Musical harmony is based on the fusing of sounds that are in simple ratio. And the history of musical scale development is the more and more sophisticated design of tone arrangements in an octave to give the best result for the different intervals among tones.

The 2nd and 3rd harmonic : Foundation of Musical Temperaments
The first thing to happen is the octave interval. This is created by blowing to the flute with tightened lips. The tone that goes out from the flute has a frequency that is twice (2nd harmonic) that of the tone blow without tightening lips. For the less experienced flute player, it is difficult to hold onto the higher pitched tone that is an octave higher than normal and the sound switches between these two tones. With some practice, it is even possible to create a even higher pitched note which has a frequency that is 3 times (3rd harmonic) that of the normal tone.

After having the 2nd and 3rd harmonics, interesting things then happen. When we create some sound, a bunch of harmonics comes out that is characteristic of the sounding equipment which is not easy to control separately. However, if we set one instrument to sound at 2 times of a certain frequency and another instrument to sound at 3 times of that frequency, then by making the two instruments to sound at different loudness, we can control their composition fairly easily. In any case, these two sounds will combine together to appear like one.

The Pentatonic Temperament
The first structural design begins when people build on the 2:3 ratio. After getting a tone that is 1.5 times of a beginning tone, another tone that is 1.5 times that of the second tone is the next to follow. This being too far away, a tone that is half that frequency brings the range back to 1.5*1.5/2 = 9/8. So we already have tones that are with ratios 8:9:12:16.

Checking the ratio between succeeding tones, we get 9/8=1.125, 12/9=1.333 and 16/12=1.333. The second and third gaps are too much wider than the first. A easy way out is to insert two tones that are 1.125 times that of the second and third tones. So we get six tones with ratios 8 : 9 : 10.125 : 12 : 13.5 : 16.

Balabiliba !!! we get our first musical temperament.

The ratios between notes are either 1.125 (which is 9/8) or 1.185 (which is 32/27). Due to the simplicity of this scale, the Pentatonic musical scale is frequently used in folk songs, especially those for kids.

In order to give the idea of relative size for different ratios, we give them a scale. For reasons to be explained later in the 12 Equal Temperament Chromatic Scale, we use 1200 cents to represent the difference between two tones that are 2/1 in frequency ratio. The gaps, which in music tonality terms, are called intervals. When represented in cents, the intervals for ratios of 9/8 and 32/27 are 204 cents and 294 cents respectively. The ratio of these two gaps is about 2:3, which is quite acceptable for such a simple structured musical scale.

The Pythagorean temperament A natural extension of the Pentatonic scale is to further subdivide the wider gaps. One tone is 8/9 times of the 12 unit tone and another is 9/8 times of the 13.5 unit tone. If we write the ratios with the lowest tone, we get 1/1, 9/8, 81/64, 4/3, 3/2, 27/16, 243/128, 2/1 respectively.

This scale keeps the ratio for big gap to 9/8, which we call the whole-tone. But there are two not very nice small gaps with ratios of 256/243 (which is 1.0595 or 90 cents) and 2187/2048 (which is 1.0679 or 114 cents) respectively. Their difference is 531441/524288 (which is 1.0136 or 23.5 cents). This difference that cannot eliminate is called the comma, which represents the smallest unit of intervals in common use.

The Just Intonation Temperament
In order to stay with simple ratios, another approach goes from the ground up to replace complicated ratios with simple ratios.

Step 1)	Examining the Pythagorus scale, the obviously OK tones are 1/1, 4/3, 3/2, 2/1.Then we use them to create further notes.
Step 2)	3/2 can be rewritten as 6/4 and 2/1 being 8/4. Naturally, we would also want to see 5/4 and 7/4. Likewise, 2/1 is 6/3 and it is good to insert 5/3.

Step 1	1/1			4/3	3/2			2/1
Step 2	4/4		5/4	4/3	6/4	5/3	7/4	8/4
Step 3	4/4		5/4	4/3	6/4	5/3		8/4
Step 4	8/8	9/8	10/8	4/3	12/8	5/3	15/8	16/8
Final	1	9/8	5/4	4/3	3/2	5/3	15/8	2

Step 3)	So far so good except that the first gap is too wide and the gap between 5/3 and 7/4 is 21/20 (which is 1.05). This is less than half of any other gaps. So we have to drop either 5/3 or 7/4. Obviously 5/3 is a simpler ratio and so 7/4 is out.
Step 4)	Like the Pentatonic scale, we now have 2 big gaps. As in most other musical scale, we repeat the wisdom of dividing of gap by treating 4/4 as 8/8 and likewise for other tones. Which naturally lead us to the addition of 9/8 and 15/8. Do you know why 14/8 is not taken ?
Step 5)	Simplify the fractions to smallest numbers to see how small they can be.

The characteristic of the just intonation is, by way of its construction method, consist of tones that are in simple ratios. Because of this, they have strong followings. The spirit of this scale is elegance and perfection, regardless of the difficulties. Indeed there are big difficulties with this scale, especially concerning the change of key.

The Just Intonation scale consists of 3 kinds of gaps, namely 16/15, 10/9 and 9/8 respectively. The intervals are 112, 182 and 204 cents respectively. In contrast to the Pythagorean scale, the Just Intonation has two kinds of whole-tones and only one kind of semi-tone.

The Quarter Comma Mean-Tone Temperament
If we compare the Pythagorean scale and Just Intonation scale, we find that they both consists of eight tones in approximately equal intervals. For convenience, we give them names unison, whole-tone, third, fourth, fifth, sixth, seventh, octave respectively. It is quite interesting that due to the existence of semi-tones, the intervals are not in proportion to the suggested numbers. For example, twice the interval of a fourth is mid-way between a sixth and a seventh, but not the octave !! Another notation is to name the notes in alphabetical order from A to G. For some mysterious reasons, we often begin in C.

The same interval name also mean differently sometimes for the Pythagorean Scale and Just Intonation Scale. When they are different, their ratio and difference in cents is shown.

Tone	C	D	E	F	G	A	B	C
Name	Unison	Wholenote	Third	Fourth	Fifth	Sixth	Seventh	Octave
Pythagorean Temperament	1	9/8	81/64	4/3	3/2	27/16	243/128	2
Just Intonation Temperament	1	9/8	5/4	4/3	3/2	5/3	15/8	2
Ratio	1	1	81/80	1	1	81/80	81/80	1

In all cases when they differ, the ratio is 81/80. The interval of this ratio is about 21.5 cents. Many new musical scales are methods to tackle this difference so that the pairs C & E can be consonant.

Note that the third is made by repreating up a fifth 4 times and then goes down 2 octaves. If we make the third of the scale exactly 5/4 as in Just Intonation, we should compress the fifth by a quarter comma so that the compensation is distributed in 4 intervals. The new fifth, although not perfect, is fairly good. This is the Quarter Comma Mean-Tone Temperament. There are other kinds of Mean-Tone Temperaments. But since this is considered the best, so sometimes we omit the Quarter Comma specifier and just call it Mean-Tone Temperament without confusion.

53-Tone Equal Temperament
If we examine the intervals in the Just Intonation and the Pythagorean Temperament, we find that they are very close to simple multiples of the comma.

Ratio	531441/524288	81/80	256/243	16/15	2187/2048	10/9	9/8
Interval	23.5 cents	21.5 cents	90.2 cents	112 cents	114 cents	182 cents	204 cents
Multiples of Comma	1	0.92	3.85	4.76	4.84	7.76	8.70

The use of intervals smaller than a semi-tone in a musical tonal arrangement is called micro-tone temperament. So we are going to design our micro-tone Temperament. Based on the Pythagorean Temperament, if we take semi-tones to be 4 units of a uniform interval, and whole-tones to be 9 such interval, we have divided an octave into 53 equal intervals. Since the Pythagorean Temperament and the Just Intonation Temperament either agree or differ by 81/80, this Temperament can represent both with high precision. The difference from exact tonal values is less than 2 cents for the Pythagorean Temperament and less than 4 cents when approximating the Just Intonation Temperament. Pianos have been built for this 53-Tone Equal Temperament. Though tonal arrangement is good, its use is difficult.

A table for the 53-Tone Equal Temperament is shown below :

53 Microtone Temperament
Division	Ratio To Base Note C	3 x Ratio	8 x Ratio	Cents	Closest Simple Ratio To C	Pythaguarean Temperament Name	Just Intonation Name
0	1.0000	3.0000	8.0000	0.0000	1/1	C	C
1	1.0132	3.0395	8.1053	22.6415	81/80
2	1.0265	3.0795	8.2120	45.2830
3	1.0400	3.1200	8.3201	67.9245
4	1.0537	3.1611	8.4296	90.5660
5	1.0676	3.2027	8.5406	113.2075
6	1.0816	3.2449	8.6530	135.8491
7	1.0959	3.2876	8.7670	158.4906
8	1.1103	3.3309	8.8824	181.1321	10/9
9	1.1249	3.3747	8.9993	203.7736	9/8	D	D
10	1.1397	3.4192	9.1178	226.4151
11	1.1547	3.4642	9.2378	249.0566
12	1.1699	3.5098	9.3594	271.6981
13	1.1853	3.5560	9.4826	294.3396
14	1.2009	3.6028	9.6074	316.9811
15	1.2167	3.6502	9.7339	339.6226
16	1.2328	3.6983	9.8620	362.2642
17	1.2490	3.7470	9.9919	384.9057	10/8		E
18	1.2654	3.7963	10.1234	407.5472	81/64	E
19	1.2821	3.8463	10.2567	430.1887
20	1.2990	3.8969	10.3917	452.8302
21	1.3161	3.9482	10.5285	475.4717
22	1.3334	4.0002	10.6671	498.1132	4/3	F	F
23	1.3509	4.0528	10.8075	520.7547
24	1.3687	4.1062	10.9498	543.3962
25	1.3867	4.1602	11.0939	566.0377
26	1.4050	4.2150	11.2400	588.6792
27	1.4235	4.2705	11.3879	611.3208
28	1.4422	4.3267	11.5378	633.9623
29	1.4612	4.3836	11.6897	656.6038
30	1.4805	4.4414	11.8436	679.2453
31	1.4999	4.4998	11.9995	701.8868	3/2	G	G
32	1.5197	4.5591	12.1575	724.5283
33	1.5397	4.6191	12.3175	747.1698
34	1.5600	4.6799	12.4797	769.8113
35	1.5805	4.7415	12.6440	792.4528
36	1.6013	4.8039	12.8104	815.0943
37	1.6224	4.8671	12.9791	837.7358
38	1.6437	4.9312	13.1499	860.3774
39	1.6654	4.9961	13.3230	883.0189	5/3		A
40	1.6873	5.0619	13.4984	905.6604	27/16	A
41	1.7095	5.1285	13.6761	928.3019
42	1.7320	5.1961	13.8561	950.9434
43	1.7548	5.2645	14.0385	973.5849
44	1.7779	5.3338	14.2233	996.2264
45	1.8013	5.4040	14.4106	1018.8679
46	1.8250	5.4751	14.6003	1041.5094
47	1.8491	5.5472	14.7925	1064.1509
48	1.8734	5.6202	14.9872	1086.7925	15/8		B
49	1.8981	5.6942	15.1845	1109.4340	243/128	B
50	1.9230	5.7691	15.3844	1132.0755
51	1.9484	5.8451	15.5869	1154.7170
52	1.9740	5.9220	15.7921	1177.3585
53	2.0000	6.0000	16.0000	1200.0000	2/1	C	C

12-Tone Equal Temperament Chromatic Scale
As always noted, interval for the whole-tone is approximately twice that of the semi-tone. So if we take the interval of a whole-tone to be twice that of a semi-tone, we have a 12-Tone Equal Temperament scale. Taking the unit for a semi-tone in this scale to be 100 cents, then one octave has 1,200 cents. This scale has uniform interval of 100 cents. So it has no problem changing keys. This musical tonal scale is also called Chromatic Scale.

Other Temperaments
Temperaments are proposed to solve problems in getting harmony.

Along the theme of the Mean-Tone scale, we can choose different whole-tone to semi-tone ratio to create different Mean-Tone Temperaments. Since the tonal arrangement in an octave is fixed, this single ratio will define notes in the whole octave.

Along the theme of Equal Temperament, 19-tone and 33 -tone systems have been proposed. They represent a solution mid-way between the 12-tone scale and the 53-tone scale.

It is even possible to have Temperaments with an octave that is not 2. For example, a Hong Kong violinist proposed an octave with frequency ratio of 81/40. This is said to create better harmony in most melodies.

The Mathematical origin of different musical temperaments Essentially, all temperaments are based on the perfect fifth with a frequency ratio of 3/2, which is 1.5. Calculating the LOG value of 3 in base 2 is the ratio between an interval for a 3 and 2.

LOG2(3) = 1.5849625

That means, the interval between the 3rd harmonic and the fundamental is about 1.585 times bigger than the interval for an octave. Unfortunately, this is not easily translated into a simple fraction. So it is impossible to create a uniform scale that covers the 3rd harmonic and the octave. But if it is not going to be uniform, then what systematic approach can be used.

To see how we can create music temperaments that approximately covers both the 2nd and 3rd harmonic, let's convert this number into approximate fractions. The first approximation is obviously 1.5849625 = 1 + 1/2. But are we happy with an octave with just 2 tones ? If not, then let's move on.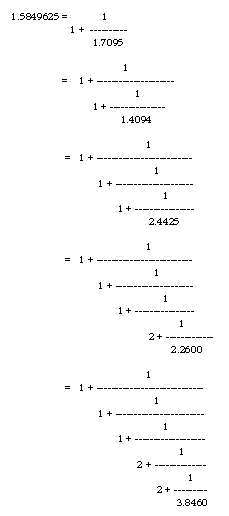


If we calculate the fraction and stop at different stages by taking the last denominator to the nearest integer, the fractions are in sequence :
3/2 , 8/5, 19/12, 84/53

If we take away one octave to see the ratio of the fifth in an octave, we have :
1/2, 3/5, 7/12, 31/53

Here we can see the Pentatonic Temperament, 12-Tone Equal Temperament Chromatic Scale, and the almost perfect 53-Tone Equal Temperament.

There is a simple way to assess how good they are. If the rounding is insignificant, the truncated fraction expansion is a good approximation to the actual value. So seeing that 2.26 is close to 2, the 7/12 octave fifth is a good approximation, and likewise for 31/53, but not for the other two.

So from a mathematical viewpoint, the development of the musical temperaments is a natural consequence of having more and more precise musical instruments and better musical actueness over many generations of cultural conditioning. If we go on with the calculation, the next fractions will be 179/306 and 389/665. I cannot foresee one day when our ears can perceive such fine details. Also in view that even the 53-Tone Equal Temperament piano did not become popular, it is unlikely some one would like to play a 306-Tone or 665-Tone Equal Temperament piano. So we can conveniently declare here the end of search for more accurate musical temperaments. If there are any new developments, it is bound to appear along other ideas than better approximation of the perfect fifth.