MATH 1.6: Trigonometric functions |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
Trigonometric functions have a wide range of application in physics; examples include the addition and resolution of vectors (such as forces), the description of simple harmonic motion and the formulation of quantum theories of the atom. Trigonometric functions are also important for solving certain differential equations, a topic which is considered in some detail elsewhere in FLAP.
In Section 2 of this module we begin by looking at the measurement of angles in degrees and in radians. We then discuss some basic ideas about triangles, including Pythagoras’s theorem, and we use right–angled triangles to introduce the trigonometric ratios (sin θ, cos θ and tan θ) and the reciprocal trigonometric ratios (sec θ, cosec θ and cot θ). In Section 3 we extend this discussion to include the trigonometric functions (sin (θ), cos (θ) and tan (θ)) and the reciprocal trigonometric functions (cosec (θ), sec (θ) and cot (θ).) These periodic functions generalize the corresponding ratios since the argument θ may take on values that are outside the range 0 to π/2. Subsection 3.2 discusses the related inverse trigonometric functions (arcsin(x), arccos(x) and arctan(x)), paying particular attention to the conditions needed to ensure they are defined. We end, in Section 4, by showing how the sides and angles of any triangle are related by the sine rule and the cosine rule and by listing some useful identities involving trigonometric functions.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 5.1Module summary and the Subsection 5.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 5.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
State Pythagoras’s theorem.
Answer F1
Pythagoras’s theorem states that the square of the hypotenuse in a right–angled triangle is equal to the sum of the squares of the other two sides.
Question F2
Define the ratios sin θ, cos θ and tan θ in terms of the sides of the right–angled triangle. What are the exact values (i.e. don’t use your calculator) of sin(45°) and tan(π/4)?
Answer F2
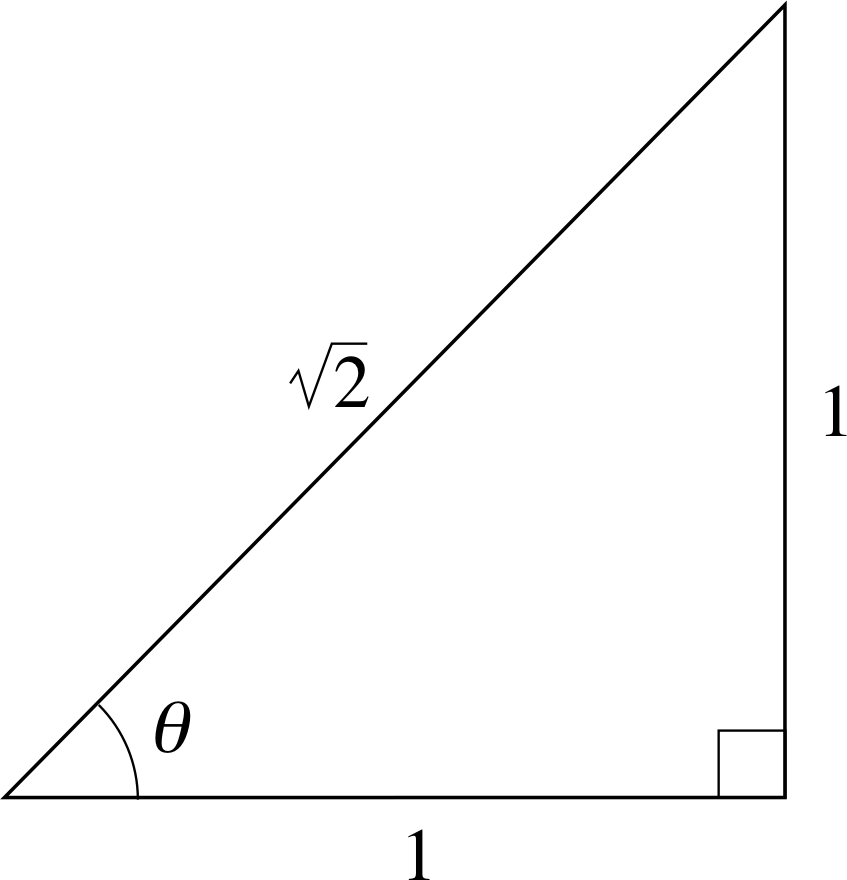
Figure 10 A right–angled triangle with two equal length sides, an isosceles triangle.
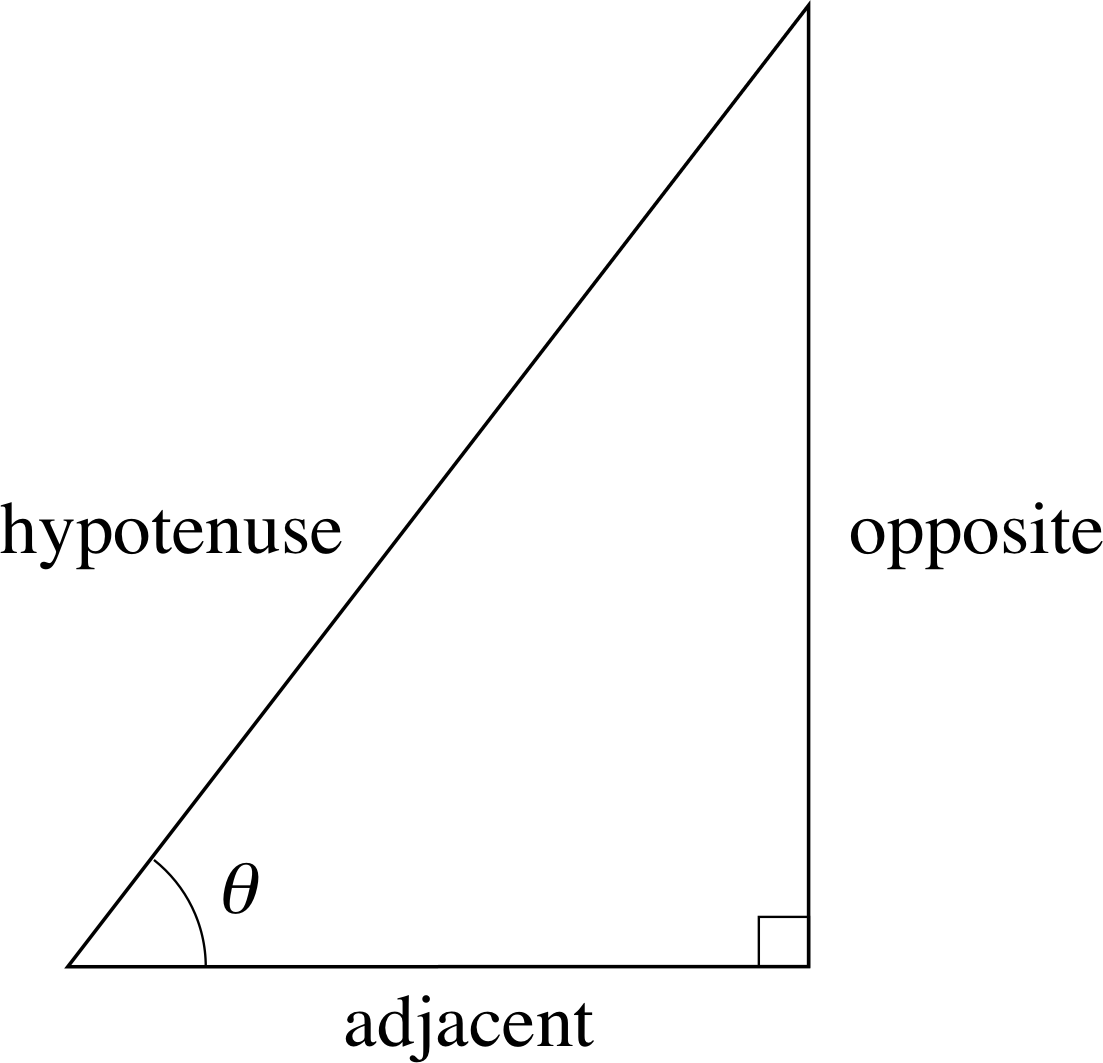
Figure 8 The labelling of sides in a right–angled triangle.
With the notation of Figure 8 (Subsection 2.2), we have:
$\sin\theta = \dfrac{\text{opposite}}{\text{hypotenuse}}\\ \cos\theta = \dfrac{\text{adjacent}}{\text{hypotenuse}}\\ \tan\theta = \dfrac{\text{opposite}}{\text{adjacent}}$
From Pythagoras’s theorem, the hypotenuse of the 45° triangle in Figure 10 (Subsection 2.2) has length 2, and therefore:
$\sin(45°) = \dfrac{\text{opposite}}{\text{hypotenuse}} = \dfrac{1}{\sqrt{2\os}}$
An angle of π/4 radians is equivalent to 45° and therefore we have:
$\tan\left(\dfrac{\pi}{4}\right) = 1$
Question F3
Write down the sine and cosine rules for a triangle. Calculate the angles of a triangle which has sides of length 2 m, 2 m and 3 m.
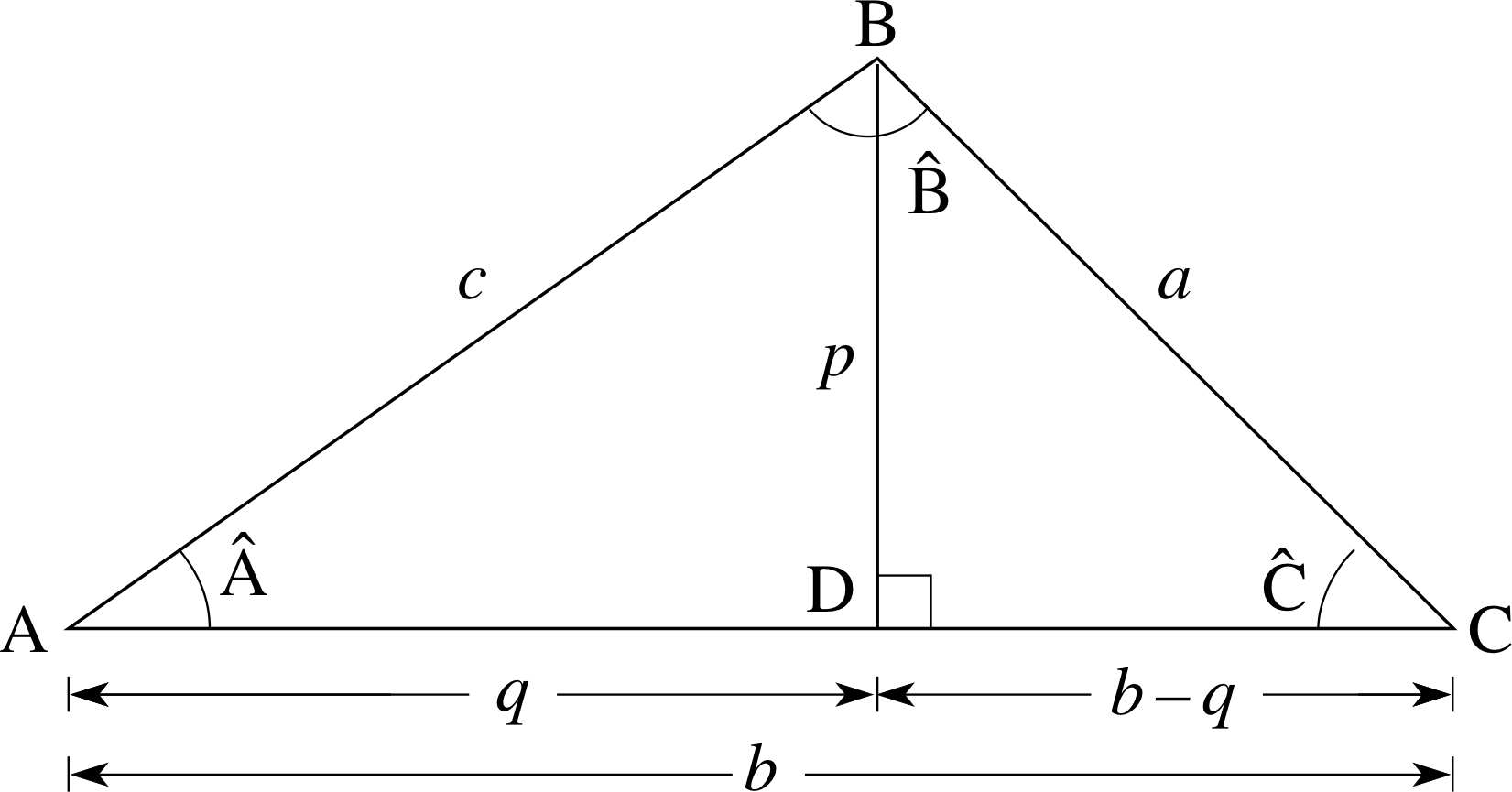
Figure 28 Construction used in deriving the sine and cosine rules.
Answer F3
The sine rule: $\dfrac{a}{\sin\hat {\rm A}} = \dfrac{b}{\sin\hat {\rm B}} = \dfrac{c}{\sin\hat {\rm C}}$
The cosine rule: a2 = b2 + c2 − 2bc cos A^
where the notation is given in Figure 28 (Subsection 4.1).
Suppose b = c = 2 m and a = 3 m. Then using the cosine rule we get:
32 = 22 + 22 − 2 × 2 × 2 cos A^
and so:
cos A^ = −1/8$
There are an infinite number of solutions to this equation for A^, but only one is relevant to our triangle problem:
A^ = arccos(1/8) = 97.2°
Since sides b and c of the triangle are equal, we have: B^ = C^ = ½ (180° − 97.2°) = 41.4°
Question F4
Sketch graphs of the functions cosec(θ) and sec(θ) for −π ≤ θ ≤ π, and cot(θ) for −3π/2 < θ < 3π/2.
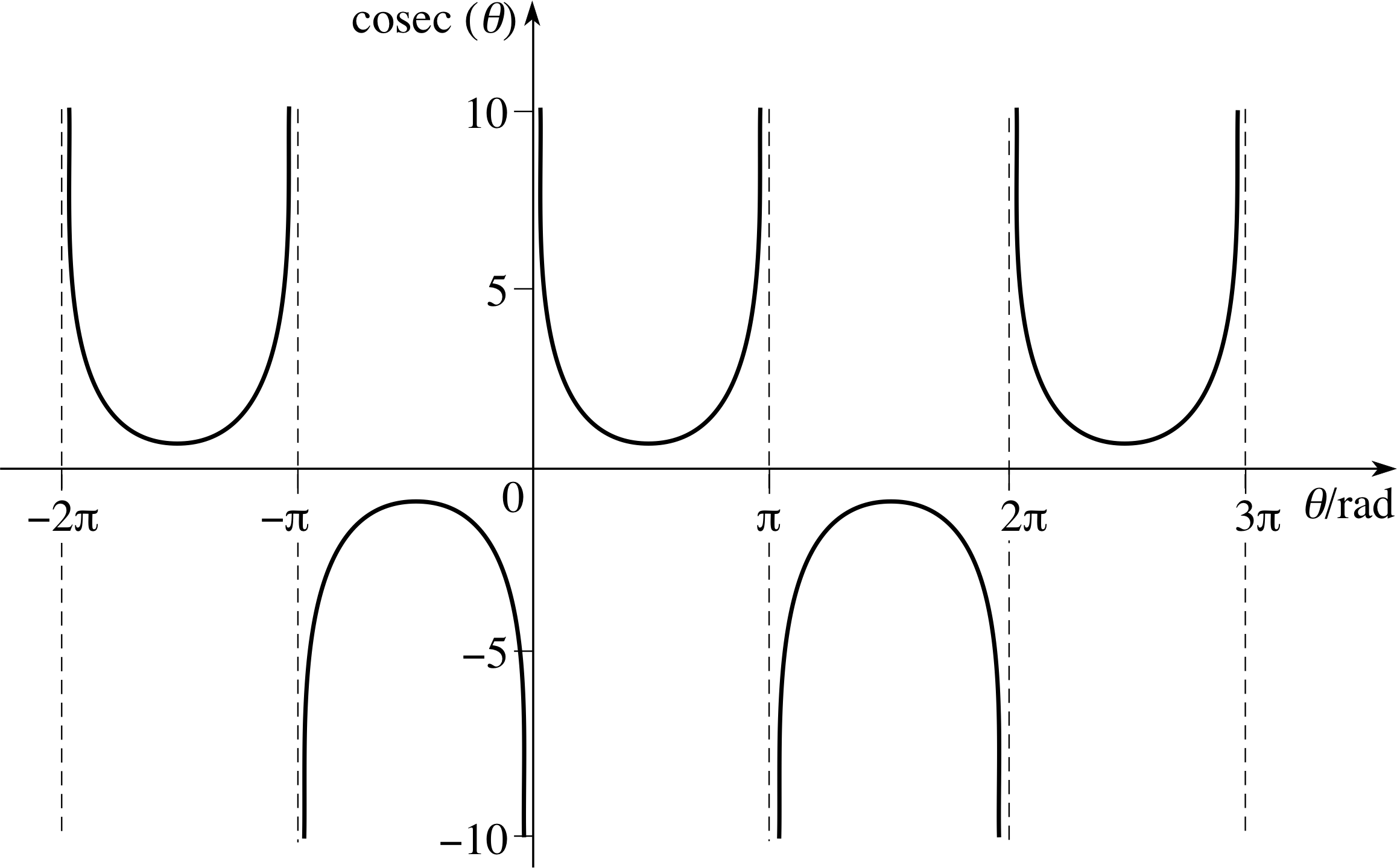
Figure 21 Graph of cosec(θ).
Answer F4
The graphs for these functions are given in Figures 21, 22 and 23.
$\sec(\theta) = \dfrac{1}{\cos(\theta)}\quad\theta\ne(2n+1)\pi/2$
$\cot(\theta) = \dfrac{\cos(\theta)}{\sin(\theta)}\quad\theta\ne n\pi$
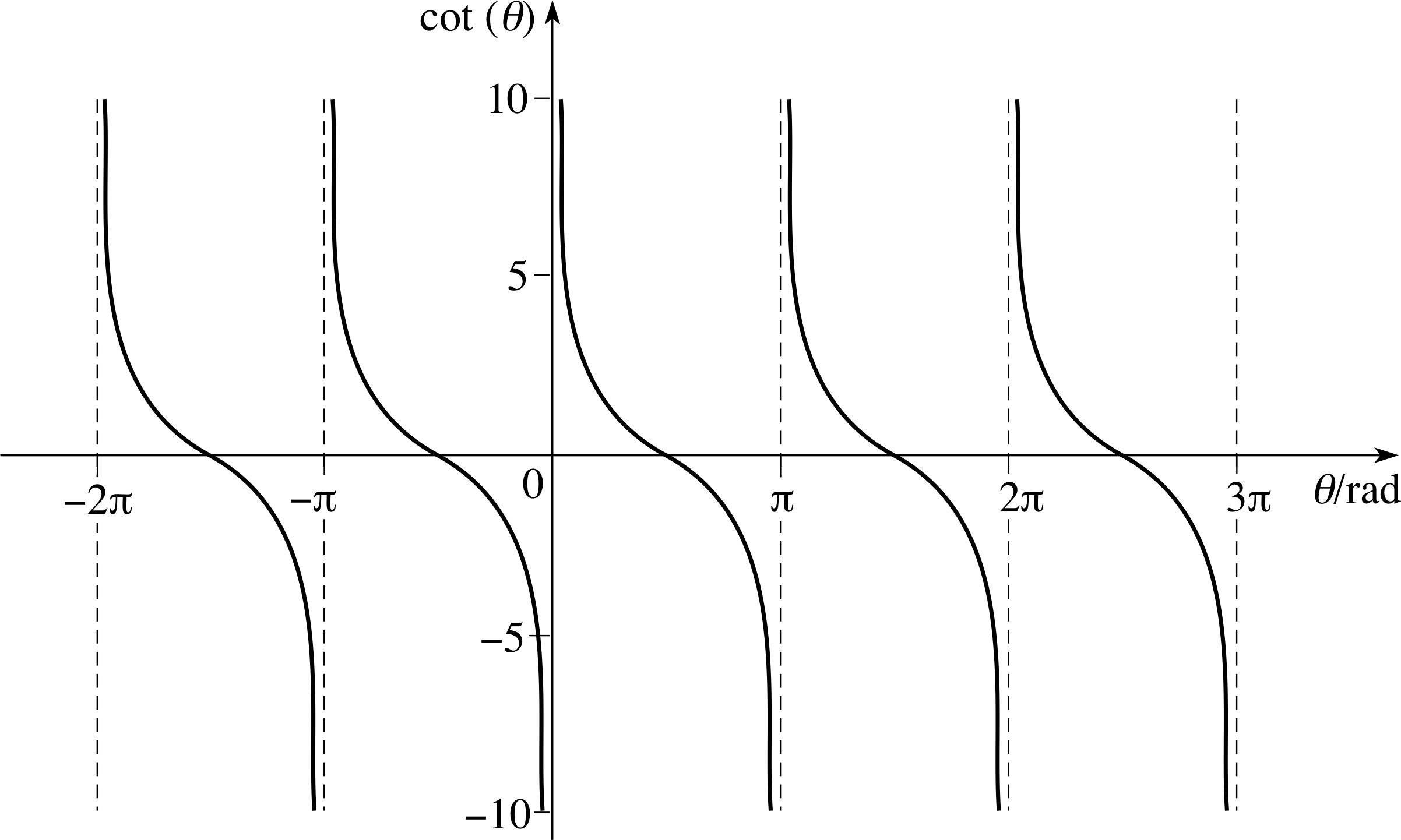
Figure 23 Graph of cot(θ).
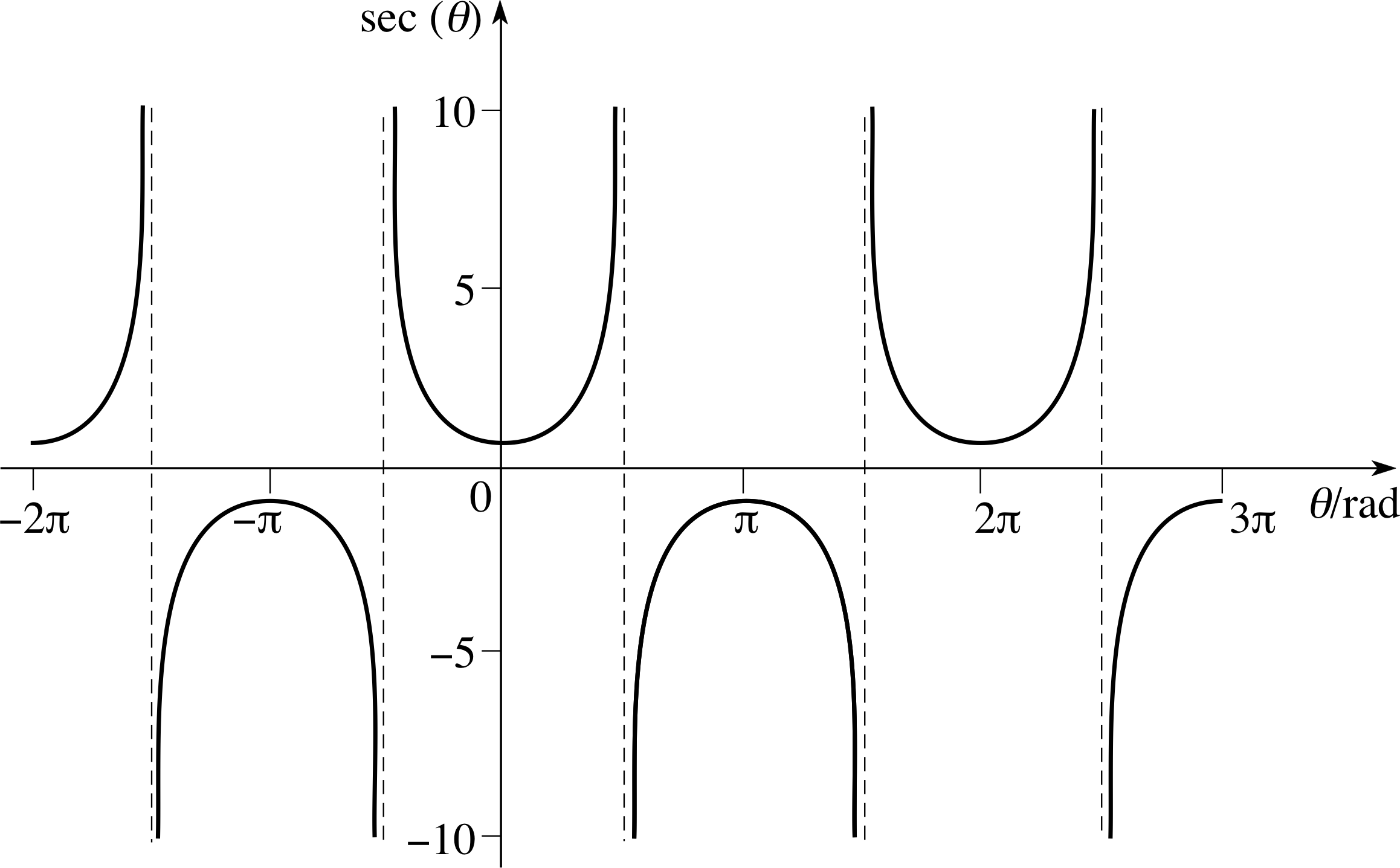
Figure 22 Graph of sec(θ).
Question F5
Sketch graphs of the functions, arccosec(x) and arccot(x) over the range −10 < x < 10.
Answer F5
The graphs for these functions are given in Figures 26a and 26c.
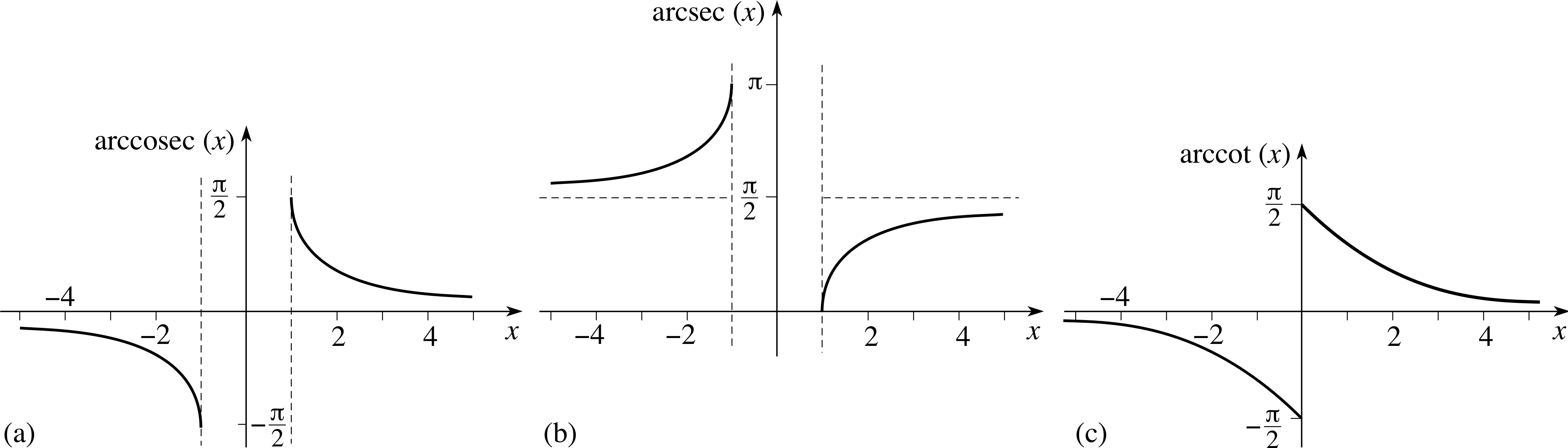
Figure 26 The graphs of (a) arccosec(x), (b) arcsec(x), and (c) arccot(x).
1.3 Ready to study?
Study comment In order to study this module you will need to understand the following terms: constant, decimal places, function, power_mathematicalpower, reciprocal and variable. An understanding of the terms codomain, domain and inverse function would also be useful but is not essential. You will need to be able to solve a pair of simultaneous_linear_equationssimultaneous equations, manipulate arithmetic and algebraic expressions – including those involving square_of_a_numbersquares, square roots, brackets and ratios – and to plot and interpret graphs. If you are uncertain about any of these terms, you should consult the Glossary, which will also indicate where in FLAP they are developed. The following questions will help you to decide whether you need to review some of these topics before embarking on this module.
Question R1
Given that x = a/h, y = b/h, and a2 + b2 = h2, rewrite the following expressions in terms of a, b and h, simplifying each as far as possible:
(a) 1/x, (b) x/y, (c) x2 + y2.
Answer R1
(a) 1/x = h/a, (b) x/y = (a/h)/(b/h) = a/b, (c) x2 + y2 = a2/h2 + b2/h2 = (a2 + b2)/h2 = 1.
(If you had difficulty with any part of this question, consult algebra and arithmetic in the Glossary.)
Question R2
Solve the following simultaneous equations:
2x + 5y = 6 and 3x − 10y = 9
Answer R2
Multiplying the first of the given equations by 2, the pair become
4x + 10y = 12 and 3x − 10y = 9
Adding the corresponding sides of the two equations in order to eliminate y, we find
7x = 21, so x = 3
Substituting x = 3 into either of the original equations shows that y = 0.
(If you had difficulty with any part of this question, consult module MATH 1.4.)
Question R3
What do we mean when we say that the position of an object is a function of time?
Answer R3
A function is a rule that assigns a single value from a set called the codomain to each value from a set called the domain. Thus, saying that the position of an object is a function of time implies that at each instant of time the object has one and only one position.
(If you had difficulty with any part of this question, consult functions in the Glossary.)
2 Triangles and trigonometric ratios
2.1 Angular measure: degrees and radians
When two straight lines pass through a common point, the angle between the lines provides a measure of the inclination of one line with respect to the other or, equivalently, of the amount one line must be rotated about the common point in order to make it coincide with the other line. The two units commonly used to measure angles are degrees and radians (discussed below) and we will use both throughout this module. Greek letters, α (alpha), β (beta), γ (gamma), ... θ (theta), ϕ (phi) ... are often used to represent the values of angles, but this is not invariably the case.
A degree is defined as the unit of angular measure corresponding to 1/360th of a circle and is written as 1°. In other words, a rotation through 360° is a complete revolution, and an object rotated through 360° about a fixed point is returned to its original position. Fractions of an angle measured in degrees are often expressed as decimals, as in 97.8°, but it is also possible to use subsidiary units usually referred to as minutes and seconds for subdivisions of a degree, with the definitions that sixty minutes are equivalent to one degree and sixty seconds are equivalent to one minute. To distinguish them from units of time, these angular units are called the minute of arc and second of arc, abbreviated to arcmin and arcsec, respectively. i The symbols ′ and ′′ are often used for arcmin and arcsec, respectively. For example, 12′ means 12 arcmin, and 35′′ means 35 arcsec.
✦ (a) Express 6° 30′ as a decimal angle in degrees. (b) Express 7.2 arcmin in terms of arcsecs.
✧ (a) 30′ = 0.5°, so 6° 30′ = 6.5°.
(b) 7.2′ = (7.2 × 60)′′ = 432′′.
The angles 180° and 90° correspond to a rotation through half and one–quarter of a circle, respectively. An angle of 90° is known as a right angle. A line at 90° to a given line (or surface) is said to be perpendicular or normal to the original line (or surface).

Figure 1 A positive rotation through a (positive) angle, θ.
It is conventional in mathematics and physics to refer to rotations in an anti–clockwise direction as positive rotations. So, a positive rotation through an angle θ would correspond to the anticlockwise movement shown in Figure 1, while a negative rotation of similar size would correspond to a clockwise movement. The negative rotation may be described as a rotation through an angle −θ.
An object which is rotated through an angle of 0° or 360° or 720° appears to remain unchanged and, in this sense, these rotations are equivalent. In the same sense rotations of 10°, 370°, 730°, −350° and so on are equivalent, since each can be obtained from the others by the addition of a multiple of 360°. When considering the orientational effect of a rotation through an angle θ it is only necessary to consider values of θ which lie in the range 0° ≤ θ < 360° i since the orientational effect of every rotation is equivalent to a rotation lying in this range.
For example, a rotation through −1072° is equivalent to one through −1072° + 3 × 360° = 8°. Notice that the range of non–equivalent rotations, 0° ≤ θ < 360°, does not include 360°. This is because a rotation through 360° is equivalent to one through 0°, which is included.
✦ Find a rotation angle θ in the range 0° ≤ θ < 360° that has the equivalent orientational effect to each of the following: 423.6°, −3073.35° and 360°.
✧ 423.6° − 360° = 63.6°; −3073.35° + 9 × 360° = 166.65°; 360° − 360° = 0°.
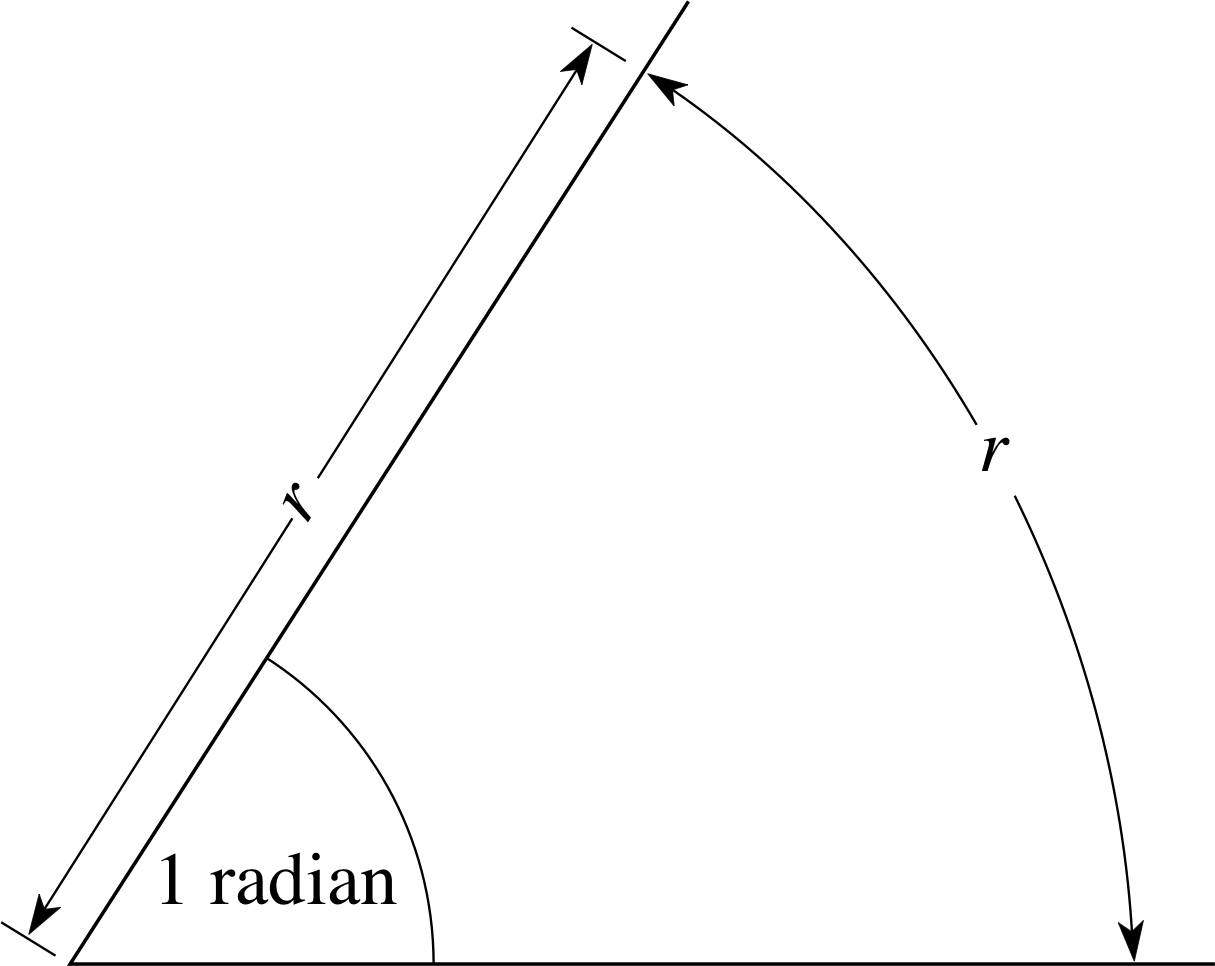
Figure 2 An angle of one radian.
Of course, angles that differ by a multiple of 360° are not equivalent in every way. For example, a wheel that rotates through 36 000° and thus completes 100 revolutions would have done something physically different from an identical wheel that only rotated through an angle of 360°, even if their final orientations were the same.
Despite the widespread use of degrees, a more natural (and important) unit of angular measure is the radian. As Figure 2 indicates, the radian may be defined as the angle subtended at the centre of a circle by an arc of the circle which has an arc length i equal to the radius of the circle. As will be shown below, it follows from this definition that 1 radian (often abbreviated as 1 rad or sometimes 1c) is equal to 57.30°, to two decimal places.
Radians are such a natural and widely used unit of angular measure that whenever you see an angular quantity quoted without any indication of the associated unit of measurement, you should assume that the missing unit is the radian.
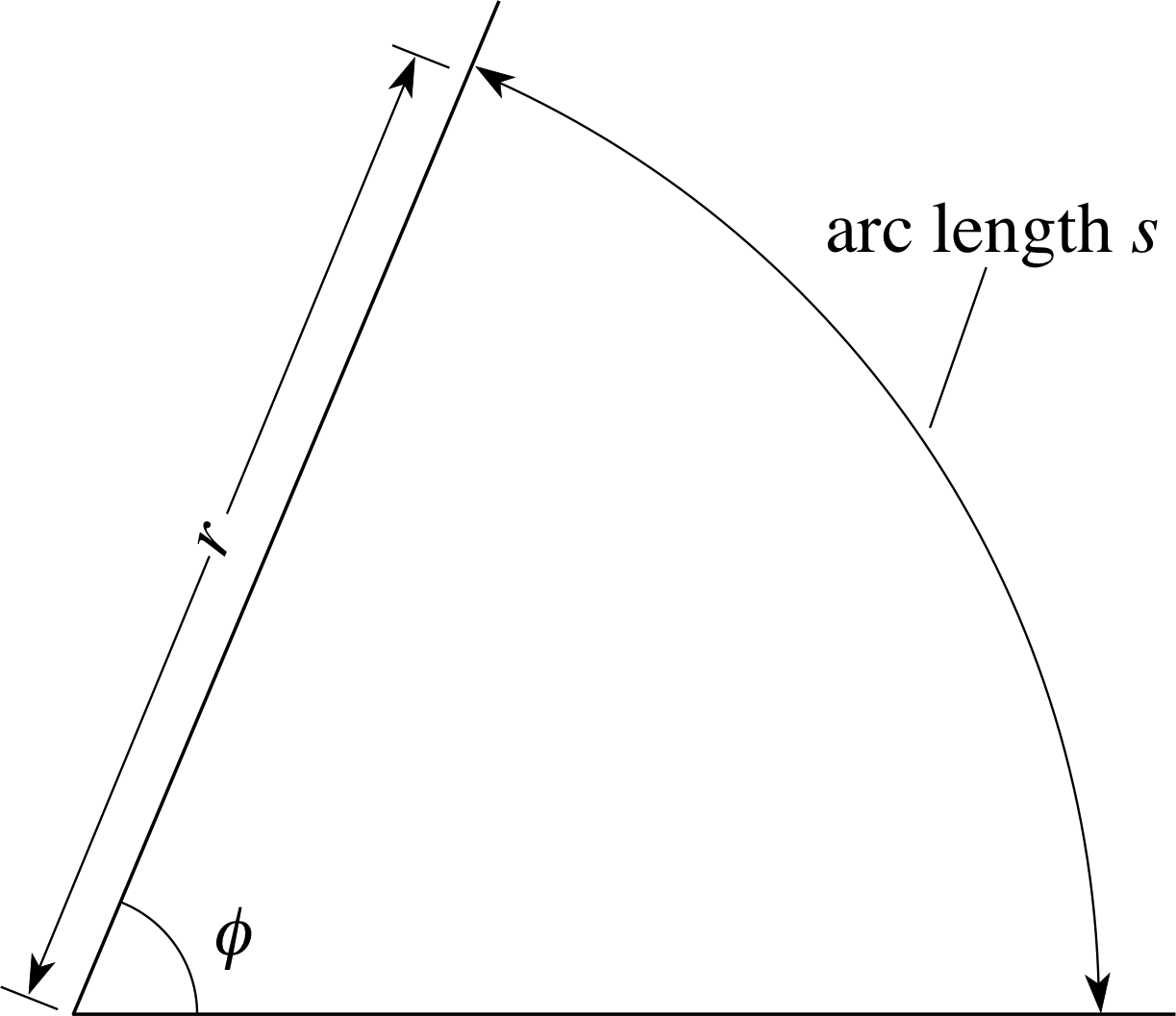
Figure 3 An angle measured in radians.
In general, as indicated in Figure 3, if an arc length s at a distance r subtends an angle ϕ at the centre of the circle, then the value of ϕ, measured in radians, is:
$\phi = \dfrac sr\,{\rm rad}$(1) i
i.e.$\phi/{{\rm rad}} = \dfrac sr$
This is a sensible definition of an angle since it is independent of the scale of Figure 3. For a given value of ϕ, a larger value of r would result in a larger value of s but the ratio s/r would be unchanged.
| Angle measured in degrees |
Angle measured in radians |
|---|---|
| 360 | 2π |
| 180 | π |
| 90 | π/2 |
| 60 | π/3 |
| 45 | π/4 |
| 30 | π/6 |
To determine the fixed relationship between radians and degrees it is probably easiest to consider the angle subtended at the centre of a circle by the complete circumference of that circle. A circle of radius r has a circumference of arc length 2πr, where π represents the mathematical constant pi, an irrational number i the value of which is 3.1416 to four decimal places. Consequently, the ratio of circumference to radius is 2π and the angle subtended at the centre of any circle by its circumference is 2π rad. But the complete angle at the centre of a circle is 360°, so we obtain the general relationship
2π radians = 360°
Since 2π = 6.2832 (to four decimal places) it follows that 1 radian = 57.30°, as claimed earlier. Table 1 gives some angles measured in degrees and radians. As you can see from this table, many commonly–used angles are simple fractions or multiples of π radians, but note that angles expressed in radians are not always expressed in terms of π. Do not make the common mistake of thinking that π is some kind of angular unit; it is simply a number.
✦ What is 10° expressed in radians?
✧ $\rm \dfrac{10°}{180°}\times\pi\,rad = \dfrac{\pi\,rad}{18}\approx 0.175\,rad$.
Question T1
The usual way of converting a quantity expressed in terms of one set of units into some other set of units is to multiply it by an appropriate conversion factor. For example, multiplying a distance measured in kilometres by the conversion factor 1000 km−1 will provide the equivalent distance in metres. What are the conversion factors from radians to degrees and from degrees to radians?
Answer T1
An angle of π radians is equivalent to 180°, so 1 radian is equivalent to 180/π ≈ 57.3°.
This means that the conversion factor from radians to degrees is (to three significant figures) 57.3 degrees radian−1. Similarly, an angle of 1° is equivalent to (π/180) rad = 0.0175 rad and so the conversion factor from degrees to radians is approximately 0.0175 radians degree−1.
Question T2
What is the non–negative rotation angle less than 2π rad that has the same orientational effect as a rotation through −201π rad?
Answer T2
First find the number of times 2π rad divides into 201π rad:
$\dfrac{201\pi}{2\pi} = 100.5$
So, in order to convert to the given range we need to add 101 × 2π rad to the given angle. Thus, −201π rad
reduces to −201π rad + 101 × 2π rad = π rad.
2.2 Right–angled triangles
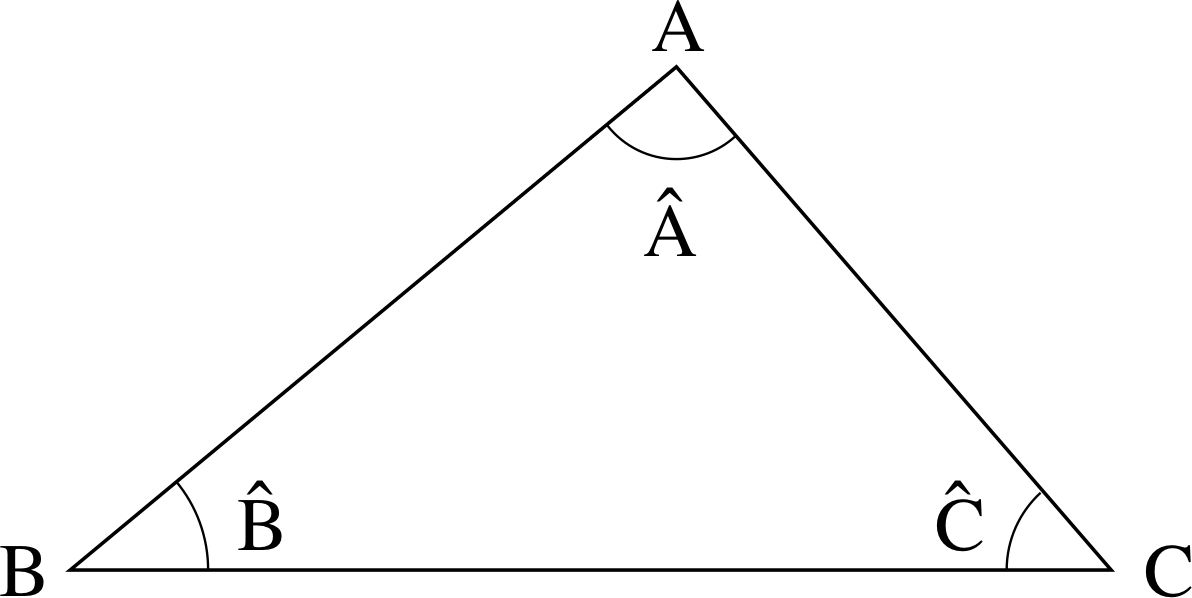
Figure 4 A general triangle.
Figure 4 shows a general triangle – a geometrical figure made up of three straight lines. There are three angles formed by the intersections of each pair of lines. By convention, the three angles are labelled according to the corresponding vertices as A^, B^ and C^. An alternative notation is to use AB^C instead of B^, where AB and BC are the two lines defining the angle. In this module we use the AB^C and B^ notations interchangeably. i
The angles A^, B^ and C^ in Figure 4 are known as the interior angles of the triangle.
The sum of the interior angles of any triangle is 180° (π radians). To see that this is so, imagine an arrow located at point A, superimposed on the line AB and pointing towards B. Rotate the arrow anticlockwise about the point A through an angle A^ so that it is aligned with AC and points towards C. Then rotate the arrow through an additional angle C^ so that it is horizontal and points to the right, parallel with BC. Finally, rotate the arrow through an additional angle B^ about point A. After this final rotation the arrow will again be aligned with the line AB, but will now point away from B having rotated through a total angle of 180°. So, rotating through A^ + B^ + C^ is equivalent to half a complete turn, i.e. 180°.
For the time being, we will be concerned only with the special class of triangles in which one interior angle is 90°. There are infinitely many such triangles, since the other two interior angles may have any values provided their sum is also 90°.
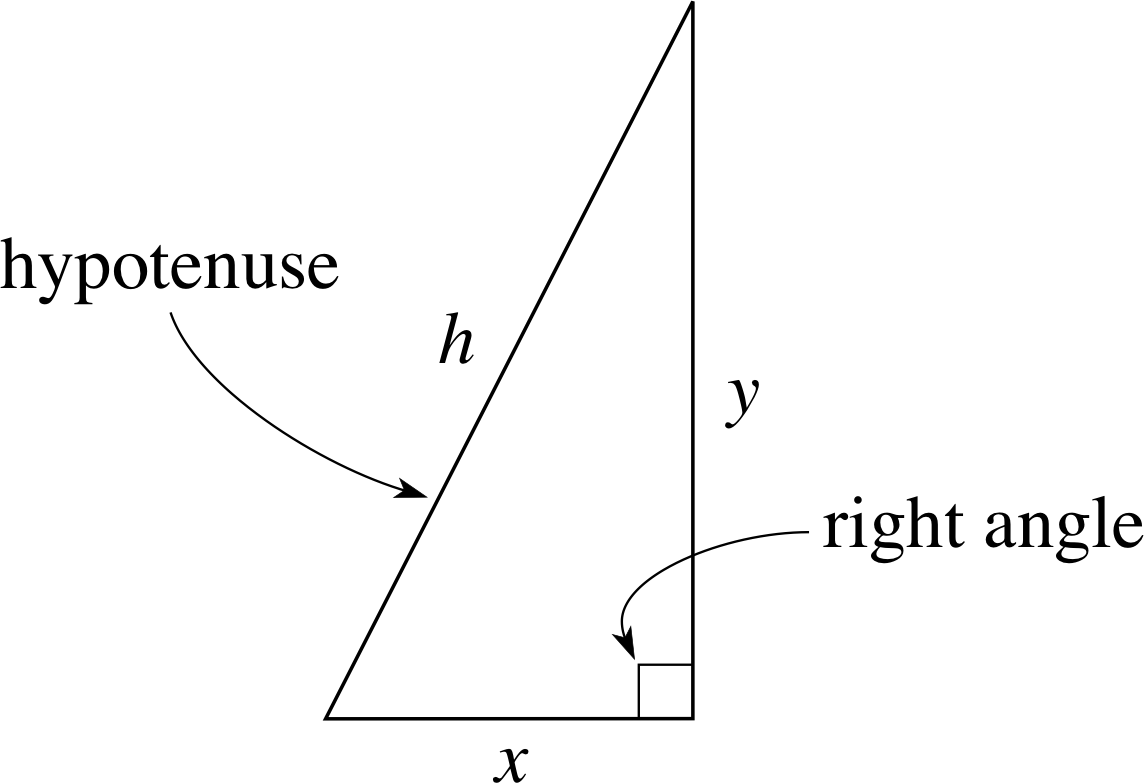
Figure 5 A right–angled triangle with sides of length x, y and h.
Any such triangle is called a right–angled triangle (see Figure 5), and the side opposite the right angle is known as the hypotenuse.
Notice the use of the box symbol, ⦜, to denote a right angle. Right–angled triangles are important because:
- There is a special relationship between the lengths of the sides (Pythagoras’s theorem.)
- There is a strong link between right–angled triangles and the trigonometric ratios (sine, cosine and tangent).
- Applications involving right–angled triangles often occur in physics (and many other branches of science and engineering).
We shall consider each of these points in this module, but the rest of this subsection will be devoted to Pythagoras’s theorem.
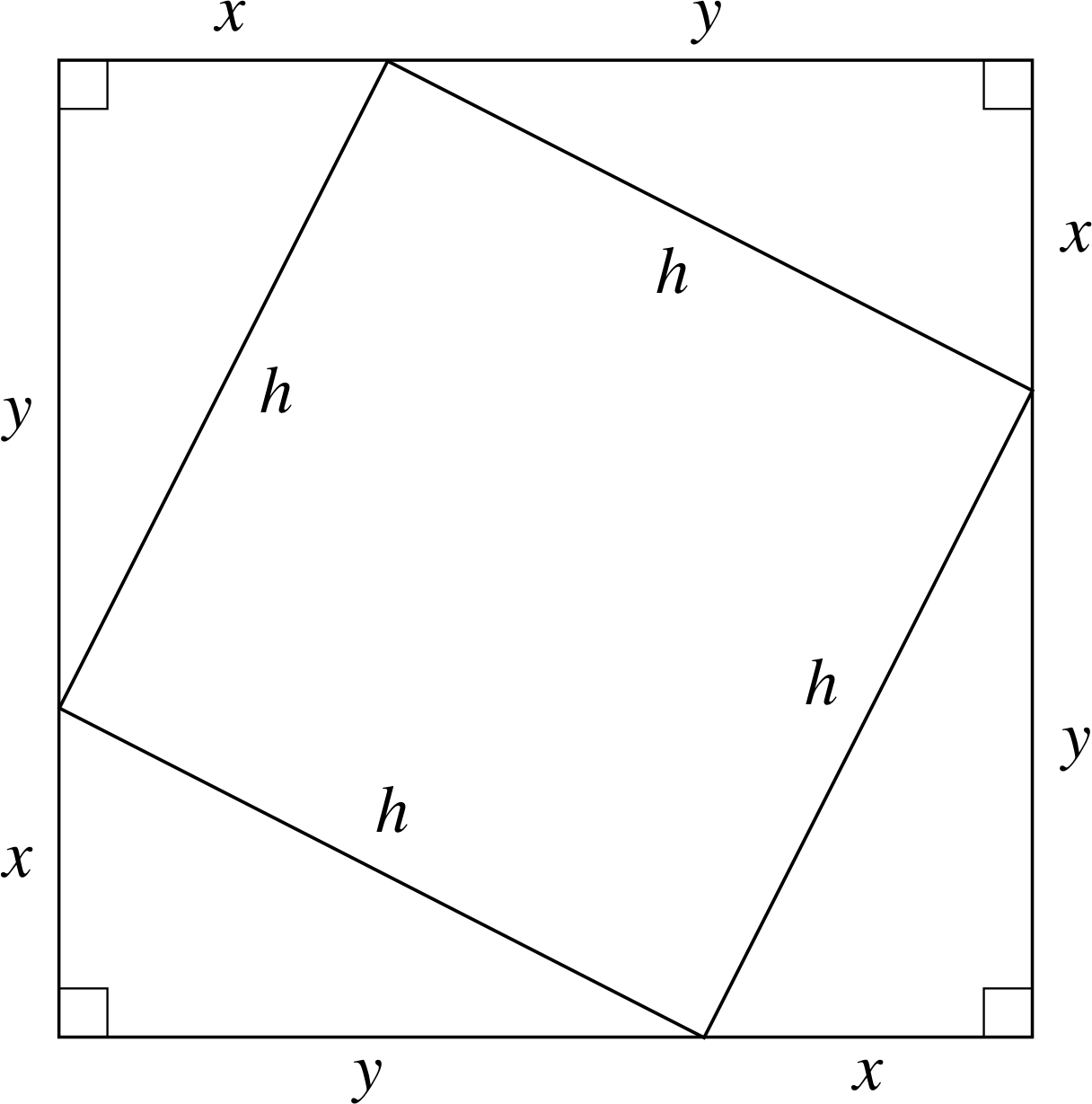
Figure 6 Pythagoras’s theorem can be derived by writing expressions for the area of the large square.
Pythagoras’s theorem states that the square of the hypotenuse of a right–angled triangle is equal to the sum of the squares of the other two sides.
i.e. h2 = x2 + y2
Consideration of Figure 6 shows how this result comes about for a general right–angled triangle of sides x, y and h. One way of finding the area of the large outer square is by squaring the length of its sides, i.e.
area = (x + y)2 = x2 + y2 + 2xy(2)
However, the area of the large square can also be found by adding the area of the smaller square, h2, to the areas of the four corner triangles. Each triangle has an area xy/2 (each is half a rectangle of sides x and y) so the area of the large square is
area = h2 + 4xy/2 = h2 + 2xy(3)
Comparing the right–hand sides of Equations 2 and 3 shows that
h2 = x2 + y2(4)
which is Pythagoras’s theorem.
The converse of Pythagoras’s theorem is also true; that is, if the sum of the squares of two sides of a triangle is equal to the square of the other side, then the triangle is right–angled. For the purpose of this module, we will accept the validity of the converse without proving it.
✦ The angles of a triangle are 45°, 90° and 45° and two of the sides (that is, those sides opposite the 45° angles) have lengths of 10 m. What is the length of the hypotenuse?
✧ By Pythagoras’s theorem, the length of the hypotenuse is $\rm \sqrt{10^2+10^2}\,m = \sqrt{200\os}\,m = 14.14\,m~~\text{(to two decimal places).}$
✦ The hypotenuse of a right–angled triangle is 7 m long while one of the other sides is of length 3 m. What is the length of the remaining side?
✧ If we denote the length of the remaining side by x, then, from Pythagoras’s theorem, 72 m2 = 32 m2 + x2, so that x2 = (72 − 32) m2 = (49 − 9) m2 = 40 m2 and therefore x = $\sqrt{40\os}$ m = 6.32 m (to two decimal places).
The sides of some right–angled triangles can be expressed entirely in terms of integers; probably the most famous is the 3 : 4 : 5 triangle where the hypotenuse has length 5 units and the other two sides have lengths 3 and 4 units: 32 + 42 = 52.
Note Throughout the remainder of this module we will not usually express lengths in any particular units. This is because we are generally interested only in the ratios of lengths. Of course, when you are considering real physical situations, you must attach appropriate units to lengths.
Question T3
Show that triangles with sides in the ratios 5 : 12 : 13 and 8 : 15 : 17 are also right–angled triangles.
Answer T3
In both cases we calculate $\sqrt{b^2+c^2}$ where b and c are the two shorter sides, obtaining:
$\sqrt{5^2+12^2}= \sqrt{25 + 144\os} = \sqrt{169\os} = 13$
and
$\sqrt{8^2+15^2} = \sqrt{64+225\os}= \sqrt{289\os}=17$
So both triangles are right–angled, by the converse of Pythagoras’s theorem.
Question T4
Use Pythagoras’s theorem to show that the hypotenuse is always the longest side of a right–angled triangle.
[Hint: Consider a2 = b2 + c2.]
Answer T4
If the hypotenuse of a right–angled triangle is labelled, a, and the other two sides are b and c, then:
a2 = b2 + c2
where a, b and c are positive. Since c2 > 0 we have:
a2 > b2 and consequently a > b.
Also, b2 > 0, and so we obtain:
a2 > c2 and consequently a > c.
2.3 The trigonometric ratios
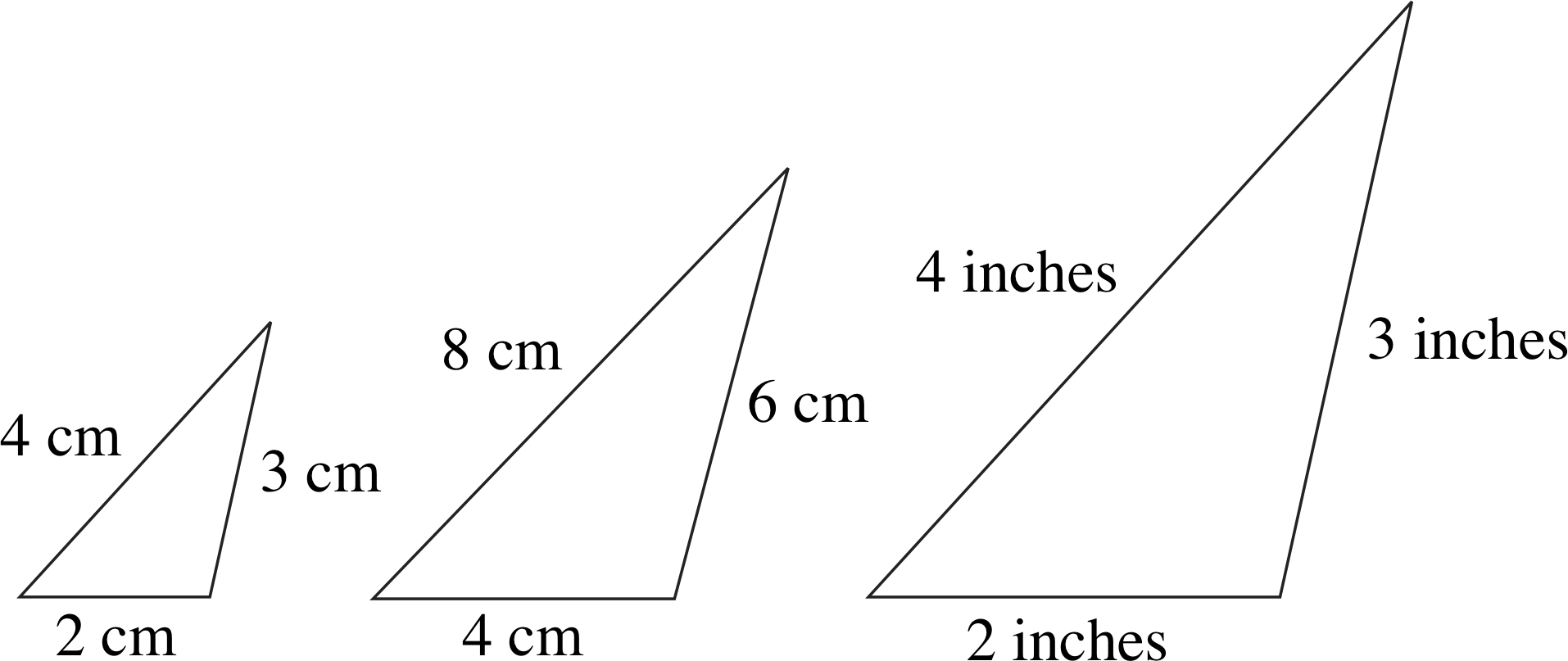
Figure 7 Some similar triangles. Each triangle has the same interior angles, and the lengths of the sides of any one triangle are in the same ratio to one another (2 : 3 : 4 in this case) as the lengths of the sides of any of the other similar triangles. (These are not to scale.)
In the previous subsection, we indicated that the ratios of the lengths of the sides of a triangle were often of more interest than the actual lengths themselves. Figure 7 shows some similar triangles, i.e. triangles that are the same shape but different sizes – in other words, triangles with corresponding angles that are equal but with corresponding sides of different lengths. Although the lengths of the sides of any one triangle may differ from those of any similar triangle, the ratios of the side lengths are the same in each triangle – for example, each triangle in Figure 7 has sides whose lengths are in the ratio 2 : 3 : 4. In future, whenever we say that two or more triangles are similar we will mean it in the technical sense that they have the same interior angles and side lengths that are in the same ratio.

Figure 8 The labelling of sides in a right–angled triangle.
Figure 8 shows a right–angled triangle in which an angle θ has been marked for particular attention and the opposite side and adjacent side to this angle have been identified. Thus the three sides may be referred to as the opposite, the adjacent and the hypotenuse, and we may use these terms or the letters o, a and h to refer to their respective lengths.
Thanks to the special properties of right–angled triangles, the whole class of triangles that are similar to the triangle in Figure 8 can be characterized by the single angle θ, or, equivalently, by the ratio of the side lengths o : a : h. In fact, because of the Pythagorean relationship that exists between the sides of a right–angled triangle, the ratio of any two side lengths is sufficient to determine θ and identify the class of similar triangles to which a given right–angled triangle belongs. The ratios of the sides of right–angled triangles are therefore of particular importance.
The study of right–angled triangles is known as trigonometry, and the three distinct ratios of pairs of sides are collectively known as the trigonometric ratios. They are called the sine, cosine and tangent of the angle θ – abbreviated to sin, cos and tan, respectively i – and defined as follows:
$\sin\theta = \dfrac{\text{opposite}}{\text{hypotenuse}}$(5)
$\cos\theta = \dfrac{\text{adjacent}}{\text{hypotenuse}}$(6)
$\tan\theta = \dfrac{\text{opposite}}{\text{adjacent}}$(7) i
The angle θ that appears in these definitions must lie between 0 rad (0°) and π/2 rad (90°), but later in this module we will extend the definitions to all angles. It should be emphasized that the value of a particular trigonometric ratio depends only on the value of θ, so the sine, cosine and tangent are effectively functions of the angle θ. More will be made of this point in Section 3 when we actually define related quantities called the trigonometric functions.
It is extremely useful to remember the definitions of the trigonometric ratios. You may find it helpful to denote the sine, cosine and tangent by the letters s, c and t and then, using h, o and a to represent hypotenuse, opposite and adjacent, the three relations read, left to right and top to bottom, as soh, cah and toa.
You can use a calculator to find the sine, cosine or tangent of an angle expressed in either degrees or radians, provided you first switch it to the appropriate mode – this is usually done by pressing a key marked ‘DRG’ (or something similar) until either ‘degrees’ or ‘radians’ appears in the display. Then key in the angle followed by one of the function keys sin, cos or tan.
✦ Use a calculator to find sin(15°); cos(72°); sin(π/4); tan(π/3); cos(0.63). i
✧ sin(15°) = 0.2588; cos(72°) = 0.3090; sin(π/4) = 0.7071; tan(π/3) = 1.732; cos(0.63) = 0.8080.
(Note that the last three angles should be assumed to be in radians since no units are stated.)
The three trigonometric ratios are not all independent since we can write:
$\tan\theta = \dfrac{\text{opposite}}{\text{adjacent}} \times \dfrac{\text{hypotenuse}}{\text{adjacent}} =\sin\theta \times \dfrac{1}{\cos\theta}$
and so we obtain the identity:
$\tan\theta = \dfrac{\sin\theta}{\cos\theta}$(8)
Furthermore, we can use Pythagoras’s theorem to obtain a second relation. Starting with:
(opposite)2 + (adjacent)2 = (hypotenuse)2
we can divide both sides by (hypotenuse)2 to obtain
$\dfrac{(\text{opposite})^2}{(\text{hypotenuse})^2} + \dfrac{(\text{adjacent})^2}{(\text{hypotenuse})^2}=1$
and therefore
(sin θ)2 + (cos θ)2 = 1
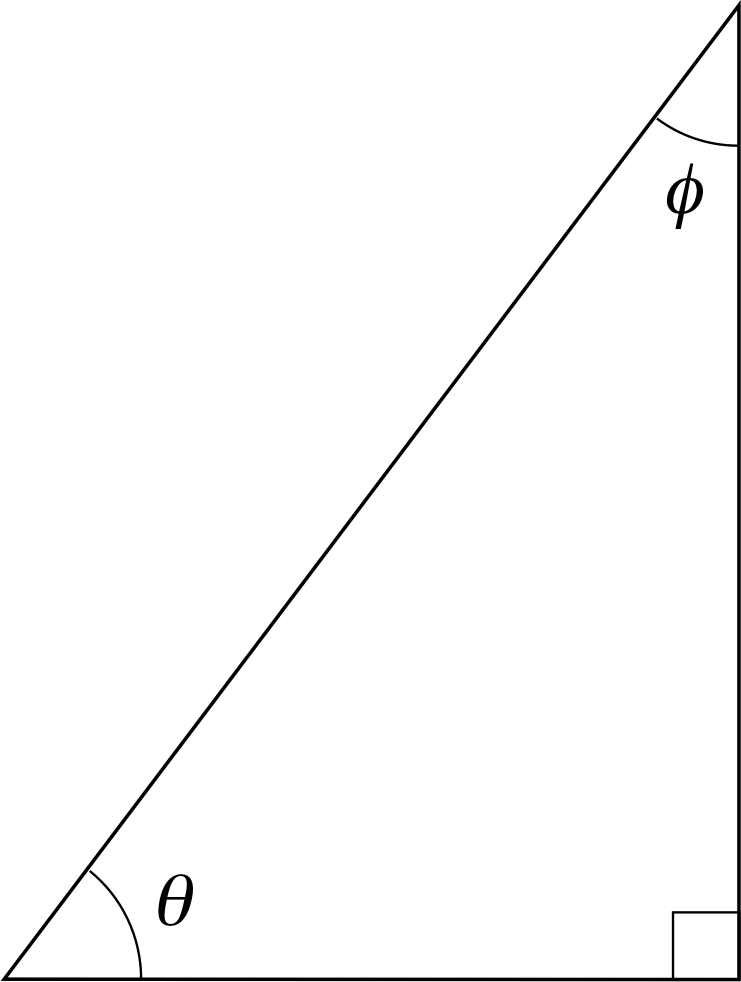
Figure 9 A right–angled triangle with angles θ and ϕ.

Figure 10 A right–angled triangle with two equal length sides, an isosceles triangle.
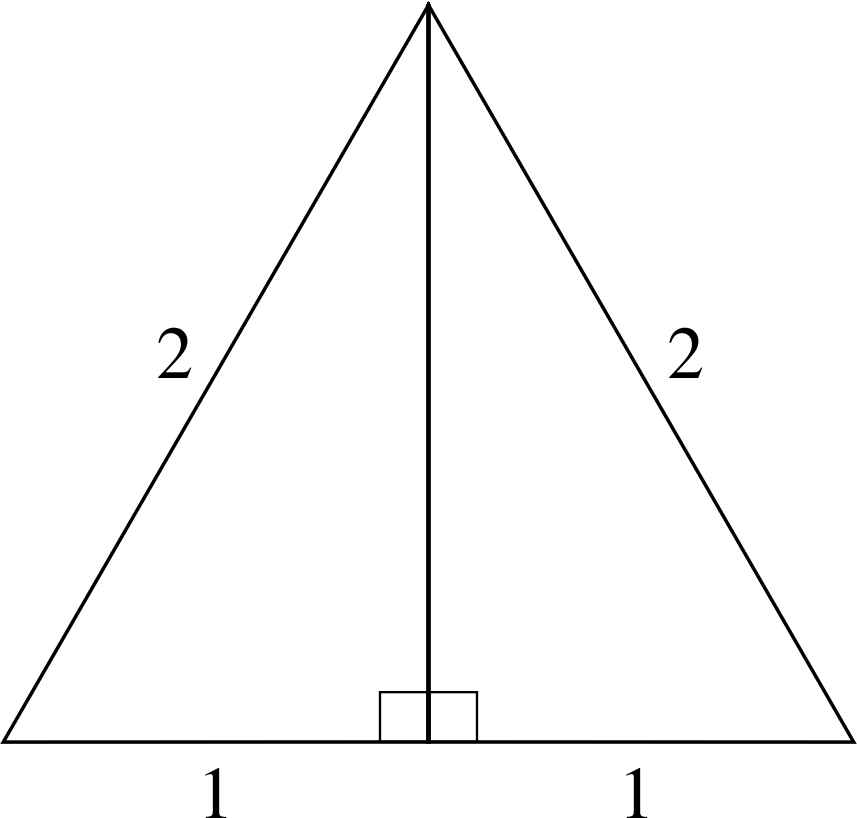
Figure 11 An equilateral triangle.
As you can see, writing powers of trigonometric functions can be rather cumbersome and so the convention that sinnθ means (sin θ)n (for positive values of n) is often used. Similar conventions are used for the other trigonometric functions. The notation cannot be used for negative values of n since sin−1θ is sometimes used for the inverse sine function, which we consider later in this module. The above relation can therefore be written as:
sin2 θ + cos2 θ = 1(9)
Since there are two identities relating the trigonometric ratios, it follows that only one ratio is independent and therefore given one ratio we can find the other two. (This assumes that the trigonometric ratios are positive, which is true for 0° ≤ θ ≤ 90°.)
The angle ϕ in Figure 9 also has its sine, cosine and tangent. But the opposite and adjacent sides appropriate to θ are interchanged for ϕ and, as a consequence we can write
$\tan\theta = \dfrac{1}{\tan\phi},\;\sin\theta = \cos\phi,\;\cos\theta = \sin\phi$
There are some special angles for which it is easy to write down the sine, cosine and tangent.
As an example, consider the right–angled triangle with two sides of equal length, as shown in Figure 10.
Any triangle with two sides of equal length is called an isosceles triangle, and any isosceles triangle must contain two equal interior angles. The isosceles triangle of Figure 10 is special because it is also a right–angled triangle. Since the interior angles of any triangle add up to 180°, the angles of this particular triangle must be 45°, 90°, 45°. Also, since the two equal sides of this particular triangle are both of unit length it follows from Pythagoras’s theorem that the length of the hypotenuse is $\sqrt{1^2 + 1^2} = \sqrt{2\os}$ and so we can write down the following results:
$\sin 45° = \dfrac{\text{opposite}}{\text{hypotenuse}} = \dfrac{1}{\sqrt{2\os}}$
$\cos 45° = \dfrac{\text{adjacent}}{\text{hypotenuse}} = \dfrac{1}{\sqrt{2\os}}$
$\tan 45° = \dfrac{\text{opposite}}{\text{adjacent}} = 1$
Figure 11 shows an equilateral triangle, i.e. one with three sides of equal length and hence three equal interior angles which must be equal to 60°. A line has been drawn from one vertex (i.e. corner) to the middle of the opposite side, so that the angle between the line and the side is 90° (that is, the line is a normal to the side).
| θ/degrees | θ/radians | sin θ | cos θ | tan θ |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 30 | $\pi/6$ | |||
| 45 | $\pi/4$ | $1/\sqrt{2\os}$ | $1/\sqrt{2\os}$ | 1 |
| 60 | $\pi/3$ | |||
| 90 | $\pi/2$ | 1 | 0 | undefined |
Question T5
By considering Figure 11, find the values of sin θ, cos θ and tan θ for θ equal to 30° (π/6 rad) and 60° (π/3 rad), and hence complete the trigonometric ratios in Table 2.
| θ/degrees | >θ/radians | sin θ | cos θ> | tan θ |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 30 | $\pi/6$ | 1/2 | $\sqrt{3\os}/2$ | $1/\sqrt{3\os}$ |
| 45 | $\pi/4$ | $1/\sqrt{2\os}$ | $1/\sqrt{2\os}$ | 1 |
| 60 | $\pi/3$ | $\sqrt{3\os}/2$ | 1/2 | $\sqrt{3\os}$ |
| 90 | $\pi/2$ | 1 | 0 | undefined |
Answer T5
By Pythagoras’s theorem, the perpendicular has length, $\sqrt{2^2-1} = \sqrt{3\os}$. Therefore the completed table is as given in Table 4.
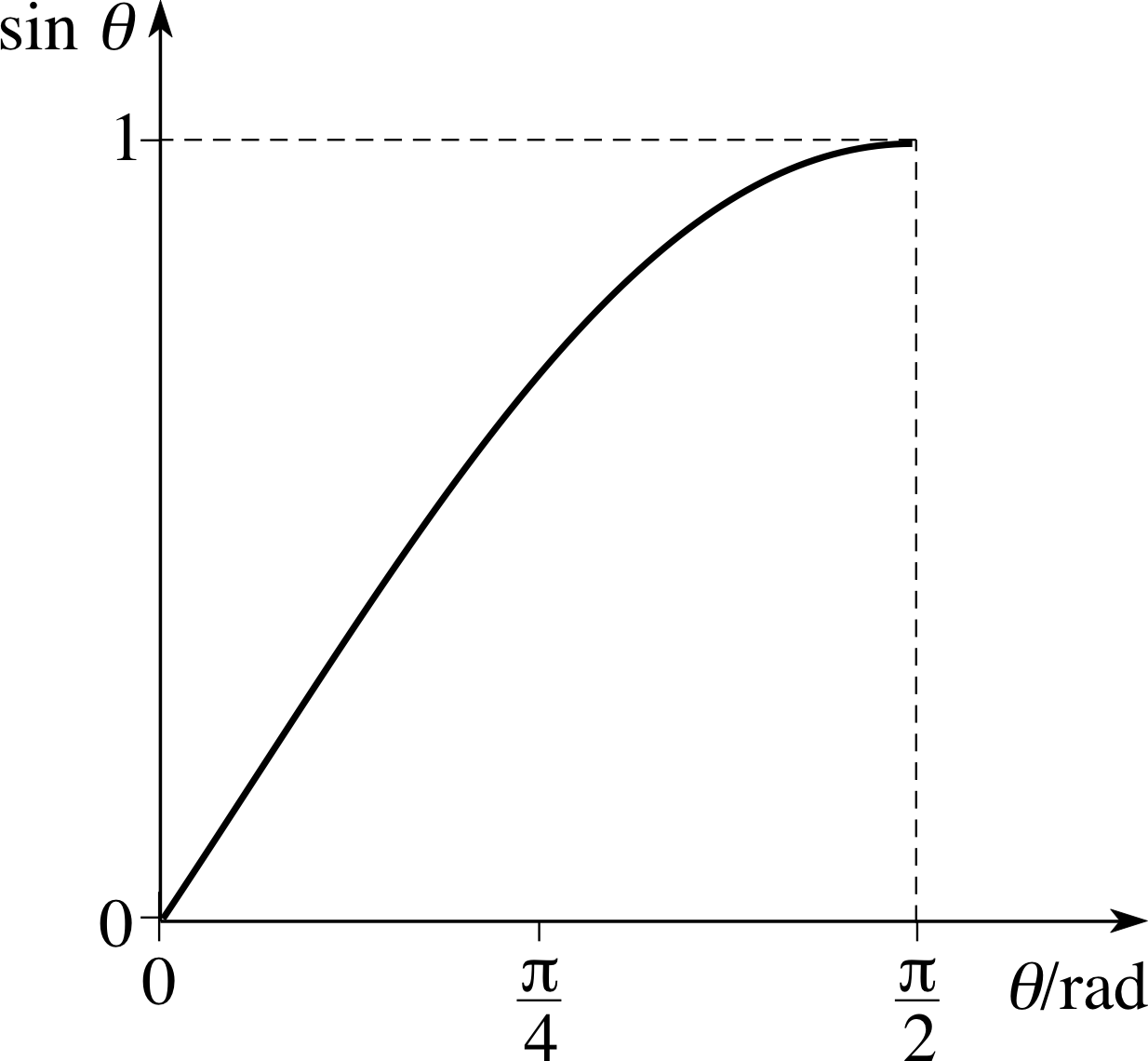
Figure 12 See Question T6.
Question T6
Figure 12 shows a graph of sin θ for 0 ≤ θ < π/2. i Using Table 2, your answer to Question T5, and any other relevant information given in this subsection, sketch corresponding graphs for cos θ and tan θ.
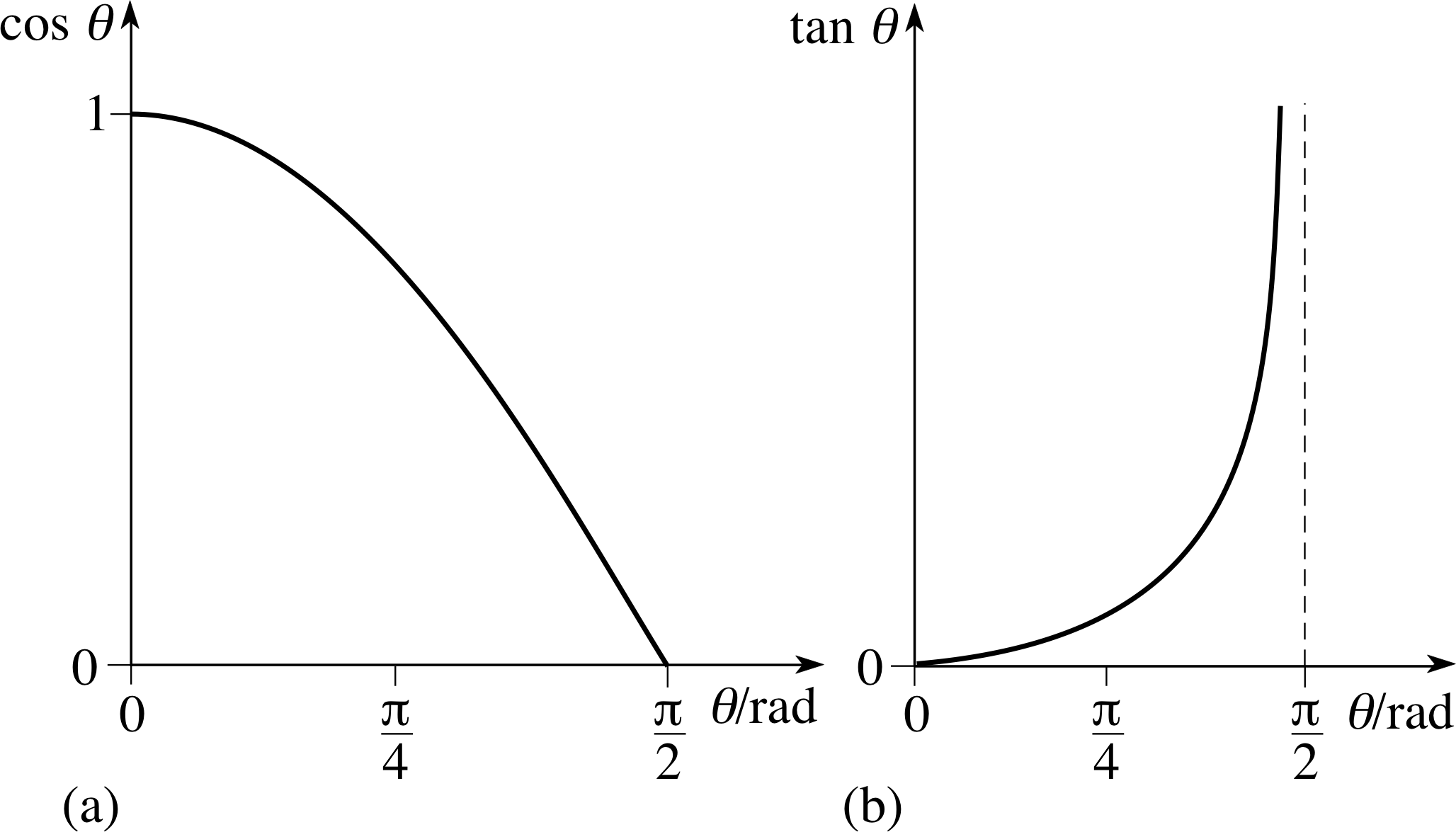
Figure 32 See Answer T6.
Answer T6
Graphs of (a) cos θ and (b) tan θ for 0 ≤ θ < π/2 are given in Figure 32.
One of the many reasons why trigonometric ratios i are of interest to physicists is that they make it possible to determine the lengths of all the sides of a right–angled triangle from a knowledge of just one side length and one interior angle (other than the right angle).
Here is an example of this procedure taken from the field of optics.
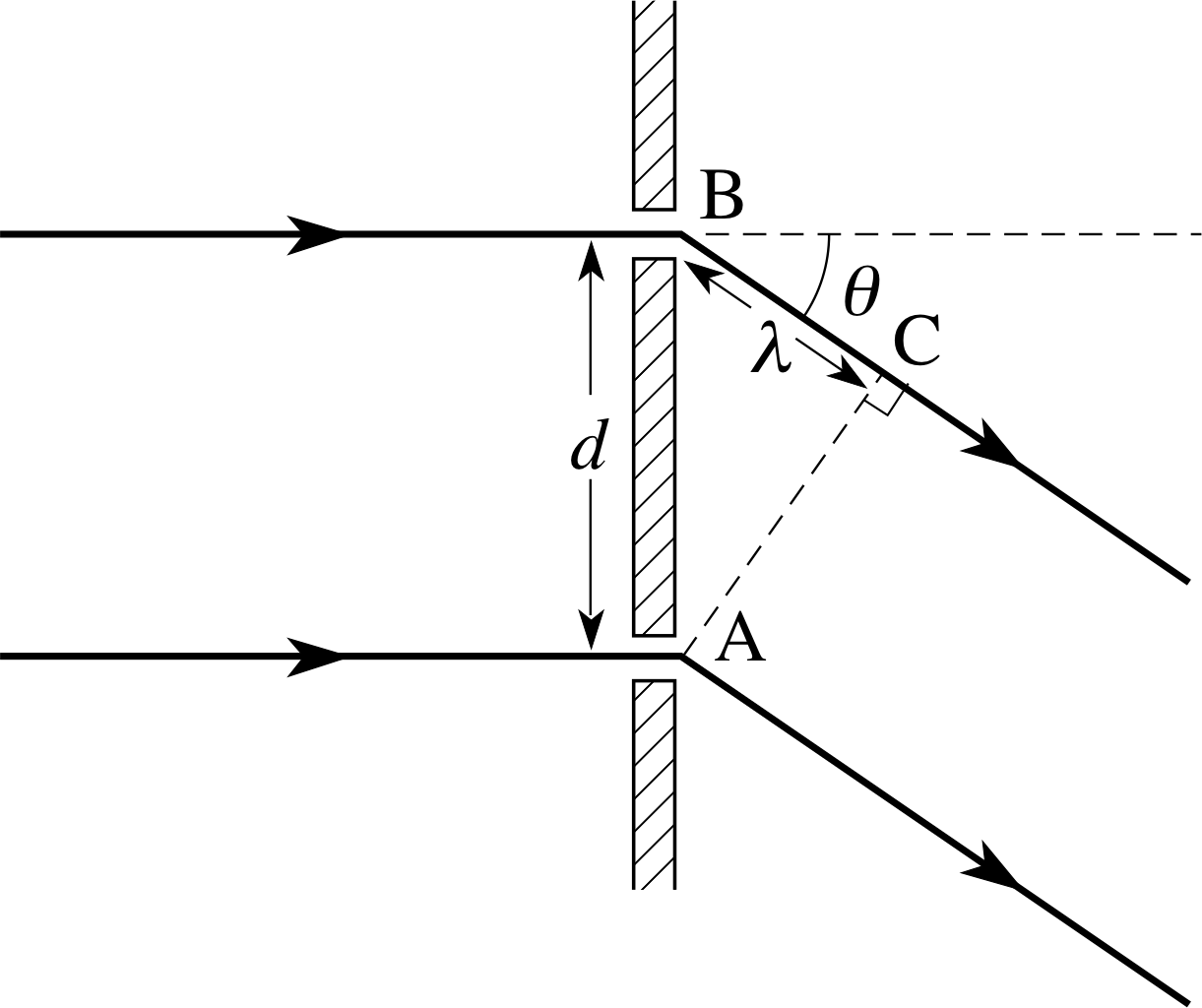
Figure 13 See Question T7.
Question T7
Figure 13 represents a two–slit diffraction experiment. i Derive a formula relating λ to d and θ. If d = 2 × 10−6 m and θ = 17.46°, what is the value of λ?
Answer T7
The angle AB^C = 90° − θ, so the angle BA^C must be θ. Since the side AB is the hypotenuse of the right–angled triangle ABC, it follows that
sin θ = λ/d
and λ = 2 × 10−6 m × sin(17.46°) = 6 × 10−7 m
2.4 The reciprocal trigonometric ratios
The ratios introduced in the previous subsection could all have been written the other way up. The resulting reciprocal trigonometric ratios occur so frequently that they too are given specific names; they are the cosecant, secant, and cotangent (abbreviated to cosec, sec and cot) and are defined by:
$\cosec\,\theta = \dfrac{1}{\sin\theta} \quad\,\text{provided }\sin\theta \ne 0$(10) i
$\sec\theta = \dfrac{1}{\cos\theta}\quad\quad\text{provided }\cos\theta \ne 0$(11)
$\cot \theta = \dfrac{1}{\tan\theta}\quad\quad\text{provided }\tan\theta \ne 0$(12)
Notice that cosec is the reciprocal of sin, and sec the reciprocal of cos. This terminology may seem rather odd but it is easily remembered by recalling that each reciprocal pair – (sin, cosec), (cos, sec), (tan, cot) – involves the letters ‘co’ just once. In other words there is just one ‘co’ between each pair. Also notice that each reciprocal trigonometric function is undefined when its partner function is zero.
Throughout the domains on which they are defined, each of the reciprocal trigonometric ratios can also be written in terms of the sides of the triangle in Figure 8:

Figure 8 The labelling of sides in a right–angled triangle.
$\cosec\,\theta = \dfrac{\text{hypotenuse}}{\text{opposite}}$(13)
$\sec\theta = \dfrac{\text{hypotenuse}}{\text{adjacent}}$(14)
$\cot\theta = \dfrac{\text{adjacent}}{\text{opposite}}$(15)
Two useful general relationships follow from Equations 13–15 and Pythagoras’s theorem:
$\cot\theta = \dfrac{\cosec\,\theta}{\sec\theta}$(16)
and$1+\tan^2\theta=\sec^2\theta$(17)

Figure 11 An equilateral triangle.
Question T8
Using Figure 11, write down the values of cosec(30°), sec(30°), cot(30°) and cosec(60°), sec(60°), cot(60°).
Answer T8
From Figure 11:
$\cosec(30°) = 2,~\sec(30°) = 2/\sqrt{3\os},~\cot(30°) = \sqrt{3\os},~\cosec(60°) = 2/\sqrt{3\os},~\sec(60°) = 2,~\cot(60°) = 1/\sqrt{3\os}$
Calculators do not generally have keys that give the reciprocal trigonometric ratios directly, but the ratios can be found using the sin, cos and tan keys and the reciprocal (1/x) key.
Question T9
Use a calculator to find cosec(23°), sec(56°), cot(π/6), cot(1.5).
Answer T9
cosec(23°) = 1/sin(23°) = 2.559; sec(56°) = 1/cos(56°) = 1.788; cot(π/6) = 1/tan(π/6) = 1.732; cot(1.5) = 1/tan(1.5) = 0.071.
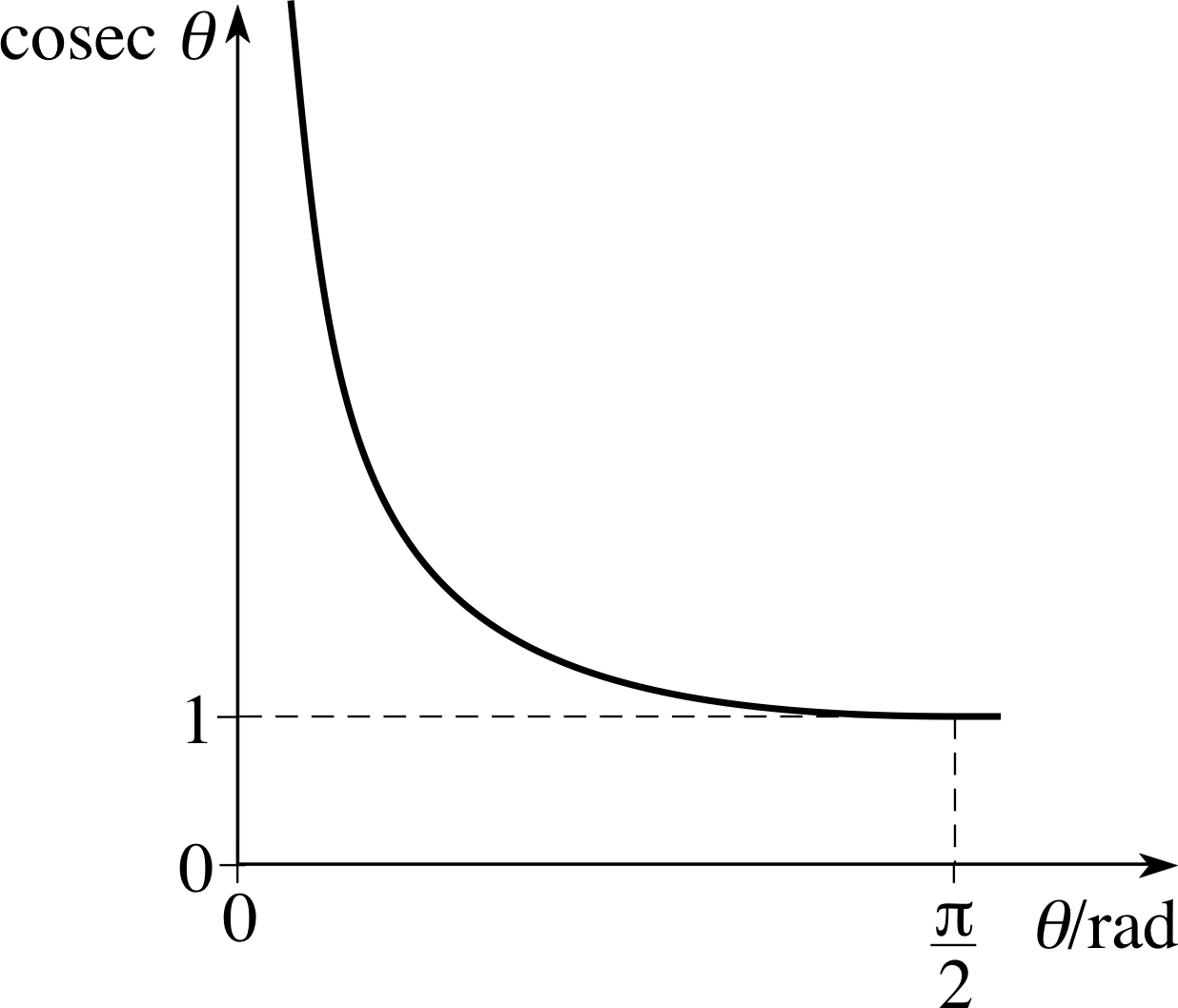
Figure 14 See Question T10.
Question T10
Figure 14 shows a graph of cosec θ for 0 < θ < π/2. Using values of reciprocal trigonometric ratios calculated above, and other information from this subsection, sketch graphs of sec θ and cot θ for 0 ≤ θ < π/2.
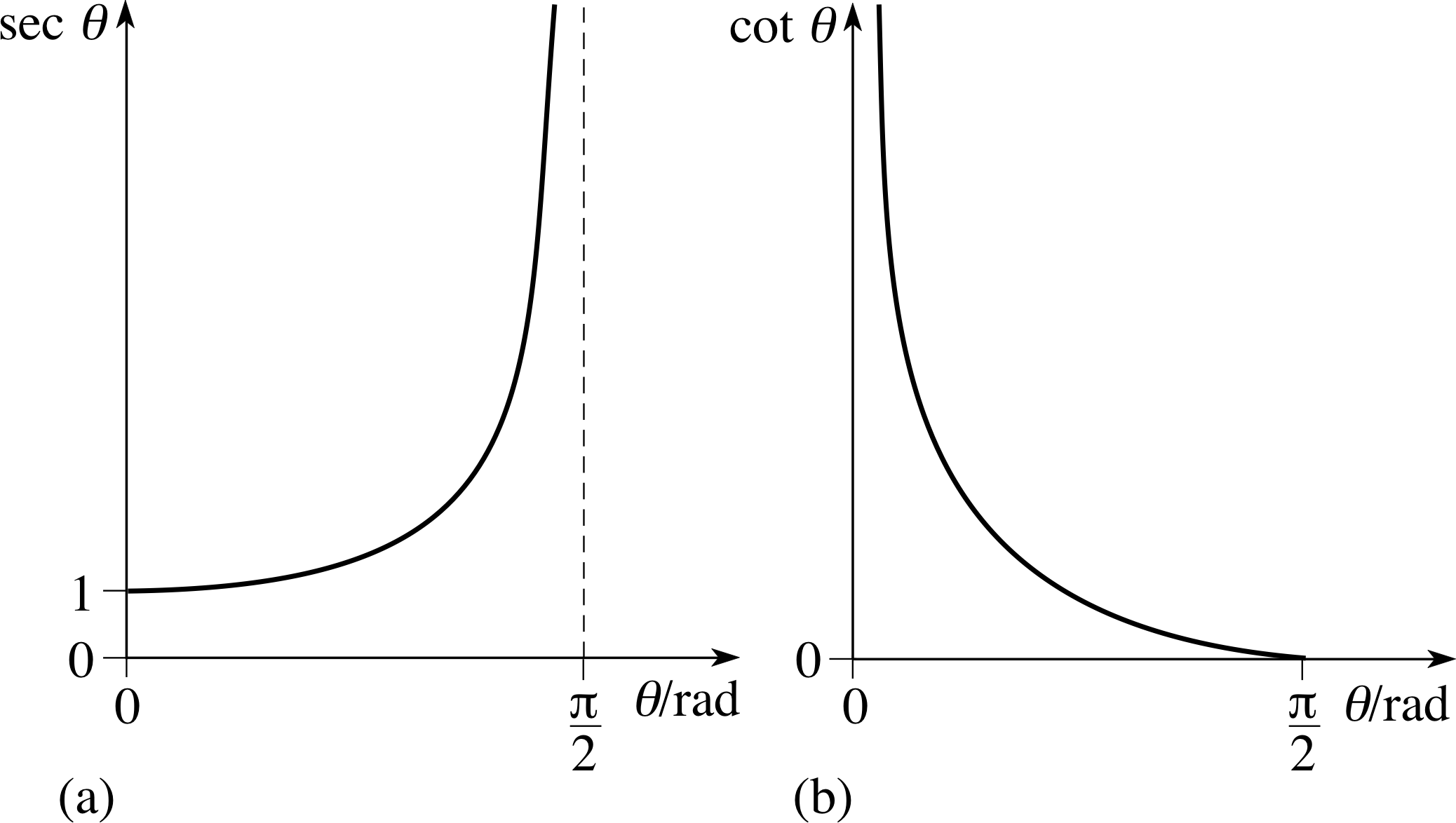
Figure 33 See Answer T10.
Answer T10
Graphs of (a) sec θ (b) cot θ for 0 ≤ θ < π/2 are given in Figure 33.
2.5 Small angle approximations
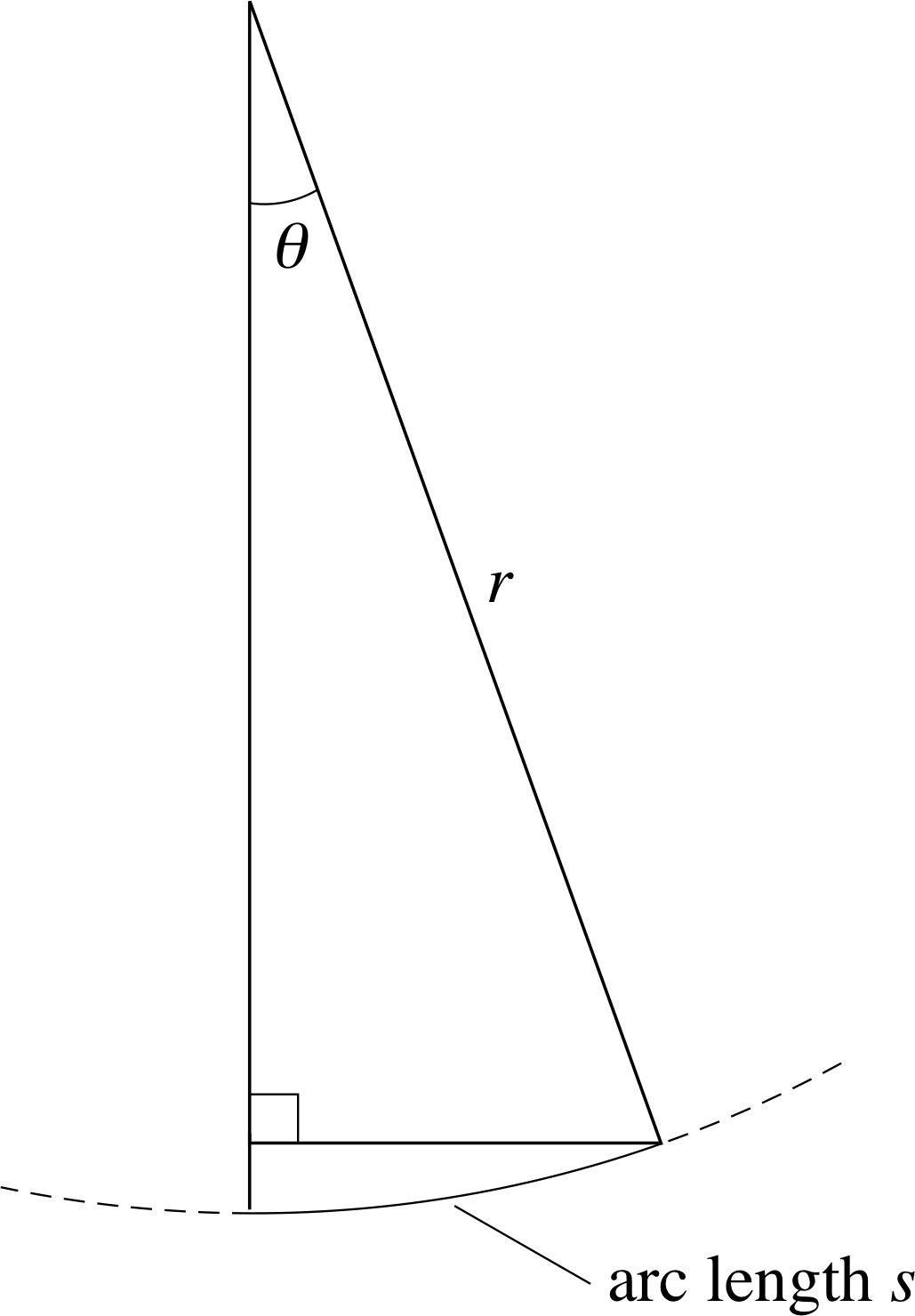
Figure 15 A right–angled triangle with a small angle θ
We end this section with some useful approximations involving small angles. Figure 15 shows a right–angled triangle with one very small angle θ and the third angle almost a right angle. If θ is at the centre of a circle radius r, where r is the hypotenuse of the triangle, you can see from the diagram that the opposite side to θ is almost coincident with the arc length s and the adjacent side to θ is almost the same length as the hypotenuse. From Equation 1, s/r is the value of θ in radians. So, for the small angle θ, Equations 5 to 7 give sin θ ≈ s/r, cos θ ≈ r/r, tan θ ≈ s/r and hence:
for a small angle θ:
cos θ ≈ 1 and sin θ ≈ tan θ ≈ θ/rad
✦ Use a calculator to find sin θ, cos θ and tan θ for a few small angles, and hence show that the approximations expressed in the boxed equations above become increasingly good as θ becomes smaller. Try, for example, θ = 0.175 00 rad (i.e. θ ≈ 10°) and θ = 0.010 00 rad, and express the answers to five decimal places. triangle with a small angle θ.
✧ sin(0.175 00) = 0.174 11; cos(0.175 00) = 0.984 73; tan(0.175 00) = 0.176 81.
sin(0.010 00) = 0.010 00; cos(0.010 00) = 0.999 95; tan(0.010 00) = 0.010 00.
✦ Write down approximate expressions for the reciprocal trigonometric ratios for a small angle θ.
✧ cosec θ ≈ cot θ ≈ 1/(θ/rad); sec θ ≈ 1.
Question T11
Seen from Earth, the diameter of the Sun subtends an angle ϕ of about 0.5°. By expressing ϕ in radians, derive an expression for the Sun’s diameter, s, in terms of its distance d from Earth. Your expression should not involve any trigonometric ratios.
Answer T11
ϕ = 0.5° = (0.5 × π/180) rad = (0.5 × 0.0175) rad = 8.73 × 10−3 rad (see Answer T1 for the origin of the conversion factor.)
Since ϕ is a small angle, ϕ/rad ≈ s/d so s ≈ d × ϕ/rad = d × 8.73 × 10−3.
3 Graphs and trigonometric functions
3.1 The trigonometric functions
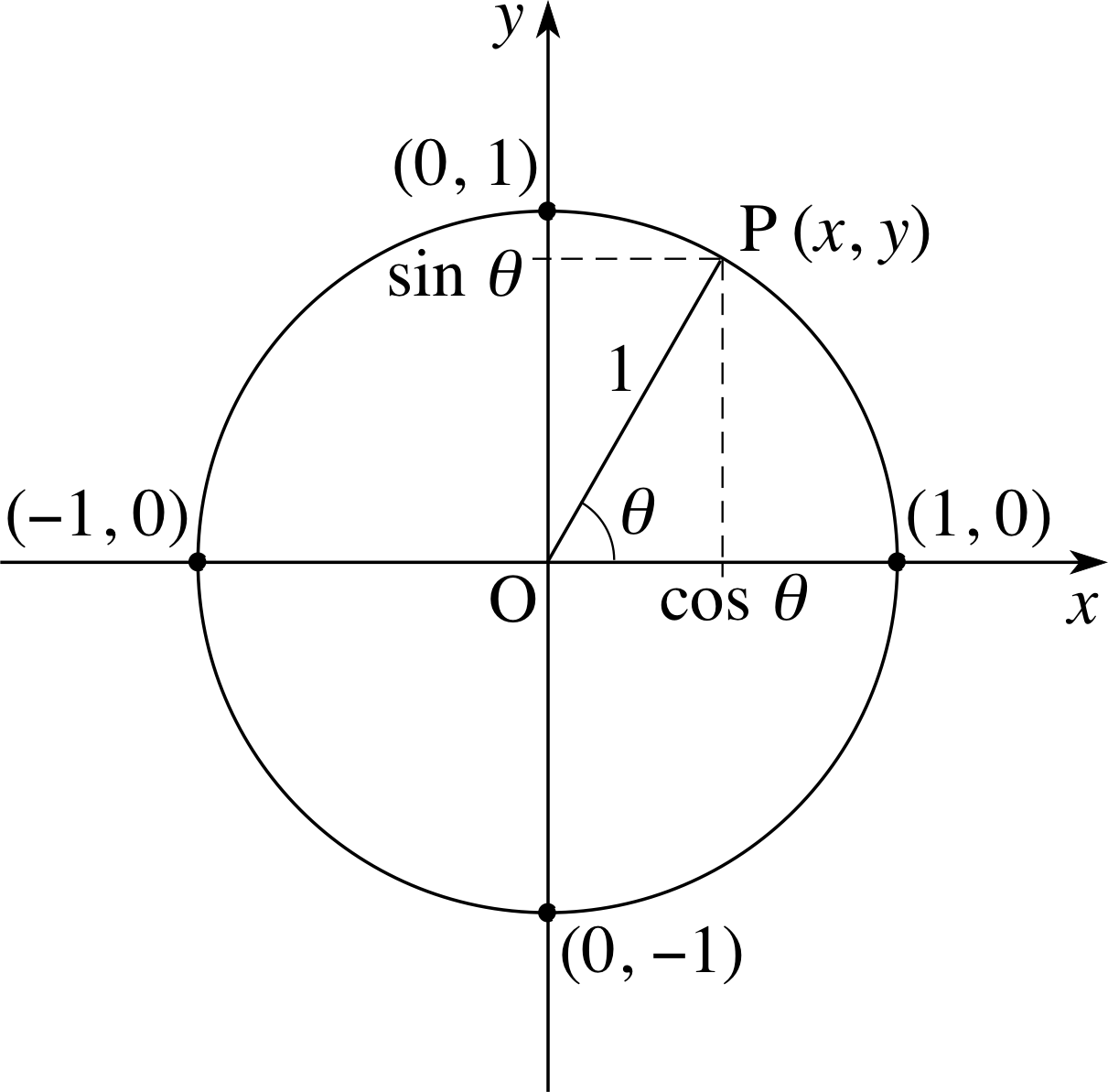
Figure 16 Defining the trigonometric functions for any angle. If 0 ≤ θ < π/2, the coordinates of P are x = cos θ and y = sin θ. For general values of θ we define sin(θ) = y and cos(θ) = x.
The ratio definitions of the sine, cosine and tangent (i.e. Equations 5, 6 and 7) only make sense for angles in the range 0 to π/2 radians, since they involve the sides of a right–angled triangle. In this subsection we will define three trigonometric functions, also called sine, cosine and tangent, and denoted sin(θ), cos(θ) and tan(θ), respectively. i These functions will enable us to attach a meaning to the sine and cosine of any angle, and to the tangent of any angle that is not an odd multiple π/2. Like the trigonometric ratios that they generalize, these trigonometric functions are of great importance in physics.
In defining the trigonometric functions we want to ensure that they will agree with the trigonometric ratios over the range 0 to π/2 radians. In order to do this, consider the point P shown in Figure 16 that moves on a circular path of unit radius around the origin O of a set of two–dimensional Cartesian coordinates (x, y).
If we let θ be the angle between the line OP and the x–axis, it follows from the definition of the trigonometric ratios that the coordinates of P are
y = sin θ for 0 ≤ θ < π/2
andx = cos θ for 0 ≤ θ < π/2
Although these trigonometric ratios are only defined over a very narrow range, it is easy to imagine the angle θ increasing in the positive (i.e. anticlockwise) direction to take up any positive value, with P crossing the positive x–axis whenever θ is equal to an integer multiple of 2π. And it is equally easy to imagine θ increasing in the negative (clockwise) direction to take up any negative value. Now, whatever the value of θ may be, large or small, positive or negative, the point P must still be located somewhere on the circle in Figure 16 and it must have a single x– and a single y–coordinate. We can use the particular values of x and y that correspond to a given value of θ to define the first two trigonometric functions
sin(θ) = y for any θ
andcos(θ) = x for any θ
Defined in this way, it is inevitable that the trigonometric functions will agree with the trigonometric ratios when 0 ≤ θ ≤ π/2, but it is also clear that the functions, unlike the ratios, make sense for arbitrary values of θ.
Having defined the functions sin(θ) and cos(θ) we also want to define a function tan(θ), but once again we want to ensure consistency with the behaviour of the trigonometric ratio tan θ that was introduced earlier. We can do this by using a generalization of Equation 8 (i.e. tan θ = sin θ1/cos θ0) as the basis of the definition. Thus, we define
$\tan(\theta)=\dfrac{\sin(\theta)}{\cos(\theta)} \quad\text{for any }\theta \ne(2n+1)\pi/2$ i
Notice that unlike the sine and cosine functions, this function is not defined for values of θ that are odd integer multiples of π/2. This restriction is imposed because cos θ = 0 at those values of θ, and the quotient sin(θ)/cos(θ) has no meaning. i
Having defined the trigonometric functions it is only natural to enquire about their graphs, since graphs are usually a good way of gaining insight into the behaviour of functions. Perhaps the first thing to notice about the trigonometric functions is that they are not always positive. If θ is in the range 0 ≤ θ < π/2 both the x– and y–coordinates of P will be positive, so both sin(θ) and cos(θ) will be positive as will their quotient tan(θ). However, as θ enters the range π/2 < θ < π the x–coordinate of P becomes negative, so cos(θ) and tan(θ) will be negative, though sin(θ) will remain positive. Similarly, when π < θ < 3π/2, x and y are both negative so sin(θ) and cos(θ) are negative while tan(θ) is positive; and if 3π/2 < θ < 2π, cos(θ) is positive while sin(θ) and tan(θ) are negative. As θ increases beyond 2π (or when θ decreases below 0) the same pattern is repeated.
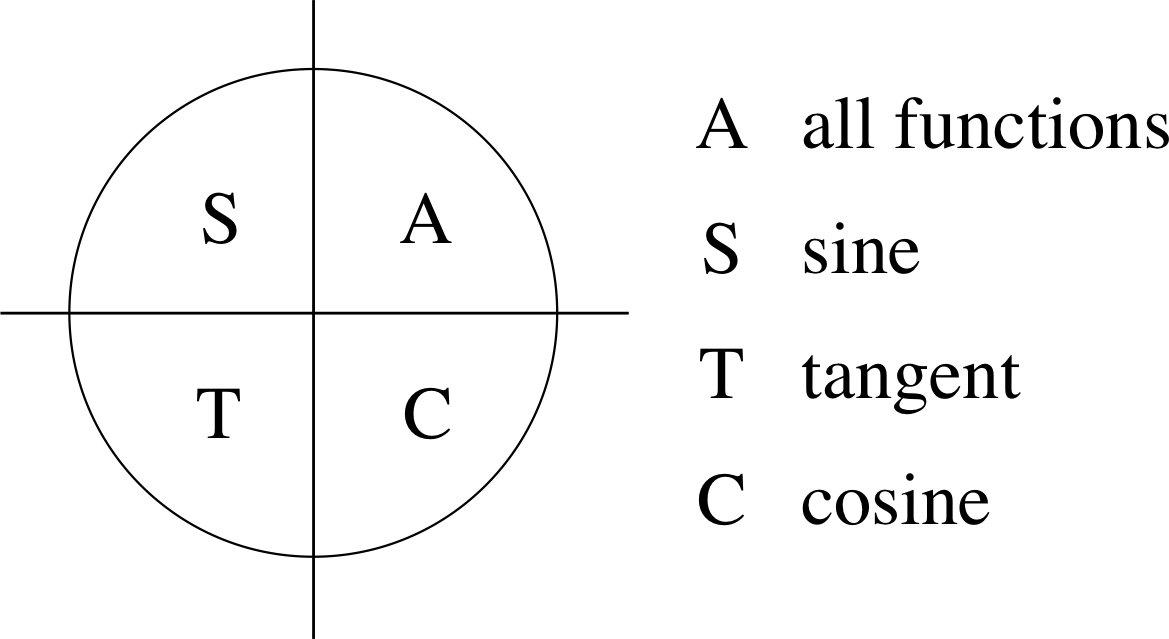
Figure 17 Quadrants in which the trigonometric functions are positive.
Figure 17 summarizes the sign behaviour of the trigonometric functions. The positive function in each quadrant i is indicated by its initial letter, or in the case of the first quadrant where all the functions are positive by the letter A. Most people who use the trigonometric functions find it helpful to memorize Figure 17 (or to remember Figure 16, so that they can work it out). A traditional mnemonic to help recall which letter goes in which quadrant is ‘All Stations To Crewe’, which gives the letters in positive (anticlockwise) order starting from the first quadrant.
Of course, it is not only the signs of the trigonometric functions that change as θ increases or decreases and P moves around the circle in Figure 16. The values of x and y, and consequently of sin(θ), cos(θ) and tan(θ) also vary.
✦ If you were asked to draw a diagram similar to Figure 17, but showing which trigonometric function(s) increase as θ increases in each quadrant, how would you have to change the lettering on Figure 17.
✧ A would become S, T (both sin(θ) and tan(θ) are increasing from zero in the first quadrant). S would become T (as sin(θ) decreases you might think that tan(θ) would also decrease, but cos(θ) is negative and decreasing in the second quadrant so tan(θ) becomes a smaller negative number as θ increases, i.e. the value of tan(θ) increases). T would become C, T (in this quadrant it is cos(θ) that is becoming less negative). C would become A, (sin(θ) and tan(θ) are both becoming less negative and cos(θ) is increasing from zero in this quadrant).
The graphs of sin(θ), cos(θ) and tan(θ) are shown in Figures 18, 19 and 20.
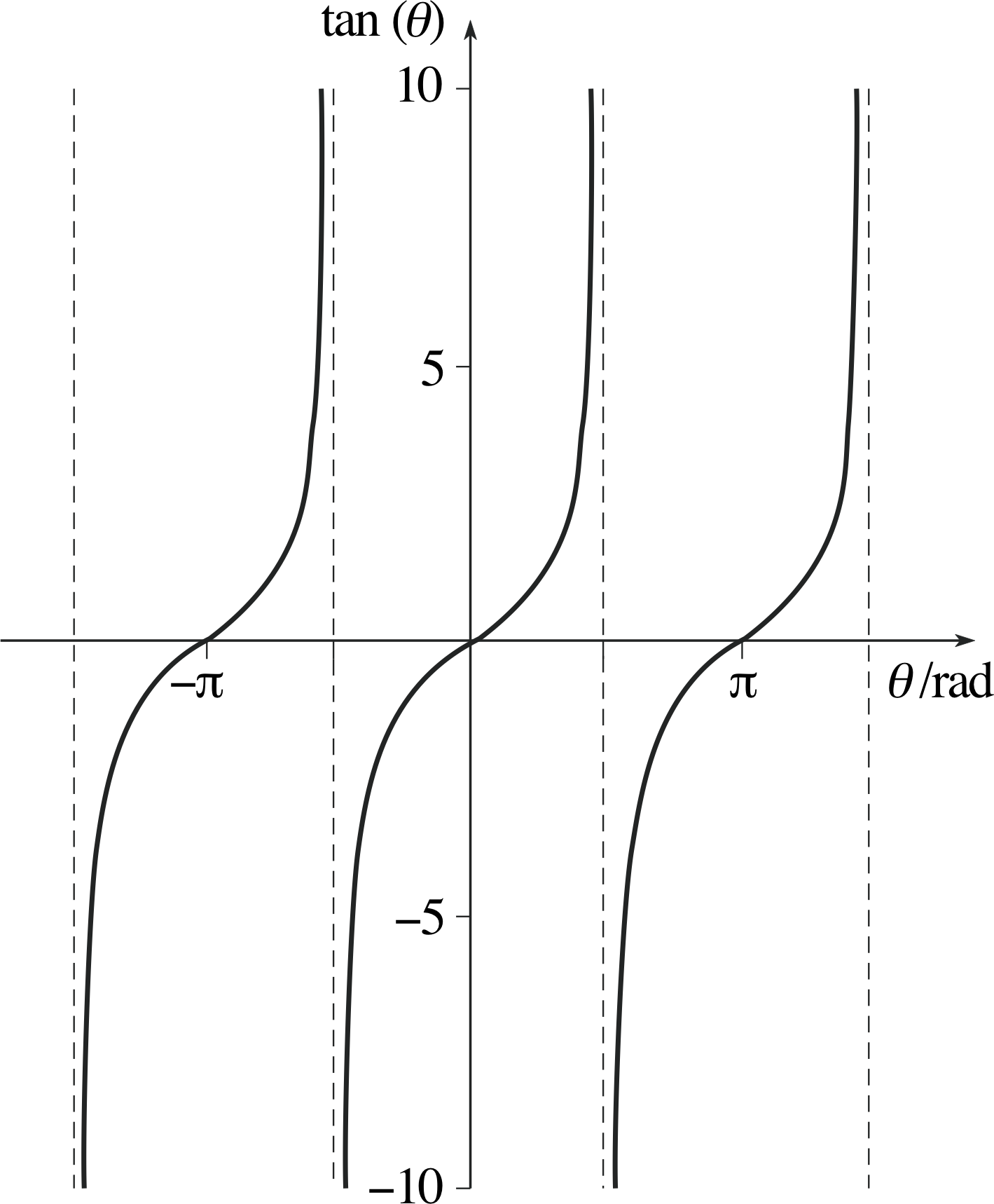
Figure 20 Graph of tan(θ).
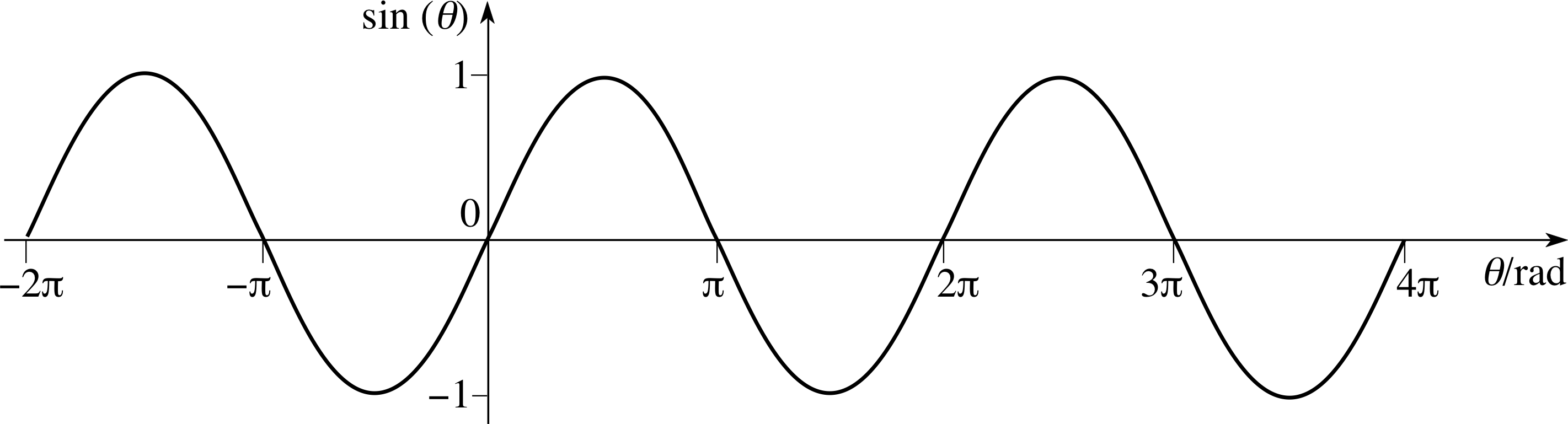
Figure 18 Graph of sin(θ).
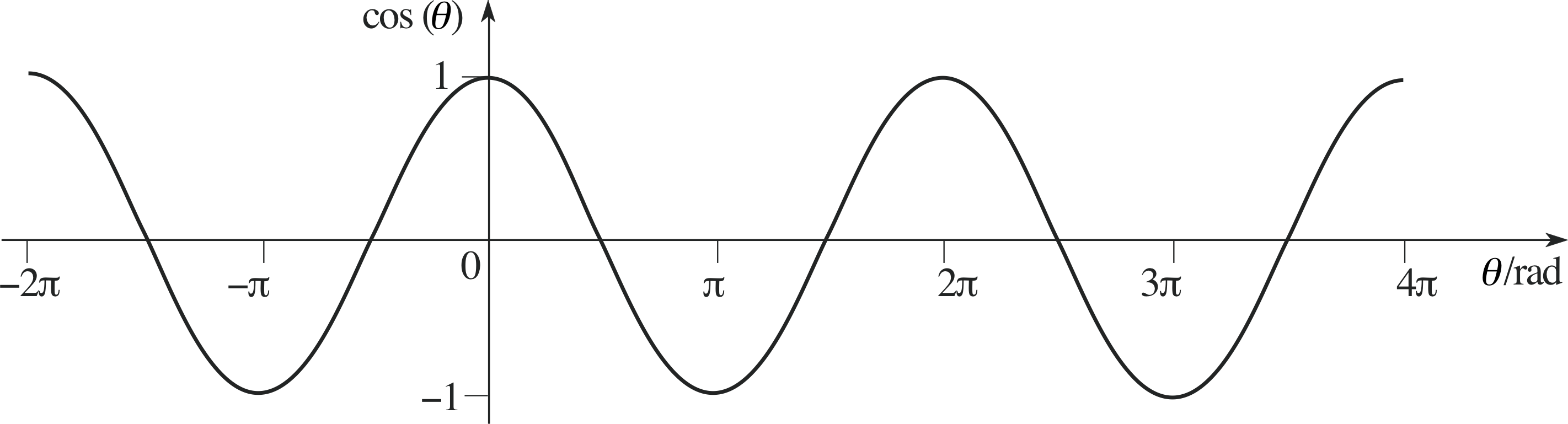
Figure 19 Graph of cos(θ).
| θ/radians | sin θ | cos θ | tan θ |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| $\pi/6$ | 1/2 | $\sqrt{3\os}/2$ | $1/\sqrt{3\os}$ |
| $\pi/4$ | $1/\sqrt{2\os}$ | $1/\sqrt{2\os}$ | 1 |
| $\pi/3$ | $\sqrt{3\os}/2$ | 1/2 | $\sqrt{3\os}$ |
| $\pi/2$ | 1 | 0 | undefined |
| $2\pi/3$ | $\sqrt{3\os}/2$ | −1/2 | −$\sqrt{3\os}$ |
| $3\pi/4$ | $1/\sqrt{2\os}$ | −$1/\sqrt{2\os}$ | −1 |
| $5\pi/6$ | 1/2 | −$\sqrt{3\os}/2$ | −$1/\sqrt{3\os}$ |
| $\pi$ | 0 | −1 | 0 |
| $7\pi/6$ | −1/2 | −$\sqrt{3\os}/2$ | $1/\sqrt{3\os}$ |
| $5\pi/4$ | −$1/\sqrt{2\os}$ | −$1/\sqrt{2\os}$ | 1 |
| $4\pi/3$ | −$\sqrt{3\os}/2$ | −1/2 | $\sqrt{3\os}$ |
| $3\pi/2$ | −1 | 0 | undefined |
| $5\pi/3$ | −$\sqrt{3\os}/2$ | 1/2 | −$\sqrt{3\os}$ |
| $7\pi/4$ | −$1/\sqrt{2\os}$ | $1/\sqrt{2\os}$ | −1 |
| $11\pi/6$ | −1/2 | $\sqrt{3\os}/2$ | −$1/\sqrt{3\os}$ |
| $2\pi$ | 0 | 1 | 0 |
As you can see, the values sin(θ) and cos(θ) are always in the range −1 to 1, and any given value is repeated each time θ increases or decreases by 2π.
The graph of tan(θ) (Figure 20) is quite different. Values of tan(θ) cover the full range of real numbers, but tan(θ) tends towards +∞ i as θ approaches odd multiples of π/2 from below, and towards −∞ as θ approaches odd multiples of π/2 from above. This emphasizes the impossibility of assigning a meaningful value to tan(θ) at odd multiples of π/2.
Table 3 lists the values of the trigonometric functions for some angles between 0 and 2π.
Question T12
Describe as many significant features as you can of the graphs in Figure 18Figures 18 and Figure 1919.
(Some of these features will be discussed in the next subsection.)
Answer T12
The sin(θ) graph repeats itself so that sin(2π + θ) = sin(θ). It is antisymmetric, i.e. sin(θ) = −sin(−θ) and continuous, and any value of θ gives a unique value of sin(θ).
The cos(θ) graph repeats itself so that cos(2π + θ) = cos(θ). It is symmetric, i.e. cos(θ) = cos(−θ) and continuous, and any value of θ gives a unique value of cos(θ).
Given the trigonometric functions, we can also define three reciprocal trigonometric functions cosec(θ), sec(θ) and cot(θ), that generalize the reciprocal trigonometric ratios defined in Equations 10, 11 and 12.
$\cosec\,\theta = \dfrac{1}{\sin\theta} \quad\,\text{provided }\sin\theta \ne 0$(Eqn 10)
$\sec\theta = \dfrac{1}{\cos\theta} \quad\quad\text{provided }\cos\theta \ne 0$(Eqn 11)
$\cot \theta = \dfrac{1}{\tan\theta} \quad\quad\text{provided }\tan\theta \ne 0$(Eqn 12)
The definitions are straightforward, but a little care is needed in identifying the appropriate domain of definition in each case. (As usual we must choose the domain in such a way that we are not required to divide by zero at any value of θ.)

Figure 21 Graph of cosec(θ).
$\cosec\,(\theta) = \dfrac{1}{\sin(\theta)} \quad\;\theta \ne n\pi$
$\sec(\theta) = \dfrac{1}{\cos(\theta)} \quad\quad\theta \ne 2n+1)\pi/2$
$\cot(\theta) = \dfrac{1}{\tan(\theta)} \quad\quad\theta \ne n\pi$
Graphs of the reciprocal trigonometric functions are shown in Figures 21, 22 and 23.

Figure 23 Graph of cot(θ).

Figure 22 Graph of sec(θ).
Throughout this subsection the argument θ of the various trigonometric and reciprocal trigonometric functions has always been an angle measured in radians. (This is true even though we have been conventionally careless about making sure that we always include the appropriate angular unit when assigning numerical values to θ.) However, the arguments of these functions do not have to be angles. If we regarded the numbers printed along the horizontal axes of Figures 18 to 23 as values of a purely numerical variable, x say, rather than values of θ in radians, we could regard the graphs as defining six functions of x; sin(x), cos(x), tan(x), etc. Strictly speaking these new functions are quite different from the trigonometric functions i and should be given different names to avoid confusion. But, given the tendency of physicists to be careless about domains and their habit of ‘dropping’ the explicit mention of radian from angular values, there is no practical difference between these new functions and the true trigonometric functions, so the confusion of names is harmless. Nonetheless, it is worth remembering that what appears as the argument of a trigonometric function is not necessarily an angle.
A common example of this arises in the study of oscillations i where trigonometric functions are used to describe repeated back and forth motion along a straight line.
In the simplest such motion, simple harmonic motion, the changing position x of a mass oscillating on the end of a spring may be represented by x = Acos(ωt + ϕ). Despite appearances none of the quantities inside the bracket is an angle (though they may be given angular interpretations); t is the time and is measured in seconds, ω is a constant known as the angular frequency that is related to the properties of the mass and spring and is measured in hertz (1 Hz = 1 s−1), and ϕ, the phase constant, is a number, usually in the range 0 to 2π.
One final point to note. As mentioned before, throughout this subsection we have been careful to use brackets (as in sin(θ)) to distinguish the trigonometric functions from the trigonometric ratios (sin θ, etc)., but since the trigonometric functions and ratios agree in those regions where they are both defined this distinction is also of little importance in practice. Consequently, as a matter of convenience, the brackets are usually omitted from the trigonometric functions unless such an omission is likely to cause confusion. In much of what follows we too will omit them and simply write the trigonometric and reciprocal trigonometric functions as sin x, cos x, tan x, cosec x, sec x and cot 1x.
3.2 Periodicity and symmetry
The trigonometric functions are all examples of periodic functions. That is, as θ increases steadily, the same sets of values are ‘recycled’ many times over, always repeating exactly the same pattern. The graphs in Figures 18, 19 and 20, show this repetition, known as periodicity, clearly. More formally, a periodic function f (x) is one which satisfies the condition f (x) = f (x + nk) i for every integer n, where k is a constant, known as the period.
Adding or subtracting any multiple of 2π to an angle is equivalent to performing any number of complete rotations in Figure 16, and so does not change the value of the sine or cosine:
sin(θ) = sin(θ + 2nπ) and cos(θ) = cos(θ + 2nπ)
for any integer n. The functions sin(θ) and cos(θ), are therefore periodic functions with period 2π.

Figure 20 Graph of tan(θ).
✦ What is the period of tan(θ)?

Figure 16 Defining the trigonometric functions for any angle. If 0 ≤ θ < π/2, the coordinates of P are x = cos θ and y = sin θ. For general values of θ we define sin(θ) = y and cos(θ) = x.
✧ Since tan(θ) = sin(θ)/cos(θ) (if cos(θ) is non–zero) it is tempting to say that tan(θ) has period 2π, but we can actually do better than this.
From Figure 20, you can see that it repeats with a period of π.
You can see why this is so if you look at Figure 16.
Rotating P through π radians leaves the sizes of x and y unchanged, but changes the sign of both of them, with the result that tan θ (= y/x) will be unaffected.

Figure 20 Graph of tan(θ).

Figure 18 Graph of sin(θ).

Figure 19 Graph of cos(θ).
As noted in the answer to Question T12, the trigonometric functions have some symmetry either side of θ = 0. From Figures 18, 19 and 20 we can see the effect of changing the sign of θ:
sin(−θ) = −sin(θ)(Eqn 18)
cos(−θ) = cos(θ)(Eqn 19)
tan(−θ) = −tan(θ)(Eqn 20)
Any function f (x) for which f (−x) = f (x) is said to be even_functioneven or symmetric_functionsymmetric, and will have a graph that is symmetrical about x = 0. Any function for which f (−x) = −f (x) is said to be odd_functionodd or antisymmetric_functionantisymmetric, and will have a graph in which the portion of the curve in the region x < 0 appears to have been obtained by reflecting the curve for x > 0 in the vertical axis and then reflecting the resulting curve in the horizontal axis. It follows from Equations 18, 19 and 20 that cos(θ) is an even function, while sin(θ) and tan(θ) are both odd functions.
✦ For each of the reciprocal trigonometric functions, state the period and determine whether the function is odd or even. i
✧ cosec(θ) is an odd function with period 2π.
sec(θ) is an even function with period 2π.
cot(θ) is an odd function with period π.
The combination of periodicity with symmetry or antisymmetry leads to further relationships between the trigonometric functions. For example, from Figures 18 and 19 you should be able to see that the following relationships hold true:
sin(θ) = sin(π − θ) = −sin(π + θ) = −sin(2π−θ)(Eqn 21)
andcos(θ) = −cos(π − θ) = −cos(π + θ) = cos(2π − θ)(Eqn 22)
Less apparent, but just as true are the following relationships
cos(θ) = sin(π/2 − θ) = sin(π/2 + θ) = −sin(3π/2 − θ) = −sin(3π/2 + θ)(23)
andsin(θ) = cos(π/2 − θ) = −cos(π/2 + θ) = −cos(3π/2 − θ) = cos(3π/2 + θ)(24)
Thanks to periodicity, all of these relationships (Equations 21 to 24) remain true if we replace any of the occurrences of θ by (θ + 2nπ), where n is any integer.
It is quite clear from Figures 18 and 19 that there must be a simple relationship between the functions sin θ and cos θ0; the graphs have exactly the same shape, one is just shifted horizontally relative to the other through a distance π/2. Equations 23 and 24 provide several equivalent ways of describing this relationship algebraically, but perhaps the simplest is that given by the first and third terms of Equation 23:
i.e. sin(θ + π/2) = cos(θ)
Clearly, adding a positive constant, π/2, to the argument of the function has the effect of shifting the graph to the left by π/2. In crude terms, the addition has boosted the argument and makes everything happen earlier (i.e. further to the left).
Simple as it is, this is just one example of an important general principle that has many physical applications and deserves special emphasis.
Adding any positive constant ϕ to θ has the effect of shifting the graphs of sin θ and cos θ horizontally to the left by ϕ, leaving their overall shape unchanged. Similarly, subtracting ϕ shifts the graphs to the right. The constant ϕ is known as the phase constant.
Since the addition of a phase constant shifts a graph but does not change its shape, all graphs of sin(θ + ϕ) and cos(θ + ϕ) have the same ‘wavy’ shape, regardless of the value of ϕ: any function that gives a curve of this shape, or the curve itself, is said to be sinusoidal.
✦ Sketch the graphs of sin(θ) and sin(θ + ϕ) where ϕ = π/6.
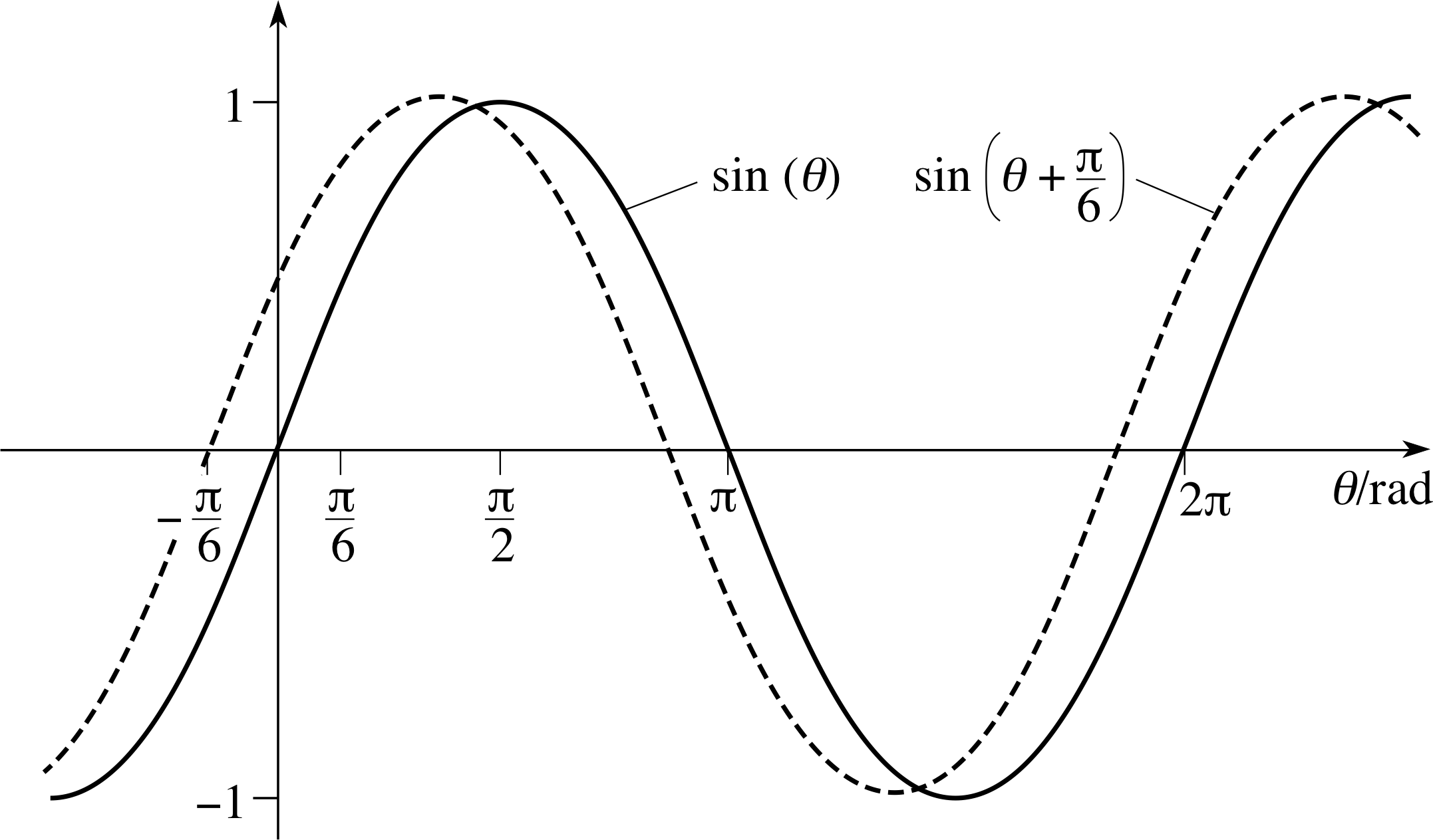
Figure 24 Graphs of sin(θ) and sin(θ + π/6).
✧ See Figure 24.
Question T13
Use the terms periodic, symmetric or antisymmetric and sinusoidal, where appropriate, to describe the function tan(θ). What is the relationship between the graphs of tan(θ) and tan(ϕ + θ)?
Answer T13
The function tan(θ) is antisymmetric, that is tan(θ) = −tan(−θ); it is periodic with period π; it is not sinusoidal. The graph of tan(θ + ϕ) has the same shape as that of tan(θ), but is shifted to the left by ϕ.
3.3 Inverse trigonometric functions
A problem that often arises in physics is that of finding an angle, θ, such that sin θ takes some particular numerical value. For example, given that sin θ = 0.5, what is θ? You may know that the answer to this specific question is θ = 30° (i.e. π/6); but how would you write the answer to the general question, what is the angle θ such that sin θ = x? The need to answer such questions leads us to define a set of inverse trigonometric functions that can ‘undo’ the effect of the trigonometric functions. These inverse functions are called arcsine, arccosine and arctangent (usually abbreviated to arcsin(x), arccos(x) and arctan(x)) and are defined so that:
arcsin(sin θ) = θ − π/2 ≤ θ ≤ π/2(25a)
arccos(cos θ) = θ 0 ≤ θ ≤ π(25b)
arctan(tan θ) = θ −π/2 < θ < π/2(25c) i
Thus, since sin(π/6) = 0.5, we can write arcsin(0.5) = π/6 (i.e. 30°), and since tan(π/4) = 1, we can write arctan(1) = π/4 (i.e. 45°). Note that the argument of any inverse trigonometric function is just a number, whether we write it as x or sin θ or whatever, but the value of the inverse trigonometric function is always an angle. Indeed, an expression such as arcsin(x) can be crudely read as ‘the angle whose sine is x.’ Notice that Equations 25a–c involve some very precise restrictions on the values of θ, these are necessary to avoid ambiguity and deserve further discussion.
Looking back at Figures 18, 19 and 20, you should be able to see that a single value of sin(θ), cos(θ) or tan(θ) will correspond to an infinite number of different values of θ. For instance, sin(θ) = 0.5 corresponds to θ = π/6, 5π/6, 2π + (π/6), 2π + (5π/6), and any other value that may be obtained by adding an integer multiple of 2π to either of the first two values. To ensure that the inverse trigonometric functions are properly defined, we need to guarantee that each value of the function’s argument gives rise to a single value of the function. The restrictions given in Equations 25a–c do ensure this, but they are a little too restrictive to allow those equations to be used as general definitions of the inverse trigonometric functions since they prevent us from attaching any meaning to an expression such as arcsin(sin(7π/6)).
In fact, the general definitions of the inverse trigonometric functions are as follows:
If sin(θ) = x, where −π/2 ≤ θ ≤ π/2 and −1 ≤ x ≤ 1(26a)
then arcsin(x) = θ
If cos(θ) = x, where 0 ≤ θ ≤ π and −1 ≤ x ≤ 1(26b)
then arccos(x) = θ
If tan(θ) = x, where −π/2 < θ < π/2(26c)
then arctan(x) = θ i
The graphs of these three inverse trigonometric functions are given in Figure 25.
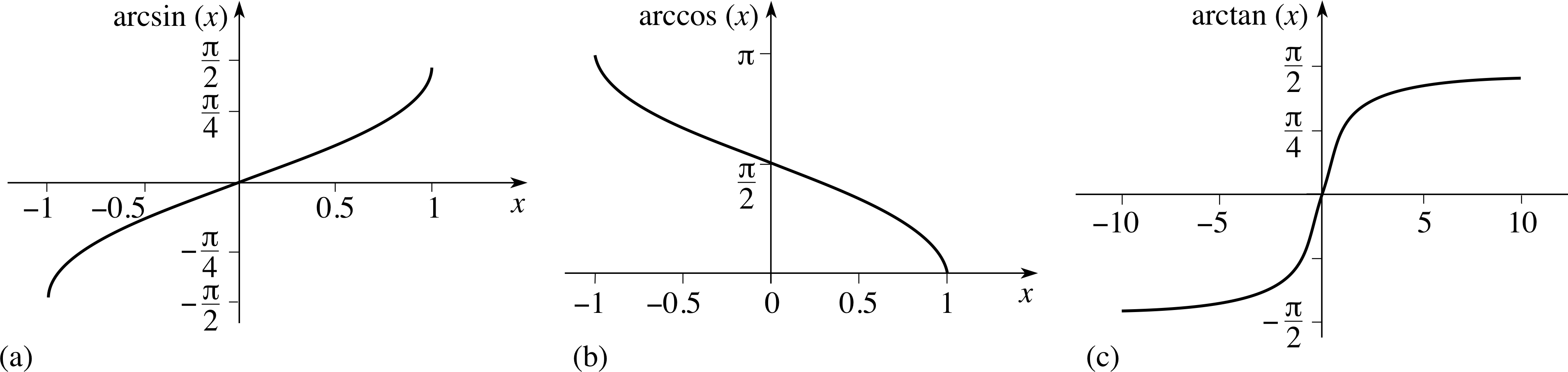
Figure 25 (a) The graph of arcsin(x). (b) The graph of arccos(x). (c) The graph of arctan(x).
Equations 26a–c look more intimidating than Equations 25a–c, but they embody the same ideas and they have the advantage of assigning meaning to expressions such as arcsin(sin(7π/6)).
arcsin(sin θ) = θ −π/2 ≤ θ ≤ π/2(Eqn 25a)
arccos(cos θ) = θ 0 ≤ θ ≤ π(Eqn 25b)
arctan(tan θ) = θ −π/2 < θ < π/2(Eqn 25c)
If sin(θ) = x, where −π/2 ≤ θ ≤ π/2 and −1 ≤ x ≤ 1 then arcsin(x) = θ(Eqn 26a)
If cos(θ) = x, where 0 ≤ θ ≤ π and −1 ≤ x ≤1 then arccos(x) = θ(Eqn 26b)
If tan(θ) = x, where −π/2 < θ < π/2 then arctan(x) = θ(Eqn 26c)
✦ What is arcsin(sin(7π/6))?
✧ sin(7π/6) = −0.5, so arcsin(sin(7π/6)) = arcsin(−0.5) = −π/6.
Inverse trigonometric functions can be found on all ‘scientific’ calculators, often by using the trigonometric function keys in combination with the inverse key. The answer will be given in either radians or degrees, depending on the mode selected on the calculator, and will always be in the standard angular ranges given in Equations 26a–c.
When dealing with functions of any kind, physicists traditionally pay scant regard to such mathematical niceties as domains (ranges of allowed argument values) and codomains (ranges of allowed function values). This attitude persists because it rarely leads to error. However, care is needed when dealing with inverse trigonometric functions. If you know the sin, cos or tan of an angle and you want to find the angle itself, the inverse trigonometric functions will give you an answer. But that answer will lie in one of the standard angular ranges and may not be the particular answer you are seeking. You will have to remember that there are other possible answers, your calculator is unlikely to warn you!
✦ Earlier, arcsin(x) was crudely interpreted as ‘the angle with a sine of x.’ What would be a more accurate interpretation?
✧ ‘The angle in the range −π/2 to π/2 with a sine of x.’
Question T14
(a) Use a calculator to find arcsin(0.65) both in radians and in degrees.
(b) Using information from earlier in this module, determine the values of:
arctan(1), $\arcsin(\sqrt{3\os}/2$), and $\arccos(1/\sqrt{2\os}$)
Answer T14
(a) With a calculator in degree mode, arcsin(0.65) = 40.5°, and in radian mode, arcsin(0.65) = 0.708 rad.
| θ/radians | sin θ | cos θ | tan θ |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| $\pi/6$ | 1/2 | $\sqrt{3\os}/2$ | $1/\sqrt{3\os}$ |
| $\pi/4$ | $1/\sqrt{2\os}$ | $1/\sqrt{2\os}$ | 1 |
| $\pi/3$ | $\sqrt{3\os}/2$ | 1/2 | $\sqrt{3\os}$ |
| $\pi/2$ | 1 | 0 | undefined |
| $2\pi/3$ | $\sqrt{3\os}/2$ | −1/2 | −$\sqrt{3\os}$ |
| $3\pi/4$ | $1/\sqrt{2\os}$ | −$1/\sqrt{2\os}$ | −1 |
| $5\pi/6$ | 1/2 | −$\sqrt{3\os}/2$ | −$1/\sqrt{3\os}$ |
| $\pi$ | 0 | −1 | 0 |
| $7\pi/6$ | −1/2 | −$\sqrt{3\os}/2$ | $1/\sqrt{3\os}$ |
| $5\pi/4$ | −$1/\sqrt{2\os}$ | −$1/\sqrt{2\os}$ | 1 |
| $4\pi/3$ | −$\sqrt{3\os}/2$ | −1/2 | $\sqrt{3\os}$ |
| $3\pi/2$ | −1 | 0 | undefined |
| $5\pi/3$ | −$\sqrt{3\os}/2$ | 1/2 | −$\sqrt{3\os}$ |
| $7\pi/4$ | −$1/\sqrt{2\os}$ | $1/\sqrt{2\os}$ | −1 |
| $11\pi/6$ | −1/2 | $\sqrt{3\os}/2$ | −$1/\sqrt{3\os}$ |
| $2\pi$ | 0 | 1 | 0 |
(b) Using Table 3 and/or Figures 10 and 11:
tan(π/4) = 1, so arctan(1) = π/4 (i.e. 45°)
sin(π/3) = $\sqrt{3\os}/2$ and so arcsin($\sqrt{3\os}/2$) = π/3 (i.e. 60°)
cos(π/4) = $1/\sqrt{2\os}$, therefore arccos(1/2) = π/4 (i.e. 45°)

Figure 11 An equilateral triangle.

Figure 10 A right–angled triangle with two equal length sides, an isosceles triangle.
It is possible to define a set of inverse reciprocal trigonometric functions in much the same way that we defined the inverse trigonometric functions. These functions are called arccosecant, arcsecant and arccotangent, and are usually abbreviated to arccosec, arcsec and arccot. Their definitions are:
If cosec(θ) = x
where either 0 < θ ≤ π/2 and x ≥ 1
or −π/2 ≤ θ < 0 and x ≤ −1
then arccosec(x) = θ
If sec(θ) = x
where either 0 ≤ θ < π/2 and x ≥ 1
or π/2 < θ ≤ π and x ≤ −1
then arcsec(x) = θ
If cot(θ) = x
where−π/2 < θ < π/2
and −∞ < x < +∞
then arccot(x) = θ i
The corresponding graphs are given in Figure 26.

Figure 26 The graphs of (a) arccosec(x), (b) arcsec(x), and (c) arccot(x).
Finally, a few words of warning. The following notation is sometimes used to represent the inverse trigonometric functions:
sin−1 (x) for arcsin(x), cos−1 (x) for arccos(x) and tan−1 (x) for arctan(x)
Notice that there is no connection with the positive index notation used to denote powers of the trigonometric functions (for example, using sin2(θ) to represent (sin(θ))2. Also notice that although this notation might make it appear otherwise, there is still a clear distinction between the inverse trigonometric functions and the reciprocal trigonometric functions.
Sosin−1 [sin(θ)] = θ
butcosec(θ) × sin(θ) = 1
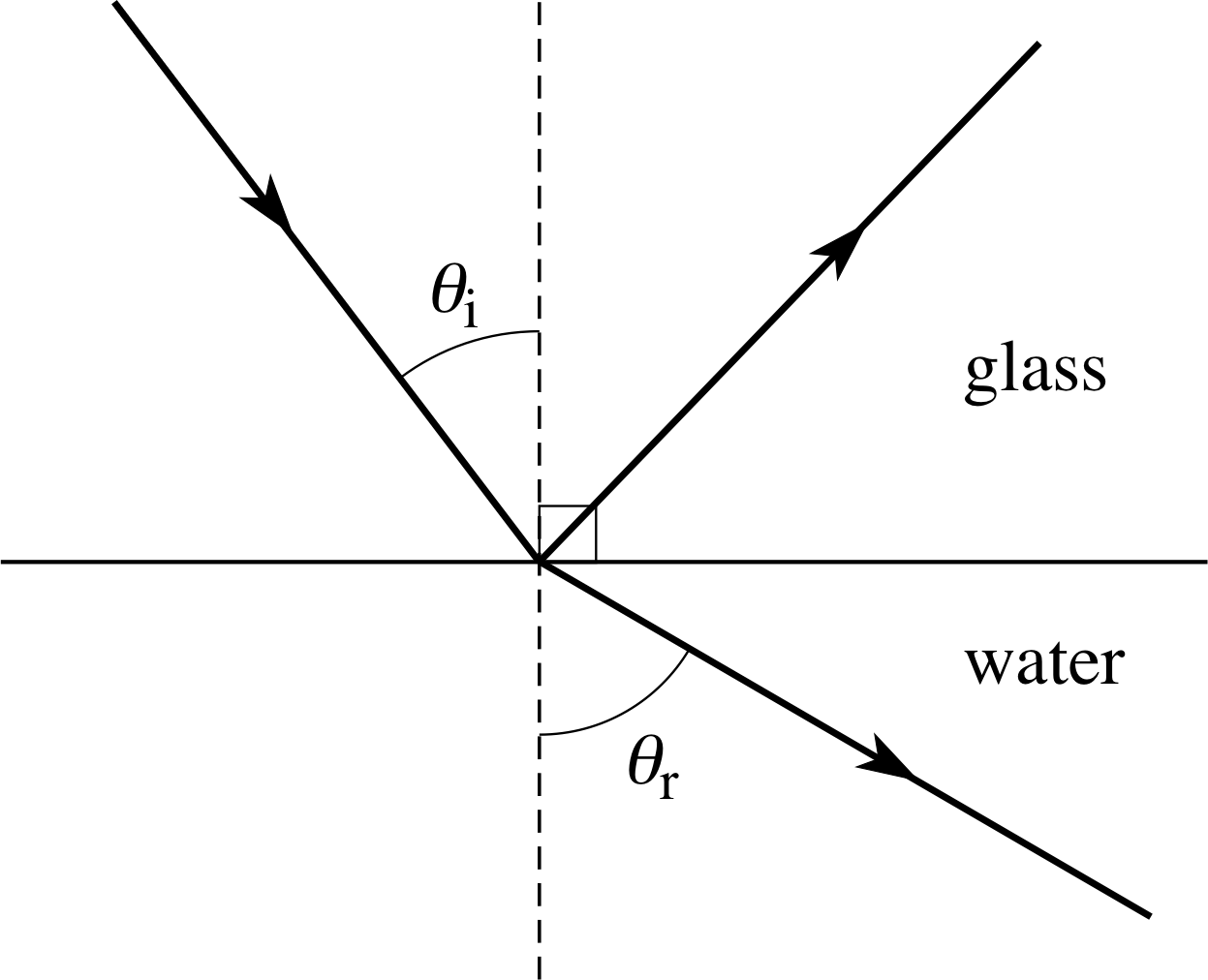
Figure 27 See Question T15.
Question T15
Figure 27 shows a ray of light travelling from glass to water. The angles, θi and θr are related by Snell’s law:
μgsin θi = μwsin θr
where μg and μw are constants.
(a) If the measured values of the angles are θi = 50.34° and θr = 60.00°, what is the value of μg/μw?
(b) The critical angle, θc, is defined as the value of θi for which θr is 90°. Use your result for μg/μw to determine the critical angle for this glass–water interface.
Answer T15
(a) Using Snell’s law we find:
$\dfrac{\mu_{\rm g}}{\mu_{\rm w}} = \dfrac{\theta_{\rm r}}{\theta_{\rm i}} = \dfrac{\sin(60°)}{\sin(50.34°)} = 1.124934 = 1.12~~ \text{(to two decimal places)}$
(b) Again using Snell’s law, we have:
$\sin\theta_{\rm i} = \dfrac{\sin(90°)}{1.124934}$
and so
$\theta_{\rm c} = \arcsin\left(\dfrac{1}{1.124\,934}\right) = 62.7°$ (to one decimal place)
Notice that if you use the approximate value μg/μw = 1.12 in (b) you obtain sin θi = 1/1.12 and θc = 63.2°. To avoid such rounding errors, you should always work to a higher degree of precision (i.e. keep more figures) at intermediate stages than will be justified in your final answer, and round to a sensible number of figures only at the last step. Also notice that, although there are an infinite number of solutions to the equation for θc, only the one given is physically admissible.
4 Trigonometric rules and identities
In this section we first extend the discussion in Section 2 to derive relationships between sides and angles of any arbitrary triangle, and then add to the discussion of Subsection 2.3Subsections 2.3 and Subsection 3.23.2 by introducing some further relationships involving trigonometric functions.
Study comment It is unlikely that you will be required to reproduce the derivations given in this section. However, you should try to ensure that you understand each step, since that will reinforce your understanding and experience of trigonometric functions.
4.1 The sine and cosine rules

Figure 28 Construction used in deriving the sine and cosine rules.
In Section 2, you saw that the sides and angles of a right–angled triangle are related by Pythagoras’s theorem and by the trigonometric ratios. These relationships are in fact special cases of relationships that apply to any triangle. To derive these general relationships, consider Figure 28, where ABC is any triangle, with sides a, b and c. BD is drawn perpendicular to AC and has length p. We have called the length of AD, q, which means that the length of DC is b − q.
From Figure 28
$\sin\hat {\rm A} = \dfrac pc \quad\text{so}\quad p = c \sin\hat {\rm A}$
$\sin\hat {\rm C} = \dfrac pa \quad\text{so}\quad p = a \sin\hat {\rm C}$
and therefore $a\sin\hat {\rm C} = c\sin\hat{\rm A}\quad\text{or}\quad\dfrac{a}{\sin\hat {\rm A}} = \dfrac{c}{\sin\hat {\rm C}}$
Similarly, by drawing a perpendicular from C to AB,
$\dfrac{a}{\sin\hat {\rm A}} = \dfrac{b}{\sin\hat {\rm B}}$
By combining the two previous equations we obtain
$\dfrac{a}{\sin\hat {\rm A}} = \dfrac{b}{\sin\hat {\rm B}} = \dfrac{c}{\sin\hat {\rm C}}$(27)
which is called the sine rule.
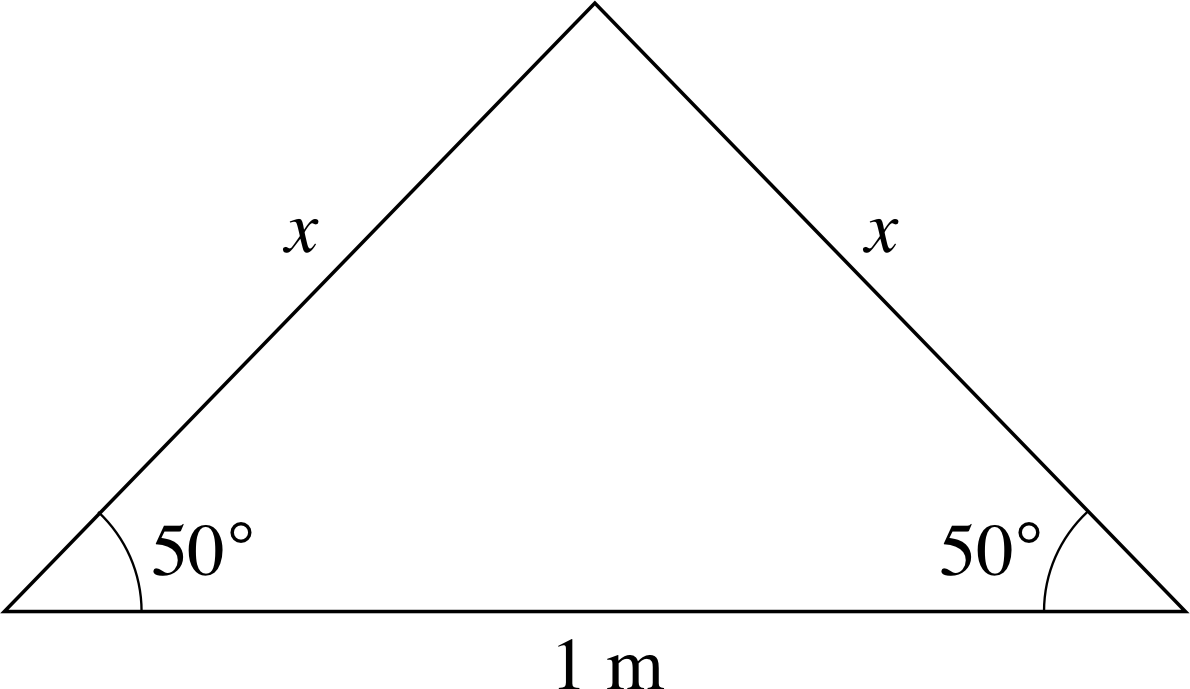
Figure 29 A triangle with two equal sides of unknown length x.
✦ What is the length, x, in Figure 29?
✧ The remaining angle is 180° − 2 × 50° = 80°, hence
$\dfrac{x}{\sin(50°} = \dfrac{1\,{\rm m}}{\sin(80°}$
and so
$x = \rm \dfrac{1\,m\times\sin(50°)}{\sin(80°)} \approx 0.778\,m$

Figure 28 Construction used in deriving the sine and cosine rules.
There is also an important relationship between the three sides of a general triangle and the cosine of one of the angles. i
To derive this rule, consider Figure 28 again. ABD is a right–angled triangle so Pythagoras’s theorem gives
c2 = q2 + p2
In a similar way, since BCD is a right–angled triangle, we have
a2 = p2 + ( b − q )2
Eliminating p2 between these two simultaneous equations gives us:
a2 = (c2 − q2) + (b − q)2
which we can simplify by expanding the bracket on the right–hand side
a2 = c2 − q2 + b2 − 2bq + q2 = c2 + b2 − 2bq
But q = ccos A^ and so
a2 = b2 + c2 − 2bc cos A^(28)
which is called the cosine rule. i
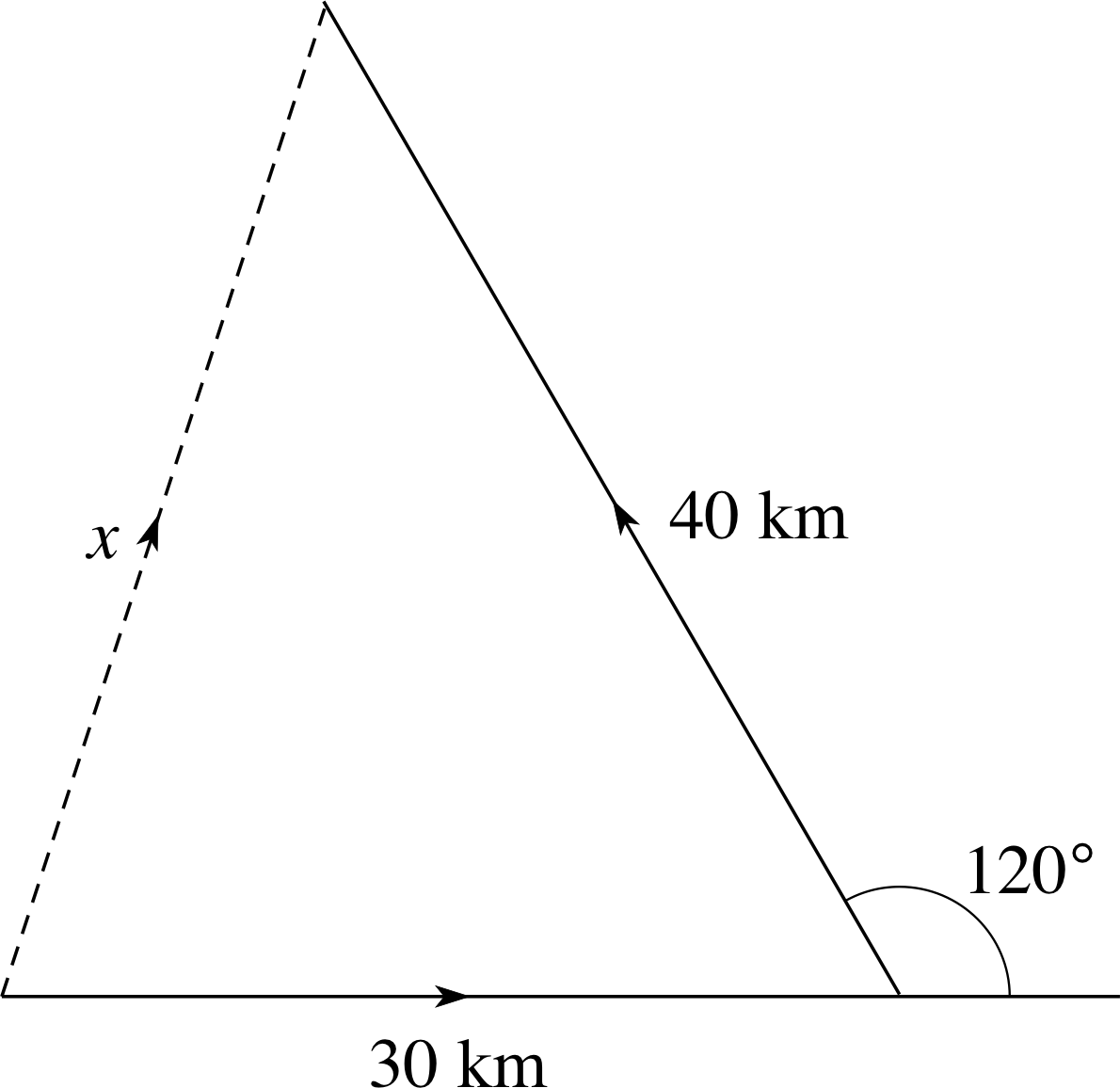
Figure 30 See Question T16.
Question T16
Figure 30 shows the path of a ship that sailed 30 km due east, then turned through 120° and sailed a further 40 km. Calculate its distance x ‘as the crow flies’ from the starting point.
Answer T16
Using the cosine rule (Equation 28):
a2 = b2 + c2 − 2bc cos A^$(Eqn 28)
x2 = (40 km)2 + (30 km)2 − 2 × 40 km × 30 km × cos(180° − 120°)
x2 = [2500 km2 − 2400 cos(60°)] km2 = 1300 km2
and hence: x = $\sqrt{1300\os}$ km = 36.1 km
Question T17
One of the interior angles of a triangle is 120°. If the sides adjacent to this angle are of length 4 m and 5 m, use the cosine rule to find the length of the side opposite the given angle.
Answer T17
Using the cosine rule (Equation 28):
a2 = b2 + c2 − 2bc cos A^(Eqn 28)
x2 = (4 m)2 + (5 m)2 − 2 × 4 m × 5 m × cos(120°)
x2 = 41 m2 − 40 cos(120°) m2 = 41 m2 + (40/2) m2 = 61 m2
and so:x = $\sqrt{61\os}$ m = 7.81 m
4.2 Trigonometric identities
A good deal of applicable mathematics is concerned with equations. It is generally the case that these equations are only true when the variables they contain take on certain specific values; for example, 4x = 4 is only true when x = 1. However, we sometimes write down equations that are true for all values of the variables, such as (x + 1)2 = x2 + 2x + 1. Equations of this latter type, i.e. ones that are true irrespective of the specific values of the variables they contain, are properly called identities. i
There are a great many trigonometric identities, i.e. relationships between trigonometric functions that are independent of the specific values of the variables they involve. These have various applications and it is useful to have a list of them for easy reference. The most important are given below – you have already met the first seven (in slightly different forms) earlier in the module and others occur at various points throughout FLAP. Note that α and β may represent any numbers or angular values, unless their values are restricted by the definitions of the functions concerned.
The symmetry relations: i
sin(−α) = −sin(α)(Eqn 18)
cos(−α) = cos(α)(Eqn 19)
tan(−α) = −tan(α)(Eqn 20)
The basic identities: i
$\tan(\alpha) = \dfrac{\sin(\alpha)}{\cos(\alpha)}$(Eqn 8)
sin2 (α) + cos2 (α) = 1(Eqn 9)
$\cot(\alpha) = \dfrac{\cosec\,(\alpha)}{\sec(\alpha)}$(Eqn 16)
$1+\tan^2(\alpha) = \sec^2(\alpha)~~~\text{for}~\alpha \ne (2n+1)\dfrac{\pi}{2}$(Eqn 17)
cot2(α) + 1 = cosec2(α)
The addition formulae: i
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)(29)
cos(α + β) = cos(α) cos(β) − sin(α) sin(β)(30)
$\tan(\alpha+\beta) = \dfrac{\tan(\alpha)+\tan(\beta)}{1-\tan(\alpha)\tan(\beta)}$(31)
$\text{for}~\alpha,~\beta~\text{and}~ (\alpha+\beta) \ne (2n+1)\dfrac{\pi}{2}$
The double–angle formulae: i
sin(2α) = 2 sin(α) cos(α)(32)
cos(α) = cos2 (α) − sin2 (α)(33)
cos(2α) = 1 − sin2 (α)(34)
cos(2α) = 2 cos2(α) − 1(35)
tan(2α) = 2 tan(α)(36)
$\text{for}~\alpha~\text{and}~2\alpha \ne (2n+1)\dfrac{\pi}{2}$
The half–angle formulae: i
$\cos^2(\alpha/2) = \dfrac12[1 + \cos(\alpha)]$(37)
$\sin^2(\alpha/2) = \dfrac12[1 - \cos(\alpha)]$(38)
and if t = tan(α/2) then, provided tan(α/2) is defined:
$\sin(\alpha) = \dfrac{2t}{1+t^2}$(39)
$\cos(\alpha) = \dfrac{1-t^2}{1+t^2}$(40)
$\tan(\alpha) = \dfrac{2t}{1-t^2} \quad\text{for }\alpha \ne (2n+1)\dfrac{\pi}{2}$(41)
The sum formulae: i
$\sin(\alpha)+\sin(\beta) = 2\sin\left(\dfrac{\alpha+\beta}{2}\right)\cos\left(\dfrac{\alpha-\beta}{2}\right)$(42)
$\sin(\alpha)-\sin(\beta) = 2\cos\left(\dfrac{\alpha+\beta}{2}\right)\sin\left(\dfrac{\alpha-\beta}{2}\right)$(43)
$\cos(\alpha)+\cos(\beta) = 2\cos\left(\dfrac{\alpha+\beta}{2}\right)\cos\left(\dfrac{\alpha-\beta}{2}\right)$(44)
$\cos(\alpha)-\cos(\beta) = -2\sin\left(\dfrac{\alpha+\beta}{2}\right)\sin\left(\dfrac{\alpha-\beta}{2}\right)$(45)
The product formulae: i
2 sin(α) cos(β) = sin(α + β) + sin(α − β)(46)
2 cos(α) sin(β) = sin(α + β) − sin(α − β)(47)
2 cos(α) cos(β) = cos(α + β) + cos(α − β)(48)
−2 sin(α) sin(β) = cos(α + β) − cos(α − β)(49)
As indicated by the marginal notes, some of these identities can be derived straightforwardly from others. Rather than deriving the unexplained identities, one by one, we will consider just one example in full and allow it to serve as an example.
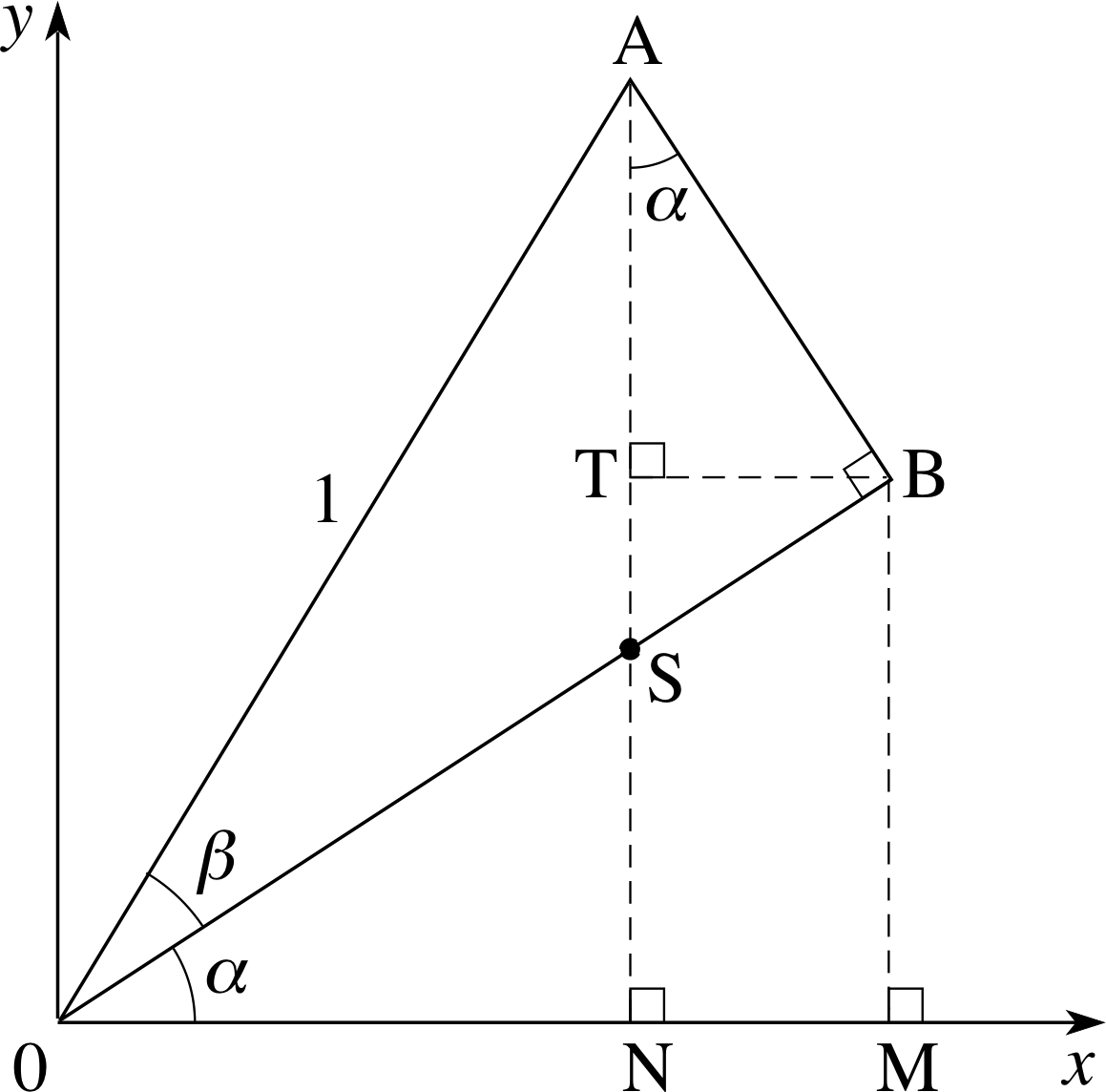
Figure 31 Construction used in deriving Equation 29.
To derive Equation 29, the addition formula for sin(α + β), we use Figure 31.
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)(Eqn 29)
The line OB is at an angle, α, to the x–axis. OA has unit length and is at an angle, β, to OB. The angle AB^O is a right angle. (This is what fixes the length of OB, which is not of unit length.) It turns out to be useful to construct lines AN, BM and TB, such that AN^O, BM^O and BT^A, are all right angles. If we let S represent the point of intersection of OB and AN, then OS^N, and consequently AS^B, are equal to α − 90°. But SAB is a right–angled triangle, so TA^B is equal to α.
Since OA has unit length, the y–coordinate of the point, A, is sin(α + β) and from the diagram we have:
sin(α + β) = NT + TA(50)
To find TA, first consider the triangle, OAB. Since OA = 1, we have:
AB = sin(β)(51)
Next, considering triangle TAB, we have
$\cos(\alpha) = \dfrac{\rm{TA}}{\rm{AB}} = \dfrac{\rm{TA}}{\sin\beta}$(52)
Therefore,
TA = cos(α) sin(β)(53)
To find NT, we start by considering triangle OAB, obtaining
OB = cos(β)(54)
Next, consideration of triangle OBM gives
$\sin(\alpha) = \dfrac{\rm{MB}}{\rm{OB}} = \dfrac{\rm{NT}}{\cos\beta}$(55)
Therefore,
NT = sin(α) cos(β)(56)
We can now substitute in Equation 50,
sin(α + β) = NT + TA(Eqn 50)
using Equations 53 and 56 to get the desired result:
TA = cos(α) sin(β)(Eqn 53)
NT = sin(α) cos(β)(Eqn 56)
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)(Eqn 29) i
The first of the double–angle identities, Equation 32, can be obtained by putting β = α in Equation 29: i
sin(α + α) = 2 sin(α) cos(α)
Therefore,
sin(2α) = 2 sin(α) cos(α)(Eqn 32)
| θ/radians | sin θ | cos θ | tan θ |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| $\pi/6$ | 1/2 | $\sqrt{3\os}/2$ | $1/\sqrt{3\os}$ |
| $\pi/4$ | $1/\sqrt{2\os}$ | $1/\sqrt{2\os}$ | 1 |
| $\pi/3$ | $\sqrt{3\os}/2$ | 1/2 | $\sqrt{3\os}$ |
| $\pi/2$ | 1 | 0 | undefined |
| $2\pi/3$ | $\sqrt{3\os}/2$ | −1/2 | −$\sqrt{3\os}$ |
| $3\pi/4$ | $1/\sqrt{2\os}$ | −$1/\sqrt{2\os}$ | −1 |
| $5\pi/6$ | 1/2 | −$\sqrt{3\os}/2$ | −$1/\sqrt{3\os}$ |
| $\pi$ | 0 | −1 | 0 |
| $7\pi/6$ | −1/2 | −$\sqrt{3\os}/2$ | $1/\sqrt{3\os}$ |
| $5\pi/4$ | −$1/\sqrt{2\os}$ | −$1/\sqrt{2\os}$ | 1 |
| $4\pi/3$ | −$\sqrt{3\os}/2$ | −1/2 | $\sqrt{3\os}$ |
| $3\pi/2$ | −1 | 0 | undefined |
| $5\pi/3$ | −$\sqrt{3\os}/2$ | 1/2 | −$\sqrt{3\os}$ |
| $7\pi/4$ | −$1/\sqrt{2\os}$ | $1/\sqrt{2\os}$ | −1 |
| $11\pi/6$ | −1/2 | $\sqrt{3\os}/2$ | −$1/\sqrt{3\os}$ |
| $2\pi$ | 0 | 1 | 0 |
✦ Use the addition identities and values from Table 3 to calculate the exact value of sin 75°.
✧ From Equation 29,
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)(Eqn 29)
sin 75° = sin(45° + 30°) = sin 45° cos 30° + cos 145° sin 30° i
sin 75° $ = \dfrac{1}{\sqrt{2\os}} \times \dfrac{\sqrt{3\os}}{2} + \dfrac{1}{\sqrt{2\os}} \times \dfrac{\sqrt{1\os}}{2} = \dfrac{1+\sqrt{3\os}}{2\sqrt{2\os}}$
Question T18
Derive the identity given in Equation 33,
cos(2α) = cos2(α) − sin2(α)(Eqn 33)
Answer T18
cos(α + β) = cos(α) cos(β) − sin(α) sin(β)(Eqn 30)
Setting α = β in Equation 30 we get:
cos(2α) = cos2 (α) − sin2 (α)
Question T19
Use Equation 34,
cos(2α) = 1 − 2 sin2 (α)(Eqn 34)
to find the exact value of sin(15°).
Answer T19
cos(2α) = 1 − 2 sin2 (α)(Eqn 34)
Let α = 15° then, from Equation 34:
cos(30°) = 1 − 2 sin2 (15°) = $\dfrac{\sqrt{3\os}}{2}$
so that2 sin 2 (15°) = $\dfrac{2-\sqrt{3\os}}{2}$
and therefore sin(15°) = $\dfrac{\sqrt{2-\sqrt{3\os}}}{2}$
Question T20
A feather trapped on the front of a loudspeaker moves back and forth whenever the speaker is in use. When a certain signal is played through the speaker, the position of the feather at time t is given by x (t) = A cos(ωt + ϕ1), where A, ω and ϕ1 are constants. A second similar signal causes a motion described by x (t) = A cos(ωt + ϕ2), where ϕ2 is another constant. Using an appropriate trigonometric identity, find a compact expression describing the motion x (t) = Acos(ωt + ϕ1) + Acos(ωt + ϕ2) that results from relaying the two signals simultaneously.
Answer T20
$\cos(\alpha) + \cos(\beta) = 2\cos\left(\dfrac{\alpha+\beta}{2}\right)\cos\left(\dfrac{\alpha-\beta}{2}\right)$(Eqn 44)
Using Equation 44 with α = ωt + ϕ1 and β = ωt + ϕ2, we find
$x(t)=2A\cos\left(\dfrac{\omega t+\phi_1-\omega t -\phi_2}{2}\right)\cos\left(\dfrac{\omega t +\phi_1+\omega t +\phi_2}{2}\right)$(Eqn 44)
so$x(t)=2A\cos\left(\dfrac{\phi_1-\phi_2}{2}\right)\cos\left(\omega t\dfrac{\phi_1+\phi_2}{2}\right)$
5 Closing items
5.1 Module summary
- 1
-
Angles are usually measured in Subsection 2.1degrees or Subsection 2.1radians. An angle of 180° is equivalent to π rad.
- 2
-
The side opposite the Subsection 2.2right angle in a right–angled triangle is called the hypotenuse.
- 3
-
Pythagoras’s theorem states that the square of the hypotenuse in a right–angled triangle is the sum of the squares of the other two sides. (The converse is also true.)
- 4
-
For a right–angled triangle, the Subsection 2.3trigonometric ratios are:
$\sin\theta = \dfrac{\text{opposite}}{\text{hypotenuse}}$(Eqn 5)
$\cos\theta = \dfrac{\text{adjacent}}{\text{hypotenuse}}$(Eqn6)
$\tan\theta = \dfrac{\text{opposite}}{\text{adjacent}}$(Eqn 7) i
- 5
-
The Subsection 2.4reciprocal trigonometric ratios are:
$\cosec\,\theta = \dfrac{1}{\sin\theta} \quad\,\text{provided }\sin\theta \ne 0$(Eqn 10)
$\sec\theta = \dfrac{1}{\cos\theta} \quad\quad\text{provided }\cos\theta \ne 0$(Eqn 11)
$\cot \theta = \dfrac{1}{\tan\theta} \quad\quad\text{provided }\tan\theta \ne 0$(Eqn 12)
- 6
-
For a small angle θ, cos θ ≈ 1
and sin θ ≈ tan θ ≈ θ/rad
- 7
-
The sides and angles of a general triangle are related by
the Subsection 4.1sine rule:
$\dfrac{a}{\sin\hat A}=\dfrac{b}{\sin\hat B}=\dfrac{c}{\sin\hat C}$(Eqn 27)
and the cosine rule:
$a^2 = b^2 + c^2- 2bc\cos\hat A$(Eqn 28)
- 8
-
The Subsection 3.1trigonometric functions generalize the trigonometric ratios; sin(θ) and cos(θ) are periodic functions (with period 2π) and are defined for any value of θ. The function tan(θ) is a periodic function (with period π) and is defined for all values of θ except odd multiples of π/2. The reciprocal trigonometric functions generalize the reciprocal trigonometric ratios in a similar way.
- 9
-
The Subsection 3.3inverse trigonometric functions; arcsin(x), arccos(x) and arctan(x) are defined as follows:
If sin(θ) = x, where −π/2 ≤ θ ≤ π/2 and −1 ≤ x ≤ 1 then arcsin(x) = θ(Eqn 26a)
If cos(θ) = x, where 0 ≤ θ ≤ π and −1 ≤ x ≤1 then arccos(x) = θ(Eqn 26b)
If tan(θ) = x, where −π/2 < θ < π/2 then arctan(x) = θ(Eqn 26c)
The inverse reciprocal trigonometric functions may be defined in a similar way.
- 10
-
There are a large number of Subsection 4.2trigonometric identities, such as
sin2(α) + cos2(α) = 1(Eqn 9)
The most important are listed in Subsection 4.2 of this module.
5.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Given an angle measured in degrees express its value in radians, and vice versa.
- A3
-
Use Pythagoras’s theorem.
- A4
-
Use trigonometric ratios, and their reciprocals, to solve geometrical problems.
- A5
-
Explain the sine and cosine rules and use these rules to solve problems involving general triangles.
- A6
-
Explain how the sine, cosine and tangent functions can be defined for general angles and sketch their graphs.
- A7
-
Recognize the most common identities for the trigonometric functions and apply them to solving mathematical and physical problems.
- A8
-
Use the inverse trigonometric functions to solve mathematical and physical problems.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
5.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions, each of which tests one or more of the Achievements.
Question E1 (A2)
Define the units commonly used in the measurement of angles.
Express the angles, −10°, 0°, 275°, in terms of radians.
Write the angles 2π/3 and π/4 in terms of degrees.
Answer E1
A degree is defined as 1/360 th of a rotation through a complete circle. A radian is the angle subtended at the centre of a circle by an arc of the circle that has an arc length equal to the radius of the circle. Since π radians is equivalent to 180°, we have:
−10° is equivalent to −(10π/180) radians = −0.175 radians
0° is equivalent to 0 radians
275° is equivalent to (275π/180) radians = 4.8 radians
2π/3 radians is equivalent to 2π/3 × 180°/π = 120°
π/4 radians is equivalent to π/4 × 180°/π = 45°
(Reread Subsection 2.1 if you had difficulty with this question.)
Question E2 (A3)
State Pythagoras’s theorem.
If the two shorter sides of a right–angled triangle have lengths of 4961 m and 6480 m, what is the length of the third side?
Answer E2
Pythagoras’s theorem states that the square of the hypotenuse in a right–angled triangle is the sum of the squares of the other two sides. If we call the hypotenuse x, then:
$x = \rm \sqrt{(4961\,m)^2 +(6480\,m)^2} = 8161\,m$
(Reread Subsection 2.2 if you had difficulty with this question.)
Question E3 (A4)
By drawing a suitable diagram, give definitions of the sine, cosine and tangent ratios.
A right–angled triangle has a hypotenuse of length 7 mm, and one angle of 55°. Determine the lengths of the other two sides.

Figure 8 The labelling of sides in a right–angled triangle.
Answer E3
Using the conventional notation (see Figure 8) the definitions are:
$\sin\theta = \dfrac{\text{opposite}}{\text{hypotenuse}}$(Eqn 5)
$\cos\theta = \dfrac{\text{adjacent}}{\text{hypotenuse}}$(Eqn6)
$\tan\theta = \dfrac{\text{opposite}}{\text{adjacent}}$(Eqn 7)
The side opposite the 55° angle has length 7.0 mm × sin(55°) = 5.7 mm.
The side adjacent to the 55° angle has length 7.0 mm × cos(55°) = 4.0 mm.
(Reread Subsection 2.3 if you had difficulty with this question.)
Question E4 (A5)
Two sides of a triangle have lengths 2 m and 3 m. If the angle between these two sides is 60°, find the length of the third side and find the remaining angles.
Answer E4
a2 = b2 + c2 − 2bc cos A^$(Eqn 28)
Using the cosine rule (Equation 28) with b = 2 m, c = 3 m and A^ = 60°, we find:
a2 = 22 + 32 − 2 × 2 × 3 × ½
and therefore $a = \sqrt{7\os}$ m.
The sine rule (Eqn 27),
$\dfrac{a}{\sin\hat {\rm A}} = \dfrac{b}{\sin\hat {\rm B}} = \dfrac{c}{\sin\hat {\rm C}}$(Eqn 27)
gives:$\dfrac{\sqrt{7\os}}{\sin 60°} = \dfrac{2}{\sin(\hat {\rm B})}$
and hence: $\sin(\hat {\rm B}) = \dfrac{2}{\sqrt{7\os}}\times \dfrac{\sqrt{3\os}}{2} = \sqrt{\dfrac{3\os}{7}}$
which implies that: B^ = 40.9°
Moreover, since the angles of a triangle add up to 180°, we also find: $\hat C$ = 180 − 60 − 40.9 = 79.1°.
(Reread Subsection 4.1 if you had difficulty with this question.)
Question E5 (A6)
Sketch the graphs of sin(θ), cos(θ) and tan(θ) for general values of θ.
Why is tan(θ) undefined when θ is an odd multiple of π/2?
Answer E5
See Figures 18, 19 and 20.

Figure 20 Graph of tan(θ).

Figure 18 Graph of sin(θ).

Figure 19 Graph of cos(θ).
From Equation 8,
$\tan\theta = \dfrac{\sin\theta}{\cos\theta}$(Eqn 8)
the function tan(θ) becomes infinite whenever cos(θ) = 0, that is whenever θ = (2n + 1)π/2 for any integer, n.
Looking at Figure 20, we see that approaching such values of θ from below, tan(θ) tends to +∞ and approaching from above, tan(θ) tends to −∞. Consequently, tan[(2n+1)π/2] is undefined.
(Reread Subsection 3.1Subsections 3.1 and Subsection 3.23.2 if you had difficulty with this question.)
Question E6 (A7)
Use Figure 10 and suitable trigonometric identities to show that:
$\sin(22.5°) = \sqrt{\dfrac{\sqrt{2\os}-1}{2\sqrt{2\os}}}$

Figure 10 A right–angled triangle with two equal length sides, an isosceles triangle.
Answer E6
From Figure 10 we obtain: $\cos(45°) = 1/\sqrt{2\os}$
We can rewrite Equation 34,
cos(2α) = 1 − 2 sin2 (α)(Eqn 34)
as: $\sin^2(\alpha) = \dfrac{1 - \cos(2\alpha)}{2}$
which gives: $\sin^2(22.5°) = \dfrac{1}{2}\left(1 - \dfrac{1}{\sqrt{2\os}}\right)$
Taking the positive square root (since we know that sin(θ) is positive for 0° < θ < 90°), we obtain:
$\sin(22.5°) = \sqrt{\dfrac{\sqrt{2\os}-1}{2\sqrt{2\os}}}$
(Reread Subsection 4.2 if you had difficulty with this question.)
Question E7 (A7)
Given that $\sin(60°) = \sqrt{3\os}/2$ and $\cos(60°) = 1/2$, use suitable trigonometric identities to find the exact values of sin(120°), cos(120°) and cot(2π/3) without using a calculator.
Answer E7
Using Equation 32,
sin(2α) = 2 sin(α) cos(α)(Eqn 32)
we have:
$\sin(120°) = 2\sin(60°)\cos(60°) = 2 \times \dfrac{\sqrt{3\os}}{2}\times\dfrac{1}{2} = \dfrac{\sqrt{3\os}}{2}$
Furthermore, using Equation 34,
cos(2α) = 1 − 2 sin2 (α)(Eqn 34)
we have:
$\cos(120°) = 1 - 2\sin(60°) = 1 - 2 \times \dfrac{3}{4} = -\dfrac{1}{2}$
But 2π/3 radians is equivalent to 2π/3 × 180/π =120°, so:
$\cot\dfrac{2\pi}{3}=\dfrac{\cos(120°)}{\sin(120°)}=-\dfrac{1}{2}\times \dfrac{2}{\sqrt{3\os}} = -\dfrac{1}{\sqrt{3\os}}$
(Reread Subsection 4.2 if you had difficulty with this question.)
Question E8 (A8)
Determine a general expression for all values of θ that satisfy the equation:
cot(θ) = 4/3
[Hint: Solve for −π/2 < θ < π/2 and then consider how tan(θ), and hence cot(θ), behaves for other angles.]
Answer E8
Since cot(θ) = 1/tan(θ), tan θ = 3/4 = 0.75. With a calculator set in radians mode, arctan(0.75) = 0.644. But tan(θ) is periodic, with a period π, so the complete solution is θ = 0.644 + nπ, where n is any integer.
In degree mode, arctan(0.75) = 36.9°, and the complete solution is θ = 36.9° + 180°n.
(Reread Subsection 3.2Subsections 3.2 and Subsection 3.33.3 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.