MATH 2.3: Conic sections |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
If you throw a stone, then to a good approximation, it follows a parabolic path. As a planet orbits the Sun it traces out a closed path in a plane, and this closed path is an ellipse. When an alpha–particleα–particle approaches the nucleus of an atom it undergoes a deflection, and the particle follows a hyperbolic path.
Parabolas, ellipses and hyperbolas are particular examples of a family of curves known as conic sections, for the very good reason that they can be obtained by taking a slice through a cone (or more precisely a double cone). The edge of the slice is called a conic section. We pursue this idea in Subsection 2.1, and then examine each of the major classes of conic section in turn in the subsequent subsections.
In Subsection 2.2Subsections 2.2 to Subsection 2.52.5 we study the circle, the parabola, the ellipse and finally the hyperbola. In each case our approach is very similar. First we introduce the equation of the curve in so–called standard form, which simply means that we choose the axes so that the equation of the curve turns out to be particularly simple. We investigate the tangents to the curve, and we consider parametric representations of the curve (this is particularly relevant to applications in physics). At the end of each subsection we consider particular properties of the curve under discussion; for example, an ellipse is a closed curve, i whereas, at a great distance from the origin, the points on a hyperbola approach one of two straight lines (called asymptotes).
In spite of their very different shapes, it turns out that the various forms of conic section have a great deal in common. In each case we introduce the polar form of the equation, and in Subsection 2.5 we show how this form of the hyperbola may be applied to a well known experiment in nuclear physics.
For the equation of a conic in standard form one or both of the coordinate axes are aligned with an axis of symmetry of the curve, and the origin of coordinates is placed at a point which ensures that the equation of the curve is particularly simple. In Subsection 3.1Subsections 3.1 and Subsection 3.23.2 we introduce the general equation of a conic, and consider the effect of moving the coordinate axes from the ‘standard position’. Finally in Subsection 3.3 we consider an application of the general form of the equation of a conic to electrostatics.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 4.1Module summary and the Subsection 4.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 4.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
(a) Find the radius and the coordinates of the centre of the circle x2 + y2 − 2x − 6y + 6 = 0.
(b) Find the coordinates of the points P and Q at which the line y = x/2 meets the circle x2 + y2 −8x + 6y −15 = 0. Also find the equation of the circle passing through P, Q and the point (1, 1).
(c) Find the equations of the tangents to the circle x2 + y2 = 25 which are parallel to the line 3x + 4y = 0.
Answer F1
(a) Rewrite the equation as ( x − 1)2 + ( y − 3)2 = 4; the radius is 2 and the coordinates of the centre are (1, 3).
(b) Substituting x/2 into the equation of the circle, we obtain x2 + (x2/4) − 8x + 3x − 15 = 0,
i.e. 5 x 2 − 20 x − 60 = 0, or x2 − 4x − 12 = 0, so that (x − 6)(x + 2) = 0.
When x = 6, y = 3 and when x = −2, y = −1, so that the coordinates of P and Q are (6, 3) and (−2, −1).
The equation of the required circle can be written as
x2 + y2 + 2Gx + 2Fy + C = 0
Since (1, 1) lies on the circle then 1 + 1 + 2 G + 2 F + C = 0
i.e.2 + 2G + 2F + C = 0(i)
Since (6, 3) lies on the circle then 36 + 9 + 12G + 6F + C = 0
i.e.45 + 12G + 6F + C = 0(ii)
Since (−2, −1) lies on the circle then 4 + 1 − 4G − 2F + C = 0
i.e.5 − 4G − 2F + C = 0(iii)
Equations (i), (ii) and (iii) can be solved simultaneously to find G, F and C. Probably the simplest method is
(ii) − (i) gives us 43 + 10G + 4F = 0
and (ii) − (iii) gives us 40 + 16G + 8F = 0
Then multiply the first of these equations by 2 and subtract to give G = −23/2, from which we find F = 18 and C = −15.
The equation of the circle is x2 + y2 − 23x + 36y − 15 = 0.
(c) The line $y=-\frac34 x + c$ is parallel to the given line. It meets the circle x2 + y2 = 25 where
$x^2+(-\frac34 x + c)^2 = 25$, i.e. $\dfrac{25}{16}x^2-\dfrac{3c}{2}x+c^2=0$
This quadratic equation has equal roots if
$\left(\dfrac{-3c}{2}\right)^2 = 4 \times \left(\dfrac{25}{16}\right) \times (c^2-25)$, i.e. $\dfrac{9c^2}{4}=\dfrac{25(c^2-25)}{4}$
so that $16c^2 -25 \times 25 = 0$, or $c^2=\left(\dfrac{25}{4}\right)^2$
hence c = ±25/4 and the equations of the tangent lines can be written
3x + 4y = 25 and 3x + 4y = −25
Question F2
(a) Find the equations of the tangents and normals to the parabola y2 = 16x at the points (16, 16) and (1, −4). If these tangents intersect at T and the normals intersect at R show that the line TR is parallel to the x–axis.
(b) Write down the parametric representation of a point on a parabola. Show that the tangents to a parabola at the ends of a chord which passes through the focus are perpendicular to each other.
Answer F2
(a) Comparing the equation of this given parabola to that of the standard form y2 = 4ax we see that a = 4. For the point (x2, y2) the tangent to the parabola at this point is y1y = 2a (x + x1). At the point (16, 16) this becomes 16y = 8 (x + 16) or 2y = x + 16. The normal has gradient −2 and passes through (16, 16); its equation is y − 16 = − 2 (x − 16) or 2x + y = 48.
Repeating the process for the point (1, −4) we obtain
for the tangent 2x + y + 2 = 0
and for the normal 2y = x − 9
The tangents meet at T = (−4, 6) and the normals at R = (21, 6).
Since T and R have the same y–coordinate the line joining them must be parallel to the x–axis.
(b) The parametric representation of a point on a parabola is (at2, 2at). The two points on the parabola at the ends of a chord can be represented as (at12,2at1)and (at22,2at2 ) The equation of the line joining them is
$\dfrac{y-2at_1}{2at_2-2at_1}=\dfrac{x-at_1^2}{at_2^2-at_1^2}$
which reduces to 2x − (t1 + t2)y + 2at1t2 = 0.
If this chord passes through the focus (a, 0) we have 2a + 2at1t2 = 0 so that t1t2 = −1.
The gradient of the tangent at the point (at2, 2at) is 1/t, so that the product of the gradients at the ends of the chord through the focus is 1/t1 × 1/t2 = 1 (t1t2) = −1. It follows that the tangents at the end points of a chord through the focus are perpendicular.
Question F3
(a) Show that the tangent to the ellipse x2/16 + y2/9 = 1 at the point (16/5, 9/5) makes equal intercepts with the coordinate axes.
(b) Find the equation of the tangent to the rectangular hyperbola xy = 12 at the point (3, 4).
Answer F3
(a) The tangent to the given ellipse at (x, y) is $\dfrac{x_1 x}{a^2}+{y_1 y}{b^2}=1$ where a = 4 and b = 3. For the point $(\frac{16}{5},\,\frac95$ this equation becomes $\dfrac{16}{5}\dfrac{x}{16} + \dfrac95\dfrac y9 = 1$ or x + y = 5. This line meets the x–axis (y = 0) where x = 5, and meets the y–axis (x = 0) where y = 5. Hence the intercepts are equal.
(b) From Equation 32,
t2y + x − 2tc = 0(Eqn 32)
the tangent to the hyperbola xy = c2 at the point (ct, c/t) is t2y + x − 2tc = 0.
Putting $c=2\sqrt{3\os}$ and $t=\sqrt{3\os}\big /2$, we have x = ct = $2\sqrt{3\os} \times \sqrt{3\os}\big /2$ = 3 and y = c/t = $\sqrt{3\os}\big /2 \times 2\big /\sqrt{3\os}$= 4 so that the tangent line at (3, 4) is
$\left(\dfrac{\sqrt{3\os}}{2}\right)^2y+x-2\left(\dfrac{\sqrt{3\os}}{2}\right)\left(2\sqrt{3\os}\right)=0$
which simplifies to give (3/4)y + x − 6 = 0 or 3y + 4x = 24.
1.3 Ready to study?
Study comment In order to study this module you will need to be familiar with the following terms: chord, coordinate axes, graph, normal, repeated roots of quadratic equations, straight lines, tangent_to_a_curvetangent. You should also be familiar with trigonometric identities (although the relevant formulae are repeated here). It would be helpful, but not essential, for you to have some knowledge of differentiation. If you are uncertain of any of these terms you can review them now by referring to the Glossary which will indicate where in FLAP they are developed. In addition, you will need to be familiar with SI units. The following questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
Calculate the distance between the points P(0, −2) and Q(3, 1) and the gradient of the line PQ.
Answer R1
$\rm{PQ} = \sqrt{(3-0)^2 + (1-(-2))^2} = \sqrt{9 + 9\os} = 3\sqrt{2\os}$.
Gradient = (1 − ( − 2))/(3 − 0) = 1.
Question R2
Find the equation of the line through the point (−2, 1) which has gradient 3. Find also the equation of the line through the same point which is perpendicular to the first line.
Answer R2
y − 1 = 3 (x − (−2)) or y = 3x + 7
The perpendicular line has gradient $-\frac13$ and equation
$y-1=-\frac13(x-(-2))$ or x + 3y −1 = 0
Question R3
Find the equation of the line passing through the points (2, −1) and (−1, 4) and find its point of intersection with the line y = 3x.
Answer R3
$\dfrac{y-(-1)}{x-2} = \dfrac{4-(-1)}{-1-2}$ or $\dfrac{y+1}{x-2} = \dfrac{5}{-3}$
so that 3y + 3 + 5x − 10 = 0 and therefore 3y + 5x − 7 = 0.
This intersects y = 3x where 3 (3x) + 5x − 7 = 0
i.e. x = 1/2 and y = 3/2 so that the point of intersection is (1/2, 3/2).
Question R4
(a) Write down the condition that the quadratic equation Ax2 + Bx + C = 0 has a repeated root at x = −B/(2A).
(b) Show that the quadratic equation x2 + (mx + c)2 = a2 has a repeated root if the constants a, c and m satisfy the equation c2 = (1 + m2)a2.
Answer R4
(a) The quadratic equation Ax2 + Bx + C = 0 has a repeated root at x = −B/(2A) if B2 = 4AC.
Recall that $x = \dfrac{-B\pm\sqrt{B^2-4AC}}{2A}$
(b) The quadratic equation x2 + (mx + c)2 = a2 can be rearranged into the form (1 + m2)x2 + 2mcx + c2 − a2 = 0, in which case A = (1 + m2), B = 2mc and C = c2 − a2. The equation has a repeated root if (2mc)2 = 4 (1 + m2)(c2 − a2), which rearranges to m2c2 = m2 c2 + c2 − (1 + m2)a2, so that c2 = (1 + m2)a2.
2 Conic sections
2.1 What are conic sections?
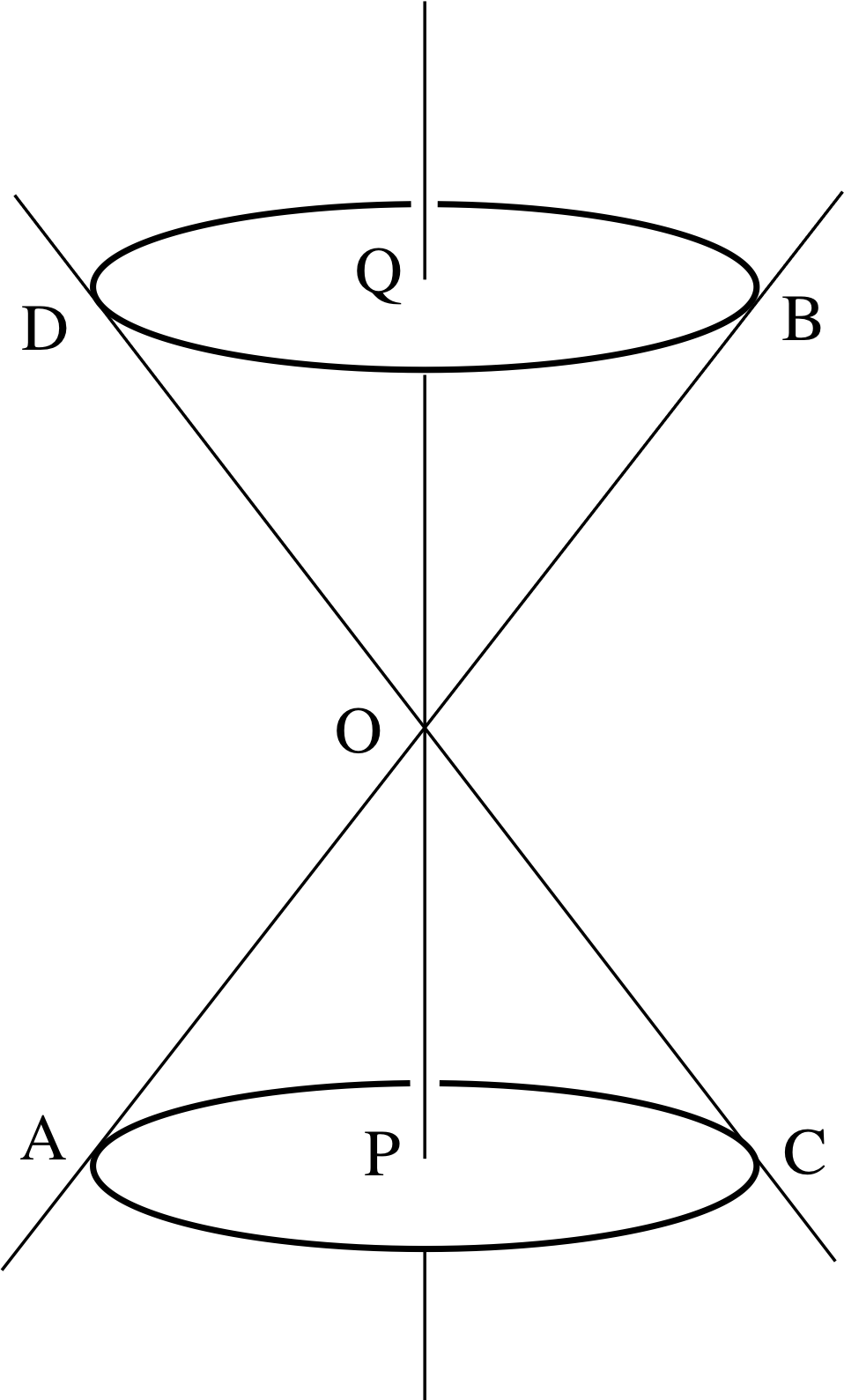
Figure 1 Double cone.
Figure 1 shows a double cone; it looks like one cone placed upside down on top of another. It is to be understood that this shape extends infinitely upwards and downwards.
To generate this figure we take the line of which AOB is a part and rotate it about a vertical axis through O in such a way that the point B traces out a circle which is perpendicular to the axis POQ and which has Q at its centre. The point A traces out a similar circle with P as its centre. The line of which POQ is a part is called the axis of symmetry of the double cone. P and Q are the centres of the circles traced out by A and B, respectively. The line through A, O and B is a generator of the double cone.
The curves we produce by cutting the double cone with a plane are called conic sections or, more simply conics. These curves are the boundaries of the sections exposed by the cuts.
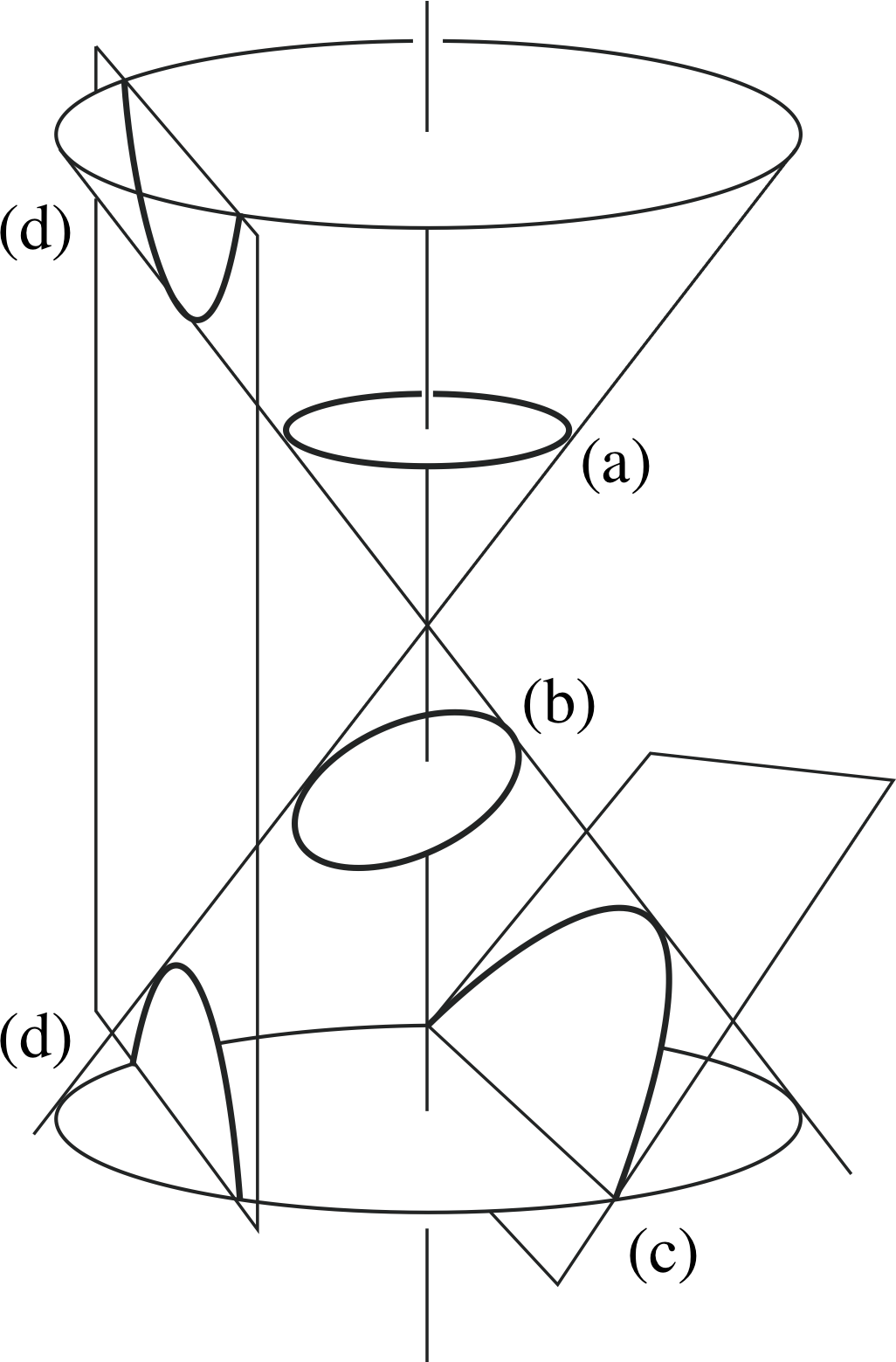
Figure 2 Conic sections. Note that the section representing the hyperbola (d) does not have to be parallel to the vertical axis – any angle of inclination steeper than (c) will suffice.
Figure 2 shows the possibilities.
(a) When the plane making the cut is perpendicular to the axis, the curve produced is a circle.
(b) When the cutting plane is inclined at an angle between the horizontal and that of a generator the boundary curve is an ellipse.
(c) When the cutting plane is parallel to a generator the resulting curve is a parabola.
(d) If the cutting plane meets both parts of the cone at any angle the curve produced is in two parts called branches and is a hyperbola.
In Subsection 2.2Subsections 2.2 to Subsection 2.52.5 we derive the equations of these four curves from quite different starting points. We shall not prove that the two approaches lead to the same curves in each case; rest assured that they do.
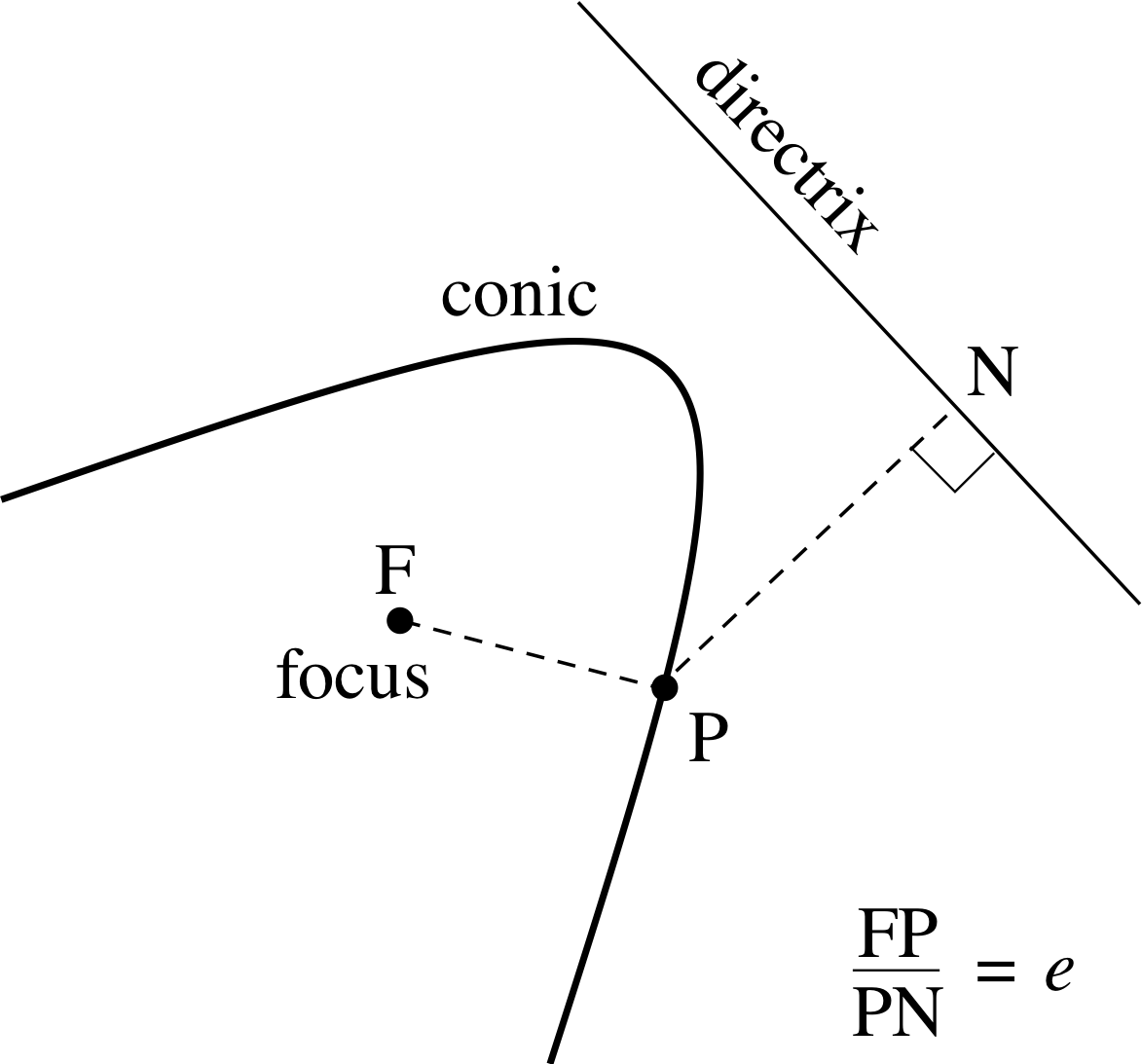
Figure 3 A conic with its focus and directrix.
The conics of various kinds have a common property that we have illustrated in Figure 3. There is a fixed point called the focus, and a fixed line called the directrix, such that for any point P on the conic, the distance to the focus and the distance to the directrix have a constant ratio, called the eccentricity and denoted by e.
In other words, $\dfrac{\rm{FP}}{\rm{PN}} = e$(1)
It is the value of the eccentricity that determines the nature of the conic, and Table 1 contains a short summary of some important results, which you may find useful as a quick reference.
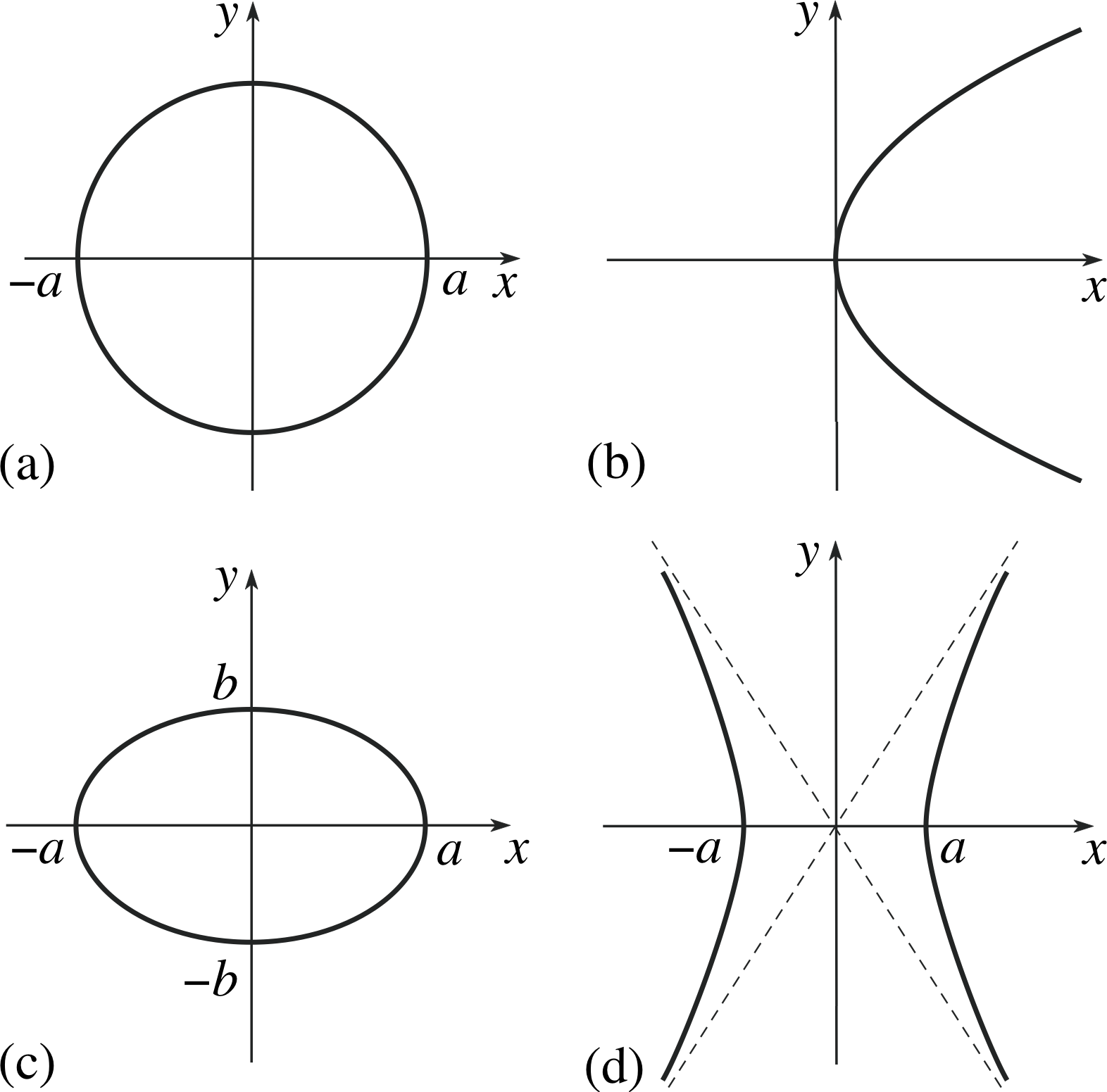
Figure 4 (a) Circle; (b) parabola; (c) ellipse; (d) hyperbola.
| Conic | Circle | Parabola | Ellipse | Hyperbola |
|---|---|---|---|---|
| eccentricity | e = 0 | e = 1 | 0 ≤ e < 1 | e > 1 |
| standard equation |
$x^2+y^2=a^2$ | $y^2=4ax$ | $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ | $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ |
| graph | see Figure 4a | see Figure 4b | see Figure 4c | see Figure 4d |
The circle can be regarded as the limiting case of an ellipse as the directrix moves further from the origin, e approaches 0, and the foci i approach the centre of the circle. It corresponds to putting b = a in the equation x2/a2 + y2/b2 = 1. In this module when we refer to ellipses we mean to exclude circles, unless we say otherwise. The equations given in Table 1 will be known as the standard equations or standard forms of the conics. (We will see later that it is sometimes convenient to represent the conics in various other forms.)
✦ Loosely speaking, a curve is symmetric about a line if it can be folded onto itself with a fold along the line. Which of the standard equations in Table 1, represent conics which are symmetric about (a) the x–axis, (b) the y–axis?
✧ The symmetries of the curves are clear from the figures in Figure 4, however we could use an algebraic approach. A curve is symmetric about the x–axis if the equation of the curve is unchanged when y is replaced by −y; it is symmetric about the y–axis if the equation of the curve is unchanged when x is replaced by −x.
The equation y2 = 4ax represents a parabola that is symmetric about the x–axis only, and the other equations represent conics that are symmetric about both axes. In general ellipses and hyperbolas have two axes of symmetry whereas parabolas have one axis of symmetry.
2.2 The circle
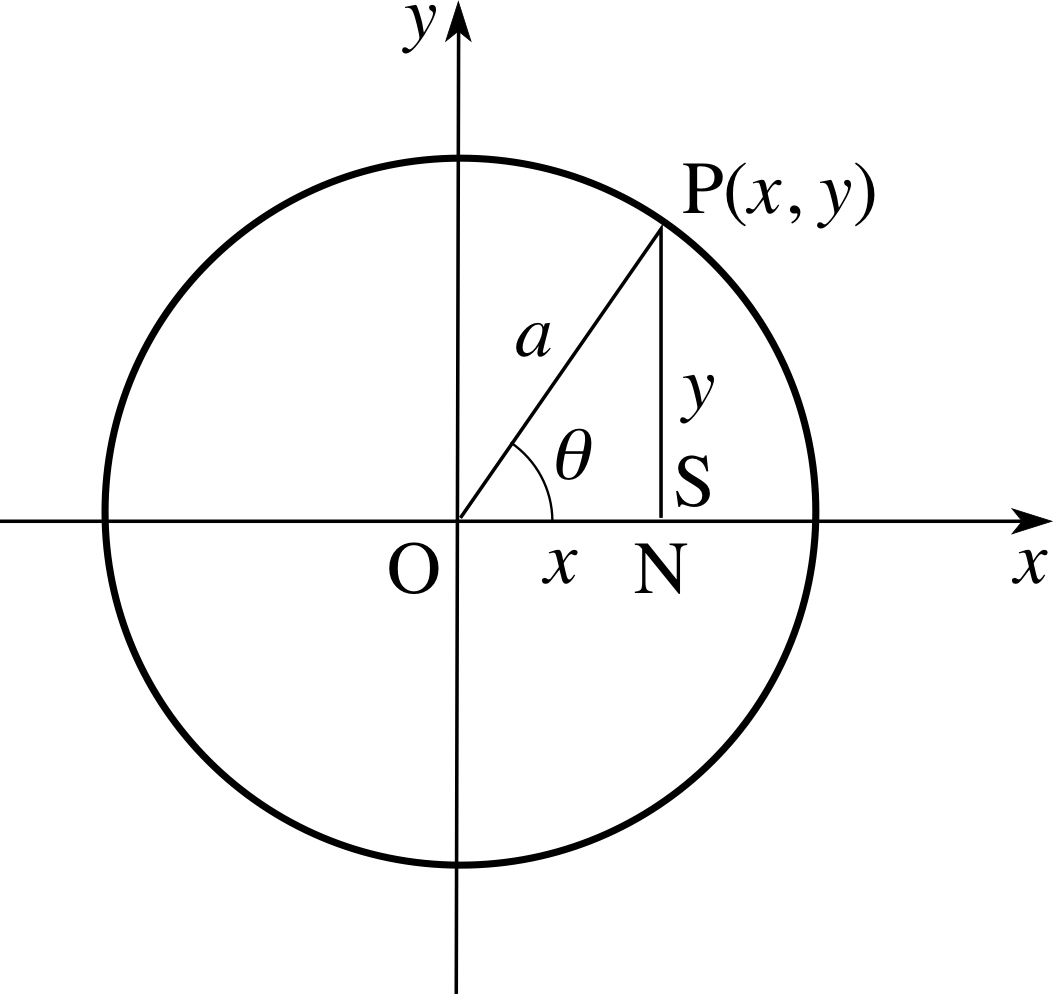
Figure 5 The circle and the angle θ. (2)
A circle is a collection of points which are at a constant distance from a fixed point. The fixed point is called the centre of the circle. Refer to Figure 5, where the fixed point O is the origin of coordinates. The point P is an arbitrary point on the circle and the distance OP is the radius of the circle denoted by a; as P moves around the circle, the length of OP is constant.
If the coordinates of P are (x, y) then the distances ON and PN are x and y, respectively, as shown in the figure. If the distance OP is denoted a then by applying Pythagoras’s theorem to the right–angled triangle ONP we find that
(ON)2 + (PN)2 = (OP)2
i.e.x2 + y2 = a2(2)
This is the standard equation of a circle.
✦ What is the radius of the circle x2 + y2 = 16 ?
✧ Since 16 = 42, the radius is 4.
✦ What is the equation of a circle, centre the origin, with radius 3?
✧ The equation is x2 + y2 = 32 or x2 + y2 = 9.
The intersection of a line with a circle
We can discover the x–coordinates of the points where a line
y = mx + c
meets the circle
x2 + y2 = a2
by substituting for y from the first equation into the second equation to obtain
x2 + (mx + c)2 = a2
and this equation may be written in the form
(1 + m2)x2 + 2mcx + (c2 − a2) = 0
Generally a line will either intersect a circle in two points, miss it entirely, or meet it in just one point (when it is a tangent). These three cases correspond to the above quadratic equation having
two real roots when (2mc)2 > 4 (1 + m2)(c2 − a2)
no real roots when (2mc)2 < 4 (1 + m2)(c2 − a2)
one real root when (2mc)2 = 4 (1 + m2)(c2 − a2)
(See Question R4.)
It is the third of the three cases that interests us here, and the equation
(2mc)2 = 4 (1 + m2)(c2 − a2)
can be rewritten in the form
c2 = (1 + m2)a2(3)
Equation 3 is thus the condition that ensures that the line y = mx + c is a tangent_to_a_curvetangent to the circle x2 + y2 = a2.
Question T1
c2 = (1 + m2)a2(Eqn 3)
Show that the quadratic equation x2 + (mx + c)2 = a2 has equal roots if m = 3, a = 5 and c = $5\sqrt{10\os}$, and then show that Equation 3 is satisfied. What can you say about the line $y=3x+5\sqrt{10\os}$ and the circle x2 + y2 = 25?
Answer T1
The quadratic equation becomes $x^2 + (3x + 5\sqrt{10\os})^2 = 5^2$ so that $10x^2+ 30\sqrt{10\os}x + 225 = 0$. The quadratic equation Ax2 + Bx + C = 0 has equal roots if B2 − 4AC = 0, and in this case B2 − 4AC = $(30\sqrt{10\os})^2- 40 \times 225 = 0$.
c2 = (1 + m2)a2(Eqn 3)
Also c2 − (1 + m2)a2 = 250 − (1 + 9) × 25 = 0 so that Equation 3 is satisfied
The line $y = 3x + 5\sqrt{10\os}$ is a tangent to the circle x2 + y2 = 25.
Tangents and normals to the circle
We may use Equation 3,
c2 = (1 + m2)a2(Eqn 3)
to show that the equation of the tangent to the circle x2 + y2 = a2 at the point (x1, y1) on the circle is
x1x + y1y = a2(4) i
and this is done in the following exercise.
✦ Show that Equation 4 is the equation of a tangent to the circle at the point (x1, y1).
✧ We are given that (x1, y1) lies on the circle, so x12 + y12 = a2.
If we put x = x1, y = y1 into Equation 4 we again get x12 + y12 = a2 and this proves that (x1, y1) lies on the line given by Equation 4.
It remains to prove that (x1, y1) is the only point of coincidence between the circle and the line.
Equation 4 can be rearranged into the form
$y = - \dfrac{x_1}{y_1}x+\dfrac{a^2}{y_1}$
so that in this case
$m = -\dfrac{x_1}{y_1}$ and $c = \dfrac{a^2}{y_1}$
It follows that
$\left(1+\dfrac{x_1^2}{y_1^2}\right)a^2 = \left(\dfrac{x_1^2+y1_2}{y_1^2}\right)a^2 = \dfrac{a^4}{y_1^2} = c^2$
and Equation 3,
c2 = (1 + m2)a2(Eqn 3)
is satisfied.
You may omit the following question if you are not familiar with calculus.
✦ Find the gradient of the tangent at the point P(x1, y1) on the circle by differentiating Equation 2,
x2 + y2 = a2(Eqn 2)
and hence show that Equation 4 represents the tangent at P.
✧ We may differentiate Equation 2,
x2 + y2 = a2(Eqn 2)
implicitly to obtain
$2x+2y\dfrac{dy}{dx}=0$ and hence $\dfrac{dy}{dx}= -\dfrac xy$
Thus, at the point P = (x1, y1) on the circle, the derivative is $-\dfrac{x_1}{y_1}$.
The tangent at P has the same slope as this derivative, and so the equation of the tangent at P is $y-y_1 = -\dfrac{ x_1}{y_1}(x - x_1)$
so thaty1y − y12 = − x1x + x12
i.e.y1y + x1x = x12 + y12 = a2
because (x1, y1) is a point on the circle.
From Equation 4 we can write $y=-\left(\dfrac{x_1}{y_1}\right)x+\dfrac{a^2}{y_1}$. Comparing this with y = mx + c we can see that the gradient of the tangent at a point (x1, y1) on the circle is $-\dfrac{x_1}{y_1}$. The normal at (x1, y1) is by definition a line perpendicular to the tangent, and so its gradient must be $\dfrac{y_1}{x_1}$. i
The equation of the normal to the circle at a point P(x1, y1) on the circle is
$y-y_1=\dfrac{y_1}{x_1}(x-x_1)$
which simplifies to
$y=\left(\dfrac{y_1}{x_1}\right)x$(5)
This is the equation of a line through the origin, as we would expect.
Question T2
What are the equations of the tangents and the normals to the circle x2 + y2 = 4 at the following points?
(a) ($\sqrt{2\os},\,\sqrt{2\os}$), (b) (0, 2), (c) (2, 0), (d) (−1,−$\sqrt{3\os}$), (e) (1.2, −1.6)
Answer T2
The general equation of a tangent at (x1, y1) is x1x + y1y = 4, while the normal is given by Equation 5,
$y = \left(\dfrac{y_1}{x_1}\right)x$(Eqn 5)
(a) tangent: $\sqrt{2\os}x + \sqrt{2\os}y = 4$ or $x + y = 2\sqrt{2\os}$; normal: y = x
(b) tangent: 2y = 4 i.e. y = 2; normal: x = 0
(c) tangent: 2x = 4 i.e. x = 2; normal: y = 0
(d) tangent: $-x-\sqrt{3\os}y = 4$; normal: $y = \sqrt{3\os}x$
(e) tangent: 1.2x − 1.6y = 4 i.e. 3x − 4y = 10; normal: y = −4x/3
Parametric equations for the circle
The equation x2 + y2 = a2 defines a set of points (x, y) that lie on a circle, but in many applications this is not quite enough. We may also need to indicate that the points on the curve are traced in a particular order or that a point is moving along the curve in an anticlockwise direction starting at the point (a, 0), for example. In Figure 5 the point P on the circle is determined by the angle θ, and from triangle OPN we see that
x = a cos θ and y = a sin θ(6)
As θ takes values in the range 0 ≤ θ < 360° then P moves round the circle in an anticlockwise direction from S(a,10). A variable such as θ, which is used to determine the position of a point on a curve is known as a parameter. In many applications to physics the natural parameter to choose would be time, so that the position of P is determined by the value of the time.
✦ Mark on the circle x2 + y2 = 4 the points P1 = (2 cos 60°, 2 sin 60°), P2 = (2 cos 240°, 2 sin 240°). Note that the points P1 and P2 are at the opposite ends of a diameter. This will be true of any two points corresponding to two values of the parameter that differ by 180°.
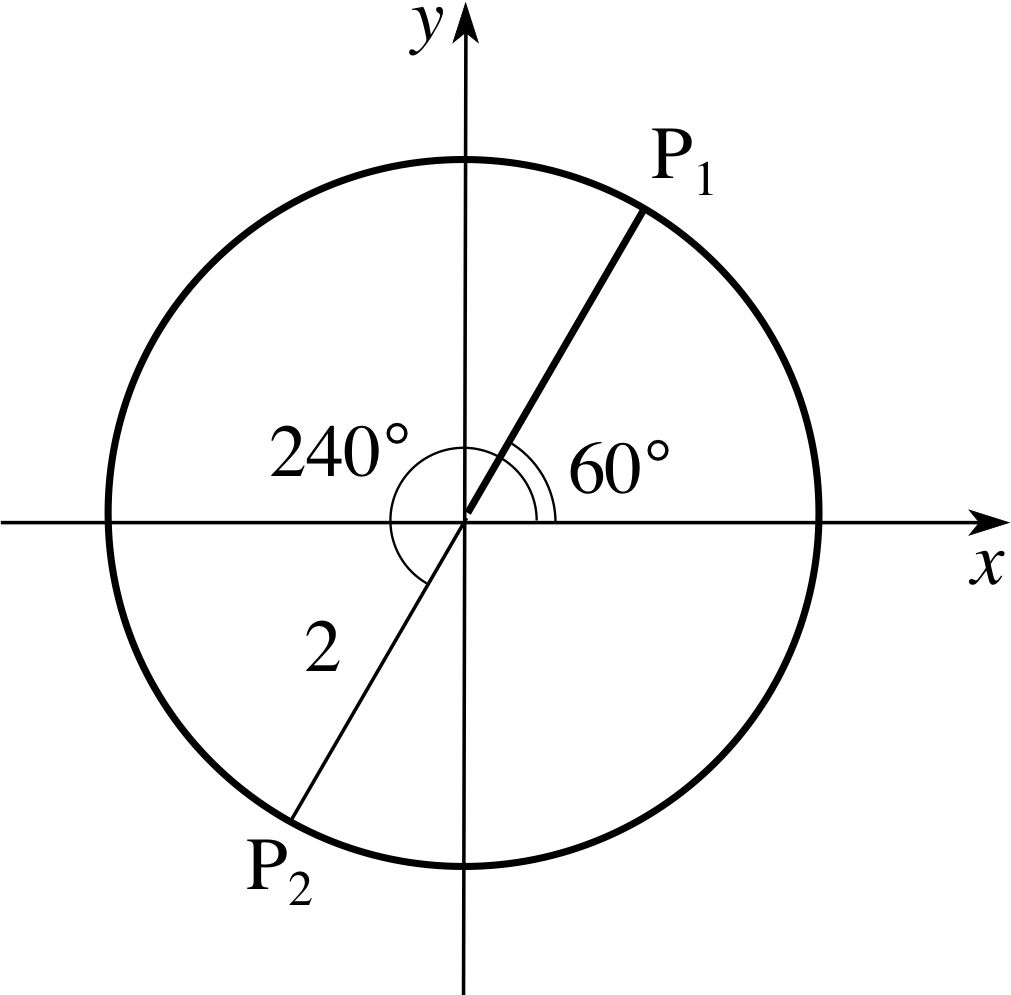
Figure 6 Points on a circle of radius 2.
✧ See Figure 6.

Figure 5 The circle and the angle θ.
✦ Suppose that the angle θ in Figure 5 is given by θ = ωt, where ω is a positive number and t is the time.
(a) Does the point P move clockwise or anticlockwise round the circle as t increases?
(b) What are x and y of Figure 5 in terms of ω and t?
✧ (a) θ increases as t increases, so P moves anticlockwise round the circle.
(b) x = a cos(ωt), y = a sin(ωt).
✦ Suppose the position of a point P on a circle is determined by a parameter t representing time in seconds, and x = 4 cos(ωt), y = 4 sin(ωt). What is the radius of the circle? In which direction does P traverse the circle if ω is negative; and if ω = −π rad s−1, how long does it take P to trace out the circle?
✧ The value of a in Figure 5 is 4 units, and θ = ωt at time t. Since ω is negative, the value of θ decreases as t increases and so the point P moves in a clockwise direction around a circle of radius 4.
When P returns to its starting point (for the first time), it will have traversed 2π radians (in the negative direction) and therefore putting θ = −2π radians and ω = −π rad s−1 into the formula θ = ωt we obtain t = 2 s.
✦ What is the equation of the tangent to the circle x2 + y2 = 16 at the point P(4 cos θ, 4 sin θ) on the circle?
✧ From Equation 4,
x1x + y1y = a2 (Eqn 4)
the equation of the tangent is
(4 cos θ)x + (4 sin θ)y = 16
which simplifies to
x cos θ + y sin θ = 4.
Question T3
What is the equation of the normal to the circle x2 + y2 = 16 at the point P(4 cos θ, 4 sin θ) on the circle?
Answer T3
The normal has equation $y = \dfrac{4\sin\theta}{4\cos\theta}x$, that is y = x tan θ.
Alternative forms of the circle
x2 + y2 = a2(Eqn 2)
x = a cos θ and y = a sin θ(Eqn 6)
We normally regard Equations 2 or 6 as the simplest forms of the equations of a circle, but we will mention several other forms because they sometimes arise naturally from physics. It will not be necessary for you to remember these alternative forms, but you may wish to refer to this subsection if you encounter them in your other work.
The first form is simply a consequence of choosing the centre of the circle to be at a point other than the origin. Such a situation might arise if we are discussing lenses with spherical surfaces for example, in which case it may be impossible to arrange for all our spheres or circles to be centred at a single point.

Figure 5 The circle and the angle θ.
When we apply Pythagoras’s theorem to the triangle OPN in Figure 5 we obtain the equation of a circle of radius a, with its centre at O, in the form x2 + y2 = a2. If we replace the point O by a point with coordinates (p, q) then the same argument gives the equation
(x − p)2 + (y − q)2 = a2(7)
for a circle of radius a with its centre at (p, q).
Alternatively you may encounter the equation of a circle in the general form
x2 + y2 + 2Gx + 2Fy + C = 0(8)
in which case the centre of the circle is at the point (−G, −F) and its radius is $\sqrt{G^2 + F^2 - C}$.
✦ Expand the brackets in Equation 7 and verify that Equation 8 represents a circle of radius $\sqrt{G^2 + F^2 - C}$ with centre at (−G, −F).
✧ Equation 7,
(x − p)2 + (y − q)2 = a2(Eqn 7)
gives
x2 − 2px + p2 + y2 − 2qy + q2 = a2 or x2 + y2 − 2px − 2qy + (p2 + q2 − a2) = 0
Then comparing the coefficients of this equation with those of Equation 8,
x2 + y2 + 2Gx + 2Fy + C = 0(Eqn 8)
we see that p = −G, q = −F, and $a = \sqrt{G^2+F^2-C\os}$.
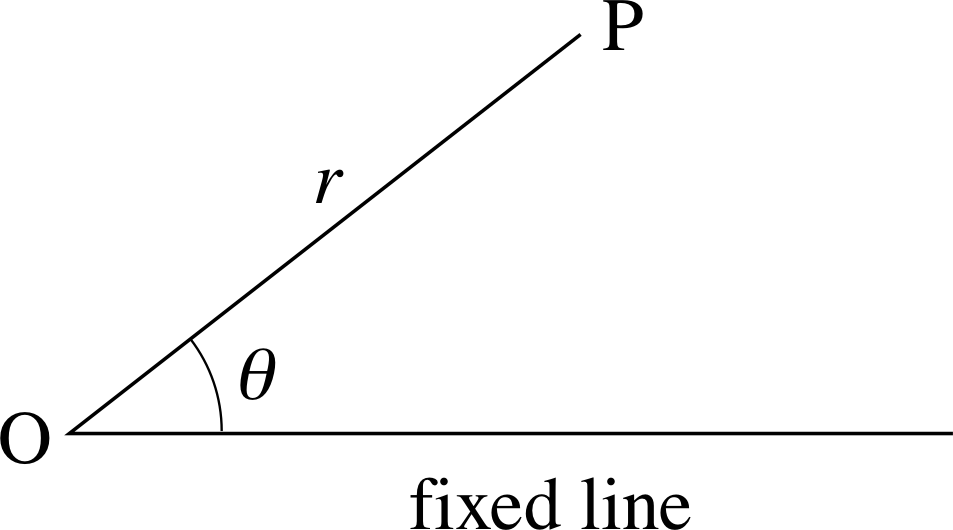
Figure 7 Polar coordinates.
Sometimes we encounter circles in polar form when investigating so called central forces, for example in electrostatics. In polar coordinates we use the distance from the origin and an angle to specify the position of a point as in Figure 7. The equation of a circle of radius a with its centre at the origin is particularly simple in such a coordinate system and is just
r = a (with a ≥ 0)(9)
You are probably familiar with the representation of curves in terms of (x, y) coordinates, but you may not be aware that we can do something very similar with (r, θ) coordinates. For example the equation
r = 2a cosθ(10)
represents a curve; but which curve?
In Figure 7 we suppose that the point P has coordinates (x, y) then r2 = x2 + y2 and cos θ = $\dfrac xr = \dfrac{x}{\sqrt{x^2+y^2}}$.
Substituting for r and cos θ in Equation 10 we obtain x2 + y2 = 2ax which gives x2 − 2ax + y2 = 0 or x2 − 2ax + y2 + a2 = a2 so that
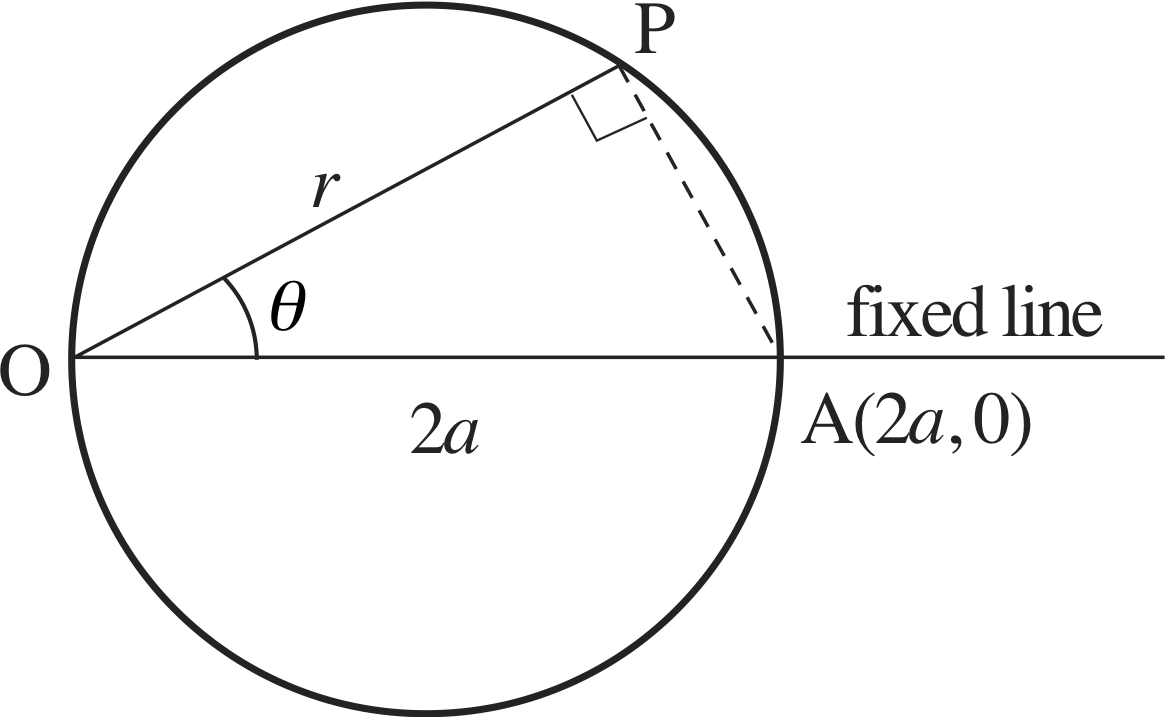
Figure 8 The polar form of a circle.
(x − a)2 + y2 = a2
Comparing this (x − a)2 + y2 = a2 with Equation 7,
(x − p)2 + (y − q)2 = a2(Eqn 7)
we see that it is a circle of radius a with its centre at (a, 0).
Equation 10,
r = 2a cosθ(Eqn 10)
therefore represents the circle shown in Figure 8.
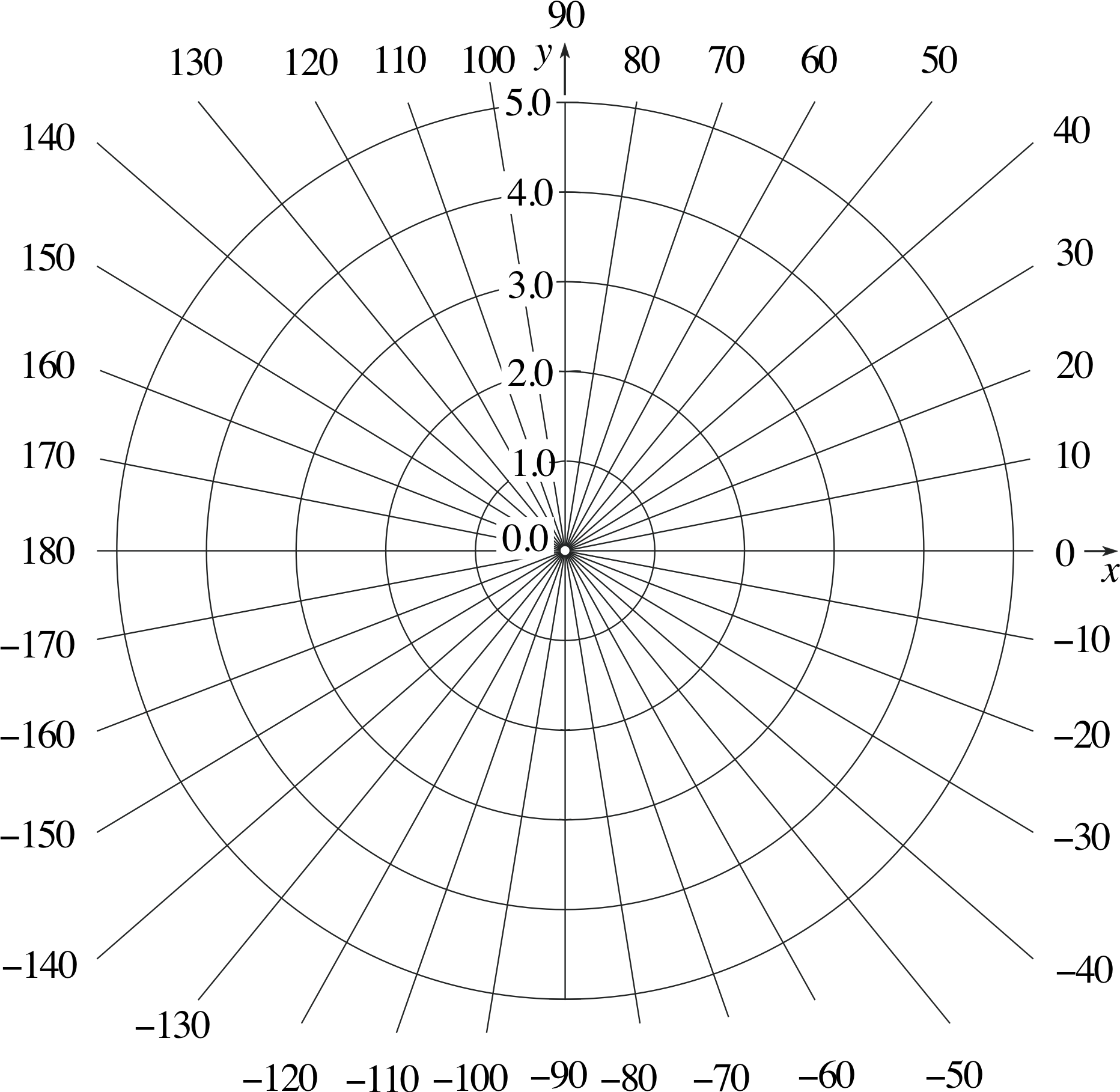
Figure 9 Polar graph paper.
✦ In Figure 9 we provide you with graph paper marked in polar coordinates, and Table 2 is obtained from the formula r = 4 cos θ cm.
Plot the points and convince yourself that they do indeed lie on a circle.
| θ /° | r/cm |
|---|---|
| −90 | 0.0 |
| −80 | 0.7 |
| −060 | 2.0 |
| −040 | 3.1 |
| −20 | 3.8 |
| −10 | 3.9 |
| 0 | 4.0 |
| 10 | 3.9 |
| 20 | 3.8 |
| 40 | 3.1 |
| 60 | 2.0 |
| 80 | 0.7 |
| 90 | 0.0 |
✧ The points lie on a circle of radius 2 cm with its centre at the point (2 cm, 0) with respect to the x– and y–axes shown in the figure.
2.3 The parabola
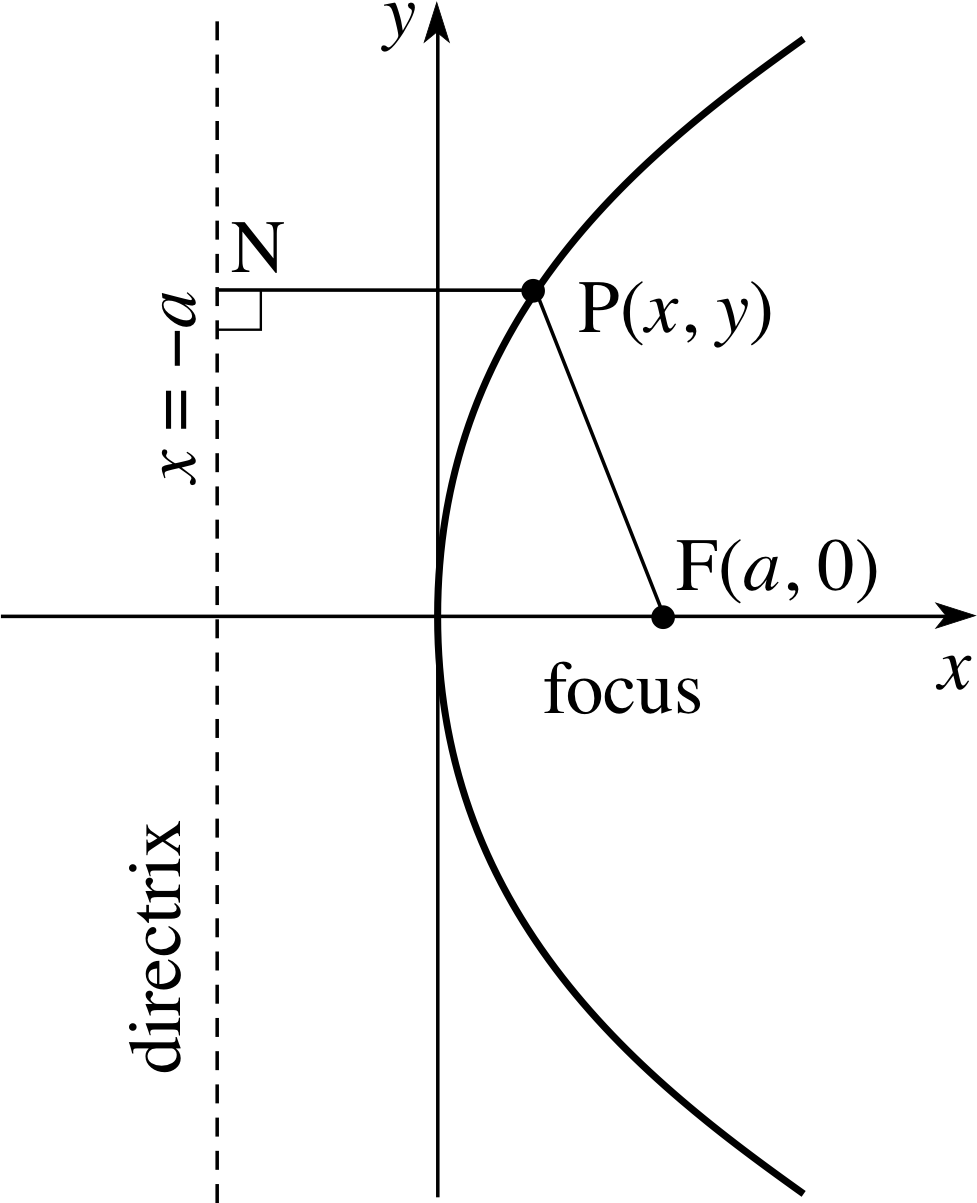
Figure 10 The parabola.
You may be aware that the graph of a quadratic function
y = Ax2 + Bx + C(11)
is a geometric shape known as a parabola, but here we begin our investigation of parabolas with the definition of a conic, Equation 1 with e = 1. Such shapes occur in many areas of physics, in particular, a simple model of the motion of a projectile i under gravity near the Earth predicts that it will move along a parabolic path.
We will choose the position of the focus and the directrix in such a way that the equation of the parabola becomes particularly simple. In Figure 10 you will see that we have placed the focus on the x–axis at the point (a, 0), and we have arranged for the parabola to pass through the origin by choosing the directrix to be the line x = −a. The point on the parabola closest to the directrix is called the vertex_of_a_parabolavertex of the parabola.
Let P be a point on the parabola. Then by Equation 1 with e = 1,
$\dfrac{\rm{FP}}{\rm{PN}} = e$(Eqn 1)
we have FP = PN where PN is perpendicular to the directrix.
✦ Given that P is the point (x, y), calculate (PN)2 and (FP)2.
✧ PN = x + a so that (PN)2 = (x + a)2
and using the expression for the distance between two points i, we have
(FP)2 = (x − a)2 + (y − 0)2 = (x − a)2 + y2
From the definition of a parabola we know that FP = PN so that (FP)2 = (PN)2 and therefore (x − a)2 + y2 = (x + a)2 which simplifies to
y2 = 4ax(12)
This is the standard equation of the parabola.
Tangents and normals to the parabola
We can find the equation of the tangent to a parabola in much the same way as we did for the circle, by constructing a line which touches the curve at one point. We will spare you the details and quote the result.
The tangent at a point P(x1, y1) on the parabola (Equation 12) has the equation i
y1y = 2a (x + x1)(13)
You may skip the following question if you are unsure of calculus.
✦ Differentiate Equation 12,
y2 = 4ax(Eqn 12)
and hence verify that Equation 13 represents the tangent at a point P(x1, y1) on the parabola.
✧ We may differentiate Equation 12,
y2 = 4ax(Eqn 12)
implicitly with respect to x to obtain
$2y\dfrac{dy}{dx} = 4a$
which can be rearranged to give
$\dfrac{dy}{dx}=\dfrac{2a}{y}$
at the point P(x1, y1) the gradient of the parabola is therefore
$\dfrac{2a}{y_1}$
The tangent line at P has the same slope as this gradient and so its equation is
$y-y_1 = \dfrac{2a}{y_1}(x-x_1)$
Multiplying by y1we obtain
y1y − y12 = 2ax − 2ax1.
Since P lies on the parabola we have
y12 = 4ax1
so that the above equation becomes
y1y − 4ax1 = 2a (x − x1)
which simplifies to
y1y = 2a (x + x1 )
as required.
You do not need to use calculus to answer the following question.
Question T4
(a) What are the equations of the tangent and the normal to the parabola 8y2 = x at the points (1/2, 1/4) and (1/2, −1/4)? [Hint: Use Equation 13.]
(b) Show that the point M (a/m2, 2a/m) lies on the parabola y2 = 4ax for any value of m ≠ 0, and then use
Equation 13 to show that the line
$y=mx+\dfrac am $(14)
is a tangent to the parabola y2 = 4ax, and hence the gradient of the parabola at M is m.
Answer T4
(a) Here 4a = 1/8 so that $a=\frac{1}{32}$ and the general equation of the tangent at (x1, y1) is given by Equation 13.
y1 y = 2a (x + x1)(Eqn 13)
The normal at this point has gradient −(y2/2a) = −16y2 and so its equation is y − y1 = −16y1(x − x1).
At the point (1/2, 1/4) these equations become:
tangent: y/4 = (x + 1/2)/16, i.e. 8y = 2x + 1
normal: y − 1/4 = − 4 (x − 1/2), i.e. 16x + 4y = 9
At the point (1/2, −1/4) these equations become:
tangent: −y/4 = (x + 1/2)/16, i.e. 8y + 2x + 1 = 0
normal: y + 1/4 = 4 (x − 1/2), i.e. 16x − 4y = 9
(b) Putting x2 = a/m2 and y2 = 2a/m we have
y12 = 4a2/m2 = 4ax1 and therefore M lies on the parabola.
From Equation 13 the tangent at M is 2ay/m = 2a (x + a/m2), which simplifies to give Equation 14.
$y = mx + \dfrac am$(Eqn 14)
✦ Which of the following lines are tangents to the parabola y2 = 8x?
(a) y = 2x + 2 (b) y = 3x + 2/3 (c) y = kx + k2
✧ The parameter a in Equation 12,
y2 = 4ax(Eqn 12)
is 2 since 4a = 8.
(a) m = 2, c = 2 and a/m = 1, is not a tangent because c ≠ a/m.
(b) m = 3, c = 2/3 and a/m = 2/3, is a tangent because c = a/m.
(c) m = k, c = k2 and a/m = 2/k and c = a/m provided that k2 = 2/k which will be so if k3 = 2 so that $k = \sqrt[{\large\raise{2pt}3}]{2\os}$. For any other values of k the line will not be a tangent.
Parametric equations for the parabola
You may recall that the use of a parameter enabled us to trace out the points of a circle in a particular order, and we may do something very similar for a parabola. If we introduce the parametric equations
x = at2 and y = 2at(15)
then both x and y are determined by the value of the parameter t. If we use the second of these equations to write t = y/(2a) and then substitute for t in the first equation, we obtain x = a (y/(2a))2, which reduces to y2 = 4ax. This means that any point (x, y) = (at2, 2at) specified by Equations 15 must lie on the parabola defined by Equation 12 y2 = 4ax. Moreover, each point on the parabola corresponds to one and only one value of t.
Many results relating to the parabola can be derived via the parametric representation. For example, consider two points P and Q corresponding to two values t1 and t2 of the parameter. The line passing through the two points P(at12, 2at1) and Q(at22, 2at2) has the equation
$\dfrac{y-at_1}{2at_2-2at_1} = \dfrac{x-at_1^2}{at_2^2-at_1^2}$ i
which can be simplified to
2x − (t1 + t2)y + 2at1t2 = 0
If the two points P and Q coincide, i.e. if t1 = t2 = t say, then this line becomes a tangent to the parabola at the point (at2, 2at) with equation
2x − 2ty + 2at2 = 0
which simplifies to $y=\dfrac xt +at$, so that the gradient of the parabola at (at2, 2at) is 1/t
(This final equation is identical to Equation 14 $y=mx+\dfrac am $ except that m has been replaced by 1/t.) You may skip the following question if you are unsure of calculus.
✦ What is the value of dy/dx in terms of t, at a general point (at2, 2at) on the parabola?
✧ Since dx/dt = 2at and dy/dt = 2a, it follows (from the chain rule) that
$\dfrac{dy}{dx} = \dfrac{dy}{dt}\left /\right. \dfrac{dx}{dt} = \dfrac{2a}{2at}=\dfrac1t$
You do not need to use calculus to answer the following question.
✦ Find the equation of the normal to the parabola at the point (at2, 2at).
✧ The normal is perpendicular to the tangent at the point of contact and so the product of their gradients is −1. Hence the gradient of the normal is −t; the equation of the normal is therefore
y − 2at = −t (x − at2)
which simplifies to
y + tx = 2at + at3(16)
Question T5
A line passing through the focus of the parabola y2 = 4ax cuts the parabola at the points P(at12, 2at1) and Q(at22, 2at2). Find a relationship between t1 and t2.
Answer T5
y − 2at1 x − at12 y − 2at1 x − at12
The line through P and Q is $\dfrac{y-at_1}{2at_2-2at_1} = \dfrac{x-at_1^2}{at_2^2-at_1^2}$ which simplifies to $\dfrac{y-at_1}{2} = \dfrac{x-at_1^2}{t_2+t_1}$
Since the line passes through the focus (a, 0) we have $-\dfrac{2at_1}{2} = \dfrac{a(1-t_1^2)}{t_2+t_1}$, so that −t1 (t2 + t1) = 1 − t12, or t2t1 = 1.
Question T6
The tangents to the parabola y2 = 4ax at P(at12, 2at1) and Q(at22, 2at2) meet at a point R. What are the coordinates of R?
Answer T6
The parametric equation of a tangent is y = x/t + at so the tangents at P and Q are x − t1y + at12 = 0 and x − t2y + at22 = 0, respectively. These meet where (t2 − t1)y + a (t12 − t22) = 0, i.e. if y = a (t1 + t2); substituting into the equation of either tangent we have x = at1t2. Hence R is (at1t2, a (t1 + t2)).
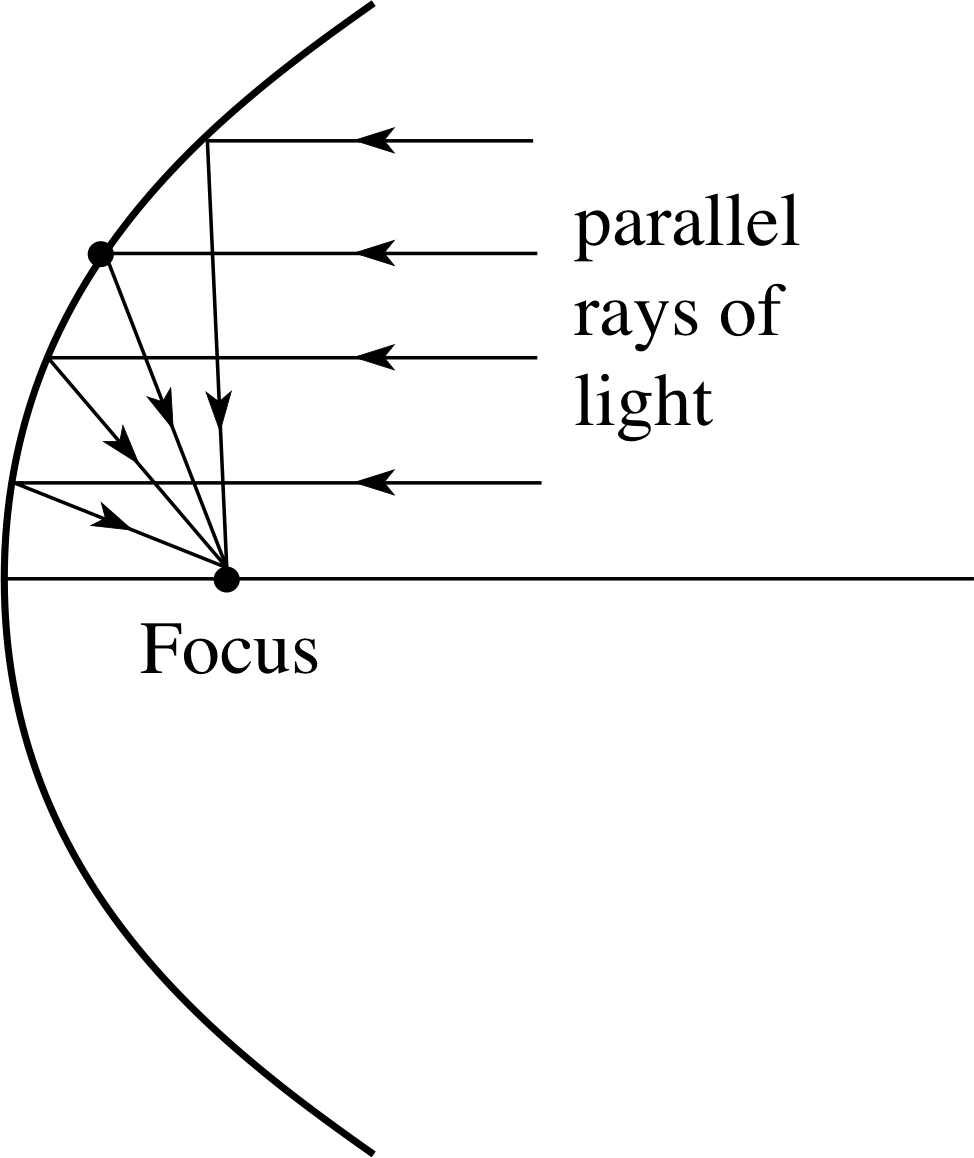
Figure 11 Reflection property of a parabola.
Reflection property of the parabola
Parabolas have the interesting and useful property, which is illustrated in Figure 11, that parallel rayrays of light striking a parabolic mirrored surface are all reflected through a fixed point – the focus of the parabola.
A distant source of light will produce a nearly parallel beam, and a receiver placed at the focus of the parabolic reflector can collect a strong signal. Receiving dishes, such as those used in radio astronomy or to recover television signals from a satellite, are usually in the shape of a paraboloid, which is the three–dimensional surface obtained by rotating a parabola about its axis of symmetry.
The property can also be used in reverse. Domestic electric fires are often provided with parabolic reflectors and the heating element is placed at the focus of the reflecting surface. Heat rays (mainly infra–red radiation) then emerge in parallel and the arrows in Figure 11 would be reversed.
✦ Give an example in which this geometric property is used to produce parallel rays of light.
✧ Examples include a motorcar headlamp, a torch, a theatre spotlight or a searchlight.
Alternative forms of the parabola
Just as for the circle, the equation of a parabola that arises from our work in physics may not be exactly like Equation 12.
y2 = 4ax(Eqn 12)
As a trivial example, the x and y may be swapped over to give y = x2/4a, and a change of origin will then lead to Equation 11 (which is probably the most common form of the equation of a parabola).
y = Ax2 + Bx + C(Eqn 11)
The polar form of a parabola
L/r = 1 + cos θ for −π < θ < π(17)
where L is a constant length, occurs quite often in the discussion of central orbits. We will not discuss this form in detail, but the following exercise is intended to convince you that the equation does indeed represent a parabola.
Question T7

Figure 9 Polar graph paper.
Table 3 shows the values of r for various values of θ (measured in degrees) obtained from the equation
L/r = 1 + cos θ(Eqn 17)
where L = 4 cm. Plot these values on the polar graph paper provided in Figure 9. Use your graph to decide which of the following equations is equivalent to Equation 17 in this case.
(a) (y − 4)2 = − x/2
(b) (y − 4)2 = x/2
(c) y2 + 16 = x/2
(d) 8y = −(x − 4)2
(e) y2 − 16 = −8x
(f) y = −2 (x + 4)2
| θ/° | r/cm |
|---|---|
| 0 | 2 |
| ±20 | 2.1 |
| ±40 | 2.3 |
| ±60 | 2.7 |
| ±80 | 3.4 |
| ±90 | 4.0 |
| ±100 | 4.8 |
Answer T7
The parabola passes through the points x = 2, y = 0 and x = 0, y = 4 and the only option that satisfies these requirements is option (e) y2 − 16 = −8x
2.4 The ellipse
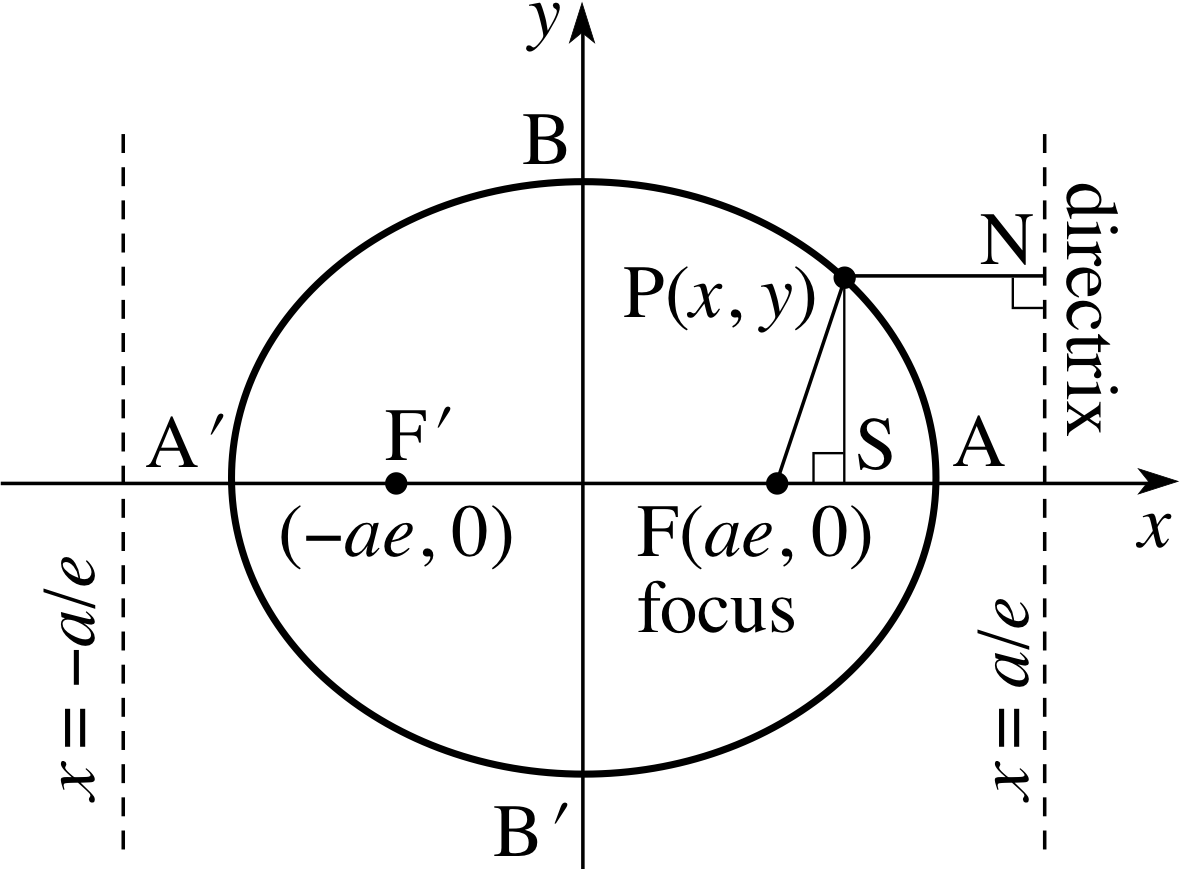
Figure 12 The ellipse.
Our discussion for the ellipse is very similar to that for the parabola. Again we begin with Equation 1, but this time with 0 ≤ e < 1. Once again we choose the axes and the origin so as to produce the simplest form of the equation, and our choice is shown in Figure 12.
Let us suppose that a is an arbitrary positive number, then the focus is chosen at the point (ae, 0) while the directrix is the line x = a/e.
From Equation 1, we have
$\dfrac{\rm{FP}}{\rm{PN}} = e$(Eqn 1)
and from the right–angled triangle FPS we have
FP2 = FS2 + PS2
so that (e × PN)2 = (x − ae)2 + y2
But PN = a/e − x and so e × PN = a − ex,
therefore(a − ex)2 = (x − ae)2 + y2
which givesa2− 2aex + e2x2 = x2− 2aex + a2e2 + y2
ora2 − a2e2 = a2(1 − e2) = (1 − e2)x2 + y2
Therefore(1 − e2)x2 + y2 = a2(1 − e2)
Dividing both sides of this final equation by a2(1 − e2) we obtain
$\dfrac{x^2}{a^2} + \dfrac{y^2}{a^2(1-e^2)} = 1$
Noting that a2(1 − e2) > 0 we may replace it by b2
so thatb2 = a2(1 − e2)
and$b=a\sqrt{1-e^2}$(18)
to produce the standard equation of an ellipse
$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$(19) i
✦ What is the equation of the standard ellipse which passes through the points (−2, 0) and (1, $\sqrt{3\os}/2$) ?
✧ Substituting (−2, 0) into Equation 19,
$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$(Eqn 19)
we obtain 4/a2 = 1 i.e. a = 2.
Substituting (1, $\sqrt{3\os}/2$) into Equation 19 gives us
$\dfrac{1}{a^2}+\dfrac{3}{4b^2}=1$
so that b = 1.
Hence the equation is
$\dfrac{x^2}{4}+\dfrac{y^2}{1}=1$

Figure 12 The ellipse.
If we put y = 0 in Equation 19 we obtain x2/a2 = 1, so that x = ±a and the ellipse meets the x–axis at the points A′(−a, 0) and A(a, 0) of Figure 12. If we put x = 0 in Equation 19 we obtain y2/b2 = 1, so that y = ±b and the ellipse meets the y–axis at the points B′(0, −b) and B(0, b) of Figure 12.
With this choice of axes, the ellipse is symmetric both about the x–axis and about the y–axis; and because of this latter symmetry there is a second focus F′(−ae, 0) and a second directrix x = −a/e which could have been used to draw the same ellipse.
Any chord passing through O is called a diameter, but, unlike those of a circle, the diameters of the ellipse are not all of the same length. The major axis is defined to be the longest diameter AA′, while the minor axis is defined to be the shortest diameter BB′. If we put y = 0 in Equation 19 we obtain x = ±a, so that the major axis is 2a. Similarly putting x = 0 in Equation 19 we have y = ±b and the minor axis is 2b.
✦ For an ellipse we require 0 ≤ e ≤ 1, but how does the shape of the ellipse change as we vary e within this range?
✧ Remember that b2 = a2(1 − e2).
When e = 0 then b = a and we get a circle. Notice that as e decreases to zero the directrix x = a/e moves further and further from the origin (until finally it is undefined when e = 0). Also as e decreases to zero the foci (±ae, 0) get closer to the origin, which is then the centre of the circle. The closer e is to 1 then the smaller is 1 − e2 and so the ratio b/a is smaller, and the ellipse departs more from a circle to a squashed oval shape.
✦ The equation x2/16 + y2/4 = 1 represents an ellipse. What are the major and minor axes of this ellipse? What is the eccentricity of this ellipse? What are the foci and the directrices of this ellipse?
✧ Comparing the given equation with Equation 19,
$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$(Eqn 19)
we see that a = 4 and b = 2 so the major axis is 8 and the minor axis is 4.
Substituting these values for a and b into Equation 18,
$b = a\sqrt{1-e^2}$(Eqn 18)
we obtain $2 = 4 \sqrt{1-e^2}$ which gives e = $\sqrt{3\os}/2$.
The foci are at (±ae, 0) = (±2$\sqrt{3\os}$, 0) while the directrices are x = ±a/e = ±8/$\sqrt{3\os}$.
Aside From Equation 18 $b=a\sqrt{1-e^2}$ and the fact that 0 ≤ e ≤ 1, it is clear that b ≤ a in the standard equation of the ellipse. Actually, Equation 19 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ with this condition b ≤ a would perhaps be more accurately described as ‘the standard equation of an ellipse with its foci on the x–axis’. If we throw away the condition b ≤ a then Equation 19 is still the equation of an ellipse, but the foci may lie on the y–axis. For example, $\dfrac{x^2}{4}+\dfrac{y^2}{16}=1$ is certainly the equation of an ellipse, with major axis 8 (in the direction of the y–axis) and minor axis 4 (in the direction of the x–axis) but its foci lie on the y–axis, rather than on the x–axis. In Equation 19 the greater of a and b is known as the semi–major axis while the lesser of a and b is known as the semi–minor axis.
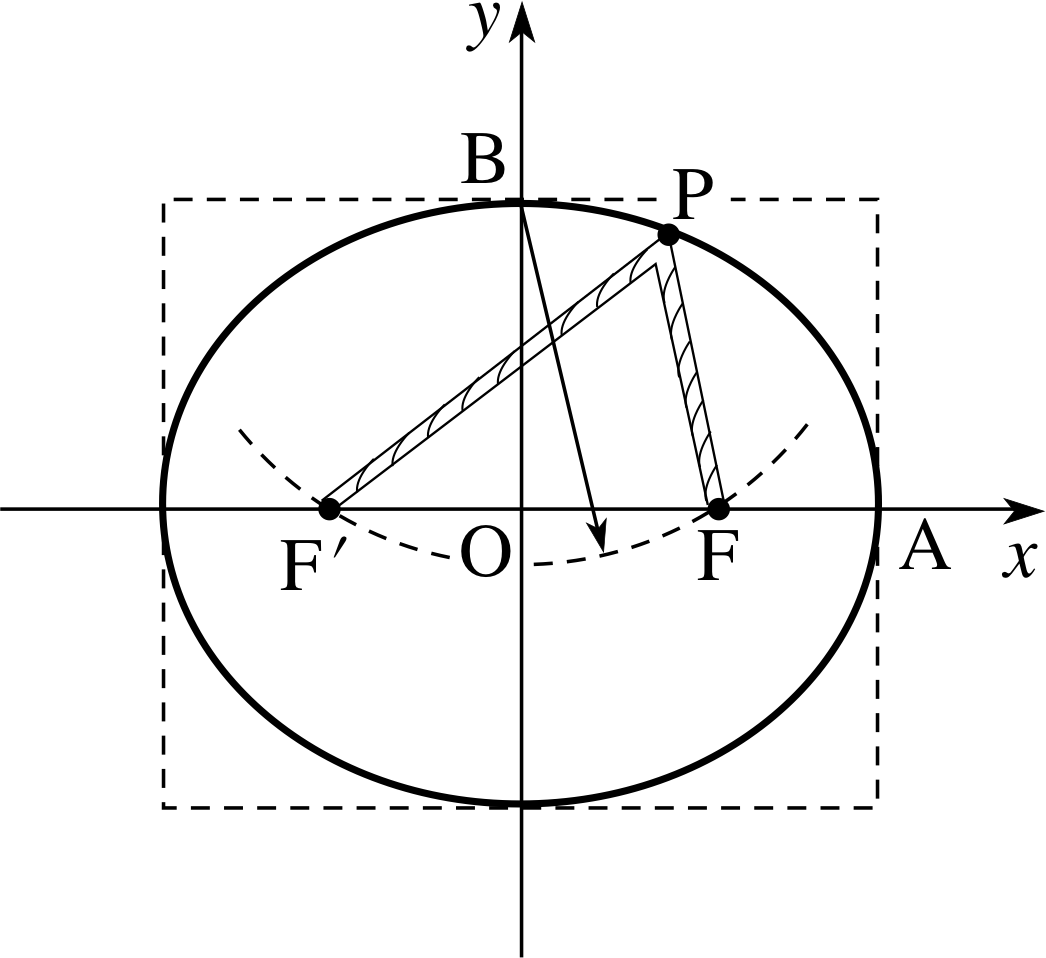
Figure 13 Drawing an ellipse with pins, string and pencil.
In Figure 12 we have shown an ellipse with its major axis along the x–axis. You would need to turn Figure 12 through 90° in order to find the foci and directrices of an ellipse for which b > a.
It is clear from Figure 13 that an ellipse is a bounded closed figure lying in a rectangle −a ≤ x ≤ a and −b ≤ y ≤ b. This figure shows a simple method of constructing an ellipse inside a given rectangle.
First, measure the length OA (the semi–major axis) then find where a circle centred at B with this length as radius meets the major axis. These two points are the foci F′ and F. Now place a loop of thread round pins through F′ and F, and keeping the thread taught, trace out the curve (so that the length F′PF is fixed).
Tangents and normals to the ellipse
$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$(Eqn 19)
The equation of the tangent to the ellipse defined by Equation 19, at a point P(x1, y1) on the ellipse, is
$\dfrac{x_1 x}{a^2} + \dfrac{y_1 y}{b^2} = 1$(20) i
This result is established in the next exercise, which you may skip if you are unsure of calculus.
✦ Show that Equation 20 is the equation of the tangent to the ellipse at a point P(x1, y1) on the ellipse.
✧ Let P(x1, y1) be an arbitrary point on the ellipse, then we differentiate Equation 19,
$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$(Eqn 19)
implicitly to obtain
$\dfrac{2x}{a^2}+\dfrac{2y}{b^2}=0$
which gives us
$\dfrac{dy}{dx}=\dfrac{-b^2 x}{a^2 y}$
It follows that at P(x1, y1) the gradient of the ellipse is
$\dfrac{-b^2 x}{a^2 y}$
and therefore the equation of the tangent at P is
$y-y_1=\dfrac{-b^2 x}{a^2 y}(x-x_1)$
so that
$\dfrac{y_1 y}{b^2} - \dfrac{y_1^2}{b^2} = \dfrac{-x_1 x}{a^2} + \dfrac{x_1^2}{a^2}$
and hence
$\dfrac{y_1 y}{b^2} +\dfrac{x_1 x}{a^2} = \dfrac{x_1^2}{a^2} + \dfrac{y_1^2}{b^2} $
However $\dfrac{x_1^2}{a^2} + \dfrac{y_1^2}{b^2}=1$, because P lies on the ellipse, and this gives Equation 20,
$\dfrac{x_1 x}{a^2} + \dfrac{y_1 y}{b^2} = 1$(Eqn 20)
✦ Write down the equation of the normal to the ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ at the point (x1, y1) on the ellipse.
✧ From Equation 20,
$\dfrac{x_1 x}{a^2} + \dfrac{y_1 y}{b^2} = 1$(Eqn 20)
the slope of the tangent at (x1, y1) is −b2x1/a2y1.
So the slope of the normal is a2y1/b2x1.
The equation of the normal at (x1, y1) is therefore
$y-y_1=\dfrac{a^2y_1}{b^2x_1}(x-x_1)$
Question T8
What are the equations of the tangent and the normal to the ellipse x2/4 + y2/16 = 1 at the points i
(a) (1, $2\sqrt{3\os}$), (b) (1, $-2\sqrt{3\os}$), (c) (−1,$2\sqrt{3\os}$), (d) (2, 0), (e) (0, −4)
Answer T8
From Equation 20,
$\dfrac{x_1 x}{a^2} + \dfrac{y_1 y}{b^2} = 1$(Eqn 20)
the equation of the tangent to the given ellipse at P (x1, y1) is x1x/4 + y1y/16 = 1.
This can be written $y = -\left(\dfrac{4x_1}{y_1}\right)x + \dfrac{16}{y_1}$ and so has gradient −4x1/y1.
Thus the normal at P has gradient y1/4x1, and the equation of the normal at P is therefore
$y-y_1 = \dfrac{y_1}{4x_1}(x-x_1)$, which simplifies to $y=\dfrac{y_1 x}{4x_1}+\dfrac{3y_1}{4}$
(a) At (1, $2\sqrt{3\os}$) the equations are:
tangent: $\dfrac14x+\dfrac{2\sqrt{3\os}}{16}y=1$ or $2x+\sqrt{3\os}y=8$
normal: $y=\dfrac{\sqrt{3\os}}{2}x+\dfrac32\sqrt{3\os}$
(b) At (1, $-2\sqrt{3\os}$):
tangent: $2x-\sqrt{3\os}y=8$
normal: $y=-\dfrac{\sqrt{3\os}}{2}x-\dfrac32\sqrt{3\os}$
(c) At (−1, $2\sqrt{3\os}$):
tangent: $-2x+\sqrt{3\os}y=8$
normal: $y=-\dfrac{\sqrt{3\os}}{2}x+\dfrac32\sqrt{3\os}$
(d) At (2, 0): tangent x = 2, normal y = 0 (the x–axis).
(e) At (0, −4): tangent: y = −4, normal x = 0 (the y–axis).
Parametric equations for an ellipse
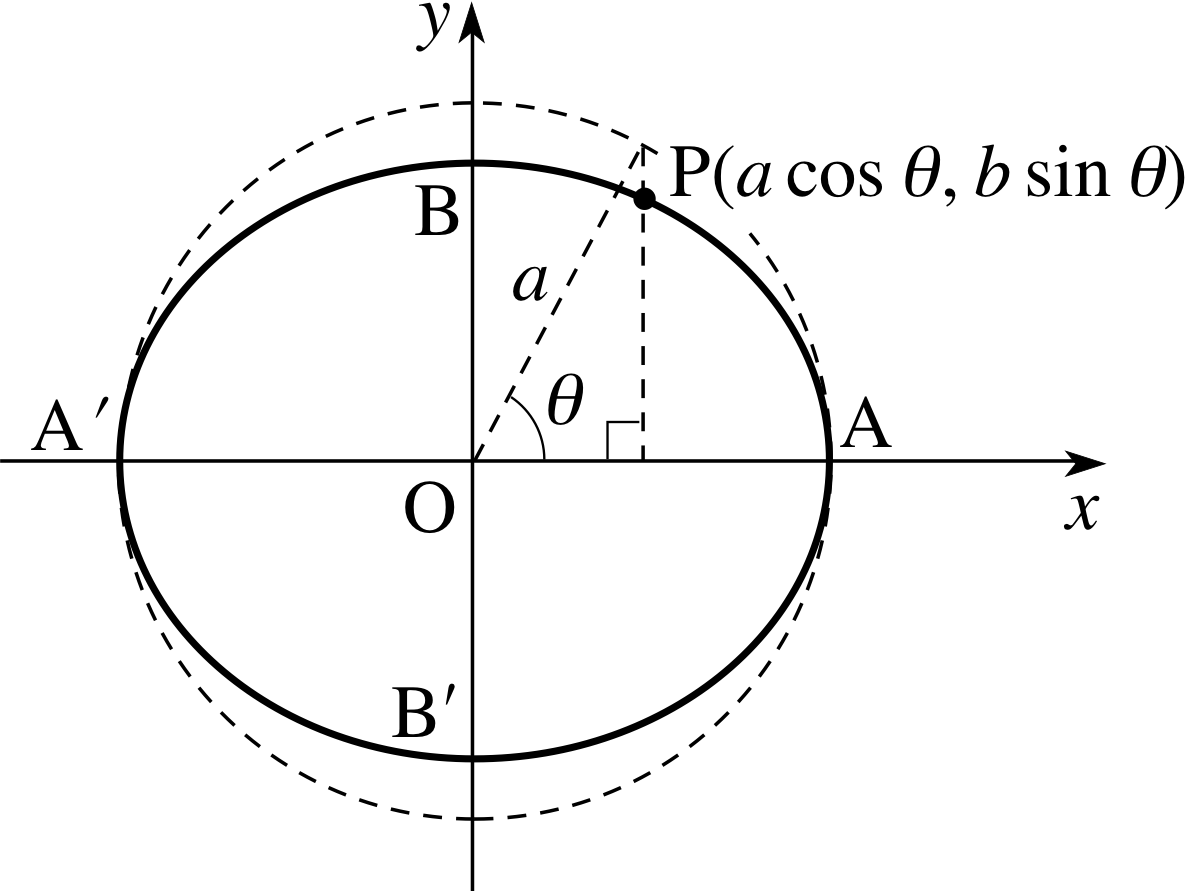
Figure 14 Parametric representation
We introduce parametric equations
x = a cos θ and y = b sin θ(21)
for the ellipse for the same reasons as for the circle and the parabola. It is clear that the point P(a cos θ, b sin θ) lies on the ellipse (Equation 19)
$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$(Eqn 19)
for any value of θ, since $\dfrac{(a\cos\theta)^2}{a^2}+\dfrac{(b\sin\theta)^2}{b^2}=\cos^2\theta+\sin^2\theta=1$.
Each value of θ in the range 0 ≤ θ < 360° ( or −180° < θ ≤ 180°) corresponds to one and only one point on the ellipse: see Figure 14. If we choose an arbitrary point x1 = a cos θ1, y1 = b sin θ1 on the ellipse, then Equation 20,
$\dfrac{x_1 x}{a^2} + \dfrac{y_1 y}{b^2} = 1$(Eqn 20)
becomes
$\dfrac{\cos\theta_1}{a}x+\dfrac{\sin\theta_1}{b}=1$(22)
and this is very often the most useful form of the equation of a tangent to the ellipse.
✦ Equation 22 gives the equation of the tangent to the ellipse at the point corresponding to choosing θ = θ1. Find the equation of the tangent line at the point corresponding to θ = θ1 + 90°.
✧ The equation of the tangent at the point corresponding to θ = θ1 + 90° is obtained by replacing θ1 by θ1 + 90° in Equation 22,
$\dfrac{\cos\theta_1}{a}x + \dfrac{\sin\theta_1}{b}y = 1$(Eqn 22)
which gives
$\dfrac{\cos(\theta_1+90°)}{a}x + \dfrac{(\sin\theta_1+90°)}{b}y = 1$
But cos(θ1 + 90°) = −sin θ1 and sin(θ1 + 90°) = cos θ1 so the equation of the tangent line becomes
$\dfrac{-\sin\theta_1}{a}x + \dfrac{\cos\theta_1}{b}y = 1$
Question T9
Show that the tangents to the ellipse $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ at the points with parameters θ1 and θ1 + 90° meet at the point x = a (cos θ1 − sin θ1), y = b (cos θ1 + sin θ1) and show that this point lies on the ellipse $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=2$
Answer T9
The tangent at the point corresponding to θ = θ1 is given by Equation 22,
$\dfrac{\cos\theta_1}{a}x+\dfrac{\sin\theta_1}{b}=1$(Eqn 22) (i)
while the tangent at the point corresponding to θ = θ2 + 90° is
$\dfrac{\cos(\theta_1+90°)}{a}x+\dfrac{\sin(\theta_1+90°)}{b}=1$
which becomes $\dfrac{-\sin\theta_1}{a^2}x+\dfrac{\cos\theta_1}{b}=1$ (ii)
The tangents meet where Equation (i) and Equation (ii) are satisfied simultaneously. Multiplying (i) by cos θ1 and (ii) by sin θ1 and then subtracting gives
$\dfrac{\cos^2\theta_1}{a}x+\dfrac{\sin^2\theta_1}{a}x=\cos\theta_1-\sin\theta_1$
so thatx = a (cos θ1 − sin θ1).
Multiplying (i) by sin θ1 and (ii) by cos θ1 and then adding them together gives
$\dfrac{\sin^2\theta_1}{b}y+\dfrac{\cos^2\theta_1}{b}x=\cos\theta_1+\sin\theta_1$
so thaty = b (cos θ1 + sin θ1).
It follows that
$\dfrac{x^2}{a^2}+ \dfrac{y^2}{b^2}= (\cos^2\theta_1-2\cos\theta_1\sin\theta_1+\sin\theta_1) + (\cos^2\theta_1+2\cos\theta_1\sin\theta_1+\sin\theta_1) = 2$
Alternative forms of the ellipse
The parabola, ellipse and hyperbola are of special interest because they are the paths which are followed by bodies which move under the so–called inverse square law. This occurs when the net force on a body is directed towards a fixed point, and is inversely proportional to the square of the distance between the body and the fixed point. Projectiles (in the absence of air resistance) travel in parabolic paths, planets i move around the Sun in ellipses, (some) meteorites passing near the Earth follow a hyperbolic orbit and, in a famous experiment by Geiger and Marsden, alpha–particlesα–particles i were deflected by nuclei along hyperbolae.
The polar equation of a conic is
L/r = 1 + e cos θ(23)
where L is a fixed length, and for 0 < e < 1 the conic is an ellipse (we have already seen the case e = 1 in Subsection 2.3 when we discussed the parabola). The following exercise is intended to convince you that Equation 23 is indeed the equation of an ellipse.
Question T10

Figure 9 Polar graph paper.
Table 4 shows the values of r for various values of θ obtained from the equation L/r = 1 + e cos θ, where L = 2.5 cm and e = 0.5. Plot these values on the polar graph paper provided in Figure 9. Is the major axis of the ellipse parallel to the x–axis or to the y–axis?
| θ /° | r/cm |
|---|---|
| 0 | 1.7 |
| ±30 | 1.7 |
| ±50 | 1.9 |
| ±70 | 2.1 |
| ±90 | 2.5 |
| ±110 | 3.0 |
| ±130 | 3.7 |
| ±150 | 4.4 |
| ±175 | 5.0 |
| ±180 | 5.0 |
Answer T10
The major axis is along the x–axis.
2.5 The hyperbola
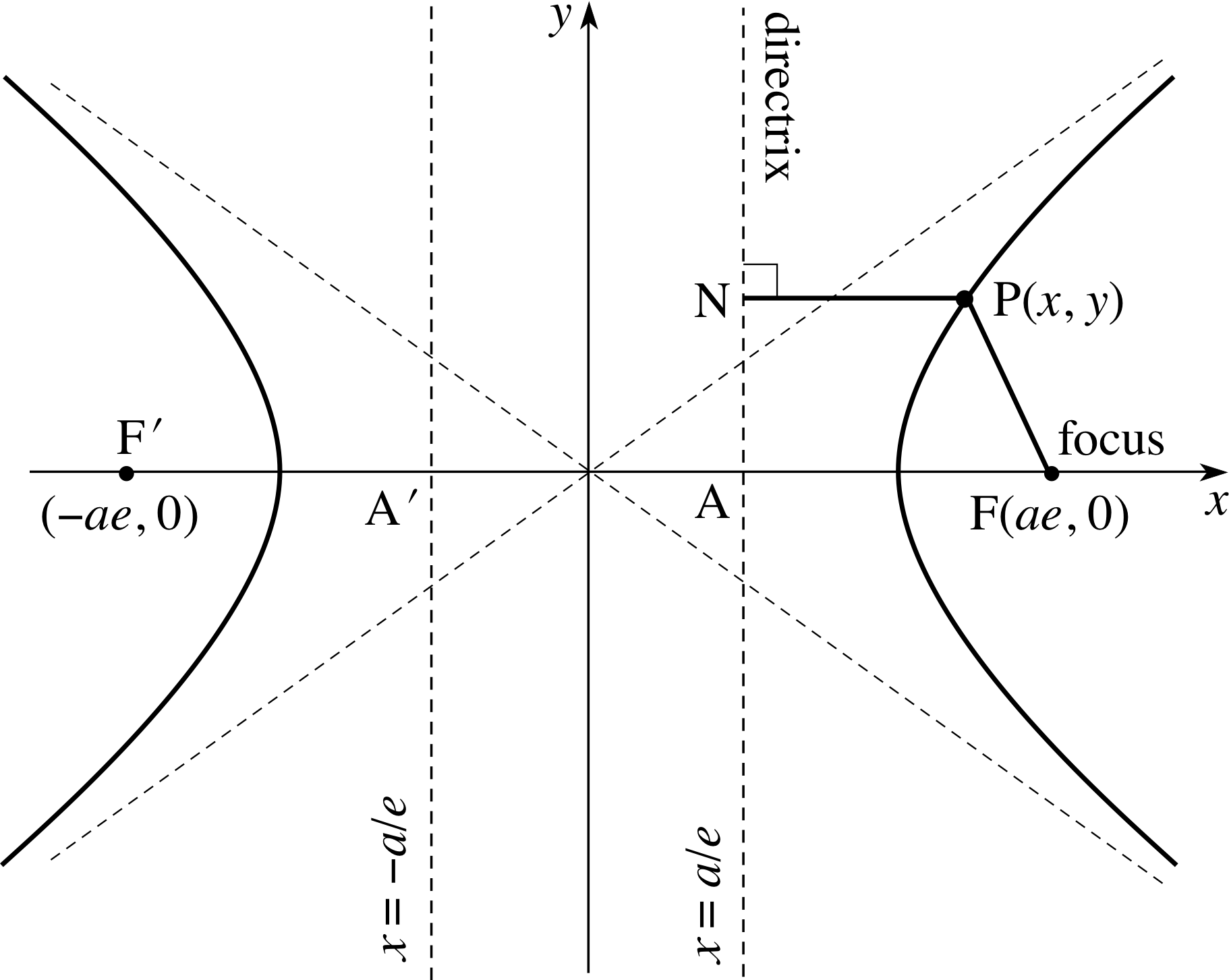
Figure 15 The hyperbola.
Our discussion for the hyperbola is very similar to that for the ellipse. Again we begin with Equation 1, but this time with e > 1. Once again we choose the axes and the origin so as to produce the simplest form of the equation, and our choice is shown in Figure 15.
Let us suppose that a is an arbitrary positive number, then the focus is chosen at the point (ae, 0) while the directrix is the line x = a/e.
From Equation 1 we have (FP)2 = e2(PN)2 so that
$(xa-e)^2 +(y-0)^2 = e^2\left(x-\dfrac ae \right)^2$
expanding gives us
x2 − 2aex + a2e2 + y2 = e2x2 − 2aex + a2
factorizing gives us
(e2 − 1)x2 − y2 = a2(e2 − 1)
Hence$\dfrac{x^2}{a^2} - \dfrac{y^2}{a^2(e^2-1)} = 1$
Since a2(e2 − 1) > 0 we may replace it by b2, where b is a constant, to obtain the standard form of the hyperbola:
$\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1$(24) i
As with the ellipse it follows from the symmetry that there is a second focus and a second directrix which will produce the same curve. The two foci are the points F(ae, 0) and F′(−ae, 0) and the two directrices have equations x = a/e and x = −a/e.
Notice from Figures 4d and 15 that the hyperbola has y two distinct branches: this is quite different from an ellipse which is always a closed curve.
We can readily verify for Equation 24 that when y = 0, x = ± a (giving the points A′ and A in Figure 15), but there is no value of y for which x = 0; indeed, since Equation 24 can be rearranged to give the equation
$\dfrac{y^2}{b^2} = \dfrac{x^2-a^2}{a^2}$
in which the left–hand side is positive, it follows that x2 ≥ a2, so there is no part of the curve in the band −a < x < a.
Asymptotes
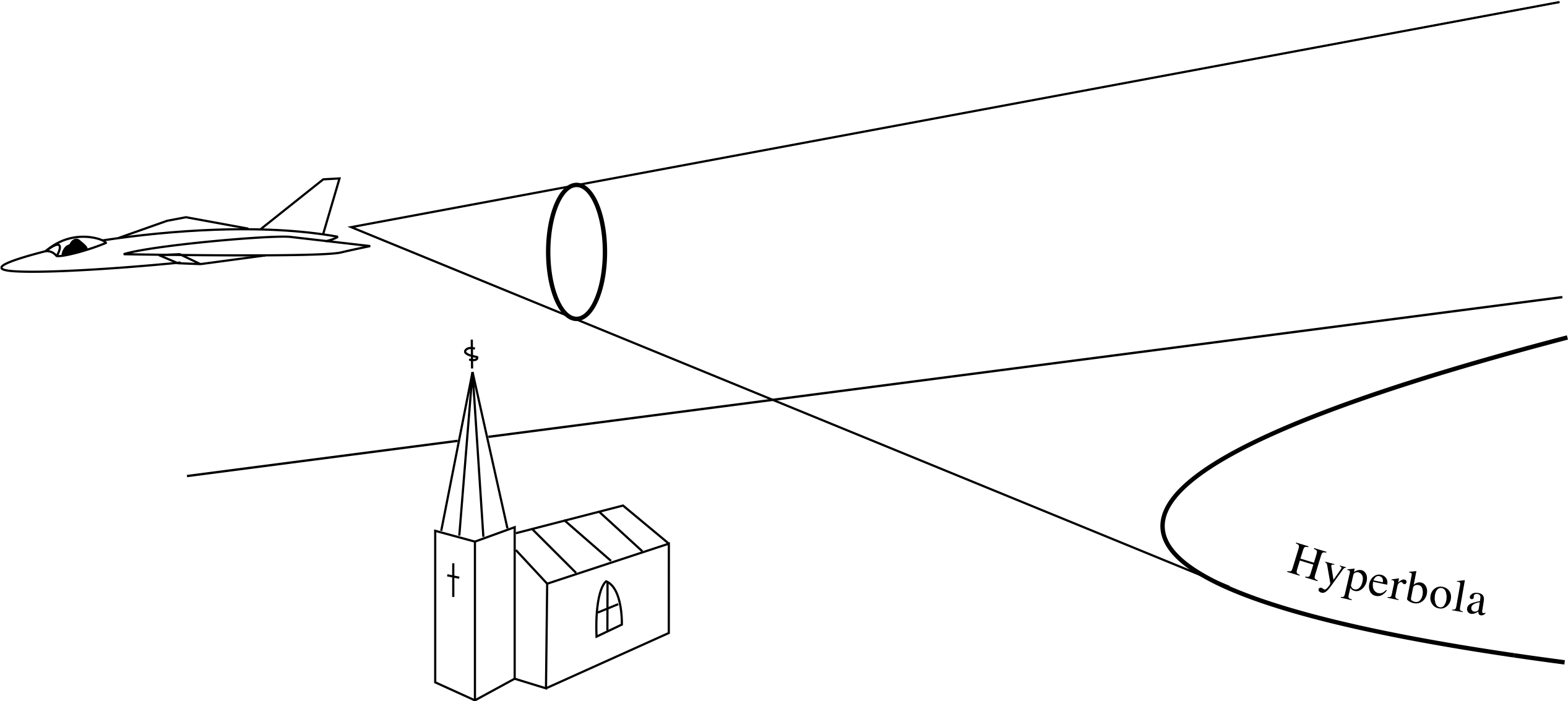
Figure 16 Effect of sonic boom.
There is one important feature of the hyperbola which is not present in the other curves we have considered. The dashed lines in Figure 15 correspond to the equations
$y=\pm\dfrac ba x$(25)
The branches of the hyperbola are ‘hemmed in’ by these lines as x and y both become large in magnitude. The hyperbola approaches one of these lines ever more closely but does not touch or cut it. These lines are called asymptotes, and the hyperbola is the only conic section which possesses them.
The sonic boom from a supersonic jet is a shock cone which trails behind the jet. At the surface of this cone there is a sudden change of pressure which causes the sonic boom. The intersection of the cone with the ground is (usually) a branch of a hyperbola, and the strength of the bang decreases as the distance from the aircraft increases. See Figure 16.
The asymptotes are a useful aid in sketching a hyperbola.
✦ What is the equation of the hyperbola which passes through the points (−4, 0) and ($2\sqrt{5\os}$, 1)? What are the equations of its asymptotes?
✧ Substituting (−4, 0) into Equation 24,
$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} = 1$(Eqn 24)
we obtain 16/a2 = 1, so that a = 4.
For ($2\sqrt{5\os}$, 1) the resulting equation is
$\dfrac{20}{16}-\dfrac{1}{b^2}=1$ so that $\dfrac{1}{b^2}=\dfrac14$ and b = 2.
Hence the equation is $\dfrac{x^2}{16}-\dfrac{y^2}{4}$, and from Equation 25,
$y=\pm\dfrac bax$(Eqn 25)
the asymptotes have equations
y = $\pm\dfrac24x$, i.e. y = ± x/2.
Tangents and normals to the hyperbola
The derivation of the equation of the tangent is almost identical to that for the ellipse. You may omit the following question if you are unsure of calculus, but notice that Equation 26 is the equation of a tangent to the hyperbola of Equation 24 at the point (x1, y1).
$\dfrac{x_1 x}{a^2} - \dfrac{y_1 y}{b^2} = 1$(Eqn 26)
$\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1$(Eqn 24)
✦ Find the equation of the tangent line at a point P(x1, y1) on the hyperbola defined by Equation 24.
✧ Differentiating Equation 24,
$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$(Eqn 24)
implicitly we obtain
$\dfrac{2x}{a^2}=\dfrac{2y}{b^2}\dfrac{dy}{dx}=0$
so that
$\dfrac{dy}{dx}=\dfrac{b^2 x}{a^2 y}$
To find the tangent at P(x1,y1) on the hyperbola we first note that the gradient at this point is $\dfrac{b^2 x_1}{a^2 y_1}$.
The equation of the tangent at P is therefore
$y-y_1 = \dfrac{b^2 x_1}{a^2 y_1}(x-x_1)$
which gives us
$\dfrac{x_1 x}{a^2}-\dfrac{y_1 y}{b^2} = \dfrac{x_1^2}{a^2}-\dfrac{y_1^2}{b^2}=1$
The equation of the tangent line at a point P(x1, y1) on the hyperbola is therefore
$\dfrac{x_1 x}{a^2}-\dfrac{y_1 y}{b^2} = 1$(Eqn 26) i
Question T11
Find the equations of the tangent and normal to the hyperbola 9x2 − 4y2 = 36 at the point (4, $3\sqrt{3\os}$).
Answer T11
The hyperbola is $\dfrac{x^2}{4} - \dfrac{y^2}{9} = 1$.
Then from Equation 26,
$\dfrac{x_1 x}{a^2} - \dfrac{y_1 y}{b^2} = 1$(Eqn 26)
the equation of the tangent at (4, $3\sqrt{3\os}$) is $4x/4-3\sqrt{3\os}y\big /9=1$, which simplifies to $3\sqrt{3\os}x-y=\sqrt{3\os}$
The gradient of this tangent is \sqrt{3\os} so that the gradient of the normal is $\dfrac{1}{\sqrt{3\os}}$.
It has equation $y-3\sqrt{3\os}=\dfrac{1}{\sqrt{3\os}}(x-4)$, which simplifies to $x+\sqrt{3\os}y=13$.
Parametric equations for a hyperbola
The hyperbolic functions cosh and sinh are defined by
$\cosh x = \dfrac{\rm{e}^x+\rm{e}^{-x}}{2}$ and $\sinh x = \dfrac{\rm{e}^x-\rm{e}^{-x}}{2}$(27)
where ex is the exponential function. i
We need to know very little about these functions in this module, except for the fact that they satisfy the following useful identity.
✦ Show that cosh2 θ − sinh2 θ = 1
✧ $\cosh^2\theta-\sinh^2\theta=\left(\dfrac{e^x+e^{-x}}{2}\right)^2-\left(\dfrac{e^x-e^{-x}}{2}\right)^2 = \left(\dfrac{e^{2x}+2+e^{-2x}}{4}\right)-\left(\dfrac{e^{2x}-2+e^{-2x}}{4}\right)=1$
✦ Show that the point x = a cosh θ, y = b sinh θ lies on the hyperbola of Equation 24.
$\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1$(Eqn 24)
✧ $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} = \cosh^2\theta-\sinh^2\theta$
We may now use the equations
x = a cosh θ and y = b sinh θ(28)
to parametrize the hyperbola because Equation 24,
$\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1$(Eqn 24)
is satisfied for any value of θ.
The functions cosh and sinh are known as hyperbolic functions precisely because of this association with the hyperbola. Just as for the ellipse, we can show that the tangent to the hyperbola at θ = θ1 has equation
$\dfrac{\cosh\theta_1}{a}x - \dfrac{\sinh\theta_1}{b}y = 1$(29)
The polar equation of a hyperbola is Equation 23,
L/r = 1 + e cos θ(Eqn 23)
where L is a fixed length, and e > 1 (we have already seen the cases e = 1 and 0 < e < 1 when we discussed the parabola and the ellipse).
A famous example from physics
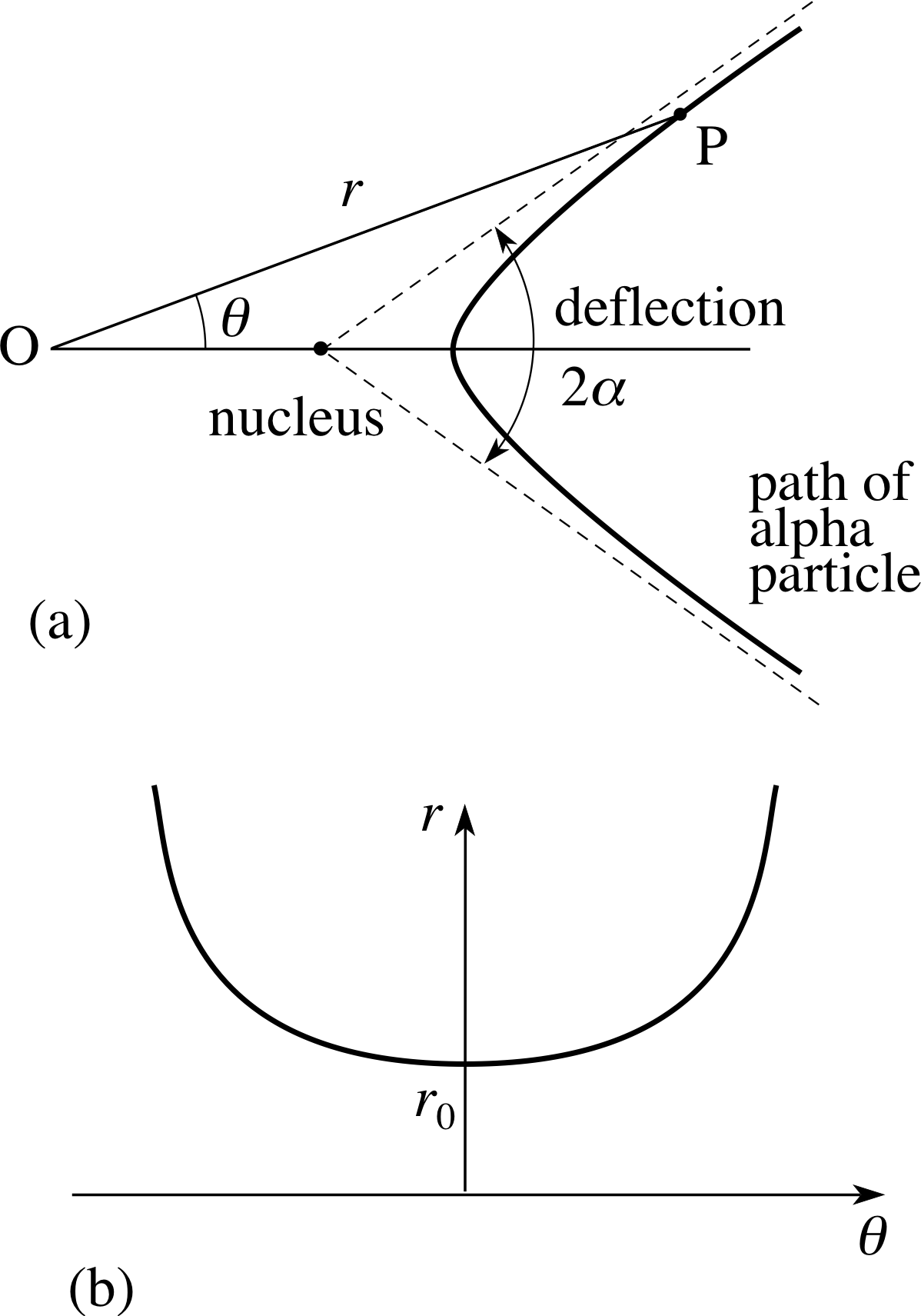
Figure 17 (a) The path of an alpha particle near the nucleus of an atom. (b) An upper estimate for the size of the nucleus.
When an alpha–particle passes close to the nucleus of an atom (of gold say) a certain mathematical model based on the inverse square law predicts that its path will be a hyperbola. We imagine an alpha–particle heading along a straight line towards the nucleus, and then being deflected through an angle, 2ϕ say, which we can measure, as in Figure 17a. The paths along which the particle approaches and retreats from the nucleus lie close to the asymptotes of a hyperbola, and when r is very large we have θ ≈ ±ϕ so that, from Equation 23 we have
1 + e cos ϕ = 0 and therefore $e = -\dfrac{1}{\cos\phi}$
and Equation 23 becomes $r = -\dfrac{L\cos\phi}{\cos\phi-\cos\theta}$
where ϕ and L are constants to be determined by experiment.
Figure 17b shows a typical graph of r plotted against θ (not a conic) and the significant point to notice is that there is a minimum value for r, say r0.
We conclude that this minimum value of r provides an upper estimate for the size of the nucleus. A similar calculation was first performed by Lord Rutherford i in the early years of the 20th century; prior to this time very little was known about the size of the nucleus.
Rectangular hyperbola
A special case arises when a = b, for then Equation 24,
$\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1$(Eqn 24)
reduces to
x2 − y2 = a2(30)
and the asymptotes (from Equation 25)
$y=\pm\dfrac ba x$(Eqn 25)
are y = x and y = −x, which are perpendicular to each other. Such a curve is known as a rectangular hyperbola.
Question T12
Find the equations of the tangents to the hyperbola $\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1$ that pass through the point S(a/2, 0).
Answer T12
From Equation 29,
$\dfrac{\cosh\theta_1}{a}x - \dfrac{\sinh\theta_1}{b}y = 1$(Eqn 29)
the tangent at the point on the hyperbola corresponding to the parameter θ is
$\dfrac{\cosh\theta}{a}x - \dfrac{\sinh\theta}{b}y = 1$, and this passes through the point (a/2, 0) if $\dfrac{\cosh\theta}{a}\left(\dfrac a2\right) - \dfrac{\sinh\theta}{b}0 = 1$, i.e. if cosh θ = 2.
Since sinh2 θ = cosh2 θ − 1 it follows that
$\sinh\theta = \pm\sqrt{\cosh^2\theta-1}=\pm\sqrt{4-1\os} = \sqrt{3\os}$
The equations of the tangent lines are therefore $\dfrac2a x\pm\dfrac{\sqrt{3\os}}{b}y=1$.
The following alternative form of the rectangular hyperbola, which you may have seen before, arises in many applications:
$y = \dfrac{c^2}{x}$(31)
Such a rectangular hyperbola has the x– and y–axes as its asymptotes. Equation 31 can be obtained from Equation 30 by rotating the axes about the origin through 90°, but the details are beyond the scope of this module.
✦ Show that x = ct, y = c/t is a parametrization of the rectangular hyperbola xy = c2.
✧ If x = ct and y = c/t then xy = (ct)(c/t) = c2.
✦ Find the equation of the line joining the points on the rectangular hyperbola (ct1, c/t1) and (ct2, c/t2).
✧ The slope of the line is
$\dfrac{(c/t_2)-(c/t_1)}{ct_2-ct_1}=-\dfrac{1}{t_1 t_2}$
The equation of the line is
$y-\dfrac{c}{t_2}=-\dfrac{1}{t_1 t_2}(x-ct_2)$
which gives us
t1t2y + x − c (t1 + t2) = 0
The result of the previous exercise can be used to find the equation of the tangent to the hyperbola at the point x = ct, y = c/t. Putting t1 = t1 = t, so that the two points coincide, we obtain
t2y + x − 2tc = 0(32)
3 The general form of a conic
3.1 Classifying conics
In this short section we mention very briefly some topics which do not arise very often in physics, but nevertheless they might cause you some difficulties on the rare occasions they do occur if you have never seen them before.
It can be shown that the general equation
Ax2 + 2Hxy + By2 + 2Gx + 2Fy + C = 0(33)
includes all the different types of conics: circles, ellipses, parabolas and hyperbolas. We state without proof that the following conditions determine the nature of the conic:
(a) H = 0, A = B ≠ 0 is a circle i
(b) H 2 = AB is a parabola
(c) H 2 < AB is an ellipse
(d) H 2 > AB is a hyperbola.
✦ What type of conic is defined by the equation 3x2 + 4xy + 3y2 − 8x + 2y + 4 = 0? (34)
✧ In this example H = 2, A = B = 3 so that H 2 = 4 and AB = 9.
Since H 2 < AB the curve is an ellipse.
Equation 34 represents an ellipse, but not the sort of ellipse with which we are familiar. Very roughly speaking, the xy term indicates that the ellipse has undergone a rotation so that its major and minor axes no longer coincide with the coordinate axes. The linear x and y terms indicate that the centre of the ellipse is not at the origin of coordinates so that the ellipse has undergone a translation.
Question T13
To which class of conic does each of the following belong?
(a) 5x2 + 6xy − 4y2 + 2x + 4y − 3 = 0
(b) 2x2 + 3xy + 2y2 + 2 = 0
Answer T13
(a) Here A = 5, B = −4, H = 3 and H 2 = 9 > −20 = AB. The curve is a hyperbola.
(b) A = 2, B = 2, H = $\frac32$ and H 2 = $\frac94$ < 4 = AB. The curve is an ellipse.
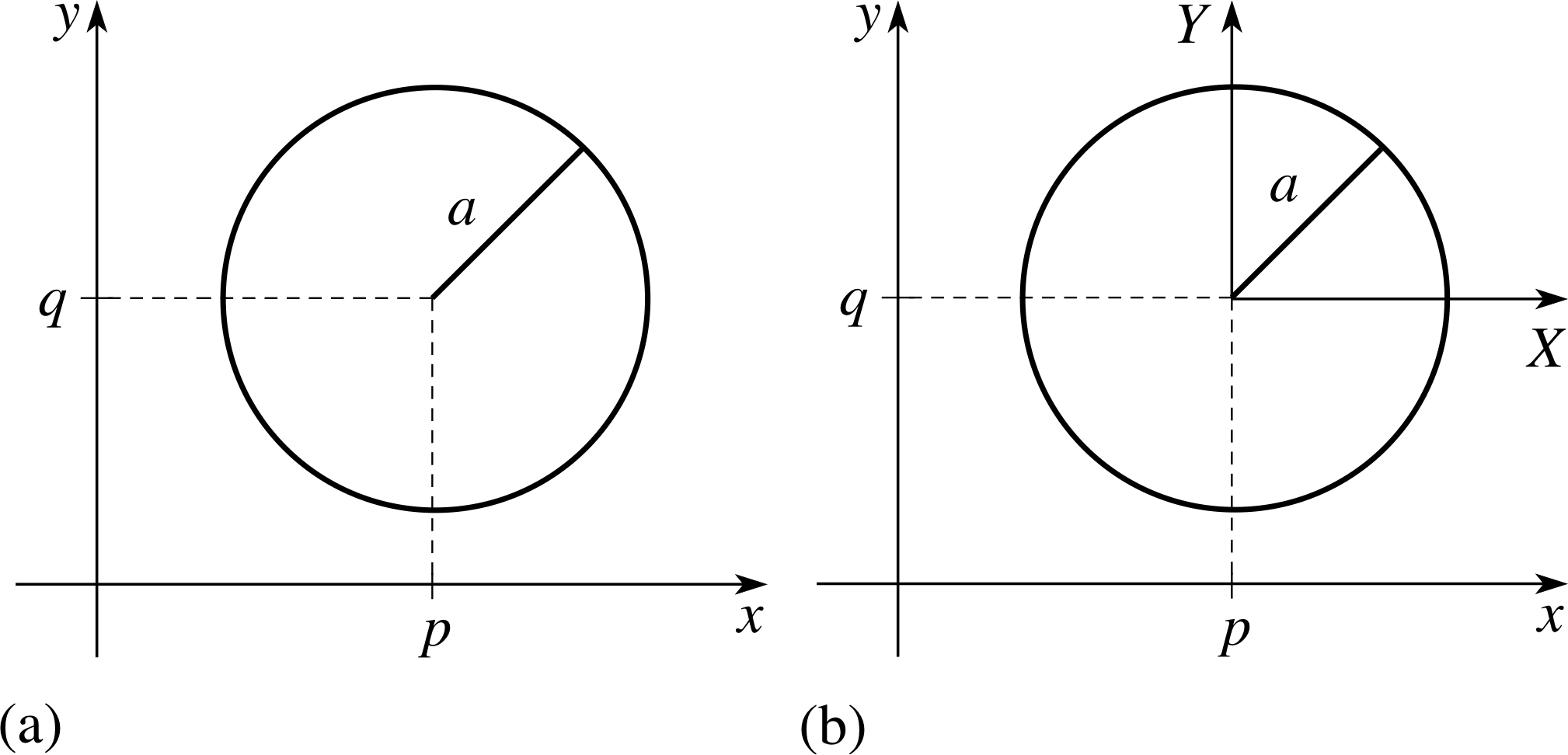
Figure 18 Translation of axes.
3.2 Changing the axes
Let us consider the equation (x − p)2 + (y − q)2 = a2. If we draw a graph of this for particular values of p, q, and a, we get a circle, with centre (p, q) and radius a (Figure 18a). Now if we make the substitutions X = x − p, and Y = y − q we get X 2 + Y 2 = a2, and this amounts to drawing the figure in a new coordinate system referred to X– and Y–axes, whose origin is at the point (p, q) (Figure 18b).
✦ What is the equation of an ellipse centred at the point (2, 4) with major axis 10 parallel to the x–axis and minor axis 6 parallel to the y–axis?
✧ If this shape of ellipse was centred at (0, 0) its equation would be $\dfrac{x^2}{5^2}+ \dfrac{y^2}{3^2}= 1$ since
a = ½ × 10 and b = ½ × 6.
To effect the transformation we replace x by x − 2 and y by y − 4. The resulting equation is
$\dfrac{(x-2)^2}{25} + \dfrac{(y-4)^2}{9}= 1$
or written out in full
9x2 + 25y2 − 36x − 200y + 211 = 0.
Question T14
What is the effect on the standard equations of the ellipse and the hyperbola if they are moved so that they are centred at the point (−1, 2) with the directions of the major and minor axes unchanged?
Answer T14
Ellipse: $\dfrac{(x+1)^2}{a^2} + \dfrac{(y-2)^2}{b^2}=1$
Hyperbola: $\dfrac{(x+1)^2}{a^2} - \dfrac{(y-2)^2}{b^2}=1$
3.3 An example from electrostatics: equipotentials
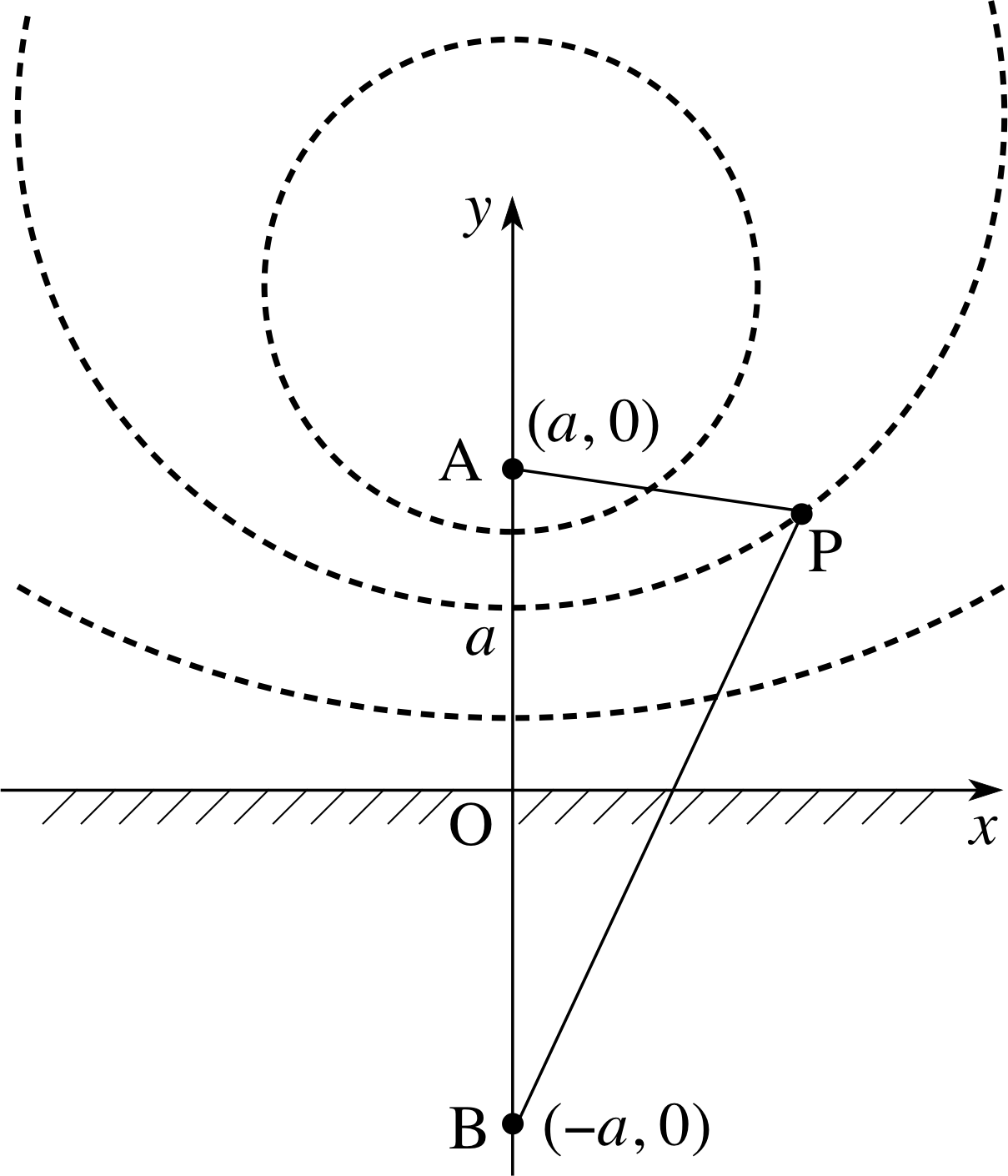
Figure 19 The equipotentials due to a line charge at A and a plane surface at zero potential along the x–axis.
You do not need to understand the physics in this example, but we will outline the physical background in order to set it in context. You have probably encountered static electricity when you comb your hair, or after walking on a nylon carpet. Lightning is probably the best known, and certainly the most impressive, manifestation of the phenomenon. Figure 19 represents an electrical charge distributed along a very long straight line at A(0, a) above a very large flat copper plate represented by the x–axis. Since we are viewing ‘edge on’, all we see of the line charge is a point (namely A) and similarly we see only the edge of the metal plate (along the x–axis). We suppose that the plate is earthed, or more technically, we say that it is at zero potential. The line charge and the metallic surface combine to create an electric field, and a small point charge will experience a force due to this field. The magnitude and direction of this force depend on where the point charge is placed. Through each chosen point there is a curve, called an equipotential lineequipotential with the property that no work is required to move a point charge along the curve. In many respects the equipotentials are similar to the contour curves on a map showing points of equal height above sea level, in that relatively little effort is required to walk along such paths.
The force experienced by a small charge is always perpendicular to the equipotential through the location of the charge.
In Figure 19 the dashed lines represent the equipotentials, and B(0, −a) is the image of the point A(0, a) in the flat surface (as in a mirror). It is known that the equipotentials have the property that AP/PB = λ, a constant. Different choices of the value of λ will produce the various equipotentials. In this example we shall investigate the nature of these curves.
First we suppose that P has coordinates (x, y). Then, (AP)2 = λ2(PB)2 we have, for a particular value of λ,
x2 + (y − a)2 = λ2[x2 + (y + a)2]
which can be rearranged to give
$x^2 + y^2 - 2ay\dfrac{1+\lambda^2}{1-\lambda^2} + a^2\lambda^2 = 0$(35)
This equation corresponds to putting H = 0 and A = B = 1 in Equation 33,
Ax2 + 2Hxy + By2 + 2Gx + 2Fy + C = 0(Eqn 33)
and we see immediately that the equipotentials are circles. If we compare Equation 35 with Equation 8,
x2 + y2 + 2Gx + 2Fy + C = 0(Eqn 8)
we see that G = 0 and F = −a (1 + λ2)/(1 − λ2), so that the centre of the Ox circle is at (0, a (1 + λ2)/(1 − λ2)) on the y–axis. For λ = 1 we have
AP = PB and the equipotential lies along the x–axis (see Figure 19). For λ < 1 the equipotentials are circles in the upper half-plane. For small values of λ, P is close to A, so that the equipotential is a circle which is close to A. In the case λ = 0 the point P is actually at A and the equipotential reduces to a single point.
(The case λ > 1 is of no interest since it gives rise to circles which lie below the x–axis, and these do not correspond to equipotentials.)
4 Closing items
4.1 Module summary
- 1
-
Section 3Conic sections, or Section 3conics, are the curves which arise when a double cone is cut by a plane. The main classes are Subsection 2.3parabolas, Subsection 2.4ellipses and Subsection 2.5hyperbolas; the Subsection 2.2circle is a special case of the ellipse.
- 2
-
The following table summarizes the main results:
Conic Circle Parabola Ellipse Hyperbola eccentricity e = 0 e = 1 0 ≤ e < 1 e >1 focus (a, 0) (±ae, 0) (±ae, 0) directrix x = −a x = ±a/e x = ±a/e standard equation $x^2+y^2=a^2$
centre (0, 0) radius a$y^2=4ax$ $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$
$b=a\sqrt{1-e^2}$$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$
$b=a\sqrt{e^2-1}$asymptotes none none none $y=\pm\dfrac ba x$ parametric form x = a cos θ
y = a sin θx = at2
y = 2atx = a cos θ
y = b sin θx = a cosh θ
y = b sinh θtangent at (x1, y1) x1x + y1y = a2 y = 2a (x + x1) $\dfrac{x_1 x}{a^2}+\dfrac{y_1 y}{b^2}=1$ $\dfrac{x_1 x}{a^2}-\dfrac{y_1 y}{b^2}=1$ polar form r = a, centre (0, 0), radius a
r = 2a cos θ, centre (a, 0), radius aL/r = 1 + cos θ L/r = 1 + e cos θ
0 ≤ e < 1L/r = 1 + e cos θ
e > 1some other forms
and special cases(x − p)2 + (x − q)2 = a2
centre (p, q) radius a
x2 + y2 + 2Gx + 2Fy + C = 0
centre (−G, −F)
radius $\sqrt{G^2+F^2-C}$y = Ax2 + Bx + C rectangular hyperbola
x2 − y2 = a2
rectangular hyperbola
$y = \dfrac kx $graph see Figure 4a see Figure 4b see Figure 4c see Figure 4d - 3
-
The general equation of a conic has the form Ax2 + 2Hxy + By2 + 2Gx + 2Fy + C = 0.
(a) H = 0, A = B ≠ 0 a circle
(b) H 2 = AB a parabola
(c) H 2 < AB an ellipse
(d) H 2 > AB a hyperbola
When the axes are translated (or rotated) then it is possible to obtain the equation of a conic relative to the new coordinates.
4.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Recognize the graphs of the main types of conic sections, write down their equations in standard form, and explain how the value of the eccentricity governs the nature of the conic.
- A3
-
Appreciate that a tangent to a curve is a line that touches the curve at one point, and use the equations of the tangents to the conics.
- A4
-
Use the parametric representations of the conics.
- A5
-
Appreciate that a circle is a particular case of an ellipse, and that ellipses are the only bounded conics.
- A6
-
Determine the equations of the asymptotes of a hyperbola in standard form.
- A7
-
Recognize the various forms of the equations of the conics, in particular a circle centred at the point (p, q), the general equation of a circle, a rectangular hyperbola and in particular a rectangular hyperbola whose asymptotes are the coordinate axes.
- A8
-
Recognize the polar forms of the conics.
- A9
-
Recognize the general form of a conic.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
4.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions each of which tests one or more of the Achievements.
Question E1 (A2, A7, A8 and A9)
Classify the following conics as circles, ellipses, parabolas or hyperbolas:
(a) y2 + (x − 1)2 = 4
(b) x (x + y) = 2
(c) 4x2 + 9y2 = 1
(d) r = 2 cos θ
(e) $\dfrac 2r = 1 + 5\cos\theta$
(f) $r = \dfrac{1}{1+\cos\theta}$
(g) xy = 4
(h) x2 + y2 + x + y = 0
Answer E1
(a) A circle with centre at (1, 0) and radius 2.
(b)The equation can be written as x2 + xy − 2 = 0. In the general equation, Equation 33, we have A = 1, B = 0 and H = 1/2. Since H 2 > AB the curve is a hyperbola.
(c) An ellipse centred at the origin, with a = 1/2 and b = 1/3 in Equation 19.
(d) The polar form of a circle centred at (1, 0) with radius 1. See Equation 10.
(e) Polar form of a hyperbola. See Equation 23, with e > 1.
(f) The equation can be written as 1/r = 1 + cos θ, the polar form of a parabola.
(g) A rectangular hyperbola (with its asymptotes along the coordinate axes).
(h) A circle with centre at (−1/2, −1/2) and radius $1/\sqrt{2\os}$.
If you had difficulty with this question look at the Table 5Table in the Section 4Module summary.
Question E2 (A3, A7 and A9)
(a) Show that the line x + 3y = 1 is a tangent to the circle x2 + y2 − 3x − 3y + 2 = 0 and find the coordinates of the point of contact. Use Equation 8 to find the centre and radius of this circle.
(b) Prove, by calculation, that the point P(3, 2.5) lies outside the circle and calculate the length of a tangent to the circle from P.
Answer E2
(a) Substitute x = 1 − 3y into the equation of the circle (rather than substituting for y since we then avoid fractions). Then (1 − 3y)2 + y2 − 3 (1 − 3y) − 3y + 2 = 0, which simplifies to give 10y2 = 0, so that y = 0 is a repeated root, and (1, 0) is the only point of contact.
A circle x2 + y2 + 2Gx + 2Fy + C = 0 has its centre at the point (−G,−F) and its radius is $\sqrt{G^2+F^2-C}$. In this case G = −3/2, F = −3/2 and C = 2 so the centre is at $\left(\frac32,\,\frac32\right)$ and its radius is $\sqrt{5\os}\big /2$.
Alternatively, you may be able to spot that the equation of the circle can be written as $\left(x-\frac32\right)^2 + \left(y-\frac32\right)^2=\frac52$, so that it is a circle centred at $\left(\frac32,\,\frac32\right)$ and its radius is $\sqrt{5\os}\big /2$.
(b) The distance of (3, 2.5) from the centre is
$\sqrt{\left(3-\frac32\right)^2+\left(\frac52-\frac32\right)^2} = \sqrt{\frac94+\frac44}=\sqrt{13\os}\big /2$
which is greater than the radius. The point P(3, 2.5) therefore lies outside the circle.
Let T be a point where a tangent from P meets the circle and let C be the centre of the circle, then, since PTC is a right–angled triangle,
we have (PT)2 = (PC)2 − (CT)2 = $\frac{13}{4}-\frac52=\frac34$ so that the distance PT = $\sqrt{3\os} \big /2$
If you had difficulty with this question, you should reread Section 2.2.
Question E3 (A2, A3, A4 and A8)
The normal to the parabola y2 = 4ax at the point P(at2, 2at) meets the x–axis at the point G, and GP is extended, beyond P, to the point Q so that PQ = GP. Show that Q lies on the curve y2 = 16a (x + 2a). What kind of curve is this?
Answer E3
From Equation 16,
y + tx = 2at + at3(Eqn 16)
the normal to the parabola at P(at2, 2at) has equation y + tx = 2at + at3.
It meets the x–axis where y = 0 and x = 2a + at2.
Since QP = PG it follows that if Q is the point (x1, y1) then y1 = 4at (twice the y–coordinate of P) and substituting this value for y into the equation of the normal gives 4at + tx1 = 2at + at3, from which we see that x1 = at2 − 2a.
Eliminating t between the equations y1 = 4at and x1 = at2 − 2a gives y12 = 16a (x1 + 2a) so that Q lies on the required curve. Using the general equation of a conic, Equation 33,
Ax2 + 2Hxy + By2 + 2Gx + 2Fy + C = 0(Eqn 33)
we see that H = 0 and A = 0 which gives H 2 = AB so that the curve is a parabola.
If you had difficulty with this question, you should reread Subsection 2.3.
Question E4 (A2, A4, A5 and A6)
Find the equations of the tangents to the ellipse x2 + 2y2 = 8 which are parallel to the asymptotes of the hyperbola 4x2 − y2 = 1.
Answer E4
The asymptotes of the hyperbola are y = ±2x. The ellipse can be written as x2/8 + y2/4 = 1 and suppose that (x1, y1) is a point P on the curve. From Equation 20,
$\dfrac{x_1 x}{a^2}+\dfrac{y_1 y}{b^2}=1$(Eqn 20)
the tangent at P is x1x/8 + y1y/4 = 1 which can be rearranged to give
$y=-\dfrac{x_1}{2y_1}+\dfrac{4}{y+1}$ and we require the slope of this line to be ±2.
Thus −x1/2y1 = ±2, which gives x1 = ±4y1 and, since P lies on the ellipse we have x12/8 + y12/4 = 1.
Substituting for x1, we have (±4y1)2/8+ y12/4 = 1 which gives $y_1 = \pm\dfrac23$ and therefore $\dfrac{4}{y_1} = \dfrac{4}{\pm 2/3} = ±6$.
It follows that there are four tangent lines that satisfy the required conditions given by the equations y = 2 x ± 6 and y = −2x ± 6.
If you had difficulty with this question, you should reread Subsection 2.4Subsections 2.4 and Subsection 2.52.5.
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 4Closing items. i