MATH 2.5: Working with vectors |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
When modelling the physical world mathematically we need to use quantities that can be measured. Such physical quantities mainly fall into two classes, scalars and vectors. The mathematics of scalars such as mass and temperature is simply the familiar mathematics of real numbers and functions, but the mathematics of vector quantities such as force and velocity, which have both a magnitude and a direction, is quite different, and is the subject of this module. Vectors are often introduced as geometric entities – more like arrows than numbers. Our main purpose in this module is to show you how the study of vectors may be transformed from geometry to algebra.
Section 2 of this module reviews the definition of scalar and vector quantities, the graphical (or geometric) representation of vectors, and the notation used in referring to vector quantities. (A more detailed introduction is given elsewhere in FLAP.) This section also reviews the basic operations of scaling, vector addition and vector subtraction in terms of the geometric representation. The section ends with a review of the resolution of vector quantities into component vectors, using the geometric representation.
Section 3 introduces the use of unit vectors to denote directions and, in particular, the use of i, j, and k to specify the directions of the x–, y–, and z–axes in a right–handed Cartesian coordinate system. Section 3 continues by showing how these Cartesian unit vectors may be used to represent any vector in three dimensions, and then how vectors represented in Cartesian form may be manipulated in some of the basic operations of vector algebra, such as scaling and vector addition.
Section 4 introduces an alternative algebraic representation of vector quantities in terms of ordered triples of numbers. Sections 3 and 4 each conclude with a specific example which illustrates how, in practice, vector operations may be carried out using the Cartesian form, or the ordered triple representations, respectively.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 5.1Module summary and the Subsection 5.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 5.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
Three forces F1, F2 and F3 acting on a particle are such as to keep the particle in equilibrium. F1 and F2 are given as F1 = (−i + 2 j + 4 k) newtons and F2 = (−i − 5 k) newtons.
(a) Find the vector F3.
(b) Suppose the magnitude of F1 is doubled, and the magnitude of F3 is tripled (without changing their directions), while F2 remains unchanged. Find the new resultant force acting on the particle, the magnitude of this resultant force, and the unit vector acting in the direction of this resultant force.
Answer F1
(a) If the particle is in equilibrium then F1 + F2 + F3 = 0 and therefore
F3 = −(F1 + F2)
so thatF3 = −[(−i + 2 j + 4 k) + (−i − 5 k)] N = −(−2 i + 2 j − k) N = (2 i − 2 j + k) N
(b) Now 2F1 = (−2 i + 4 j + 8 k) N, F2 = (−i − 5 k) N
and3F3 = (6 i − 6 j + 3 k) N
so that2F1 + F2 + 3F3 = (3 i − 2 j + 6 k) N
Using Equation 8,
| a | = (ax2 + ay2 + az2)1/2(Eqn 8)
| 2F1 + F2 + 3F3 | = [32 + (−2)2 + 62]1/2 N = 7 N
Using Equation 1,
$\hat{\boldsymbol a} = \dfrac{{\boldsymbol a}}{\left\lvert\,{\boldsymbol a}\,\right\rvert}$(Eqn 1)
the required unit vector is obtained by dividing the vector 2F1 + F2 + 3F3 by | 2F1 + F2 + 3F3 |
it is therefore
$\left(\dfrac37{\boldsymbol i} - \dfrac27{\boldsymbol j} + \dfrac37{\boldsymbol k}\right)$ ≈ 0.429 i − 0.286 j + 0.857 k
Question F2
In the absence of an air current, the velocity of a particle is given by υp = (2, 2, −1) m s−1. Find the resultant velocity of the particle, and the time taken for the particle to travel a distance of 5 m along its resultant path, when an air current of velocity υc = (−1, 1, 3) m s−1 is present.
Answer F2
υp + υc = (2, 2, −1) m s−1 + (−1, 1, 3) m s−2 = (1, 3, 2) m s−2
therefore | υp + υc | = [12 + 32 + 22]1/2 m s−2 = $\sqrt{14\os}$ m s−2
therefore time = distance/speed = (5/$\sqrt{14\os}$) s = 1.34 s
1.3 Ready to study?
Study comment Although the basic concepts of scalar and vector quantities are reviewed briefly in this module, it is assumed that you have some knowledge of these already. For example, you should be familiar with the definitions and methods of representation of scalar and vector quantities, and terms such as zero vector. You should understand the ideas of the scaling_of_a_vector by a scalarscaling of a vector quantity, the addition_of_vectorsaddition and vector_difference, and the resolution of vectors into component vectors. Also, you should be familiar with the terms: acceleration, displacement, electric charge, mass, momentum, temperature and velocity. In addition, it is assumed that you have met Newton’s laws of motion, and that you appreciate the conditions required for a particle to be in equilibrium. You should be familiar with basic mathematical concepts including the ideas of Cartesian coordinate systems, Pythagoras’s theorem and the use of trigonometric functions. You should understand also the ways in which directions may be given with respect to points of the compass. If you are uncertain about any of these terms then you can review them by reference to the Glossary which will indicate also where in FLAP they are developed. The following questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
A right–angled triangle ABC has sides AB and BC of length 12 cm and 5 cm, respectively. Angle AB^C is 90°. Determine the angles BA^C and AC^B and the length of the side AC.
Answer R1
From the definition of the tangent of an angle:
$\tan B\hat AC = \left(\dfrac{5}{12}\right)$ so that $B\hat AC = \arctan\left(\dfrac{5}{12}\right)$ ≈ 22.6°
so$A\hat CB$ ≈ 90° − 22.6° ≈ 67.4°
From Pythagoras’s theorem: AC = (25 + 144)1/2 cm = 13 cm
Consult Pythagoras’s theorem and tangent_to_a_curvetangent in the Glossary for further information.
Question R2
A ladder 5 m long stands on level ground with its highest point against a wall at a point 4.5 m above the ground. Determine the angle of inclination of the ladder to the ground, and the distance of the foot of the ladder from the bottom of the wall.
Answer R2
Let the angle of inclination be θ (i.e. the angle between the ladder and the ground), then from the definition of the sine of an angle:
sin θ = 4.5/5 so that θ = arcsin(4.5/5) ≈ 64.2°
From the definition of cosine, the distance of the foot of the ladder from the wall is
(5 cos θ) m = (5 cos 64.2°) m ≈ 2.18 m
Consult cosine and sine of an angle in the Glossary for further information.
Question R3
Points A and B are given by their Cartesian coordinates in two dimensions as (1, 2) and (4, 3), respectively. Determine the lengths OA, OB and AB, and the angle AO^B, where O is the origin of the coordinate system.
Answer R3
You may find it helpful to plot A and B on a Cartesian coordinate system.
From Pythagoras’s theorem: OA = (12 + 22)1/2 = 51/2 ≈ 2.24
Similarly: OB = (42 + 32)1/2 = 251/2 = 5
Also: AB = [(4 − 1 )2 + (3 − 2)2]1/2 = 101/2 ≈ 3.16
The angle between OA and the x-axis is arctan(2), while the angle between OB and the x-axis is arctan(3/4), so that
$A\hat OB$ = arctan(2) − arctan(3/4) ≈ 63.43° − 36.87° ≈ 26.6°
2 A brief review of scalars and vectors
2.1 What are scalars and vectors?
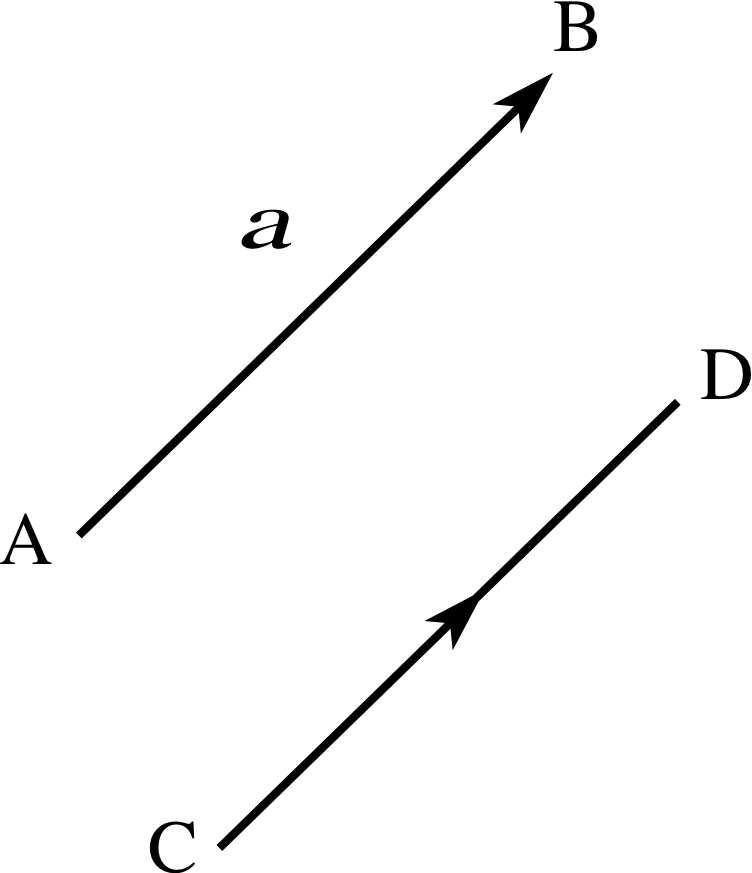
Figure 1 Vector a or $\overrightarrow{AB}$ is represented by an arrow, and $\overrightarrow{CD}$ by a directed line segment. Notice that while the vectors $\overrightarrow{AB}$ and $\overrightarrow{BA}$ have the same magnitude, they do not have the same direction, and they are therefore distinct vectors.
A vector is a mathematical object that has both magnitude and direction. Vectors may be represented diagramatically by arrows or directed line segments, as shown in Figure 1 where the magnitude and direction of a vector are indicated by the length and orientation of an arrow or line segment. These graphical representations of vectors are sometimes referred to as geometric vectors.
It is customary to use distinctive notation when referring to vectors in order to emphasize the importance of their direction as well as their magnitude. For example, the vector from A to B in Figure 1 can be denoted by $\overrightarrow{AB}$ and, similarly, the vector from C to D can be denoted $\overrightarrow{CD}$. Alternatively, and more commonly, we might denote the vector $\overrightarrow{AB}$ by a, where the bold typeface warns us that a is a vector with direction as well as magnitude.
It should be noted that geometric vectors are completely specified by their magnitude and direction so $\overrightarrow{AB}$ = $\overrightarrow{CD}$, even though they have been drawn at different points on the page.
The sum of two vectors is determined by the triangle rule, see Figure 2a, and the vector sum a + b is often known as the resultant vector. The result of adding any number of vectors, such as a, b, c, and d in Figure 2b, is obtained by simply joining them ‘nose to tail’.
While ‘geometric’ vectors are valuable concepts, their practical use is limited by the difficulty of drawing such objects in three dimensions, and the major purpose of this module is to show you how a geometric construction like that shown in Figure 2b for the sum of four ‘geometric’ vectors can be replaced by a simple form of algebra.
Scalar quantities
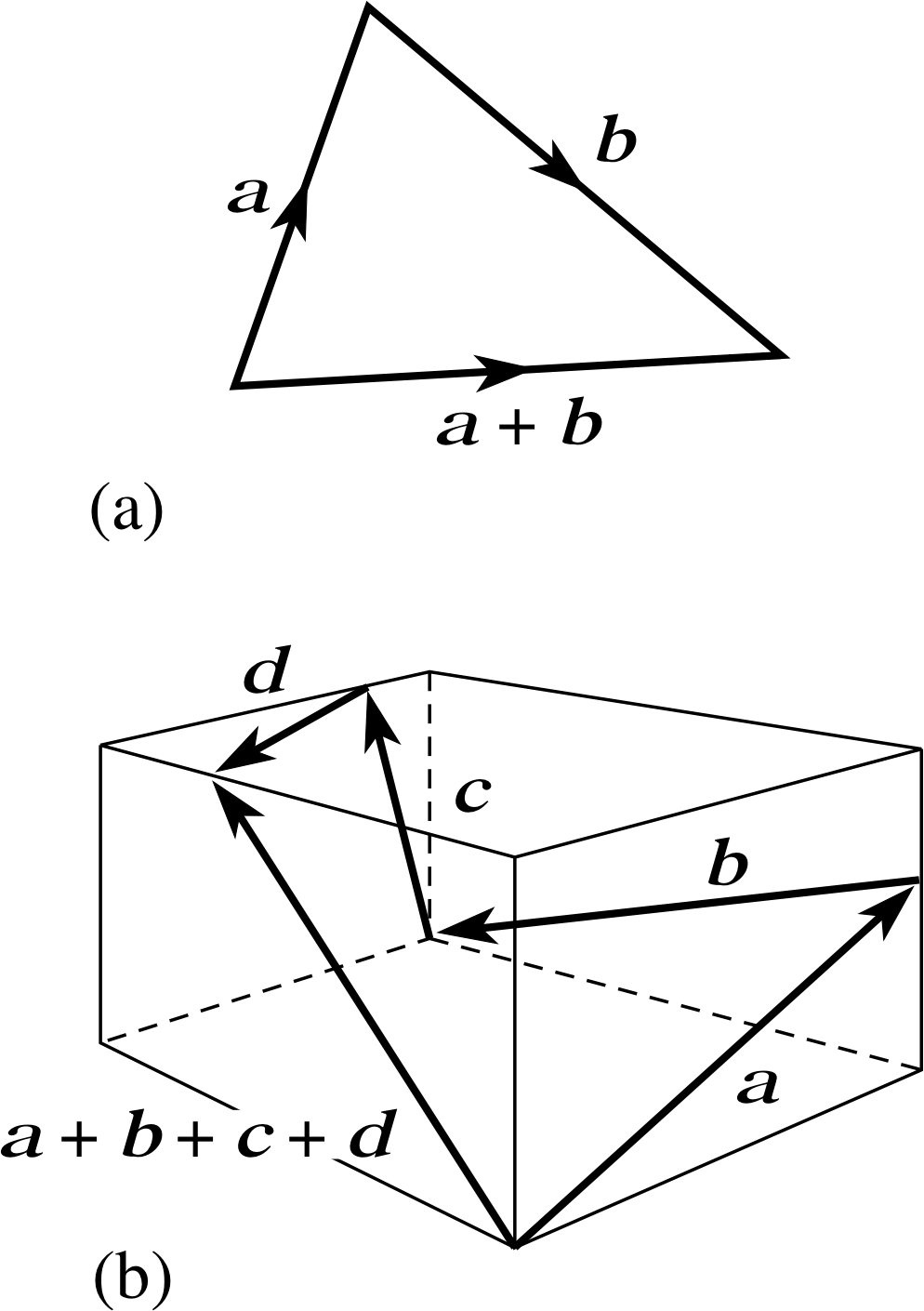
Figure 2 (a) The sum of two vectors obtained from the triangle rule. (b) The sum of four vectors (in three dimensions).
Many physical quantities can be specified completely by a single number together with an appropriate unit of measurement, for example length, mass, time and temperature. Such quantities are called scalar quantities or simply scalars, and we commonly denote them by symbols such as L, m, t and T. i
Vector quantities
There are many physical quantities, for example displacement, velocity, acceleration and force, which cannot be completely defined by their magnitudes (in the appropriate units); each of them is only really specified if we are also told the direction in which they act. The essence of such quantities is that they have both magnitude and direction, where the magnitude_of_a_vector_or_vector_quantitymagnitude is a non–negative scalar quantity which gives the ‘size’ of the quantity.
Vector quantities are physical quantities that have both magnitude and direction (and which can be adequately represented by geometric vectors).
Notation
In this module (and generally in FLAP) we will follow the standard convention of using bold type to indicate vectors, but in handwritten work it is usual to indicate a vector, a, by a wavy underline, $\underset{\boldsymbol{\raise 6pt \sim}}{a}$, i while a geometric vector or displacement vector from A to B may be written $\overrightarrow{AB}$.
In FLAP we usually denote the magnitude of a vector a by | a |, while in your written work you should use $\lvert\,\underset{\boldsymbol{\raise 6pt \sim}}{a}\,\vert$. (It is important that you remember to include the underline to denote a vector, and the vertical lines for a magnitude, in your written work.) i
You will also encounter an alternative notation, used by many authors, in which the magnitude of the vector a is denoted by an unemboldened a.
✦ Which of the following are vector quantities?
(a) Your weight, (b) the pressure at a certain depth in the sea, (c) a charging rhinoceros.
✧ (a) Your weight is a force, and is therefore a vector quantity. (Your mass, which is what you try to reduce when you diet, is a scalar.)
(b) The pressure in a liquid doesn’t have a direction, and is therefore a scalar.
(c) A charging rhinoceros certainly has magnitude and direction, but it is not a vector; the resultant of two rhinos, one heading north and another east, is not $\sqrt{2\os}$ rhinos heading north-east. i
✦ Is it generally true that | a + b | = | a | + | b |?
✧ No, it is not generally true, as we can see from Figure 2a. The length | a + b | of one side of the triangle is not generally equal to the sum of the lengths of the other two sides.
2.2 Scaling a vector, unit vectors and the zero vector
In order to scaling_of_a_vectorscale a vector a by a factor 2 say, we simply double its length, and denote the result by 2a, which is compatible with the triangle rule of addition because (as we would expect) we then have a + a = 2a.
The scaling factor may be positive or negative, so that, for example, if s is a displacement of 10 km north, then 3 s is a displacement of 30 km north; −2 s is a displacement of 20 km south, and dividing by 2, we have 1/2 s, or s/2, a displacement of 5 km north.
Unit vectors
If s is a displacement of 10 km north, then dividing s by 10 km produces a vector of magnitude 1 in the northerly direction.
In general, if we divide an arbitrary vector a by its magnitude we obtain a (dimensionless) vector in the same direction as a and of magnitude 1 (a dimensionless number). Such a vector is known as a unit vector in the direction of the vector a, and is denoted by $\hat{\boldsymbol a}$, so that
$\hat{\boldsymbol a} = \dfrac{{\boldsymbol a}}{\left\lvert\,{\boldsymbol a}\,\right\rvert}$(1)
✦ If $\hat{\boldsymbol n}$ is a unit vector pointing north, and $\hat{\boldsymbol w}$ is a unit vector pointing west, what is the magnitude of $\hat{\boldsymbol n} + \hat{\boldsymbol w}$?
✧ Adding according to the triangle rule, the magnitude of $\hat{\boldsymbol n} + \hat{\boldsymbol w}$ is $\sqrt{1^2 + 1^2} = \sqrt{2\os}$, from Pythagoras’s theorem. (Notice that it must be the positive square root, since magnitudes are always positive; and there are no dimensions.)
Question T1
If F represents a force directed vertically downwards, find a unit vector directed vertically upwards.
Answer T1
If F is vertically downwards, then the required unit vector upwards = −F/| F |.
The zero vector
We are intent on establishing an algebra of vectors, so clearly one of our requirements is a zero vector, 0, which is defined so that
a + (−1)a = 0(2)
for any vector a. The zero vector has magnitude zero, and its direction is undefined (since it is irrelevant). You may have noticed that we have written zero as a vector, since the sum of two vectors must of course be a vector, and you should use a wavy underline with every occurrence of the zero vector in your written work.
2.3 Addition and subtraction of vectors
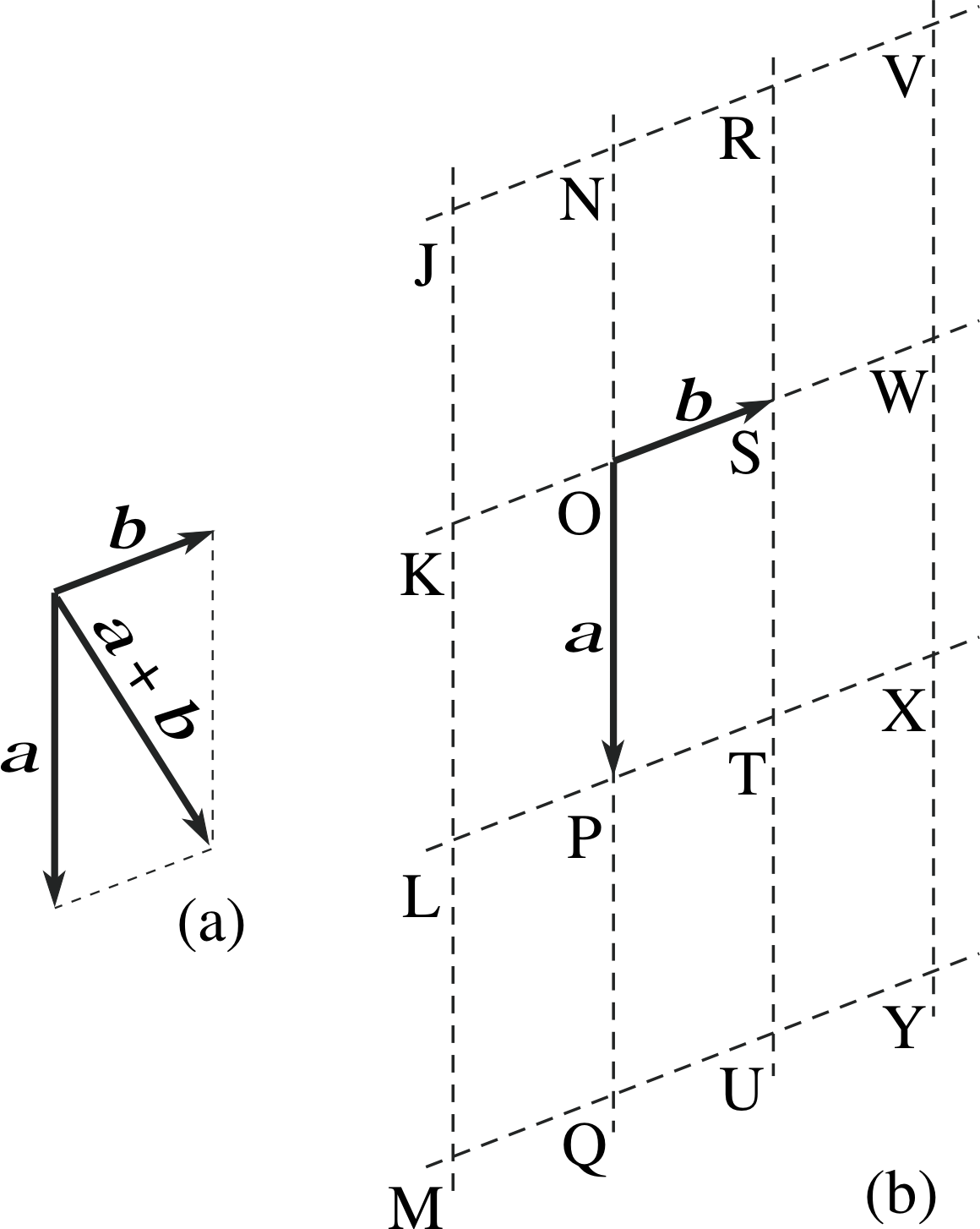
Figure 3 (a) The parallelogram rule of addition. (b) An array of points defining many different vectors.
The result of adding two vector quantities, say a and b, is determined by the triangle rule of Figure 2a, or equivalently by the parallelogram rule illustrated in Figure 3a and is of the same physical type as the original vectors. (The choice of rule is merely a matter of taste.)
We follow the practice of ordinary algebra and usually replace (−1)a by −a. The vector −a has the same magnitude as the vector a, but it acts in the opposite direction (it is antiparallel to a), for example, in Figure 3b $\overrightarrow{JN} = -\overrightarrow{NJ}$. One further point, which we take for granted in ordinary algebra, is that the order in which we add vectors is immaterial, so
a + b = b + a(3)
and
a + (b + c) = (a + b) + c(4)
Note A mathematician would recognize Equations 3 and 4 as the commutative and associative properties of vector addition, respectively.
Vector subtraction is achieved by scaling a vector by −1 and then using vector addition as before. i For example, in Figure 3b $\overrightarrow{OS}$ = b and therefore $\overrightarrow{SO}$ = −b, then $\overrightarrow{SP} = \overrightarrow{OP} + \overrightarrow{SO}$ = a + (−b) = a − b.
✦ With reference to Figure 3:
(a) Express the vector $\overrightarrow{JW}$ in terms of a and b,
(b) What is the final position of an object which is placed at R and then displaced by the vector 3 a − 2 b?
(c) Write down two vectors equal to 2 a + 2 b.
✧ (a) $\overrightarrow{JW}$ = $\overrightarrow{JN}$ + $\overrightarrow{NR}$ + $\overrightarrow{RV}$ + $\overrightarrow{VW}$ = b + b + b + a = 3 b + a.
(b) 3 a − 2 b =$\overrightarrow{RM}$ and so the final position of the object is M.
(c) $\overrightarrow{NX}$ = $\overrightarrow{KU}$ = 2 a + 2 b.
Remember that the position in which a geometric vector is drawn is not relevant, and the vectors $\overrightarrow{NX}$ and $\overrightarrow{KU}$ in Figure 3 are equal, in spite of the fact that they are defined by distinct line segments (and the vectors $\overrightarrow{JT}$ and $\overrightarrow{OY}$ would do equally well). Notice also 2 a + 2 b = 2 (a + b), which is a particular case of a more general rule, which states that for any scalar k:
k a + k b = k (a + b)(5) i
Question T2
With reference to Figure 3:
(a) express the vectors $\overrightarrow{KU}$, $\overrightarrow{WL}$ and $\overrightarrow{YK}$ in terms of a and b, (b) write down two vectors equal to 2 a − 3 b.
Answer T2
(a) In Figure 3,
$\overrightarrow {KU}$ = 2a + 2b, $\overrightarrow {WL}$ = a − 3b and $\overrightarrow {YK}$ = −2a − 3b.
(b) 2a − 3b = $\overrightarrow {WM} = \overrightarrow {VL}$.
2.4 Resolution of vectors, and component vectors
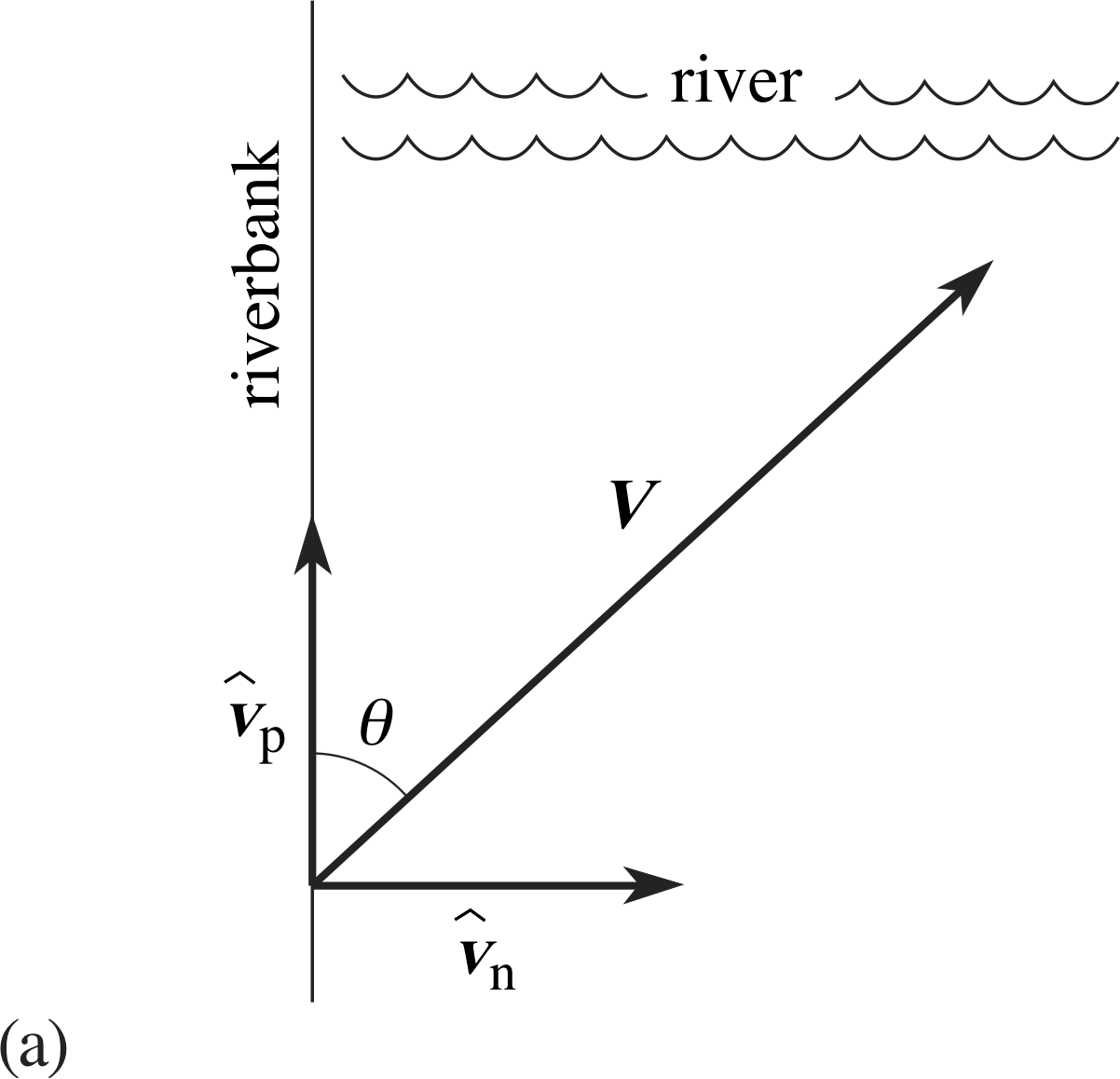
Figure 4 (a) Velocity V at an angle θ to the river bank, with unit vectors $\hat{\boldsymbol v}_{\rm n}$ and $\hat{\boldsymbol v}_{\rm p}$..
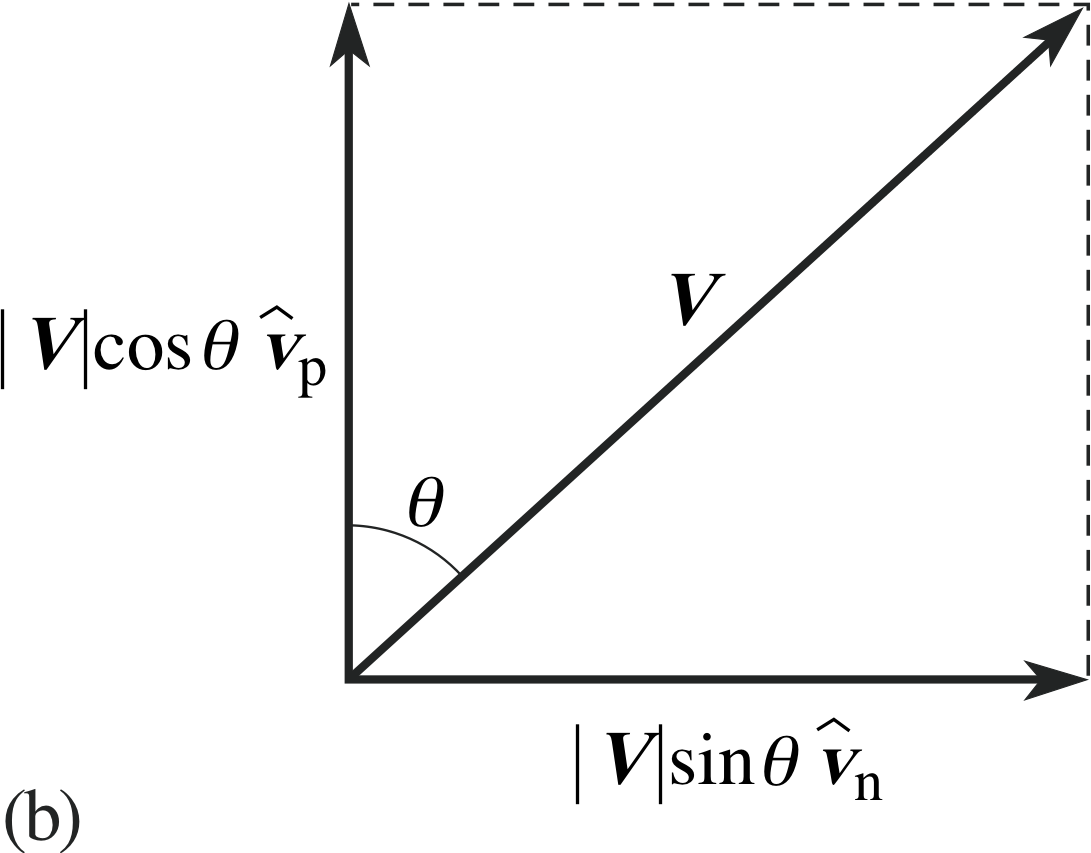
Figure 4 (b) Velocity V resolved into component velocities | V | sin θ $\hat{\boldsymbol v}_{\rm n}$ and | V | cos θ $\hat{\boldsymbol v}_{\rm p}$ normal to, and parallel to, the river bank.
Often when dealing with a vector quantity, we need to know how much the vector contributes in a given direction. For example, consider the two–dimensional situation in which a boat moves with velocity V across a river at an angle θ to the bank, as shown in Figure 4a. To find how long the boat takes to cross the river we need to find the effective velocity normal to (i.e. perpendicular to) the river bank. This can be obtained by treating the vector V as the vector sum of two orthogonal i component vectors normal to the bank and parallel to it. i
If $\hat{\boldsymbol v}_{\rm n}$ and $\hat{\boldsymbol v}_{\rm p}$ are unit vectors normal to, and parallel to the bank, respectively, then V can be written as the sum of two component vectors
so thatV = | V | sin θ $\hat{\boldsymbol v}_{\rm n}$ + | V | cos θ $\hat{\boldsymbol v}_{\rm p}$
The component vectors of V are in this case (see Figure 4b): | V | sin θ $\hat{\boldsymbol v}_{\rm n}$ in a direction normal to the bank, and of magnitude | V | sin θ, and | V | cos θ $\hat{\boldsymbol v}_{\rm p}$ in a direction parallel to the bank, and of magnitude | V | cos θ.
If the width of the river is d, we can now see that the time taken for the boat to cross is d/(| V | sin θ).
This process of resolution_of_a_vectorresolution (i.e. splitting) into component vectors can be thought of as the reverse of vector addition; instead of adding two (or more i) vectors to produce a single resultant vector, we are replacing a single vector by the sum of two orthogonal component vectors. Note that when these component vectors are added together we obtain our original vector.
✦ The string of a simple pendulum exerts a force F of magnitude 15 N on the pendulum bob, at an angle of 15° to the (upward) vertical. Resolve this force into horizontal and vertical component vectors.
✧ If $\hat{\boldsymbol v}$ and $\hat{\boldsymbol h}$ are unit vectors in the (upward) vertical direction and horizontal direction, respectively, then the force in the horizontal direction is
$\lvert\,F\,\vert \sin\theta\,\hat{\boldsymbol h} = (15 \sin 15°)\,\hat{\boldsymbol h} = (3.88\,{\rm N})\,\hat{\boldsymbol h}$
and the force in the vertical direction is
$\lvert\,F\,\vert \cos\theta\,\hat{\boldsymbol v} = (15 \cos 15°)\,\hat{\boldsymbol v} = (14.5\,{\rm N})\,\hat{\boldsymbol v}$
Question T3
A block of wood lies on a rough plane which is inclined at an angle of 25° to the horizontal. It is prevented from sliding down the plane by a static frictional force of magnitude 20 N acting up the plane. Find the horizontal and vertical component vectors of that frictional force.
Answer T3
If $\hat{\boldsymbol v}$ and $\hat{\boldsymbol h}$ are unit vectors in the direction of the upward vertical, and a horizontal in the direction of steepest slope, respectively, then the horizontal and vertical component vectors are:
[(20 cos 25°) N] $\hat{\boldsymbol h}$ ≈ (18.13 N) $\hat{\boldsymbol h}$
and[(2 sin 25°) N] $\hat{\boldsymbol v}$ ≈ (8.45 N) $\hat{\boldsymbol v}$
3 Vectors in a Cartesian coordinate system
In the previous section you saw how it was possible to represent the velocity of a boat in terms of the unit vectors $\hat{\boldsymbol v}_{\rm n}$ and $\hat{\boldsymbol v}_{\rm p}$ normal to, and parallel to, the bank of a river. This same idea can be extended to three dimensions, and provides a very convenient means of specifying three–dimensional vectors.
3.1 Cartesian unit vectors
The use of unit vectors is of particular importance in specifying the positive directions of the axes in a Cartesian coordinate system. In two dimensions the Cartesian unit vectors i and j are used to specify the directions of the x– and y–axes as shown in Figure 5.
In three dimensions a third Cartesian unit vector k is added to specify the direction of the z–axis. However, there are two possible directions, opposite to one another, in which the z–axis can be directed so that it is normal to both the x– and y–axes. To remove any ambiguity about the choice of direction of the z–axis a right-handed Cartesian coordinate system is almost invariably used. There are various ways of describing this system, but one simple method only is included here.
If the thumb and first two fingers of your right hand are arranged approximately mutually perpendicular as in Figure 6, then, if the first and second finger point along the x– and y–axes, respectively, the thumb points along the z–axis in a right–handed system.
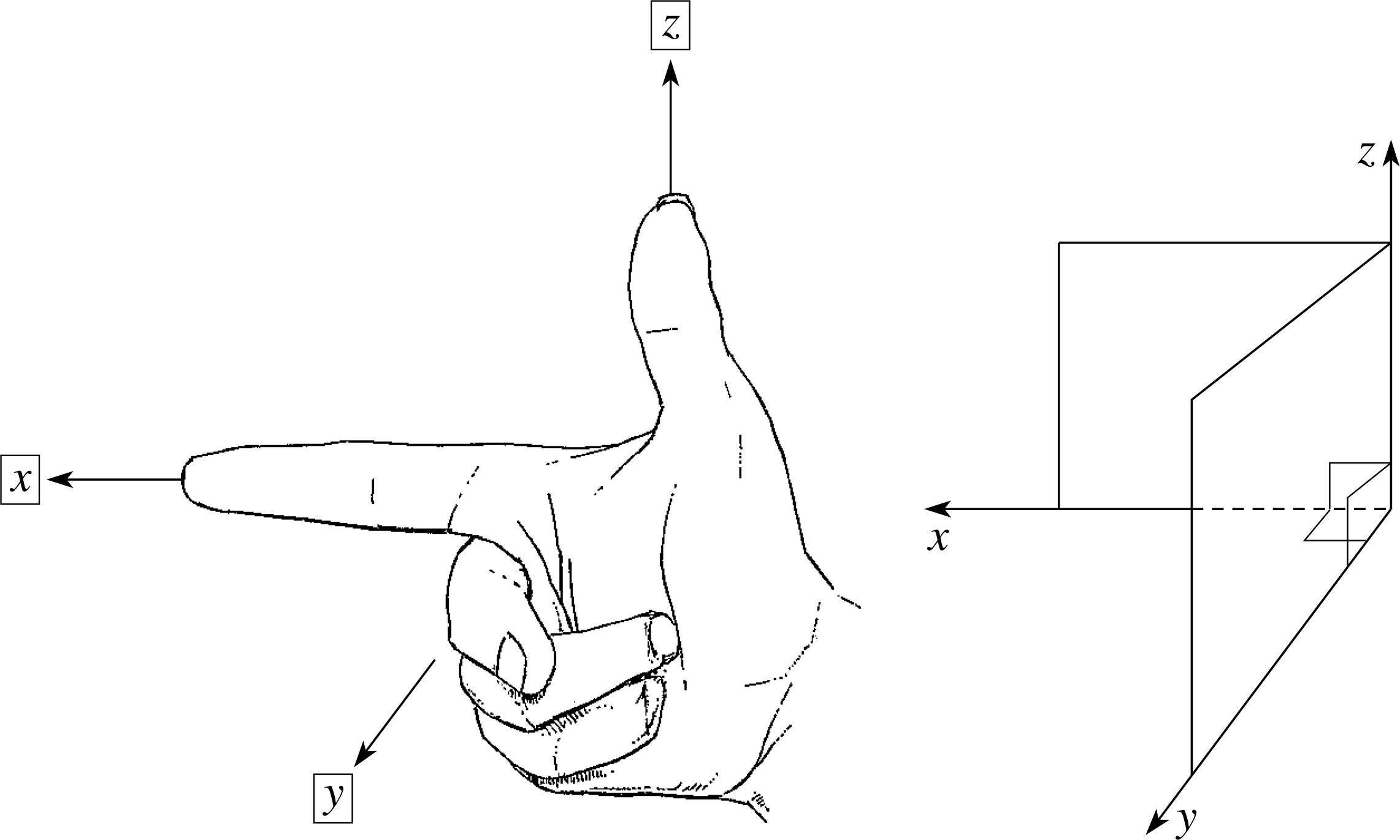
Figure 6 Directions of the axes in a right–handed Cartesian coordinate system.
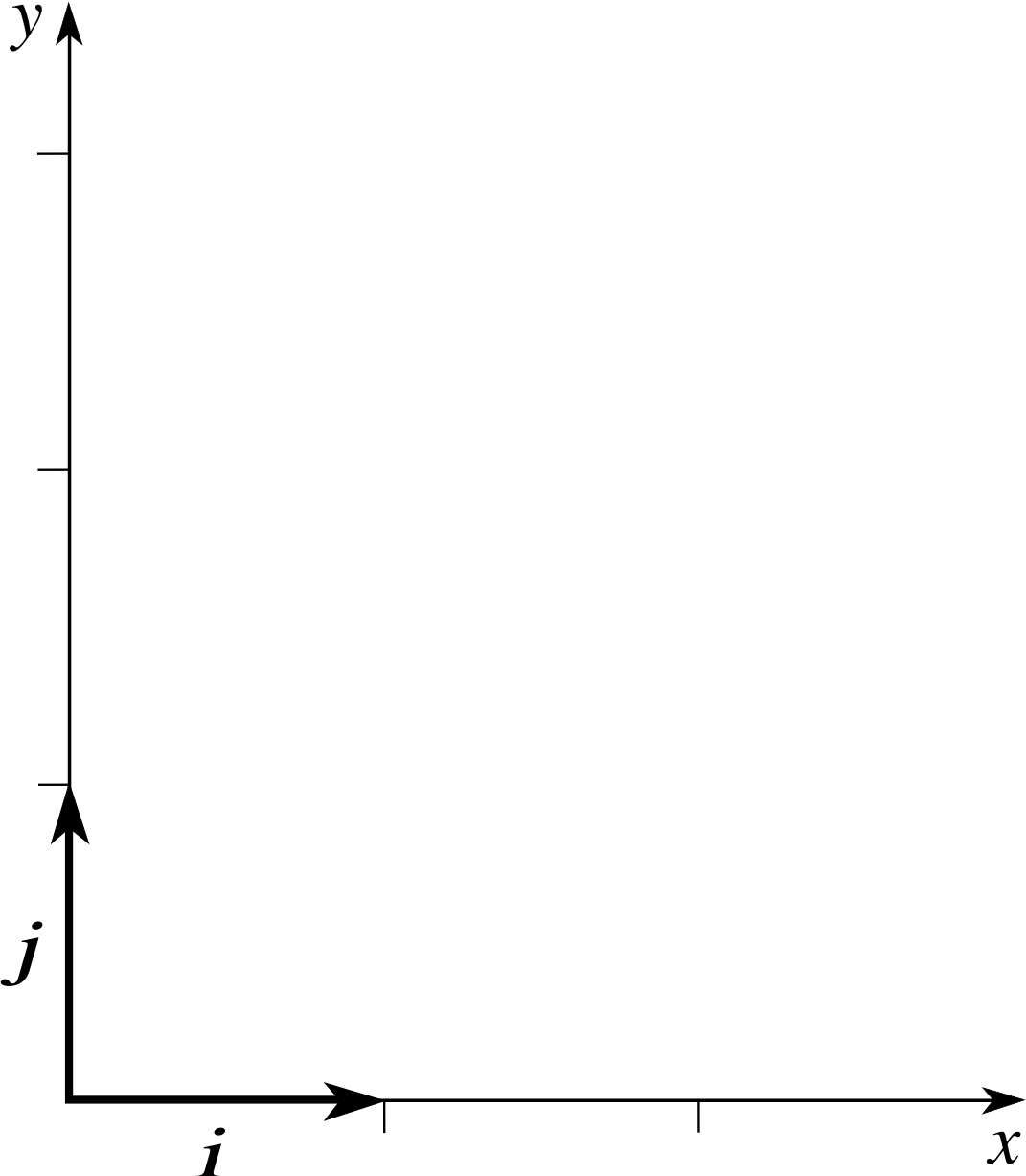
Figure 5 Unit vectors i and j are directed along the x– and y–axes.
✦ Which of the following is a right–handed coordinate system:
(a) i points west, j points north and k points vertically upward,
(b) i is vertically downward, j points south and k points west?
✧ Case (b) is right-handed, case (a) is not. i
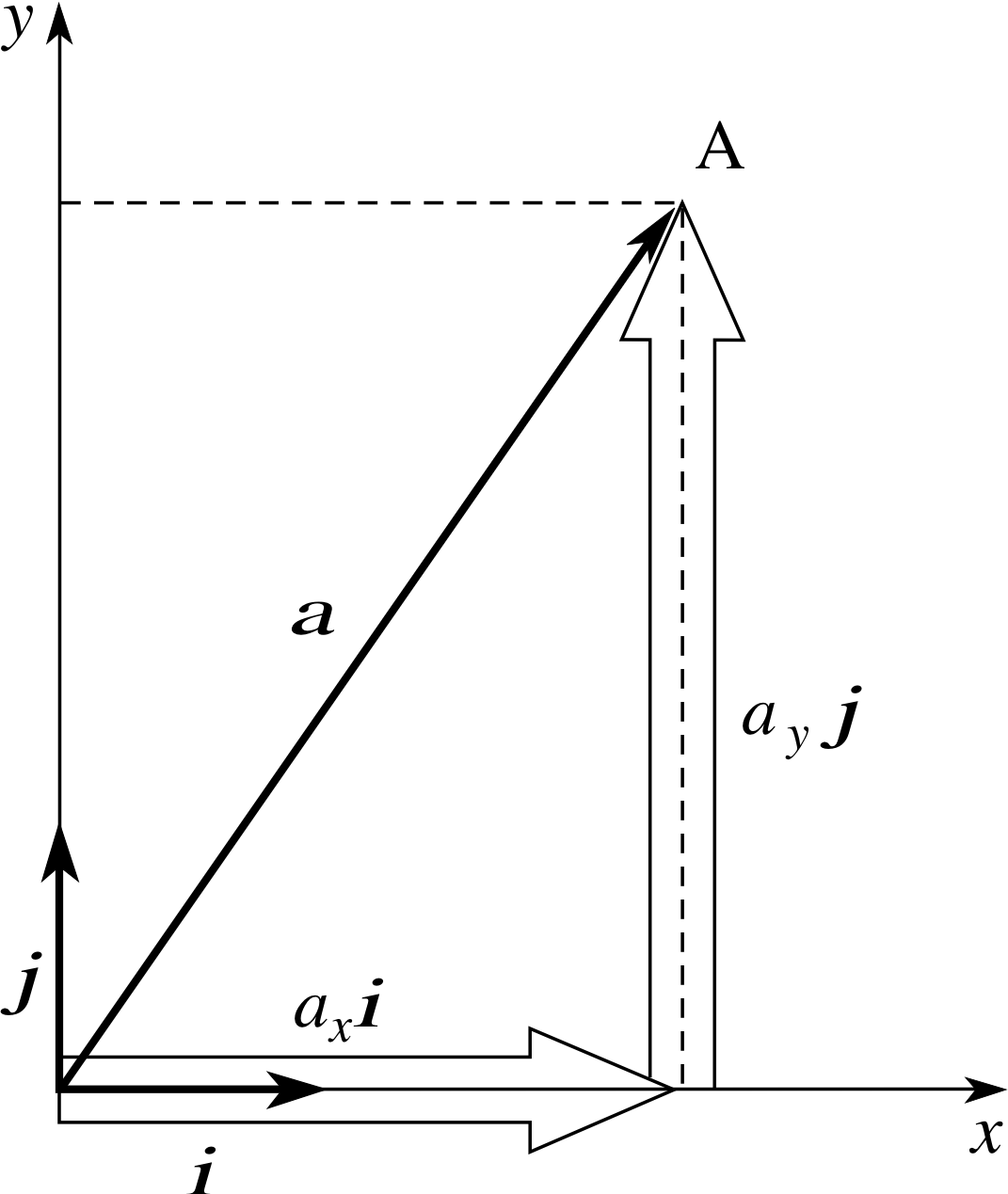
Figure 7 The component vectors of vector a in terms of i and j.
Now let us consider how these Cartesian unit vectors may be used to specify the Cartesian component vectors of any vector a in the (x, y) plane, i.e. an arbitrary vector in two dimensions. The vector a can be resolved into two orthogonal component vectors parallel to the x– and y–axes, respectively, as shown in Figure 7. If ax and ay are the coordinates of the point A, then the component vectors will have magnitudes ax and ay. Hence the component vectors will be ax i and ay j. From vector addition, a can be expressed as:
a = ax i + ay j(6)
The important point to notice about Equation 6 is that, once we have specified the directions of i and j the vector a is completely determined (both in magnitude and direction) by the pair of scalar quantities ax and ay.
The values ax and ay are known as the Cartesian scalar components of a (or simply the components i of a), ax i and ay j are the Cartesian component vectors of a (or simply the component vectors of a).
We obtain the full benefit from this method of representing vectors when the idea is extended to three dimensions. In Figure 8 we show how a vector a in three dimensions can be resolved into three orthogonal component vectors parallel to the x–, y– and z–axes. If ax, ay and az are the coordinates of the point A, then
a = ax i + ay j + az k(7)
In this case the Cartesian component vectors of a are
ax i, ay j and az k
while the Cartesian scalar components of a are
ax, ay and az and when we write
a = ax i + ay j + az k
we say that a is expressed in cartesian_form_of_a_vectorCartesian form.
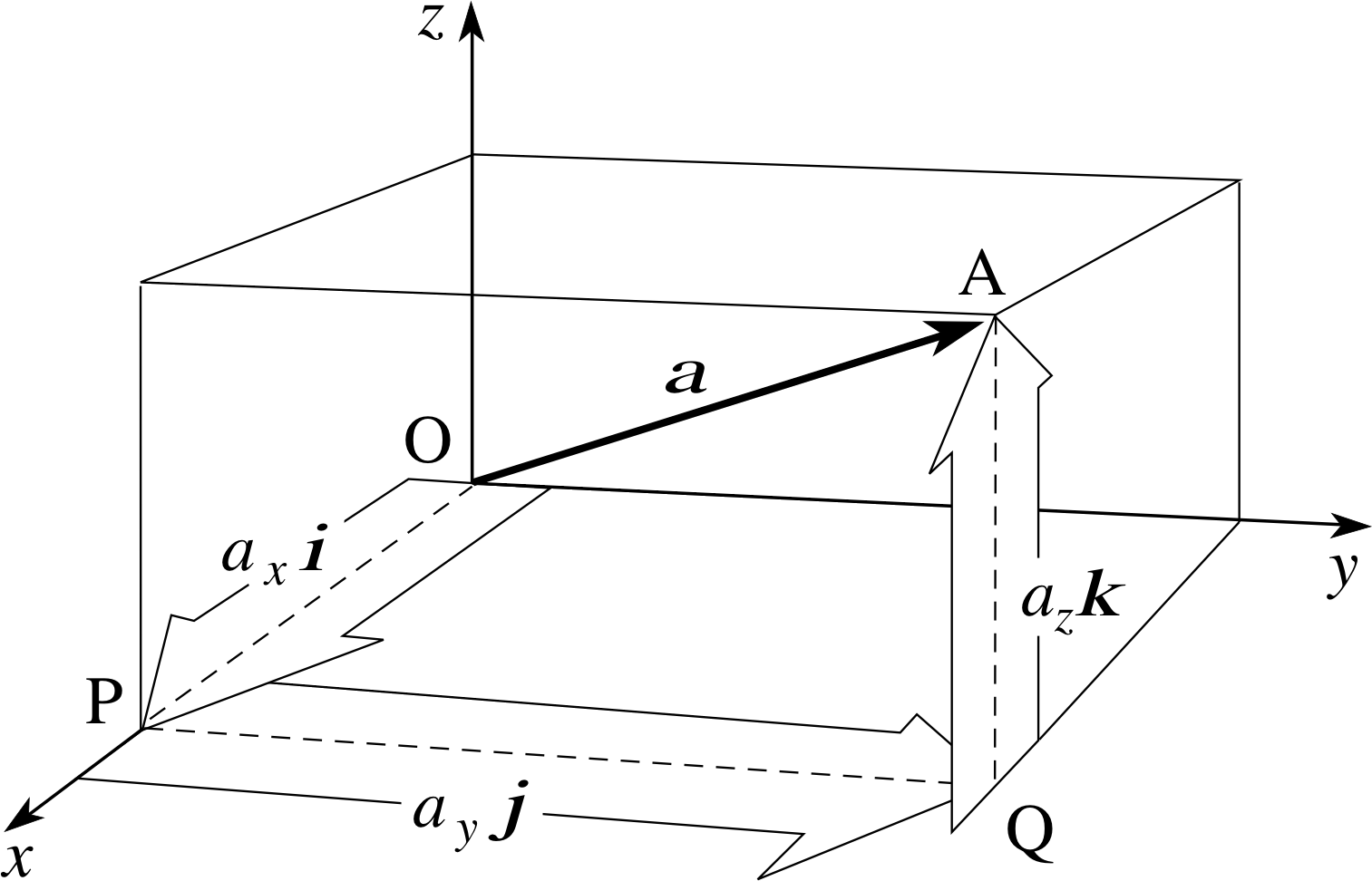
Figure 8 The Cartesian component vectors of a vector a in terms of i, j and k.
The suffix notation used in the above definitions is quite convenient, and it is natural to express any given vector, r say, in the same form. Thus rx i is the natural choice of notation for the vector component i in the x–direction of the vector r, while ry j and rz k denote its y and z–component vectors.
Most of us have great difficulty visualizing objects, and their relative distances from each other, in three dimensions; vector methods largely overcome these problems.
✦ A portable rectangular cabin is 3 m wide, 5 m long and 2.5 m high, and it is placed on a horizontal foundation with its long axis pointing north/south. An origin is chosen in the bottom south–west corner of the cabin, with i pointing east, j pointing north, and k pointing vertically upward.
What vector displacement r is required to move an object from the origin to a point at the centre of the ceiling?
✧ The vector a = (3 i + 5 j) m is the displacement from the origin to the opposite corner of the floor of the cabin.
It follows that $\frac12$ a = (1.5 i + 2.5 j) m is the displacement from the origin to the centre of the floor. The centre of the ceiling is 2.5 m above this point, and so its displacement from the origin is given by r = (1.5 i + 2.5 j + 2.5 k) m.
Once we have found the vector displacement r from the origin to the centre of the ceiling, then it is possible to find displacements from this new point. For example, the vector displacement of the opposite corner of the floor of the cabin from the origin is a = 3 i + 5 j, and therefore the displacement of the opposite corner of the cabin from the centre of the ceiling is i
−r + a = −(1.5 i + 2.5 j + 2.5 k) m + (3 i + 5 j) m = (1.5 i + 2.5 j − 2.5 k) m
Question T4
Is the suggested coordinate system for the cabin described above right-handed? What vector displacement s will move an object from the centre of the ceiling to the mid–point of the northern wall?
Answer T4
The coordinate system is right-handed. The displacement from the origin to the mid–point of the north wall is p = (1.5 i + 5 j + 1.25 k) m. The displacement from the centre of the ceiling to the mid–point of the north wall is given by
s = −r + p = −(1.5 i + 2.5 j + 2.5 k) m + (1.5 i + 5 j + 1.25 k) m = (2.5 j − 1.25 k) m
3.2 The magnitude and combination of vectors in Cartesian form

Figure 8 The Cartesian component vectors of a vector a in terms of i, j and k.
We can regard vectors in two dimensions as merely a special case of vectors in three dimensions; their z–component just happens to be zero. So hereafter our results apply equally well to vectors in two or three dimensions.
It is convenient to be able to determine the magnitude of a vector in terms of its Cartesian components, and this may be easily done if we apply Pythagoras’s theorem to vector a in Figure 8. First we consider the (x, y) plane only. Triangle OPQ is a right–angled triangle and so:
OQ2 = OP2 + PQ2
But OP = ax and PQ = ay, and so:
OQ2 = ax2 + ay2
Now we consider the right–angled triangle OQA:
OA2 = OQ2 + QA2
ButOQ2 = ax2 + ay2 and QA2 = az2
and so: OA2 = ax2 + ay2 + az2
But OA = | a | therefore:
| a | = (ax2 + ay2 + az2)1/2(8)
✦ Given that a = 2 i + 3 j + 4 k calculate | a |.
✧ | a | = (22 + 32 + 42)1/2 = $\sqrt{29\os}$. i
Question T5
In Question T4 you were asked to determine a vector displacement s.
s = (2.5 j − 1.25 k) m
Now determine the magnitude of that displacement.
Answer T5
The magnitude of the displacement is given by Equation 8,
| a | = (ax2 + ay2 + az2)1/2(Eqn 8)
| s | = [02 + (2.5)2 + (1.25)2 ]1/2 m ≈ 2.80 m
As we saw in Subsection 2.2, the scaling of a vector is simply multiplication of the vector by a scalar quantity, and this operation is very straightforward when a vector is expressed in Cartesian form. For example let α i be a scalar quantity and let a = ax i + ay j + az k, then:
α a = α ax i + α ay j + α az k(9)
The sum of two vectors in Cartesian form is equally easy.
Let a = ax i + ay j + az k and b = bx i + by j + bz k, then:
a + b = (ax + bx) i + (ay + by) j + (az + bz) k(10)
and similarly for subtraction
a − b = (ax − bx) i + (ay − by) j + (az − bz) k(11)
✦ At 3 a.m. a hedgehog of mass 1.5 kg starts crossing the M1 from west to east at a speed of 2.0 km h−1. What is the momentum i of the hedgehog?
✧ Taking i to be a unit vector pointing east, the momentum is given by
h = (1.5 kg) × (2.0 km h−1) i = 3.0 i kg km h−1.
✦ At 3.05 a.m. a truck of mass 15 000 kg and speed 50 km h−1 passes the same spot travelling north. What is the momentum of the truck?
✧ Taking j to be a unit vector pointing north, the momentum of the truck is
t = (15 000 kg) × (50 km h−1) j = 75 × 104 j kg km h−1.
Question T6
What is the magnitude of the combined momentum of the truck and the hedgehog at 3.06 a.m., (and what was the name of the hedgehog)?
Answer T6
The combined momentum is
h + t = (3.0 i + 75 × 104 j) kg km h−1
and
| h + t | = $\sqrt{\smash[b]{(3.0)^2+(75\times 10^4)^2}}$ kg km h−1 ≈ 75 × 104 kg km h−1
In the five minutes between 3 a.m. and 3.05 a.m. the hedgehog covered a distance of about 167 m, and since the total width of the M1 (including both carriageways, the central reservation and the emergency lanes) is about 40 m, the hedgehog was long gone by the time the truck passed. The answer for the momentum is the same whether they collide or not. (The hedgehog’s name was Lucky!)
Having considered the operations of scaling, addition and subtraction separately, we are now in a position to combine these processes when using the Cartesian component approach.
Suppose, for example, that a = 2 i + 3 j + 4 k and b = 3 i − j + 4 k then
4a − 3b = 4 (2 i + 3 j + 4 k) − 3 (3 i − j + 4 k) = −i + 15 j + 4 k
and more generally, for scalars α and β,
α a + β b = (α ax + β bx) i + (α ay + β by) j + (α az + β bz) k(12) i
✦ Is there any physical restriction on α, β, a and b in order that Equation 12 makes sense?
✧ Yes, the dimensions of α a and β b must be the same.
3.3 An application of vectors in Cartesian form
To complete Section 3 let us consider how the concepts covered in this section may be applied in a specific example.
✦ A particle travels at velocity υ1 for 3 s and then velocity υ2 for 2 s, where υ1 and υ2 are given by:
υ1 = (2 i − 3 j + 6 k) m s−1 and υ2 = (4 i + 12 j −3 k) m s−1
Determine:
(a) the magnitudes of the velocities υ1 and υ2;
(b) the displacements s1 and s2 over the first and second intervals;
(c) the distances associated with these displacements;
(d) the total displacement, st;
(e) the magnitude of the total displacement; and
(f) the unit vector $\hat{\boldsymbol s}_{\rm t}$ in the direction of st.
✧ (a) To determine the magnitudes of υ1 and υ2 we apply Equation 8 which we deduced from Pythagoras’s theorem.
$\lvert\,{\boldsymbol a}\,\vert = \left(a_x^2+a_y^2+a_z^2\right)^{1/2}$(Eqn 8)
For υ1, the components in m s−1 are 2, −3 and 6, and therefore:
$\lvert\,{\boldsymbol v_1}\,\vert = \left(2^2+(-3)^2+6^2\right)^{1/2}$ = 491/2 m s−1 = 7 m s−1i
Similarly:
$\lvert\,{\boldsymbol v_2}\,\vert = \left(4^2+12^2+(-3)^2\right)^{1/2}$ = 1691/2 m s−1 = 13 m s−1
(b) The displacement s corresponding to a constant velocity υ for a time t is given by s = tυ, so we can find s1 and s2 by scaling the vectors υ1 and υ2 by the appropriate times. Hence:
s1 = (3 s)υ1 = (6 i − 9 j + 18 k) m
ands2 = (2 s)υ2 = (8 i + 24 j − 6 k) m
(c) The required distances are simply the magnitudes of s1and s2. The direct approach to the determination of | s1 | and | s2 | would appear to involve the application of Equation 8 to the vectors s1 and s2 found in part (b). However, it is easier to make use of the answers obtained for | υ1 | and | υ2 | in part (a), since | s1 | = (3 s) | υ1 | and | s2 | = (2 s) | υ2 |. Therefore:
| s1 | = 3 s × 7 m s−1 = 21 m
and| s2 | = 2 s × 13 m s−1 = 26 m
(d) The total displacement is simply the vector sum st = s1+ s2, where s1and s2, are the answers obtained for part (b). Following the Cartesian component vector method for addition, we obtain:
s1 + s2 = st = [(6 + 8) i + (−9 + 24) j + (18 − 6) k] m
and therefore st = [14 i + l5 j + 12 k] m
(e) The value of | st | can be obtained using Equation 8,
$\lvert\,{\boldsymbol a}\,\vert = \left(a_x^2+a_y^2+a_z^2\right)^{1/2}$(Eqn 8)
$\lvert\,{\boldsymbol s}_{\rm t}\,\vert = \left(14^2+15^2+12^2\right)^{1/2}$ = 5651/2 m s−1 = 23.8 m s−1
(f) The required unit vector is obtained using Equation 1,
$\hat{\boldsymbol s}_{\rm t} = \dfrac{{\boldsymbol s}_{\rm t}}{\lvert\,{\boldsymbol s}_{\rm t}\,\vert} = \dfrac{14\,{\boldsymbol i}+15\,{\boldsymbol j}+12\,{\boldsymbol k}}{\sqrt{565\os}}$ i
therefore$\hat{\boldsymbol s_{\rm t}}$ = 0.589 i + 0.631 j + 0.505 k
Question T7
Particle A, of mass 2 kg, travelling with velocity υA = (i − 2 j + 4 k) m s−1 collides with particle B, of mass 3 kg, travelling with velocity υB = (3 i + j − 2 k) m s−1. The particles stick together on collision and then move as one combined body with momentum the same as the total momentum of A and B before the collision. Determine:
(a) the momenta i of A and B before the collision;
(b) the total (resultant) momentum of A and B before the collision;
(c) the magnitudes of the momenta of A and B before the collision; and
(d) the velocity of the combined body after the collision.
Answer T7
(a) Since momentum = mυ, the required momenta are obtained by scaling the given velocities by the appropriate masses. Hence:
momentum of A = (2 kg) υA = 2 (i − 2 j + 4 k) kg m s−1 = (2 i − 4 j + 8 k) kg m s−1
and momentum of B = (3 kg) υB = 3 (3 i + j − 2 k) kg m s−1 = (9 i + 3 j − 6 k) kg m s−1
(b) The total momentum = (2 kg) υA + (3 kg) υB = [(2 i − 4 j + 8 k) + (9 i + 3 j − 6 k)] kg m s−1 = (11 i − j + 2 k) kg m s−1
(c) The magnitudes of the initial momenta are obtained using Equation 8,
| a | = (ax2 + ay2 + az2)1/2(Eqn 8)
| (2 kg) υA | = [22 + (−4)2 + 82]1/2 kg m s−1 = 841/2 kg m s−1 ≈ 9.17 kg m s−1
and| (3 kg) υA | = [92 + 32 + (−6)2]1/2 kg m s−1 = 1261/2 kg m s−1 ≈ 11.2 kg m s−1
(d) The final total momentum equals the total mass of the combined body multiplied by the final velocity, υF, say. Therefore υF is obtained by dividing the final momentum by the total mass, so that
υA = $\left(\dfrac{11\,{\boldsymbol i} - {\boldsymbol j} + 2\,{\boldsymbol k}}{5}\right)$ m s−1 = (2.2 i − 0.2 j + 0.4 k) m s−1
4 Vectors as ordered triples
4.1 Ordered triples and ordered pairs
A vector, a = 3 i − j + 4 k say, in Cartesian form, is often abbreviated to three numbers in brackets, (3, −1, 4), in which the order of the numbers is of crucial importance, for otherwise we would not know which number referred to which component. Such a collection of numbers is called an ordered triple.
In general we write
a = ax i + ay j + az k = (ax, ay, az)(13)
An ordered triple, such as (3, −1, 4), can mean the coordinates of a point in three dimensions or the vector 3 i − j + 4 k, but the context will make it clear which is intended. (In fact this dual meaning is an advantage, as you will see in Subsection 4.4).
✦ Express the vector 2 i − j + 3 k as an ordered triple.
✧ 2 i − j + 3 k = (2, −1, 3)
In the case of two–dimensional vectors, we refer to s rather than ordered triples, for example, υ = 2 i + 5 j = (2, 5). Therefore (2, 5) is the ordered pair which represents the vector υ.
4.2 Manipulation of ordered triples
The extension of the calculations of the last section, for vectors in Cartesian form, to vectors represented as ordered triples is very easy, but we will state the results ‘for the record’.
If a = (ax, ay, az) and b = (bx, by, bz) then i
| a | = (ax2 + ay2 + az2)1/2(Eqn 8)
α a = α ax i + α ay j + α az k(Eqn 9)
a + b = (ax + bx) i + (ay + by) j + (az + bz) k(Eqn 10)
α a +β b = (α ax + β bx, α ay + β by, α az + β bz)(Eqn 12)
Question T8
Find the magnitude of the vector represented by the ordered triple (5, −2, −1).
Answer T8
Equation 8,
| a | = (ax2 + ay2 + az2)1/2(Eqn 8)
gives the expression for the magnitude of the vector. Hence:
| (5, −2, −1) | = [52 + (−2)2 + (−1)2]1/2 = 301/2 ≈ 5.48
✦ Express 2 (2 i − j + 3 k) as an ordered triple and find the ordered triple which represents the sum of (i + 2 j − k) and (3 i − j + 4 k).
✧ 2 (2 i − j + 3 k) = 2 (2, −1, 3) = (4, −2, 6) (i + 2 j − k) + (3 i − j + 4 k) = (1, 2, −1) + (3, −1, 4) = (4, 1, 3)
Question T9
Find the ordered triple that represents the resultant of the vectors (2, −1, −2) and (3, −2, 7), and find also the ordered triple which represents the unit vector in the direction opposite to that of the resultant.
Answer T9
The resultant of (2, −1, −2) and (3, −2, 7) is given by (5, −3, 5) in ordered triple notation. To find the required unit vector we need to find the magnitude of the resultant, and this is done using Equation 8,
| a | = (ax2 + ay2 + az2)1/2(Eqn 8)
Therefore:
magnitude = [52 + (−3)2 + 52]1/2 = 591/2 = 7.68
The required unit vector is oppositely directed to the resultant and can be obtained using Equation 1,
$\hat{\boldsymbol a} = \dfrac{{\boldsymbol a}}{\left\lvert\,{\boldsymbol a}\,\right\rvert}$(Eqn 1)
required unit vector = $-\dfrac{(5,\,-3,\,5)}{\sqrt{59\os}}$ ≈ (−0.651, 0.391, −0.651)
4.3 An application of ordered triples
The following exercises are intended to illustrate how vectors may be manipulated using the ordered triple notation.
✦ Forces F1 = (2, −1, 4) N and F2 = (1, 3, 1) N act simultaneously on a particle. Determine:
(a) the magnitudes of F1 and F2;
(b) the resultant of F1 and F2;
(c) the magnitude of this resultant;
(d) the vector required to cancel the combined effect of F1 and F2; and
(e) the vectors 2F1, 5F2 and 2F1 + 5F2.
✧ (a) | F1 | = [22 + (−1)2 + 42]1/2 N = [4 + 1 + 16]1/2 N = 211/2 N = 4.58 N.
| F2 | = [12 + 32 + 12]1/2 N = [1 + 9 + 1]1/2 N = 111/2 N = 3.32 N
(b) F1 + F2 = (2 + 1, −1 + 3, 4 + 1) N = (3, 2, 5) N.
(c) | F1 + F2 | = [32 + 22 + 52]1/2 N = [9 + 4 + 25]1/2 N = 381/2 N = 6.16 N.
(d) If F1 + F2 = (3, 2, 5) N, then the force vector required to cancel the effect of F1 + F2 is
−(F1 + F2) = (−3, −2, −5) N.
(e) 2F1 = 2 (2, −1, 4) N = (4, −2, 8) N.
5F2 = 5 (1, 3, 1) N = (5, 15, 5) N
so that 2F1 + 5F2 = (4 + 5, −2 + 15, 8 + 5) N = (9, 13, 13) N.
Question T10
A particle travels with velocity υ1 = (2, 1, −2) m s−1 for 5 s, then with velocity υ2 = (−1, 2, 3) m s−1 for 2 s, and finally with velocity υ3 = (−2, −1, 2) m s−1 for 3 s. Find the total displacement of the particle over the 10 s, the magnitude of this total displacement, and the unit vector in the direction of the total displacement.
Answer T10
The individual displacements s1, s2 and s3, say, are obtained by scaling the velocities by the appropriate time intervals. Therefore
s1 = t1υ1, s2 = t2υ2 and s3 = t3υ3
so that
s1 = 5 (2, 1, −2) m = (10, 5, −10) m
s2 = 2 (−1, 2, 3) m = (−2, 4, 6) m
ands3 = 3 (−2, −1, 2) m = (−6, −3, 6) m
The resultant displacement is obtained by adding s1, s2 and s3.
Therefores1, s2 and s3 = (2, 6, 2) m
The magnitude of this resultant is given by Equation 8,
| a | = (ax2 + ay2 + az2)1/2(Eqn 8)
| s1, s2 and s3 | = [22 + 62 + 22]1/2 m = 441/2 m ≈ 6.631 m
The unit vector is given by Equation 1,
$\hat{\boldsymbol a} = \dfrac{{\boldsymbol a}}{\left\lvert\,{\boldsymbol a}\,\right\rvert}$(Eqn 1)
unit vector = $\dfrac{{\boldsymbol s}_1 + {\boldsymbol s}_2 + {\boldsymbol s}_3}{\lvert\,{\boldsymbol s}_1 + {\boldsymbol s}_2 + {\boldsymbol s}_3\,\vert}$ = (2, 6, 2) ≈ (0.302, 0.905, 0.302)
4.4 Position vectors
There are two main applications of vectors in physics. The first concerns the mathematical modelling (or representation, if you prefer) of physical quantities such as force, displacement and velocity. The second is equally important, and concerns the location of objects in three dimensions, and is essentially a form of geometry. Generally we do not associate a vector with a particular point in space (although later you may encounter applications where it is desirable to do just that), and vectors such as $\overrightarrow{\rm JN}$ and $\overrightarrow{\rm UY}$ in Figure 3 are defined to be the same vector. On the other hand, the vector a in Figure 8 specifies the position of the point A provided that we know that the end of the vector is fixed at the origin. Vectors that are used in this way to determine the positions of points are often known as position vectors.
✦ Two points A and B are specified by the position vectors $\overrightarrow{\rm OA}$ = (1, −3, 5) cm and $\overrightarrow{\rm OB}$ = (−2, 2, 4) cm
Find the distance between the points A and B, and the position vector of the mid–point M of AB. Is a position vector r identical to a displacement vector r?
✧ The displacement vector from A to B is defined by
$\overrightarrow{AB} = \overrightarrow{AO} +\overrightarrow{OB}$ = [(−2, 2, 4) − (1, −3, 5)] cm = (−3, 5, −1) cm
so that the distance from A to B is $\overrightarrow{AB}$ = [(9 + 25 +1)1/2] cm ≈ 5.92 cm.
The mid–point of AB has coordinates $\frac12$ [(−2, 2, 4) + (1, −3, 5)] cm so that the position vector $\overrightarrow{OM}$ = $\frac12$ [(−2, 2, 4) + (1, −3, 5)] cm = (−0.5, −0.5, 4.5) cm
The position vector r and the displacement vector r are identical, they are the same vector; but the interpretation of them is different. The fact that we are told that r is a displacement vector tells us only the magnitude and direction of the displacement. We can use that displacement to specify a particular point only if we first specify a point from which to make the displacement. On the other hand, if we are told that r is a position vector we know that the position of the point A is determined if the vector is placed with its tail at the origin. In a sense, position vectors are simply a special class of displacement vectors since position vectors define displacements from the origin.
Notice that in the above exercise we were quite happy to use exactly the same notation for the coordinates of M and for the position vector $\overrightarrow{\rm OM}$. The context makes it absolutely clear which is intended, and, in any case, there is very little difference between saying that a point P is determined by the coordinates (1, 2, 3) and that P is determined by the position vector (1, 2, 3).
Question T11
A particle is moving with velocity υ = (1, 1, 2) m s−1 and at time t = 0 it is at the point P with position vector $\overrightarrow{\rm OP}$ = (2, 3, −4) m. What is the position vector $\overrightarrow{\rm OQ}$ of the particle at time t = 5 s?
Answer T11
The displacement of the particle after 5 s is
$\overrightarrow{PQ}$ = (5 s) υ = 5 (1, 1, 2) m
so that
$\overrightarrow{OQ} = \overrightarrow{OP} + \overrightarrow{PQ}$ = (2, 3, −4) m + 5 (1, 1, 2) m = (7, 8, 6) m
5 Closing items
5.1 Module summary
- 1
-
Scalar quantities can be specified completely by a single number together with an appropriate unit of measurement.
- 2
-
Vector quantities can be specified by a magnitude and a direction. Geometric vectors are represented by arrows or Subsection 2.1directed line segments and vector quantities are often represented pictorially by geometric vectors. In print, vectors are denoted by bold typeface, and in handwritten material, by a wavy underline.
- 3
-
The magnitude of a vector is a non–negative scalar that represents the ‘length’ or ‘size’ of that vector. The magnitude of a is denoted by | a | (or sometimes by a) in print, and by | $\underset{\boldsymbol{\raise 6pt \sim}}{a}$ | in handwritten material.
- 4
-
Any vector a may be multiplied by a scalar α to produce a scaled vector α a which points in the same direction as a if α > 0 and in the opposite direction if α < 0. The magnitude of α a is | α a | = | α | | a |.
- 5
-
If any non–zero vector a is divided by | a |, a vector of unit magnitude is obtained which points in the same direction as a. Such a vector is called a unit vector and is denoted by $\hat{\boldsymbol a}$.
- 6
-
Vectors may be added geometrically using either the Subsection 2.3triangle or Subsection 2.3parallelogram rule (see Figure 2Figures 2 and Figure 33).
- 7
-
A vector may be Subsection 2.4resolved into component vectors along appropriately chosen directions. Given a vector a, its orthogonal component vectors parallel and normal to a direction inclined at an angle θ to a are of magnitude
| ap | = | a | cos θ and | an | = | a | sin θ
- 8
-
The Subsection 3.1Cartesian unit vectors in the directions of the Cartesian axes x, y and z are denoted by i, j and k.
- 9
-
A vector a can be expressed in Cartesian form as
a = ax i + ay j + az k(Eqn 7)
The scalars ax, ay and az are called the Cartesian scalar components of a, whereas the vectors ax i, ay j and az k are called the Cartesian component vectors of a. i
- 10
-
The magnitude of the vector a is given by
| a | = (ax2 + ay2 + az2)1/2(Eqn 8)
- 11
-
The operations of Subsection 2.2scaling and Subsection 2.3vector addition take the following Cartesian algebraic forms (for any scalar α and vectors a and b):
α a = α axi + α ay j + α az k
anda + b = (ax + bx) i + (ay + by) j + (az + bz) k(Eqn 10)
- 12
-
A vector represented by a = ax i + ay j + az k can also be represented by the abbreviated notation of an Subsection 4.1ordered triple:
a = (ax, ay, az)
- 13
-
The operations of scaling and vector addition take the following abbreviated forms (for any scalar α and vectors a and b):
α a = (α ax, α ay, α az)
anda + b = (ax + bx, ay + by, az + bz)
- 14
-
Vectors may be used to determine the position of points relative to a chosen origin, and they are then known as Subsection 4.4position vectors.
5.2 Achievements
Having completed this module, you should be able to:
- A1
-
A1 Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Identify quantities as being scalars or vectors, given the definitions of the quantities.
- A3
-
Recognize and use the notations (a, $\underset{\boldsymbol{\raise 6pt \sim}}{a}$, | a |, | $\underset{\boldsymbol{\raise 6pt \sim}}{a}$ |) to represent vectors and their magnitudes.
- A4
-
Carry out and represent graphically the operations of scaling, addition and subtraction of vectors, and of resolving a vector into orthogonal component vectors.
- A5
-
Determine a unit vector in the same direction as a given vector.
- A6
-
Use Cartesian unit vectors and Cartesian scalar components to represent a given vector in Cartesian form.
- A7
-
Evaluate the magnitude of any vector in terms of its Cartesian components.
- A8
-
Scale, add and subtract vectors in Cartesian form.
- A9
-
Use Cartesian scalar components to represent a given vector as an ordered triple (or an ordered pair in two dimensions).
- A10
-
Scale, add and subtract vectors using the ordered triple notation for vectors.
- A11
-
Use a position vector to specify the location of a point.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
5.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions, each of which tests one or more of the Achievements.
Question E1 (A2)
The electric field at any point in space can be defined as the electrical force experienced by a positive charge at that point, divided by the magnitude of the charge. Given that charge is a scalar quantity, decide whether electric field is a scalar or a vector quantity, and justify your decision.
Answer E1
Since electric field is a vector divided by a scalar it must be a vector quantity. (Reread Subsection 2.1 if you had difficulty with this question.)
Question E2 (A4)
On Treasure Island, Captain Flint decides to bury his treasure at the point at which he arrives after making a displacement of 20 m west and then a displacement of 10 m north, starting from a distinctive rock which he uses as his reference point. Illustrate these displacements graphically, and find the magnitude and direction of the resultant displacement. Find also the component of the resultant displacement in the north–west direction.
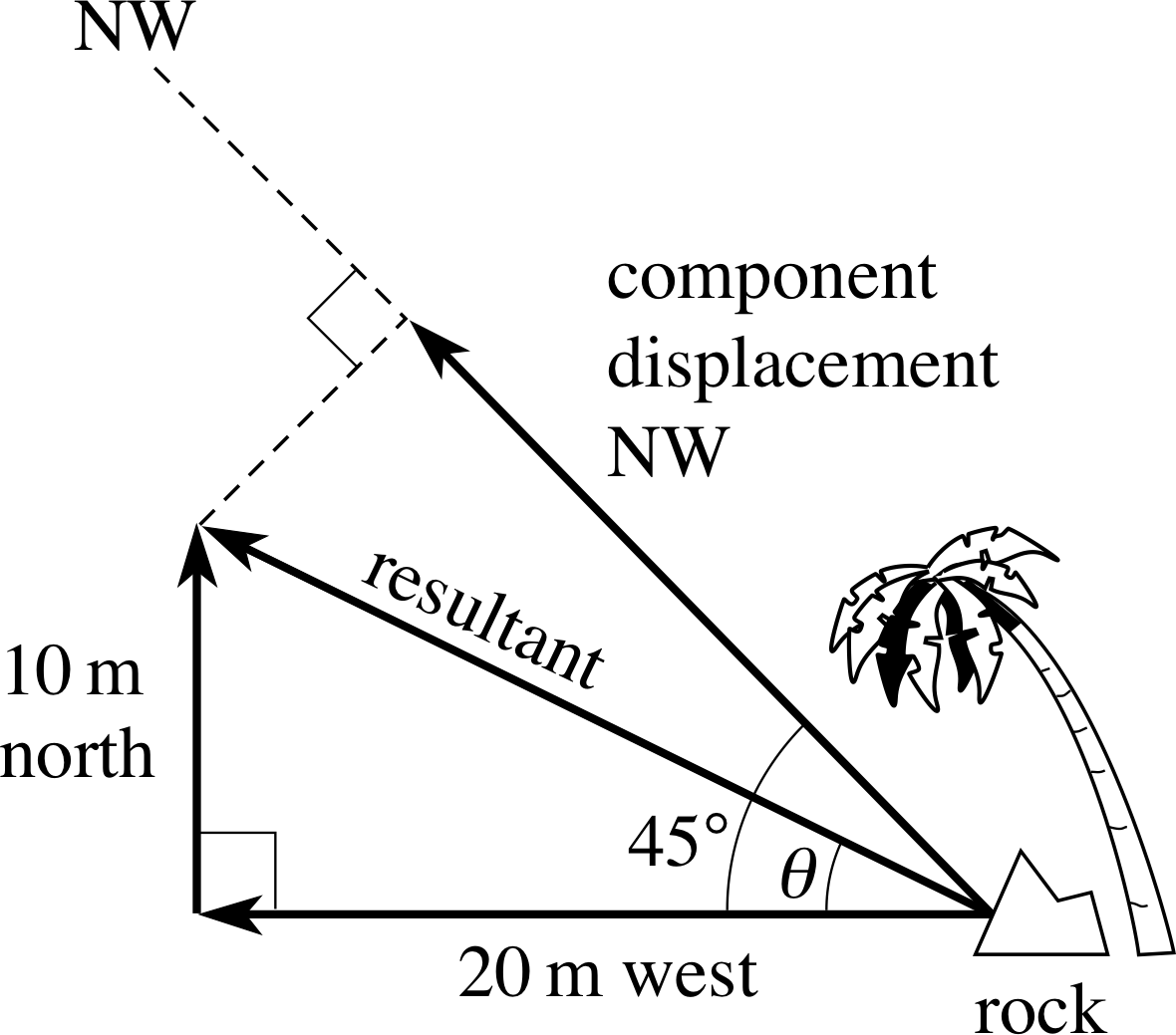
Figure 9 See Answer E2.
Answer E2
See Figure 9. From this diagram the resultant displacement can be seen to be represented by the hypotenuse of the right–angled triangle. Therefore, from Pythagoras’s theorem, the magnitude of the resultant displacement is:
[202 + 102]1/2 m ≈ 22.4 m
Since tan θ = 1/2 it follows that θ = arctan(1/2) ≈ 26.6°
The component in the north–west direction is given by
22.4 cos(45° − θ) m ≈ 22.4 cos(45 − 26.6°) m ≈ 21.2 m
(Reread Subsection 2.3Subsections 2.3 and Subsection 2.42.4 if you had difficulty with this question.)
Question E3 (A3, A5, A6, A7 and A8)
Vectors a and b are given by a = −i + 5 j − 2 k and b = 3 i − 2 j − 4 k
Find a + b, | a + b | and the unit vector in the direction of a + b.
Answer E3
a = i + 5 j − 2 k and b = 3 i − 2 j − 4 k
and therefore a + b = 2 i + 3 j − 6 k
The magnitude of a + b is given by Equation 8,
| a | = (ax2 + ay2 + az2)1/2(Eqn 8)
| a + b | = [22 + 32 + (−6)2]1/2 = $\sqrt{49\os}$ = 7
The unit vector = $\dfrac{{\boldsymbol a}+{\boldsymbol b}}{\lvert\,{\boldsymbol a}+{\boldsymbol b}\,\vert} = \dfrac{2\,{\boldsymbol i}+3\,{\boldsymbol j}-6\,{\boldsymbol k}}{7}$ ≈ 0.286 i + 0.429 j − 0.857 k
(Reread Subsections Subsection 2.22.2, Subsection 3.13.1 and Subsection 3.23.2 if you had difficulty with this question.)
Question E4 (A3, A6, A7 and A8)
Given the forces: F1 = (i − 2 j + 3 k) N, and F2 = (3 i + j − 4 k) N, find the force given by 3F1 + 2F2, the magnitude of this force and its Cartesian vector component along the z–axis.
Answer E4
Given F1 and F2, we first evaluate 3F1 and 2F2 by scaling:
3F1 = 3 (i − 2 j + 3 k) N = (3 i − 6 j + 9 k) N
and2F2 = 2 (3 i + j − 4 k) N = (6 i + 2 j − 8 k) N
Now we simply add these two vectors:
3F1 + 2F2 = (9 i − 4 j + k) N
The magnitude of this vector is found from Equation 8:
| a | = (ax2 + ay2 + az2)1/2(Eqn 8)
| 3F1 + 2F2 | = [92 + (−4)2 + 12]1/2 N = $\sqrt{98\os}$ N ≈ 9.90 N
The Cartesian component vector along the z–axis is obtained from the expression for the resultant. It is simply the ‘k term’, which in this case is k N.
(Reread Subsections Subsection 3.13.1 and Subsection 3.23.2 if you had difficulty with this question.)
Question E5 (A3, A9 and A10)
Given the vectors a and b in Cartesian form as:
a = −i + 4 j − 2 k and b = 2 i − j + 2 k
express the vectors a, b and a + b in terms of ordered triples. What physical restriction must apply to vectors a and b for the resultant to have any sensible meaning?
Answer E5
Using the ordered triple notation:
a = −i + 4 j − 2 k = (−1, 4, −2)
andb = 2 i − j + 2 k = (2, −1, 2)
so thata + b = (−1, 4, −2) + (2, −1, 2) = (1, 3, 0)
For the resultant to have any physical meaning, the vectors a and b must have the same dimensions.
(Reread Subsections Subsection 4.14.1 and Subsection 4.24.2 if you had difficulty with this question.)
Question E6 (A9 and A10)
Vectors a and b are given by: a = (2, 1, −1) and b = (1, −3, 2). Find, in ordered triple notation, the vectors 2 a + 5 b, 3 a − 2 b, and the vector c such that a + b + c = (0, 0, 0).
Answer E6
To find 2a + 5b, first we scale vectors a and b by 2 and 5, respectively:
2a = 2 (2, 1, −1)= (4, 2, −2)
and5b = 5 (1, −3, 2) = ( 5, −15, 10)
then 2a + 5b = (4, 2, −2) + (5, −15, 10) = (9, −13, 8)
Similarly,3a − 2b = (6, 3, −3) − (2, −6, 4) = ( 4, 9, −7)
Since a + b + c = 0 it follows that
c = −(a + b) = −[(2, 1, −1) + (1, −3, 2)] = (−3, 2, −1)
(Reread Subsections Subsection 4.24.2, Subsection 4.34.3, and Subsection 4.44.4 if you had difficulty with this question.)
Question E7 (A9 and A10)
Given the forces F1 = (2, 0, 2) N, F2 = (1, −2, 3) N and F3 = (−3, 1, 2) N, determine:
(a) the ordered triple representing F1 + F2 + F3;
(b) the magnitude of F1 + F2 + F3
(c) the ordered triple representing the unit vector in the direction of F1 + F2 + F3;
(d) the component vector in the z–direction of the force which would completely counteract the force F1 + F2 + F3;
(e) the scalar component of F1 + F2 − F3 in the y–direction.
Answer E7
(a) F1 + F2 + F3 = [(2, 0, 2) + (1, −2, 3) + (−3, 1, 2)] N = (0,−1, 7) N
(b) The magnitude is obtained from Equation 8,
| a | = (ax2 + ay2 + az2)1/2(Eqn 8)
| F1 + F2 + F3 | = [02 + (−1)2 + 72]1/2 N = $\sqrt{50\os}$ N ≈ 7.07 N
(c) The unit vector is $\dfrac{{\boldsymbol F}_1+{\boldsymbol F}_2+{\boldsymbol F}_3}{\lvert\,{\boldsymbol F}_1+{\boldsymbol F}_2+{\boldsymbol F}_3\,\rvert} = \left(0,\,\dfrac{1}{\sqrt{50\os}}, \dfrac{7}{\sqrt{50\os}}\right)$ ≈ (0, −0.141, 0.990)
(d) The force which would counteract F1 + F2 + F3 is −(F1 + F2 + F3) = −(0, −1, 7) N
and the vector component of this force in the z–direction is (0, 0, −7) N, alternatively written as −7 k N.
(e) F1 + F2− F3 = [(2, 0, 2) + (1, −2, 3) − (−3, 1, 2)] N = (6, −3, 3) N
Therefore the scalar component in the y–direction is −3 N.
(Reread Subsections Subsection 4.24.2 and Subsection 4.34.3 if you had difficulty with this question.)
Question E8 (A11)
A pyramid has a square base of length 100 m and its height is 20 m. Cartesian coordinates are chosen with one corner of the base as the origin, with i and j in the direction of the adjacent edges of the base, and with k vertically upward. Find the position vector of the vertex of the pyramid.
Answer E8
The centre of the (square) base is at (50, 50, 0) m and the vertex is 20 m above this point at (50, 50, 20) m.
(Reread Subsection Subsection 4.44.4 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment
Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 5Closing items.