PHYS 11.2: The quantum harmonic oscillator |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
A study of the simple harmonic oscillator is important in classical mechanics and in quantum mechanics. The reason is that any particle that is in a position of stable equilibrium will execute simple harmonic motion (SHM) if it is displaced by a small amount. A simple example is a mass on the end of a spring hanging under gravity. The system is stable because the combination of the tension in the spring and the gravitational force will always tend to return the mass to its equilibrium position if the mass is displaced. Another example is an atom of hydrogen in a molecule of hydrogen chloride HCl. The mean separation between the hydrogen and the chlorine atoms corresponds to a position of stable equilibrium. The electrical forces between the atoms will always tend to return the atom to its equilibrium position provided the displacements are not too large. Such examples of motion about a position of stable equilibrium can be found in all branches of mechanics, and in atomic, molecular and nuclear physics.
The key to understanding both the classical and quantum versions of harmonic motion is the behaviour of the particle potential energy as a function of position. The potential energy function of a particle executing pure simple harmonic motion has a parabolic graph (see Figure 2), and it may be shown that sufficiently close to a position of stable equilibrium almost all systems have a parabolic potential energy graph and hence exhibit SHM. For oscillations of large amplitude, the potential energy often deviates from the parabolic form so that the motion is not pure SHM.
In this module, we will review the main features of the harmonic oscillator in the realm of classical or large–scale physics, and then go on to study the harmonic oscillator in the quantum or microscopic world. We will solve the time–independent Schrödinger equation for a particle with the harmonic oscillator potential energy, and hence determine the allowed energy levels of the quantum oscillator, the corresponding spatial wavefunctions and the probability density distributions. Comparisons will be made between the predictions of classical and quantum theories, bearing in mind their very different regions of applicability.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 3.1Module summary and the Subsection 3.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 3.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
What is meant by the term simple harmonic oscillation in classical mechanics? Suggest a criterion for deciding whether classical mechanics or quantum mechanics should be used in a problem involving harmonic oscillation.
Answer F1
In classical mechanics, a particle executes simple harmonic motion (SHM) if the particle acceleration is directly proportional to the distance from a fixed point and is directed towards that point. If the motion is along the x–axis and the origin is the fixed point, then we write $\ddot{x} = -\omega^2x$ where ω is the angular frequency of the oscillation.
In quantum mechanics, the total energy of an SHM oscillator is quantized in units of hf, where f is the frequency calculated by classical theory. If the total energy E ≫ hf, then classical theory may be used; otherwise quantum theory must be used.
Question F2
Write down an expression for the allowed energies of the harmonic oscillator in quantum mechanics in terms of the quantum number n, Planck’s constant and the frequency of the corresponding classical oscillator. Sketch the energy eigenfunctions (i.e. spatial wavefunctions) of the n = 0 and n = 1 states.
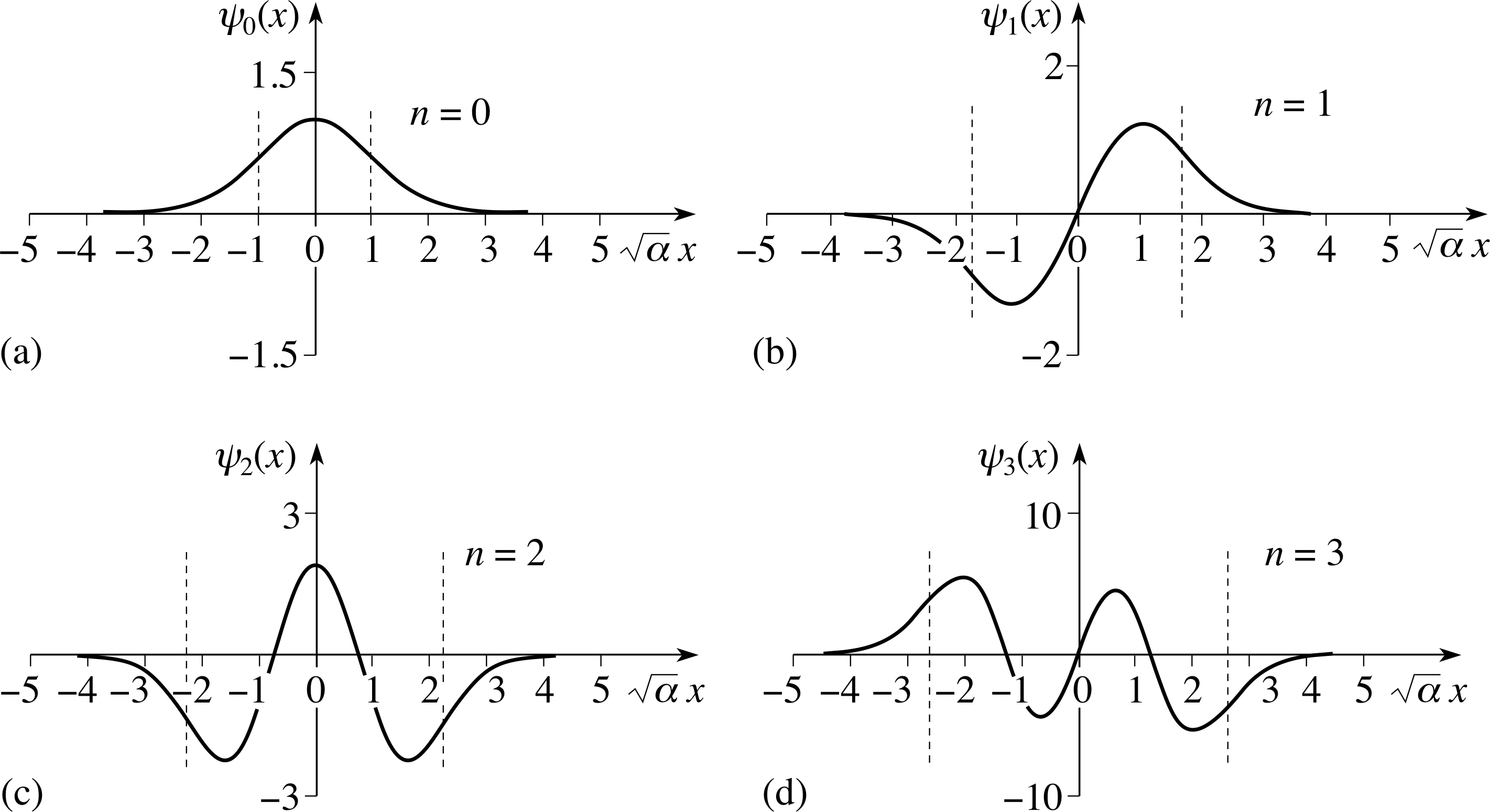
Figure 4 The first four energy eigenfunctions for the quantum simple harmonic oscillator (not normalized). The limits of motion for a classical oscillator with the same energy are indicated by the vertical dashed lines. The horizontal axis is marked in the dimensionless variable $\sqrt{\alpha\os}x$.
Answer F2
The allowed energies of the harmonic oscillator in quantum mechanics are
$E_n = \left(n + \frac12\right)hf = \left(n + \frac12\right)\hbar\omega$
where ω = 2πf and $\hbar = h/2\pi$. The quantum number n takes the integer values 0, 1, 2, 3 ....
The n = 0 wavefunction (eigenfunction) has a single maximum at x = 0; the n = 1 wavefunction has a node there.
The wavefunctions go to zero exponentially when | x | is outside the classically allowed region.
Your sketches should look like those in Figure 4.
Question F3
Write down the time–independent Schrödinger equation for a particle of mass m in a one–dimensional harmonic oscillator potential centred at x = 0. Show that the spatial wavefunction
$\psi(x) = A\exp\left(-\frac12\alpha x^2\right)$
is an energy eigenfunction with total energy eigenvalue $E = \frac12\hbar\omega$, where ω is the angular frequency of the corresponding classical oscillator. Can the quantum oscillator have a lower energy?
Answer F3
The SHM potential energy function is $U(x) = \frac12k_{\rm s}x^2$, where ks is the ‘spring force constant’. Consequently, the time–independent Schrödinger equation is
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} + \frac12k_{\rm s}x^2\psi(x) = E\psi(x)$
Solutions of this equation are the total energy eigenfunctions, and the corresponding values of E are the allowed values of the total energy or eigenvalues of energy. If we substitute the suggested wavefunction
$\psi(x) = A\exp\left(-\frac12\alpha x^2\right)$
into the Schrödinger equation, we find the identity
$x^2\left(\dfrac{\hbar^2\alpha^2}{2m\os} - \frac12k_{\rm s}\right)\psi(x) + \left(E - \dfrac{\alpha\hbar^2}{2m}\right)\psi = 0$
which must be true for all values of x. (See Question R3 for some mathematical detail; also Subsection 2.4.) It follows that the coefficient of x2 and the constant term are each equal to zero.
From the x2 term:
$\dfrac{\hbar^2\alpha^2}{2m\os} = \dfrac{k_{\rm s}}{2}\quad\text{or}\quad\alpha^2 = \dfrac{k_{\rm s}m}{\hbar^2}$
Using $\omega = \sqrt{k_{\rm s}/m\os}$, we confirm that $\alpha = \omega m/\hbar$.
From the constant term:
$E = \dfrac{\hbar^2\alpha}{2m}$
and substituting $\alpha = \omega m/\hbar$: $E = \frac12\hbar\omega$
This is the lowest energy eigenvalue for a quantum harmonic oscillator.
1.3 Ready to study?
Study comment In order to study this module, you will need to be familiar with the following physics terms and physics principles: simple harmonic motion in classical mechanics; the nature of a conservative force and the importance of the potential energy; the potential energy function for a particle executing SHM (U (x) = ksx2/2); the solutions of the time–independent Schrödinger equation for a particle moving in one dimension in a region of constant potential energy; the allowed wavefunctions or eigenfunctions and the corresponding allowed energies or eigenvalues of energy of a particle in a stationary state of definite energy in a one–dimensional box; photons, the Planck–Einstein formula, the de Broglie wavelength, the Heisenberg uncertainty principle; the Born probability interpretation (of the wavefunction). If you are uncertain of any of these terms, you can review them now by referring to the Glossary which will indicate where in FLAP they are developed. You should be familiar with the mathematics of elementary trigonometric functions and the exponential function; the use of complex numbers (including complex conjugates and the role of arbitrary constants in the solution of second–order differential equations). We will frequently use both integral and calculusdifferential calculus involving elementary functions. The following Ready to study questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
A particle of mass m is confined in an infinitely deep potential well such that V = 0 for −a/2 ≤ x ≤ +a/2 and V → ∞ for | x | > a/2. Write down the time–independent Schrödinger equation for the particle inside the well. Confirm that within the well ψ (x) = A cos(πx/a) is a solution to the Schrödinger equation when the total energy $E = \pi^2\hbar^2/(2ma^2)$. Show that this solution satisfies the boundary condition ψ (x) = 0 at x = ±a/2.
Answer R1
Inside the well, U (x) = 0, so the Schrödinger equation becomes:
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = E\psi(x)$
Try the solution ψ (x) = A cos(πx/a):
$\dfrac{d^2\psi(x)}{dx^2} = -\dfrac{A\pi^2}{a^2}\cos\left(\dfrac{\pi x}{a}\right) = -\dfrac{\pi^2}{a^2}\psi$
Substitute into the Schrödinger equation and we find:
$\dfrac{\hbar^2\pi^2}{2ma^2}\psi = E\psi$
which is satisfied if $E = \dfrac{\hbar^2\pi^2}{2ma^2}$
The wavefunction must be continuous_functioncontinuous everywhere and ψ (x) = 0 for | x | > a/2.
Therefore we must have ψ (x) = 0 at the boundary x = ±a/2.
So$\psi\left(\pm\dfrac a2\right) = A\cos\left(\pm\dfrac{\pi a}{2a}\right) =A\cos\left(\pm\dfrac{\pi}{2}\right) = 0$
as required.
Question R2
Write down the time–independent Schrödinger equation for a particle of mass m moving in the x–direction where the potential energy has a constant value V that is greater than the total energy E. Show by substitution that
ψ (x) = A exp(αx) + B exp(−αx)
is a solution with A and B arbitrary constants and α real. Find an expression for α in terms of E and V.
Answer R2
When the potential energy function U (x) = V, the Schrödinger equation becomes:
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} + V\psi(x) = E\psi(x)$
i.e.$\dfrac{\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = (V-E)\psi(x)$
Try the function ψ (x) = A exp(αx) + B exp(−αx):
We use the notation ψ = ψ (x), ψ′ = dψ (x)/dx, and ψ′′ = d2ψ (x)/dx2
Soψ′ = Aα exp(αx) − Bα exp(−αx)
andψ′′ = Aα2 exp(αx) + Bα2 exp(−αx) = α2ψ
Substituting in the Schrödinger equation, we find:
$\dfrac{\hbar^2}{2m\os}\alpha^2\psi = (V-E)\psi$
Thus, the trial function is a solution, provided
$\alpha^2 = \dfrac{2m(V-E)\os}{\hbar^2}\quad\text{i.e.}\quad\alpha = \pm\dfrac{\sqrt{2m(V-E)\os}}{\hbar}$
α is real since V > E.
Question R3
If $\psi(x) = A\exp\left(-\frac12\alpha x^2\right)$, show that d2ψ (x)/dx2 = (x2α2 − α) ψ (x).
Answer R3
We will use the techniques demonstrated in this question many times in this module, so make sure you follow each step carefully.
Note:
Step 1 uses the ‘chain rule of differentiation’ to differentiate a function of a function.
Step 2 uses the ‘differentiation of a product’ rule.
$\psi = A\exp\left(-\frac12\alpha x^2\right)$
$\psi' = -\alpha xA\exp\left(-\frac12\alpha x^2\right) = -\alpha x\psi$
Henceψ′′ = −αψ − αxψ′ = −αψ − αx (−αxψ)
i.e.ψ′′ = −αψ + α2x2ψ = (x2α2 − α)ψ
2 The harmonic oscillator
2.1 Classical description of the problem; classical predictions
We consider a particle of mass m constrained to move in the x–direction. It is subject to a force Fx also directed in the x–direction, proportional to the distance from the origin and directed towards the origin:
Fx = −ksx(1) i
The constant ks is called the force constant, and it plays an important role in our treatment of harmonic motion. A good example of this kind of force is the restoring force on a particle attached to a spring which is free to expand or contract. Newton’s second law is now applied, and we immediately obtain a differential equation relating the position x and the time t:
$m\ddot{x} = -k_{\rm s}x$ i
so$\ddot{x} = -\left(\dfrac{k_{\rm s}}{m}\right)x$(2)
Notice that the negative sign in Equation 2 says that the acceleration is in the negative x–direction when x is positive and is in the positive x–direction when x is negative. Equation 2 is often regarded as the definition of classical harmonic oscillation:
A particle executes simple harmonic motion about a fixed point O if the acceleration is proportional to the displacement from O and directed towards O.
The solutions of Equation 2 have been obtained elsewhere in FLAP:
x = A cos(ωt) + B sin(ωt) with $\omega = \sqrt{k_{\rm s}/m\os}$
Question T1
Confirm by direct substitution that x = A cos(ωt) + B sin(ωt) with $\omega = \sqrt{k_{\rm s}/m\os}$ is the general solution of Equation 2.
Answer T1
Equation 2 is $\ddot{x} = -\left(\dfrac{k_{\rm s}}{m}\right)x$.
Start with the suggested solution:
$x = A\cos(\omega t) + B\sin(\omega t)$
$\dot{x} = -\omega A\sin(\omega t) + \omega B\cos(\omega t)$
$\ddot{x} = -\omega^2A\cos(\omega t) - \omega^2B\sin(\omega t) = -\omega^2x$
Substitute into Equation 2: $-\omega^2x = -\left(\dfrac{k_{\rm s}}{m}\right)x$
This must be true for all values of x, and hence ω2 = ks/m and $\omega = \sqrt{k_{\rm s}/m\os}$ as required.
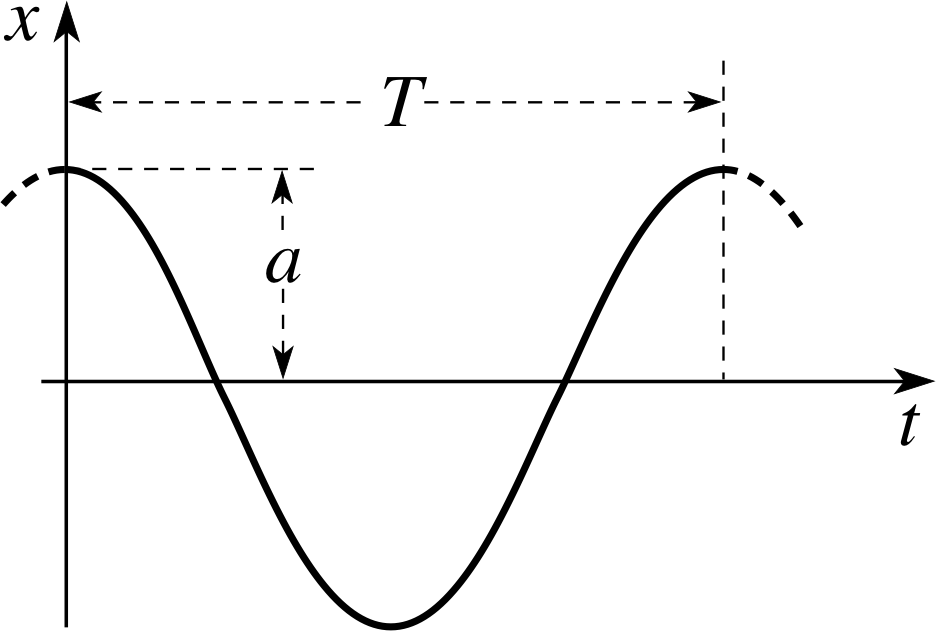
Figure 1 A graph of the oscillation x = a cos(ωt), showing how the amplitude a and the period T are defined.
The arbitrary constants A and B may be determined from the velocity and displacement of the particle at t = 0. For example, we can take x = a and $\dot{x} = 0$ at t = 0; then:
x = a cos(ωt)(3)
The amplitude of this simple harmonic oscillation is a, and it is illustrated in Figure 1. The period T determines the frequency f = 1/T and the angular frequency ω = 2π/T. Consequently, in this particular case:
$\omega = \sqrt{\dfrac{k_{\rm s}}{m}}\quad T = 2\pi\sqrt{\dfrac{m}{k_{\rm s}}}\quad\text{and}\quad f = \dfrac{1}{2\pi}\sqrt{\dfrac{m}{k_{\rm s}}}$(4)
For comparisons with the quantum–mechanical treatment, we need to relate the total energy of the oscillator to its amplitude and also find an expression for the particle velocity in terms of the displacement. The force defined by Equation 1,
Fx = −ksx(Eqn 1)
is a conservative force since it can be derived from a potential energy function U (x):
$F_x = -\dfrac{dU(x)}{dx}$
$\displaystyle U(x) = -\int F_x\,dx = -\int(-k_{\rm s}x)\,dx$
Therefore$U(x) = \frac12k_{\rm s}x^2 + C$
It is usual to put the arbitrary constant C = 0, and the potential energy function then becomes:
The potential energy function for a one–dimensional simple harmonic oscillator:
$U(x) = \frac12k_{\rm s}x^2 + C$(5)
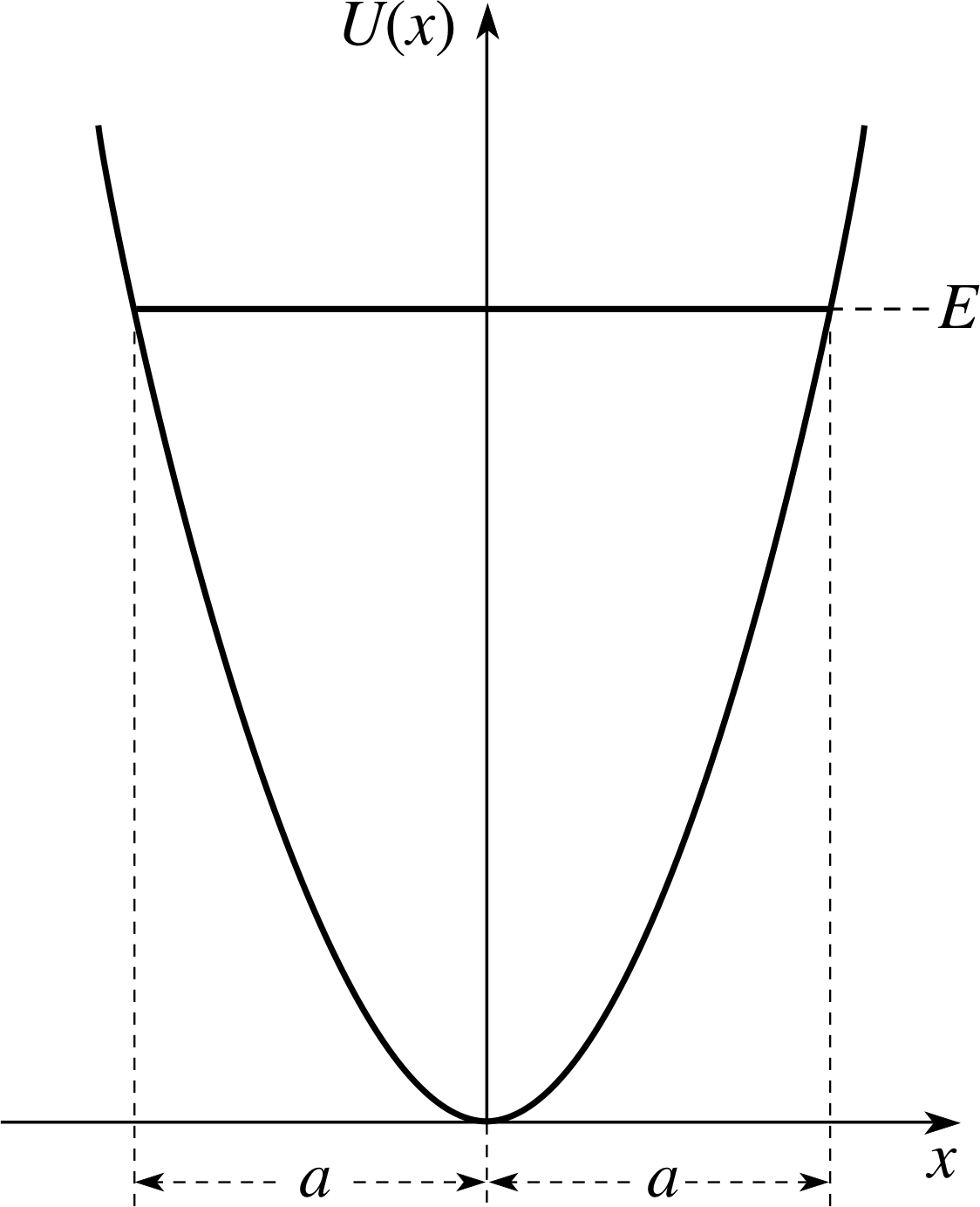
Figure 2 The potential energy function for a simple harmonic oscillator. A possible energy E is represented by a horizontal line, and the corresponding amplitude a is indicated. The potential energy function has a parabolic form.
A graph of the potential energy function has a parabolic form and is shown in Figure 2.
Since the only force acting on the particle is the restoring force, given by Equation 1, the sum of the kinetic and potential energies is constant. We call this constant the total energy E:
$E = \frac12m\dot{x}^2 + \frac12k_{\rm s}x^2$(6)
However when $\dot{x} = 0$, then x = a, and we have:
$E = \frac12k_{\rm s}a^2\quad\text{or}\quad a = \sqrt{\dfrac{2E\os}{k_{\rm s}}}$(7)
The amplitude of the oscillation increases as the square root of the total U (x) energy. The relation between the total energy E and the amplitude a is also illustrated in Figure 2.
We can rearrange Equation 6 to obtain the desired expression for the particle velocity:
$\dot{x}^2 = \dfrac{2E}{m} - \left(\dfrac{k_{\rm s}}{m}\right)x^2$
Substituting in Equation 7:
$\dot{x}^2 = \left(\dfrac{k_{\rm s}}{m}\right)(a^2-x^2)$
It is convenient to replace the ratio ks/m by ω2 using Equation 4,
$\omega = \sqrt{\dfrac{k_{\rm s}}{m}}\quad T = 2\pi\sqrt{\dfrac{m}{k_{\rm s}}}\quad\text{and}\quad f = \dfrac{1}{2\pi}\sqrt{\dfrac{m}{k_{\rm s}}}$(Eqn 4)
so that:
$\dot{x} = \pm\omega\sqrt{a^2-x^2}$(8)
The speed $\lvert\,\dot{x}\,\rvert$ is maximum at x = 0 and is zero at the extremes x = ±a.
Now, imagine making observations on the position of the particle as it oscillates, and assume they are made at random times. Obviously, you are more likely to find the particle in regions where it is moving slowly, and conversely less likely to find it where it is moving quickly. We can quantify this argument as follows:
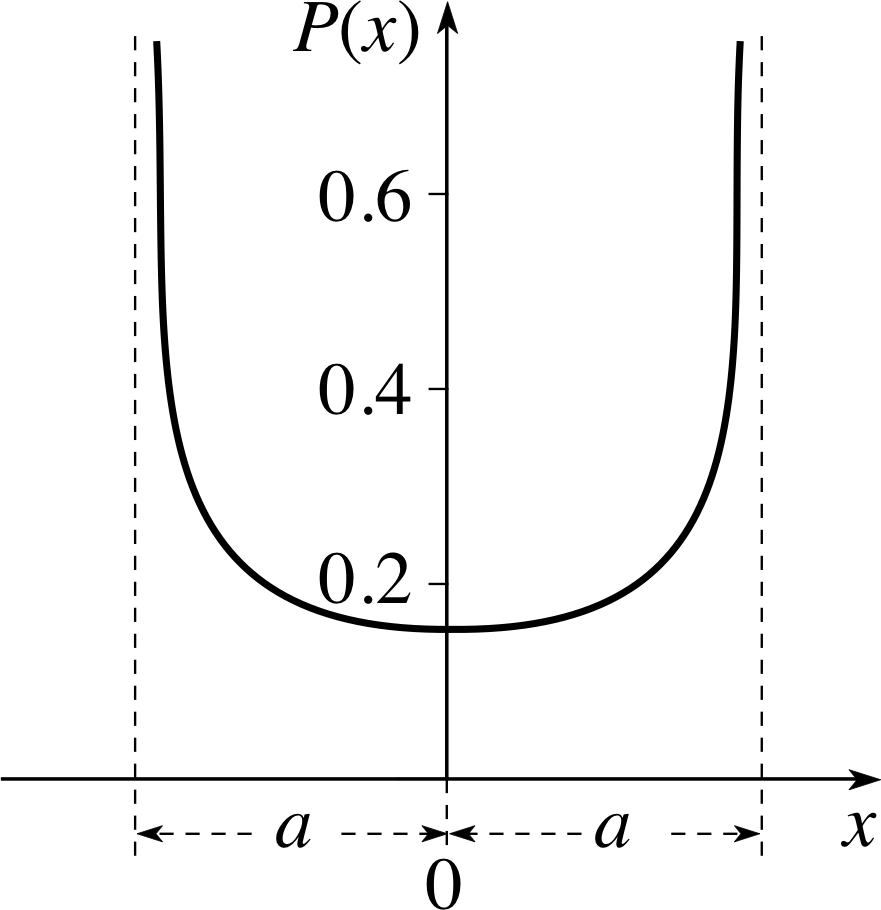
Figure 3 The classical probability density for a particle executing simple harmonic motion. The amplitude of the oscillation is a. The corresponding classical probability of finding the particle in any finite region between x = x1 and x = x2 is given by $\displaystyle \int_{x_1}^{x_2}P(x)\,dx$
Let the probability of finding the particle in a narrow region of length ∆x at position x be P (x) ∆x, and let ∆t be the time required for the particle to cross ∆x. Since the particle crosses ∆x twice during each complete oscillation, we have:
P (x) ∆x = 2∆t/T
where T is the period. In the limit as ∆x and ∆t tend to zero, ∆x/∆t tends to $\dot{x}$ and so:
$P(x) = \dfrac{2}{\lvert\,\dot{x}\,\rvert T}$ i
Using Equations 4 and 8, we find:
$P(x) = \dfrac{\omega}{\pi\os}\dfrac{1}{\omega\sqrt{a^2-x^2}}$
Hence$P(x) = \dfrac{1}{\pi\sqrt{a^2-x^2}}$(9)
The function P (x) is the classical probability density, and we will compare it with the corresponding quantum probability density in due course. Figure 3 shows the graph of P (x). You can see the probability density increasing as the displacement increases and the speed decreases; eventually, the probability density goes asymptotically to infinity when x → ±a. However, the probability of finding the particle in any finite region remains finite.
2.2 The Schrödinger equation for a simple harmonic oscillator
Before you embark on any mechanics problem, it is important to decide whether to use the classical approximation or quantum mechanics. One test is to compare a typical de Broglie wavelength with an important linear dimension in the problem. If the de Broglie wavelength is negligibly small, then classical mechanics may safely be used. In the harmonic oscillator problem, we can compare the de Broglie wavelength with the amplitude of the oscillation. This leads to the following conditions:
If E is the total energy, h is Planck’s constant and f is the classical oscillator frequency:
Use classical mechanics if E ≫ hf. Otherwise use quantum mechanics! i
In the quantum–mechanical description of particle motion, the concept of a particle trajectory is completely lost. We cannot know the particle position and momentum simultaneously, and this fundamental limitation is formalized in the Heisenberg uncertainty relation $\Delta x\,\Delta p_x \ge \hbar$. In the case of the quantum simple harmonic motion, you must stop visualizing a particle oscillating about a mean position and concentrate on the wavefunction! The wavefunction corresponding to a particular state tells you all that can be known about the behaviour of the particle in that particular state.
Study comment The one–dimensional wavefunction Ψ (x, t) is time–dependent and satisfies the time–dependent Schrödinger equation. For a stationary state of definite energy E the wavefunction takes the form:
${\it\Psi}\,(x,\,t) = \psi(x)\exp\left(-i\dfrac E\hbar t\right)$
Since this module is entirely concerned with such states we will concentrate on determining the spatial wavefunctions ψ (x) which satisfy the time–independent Schrödinger equation, and the corresponding values of E. Because of this restriction we may conveniently refer to ψ (x) as the wavefunction since Ψ (x, t) follows immediately from ψ (x) and E.
The time–independent Schrödinger equation for particle motion in one dimension is:
$\dfrac{-\hbar}{2m\os}\dfrac{d^2\psi(x)}{dx^2} + U(x)\psi(x) = E\psi(x)$(10)
Here, U (x) is the potential energy function, and we have to solve the equation with appropriate boundary conditions to obtain the allowed values of the total energy E and the corresponding wavefunctions. Solutions of the time–independent Schrödinger equation for a particle trapped in a one–dimensional box, discussed elsewhere in FLAP, show that confinement leads to quantized_quantityquantized energy levels labelled by an integer quantum number n and that each energy level has a corresponding wavefunction ψn(x). Much can be learned from this example and the lessons applied to the harmonic oscillator.
First we substitute Equation 5,
$U(x) = \frac12k_{\rm s}x^2 + C$(Eqn 5)
into Equation 10 to produce the Schrödinger equation for the quantum harmonic oscillator:
$\dfrac{-\hbar}{2m\os}\dfrac{d^2\psi(x)}{dx^2} + \frac12k_{\rm s}x^2\psi(x) = E\psi(x)$
and, after rearrangement:
The time–independent Schrödinger equation for a quantum harmonic oscillator:
$\dfrac{\hbar}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = \left(\frac12k_{\rm s}x^2 - E\right)\psi(x)$(11)
2.3 The energy eigenfunctions
There are very many solutions of Equation 11 and we have to select those which satisfy the appropriate boundary conditions. i In the case of the one–dimensional box, or infinite square well, the allowed wavefunctions are constrained to zero at the edges where the potential energy goes to infinity. i However, the harmonic oscillator potential energy function has no such rigid boundary but it does go to infinity at infinite distance from the origin. Our boundary condition is that the allowed wavefunctions approach zero as x approaches +∞ or −∞. You may think that this condition is easy to arrange with any value of the total energy E since the solution to any second–order differential equation contains two arbitrary constants. This is not so! One of the constants fixes the overall normalization of the wavefunction, and the remaining constant and the value of E are used to satisfy the two boundary conditions. In fact, it turns out that there are an infinite number of discrete values of E which we label E1, E2, E3, ..., En, and to each of these there is a corresponding allowed wavefunction ψ1, ψ2, ψ3, ..., ψn. If E is varied, even infinitesimally, from any one of the allowed values, then the wavefunction will diverge to infinity as x approaches +∞ or −∞. The allowed values of E are called eigenvalues of total energy and the corresponding wavefunctions are eigenfunctions of total energy.

Figure 2 The potential energy function for a simple harmonic oscillator. A possible energy E is represented by a horizontal line, and the corresponding amplitude a is indicated. The potential energy function has a parabolic form.
Physical intuition can give us some idea of the form of the allowed U (x) wavefunctions (eigenfunctions). For any given energy E, there will be a region of space (see Figure 2) where the potential energy is less than the total energy; this is the so–called classically allowed region. i Here, we expect the wavefunction to have properties similar to the standing waves inside a one–dimensional box. In particular, we expect the number of points at which ψn (x) = 0, the number of node_in_a_spatial_wavefunctionnodes of the wavefunction, to increase with increasing energy. In the region of large x where the particle energy is much less than the potential energy, the classically forbidden region, we might expect a solution of the Schrödinger equation of an exponential form. It would be incorrect to anticipate ψn (x) ≈ exp(−αx) here since this would not fall asymptotically to zero for negative x. We require instead a symmetric_functionsymmetric function of x such as ψn (x) ≈ exp(−αx2), which tends to zero as x → ∞ or x → −∞, as required physically.
In fact, each wavefunction will include a term of the form:
$\psi(x) = A\exp\left(-\frac12\alpha x^2\right)$(12)
where A is a constant and $\alpha = \omega m/\hbar$. i
Study comment You can omit the following question at first reading if you wish.
✦ Show by substitution that Equation 12,
$\psi(x) = A\exp\left(-\frac12\alpha x^2\right)$(Eqn 12)
is a solution of Equation 11,
$\dfrac{\hbar}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = \left(\frac12k_{\rm s}x^2 - E\right)\psi(x)$(Eqn 11)
when x is large. i
✧ As in Question R3 we use the notation:
ψ′ = dψ (x)/dx and ψ′′ = d2ψ (x)/dx2.
$\psi = A\exp\left(-\frac12\alpha x^2\right)$
$\psi' = -\alpha xA\exp((-\frac12\alpha x^2) = -\alpha x\psi$
$\psi'' = -\alpha x\psi' +\alpha\psi = (\alpha^2x^2-\alpha)\psi$
Substitute in Equation 11,
$\dfrac{\hbar^2}{2m}\dfrac{d^2\psi(x)}{dx^2} = \left(\frac12k_{\rm s}x^2-E\right)\,\psi(x)$(Eqn 11)
$\dfrac{\hbar^2}{2m}(\alpha^2x^2-\alpha)\psi = \left(\frac12k_{\rm s}x^2-E\right)\psi$
When x is large, we may neglect E and α with respect to $\frac12k_{\rm s}x^2$ and α2x2 to obtain:
$\dfrac{\hbar^2}{2m}\alpha^2x^2\psi = \frac12k_{\rm s}x^2\psi$
and if ψ ≠0:
$\dfrac{\hbar^2}{2m}\alpha^2x^2 = \frac12k_{\rm s}\quad\text{i.e.}\quad\alpha=\dfrac{\sqrt{k_{\rm s}m}}{\hbar}$
Remember that $\omega = \sqrt{k_{\rm s}m}$, so we can rewrite α as $\alpha =\omega m/\hbar$. This shows that Equation 12,
$\psi(x) = A\exp\left(-\frac12\alpha x^2\right)$(Eqn 12)
is a solution of the Schrödinger equation for any value of the energy E provided x is large.
Solutions to Equation 11 for all values of x can now be found by multiplying Equation 12 by suitable polynomial functions fn(x) of degree n. This results in wavefunctions similar to standing waves in the classically allowed region joining smoothly to the falling exponential shape in the classically forbidden region:
$\psi_n(x) = A_nf_n\exp\left(-\frac12\alpha x^2\right)$ with n = 0, 1, 2, 3 ...(13) i
These are the energy eigenfunctions, and to each one there is a corresponding energy eigenvalue (see Subsection 2.4).

Figure 4 The first four energy eigenfunctions for the quantum simple harmonic oscillator (not normalized). The limits of motion for a classical oscillator with the same energy are indicated by the vertical dashed lines. The horizontal axis is marked in the dimensionless variable $\sqrt{\alpha\os}x$.
The first four of the relevant polynomial functions fn(x) are listed below, and the eigenfunctions are illustrated in Figure 4:
$\left.\begin{align}f_0 &= 1\\f_1 &= 2\sqrt{\alpha\os}x\\f_2 &= 2 - 4\alpha x^2\\f_3 &= 12\sqrt{\alpha\os}x - 8\alpha\sqrt{\alpha\os}x^3\end{align}\right\}$(14)
The exponential combined with the polynomials produces functions that have n nodes in the classically allowed regions.
As the number of nodes increases, so does the corresponding energy as expected.
The boundaries of the classically allowed regions are marked in Figure 4, so you can clearly see the transition from the standing wave forms to the falling exponential.
The falling exponential with argument proportional to x2 ensures that the wavefunctions go smoothly to zero as x → ±∞.
Notice that each allowed wavefunction has a definite symmetry, it is either an odd_functionodd or an even_functioneven function of x. A wavefunction is odd or even depending on whether or not ψ (x) changes sign under the transformation x → −x:
- If ψ (x) = +ψ (−x), then ψ (x) is even.
- If ψ (x) = −ψ (−x), then ψ (x) is odd.
Inspection of the first four eigenfunctions (Figure 4) shows that ψn(x) is even or odd according to whether n is even or odd.
This property of the wavefunction is extremely important and follows from the nature of the potential function $U(x) = \frac12kx^2$. Clearly, U (x) = U (−x), i.e. the potential is symmetric about x = 0. This means that any physical observable must also be symmetric about x = 0, including the stationary state probability density functions: Pn(x) = ψn*(x) ψn(x) = | ψn(x) |2. We must have Pn(x) = Pn(−x), and therefore:
| ψn(x) |2 = | ψn(-x) |2
In this case the wavefunctions are real, so the condition becomes:
ψn2(x) = ψn2(−x) i
and taking the square root we obtain
ψn(x) = ±ψn(−x)
The eigenfunctions are therefore necessarily either odd or even when the potential function is symmetric about the origin.
Question T2
Within a one–dimensional box between x = −a/2 and x = a/2 the eigenfunctions of a confined particle are ψn(x) = A cos(nπx/a) for n = 2, 4, 6 ... and ψn(x) = A sin(nπx/a) for n = 1, 3, 5 .... Confirm that these are even and odd functions, as required by symmetry.
Answer T2
ψn(x) = A cos(nπx/a) for n = 2, 4, 6 ... and ψn(x) = A sin(nπx/a) for n = 1, 3, 5 ...
Consider the even quantum number states first, and make the transformation x → −x:
$\psi_n(-x) = A\cos\left(\dfrac{-n\pi x}{a}\right) = +A\cos\left(\dfrac{n\pi x}{a}\right)$ (remember cos(−θ) = cos θ for any θ)
so that ψn(−x) = ψn(x)
ψn(x) is an even function when n is an even number.
Now consider the odd quantum number states:
$\psi_n(-x) = A\sin\left(\dfrac{-n\pi x}{a}\right) = -A\sin\left(\dfrac{n\pi x}{a}\right)$ (remember sin(−θ) = −sin θ for any θ)
so that ψn(−x) = −ψn(x)
ψn(x) is an odd function when n is an odd number.
2.4 The energy eigenvalues
The allowed total energies or eigenvalues of total energy corresponding to the first few eigenfunctions given by Equations 13 and 14
$\psi_n(x) = A_nf_n\exp\left(-\frac12\alpha x^2\right)$ with n = 0, 1, 2, 3 ...(Eqn 13)
$\begin{align}f_0 &= 1\\f_1 &= 2\sqrt{\alpha\os}x\\f_2 &= 2 - 4\alpha x^2\\f_3 &= 12\sqrt{\alpha\os}x - 8\alpha\sqrt{\alpha\os}x^3\end{align}$(Eqns 14)
may be found by direct substitution into the Schrödinger equation. We will do the first one, and then you can try the second!
Starting with $\psi_0(x) = A_0\exp\left(-\frac12\alpha x^2\right)$ we get by successive differentiation i:
ψ′′ = (α2x2 − α)ψ
Substitute this into Equation 11,
$\dfrac{\hbar}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = \left(\frac12k_{\rm s}x^2 - E\right)\psi(x)$(Eqn 11)
$\dfrac{\hbar}{2m}(\alpha^2x^2 - \alpha)\psi = \left(\frac12k_{\rm s}x^2 - E\right)\psi$
Collecting terms:
$x^2\left(\dfrac{\hbar^2\alpha^2}{2m}-\frac12k_{\rm s}\right)\psi + \left(E - \dfrac{\alpha\hbar^2}{2m}\right)\psi = 0$
This is not an equation to be solved for a particular value of x – rather it is an identity that is true for all values of x. It follows that the coefficient of x2 and of the constant term must each be equal to zero. From the x2 term:
$\dfrac{\hbar^2\alpha^2}{2m} = \frac12k_{\rm s}\quad\text{i.e.}\quad\alpha^2 = \dfrac{k_{\rm s}m}{\hbar^2}$
Using $\omega = \sqrt{k_{\rm s}/m\os}$, we confirm that $\alpha = \dfrac{\omega m}{\hbar}$
Now, from the constant term:$E = \dfrac{\hbar^2\alpha}{2m}$
and substituting $\alpha = \dfrac{\omega m}{\hbar}$ gives:$E = \frac12\hbar\omega$
or in terms of the frequency f = ω/(2π):$E = \frac12hf$
We have confirmed that $\psi_0(x) = A_0\exp\left(-\frac12\alpha x^2\right)$ is an energy eigenfunction of the system and the corresponding eigenvalue is $E_0 = \frac12hf$. This is in fact the lowest possible value of the energy of the quantum harmonic oscillator. There is a zero point energy of the harmonic oscillator (just as there is for a particle confined in a one–dimensional box). In Question T5, you can show that this is a consequence of the Heisenberg uncertainty principle $\Delta p_x\,\Delta x \ge \hbar$.
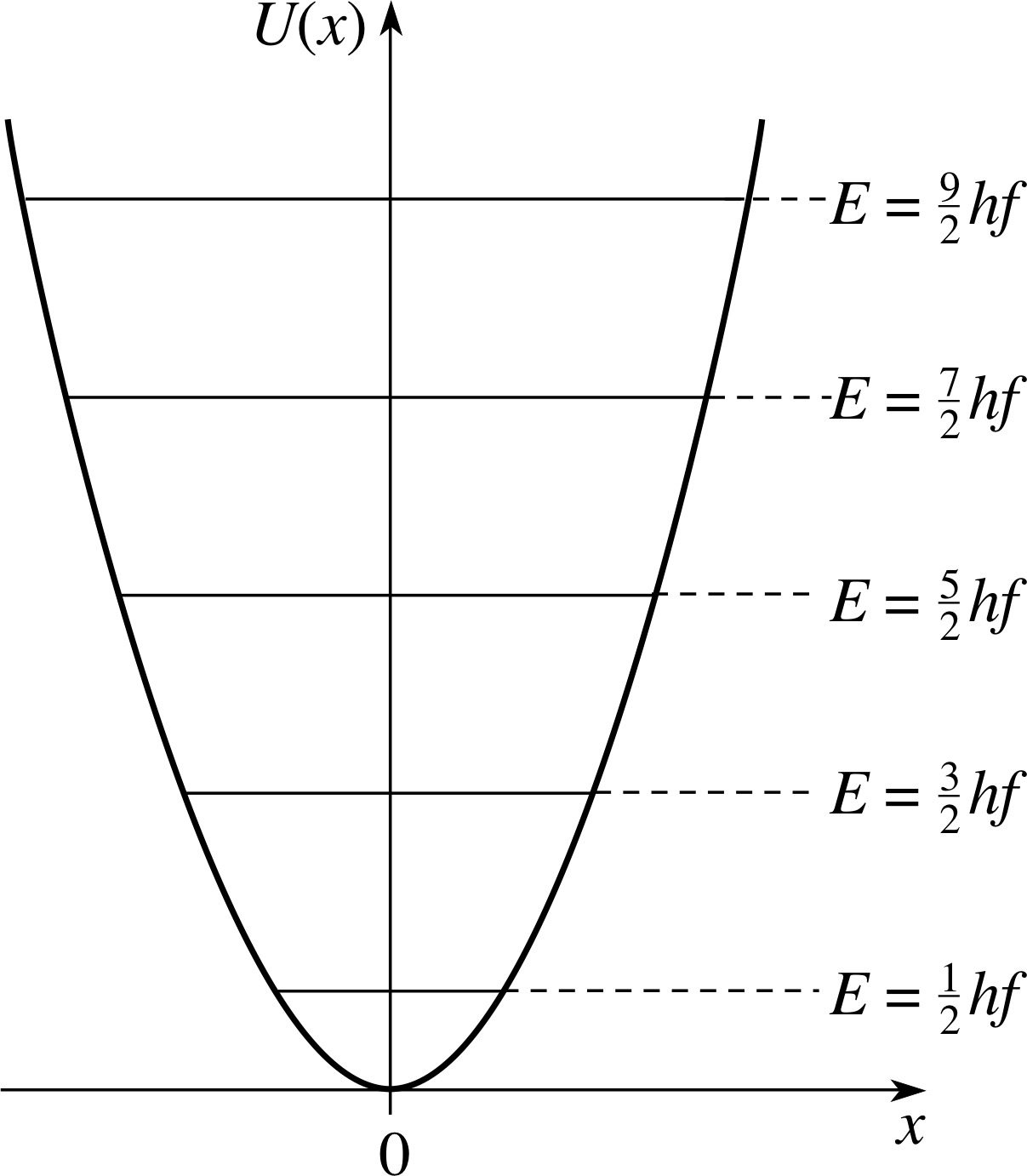
Figure 5 The quantum harmonic oscillator energy levels superimposed on the potential energy function.
In exactly the same way, it can be shown that the eigenfunctions ψ1(x), ψ2(x) and ψ3(x) have eigenvalues $\frac32hf,~\frac52hf\text{ and }\frac72hf$, respectively. This suggests a general rule which, although true, we will not attempt to prove:
The allowed energy eigenvalues of the quantum harmonic oscillator are:
$E_n = \left(n + \frac12\right)hf$ with n = 0, 1, 2, 3 ...(15)
where the quantum number n characterizes the allowed energies and wavefunctions.
Question T3
Show that $\psi_1(x) = A_12\sqrt{\alpha\os}x\exp\left(-\frac12\alpha x^2\right)$ is an eigenfunction of the quantum harmonic oscillator and that the corresponding total energy eigenvalue is $E_1 = \frac32hf$. (A1 is an arbitrary constant.)
Answer T3
The SHM potential energy function is $U(x) = \frac12k_{\rm s}x^2$, so that the Schrödinger equation in one dimension is:
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} + \frac12k_{\rm s}x^2\psi(x) = E\psi(x)$
Try the suggested function $\psi(x) = A_12\sqrt{\alpha\os}x\exp\left(-\frac12\alpha x^2\right)$. If this is an eigenfunction, then it satisfies the Schrödinger equation for all values of x. We need the derivatives of ψ (x):
$\psi' = A_12\sqrt{\alpha\os}\exp\left(-\frac12\alpha x^2\right) - A_12\sqrt{\alpha\os}\alpha x^2\exp\left(-\frac12\alpha x^2\right) = \psi\left(\dfrac1x-\alpha x\right)$
$\psi'' = \psi'\left(\dfrac1x-\alpha x\right) + \psi\left(\dfrac{-1}{x^2}-\alpha\right)$
Substitute for ψ′: $\psi'' = \psi\left(\dfrac1x-\alpha x\right)\left(\dfrac1x-\alpha x\right) + \psi\left(\dfrac{-1}{x^2}-\alpha\right) = (-3\alpha+\alpha^2x^2)\psi$
Substitute this into the Schrödinger equation, and we obtain:
$\dfrac{-\hbar^2}{2m\os} (-3\alpha+\alpha^2x^2)\psi + \frac12k_{\rm s}x^2\psi(x) = E\psi(x)$
Collect terms to get the identity:
$\left(\dfrac{3\alpha\hbar^2}{2m}-E\right)\psi + \left(\frac12k_{\rm s} - \dfrac{\hbar^2}{2m}\right)x^2\psi = 0$
This is true for all values of x, so the coefficient of x2 and the constant term are both equal to zero;
so $k_{\rm s} = \hbar^2\alpha^2/m$, giving $\alpha^2 = mk_{\rm s}/\hbar^2$. Using ω2 = ks/m we find $\alpha^2 = \omega^2m^2/\hbar^2$. This confirms that $\alpha = \omega m/\hbar$.
Using the x2 term: $E = 3\alpha\hbar^2/(2m)$ and substituting $\alpha = \omega m/\hbar$, we get the final result $E = \frac32\omega\hbar$ or $E = \frac32hf$.
Congratulations if you got this out correctly first time!
The energy eigenvalues given by Equation 15 are often referred to as the harmonic oscillator energy levels. The levels are spaced equally by an amount hf. They are shown schematically in Figure 5 superimposed on the potential energy function.

Figure 4 The first four energy eigenfunctions for the quantum simple harmonic oscillator (not normalized). The limits of motion for a classical oscillator with the same energy are indicated by the vertical dashed lines. The horizontal axis is marked in the dimensionless variable $\sqrt{\alpha\os}x$.
You should now refer to Figure 4 and associate each eigenfunction shape with the corresponding energy eigenvalue. Notice, in particular, the following:
- The energy levels are equally spaced.
- The number of nodes in the eigenfunctions, given by n, increases with energy.
- The eigenfunctions spread out in space as the energy increases.
For each of the energy eigenvalues En, we can work out, from Equation 7,
$E = \frac12k_{\rm s}a^2$(Eqn 7)
the region of space in which a classical simple harmonic oscillator with that energy would be confined.
Let the region for energy En be bounded by x = ±an then:
since$E = \frac12k_{\rm s}a^2\quad a = \sqrt{\dfrac{2E\os}{k_{\rm s}}}$
but$E_n = (n + \frac12)hf = (n + \frac12)\hbar\omega$
However, $\alpha = \omega m/\hbar = k_{\rm s}/(\hbar\omega)$, so that $E_n = (n + \frac12)k_{\rm s}/\alpha\quad\text{and}\quad a_n = \sqrt{\dfrac{2n+1}{\alpha}}$
making the equation dimensionless:
$\sqrt{\alpha\os}a_n = \sqrt{2n + 1\os}$(16)
These boundaries are marked in Figure 4 which showed the eigenfunctions.
Notice that for the quantum oscillator the amplitude ceases to have direct physical meaning, since there is no definite limit to the region of space in which the particle may be found. Also the eigenfunctions are stationary states and imply no particle oscillation, as in the classical model.
If we associate energy emission with a transition between two stationary states then we need to consider the time dependence of the full wavefunction. This complication is beyond the scope of this module but is developed in the FLAP module dealing with the one–dimensional box.
Question T4
In classical theory, a charged particle executing SHM of frequency f emits electromagnetic radiation, also of frequency f. Write down an expression for the allowed energies of the equivalent quantum oscillator.
What is the energy of a photon emitted when the quantum oscillator jumps from level n1 to level n2 (n1 > n2)? Show that it is only when n2 = n1 − 1 that the frequency of the radiation associated with such photons is equal to the classical frequency f.
Answer T4
The total energy eigenvalues are given by Equation 15,
$E_n = \left(n + \frac12\right)hf$ with n = 0, 1, 2, 3 ...(Eqn 15)
where f is the frequency of the classical oscillator with the same m and k. The energy of a photon emitted is
E = En1 −En2 = (n1 − n2)hf
The radiation associated with a photon of energy E has frequency fr given by E = hfr. Hence hfr = (n2 − n2)hf, and fr = f if n2 = n1 −1. This important result shows us another connection between the classical and quantum theories of radiation.
2.5 Probability densities and comparison with classical predictions
We must be particularly careful when comparing the predictions of quantum mechanics and classical mechanics. The two theories were developed for very different systems. Classical mechanics is the appropriate tool, in general, for the large–scale world of objects we sense directly, and it was developed on the basis of experimental observations on such objects. Quantum mechanics applies, in general, to the world of atoms and nuclei, where the relevant objects – electrons, nucleons etc. – cannot be sensed directly. It is hardly surprising that the predictions of quantum mechanics seem strange and often defy common sense when compared with the predictions of classical mechanics which accord with everyday experience.
Although it is beyond the scope of FLAP, one can show that the laws of quantum mechanics do agree with the laws of classical mechanics in the limit of large distances or high energies or large quantum numbers. We can therefore regard quantum mechanics as the more fundamental theory and classical mechanics as an approximation that becomes more exact as we move from the microscopic to the macroscopic world. The notion that classical physics can be obtained from some limiting case of quantum physics is known as the correspondence principle.
The most important result we derived from the quantum mechanics of the harmonic oscillator was the prediction of quantized energy levels. If the potential energy function of a particle of mass m moving along the x–axis is $U(x) = \frac12k_{\rm s}x^2$, then the total energy can be one of the discrete set $E_n = \left(n + \frac12\right)hf$ with $f = \dfrac{1}{2\pi}\sqrt{\dfrac{k_{\rm s}}{m}}$ and the quantum number n = 0, 1, 2, 3 .... No other value of E is possible. The difference between adjacent energy levels ∆E = En − En−1 = hf, and in the limit of large quantum numbers this becomes negligible compared with En:
$\dfrac{\Delta E}{E_n} = \dfrac{hf}{\left(n+\frac12\right)hf} \to 0$ as n → ∞
For very large quantum numbers the energy levels become so close to each other that the essential ‘granularity’ is not noticed. This corresponds to classical mechanics, which predicts a continuum of values of the total energy. It is also in agreement with our condition for the applicability of classical mechanics E ≫ hf, and is an example of the correspondence principle.
Another important prediction of quantum mechanics is the so–called zero point energy. When the quantum number n = 0, the total energy is $E_0 = \frac12hf$, and this is the smallest possible value of the total energy of any harmonic oscillator. The zero point energy is a purely quantum effect and it has no parallel in classical mechanics, which allows energies arbitrarily close to zero.
Quantum mechanics predicts:
- discrete energy levels: $E_n = \left(n + \frac12\right)hf$
- the zero point energy: $E_0 = \frac12hf$
Classical mechanics predicts:
- a continuum of energies from zero upwards
Quantum mechanics → classical mechanics as n → ∞.
The essential lumpy or grainy characteristic of quantum mechanics and the smoothness of classical mechanics is also evident in the probability density distributions P (x). We worked out a probability density for the classical harmonic oscillator under the assumption that observations on the particle position were made at random times during the oscillation. This was found to be:
$P(x) = \dfrac{1}{\pi\sqrt{a^2-x^2}}$(Eqn 9)
In quantum mechanics, there is a fundamental uncertainty in the position of the particle before the observation is made, and the probability of finding the particle in the range x to x + ∆x is given by | ψ (x) |2 ∆x. The quantum probability density is then P (x) = | ψ (x) |2. The quantum probabilities are readily worked out by squaring the real eigenfunctions given by Equations 13 and 14:
$\psi_n(x) = A_nf_n\exp\left(-\frac12\alpha x^2\right)$ with n = 0, 1, 2, 3 ...(Eqn 13)
$\begin{align}f_0 &= 1\\f_1 &= 2\sqrt{\alpha\os}x\\f_2 &= 2 - 4\alpha x^2\\f_3 &= 12\sqrt{\alpha\os}x - 8\alpha\sqrt{\alpha\os}x^3\end{align}$(Eqns 14)
Quantum probability densities for the harmonic oscillator:
$P_n(x) = A_n^2f_n^2(x)\exp(-\alpha x^2)$ with n = 0, 1, 2, ...(17)
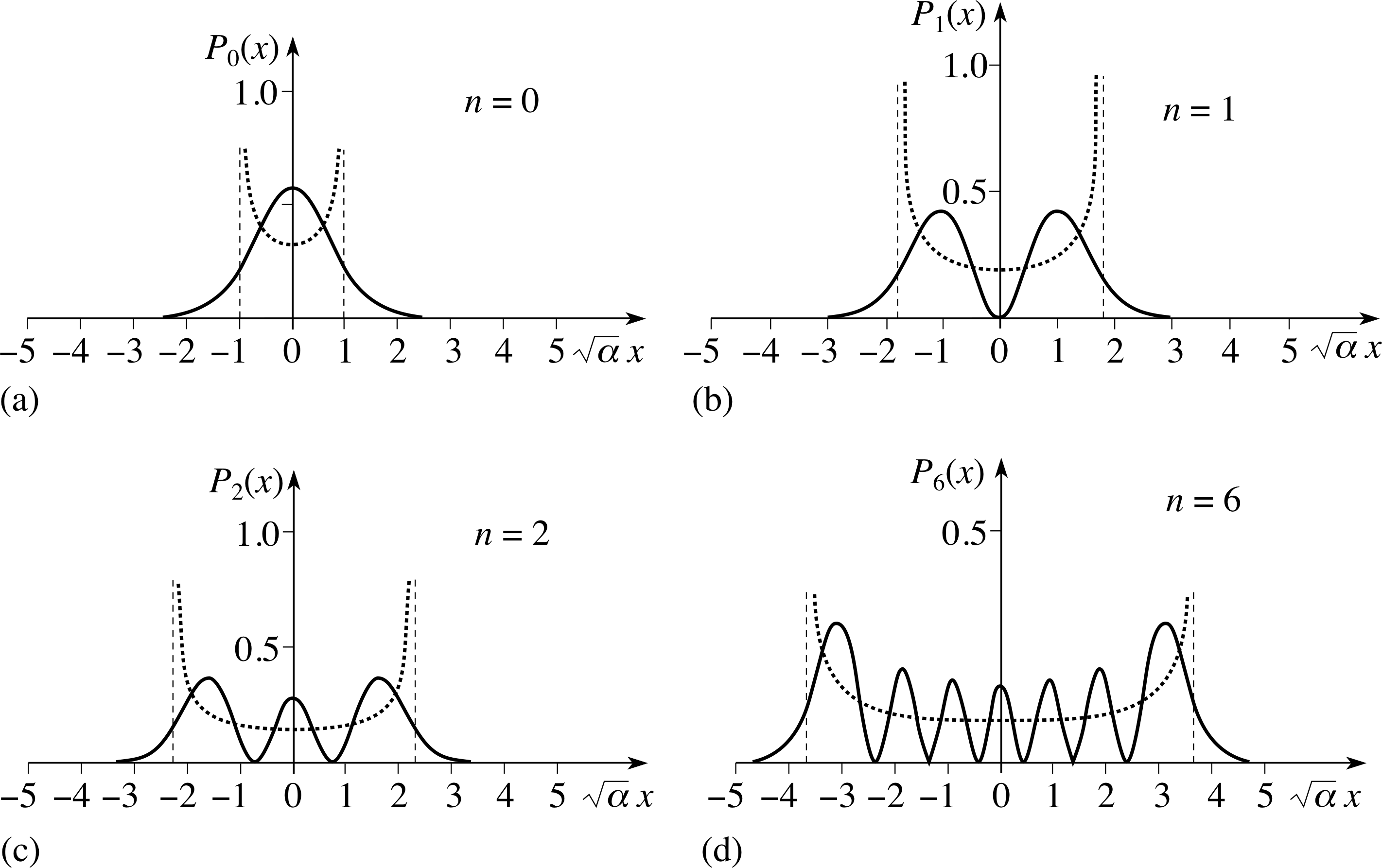
Figure 6 The probability density functions for the harmonic oscillator. Four cases are shown for particles in energy levels given by the quantum number n = 0, 1, 2, and 6. The dotted curves show the corresponding classical calculation of the probability density, with the dashed lines the classical limits of the oscillation.
The graphs of the probability functions given by Equation 17 for the three lowest energy levels and for the n = 6 energy level are shown in Figure 6, plotted as a function of the dimensionless variable $\sqrt{\alpha\os}x$.
Also shown in Figure 6 are the corresponding classical probability distributions given by Equation 9. These are obtained by finding the amplitude of the classical oscillator from Equation 16,
$\sqrt{\alpha\os}a_n = \sqrt{2n + 1\os}$(Eqn 16)
Of course, it is really absurd to suggest that the classical calculation is relevant in the region of small quantum numbers, and the classical and quantum probability distributions bear little resemblance to each other for n = 1, 2 or 3. But for n = 6, you can see that the quantum distribution is beginning to approach the classical one. It does not stretch the imagination too much to see that the two forms become indistinguishable as n → ∞. This is another instance of the correspondence principle.
Question T5
Write down the probability density function P (x) for the n = 0 state of the quantum oscillator.
Show that at a distance $\Delta x = 1/\sqrt{\alpha\os}$ from the origin, P (x) falls to 1/e of its maximum. ∆x is regarded as the uncertainty in the position of the particle. Now estimate the momentum of the particle using the relation $p_x \approx \pm\sqrt{2mE\os}$, and hence estimate the
uncertainty in the momentum ∆px. Find the product ∆x ∆px, and comment on the result.
Answer T5
The eigenfunction labelled by n = 0 describes the lowest energy state or ground state of the quantum oscillator. From Equations 13 and 14,
$\psi_n(x) = A_nf_n\exp\left(-\frac12\alpha x^2\right)$ with n = 0, 1, 2, 3 ...(Eqn 13)
$\begin{align}f_0 &= 1\\f_1 &= 2\sqrt{\alpha\os}x\\f_2 &= 2 - 4\alpha x^2\\f_3 &= 12\sqrt{\alpha\os}x - 8\alpha\sqrt{\alpha\os}x^3\end{align}$(Eqns 14)
we find:
$\psi_0(x) = A\exp\left(\frac12\alpha x^2\right)$
We do not need the normalization constant A. The probability density is then P0(x) = A2 exp(−αx2).
The maximum value of P0(x) is at x = 0, and we have P0(0) = A2.
At a distance $\Delta x = 1/\sqrt{\alpha\os}$ from the origin, P0(∆x) = A2exp(−α/α) = A2/e
The probability of finding the particle at distance $\Delta x = 1/\sqrt{\alpha\os}$ is 1/e of its value at the origin. A measurement of position of the particle is likely to get a result in the range −∆x to +∆x, so the uncertainty in the position of the particle is $\Delta x = 1/\sqrt{\alpha\os}$. Since $\alpha = \omega m/\hbar$, this is written $\Delta x = \sqrt{\hbar/(\omega m)}$.
The wavefunction is not an eigenfunction of momentum, but we can estimate the momentum from $p_x \approx \pm\sqrt{2mE\os}$. The particle can be moving in either direction, so $\Delta p_x \approx \sqrt{2mE\os}$.
The total energy is $E = \frac12\hbar\omega$, so that $\Delta p_x \approx \sqrt{m\hbar\omega\os}$. Immediately we can write:
$\Delta x\,\Delta p_x \approx \sqrt{\hbar/(\omega m)\os}\,\sqrt{m\hbar\omega} \approx \hbar$
This is consistent with the Heisenberg uncertainty principle $\Delta x\,\Delta p_x \ge \hbar/2$, which places a fundamental limit on our simultaneous knowledge of a particle’s position and momentum.
3 Closing items
3.1 Module summary
- 1
-
If a particle of mass m is subject to a force Fx = −ksx, then classical (Newtonian) mechanics shows that it will execute simple harmonic motion (SHM) about the origin with frequency
$f = \dfrac{1}{2\pi}\sqrt{\dfrac{k_{\rm s}}{m}}$
- 2
-
The potential energy function of a particle executing SHM is $U(x) = \frac12k_{\rm s}x^2$. The total energy of a particle executing SHM is related to the amplitude of the oscillation by the equation
$E = \frac12k_{\rm s}a^2\quad\text{or}\quad a = \sqrt{\dfrac{2E\os}{k_{\rm s}}}$(Eqn 7)
- 3
-
The classical probability density for a particle executing SHM is
$P(x) = \dfrac{1}{\pi\sqrt{a^2-x^2}}$(Eqn 9)
- 4
-
E ≫ hf is a condition for the use of classical mechanics in oscillator problems. Otherwise use quantum mechanics.
- 5
-
The Schrödinger equation for the quantum harmonic oscillator is:
$\dfrac{\hbar}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = \left(\frac12k_{\rm s}x^2 - E\right)\psi(x)$(Eqn 11)
- 6
-
The energy eigenfunctions are given by
$\psi_n(x) = A_nf_n\exp\left(-\frac12\alpha x^2\right)$ with n = 0, 1, 2, 3 ...(Eqn 13)
where fn(x) is a polynomial function of degree n and has n nodes. The first few polynomials are given by Equations 14 and the eigenfunctions illustrated in Figure 4.
- 7
-
Since the potential function is symmetric about the x = 0 line, the eigenfunctions are odd or eveneven functions. They are odd when n is odd, and even when n is even.
- 8
-
The total energy Subsection 2.4eigenvalues are given by the formula:
$E_n = \left(n + \frac12\right)hf$ with n = 0, 1, 2, 3 ...(Eqn 15)
When n = 0, we have the zero point energy. This prediction of discrete energies, with the lowest energy not equal to zero, is in contrast to classical mechanics which allows a continuum of possible energies from zero upwards.
- 9
-
The quantum probability density function is given by:
$P_n(x) = A_n^2f_n^2(x)\exp(-\alpha x^2)$ with n = 0, 1, 2, ...(Eqn 17)
The probability density functions are bounded approximately by the classically allowed region. They decay exponentially outside this region. As n → ∞, the quantum probability function becomes comparable with the classical probability function which is an illustration of the correspondence principle. Some of the functions Pn(x) are illustrated in Figure 6.
3.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Define simple harmonic motion (SHM) in classical mechanics in terms of the restoring force and the potential energy function.
- A3
-
Calculate the frequency and period of SHM from the particle mass and the force constant. Relate the amplitude of the oscillation to the total energy. Sketch the classical probability function.
- A4
-
Decide whether to use classical or quantum mechanics in a particular SHM problem.
- A5
-
Write down the Schrödinger equation for quantum SHM. Verify the first few energy eigenfunctions and eigenvalues. Recall the general formula $E_n = \left(n + \frac12\right)hf$, and use it to calculate the energy eigenvalues given the particle mass and the force constant.
- A6
-
Sketch the shape of the first few energy eigenfunctions, and relate the number of nodes to the quantum number n. Distinguish the even and odd eigenfunctions.
- A7
-
Understand and use the quantum probability density functions Pn(x) = ψn2(x), and sketch their shapes for n = 0, 1, 2, 3. Compare the classical probability density distribution with the quantum distributions.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
3.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions each of which tests one or more of the Achievements.
Question E1 (A2, A3 and A4)
A small mass of 0.002 kg is hung on a light spring producing an extension of 0.01 m. Calculate the spring constant ks. Find the frequency of small vertical oscillations of the mass about its equilibrium position.
Show that the condition E ≫ hf for the validity of the classical approximation is easily satisfied if the amplitude of the oscillation is 1 mm.
Answer E1
The spring restoring force is proportional to the extension Fx = −ksx.
When the mass hangs in equilibrium, mg = ks × extension.
Substituting: 0.002 kg × 10 m s−2 = ks × 0.01 m, so that ks = (0.02/0.01) N m−1 = 2 N m−1.
The frequency of oscillation is given by Equation 4,
$\omega = \sqrt{\dfrac{k_{\rm s}}{m}}\quad T = 2\pi\sqrt{\dfrac{m}{k_{\rm s}}}\quad\text{and}\quad f = \dfrac{1}{2\pi}\sqrt{\dfrac{m}{k_{\rm s}}}$(Eqn 4)
If the amplitude of small oscillations is 1 mm, then: $E = \frac12k_{\rm s}a^2 = \rm (2\times10^{-6}/2)\,J = 10^{-6}\,J$.
Compare this with the quantum unit: hf = 6.6 × 10−34 J s × 5 s−1 ≈ 3 × 10−33 J.
Clearly, in this case, E ≫ hf, and the classical approximation is valid. An energy 10−6 J corresponds to a quantum number n ≈ 1027 at frequency 5 Hz.
(Reread Subsections 2.1 and 2.2 if you had difficulty with this question.)
Question E2 (A5 and A6)
A particle moves in a region where its potential energy is given by $U(x) = \frac12k_{\rm s}x^2$. The wavefunction is the eigenfunction
$\psi(x) = A(1-2\alpha x^2)\exp\left(-\frac12\alpha x^2\right)$
with α = 5 × 1010 m−1, and A is a normalization constant. Is this an odd or an even function? Find the positions where ψ (x) = 0, and sketch the shape of the wavefunction (use the dimensionless variable $\sqrt{\alpha\os}x$). What is the result of measuring the total energy if the particle is an electron? Calculate the result in electronvolts.
Answer E2

Figure 4 The first four energy eigenfunctions for the quantum simple harmonic oscillator (not normalized). The limits of motion for a classical oscillator with the same energy are indicated by the vertical dashed lines. The horizontal axis is marked in the dimensionless variable $\sqrt{\alpha\os}x$.
The potential energy function $U(x) = \frac12k_{\rm s}x^2$ defines harmonic motion. The quoted value $\sqrt{\alpha\os} = \rm 5\times10^{10}\,m^{-1}$ shows that the wavefunction extends over a range of the order $1/\sqrt{\alpha\os}\approx \rm 10^{-11}\,m$; this is roughly one–tenth of an atomic radius. If you make the transformation x → −x, then you will see that ψ (−x) = +ψ (+x), so the wavefunction is an even function of x; it is symmetric about the line x = 0.
$\psi(x) = A(1-2\alpha x^2)\exp\left(-\frac12\alpha x^2\right)$, so that if ψ (x) = 0, then either x2 = 1/2α or $\exp\left(-\frac12\alpha x^2\right) = 0$. The wavefunction passes through zero when $x = \pm1/\sqrt{2\alpha\os}$, i.e. $\sqrt{\alpha\os}x = 0.707$.
The wavefunction also goes smoothly to zero as x → ±∞.
This information allows you to sketch the shape of the wavefunction, and your effort should look like the n = 2 eigenfunction shown in Figure 4.
The result of measuring the total energy of the particle is the energy eigenvalue: $E_2 = (2 + \frac12)hf = \frac52\hbar\omega$.
The angular frequency ω is calculated from the parameter α:
Equation 12 gives $\alpha = \omega m /\hbar$, so that $\omega = \alpha\hbar/m$. Substitute this into the total energy equation and we find:
$E_2 = \dfrac52\dfrac{\hbar\alpha\hbar}{m} = \dfrac{5\alpha\hbar^2}{2m}$
Substitute the appropriate values, and then convert from joules into electronvolts:
$E_2 = \rm 5\times5^2\times10^{20}\times\dfrac{(1.05\times10^{-34}\,J\,s)^2}{2\times9.1\times10^{-31}\,kg} = 7.6\times10^{-17}\,J\\ \phantom{E_2 }=\dfrac{7.6\times10^{-17}}{1.6\times10^{-19}}\,eV = 4.7\times10^2\,eV$
This is typical of SHM energy levels at the atomic scale.
(Reread Subsections 2.3 and 2.4 if you had difficulty with this question.)
Question E3 (A6 and A7)
Write down an expression for the probability density P (x) for the n = 1 state of a quantum simple harmonic oscillator in one dimension. (Refer to Equation 13Equations 13 and Equation 1414 for the eigenfunctions.) Find the points where P (x) is zero, the points where P (x) is a maximum, and the boundaries of the classically allowed region. Sketch the shape of P (x). What can you say about the result of a measurement of (a) the position of the particle, (b) the total energy of the particle?
Answer E3
From Equations 13 and 14,
$\psi_n(x) = A_nf_n\exp\left(-\frac12\alpha x^2\right)$ with n = 0, 1, 2, 3 ...(Eqn 13)
$\left.\begin{align}f_0 &= 1\\f_1 &= 2\sqrt{\alpha\os}x\\f_2 &= 2 - 4\alpha x^2\\f_3 &= 12\sqrt{\alpha\os}x - 8\alpha\sqrt{\alpha\os}x^3\end{align}\right\}$(Eqn 14)
we have$\psi(x) = 2A_1\sqrt{\alpha\os}x\exp\left(-\frac12\alpha x^2\right)$
so that$P(x) = \vert\,\psi(x)\,\rvert^2 = 4A_1^2\alpha x^2\exp(-\alpha x^2)$
We do not need to know the normalization constant A1. This function is obviously zero at x = 0, and also goes to
zero as x → ∞. (It cannot be negative!)
The function has maxima or minima where dP (x)/dx = 0:
$\dfrac{dP(x)}{dx} = 8A_1^2\alpha x\exp(-\alpha x^2) + (-2\alpha x)4A_1^2\alpha\exp(-\alpha x^2) = (8-8\alpha x^2)\alpha xA_1^2\exp(-\alpha x^2)$
dP (x)/dx = 0 when x = 0 and x → ±∞. These are the points where P (x) reaches its minimum value of zero.
dP (x)/dx = 0 also when 8αx2 = 8 or $\sqrt{\alpha\os}x = \pm1$. These are the points where P (x) reaches its maximum.

Figure 6 The probability density functions for the harmonic oscillator. Four cases are shown for particles in energy levels given by the quantum number n = 0, 1, 2, and 6. The dotted curves show the corresponding classical calculation of the probability density, with the dashed lines the classical limits of the oscillation.
The boundaries of the classically allowed region are given by Equation 16: $\sqrt{\alpha\os}a_n = \sqrt{2n + 1\os}$, so that for n = 1 we have $\sqrt{\alpha\os}a_1 = 1.732$. Remember that when | x | > an, the wavefunctions fall exponentially to zero.
You should now be able to sketch P (x) fairly accurately, and the result should look like Figure 6 (n = 1 case).
(a) A measurement of position will usually give a result close to points where the probability density function is maximum, i.e. close to $x = \pm1/\sqrt{\alpha\os}$. The measurement will rarely give a result close to x = 0 where the probability density is zero.
(b) A measurement of the total energy will certainly give the eigenvalue $E_1 = \frac32hf$, since the wavefunction is the eigenfunction for n = 1.
(Reread Subsections 2.4 and 2.5 if you had difficulty with this question.)
Question E4 (A3, A4, A5 and A7)
A simple model of the HCl molecule indicates that the hydrogen ion is held in an SHM potential with force constant ks = 470 N m−1. i Calculate the frequency of oscillations in the classical approximation (neglecting the motion of the chlorine atom). i The amplitude of oscillations is approximately 10−11 m, or one–tenth of the interatomic spacing. Is the classical approximation valid? Obtain an expression for the vibrational energy levels using quantum theory. Where is the boundary of the classically allowed region when n = 0? Calculate the frequency and wavelength of electromagnetic radiation emitted when molecules of HCl jump from one of these energy levels to the one immediately below.
Answer E4
The mass of the hydrogen ion is 1.67 × 10−27 kg. A classical calculation of the oscillator frequency, using Equations 4,
$\omega = \sqrt{\dfrac{k_{\rm s}}{m}}\quad T = 2\pi\sqrt{\dfrac{m}{k_{\rm s}}}\quad\text{and}\quad f = \dfrac{1}{2\pi}\sqrt{\dfrac{m}{k_{\rm s}}}$(Eqn 4)
gives:
$f = \dfrac{1}{2\pi}\sqrt{k_{\rm s}{m}} = \rm \dfrac{1}{2\pi}\sqrt{\dfrac{470\,N\,m^{-1}}{1.67\times10^{-27}\,kg}} = 8.4\times10^{13}\,Hz$
This is a frequency typical of atomic oscillators. If the amplitude of the oscillation is a = 10−11 m, then the total
energy is given by Equation 7,
$E = \frac12k_{\rm s}a^2$(Eqn 7)
So$E = \rm \dfrac{470\,N\,m^{-1}\times10^{-22}\,m^2}{2} = 2.4\times10^{-20}\,J$
We must compare E with the quantum unit hf, and if E ≫ hf, classical theory is valid; otherwise quantum mechanics must be used:
hf = 6.6 × 10−34 J s × 8.4 × 1013 s−1 = 5.5 × 10−20 J
Thus E < hf, and we must use quantum theory. The eigenvalues of total energy are given by Equation 15 (which you really should know by heart!):
$E_n = \left(n + \frac12\right)hf = \rm \left(n + \frac12\right)\times2.4\times10^{-20}\,J$
Converting into electronvolts, we obtain:
$E_n = \rm \left(n + \frac12\right)\times1.5\,eV$
The energy of a photon emitted in a transition En → En − 1 is:
$E = \rm (n + \frac12 -(n-1)-\frac12)\times0.15\,eV = 0.15\,eV$
Clearly, the frequency of the associated radiation is the same as the frequency of the classical oscillator f = 8.4 × 1013 Hz. The wavelength of the radiation is:
$\lambda = \dfrac cf = \rm \dfrac{3\times10^8\,m\,s^{-1}}{8.4\times10^{13}\,s^{-1}} = 3.6\times10^{-6}\,m$
Converting to nanometres: λ = 3600 nm. This radiation is in the infrared region of the electromagnetic spectrum and is typical of the spectral lines produced by molecular vibrations.
(Reread Section 2 if you had difficulty with this question.
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 3Closing items.