PHYS 2.5: Momentum and collisions |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
When two billiard balls collide they remain in contact for only a very short time, during which the forces between them vary rapidly. To predict the outcome of such a collision by calculating the acceleration of each ball at each instant of time we would need to know exactly how the forces vary with time, and this is not an easy matter. However, we may predict the outcome in a simpler way, using the concept of linear momentum – the subject of this module.
The total linear momentum involved in a collision is important because, under certain conditions, it has the same value both before and after the collision. In other words, it is a conserved quantity. Interestingly, when appropriately interpreted, the principle of conservation of linear momentum extends beyond the confines of classical Newtonian mechanics, into the realms of relativistic mechanics and even quantum mechanics. It is, therefore, along with the conservation of energy, one of the most wide ranging and far reaching principles in the whole of physics.
We introduce linear momentum in Section 2 and show how Newton’s second law of motion may be expressed in terms of linear momentum. The principle of conservation of linear momentum is then derived from Newton’s second and third laws of motion and it is illustrated with some simple one–dimensional applications.
In Section 3 we extend this to study collisions, and introduce the idea of energy, translational kinetic energy and the principle of conservation of energy. Collisions are classified as elastic or inelastic, according to whether kinetic energy is conserved. Elastic and inelastic collisions are then analysed in terms of the conservation principles, using examples that involve one– and two–dimensional motions. Finally, brief mention is made of a revised definition of momentum, necessary for the extension of momentum conservation into relativistic mechanics.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 5.1Module summary and the Subsection 5.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 5.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
A railway truck is moving horizontally under a stationary hopper, and is receiving coal at a rate of 200 kg s−1 from the hopper. The coal is delivered with negligible speed, and the truck and its contents are subject to no resultant force. Find the rate of change of the truck’s speed at the instant when the total mass of the truck and its contents is 4 × 103 kg and the speed of the truck is 2 m s−1.
Answer F1
From Newton’s second law the resultant force is given by:
$\boldsymbol{F} = \dfrac{d\boldsymbol{p}}{dt} = \dfrac{d(m\boldsymbol{\upsilon})}{dt} = m\dfrac{d\boldsymbol{\upsilon}}{dt} + \boldsymbol{\upsilon}\dfrac{dm}{dt}$
Therefore, if F = 0
$m\dfrac{d\boldsymbol{\upsilon}}{dt} = -\boldsymbol{\upsilon}\dfrac{dm}{dt}$
Since the direction of the motion is not changing, the rate of change of the truck’s speed is
$\dfrac{d\upsilon}{dt} = -\dfrac{\upsilon}{m} \dfrac{dm}{dt} = \rm \dfrac{2\, m\,s^{-1}\times 200\,kg\,s^{-1}}{4 \times 10^3\,kg} = -0.1\,m\,s^{-2}$
Question F2
A neutron of mass m travelling east at a speed of 4 × 104 m s−1 collides with a helium nucleus of mass 4m which is travelling north at a speed of 3 × 104 m s−1. If the neutron travels with unchanged speed after the collision, but moves in a direction 36.9° west of north, find the final speed and direction of the helium nucleus.
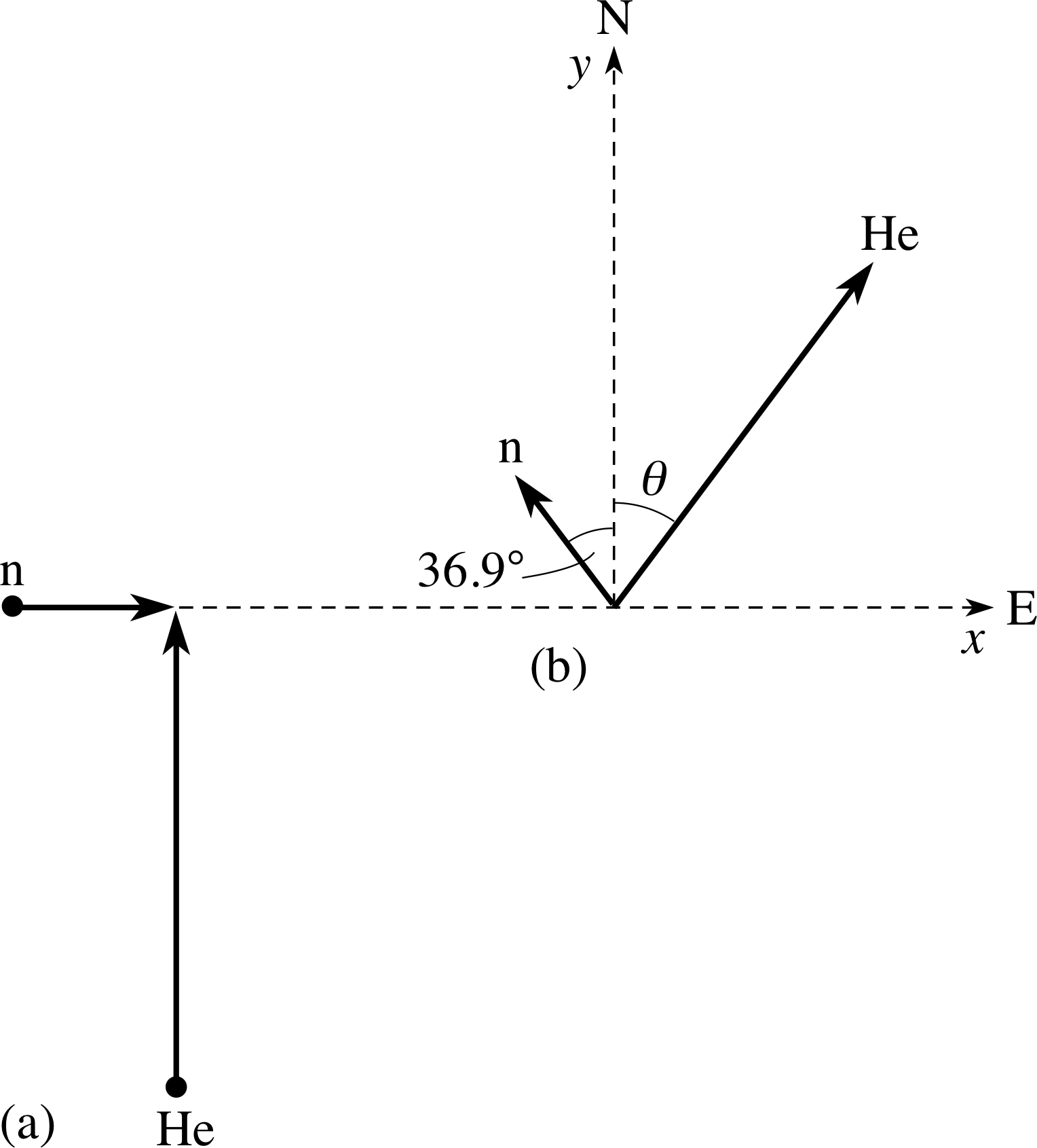
Figure 4 See Answer F2.
Answer F2
We will define east along the positive x–axis and north along the positive y–axis. After the collision, let the helium nucleus travel at a speed υ2 in a direction inclined at an angle θ to the positive y–axis. The pre– and post–collision situations are shown in Figure 4a and b. Using conservation of momentum in the x– and y–directions we find:
along the x–direction:
mun = 4mυHe sin θ − mun sin 36.9°
so$\sin\theta = \dfrac{u_n(1 + \sin\,36.9°)}{4\upsilon_{\rm He}}$
along the y–direction:
4muHe = 4mυHe cos θ + mun cos 36.9°
so$\cos\theta = \dfrac{4u_{\rm He} - u_n\cos\,36.9°}{4\upsilon_{\rm He}}$
Dividing these two expressions to find tan θ we obtain:
$\tan\theta = \dfrac{\sin\theta}{\cos\theta} = \dfrac{u_n(1 + \sin\,36.9°)}{4u_{\rm He} - u_n\cos\,36.9°} = \dfrac{4 \times 0^4 \times 160}{12 \times 10^4 -(4 \times 0.800 \times 10^4)} = 0.727$
This gives θ = 36.0°. The expression for sin θ can be rearranged to give:
$\upsilon_{\rm He} = \dfrac{u_n(1 + \sin\,36.9°)}{4\sin\theta} = \dfrac{4 \times 10^4(1+\sin\,36.9°)}{4 \sin\,36.9°}\,{\rm m\,s^{-1}} = 2.72 \times 10^4\,{\rm m\,s^{-1}}$
Therefore, after the collision the helium nucleus is travelling at a speed of 2.72 × 104 m s−1 at 36.0° east of north.
Question F3
A golf ball of mass 45 g is hit with a golf club. The mass of the club head is 0.30 kg and the mass of the shaft is negligible compared with that of the head. Immediately before the head strikes the ball, the speed of the club head is 30 m s−1. Assuming that the collision is elastic, calculate the speed with which the ball is propelled.
Answer F3
We assume that the club head and the ball move along the x–axis, the initial velocity of the club head is u2 and the masses and final velocities of the club head and ball are m2, υ2, and m2, υ2, respectively. From this, the conservation of momentum along the x–direction gives:
m1u1 = m1υ1 + m2υ2
and conservation of energy
½ m1u1x2 = ½ m1υ1x2 + ½ m2υ2x2
We are not interested in υ2, so let us eliminate it. The first equation gives
υ1x = u1x − (m2 /m1)υ2x
and the second υ1x2 = u1x2 − (m2/m1)υ2x2
Substituting for υ1x in this last equation gives us
u1x2 − 2 (m2/m1)u1xυ1x2 + (m2/m1)2υ2x2 = u1x2 − (m2/m1)υ2x2
Cancelling u1x2 on both sides, and then dividing both sides by (m2/m1)υ2x
we find−2u1x + (m2 /m1)υ2x = −υ2x
so thatυ2x = 2u1x /(1 + m2 /m1)
i.e.υ2x = 2 × 30 m s−1/(1 + 0.045 kg/0.30 kg) = 52 m s−1
1.3 Ready to study?
Study comment In order to study this module you will need to be familiar with the following terms: acceleration, components_of_a_vectorcomponent (of a vector), force, mass, Newton’s laws of motion, scalar, speed, vector, vector addition and velocity. Also, you will need to be familiar with the use of Cartesian coordinate systems, Pythagoras’s theorem, trigonometric functions, the sine rule, and the cosine rule. Additionally, this module makes some use of the derivativederivative notation of basic differentiation to represent rates of change and assumes you are familiar with symbols such as dυ/dt. If you are uncertain of any of these terms you can review them now by referring to the Glossary which will indicate where in FLAP they are developed. The following questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
Describe the difference between scalar and vector quantities, and how the resultant or sum of two vector quantities is found diagramatically.

Figure 5 See Answer R1.
Answer R1
Scalar quantities have magnitude only whereas vector quantities have magnitude and direction and may be represented by arrows. Two vectors of similar type may be added diagrammatically using the triangle rule by placing the initial point of the second vector on the terminal point of the first vector, and then joining the initial point of the first vector to the terminal point of the second vector. (See Figure 5 for an example.)
Consult scalar and vector in the Glossary for further information.
Question R2
A triangle ABC has side AB of length 4.00 m and the angles at A and B equal to 60° and 80°, respectively. Find the lengths of the sides BC and CA.
Answer R2
Since the interior angles of a triangle must add up to give 180°, angle at C must be 40°. The sine rule gives:
$\dfrac{{\rm BC}}{\sin\,60°} = \dfrac{\rm CA}{\sin\,80°} = \dfrac{4.00\,{\rm m}}{\sin\,40°}$
soBC = (4.0 sin 60°/sin 40°) m = 5.39 m
andCA = (4.0 sin 80°/sin 40°) m = 6.13 m
Consult trigonometric functions in the Glossary for further information.
Question R3
A horizontal force of magnitude 20 N acts in a direction 40° west of north. Find the components_of_a_vectorcomponents of the force in the north and west directions.
Answer R3
The north component of force = (20 cos 40°) N = 15.3 N
the west component of force = (2 sin 40°) N = 12.9 N
Consult components of a vector in the Glossary for further information.
Question R4
A horizontal force of magnitude 40 N applied to a block on a frictionless horizontal surface produces an acceleration of magnitude 2 m s−2. What is the mass of the block?
Answer R4
Using Newton’s second law of motion F = ma, we see that
m = F/a = 40 N/2 m s−1 = 20 kg
Consult Newton’s second law of motion in the Glossary for further information.
Question R5
(a) If υ (t) represents the speed υ of a particle at time t, what is the meaning of dυ/dt in terms of a graph of υ against t ?
(b) If m is a constant, what would be the graphical interpretation of d (mυ)/dt ?
(c) If m is not a constant, would you expect to find that $m\dfrac{d\upsilon}{dt} = \dfrac{d}{dt}(m\upsilon)$?
Answer R5
(a) At any particular time t, the value of dυ/dt represents the gradient of the graph of υ against t at that particular time.
(b) d (mυ)/dt would represent the gradient of the graph of m × υ against t at any particular time. Since the effect of multiplying υ by a constant m is to uniformly rescale the υ–axis, the gradient of the new mυ against t graph will be just m times the gradient of the original υ against t graph. In other words, provided m is a constant
$\dfrac{d}{dt}(m\upsilon) = m \dfrac{d\upsilon}{dt}$
(c) if m is not a constant there is no reason to expect that the above result will hold true. In fact, when m and υ both vary with time the product rule of differentiation tells us that
$\dfrac{d}{dt}(m\upsilon) = m \dfrac{d\upsilon}{dt} + \upsilon \dfrac{dm}{dt}$
Consult basic differentiation in the Glossary for further information.
2 Linear momentum and Newton’s second law
2.1 Definition of linear momentum
It is easy to imagine that a lorry travelling at 40 m s−1 is more difficult to stop than the same lorry travelling at 20 m s−1. Similarly, a lorry travelling at 40 m s−1 is more difficult to stop than a car travelling at 40 m s−1. From this it is apparent that the difficulty in stopping a body depends on both the mass and the velocity of the body. The scientific quantity identifying this property of a moving body, which we have loosely described in terms of the ‘difficulty in stopping’ is called linear momentum (more often simply momentum), p. In Newtonian mechanics, a body of mass m moving with velocity υ, has a momentum p defined by:
p = mυ(1)
As velocity is a vector quantity, linear momentum is also a vector quantity, with magnitude mυ and a direction
which is the same as that of the velocity vector. The SI units of linear momentum are kg m s−1.
It is often convenient to express the momentum i vector p in terms of its components. If the components of the velocity vector υ are υx, υy and υz, then we write: υ = (υx, υy, υz) and p = (px, py, pz), where the components of the momentum vector are given by:
px = mυx py = mυy pz = mυz(1a)
In dealing with momentum we frequently encounter problems in which motion is not restricted to a single line. Bodies moving in different directions may collide and may change directions. Since momentum is a vector quantity, a change in direction represents a change in momentum, even if the magnitude of the momentum is unchanged.
Question T1
A body of mass 4 kg is moving with speed 15 m s−1 in a direction 36.9° east of north. What are the components of the momentum of the body in the north and east directions?
Answer T1
The magnitude of the momentum of the body is 4 kg × 15 m s−1 = 60 kg m s−1. The north and east components of the momentum are:
north:(60 cos 36.9°) kg m s−1 = 48 kg m s−1
east:(60 sin 36.9°) kg m s−1 = 36 kg m s−1
Question T2
In a game of volleyball, player 1 near the back of the court passes the ball to player 2, who is standing near the net. As it approaches player 2 the ball is moving horizontally at 3.0 m s−1. Player 2 taps the ball with a vertical force so that it acquires a 0.8 kg m s−1 component of momentum in the vertical direction. If the mass of the ball is 400 g, determine the magnitude and direction of the ball’s resultant momentum.
Answer T2
The x–component (horizontal) of momentum of the ball is the same before and after player 2 strikes the ball, and is given by
px = mυx = 0.40 kg × 3.0 m s−1 = 1.2 kg m s−1
The question tells us that the vertical component of momentum py = 0.8 kg m s−1 after player 2 strikes the ball. All we have to do now is to find the magnitude and direction of the momentum vector. The magnitude of the momentum is given by:
p2 = px2 + py2 = (1.2 kg m s−1)2 + (0.8 kg m s−1)2 = 2.08 kg2 m2 s−2
so thatp = 1.4 kg m s−1
If the angle of the ball to the horizontal is θ, then px = p cos θ, and py = p sin θ. We have tan θ = px /py = 0.8/1.2, and so θ = 34°.
2.2 Relationship between force and rate of change of momentum
Momentum is closely associated with Newton’s second law of motion, F = ma. Indeed, if we assume that the mass m is constant, then we can express Newton’s second law in terms of momentum. To see this first note that:
$\boldsymbol{F} = m\boldsymbol{a} = m\dfrac{d\boldsymbol{\upsilon}}{dt}$
Then note that if m is constant
$m\dfrac{d\boldsymbol{\upsilon}}{dt} = \dfrac{d(m\boldsymbol{\upsilon})}{dt} = \dfrac{d\boldsymbol{p}}{dt}$ i
and so$\boldsymbol{F} = \dfrac{d\boldsymbol{p}}{dt}$(2)
i.e. the resultant force acting on a body is equal to the rate of change of its momentum.
Equation 2 is a vector equation and so represents the three equations, one for each of the three components of force:
$F_x = \dfrac{dp_x}{dt} \quad F_y = \dfrac{dp_y}{dt} \quad F_z = \dfrac{dp_z}{dt}$(2a)
We now have two forms of Newton’s second law when m is constant:
$\boldsymbol{F} = m\boldsymbol{a} \quad\text{and}\quad F = \dfrac{d\boldsymbol{p}}{dt}$
Faced with two ways of expressing Newton’s second law it is legitimate to ask if one is more general or more fundamental than the other. In fact, the general view is that Equation 2 is the more fundamental. It can be applied directly to systems of particles as well as to single bodies, and, in some cases, it can even be applied to bodies with changing mass, such as a rocket that accelerates by expelling the fuel that it carries.
Given experimental fact that F = dp/dt is more generally applicable throughout classical mechanics you might wonder how F = ma fails in various contexts, such as that of varying mass. In that particular case the inadequacy of F = ma is easy to demonstrate provided you are familiar with the product_rule_of_differentiationproduct rule of differentiation which enables us to write the derivative of a product as a sum of products.
If we start from Equation 2,
$\boldsymbol{F} = \dfrac{d\boldsymbol{p}}{dt}$(Eqn 2)
but do not assume constant mass, then:
$\boldsymbol{F} = \dfrac{d\boldsymbol{p}}{dt} = \dfrac{d(m\boldsymbol{\upsilon})}{dt} = m\dfrac{d\boldsymbol{\upsilon}}{dt} + \boldsymbol{\upsilon}\dfrac{dm}{dt}$(3)
From this we see that if m is not constant then we have to add a further term υdm/dt to ma to obtain the correct expression for F. There are several surprising aspects of this. First, a resultant force acting on a body does not always cause acceleration; it could be that the mass of the body is increasing with time at just the correct rate to allow constant velocity. Second, even when there is no resultant force acting on the body it may nevertheless accelerate, if its mass is changing.
✦ What force is required to push a truck across a frictionless surface at a constant velocity of 5 m s−1 in a given direction if sand is being poured into the truck at a rate of 6 kg s−1?
✧ If the velocity is constant the acceleration is zero. Therefore, from Equation 3,
$\boldsymbol{F} = \dfrac{d\boldsymbol{p}}{dt} = m\dfrac{ d\boldsymbol{\upsilon}}{dt} + \boldsymbol{\upsilon} \dfrac{dm}{dt}$(Eqn 3)
with the direction of motion along the x–axis we find:
$F_x = 0 + \upsilon_x \dfrac{dm}{dt}$ = (5 m s−1) × (6 kg s−1) = 30 N
The identification of ‘force’ with ‘rate of change of momentum’ sanctioned by Equation 2,
$\boldsymbol{F} = \dfrac{d\boldsymbol{p}}{dt}$(Eqn 2)
also has another important consequence; if F = 0 i then dp/dt = 0 thus:
If no resultant force acts on a body then its momentum does not change.
As you will see in Subsection 2.3 a generalization of this result leads to the important principle of momentum conservation.
Impulse
There are many situations where the force on a body acts only for a very short time (e.g. bats on balls) and we are concerned only with the consequent changes in the motion of the body. If the force F is constant and acts for a short time ∆t, it follows from Equation 2 that the momentum of the body will change by an amount
∆p = F∆t(4) i
The quantity F∆t is called the impulse of the force. i
In many situations where varying forces act for short times it is only their effects (i.e. the momentum changes they cause) that are of real interest. In such cases Equation 4 may be used to find the constant force that would produce the same overall effect as the varying force that actually acted. This procedure can give surprising insights into the rapidly varying forces that arise in various impulsive interactions. For example, in American baseball the bat and ball are typically in contact for one or two thousandths of a second, during which the effective average force has a magnitude of about 6000 N. Such large forces are not unusual.
2.3 Conservation of momentum
The concept of momentum is particularly useful when dealing with situations where there are two or more interacting bodies which interact with each other but not with their surroundings. We call such a system an isolated system. Any forces which act on parts of an isolated system arise from the mutual interactions between bodies within the system. Each force is then one member of a Newton’s third law pair of action–reaction forces. Such forces are called internal forces, to distinguish them from the external forces which act on the system or parts of the system from outside. We will begin by considering an isolated system in which there are only two bodies and they only interact with one another.
Let p1 = m1υ1 and p2 = m2υ2 be the momenta of the two bodies in the system. These two momenta will change with time, due to the mutual interaction. The total momentum of the system, p, is given by the vector sum of the momenta of the two bodies:
p = p1 + p2
The rate of change of p with time is therefore determined by the rates of change of p1 and p2:
$\dfrac{d\boldsymbol{p}}{dt} = \dfrac{d\boldsymbol{p}_1}{dt} + \dfrac{d\boldsymbol{p}_2}{dt}$ i
At a given instant let F12 be the force on the first body due to the second and F21 be the force on the second body due to the first. Equation 2,
$\boldsymbol{F} = \dfrac{d\boldsymbol{p}}{dt}$(Eqn 2)
gives:$\boldsymbol{F}_{12} = \dfrac{d\boldsymbol{p}_1}{dt}\quad\text{and}\quad\boldsymbol{F}_{21} = \dfrac{d\boldsymbol{p}_2}{dt}$
Newton’s third law of motion tells us that:
F12 = −F21 or F12 + F21 = 0
Therefore$\dfrac{d\boldsymbol{p}_1}{dt} + \dfrac{d\boldsymbol{p}_2}{dt} = \dfrac{d\boldsymbol{p}}{dt} = \boldsymbol{0}$(5)
Thus p = p1 + p2 is constant with time, although both p1 and p2 may be varying. At every instant of time the total momentum is the same (since p does not depend on t). We can summarize the situation by saying that the total momentum of the isolated system is a conserved quantity.
Note that in deriving Equation 5 we have assumed that the only forces acting on the bodies are F12 and F21. If an external force F had been acting on the bodies then the system would not be isolated, Equation 5 would not be valid and the total momentum of the system would not be conserved; rather the total momentum would vary according to Equation 2,
$\boldsymbol{F} = \dfrac{d\boldsymbol{p}}{dt}$(Eqn 2)
Although we have considered only two bodies in deriving Equation 5, the conservation of momentum result can be extended to any number of bodies in an isolated system. The same reasoning as before may be used: the rate of change of total momentum of the isolated system is zero because the vector sum of the impulses from each action–reaction pair of forces is zero. This result constitutes one of the most important principles of physics:
The principle of conservation of momentum:
The total momentum of any isolated system is constant with time.
Alternatively, we can say that the total momentum of any system does not change through mutual interactions within the system.
✦ When a ball bounces from a wall, its momentum changes, and so it appears that momentum is not conserved. Explain why this is not so.
✧ The ball is not an isolated system when it strikes the wall. Since the wall is fixed to the Earth, the isolated system must be the ball plus the wall plus the Earth and it is the momentum of this system that is conserved. The change in momentum of the ball is equal in magnitude and opposite in direction to the change in momentum of the wall plus the Earth. However, since the Earth is so massive, you will not see any recoil of the wall when the ball strikes it; the required momentum change of the Earth corresponds to only an imperceptible change in its velocity.
Question T3
Derive the principle of conservation of momentum from Newton’s laws as applied to an isolated system consisting of three interacting particles.
Answer T3
The total momentum p of the three particles is given by:
p = p1 + p2 + p3
Thus$\dfrac{d\boldsymbol{p}}{dt} = \dfrac{d\boldsymbol{p}_1}{dt} + \dfrac{d\boldsymbol{p}_2}{dt} + \dfrac{d\boldsymbol{p}_3}{dt}$
However, $\dfrac{d\boldsymbol{p}_1}{dt} = \boldsymbol{F}_{12} + \boldsymbol{F}_{13}, \quad\dfrac{d\boldsymbol{p}_2}{dt} = \boldsymbol{F}_{21} + \boldsymbol{F}_{23} \quad\text{and}\quad\dfrac{d\boldsymbol{p}_3}{dt} = \boldsymbol{F}_{31} + \boldsymbol{F}_{32}$
so$\dfrac{d\boldsymbol{p}}{dt} = (\boldsymbol{F}_{12} +\boldsymbol{F}_{21}) + (\boldsymbol{F}_{23} + \boldsymbol{F}_{32}) + (\boldsymbol{F}_{13} + \boldsymbol{F}_{31})$
But from Newton’s third law of motion: F12 = −F21, F23 = −F32, F13 = −F31
so$\dfrac{d\boldsymbol{p}}{dt} = \boldsymbol{0}$ Therefore p must remain constant.
Question T4
When you walk along the road with constant velocity you have constant momentum. When you stop walking you have zero momentum. Where has your momentum gone?
Answer T4
When you are walking, you are not an isolated system. When you start from rest, the Earth recoils imperceptibly in the opposite direction to your motion. Similarly when you slow down and stop, you transfer momentum to the Earth in the same direction as your original motion.
2.4 Symmetry and conservation
If an object or a system of objects can be altered in some way without changing its overall behaviour or appearance, that object or system is said to exhibit symmetry under the alteration. For instance, a uniform sphere may be rotated through an arbitrary angle about its centre point without changing its properties or appearance in any way; such a sphere is consequently said to exhibit rotational symmetry and to be invariant (i.e. unchanging) under arbitrary rotations about its centre.
Symmetries and their related invariances are common features of physical systems and of the laws that describe them. Some of these symmetries are so readily taken for granted that it is easy to overlook them. For example, it is generally assumed amongst physicists that the outcome of a fundamental experiment does not depend on where or when it is performed. There is, of course, a good deal of evidence in support of this belief but it is impossible to test every case. Consequently, our expectation that the fundamental behaviour of physical systems will not vary from country to country or from day to day is largely based on our belief in the symmetry of nature under translations (i.e. ‘shifts’ or ‘transfers’) through space and time. In fact, much of modern science is based on the following assumptions:
- The laws of physics must be invariant under arbitrary translation through space.
- The laws of physics must be invariant under arbitrary translation through time.
If either of these fundamental invariances was violated, if momentum was only conserved on Tuesdays say, or only in Western Europe, then physics would be a much less interesting subject and even harder to master.
The reason for embarking on this discussion of symmetry and invariance is that it has been known for a long time that there is a deep link between the symmetries of nature and the existence of conserved physical quantities. It can be argued, for instance, that the invariance of physical laws under translations through time implies the existence of a conserved scalar quantity which may be identified as energy (about which more is said later in the module). Similarly, the invariance of physical laws under translation through space implies the existence of a conserved vector quantity which may be identified as momentum. Thus the principle of momentum conservation may be regarded as one of the fundamental principles of physics and you should not be surprised to learn that its validity extends beyond the confines of classical Newtonian mechanics.
The mathematical techniques needed to establish the link between symmetry and conservation are beyond the scope of FLAP but the importance of the result would be hard to overestimate. The search for fundamental symmetries, of which we have mentioned only two, has been one of the central pillars of modern physics and has fuelled much of the progress made in the last 40 years.
2.5 Worked examples involving conservation of momentum
In a scientific context, the term collision means a brief but powerful interaction between two particles or bodies in close proximity. To illustrate the value of the principle of conservation of momentum in solving problems, let us begin with the simple case of two bodies moving in one dimension which collide and stick together on impact. Later, we will extend our discussion to two– and three–dimensional motion and to collisions where the bodies do not stick together.
Collisions in one dimension, where the two bodies stick together
Example 1
A body of mass 2 kg moving with a speed of 6 m s−1 along the x–axis collides with a stationary body of mass 4 kg. The bodies stick together on impact and move off as one combined body along the x–axis with speed υx. Find the value of υx, assuming this is an isolated system.
Solution
In applying the principle of conservation of momentum to the isolated system we equate the total momentum before the collision to the total momentum after the collision. Therefore, conserving momentum along the x–axis:
m1u1x + m2u2x = (m1 + m2)υx(6)
where u1x and u2x are the initial velocities of the masses m1and m2.
Thusυx = (m1u1x + m2u2x)/(m1 + m2)
i.e.υx = (2 kg × 6 m s−1 + 4 kg × 0 m s−1)/(2 kg + 4 kg)
soυx = 12 kg m s−1/6 kg = 2 m s−1
Example 2
A radioactive nucleus i at rest decays by forming an alpha–particle (an α–particle is a helium nucleus) and a daughter nucleus. The mass of the daughter nucleus is 54 times that of the α–particle. What is the velocity of the daughter nucleus if the velocity of the α–particle υα is 1 × 107 m s−1 along the positive x–axis? This can be thought of as a ‘sticking collision’, but in reverse.
Solution
The total momentum before the decay is zero and so the total momentum afterwards must also be zero. This means that the vector sum of the momenta of the two particles after the decay must be zero. To satisfy this condition the magnitudes of the two momenta must be equal and their directions must be opposite. Let m be the mass of the α–particle and υx the required velocity of the daughter nucleus. Conserving momentum along the x–axis, we have:
mυα + 54mυx = 0
soυx = −υα /54 = −1 × 107 m s−1/54 = −1.85 × 105 m s−1
This confirms that the daughter nucleus recoils in the opposite direction to the α–particle, as expected.
Question T5
Two blocks of masses 0.3 kg and 0.2 kg are moving towards one another along a frictionless, horizontal surface with speeds 1.0 m s−1 and 2.0 m s−1, respectively. If the blocks stick together on impact, find their final velocity.
Answer T5
Let the 0.3 kg block move in the −x–direction and the 0.2 kg block in the +x–direction. The total momentum of the two blocks before the impact is the vector sum of the momenta of the two blocks. We use Equation 6,
m1u1x + m2u2x = (m1 + m2)υx(Eqn 6)
which leads to υx = (m1u1x + m2u2x)/(m1 + m2)
Here$\upsilon_x = \dfrac{0.2\,{\rm kg} \times 2\,{\rm m\,s^{-1}} - 0.3\,{\rm kg} \times 1\,{\rm m\,s^{-1}}}{0.2\,{\rm kg} + 0.3\,{\rm kg}}$
i.e.υx = 0.1 kg m s−1/0.5 kg = 0.2 m s−1 (i.e. along the positive x–direction).
Question T6
Consider the following scenario. The population of the Earth (5.6 × 109 people in September 1994) all begin walking in the same direction at 1.0 m s−1. Estimate the effect on the Earth. (Take the mass of the Earth as 6.0 × 1024 kg.) What would happen when everybody stopped walking? i
Answer T6
The total momentum of the isolated system of the Earth plus the walkers is constant. On starting the walk, the walkers’ total momentum increases in the direction of the walk by an amount given by their total mass multiplied by their speed. If we estimate the average mass per person as 50 kg then this total increase is
mυ = 5.6 × 109 × 50 kg × 1.0 m s−1 = 2.8 × 1011 kg m s−1
The Earth’s momentum in this same direction decreases by this same amount. The change in the Earth’s velocity, ∆υ, is equal to the change in the momentum, ∆p, divided by the Earth’s mass, so its speed changes by the amount:
∆υ = ∆p/ME = 2.8 × 1011 kg m s−1/6.0 × 1024 kg = 4.7 × 10−14 m s−1
When the walkers stop, the changes are reversed and the Earth returns to its original velocity, although the changes would have been imperceptibly small.
Collisions in two dimensions, where the two bodies stick together
In problems in which motion is in more than one dimension we have to take care over the directions of motion of the bodies involved. This means that in applying conservation of momentum we need to remember the vector nature of momentum. In our discussions so far we have prepared the ground for this extension by stressing the vector approach throughout and by insisting on the use of component notation, even with one–dimensional problems where there was the temptation to drop the subscripts! For two– or three–dimensional problems there are two possible approaches which may be used: vector summation or use of components. We will consider these alternative approaches in the following worked examples.
Example 3
A 2000 kg van, travelling due east at 20 m s−1 collides on an icy patch of road with a 1000 kg car travelling due north at 30 m s−1. The vehicles lock together on impact and then move off as one body over the frictionless surface. Find the velocity of the vehicles after the collision.
Study comment Beware – problems which ask for the velocity cannot be fully answered until you have given the direction of motion as well as the speed of motion. This same warning applies equally for any other vector quantity, such as momentum. It is very easy to forget this!
Solution
Let the final velocity of the vehicles be υ. We need to determine both the magnitude and direction of υ in order to specify it completely. First, let us consider the vector summation approach. The magnitudes of the momenta of the van and car before the collision are:
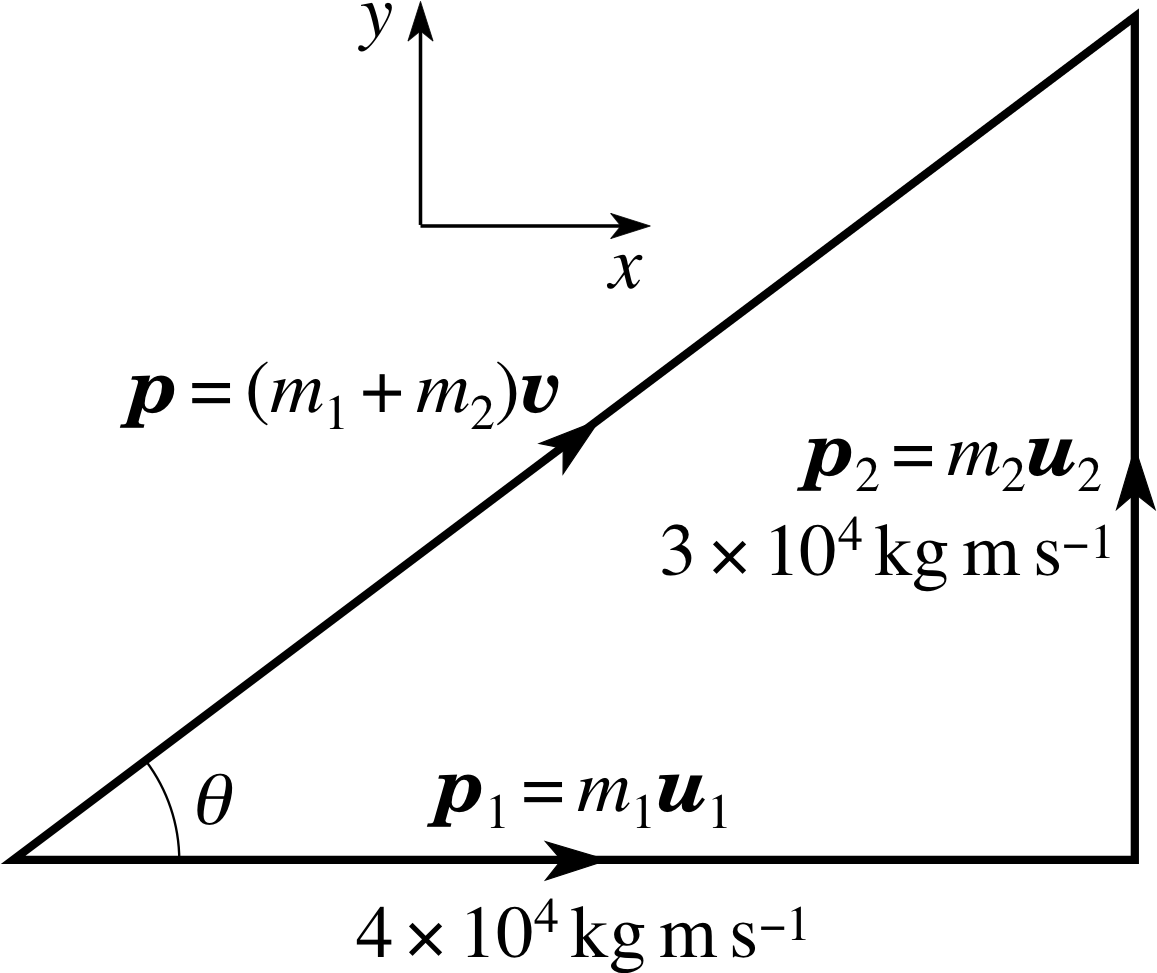
Figure 1 The resultant momentum p of two vehicles moving east and north is constructed from the vector sum of the momenta of the vehicles.
for the van p1 = (2000 kg × 20 m s−1) = 4.0 × 104 kg m s−1
for the car p2 = (1000 kg × 30 m s−1) = 3.0 × 104 kg m s−1
These two momenta must be added vectorially, as shown in Figure 1, to determine the total momentum, p = p1 + p2 before the collision. The direction of p is at an angle θ to the original direction of the van. Using Pythagoras’s theorem or by inspection of Figure 1 (a ‘3, 4, 5 triangle’) we find the magnitude of p is 5.0 × 104 kg m s−1; also we see that tan θ = 3/4.
Since the two vehicles on a frictionless surface constitute an isolated system, conservation of momentum tells us that the total initial momentum is equal to the total final momentum and so we know that p also represents the total final momentum of the locked–together vehicles.
Sincep = (m1 + m2)υ(7)
the magnitudes of the vectors p and υ are related by
υ = p/(m1 + m2) = 5.0 × 104 kg m s−1/3000 kg = 16.7 m s−1
Furthermore, since tan θ = 3/4, it follows that θ = 36.9°.
Let us now try the alternative approach, using components. The component approach is based on the fact that if the total momentum vector, p, remains constant in an isolated system, then so too must the component of p in any given direction. In our example we need to consider, in turn, the component in the east direction (say the positive x–direction) and the component in the north direction (say the positive y–direction). In this example the van has the total x–component of momentum and the car has the total y–component of momentum. Conservation of x and y momentum then immediately gives:
px = p cos θ = p1 = m1u1x = 4.0 × 104 kg m s−1
and py = p sin θ = p2 = m2u2y = 3.0 × 104 kg m s−1
withp = (px2 + py2)1/2 = 5.0 × 104 kg m s−1
andθ = arctan(py /px ) = arctan(3/4) = 36.9°
As before, υ = p/(m1 + m2) = 5.0 × 104 kg m s−1/3000 kg = 16.7 m s−1
Study comment Whilst you should practice using both the vector summation method and the component method in solving problems on momentum involving more than one dimension, the component approach is easier to use with more complicated examples. A good general strategy is to set up a clearly labelled diagram of the collision, with appropriately chosen Cartesian coordinate axes x, y, z shown. These axes are chosen so as to simplify the solution – perhaps by arranging them in such a way that one of the incoming particles is moving only along the x–axis. Then momentum conservation is applied for components along each of the axes in turn, with each direction treated entirely independently. Finally, the components are recombined to give the magnitude and direction of the required vector.
Question T7
A body of mass 6 kg moving north over a frictionless horizontal surface at a speed of 6 m s−1 collides with a stationary body of mass 4 kg. After the collision the more massive body moves in a direction 30° west of north and the less massive body in a direction 25° east of north. Find the speeds of the bodies after the collision. Use the vector summation method, then repeat the calculation using components.

Figure 5 See Answer T7.
Answer T7
First let us try the vector summation approach to this problem. Let υ1 and υ2 be the speeds of the more and less massive bodies, respectively. The principle of conservation of momentum tells us that the vector sum of the two final momenta is equal to the initial momentum of the more massive body. This initial momentum has magnitude 36 kg m s−1. The vector diagram is illustrated in Figure 5.
The sine rule is particularly useful in this example, as it enables us to determine the two unknown sides of the vector triangle. Applying the sine formula we find
$\dfrac{36\,{\rm kg\,m\,s^{-1}}}{\sin\,125°} = \dfrac{6\,{\rm kg} \times \upsilon_1}{\sin\,25°} = \dfrac{4\,{\rm kg} \times \upsilon_2}{\sin\,30°}$
soυ1 = 6 m s−1(sin 25°/sin 125°) = 3.10 m s−1
andυ2 = 9 m s−1(sin 30°/sin 125°) = 5.49 m s−1
Now let us try the component approach in solving this problem. As usual, we define east as the positive x–direction and north as the positive y–direction. First, consider components:
in the x–direction: p2 sin 25° − p1 sin 30° = 0
sop2 = p1 sin 30°/sin 25°
in the y–direction: p = p2 cos 25° + p1 cos 30°
We can substitute for p2 from the first expression into the second expression:
p = p1 sin 30° cos 25°/sin 25° + p2 cos 30° = 1.938 p1
Sop1 = p/1.938 = (36/1.938) kg m s−1 = 18.57 kg m s−1
andυ1 = 18.57 kg m s−1/6 kg = 3.10 m s−1
Using the x–direction expression we can find p2 and then υ2:
p2 = p1 sin 30°/sin 25° = 21.97 kg m s−1
andυ2 = 21.97 kg m s−1/4 kg = 5.49 m s−1
3 Momentum and kinetic energy in collisional problems
In the collision problems tackled so far we have always either finished up with a single body, or started with a single body (e.g. in α–decay). The reason for this limitation is that only such problems have a unique solution, obtainable by applying momentum conservation alone. For all other collisions we need to involve other principles in addition to momentum conservation. To illustrate this we can consider a one–dimensional problem in which two colliding bodies with known masses m1 and m2, and with known initial velocities u1x and u2x collide and then separate with final velocities υ1x and υ2x. In general, when the initial conditions are given, the problem involves finding the two unknowns υ1x and υ2x. However, consideration of momentum conservation along the x–direction:
m1u1x + m2u2x = m1υ1x + m2υ2x
gives only one equation connecting these two unknowns and so the problem is insoluble without more information. i
The additional information is provided by introducing the idea of energy. i Energy can exist in several forms, but the energy that a body has due to its instantaneous linear motion is called its translational kinetic energy. In classical Newtonian mechanics the translational kinetic energy of a body of mass m and speed υ is defined as:
Etran = ½ mυ2(8)
Energy is a scalar quantity. In the SI system, the unit of energy is the joule (J) where 1 J = 1 kg m2 s−2.
Translational kinetic energy i is only one of several forms in which energy can appear. A body may also have potential energy due to its position or internal state, as in the case of a mass suspended above the surface of the Earth, or a compressed spring. Quite apart from these various forms of mechanical energy we can also associate energy with other physical phenomena, so we may speak of electrical energy, light energy, sound energy and thermal energy. Energy may be transformed between these different forms by physical and chemical processes but it is generally accepted that, for an isolated system, the sum of all these different forms of energy remains constant. This fundamental principle is known as the principle of conservation of energy.
Collisions may be categorized by comparing the total kinetic energy of the colliding bodies before and after the collision. If there is no change in the total kinetic energy, then the collision is an elastic collision. If the kinetic energy after the collision is less than that before the collision then the collision is an inelastic collision. In some situations (e.g. where internal potential energy is released) the total kinetic energy may increase in the collision; this type of collision is a superelastic collision.
Collisions between macroscopic objects are usually inelastic but some collisions, such as those between steel ball bearings or between billiard balls, are very nearly elastic. Collisions between subatomic particles, such as electrons, protons, commonly are elastic. The kinetic energy which is lost in an inelastic collision appears as energy in a different form, e.g. thermal energy, sound energy, light energy, so that the total energy is conserved. The collisions which we have dealt with so far, in which the bodies stick together on collision and move off together afterwards, are examples of completely inelastic collisions. In these cases the maximum amount of kinetic energy consistent with momentum conservation, is converted into other forms of energy.
3.1 Elastic collisions in one dimension
We begin this discussion with an example of a simple one–dimensional elastic collision between two identical masses, where one incoming projectile strikes another, initially stationary target. We wish to know the final velocities of each mass after the collision.
Example 4
A mass m moves along the x–axis with velocity u1x and collides elastically with another identical mass at rest. What are the velocities of the two masses after collision?
Solution
Let the final velocities be υ1x and υ2x. Conservation of momentum along the x–axis gives
mu1x = mυ1x + mυ2x(9)
and conservation of kinetic energy gives
½ mu1x2 = ½ mυ1x2 + ½ mυ2x2(10) i
By eliminating common factors, Equations 9 and 10 can be simplified to give
u1x = υ1x + υ2x
i.e.υ2x = u1x− υ1x(9a)
andu1x2 = υ1x2 + υ2x2
i.e.υ2x2 = u1x2 − υ1x2 = (u1x − υ1x)(u1x + υ1x)(10a)
Dividing this last equation by υ2x = u1x − υ1x gives us:
υ2x = u1x + υ1x
Comparing this expression with that in Equation 9a shows us υ1x = 0 and υ2x = u1x
This result is familiar to anyone who has seen the head–on collision of two bowls on a bowling green. The moving one stops, and the stationary one moves off with the original velocity of the first.
✦ In the situation above, the two masses were equal. What would you expect to happen if the two masses were not equal? Can you predict qualitatively, i.e. without calculation, what would happen with the target mass m2 at rest if: (a) m1 ≫ m2, (b) m2 ≫ m1. i
✧ Experience should tell you (a) that a high mass projectile fired at a low mass target would be essentially undeflected by the collision, whereas (b) a low mass projectile fired at a massive target would bounce back with unchanged speed.
✦ In this last question we used terms such as ‘high mass’ and ‘low mass’ rather than ‘heavy’ and ‘light’. Why do you think we did this?
✧ The point is that these observations concern mass not weight. The results would be identical if the experiment were carried out well away from the Earth, where there was no gravity and therefore the objects were weightless. Terms like ‘heavy’ and ‘light’ are naturally associated with weight rather than mass, although when gravity is present these two quantities are related.
Now we consider the mathematical solution of the general one–dimensional case of an elastic collision between particles of mass m1 and m2 which move with speeds u1x and u2x before the collision and speeds υ1x and υ2x after the collision. Since the collision is elastic the kinetic energy is conserved and so we can write:
½ m1u1x2 + ½ m2u2x2 = ½ m1υ1x2 + ½ m2υ2x2(11)
This equation, together with the momentum conservation equation,
m1u1x + m2u2x = m1υ1x + m2υ2x(12)
allows υ1x and υ2x to be found, if we know the values of m1, m2 and the initial velocities u1x and u2x. The algebra is rather lengthy but it is worth the trouble because on the way we derive another useful expression relating the velocities. From Equation 11 we have:
m1(u1x − υ1x)(u1x + υ1x) = m2(υ2x − u2x)(υ2x + u2x)(13)
and from Equation 12:
m1(u1x − υ1x) = m2(υ2x − u2x)(14)
If we divide each side of Equation 13 by the corresponding side of Equation 14 we obtain:
u1x + υ1x = υ2x + u2x
i.e.u1x − u2x = −(υ1x − υ2x) = υ2x − υ1x(15)
Equation 15 shows that the following general result holds true:
In an elastic collision between two masses the relative velocity of approach is the negative of the relative velocity of separation.
Equation 15 can be combined with Equation 14 to solve simultaneously for υ1x and υ2x. We multiply Equation 15 by m2 to obtain:
m2u1x − m2u2x = m2υ2x − m2υ1x
If we subtract this equation from Equation 14 we have:
u1x(m1 − m2) + 2m2u2x = υ1x(m1 + m2)
soυ1x = [u1x(m1 − m2) + 2m2u2x]/(m1 + m2)(16)
Similarly we can derive the following expression for υ2x:
υ2x = [u2x(m2 − m1) + 2m1u1x]/(m1 + m2)(17)
It is interesting to examine these results for υ1x and υ2x in a few special cases, including some that have been mentioned earlier.
- 1
-
m1 = m2
If two objects of equal mass collide, Equations 16 and 17 give υ1x = u2x and υ2x = u1x. This means that the particles simply exchange velocities on collision. For example, if particle 2 is at rest initially (u2x = 0), then finally particle 1 is at rest (υ1x = 0) and particle 2 moves with the initial velocity of particle 1 (υ2x = u1x). We saw this result earlier in this subsection; it is a familiar tactic in bowls.
- 2
-
m1 ≫ m2; u2x = 0
If m2 is very small compared with m1, and u2x = 0, Equations 16 and 17 give υ1x ≈ u1x and υ2x ≈ 2u1x. Thus the motion of the high mass particle is virtually unchanged by the collision but the low mass particle moves off with a velocity of twice that of the high mass particle. Tennis players serving will be familiar with this case.
- 3
-
m2 ≫ m1; u2x = 0
If m1 is very small compared with m2 (which is stationary), then Equations 16 and 17 lead to υ1x ≈ −u1x and υ2x ≈ 0. i Therefore, the low mass particle rebounds with almost unchanged speed while the high mass particle remains essentially at rest. Golfers whose ball hits a tree will recognize this situation.
- 4
-
m2 ≫ m1; u2x ≈ −u1x
If m1 is negligible compared with m2, and the two bodies approach head–on with equal speeds then Equations 16 and 17 lead to υ1x ≈ −3u1x and υ2x ≈ u2x. This shows that the low mass particle bounces back with three times its initial speed, while the high mass particle continues essentially unaffected by the collision. This case will be recognized by a batsman playing cricket or by a tennis player returning a serve; a less familiar example is covered in the Exit test.
The results for these four special cases accord with common experience. The results quoted above in cases 2, 3 and 4 give an upper limit to the speed that can be imparted to a ball hit by a club, bat or racquet.
Question T8
A neutron of mass m rebounds elastically in a head–on collision with a gold nucleus at rest and of mass 197m. What fraction of the neutron’s kinetic energy is transferred to the recoiling gold nucleus? Repeat this calculation when the target is a carbon nucleus at rest and of mass 12m.
Answer T8
We need to calculate the loss of kinetic energy for the neutron, divided by its initial kinetic energy:
$\dfrac{\Delta{\rm E_{tran}}}{{\rm E_{tran}}} = \dfrac{u_{1x}^2-\upsilon_{1x}^2}{u_{1x}^2} = 1 - \upsilon_{1x}^2/u_{1x}^2$
We use Equations 16 and 17, with u2x = 0
υ1x = [u1x(m1 − m2) + 2m2u2x]/(m1 + m2)(Eqn 16)
andυ2x = [u2x(m2 − m1) + 2m1u1x]/(m1 + m2)(Eqn 17)
so∆Etran /Etran = 1 − (υ1x /u1x)2 = 1 − [(m1− m2)/(m1 + m2)]2
for gold:∆Etran /Etran = 1 − (196/198)2 = 0.020 (i.e. 2.0%)
for carbon:∆Etran /Etran = 1 − (11/13)2 = 0.284 (i.e. 28.4%)
We see that a low mass nucleus is much more effective than a more massive nucleus when it comes to slowing down fast neutrons by elastic collisions. As an aside, it is interesting to note that it is because of this fact that carbon is used in a nuclear reactor for just this purpose.
Question T9
A tennis player returns a service ball back in the direction of the server. The ball of mass 50 g arrives at the racquet of mass 350 g with a speed of 45 m s−1 and the racquet is travelling at 10 m s−1 at impact. Calculate the velocity of the returning ball, assuming elastic conditions.
Answer T9
We designate the ball as particle 1 and the racquet as particle 2, with the ball initially travelling along the positive x–direction. From Equation 16,
υ1x = [u1x(m1 − m2) + 2m2u2x]/(m1 + m2)(Eqn 16)
soυ1x = [45 m s−1 × (− 0.3 kg) + 2 × 0.35 kg(−10 m s−1)]/0.4 kg
υ1x = (−13.5 kg ms−1 − 7.0 kg m s−1)/0.4 kg = −51.3 m s−1
The server receives the ball back with interest!
3.2 Inelastic collisions in one dimension
We now extend our discussion to include cases where the total kinetic energy changes during the one–dimensional collision.
Completely inelastic collisions
First we return to our original case, where the two particles stick together on impact; this is an example of a completely inelastic collision, which occurs with the maximum loss of kinetic energy consistent with momentum conservation. As a simple example, suppose we have two bodies of equal mass, with one initially at rest. If the initial velocity of the other is ux, the initial momentum is mux; the final momentum must be the same so, since the mass has been doubled, the final velocity is ux /2 and the final kinetic energy is 2m (ux /2)2/2 = mux2 /4. Half the original kinetic energy has been transformed into other forms, mainly heat, during the collision.
For the more general case where the colliding masses are unequal, but they stick together at collision, we still have υ1x = υ2x = υx and so Equation 12 simplifies to our earlier Equation 6,
m1u1x + m2u2x = (m1 + m2)υx(Eqn 6)
and provides a full solution of the problem, without recourse to energy.
Question T10
A mass m1 travels along the x–axis with speed ux and collides with a mass m2 at rest. If the two masses stick together on impact derive an expression for the fraction of the original kinetic energy lost in the collision. What happens when m2 ≫ m1?
Answer T10
This is a completely inelastic collision, solvable using only the conservation of momentum along the x–axis. Equation 6 gives:
m1u1x + m2u2x = (m1 + m2)υx(Eqn 6)
Withu2x = 0, υx = m1u1x /(m1 + m2)
The initial kinetic energy is m1u1x2/2 and the final kinetic energy is (m1 + m2)υx2/2 and so the fractional loss of kinetic energy is given by:
$\dfrac{\Delta{\rm E_{tran}}}{{\rm E_{tran}}} = \dfrac{m_1u_{1x}^2-(m_1+m_2)\upsilon_{x}^2}{m_1u_{1x}^2} = 1 - \left(\dfrac{m_1+m_2}{m_1}\right)\left(\dfrac{\upsilon_x}{u_{1x}}\right)^2$
Substituting for υx /u1x we find:
$\dfrac{\Delta{\rm E_{tran}}}{{\rm E_{tran}}} = 1 - \left(\dfrac{m_1+m_2}{m_1}\right)\left(\dfrac{m_1}{m_1+m_2}\right)^2 = 1 - \left(\dfrac{m_1}{m_1+m_2}\right) = \dfrac{m_2}{m_1+m_2}$
For the case where m2 ≫ m1, i.e. a negligibly small mass object strikes a very massive object, the whole of the kinetic energy is lost.
The general case of an inelastic collision in one dimension
To complete the picture, let us mention the general case where two particles collide but where the transfer of kinetic energy into other forms is less than that for the completely inelastic case. This problem has no general solution without more information, such as the fraction of kinetic energy converted. Such problems have solutions which lie between those for the two extremes of elastic and completely inelastic collisions but they must be tackled on an individual basis, using the general principles of conservation of momentum and energy.
You will see that in all these calculations we have not needed to invoke the rather complicated forces involved in the interaction of the two particles, but rather have been able to solve the problems using only the principles of conservation of momentum and energy. This is a great simplification and illustrates the power of using conservation principles whenever possible.
3.3 Collisions in two or three dimensions
The same principles apply when we look at collisions in two or three dimensions. We have already considered this in Subsection 2.5, for the case of completely inelastic collisions. The extension to include elastic collisions is straightforward. We simply treat the motions in each dimension as independent motions, as we did in Subsection 2.5, and apply momentum conservation separately along each Cartesian coordinate axis, with the scalar quantity of kinetic energy and its conservation providing one additional equation relating the squares of the particle speeds. Once again, since we have been careful to use vector notation throughout, this extension to two or three dimensions is easily made.
Elastic collisions between two equal masses, with one mass at rest
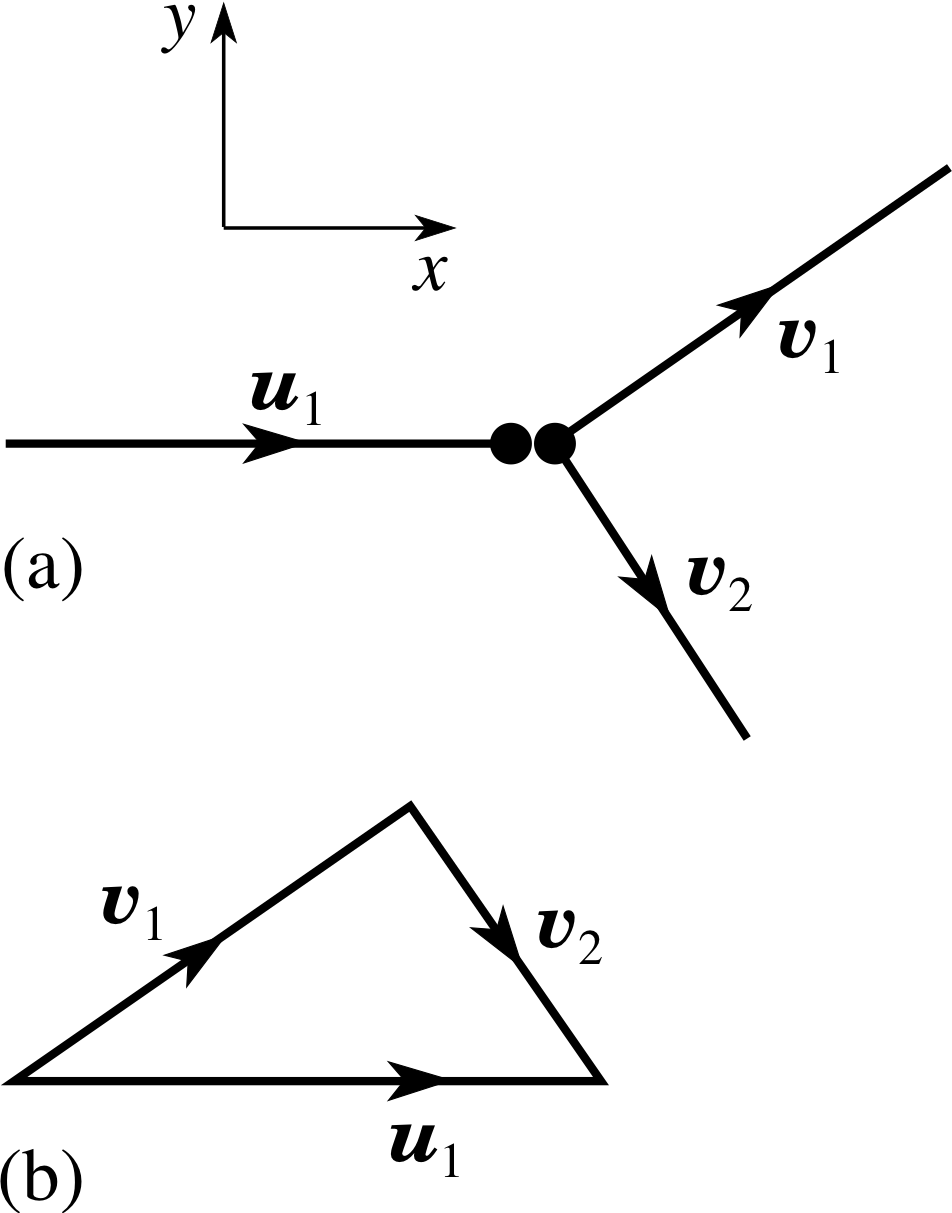
Figure 2 (a) Elastic collision between equal masses, with one at rest; (b) the corresponding vector triangle.
Consider the elastic collision between two identical bodies of mass m, one at rest and the other approaching with velocity u1. The particles are no longer confined to move in one dimension, so our x–component equations (Equations 9 and 10), embodying momentum and kinetic energy conservation,
mu1x = mυ1x + mυ2x(Eqn 9)
½ mu1x2 = ½ mυ1x2 + ½ mυ2x2(Eqn 10)
become full vector equations:
mu1 = mυ1 + mυ2(18)
and½ mu12 = ½ mυ12 + ½ mυ22(Eqn 19)
These can be simplified to:
u1 = υ1 + υ2(20)
andu12 = υ12 + υ22(21)
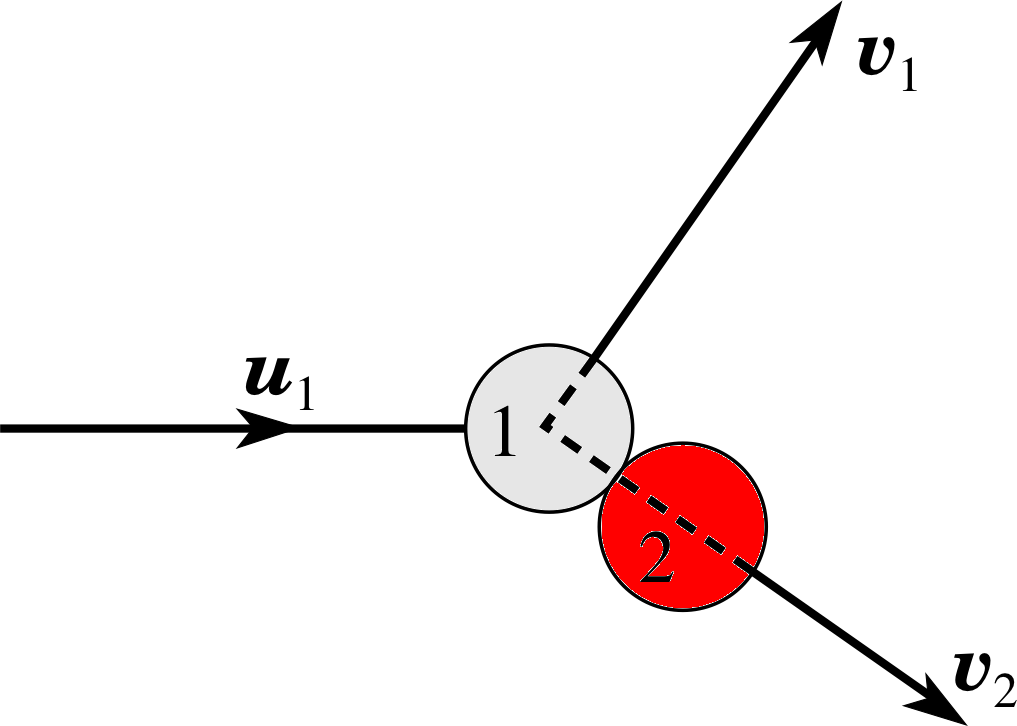
Figure 3 When ball 1 strikes ball 2, the reaction forces at the contact ensure that ball 2 is propelled away along the line of centres, as in snooker.
Equation 20 tells us that all three velocity vectors must lie in a single plane, in order for their vector sum to be zero. These equations are most easily interpreted by a diagram. Figure 2 shows how the three vectors u1, υ1 and υ2 are related to one another. They form a triangle which must be a right–angled triangle, since the sides obey Pythagoras’s theorem. The implication of this is striking; when two equal masses collide elastically they move away at 90° to each other. This is the simplifying feature of equal–mass collisions in two or three dimensions, corresponding to the simple result of the exchange of velocities, which we found in one dimension. i
You may have noticed that this result does not tell us exactly where the bodies go after the collision. Any pair of final velocities which can be represented by Figure 2 will be equally satisfactory, and there are an infinite number of these. The reason for this is that we have said nothing about the shape or size of the bodies, and just how they collide. If we have any information about how the bodies collide, as for example in the situation shown in Figure 3, then we will usually be able to find the final velocities.
Question T11
In the example above (illustrated in Figure 2), if the moving body has an initial speed of 10 m s−1, and is deflected through 20° in the collision, find the magnitudes and directions of the velocities υ1 and υ2.
Answer T11
From the triangle shown in Figure 2, υ1 has a magnitude 10 cos 20° m s−1 = 9.40 m s−1 and is at the given angle of 20° to the x–axis; υ2 has a magnitude 10 sin 20° m s−1 = 3.42 m s−1 and must be at 70° to the x–axis.
Question T12
In the example above (illustrated in Question T11), if instead of the conditions in Question T11 the speed of the moving body is reduced from 10 m s−1 to 6 m s−1 by the collision, find the final velocities.
Answer T12
Using the triangle in Figure 2 again,
υ22 = u12 − υ12 = (102 − 62) m2 s−2
so that υ2 = 8 m s−1. υ1 is at an angle cos−1 (6/10) = 53.1°, and υ2 at an angle cos−1 (8/10) = 36.9° to the x–axis. You will observe that the two angles add up to 90°, as they should.
When the two masses are unequal the algebraic manipulations required to solve collision problems become rather complex, but no new physics is involved in the solution and we will not pursue such problems here.
3.4 Relativistic momentum
It is now quite easy to study collisions in which the particles are travelling at a significant fraction of c, the speed of light in vacuum. These experiments fall mainly into the realm of nuclear and particle physics and an example might be the elastic collision between a very fast electron from a particle accelerator and an electron in the material of a stationary target. From what we have said in Subsection 3.3 we would predict that the angle between the outgoing tracks of the scattered electron and the target electron ought to be 90°. The prediction proves correct at low impact speeds but as this speed is increased the angle becomes less than 90° and the reduction in the angle increases with the impact speed. At the highest attainable speeds the incident electron is barely deflected at all by its collision with the target electron while the target electron also moves off in about this same direction. The collision essentially reverts to a one–dimensional bat–ball type of collision. From our discussions in Subsection 3.1Subsections 3.1 and Subsection 3.33.3 we recognize that this is exactly what would happen if the incoming electron had a mass which increases with speed, so that its mass eventually becomes much greater than that of the target electron and it is essentially unaffected by the collision. This suggestion, that the mass of a particle is not a constant but rather increases with speed is one of the possible interpretations of this experiment. However, this experiment does not measure mass but rather momentum and so its interpretation is best made in terms of the momentum, rather than in terms of either mass or speed separately. All we can be sure of is that if momentum conservation is valid then the magnitude of the momentum at high speeds cannot simply be given by the product of mass and speed.
The magnitude of the momentum of a particle with mass m and speed υ must always be greater than mυ. Although mυ is a good approximation at sufficiently low speeds, it underestimates the momentum progressively as the speed increases.
In 1905 Albert Einstein (1879–1955) postulated his special theory of relativity and amongst its consequences was a new definition for the momentum of a moving particle. The new definition of the relativistic momentum of a mass m when moving with velocity υ is:
$\boldsymbol{p} = \dfrac{m\boldsymbol{\upsilon}}{\sqrt{1-\dfrac{\upsilon^2}{c^2}}}$(22) i
This definition incorporates the features required to explain our experiment.
✦ What is the expression for the relativistic momentum of a particle moving at low speeds, so that υ/c ≪ 1?
✧ The denominator in Equation 22 relativistic momentum
$\boldsymbol{p} = \dfrac{m\boldsymbol{\upsilon}}{\sqrt{1-\dfrac{\upsilon^2}{c^2}}}$(Eqn 22)
simplifies to unity so p ≈ mυ.
✦ What is the magnitude of the relativistic momentum of a particle moving at a speed of, (a) υ/c = 0.1, (b) υ/c = 0.9, and (c) what happens as υ/c approaches 1?
✧ (a) The denominator in Equation 22 relativistic momentum
$\boldsymbol{p} = \dfrac{m\boldsymbol{\upsilon}}{\sqrt{1-\dfrac{\upsilon^2}{c^2}}}$(Eqn 22)
becomes $\sqrt{0.99\os}$, so p = 1.005mυ,
(b) p = 2.29mυ, and
(c) p tends to infinity.
The result for part (c) (i.e. where υ/c = 1) illustrates why it is not possible to accelerate a body to c, the speed of light in vacuum; to do so would require either an infinite force or an infinite time. Note, however, that it is the speed of light in a vacuum which is the limiting speed, not the speed of light in any other material, which is always less than c. So, it is perfectly possible to have a body travelling faster than the speed of light in glass or in water or even in air! i This discussion is only the briefest mention of relativity, about which more is said elsewhere is FLAP.
4 Closing items
4.1 Module summary
- 1
-
The momentum of a body, a vector quantity, is defined as the product of its mass and its velocity in classical Newtonian mechanics
p = mυ(Eqn 1)
At high speeds this definition must be modified into that for relativistic momentum
$\boldsymbol{p} = \dfrac{m\boldsymbol{\upsilon}}{\sqrt{1-\dfrac{\upsilon^2}{c^2}}}$(Eqn 22)
- 2
-
The force acting on a body is equal to the rate of change of momentum
$\boldsymbol{F} = \dfrac{d\boldsymbol{p}}{dt}$(Eqn 2) i
This statement is a more fundamental statement of Newton’s second law of motion than that in which force is equated to the product of mass and acceleration, since the latter form is applicable only for situations in which mass is constant.
- 3
-
The principle of conservation of momentum for an isolated system can be derived from Newton’s second and third laws of motion.
- 4
-
The principle of conservation of momentum plays an essential part in the solution of collision problems.
- 5
-
Translational kinetic energy is the energy that a body has as a result of its motion. In classical Newtonian mechanics
Etran = ½ mυ2(Eqn 8)
- 6
-
One-dimensional problems involving elastic collisions, in which kinetic energy is conserved, may be solved completely.
- 7
-
Problems involving motion in more than one dimension can only be solved fully if some details of the collision are known. One example is the elastic collision between two equal masses, where one mass initially is at rest. Here, the departing trajectories always make an angle of 90°.
4.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Determine the momentum of a body or system of bodies, given the mass and velocity of each body.
- A3
-
State and apply Newton’s second law in terms of momentum.
- A4
-
Show that the force acting on a body can be expressed as the sum of two terms, one involving rate of change of velocity and the other involving the rate of change of mass.
- A5
-
Derive the principle of conservation of momentum from Newton’s second and third laws of motion.
- A6
-
Describe the essential features of elastic and inelastic collisions.
- A7
-
Use the principle of conservation of momentum to solve problems involving completely inelastic collisions in one– or two–dimensional motion or ones involving the disruption of a single mass by explosion or decay.
- A8
-
Use the principles of conservation of momentum and kinetic energy to solve elastic collision problems.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
4.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions, each of which tests one or more of the Achievements.
Question E1 (A2)
Find the ratio of the magnitudes of the momenta associated with a rifle bullet of mass 30 × 10−3 kg moving at 400 m s−1 and a brick of mass 1 kg moving at 10 m s−1.
Answer E1
The magnitudes of the momenta are as follows:
the bullet’s is:30 × 10−3 kg × 400 m s−1 = 12 kg m s−1
and the brick’s is:1 kg × 10 m s−1 = 10 kg m s−1
Therefore the ratio is 12 : 10 or 1.2 : 1.0
These two momenta are similar in size.
(Reread Subsection 2.1 if you had difficulty with this question.)
Question E2 (A3 and A4)
Explain quantitatively how it is possible for a body on which a resultant force acts to move with constant velocity.
Answer E2
Equation 3 gives:
$\displaystyle \boldsymbol{F} = \dfrac{d\boldsymbol{p}}{dt} = \dfrac{d(m\boldsymbol{\upsilon})}{dt} = m\dfrac{d\boldsymbol{\upsilon}}{dt} + \boldsymbol{\upsilon}\dfrac{dm}{dt}$(Eqn 3)
Thus if $\dfrac{dm}{dt}$ is not zero, $\dfrac{d\boldsymbol{\upsilon}}{dt}$ may be zero even if F is not zero. Thus if the mass is changing with time then a force is required to keep the body moving at constant velocity.
(Reread Subsection 2.2 if you had difficulty with this question.)
Question E3 (A7 and A8)
A particle of mass m moves along the x–axis with velocity ux and collides head–on with a stationary particle of mass 2m. If in the collision the first particle is brought to rest, find the velocity of the second particle. This second particle then collides head–on with a stationary third particle of mass 3m. If the second and third particles stick together on impact, find their subsequent velocity after the collision.
Answer E3
Let the speed of the second particle after the first collision be υ2x and the speed of the combined second and third particles after the second collision be υx. Using conservation of momentum along the x–axis:
First collision:mux + 0 = 2mυ2x and so υ2x = ux /2
Second collision:2mυ2x + 0 = (2m + 3m)υx
soυx = 2υ2x /5 = 2 (ux /2)/5 = ux /5
(Reread Subsection 2.3 if you had difficulty with this question.)
Question E4 (A3)
Two balls of the same mass travelling at the same velocity strike a window perpendicularly. The first bounces back but the second breaks the window. Explain how this could be so.
Answer E4
The difference between the situations must be that one of the balls is more rigid than the other and so the time of contact during which the momentum of the ball changes on impact will then be less. The average force F required to effect this momentum change ∆p is related to the time of contact ∆t through the expression for the impulse:
∆p = F∆t(Eqn 4)
This implies that a much larger force must be exerted by the window to bring about any given change in momentum of the more rigid ball. If this force exceeds the maximum force which the window can safely exert then the window will break.
(Reread Subsection 2.2 if you had difficulty with this question.)
Question E5 (A3)
A car travelling at 15 m s−1 goes out of control and hits a tree, with the car and driver coming to rest in 0.6 s. What is the initial momentum of the driver, whose mass is 70 kg? What is the magnitude of the average force exerted on the driver during the crash, and how does this force compare with the magnitude of the driver’s weight?
Answer E5
The magnitude of the momentum of the driver is 70 kg × 15 m s−1 = 1050 kg m s−1. Equation 4,
∆p = F ∆t(Eqn 4)
gives the magnitude of the average force as:
∆p/∆t = (1050 kg m s−1)/(0.6 s) = 1750 kg m s−2 = 1750 N
The driver’s weight is of magnitude 70 kg × 9.8 m s−2 = 686 N, so the average impact force is about 2.5 times the weight of the driver in terms of magnitude.
(Reread Subsection 2.3 if you had difficulty with this question.)
Question E6 (A8)
A spacecraft approaches the planet Jupiter, passes round behind it, and departs in precisely the opposite direction to that with which it approached. Initially, when the spacecraft is a large distance from the planet, the spacecraft is moving in the negative x–direction at a speed of 10 km s−1, and Jupiter is moving in the positive x–direction at 13 km s−1. Assuming elastic conditions, find the final speed of the spacecraft when it is once again at a large distance from the planet. i
Answer E6
Let the masses of the spacecraft and Jupiter be m and M, respectively, the initial velocities u1x and u2x and the final velocities υ1x and υ2x. The principle of conservation of momentum, applied along x tells us that
mu1x + Mu2x = mυ1x + Mυ2x
and if there is no loss of kinetic energy during the interaction
½ mu1x2 + ½ Mu2x2 = ½ mυ1x2 + ½ Mυ2x2
In these two equations there are two unknowns, υ1x and υ2x, but we are only interested in υ1x, so that we should eliminate υ2x. The neatest way to do this is to rewrite the two equations as
υ2x = u2x + (m/M)(u1x − υ1x)
and(mM)(u1x2 − υ1x2) = υ2x2 − u2x2
substituting for υ2x in the second equation gives us
$\dfrac{m}{M}(u_{1x}^2-\upsilon_{1x}^2) = u_{2x}^2 + \left(\dfrac{m}{M}\right)^2\left(u_{1x}-\upsilon_{1x}\right)^2 + 2 u_{2x}\left(\dfrac{m}{M}\right)\left(u_{1x}-\upsilon_{2x}\right)^2$
cancelling the u2x2 terms, and dividing through by (m/M) × (u1x − υ1x) gives:
$\displaystyle \dfrac{(u_{1x}^2-\upsilon_{1x}^2)}{u_{1x}-\upsilon_{1x})} = (u_{1x}-\upsilon_{2x}) = \left(\dfrac{m}{M}\right)(u_{1x}-\upsilon_{1x}) + 2u_{2x}$
The mass of Jupiter is so much greater than that of the spacecraft that m/M is very small and the first term on the right can be neglected compared to the second term and compared to the term on the left–hand side. In fact, this neglected term can be shown to be equal to the change in velocity of Jupiter, which is very small (even though Jupiter’s change of momentum cannot be neglected compared to that of the spacecraft). This illustrates what we saw in Equation 15 in Subsection 3.1,
u1x − u2x = − (υ1x −υ2x) = υ2x −υ1x(Eqn 15)
that the relative velocity after collision is equal to the negative of the relative velocity before collision. So, neglecting the term, we find to a very good approximation:
u1x + υ1x ≈ 2u2x
(this is an approximation of Equation 16 with m2 ≫ m1)
υ1x = [u1x(m1− m2) + 2m2u2x]/(m1 + m2)(Eqn 16)
soυ1x ≈ 2u2x − u1x = 2 × 13 km s−1 − (−10 km s−1) = 36 km s−1
The spacecraft has been speeded up very substantially! This is a simplified example of the so–called ‘slingshot’ method, used to give a spacecraft enough energy to reach the outermost parts of the solar system. This additional energy comes from a reduction in the planet’s kinetic energy.
(Reread Subsection 3.1 if you had difficulty with this question.)
Question E7 (A8)
Two steel balls travelling at the same speed collide elastically head-on. One of them is stationary after the collision. If its mass is 900 g, what is the mass of the other?
Answer E7
If the initial velocities of the balls are ux and −ux and the final velocity of the moving ball is υ1x, then the conservation of momentum along the x–axis gives:
m1ux − m2ux = m1υ1x
and conservation of energy gives:
½ m1ux2 + ½ m2ux2 = ½ m1υ1x2
Rearranging these equations gives us
υ1x /ux = (m1− m2)/m1 and (υ1x /ux)2 = (m1 + m2)/m1
so that(m1− m2)2/m12 = (m1 + m2)/m1
which can be simplified to: m2 = 3m1, and so m1 = 300 g.
(Reread Subsection 3.1 if you had difficulty with this question.)
Question E8 (A7)
A block of stone at a quarry is blown up into three separate pieces of masses 10 tonnes, 8 tonnes, and 6 tonnes (1 tonne = 1000 kg). The 10 tonne piece moves off in the positive x–direction at a speed of 8 m s−1, and the 8 tonne piece moves in the negative y–direction at 5 m s−1. Find (a) the momentum of the third piece, and (b) the energy of the explosion, which must be equal to the extra kinetic energy after the explosion.
Answer E8
(a) If we take m1 = 104 kg, m2 = 8 × 103 kg, m3 = 6 × 103 kg, υ1x = 8 m s−1, and υ2y = −5 m s−1, the momentum of the third block is given by
p3x + m1υ1x = 0 and p3y + m2υ2y = 0
sop3x = −(104 kg) × (8 m s−1) = −8 × 104 kg m s−1
p3y = −(8 × 103 kg) × (−5 m s−1) = 4 × 104 kg m s−1
Alternatively
p = $\sqrt{\smash[b]{(8^2 + 4^2)}}$ × 104 kg m s−1 = 8.94 × 104 kg m s−1
at an angle to the negative x–axis of arctan(4 × 104/8 × 104) = 26.6°
(b) The speed of the third block is (8.94 × 104 kg m s−1)/(6 × 103 kg) = 14.9 m s−1
The total kinetic energy of the three blocks Etran is then
½ [(104 kg) × (8 m s−1)2 + (8 × 103 kg) × (5 m s−1)2 + (6 × 103 kg) × (14.9 m s−1)2]
So Etran = 1.09 × 106 J, equal to the total energy released in the explosion.
(Reread Section 3 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 4Closing items.