PHYS 5.2: Energy, damping and resonance in harmonic motion |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
When an object vibrates there are always some points in its oscillatory motion where it is momentarily at rest and other points at which it is moving with maximum speed. Consequently, the kinetic energy of the system is sometimes zero and sometimes a maximum; if the motion is periodic then so too is the kinetic energy. However, if the oscillator is isolated from its surroundings, so that the principle of energy conservation applies, its total energy will be constant. Such an oscillator must therefore have potential energy and this too must be periodic in order that the sum of kinetic and potential energy can be constant; the potential energy is maximum when the kinetic energy is minimum and vice versa. Section 2 deals with the energy in vibrating mechanical systems, particularly systems in one–dimensional simple harmonic motion (SHM); among other things it provides a mathematical expression for the kinetic and potential energy in an isolated simple harmonic oscillator.
It is a matter of common experience that the amplitude of any mechanical vibration tends to decrease with time, until the motion eventually stops. The total energy of the vibrating system is clearly not constant in this situation. However, the principle of energy conservation still applies on a larger scale, so the vibrating system must be transferring energy elsewhere, and cannot be treated as an isolated system. When a vibrating system loses mechanical energy in this way it is said to be damped. Any vibrating system will have some damping, although it may be very small.
The damping of vibrations is of great technological importance and many engineers spend time designing systems to have particular levels of damping – either low or high or optimal. For example, in a mechanical clock the oscillations of the balance wheel or pendulum should be as lightly damped as possible, to minimize the energy input needed to sustain the oscillations. In contrast, a car suspension system uses heavily damped shock–absorbers to prevent the car and its passengers being driven into excessive vertical oscillations or being jolted to destruction by bumps in the road surface; the main function of the suspension system is to absorb and dissipate (as heat) the energy from unwanted vibrations. Electrical meters and weighing balances are other examples where the correct level of damping is important – too much damping and the instrument will be too slow to respond to a changing reading, too little damping and the instrument will oscillate about the true reading. Section 3 describes damped harmonic motion. It provides a mathematical treatment of lightly damped harmonic motion, in which the amplitude of the oscillation decays gradually, and a qualitative discussion of more heavily damped oscillations. The module closes with a brief qualitative introduction to driven oscillations and resonance.
Although the mathematical expressions introduced in this module are developed in the context of mechanical oscillations, the results are equally applicable to many other situations, including the oscillations of electric charge in circuits – some of these applications are covered elsewhere in FLAP.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 4.1Module summary and the Subsection 4.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 4.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
An object of mass 0.20 kg is suspended from the end of a spring with a spring constant of 125 N m−1 and is set into simple harmonic motion (SHM). Calculate the angular frequency ω of the resulting oscillation, in the absence of damping. The system is then damped and the magnitude of the damping force is linearly proportional to the speed, with a damping constant of 1.4 s−1. Explain what this statement means. Calculate the Q–factor for this oscillator.
Answer F1
The undamped angular frequency is given by
$\omega_0 = \sqrt{\dfrac km} = \rm \sqrt{\dfrac{125\,N\,m^{-1}}{0.20\,kg}} =\sqrt{\dfrac{125\,kg\,m\,s^{-2}\,m^{-1}}{0.20\,kg}} = 25\,s^{-1}$
The statement means that this oscillator is subject to a damping force given by F2 = −bυ2 with the damping constant γ = b/m = 1.4 s−1 or b = 0.2 kg × 1.4 s−1 = 0.28 kg s−2.
The Q–factor is given as Q = ω0/γ (Equation 28),
$Q = \dfrac{2\pi E(t)}{\left\lvert\,(\Delta E)_T\,\right\rvert} = \dfrac{2\pi}{\gamma T_0} = \dfrac{\omega_0}{\gamma}$(Eqn 28)
with γ = b/m (Equation 24),
$\dfrac{dE(t)}{dt} = -\dfrac{bE(t)}{m} = -\gamma E(t)$(Eqn 24)
so $Q = \dfrac{\omega_0}{\gamma} = \rm \dfrac{25\,s^{-1}}{1.4\,s^{-1}} = 18$. This is a fairly low Q-factor oscillator.
Question F2
The object described in Question F1 is displaced by 0.1 m from its equilibrium position and then released. Sketch graphs showing how (i) the amplitude, (ii) the kinetic energy, (iii) the potential energy, and (iv) the total energy vary with time for (a) the undamped situation, and (b) the damped situation as given in Question F1.
Answer F2
The graphs for these situations are shown in Figure 8. The oscillatory functions for the kinetic energy Ekin and potential energy Epot have twice the frequency of the displacement oscillation (Ekin = 0 at t = 0 since it is released from rest at maximum displacement or maximum Epot).
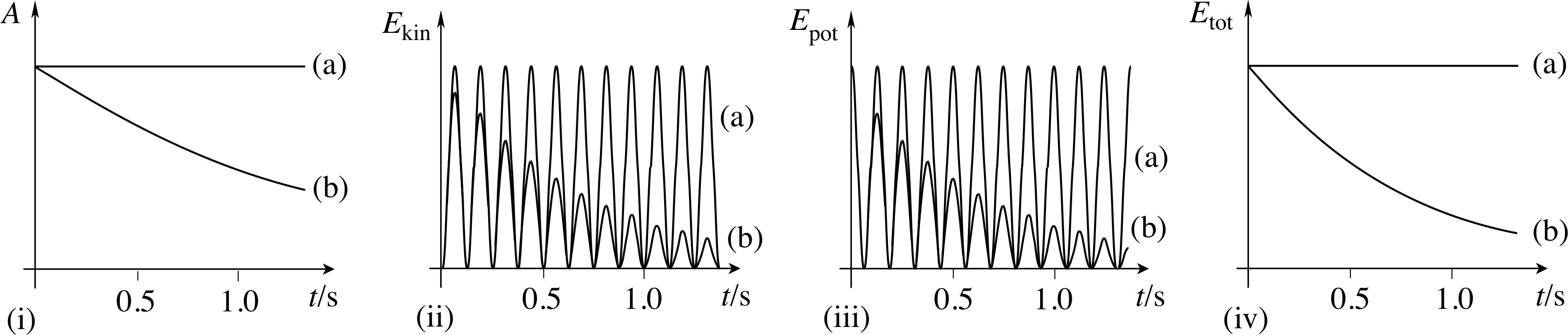
Figure 8 See Answer F2.
The total energy is constant for (a). In (b) all three energies decay as e−γt and the amplitude decays as e−γt/2. The energies each decay to 1/e of their original levels in a time t = 1/γ = 0.71 s while the amplitude decays to 1/e of its original level in t = 2/γ = 1.4 s.
The period is T = 2π/ω0 = 0.25 s. The graphs show these relative scales.
1.3 Ready to study?
Study comment In order to study this module you will need to be familiar with the following terms: acceleration, components_of_a_vectorcomponent (of a vector), displacement, energyenergy transfer (or work done) by a force, equilibrium, kinetic energy, mass, momentum, Newton’s laws of motion, potential energy, conservation_of_mechanical_energyprinciple of energy conservation, speed, tension, velocity and weight. In addition you should be familiar with the general description of one_dimensional_simple_harmonic_motionone–dimensional simple harmonic motion (SHM) and the concepts of amplitude, angular frequency, cycle, force constant, frequency, pendulum, period, phase, phase constant, restoring force and spring constant. The module also assumes you are familiar with the expressions for displacement, velocity and restoring force in one–dimensional SHM. These expressions are developed elsewhere in FLAP and, if necessary, you can review them through the Glossary entry for simple harmonic motion. The module also requires familiarity with the following mathematical concepts: exponential function, gradient, linear function, modulus, natural logarithm, parabola, quadratic function and trigonometric function. The trigonometric identities sin2θ = ½ [1 − cos(2θ)] and sin2θ + cos2θ = 1 are used, together with the approximation cos θ = 1 − θ2/2 for small θ. You do not need to be fully conversant with differentiation in order to study this module, but you should be familiar with the calculus notation dx/dt used to represent the rate of change of x with respect to t. If you are unsure about any of these items you should refer to the Glossary, which will also indicate where in FLAP they are developed. The following Ready to study questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
Write down the values of the phase constant ϕ that make the function
x (t) = A cos(ωt + ϕ)
equivalent to
x (t) = A sin(ωt)
Answer R1
If we put ϕ = −π/2
we have $A\cos\left(\omega t - \dfrac{\pi}{2}\right) = A\cos\left(\dfrac{\pi}{2} - \omega t\right) = A\sin(\omega t)$
So, ϕ = π/2 is an answer, but so is ϕ = 2nπ − π/2 where n is any whole number.
(If you are unclear about the answer to Questions R1 consult phase constant in the Glossary.)
Question R2
Sketch the graph of the function
x (t) = A cos(ωt + ϕ)
over the time interval from t = 0 to t = 4π/ω (i.e. t = 2T) for the situations where (a) ϕ = 0, (b) ϕ = π/2, and (c) ϕ = −π/2.
Answer R2
The displacement–time graphs are shown in Figure 9, corresponding to the given equation with phase constants ϕ of (a) 0, (b) π/2, and (c) −π/2.
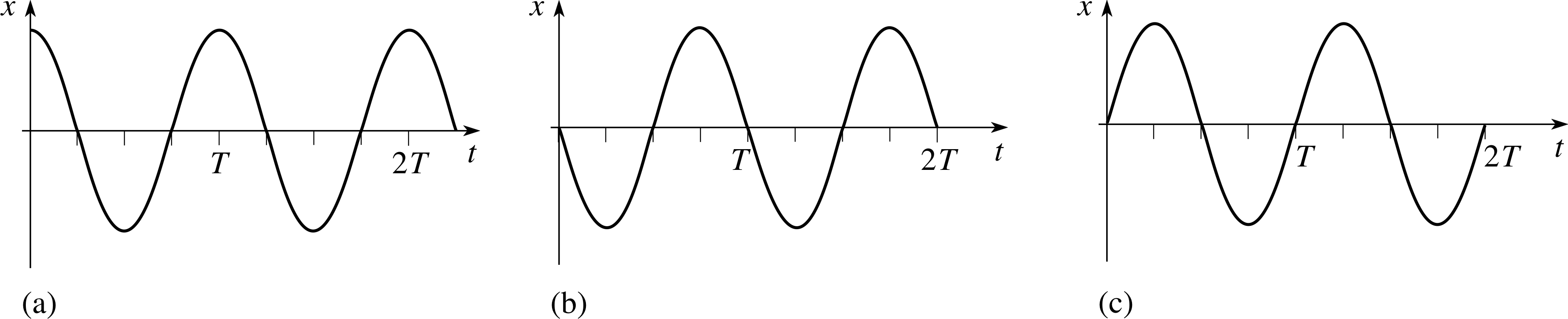
Figure 9 See Answer R2.
(If you are unclear about the answer to Questions R2 consult phase constant in the Glossary.)
Question R3
Using the function x (t) given in Question R2
x (t) = A cos(ωt + ϕ)
for the case ϕ = 0, sketch dx (t)/dt, its derivative with respect to t, as a function of t.
(dx (t)/dt denotes the rate of change of x with respect to t.)
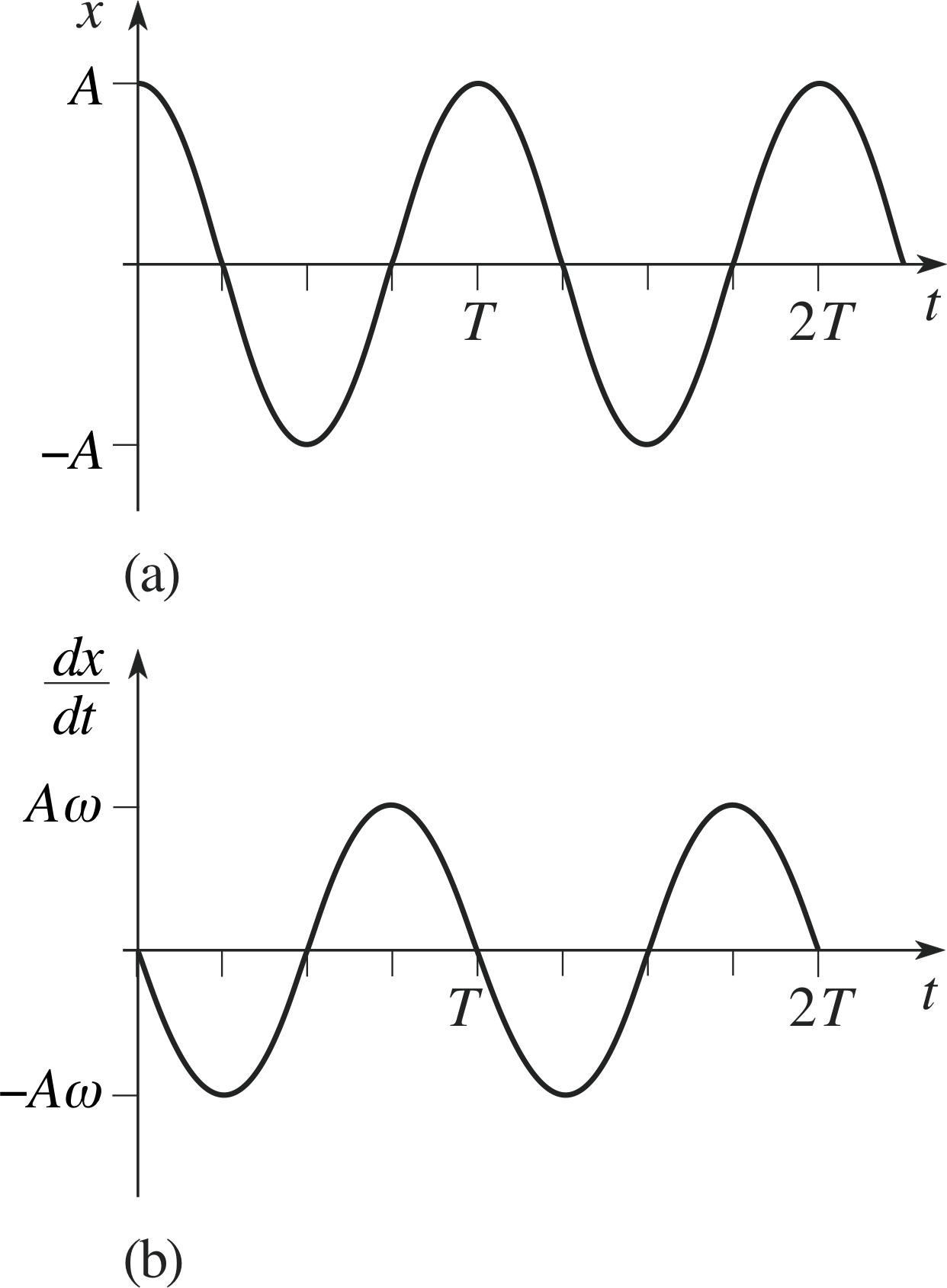
Figure 10 See Answer R3.
Answer R3
The derivative of the function x (t) = A cos(ωt) is
$\dfrac{dx(t)}{dt} = -A\omega\sin(\omega t)$
The graphs of these two functions are shown in Figure 10.
(If you are unclear about the answer to Question R3 consult derivative in the Glossary.)
Question R4
A body of mass 0.40 kg is suspended from the end of a spring of spring constant 160 N m−1. Calculate the angular frequency, the frequency and the period of small oscillations of the system about equilibrium. If the body is pulled down to a position 0.05 m below its equilibrium position, and released from rest at time t = 0, write down an expression which gives the displacement in the subsequent oscillation as a function of time.
Answer R4
The angular frequency is given by
$\omega_0 = \sqrt{\dfrac km} = \rm \sqrt{\dfrac{160\,N\,m^{-1}}{0.40\,kg}} =\sqrt{\dfrac{160\,kg\,m\,s^{-2}\,m^{-1}}{0.40\,kg}} = 20\,s^{-1}$
which implies a frequency of f = ω/2π = 3.2 s−1 = 3.2 Hz. The period is thus T = 2π/ω = 1/f = 0.1π s = 0.31 s. The amplitude is the maximum extension, which in this case is the initial displacement 0.05 m, so the displacement is given by x (t) = A cos(ωt) = (0.05 m) × cos(t × 20 s−2). The initial condition, a maximum displacement at t = 0, forces us to use the cosine function with the initial phase constant ϕ = 0.
2 Energy in oscillating systems
In a mechanical oscillation the moving mass m has kinetic energy by virtue of its motion. In the case where the object is in one–dimensional motion along the x–axis, with velocity of magnitude υx, the kinetic energy Ekin is:
$E_{\rm kin} = \frac12 m\upsilon_x^2$(1)
In addition to this, the mass has potential energy by virtue of its position. Potential energy might arise from a variety of sources. For example, the mass may change its height above the Earth’s surface (as for a swinging pendulum bob), in which case there will be corresponding changes in the gravitational potential energy. Alternatively, the mass may be attached to a spring or to some other elastic body and there will then be changes in the stored strain potential energy during the motion. In this latter context we use the term elastic to describe a body which will deform when subjected to appropriate forces but which fully recovers its original form when the forces are removed; the deformation does not produce any permanent distortion. The fact that energy can be stored in a compressed or stretched elastic body is well known to any archer or child with a catapult!
In physics, it is generally true that the calculation of potential energy poses far greater difficulties than the calculation of kinetic energy does. i Kinetic energy is simply determined from the mass and speed whereas potential energy calculations require some knowledge of the forces acting – and these are often not simple. In the case of strain potential energy in particular, the internal forces involved in a deformation may be very complicated and the energy difficult to calculate. A second but less serious problem is that while kinetic energy has an obvious zero, when the particle is stationary, potential energy often has no obvious zero. For example, when dealing with gravitational potential energy we might choose the position of zero potential energy to be at the Earth’s surface, or at the height of our laboratory floor or maybe even at the centre of the Earth, or totally remote from any gravitating body such as the Earth. This problem may be simplified because it is only changes in potential energy that have physical significance, so the zero point can be chosen arbitrarily. When dealing with strain potential energy there is an obvious zero point – at the position where the elastic body is not deformed. Nonetheless, the choice of zero point remains arbitrary and we may always choose some other zero point in order to simplify the problem in hand.
If the position of zero potential energy of an oscillator is chosen in such a way that it is also the position at which the oscillator has its maximum kinetic energy, then the total energy itself will ‘oscillate’ between being totally kinetic and totally potential. It is the purpose of this section to provide mathematical expressions for the total energy of a mechanical oscillator that show how this energy oscillation occurs. As a first step towards this goal we will investigate the behaviour of the potential energy in three particular oscillators; a simple pendulum, a mass attached to a spring and sliding on a table, and a mass hanging from a spring. We will then combine the general expression for potential energy that emerges from these investigations with the general expression for kinetic energy to find a general expression for the total energy of any one–dimensional simple harmonic oscillator.
2.1 Gravitational potential energy for the simple pendulum
We can approach the problem of potential energy in vibrational motion by considering a simple example in which the potential energy involves only gravitational energy – the swinging of a simple pendulum. As the pendulum bob rises and falls during its oscillation, its gravitational potential energy changes in proportion to its height above a chosen reference level, such as the surface of the Earth. If the height of the bob (mass m) above the surface is h and the magnitude of the acceleration due to gravity is g then the gravitational potential energy Epot is:
Epot = mgh(2) i
This expression may be interpreted as a special case of the formula for the energy transferred (or work done) by a force Fx when it acts through a displacement sx: i
∆Epot = −Fxsx(3)
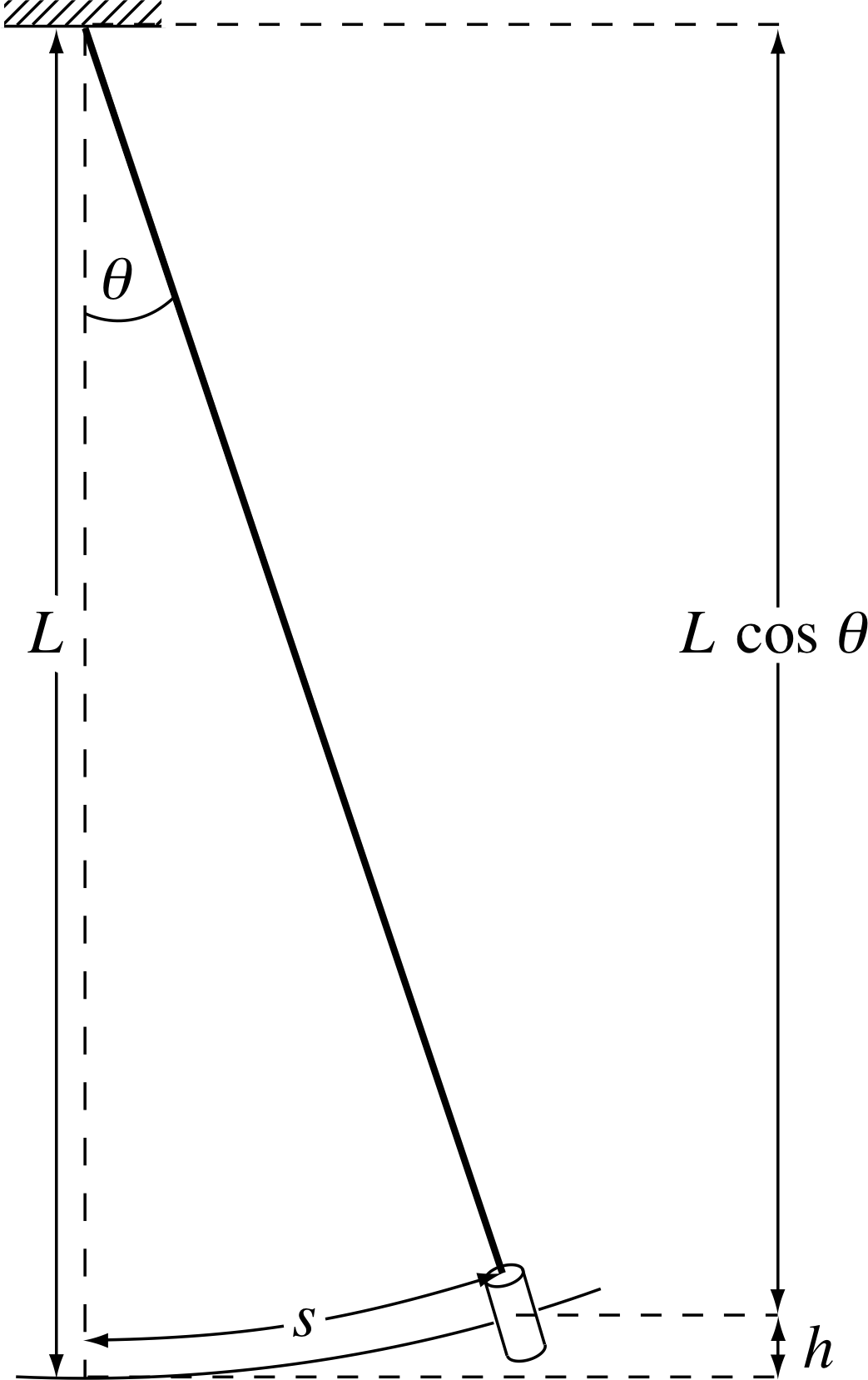
Figure 1 The simple pendulum.
In our case Fx is the gravitational force downwards of magnitude mg and sx is h, measured upwards as positive. If we take the point where h = 0 to be a point of zero gravitational potential energy, it follows that the energy transferred when Fx acts over a displacement sx is equal to mgh the gravitational potential energy at height h. i
We may apply Equation 2 to the simple pendulum, as shown in Figure 1. When the bob is displaced a distance s along the arc from the equilibrium position the additional height h is given by
h = L − L cos θ = L (1 − cos θ )
If we take the equilibrium position of the bob (h = 0) as the point of zero potential energy
Epot = mgh = mgL (1 − cos θ)
During the oscillation the angle θ varies and with it the potential energy. We could also express θ in terms of the displacement along the arc s by noting that in radians θ = s/L and by using the approximation for small θ that cos θ ≈ 1 − θ2/2 i thus:
The stored gravitational potential energy, when a pendulum is displaced by a small amount θ = s/L from its equilibrium, is given by
$E_{\rm pot} = mgL\left[1-\left(1-\theta^2\right)\right] = mgL\left(\dfrac{s^2}{2L^2}\right) = \dfrac12 \left(\dfrac{mg}{L}\right)s^2$(4)
where L is the length of the pendulum.
Notice that this motion can still be described as one–dimensional motion along the arc, even though the motion is not along a straight line. Restoring forces and stored energy can be written in terms of a single variable s, the displacement along the arc from equilibrium.
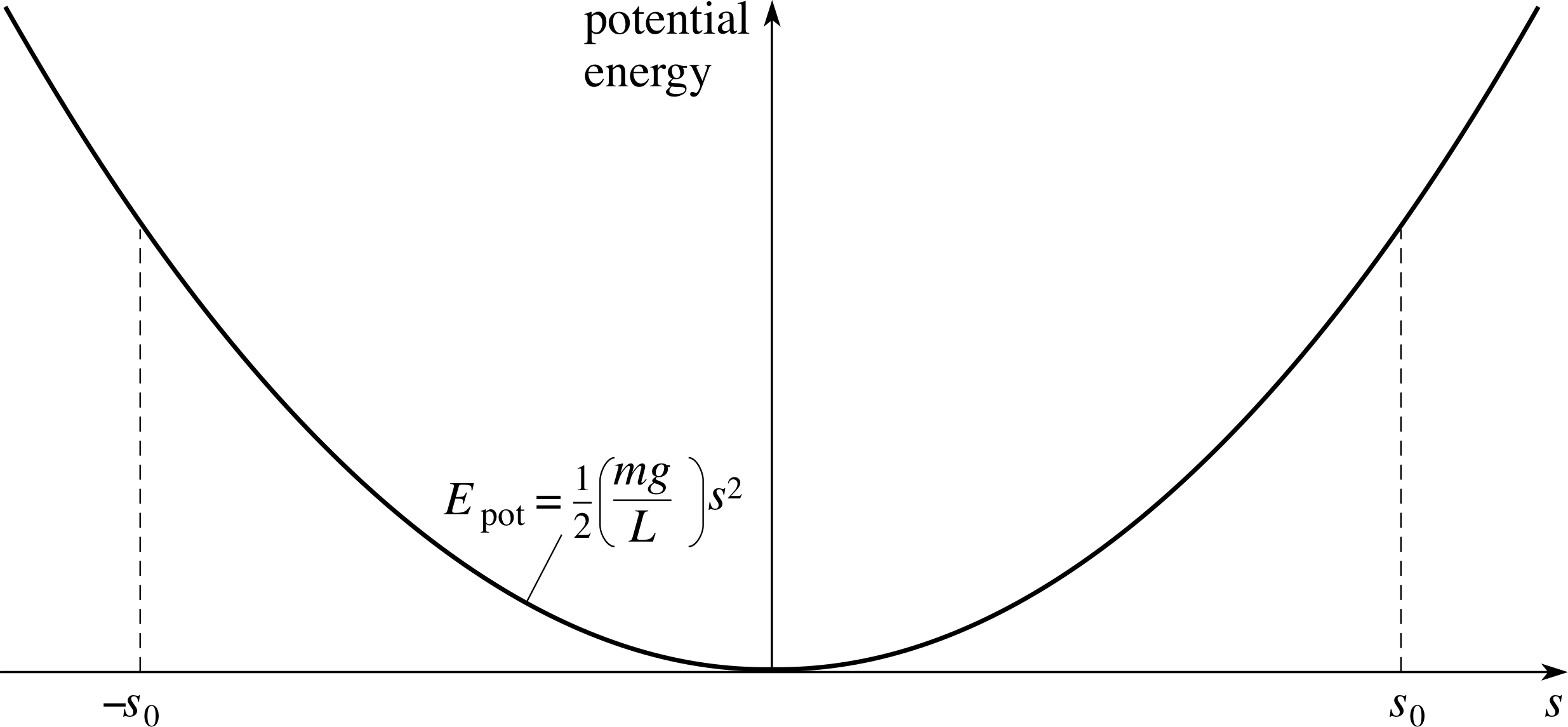
Figure 2 See Question T1.
Question T1
Figure 2 shows the potential energy of the simple pendulum as a function of the (small) displacement along the arc, as given by Equation 4.
The potential energy is taken as zero at the equilibrium position. What is the shape of the graph?
Answer T1
The graph is parabolic – it is the graph of a quadratic function of s. If the displacement is doubled the potential energy is quadrupled.
2.2 Strain potential energy in a stretched or compressed spring

Figure 3a Motion of a mass attached to a spring and oscillating along a horizontal frictionless surface.
Potential energy may also appear as stored strain potential energy in a stretched or compressed spring. An illustration of an oscillator based on this idea is shown in Figure 3a. Here a mass is attached to a spring and rests on a horizontal frictionless surface. If the mass is initially displaced by stretching the spring and is then released, it will oscillate – producing alternately, compressions and extensions in the spring.
We can find the stored strain potential energy by using Equation 3,
∆Epot = −Fxsx(Eqn 3)
to calculate the energy transferred by the tension force Fx in compressing or extending the spring from its unstretched length. The calculation is a little more complicated than for the previous example because the magnitude of the tension force increases as the extension increases, and so it is not constant throughout the energy transfer. Extensions and compressions take place along a single axis, the x–axis, so the problem is one–dimensional with the x–components of displacement and force given by x and Fx, respectively. i
Provided the spring is not stretched too far, this tension force is linearly proportional to x, but has the opposite sign since it is directed towards the origin. Thus,
Fx = −ksx(5)
Equation 5 is a statement of Hooke’s law.
Suppose the spring is stretched to some maximum extension x = xmax. Equation 3 then gives the potential energy of the system when the mass m is at the position x = xmax as
$(E_{\rm pot})_{\rm max} = -\langle F_x\rangle x_{\rm max} = \langle -F_x\rangle x_{\rm max}$(6) i
where we have replaced the varying tension force Fx over the range from x = 0 to x = xmax by its average value
$\langle F_x\rangle$ over this range. Since Fx varies linearly with x the average force $\langle F_x\rangle$ is just half the final force (Fx)max = −ksx2max.
Equation 6 then gives
$(E_{\rm pot})_{\rm max} = \frac12 k_sx_{\rm max}^2$(7)

Figure 3b Motion of a mass attached to a spring and oscillating along a horizontal frictionless surface; minus the tension force, plotted against displacement for this oscillator.
Aside If you are familiar with integral calculus you will perhaps recognize Equation 7 as the integral of Equation 3,
∆Epot = −Fxsx(Eqn 3)
over the extension x, i.e.
$\displaystyle E_{\rm pot} = -\int_0^x F_x\,dx = k_s\int_0^x x\,dx = \frac12 k_sx^2$
If you are unfamiliar with this approach it is not essential here − it amounts to finding the area under the graph in Figure 3b; by integration we have done this here directly from the graph. Details of integration can be found in the maths strand of FLAP.
A related point is that there is a general relationship between the conservative force acting on an object and the way its potential energy changes with position. The general relationship is: $F_x = -\dfrac{dE_{\rm pot}}{dx}$. If we differentiate the general form of Epot (i.e. ½ksx2) with respect to x we obtain the tension Fx = −ksx, as in Equation 5.
It can be seen that the quantity in Equation 7,
$(E_{\rm pot})_{\rm max} = \frac12 k_sx_{\rm max}^2$(Eqn 7)
is equal to the area under the graph of Figure 3b between x = 0 and x = xmax. It is straightforward to generalize Equation 7 for any extension x as:
The stored strain potential energy when a spring is stretched (x > 0) or compressed (x < 0) by an amount x from its original length is given by
Epot = ½ksx2(8)
where ks is the spring constant.

Figure 3c Motion of a mass attached to a spring and oscillating along a horizontal frictionless surface; graph showing the potential energy of this oscillator as a function of its displacement from the equilibrium position (Equation 7).
Notice that since x appears as a squared quantity in Equation 8 the magnitude but not the sign of x is important; the energy stored is the same for an extension or a compression of the same magnitude.
The potential energy of the horizontal spring oscillator as a function of the displacement, as given by Equation 8, is shown in Figure 3c. The similarity between Figure 3c for the spring oscillator and Figure 2 for the pendulum is obvious – both relationships describe parabolic curves and for the pendulum the quantity mg/L plays the same role as the spring constant ks. This similarity in the mathematical expressions for potential energy of the pendulum and the spring oscillator will be useful at the end of this section where we set up a mathematical model for the general energy oscillations in any SHM.
Question T2
A spring–powered gun fires a pellet of mass 0.1 g using a spring of spring constant 5 × 103 N m−1. If the maximum compression of the spring is 0.1 m and 30% of the strain potential energy is given to the pellet, calculate its speed on leaving the gun.
Answer T2
We use Equation 1,
$E_{\rm kin} = \frac12 m\upsilon_x^2$(Eqn 1)
for the kinetic energy of the pellet and equate this to 30% of the strain potential energy, as given by Equation 7,
$(E_{\rm pot})_{\rm max} = \frac12 k_sx_{\rm max}^2$(Eqn 7)
to obtain:
$\frac12 m\upsilon_x^2 = 0.3\left(\frac12k_sx^2\right)$
and so$\upsilon_x^2 = 0.3\left(\dfrac{k_sx^2}{m}\right) = \rm \dfrac{0.3\times5\times10^3\,N\,m^{-1}(0.1\,m)^2}{10^{-4}\,kg} = \dfrac{1.5\times10^5\,N\,m}{kg} = 1.5\times10^5\,m^2\,s^{-2}$
i.e.υx = ±3.9 × 102 m s−1. It follows that the speed is υ = | υx | = 3.9 × 102 m s−1.
2.3 Total potential energy for a mass suspended on a spring
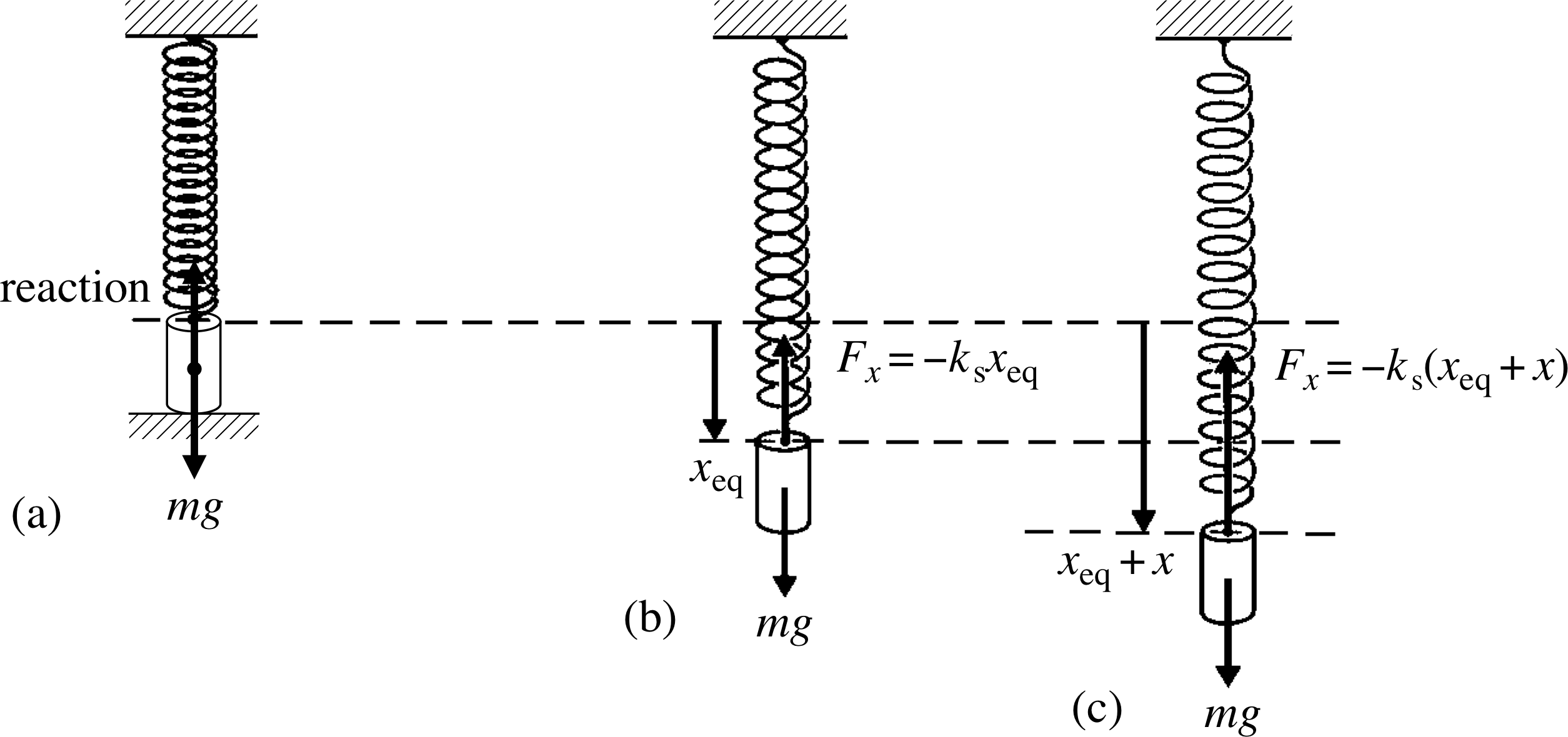
Figure 4 A light coil spring shown (a) unloaded (with a supported mass held at the unstretched spring position), (b) at the position of equilibrium under the load, and (c) loaded and displaced below its position of equilibrium. Note that x is taken to be positive in the downward direction.
A vertical spring oscillator, with a mass hanging from a light spring i, is shown in Figure 4. Figure 4a shows the unstretched spring, with the mass attached but supported externally, rather than by the spring; Figure 4b shows the mass hanging freely at rest at its equilibrium position xeq and Figure 4c shows the mass displaced to some position xeq + x below its equilibrium position, as it might be at some point during an oscillation of the spring.
Calculating the potential energy of this oscillator requires some care, since the gravitational energy of the mass must be added to the strain energy of the spring. Moreover, we have to choose zero points for both the strain energy and the gravitational energy, and they need not be the same. Should we choose the zero point of the strain energy so that it corresponds to the unstretched length or to the equilibrium position? What position of the mass should correspond to the zero point of gravitational energy? From what was said at the start of Section 2 we can choose these zero points arbitrarily, but we would be wise to choose them in such a way that they make the calculations as simple as possible. Let us investigate some possible choices to see what is best. i
If we take the unstretched spring (Figure 4a) as having zero strain potential energy, as we did in Subsection 2.2, the strain potential energy at the equilibrium position (Figure 4b) is ksx2eq/2 and at displacement x below the equilibrium position (Figure 4c) it is ks(xeq + x )2/2. If we take the zero of gravitational potential energy with the mass at the equilibrium position (Figure 4b) then at displacement x below the equilibrium position (Figure 4c) it is −mgx. When the mass is at the equilibrium position, the net force on it is zero and its weight, mg downwards, is balanced by the spring tension, ksxeq, upwards. So,
| Position | Gravitational potential energy Egrav |
Strain potential energy Estrain |
Total potential energy Epot |
|---|---|---|---|
| As in Figure 4a | mgxeq = ks(xeq)2 | 0 | ks(xeq)2 |
| As in Figure 4b | 0 | ks(xeq)2/2 | ks(xeq)2/2 |
| As in Figure 4c | −mgx = −ksxeqx | ks(xeq + x)2/2 | ks(xeq)2/2 + ksx2/2 |
mg = ksxeq
We may therefore write the gravitational energy at displacement x as −mgx = −ksxeqx. i
Table 1 summarizes the potential energy situation as shown in Figure 4, taking these potential energy zeros.
Question T3
For the system shown in Figure 4, construct a table similar to Table 1 but with both the strain potential energy zero and the gravitational potential energy zero for the unstretched spring, as shown in Figure 4a.
| Position | Gravitational potential energy Egrav |
Strain potential energy Estrain |
Total potential energy Epot |
|---|---|---|---|
| As in Figure 4a | 0 | 0 | 0 |
| As in Figure 4b | −mgxeq = −ks(xeq)2 | ks(xeq)2/2 | −ks(xeq)2/2 |
| As in Figure 4c | −mg (xeq + x) = −ks(xeq + x) | ks(xeq + x)2/2 | −ks(xeq)2/2 + ksx2/2 |
Answer T3
Your table should look like Table 3.
All gravitational potential energies are negative (below the zero potential height) and all strain energies are positive, determined by the total extension from the unstretched position.
In the next question you will need to think carefully about how to deal with a potential energy zero defined where the spring is already stretched. Y ou must remember that it is the real extension from the unstretched length which controls the stored energy.
Question T4
For the system shown in Figure 4, construct a table similar to Table 1 but with the gravitational potential energy zero for the unstretched spring and the strain potential energy zero at the equilibrium position.
| Position | Gravitational potential energy Egrav |
Strain potential energy Estrain |
Total potential energy Epot |
|---|---|---|---|
| As in Figure 4a | 0 | −ks(xeq)2/2 | −ks(xeq)2/2 |
| As in Figure 4b | −mgxeq = −ks(xeq)2 | 0 | −ks(xeq)2/2 |
| As in Figure 4c | −mg (xeq + x) = −ks(xeq + x) | ks(xeq + x)2/2 | −ks(xeq)2/2 + ksx2/2 |
Answer T4
Your table should look like Table 4.
Again, all gravitational potential energies are negative (below the zero potential height) but now we must attribute zero strain energy to the situation of Figure 4b and therefore in Figure 4a, where the spring is not stretched, the strain energy must be less and thus must be given a negative value −k (xeq)2/2 with respect to our chosen zero – although in reality the spring has no stored energy in the unstretched length. This is a rather strange choice of zero for strain potential energy! If, in your answer, you were tempted to write k (xeq)2/2 for the strain energy in Figure 4a you were treating the situation as if the spring were being stretched by xeq from its unstretched length rather than being allowed to relax back to its unstretched length.
There are two lessons to be learned from Table 1 and Answers T3 and T4. First, it is clear that although any choice for the zero point of the strain energy is equally valid, the most natural choice is that in which the spring is neither stretched nor compressed.
The reason for this is that the strain potential energy is a quadratic function of displacement, so the graph of Estrain against x is a parabola with a unique minimum at x = −xeq.
It makes good sense to let this minimum value of Estrain correspond to the zero point of the strain energy to avoid assigning a negative value to the strain energy of the unstretched spring. i
The second lesson from Table 1 and Answers T3 and T4 is that when the mass has been displaced by an amount x from the equilibrium position the total potential energy is always a quadratic function of the form
Epot = ½ksx2 + constant
where the value of the constant depends on the choice of zero points for the gravitational and strain energies. Now you may find this surprising since the gravitational potential is a linear function of x, yet there is no term proportional to x in the expression for Epot. It is worth noting how this comes about:
If we take the unstretched spring as having zero strain energy, then
Estrain = ½ks(x + xeq)2
while the gravitational potential energy is given by
Egrav = −mgx + E0
where E0 is a constant determined by the location of the zero point of the gravitational potential energy. Hence
Epot = Estrain + Egrav = ½ks(x + xeq)2 − mgx + E0
i.e.Epot = ½ksx2 + E0 + ½mgxeq
Note that the linear terms, proportional to x alone, have cancelled. Also note that Epot becomes especially simple if E0 = −½mgxeq. In other words the expression for the total potential energy becomes as simple as possible if we require that
Egrav = −mgx − ½mgxeq
SoEgrav = 0 corresponds to x = −xeq/2.
✦ If the zero point of the strain energy corresponds to the unstretched spring, and the zero point of gravitational energy corresponds to x = −xeq/2, what value of x corresponds to the zero point of Epot = Estrain + Egrav?
✧ Since Epot = ksx2/2 with these choices, it follows that x = 0 corresponds to Epot = 0, i.e. the zero point of the (total) potential energy corresponds to the equilibrium position xeq.
The stored potential energy when a mass suspended from a spring is displaced by a small amount x from its equilibrium position is given by
Epot = ½ksx2(Eqn 8)
where ks is the spring constant and the equilibrium position (x = 0) is the position of zero point of potential energy.
Question T5
The introduction to Section 2 claimed that we were free to choose any position of zero of potential energy since it was only the differences in potential energy which were significant. Look at the data in Tables 1, 3 and 4, which encompass two different choices of the zero for each of the two types of potential energy. What support for this claim can you find in these tables?
| Position | Gravitational potential energy Egrav |
Strain potential energy Estrain |
Total potential energy Epot |
|---|---|---|---|
| Fig. 4a - Fig 4b from Table 1 |
ks(xeq)2 | −ks(xeq)2/2 | ks(xeq)2/2 |
| Fig. 4a - Fig 4b from Table 3 |
ks(xeq)2 | −ks(xeq)2/2 | ks(xeq)2/2 |
| Fig. 4a - Fig 4b from Table 4 |
ks(xeq)2 | −ks(xeq)2/2 | ks(xeq)2/2 |
Answer T5
To test the claim we need to check that the differences in potential energy between the three positions shown in Figure 4 are the same for each of the two choices of zero of potential energy. Tables 1, 3 and 4 allow us to make this comparison for each of the two types of potential energy and also for the total potential energy. The comparison is easy to see when the differences are shown directly, as in Table 5. It is clear that the potential energy differences are independent of the choice of potential energy zero.
Study comment This subsection draws on the results of the general mathematical description of one–dimensional SHM – in particular, the expressions for the displacement, velocity and restoring forces. These equations are developed elsewhere in FLAP and if you are unfamiliar with the results you should review them now through the Glossary entries under simple harmonic motion.
2.4 Energy oscillations in SHM
The results of Subsections 2.1, 2.2 and 2.3 have all shown that the potential energy of a simple harmonic oscillator can be written in the form
Epot = ½kx2(9)
| Oscillator | k | x |
|---|---|---|
| pendulum | mg/L | displacement, s along the arc from the equilibrium position |
| sliding mass on a spring | ks | displacement from the unstretched position |
| suspended mass on a spring | ks | displacement from the equilibrium position |
provided we interpret k and x appropriately (see Table 2), and provided we take due care over the choice of the zero point of potential energy.
This common form for the potential energy of a simple harmonic oscillator given in Equation 9 is in fact quite general. It follows directly from the force law that characterizes one–dimensional SHM. SHM is generally characterized by a restoring force and an acceleration that is linearly proportional to the displacement from some stable position of equilibrium.
The implication of this is that for any one–dimensional SHM we may write
Fx = −kx(10)
and that this is consistent with the general relation between a conservative force and potential energy $\left(F_x = -\dfrac{dE_{\rm pot}}{dx}\right)$ which also yields Equation 9, where k is the general SHM force constant and x is the displacement from the equilibrium position, provided we choose Epot = 0 when x = 0.
Let us now move on to consider the kinetic energy and then the total energy of an oscillator in SHM. From Equation 1,
$E_{\rm kin} = \frac12 m\upsilon_x^2$(Eqn 1)
and we may write the general expression for the total energy of any one–dimensional simple harmonic oscillator
$E_{\rm tot} = E_{\rm kin}(x) + E_{\rm pot}(x) = \frac12 m\upsilon_x^2(x) + \frac12 kx^2$ i
Here we have recognized that both kinetic and potential energies vary with displacement x although the total energy should not vary with x, to be consistent with the conservation_of_mechanical_energyprinciple of energy conservation. Since x itself is an oscillatory quantity it must be a function of time, we can write:
$E_{\rm tot} = E_{\rm kin}(t) + E_{\rm pot}(t) = \frac12 m\upsilon_x^2(t) + \frac12 kx^2(t)$(11)
To take the discussion further we need to use the general expressions for x (t) and υx(t) in one–dimensional SHM.
These expressions are:
$x(t) = A\cos\left(\dfrac{2\pi t}{T} + \phi\right) = A\cos(\omega t+\phi)$(12) i
$\upsilon_x(t) = \dfrac{dx(t)}{dt} = -A\omega\sin(\omega t+\phi)$(13)
where A is the amplitude, ϕ the initial phase or phase constant, ω the angular frequency, T the period or periodic time and (ωt + ϕ) the phase.
Expressions for the acceleration and the force acting can be obtained by further differentiation and by Newton’s second law, respectively:
$a_x(t) = \dfrac{d\upsilon_x(t)}{dt}= \dfrac{d^2x(t)}{dt^2} = -A\omega^2\cos(\omega t+\phi) = -\omega^2x(t)$(14) i
andFx(t) = max(t) = −mω2x (t)(15) i
A comparison of Equation 15 with Equation 10,
Fx = −kx(Eqn 10)
identifies the force constant k with mω2 and so the angular frequency ω is determined by the force constant k and the mass m of the oscillating object:
$k = -\dfrac{F_x(t)}{x(t)} = m\omega^2$
so$\omega = \sqrt{\dfrac km}$(16)
and$T = \dfrac{2\pi}{\omega} = 2\pi \sqrt{\dfrac km}$(17)
It is important to note that Equations 12 to 17 are valid for any one–dimensional SHM, irrespective of the specific system, providing k is interpreted as the appropriate force constant – this ‘universality’ is the great power of the mathematical model.
Now we can return to our discussion of energy in SHM by using Equations 12 and 13,
$x(t) = A\cos\left(\dfrac{2\pi t}{T} + \phi\right) = A\cos(\omega t+\phi)$(Eqn 12)
$\upsilon_x(t) = \dfrac{dx(t)}{dt} = -A\omega\sin(\omega t+\phi)$(Eqn 13)
to eliminate x (t) and υx(t) from Equation 11,
$E_{\rm tot} = E_{\rm kin}(t) + E_{\rm pot}(t) = \frac12 m\upsilon_x^2(t) + \frac12 kx^2(t)$(Eqn 11)
We find:
$E_{\rm tot} = \frac12 m\left[-A\omega\sin(\omega t+\phi)\right]^2 + \frac12 k\left[A\cos(\omega t+\phi)\right]^2$
i.e.$E_{\rm tot} = \dfrac{A^2}{2}m\omega^2\sin^2(\omega t+\phi) + \dfrac{A^2}{2}k\cos^2(\omega t+\phi)$
in which we can identify the kinetic and potential energy expressions:
$E_{\rm kin} = \dfrac{A^2}{2}m\omega^2\sin^2(\omega t+\phi)$(18)
$E_{\rm pot} = \dfrac{A^2}{2}k\cos^2(\omega t+\phi)$(19)
The relationship between ω and k as given in Equation 16,
$\omega = \sqrt{\dfrac km}$(Eqn 16)
allows the total energy to be written in either of two equivalent forms:
$E_{\rm tot} = \dfrac{A^2}{2}m\omega^2\left[\sin^2(\omega t+\phi) + \cos^2(\omega t+\phi)\right] = \dfrac{A^2}{2}m\omega^2$(20a)
or$E_{\rm tot} = \dfrac{A^2}{2}k\left[\sin^2(\omega t+\phi) + \cos^2(\omega t+\phi)\right] = \dfrac{A^2}{2}k$(20b)
In Equations 20a and 20b we have used the trigonometric identity that sin2θ + cos2θ = 1 for any angle θ.
Study comment We can now draw some important conclusions from Equations 18, 19, 20a and 20b. This will be done via Questions T6 to T9. You should be sure you understand the answers to these questions before moving on.
Question T6
Are Equations 18, 19, 20a and 20b consistent with the principle of the conservation of energy in an isolated system?
Answer T6
According to Equations 20a and 20b,
$E_{\rm tot} = \dfrac{A^2}{2}m\omega^2\left[\sin^2(\omega t+\phi) + \cos^2(\omega t+\phi)\right] = \dfrac{A^2}{2}m\omega^2$(Eqn 20a)
$E_{\rm tot} = \dfrac{A^2}{2}k\left[\sin^2(\omega t+\phi) + \cos^2(\omega t+\phi)\right] = \dfrac{A^2}{2}k$(Eqn 20b)
the total energy is independent of time, so the total energy is constant and therefore consistent with the principle of energy conservation for an isolated system.
Question T7
For the special case where the phase constant is zero, draw graphs (on the same piece of graph paper) showing the behaviour of the kinetic, potential and total energies over two periods of the displacement. What is the period of any oscillations in these energies? Describe what is happening over the time interval.
Answer T7
When the phase constant is zero, the expressions for the kinetic and potential energies become
$E_{\rm kin} = \dfrac{A^2}{2}m\omega^2\sin^2(\omega t) = \left(E_{\rm kin}\right)_{\rm max}\sin^2(\omega t) = \frac12 \left(E_{\rm kin}\right)_{\rm max}\left[1-\cos(2\omega t)\right]$
and$E_{\rm pot} = \dfrac{A^2}{2}m\omega^2\cos^2(\omega t) = \left(E_{\rm pot}\right)_{\rm max}\cos^2(\omega t) = \frac12 \left(E_{\rm pot}\right)_{\rm max}\left[1+\cos(2\omega t)\right]$
where we have introduced
$\left(E_{\rm kin}\right)_{\rm max} = \dfrac{m\omega^2A^2}{2}\quad\text{and}\quad\left(E_{\rm pot}\right)_{\rm max} = \dfrac{kA^2}{2}$
and we have written sin2(ωt) and cos2(ωt) in terms of cos(2ωt) using the trigonometric identity
cos(2ωt) = 1 − 2 sin 2(ωt) = 2 cos2(ωt) − 1
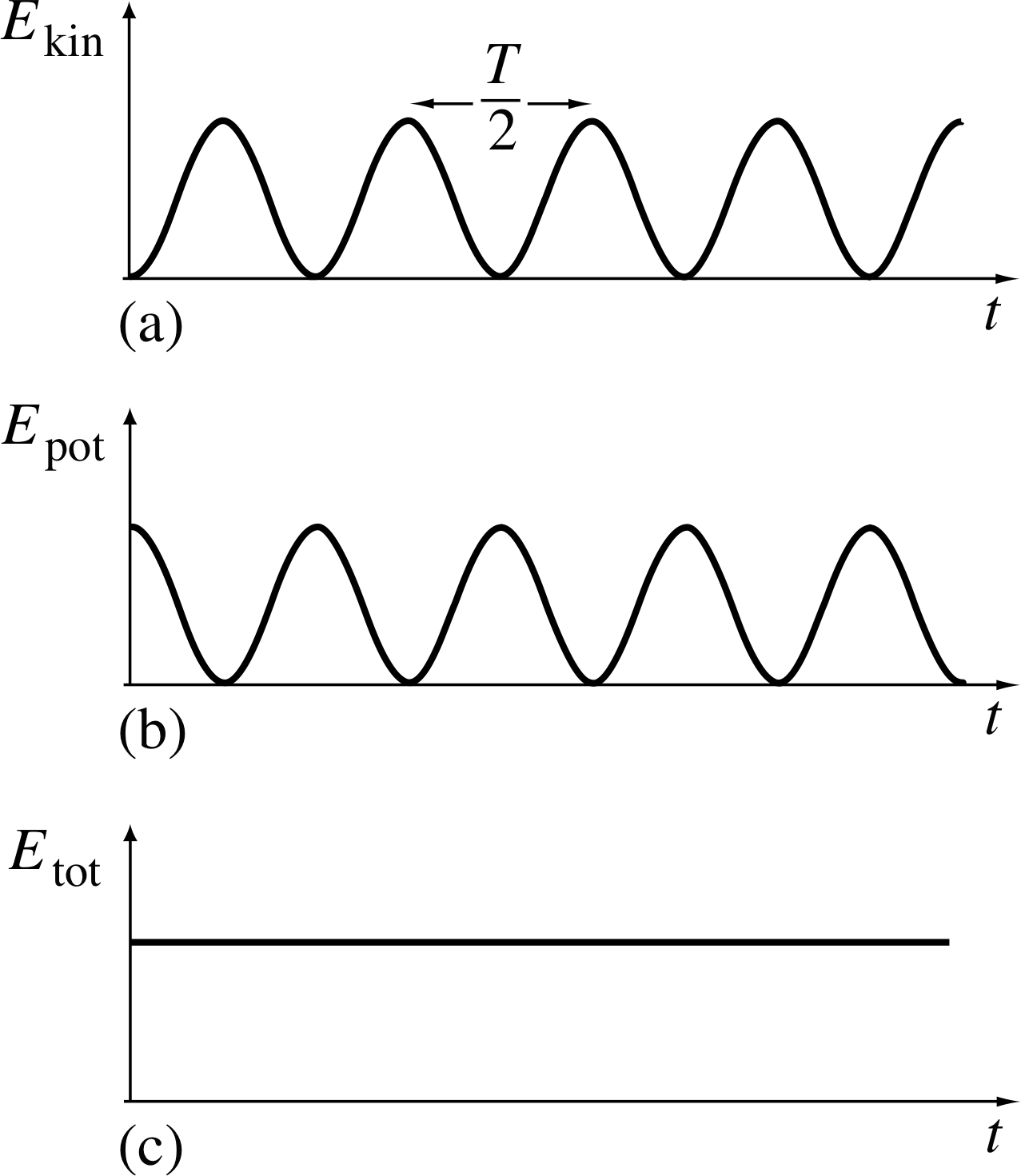
Figure 11 See Answer T7.
Both the kinetic energy Ekin and the potential energy Epot oscillate with time.
Since ω2 = k/m it is clear that the maximum values of Epot and Ekin are equal to each other but since the (sin2) function and the (cos2) function are out of phase they do not reach their maxima together, rather one lags the other by T/4.
Because the energies can both be expressed in terms of sin(2ωt) rather than sin(ωt) it follows that the oscillations in kinetic and potential energy have twice the frequency of the displacement oscillations.
In descriptive terms the energy is oscillating between being kinetic and potential at a frequency which is twice the frequency of the displacement. This doubling of the frequency is because in each cycle of the displacement there are two occasions when the kinetic energy reaches a maximum (passing through x = 0, travelling in either direction), and two occasions when the potential energy reaches a maximum (stationary at either extremity). Graphs of the kinetic and potential energy variations and the constant total energy are shown in Figure 11.
Question T8
By inspecting your answer to Question T7 determine the average values of each of Epot and Ekin over a full period of the oscillation.
Answer T8
The average value of each of the kinetic and potential energies is half the total energy; this must be so since their oscillations have equal amplitude and frequency and their sum is the total energy. The equations given in Answer T7,
$E_{\rm kin} = \dfrac{A^2}{2}m\omega^2\sin^2(\omega t) = \left(E_{\rm kin}\right)_{\rm max}\sin^2(\omega t) = \frac12 \left(E_{\rm kin}\right)_{\rm max}\left[1-\cos(2\omega t)\right]$
and$E_{\rm pot} = \dfrac{A^2}{2}m\omega^2\cos^2(\omega t) = \left(E_{\rm pot}\right)_{\rm max}\cos^2(\omega t) = \frac12 \left(E_{\rm pot}\right)_{\rm max}\left[1+\cos(2\omega t)\right]$
where
$\left(E_{\rm kin}\right)_{\rm max} = \dfrac{m\omega^2A^2}{2}\quad\text{and}\quad\left(E_{\rm pot}\right)_{\rm max} = \dfrac{kA^2}{2}$
confirm this and show that the average of each is kA2/4, while the total energy is kA2/2.
Question T9
Explain, in your own words, what factors determine the total energy in the oscillation; are these dependencies linear?
Answer T9
The total energy is determined by the amplitude (squared) and the force constant. You may have said that the energy was determined by the amplitude, mass and the angular frequency (squared) since Equation 20a,
$E_{\rm tot} = \dfrac{A^2}{2}m\omega^2\left[\sin^2(\omega t+\phi) + \cos^2(\omega t+\phi)\right] = \dfrac{A^2}{2}m\omega^2$(Eqn 20a)
involves all of these factors, but because the angular frequency itself involves the mass, the product of m and ω2 is independent of m. The relationship between energy and amplitude squared is of particular note; it is not linear.
3 Damped and driven harmonic oscillators
Our discussions in Section 2 have assumed that in SHM the amplitude is constant. From Equations 20a and 20b,
$E_{\rm tot} = \dfrac{A^2}{2}m\omega^2\left[\sin^2(\omega t+\phi) + \cos^2(\omega t+\phi)\right] = \dfrac{A^2}{2}m\omega^2$(Eqn 20a)
$E_{\rm tot} = \dfrac{A^2}{2}k\left[\sin^2(\omega t+\phi) + \cos^2(\omega t+\phi)\right] = \dfrac{A^2}{2}k$(Eqn 20b)
or from Answer T9 you will appreciate that it is the amplitude (together with the force constant) that determines the total energy in SHM. If the amplitude is constant the total energy is constant and vice versa. Now, the total energy is certainly constant if the oscillating system is completely isolated from its environment since no energy can then pass to or from the oscillator. In practice, however, this condition is never rigorously true for any oscillator; there is always some exchange of energy with the environment. In this section we will examine the consequences of such energy exchanges.
There are two situations in which changes in the energy of an oscillator are of particular importance.
The first arises when we deliberately put energy into the oscillator – this is the case of the driven oscillator or of forced vibrations, which will be discussed in Subsection 3.5. The second is where energy is transferred out of the oscillator i and the total energy of the oscillator (and hence its amplitude) decreases with time. This is the case of the damped oscillator and the process by which energy is transferred out of the oscillator is called damping; this will be discussed in Subsections 3.1 to 3.4. All natural oscillations are damped to some extent and there are many cases where we wish to change this damping artificially. For both these reasons, damping is an important topic.
3.1 The mechanisms of damping: friction
There are several mechanisms by which energy may be transferred away from a moving object. These mechanisms frequently involve frictional forces or, more succinctly, simply friction. Frictional forces act to prevent or reduce relative motion between two parts of a system and hence produce a reduction in kinetic energy. The origin of frictional forces is complex, involving intermolecular interactions between materials in close contact. Fortunately for our purpose here we need not understand the details of these processes, provided we appreciate the following characteristics of frictional forces:
- Frictional forces occur whenever there is relative motion between two surfaces or where there would be such motion if it were not being prevented by friction. The frictional forces are generally different in these two situations. When relative motion does occur it is said to be opposed by dynamic friction which is usually less than the static friction that acts to prevent relative motion. This difference explains why it is usually easier to keep something moving (thus overcoming dynamic friction) than it is to start the object moving in the first place (thus overcoming static friction). An example of dynamic friction would be the force that opposes the motion of a book sliding down a steeply inclined plane. An example of static friction would be the force that stops a book from sliding down an inclined plane when the angle of inclination is small.
- Frictional forces always act in a direction that opposes relative motion or the tendency to begin relative motion.
- In dynamic friction the general mechanism of the force is that momentum is exchanged between the surfaces or particles at the molecular level so that their relative velocity is reduced.
- The magnitude F of the dynamic frictional force often (but not always) depends on the relative speed υ. Sometimes this dependence can be approximated by a linear relationship:
F = bυ(21)
where b is a positive constant (known as the damping coefficient).
- The effect of dynamic friction is to reduce the relative motion and to convert the kinetic energy of directed motion into kinetic energy of random motion at the molecular level – that is, into heat energy.
In this section we are concerned with damping which is attributable to friction between the moving parts of a system – that is to dynamic friction. Within the general principles outlined above it is possible to identify several types of dynamic friction which may be involved in damped SHM:
- 1
-
Friction between two solid surfaces in relative motion. For example, a mass sliding on a surface as in our horizontal spring oscillator of Subsection 2.2. Equation 21 is not valid in such cases and the sliding friction is almost independent of the relative speed υ.
- 2
-
Friction between a moving solid and a liquid (or vice versa). For example, a ship rolling in a rough sea. Friction involving liquids (and sometimes gases) is often called viscosity and the forces involved are termed viscous forces. Equation 21 works quite well here.
- 3
-
Friction affecting solids or liquids moving through gases. For example, a swinging pendulum in air or a vehicle travelling through air. This is usually referred to as air friction or air resistance.
All of these processes result in the relative motion being reduced and heat being produced. Because the kinetic energy is dissipated by friction, frictional forces are often called dissipative forces.
3.2 Frictional forces as dissipative forces in mechanical SHM
The rate at which a damped oscillator loses energy depends on the nature of the damping force. As an example, let us consider the energy transferred from an object that oscillates along the x–axis while subject to a damping force that satisfies Equation 21,
F = bυ(Eqn 21)
that is, one where its magnitude is proportional to the instantaneous speed of the oscillator. i
✦ What is the x–component of such a damping force at a time when the x–component of the instantaneous velocity is υx?
✧ Fx = −bυx
Note that (unlike F and υ) Fx and υx may be positive or negative but they always have opposite signs, so Fx always opposes υx.
If we consider a very short interval of time, ∆t, we can assume that the instantaneous velocity is effectively constant throughout that interval, so the oscillator will change its position by an amount ∆x = υx ∆t and the energy transferred to the oscillator by the damping force will be
∆E = Fx ∆x
If we substitute for Fx and ∆x, we find
∆E = −bυxυx ∆t = −bυx2∆t(22)
In Equation 22 both b and υx2 are positive, so the energy transferred to the moving object must be negative. Thus the effect of the damping force is to reduce the energy of the oscillator, irrespective of its direction of motion. (Reversing the sign of υx does not change the sign of ∆E.)
The instantaneous rate at which energy is transferred to the oscillator by the damping force is obtained by rearranging Equation 22 to find ∆E/∆t and then considering the limit in which ∆t tends to zero. In terms of calculus notation this instantaneous rate is
$\displaystyle \dfrac{dE}{dt} = \lim_{\Delta t\rightarrow 0}\left(\dfrac{\Delta E}{\Delta t}\right) = -b\upsilon_x^2$(23)
Notice that dE/dt is also negative, as we would expect for a damping force that reduces the energy of the oscillator.
✦ At what stage in the oscillatory cycle is energy transferred most rapidly according to Equation 23?
✧ When υx2 is greatest, i.e. when the displacement from the equilibrium position is zero.
Of course, Equations 22 and 23 only apply to the particular case where the damping force is given by Fx = −bυx, but similar analyses can be applied to other cases.
Question T10
Suppose that a one–dimensional oscillator is subject to a damping force of constant magnitude.
(a)Write down an expression for the damping force.
(b) Find an expression for the instantaneous rate of energy transfer to the oscillator by this force.
(c) At what stage in the oscillation is energy transferred most rapidly because of the damping?
Answer T10
(a) The damping force has constant magnitude and points in a direction that opposes the instantaneous motion. Such a force may be represented by the expression
Fx = −b υx ≥ 0
Fx = b when υx ≤ 0
Alternatively, these may be combined into the single expression
Fx = −bυx /υ where υ = | υx |
(b) The energy transferred to the oscillator in a short time ∆t is
$\Delta E = F_x\Delta x = \dfrac{-b\upsilon_x}{\upsilon}\upsilon_x\Delta t = \dfrac{-b\upsilon_x^2}{\upsilon}\Delta t$
so$\displaystyle \dfrac{dE}{dt} = \lim_{\Delta t\rightarrow 0}{\left(\dfrac{\Delta E}{\Delta t}\right)} = \dfrac{-b\upsilon_x^2}{\upsilon}$
But υx2 = υ2, so this may be simplified to give
$\dfrac{dE}{dt} = -b\upsilon$ (which is always negative).
(c) The energy transfer is most rapid when the speed of the oscillator is greatest, i.e. when it passes through the equilibrium position x = 0.
3.3 Lightly damped harmonic motion
We now return to the case of a one–dimensional oscillator subject to a damping force Fx = −bυx, and consider the influence of the damping on the motion itself. Equation 23,
$\displaystyle \dfrac{dE}{dt} = \lim_{\Delta t\rightarrow 0}\left(\dfrac{\Delta E}{\Delta t}\right) = -b\upsilon_x^2$(23)
has already shown us that the energy of such an oscillator decreases continuously, and it follows from this that the amplitude of the oscillation must also decrease with time. What we now want to do is to develop a mathematical expression for x (t), the displacement of the oscillator as a function of time, which will (among other things) show us exactly how the amplitude diminishes as times passes.
The general solution to this problem involves some quite challenging mathematics. Instead of undertaking this task we will follow a simpler approach by assuming that the energy is transferred slowly, so that the total energy of the oscillator is almost constant over any one cycle even though it will change appreciably over many cycles. This amounts to assuming that the damping force is weak, so that the oscillator is certain to undergo many oscillations before the damping brings it to rest. Because of this limitation we can only claim to be dealing with the motion of the oscillator in the case of light damping. More will be said about the general case where the damping force may be strong or weak in the next subsection.
Since Equation 23 is true moment by moment, it must be the case that the average value of the right–hand side of Equation 23, taken over a full period of oscillation, is equal to the average value of the left–hand side taken over the same period. Thus, using angular brackets to indicate the mean:
$\left\langle\dfrac{dE}{dt}\right\rangle = \left\langle-b\upsilon_x^2\right\rangle$
but b is a constant and υx2 = 2Ekin/m, so
$\left\langle\dfrac{dE}{dt}\right\rangle = -b\left\langle\dfrac{2E_{\rm kin}}{m}\right\rangle = -\dfrac{2b}{m}\left\langle E_{\rm kin}\right\rangle$
Now, Subsection 2.4 and Question T8 have shown us that in SHM the average kinetic energy and the average potential energy over a full oscillation are each equal to half the total energy so, over a full oscillation it must still be the case that
$\left\langle E_{\rm kin}\right\rangle = \dfrac12\langle E\rangle$
Thus$\left\langle\dfrac{dE}{dt}\right\rangle = -\dfrac bm\langle E\rangle$
Now, if we introduce the light damping assumption so that the total energy only changes slowly with time, the average rate of change of energy will be equal to the rate of change of the average energy, i.e.
$\left\langle\dfrac{dE}{dt}\right\rangle = \dfrac{d\langle E\rangle}{dt}$
Moreover, if we represent the slowly varying average energy $\langle E\rangle$ by E (t) then we have
$\dfrac{dE(t)}{dt} = -\dfrac{bE(t)}{m} = -\gamma E(t)$(24) i
where the positive quantity b/m has been written as γ.
Study comment Equation 24 is an example of a differential equation. Such equations are the subject of a block of modules in the maths strand of FLAP. If you are already familiar with differential equations you will probably know how to solve Equation 24 and you will be able to consider the following question. If not, you should simply read the question and its answer, and pursue the topic of differential equations on some other occasion.
✦ Equation 24 tells us that the function E (t) is such that its rate of change is proportional to the instantaneous value of E (t) at any time t. What is the form of such a function?
✧ An exponential function has the required property. In fact the general solution to Equation 24,
$\dfrac{dE(t)}{dt} = -\dfrac{bE(t)}{m} = -\gamma E(t)$(Eqn 24)
may be written
E (t) = E0e−γt i
where E0 is a constant and e represents the mathematical constant that has the value 2.718 to three decimal places.

Figure 5 Graphs of E (t) = E0e−γt for different values of the damping constant γ. (γ1 > γ2)
Graphs of E (t) = E0e−γt for two different values of γ are shown in Figure 5. It is apparent that the larger value of γ corresponds to a more rapidly decaying average energy for the oscillator. The coefficient γ = b/m is called the damping constant of the oscillator. Over any time interval of duration 1/γ the value of E (t) changes by a factor of e−1 (from e−γt to e−γ (t+1/γ) = e−1e−γt).
Thus, γ determines the rate of exponential decay of the average energy. The time required for any exponentially decaying quantity to decrease by a factor of e−1 is known as the time constant of the decay, so in our example the time constant is 1/γ and we may write
E (t) = E0e−γt = E0e−γ/τ(25)
where τ = 1/γ represents the time constant.
Question T11
Confirm that the function E (t) = E0e−γt satisfies Equation 24,
$\dfrac{dE(t)}{dt} = -\dfrac{bE(t)}{m} = -\gamma E(t)$(Eqn 24)
and explain the physical significance of the constant E0.
(If you are familiar with the process of differentiation you can use it to show that Equation 25 provides a solution to Equation 24. If not, you should add arbitrary scales to Figure 5, select a point on one of the curves, determine the gradient of the curve at that point (this corresponds to dE/dt at that point) and then confirm that at that particular point dE/dt = −γE (t)).
Answer T11
If we substitute E (t) = E0e−γt into Equation 24,
$\dfrac{dE(t)}{dt} = -\dfrac{bE(t)}{m} = -\gamma E(t)$(Eqn 24)
we find
$\dfrac{dE(t)}{dt} = -\dfrac{d}{dt}\left(E_0{\rm e}^{-\gamma t}\right) = -\gamma E(t)$
as required for a solution. The same conclusion may also be reached graphically. E0 is the value of E at t = 0, i.e. it is the initial energy.
Question T12
For damped one–dimensional harmonic motion, write down expressions for (a) the damping constant for the energy and (b) the time constant of the energy decay, in terms of the damping coefficient b and the oscillator mass m.
Answer T12
(a) The damping constant γ is defined to be b/m and (b) the time constant of the energy decay τ is defined in Equation 25,
E (t) = E0e−γt = E0e−t/τ(Eqn 25)
as τ = 1/γ = m/b.
Question T13
Use the SHM relationship between total energy and amplitude to derive expressions for (a) the amplitude A (t) and (b) the time constant of the amplitude decay, in terms of the damping coefficient b and the oscillator mass m.
Answer T13
Either Equations 20a and 20b,
$E_{\rm tot} = \dfrac{A^2}{2}m\omega^2\left[\sin^2(\omega t+\phi) + \cos^2(\omega t+\phi)\right] = \dfrac{A^2}{2}m\omega^2$(Eqn 20a)
$E_{\rm tot} = \dfrac{A^2}{2}k\left[\sin^2(\omega t+\phi) + \cos^2(\omega t+\phi)\right] = \dfrac{A^2}{2}k$(Eqn 20b)
or Answer T8 gives the relationship between energy and amplitude as kA2/2. Substituting E0 = kA2/2 into Equation 29,
E (t) = E0exp(−γt) = E0exp(−ω0t/Q)(Eqn 29)
gives us $E(t) = E_0\exp(-\gamma t) = \frac12 k\left[A(t)\right]^2$
which leads to A (t) = A0 exp(−γt/2) when we take the positive square root. The time constant of the amplitude decay τA is defined by A (t) = A0 exp(−t/τA) and τA is thus 2/γ, which is twice the time constant for the energy decay τ = 1/γ as in Answer T12. τA = 2/γ = 2m/b in terms of b/m.
Question T14
In Question T13 you derived an expression for A (t). Use this result as the amplitude in Equation 12,
$x(t) = A\cos\left(\dfrac{2\pi t}{T} + \phi\right) = A\cos(\omega t+\phi)$(Eqn 12)
to write down an expression for x (t) for damped one–dimensional SHM. Sketch the graph of this function.

Figure 12 See Answer T14.
Answer T14
If we substitute the expression A (t) = A0 exp(−γt/2) into Equation 12,
$x(t) = A\cos(\omega t+\phi)$(Eqn 12)
we find:
x (t) = A0 exp(−γt/2) cos(ωt + ϕ)
The graph of this expression (for the displacement in lightly damped SHM) is shown in Figure 12. The dashed line represents the line exp(−γt/2).
Study comment The rigorous mathematical treatment of damped harmonic motion shows that the introduction of damping, even light damping, modifies the angular frequency of the motion as well as its amplitude. The changes for light damping are very small so we will continue to use the values of angular frequency and period that pertain in the undamped situation, but in recognition of this we will henceforth denote the undamped angular frequency by ω0 and use T0 to represent the corresponding period (ω02 = k/m and T0 = 2π/ω0). You should not forget that in the case of damped harmonic motion, ω0 and T0 are only approximations to the true angular frequency and period.
In the case of damped harmonic motion, the natural logarithm of the ratio of two successive maximum displacements (i.e. one period apart) is known as the logarithmic decrement of the decay. Question T13 shows that the damping constant for the amplitude is half that for the energy, since E (t) ∝ A2(t). This gives the damping constant for the amplitude as γ/2 and it follows that
logarithmic decrement = $\loge \left[exp\left(\dfrac{\gamma T_0}{2}\right)\right] = \dfrac12\gamma T_0 = \dfrac{\pi\gamma}{\omega_0}$(26) i
The case of light damping applies well to the important class of applications where engineers seek to minimize the natural damping of an oscillator in order to prolong its natural oscillation or to minimize the energy input needed to maintain the oscillations – a pendulum clock, for example. In such cases, the quality of the oscillator is determined by the fraction of its energy which is lost per cycle of the displacement (remember from Question T7 that one displacement cycle corresponds to two cycles of the energy oscillation). The larger this fraction, the poorer the performance of the oscillator, so its reciprocal can be taken as a ‘figure of merit’ for the oscillator. This inverted fraction, when multiplied by 2π, is known as the quality factor or Q–factor of the oscillator.
So,$Q = \dfrac{2\pi E(t)}{\left\lvert\,(\Delta E)_T\,\right\rvert}$(27) i
where E (t) is the average energy at time t and | (∆E)T | is the energy transferred from the oscillator in one complete oscillation at time t. i
A very lightly damped oscillator has a Q ≪ 1, while a more severely damped oscillator has a Q of order 1. An oscillator with a large Q–factor damps slowly and oscillations are maintained for many periods. A high Q–factor mechanical oscillator, such as a tuning fork, might have a Q–factor of several thousand.
Now, according to Equation 24,
$\dfrac{dE(t)}{dt} = -\dfrac{bE(t)}{m} = -\gamma E(t)$(Eqn 24)
the average rate of energy transfer from the lightly damped oscillator is dE (t)/dt = −γE (t), so the energy transferred from the lightly damped oscillator over one period of duration T0 is
$\left\lvert\,(\Delta E)_T\,\right\rvert = T_0 \left\lvert\,\dfrac{dE(t)}{dt}\,\right\rvert = T_0\gamma E(t) = \dfrac{2\pi\gamma}{\omega_0}E(t)$
so$Q = \dfrac{2\pi E(t)}{\left\lvert\,(\Delta E)_T\,\right\rvert} = \dfrac{2\pi}{\gamma T_0} = \dfrac{\omega_0}{\gamma}$(28)
We can now summarize our results as follows
In lightly damped harmonic motion
E (t) = E0exp(−γt) = E0exp(−ω0t/Q)(29)
A (t) = A0exp(−γt/2) = A0exp(−ωt/(2Q))(30)
andx (t) = A0exp(−γt/2) cos(ωt + ϕ) = A0exp(−ωt/(2Q)) cos(ωt + ϕ)(31)
Question T15
By what factor does the energy of a damped oscillator decrease in Q cycles?
Answer T15
The expression for the decaying energy in the damped oscillator is given in Equation 29 as
E (t) = E0exp(−γt) = E0exp(−ω0t/Q)(Eqn 29)
Each cycle takes a time t = 2π/ω0, so Q cycles take a time t = 2πQ/ω0. If we substitute this time in the expression for the energy we find
$E(t) = E_0\exp\left(\dfrac{-\omega_0}{Q}\dfrac{2\pi Q}{\omega_0}\right) = E_0{\rm e}^{-2\pi}$
After Q cycles the energy is reduced by a factor of about 2 × 10−3. More memorably, after Q/2π oscillations, the energy is reduced by a factor e−1.
We see from Answer T15 that when a high Q–factor oscillator is excited it completes Q/2π cycles before its energy has fallen by a factor of 1/e. If we call this time the ringing time then Q is 2π × the ringing time of the oscillator, expressed in periods.
3.4 Qualitative discussion of general damping
When the damping can no longer be considered to be light, the mathematics becomes quite complicated. This topic is dealt with elsewhere in FLAP. i Here, we will describe the results qualitatively, so that you can identify and describe the types of behaviour that damped oscillators exhibit.
We have already covered light damping quantitatively in this module. In that discussion we were able to use the undamped angular frequency ω0 as an approximation to the angular frequency of the damped motion. The full mathematical treatment shows that the angular frequency ω of the damped motion is slightly different from ω0, but not significantly so in the case of light damping. However, as the damping is increased this approximation begins to break down, and we need to distinguish between ω and ω0.

Figure 6 The effect of different damping levels on the one–dimensional oscillator: (a) underdamped, (b) overdamped, (c) heavily overdamped, (d) critically damped.
As the damping is increased progressively, fewer and fewer oscillations are completed before the oscillator comes to rest; the various forms of behaviour that might arise are shown in Figure 6. The most familiar is illustrated by curve (a) and is generally known as underdamping; light damping is an extreme case of this. If we increase the damping beyond a certain level we eventually find the behaviour indicated by curve (b) in which the oscillator fails to complete even a single full oscillation. It may overshoot the equilibrium position once only, after which its displacement decays exponentially as it returns to the equilibrium position. This situation is generally known as overdamping. i
If we continue to increase the damping further we reach an extreme case of heavy overdamping (curve (c)) in which the system does not pass through the equilibrium position at all, but decays exponentially and very slowly back to the equilibrium position. The situation between underdamping (curve (a)) and overdamping (curve (b)) is called critical damping and is shown in curve (d). In the case of critical damping, the damping force has the minimum value that will avoid an oscillation and, after one overshoot, the displacement decays exponentially to reach the stable equilibrium position in the shortest overall time. This condition of critical damping is the one sought by designers of electrical meters and shock–absorbers.
3.5 Qualitative discussion of forced vibrations: resonance
If the oscillations of a damped oscillator are to be maintained at a constant level then we must apply an external force which will, on average, transfer energy to the oscillator at the same rate that energy is transferred into heat by friction. This external force is called a driving force and the oscillator is then a driven oscillator. In this subsection we present a qualitative treatment of this problem; the quantitative treatment is covered elsewhere in FLAP. i
A familiar example of a driving force is the force that every child learns to apply to a swing to establish and maintain its motion. If we ask how best to apply this driving force in order to minimize effort and maximize the amplitude then, as every child discovers, the answer is that the force should be applied periodically and should be timed to coincide closely with the natural motion of the swing. In other words, a driven oscillator responds most strongly when driven by a periodically varying force, the frequency of which is closely matched to the frequency with which the system would freely oscillate if left to itself. This frequency is called the natural frequency of the oscillator.
A one–dimensional oscillator of mass m and force constant k, has a natural frequency $\omega_0 = \sqrt{k/m}$. It can be shown that this system, when subject to a damping force Fx = −bυx and a periodic driving force Fx = F0 sin(Ωt), will eventually exhibit displacement oscillations described by
x (t) = A0 sin(Ωt + ϕ)(32)
where$A_0 = \dfrac{F_0/m}{\sqrt{\smash[b]{(\omega_0^2-\Omega^2)^2+(\gamma\Omega)^2}}} \quad\text{and}\quad\phi = \arctan{\dfrac{-\gamma\Omega}{\omega_0^2-\Omega^2}}$
Note that the angular frequency of these steady oscillations is determined by the angular frequency of the driving force and not by the natural frequency of the oscillator. Also note that the amplitude of the driven oscillations A0 is independent of time but does depend on the amplitude and angular frequency of the driving force. In particular, the amplitude will be large when Ω ≈ ω0.
(It can be shown that the maximum value of A0 actually occurs when Ω2 = ω02 − γ2/2).
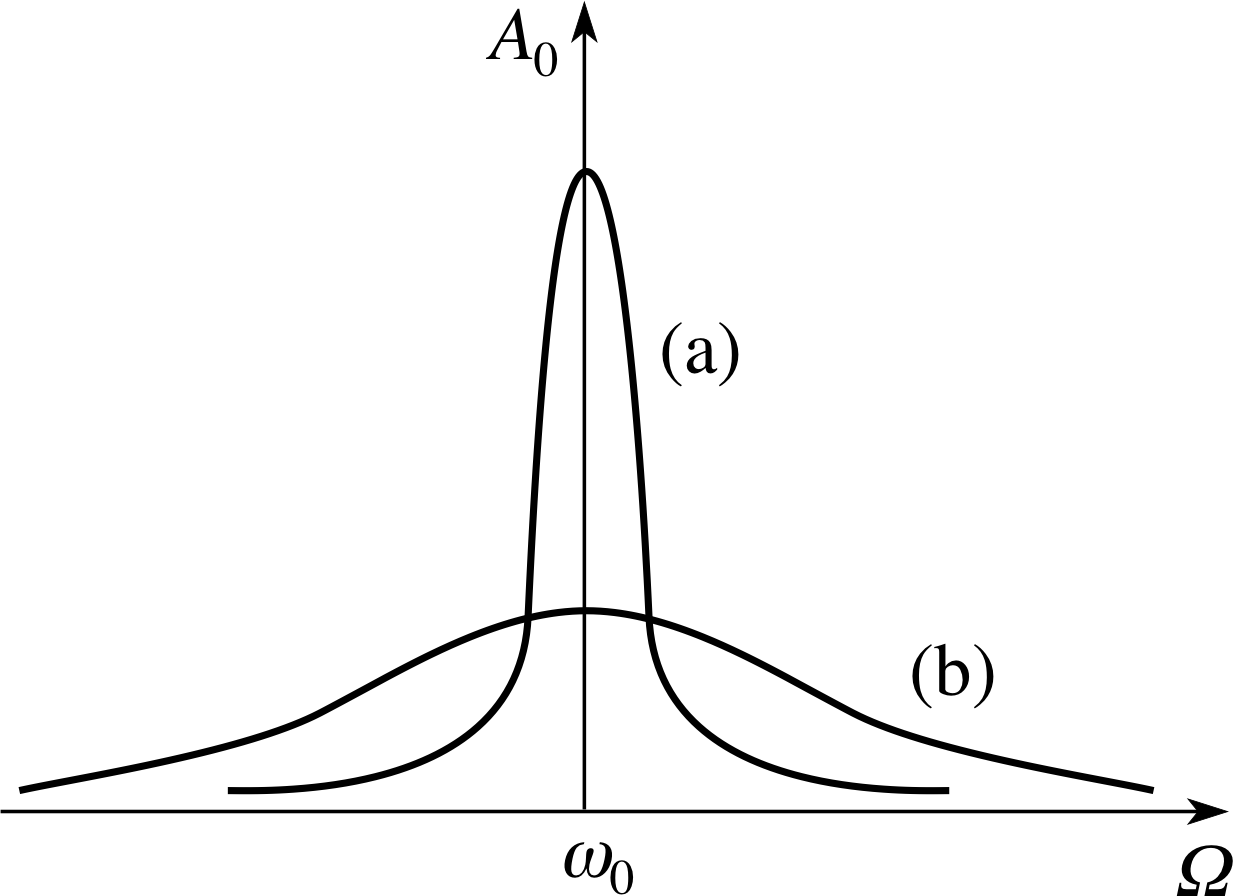
Figure 7 The resonant response of a driven damped oscillator under two levels of damping. (a) The steady state amplitude established in a high Q–factor oscillator with very small γ, (b) the steady state response in a low Q–factor oscillator with larger γ. The effect of γ on the resonant frequency has been ignored in this graph.
The eventual steady amplitude of the driven oscillator for a range of driving frequencies is shown in Figure 7. There are two curves in the figure, corresponding to different values of the damping constant γ. As you can see, although the location of the peak is mainly determined by ω0, the height and width of the peak both depend on γ. The role of γ in determining the amplitude is not surprising. Most damping losses increase with the speed of the oscillator and so the dissipative losses rise as the oscillation amplitude grows. With any given driving force applied, the oscillation amplitude will grow until the energy transferred from the oscillator by the damping force exactly balances the energy transferred to the oscillator by the driving force. Steady oscillation conditions are then established.
The condition in which an oscillator responds with maximum amplitude to a periodic driving force is called resonance. For a lightly damped oscillator this condition occurs when the angular frequency of the driving force is close to but slightly less than the natural frequency of the oscillator and corresponds to the state of affairs in which the energy transferred to the oscillator by the driving force is a maximum.
If we refer back to Equation 32,
x (t) = A0 sin(Ωt + ϕ)(Eqn 32)
you will see that there is a phase difference ϕ between the displacement oscillation and the driving force.
✦ What is the value of ϕ when the resonance condition is satisfied?
✧ In resonance Ω2 = ω02 − γ2/2, so
$\phi \approx \arctan\left(\dfrac{\gamma\omega_0}{\gamma^2/2}\right) = \arctan\left(\dfrac{2\omega_0}{\gamma}\right)$
For a small value of γ the value of 2ω0/γ will be large and so
arctan(2ω0/γ ) ≈ 90°
So, in resonance, in the steady condition, the displacement of a lightly damped oscillator lags 90° behind the driving force. You may find it surprising that the displacement is not in phase with the driving force, but you saw in Subsection 3.2 that the power transferred to an oscillator depends on the velocity of the oscillator, not its displacement. A phase lag of 90° between the driving force and the displacement ensures that the driving force is in phase with the oscillator’s velocity rather than displacement.
Thus a given force gives the oscillating mass its greatest rate of transfer of energy (i.e. power) just when its speed is greatest. This is exactly the principle most children learn to apply when pushing a swing.
There are many important illustrations and applications of resonance. Mechanical resonance plays a crucial role in many pieces of machinery, such as when one part of a machine vibrates and drives another part into vibration. If the driven part is underdamped, the resonant response can build up a very large amplitude, which might end in the destruction of the machine. The suspension bridge across the Tacoma Narrows on the western coast of the USA was driven into resonance by unusually violent winds in 1940; it was destroyed. A similar incident took place in 1850 at Angers (in France) where the marching of about 500 soldiers across a bridge resonantly excited the structure, with the resultant death of more than 200 soldiers.
Perhaps some of the most important applications of resonance occur in electrical_oscillatorelectrical oscillations. i Electrons are charged particles and electrical forces can be exerted on them by electric fields. In an electrical conductor some electrons are free to move and this motion can constitute an electric current. In an circuitelectrical circuit, electrical energy can be stored as potential energy, by electrons in electric fields, or associated with the kinetic energy of the moving electrons, through the magnetic field caused by the electric current. Electrical energy oscillations can be produced by the action of electric or magnetic fields on the electrons in a conductor. A good example of this process is when the oscillating electric and magnetic fields associated with an electromagnetic wave (such as a radio wave or a light wave) interact with electrons in a circuit. An electrical oscillator has a natural frequency and a resonant response when driven at this frequency. The driving force for an electrical oscillator can be provided by the currents from an aerial. At the circuit’s resonant frequency large oscillatory currents may be produced, and these can easily be detected. We have described here a radio or TV receiver, which must be set or tuned to the required resonant frequency.
A surprising example of electrical resonance is the response of the electrons in an atom to an incoming light wave. At some characteristic resonant frequencies (or wavelengths of light) these electrons respond strongly, absorbing the light. This is why materials absorb some colours of light but not others.
Resonance is an extremely widespread and important topic in physics. Although we have been concerned with mechanical oscillators in this module it is important to remember the wide applicability of all the ideas discussed here.
4 Closing items
4.1 Module summary
- 1
-
In simple harmonic motion, the displacement of an oscillator may be described by the sinusoidal function x (t) = A cos(ωt + ϕ) where A is the amplitude, ϕ is the phase constant, and the angular frequency ω is given by $\omega = \sqrt{k/m}$, where k is the force constant and m the mass. The period of such an oscillator is
$T = \dfrac{2\pi}{\omega} = 2\pi \sqrt{\dfrac km}$(Eqn 17)
- 2
-
Kinetic energy and potential energy are associated with SHM. In one–dimensional mechanical oscillators the kinetic energy ½mυx2 is associated with a moving mass and the potential energy ½kx2 with gravitational or Subsection 2.2strain energy. The zero of strain energy is best taken where the elastic body is un-deformed, the zero of gravitational energy should be chosen to simplify the problem.
- 3
-
In undamped SHM the kinetic energy and potential energy each oscillate with time at a frequency which is twice that of the displacement oscillation, but the sum of kinetic and potential energy, the Subsection 2.3total energy, remains constant.
- 4
-
The average values for kinetic energy and potential energy over one cycle of undamped SHM are each equal to half the total energy – which is itself determined by the square of the amplitude through the expression:
$E_{\rm tot} = \dfrac{A^2}{2}k = \dfrac{A^2}{2}m\omega$(Eqn 20)
- 5
-
When Section 3dissipative forces, such as friction, are present the energy of an oscillator is gradually transferred to the environment, often as heat, and the amplitude falls with time. The oscillator is then said to be Subsection 3.1damped.
- 6
-
Frictional forces often depend on the relative motion and oppose this motion; in some cases their magnitude is linearly proportional to the relative speed and then the power loss from the damped oscillator is proportional to the square of this speed.
- 7
-
In light damping the oscillation takes many cycles to damp away and, to a good approximation, the motion remains periodic with the undamped frequency. The energy decays exponentially with a damping constant γ given by
E (t) = E0exp(−γt)(Eqn 29)
where γ = b/m (and b is a positive constant). The amplitude also decays exponentially, as given by
A (t) = A0exp(−γt/2)(Eqn 30)
and the displacement is given by
x (t) = A0exp(−γt/2) cos(ωt + ϕ)(Eqn 31)
- 8
-
The degree of damping is indicated by the Q-factor of the oscillator, which is 2π times the reciprocal of the fractional energy loss per cycle
$Q = \dfrac{2\pi E(t)}{\left\lvert\,(\Delta E)_T\,\right\rvert}$(Eqn 27)
For a lightly damped oscillator Q = ω0/γ and oscillations take many cycles to decay away.
- 9
-
In general, three levels of damping can be identified. Underdamping, when the oscillator completes several oscillations before being damped to rest. Overdamping when the displacement is no longer periodic but decays exponentially, or where it may overshoot the equilibrium position once, before decaying exponentially to the equilibrium position. Critical damping, when the displacement decays to rest without oscillatory behaviour but does so in the minimum time, passing through the equilibrium position no more than once.
- 10
-
When a damped oscillator is subject to a periodic external driving force at or near to its natural undamped frequency it exhibits resonance. In resonant behaviour the amplitude builds up to a high value, until the power lost through dissipative forces equals the power input from the driving force. The amplitude at resonance and the sharpness of the response near ω0 are each determined by the damping constant γ (or the Q–factor), and with low damping (high Q–factor) this amplitude can be very large and the response very sharp. Resonance is an important and widespread process in physics and engineering.
4.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Account for and describe, qualitatively, the oscillations of kinetic and potential energy in undamped one–dimensional SHM, and explain why the total energy is constant.
- A3
-
Derive and use expressions for the kinetic, potential and total energies in undamped one–dimensional SHM, from an expression for the displacement as a function of time. Show how the total energy depends on the amplitude.
- A4
-
Sketch the variations in kinetic and potential energy in undamped one–dimensional SHM and identify their average values over one oscillation.
- A5
-
Describe the operation of frictional forces and their qualitative effect on one–dimensional harmonic motion.
- A6
-
Describe the motion of lightly damped one–dimensional harmonic motion in terms of an energy–time graph, an amplitude–time graph and a displacement–time graph.
- A7
-
Use the approximation of light damping, with a damping force which is proportional to the velocity, to derive expressions for the energy and displacement in one–dimensional harmonic motion.
- A8
-
Describe and identify the general behaviour of damped one–dimensional harmonic motion when conditions are no longer those of light damping.
- A9
-
Describe the process of driving and resonance in harmonic motion, explaining its significance and its dependence on the damping constant or the Q–factor.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
4.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions each of which tests one or more of the Achievements.

Figure 4 A light coil spring shown (a) unloaded (with a supported mass held at the unstretched spring position), (b) at the position of equilibrium under the load, and (c) loaded and displaced below its position of equilibrium. Note that x is taken to be positive in the downward direction.
| Position | Gravitational potential energy Egrav |
Strain potential energy Estrain |
Total potential energy Epot |
|---|---|---|---|
| As in Figure 4a | mgxeq = ks(xeq)2 | 0 | ks(xeq)2 |
| As in Figure 4b | 0 | ks(xeq)2/2 | ks(xeq)2/2 |
| As in Figure 4c | −mgx = −ksxeqx | ks(xeq + x)2/2 | ks(xeq)2/2 + ksx2/2 |
Question E1 (A2)
For the system shown in Figure 4, construct a table such as Table 1 but with the gravitational potential energy and the strain potential energy both zero at the equilibrium position.
Answer E1
| Position | Gravitational potential energy Egrav |
Strain potential energy Estrain |
Total potential energy Epot |
|---|---|---|---|
| As in Figure 4a | mgxeq = ks(xeq)2 | −ks(xeq)2/2 | ks(xeq)2/2 |
| As in Figure 4b | 0 | 0 | 0 |
| As in Figure 4c | −mgx = −ksxeqx | ks[(xeq + x)2−(xeq)2]/2 | ksx2/2 |
Your table should look like Table 6.
The gravitational potential energy is positive in Figure 4a and negative in Figure 4c (below the zero potential height of Figure 4b). The strain energies are those shown in Table 4 of Answer T4 for the reasons given there. The sum of the two potential energies appears in the final column.
(Reread Subsection 2.3 if you had difficulty with this question.)
Question E2 (A3 and A4)
Show that in a one–dimensional SHM the kinetic energy, potential energy and the total energy all depend on the square of the amplitude. Sketch each of these energies over one cycle of the displacement oscillation and give their average values over this interval.

Figure 11 See Answer E2.
Answer E2
The arguments are given in Subsection 2.4 and are expressed in Equations 20a and 20b,
$E_{\rm tot} = \dfrac{A^2}{2}m\omega^2\left[\sin^2(\omega t+\phi) + \cos^2(\omega t+\phi)\right] = \dfrac{A^2}{2}m\omega^2$(Eqn 20a)
$E_{\rm tot} = \dfrac{A^2}{2}k\left[\sin^2(\omega t+\phi) + \cos^2(\omega t+\phi)\right] = \dfrac{A^2}{2}k$(Eqn 20b)
Also see Answer T7 and Figure 11.
Question E3 (A5 and A6)
Describe the motion of a lightly damped oscillator, and explain why its total energy is not conserved.
Answer E3
The motion is oscillatory and, in the approximation of light damping, the frequency is unchanged from the undamped case. The amplitude decays exponentially with time as
A (t) = A0exp(−γt/2) = A0exp(−bt/2m) = A0exp(−ω0t/2Q)
Energy is transferred because the system is affected by dissipative forces. Such forces depend on the velocity rather than the displacement, and always oppose the motion.
(Reread Subsection 3.1 if you had difficulty with this question.)
Question E4 (A5)
A body of mass 0.30 kg is suspended from the end of a spring with a spring constant of 120 N m−1. When oscillating, it is subject to a damping force that varies in proportion to the velocity, with constant of proportionality −b = −0.60 N s m−1.
Calculate the damping constant, logarithmic decrement and Q–factor of the system.
Answer E4
The damping constant is given by Equation 24,
$\dfrac{dE(t)}{dt} = -\dfrac{bE(t)}{m} = -\gamma E(t)$(Eqn 24)
as γ = b/m; the logarithmic decrement is given by Equation 26,
logarithmic decrement = $\loge \left[exp\left(\dfrac{\gamma T_0}{2}\right)\right] = \dfrac12\gamma T_0 = \dfrac{\pi\gamma}{\omega_0}$(Eqn 26)
as πω0/γ; Q is given by Equation 28,
$Q = \dfrac{2\pi E(t)}{\left\lvert\,(\Delta E)_T\,\right\rvert} = \dfrac{2\pi}{\gamma T_0} = \dfrac{\omega_0}{\gamma}$(Eqn 28)
as ω0/γ.
The numerical values for k, b and m give:
$\omega_0 = \sqrt{\dfrac km} = \rm \sqrt{\dfrac{120\,N\,m^{-1}}{0.30\,kg}} = 20\,s^{-1}$
$\gamma = \dfrac bm = \rm \dfrac{0.60\,N\,s\,m^{-1}}{0.30\,kg} = \dfrac{0.60\,m\,s^{-2}\,m^{-1}}{0.30\,kg} = 2\,s{-1}$
the logarithmic decrement = $\dfrac{\pi\gamma}{\omega_0} = \dfrac{2\pi\,{\rm s^{-1}}}{20\,{\rm s^{-1}}} = \dfrac{10}{\pi} = 0.31$
(Reread Subsection 3.3 if you had difficulty with this question.)
Question E5 (A7)
A lightly damped oscillator with undamped angular frequency 16 s−1 is set in motion by releasing it from rest at a displacement of 0.10 m from its equilibrium position. It is found that the turning point at the end of the first cycle has a displacement of 0.08 m. What are the logarithmic decrement, damping constant and Q–factor of the system? Estimate the amplitude of the oscillation after five cycles.
Answer E5
We have ω0 = 16 s−1; A0 = 0.10 m. The logarithmic decrement is the natural logarithm of two successive maximum displacements:
the logarithmic decrement = $\rm \loge\left(\dfrac{0.10\,m}{0.08\,m}\right) = 0.22$
also, the logarithmic decrement = $\dfrac{\pi\gamma}{\omega_0} = 0. 22$
so the damping constant γ is:
$\gamma = \dfrac{0.22\omega_0}{\pi} = 0.07\omega_0 = \rm 0.07\times16\,s^{-1} = 1.12\,s^{-1}$
The Q–factor is given by
$Q = \dfrac{\omega_0}{\gamma} = \rm \dfrac{16\,s^{-1}}{1.12\,s^{-1}} = 14$
After five cycles t = 5 × 2π/ω0 = (10π/16) s. Equation 30,
A (t) = A0exp(−γt/2) = A0exp(−ω0t/(2Q))(Eqn 30)
gives A (t) as:
$A(t) = A_0\exp(-\gamma t) = A_0\exp\left(\dfrac{-1.12\times10\pi}{32}\right) = [0.10\exp(-0.35\pi)]\,{\rm m} = 0.033\,{\rm m}$
(Reread Subsection 3.3 if you had difficulty with this question.)
Question E6 (A8)
For one–dimensional damped harmonic motion explain what is meant by (a) underdamped, (b) overdamped, and (c) critically damped, explaining how these conditions might be established.

Figure 6 The effect of different damping levels on the one–dimensional oscillator: (a) underdamped, (b) overdamped, (c) heavily overdamped, (d) critically damped.
Answer E6
In (a) the underdamped case, the displacement completes at least one full oscillation before coming to rest at the equilibrium position.
In (b) the overdamped case, the displacement does not complete one full oscillation but may pass through the equilibrium position once only, before decaying exponentially back to the equilibrium position.
In (c) the critically damped case, the displacement does not complete one full oscillation but may pass through the equilibrium position once only, before decaying exponentially back to the equilibrium position in the shortest overall time.
See Subsection 3.4 and Figure 6. The different x levels of damping can be established by changing the frictional damping.
(Reread Subsection 3.4 if you had difficulty with this question.)
Question E7 (A9)
Describe the process of resonance in SHM and its significance. Describe qualitatively how resonant behaviour depends on the level of damping.
Answer E7
Resonance is when an underdamped oscillatory system responds maximally to a periodic driving force. When the frequency of the driving force approaches the natural frequency of the undamped system the amplitude response of the system becomes very large. The resonant amplitude response and the width of the resonance are controlled by the level of damping; as the damping is reduced the amplitude increases and the width decreases. Resonance is a very important feature of many mechanical, electrical and atomic systems.
(Reread Subsection 3.5 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 4Closing items.