PHYS 5.3: Forced vibrations and resonance |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
In order to sustain vibrations, energy must be supplied to a system to make up for the energy transferred out of the vibrating system due to dissipative forces or damping. The resulting vibrations are called forced vibrations. In a clock or watch, the ‘pushes’ that maintain the vibrations are applied at the frequency at which the pendulum or balance wheel normally vibrates, i.e. at its natural frequency. Pushing at the natural frequency is the most efficient way to transfer energy into a vibrating system, as your childhood experiences on a swing should confirm.
In Section 2 the equation of motion for the linearly damped oscillator is developed, both for an undriven oscillator and in the presence of a harmonic driving force. We examine the steady state motion of this latter system as the amplitude and frequency of the driving force is varied, considering the low and high frequency response and the resonance response. We then look at the energy balance in the steady state system, considering the kinetic, potential and total energies. The transient motion is distinguished from the steady state motion and examined briefly. Other mechanical and non–mechanical cases of driven oscillators are considered and the application of the principle of resonance absorption in clocks and frequency standards is discussed. The cases of quartz crystal oscillators, the caesium atomic clock and the potential use of frequency-stabilized lasers are considered briefly.
In Section 3 we look at the related situation where the exciting force is due to another oscillator and consider how two coupled oscillators interact. The important idea of normal modes is introduced, along with the idea of beats between these modes.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 5.1Module summary and the Subsection 5.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 5.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
Write down the equation of motion of a damped harmonic oscillator driven by an external force which varies sinusoidally (harmonically) with the time. Explain what is meant by the terms steady state motion and transient motion. Give a qualitative description of these motions and explain the relationship between them.
Answer F1
The equation of motion may be written
$\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega_0^2x = a\sin({\it\Omega}t)$
where x is the displacement from the equilibrium position. The oscillator is characterized by its undamped angular frequency ω0 and the damping constant γ. The maximum magnitude of the driving force is F0 = ma for an oscillator of mass m.
Once the motion has started, a struggle ensues between the natural tendency of the oscillator to undergo free oscillations with angular frequency near to ω0 and the oscillations of frequency Ω imposed by the driving force. During this transient motion, beats occur between the two frequencies. However, the free oscillations soon die away, due to damping, leaving the oscillator vibrating in sympathy with the driving force. In this steady state motion the oscillator executes simple harmonic motion with angular frequency Ω and with a phase difference δ from the driving force.
Question F2
What two parameters characterize the steady state motion of an oscillator which is driven harmonically at an angular frequency Ω? Make sketches indicating how these parameters vary with the angular frequency Ω of the driving force. With reference to your sketches, describe the main features of the phenomenon of resonance.
Answer F2
In the steady state, the motion is given by:
x (t) = A sin(Ωt − δ)
where the two characterizing parameters are the amplitude A and the phase lag δ from the driving force.
The dependence of A and δ on angular frequency Ω is shown in Figures 2 and 3.
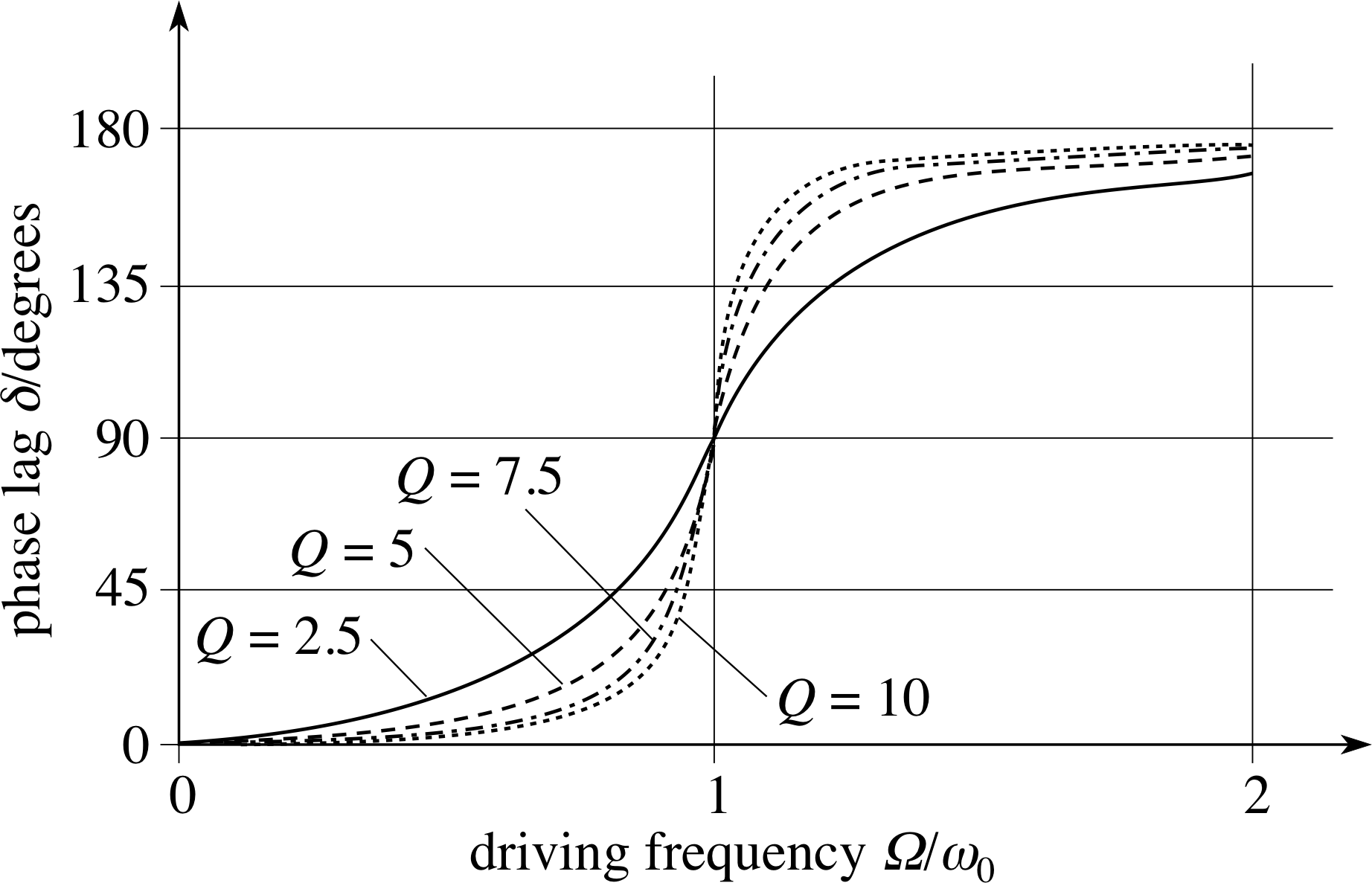
Figure 3 Graphs of phase lag δ (expressed in degrees) against driving frequency Ω (expressed as a multiple of ω0) for oscillators of different Q.
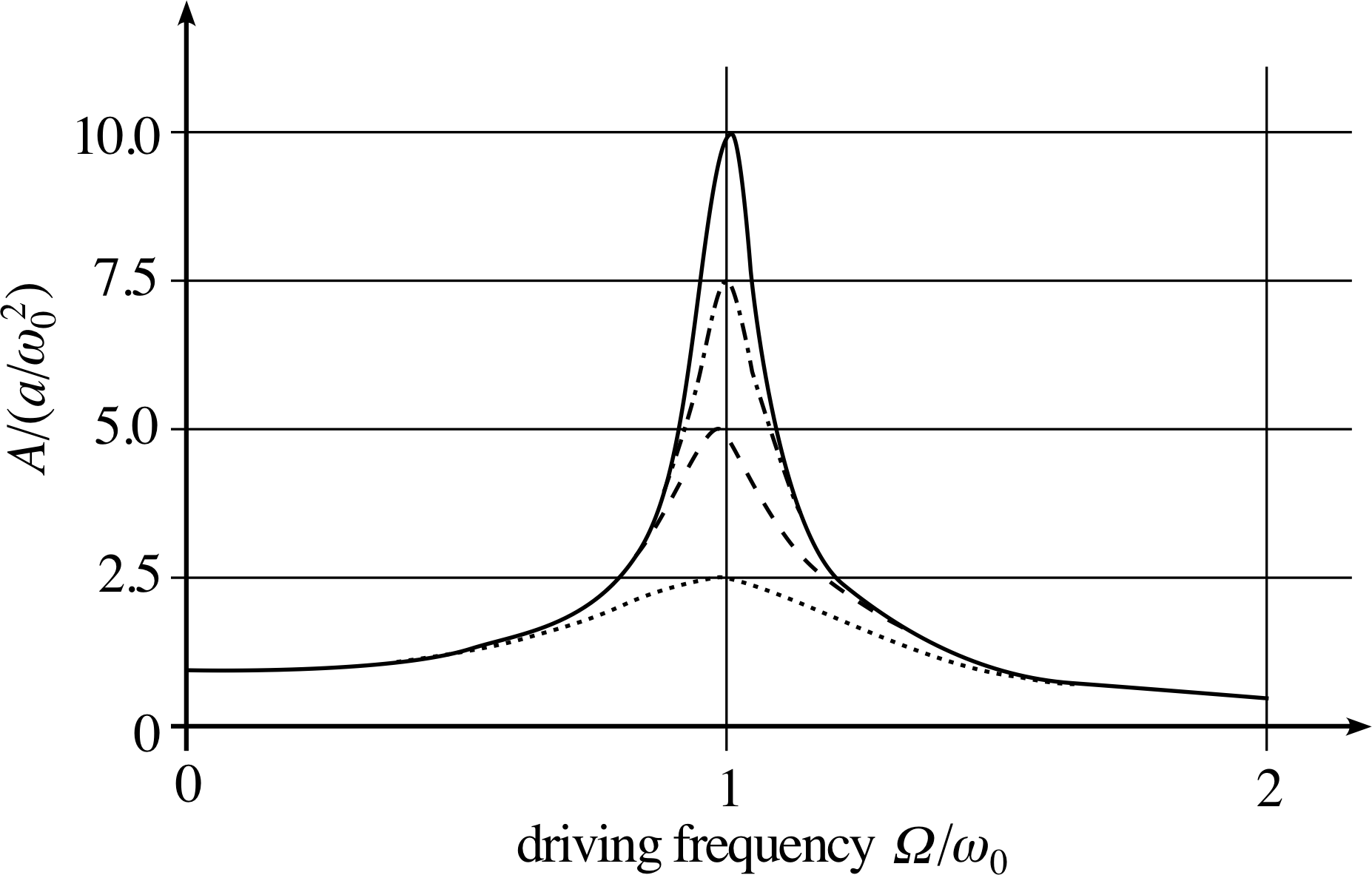
Figure 2 Graphs of amplitude A (expressed as a multiple of a/ω02) against driving frequency Ω (expressed as a multiple of ω0) for oscillators of different Q.
The amplitude shows a tall narrow peak at resonance which occurs when Ω ≈ ω0, implying that the oscillator responds very strongly when driven at any frequency within a narrow band of frequencies centred on its natural frequency ω0. The resonance peak is taller and narrower for oscillators with lighter damping (high Q–factor).
For such oscillators the phase lag rises rapidly through 90° near resonance, steepening as the Q–factor increases.
1.3 Ready to study?
Study comment In order to study this module you will need to be familiar with the following terms: acceleration, Cartesian coordinate system, displacement, displacement–time graph, energy, equilibrium, force, Hooke’s law, mass, kinetic energy, Newton’s laws of motion (including the use of the second law to formulate the equation of motion of a system), period, position, potential energy, power and velocity. You should also be familiar with simple harmonic motion (see Question R2), and aware of the general features of damped_mechanical_oscillatordamped harmonic motion (though this is briefly reviewed in the module). Mathematically, you will need to be familiar with exponential_functionexponential and trigonometric functions and with the inverse trigonometric function arctanarctan(x). You will also be required to use various trigonometric identities. The notation of differentiation (dx/dt, d2x/dt2) is used freely throughout this module, and you must be familiar with it, however you are not actually required to evaluate derivatives for yourself. An averaging process is introduced which requires a knowledge of integration if it is to be fully understood, but again you are not required to evaluate any integrals for yourself. Simple differential equations are also introduced in the module but a familiarity with this topic is not assumed. Mathematical requirements are a familiarity with trigonometry (including angle, cosine, degree, periodic functions, radian, sine, tangent, trigonometric identities), the differentiation (including higher derivatives) and integration of polynomial_functionpolynomial and trigonometric functions. If you are unsure about any of these items you can review them now by reference to the Glossary, which will also indicate where in FLAP they are developed. The following Ready to study questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
A body of mass m moves along the x–axis of a Cartesian coordinate system, subject to two forces F1x and F2x. If its instantaneous position is denoted by x (t), write down its equation of motion.
Answer R1
From Newton’s second law:
$ma_x = m\dfrac{d^2x}{dt^2} = F_{1x} + F_{2x}$
Consult Newton’s second law in the Glossary for further information.
Question R2
A simple harmonic oscillator moves in such a way that its displacement from its equilibrium position at time t is given by x (t) = A0 sin(ωt + ϕ). Explain the physical significance of the constants A0, ω and ϕ.
Answer R2
A0 is called the amplitude of the oscillator and represents its maximum displacement from the equilibrium position during each cycle of oscillation. ω is called the angular frequency of the motion and it is equal to 2πf, where f is the frequency of the oscillator (i.e. the number of oscillations per second). ϕ is called the phase constant (or initial phase) of the oscillator, it is the value of the phase, ωt + ϕ, when t = 0 and determines the initial position of the oscillator since x (0) = A0 sin ϕ.
Consult the relevant terms in the Glossary for further information.
Question R3
A simple harmonic oscillator has period T = 5.00 s. What is the frequency of the oscillator? What is the corresponding value of ω?
Answer R3
The frequency is given by f = 1/T = 0.200 Hz
The angular frequency is given by ω = 2π/T = 1.26 rad s−1
Consult frequency and angular frequency in the Glossary for further information.
Question R4
(a) Given the trigonometric identity
cos(θ + ϕ ) = cos θ cos ϕ − sin θ sin ϕ
show that cos2θ + sin2θ = 1 and cos2θ − sin2θ = cos(2θ)
(b) Use the trigonometric identity
sin(θ + ϕ) = sin θ cos ϕ + cos θ sin ϕ
to show that sin(θ − π) = −sin θ
Answer R4
(a) For the first case we put ϕ = −θ, remembering that cos(−θ) = cos θ and sin(−θ) = − sin θ, using the symmetry properties of cos θ and sin θ, to obtain:
cos(0) = 1 = cosθ cos(−θ) − sinθ sin(−θ) = cos2θ + sin2θ
For the second case, we put ϕ = θ and we find:
cos(2θ) = cos θ cos(θ) − sinθ sin(θ) = cos2θ − sin2θ
(b) To show that sin(θ − π) = −sin θ, simply substitute ϕ = −π into the given identity and note that
sin(θ −π) = sin θ cos(−π) + cos θ sin(−π) = −sinθ
since cos(−π) = −1 and sin(−π) = 0
Question R5
Use the first identity in Question R4 and the simple values for the sine and cosine of π/4 and π/6 to show that:
$\cos\left(\dfrac{5\pi}{12}\right) = \dfrac{\sqrt{3\os}-1}{2\sqrt{2\os}}\quad\text{and}\quad\cos\left(\dfrac{\pi}{12}\right) = \dfrac{\sqrt{3\os}+1}{2\sqrt{2\os}}$
Answer R5
As $\dfrac{5\pi}{12} = \dfrac{\pi}{4} + \dfrac{\pi}{6}$ we have:
$\cos\left(\dfrac{5\pi}{12}\right) = \cos\left(\dfrac{5\pi}{4}\right)\cos\left(\dfrac{5\pi}{6}\right) - \sin\left(\dfrac{5\pi}{4}\right)\sin\left(\dfrac{5\pi}{6}\right) = \left(\dfrac{1}{\sqrt{2\os}}\right)\times\left(\dfrac{\sqrt{3\os}}{2}\right) - \left(\dfrac{1}{\sqrt{2\os}}\right)\times\left(\dfrac12\right) = \dfrac{\sqrt{3\os}-1}{2\sqrt{2\os}}$
Similarly,$\dfrac{\pi}{12} = \dfrac{\pi}{4} - \dfrac{\pi}{6}$ and so:
$\cos\left(\dfrac{\pi}{12}\right) = \cos\left(\dfrac{\pi}{4}\right)\cos\left(\dfrac{-\pi}{6}\right) - \sin\left(\dfrac{\pi}{4}\right)\sin\left(\dfrac{-\pi}{6}\right)$
So$\cos\left(\dfrac{\pi}{12}\right) = \cos\left(\dfrac{\pi}{4}\right)\cos\left(\dfrac{\pi}{6}\right) + \sin\left(\dfrac{\pi}{4}\right)\sin\left(\dfrac{\pi}{6}\right) = \left(\dfrac{1}{\sqrt{2\os}}\right)\times\left(\dfrac{\sqrt{3\os}}{2}\right) + \left(\dfrac{1}{\sqrt{2\os}}\right)\times\left(\dfrac12\right) = \dfrac{\sqrt{3\os}+1}{2\sqrt{2\os}}$
Consult trigonometric functions in the Glossary for further information.
2 Driven oscillators
2.1 Qualitative discussion of driven oscillators and resonance
Oscillating systems typically have one or more characteristic natural frequencies at which they vibrate when disturbed. These natural frequencies can be very useful. In the case of a simple pendulum for instance, the single natural frequency may be used for time keeping, as in a pendulum clock. However, when using oscillating systems in technical and scientific applications it is often necessary to suppress natural oscillations and replace them by externally imposed oscillations. An example of this kind arises in the case of loudspeakers. In order to reproduce a wide range of sounds, loudspeakers must be made to vibrate over a large range of frequencies, and if sounds are to be reproduced faithfully any natural frequencies associated with the loudspeaker must not be unduly accentuated.
When we wish to produce oscillations in a system we do so by applying a driving force which has its own frequency associated with it. An oscillator responding to such a force is said to be a forced oscillator or a driven oscillator. Examples of forced oscillators are plentiful, even a device as simple as a child’s playground swing can serve the purpose.
Imagine a playground swing with a small child seated on it. If you pull the swing back a little from equilibrium, into a raised position, and then release it from rest, it will oscillate back and forth about its equilibrium position. To a first approximation, the swing will behave like an ideal pendulum, oscillating with constant total energy, and may be represented by a simple harmonic oscillator. Of course, this is only a crude approximation to the true behaviour; the swing will actually lose energy due to dissipative forces, such as friction and air resistance, and the oscillations will eventually die away. A more accurate description of the swing would take into account these various dampingdamping effects that dissipate the energy, and, provided they were relatively weak, would represent the swing as a light_dampinglightly damped harmonic oscillator with an amplitude that decreases gradually with time. i
Question T1
If the amplitude of the oscillations of the swing decays to half its initial value after five oscillations, sketch a displacement–time graph for the first ten oscillations.
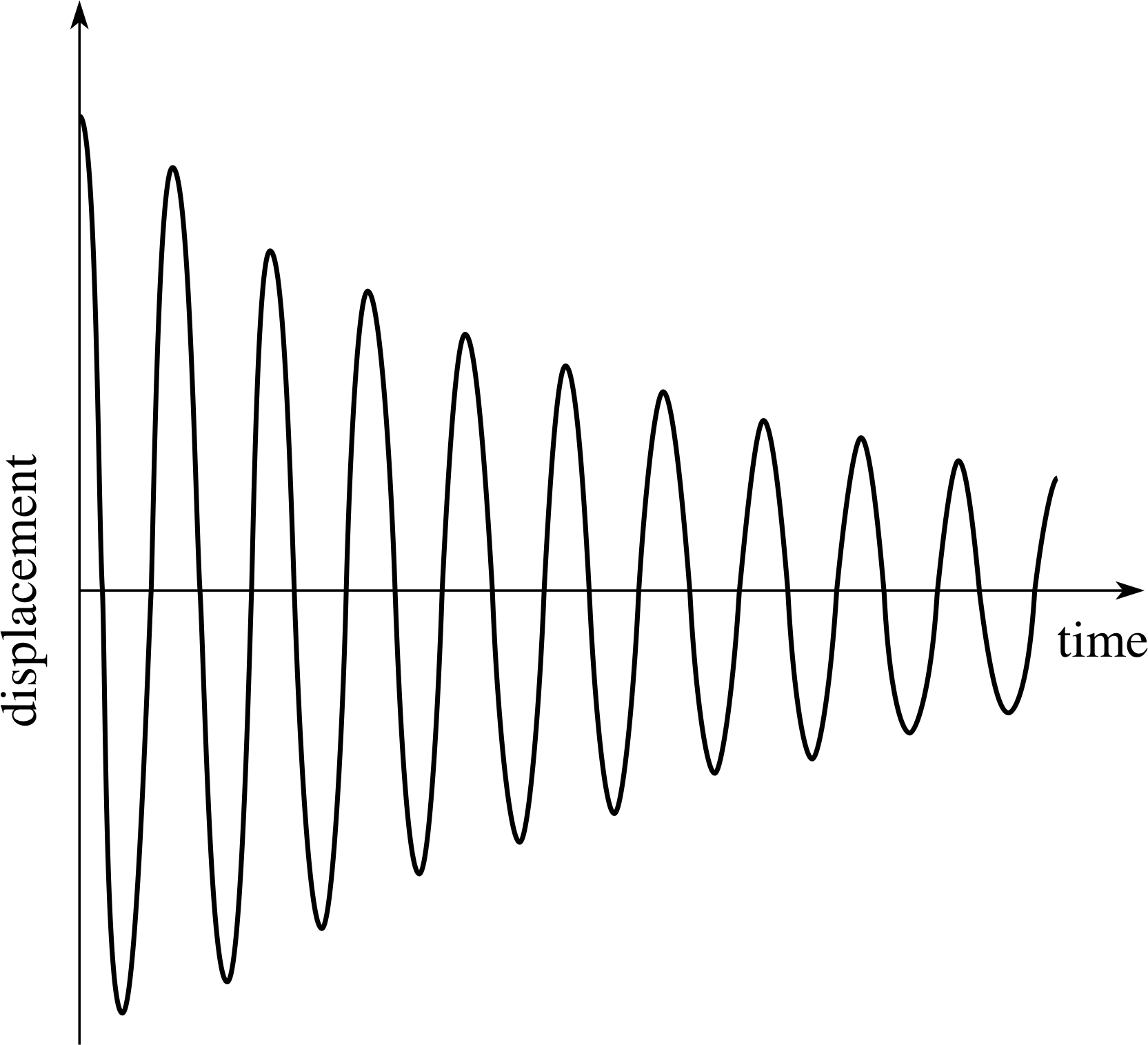
Figure 10 See Answer T1.
Answer T1
The first ten oscillations of the swing are shown in Figure 10.
Left to themselves the oscillations of the swing die away, but if you catch the swing at its highest point, at the completion of each oscillation, and push it back towards the equilibrium position, then the oscillations can be sustained despite the damping. The swing may now be described as a driven_oscillatordriven damped oscillator, or simply a forced oscillator, driven by the force you provide during part of each cycle of oscillation.
Question T2
Sketch a possible displacement–time graph for this case, superimposing on your sketch a graph of the force you would have to supply to sustain the oscillation. Assume that the driving force has a constant magnitude Fd during the time you are in contact with the swing, and that you never apply the force when the swing’s displacement from its equilibrium position is negative. Your sketch should be guided by your answers to the following questions: Is the motion periodic? What governs the pushing frequency? During what part of the cycle would you push the swing? Is the motion symmetric about the equilibrium position?
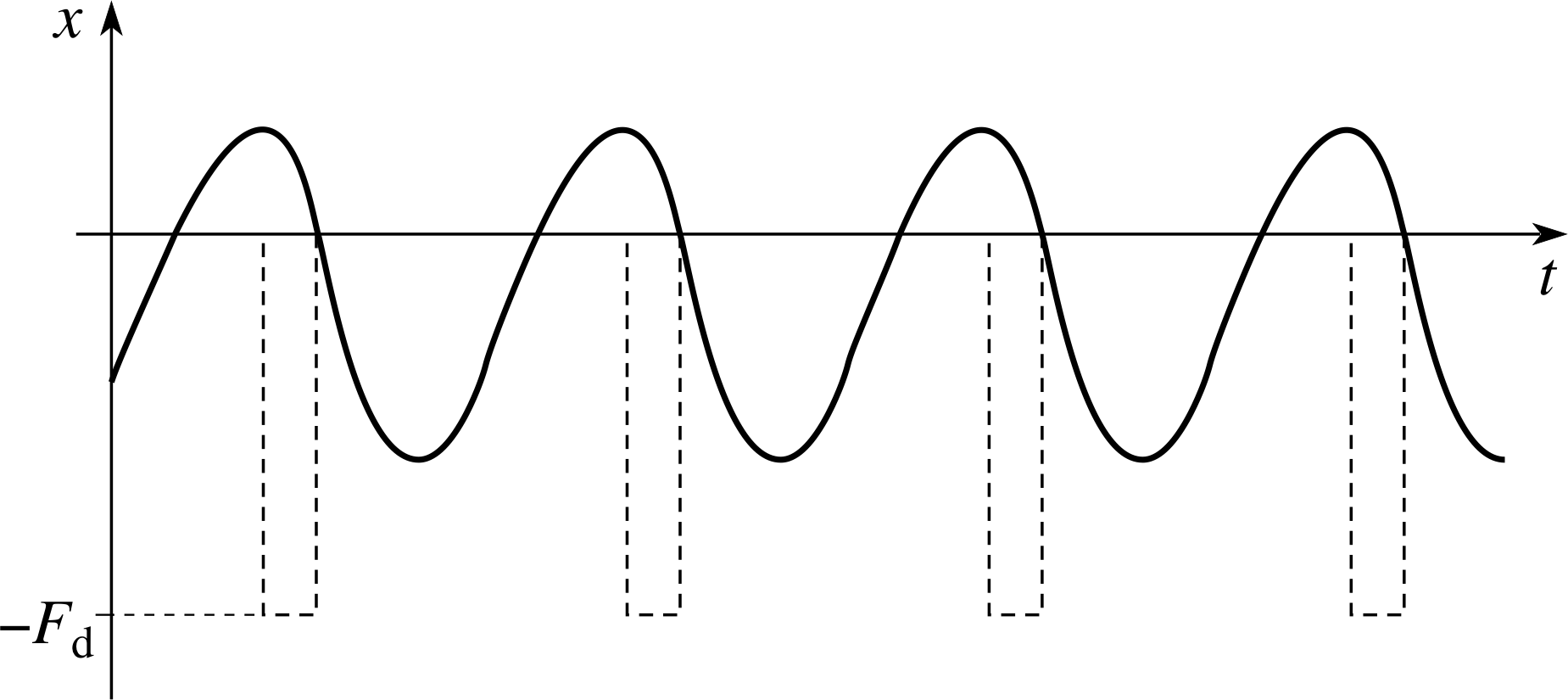
Figure 11 See Answer T2.
Answer T2
Once a steady rhythm has been set up, the motion is periodic. The pusher pushes briefly each time the swing returns, so that the pusher’s frequency is the same as the natural frequency of the swing. As the swing is being pushed from only one side, we would expect the motion to be asymmetric with respect to the vertical. For most of the cycle the pusher and swing are disconnected, and the swing is essentially a free oscillator. Figure 11 shows the steady state oscillation x (t) and the driving force.
The driving force shown in the answer to Question T2 is similar to the force you really would supply if you wanted to keep the swing oscillating with the minimum effort. It is a periodic force with a frequency that closely matches the natural frequency of the swing. Driving an oscillator in this way, at a frequency that is close to its natural frequency, can result in the efficient transfer of energy to the oscillator and may cause the amplitude of the oscillations to become very large. This is the condition known as resonance, an understanding of which is important in many fields of science and technology.
The large amplitude forced oscillations that occur near to the natural frequency of a system, due to resonance, can be disastrous. At Angers in France, in 1850, almost half of a column of about 500 soldiers were killed when the suspension bridge across which they were marching collapsed. The rhythmic marching of the soldiers excited a natural swinging motion of the bridge, which brought about its destruction. Similarly, gusting wind in the Tacoma_Narrows_Bridge_(1940)Tacoma Narrows in the north–western USA, in November 1940, caused a new suspension bridge to vibrate rather in the same way as the metal slats of a venetian blind flutter when air rushes over them. Energy was supplied to the bridge at its natural frequency and the amplitude of the vertical and then the twisting vibrations became so large that the roadway ripped from its hangers and plunged into the water below. You may have seen the classic film footage of this spectacular disaster. In the same way, tall buildings, radio aerials and factory chimneys can also sway in the wind and must be constructed so that resonance is avoided.
In contrast to these negative aspects of resonance, there are situations in which resonance is desirable and can be usefully exploited. i Many examples of this kind occur in the production and detection of sound. For instance, it is quite easy to produce sound by applying a driving force to a small body of air and causing it to resonate. A tone of about 200 Hz can be obtained from an empty one–pint milk bottle, simply by blowing across the opening. Organ pipes and some other wind instruments work in a similar way. The same principle is also widely used in nature. Howler monkeys and some frogs and toads have large vocal sacs that allow forced oscillations at a near natural frequency to produce surprisingly loud sounds. In fact, such systems often resonate over quite a wide range of frequencies, a point to which we will return later in the module.
Aside The phenomenon of resonance is not confined to macroscopic systems; examples abound in the microscopic world of atoms and nuclei, where physical systems are described by quantum physics rather than classical physics. While quantum systems are beyond the scope of this module, it is worth mentioning that useful insights into their behaviour can sometimes be gained from classical ideas. For example, the strong absorption by atomic nuclei of gamma-raysγ–rays in the wavelength range from 6 to 9 × 10−14 m may be thought of as the resonant excitation of a vibration in which the protons and neutrons in a nucleus oscillate, in anti-phase, about the nuclear centre of mass.
2.2 The equation of motion of a harmonically driven oscillator
Figure 1 A simple driven oscillator. The driving force has been omitted from the figure because its sign may change with time.
Another simple example of a forced oscillator is shown in Figure 1. A body of mass m is attached to one end of a horizontal spring, the other end of which is attached to a fixed point P. The body can slide back and forth along a straight line, which we will take to be the x–axis of a system of Cartesian coordinates, and is subject to three forces all acting in the x–direction (they may be positive or negative):
A restoring force F1x due to the spring that tends to return the body to its equilibrium position.
A damping force F2x due to friction and air resistance that opposes the motion of the body.
A driving force F3x provided by an external agency.
In the absence of any driving force, the system would have a natural equilibrium configuration in which the spring was neither extended nor compressed. If we take the equilibrium position of the mass to be the origin of the coordinate system, we can say that the mass’s displacement from equilibrium at time t is given by its instantaneous position coordinate x (t).
Using calculus notation, it follows that at any time t the velocity and acceleration of the mass are, respectively
$\upsilon_x = \dfrac{dx}{dt}\quad\text{and}\quad a_x = \dfrac{d\upsilon_x}{dt} = \dfrac{d^2x}{dt^2}$
Using Newton’s second law of motion we can then say that the sliding body must obey an equation of motion of the form
$m\dfrac{d^2x}{dt^2} = F_{1x} + F_{2x} + F_{3x}$(1)
To make further progress we now need to relate the forces that act on the sliding body to the time t or to the body’s instantaneous position x. This is easily done provided we idealize the system to some extent. First, let us suppose that the spring is ideal, which means that it obeys Hooke’s law perfectly, so that
F1x = −kx(2a)
where k is the spring constant that characterizes the spring.
Second, let us assume that damping forces which oppose the motion have magnitudes that are proportional to the instantaneous speed of the sliding body, so that
$F_{2x} = -b\dfrac{dx}{dt}$(2b) i
where b is a constant that characterises the dissipative forces. Third, let us suppose that the driving force is periodic, and has the relatively simple form
F3x = F0 sin(Ωt)(2c) i
where F0 is the maximum magnitude that the driving force attains, and Ω is the angular frequency of the driving force. Note that the angular frequency Ω is externally imposed and is not necessarily related in any way to the natural frequency of the system in Figure 1.
Substituting Equations 2a, 2b and 2c into Equation 1, we see that the behaviour of the sliding mass must now be described by the equation
$m\dfrac{d^2x}{dt^2} = -kx -b\dfrac{dx}{dt} + F_0\sin({\it\Omega}t)$
which can be rearranged to isolate the time–dependent driving term as follows
$m\dfrac{d^2x}{dt^2} + b\dfrac{dx}{dt} + kx = F_0\sin({\it\Omega}t)$(3)
A driving force that depends sinusoidally on time is sometimes described as a harmonic driving force, and a damping force with magnitude proportional to velocity is sometimes called a linear damping force. Equation 3 may therefore be described as the equation of motion of a harmonically_driven_linearly_damped_harmonic_oscillatorharmonically driven linearly damped oscillator. This equation arises in a number of physical contexts, though it is often presented in a form that differs somewhat from Equation 3. One of the most common variants is obtained by dividing both sides of Equation 3 by the mass m, and then introducing
the damping constant γ = b/m
the maximum magnitude of the driving acceleration a = F0/m
and the natural angular frequency $\omega_0 = \sqrt{k/m\os}$ i
The last of these is the angular frequency the oscillator would have if it were just a simple harmonic oscillator without any damping or driving.
Substituting these expressions into Equation 3 we can say that:
for the harmonically driven linearly damped oscillator:
$\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega_0^2x = a\sin({\it\Omega}t)$(4)
Equations of this kind, involving an independent variable (t), a dependent variable (x (t)) and derivatives of the dependent variable with respect to the independent variabsimple harmonic oscillator. le, are known as differential equations. From a mathematical point of view, Equation 4 involves only the first power of x and its derivatives (i.e. it is a linear equation) and the derivative of highest order that it contains is a second derivative. Equation 4 is therefore classified as a linear second–order differential equation.
From a physical point of view, it is clear that the driving force is represented by the term on the right–hand side of Equation 4. So, if we set a = 0 we obtain the equation of motion for an undriven linearly_damped_harmonic_oscillatorlinearly damped oscillator:
linearly damped oscillator: $\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega_0^2x = 0$(5)
If, in addition, we suppose that there is no damping, so γ = 0, the equation of motion becomes that of a simple harmonic oscillator:
simple harmonic oscillator: $\dfrac{d^2x}{dt^2} + \omega_0^2x = 0$(6)
We will approach the solution of Equation 4 through the simpler Equation 6 and then Equation 5.
First we look at Equation 6. Now, you should be familiar with simple harmonic motion in one-dimension, and you should know that it can generally be described by an equation of the form
x (t) = A0 sin(ω0t + ϕ)(7) i
where the amplitude A0 is a constant that determines the maximum displacement from the equilibrium position, and the phase constant ϕ determines the initial position of the oscillator at t = 0, since x (0) = A0sin ϕ.
If you know how to differentiate the function that appears in Equation 7 you should be able to show that
$\upsilon_x = \dfrac{dx}{dt} = A_0\omega_0\cos(\omega_0t+\phi)$
and$a_x= \dfrac{d^2x}{dt^2} = A_0\omega_0^2\sin(\omega_0t+\phi)$
and hence confirm that Equation 7 is a solution to Equation 6. To a mathematician, the presence of two arbitrary constants (A0 and ϕ) in Equation 7 also shows that it is the general solution to Equation 6, i.e. every solution to Equation 6 can be written in the form of Equation 7 by assigning suitable values to A0 and ϕ. i
In a similar way, but with more mathematical manipulation, it can be shown that damped harmonic motion, with its exponentially decaying amplitude can be described by an expression of the form
x (t) = A0 e−γt/2sin(ωt + ϕ) where $\omega = \sqrt{\smash[b]{\omega_0^2-\gamma^2/4}}$(8)
which is the general solution to Equation 5.

Figure 1 A simple driven oscillator. The driving force has been omitted from the figure because its sign may change with time.
If we want to determine how the sliding body of Figure 1 moves when subjected to the three forces specified above we need to find a solution to Equation 4,
$\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega_0^2x = a\sin({\it\Omega}t)$(Eqn 4)
i.e. we need to find an expression relating the instantaneous position x of the body to the time t, that satisfies Equation 4 and any other condition that the oscillator is known to satisfy. Solving Equation 4 is actually somewhat more complicated than solving Equations 5 and 6.
linearly damped oscillator: $\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega_0^2x = 0$(Eqn 5)
simple harmonic oscillator: $\dfrac{d^2x}{dt^2} + \omega_0^2x = 0$(Eqn 6)
This is because Equations 5 and 6 are homogeneous differential equations in which each term is proportional to x or to one of its time derivatives, whereas Equation 4,
$\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega_0^2x = a\sin({\it\Omega}t)$(Eqn 4)
is an inhomogeneous differential equation because it contains the driving term, a sin(Ωt), which does not involve the displacement at all, but does depend explicitly on the time. The mathematical procedure for solving such equations is described in detail in the maths strand of FLAP, where it is applied to Equation 3,
$m\dfrac{d^2x}{dt^2} + b\dfrac{dx}{dt} + kx = F_0\sin({\it\Omega}t)$(Eqn 3)
(see second–order differential equation in the Glossary for references), but we will not employ such methods here.
In this module we will adopt a more physical approach in which we will use physical arguments to determine the overall form of a solution, and mathematical techniques to work out the details. Methods of this kind are much used by physicists.
Question T3
Devise and describe two simple systems that, like the system in Figure 1, are capable of oscillatory motion and which may be acted upon by an externally produced periodic driving force.
Answer T3
There are many examples you could cite, but two possibilities are:
(i) A simple pendulum with its point of support able to move horizontally or vertically, so that it can be vibrated from side to side or up and down.
(ii) Moving your hands back and forth like paddles through the water when you are sitting in the bath. This can cause oscillation of the water from end to end of the bath and if the amplitude of the oscillations becomes sufficiently large, which it will do near resonance, you may have some cleaning up to do afterwards!
Question T4
A student claims that the action of an external driving force must eventually lead to an increase in the mechanical energy of the sliding body of Figure 1. The student therefore concludes that in the absence of friction, or any other dissipative effect, the sliding body will gain energy continuously and the oscillation will grow without limit, at least until the spring fractures. Do you agree with this argument?
Answer T4
It is not true to say that the driving force can only increase the energy of the mass. The work done on the mass by the external force is positive when the force acts in the same direction as the motion but it is negative when the force opposes the motion. It is not obvious that the net effect of this will be positive. In fact, as we will see in the next subsection, the net effect depends critically on the frequency of the driver in relation to the natural frequency of the oscillator – read on!
2.3 Steady state motion
$\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega_0^2x = a\sin({\it\Omega}t)$(Eqn 4)
Equation 4 represents a struggle. The oscillator, when disturbed, tends to oscillate with its natural angular frequency ω0, but it is being driven at a different angular frequency, Ω. It is clear that the driving force must eventually win this struggle, because the oscillator loses energy due to damping and is only sustained in perpetuity by the external agency that provides the driving force. The motion during the struggle is usually called the transient motion and its finite duration is determined by the time taken for free oscillations to decay to a negligible amplitude. This time is of the order of 2π/γ, as you will see in Subsection 2.5, where we consider the transient motion in more detail. In this subsection we will be concerned with the steady state motion that persists after the transient motion has decayed.
The steady state motion of the driven oscillator can be expected to be in sympathy with the driving force, so it is likely to be harmonic motion with the same angular frequency as the driving force. However, there is no reason why it should be exactly in–phase with the driving force, indeed on physical grounds you might well expect the displacement to lag somewhat behind the force that causes it.
For these reasons we will assume that the steady state motion of the harmonically driven linearly damped oscillator is described by an expression of the form:
steady state motion x (t) = A sin(Ωt − δ)(9) i
where A represents the amplitude of the steady state motion, and δ the phase lag between the steady state motion and the driving force (F3x = F0sin(Ωt)). Having arrived at Equation 9 on the basis of physical arguments, rather than by straightforward mathematical deduction from Equation 4, we must treat it with caution. As is usual in such circumstances we will regard Equation 9 as a trial solution of Equation 4 and investigate its physical implications. In particular, we will use it to determine the way in which the values of A and δ depend on the characteristics of the driving force (a and Ω) and the oscillator (ω0 and γ). By doing this we should gain insight into our trial solution and either convince ourselves of its correctness or expose its shortcomings.
We will start these investigations by considering separately the steady state behaviour of the oscillator when the angular frequency of the driving force is first much smaller than the natural angular frequency (Ω ≪ ω0), then when it is much larger than the natural angular frequency (Ω ≫ ω0), and finally when the two angular frequencies are equal (Ω = ω0) and the oscillator is near to resonance.
✦ Using Equation 9,
steady state motion x (t) = A sin(Ωt − δ)(Eqn 9)
express the first two terms of Equation 4,
$\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega_0^2x = a\sin({\it\Omega}t)$(Eqn 4)
in terms of Ω, A, t and δ.
✧ Since
$\dfrac{d[\sin({\it\Omega}t)]}{dt} = {\it\Omega}\cos({\it\Omega}t)\quad\text{and}\quad\dfrac{d[\cos({\it\Omega}t)]}{dt} = -{\it\Omega}\sin({\it\Omega}t)$
we have
$\dfrac{d^2x}{dt^2} = -{\it\Omega}^2\sin({\it\Omega}t-\delta) = {\it\Omega}^2x(t)\quad\text{and}\quad\gamma\dfrac{dx}{dt} = {\it\Omega}\cos({\it\Omega}t-\delta)$
Now let us look at the first of the frequency regimes in which our trial solution to Equation 4 is to be investigated.
Low frequency limit: Ω ≪ ω0
As we have just seen, our trial solution implies that the first two terms in Equation 4,
$\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega_0^2x = a\sin({\it\Omega}t)$(Eqn 4)
involve factors of Ω2 and Ω, respectively. If Ω ≪ ω0 the first term (Ω2x) is small compared to the third term (ω2x). For light damping (small γ) the second term will also be small compared with the third term (except very near x = 0). As a first approximation we can therefore neglect these first two terms, so that Equation 4 becomes:
ω2x (t) ≈ a sin(Ωt)
in the low frequency limit: $x(t) = \left(\dfrac{a}{\omega_0^2}\right)\sin({\it\Omega}t)$(10)
This confirms that the oscillator is moving at the driving angular frequency Ω, as expected. In terms of the trial solution it also implies that, in the low frequency limit, the amplitude is A = (a/ω2 ), which is independent of the driving frequency, and the displacement is in phase with the driving force; i.e. δ = 0. In practice, this limit usually results in small amplitude oscillations in phase with the driving force.
High frequency limit: Ω ≫ ω0
In this case the first term in Equation 4,
$\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega_0^2x = a\sin({\it\Omega}t)$(Eqn 4)
is the important one, if the oscillator is lightly damped, since it involves a factor of Ω2 which will be large. Thus a reasonable approximation to Equation 4 is:
$\dfrac{d^2x}{dt^2} = a\sin({\it\Omega}t)$
but in the steady state described by Equation 9,
steady state motion x(t) = A sin(Ωt − δ)(Eqn 9)
we have
$\dfrac{d^2x}{dt^2} = -{\it\Omega}^2x(t)$
Hence$x(t) \approx -\left(\dfrac{a}{{\it\Omega}^2}\right)\sin({\it\Omega}t)$
Using one of the trigonometric identities discussed in Question R4, we can rewrite this in a form that is directly comparable to Equation 9:
in the high frequency limit: x (t) = a sin(Ωt − π)(11)
Thus the oscillator still moves with the angular frequency of the driving force, but it is now in anti–phase with that force, i.e. δ = π, and its amplitude is A = (a/Ω2), which does depend on Ω and decreases rapidly as Ω increases.
Resonance limit: Ω ≈ ω0
The driving angular frequency at which resonance occurs depends on the damping constant, but for light damping it is very close to the natural angular frequency ω0. For our present purposes we will assume that the damping is light and that resonance implies Ω = ω0. Using the steady state expression for x (t) from Equation 9,
steady state motion x(t) = A sin(Ωt − δ)(Eqn 9)
and setting Ω = ω0, Equation 4,
$\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega_0^2x = a\sin({\it\Omega}t)$(Eqn 4)
now becomes
−ω02x + γω0A cos(ω0t − δ) + ω02x = a sin(Ωt)
On the left–hand side the first and last terms cancel, so that:
γω0A cos(ω0t − δ) = a sin(Ωt)
We can use the trigonometric identity cos θ = sin(π/2 + θ) to rewrite this in the form
γω0A sin(π/2 + ω0t − δ) = a sin(Ωt)
If this relation is to hold true for all values of t, then it must be the case that Ω = ω0 and δ = π/2. In addition, it must also be the case that γω0A = a. It then follows from Equation 9 that
in the resonance limit: $x(t) = \left(\dfrac{a}{\gamma\omega_0}\right)\sin\left({\it\Omega}t-\dfrac{\pi}{2}\right)$(12)
where the amplitude at resonance is given by A = a/γω0 which exceeds the amplitude in the low frequency limit by a factor $\dfrac{a}{\gamma\omega_0}\dfrac{\omega_0^2}{\gamma} = \dfrac{\omega_0}{\gamma}$. We will call this factor the quality factor or Q–factor of the lightly damped oscillator.
We will have more to say about the Q–factor in the next subsection, but it worth pointing out now that it provides a useful way of characterizing oscillators that will be used throughout the rest of this module. For a very lightly damped oscillator, the Q–factor is usually very large. Indeed, in the absence of damping it would be infinite and the response of the system would be unbounded – to destruction.
For a lightly damped oscillator at resonance the phase of the displacement lags 90° behind that of the driving force, and the amplitude is given by Q × (a/ω02) where Q = ω0/γ. i
Question T5
Three lightly damped oscillators A, B and C are driven by the same harmonic force. The natural frequency of oscillator A is much higher than the frequency of the driving force, and that of B much lower. Oscillator C has a natural frequency very close to the driving frequency. Make a sketch showing the time dependence of the driving force and the displacements of the three oscillators in their steady state motion.
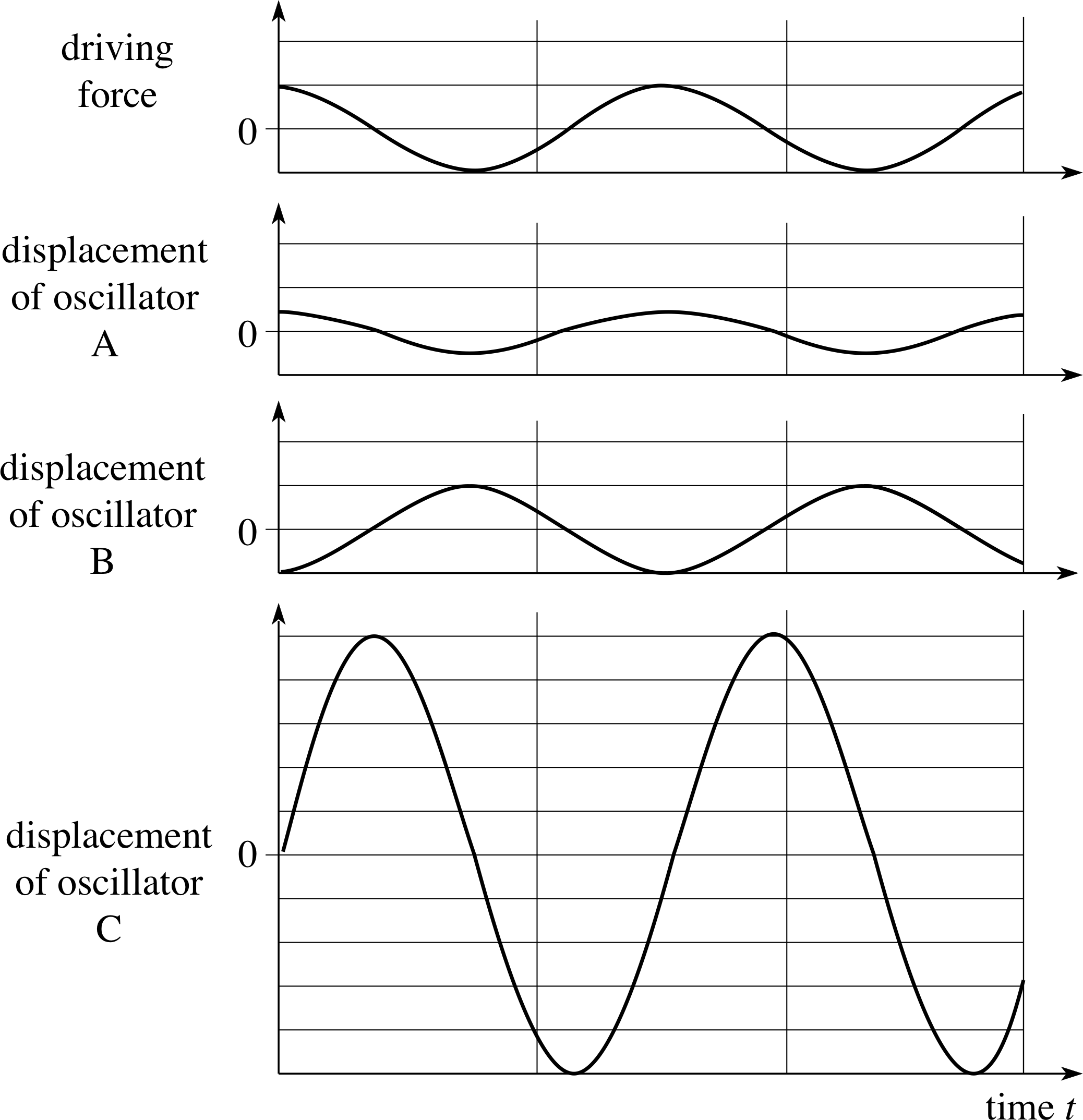
Figure 12 See Answer T5. Note that the amplitude of B should actually be smaller than that of A, but the scale has been expanded for clarity.
Answer T5
Figure 12 shows the sketches.
The following points should be noted:
Oscillator A: low frequency limit; displacement in phase with the driver.
Oscillator B: high frequency limit; small amplitude response, in anti-phase.
Oscillator C: resonance; large amplitude displacement with a phase lag of 90° on the driver.
Question T6
Using the three limiting cases as guidance, summarize how the amplitude and phase lag of the steady state motion of the driven oscillator change as the driving frequency is increased from a low value, through the natural frequency, to a high value.
Answer T6
When the angular frequency Ω of the driving force is low, the amplitude of the forced oscillation is F0/(mω0), where F0 is the maximum magnitude of the driving force, m is the mass of the sliding body and ω0 is the natural frequency of the oscillator in the absence of driving and damping. As the driving frequency increases, the amplitude rises, reaching a maximum value that exceeds the low frequency amplitude by a factor of Q (=ω0/γ) at resonance, when Ω has a value close to ω0. Thereafter the amplitude decreases, becoming vanishingly small at high frequency where it behaves like F0/(mΩ2). The displacement of the oscillator lags the driving force by a phase which increases from zero at low frequency, through 90° near to resonance, to 180° at high frequency.
Our considerations of the frequency limits of the solution have led to sensible predictions, in accord with experimental results. Accordingly, we are encouraged to believe that Equation 9,
steady state motion x(t) = A sin(Ωt − δ)(Eqn 9)
is indeed a solution to Equation 4,
$\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega_0^2x = a\sin({\it\Omega}t)$(Eqn 4)
Let us press on with this line of investigation.
The most direct way to obtain the precise dependencies of A and δ on Ω is to substitute Equation 9 into Equation 4.
When this is done we find:
A (ω02 − Ω2) sin(Ωt − δ) + AγΩ cos(Ωt − δ) = a sin δ cos(Ωt − δ) + a cos δ sin(Ωt − δ)(13) i
Examine Equation 13 carefully. Notice that the time t occurs in two different sinusoidal functions.
For Equation 9 to be a solution of Equation 4, it is necessary that Equation 13 should be an identity, valid for all t. This is true if, and only if, the coefficients of cos(Ωt − δ) on each side of the equation are identical; the same must be true of the coefficients of sin(Ωt − δ) on each side. Equating the two sets of coefficients leads immediately to the pair of equations:
$\sin\delta = \dfrac{A\gamma{\it\Omega}}{a}$(14a)
$\cos\delta = \dfrac{A(\omega_0^2-{\it\Omega}^2}{a}$(14b)
Squaring and adding these equations to eliminate δ, through the identity sin2δ + cos2δ = 1, gives the amplitude as:
general case amplitude $A = \dfrac{a}{\sqrt{\smash[b]{(\omega_0^2-{\it\Omega}^2)^2+(\gamma{\it\Omega})^2}}}$(15)
Dividing Equation 14a by 14b leads to:
$\tan\delta = \dfrac{\sin\delta}{\cos\delta} = \dfrac{\gamma{\it\Omega}}{\omega_0^2-{\it\Omega}^2}$
Therefore we can write
general case phase lag: $\delta = \arctan\left(\dfrac{\gamma{\it\Omega}}{\omega_0^2-{\it\Omega}^2}\right)$(16)
Graphs of A and δ as functions of angular frequency, as calculated from Equations 15 and 16, are shown in Figures 2 and 3, respectively, for oscillators with Q = 2.5, 5, 7.5 and 10. It may be seen that they exhibit the expected qualitative behaviour.

Figure 3 Graphs of phase lag δ (expressed in degrees) against driving frequency Ω (expressed as a multiple of ω0) for oscillators of different Q.

Figure 2 Graphs of amplitude A (expressed as a multiple of a/ω02) against driving frequency Ω (expressed as a multiple of ω0) for oscillators of different Q.
Notice that the maximum amplitude response in Figure 2 occurs at a value of ω that is slightly less than ω0, the effect being more marked for the more heavily damped oscillators with lower values of Q. We normally define the resonance angular frequency ωres and the corresponding resonance frequency fres = ωres/2π as the frequency at which the system has a maximum response. i This means that the resonance frequency of a damped oscillator is slightly less than the natural frequency of the undamped oscillator.
The natural frequency of the undamped system can be found from measurements on the damped system by noting the frequency at which the phase lag becomes 90°. The curves in Figures 2 and 3 are not symmetric, since the low and high frequency limits are different, but the phase lag is antisymmetric about 90°, for which Ω = ω0 exactly. Notice also that the gradient in the phase lag curves as the angular frequency goes through resonance is steeper for higher values of Q, i.e. for oscillators with lighter damping.
Question T7
Use Equations 15 and 16,
general case amplitude $A = \dfrac{a}{\sqrt\smash[b]{{(\omega_0^2-{\it\Omega}^2)^2+(\gamma{\it\Omega})^2}}}$(Eqn 15)
general case phase lag: $\delta = \arctan\left(\dfrac{\gamma{\it\Omega}}{\omega_0^2-{\it\Omega}^2}\right)$(Eqn 16)
to confirm the results obtained at the beginning of this subsection for the low frequency, high frequency and resonance limits.
Answer T7
Low frequency limit: Ω = 0.
Immediately this gives A = a ω02 and δ = 0, as expected.
Resonance limit: Ω = ω0.
In this case A = a/(γω0) and δ = arctan(∞) = 90°
High frequency limit: Ω → ∞
In the denominator of Equation 15,
general case amplitude $A = \dfrac{a}{\sqrt{\smash[b]{(\omega_0^2-{\it\Omega}^2)^2+(\gamma{\it\Omega})^2}}}$(Eqn 15)
ω02 can be neglected in comparison with Ω2; also (γΩ)2 is negligible compared to Ω4, so the result is A = a/Ω2. From Equation 16,
$\delta = \arctan\left(\dfrac{\gamma{\it\Omega}}{\omega_0^2-{\it\Omega}^2}\right)$(Eqn 16)
$\delta = \arctan\left(-\dfrac{\gamma}{\it\Omega}\right) \rightarrow \delta = 180°$
Question T8
An oscillator with ω0 = 100 s−1 and Q = 5 is driven by a harmonically varying force of maximum magnitude 2 N. If the mass of the oscillator is 0.2 kg, calculate the amplitude and phase lag of the steady state oscillations when the angular frequency of the driving force is: (a) 50 s−1, (b) 100 s−1 and (c) 200 s−1.
Answer T8
Here $\gamma = \dfrac{\omega_0}{Q} = 20\,{\rm s^{-1}}\quad\text{and}\quad a = \dfrac{F_0}{m} = \rm \dfrac{2\,N}{0.2\,kg} = 10\,m\,s^{-2}$
Hence, using Equations 15 and 16
$A = \dfrac{a}{\sqrt{\smash[b]{(\omega_0^2-{\it\Omega}^2)^2+(\gamma{\it\Omega})^2}}}$(Eqn 15)
$\delta = \arctan\left(\dfrac{\gamma{\it\Omega}}{\omega_0^2-{\it\Omega}^2}\right)$(Eqn 16)
with Ω = 50 s−1, 100 s−2, 200 s−2, we obtain:
(a) Ω = 50 s−1: A = 1.3× 10−2 m; δ = 7.6° Ω = 100 s−2;
(b) A = 5 × 10−2 m; δ = 90° Ω = 200 s−2;
(c) A = 0.33 × 10−2 m; δ = 172.4°
2.4 Steady state energy balance and power transfer
Equation 9,
steady state motion x(t) = A sin(Ωt − δ)(Eqn 9)
indicates that the oscillator, in its steady state, undergoes pure harmonic motion with the same angular frequency, Ω, as the driving force. However, when the behaviour is compared with that of a simple, undamped harmonic oscillator, important differences emerge, particularly regarding the energy of the oscillator. As usual, the total energy is the sum of the kinetic and potential energies, and ω02 = k/m so we have:
$E_{\rm tot} = E = E_{\rm kin} + E_{\rm pot} = \dfrac12 m\left(\dfrac{dx}{dt}\right)^2 + \dfrac12 kx^2 = \dfrac12 m\left(\dfrac{dx}{dt}\right)^2 + \dfrac12 m\omega_0^2x^2$(17)
In the steady state we can use Equation 9 to express this total energy in terms of t rather than x, giving:
$E = \dfrac12 mA^2{\it\Omega}^2\cos^2({\it\Omega}t - \delta) + \dfrac12 m\omega_0^2A^2\sin^2({\it\Omega}t - \delta)$
For the harmonically driven oscillator:
total energy$E = \dfrac12 mA^2\left[{\it\Omega}^2\cos^2({\it\Omega}t - \delta) + \omega_0^2A^2\sin^2({\it\Omega}t - \delta)\right]$(18)
kinetic energy$E_{\rm kin} = \dfrac12 mA^2{\it\Omega}^2\cos^2({\it\Omega}t - \delta)$(19)
potential energy$E_{\rm pot} = \dfrac12 mA^2\omega_0^2A^2\sin^2({\it\Omega}t - \delta)$(20)
Equations 18 to 20 have several important consequences for the driven oscillator:
- The instantaneous total energy E of the driven oscillator depends on time unless Ω = ω0, in which case
$\quad E = \dfrac12 mA^2\omega_0^2$
- The average total energy over a complete cycle, denoted by $\langle E\rangle$, does not depend on time. In fact it can be shown that
$\langle E\rangle = \langle E_{\rm kin}\rangle + \langle E_{\rm pot}\rangle = \dfrac14 mA^2{\it\Omega}^2 + \dfrac14 mA^2\omega_0^2 = \dfrac14 mA^2({\it\Omega}^2+\omega_0^2)$(21) i
- We also see from Equation 21 that (unless Ω = ω0) the averages of kinetic and potential energies over a full period are not equal, as they are in free SHM. In the low frequency limit (Ω ≪ ω0) potential energy dominates, while at high frequency (Ω ≫ ω0) the energy is almost entirely kinetic.
- Since the average total energy over a cycle is constant, the driving force must provide precisely sufficient energy over a full period to compensate for the energy lost due to damping over a full period.
It is interesting to look at this last result from another point of view, by investigating the rate of energy transfer in more detail. When a general one–dimensional force Fx, acts on a body along the line of the force with instantaneous velocity dυx /dt, the instantaneous rate of energy transfer to the body is just the instantaneous power
$P(t) = F_x(t)\dfrac{dx}{dt}$
but, from Equation 3,
$m\dfrac{d^2x}{dt^2} + b\dfrac{dx}{dt} + kx = F_0\sin({\it\Omega}t)$(Eqn 3)
the driving force of the oscillator, F3x = F0 sin(Ωt) is given by
$F_{3x} = m\dfrac{d^2x}{dt^2} + m\omega_0^2x + m\gamma\dfrac{dx}{dt}$
so in the steady state, when x (t) = A sin(Ωt − δ),
$F_{3x} = m(\omega_0^2-{\it\Omega}^2)x + m\gamma\dfrac{dx}{dt}$
It follows that the instantaneous power delivered by this particular force is
$P(t) = F_{3x}\dfrac{dx}{dt} = m(\omega_0^2-{\it\Omega}^2)x\dfrac{dx}{dt} + m\gamma\left(\dfrac{dx}{dt}\right)^2$
and the corresponding average power over a full period will be
$\langle P\rangle = m(\omega_0^2-{\it\Omega}^2)\left\langle x\dfrac{dx}{dt}\right\rangle + m\gamma\left\langle\left(\dfrac{dx}{dt}\right)^2\right\rangle$
Now, as you will shortly be asked to demonstrate, $\left\langle x\dfrac{dx}{dt}\right\rangle = 0$.
Anticipating this result,
$\langle P\rangle = m\gamma\left\langle\left(\dfrac{dx}{dt}\right)^2\right\rangle$(22)
However if we identify the damping force $F_{2} = -m\gamma\dfrac{dx}{dt}$, it is clear that we can rewrite this last expression as
$\langle P\rangle = -\left\langle F_{2x}\dfrac{dx}{dt}\right\rangle$
Hence, as claimed, the rate at which energy is transferred to the oscillator by the driving force, averaged over a full period, is equal to the rate at which energy is transferred from the oscillator by damping, averaged over the same period.
✦ Formulate a convincing physical argument to show that over a full period of oscillation $\left\langle x\dfrac{dx}{dt}\right\rangle = 0$, as claimed above.
✧ The oscillating body passes through any given point, x, twice in a cycle. If it is moving to the right on the first transit, it is moving to the left on the second. Since this is steady state motion the speeds on these two occasions are the same, so that the two contributions to the average cancel. As this is true for every point on the cycle, except the turning points, where the velocity is zero anyway, the average of $x \dfrac{dx}{dt}$ over a full cycle (in the steady state) must vanish.
Using Equation 22 we can now obtain a useful explicit expression for the average rate of energy transfer over a full period. There are many ways of doing this, one is to note that
$\langle E_{\rm kin}\rangle = \dfrac12 m\langle \upsilon_x^2\rangle = \dfrac m2 \left\langle\left(\dfrac{dx}{dt}\right)^2\right\rangle$
so that Equation 22 can be written in the form
$\langle P\rangle = m\gamma \left\langle\left(\dfrac{dx}{dt}\right)^2\right\rangle = 2\gamma\langle E\rangle$
and then use Equation 21,
$\langle E\rangle = \langle E_{\rm kin}\rangle + \langle E_{\rm pot}\rangle = \dfrac14 mA^2{\it\Omega}^2 + \dfrac14 mA^2\omega_0^2 = \dfrac14 mA^2({\it\Omega}^2+\omega_0^2)$(Eqn 21)
which gives $\langle E_{\rm kin} = \dfrac14 mA^2{\it\Omega}^2$, to rewrite it as
$\langle P\rangle = \dfrac12 m\gamma(A{\it\Omega})^2$(23)
As we saw in the last subsection, in the case of a lightly damped oscillator, resonance occurs when Ω = ω0, which implies that A = a/(γω0) and δ = 90°. It follows from Equation 23 that the average rate of energy transfer at resonance will be
$\langle P_{\rm res}\rangle = \dfrac{ma^2}{2\gamma}$(24)
and substituting this into Equation 23 we see that at any driving frequency Ω
$\langle P\rangle = \left(\dfrac{\gamma A{\it\Omega}}{a}\right)^2\langle P_{\rm res}\rangle$(25a) i
According to Equation 14a, γAΩ/a = sin δ, so we can also write the above result in the form:
$\langle P\rangle = \langle P_{\rm res}\rangle\sin^2\delta$(25b) i
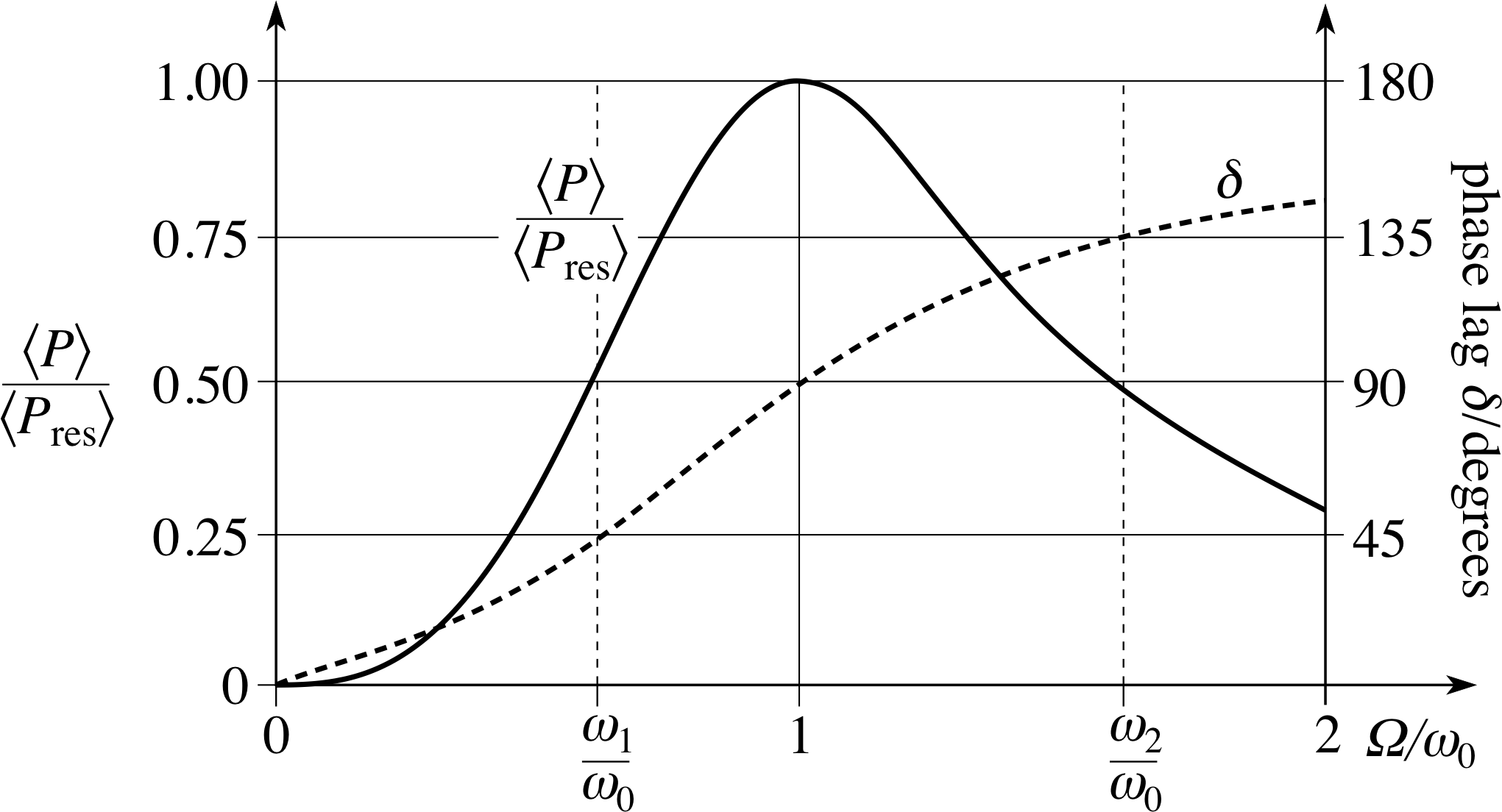
Figure 4 Graphs of $\langle P\rangle / \langle P_{\rm res}\rangle$ and δ against Ω/ω0 for an oscillator with Q = 1.
For a given oscillator, driven at a given frequency Ω, the quantity sin2 δ in Equation 25b is called the power factor and measures the ratio of the average power absorbed at the driving frequency to the average power absorbed at resonance.
The way in which $\langle P\rangle$ varies with Ω for an oscillator with Q = ω0/γ = 1 can be seen from Figure 4. Note that by plotting values of $\langle P\rangle / \langle P_{\rm res}\rangle$ against Ω/ω0 we are effectively measuring $\langle P\rangle$ in units of $\langle P_{\rm res}\rangle$ and Ω in units of ω0. The graph also shows how the phase lag δ between the driving force and the displacement varies with Ω for this Q = 1 oscillator, making it possible to see how $\langle P\rangle / \langle P_{\rm res}\rangle$ varies with δ. As you can see the average power transfer per cycle is greatest at resonance, and in the lightly damped case this occurs when Ω = ω0 and δ = 90°.
Question T9
Show that in the resonance limit, for a lightly damped oscillator, the average power transferred by the driving force in each full cycle is $\langle P\rangle = maA\omega_0/2$, but in both the low frequency limit and the high frequency limit the power transfer averages to zero.
Answer T9
In the resonance limit
Ω = ω0 and x (t) = A0 sin(ω0t − 90°) = −A0 cos(ω0t)
where A0 = a/(γω0). The instantaneous power Pres(t) is then:
$P_{\rm res}(t) = F_{3x}(t)\dfrac{dx}{dt} = ma\sin(\omega_0t)\dfrac{d[-A_{\rm res}\cos(\omega_0t)]}{dt} = maA_{\rm res}\omega_0\sin^2(\omega_0t)$
The average value of sin2(ωt) over a full period is 1/2, as explained in the discussion (and marginal comments)
associated with Equation 21,
$\langle E\rangle = \langle E_{\rm kin}\rangle + \langle E_{\rm pot}\rangle = \dfrac14 mA^2{\it\Omega}^2 + \dfrac14 mA^2\omega_0^2 = \dfrac14 mA^2({\it\Omega}^2+\omega_0^2)$(Eqn 21)
Averaged over a full cycle, at resonance: $\langle P_{\rm res}\rangle = maA_{\rm res}\omega_0/2 = ma^2/(2\gamma)$.
(This result may also be obtained directly from Equation 25a,
$\langle P\rangle = \left(\dfrac{\gamma A{\it\Omega}}{a}\right)^2\langle P_{\rm res}\rangle$(Eqn 25a)
by making appropriate substitutions.)
In the low frequency limit Ω ≪ ω0, δ = 0° and x (t) = A sin(Ωt)
The instantaneous power P (t) is then:
$P(t) = ma\sin({\it\Omega}t)\dfrac{d[A\sin({\it\Omega}t)]}{dt} = maA{\it\Omega}\sin({\it\Omega}t)\cos({\it\Omega}t) = -\dfrac{maA{\it\Omega}}{2}\sin(2{\it\Omega}t)$
By considering the graph of sin(2Ωt), it can be seen that this quantity averages to zero over a full period from t = 0 to t = 2π/Ω, since every positive value is matched by an equivalent negative value.
(Alternatively, simply note that Equation 25b,
$\langle P\rangle = \langle P_{\rm res}\rangle\sin^2\delta$(Eqn 25b)
implies $\langle P\rangle = 0$ when δ = 0°.)
In the high frequency limit
Ω ≫ ω0 and x (t) = A sin(Ωt − 180°) = −A sin(Ωt)
The instantaneous power P (t) is then:
$P(t) = ma\sin({\it\Omega}t)\dfrac{d[-A\sin({\it\Omega}t)]}{dt} = -maA{\it\Omega}\sin({\it\Omega}t)\cos({\it\Omega}t) = -\dfrac{-maA{\it\Omega}}{2}\sin(2{\it\Omega}t)$
This is zero, as sin(2Ωt) averages to zero over a full period from t = 0 to t = 2π/Ω.
(Alternatively, simply note that Equation 25b,
$\langle P\rangle = \langle P_{\rm res}\rangle\sin^2\delta$(Eqn 25b)
implies $\langle P\rangle = 0$ when δ = 0°.)
Figure 4 was drawn for an oscillator with the rather small Q–factor of 1. It is interesting to enquire how the situation would be changed if an oscillator with a larger value of Q had been considered. (For a fixed natural frequency, higher values of Q correspond to lighter damping.) Using the light damping result,
$\langle P_{\rm res}\rangle = \dfrac{ma^2}{2\gamma}$(Eqn 24)
this may be written in the form
$\langle P_{\rm res}\rangle = \dfrac{ma^2}{2\gamma} = \dfrac{ma^2Q}{2\omega_0}$
showing that for oscillators of the same natural frequency and mass, driven by the same force, the average power transfer over a full cycle at resonance is proportional to the Q–value. Thus Q acts as an amplification factor for the power absorbed. This explains why very lightly damped oscillators resonate more powerfully than heavily damped ones.
In addition to its height, given by Equation 25a,
$\langle P\rangle = \left(\dfrac{\gamma A{\it\Omega}}{a}\right)^2\langle P_{\rm res}\rangle$(Eqn 25a)
the power resonance curve of Figure 4 is also characterized by its width. This may be defined as the (positive) difference between the half–power points $\dfrac{\omega_1}{\omega_0}\;\text{and}\;\dfrac{\omega_2}{\omega_0}$ at which $\langle P\rangle = \frac12 \langle P_{\rm res}\rangle$. In order that they should correspond to half–power points, ω1 must be the driving angular frequency at which δ = 45° and ω2 that at which δ = 135°. At both of these values the power factor is 0.5, so that $\langle P\rangle$ exceeds $\langle P_{\rm res}/2\rangle$ in the range ω1 < Ω < ω2. This is illustrated in Figure 4.
The average power absorption $\langle P\rangle$ attains its maximum at the resonance frequency f0, but it remains significant throughout the range of angular driving frequencies between the half–power points.
The corresponding frequency range
∆f = (ω2 − ω1)/2π
is called the resonance absorption bandwidth of the oscillator. This too depends on the Q–factor of the oscillator, since it can be shown that ω2 − ω1 = γ, (see Question T11) implying that
resonance absorption bandwidth $\Delta f = \dfrac{\omega_2-\omega_1}{2\pi} = \dfrac{\gamma}{2\pi} = \dfrac{\omega_0}{2\pi Q} = \dfrac{f_0}{Q}$(26)
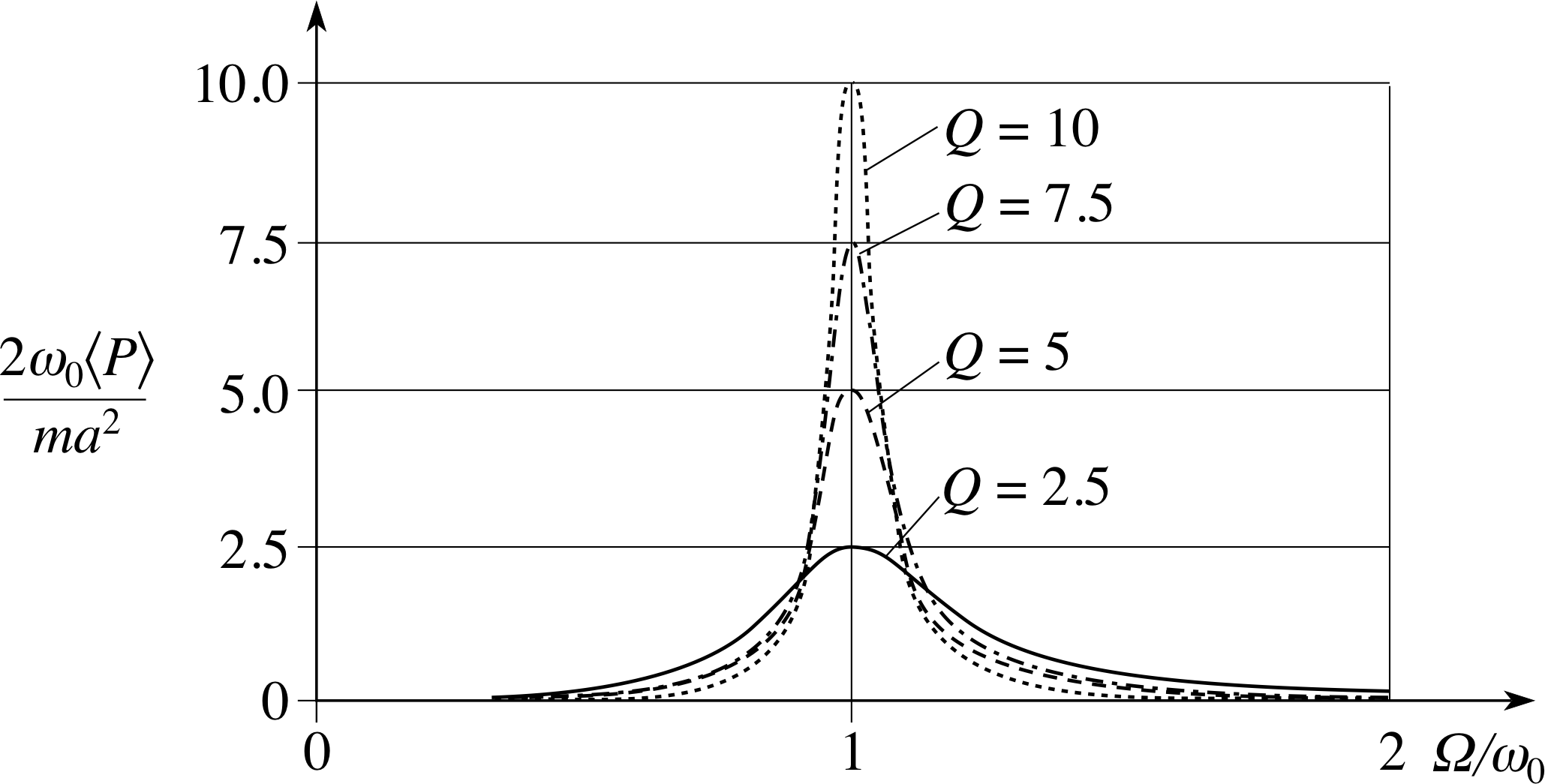
Figure 5 Graphs of $2\omega_0\langle P\rangle/(ma^2)$ against Ω/ω0 for oscillators of different Q.
The resonance absorption bandwidth therefore becomes narrower as the Q–factor increases, and it follows from Equation 26 that a simple expression for the Q–factor is Q = f0/∆f. It follows that for high Q oscillators the power resonance is proportionally very tall and narrow. Power resonance curves for a few Q–values are shown in Figure 5.
Question T10
Describe two features of the performance of an oscillator that are determined by its quality factor Q.
Answer T10
For a given driven oscillator, in the steady state, Q determines the ratio of the amplitude at resonance to the amplitude in the low frequency limit. The Q–factor of an oscillator also determines the relative sharpness of the peak of its average power absorption curve (a plot of $\langle P\rangle$ against Ω), in the sense that the peak value of $\langle P\rangle$ increases with Q and the resonance absorption bandwidth decreases in proportion to Q−1.
Question T11
Show that the power factor of an oscillator may be written in the form:
$\dfrac{\langle P\rangle}{\langle P_{\rm res}\rangle} = \left[1 + Q^2\left(\dfrac{{\it\Omega}}{\omega_0} - \dfrac{\omega_0}{{\it\Omega}}\right)^2\right]^{-1}$
and use this to obtain expressions for ω1 and ω2. Hence show that ω2 − ω1 = γ, as claimed above.
Answer T11
The power factor is
$\sin^2\delta = \gamma^2{\it\Omega}^2\left(\dfrac Aa\right)^2$
Using Equation 15,
$A = \dfrac{a}{\sqrt{\smash[b]{(\omega_0^2-{\it\Omega}^2)^2+(\gamma{\it\Omega})^2}}}$(Eqn 15)
we can write:
$\sin^2\delta = \dfrac{\gamma^2{\it\Omega}^2a^2}{a^2[(\omega_0^2-{\it\Omega}^2)^2+(\gamma{\it\Omega})^2]} = \left[\dfrac{[(\omega_0^2-{\it\Omega}^2)^2+(\gamma{\it\Omega})^2]}{\gamma^2{\it\Omega}^2}\right]^{-1}\\\phantom{\sin^2\delta} = \left[1 + \dfrac{(\omega_0^2-{\it\Omega}^2)^2}{\gamma^2{\it\Omega}^2}\right]^{-1} = \left[1 + \left(\dfrac{\omega_0^2}{\gamma{\it\Omega}}\right)^2 - \left(\dfrac{\it\Omega^2}{\gamma{\it\Omega}}\right)^2\right]^{-1} = \left[1+\left(\dfrac{\omega_0}{\gamma}\right)^2\left(\dfrac{\omega_0}{\it\Omega} - \dfrac{\it\Omega}{\omega_0}\right)^2\right]^{-1}$
This is the required result since Q = ω/γ.
At ω1 and ω2, the power factor is 1/2, so that:
$\dfrac12 = \left[1+\left(\dfrac{\omega_0}{\gamma}\right)^2\left(\dfrac{\omega_0}{\it\Omega} - \dfrac{\it\Omega}{\omega_0}\right)^2\right]^{-1}$
$2 = 1+\left(\dfrac{\omega_0}{\gamma}\right)^2\left(\dfrac{\omega_0}{\it\Omega} - \dfrac{\it\Omega}{\omega_0}\right)^2$
$\left(\dfrac{\gamma}{\omega_0}\right)^2 = \left(\dfrac{\omega_0}{\it\Omega} - \dfrac{\it\Omega}{\omega_0}\right)^2$
$\dfrac1Q = \left\lvert\,\dfrac{\omega_0}{\it\Omega} - \dfrac{\it\Omega}{\omega_0}\,\right\rvert$
Since ω1 < ω0, we have
$\dfrac{\omega_0}{\omega_1} - \dfrac{\omega_1}{\omega_0} = \dfrac1Q$
so$\dfrac{\omega_0^2-\omega_1^2}{\omega_1\omega_0} = \dfrac1Q$
or$\omega_1^2 + \left(\dfrac{\omega_0}{Q}\right)\omega_1 - \omega_0^2 = 0$
Solving this quadratic equation for ω1, we have
$\omega_1 = -\dfrac{(\omega_0/Q) \pm \sqrt{\smash[b]{(\omega_0^2/Q^2)+4\omega_0^2}}}{2}$
or$\omega_1 = -\dfrac{\omega_0}{2Q} \pm \omega_0\sqrt{1+\dfrac{1}{4Q^2}}$
Similarly, since ω2 > ω0, we have
$\dfrac{\omega_2}{\omega_0} - \dfrac{\omega_0}{\omega_2} = \dfrac1Q$
$\omega_2^2 + \left(\dfrac{\omega_0}{Q}\right)\omega_2 - \omega_0^2 = 0$
Solving this quadratic equation for ω2, we have
$\omega_2 = \dfrac{(\omega_0/Q) \pm \sqrt{\smash[b]{(\omega_0^2/Q^2)+4\omega_0^2}}}{2}$
or$\omega_2 = \dfrac{\omega_0}{2Q} \pm \omega_0\sqrt{1+\dfrac{1}{4Q^2}}$
Thus, taking the positive roots, ω2 − ω1 is given by
$\omega_2-\omega_1 = \dfrac{\omega_0}{2Q} + \dfrac{\omega_0}{2Q} = \dfrac{\omega_0}{Q} = \gamma$
2.5 Transient motion
The steady state motion, expressed by Equation 9,
steady state motion x(t) = A sin(Ωt − δ)(Eqn 9)
is just one possible motion for a harmonically driven oscillator. In the present subsection we will refer to the steady state motion as xss(t). In contrast, the general solution of the homogeneous differential equation,
linearly damped oscillator: $\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega_0^2x = 0$(Eqn 5)
that describes an undriven linearly damped oscillator is a transient motion of the form:
transient motion: xtr (t) = Be−γt/2 cos(ωt + ϕ)(27) i
where B and ϕ are arbitrary constants determined by the initial conditions of the motion, and $\omega = \sqrt{\omega_0^2-\dfrac{\gamma^2}{4}}$
Interestingly this kind of transient motion is also relevant to a driven oscillator. To see why this is so note that the steady state motion is a solution to Equation 4,
$\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega_0^2x = a\sin({\it\Omega}t)$Eqn (4)
so$\dfrac{d^2x_{\rm ss}}{dt^2} + \gamma\dfrac{dx_{\rm ss}}{dt} + \omega_0^2x_{\rm ss} = a\sin({\it\Omega}t)$
but the transient motion of Equation 27,
transient motion: xtr (t) = Be−γt/2 cos(ωt + ϕ)(Eqn 27)
is a solution to Equation 5,
linearly damped oscillator: $\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega_0^2x = 0$(Eqn 5)
so$\dfrac{d^2x_{\rm tr}}{dt^2} + \gamma\dfrac{dx_{\rm tr}}{dt} + \omega_0^2x_{\rm tr} = 0$
adding corresponding terms in these two equations,
$\left(\dfrac{d^2x_{\rm ss}}{dt^2} + \dfrac{d^2x_{\rm tr}}{dt^2}\right) + \gamma\left(\dfrac{dx_{\rm ss}}{dt} + \dfrac{dx_{\rm tr}}{dt} \right) + \omega_0^2(x_{\rm tr} + x_{\rm tr}) = a\sin({\it\Omega}t)$
and using the mathematical property that the derivative of a sum is a sum of derivatives:
$\dfrac{d^2(x_{\rm ss}+x_{\rm tr})}{dt^2} + \gamma\dfrac{d(x_{\rm ss}+x_{\rm tr})}{dt} + \omega_0^2(x_{\rm tr} + x_{\rm tr}) = a\sin({\it\Omega}t)$
This is just Equation 4 with (xss + xtr) in place of x. Hence (xss + xtr) is also a solution of the inhomogeneous differential equation that describes a damped driven harmonic oscillator. The full solution, including both the steady state and the transient motion is therefore:
x (t) = xss(t) + xtr(t) = A sin(Ωt − δ) + B e−γt/2 cos(ωt + ϕ)(28) i
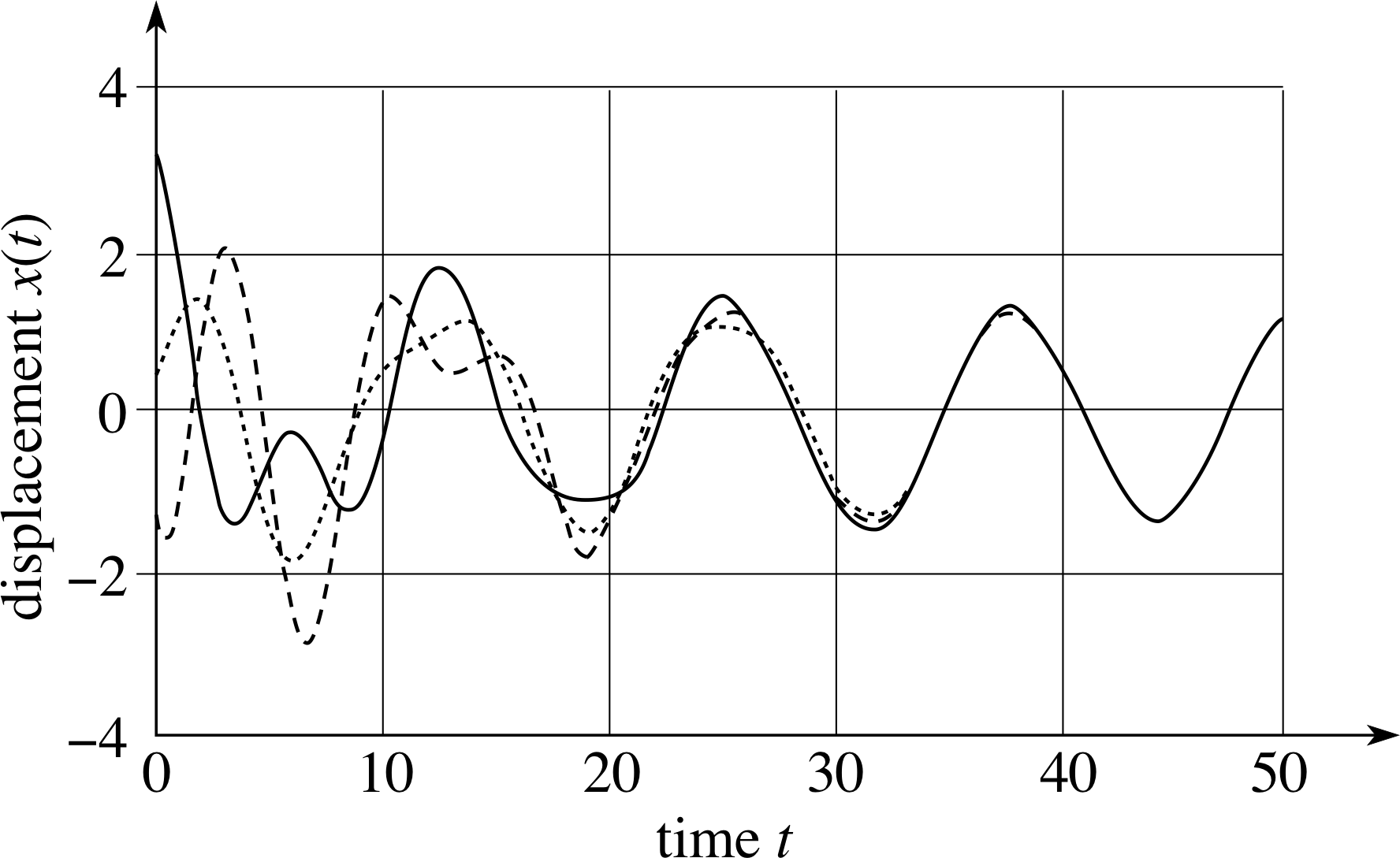
Figure 6 Displacement–time graphs for the same oscillator with three different sets of initial conditions (different choices of B and ϕ).
Equation 28 gives a complete representation of the motion of this driven oscillator, including the transient phase. Whatever the starting conditions, as embodied in the values of B and ϕ, the transient term, xtr, in Equation 28 becomes negligible for t ≫ 2π/γ, so that when t ≫ 2π/γ
x (t) ≈ xss(t) = A cos(ωt − δ)
This is illustrated in Figure 6, which shows the displacement–time graphs of a driven oscillator with various starting conditions. The transient behaviour and the onset of steady state motion can both be clearly seen.
Question T12
The constants B and ϕ that appear in Equation 28 are the arbitrary constants that are determined by the starting conditions of the oscillator. Why can’t the constants A and δ be regarded in the same way?
Answer T12
As we saw in Subsection 2.3, the constants A and δ that appear in the steady state motion are determined by the value of Ω and the various constants that characterize the oscillator, they are not adjustable in the sense that they cannot be altered by changing the starting position or initial velocity of the oscillator. This feature distinguishes them from B and ϕ.
2.6 Resonance and frequency standards
So far we have developed the mathematical model of the driven oscillator by thinking of mechanical oscillations and mechanical resonance. As we mentioned in the introduction there are many other examples of resonance from non–mechanical oscillator systems. The electrical response of a tuned circuit or the resonant response of a tuned cavity or an atom or nucleus to an electromagnetic wave are cases in point. The damping is caused by any process through which energy can be transferred out of the vibrational system, often through heating. For example, in an electrical circuit the dissipation arises from the heating effect of the current as it flows through any circuit resistance. While these other systems are not always amenable to the simple linearly damped mathematical model introduced here, the model enables us to appreciate the processes involved.
We can describe all these systems in terms of resonance, with an appropriate Q–factor implied by the frequency response shown on the power absorption curve. In some cases these systems have Q–factors which are very much larger than those of the mechanical systems considered thus far and so the frequency response is a great deal narrower and more selective. If the frequency of an oscillator is narrowly defined then the period of the oscillation is also narrowly defined and the oscillator can be used as a clock. For this reason, resonant systems find widespread application in the maintenance of frequency or time standards. The higher the Q–factor of the oscillator the greater the potential for using the resonant oscillator as a well–defined frequency standard. Here we cannot describe these systems in any detail but it is worth mentioning a few important examples and quoting the Q–factors that typify them.
We begin with a simple familiar mechanical oscillator, the pendulum clock.
The pendulum oscillations are sustained by energy input to compensate for dissipative processes, such as friction. The damping of the system is minimized and an estimate for the Q–factor achieved can be found from Equation 26,
resonance absorption bandwidth $\Delta f = \dfrac{\omega_2-\omega_1}{2\pi} = \dfrac{\gamma}{2\pi} = \dfrac{\omega_0}{2\pi Q} = \dfrac{f_0}{Q}$(Eqn 26)
knowing the typical performance of a good mechanical clock. If the clock is to gain or lose by no more than 10 s a day then this is a fractional time error of 10 s in 24 × 3600 s, or about 10−4. The fractional frequency error is the same as the fractional time error and if we take a typical frequency error to be the full width of the power curve at half height i (i.e. ∆f) then Equation 26 gives the required Q–value as f0/∆f = 104.
Our next example is a quartz crystal oscillator, such as is used in a watch. This is another mechanical oscillation, but on a smaller size scale and at a much higher frequency (a few tens of kHz). Some materials (quartz, for example) have the property that an applied electric field causes mechanical stresses in the material. They are said to be piezoelectric materials and an oscillating voltage applied across them causes them to vibrate at the driver frequency, rather like a loudspeaker, but piezoelectric crystals can respond at much higher driver frequencies than is possible for a conventional loudspeaker. In the quartz crystal oscillator the mechanical oscillations of the crystal are maintained by electrical oscillations in a circuit which drives the crystal. The crystal resonance stabilizes the frequency of these oscillations and makes the resonance of the tuned circuit much sharper. The oscillations are then counted and this is converted into a time display. Such watches are capable of an order of magnitude better time–keeping than the pendulum clock and so the required Q–value is about 105. High quality quartz–controlled clocks can do rather better than this but our next example shows a spectacular improvement on this.
The caesium atomic clock is so precise that its oscillations are used to establish and maintain our fundamental unit of time, the second. The oscillations here are rather far removed from mechanical oscillations; they correspond to a characteristic internal transition frequency within single caesium atoms. This is not the place to go into details of this process but suffice to say that caesium atoms can absorb electromagnetic radiation at a frequency of around 9192 MHz, in a resonant process. i For our purpose here the important point is that the sharpness of the atomic resonance can be made so great that the full resonance absorption bandwidth is as low as 1 Hz. With a basic resonance frequency of 9192 MHz this gives a Q–factor of about 1010!
Sophisticated technology is used to stabilize the frequency to within a small fraction of this bandwidth and the frequency of such clocks can then be made reproducible to about 1 part in 1013. Two such clocks will keep the same time to within about 3 seconds in a million years! Unfortunately, these clocks are of a size which would fill a medium–sized room and you would not want one strapped around your wrist. Their use is confined to establishing the international time standard and in calibrating other more portable clocks. Such high precision is needed in certain scientific experiments. For example, caesium clocks flown in aircraft have enabled the direct observation of the tiny time changes for moving clocks, predicted by Einstein’s special theory of relativity.
Even the caesium clock could be made to look rather crude when compared to future clocks that may be based on frequency-stabilized lasers. In a laser the oscillators are effectively an ensemble of atoms in a cavity, rather than individual atoms, and the driver is an electromagnetic wave (light), trapped within the same cavity, between mirrors. The atoms absorb and re–emit the wave within the cavity but because they are all in communication with the same wave they all absorb and emit with well–defined phases, rather than with random phases as would be the case if they were acting individually. Such phase–organized light is called coherent light. The process by which an incoming wave drives an atom to emit is known as stimulated emission and it is the counterpart to absorption. If the stimulated emission exceeds the absorption then this will give rise to laser action, or Light Amplification by Stimulated Emission of Radiation. Within the cavity of a laser oscillator there is a single giant amplitude oscillation with a well–defined phase and an extremely well–defined frequency. The frequency output bandwidth for the laser is very much narrower than would be the case if the same atoms were placed outside the cavity, as in an ordinary lamp.
Lasers have many advantages over conventional light sources but the one that concerns us here is this very narrow bandwidth. It gives rise to an enormous value for the Q–factor of the oscillator. The full resonance bandwidth of a laser oscillator can be made to be only a few Hz, even when the laser is operating in the visible spectrum, at frequencies of around 5 × 1014 Hz. If such a laser could also have its frequency stabilized sufficiently to capitalize on this low bandwidth then the resulting frequency–stabilized laser could have a Q–factor of around 1014, with a potential improvement factor of 104 over the caesium clock. The technology for this is under development and stabilized lasers could well be the reference clocks of the future.
3 Coupled oscillators
In the previous section we considered how an oscillator is affected by an oscillatory (harmonic) driving force. This force has been taken to be so robust that its driving mechanism is not affected by the oscillator. Let us now take a look at what happens when the driving force is replaced by another oscillator.
3.1 Normal modes
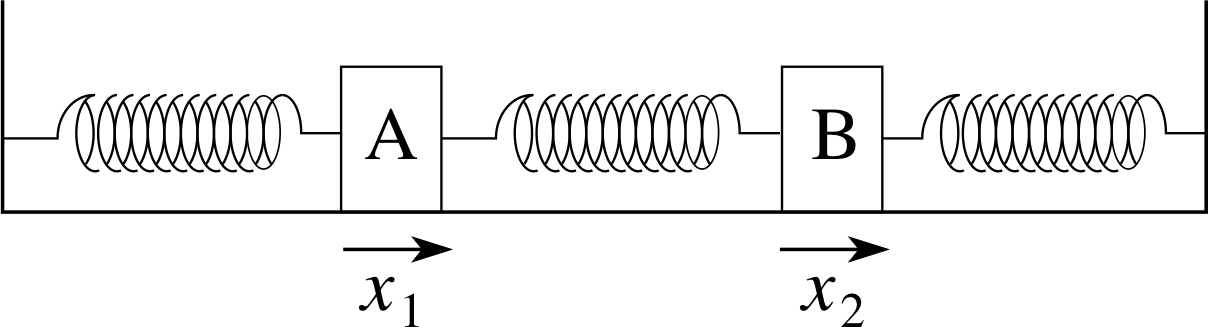
Figure 7 A model of two coupled oscillators.
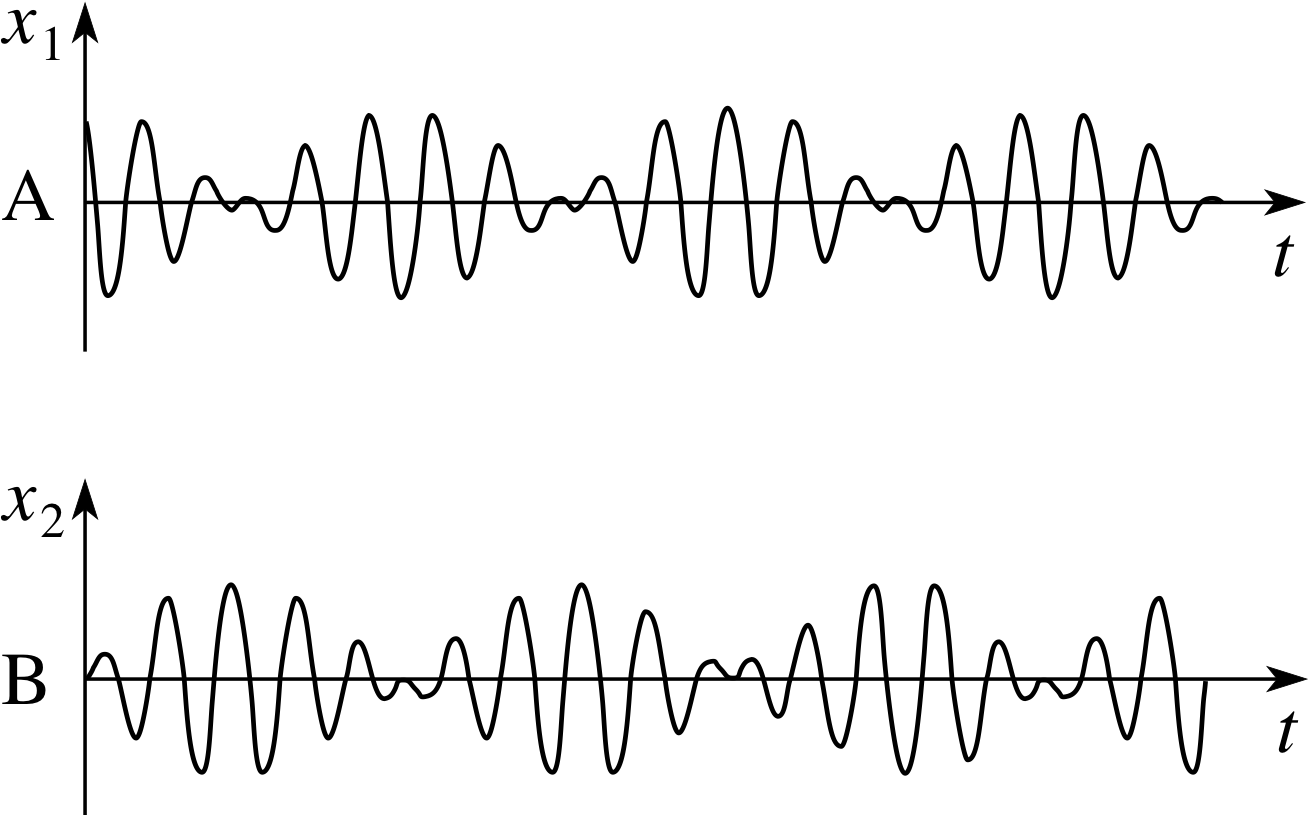
Figure 8 The transfer of energy between two coupled oscillators.
As a specific example, consider two identical oscillators, consisting of equal masses A and B, resting on a smooth horizontal surface and connected by identical springs to two rigid walls, as shown in Figure 7. The two masses are also connected together by another spring, which we will suppose to be much weaker than the two main ones. Initially the two masses are at rest at their equilibrium positions.
Now let us move A from its equilibrium position, while holding B fixed, and then let go of both. A will immediately start to oscillate, but because of the coupling between the two masses, it will excite an oscillation of increasing amplitude in B. There is only a limited amount of energy to supply these oscillations, so as the amplitude of B increases that of A must decrease. Surprisingly, this exchange of energy does not stop when the two amplitudes are equal, but continues until A is stationary and B is moving with the full amplitude that A had at the start. The process is then reversed, with the B amplitude decreasing and that of A increasing until the starting configuration is reached and the whole process is repeated ad infinitum, or until damping reduces the vibrational energy to zero.
Figure 8 shows how the two displacements vary with time.
✦ Are these the sort of time variations we should expect for two harmonic oscillators?
✧ No, because in a harmonic oscillator the amplitude is constant and the form of the displacement is
x = x0 sin(ωt + ϕ)
with x0 constant.
The form of the curves in Figure 8 is more like:
x (t) = x0 cos(ω ′ t) cos(ωt + ϕ)
the constant amplitude x0 has been replaced by a variable one x0 cos(ω ′ t), where the angular frequency ω ′ is much less than the angular frequency ω.
The overall motion of the two coupled oscillators looks quite complicated and neither oscillator moves with simple harmonic motion. However, the motion is periodic and this encourages us to A ask whether there is any concealed simple harmonic motion in this system. As you will soon see, the answer is yes, and these motions are remarkably simple in this case – once we expose them.
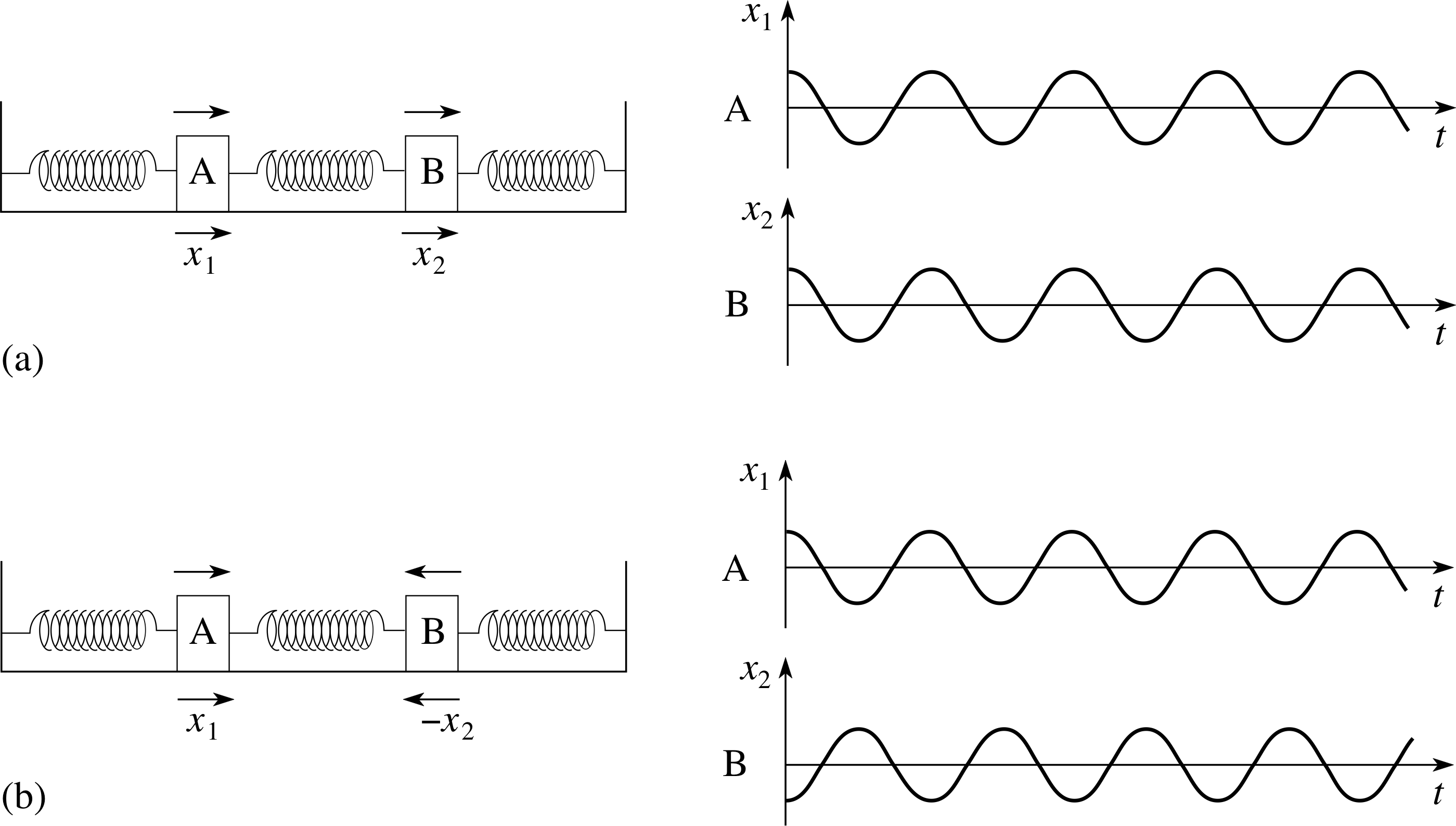
Figure 9 (a) Masses moving in phase; (b) masses moving out of phase.
When we disturb the system of Figure 7 in different ways we notice that, as we have described, usually the state of motion changes with time, with one mass first oscillating vigorously then becoming quiescent, while the other does the same but with opposite periods of activity, as the energy is switched back and forth. However, there are two particular patterns of relative motion in which the motion continues unchanged, with neither mass changing its energy with time.
In one of these motions the two identical masses move together, in phase, with equal amplitude, as shown in Figure 9a. The distance between the two will remain unchanged, so the coupling spring will have no effect on the motion, and the frequency of oscillation will be just the same as if the two were uncoupled. In the other motion the two masses move in opposite directions with equal amplitude, as shown in Figure 9b.
✦ Would you expect this second oscillation to have the same frequency as the first? If not, will the frequency be higher or lower?
✧ In the second case the coupling spring is alternately stretched and compressed, so that the restoring force is greater than before, and the resulting frequency will thus be higher than before.
These two forms of steady state oscillation are simple harmonic motions, with constant amplitudes, and are known as the two normal modes of this system. Such normal modes always appear whenever two or more oscillators are coupled together. Any motion of the system can be analysed in terms of an appropriate superposition of these normal modes of the system, as we will see shortly, so the normal modes can be considered as the basic SHM building blocks of any oscillation of the system.
These two normal modes may then be identified through the mass displacements x1(t) and x2(t) as:
for ω = ω1 = ωx1(t) = x0 cos(ω0t) and x2(t) = x0 cos(ω0t)(29a)
for ω = ω2x1(t) = x0 cos(ω2t) and x2(t) = −x0 cos(ω2t)(29b)
We will now show that the complicated motions depicted in Figure 8 and the simple normal modes in Figure 9 are related. To do this we need to invoke the idea of the superposition of two simple harmonic motions.
The principle of superposition states that:
When several oscillations are added, the resultant displacement at any time is the sum of the displacements due to each oscillation at that time. i
Now let us construct an oscillation representing 50% of mode 1 and 50% of mode 2 by superposing the two
normal modes of Equation 29. We obtain:
$x_1(t) = \frac12[x_0\cos(\omega_0t) + x_0\cos(\omega_2t)]$
$x_2(t) = \frac12[x_0\cos(\omega_0t) - x_0\cos(\omega_2t)]$
Using an identity from Question R4 we can write these as
$x_1(t) = x_0\cos\left(\dfrac{\omega_2-\omega_0}{2}\right)\cos\left(\dfrac{\omega_2+\omega_0}{2}\right)$(30a)
$x_2(t) = x_0\sin\left(\dfrac{\omega_2-\omega_0}{2}\right)\sin\left(\dfrac{\omega_2+\omega_0}{2}\right)$(30b) i
Question T13
Verify Equations 30a and 30b.
Answer T13
From Question R4 we have
cos(θ + ϕ) = cos θ cosϕ − sin θ sin ϕ
andcos(θ − ϕ) = cos θ cos ϕ + sin θ sin ϕ
thencos(θ + ϕ) + cos(θ − ϕ) = 2 cos θ cos ϕ
andcos(θ + ϕ) − cos(θ − ϕ) = 2 sin θ sin ϕ
If we now substitute
$\theta = \dfrac12 (\omega_2+\omega_0)t\quad\text{and}\quad\phi = \dfrac12(\omega_2-\omega_0)t$,
we have
θ + ϕ = ω2t and θ − ϕ = ω0t
and the answer follows at once.

Figure 8 The transfer of energy between two coupled oscillators.
Since ω0 and ω2 are different, but usually not greatly different, each of the right–hand sides in these equations is a product of a slowly oscillating term, involving (ω2 − ω0), and a rapidly oscillating one involving (ω2 + ω0).
If we refer back to Figure 8 we can see that this slowly oscillating term can be interpreted as describing the overall slowly changing amplitude of the motion of each mass, often referred to as beating, at the difference frequency of the two modes. The rapid oscillation of each mass is represented by the mean frequency of the two modes.
Question T14
After what time does the mass A come to rest, with all the motion passed to mass B? How long is it before A is moving again with maximum amplitude and with B stationary?
Answer T14
If we think of $x_0\cos\left(\dfrac{\omega_2-\omega_0}{2}\right)t$ as the slowly varying amplitude of the A oscillation, and $x_0\sin\left(\dfrac{\omega_2-\omega_0}{2}\right)t$ as the slowly varying amplitude of the B oscillation, then we can see that after time t = π/(ω2 − ω0) the amplitude of A is zero, and that of B is a maximum. After time t = 2π/(ω2 − ω0) the situation is reversed and the amplitude of A is a maximum again and that of B is zero.
Normal modes appear in any situation where we have oscillations coupled together, and when there is a large number of oscillators – an extreme case is the atoms in a crystal, the forms of oscillation and their frequencies can become extremely complex. However, the main points to bear in mind are:
Any set of oscillators coupled together will result in normal modes which carry out simple harmonic motion.
The frequencies of the normal modes are almost always different from the frequencies of the uncoupled oscillators.
4 Closing items
4.1 Module summary
- 1
-
Freely oscillating systems are characterised by natural frequencies of oscillation. The action of damping forces will generally modify the frequency of an oscillator, and cause its amplitude to diminish with time. Oscillations in damped systems may be sustained by means of an externally applied driving force; such oscillators are called forced or driven oscillators. Under appropriate conditions, a periodic driving force with a period close to the natural period of an oscillator can cause a driven oscillator to develop oscillations of relatively large amplitude; this condition is known as resonance.
- 2
-
The harmonically driven linearly damped oscillatorequation of motion of a harmonically driven, linearly damped oscillator is a inhomogeneous differential equation of the form:
$\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega_0^2x = a\sin({\it\Omega}t)$Eqn (4)
If the driving force is absent (a = 0) the remaining (homogeneous) differential equation describes a linearly damped oscillator:
linearly damped oscillator: $\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega_0^2x = 0$(Eqn 5)
and if γ = 0, we obtain the equation of motion of a simple harmonic oscillator
simple harmonic oscillator: $\dfrac{d^2x}{dt^2} + \omega_0^2x = 0$(Eqn 6)
- 3
-
The full solution of the driven oscillator equation can be regarded as the sum of two parts; one describing the transient motion which effectively decays to zero after a time of order 2π/γ, and one describing the persisting steady state motion that is sustained by the driving force.
- 4
-
Once it has entered the steady state, the driven oscillator acquires the same frequency as the driving force, though there is generally a constant phase lag between the driving force (F3x = ma sin(Ωt)) and the oscillator’s displacement. The steady state motion is therefore independent of the starting conditions and can be written as
x (t) = A sin(Ωt − δ)(Eqn 9)
- 5
-
In the steady state, the amplitude A and the phase lag δ both depend on the driving frequency Ω and are given by:
general case amplitude $A = \dfrac{a}{\sqrt{\smash[b]{(\omega_0^2-{\it\Omega}^2)^2+(\gamma{\it\Omega})^2}}}$(Eqn 15)
general case phase lag: $\delta = \arctan\left(\dfrac{\gamma{\it\Omega}}{\omega_0^2-{\it\Omega}^2}\right)$(Eqn 16)
The amplitude is almost independent of Ω at low frequencies, attains a maximum value at resonance, which defines the resonance frequency, and then decreases at high frequency. The phase lag is small at low frequency, 90° at the undamped natural frequency, which is near resonance and approaches 180° at high frequency. In particular:
in the low frequency limit: $x(t) = \left(\dfrac{a}{\omega_0^2}\right)\sin({\it\Omega}t)$(Eqn 10)
in the high frequency limit: x (t) = a sin(Ωt − π)(Eqn 11)
and in the resonance limit (Ω = ω0 for the case of light damping):
$x(t) = \left(\dfrac{a}{\gamma\omega_0}\right)\sin\left({\it\Omega}t-\dfrac{\pi}{2}\right)$(Eqn 12)
In the latter case the resonance amplitude exceeds the low frequency amplitude by the oscillator’s quality factor Q = ω0/γ.
- 6
-
In the steady state, the total energy, kinetic energy and potential energy are all functions of time, and are given by
Equation 18total energy$E = \dfrac12 mA^2\left[{\it\Omega}^2\cos^2({\it\Omega}t - \delta) + \omega_0^2A^2\sin^2({\it\Omega}t - \delta)\right]$(18)
Equation 19kinetic energy$E_{\rm kin} = \dfrac12 mA^2{\it\Omega}^2\cos^2({\it\Omega}t - \delta)$(19)
Equation 20potential energy$E_{\rm pot} = \dfrac12 mA^2\omega_0^2A^2\sin^2({\it\Omega}t - \delta)$(20)
However, the average value of each of these quantities, taken over a full period of oscillation, has a constant value, as given by
$\langle E\rangle = \langle E_{\rm kin}\rangle + \langle E_{\rm pot}\rangle = \dfrac14 mA^2{\it\Omega}^2 + \dfrac14 mA^2\omega_0^2 = \dfrac14 mA^2({\it\Omega}^2+\omega_0^2)$(Eqn 21)
The average total energy is mostly potential energy below resonance, and mostly kinetic energy above resonance. At resonance, in the case of light damping (when Ω = ω0), the total energy is independent of time, potential and kinetic energy contribute equally to the total, and
$E = \langle E_{\rm kin}\rangle = \dfrac12 mA^2\omega_0^2$
- 7
-
In the steady state, the average power $\langle P\rangle$ transferred to the oscillator from the driving force, is exactly equal to the average power dissipated by the damping force.
- 8
-
The average power absorption, $\langle P\rangle$, exhibits resonance behaviour, i.e. it rises to a maximum when the driving frequency is close to the undamped natural frequency. The height of the maximum is proportional to Q, and its width is proportional to Q−1. Thus, more lightly damped oscillators (characterized by larger values of Q), have taller and narrower resonance peaks. The average power transfer at resonance is:
$\langle P_{\rm res}\rangle = \dfrac{ma^2}{2\gamma}$(Eqn 24)
and the resonance absorption bandwidth is:
$\Delta f = \dfrac{\omega_2-\omega_1}{2\pi} = \dfrac{\gamma}{2\pi} = \dfrac{\omega_0}{2\pi Q} = \dfrac{f_0}{Q}$(Eqn 26)
- 9
-
One important application of resonance absorption is to establish oscillators whose frequencies are very well-defined; these can constitute frequency and time standards.
- 10
-
The transient motion for the driven oscillator can be represented by:
transient motion: xtr (t) = Be−γt/2 cos(ωt + ϕ)(Eqn 27)
where B and ϕ are arbitrary constants determined by the initial conditions of the motion, and $\omega = \sqrt{\omega_0^2-\dfrac{\gamma^2}{4}}$
- 11
-
The general solution to the equation of motion for the harmonically driven, linearly damped harmonic oscillator may be written
x (t) = xss(t) + xtr(t) = A sin(Ωt − δ) + B e−γt/2 cos(ωt + ϕ)(Eqn 28)
- 12
-
When two oscillators are coupled together, the energy of oscillation may be exchanged continually between them.
- 13
-
The simple harmonic motions of a pair of identical coupled oscillators are the normal modes, consisting of in–phase and out-of-phase motions of the two. These can be represented as:
for ω = ω1 = ωx1(t) = x0 cos(ω0t) and x2(t) = x0 cos(ω0t)(Eqn 29a)
for ω = ω2x1(t) = x0 cos(ω2t) and x2(t) = −x0 cos(ω2t)(Eqn 29b)
When these two normal modes are superposed the resulting oscillation has the average frequency of the two modes and the superposed amplitude shows beats at the difference frequency:
$x_1(t) = x_0\cos\left(\dfrac{\omega_2-\omega_0}{2}\right)\cos\left(\dfrac{\omega_2+\omega_0}{2}\right)$(Eqn 30a)
$x_2(t) = x_0\sin\left(\dfrac{\omega_2-\omega_0}{2}\right)\sin\left(\dfrac{\omega_2+\omega_0}{2}\right)$(Eqn 30b)
- 14
-
Any set of oscillators coupled together will result in normal modes which carry out simple harmonic motion. The frequencies of the normal modes are almost always different from the frequencies of the uncoupled oscillators.
4.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Describe what is meant by a driven oscillator, explaining its main response features in steady state motion and transient motion and how these may be varied, giving specific examples.
- A3
-
Write down the equation of motion of a harmonically driven linearly damped oscillator.
- A4
-
Derive the properties of the steady state motion from this equation.
- A5
-
Account for the main features of resonant behaviour in terms of the frequency dependence of the amplitude and phase lag in the steady state motion.
- A6
-
Show that the average value of the total energy of the oscillator is constant, and that the proportion of kinetic energy increases from zero at low frequency to 50% at resonance and approaches 100% at high frequency.
- A7
-
Show that the average power absorbed from the driving force is equal to the average power dissipated by damping.
- A8
-
Discuss the resonance phenomenon in terms of the graph of average power absorbed against driving frequency, showing (in the case of light damping) that it possesses a peak of height proportional to Q and width proportional to Q−1, centred on the natural frequency.
- A9
-
Describe the importance of resonance and the Q–factor of an oscillator in relation to frequency standards, illustrating this with some examples.
- A10
-
Describe the possible motions that follow when two identical oscillators are coupled together, and explain how they can be described in terms of the normal modes of the system.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
4.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions each of which tests one or more of the Achievements.
Question E1 (A3 and A4)
An oscillator consists of a mass of 0.02 kg suspended from a spring with spring constant 50 N m−1. It is subject to a damping force of the form −bυx, where υx is the velocity and b = 0.5 kg s−1, and is driven by a harmonically varying force of amplitude 4 N and frequency 550 rpm. Calculate the amplitude and phase lag of the resulting steady state vibration.
Answer E1
The equation of motion of the oscillator is given by Equation 4,
$\dfrac{d^2x}{dt^2} + \gamma\dfrac{dx}{dt} + \omega_0^2x = a\sin({\it\Omega}t)$Eqn (4)
with γ = b/m, ω02 = k/m and a = F0/m
The steady state solution is:
x (t) = A sin(Ωt − δ)(Eqn 9)
where$A = \dfrac{a}{\sqrt{\smash[b]{(\omega_0^2-{\it\Omega}^2)^2+(\gamma{\it\Omega})^2}}}$(Eqn 15)
and$\delta = \arctan\left(\dfrac{\gamma{\it\Omega}}{\omega_0^2-{\it\Omega}^2}\right)$(Eqn 16)
The driving frequency is 550 rpm, which corresponds to 9.17 Hz, so that Ω = 57.6 s−1. The natural frequency
ω0 = (k/m)1/2 = (50 N m−1/0.02 kg)1/2 = 50.0 s−1
The factor (ω02 − Ω2) = −818 s−2
and a = F0/m = 4 N/0.02 kg = 200 m s−2
So$A = \rm \dfrac{200\,m\,s^{-1}}{\sqrt{(-818\,s^{-2})^2+\left(\cfrac{0.5\,kg\,s^{-1}\times57.6\,s^{-1}}{0.02\,kg}\right)^2}} = \dfrac{200\,m\,s^{-2}}{1.66\times10^3\,s^{-2}} = 0.121\,m$
and$\delta = \arctan\left(\dfrac{\gamma{\it\Omega}}{\omega_0^2-{\it\Omega}^2}\right) = \rm \arctan\left(\dfrac{0.5\,kg\,s^{-1}\times57.6\,s^{-1}}{0.02\,kg\times-818\,s^{-2}}\right) = 119.6°$
In the expression for δ we have taken the angle between 0 and 180°.
(Reread Subsections 2.2, 2.3 and 2.4 if you had difficulty with this question.)
Question E2 (A6)
For the oscillator in Question E1 calculate the average potential energy, the average kinetic energy and the average power absorbed.
Answer E2
From Equation 21,
$\langle E\rangle = \langle E_{\rm kin}\rangle + \langle E_{\rm pot}\rangle = \dfrac14 mA^2{\it\Omega}^2 + \dfrac14 mA^2\omega_0^2 = \dfrac14 mA^2({\it\Omega}^2+\omega_0^2)$(Eqn 21)
$\langle E_{\rm kin}\rangle = \dfrac14 m(A{\it\Omega})^2 = \rm 14\times0.02\,kg\times(0.12\,m\times57.6\,s^{-1})^2 = 0.243\,J$
$\langle E_{\rm pot}\rangle = \dfrac14\times0.02\,kg\times(0.12\,m\times50.0\,s^{-1})^2 = 0.183\,J$
The average power absorbed is given by Equation 23,
$\langle P\rangle = \dfrac12 m\gamma(A{\it\Omega})^2$(Eqn 23)
$\langle P\rangle = \rm \dfrac12\times0.02\,kg\times\dfrac{0.50\,N\,m^{-1}}{0.02\,kg}\times(0.121\,m\times57.6\,s^{-1})^2 = 12.1\,W$
(Reread Subsection 2.4 if you had difficulty with this question.)
Question E3 (A2, A5, A8 and A7)
Under what practical circumstances does one try to minimize the amplitude of a forced vibration? What methods can one use to do this?
Answer E3
There are many circumstances in engineering where unwanted vibrations occur; in particular, in almost any piece of machinery containing rotating parts, when unbalanced rotors may cause dangerous vibrations. A common example of this happens with unbalanced car wheels, which may start to vibrate at a particular road speed and make the car difficult to control. Other examples include bridges and tall buildings, which may be subject to wind–induced or earthquake–induced vibrations. The amplitude of such vibrations must be reduced by decreasing the Q–value of the oscillator; in other words, by increasing the damping of the system.
(Reread Section 2 if you had difficulty with this question.)
Question E4 (A2, A5, A8 and A7)
In designing a loudspeaker one wants to have as ‘flat’ a response as possible to different frequencies so the amplitude is independent of the driver frequency. What principles should one bear in mind when trying to achieve this? What unavoidable disadvantage accompanies the process?
Answer E4
A loudspeaker may have a number of resonant frequencies, associated with the different modes of vibration of the diaphragm, and with air vibrations in the cabinet. These may result in a very uneven response to music. To avoid these the Q–values of the different oscillating systems should be reduced as far as possible; one way of doing this is to fill the cabinet with damping material. The unavoidable disadvantage of this is the increased power required to obtain the same level of sound; a large proportion of the power supplied is dissipated in the damping material.
(Reread Subsections 2.5 and 2.6 if you had difficulty with this question.)
Question E5 (A2, A5, A8 and A9)
Under what practical circumstances does one try to maximize the amplitude of a forced vibration? How can one achieve this?
Answer E5
The amplitude of a forced vibration must be maximised when one is seeking a particular isolated frequency. One of the commonest examples of this is the resonant (tuned) circuit in a radio receiver, where it is often essential to eliminate the frequencies due to other transmitters. The Q–value can be increased by reducing the damping (resistance) in the circuit or by incorporating a piezoelectric crystal into the circuit, as in the quartz crystal oscillator. Many musical instruments, such as the xylophone or pipe organ, use resonators to enhance one frequency over other unwanted ones.
(Reread Subsection 2.6 if you had difficulty with this question.)
Question E6 (A10)
Two identical oscillators are connected together by weak coupling. Initially they are at rest.
(a) Describe what happens when one is made to oscillate.
(b) How does this behaviour change if the coupling is made stronger?
(c) What simple harmonic motions are possible in the system?
Answer E6
(a) First of all one oscillator, say A, is vibrating on its own; then the other, B, begins to vibrate with increasing amplitude, while the amplitude of A decreases. Eventually A comes to rest, and B is vibrating with the same amplitude that A had originally. Then the process is reversed; B gradually loses amplitude, which is regained by A, and after the same time as before A is vibrating alone and B is stationary. The whole process is then repeated over and over again.
(b) If the coupling is increased the frequency with which the motion oscillates between A and B increases. There may also be a change in the vibration frequency of the individual oscillators. In the example used in the module this frequency increases.
(c) Two normal modes of oscillation are possible. In one of these, A and B are oscillating in phase; in the other, they are oscillating out of phase. The first one has the lower frequency. In the example used in the module this is the frequency of the isolated oscillators, but more usually it will be lower than for the original, uncoupled case.
(Reread Section 3 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 4Closing items.