PHYS 6.2: Rays and geometrical optics |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
From the earliest period of civilization people have pondered over their reflections in pools of water and contemplated the distorted images of objects under the surface of those pools. Such everyday phenomena have intrigued and challenged natural philosophers for millennia, yet it was not until the end of the 16th century that the simple rules that govern them were presented in something akin to their modern mathematical form. These rules, all of which assume that light in a uniform medium travels along linear paths called rays, now provide the basis of geometrical optics, a field of study in which many optical conundrums are reduced to problems in geometry and trigonometry.
This module provides an introduction to geometrical optics. It describes the conditions under which the behaviour of light may be adequately described in terms of rays and uses the ray concept to describe reflection at a plane mirror (Section 3), refraction at a plane interface (Subsection 4.2), total internal reflection in a medium of relatively high refractive index and continuous refraction in a medium where the refractive index changes from place to place (Subsections 4.3 and 4.4). The phenomenon of optical mirages will be described as will the passage of light through an optical fibre (Subsection 4.4).
The module closes with a discussion (in Section 5) of Fermat’s principle which provides a unified basis for geometrical optics from which all of the subject’s basic laws and principles can be derived.
Most of the basic ideas in geometrical optics have been known for almost four hundred years, but do not fall into the trap of thinking that geometrical optics is a dead subject, of little relevance to the modern world – far from it. The very latest designs for camera lenses or telescope mirrors depend on intelligent application of the laws of optics, now augmented by computer power. Similarly, modern communication networks use the latest developments in optical fibre technology and rely on these same ideas.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 6.1Module summary and the Subsection 6.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 6.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
What is meant by the ray approximation in optics? Under what conditions can one use the ray approximation to describe the transmission of light?
Answer F1
The ray approximation in optics assumes that light travels from one point to another along a narrow path called a ray that may be represented by a directed line (i.e. a line with an arrow on it). In a uniform medium (where the refractive index is the same everywhere) the rays are straight lines, though they may be kinked at mirror surfaces or upon passing through the interface between two different media and they may bend continuously in non–uniform media where the refractive index changes smoothly with position.
The ray approximation gives an adequate description of light transmission provided diffraction effects can be ignored. This happens when the transverse dimensions of the optical systems or obstacles through or around which the light is passing are large compared with the wavelength of light.
Question F2
Using the laws of reflection of light, draw a diagram to show how your eye can see the virtual image of a point object in a plane mirror. If the object is 20 cm from the mirror, where is the image?
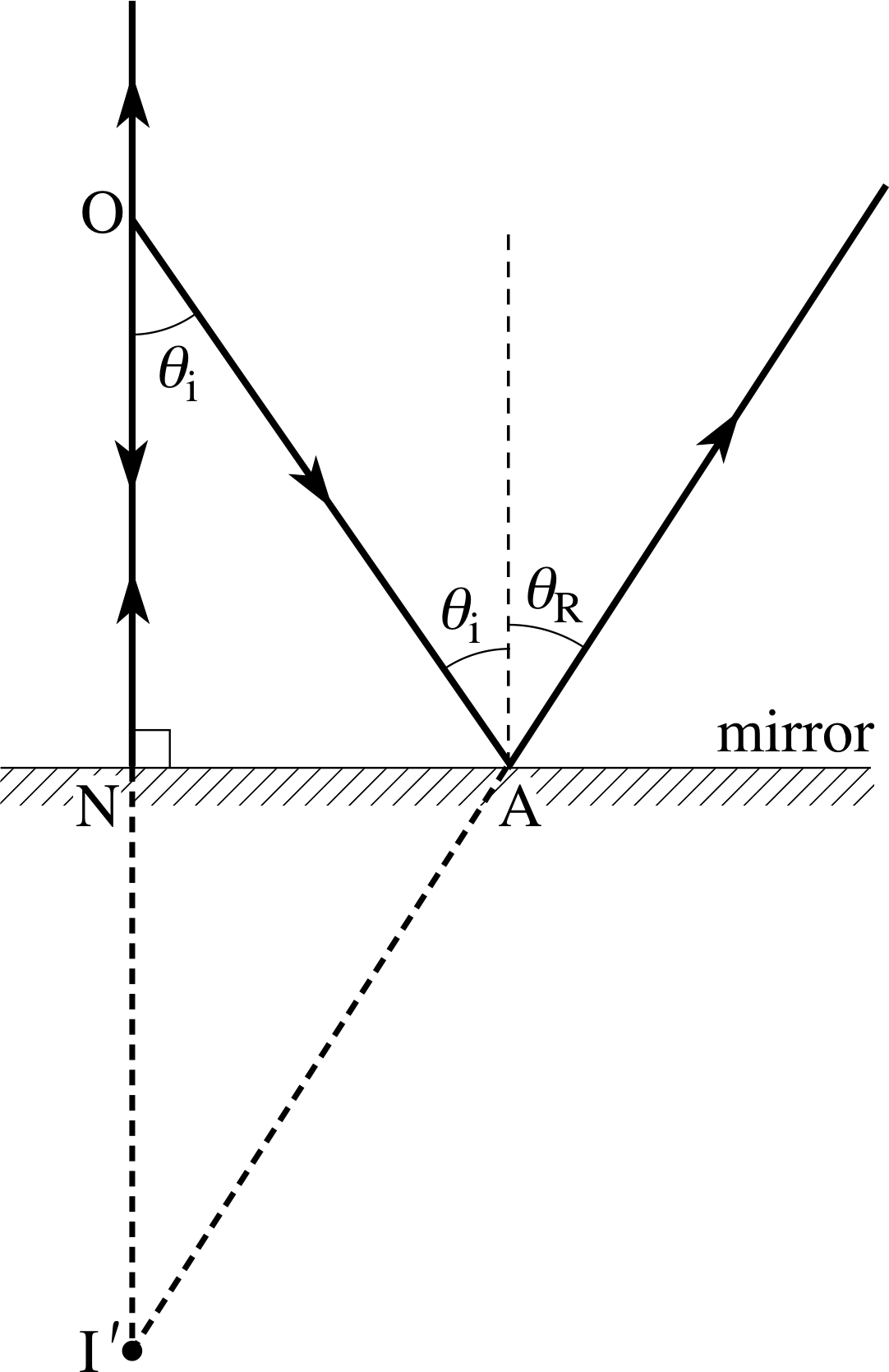
Figure 24 See Answer T2.
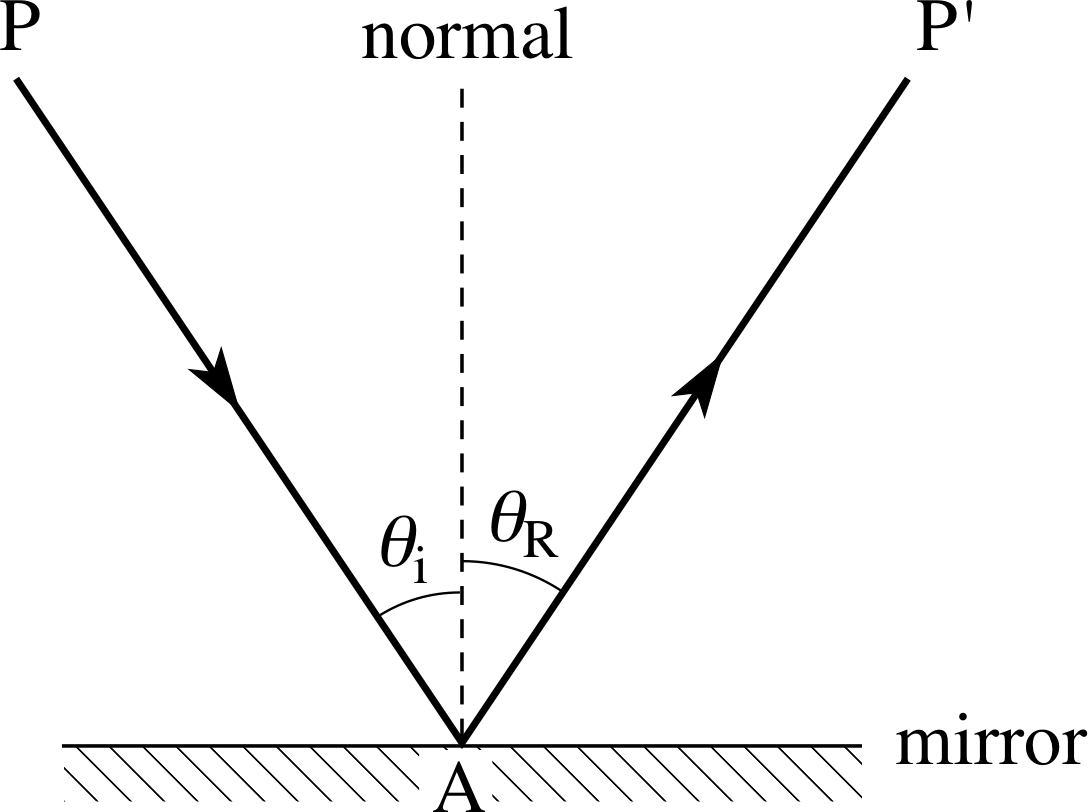
Figure 3 A ray of light reflected from a plane mirror.
Answer F2
A ray from the object to the eye is constructed by drawing the incident and reflected parts of the ray in the same plane as the normal at the point of incidence, and by making the angles of incidence and reflection equal (see Figure 3). From the geometry of the (similar) triangles shown in Figure 24, we can see that the virtual image will be 20 cm behind the mirror and located along the extended normal from the object to the mirror.
Question F3
(a) A light ray inside a glass block (refractive index 1.50) strikes a glass–air interface at an angle θ1 to the normal. Find the critical angle θ1c beyond which the ray is totally internally reflected. (Take the refractive index of air to be 1.00).
(b) Explain how total internal reflection is used in optical fibres.
Answer F3
(a) We use Snell’s law and assume the refractive index of air is 1.00:
$\dfrac{\sin\theta_1}{\sin\theta_2} = \dfrac{1.00}{1.50}$
thereforesin θ1 = 0.667 sin θ2
The maximum value of sin θ2 is 1.00 and at this limiting value
θ1c = arcsin(0.667) = 41.8°
This is the critical angle. When θ1 > 41.8° there can be no refracted ray and total internal reflection occurs.
(b) Light rays are confined in optical fibres by total internal reflection. These devices are used extensively in modern optical communication systems. See also Subsections 4.3 and 4.4.
1.3 Ready to study?
Study comment In order to study this module you will need to be familiar with certain ideas concerning the wave model of light. In particular you should know that many of the properties of light can be accounted for by assuming that light travels as waves characterized by a wavelength λ, a frequency f and a speed υ that are related by υ = f λ; that different colours of light correspond to different frequencies or wavelengths, and that the phenomena of interference and diffraction provide evidence in support of the wave model. It is not assumed that you have a detailed knowledge of these topics, indeed most of them are given a brief introduction when they first arise. However, if you are completely unfamiliar with these ideas you may find the introductions too brief, in which case you should refer to the Glossary which will indicate where they are more fully developed. The mathematical requirements of this module include trigonometry, and the geometry of triangles. In Section 5 some use will be made of differentiation to determine the stationary points (in this case local minima) of a function, but if this technique is unfamiliar to you then you should nevertheless still be able to meet the achievements of the module. If you are unsure about any of these items you can review them now by reference to the Glossary, which will also indicate where in FLAP they are developed. The following Ready to study questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
θ is an angle between 0° and 90° satisfying the equation sin θ = 0.45. Find θ.
Answer R1
If sin θ = 0.45, then θ = arcsin(0.45). To three significant figures this gives: θ = 26.7°. Consult trigonometry in the Glossary for further information.
Question R2
Given the approximate values for the wavelengths in a vacuum of blue and red light as 450 nm and 650 nm, respectively, calculate the frequency of the light in each case given that the speed of light in a vacuum is 3.00 × 108 m s−1. (Note that 1 nm = 10−9 m.)
Answer R2
The relation between wavelength λ, speed c and frequency f of a wave is c = f λ. The values for blue and red light are as follows:
blue lightλ = 450 nm, therefore f = 6.67 × 1014 Hz
red lightλ = 650 nm, therefore f = 4.62 × 1014 Hz
Consult the relevant terms in the Glossary for further information.
Question R3
What is meant by saying two waves are in phase at a certain point? What is meant by saying two waves arriving at a common point by different routes interfere when they meet?
Answer R3
The rise and fall of a wave creates a vibration or oscillation at any point through which the wave passes. The term phase is generally used to describe the stage that an oscillator has reached in its repetitive oscillatory cycle, and is often expressed as a fraction of 2π since 2π radians represents one complete cycle. Two waves are said to be in phase at a certain point if the oscillations they would individually cause at that point are exactly in step, rising and falling together with equal phases at each moment. Under appropriate conditions, two waves arriving simultaneously at a given point may cause a joint disturbance at that point which is equal to the sum of the disturbances they would cause individually; under these circumstances the waves are said to interfere when they meet.
Consult the relevant terms in the Glossary for further information if required, but few other ‘wave’ concepts are needed in this module.
2 Waves, rays and geometrical optics
2.1 Rays and rectilinear propagation
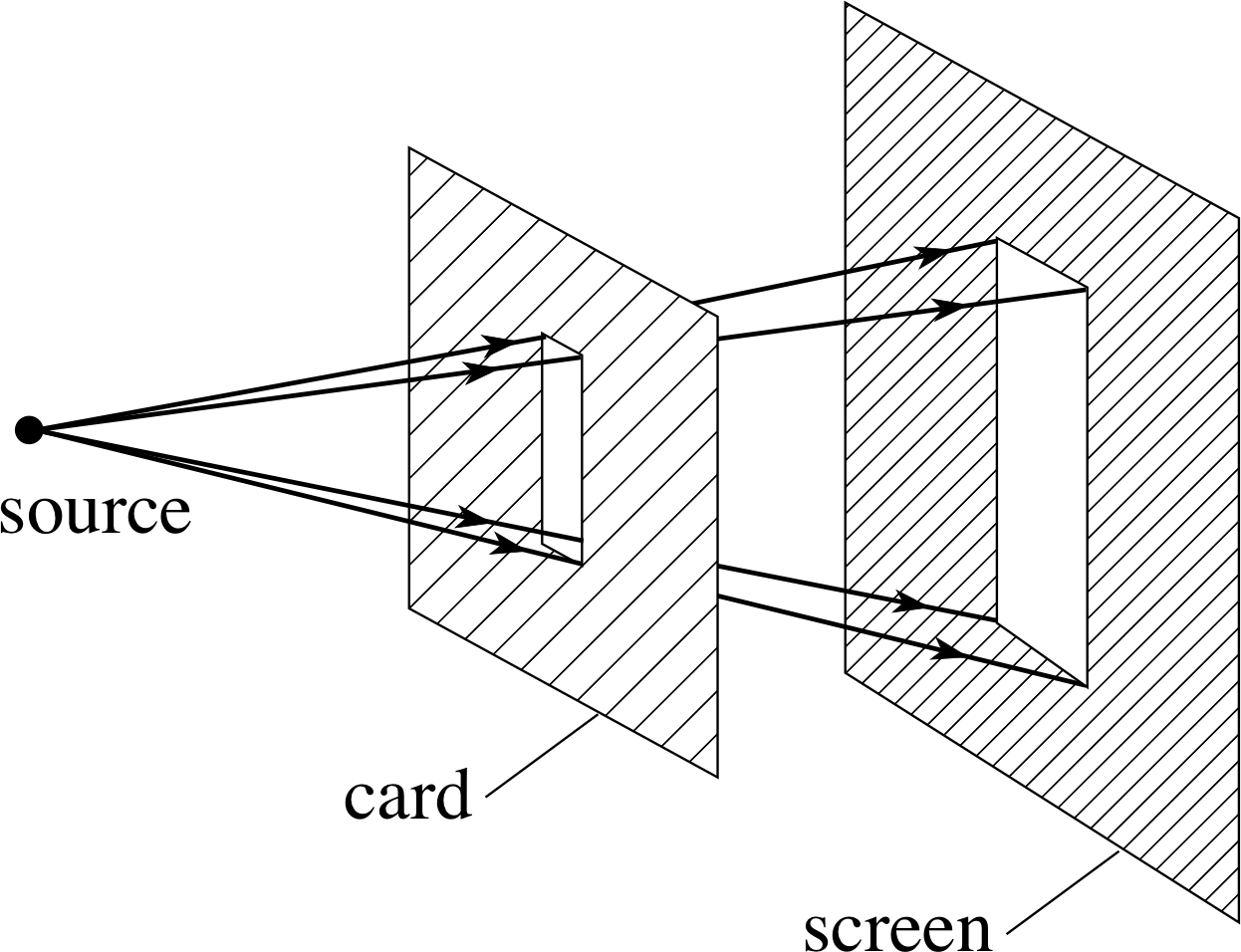
Figure 1 Light from a small source passes through a rectangular aperture to form a well defined bright patch on a screen.
‘Light,’ it is often said, ‘travels in straight lines’. Of course, this is an oversimplification; lenses and mirrors can alter the course of a light beam, as can changes or irregularities in the medium (i.e. material) through which the light is moving. Nonetheless, the idea that light travels in straight lines in a uniform medium, sometimes referred to as the principle of rectilinear propagation, does provide a simple characterization of the behaviour of light under a wide range of circumstances. i Evidence in support of the principle is provided by the ‘shafts’ of sunlight that can sometimes be seen streaming through open windows or through gaps in clouds and by countless other natural phenomena. The effect can easily be demonstrated in the laboratory by letting light from a very small source pass through an aperture (cut in an otherwise opaque piece of card) and fall on a screen. This is shown in Figure 1, where the aperture has a rectangular shape. The precise shape of the bright patch on the screen can be predicted by drawing straight lines from the source to the screen. Any line hitting the opaque part of the card is stopped, otherwise it passes through to the screen.
The idea that light travels in straight lines leads naturally to the concept of a ray of light.
A ray is a directed line (i.e. a line with an arrow on it) showing a possible path along which light can travel and indicating the direction in which such light would transport energy.
The principle of rectilinear propagation leads us to expect that light rays in a uniform medium will be straight lines (this is sometimes referred to as a pencil of rays), like those shown in Figure 1, though we know that rays may be kinked or reversed at mirrors or at the boundaries between different transparent media, and we should also expect rays to be bent or curved when the optical properties of a medium change from place to place. i
2.2 Waves and the ray approximation
Although the idea of rectilinear propagation is intuitively appealing and accords with much of our everyday experience, it is still not fully consistent with all the observed properties of light. It has been known at least from the time of Isaac Newton (1642–1727) that when light travels through a very small aperture or passes close to a very small obstacle it spreads out in a way that cannot be simply explained in terms of motion in straight lines. For example, if the rectangular aperture in Figure 1 is less than about 0.1 mm wide then the bright patch on a screen placed 1 m away will not be perfectly sharp, even for the smallest possible source. Moreover, the blurring of the bright patch will become progressively greater if the size of the aperture is made even smaller. The implication of this is that, in this situation, light does not travel along straight lines and the concept of a light ray is not useful.
The tendency of light to spread out when passing through narrow apertures is one manifestation of a widespread phenomenon known as diffraction. In general diffraction is characteristic of wave phenomena, such as water waves on a pond or sound waves in air. It arises because of the natural tendency of waves to spread out when they encounter obstacles or pass through apertures comparable in size to the wavelength of the waves. The diffraction of light by narrow slits is evidence that light too is a wave phenomenon and that the relevant waves have a very small wavelength. i
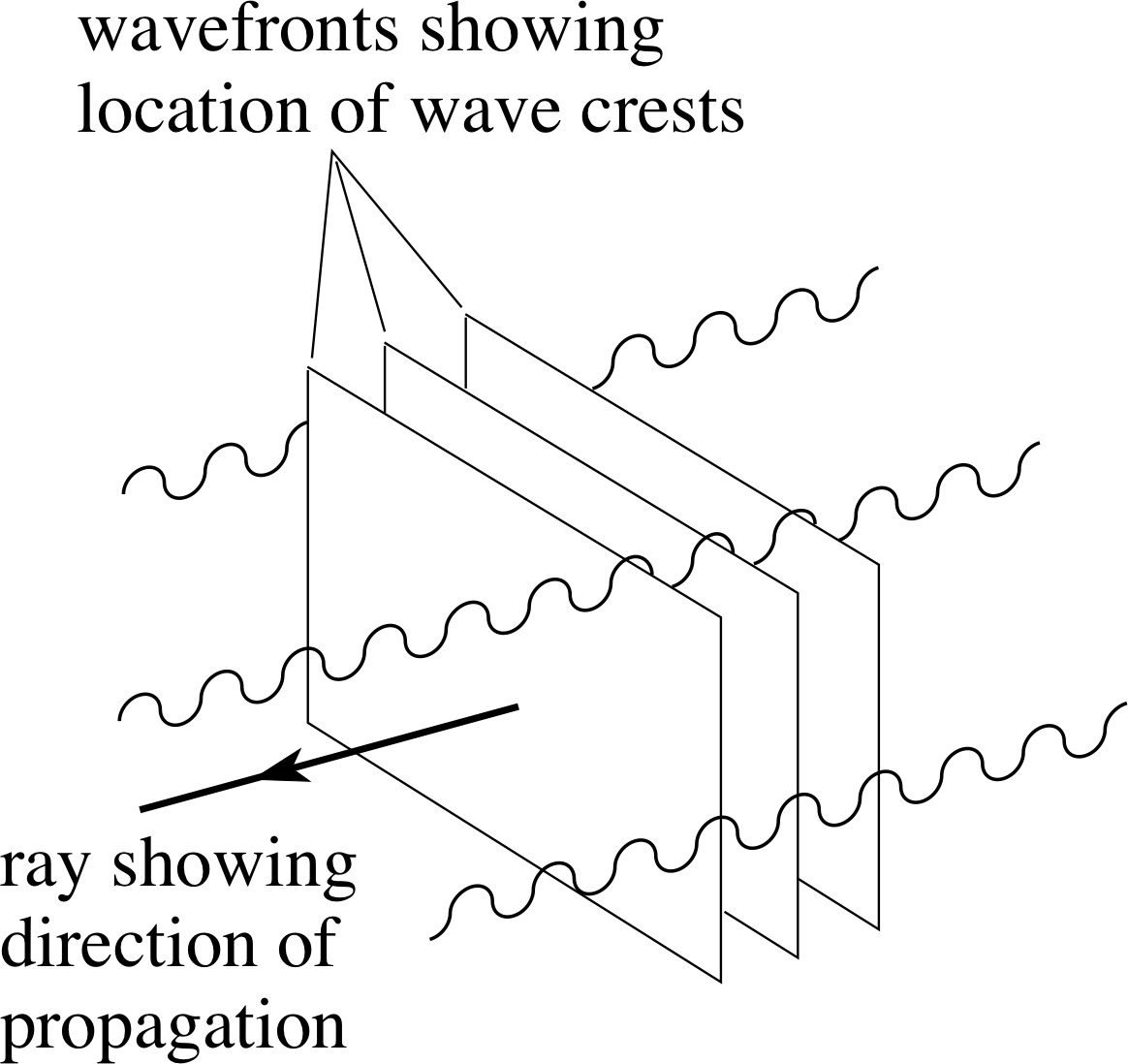
Figure 2 In terms of the wave model of light, rays are drawn perpendicular to wavefronts at any point and indicate the direction in which those wavefronts are moving.
The wave model of light, according to which light travels in the form of waves, with different wavelengths corresponding to different colours, is discussed more fully elsewhere in FLAP. Although we will mention it from time to time, we will not pursue it in any detail in this module. However, it should be noted that the use of rays to indicate possible pathways for light is entirely consistent with the wave model. In the context of the wave model, light of a given colour spreading out from a point–like source can be viewed as roughly analogous to the concentric ripples that spread out from a point of disturbance on the surface of a pond. Each expanding circular ripple can be thought of as representing an expanding spherical wavefront i of the light, and the unimpeded movement of such wavefronts through a uniform medium can be indicated at any point by drawing a suitably directed ray perpendicular to the wavefront at that point.
The same principle, that rays are perpendicular to wavefronts in a uniform medium (see Figure 2), can be applied in other situations, provided diffraction effects are negligible. Thus, rays provide a useful way of describing the propagation of waves. Of course, the applicability of the ray description is limited by diffraction, so it is customary to speak of the ray approximation – an approximation that should be expected to break down when light passes through a narrow aperture or in any other situation where diffraction cannot be neglected.
Despite this limitation, there are many problems involving light that can be adequately treated by considering rays. These problems fall within the domain of geometrical optics, the field of study in which the ray approximation is valid. This module provides an introduction to some of the principles and applications of geometrical optics.
3 Reflection
An important topic in geometrical optics is the reflection of light. In reflection, light strikes a surface and is returned to the medium from which it came. A surface which reflects strongly is said to have a high reflectivity and to be a good reflector. Such a reflector is commonly called a mirror. The simplest type of mirror, and the only type we will consider in this module, is a flat or plane mirror. A plane mirror can be made by coating a smooth flat surface (e.g. glass) with a metal film (e.g. silver) of thickness greater than a few wavelengths of light. Light which strikes the mirror cannot penetrate far into the metal and is almost entirely reflected. Some light however will be absorbed by the metal film and the extent of this absorption will generally depend on the wavelength of the incident light. For example, silver and aluminium are particularly good for mirrors because their absorption is almost independent of wavelength; in contrast, gold selectively absorbs the shorter visible wavelengths which causes a gold mirror to have its characteristic colour when viewed in ordinary daylight.
3.1 The law of reflection
Figure 3 shows a light ray from any point P striking a mirror at point A, which is called the point of incidence, and, after reflection, passing through a point P′. The line drawn perpendicular to the mirror at A is called the normal and the angles made by the incoming incident ray and the outgoing reflected ray to the normal at the point of incidence are known as the angle of incidence θi and the angle of reflection θR, respectively. i Experiments clearly demonstrate the following law of reflection, which has been known since ancient times.

Figure 3 A ray of light reflected from a plane mirror.
Law of reflection
- The reflected ray, the incident ray and the normal all lie in the same plane.
- The angle of reflection is equal to the angle of incidence: θR = θi
The two parts of this law can be derived from the wave model of light but here we take them as being justified by experimental observations. Notice that in Figure 3 the direction of the rays is reversible, that is, a ray from P′ to A will be reflected in such a way that it passes through P. This is a particular example of another general principle of geometrical optics to which we will return later.
Question T1
Two plane mirrors are fixed together at right angles in the form of a letter ‘L’ with the reflecting surfaces on the inside. Show that any ray of light striking both mirrors will be reflected back in a direction parallel to its original direction.
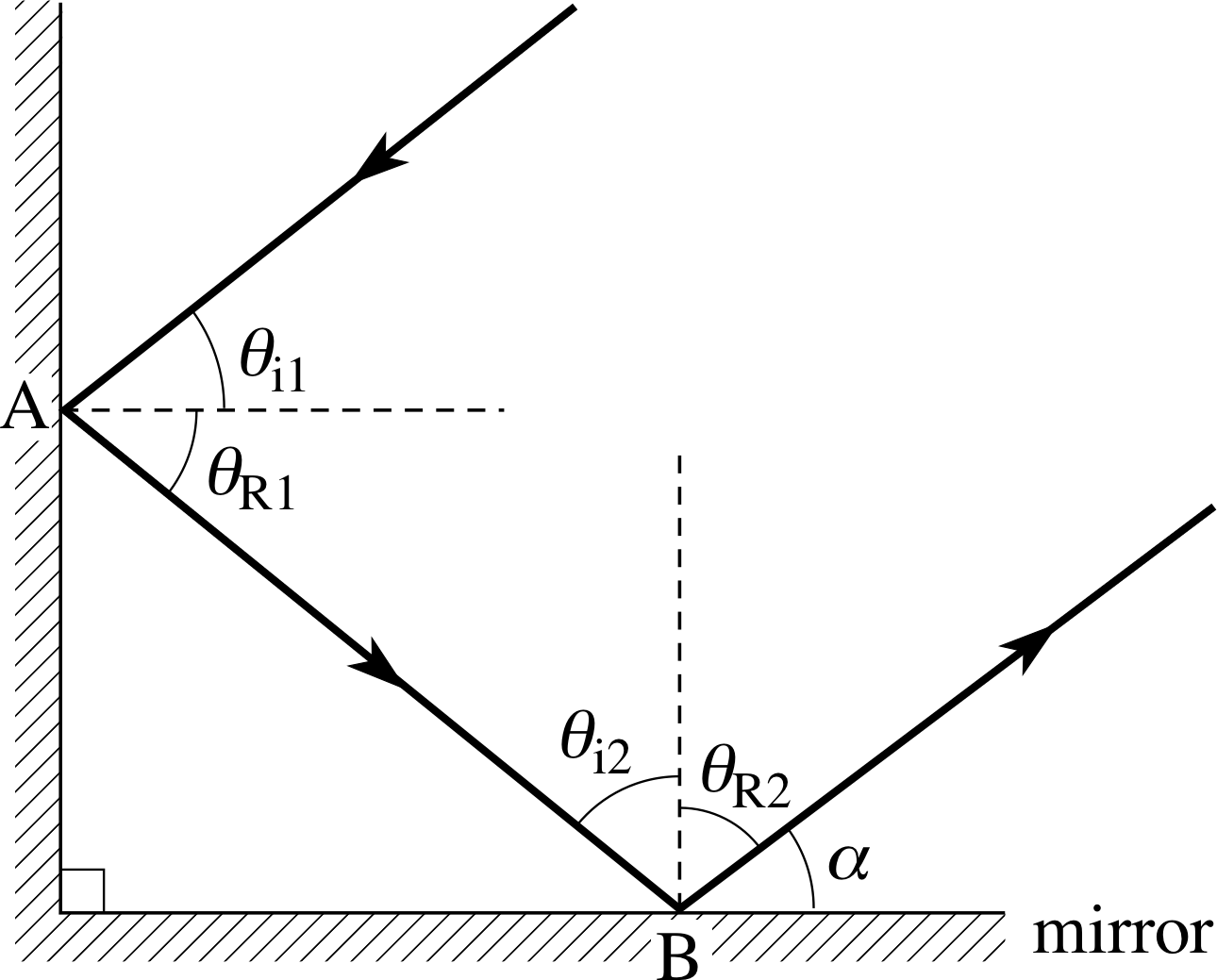
Figure 23 See Answer T1.
Answer T1
See Figure 23. At the first reflection, point A, the reflected angle θR1 is equal to the incident angle θi1. The mirrors are at right angles so that at the second reflection, point B, θi2 = 90° − θR1 and θR2 = θi2 = 90° − θR1. The angle of the ray relative to the horizontal after the second reflection is given by:
α = 90° − θR2 = 90° − (90° − θR1) = θR1 = θi1.
The ray is finally reflected back parallel but the direction of travel is reversed. This is the basic principle of operation for a bicycle reflector and also for the reflectors placed on the Moon by the Apollo 11 astronauts (used to reflect laser beams sent from Earth and thereby to measure the distance from the Earth to the Moon – the lunar ranging experiment).
3.2 Image formation in a plane mirror
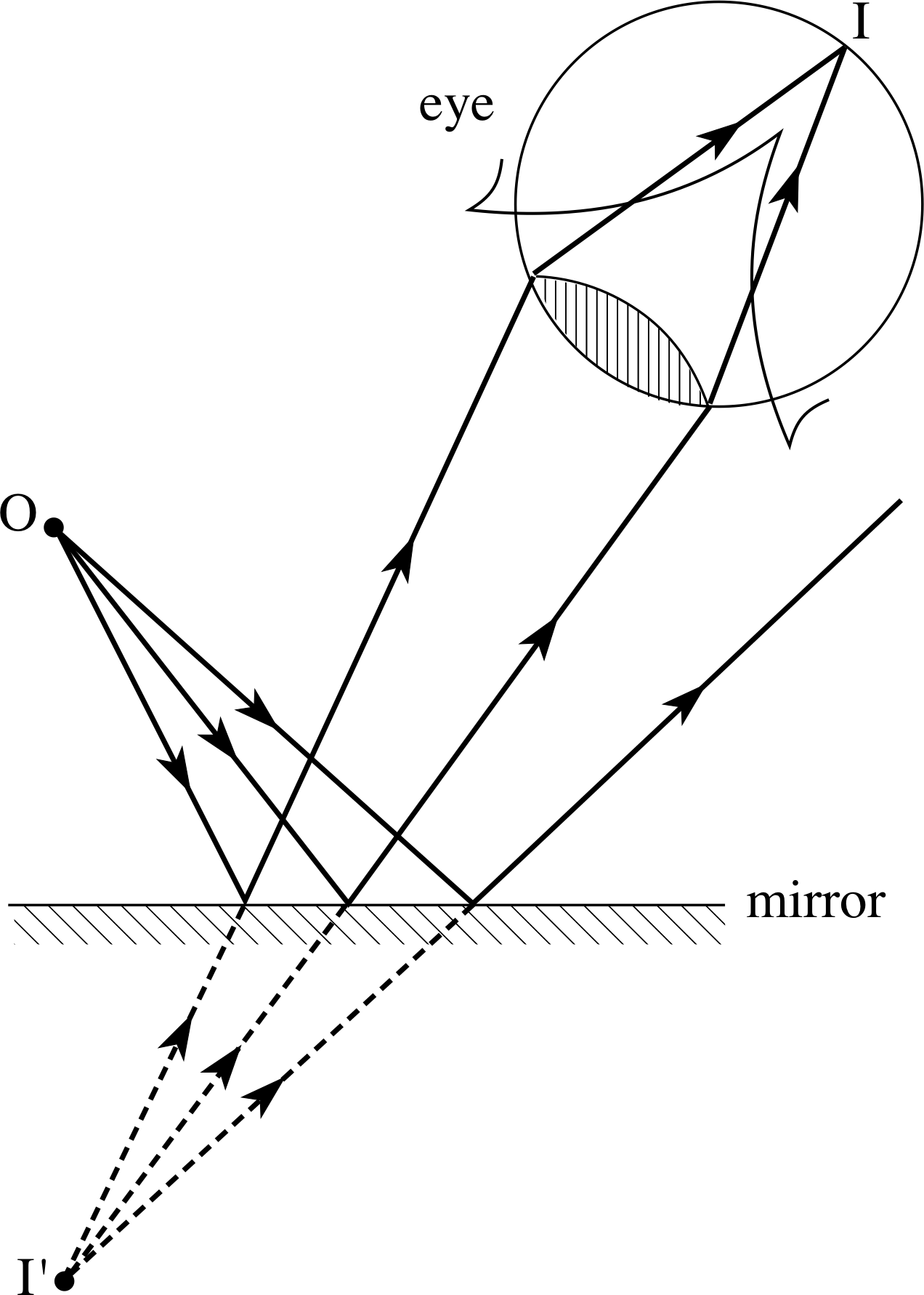
Figure 4 A bundle of rays diverging from O and reflected by a plane mirror, forms a virtual image at I′ behind the mirror, while the human eye forms a real image at I.
Mirrors and lenses are often used to make a bundle of light rays that diverge (i.e. spread out) from one point come together (i.e. converge) at some other point. This process is illustrated in Figure 4 where some of the rays diverging from a point object at O are reflected from a plane mirror and then brought together at a point I by a human eye. Under such circumstances we say that there is a real image of the object at the point I.
If the eye shown in Figure 4 was your own, and you were asked where the object O appeared to be you would probably say that you could see it ‘in’ the mirror. The reason for this is fairly clear: the reflected rays travel in such a way that if it is assumed they always travel in straight lines then they must have come from the point I′ behind the mirror. Because the rays do not really diverge from this point but only appear to do so, we say that there is a virtual image of O at the point I′.
Note that this virtual image at I′ exists even when there is no eye to form the real image at I: it is sufficient that the reflected rays can be continued back to the point I′. i
Bearing in mind the law of reflection, which tells us that the angles of incidence and reflection must be equal for each of the rays in Figure 4, it is fairly easy to demonstrate that the virtual image at I′ is as far behind the mirror surface as the object at O is in front of it.
Question T2
Show that all rays coming from O that are reflected by the mirror in Figure 4 will, after reflection, behave as though they came from a single fixed point I′. Prove that the virtual image at I′ is at the same distance from the mirror as the object at O.
[Hint: Consider one ray along the normal from O to the mirror and a general ray at an angle θi to the normal.)]

Figure 24 See Answer T2.
Answer T2
See Figure 24. Consider two rays from O – one along the normal to the mirror and the other at any angle of incidence θi. The ray ON is reflected back towards O so the virtual image must lie somewhere along the normal. For the ray reflected at the arbitrary point A, the angle of incidence equals the angle of reflection: θi = θR. Hence the angle NI′A = θR. But the angle NOA = θi = θR so that the triangles ONA and I′NA are identical. This means that side I′N is equal to side ON for any value of θi. All rays reflected in the mirror from O appear to diverge from I′ with I′N = ON, so the image appears to be at the same distance from the mirror as the object.
We can formalize the result of Question T2 by associating a Cartesian coordinate system with the mirror, as shown in Figure 5, with the x- and y–axes in the plane of the mirror and the z–axis normal to the mirror. If the coordinates of the object at point O are (X, Y, Z) then the coordinates of the point N (where the normal from O meets the mirror) will be (X, Y,, 0), and since the length NI′ is Z, the coordinates of the virtual image point I′ are (X, Y, −Z). Thus, when a plane mirror is used to form a virtual image of a point object, the coordinates of the image may be found from the coordinates of the object by changing the sign of the coordinate measured normal to the mirror while leaving the coordinates measured parallel to the mirror unchanged.
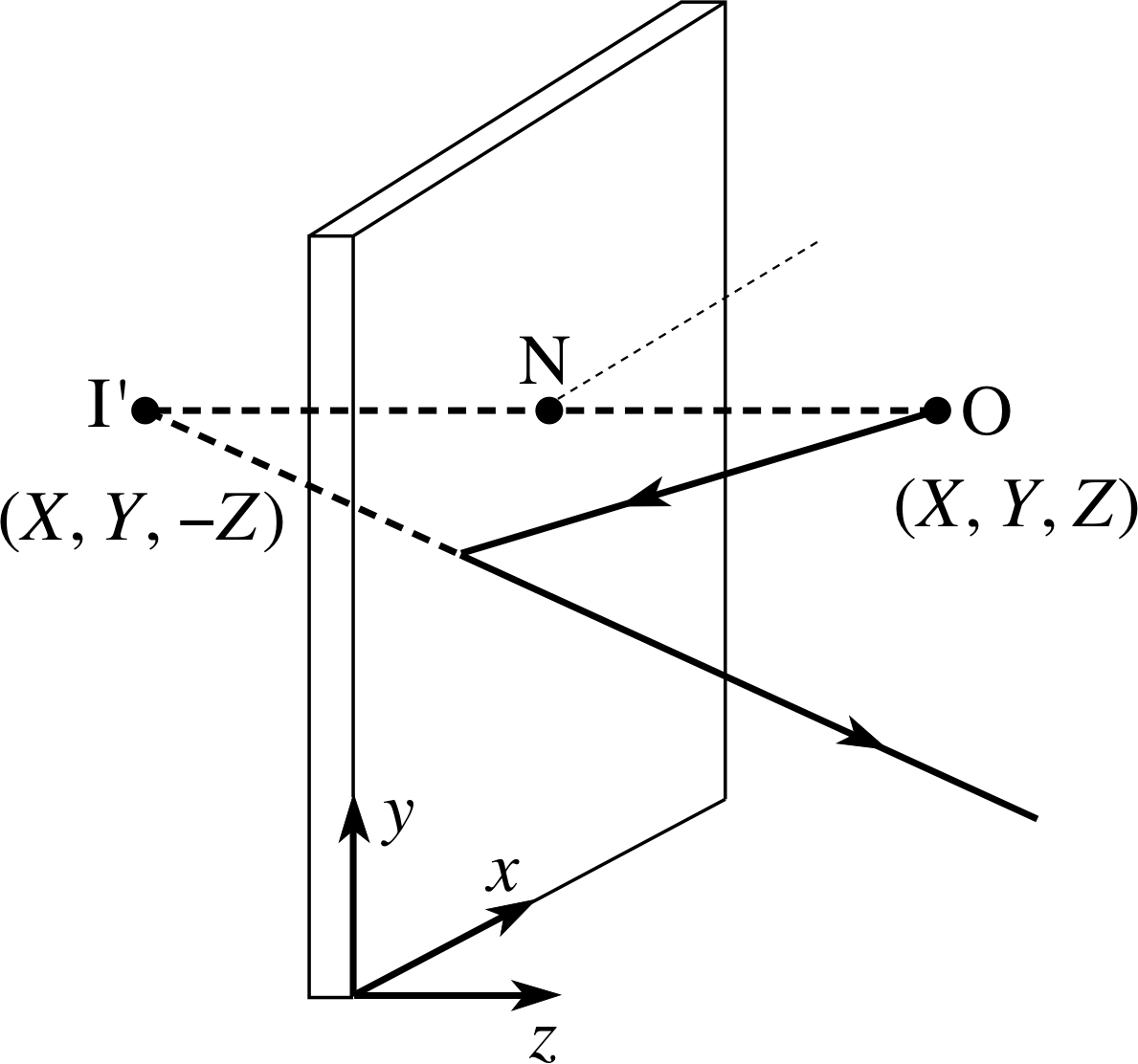
Figure 5 A coordinate system fixed in a mirror. (The mirror is in the (x, y) plane.)
Now imagine looking at yourself in a mirror. Better still, try it! Your body is an example of an extended object rather than a point object, but the principle outlined above still applies. Each point on your body will correspond to a unique virtual image point behind the mirror, thus creating a virtual image of yourself which will be the same size as the original but which will appear to differ in one important respect. If you wave your right hand your mirror image will wave its left hand, and if you shut your left eye your mirror image will shut its right eye. We describe this by saying that the image is reversed_imagereversed, i.e. left and right appear to have been interchanged.
At the same time, the image is said to be erect, i.e. the right way up – the mirror does not appear to interchange your head and your feet. The ability of a mirror to produce an image that is simultaneously reversed and yet erect has been used to perplex students for generations and you are not going to be spared that perplexity!
In the Exit test at the end of this module you will be asked to explain how a plane mirror can apparently interchange left and right without interchanging top and bottom. You might like to keep that in mind as you read the next paragraph; it won’t tell you the answer, but it may help you to formulate one.
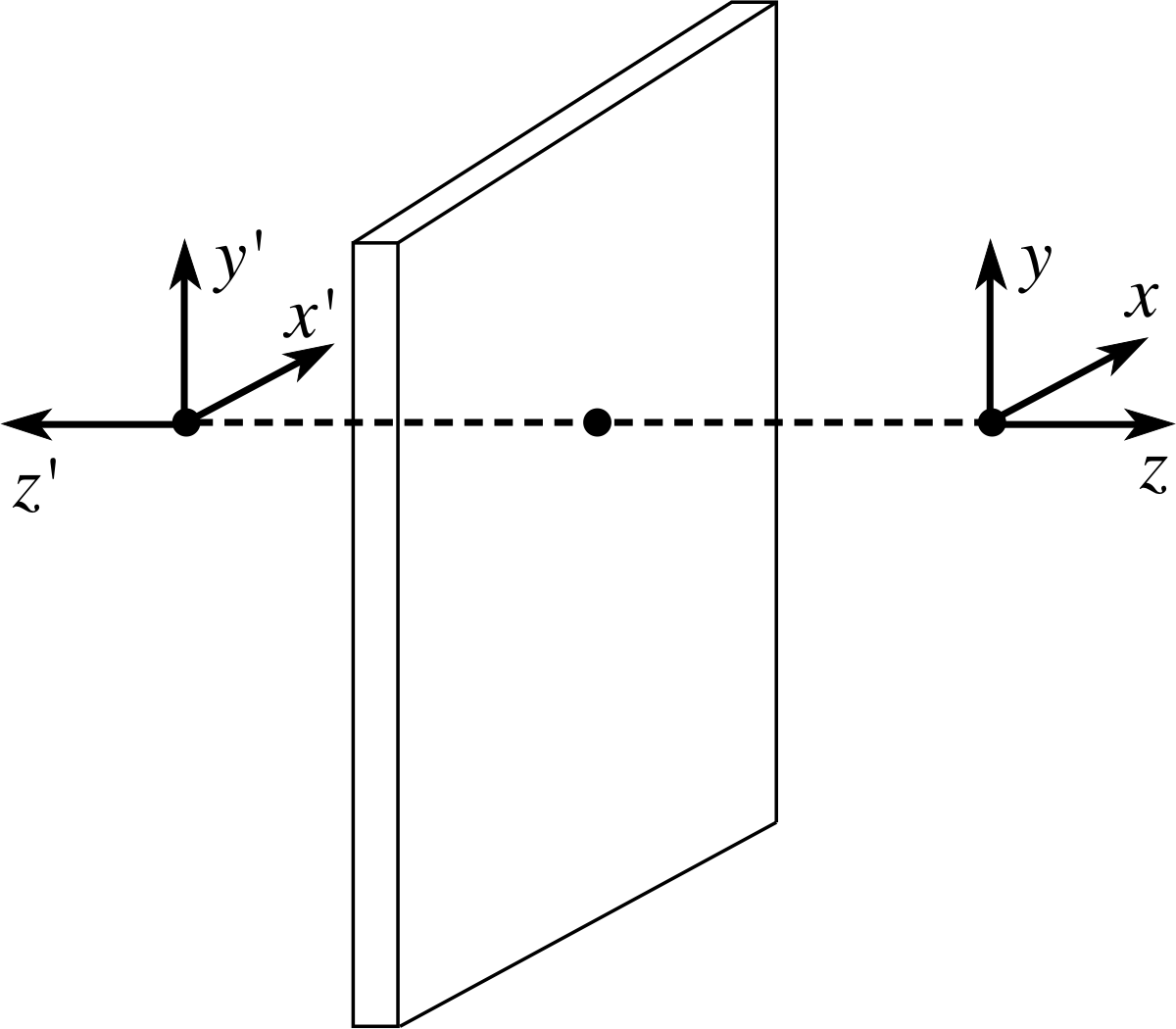
Figure 6 A right–handed coordinate system, reflected in a plane mirror, forms an image which is a left–handed system. (The mirror is in the (x, y) plane.)
We can gain more insight into the nature of the reflected image by supposing that the origin of a coordinate system is located at some point in front of a plane mirror, as shown in Figure 6, so that the system itself can be seen reflected in the mirror. How does the virtual image formed by the mirror differ from the real coordinate system? As indicated in Figure 6, the x– and y–axes of the image are parallel to those of the real system, but the z–axis is reversed. This might seem a rather insignificant change – you might think that by rotating the real system you could reorientate it so that all of its axes are parallel to the corresponding axes of the image, but if so, you would be wrong. The real system and its mirror image are fundamentally different in the same sense that your right hand is fundamentally different from your left hand; no matter how you rotate your right hand it never becomes a left hand, and no matter how you rotate the real coordinate system in Figure 6 you will never completely align it with its mirror image.
In fact the real system shown in Figure 6 is called a right–handed coordinate system because if you imagine yourself at the origin of the coordinate system, looking in the direction of increasing z, it requires a right–handed (clockwise) screw rotation to go from the x–axis to the y–axis, whereas the image system is called a left–handed coordinate system because it requires a left–handed (anticlockwise) screw rotation to go from the x′-axis to the y′-axis if you are looking in the direction of increasing z′.
No rotation will ever succeed in aligning a right–handed coordinate system with a left–handed system nor a left–handed system with a right–handed system. However, the mirror image of a right–handed system is a left–handed system which may be rotated into alignment with any other left–handed system; and the mirror image of a left–handed system is a right–handed system which may be rotated into alignment with any other right–handed system. This interchange of right–handed and left–handed coordinate systems is the essence of image reversal.
To summarize:
When light from an object is reflected in a plane mirror a reversed virtual image is formed. This image is erect, the same size as the original object and located as far behind the mirror as the object is in front.
Although we have described the formation of images in plane mirrors produced by coating a glass surface with a metallic film, you will undoubtedly have seen reflections from other surfaces such as polished bench tops or unsilvered glass. Any surface acts to some extent as a reflector, though its reflectivity generally depends on the angle of incidence and increases as that angle approaches 90°. This phenomenon can be explained by the wave model of light but not in terms of rays and geometrical optics. Nonetheless, it is interesting to note that mirrors can be made from some rather unlikely materials, provided we restrict the angle of incidence to be nearly 90° – a condition usually referred to as grazing incidence.
For example, a piece of paper is a very poor reflector of light at or near normal incidence, but at grazing incidence it can actually be quite good. Try this for yourself – hold a piece of paper up so that you can look along its surface at a light bulb and you should see a surprisingly bright reflection of the bulb. The quality of this image will not be very good because the surface of the paper will not be very flat when measured on the scale of the wavelength of light, still, it is quite surprising that paper can perform this function at all.
4 Refraction
If you stand by a window in a brightly lit room at night, with the curtains open, you can usually see your own reflection in the window while someone outside can see you through the window. Your ability to see yourself in a ‘transparent’ window demonstrates the phenomenon of partial reflection. When light strikes the interface (i.e. boundary) between two different materials some light is usually reflected back into the first material while the rest is transmitted or absorbed by the second material. If both the materials involved are transparent then relatively little energy will be absorbed and any incident ray will split into two at the interface, one part being reflected while the other is transmitted. The light entering the second material is said to undergo refraction at the interface, which may cause it to travel in a different direction from the incident light. The proportions reflected and refracted at the interface will depend on the nature of the two materials and the angle of incidence, and will generally vary with wavelength.
4.1 The law of refraction
Figure 7 shows a single ray of light travelling through a transparent medium (material 1) and striking the interface with a different transparent medium (material 2). The ray is partly reflected and the reflected ray obeys the usual law of reflection. The remaining part of the ray is refracted at the interface and then travels through the second material; this is called the refracted ray. The direction of the refracted ray is described by the angle of refraction θr, which is the angle between the refracted ray and the normal (in material 2) to the interface at the point of incidence.
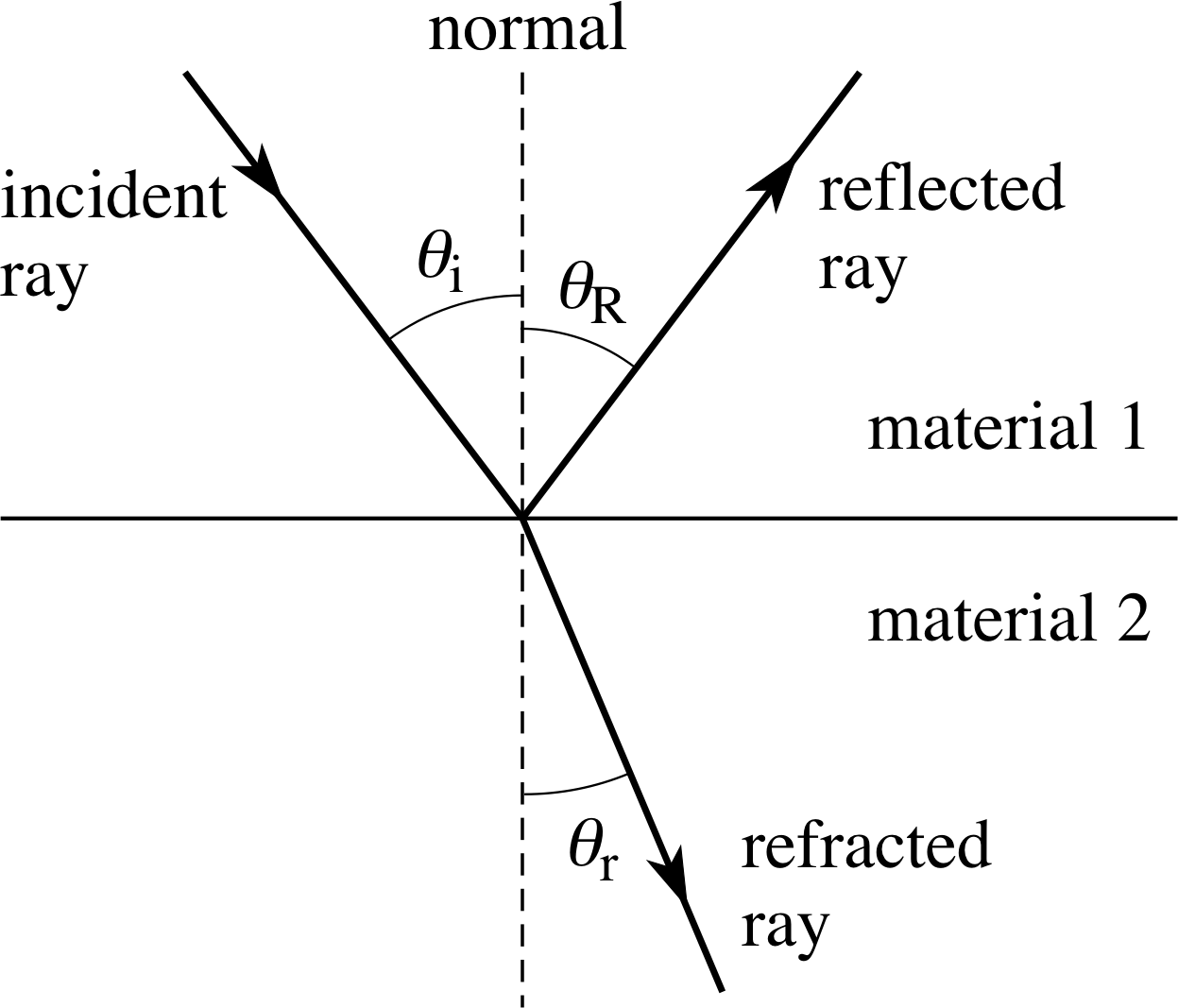
Figure 7 Reflection and refraction of a ray of light at the interface between two different transparent materials, where μ2 > μ1.
Extensive experimentation with many kinds of transparent materials supports the following law of refraction.
Law of refraction
- The incident ray, the refracted ray and the normal all lie in the same plane.
- The angle of incidence and the angle of refraction are related by
$~~~~\dfrac{\sin\theta_{\rm i}}{\sin\theta_{\rm r}} = \text{constant}$(1a)
where the constant depends on the two materials involved and on the wavelength of the light. i
This law was first propounded in 1621 by the Dutch mathematician and astronomer Willebrord Snell (1591–1626) and was published after his death by the French philosopher René Descartes (1596–1650). Equation 1a is usually referred to as Snell’s law, though that term is also applied to a more detailed form of the law that we will now introduce.
As in the case of reflection, the directions of the incident and refracted rays in Figure 7 are reversible, that is, a ray incident at an angle θr in material 2 will be refracted at an angle θi in material 1. Because of this it makes good sense to replace θi and θr in Equation 1a by θ1 and θ2 since the numerical subscripts show the material in which each angle is to be measured but don’t imply that either is necessarily an angle of incidence or refraction. Moreover, experience shows that the constant in Equation 1a can be written as the quotient μ2/μ1, where μ1 is a property of material 1, called the refractive index of material 1, and μ2 the refractive index of material 2.
Taking these points into account we obtain a more informative version of Equation 1a:
Snell’s law $\dfrac{\sin\theta_1}{\sin\theta_2} = \dfrac{\mu_2}{\mu_1}$(1b) i
Question T3
A ray of light passes through a parallel–sided block of glass surrounded by air. Show that the ray leaving the block is parallel to the ray entering it.
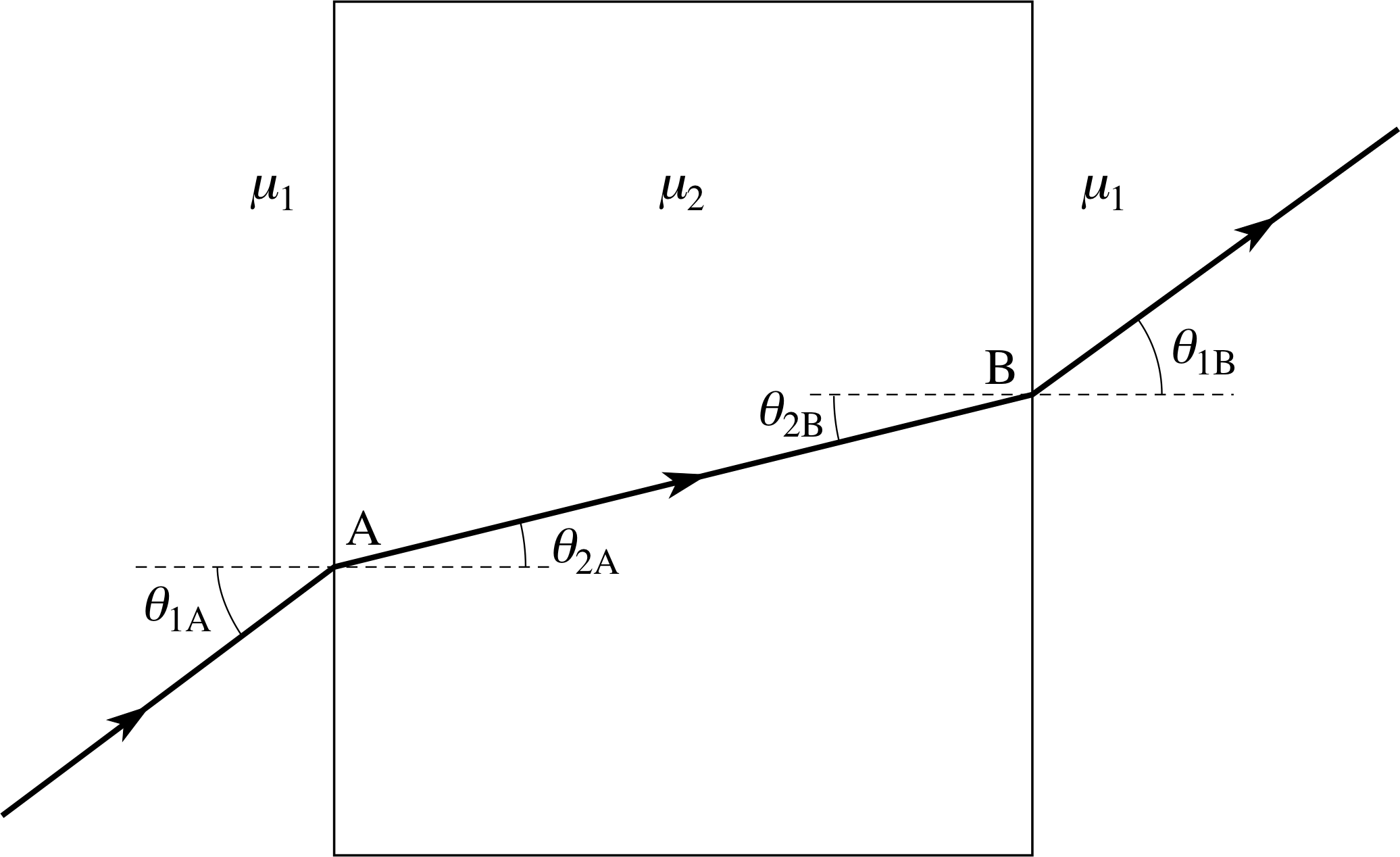
Figure 25 See Answer T3.
Answer T3
The ray diagram for refraction through a parallel–sided glass block is shown in Figure 25.
At A (the point where the light enters the block):
$\dfrac{\mu_1}{\mu_2} = \dfrac{\sin\theta_{2A}}{\sin\theta_{1A}}$
At B (the point where the light leaves the block):
$\dfrac{\mu_2}{\mu_1} = \dfrac{\sin\theta_{1B}}{\sin\theta_{2B}}$
Multiplying these two equations together, and noting that θ2A = θ2B gives us:
$1 = \dfrac{\sin\theta_{2A}}{\sin\theta_{1A}} \times \dfrac{\sin\theta_{1B}}{\sin\theta_{2B}} = \dfrac{\sin\theta_{1B}}{\sin\theta_{1A}}$
i.e. sin θ1B = sin θ1A and θ1B = θ1A; hence the ray emerging from the block is parallel to the ray entering the block.
| Material | Refractive index |
|---|---|
| vacuum | 1.00 (exactly) |
| air* | 1.000 29 |
| water | 1.33 |
| crown glass | 1.52 |
| fused quartz | 1.46 |
| diamond | 2.42 |
| *at 0°C and 1 atm | |
For light of a given wavelength, the refractive index of a medium is a dimensionless quantity that depends on the physical properties of that medium. Table 1 gives the refractive indices of a variety of transparent materials for light of one particular wavelength. Media of high (or low) refractive index are said to have a high (or low) optical density. It is often useful to identify which of the two media at an interface is the more optically dense since this will determine whether or not rays entering that material will be refracted towards the normal or away from it.
✦ If light passes from material A to material B, where material B is more optically dense than material A, in which direction will the light be deflected? (Assume θi ≠ 0).
✧ From Snell’s law
$\dfrac{\sin\theta_1}{\sin\theta_2} = \dfrac{\mu_2}{\mu_1}$(Eqn 1b)
as μB > μA we can see that θA > θB.
Therefore the light would bend towards the normal as it passes from material A to B.
The refractive index of a medium also determines the speed of light in that medium. If we let c represent the speed of light in a vacuum (c = 3.00 × 108 m s−1, to three significant figures) and υ the speed of light in a medium, then the refractive index μ of that medium is given by:
$\mu = \dfrac{c}{\upsilon}$(2)
Applying this relationship to both of the media at an interface allows us to rewrite Snell’s law in terms of υ1 and υ2, the respective speeds of light in materials 1 and 2:
$\dfrac{\sin\theta_1}{\sin\theta_2} = \dfrac{\upsilon_1}{\upsilon_2}$(1c)
This equation not only shows that a light ray is generally refracted towards the normal when it enters an optically denser medium (if υ2 is less than υ1, then θ2 must be less than θ1), it also gives some physical insight into why this should be so.
The situation is analogous to that of a car driving across a field that suddenly encounters a patch of mud. Whichever wheel enters the mud first will be slowed down so that the car as a whole tends to turn around that wheel until both wheels are in the mud and both wheels are moving forward at the same speed to each other. Once the speed of the wheels has been matched the car will proceed in a straight line, albeit at a somewhat reduced rate. A similar argument can be applied in reverse to explain why light entering a less optically dense medium tends to be refracted away from the normal as its speed increases.
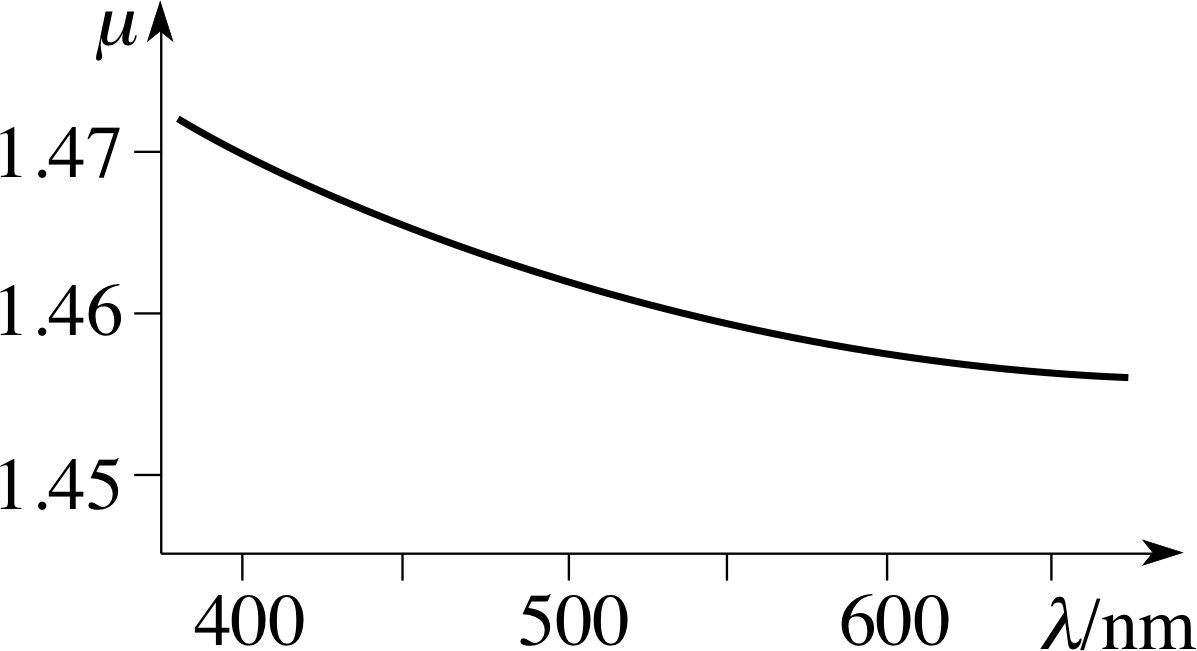
Figure 8 The variation of the refractive index with wavelength for ‘fused quartz’ glass. (The wavelength is measured in a vacuum.)
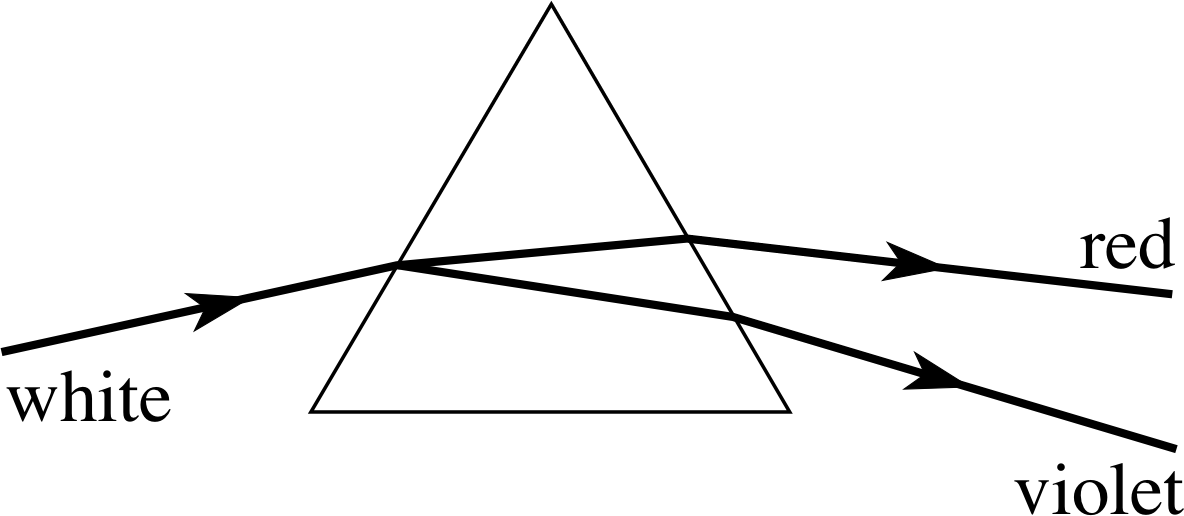
Figure 9 A ray of white light is split into its constituent colours by dispersion in a prism.
It has already been mentioned that the refractive index of a material depends on the wavelength of the light involved. The nature of this dependence for one form of glass, fused quartz, is shown in Figure 8. The variation in μ is not very great, just 1% or so over the full range of visible wavelengths, but it is sufficient to have easily observable consequences. Because μ varies with wavelength, the extent to which a ray of light is refracted at an interface will depend on the colour (wavelength) of the light, and light of different colours incident at the same point and at the same angle will be refracted by different amounts. This effect is called dispersion.
The dispersion of sunlight (which is a specific mix of visible wavelengths) in airborne water droplets is the fundamental cause of rainbows. A similar effect is shown in Figure 9, where a ray of white light (i.e. a similar mix of wavelengths to daylight) is shown splitting into a continuous band of colours as it passes through a glass prism. i
When Isaac Newton discovered this phenomenon he correctly interpreted it as indicating that white light was composed of all the colours that are usually seen in a rainbow. The extreme red and violet rays are shown and in between these are all the other colours that comprise the visible spectrum; orange, yellow, green, blue and indigo. Since the refractive index of glass decreases as the wavelength increases (as in Figure 8), red light will be refracted less at each interface than the shorter wavelength violet light, and will emerge travelling in a direction closer to that of the incident ray of white light.
Question T4
A light ray is composed of a mixture of red and blue light, and is incident on a block of fused quartz glass at an angle of 40°. Use the data from Figure 8 to estimate the difference in the angles of refraction inside the quartz for the two colours. (Assume λ = 650 nm for red light and λ = 450 nm for blue light.)
Answer T4
We use the data given in Figure 8 for the variation of refractive index of a form of glass called ‘fused quartz’.

Figure 8 The variation of the refractive index with wavelength for ‘fused quartz’ glass. (The wavelength is measured in a vacuum.)
Snell’s law gives us:
$\dfrac{\sin\theta_{\rm air}}{\sin\theta_{\rm glass}} = \dfrac{\mu_{\rm glass}}{\mu_{\rm air}}$
and we put μair = 1.00.
At λ = 650 nm, μglass = 1.46, hence :
$\sin\theta_{\rm glass} = \dfrac{\sin40°}{1.46} = 0.4403\quad\text{and}\quad\theta_{\rm glass} = 26.12°$
At λ = 450 nm, μ2 = 1.465, hence:
$\sin\theta_{\rm glass} = \dfrac{\sin40°}{1.465} = 0.4883\quad\text{and}\quad\theta_{\rm glass} = 26.02°$
The difference in angles is 26.12° − 26.02° = 0.10°
Question T5
A ray of light strikes the interface between air and a block of glass so that the angle of incidence is 35°. It is observed that the angle of refraction is 22°. Calculate the speed of light inside the glass block.
Answer T5
Using Snell’s law for the glass–air interface:
μair sin θair = μglass sin θglass
We can set μair = 1.00 and then find:
μglass = sin(35°)/sin(22°) = 0.574/0.375 = 1.53
The refractive index of a material is defined as the ratio of the speed of light in a vacuum to the speed of light in the material, i.e. μ = c/υ, so we have:
υglass = c/μglass = (3.00 × 108/1.53) m s−1 = 1.96 × 108 m s−1
4.2 Image formation by a plane interface
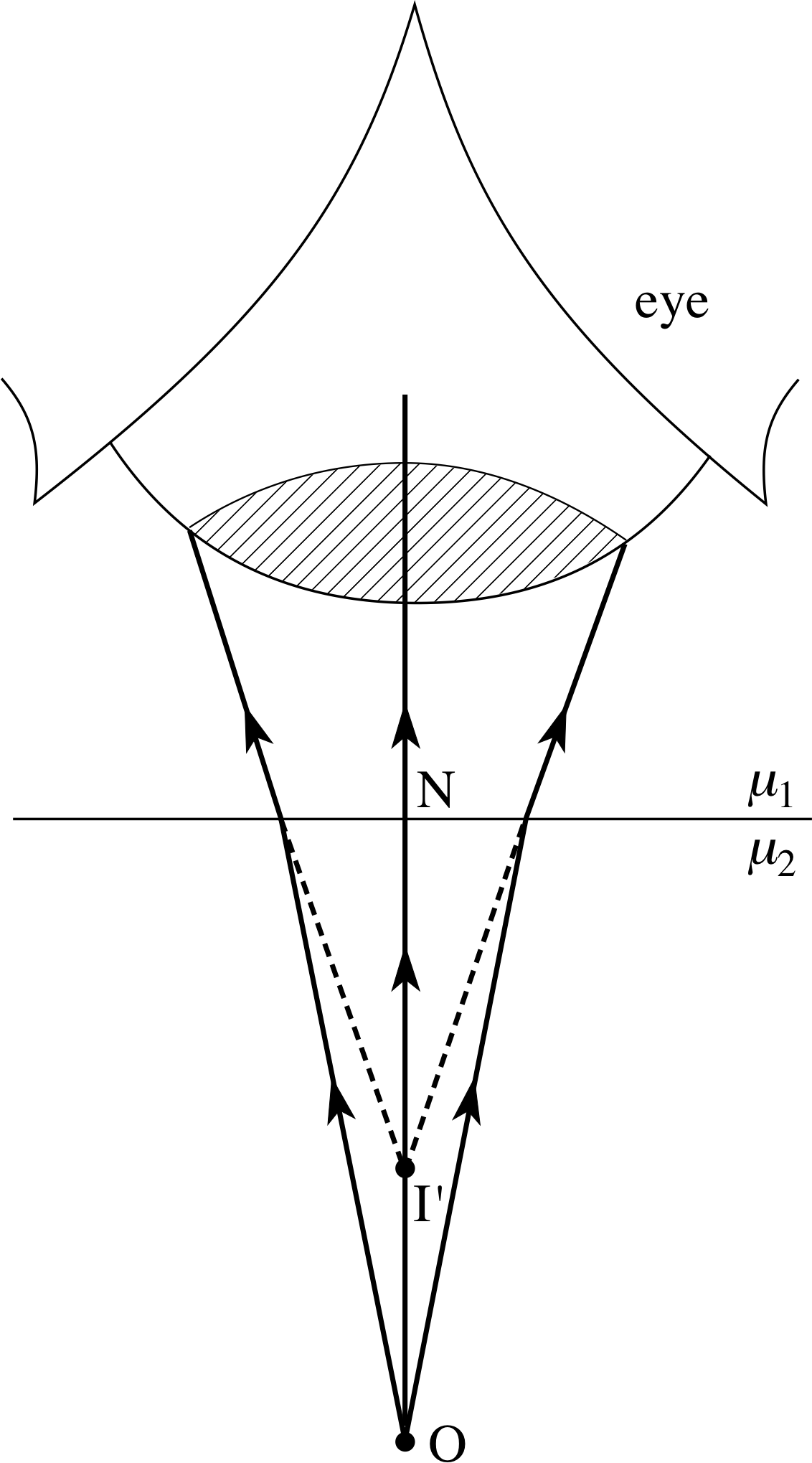
Figure 11 The real and apparent depth of an object in a transparent material.
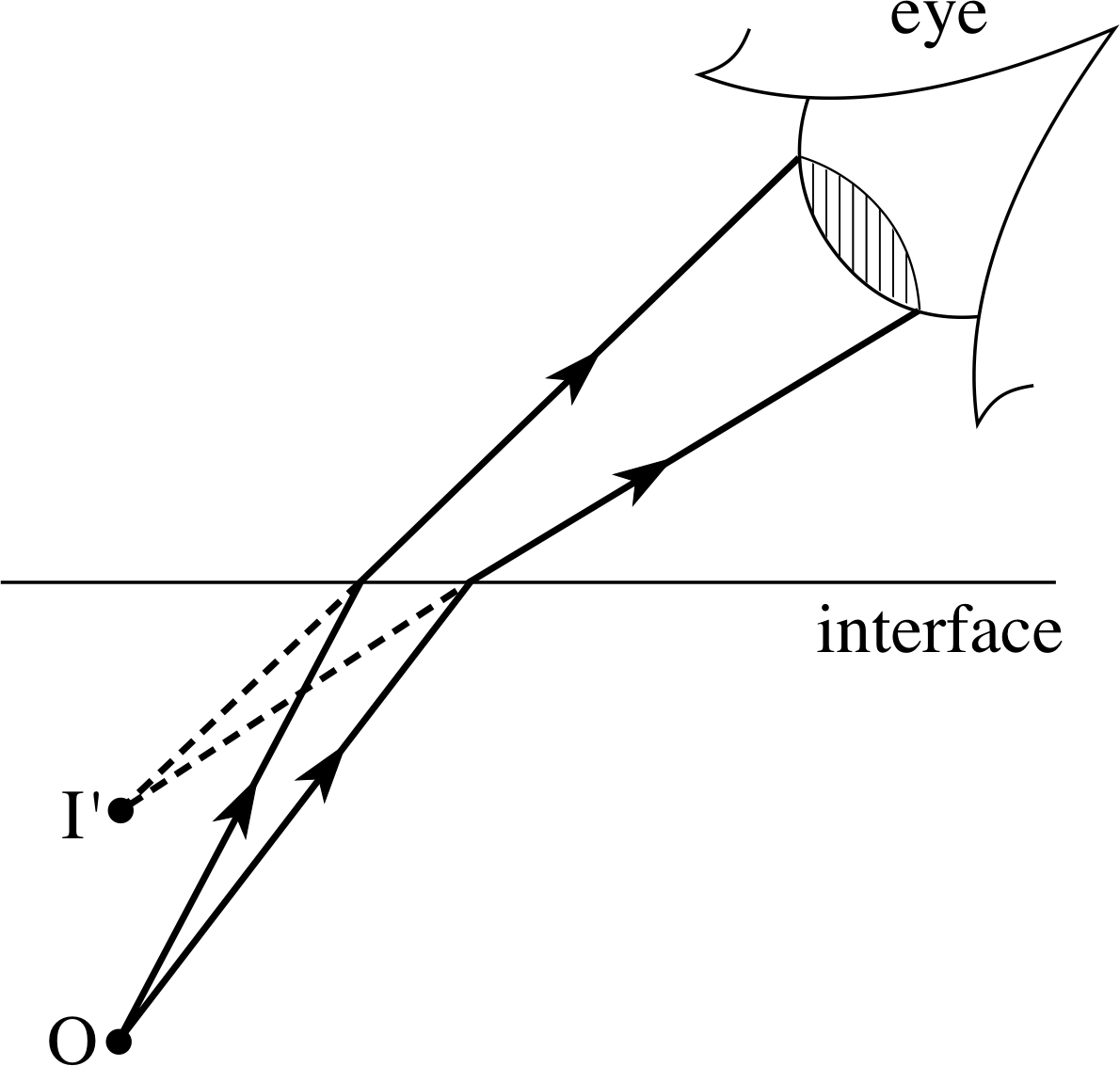
Figure 10 Formation of a virtual image by refraction at an interface.
If you look into a calm swimming pool you can see images of objects below the surface. Ray diagrams can be used to investigate these refracted images, just as they were used in the case of reflection. Figure 10 shows two rays from a point object O that are refracted at the interface between two different transparent materials. The two refracted rays appear to come from a virtual image at the point I′. Unfortunately, if we choose any other two rays from O, at different angles of incidence to the surface, we will find that they will appear to come from a virtual image which is slightly displaced from I′. This means that the virtual image of a point object formed by refraction at a plane interface is never perfectly sharp; it suffers from what are called aberrations.
Fortunately these aberrations are reduced when the eye receives refracted rays from only a small range of angles, and also when the angle of incidence is small. This is indicated in Figure 11, which shows an object at O in a material with refractive index μ2, viewed from directly above by an eye in a material with refractive index μ1. As drawn, the rays are refracted away from the normal as they enter material 1, indicating that μ2 is greater than μ1. Using Snell’s law it is possible to show that in this or similar situations, the real depth of the object below the interface (the distance ON) is related to its apparent depth (the depth of the image I′N), by:
$\dfrac{\text {apparent depth}}{\text {real depth}} = \dfrac{\rm ON}{\rm I'N} = \dfrac{\mu_2}{\mu_1}$(3)
provided the angles of incidence and refraction are small.
| Material | Refractive index |
|---|---|
| vacuum | 1.00 (exactly) |
| air* | 1.000 29 |
| water | 1.33 |
| crown glass | 1.52 |
| fused quartz | 1.46 |
| diamond | 2.42 |
| *at 0°C and 1 atm | |
Question T6
Derive Equation 3, using Snell's Law,
$\dfrac{\sin\theta_1}{\sin\theta_2} = \dfrac{\mu_2}{\mu_1}$(Eqn 1b)
An object O at the bottom of a swimming pool, viewed from above, appears to be 1 m below the surface. Use the data in Table 1 to find the real depth.
[Hint: If θ is small, sin θ ≈ tan θ.]
Answer T6
The real and apparent depth due to refraction are shown in Figure 26. If we take one ray normal to the interface along the line ON and another ray at angle θ1 along OA, Snell’s law gives us:
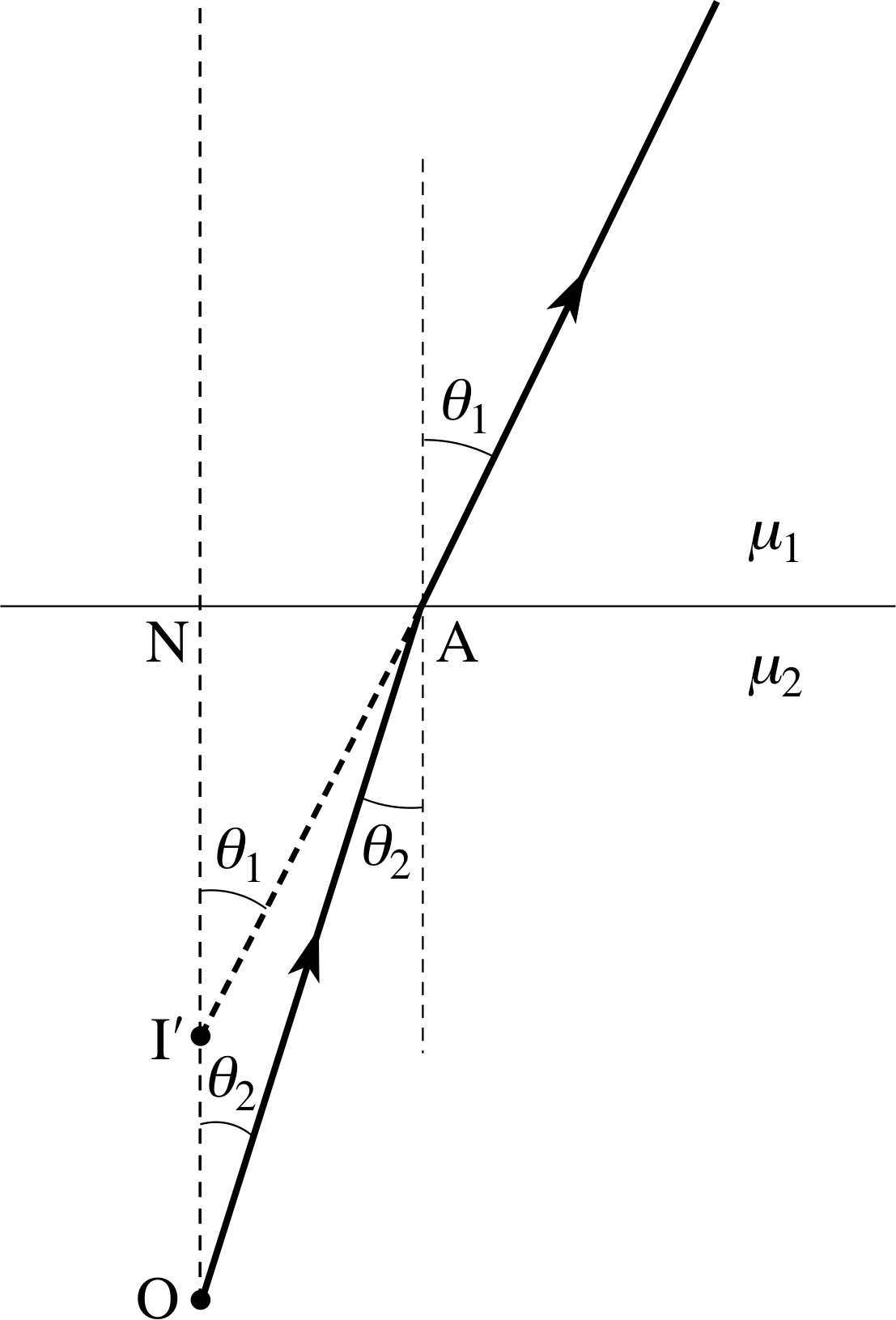
Figure 26 See Answer T6.
$\dfrac{\sin\theta_1}{\sin\theta_2} = \dfrac{\mu_2}{\mu_1}$
But when θ1 and θ2 are small:
sin θ1 ≈ tan θ1 and sin θ2 ≈ tan θ2
so that$\dfrac{\tan\theta_1}{\tan\theta_2} = \dfrac{\mu_2}{\mu_1}$
therefore$\dfrac{\rm NA/I'N}{\rm NA/ON} =\dfrac{\mu_2}{\mu_1}$
thus$\dfrac{\rm ON}{\rm I'N} =\dfrac{\mu_2}{\mu_1}$ as required in Equation 3,
$\dfrac{\text {apparent depth}}{\text {real depth}} = \dfrac{\rm ON}{\rm I'N} = \dfrac{\mu_2}{\mu_1}$(Eqn 3)
From Equation 3 we have:
$\dfrac{\text {apparent depth}}{\text {real depth}} = \dfrac{\mu_{\rm water}}{\mu_{\rm air}} = \dfrac{1.33}{1.00}$
i.e. real depth = (1.33 × 1.0) m = 1.33 m
Analysis of the images of extended objects, especially when viewed at large angles of incidence, is more complicated in the case of refraction than reflection. We will not pursue the formation of such images systematically in this module but one of the complicating factors that may arise, total internal reflection, is dealt with in the next subsection.
4.3 Total internal reflection and optical fibres
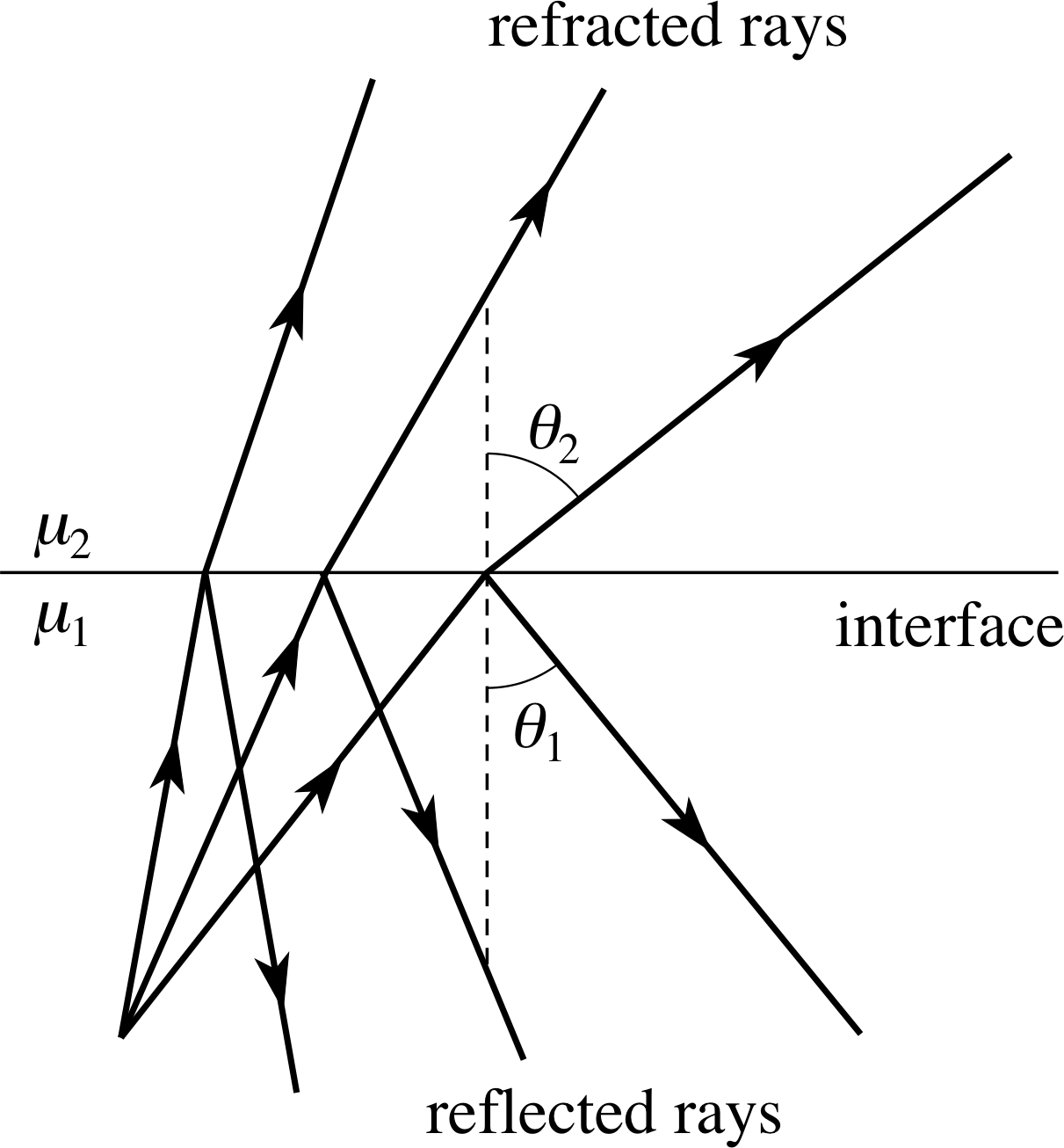
Figure 12 Light rays of a particular wavelength and a range of angles of incidence pass from one material to another material of lower optical density.
When light of a particular wavelength passes from one transparent material to another of lower optical density (i.e. μ1 > μ2), as shown in Figure 12, we are usually able to observe both reflection and refraction. From Snell’s law we know that for any given ray the angle of refraction θ2 will generally be greater than the angle of incidence θ1 since μ1 > μ2. In such cases Equation 1b,
Snell’s law $\dfrac{\sin\theta_1}{\sin\theta_2} = \dfrac{\mu_2}{\mu_1}$(Eqn 1b)
can be rearranged to give:
$\sin\theta_1 = \dfrac{\mu_2\sin\theta_2}{\mu_1}$(4)
The largest possible value of sin θ2 is 1 and this occurs when θ2 = 90°, that is when the refracted ray is parallel to the interface. Now, it is clear from Equation 4 that the corresponding value of sin θ1 is μ2/μ1, which is less than 1, so it follows that there is a limited range of angles of incidence that can give rise to refracted rays in medium 2.
The upper limit to this range, the angle of incidence which gives the refracted ray along the interface, is called the critical angle θc. Since the critical angle is the value of θ1 that ensures θ2 = 90° it follows from Equation 4 that:
$\theta_{\rm c} = \arcsin\left(\dfrac{\mu_2}{\mu_1}\right)$(5)
The question that now arises is what happens to an incident ray which reaches the interface at an angle of incidence greater than θc? According to Equation 4 there is no value of θ2 which can satisfy the equation (it would require sin θ2 to be greater than 1) and so there is no refracted ray – the light cannot pass through into the material of lower optical density and so all the incident energy must be reflected at the boundary. We have here a mechanism for perfect 100% reflection! The phenomenon is called total internal reflection and it has many important applications.
Question T7
A light ray passes from a block of glass (μglass = 1.50) into water (μwater = 1.33). Find the critical angle θc. Repeat the calculation for a ray passing from glass into air (μair = 1.00).
Answer T7
The critical angle is given by Equation 5,
$\theta_{\rm c} = \arcsin\left(\dfrac{\mu_2}{\mu_1}\right)$(Eqn 5)
so$\theta_{\rm c} = \arcsin\left(\dfrac{\mu_{\rm water}}{\mu_{\rm glass}}\right) = \arcsin\left(\dfrac{1.33}{1.50}\right) = 62.5°$
At incident angles greater than 62.5° the ray is totally internally reflected.
Replacing the water by air gives:
θc = arcsin(1.00/1.50) = 41.8°.
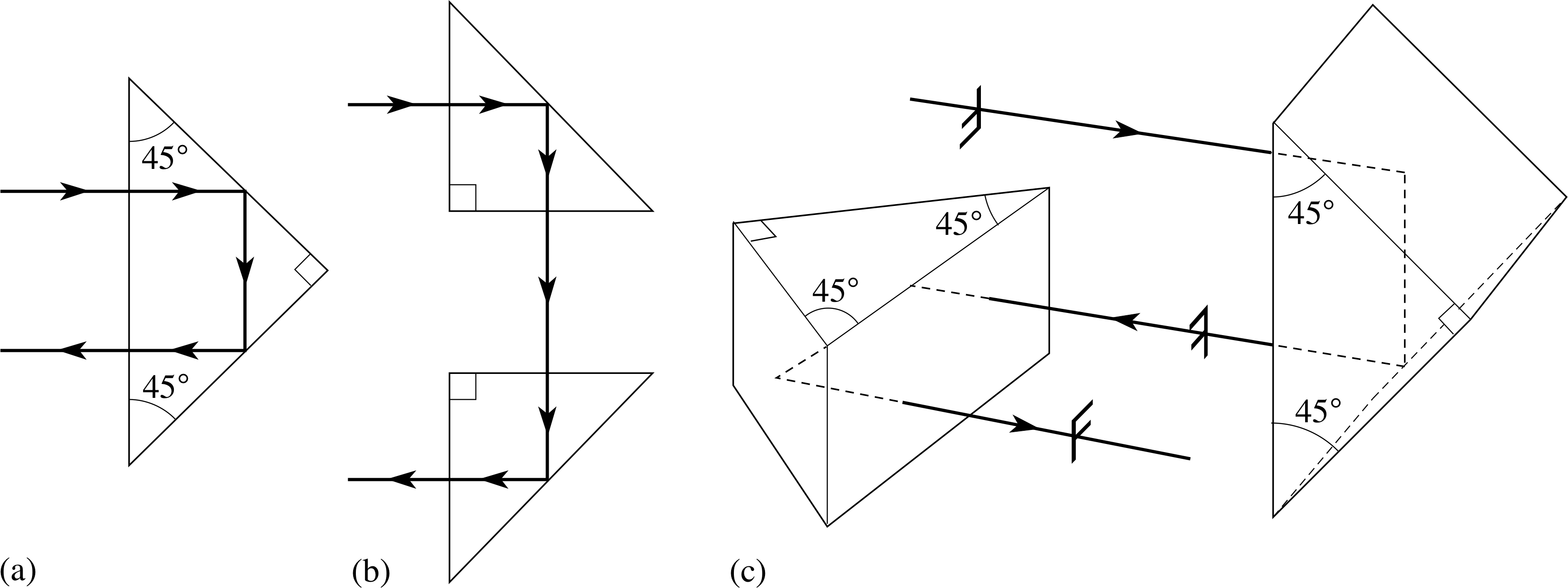
Figure 13 Total internal reflection in 45° prisms. (a) A single prism, (b) two prisms separated as in a periscope, (c) two prisms as in prismatic binoculars.
Total internal reflection is exploited in many commercial applications where energy losses at reflecting surfaces must be minimized. For example, in Figure 13a we show a 45° glass prism used as a prismatic reflector, in Figure 13b two such prisms as used in a periscope, and in Figure 13c two such prisms with their 45° faces rotated through 90°, as might be found in prismatic binoculars. i
The prisms are made of glass with refractive index close to 1.5 so that their critical angle with air is 41.8°. When a ray enters such a prism, as shown, its angle of incidence within the glass is 45° which is greater than the critical angle, so it is totally internally reflected and turned through 90° at each reflection as shown. The energy loss at the air–glass interfaces is lower than that at a silvered mirror surface, so the images seen are brighter.

Figure 14 A section of optical fibre and a confined light ray.
Perhaps the most important application of total internal reflection lies in the field of optical fibre technology. This is of vital importance in modern telecommunications networks. Optical fibres are usually made from very thin strands of quartz glass (often 0.2 mm or less in diameter), specially made to be as free as possible from impurities and imperfections. If a parallel beam of light (usually from a laser) enters one end of the fibre at a small angle to the axis then the constituent light rays may be arranged to have large incidence angles (larger than the critical angle) at the fibre wall. Under these circumstances total internal reflections will prevent the light from escaping through the sides of the fibre and it can be conveyed over distances of the order of tens of kilometres to emerge at the other end without much loss of energy. A section of optical fibre, with an incident ray at a small angle to the axis of the fibre, is shown in Figure 14. The ray is confined within the fibre by successive reflections at the surface, provided the angle of incidence remains greater than the critical angle.
Optical fibres can carry an incredible amount of information. It is not the purpose of this module to describe exactly how this encoding is done but suffice it to say that the light often consists of very short pulses from a laser and these pulses can convey coded information in a variety of ways. In this application the optical fibre link behaves in many ways like the radiowave and microwave links that have been used for decades by the communications industry. Apart from the need for a fibre pathway between the source and the detector, the main difference is the much shorter wavelength (i.e. higher frequency) of the optical signal. i
This has the consequence that fibre–based systems can carry much more information than either radiowave or microwave links or even a normal wire connection.

Figure 15 A stepped–index fibre in which the refractive index changes at a fixed distance from the fibre axis (as indicated by the dashed line).
For all their virtues, simple optical fibres may lose energy if their surfaces are damaged in any way. An improvement in the performance of optical fibres can therefore be made by preventing the light rays from ever touching the outer surface. This improved design can be achieved in two ways. First, a fibre can be constructed so that the refractive index decreases by a finite step at a fixed distance from the axis; the rays may then be totally reflected from this internal protected interface. This is called a stepped–index fibre and is illustrated in Figure 15. Alternatively, a fibre can be made so that the refractive index decreases gradually with distance from the axis; this is called a graded-index fibre and will be discussed in the next subsection. The only major source of energy loss in the stepped–index or graded–index fibre is the absorption in the glass itself, which can be made very low.
Over the next few years optical fibres are likely to replace the hard–wire telephone–grid land lines throughout the UK and since 1988 a fibre optic undersea cable has been used for transatlantic telecommunication. The next phase of the transatlantic cable development (planned for 1996) will link the UK and France with two sites in the USA in a ring network involving two transatlantic fibre optic cables. Each of these cables will have two pairs of fibres, each 5 μm (or about ten wavelengths of light) in diameter.
In each cable only one fibre pair is active, with the other pair as a spare in the event of damage. The power of this technology can be appreciated by realizing that, in principle, a single active pair of these fibres can carry the equivalent of 300 000 simultaneous telephone conversations!
Sometimes many hundreds or thousands of optical fibres are packaged together to form a flexible fibre bundle that will confine rays within individual fibres, provided they are not bent into too tight a curve. These bundles may be used in large communication networks, where there are many sites for sending and receiving information. Fibre bundles can also be used to convey pictures in a very straightforward way. If a real image of an object is projected on to the end of a fibre bundle, each point in the image will correspond to a particular fibre and hence to a particular point at the output end of the bundle. So, if the relative fibre positions at each end of the bundle are the same, the image fed into one end of the bundle can be seen at the other end. These organized bundles are called coherent fibre bundles and they can be used, for example, in ‘non-invasive’ medicine for diagnosis, exploratory investigations or to assist surgeons.
4.4 Continuous refraction and atmospheric optics
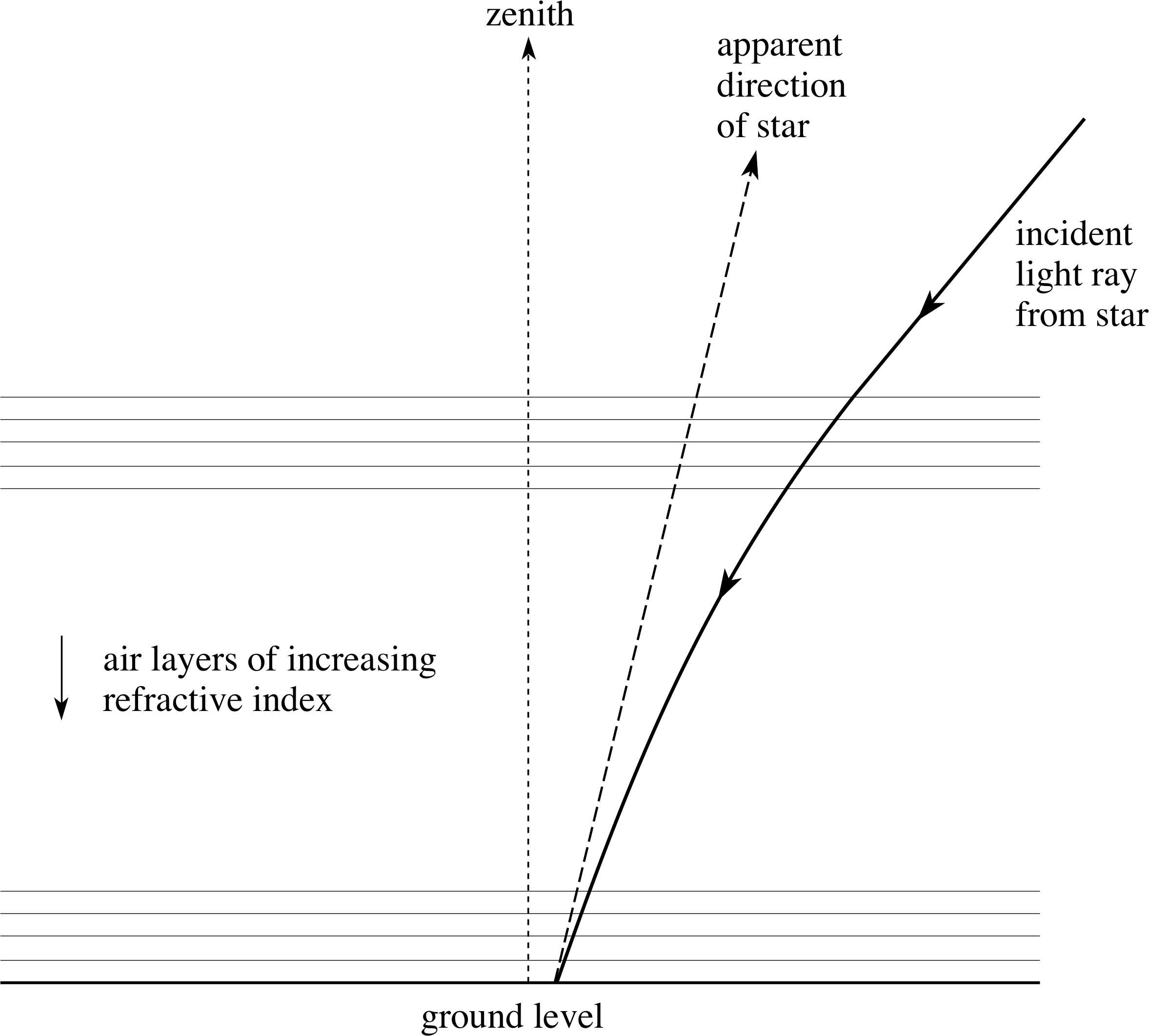
Figure 16 Atmospheric refraction in a plane stratified atmosphere where the refractive index decreases as the altitude increases. The incident ray bends towards the optically denser air. (The effect has been greatly exaggerated for clarity.)
To close this section it is interesting to consider what happens when a light ray travels through a medium in which the refractive index is changing continuously, rather than changing suddenly at an interface. Such situations lead to the phenomenon of continuous refraction which may arise, for example, when a ray of light travels through the atmosphere at an angle to the ground. The refractive index of air varies with density and temperature and, since both of these vary with altitude, the refractive index will also vary with altitude. Density is usually the dominant factor, as a result of which the refractive index usually decreases as the height above the ground increases.
Continuous refraction in the atmosphere has a number of interesting consequences. For example, when astronomers attempt to determine the precise position of a star they usually have to take the effect of continuous refraction into account. If the star is fairly close to the overhead point (the zenith) this is not too difficult; the curvature of the Earth can be ignored and the atmosphere can be treated as though it consisted of several horizontal layers with slightly different refractive indices.
The effect of this, as shown in Figure 16, is to make the star appear closer to the overhead point than it truly is.
On the other hand the effect of continuous refraction on the light from stars near the horizon is much greater and much harder to calculate, partly because of the need to take account of the Earth’s curvature but mainly because a greater part of the ray is in the lower part of the Earth’s atmosphere where turbulence, localized atmospheric disturbances and pollution are all more likely to distort the light rays. This is part of the reason why sunsets are so dramatic and have so many colourful effects associated with them. i
✦ Does the atmosphere affect the time at which the Sun appears to set as seen from a fixed point on Earth? If so, would the Sun set earlier or later in the absence of atmospheric refraction?
✧ Yes. The tendency of incident rays to bend towards the optically denser medium (as in Figure 16) will cause the Sun to appear closer to the zenith (i.e. higher above the horizon) than it really is. Thus the Sun would set earlier in the absence of atmospheric refraction.
Another atmospheric phenomenon associated with continuous refraction is the mirage familiar from films and advertisements where a weary desert traveller sees the illusion of water (or some similar liquid) in the distance. There are in fact several different kinds of mirage. The simplest may sometimes be seen when driving on a long straight road on a hot clear sunny day. You may notice what appear to be ‘wet’ patches on the road surface well ahead, but as you approach them they disappear and reappear further ahead. What you are seeing is a ‘reflection’ of the sky or some other object caused by continuous refraction in the layers of air near the hot road surface.

Figure 17 A ‘hot road’ or ‘desert’ mirage.
The ray diagram explaining such mirages is shown schematically in Figure 17; in this case the air closest to the ground is hotter and optically less dense than that above, so the usual arrangement is reversed and rays bend away from the ground. If the rate at which the temperature changes with height (i.e. the temperature gradient dT/dh) itself decreases appropriately with height then those rays that get closest to the ground will undergo the greatest degree of bending, as shown. The main effect takes place very near the road surface, where the temperature gradient in the air is quite large, but the angles of refraction are very small and so this mirage is only possible near to grazing incidence. That is why the ‘wet’ patches are usually seen far away on a flat road, though they can sometimes be seen much closer when you approach the brow of a hill. convectionConvection currents in the air near the road surface cause the shimmering which usually accompanies this mirage effect.
Question T8
A ray of light that rises into the Earth’s atmosphere leaves the ground at approximately 45° to the surface. If the refractive index of the atmosphere decreases gradually with height, how will refraction affect the path of the ray? How might this behaviour lead to a mirage?
Answer T8
Since it is continually entering layers of lower and lower refractive index it must be refracted smoothly and progressively further and further from the normal to the Earth’s surface. The ray will follow a smooth curve and eventually will be bent back towards the surface, following a symmetric path and arriving at the surface some distance from its departure point. The atmosphere here acts like a mirror.
It is possible to demonstrate continuous refraction in a simple laboratory experiment using a laser beam and a tank of sugar solution. The refractive index of a sugar solution depends on the concentration of the sugar. If a tank of sugar solution is created by allowing water to settle over a large amount of sugar and the system is then allowed to reach equilibrium, the sugar concentration will be highest immediately above the undissolved sugar and will fall smoothly with height above this. This creates a situation where the refractive index of the solution decreases with height. If a laser beam is shone into the tank the curved path of the continuously refracted beam through the solution can be easily seen and the mirage effect demonstrated.

Figure 18 A graded–index optical fibre, with a refractive index that decreases as the distance from the axis increases.
Continuous refraction is also used in fibre optics. A fibre can be made so that the refractive index decreases gradually with distance from the axis; this is called a graded–index fibre. Figure 18 shows how a graded index fibre works. Rays at small angles to the axis always bend away from the optically less dense material near to the surface so they can progress down the fibre without ever touching the surface. i This has a similar power loss to the stepped-index fibre and in some applications is a preferred solution.
Question T9
What would happen to a light ray passing through a medium in which the refractive index changes continuously along the ray, but does so in such a way that at no point are there any changes in refractive index perpendicular to the ray?
Answer T9
Since the light ray is travelling along the direction of the changing refractive index it is always travelling along the normal, with an angle of incidence equal to 90°, and so is not refracted at all – although its speed through the medium will change with the refractive index.
5 Fermat’s principle
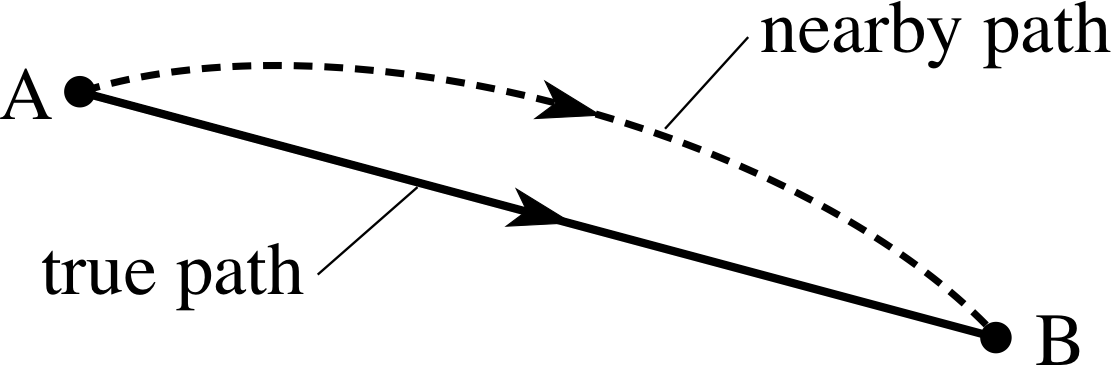
Figure 19 A light ray follows the shortest route between two fixed points. Any nearby path is longer.
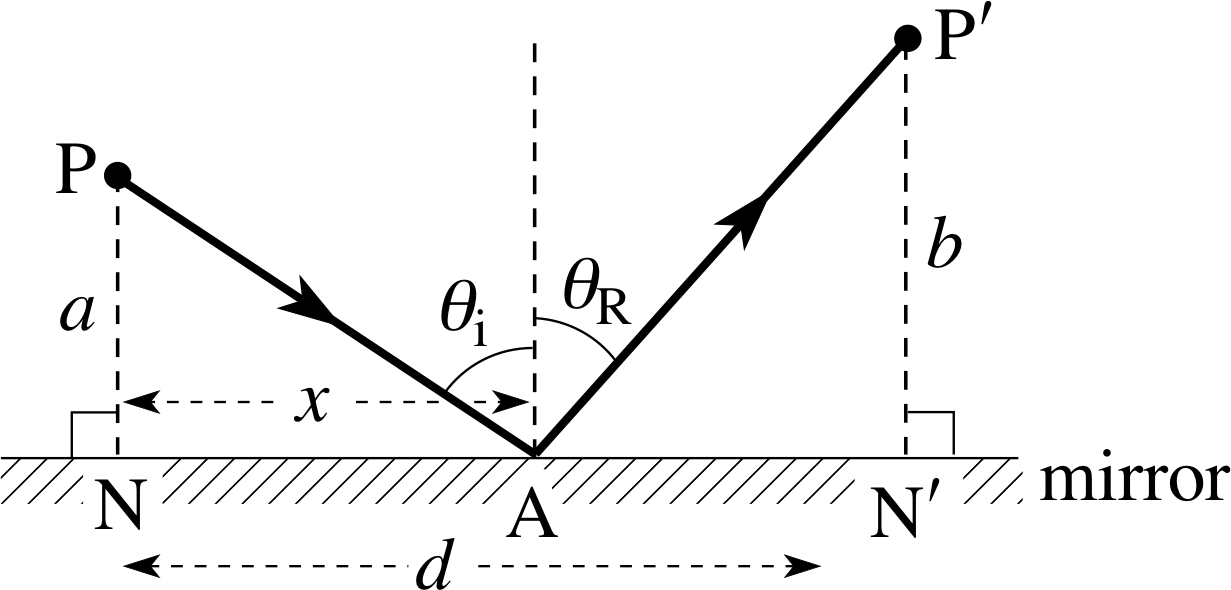
Figure 20 A conceivable route for light rays passing from P to P′ via a reflection at A; but is it the route the rays will actually follow?
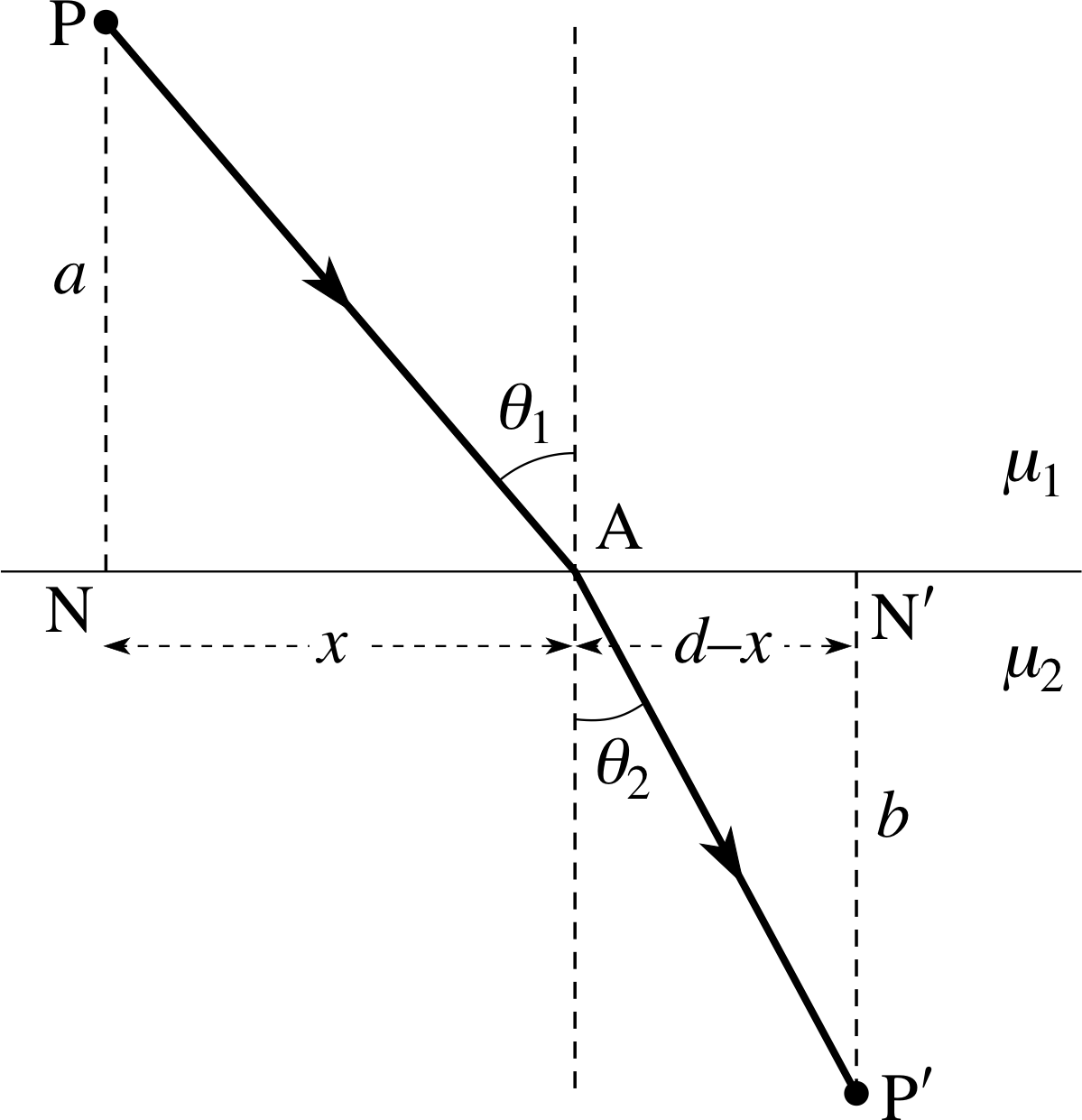
Figure 21 The refraction of a light ray at a plane surface – Fermat’s principle of least time can be used to determine the correct location of point A.
Hero of Alexandria, who probably lived some time around 50 (± 30) AD, proposed the following rule which he believed governed the propagation of light:
When light travels between two fixed points it does so in such a way that its path has the shortest possible length.
If correct, this rule can certainly explain rectilinear propagation; it would simply be a consequence of the geometrical fact that given any two points A and B (see Figure 19), a straight line provides the shortest path between them.
Figure 20 shows how Hero’s rule can be used to deduce the law of reflection. In this case the problem is to find the shortest path from P and P′ that includes a reflection in the mirror. It is pretty clear that the solution must involve two straight lines, such as PA and AP′, but where must A be located to ensure that the total path length is as small as possible? As Hero realized (and as we will prove in Subsection 5.1), A must be located in such a way that θi = θR. Thus the particular path that obeys the law of reflection is also the path of shortest possible length, and the law of reflection may be viewed as a consequence of Hero’s rule.
It took about 1600 years to take the next step. In 1657 the French mathematician Pierre de Fermat (1601–1665) published his now famous ‘principle’ which extended Hero’s rule to include cases of refraction. If you look at Figure 21 it is obvious that the ray path PAP′ between P and P′ is not the shortest path – that would be the straight line path from P to P′ and the ray does not follow that path. Now, although Hero’s rule does not work in this case, Fermat realized that a simple modification to the ancient rule would lead to the known laws of reflection and refraction. According to Fermat the path taken by the light was not that of shortest length but rather that which required the least time. In the case of reflection, where only one medium is involved, the path of minimum time is also the path of minimum length. But in the case of refraction, where the two parts of the path are traversed in different media and therefore at different speeds, the minimum time condition can be used to predict the correct path but the minimum length condition cannot.
✦ If the light in Figure 21 followed a straight line path from P to P′, rather than the true path PAP′, would the time it spent in the medium with refractive index μ1 be increased? What can you say about the time spent in the medium of refractive index μ2?
✧ No, the distance from P to the interface would be shorter along the straight line path, so the time spent in the first medium would be reduced. In contrast, the distance from the interface to P′ is longer than along the actual path, so the time spent in the second medium would be increased. Moreover, since we have asserted (and will shortly prove) that the actual path PAP′ is the path of least time, it must be the case that the extra time spent in the second medium exceeds the reduction in the time spent in medium 1.
In its original formulation, Fermat’s principle was stated as follows:
The actual path taken by a light ray in travelling between two points is the one that is traversed in the least time.
Fermat’s principle presents an intriguing new perspective on the laws of geometrical optics, though it needs some further modification to enable it to deal with all the cases that arise in practice. For instance, it is now known that there are many situations involving highly curved reflectors in which the rays are such that the time taken to traverse them is greater than the time taken to traverse other conceivable rays. The somewhat technical reformulation of Fermat’s principle that covers these and other such cases will now be stated and then explained.
The modern form of Fermat’s principle is stated as follows:
If a light ray passes from one fixed point to another fixed point then the time taken to traverse the actual path will, to a first approximation, be equal to the time taken for light rays to traverse adjacent paths, i.e. the time taken to traverse the path will be stationary with respect to small variations in the path. i
The key to understanding this form of Fermat’s principle is the word stationary.
Mathematically speaking a function f (x) is said to be stationary at any point where the tangent to its graph is horizontal, and the point at which this occurs is called a stationary point.
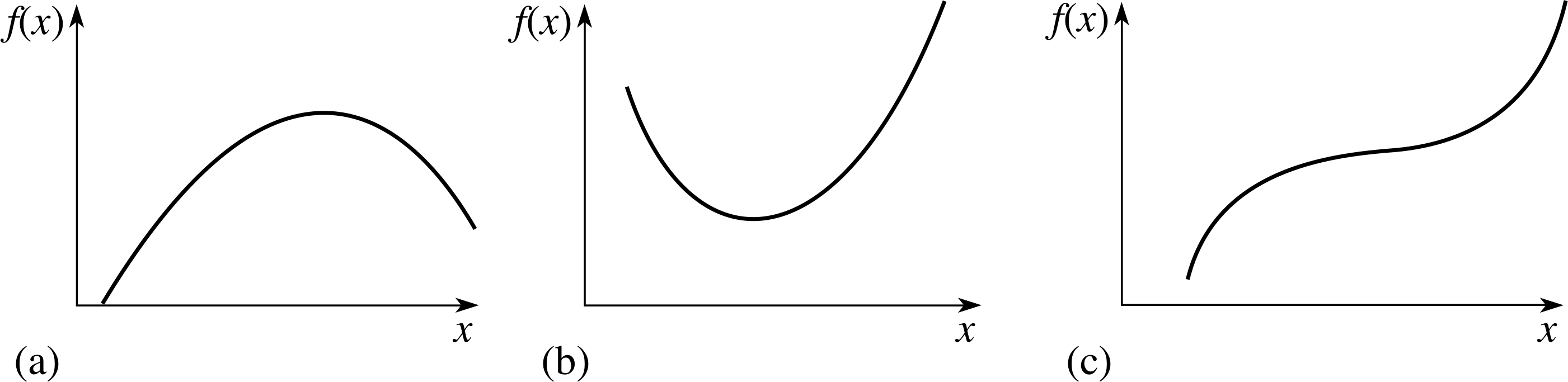
Figure 22 The three situations in which a function may be stationary: (a) a local maximum, (b) a local minimum, and (c) a point of inflection with a horizontal tangent.
At such a point the gradient of the graph must be zero, i.e. the derivative df/dx = 0. The three situations in which functions become stationary are shown in Figure 22a, b and c; they are, respectively, referred to as a local maximum, a local minimum and a point of inflection (with a horizontal tangent). i Since the tangent to the graph of f (x) is horizontal in each of these cases it is clear that the function is neither increasing nor decreasing at the stationary point and that the values of f (x) immediately to the right and to the left of the stationary point will be very close to the value of f (x) at the stationary point itself (i.e. the value of f (x) at the stationary point will be equal to the value of f (x) at adjacent points, to a first approximation).
In the context of reflection and refraction (see Figures 20 and 21), the time T taken to traverse a particular path from P to P′ via A will depend on the exact location of A, and this is determined by the value of x. Thus, we may write the time required to traverse any particular path as T (x) and we may interpret Fermat’s principle as asserting that the actual path followed by the light will be that which makes T (x) stationary. i In other words we can locate A and identify the actual path in either case by finding the value of x for which dT/dx = 0. This is exactly what we will do in the next two subsections.
Study comment Subsections 5.1 and 5.2 contain proofs of the assertions made above but they assume some knowledge of differential calculus. If you are unfamiliar with calculus you may omit these two subsections without endangering your ability to meet the achievements of this module, provided you can state Fermat’s principle and relate it to the laws of geometrical optics.
5.1 Reflection at a plane mirror

Figure 20 A conceivable route for light rays passing from P to P′ via a reflection at A; but is it the route the rays will actually follow?
Consider the path of a light ray from P reflected in a plane mirror so that it passes through the point P′ as shown in Figure 20. The points P and P′ are at fixed distances a and b from the mirror and d is the fixed length NN′. The light ray strikes the mirror at a point A and we let the distance NA be represented by the variable x, which defines the path of the ray. We assume that P, A and P′ all lie in the same plane, although we could use Fermat’s principle to prove this. Fermat’s principle requires that the actual path has the particular value of x such that dT/dx = 0. We will show that this condition leads to the result θi = θR, as expected.
We will suppose that all the rays in Figure 20 are in a vacuum (though we could equally well deal with the case where they were all in some other uniform medium), so the time taken for the light to travel the distance (PA + AP′) is given by T = (PA + AP′)/c.
We can write the path (PA + AP′) in terms of x, with
$cT = (\rm {PA + AP'}) = \sqrt{\smash[b]{a^2 + x^2\vphantom{(d)^2}}} + \sqrt{\smash[b]{b^2 + (d-x)^2}}$
Differentiating this expression with respect to x we have:
$c\dfrac{dT}{dx} = \dfrac12 \left[2x(a^2 +x^2)^{-1/2}\right] - \left\{2(d-x)\left[b^2 + (d-x)^2\right]^{-1/2}\right\}$ i
or$c\dfrac{dT}{dx} = \dfrac{x}{\rm PA} - \dfrac{d-x}{\rm AP'}$
If we set dT/dx = 0, as is required by Fermat’s principle, then
$\dfrac{x}{\rm PA} - \dfrac{d-x}{\rm AP'} = 0$(6)
Since the angle $N\hat PA$ = θi and the angle $A\hat{P'}N'$ = θR we can write
$\dfrac{x}{\rm PA} = \sin\theta_{\rm i}\quad\text{and}\quad\dfrac{d-x}{\rm AP'} = \sin\theta_{\rm R}$
so Equation 6 gives sin θi − sin θR = 0 i.e. θi = θR
Thus, as claimed earlier, the law of reflection is a consequence of Fermat’s principle. i Any allowable path with θi ≠ θR would take a greater time to traverse than the actual path. Though we have proved this mathematically you may still like to confirm it ‘experimentally’ – the next question will allow you to do so.
Question T10
Consider a special case of reflection, as in Figure 20, with the distances: a = 10.0 cm, b = 7.0 cm and d = 20.0 cm. Use the laws of reflection to find the distance NA for a true reflection. Now, make a full scale drawing and, by directly measuring paths, check that this path length is less than that where the point A lies 2 cm nearer to N or 2 cm further from N, as predicted by Fermat’s principle.
Answer T10

Figure 20 A conceivable route for light rays passing from P to P′ via a reflection at A; but is it the route the rays will actually follow?
See Figure 20. If the angles of incidence and reflection are to be equal then, with NA = x:
$\dfrac xa = \dfrac{d-x}{b}$
i.e.xb = ad − ax
Gathering terms involving x on the left–hand side,
x (a + b) = ad
so$x = \dfrac{ad}{a+b}$
Putting in the values for a, b and d we find:
$x = \rm \dfrac{10\,cm\times20\,cm}{(10+7)\,cm} = 11.8\,cm$
A careful drawing, using this value of x, gives a total true path length of 26.3 mm. Nearby paths, with NA = 9.8 cm or 13.8 cm, are about 1.33 mm longer, confirming that the true path is a minimum path.
5.2 Refraction at a plane interface

Figure 21 The refraction of a light ray at a plane surface – Fermat’s principle of least time can be used to determine the correct location of point A.
We now give a similar derivation of the law of refraction. Remember, in Figure 21, the point P is in a transparent material of refractive index μ1 and the point P′ is in a material of refractive index μ2. The interface between the two media is a plane, and it is perpendicular to the plane containing the points P, P′, N and N′. We will let PN = a, P′N′ = b and NN′ = d. The path of the light ray from P to P′ crosses the interface at point A, which is an unknown distance x from N. Fermat’s principle, applied to the path PAP′, should tell us the true value of x and hence the relation between the incident and refracted angles θ1 and θ2. Again we assume that P, A and P′ lie in a plane, but this could also be deduced from Fermat’s principle. Remembering that the speed of light in a material is c/μ, the time taken for the ray path PAP′ is given by:
T = μ1PA/c + μ2AP′/c
so thatcT = μ1(a2 + x2)1/2 + μ2[b2 + (d − x)2]1/2
Differentiating this with respect to x we find:
$c\dfrac{dT}{dx} = \mu_1\dfrac12 \left[2x(a^2 + x^2)^{-1/2}\right] - \mu_2\dfrac12 \left\{2(d-x)\left[b^2 + (d-x)^2\right]^{-1/2}\right\}$
i.e.$c\dfrac{dT}{dx} = \mu_1\dfrac{x}{\rm PA} - \mu_2\dfrac{d-x}{\rm AP'}$ i

Figure 4 A bundle of rays diverging from O and reflected by a plane mirror, forms a virtual image at I′ behind the mirror, while the human eye forms a real image at I. I′
From Fermat’s principle, we set dT/dx = 0 and thus obtain:
$\mu_1\dfrac{x}{\rm PA} - \mu_2\dfrac{d-x}{\rm AP'} = 0$(7)
Also, since $\dfrac{x}{\rm PA} = \sin\theta_1\quad\text{and}\quad\dfrac{d-x}{\rm AP'} = \sin\theta_2$
we have μ1 sin θ1 = μ2 sin θ2
Thus, as claimed earlier, the law of refraction is a consequence of Fermat’s principle. i This is precisely what we expect – Fermat’s principle has given us Snell’s law of refraction. Any closely similar path from P to P′ would take a longer time than the actual path.
We now refer back to Figure 4, which shows the formation of a real image by reflection at a plane mirror followed by refraction in a human eye. In this case there are many different rays from a point on the object to the corresponding point on the (real) image. Since all of these rays are equally valid no one of them can be singled out as corresponding to the minimum (or maximum) time; indeed, we can conclude from Fermat’s principle that light takes the same amount of time to traverse each of these rays. This situation must generally occur when a real image is formed and provides another way of thinking about images and about Fermat’s principle: all rays from a point on an object to the corresponding point on its image must take the same time to traverse.
5.3 The principle of reversibility
It was noted earlier, in Subsections 3.1 and Subsection 4.14.1, that the directions of rays can always be reversed. Though perhaps not as important as the rules of reflection and refraction, this too is a general principle of geometrical optics and is usually referred to as the principle of reversibility.
It may be stated formally as follows:
The result of reversing the direction of a light ray is another valid light ray.
Fermat’s principle provides a general basis for the principle of reversibility. Since the time light requires to traverse any part of a path depends only on the length of the path and the refractive index along that path, it is quite clear that the direction in which the light is travelling plays no role in determining the travel time. Thus, if a particular path is the path of stationary travel time for light travelling in one direction, it will also be the path of stationary travel time for light travelling in the opposite direction. Thus all rays should be reversible, as the principle asserts.
5.4 The physical basis of Fermat’s principle
So far we have stated Fermat’s principle and shown that it is consistent with the principles of geometrical optics (the principles of rectilinear propagation and reversibility, and the laws of reflection and refraction). If we were to ask for a physical justification of Fermat’s principle we would have to resort to a discussion of the (electromagnetic) wave model of light. Whilst a full discussion of this would be out of place in this module, it is interesting to point out some features of the argument, since it gives a valuable insight into the relationship between the full wave model of light and the ray approximation.
Imagine an idealized ray of light as a line joining two fixed points P and P′. This path is a straight line in any material with constant refractive index. Imagine also a second route between P and P′ which deviates from the first only by very small amounts. Fermat’s principle requires that, to a first approximation, the second route has the same journey time as the first since the first corresponds to a stationary journey time. From the perspective of the wave model, it follows that waves that start out in phase from P and travel along the two different routes will, to a first approximation, still be in phase when they arrive at P′. Such waves will tend to reinforce one another when they arrive, giving constructive interference.
This implies that there will be a group of wavelets travelling close to the actual path which will add constructively and maximum energy can be transmitted along the path. In contrast, if we consider any other path from P to P′ which does not correspond to a stationary journey time then slightly different nearby paths are less likely to have similar journey times and it is unlikely that waves starting out in phase from P and travelling along those paths will interfere constructively when they arrive at P′. Thus, the wave phenomenon of interference provides a justification for Fermat’s principle. What is required for the actual path of the ray is that nearby rays have the same journey time, not necessarily that this time should be a minimum – it could equally well be a maximum or any stationary value. The condition that nearby paths have the same journey time, to first approximation, is simply that dT/dx = 0.
6 Closing items
6.1 Module summary
- 1
-
Although light is fundamentally a wave phenomenon there are important simplifications which can be made when the wavefronts are not restricted by apertures or obstacles whose size is comparable with the wavelength. Under these conditions diffraction is usually negligible and the ray approximation is valid. This is the domain of geometrical optics.
- 2
-
A ray is a directed line (i.e. a line with an arrow on it) showing a possible path along which light can travel and indicating the direction in which such light would transport energy. According to the principle of rectilinear propagation light travels in straight lines in a uniform medium. According to the principle of reversibility the result of reversing the direction of a light ray is another valid light ray.
- 3
-
According to the law of reflection when a light ray is Figure 3reflected from a surface, (i) the incident ray, the reflected ray and the normal all lie in the same plane, and (ii) the angle of incidence is equal to the angle of reflection: θi = θR.
- 4
-
When light from an object is reflected in a plane mirror a reversedreversed virtual image is formed. This image is erect, the same size as the original object and located as far behind the mirror as the object is in front.
- 5
-
When light travels through a transparent medium it always travels more slowly than in a vacuum and the refractive index μ of the medium is defined as the ratio of the speed of light in a vacuum to the speed of light in the medium, i.e. μ = c/υ.
- 6
-
According to the law of refraction when a light ray is Figure 7refracted at the interface between two transparent media with different refractive indices, (i) the incident ray, the refracted ray and the normal all lie in the same plane, and (ii) the angle of incidence and the angle of refraction are related by Snell’s law
$\dfrac{\sin\theta_1}{\sin\theta_2} = \dfrac{\mu_2}{\mu_1}$(Eqn 1b)
- 7
-
When a light ray reaches a boundary with a less optically dense medium (i.e. one of lower refractive index) there is a critical angle of incidence, above which total internal reflection occurs. Optical fibres are an important commercial application of total internal reflection.
- 8
-
When a light ray travels through a region where there is a smooth variation in the refractive index the ray is continuously refracted and may follow a curved path. This effect explains various optical effects of the atmosphere, such as mirages, and finds commercial applications in the production of graded-index optical fibres.
- 9
-
According to Section 5Fermat’s principle, if a light ray passes from one fixed point to another fixed point then the time taken to traverse the actual path will, to a first approximation, be equal to the time taken for light rays to traverse adjacent paths, i.e. the time taken to traverse the path will be stationary with respect to small variations in the path. This principle can be justified in terms of the wave model of light and provides a basis for geometrical optics from which the principles of rectilinear propagation and reversibility, and the laws of reflection and refraction can all be deduced.
6.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Recall and use the law of reflection at plane mirrors, and describe the image formed at a plane mirror.
- A3
-
Define the refractive index of a transparent material. Recall and use the law of refraction (including Snell’s law), and describe the image formed at a plane interface between transparent media.
- A4
-
Calculate the critical angle at appropriate interfaces, describe the phenomenon of total internal reflection, and explain how this phenomenon is used in fibre optics and in other optical systems.
- A5
-
Describe the phenomenon of continuous refraction and explain how it is involved in the operation of graded–index optical fibres and in atmospheric phenomena such as mirages.
- A6
-
State the modern form of Fermat’s principle. Justify it in terms of the wave model of light, and explain (without proof) its relation to the principles of rectilinear propagation and reversibility, and to the laws of reflection and refraction.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
6.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions each of which tests one or more of the Achievements.
Question E1 (A2 and A3)
State the principles of rectilinear propagation and reversibility, and the laws of reflection and refraction.
Answer E1
You will find the principles of rectilinear propagation and reversibility in Subsections 2.1 and 5.3, respectively, and the laws of reflection and refraction in Subsections 3.1 and 4.1, respectively.
(Reread these subsections if you had difficulty with this question.)
Question E2 (A1)
Explain what is meant by the terms virtual image and real image of a point object. Give one example of each kind of image.

Figure 4 A bundle of rays diverging from O and reflected by a plane mirror, forms a virtual image at I′ behind the mirror, while the human eye forms a real image at I.
Answer E2
A virtual image of a point object occurs at a point from which light rays appear to diverge. An example is the virtual image of a point object formed in a plane mirror. In Figure 4 the eye sees the object as though it were at I′. A real image of a point object occurs at a point where the light rays from the object converge. An example is the real image formed at the back of the eye (on the retina) by the action of the eye lens.
(Reread Subsections 3.2 and 4.2 if you had difficulty with this question.)
Question E3 (A2)
When you look in a mirror your left hand appears to be your mirror image’s right hand. Why is the mirror image not also upside down?
Answer E3

Figure 6 A right–handed coordinate system, reflected in a plane mirror, forms an image which is a left–handed system. (The mirror is in the (x, y) plane.)

Figure 5 A coordinate system fixed in a mirror. (The mirror is in the (x, y) plane.)
The coordinates of points on an image seen in a plane mirror are obtained from the coordinates of the corresponding points on the original object by reversing the signs of coordinates measured perpendicular to the mirror while leaving unchanged the coordinates measured parallel to the mirror. (This is illustrated in Figure 5). The effect of this ‘near-to-far’ or ‘back-to-front’ reversal is to make the image of a left–handed object into a right–handed object (as shown in Figure 6) but it does not involve any left-to-right interchange in the plane of the mirror nor will it involve any top-to-bottom interchange in that plane.
(Reread Subsection 3.2 if you had difficulty with this question.)
Question E4 (A3)
Draw a ray diagram to show how a person, looking directly down into a pool of water, can see a virtual image of an object at the bottom. If the real depth of the pool is 2.00 m what is the apparent depth of the object, given that the refractive index of water is 1.33?

Figure 11 The real and apparent depth of an object in a transparent material.
Answer E4
Your diagram should look like Figure 11. The image distance I′N is less than the object distance ON. Equation 3 gives:
$\dfrac{\rm ON}{\rm I'N} = \dfrac{\mu_{\rm water}}{\mu_{\rm air}}\quad\text{and}\quad\rm ON = 2.00\,m$
therefore$\rm I'N = \dfrac{2.0\,m}{1.33} = 1.50\,m$
The apparent depth of the object is 1.50 m.
(Reread Subsection 4.2 if you had difficulty with this question.)
Question E5 (A3)
A ray of light passes from a material with refractive index μ1 into another with refractive index μ2 and then into a third material with index μ3. Show that the ray finally emerges with the same angle as if it had passed directly from the first to the third material. (Assume that all the interfaces are parallel.) Explain whether this would be true for any number of parallel layers of different transparent materials.
Answer E5
Using Snell’s law,
$\dfrac{\sin\theta_1}{\sin\theta_2} = \dfrac{\mu_2}{\mu_1}$(Eqn 1b)
and noting that the subscript refers to the number of the layer:
At the interface between layer 1 and 2:
$\dfrac{\mu_1}{\mu_2} = \dfrac{\sin\theta_2}{\sin\theta_1}$
At the interface between layer 2 and 3:
$\dfrac{\mu_2}{\mu_3} = \dfrac{\sin\theta_3}{\sin\theta_2}$
If we multiply the equations together, we find:
$\dfrac{\mu_1}{\mu_2}\times\dfrac{\mu_2}{\mu_3} = \dfrac{\sin\theta_2}{\sin\theta_1}\times\dfrac{\sin\theta_3}{\sin\theta_2}$
Eliminating sin θ2 we have:
$\dfrac{\mu_1}{\mu_3} = \dfrac{\sin\theta_3}{\sin\theta_1}$
This is precisely the relation between incident and refracted angles that would be expected to hold at a direct interface between materials 1 and 3. Now for any number of layers, m, we proceed in the same way and multiply m equations together:
$\dfrac{\mu_1}{\mu_2}\times\dfrac{\mu_2}{\mu_3}\times\dots\times\dfrac{\mu_m}{\mu_{m+1}} = \dfrac{\sin\theta_2}{\sin\theta_1}\times\dfrac{\sin\theta_3}{\sin\theta_2}\times\dots\times\dfrac{\sin\theta_{m+1}}{\sin\theta_m}$
Eliminating sin θ2, sin θ3, sin θ4, ... sin θm gives us:
$\dfrac{\mu_1}{\mu_{m+1}} = \dfrac{\sin\theta_{m+1}}{\sin\theta_1}$
This is of course just Snell’s law for the interface between material 1 and material (m + 1) and the ray does emerge as if it had passed directly from the 1st to the (m + 1)th material.
(Reread Subsections 4.1 and 4.2 if you had difficulty with this question.)

Figure 13a Total internal reflection in a 45° prism.
Question E6 (A4)
A light ray passes into a right–angled prism in the way shown in Figure 13a. Calculate the smallest value of the refractive index of the glass for which total internal reflection would take place when the prism is in air (μair = 1.00).
Answer E6
Referring to Figure 13a the incident angle at the glass to air interface is 45°.
The critical angle for the glass–air interface is given by Equation 5:
$\theta_{\rm c} = \arcsin\left(\dfrac{\mu_{\rm air}}{\mu_{\rm glass}}\right)$
The critical angle must be less than 45° otherwise there would be a refracted ray. We have μair = 1.00 so that:
$\arcsin\left(\dfrac{1.0}{\mu_{\rm glass}}\right) \le 45°$
therefore$\dfrac{1.0}{\mu_{\rm glass}} \le \sin(45°) = 1/\sqrt{2\os}$
thus$\mu_{\rm glass} \ge \sqrt{2\os} = 1.41$
The refractive index of the glass of the prism must be greater than 1.41.
(Reread Subsection 4.3 if you had difficulty with this question.)
Question E7 (A3)
A light ray in air strikes a glass block at an angle of 15.0° to the normal. The ray is refracted into the block at an angle of 9.9°. Calculate the refractive index of the glass.
Answer E7
We use Snell’s law of refraction: μ1 sin θ1 = μ2 sin θ2, where θ1 is the angle of incidence and θ2 is the angle of refraction. Assuming μ1 = 1.00 for air we have:
$\mu_2 = \dfrac{\sin\theta_1}{\sin\theta_2} = \dfrac{\sin15°}{\sin9.9°} = 1.51$
(Reread Subsection 4.1 if you had difficulty with this question.)
Question E8 (A5)
What is meant by saying that a light ray can be continuously refracted? Describe the conditions in which such a phenomenon might occur.
Answer E8
Refer to the discussion and the figures given in Subsection 4.4. The direction of a continuously refracted ray changes smoothly rather than abruptly, thus the ray is a curve rather than a straight line. For a ray to be continuously refracted there must be some variation of the refractive index from place to place, i.e. the medium must be of non–uniform optical density. A ray of light entering the Earth’s atmosphere with a non–zero angle of incidence provides a good example of the kind of ray that will be continuously refracted. Continuous refraction is responsible for the production of optical mirages and for the operation of graded–index optical fibres.
Question E9 (A6)
State Fermat’s principle and explain (without proof) how it is related to the principles of rectilinear propagation and reversibility, and the laws of reflection and refraction.
Answer E9
Refer to the discussion and the figures given in Section 5. The key feature is that the condition on an actual ray path is that the travel time T is stationary for small variations about this path, i.e. dT/dx = 0, where x is a parameter which characterizes a particular route. This time may be a maximum, or a minimum or a point of inflection (with horizontal tangent). The principles of rectilinear propagation and reversibility, and the laws of reflection and refraction can all be deduced from Fermat’s principle. It therefore provides a basis for geometrical optics.
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 6Closing items.