PHYS 8.1: Introducing atoms |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
One of the greatest achievements of modern science has been the demonstration that all the common forms of matter are made of atoms – entities too small to be seen with even the most powerful optical microscopes. Despite our inability to ‘see’ atoms in the conventional sense, they are now so familiar to us that it is easy to forget that their existence was still doubted by some scientists as little as 90 years ago.
The main purpose of this module is to introduce you to atoms and to the major atomic constituents. A subsidiary aim is to give you some insight into the early historical development of atomic physics, since this too is part of the common culture that all physicists share.
Section 2 contains a brief sketch of the historical origins of the idea that matter is composed of atoms and relates the modern concept of an atom to that of a chemical element. (An atom is usually defined as the smallest part of an element that retains the chemical identity of that element.) A description is then given of how the size of an atom can be estimated and how the electron, the first atomic constituent to be identified, was discovered. The section ends with an introduction to ions, atoms that have become electrically charged, usually by gaining or losing electrons.
An explanation is given in Section 3 of how the mass of an atom can be measured with a mass spectrometer, and how such measurements demonstrate that pure samples of a single element usually consist of several different isotopes – chemically similar substances that may be distinguished from one another by the masses of their atoms.
Section 4 describes an early model for the internal structure of atoms proposed by Ernest Rutherford (1871–1937) following his analysis of experiments performed around 1910 by his collaborators at Cambridge University. According to Rutherford’s model, each atom consists of one or more negatively charged electrons orbiting a tiny positively charged nucleus in which most of the atom’s mass is concentrated. Further experiments showed that the nucleus itself consists of other particles, predominantly protons and neutrons.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 5.1Module summary and the Subsection 5.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 5.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
Explain how Rutherford used data from α–particle scattering experiments to propose that each atom contains a tiny, heavy nucleus with a positive electrical charge.
Answer F1
Rutherford’s collaborators (Geiger and Marsden) demonstrated that a thin piece of gold foil scattered high–energy α–particles to a remarkable degree – some of the α–particles were scattered backwards. Rutherford argued that this scattering could be explained only if the α–particle encountered, during its path through the atom, a very large electrostatic force which must, therefore, act over a very short distance. He also inferred from the experiment that the electrostatic force responsible for the scattering must be associated with a very small body that is much heavier than the α–particle. Because he knew that atoms contain electrons, which have very low mass and have negative charge, Rutherford proposed that the scattering was caused by a nucleus with a comparatively high mass (approximately the mass of the atom) and with a positive charge that exactly balances the sum of the negative charges of the electrons.
Question F2
Consider the nitrogen isotope 157N. (a) How many protons does this nucleus contain? (b) How many neutrons does it contain? (c) How many electrons orbit the nucleus of a (neutral) nitrogen atom?
Answer F2
(a) Seven. The number of protons is equal to the atomic number of the isotope, which is the subscript number that precedes the chemical symbol of the chemical element.
(b) Eight. The number of neutrons is equal to the difference between the mass number (the superscript number that precedes the chemical symbol) and the atomic number (the subscript number that precedes the chemical symbol).
(c) Seven. The number of electrons must be equal to the total number of protons in the nucleus because the total charge of the atom must be zero.
Question F3
Describe the essential features of a simple mass spectrometer.
Answer F3
Subsection 3.1 is devoted to the subject of the mass spectrometer. You may treat the instrumental part of that subsection as a rather wordy answer to this question.
1.3 Ready to study?
This is an introductory module that does not presume a high level of prior technical knowledge, nonetheless you will be expected to have some understanding of the following concepts and in a few cases you will be asked to use them in calculations: Coulomb’s law, electric charge, electric field, electrostatic force, force, kinetic energy, magnetic field, mass, Newton’s laws of motion, speed, orbit, potential difference and X–rays. In addition you will need an everyday understanding of the terms: acceleration, chemical reaction, electric current, pressure, radioactivity and voltage. You will also need to know that to keep a particle of mass m moving with speed υ in a circle of radius r there must be a force of magnitude mυ2/r acting on the particle, directed towards the centre of the circle. You will need to be able to use scientific_notationscientific (powers of ten) scientific_notationnotation and SI units in calculations, and you should be aware of the meaning of such basic mathematical terms as product, ratio (used as a synonym for quotient) and sum. You will also be asked to rearrange a simple equation and to make use of square roots. If you are uncertain of any of these terms, you can review them by reference to the Glossary, which will indicate where in FLAP they are developed. The following Ready to study questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
Define kinetic energy. What is the kinetic energy of a particle of mass m and speed υ?
Answer R1
Kinetic energy is the energy that an object has by virtue of its motion. A particle of mass m moving with speed υ has a kinetic energy of ½mυ2.
Consult kinetic energy in the Glossary for further details.
Question R2
Describe the force between two point particles carrying positive charges Q1 and Q2 and separated by a distance r. How would your answer change if one of the charges were negative?
Answer R2
According to Coulomb’s law, each particle experiences a force directed away from the other particle (because like charges repel). The magnitude (i.e. strength) of that force is the same for both particles and is given by the positive quantity AQ1Q2/r2, where A is a positive constant. If one of the charges was negative while the other remained positive the particles would attract each other and the directions of the forces would be reversed. The magnitude of each force would be the same as above, but the expression given earlier becomes negative, reflecting the change in direction of the fields.
Consult Coulomb’s law in the Glossary for further details.
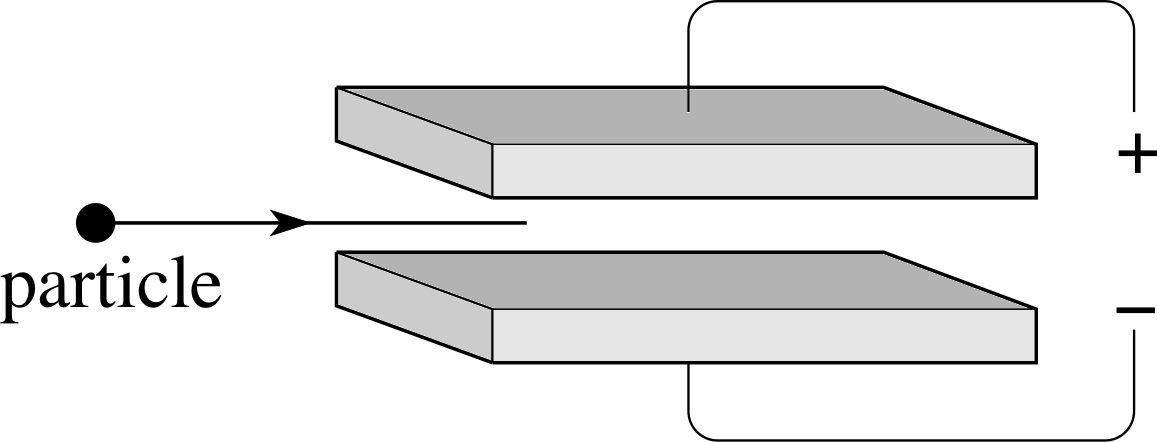
Figure 1 See Questions R3 and R4.
Question R3
Figure 1 shows two plates connected to a power supply. What is the direction of the electric field between the plates? If a negatively charged particle or a positively charged particle entered the space between the plates as shown, in which direction would the particle move?
Answer R3
The electric field is directed vertically downwards, from positive to negative. A positively charged particle would move downwards, a negatively charged particle upwards.
Consult electric field in the Glossary for further information.
Question R4
Still referring to Figure 1, suppose that a magnetic field directed into the page had been present in the region between the plates, in addition to the electric field discussed in Question R3. What would be the direction of the additional force that such a field would have imposed on a negatively charged particle or a positively charged particle entering from the left?
Answer R4
The magnetic field would exert an upwards force on a positive charge and a downwards force on a negative charge. These results follow from the Lorentz force law, which also shows that the magnitude of the additional force is equal to $\lvert\,q\,\rvert\upsilon B$, where $\lvert\,q\,\rvert$ is the (positive) magnitude of the charge on the particle, υ is its speed and B is the strength of the magnetic field.
Consult magnetic field and Lorentz force in the Glossary for further information.
2 Atomic sizes and subatomic particles
2.1 Elements and atoms
The idea that matter consists of atoms seems to have been first suggested by the ancient Greeks. In the 5th century BC, the philosopher Democritus (c. 460–361BC) speculated that matter consisted of hard, unchanging atoms of various shapes and sizes moving in a void. This was not a universally held view, even among the Greeks, but it was sufficiently influential to be passed down to us, notably in the poem De rerum natura (On the nature of things) by the Roman author Lucretius (c. 95–55BC).
The atomic hypothesis (in a suitably modified form) was revived in the early 19th century by the English chemist John Dalton (1766–1844), who proposed it as the most satisfactory explanation of a series of experiments concerning the proportions in which substances combine with each other to form compounds. Investigations of this kind led naturally to the idea that all matter consists of atoms, and that atoms may combine in various ways to form entities called molecules that were supposed to be the smallest part of a compound capable of independent existence while retaining the chemical identity of the compound. However, the usefulness of the atomic hypothesis in simplifying chemical calculations did not provide any ‘proof’ that atoms and molecules actually existed as physical entities.
Convincing evidence of the reality of atoms emerged only in the 20th century, most strikingly in the interpretation given by Albert Einstein (1879–1955) of the previously incomprehensible random zig–zag motion exhibited by tiny fragments of pollen and other such particles suspended in air or water.
In 1905, Einstein suggested that this so–called Brownian motion i was due to the continual buffeting of the fragments by unseen molecules. Subsequent investigations confirmed Einstein’s brilliantly simple explanation and it is now widely accepted that this furnished the first convincing evidence of the physical existence of atoms and molecules.
If all chemical substances are composed of atoms, how many different sorts of atom must there be? Some of the ancients thought that the changing make–up of the world could be explained in terms of combinations of a relatively small number of basic elements. The best known version of this proposal is that associated with Aristotle (384–322 BC) who countenanced four terrestrial elements Air, Earth, Fire and Water. i Unfortunately this is regarded as rather too few by modern chemists who insist that the number of chemical elements (or chemical_elementselements for short) should be closer to 100. At the present time about 111 elements are known, though only about 90 are found naturally on the Earth, the remainder having to be artificially created.
Does the fact that all the known chemical compounds (of which about 8 000 000 are listed in the chemical literature) can be explained as combinations of just 100 or so elements mean that there are only a hundred or so different sorts of atom? The answer to this depends on what is meant by a ‘sort’ of atom. From a chemical point of view, all the atoms found in a pure sample of any element behave almost identically, so we may say that each element corresponds to a single ‘sort’ of atom. However, if all the chemically similar atoms of a particular element are examined it is generally the case that they can be divided into a number of classes according to their mass. We will have more to say about these different ‘versions’ of a given ‘sort’ of atom later, when we discuss isotopes, but for the moment we note that counting each ‘version’ (isotope) separately would increase the total number of atomic ‘types’ to a few hundred.
| Element | Symbol | Atomic number | Relative atomic mass |
|---|---|---|---|
| aluminium | Al | 13 | 26.981 54 |
| calcium | Ca | 20 | 40.08 |
| carbon | C | 6 | 12.011 15 |
| chlorine | Cl | 17 | 35.453 |
| copper | Cu | 29 | 63.55 |
| gold | Au | 79 | 196.967 |
| helium | He | 2 | 4.0026 |
| hydrogen | H | 1 | 1.007 94 |
| iodine | I | 53 | 126.9045 |
| iridium | Ir | 77 | 192.2 |
| magnesium | Mg | 12 | 24.305 |
| neon | Ne | 10 | 20.18 |
| nitrogen | N | 7 | 14.0067 |
| oxygen | O | 8 | 15.9994 |
| silver | Ag | 47 | 107.8682 |
| sodium | Na | 11 | 22.9898 |
Each chemical element has an internationally agreed name and can be represented by an agreed chemical symbol, which often consists of the first one or two letters of the name; the first letter is always upper case and the second always lower case. Thus, the elements oxygen and aluminium are symbolized by O and Al, respectively. Some of the chemical symbols are less obvious as they are derived from other languages. For example, the chemical symbols for gold and silver, Au and Ag, respectively, come from their Latin names, aurum and argentum.
Table 1 lists the chemical symbols of some common elements, together with their atomic numbers and relative atomic masses, concepts that will be explained in Subsections 4.3 and 3.1, respectively.
We can use the chemical symbols as a shorthand when referring to atoms (e.g. H atom rather than hydrogen atom) or when writing the chemical formula that shows the relative numbers of various types of atom in a compound (e.g. H2O for water). Since molecules are actually specific combinations of atoms we may also make use of chemical symbols when referring to them, thus the water molecule which consists of two hydrogen atoms bound to one oxygen atom may be referred to as the H2O molecule. i
2.2 The size of atoms
Although atoms are often visualized as spheres, they are not like billiard balls; they do not have a sharp perimeter edge, such as that of a billiard ball and so there is no unique meaning attached to the phrase ‘the size of an atom’. Nonetheless, it is possible to associate a typical size with what may be loosely termed an ‘atomic diameter’ and it is the determination of that typical atomic ‘scale’ (i.e. a rough order of magnitude estimate) that concerns us in this subsection.
You have probably noticed how oil spreads on a wet road to produce a thin film, resulting in coloured patterns. Some oily substances spread on water in this way to make a very thin film, called a monolayer, that is a film that is only one molecule thick. Each molecule of such a substance consists of many atoms linked together, and the corresponding monolayer may therefore have a thickness that is greater than the diameter of a single atom. Nonetheless, the thickness of a monolayer can be easily determined in some instances, so measurements of monolayers provide a simple way of finding a reasonable upper limit on the size (diameter) of an atom.
A suitable substance for this kind of experiment is stearic acid, which is an oily liquid at room temperature. It is first dissolved in a liquid that evaporates easily (such as pentane). Then a single drop of the resulting solution is dropped on to the surface of a dish of water. The drop spreads and the pentane quickly evaporates, leaving a monolayer of the stearic acid on the surface of the water. When a second drop of solution is added to this film of stearic acid the area of the monolayer increases.
| Number of drops | Area/cm2 | Area per drop/cm2 |
|---|---|---|
| 1 | 32 | 32 |
| 2 | 59 | 30 |
| 3 | 106 | 35 |
| 5 | 168 | 34 |
| average: 33 |
It is easy to estimate the surface area of the monolayer by measuring the length (diameter) of the film in various directions. The film can be made more visible if the surface of the water is covered with a fine powder before the stearic acid is added. The powder is then pushed aside by the expanding monolayer. Table 2 gives some typical results obtained by successively adding drops.
Notice from Table 2 that the area per drop remains roughly constant as the number of drops increases.
✦ What do you conclude from the roughly constant value of the area of the layer per drop?
✧ The film appears to have a roughly constant thickness. As the number of drops increases, the area increases proportionately, maintaining the thickness of the film.
This constant film thickness is precisely what should be expected if a monolayer has formed, but it does not prove that the film is a monolayer. Nevertheless, the thickness of the layer can be calculated and is certainly an upper limit to the size of an atom because the film cannot be less than one atom thick.
If the volume of one drop is 0.01 cm3 and if the solution contains 0.05% stearic acid (i.e. 0.05 cm3 of stearic acid in 100 cm3 of solution), we can calculate the thickness of the monolayer.
The volume V of stearic acid in one drop is
V = volume of drop (in cm3) × (0.05 cm3/100 cm3) = 5.0 × 10−6 cm3
This volume is related to thickness by the expression V = thickness × area. i The thickness d of the monolayer is therefore
$d = \dfrac{\text{volume of stearic acid}}{\text{area of monolayer}}$
Taking the average area per drop from Table 2, we find:
d = ( 5.0 × 10−6 cm3)/(33 cm2) = 1.5 ×10−7 cm
i.e.d = 1.5 × 10−9 m
Thus we arrive at a rough upper limit on the size of an atom using an extremely simple experiment. Of course, the extent to which this upper limit exceeds the diameter of a single atom depends on the arrangement of atoms in the monolayer but even without knowing much about stearic acid it seems reasonable to guess that this won’t be much more than a few atomic diameters.
There are many other methods of determining the atomic size scale, some of them much more precise (but also more complicated) than the one described above. Many of these methods involve using the atoms in a gas or a solid as a ‘target’ and observing what happens in a collision when some sort of ‘projectile’ is ‘scattered’ by the target atoms. Scattering experiments of this kind may be difficult to analyse, but if the ‘projectile’ is sufficiently simple and well–understood they can provide very direct information about atomic sizes. Similarly, a careful analysis of the way in which X–rays are scattered from a crystal in which atoms are regularly arranged can reveal the spacing between adjacent atoms in the crystal and hence provide insight into atomic sizes. i
Since the 1950s it has even been possible to record the images of individual atoms by various techniques, though the nature of these techniques is such that the images still don’t provide an unambiguous way of determining the size of an atom.
Using these techniques and many others, the size scale associated with atoms has come to be well known, even though the ‘diameter’ i of any particular sort of atom will depend on the definition of diameter that has been adopted. We can sum up the situation as follows:
In general, atoms should not be thought of as hard spheres with definite diameters. However, for many purposes the ‘diameter’ of an atom may be taken to be a few times 10−10 m, irrespective of its chemical nature.
Question T1
Approximately how many atoms are there in a cup of tea? [Hint: First estimate the volume of a cup of tea, and then assume that all atoms are roughly the same size and that the atoms are small cubes, of side 5 × 10−10 m, which touch each other.]
Answer T1
The volume of a cup of tea is typically about 200 cm3.
200 cm3 = 200 × 10−6 m2 = 2 × 10−4 m2
If each atom is assumed to be a cube of length L, and L = 5 × 10−10 m, then
volume of an atom = L3 = 125 × 10−30 m2 = 1.25 × 10−28 m3
So the number of atoms in a cup of tea is:
$\dfrac{\text{volume of tea}}{\text{volume of atom}} = \rm \dfrac{2\times10^{-4}\,m^3}{1.25\times10^{-28}\,m^3} \approx 10^{24}$
Note the size of this huge number: a cup of tea comprises roughly a million, million, million, million atoms!
2.3 Electrons
Even before the existence of atoms was universally accepted, evidence existed that atoms had constituents, implying the existence of subatomic particles. This subsection concerns the discovery and investigation of the first subatomic particle to be found – the electron.
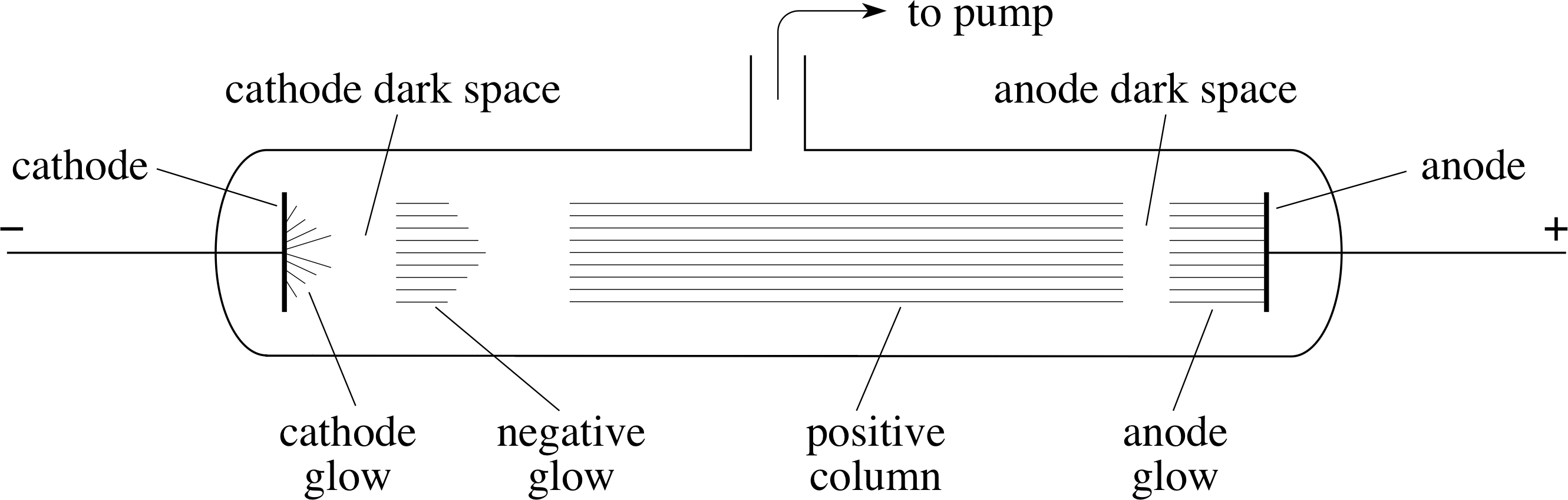
Figure 2 A discharge tube illustrates the conduction of electricity through a low–pressure gas. (The pressure within the tube shown schematically in the figure is about 103 Pa.)
The discovery of the electron had its origin in studies of the conduction of electricity by gases at very low pressures. In this type of experiment, the gas is contained in a discharge tube (see Figure 2); typically a glass tube in which the pressure can be reduced by means of a pump, and which contains metal plates (electrodes) connected to a high voltage supply. The electrode connected to the positive terminal of the supply is called the anode and the one connected to the negative terminal is called the cathode.
As the gas is pumped out of the discharge tube, nothing much happens until the pressure falls to about 104 Pa i (~10% of atmospheric pressure), at which point a current begins to flow and thin streamers of luminous gas appear between the electrodes. By the time the pressure has fallen to about 103 Pa (~1% of atmospheric pressure), the streamers are replaced by a steadily glowing column that is interrupted by darker regions, with the one nearest the cathode especially dark and difficult to see (this is indicated in Figure 2). This particular dark region is called the cathode dark space. As the pressure of the gas is reduced still further, the dark spaces swell until the cathode dark space eventually occupies the whole of the region between the electrodes, at which stage the walls of the glass tube glow with a pale green light. (This glow is an example of fluorescence.)
The German scientist Johann Hittorf (1824–1914), working in Bonn in 1869, was the first to recognize the cause of the glowing walls. He found that small obstacles positioned between the electrodes cast sharp–edged shadows on the walls of the tube, and from their location he concluded that ‘glow rays are emitted by the cathode and from there follow straight paths.’ These ‘glow rays’ were named cathode rays in the mid-1870s, and as such became part of the systematic investigation of gas discharge phenomena carried out by Sir William Crookes (1832–1919). Crookes confirmed that cathode rays normally moved in straight lines, that they could be deflected by a magnet and that they behaved as though they were composed of negatively charged particles. At about the same time it was independently established that cathode rays could deposit negative charge on a body, so by the early-1880s many scientists were convinced that cathode rays really were beams of negatively charged particles. However, this view was not universally accepted because no one had been able to show that cathode rays were deflected by electric fields, as charged particles would be.
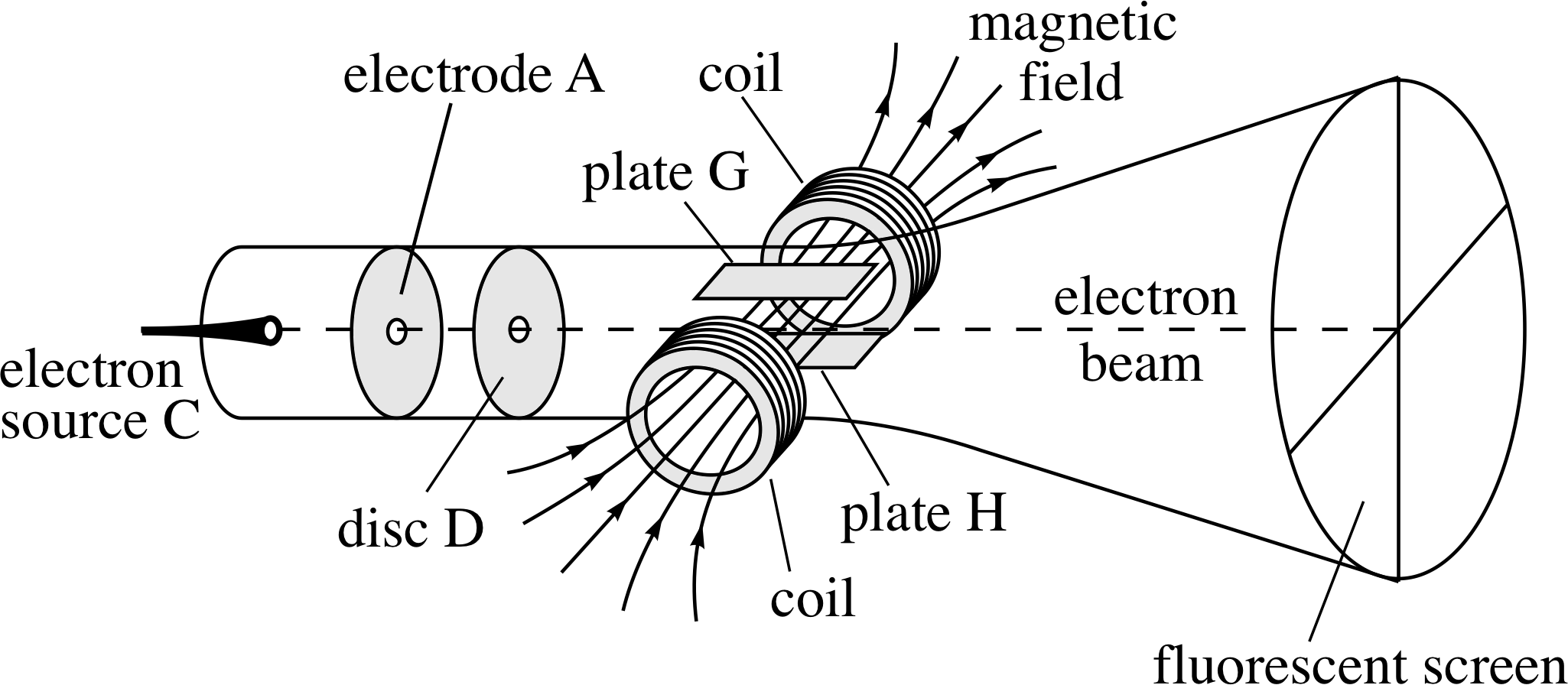
Figure 3 A schematic representation of Thomson’s apparatus to determine the charge-to-mass ratio of the electron. Electrons are emitted at C and accelerated along an evacuated tube towards A. The electrons then pass through the hole in disc D and cease to accelerate as they are now shielded from A. This electron beam then passes through mutually perpendicular electric and magnetic fields (like those discussed in Questions R3 and R4) that are adjusted so that they have compensating effects on the electron beam. This is illustrated in the diagram where the beam is shown travelling straight through with no deflection.
The debate about the nature of cathode rays was finally settled in 1897 by the British physicist J. J. Thomson (1856–1940). i He felt that previous attempts to show that electric fields could deflect cathode rays had failed because too much gas had been left in the discharge tube; this had been broken–up into charged particles by the cathode rays and had neutralized the applied electric field. Obviously the way to overcome this problem was to remove the excess gas. Thomson therefore evacuated a discharge tube more completely than before, and was then able to show that an electric field created by a second pair of electrodes (plates G and H in Figure 3) built into the tube did deflect the cathode rays. This was a notable achievement and harder than it sounds, but his experiments went further still.
By using the deflecting effect of a known magnetic field to counteract the deflecting effect of the second electric field, Thomson was able to determine the so–called charge–to–mass ratio of his cathode ray particles – the result of dividing the charge of a particle by its mass. i It had been expected by some that cathode ray particles, if they existed, would be electrically charged atoms or molecules, but Thomson’s values for the charge-to-mass ratio were much larger than those expected for charged atoms or molecules. Moreover, they did not depend on the kind of gas in the tube nor on the composition of the electrodes. After a great deal of thought and some further work Thomson concluded that:
- Cathode ray particles are all of the same mass and charge and are a constituent of all atoms.
- The mass of these particles is less than one–thousandth of the mass of a hydrogen atom. (Actually, it is more like one two-thousandth.)
- Atoms are not indivisible, since cathode ray particles can be torn from them. i
In Thomson’s own words, ‘... On this view we have in the cathode rays matter in a new state, a state in which the subdivision of matter is carried very much further than in the ordinary gaseous state: a state in which all matter ... is of one and the same kind.’
Thomson himself initially referred to his new subatomic particles as corpuscles but the term electron (which had been introduced some years earlier to describe a supposedly fundamental quantity of electric charge) was soon applied to them, and electrons they have remained ever since. Because the magnitude of the electron’s charge is denoted by e and its mass by m, the ratio that Thomson determined may be written e/m and this classic investigation is now generally known as Thomson’s e/m experiment. i It is worth noting that Thomson’s experiment did not directly provide a value for either the mass or the charge of the electron, only the ratio of the two quantities was measured.
In the years that followed Thomson’s discovery a number of experiments were performed to determine the charge on the electron. These met with varying degrees of success, but in 1911 the American physicist Robert A. Millikan (1868–1953) managed to measure e very precisely by making careful observations of the motion of electrically–charged oil drops in a vertical electric field. Once this had been achieved the known value of e/m could be used to make a precise determination of the electron’s mass m. To three decimal places, the currently accepted values of e, m and e/m are:
- charge of the electron −e = −1.602 × 10−19 C
- mass of the electron m = 9.110 × 10−31 kg
- charge-to-mass ratio of the electron e/m = −1.759 × 1011 C kg−1
2.4 Ions
Matter is not normally electrically charged, so it is reasonable to suppose that atoms each have zero electrical charge (i.e. they are electrically neutral). It is, however, relatively easy for many types of atom in their usual electrically neutral state to lose or to gain one or more electrons. An atom (or molecule) that has lost its electrical neutrality in this, or any other, way is known as an ion.
If we bombard the gaseous element neon with a stream of fast electrons the effect will be to dislodge some of the electrons that are within the neon atoms. As a result some positively–charged ions will be produced from the neon. As with atoms, we can use internationally agreed symbols to describe a particular ion. For example, a neon atom that has lost a single electron gains a net positive charge and is therefore represented by Ne+. Such an atom is said to be singly ionized. Similarly, an atom of neon that has lost two electrons is said to be doubly ionized and is represented by Ne2+. Equipped with this notation it is easy to indicate the sort of process in which an ion is formed:
✦ If the symbol e− is used to denote the electron, describe in words the process represented below: Ne + e− → Ne+ + 2 e− (1)
✧ The process is one in which an electron (e−) collides with an atom of neon (Ne) and knocks an electron out of the atom. The outcome is a positive ion of neon (Ne+) and two free electrons (2e−).
Note that it is also possible to have negatively charged ions, in which electrons have been added to neutral atoms.
✦ During a collision, a chlorine atom Cl absorbs three electrons. Describe this using symbols.
✧ Cl + 3e− → Cl3−
Once it had been established that atoms each have negatively charged constituents, it also became plain that they must have positively charged constituents in order that the total charge of the atom can be zero. We will return to these and other atomic constituents in Section 4. First, however, we will consider how atomic masses are measured.
Question T2
What does the symbol Hg+ mean? (Hg is the chemical symbol for mercury.)
Answer T2
Hg+ represents a mercury ion with a single positive charge, that is, an atom of mercury that has lost one electron and is hence singly ionized.
3 Atomic masses
3.1 The mass spectrometer
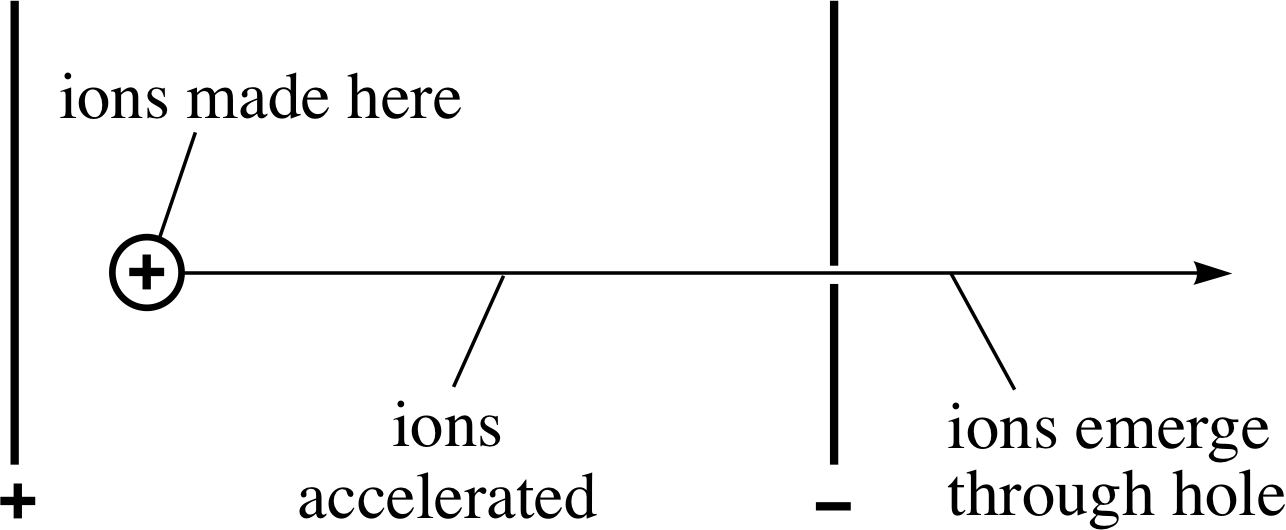
Figure 4 The acceleration of ions in a mass spectrometer.
As atoms are so small it is impossible to measure their masses with anything like a conventional balance. However, by using a device called a mass spectrometer it is possible to determine the mass of any particular kind of ion and hence of the atoms that give rise to those ions. i
The basic design of a mass spectrometer exploits the behaviour of a beam of electrically charged particles in electric and magnetic fields. The beam of charged particles in this case consists of ions which are created by bombarding neutral atoms with high speed electrons in the space between two oppositely charged metal plates (marked + and − in Figure 4). A potential difference of several hundred volts is maintained between the plates by connecting them to the two terminals of a high–voltage power supply. As soon as the positive ions are created they accelerate towards the negative plate, where a carefully positioned hole allows some of them to pass through, thus providing a beam of positive ions.
The detailed arrangements are such that each ion is accelerated through ions made here essentially the same potential difference V with the consequence that any ion of charge q will emerge from the hole with energy E given by
E = qV
This energy takes the form of the kinetic energy of the emerging ions, so the mass m and speed υ of such an ion will be related by
$\dfrac12m\upsilon^2 = qV$
Rearranging this equation, shows that the speed υ of an emerging ion will depend on its charge-to-mass ratio, q/m, since
$\upsilon = \sqrt{\dfrac{2qV}{m}}$(2)
So, after this first stage of acceleration the ions in a mass spectrometer all travel in the same direction but those with a comparatively high charge-to-mass ratio will move faster than those with a lower charge-to-mass ratio.
Question T3
If you were to examine all the accelerated ions of a given charge q, how would their speed depend on their mass?
Answer T3
Since V is the same for all the accelerated ions, and
$\upsilon = \sqrt{\dfrac{2qV}{m}}$(Eqn 2)
it follows that if we were to examine all the ions of a given charge q we would find that those with a comparatively low mass would emerge with a higher speed than those with a comparatively high mass. More quantitatively, $\upsilon \propto 1{\big /}\sqrt{m\os}$ (where ∝ is read as ‘is proportional to’).
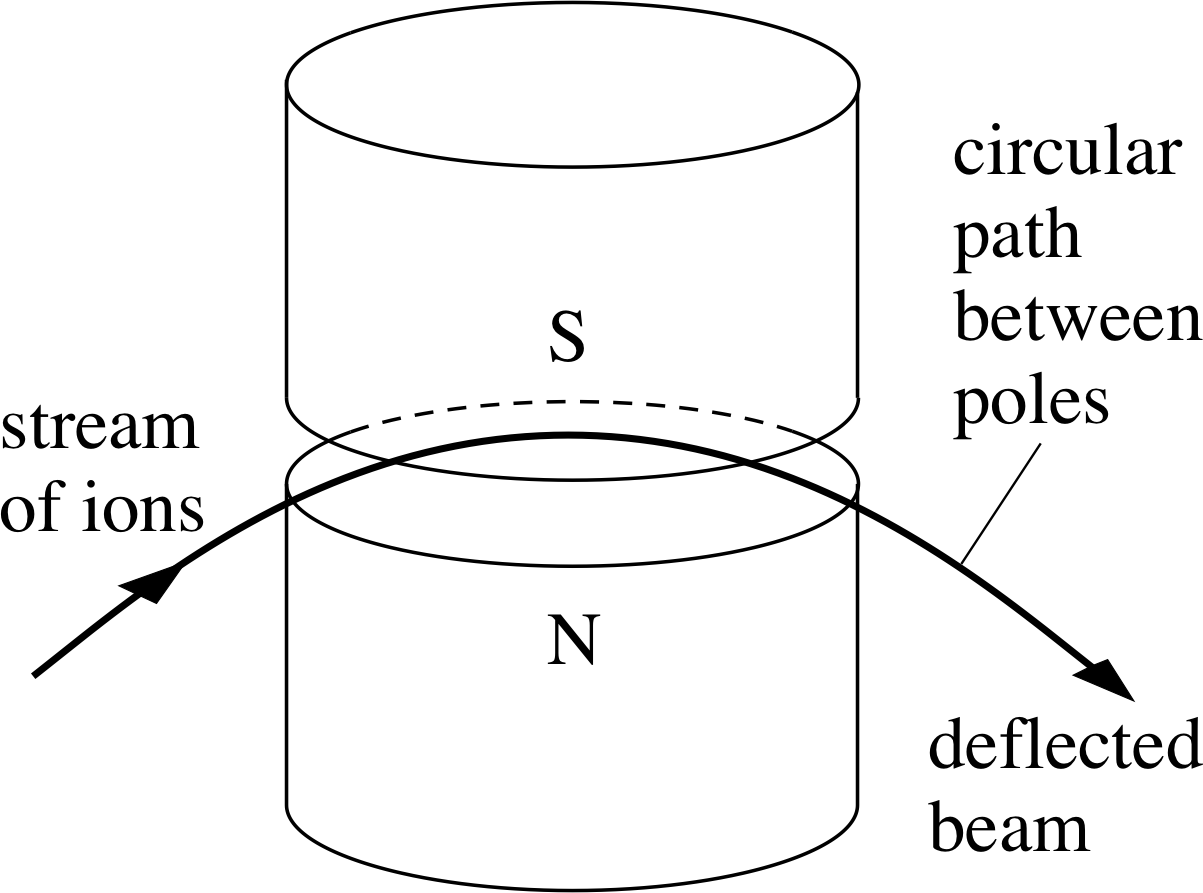
Figure 5 The path of a charged particle moving in a horizontal plane between the poles of a magnet is an arc of a circle.
The accelerated ion beam that emerges from the hole in the negative plate is next directed between the poles of a large magnet. When a charged particle such as an ion moves through a magnetic field, it generally experiences a force at right angles to its direction of motion and is consequently deflected by the field. The size of the deflection will depend on the charge, mass and speed of the particle, the strength of the magnetic field and the direction of motion of the particle relative to the direction of the magnetic field. In the simplest kind of mass spectrometer the ions travel at right angles to a uniform magnetic field of strength B, and the force that acts on them is of magnitude
F = qυB(3) i
The direction of the force is at right angles to both the magnetic field and the direction of motion of the ions, so its effect is to cause the ions to move at constant speed along a circular arc in the plane perpendicular to the magnetic field, as shown in Figure 5.
Now, the force required to keep a charged particle of mass m moving with constant speed υ around a circle of radius R is of magnitude
$F = \dfrac{m\upsilon^2}{R}$ i
Equating these last two expressions for the force magnitude and rearranging the resulting equation we see that the radius R of the circular arc followed by an ion of mass m, speed υ and charge q is:
$R = \dfrac{m\upsilon}{qB}$(4)
Question T4
Use Equations 2 and 4 to show that an ion of charge q following a path of radius R has a mass given by
$m = \dfrac{R^2B^2q}{2V}$
Answer T4
From Equation 4,
$R = \dfrac{m\upsilon}{qB}$(Eqn 4)
m = RqB/υ
Substituting the expression for υ given in Equation 2,
$\upsilon = \sqrt{\dfrac{2qV}{m}}$(Eqn 2)
gives us
$m = (RqB)\sqrt{\dfrac{m}{2qV}} = RB\sqrt{\dfrac{mq}{2V}}$
Dividing both sides by the (positive) square root of m gives us
$\sqrt{m\os} = RB\sqrt{\dfrac{q}{2V}}$
Squaring both sides, we find the required result
$m = \dfrac{R^2B^2q}{2V}$
Figure 6 shows the combined effect of the electric and magnetic fields in a simple mass spectrometer. The magnetic field causes ions with different charge-to-mass ratios to travel along arcs of different radii and hence to arrive at different points on a collector attached to an electronic measuring device or a photographic film.
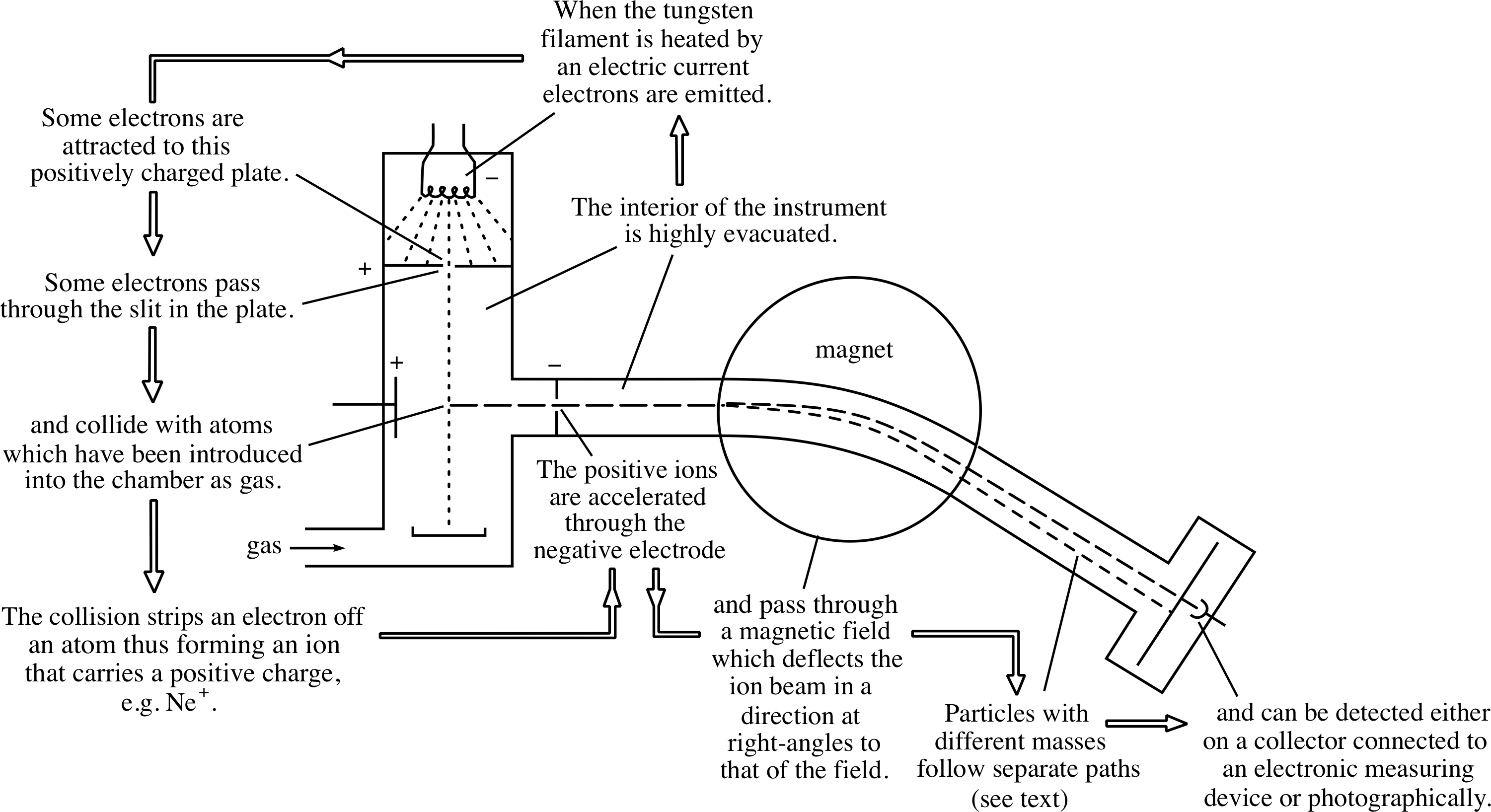
Figure 6 A schematic diagram of a mass spectrometer.
From Question T4 you should also be able to see that, in order to use a mass spectrometer to determine the mass of an ion, we need to know the charge of the ion, the radius of the curved path that it follows, the electric potential difference through which it was accelerated and the strength of the magnetic field by which it was deflected. Apart from the charge q, which must be an integer multiple of e, each of these quantities can be measured directly in the mass spectrometer. Consequently it is a fairly simple matter to determine the masses. Moreover, thanks to the mass spectrometer’s ability to separate ions of different masses, the technique of mass spectroscopy also makes it possible to determine the composition of an unknown mixture.
When a mass spectrometer is used to determine the mass of a neon atom (for example) the result is found to be about 3.32 × 10−26 kg – roughly a hundredth of a millionth of a billionth of a billionth of a kilogram! This tiny mass is not a convenient value to use in calculations, so atomic physicists often express atomic masses in terms of a more appropriate unit called the atomic mass unit which is represented by the symbol u. i For practical reasons the atomic mass unit is defined to be exactly one–twelfth of the mass of a particular sort of carbon atom, called the carbon-12 atom.i According to current measurements:
$\text{1 atomic mass unit} = 1\,{\rm u} = \dfrac{\text{mass of one carbon-12 atom}}{12} = 1.6606\times10^{-27}\,{\rm kg}$
Expressed in terms of atomic mass units, the mass of the neon atom mentioned earlier is about 20 u. (More accurate determinations give 19.992 u.)
In many situations, it is more convenient to avoid units entirely and to specify the mass of an atom by simply quoting the ratio of the mass in question to the atomic mass unit. This ratio is denoted Ar and is called the relative atomic mass. In view of the definition of the atomic mass unit we can write the following relationships:
$A_{\rm r}r = \dfrac{\text{mass of atom}}{1\,{\rm u}} = \dfrac{12 \times\text{ mass of atom}}{\text{mass of one carbon-12 atom}}$
✦ What is the relative atomic mass of the neon atom discussed above?
✧ 19.992 u/1 u = 19.992. It is just the numerical value of the mass in atomic mass units, without the units.
A number of relative atomic masses were listed in Table 1.
It is worth noting that the use of the atomic mass unit and relative mass measurements is not restricted to atomic physics. The atomic mass unit is sometimes employed by nuclear physicists and is frequently used to quantify molecular masses. It is also common to see references to relative molecular mass, which is defined as the ratio of the mass of one molecule of a compound to one–twelfth of the mass of a carbon-12 atom. i
3.2 Isotopes
Throughout our discussion of atomic masses we have repeatedly referred to the carbon-12 atom as a particular type of carbon atom, implying that there is more than one kind of carbon atom. In fact there are several kinds of carbon atom, just as there are several kinds of atom for most other elements. The different kinds of atom corresponding to a single chemical element are called the isotopes of that element.
The existence of isotopes was first recognized by the British chemist Frederick Soddy (1877–1966) in 1913. They were named isotopes (from Greek words meaning same place) because from a chemical point of view the isotopes of an element all occupy the ‘same place’ in a list of the known elements. (The sort of ‘list’ we have in mind here is the periodic table, which is discussed elsewhere in FLAP. See the Glossary for details.)
Evidence in support of Soddy’s idea was soon supplied by the mass spectrometers which were being developed by Thomson and others at that time and as a result Soddy was awarded the Nobel Prize for Chemistry in 1921. With the aid of modern mass spectrometers it is now relatively easy to determine the number of isotopes of each chemical element, though entirely new isotopes are still discovered (or deliberately created) from time to time.
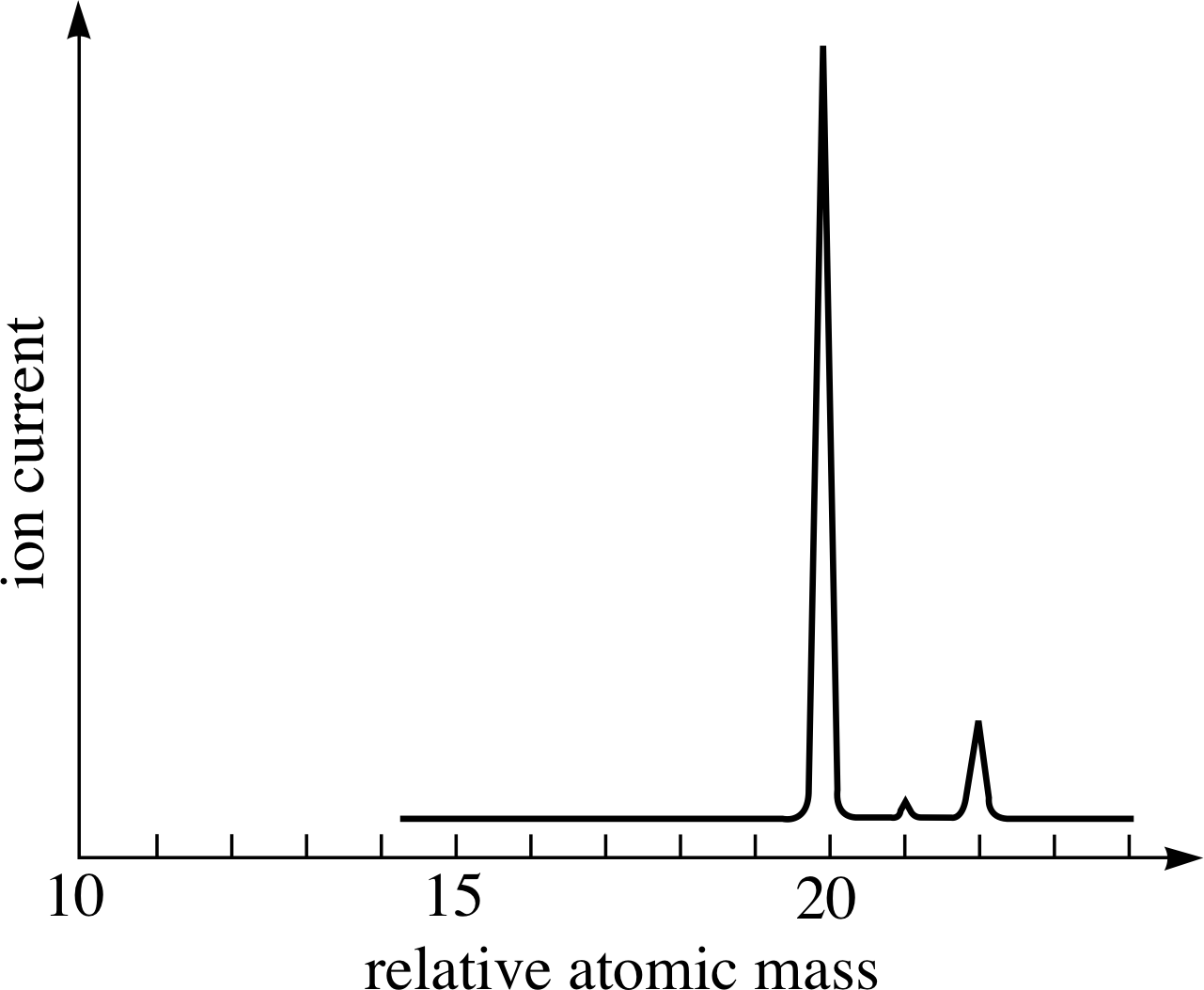
Figure 7 The (idealized) mass spectrum of neon. The relative heights of the peaks give the relative numbers of atoms of each isotope. These relative numbers reflect the relative abundances of the various isotopes in the sample.
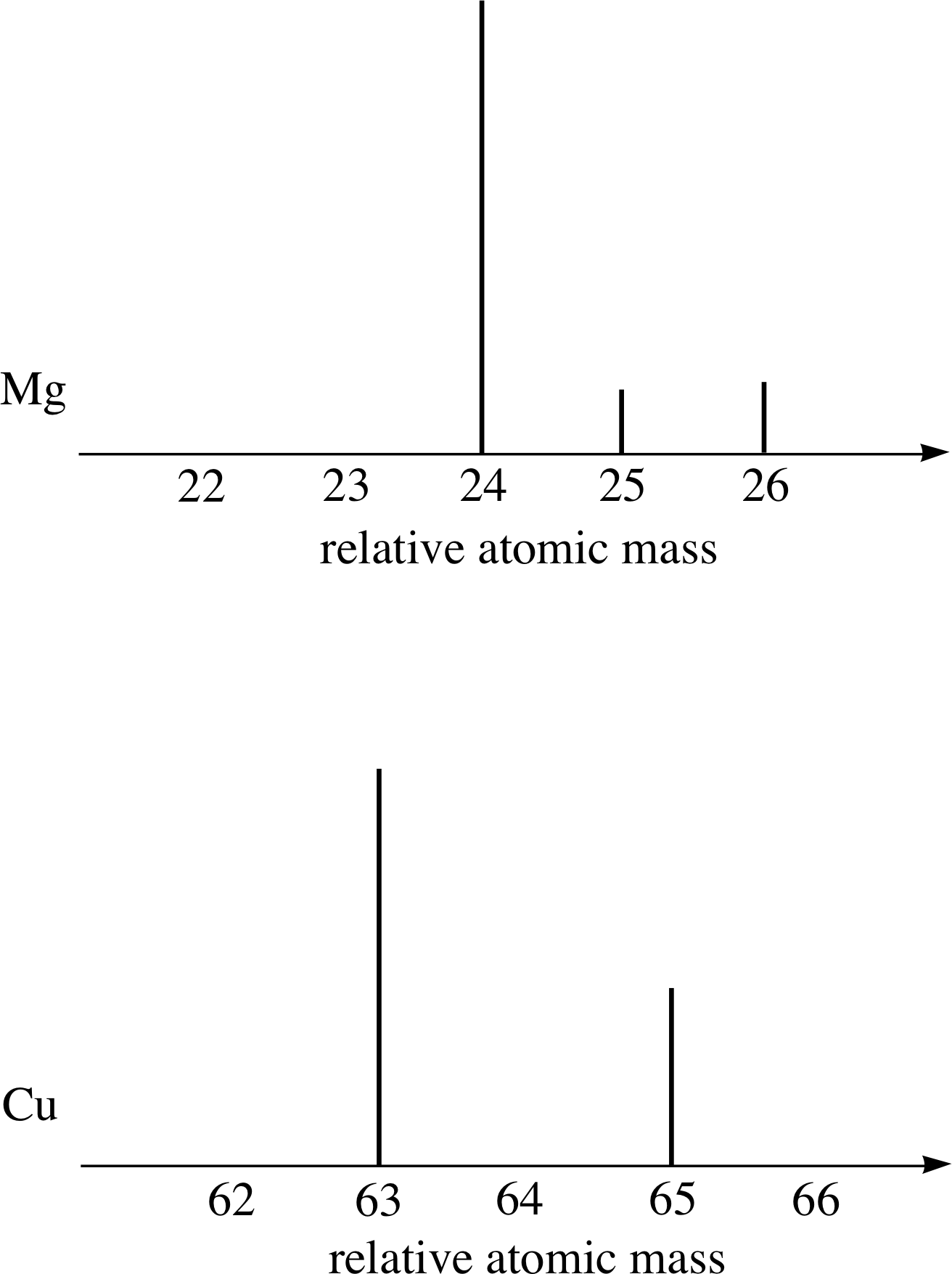
Figure 8 Schematic diagram of the mass spectra of magnesium and copper.
As explained in the last subsection mass spectrometers are able to separate ions according to their mass. When analysing a sample of matter, a modern mass spectrometer provides a mass spectrum which is typically presented as a graph of the ion current as a function of ion relative mass. Figure 7 is an (idealized) example of such a spectrum, showing the results obtained using a sample of pure neon.
The most important points to note about the mass spectrum in Figure 7 are that it has three peaks, not one, and that the peaks have different heights. The presence of three peaks demonstrates that this sample of pure neon contains three different types of atom; each is a neon atom, but each type has its own characteristic mass. Thus, neon has three isotopes with relative atomic masses of approximately 20, 21 and 22. The relative heights of the peaks indicate the relative number of each type of ion and hence the relative abundance of each isotope within the sample.
Most elements consist of a mixture of isotopes. For example, Figure 8 shows schematic mass spectra of magnesium (Mg) and copper (Cu) samples which, respectively, contain three and two isotopes. In contrast, naturally–occurring sodium gives a mass spectrum that has only one peak; naturally–occurring sodium consists of only one isotope of relative atomic mass 23.
The relative atomic masses of all the isotopes shown in Figures 7 and 8 are very close to whole numbers.
This is generally the case, and is no accident; it suggests that atoms consist of common structural units. The relative atomic mass of hydrogen is very close to 1, so atoms appear to consist of particles that have masses about equal to the mass of a hydrogen atom. We have already seen that electrons are common to all atoms, but their mass is far too low to allow them to be the common structural units. We will return to the nature of these ‘common structural units’ in the next section, for the moment let us just exploit their consequences.
Since the relative atomic mass of every isotope is close to a whole number, we can use that whole number to distinguish one isotope of an element from any other isotope of that same element. For example, we can refer to the three neon isotopes shown in Figure 7 as neon-20, neon-21 and neon-22. The whole number that characterizes the mass of each isotope in this way is called the mass number A of the isotope.
It is often useful to represent atoms (or even their nuclei) using symbols that show the mass number. This is done by writing the relevant mass number in front of the chemical symbol in accordance with the following convention (where X is the chemical symbol) AX. For example, the three neon isotopes can be represented by the symbols: 20Ne, 21Ne and 22Ne.
When we referred to carbon-12 in the last subsection we were referring to a particular isotope of carbon, with mass number A = 12. Samples of naturally–occurring carbon are usually mixtures of three isotopes. The most common one is the standard isotope 12C (used as the reference standard), but this is accompanied by about 1% of 13C and a very small proportion of 14C.
✦ The isotopes 16N and 16O both have the same mass number. Must they also have the same mass?
✧ No, the mass number is simply the nearest whole number to the relative atomic mass in each case. The masses will be very similar but they need not be identical.
Different isotopes of the same chemical element have different masses but almost identical chemical properties: it is not usually possible to distinguish between the different isotopes of an element in a chemical reaction. i The reason for this close chemical similarity between the isotopes is now well understood. The chemical properties of a neutral atom are almost entirely determined by the number of electrons that atom contains, and, as you will learn in the next section, it is now known that all (neutral) atoms of a given element contain the same number of electrons, irrespective of which isotope that atom represents. Only when we go from one element to another does the number of electrons in a neutral atom vary.
We usually work with substances that consist of a mixture of isotopes, so the relative atomic mass of the mixture is therefore important. It is determined by the relative atomic masses of the isotopes present and by their relative abundances. For example, neon contains 90.51% 20Ne, 0.27% 21Ne and 9.22% 22Ne, with relative atomic masses of 19.99, 20.99 and 21.99, respectively. To calculate the relative atomic mass of the element as it occurs naturally (as a mixture of isotopes), you simply multiply each isotopic mass by the relative abundance of the isotope and add the products. Thus, the relative atomic mass of (naturally-occurring) neon is:
Ar(neon) = (19.99 × 0.9051) + (20.99 × 0.0027) + (21.99 × 0.0922) = 20.2 (to three significant figures)
If you refer back to Table 1 in Subsection 2.1, you will see that it gives the relative atomic masses of some common elements. Each of these values is calculated according to the abundance on Earth of the element’s isotopes, just as we have just calculated the value for neon. If you examine these values, you will find that several elements have relative atomic masses that are close to whole numbers.
✦ Why do you think that the relative atomic masses of these particular chemical elements are close to whole numbers? (Note that this is a question about the relative atomic mass of an element, not about a particular isotope.)
✧ Because these elements each have only one common isotope.
Other elements have relative atomic masses that are not close to whole numbers, indicating that they consist of a mixture of isotopes.

Figure 9 See Question T5.
Question T5
Figure 9 shows a sketch of the data taken from a mass spectrum of a hypothetical element M. The numbers on each of the peaks represent their relative ion currents and hence the relative abundance of each isotope of M in the measured sample. Assuming that the sample is a representative one, calculate the relative atomic mass of the element M.
Answer T5
The relative ion current is proportional to the relative isotopic abundance. The sum of relative ion currents of isotopes = 0.045 + 0.840 + 0.095 + 0.02 = 1.00. Hence, isotopic abundance of the isotope with relative atomic mass of 50 = 0.045/1, i.e. 0.045 and isotopic abundance of isotope with relative atomic mass 52 = 0.840, etc. Therefore the relative atomic mass of M is
(0.045 × 50) + (0.840 × 52) + (0.095 × 53) + (0.020 × 54) = 52.045
i.e.52.05 to two decimal places.
4 Atomic structure: the nuclear model
Once the existence of the atom and its constituent electrons had been conclusively demonstrated, it was obviously important to understand the structure of the atom. How are electrons accommodated within an atom?
Scientists in Japan, France and Germany had put forward atomic models, but it was two physicists working in England – J. J. Thomson and Ernest Rutherford – whose work in the field is now recognized to have been the most important. In this section, we will begin by describing Thomson’s model before going on to say why Ernest Rutherford (1871–1937) saw fit to suggest an entirely different model on the basis of just one piece of experimental evidence. Also, we will briefly compare the successes and failures of the two models.
In 1903, J. J. Thomson put forward his so–called plum–pudding model of the atom. He suggested that atoms consisted of electrons contained inside a uniform sphere of positive charge, i whose total positive charge was exactly balanced by the sum of the negative charges on the electrons. Thomson proposed that the positively charged sphere has a diameter of about 5 × 10−10 m (the typical atomic size) and that, in most atoms, the constituent electrons moved in concentric, circular orbits.
This model had several major problems, one being that it predicted that atoms would be unstable. Because the electrons in the sphere are supposed to be confined, a net force must be acting on them and therefore, according to Newton’s second law, they must be accelerating. However, classical electromagnetic theory predicted that accelerating charged particles always continuously emit electromagnetic radiation which carries away energy. The kinetic energy of the electrons should therefore gradually decrease as the radiation is emitted, making the atom unstable. Despite this (and other) problems, by 1909 Thomson’s plum–pudding model had become widely accepted as the best available picture of the atom.
4.1 Evidence from the scattering of α–particles
The experiment that caused serious trouble for the plum–pudding model was suggested by Ernest Rutherford. It involved bombarding atoms with α–particles, i which we must pause briefly to introduce.
It had been known since 1896 that some elements such as uranium and radium were unstable (i.e. radioactive), and that they spontaneously emitted radiation and particles of various types. Amongst the emitted particles were alpha_particlesα–particles (alpha-particles), which Rutherford, together with his assistant Hans Wilhelm Geiger (1882–1945), had identified as ionized helium atoms with positive charge 2e.
Question T6
Write down the symbol for an α–particle, according to Rutherford’s identification. (The chemical symbol for helium is He.)
Answer T6
The symbol He2+ represents a doubly ionized helium atom with charge 2e. Note that an α–particle is actually a type of helium ion.
Rutherford found that the α–particles emerging from decaying radium atoms travel at very high speed, up to about 2 × 107 m s−1. However, due to collisions with molecules, the α–particles slow down and stop after travelling only a few centimetres in air.
Rutherford, working at the University of Manchester, brilliantly saw how to use these α–particles to probe the inner structure of the atom. He advised his student Ernest Marsden to try to find out whether the high–energy α–particles from a radioactive source were directly reflected from metals. This would have been a surprising finding, because the plum–pudding model predicted that practically none of the α–particles would be reflected. When high–speed α–particles reached the surface of the metal they might have been expected to undergo some loss of energy as they ‘shouldered their way through’ the plum puddings, but it was highly unlikely that any would ‘bounce back’.
More precisely, the positively charged α–particles should be subject to repulsive forces due to the positive charge in each atom, and to attractive forces due to the negatively charged electrons. Taking the Thomson model seriously it was possible to work out the average influence these forces would be expected to have during the very short time that a rapidly moving α–particle was in the vicinity of any particular atom. Calculations based on Thomson’s model indicated that an atom of gold should deflect an α–particle moving at 2 × 107 m s−1 by, on average, 0.006°. This deflection is very small because the electrons are too light to deflect the α–particles significantly and the positive charge is too thinly spread out over the whole volume of the atom to cause much deflection.
If the α-particle were to impinge on a piece of gold foil 10−6 m thick, it would be expected that it would be deflected because it would encounter about 10 000 atoms in traversing the metal. The deflections were expected to be random so after the α–particle had been deflected in one direction, the next encounter could cause it to be deflected further in that direction, or deflected back on itself. So when calculating the average deflection of the α–particle, it was necessary to work out the most likely result of a multiple–scattering process. When the statistical theory of multiple scattering was applied under the assumption that the gold foil was made of Thomson atoms, it turned out that the average deflection to be expected was about 0.6 of a degree. Therefore, according to this theory, practically all the α–particles fired at the target should emerge having hardly deviated at all from their original paths. Moreover, the theory predicted that if the target of gold foil were made of Thomson atoms, only 1 in 1035 of the incident α–particles should be scattered backwards, i.e. reflected. This is, for all practical purposes, a negligible number.
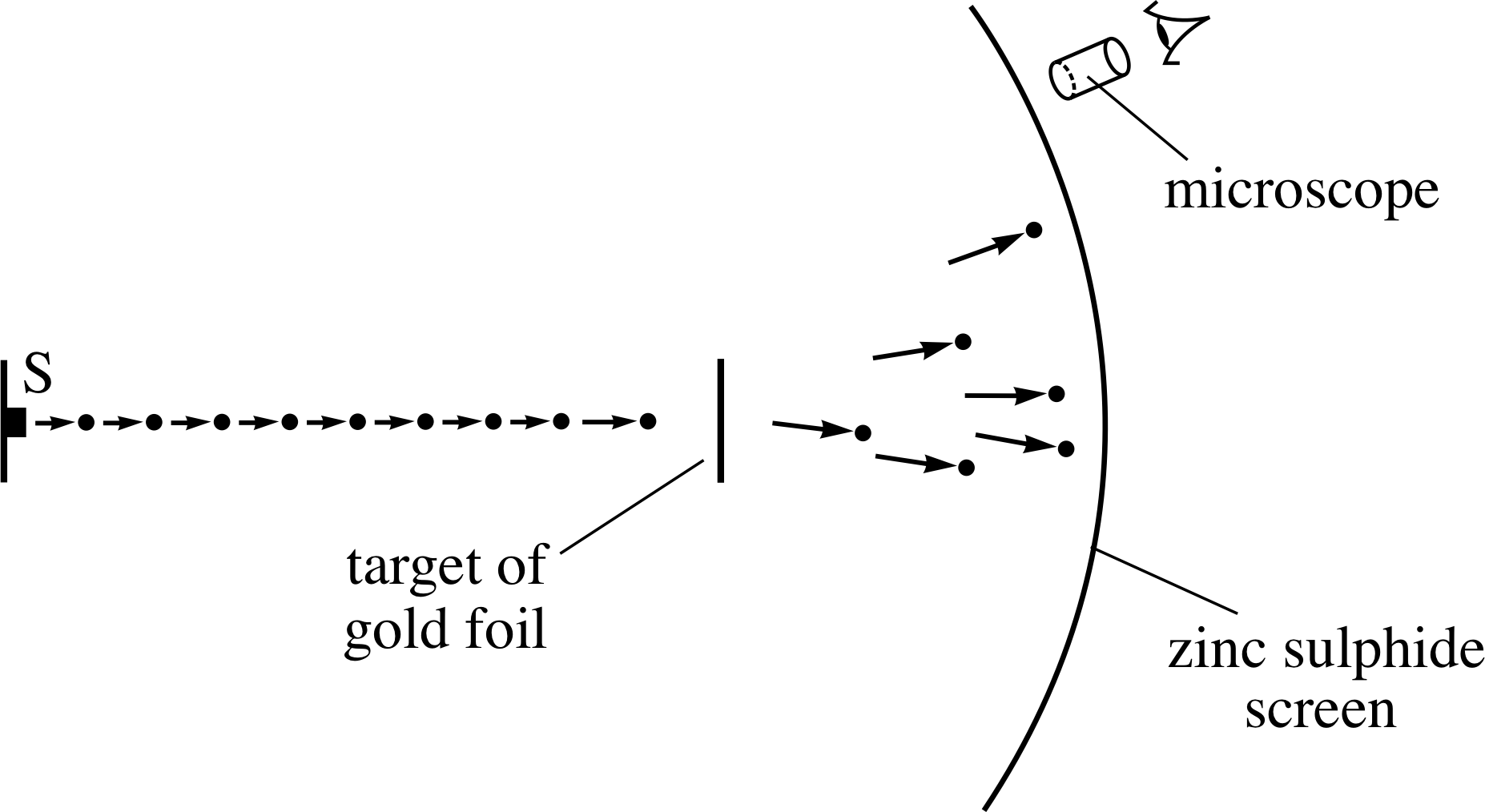
Figure 10 A schematic diagram of Geiger and Marsden’s apparatus – the α–particles emerged from the radioactive source S and impinged on the target of gold foil.
Figure 10 is a schematic diagram of the apparatus Geiger and Marsden used to perform the experiment.
A specimen of the radioactive element radon provided the source of high–energy α–particles, which were directed towards a target of gold foil. The deflected α–particles were detected by monitoring the flashes of light that were emitted when they struck the zinc sulphide screen. In order to find the relative number of α–particles that were deflected at different angles, Geiger and Marsden measured the rate at which flashes occurred in different areas of the screen.
Their painstaking work produced a result that was entirely different from the predictions based on Thomson’s model. In particular, some α–particles were deflected through very large angles, so that they did ‘bounce back’ towards the source. So although most of the particles passed almost straight through the foil, some rebounded as if from a head–on collision with something immovable in the foil. Geiger and Marsden established that one α–particle in 104 was reflected from a target of gold foil. This was 1031 times as many reflections as had been expected on the basis of the ‘plum-pudding’ model! Ernest Rutherford’s reaction to this astonishing result is captured by his often quoted remark:
‘It was quite the most incredible event that has ever happened to me in my life. It was almost as if you fired a fifteen inch shell at a piece of tissue paper and it came back and hit you.’
4.2 Rutherford’s nuclear model
In March 1911, Rutherford i proposed a new model of the atom, radically different from Thomson’s, that could explain the results of Geiger and Marsden’s α–scattering experiment. Rutherford suggested that atoms consisted of a small positively charged central core, which he called the nucleus, i which was orbited by negatively charged electrons. In Rutherford’s nuclear model almost the entire mass of the atom, apart from the tiny fraction accounted for by the electrons, was concentrated in the nucleus.
According to Rutherford, the behaviour of the α–particles that were scattered through large angles could be explained by assuming that they had undergone just one major collision – a more or less head–on collision with the nucleus of a single atom of gold. The collision did not involve direct contact between the α–particle and the nucleus or any new kind of force, the mechanism was still presumed to be electrical repulsion, but thanks to the concentration of positive charge at the centre of the atom, the electrical forces involved could be very great. Moreover, because of the concentration of mass in the nucleus the α–particle would sometimes be unable to barge its way through the atom as it could in Thomson’s model. The analogy that is often quoted is that of a game of marbles where a light marble usually bounces off a heavy one without having much effect on the heavy marble, but a heavy marble will knock a much lighter one out of its way. The mass of the gold nucleus is something like 50 times the mass of an α–particle while an electron is only about 1/7000 the mass of an α–particle, so in the Rutherford model the α–particle will not rebound from electrons, but it will do so from a nucleus.
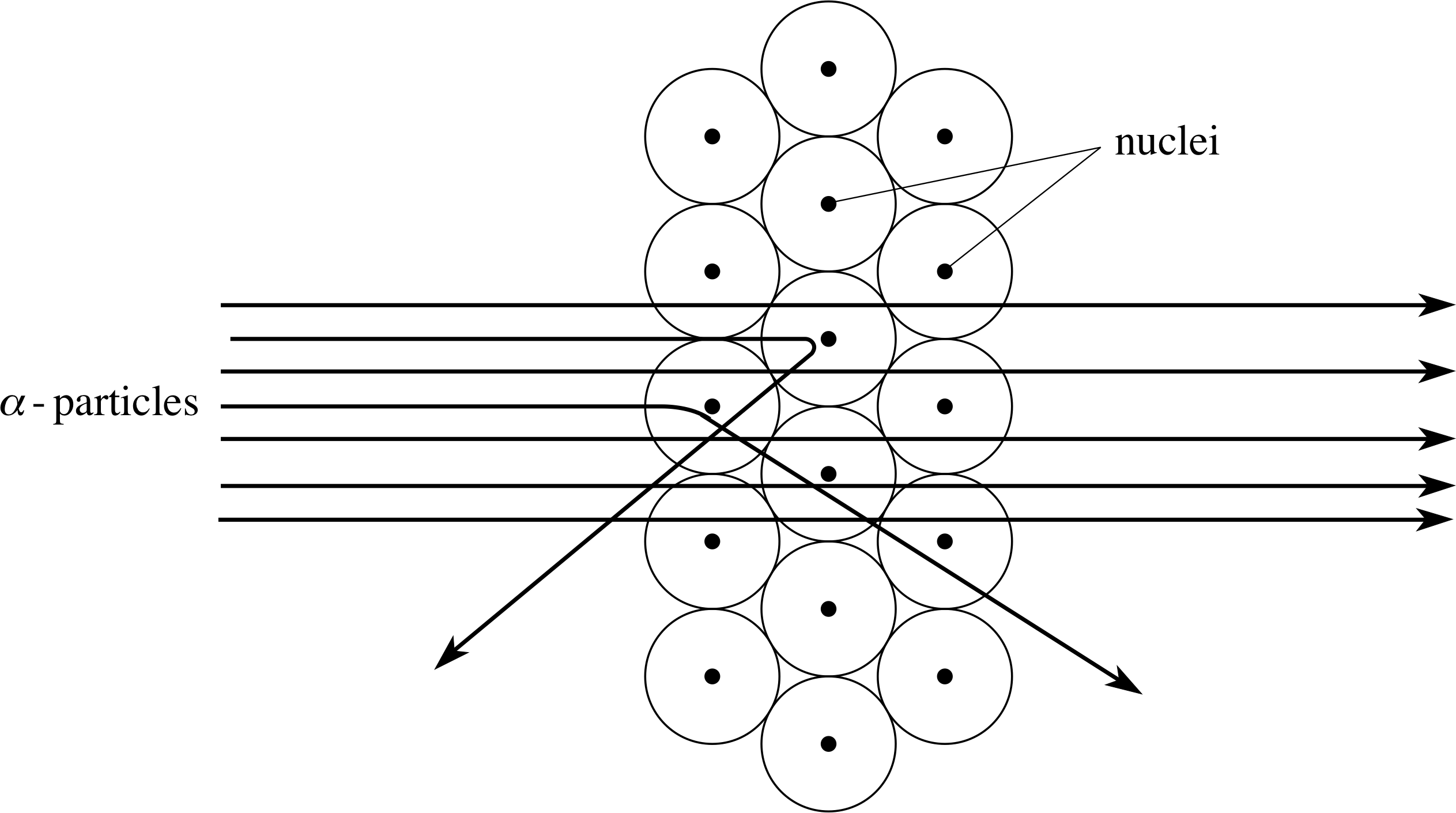
Figure 11 The scattering of α–particles by atoms in a metal foil. The relative size of the nuclei has been exaggerated for the sake of clarity.
Using the nuclear model of the atom, the interaction of a beam of α–particles and a thin foil (layers of atoms) can be crudely represented by the paths shown in Figure 11. Most of the α–particles pass straight through the foil, but sometimes an α–particle is deflected, occasionally turning through a large angle. The average deflection is less than 1°, but about one α–particle in 104 is deflected through an angle greater than 90°. In order to achieve these results the nucleus should be no more than about 10−14 m across. (As in the case of atoms, this figure should be regarded as indicative of the nuclear size scale rather than a precise diameter.)
✦ What is the ratio of the diameter of a typical atom to that of a typical nucleus? It is important to note from the answer to the previous question how small the nucleus is, compared with the atom. Question T7 is intended to give you a better feel for the size of the nucleus.
✧ The ratio is roughly (5 × 10−10 m)/(10−14 m) = 50 000, though either or both of the values in the ratio might legitimately be reduced by a factor of five or so.
Question T7
Imagine that you scale up an atom so that its diameter matches that of a large athletics stadium that is 300 m in diameter. How big would the nucleus be?
Answer T7
The ratio of the diameter of an atom to that of a nucleus is 50 000 as we have just discussed. Hence, if the athletics stadium (representing the atom) has a diameter of 300 m, the diameter that represents the nucleus is 300 m/50 000 = 0.006 m, i.e. 6 mm.
The Rutherford (or nuclear) model of an atom is illustrated in Figure 12, for the simplest possible case – the hydrogen atom, which comprises a single electron orbiting the nucleus. It is much like a minute model of the Earth orbiting the Sun, with the planet moving around in a vast void of empty space. The model has the virtue of simplicity and successfully accounts for the results of Geiger and Marsden’s experiment. However, it also has certain shortcomings and could not be regarded as entirely satisfactory, even in Rutherford’s time.
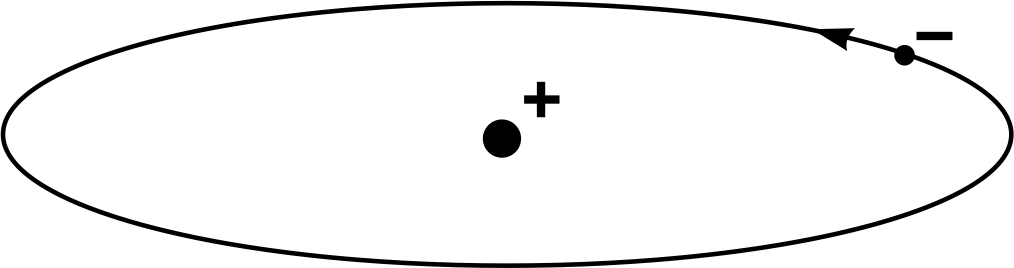
Figure 12 The Rutherford model of the hydrogen atom.
A major flaw in the Rutherford model is that the orbiting electron should continuously emit electromagnetic radiation. This should cause the electron to lose energy rapidly and spiral into the nucleus in a fraction of a second. Thus, there is an inherent instability in the Rutherford model that is certainly not observed in nature. i This point and many others were taken up in later models of the atom that made use of quantum theory. We will not explore those models here, but they are briefly discussed in Subsection 4.4 and more fully developed elsewhere in FLAP.
Despite its shortcomings, the Rutherford nuclear model of the atom was a major landmark in the development of physics. It introduced the nucleus and, as in our current theories, placed it at the heart of the atom. For many people it still represents the most sophisticated model of the atom they are ever likely to meet.
4.3 Nuclear charges and constituents
At the time of writing there is no experimental evidence that the electron is anything other than a point–like particle. The same is most certainly not true of the nucleus which clearly has its own internal structure. This subsection introduces the major nuclear constituents and discusses the electric charge of the nucleus.
When an α–particle interacts with a nucleus (Figure 11) the electrostatic force between the α -particle and the nucleus is determined by their charges and by their separation in accordance with Coulomb’s law.
Thus, knowing that the (positive) charge on an α–particle is 2e, it should be possible to determine the charge on a nucleus by scattering α–particles from it and analysing the results.
The results of Geiger and Marsden’s experiment were too imprecise to allow Rutherford to determine the nuclear charge of gold with any reliability, but in 1920 his co–worker James Chadwick (1891–1974) i was able to determine the charges of several different nuclei by essentially the same method. Chadwick found that the charge on each nucleus was a whole–number multiple of e, the magnitude of the charge of the electron, and that the value of the nuclear electric charge was characteristic of the element being investigated. In particular, Chadwick found the following values for the charges of certain nuclei:
copper, Cu: +29e; silver, Ag: +47e; iridium, Ir: +77e; gold, Au: +79e
✦ What is the charge, in units of coulombs, of a gold nucleus?
✧ The charge is +79e, where e is the magnitude of the charge of the electron (e = 1.602 × 10−19 C). Hence the charge of a gold nucleus is 79 × 1.602 × 10−19 C = 1.3 × 10−17 C.
The gold foil is electrically neutral because the positive charge of each nucleus is exactly compensated by the negative charge carried by the electrons. Thus, according to the Rutherford model each electrically neutral gold atom must have 79 orbiting electrons to balance the positive charges of 79e on the nucleus. Similarly, an atom of copper has a nuclear charge of 29e and must have 29 orbiting electrons to ensure electrical neutrality.
Chadwick’s results confirmed a well–established notion that each chemical element could be uniquely specified by a single whole number Z, now known as the atomic number, and showed that the atomic number of any element was equal to the nuclear charge in units of e (or, equivalently, to the number of orbiting electrons required to balance that charge). This was an important achievement, though it had already been assumed to be the case by some of those proposing theoretical models of the atom. The atomic numbers of some common elements were given in Table 1 (Subsection 2.1). i
✦ A neutral argon atom contains 18 orbiting electrons. What is the atomic number of argon and what is its nuclear charge?
✧ The atomic number of argon is Z = 18, and the nuclear charge is 18e.
No nucleus has ever been observed with a lower mass than the nucleus of the lightest hydrogen isotope. Furthermore, all nuclei carry charges that are whole–number multiples of the charge on the hydrogen nucleus and, as pointed out in Section 3, all known isotopes have masses that are fairly close to whole–number multiples of the mass of that nucleus. In view of this it is hardly surprising that the hydrogen nucleus has long been regarded as a ‘building block’ from which all other nuclei could be constructed. It was clear that this proton, as Rutherford called it, could not be the only constituent of the nucleus because the commonest helium nucleus (for example) has four times the mass of a proton but only twice the charge.
Nonetheless, for many years it was thought that all nuclei consisted of protons and electrons, that the number of protons determined the mass number A of the nucleus, and that the difference between the number of protons and electrons determined the atomic number Z. Note that the electrons we are referring to here are supposed to be within the nucleus, they have nothing to do with the orbiting electrons that are responsible for the chemical properties of the atom.
It is now known that the idea that nuclei might contain electrons is quite wrong and that the number of protons present in a nucleus is in fact exactly equal to the atomic number. The error of thinking otherwise arose because physicists were unaware of the existence of another nuclear constituent called the neutron which has a similar mass to the proton, but no electric charge. Rutherford suggested the existence of the neutron in 1920, but proving that such a neutral particle was really present took a considerable time. It was eventually accomplished by James Chadwick in 1932, as will now be described.
In 1930, the German physicist Walter Bothe (1891–1957) and his collaborators had shown that when α–particles were incident on a piece of beryllium, a very penetrating radiation was produced. Because the radiation had no charge, it was thought to be high–energy electromagnetic radiation (gamma rays). But this interpretation was incorrect as Chadwick was to demonstrate.
While investigating this ‘penetrating radiation’ in 1932, Chadwick observed it could cause protons and atoms to be ejected from a range of materials. He measured the speeds of the ejected particles and used some of the most basic principles of physics (the conservation of energy and of linear momentum) to analyse the collision processes that had caused the ejections. Making reasonable assumptions he found that his observations contradicted the idea that the penetrating radiation was electromagnetic, but they were consistent with the notion that the radiation consisted of identical uncharged particles with the same mass as the proton. Chadwick called these neutral particles neutrons. Later, more accurate, experiments showed that although the proton and neutron are similar in many respects the neutron is slightly more massive than the proton. i
The currently accepted values of the masses of the proton and neutron are (to three decimal places) as follows:
- mass of a proton 1.673 × 10−27 kg = 1.007 u
- mass of a neutron 1.675 ×10−27 kg = 1.009 u
The conclusion is that the building blocks of atomic nuclei are protons and neutrons: all nuclei are made of protons and, with the single exception of the lowest–mass hydrogen nucleus, neutrons. The mass number A of a nucleus is the total number of protons and neutrons that it contains while the atomic number Z, as stated earlier, is simply the number of protons.
The existence of the neutron provides a very simple explanation of the occurrence of isotopes. The various isotopes of an element all have the same atomic number and therefore must contain the same number of protons. However, they also have different mass numbers and must therefore contain different numbers of neutrons.
It is often useful to represent atoms (or even their nuclei) using symbols that show both the mass number and the atomic number, and hence allow us to identify the number of protons and neutrons in the nucleus. This is done by writing the relevant mass number A and atomic number Z in front of the chemical symbol in accordance with the following convention:
${}^{\;\;\text{mass number}}_{\text{atomic number}}\text{chemical symbol} $
For example, all atoms of neon contain ten protons so Z = 10, but neon isotopes occur with mass numbers of 20, 21 and 22, so these three neon isotopes can be represented by the symbols: 2010Ne, 2110Ne and 2210Ne.
For the lowest–mass elements apart from hydrogen, the relative atomic mass is approximately twice the atomic number; for the heaviest elements, it is nearer two and a half times. Hence, the ratio of the number of neutrons to the number of protons is found empirically to increase with Z. In other words, heavy nuclei always contain more neutrons than protons.
Question T8
Copper has two isotopes with relative atomic masses very close to 63 and 65. Write symbols to represent these two isotopes, showing the atomic numbers and mass numbers. (A copper nucleus has a charge of 29e.)
Answer T8
The symbols are ${}^{63}_{29}{\rm Cu}\text{ and }{}^{65}_{29}{\rm Cu}$. The mass number of each isotope is simply the whole number closest to the relative atomic mass of the isotope (that is, the total number of protons and neutrons in the nucleus) and the atomic number is the number of protons (equal to the positive nuclear charge, measured in units of e).
Question T9
How many neutrons are in each of the two isotopes of copper?
Answer T9
The number of neutrons is the difference between the mass number and the number of protons. Hence:
- for ${}^{63}_{29}{\rm Cu}$, the number of neutrons in each nucleus is 63 − 29 = 34;
- for ${}^{65}_{29}{\rm Cu}$, the number of neutrons in each nucleus is 65 − 29 = 36.
Question T10
Rutherford found that the α–particle was a helium atom that had become doubly ionized due to the loss of two electrons. Given that the atom concerned is an atom of 42He, how else might you describe the α–particle?
Answer T10
A neutral ${}^4_2{\rm He}$ atom has only two orbiting electrons, so when such an atom loses both of those electrons all that remains is an ${}^4_2{\rm He}$ nucleus. Thus, the α–particle must be an ${}^4_2{\rm He}$ nucleus.
4.4 Beyond the Rutherford model
As indicated earlier, the Rutherford model of the atom is not without flaws and it was soon superseded by other models that built on its success. These later models are considered elsewhere in FLAP (see the Glossary for details), but it is appropriate to say a few words about them at this point to emphasize how they differ from the Rutherford model.
The major difference between the Rutherford model and its historically important successors is that those later models attempted to take account of the ideas of quantum theory that had been developing since 1900. At first, as in the Bohr model of 1915, the modifications were relatively mild but by the mid-1920s, when the first fully–fledged quantum models appeared, the departures were substantial. Indeed, by then it was realized that the laws of classical physics (such as Newton’s laws of mechanics) simply could not be applied to matter on a subatomic scale since quantum theory implied that electrons in atoms did not have well–defined orbits at all.

Figure 13 A section through an orbital of the electron in a hydrogen atom.
In the quantum model of the atom, the notion of a well–defined electron orbit is replaced by the idea that within the atom there are regions where an electron is highly likely to be detected and other regions where it is less likely to be detected. The likelihood of detection in any given region is precisely determined in the quantum model of the atom but the exact position of the electron at any time is neither known nor even defined unless and until an appropriate measurement is made.
According to these quantum models, most of which are directly descended from Schrödinger’s model of 1925/6, the likelihood of finding an electron with a given amount of energy in a given region of space is specified by a mathematical entity called a wavefunction that may be represented pictorially (with some difficulty) as a three–dimensional ‘cloud’ shaded so as to show the relative probability of finding the electron in different regions. Figure 13 is an attempt to show the densest part of such an electron probability cloud for a hydrogen atom in its lowest energy state. In this case the region where the electron is highly likely to be found is spherical, centred on the nucleus and has a diameter of roughly 10−10 m.
5 Closing items
5.1 Module summary
- 1
-
All matter is made up of simple chemical substances called chemical elements, each of which is represented by a chemical symbol. The smallest portion of any element that retains the chemical identity of that element is called an atom.
- 2
-
For many purposes the ‘diameter’ of an atom may be taken to be a few times 10−10 m, irrespective of its chemical nature.
- 3
-
Investigations of the conduction of electricity through gases showed that a common constituent of all atoms was the electron, a negatively charged particle with a mass of only about 1/2000 times that of the hydrogen atom. The charge of the electron is denoted by −e, where the positive quantity e = 1.602 × 10−19 C represents the magnitude of the charge of the electron.
- 4
-
When one or more electrons are removed from an atom, a positively charged ion is formed. Similarly, when one or more electrons are added to an atom, a negatively charged ion is formed.
- 5
-
The masses of ions can be measured using a mass spectrometer. Such studies show that nearly all chemical elements consist of a mixture of atoms of different masses. Atoms of a given element that differ in their masses are said to belong to different isotopes of that element.
- 6
-
The masses of atoms and ions are often expressed in terms of the atomic mass unit, u, which is defined in such a way that the mass of one atom of the commonest carbon isotope (126C) is 12 u. According to current measurements 1 u = 1.6606 × 10−27 kg.
- 7
-
The relative atomic mass Ar of an element may be determined from measurements on appropriate macroscopic samples of matter. When the element consists of just one isotope, it is related to the mass of an individual atom by
$A_{\rm r} = \dfrac{\text{mass of atom}}{\rm 1\,u} = \dfrac{12\times\text{mass of atom}}{\text{mass of one }\rm{}^{12}_{\phantom{0}6}C\text{ atom}}$
- 8
-
In general, the relative atomic mass of a naturally–occurring element is obtained by multiplying the relative atomic mass of each of its isotopes by the corresponding relative abundance and adding together the resulting products.
- 9
-
Ernest Rutherford used data from α–particle scattering experiments to argue that the atom consists, in general, of a positively charged central core (the nucleus) which is orbited by negatively charged particles (electrons). Almost all the mass of the atom is concentrated in the nucleus even though the typical nuclear size scale is only about 10−14 m.
- 10
-
The nuclei of all atoms heavier than the lightest isotope of hydrogen consist of positively charged protons and electrically neutral neutrons. The nucleus of the lowest–mass hydrogen atom consists only of one proton. Protons and neutrons have approximately equal masses, though precise measurements show that the neutron is actually slightly heavier than the proton.
- 11
-
The atomic number Z of an element represents the number of protons in the nucleus of each atom of that element. It also represents the charge on that nucleus in units of e (i.e. the nuclear charge is Ze), and also the number of electrons required to balance that charge. Each chemical element has a uniquely characteristic atomic number.
- 12
-
The mass number A of an isotope represents the total number of protons and neutrons in the nucleus of each atom of that isotope. For each of the known isotopes it is the nearest whole number to the relative atomic mass of that isotope. The different isotopes of any given element are distinguished by the number of neutrons they contain, and therefore correspond to different mass numbers.
- 13
-
The number of protons and neutrons in the nucleus of a particular atom (e.g. X) is often indicated by writing the mass number and atomic number of the atom to its chemical symbol according to the convention AZX. Thus, 32He represents a helium nucleus containing 2 protons (as all helium nuclei must) and (3 − 2 = 1) neutron.
- 14
-
Although the idea of a massive positively charged nucleus surrounded by negatively charged electrons is still central to modern notions of atomic structure, current models of the atom are rooted in quantum theory and do not presume the existence of well defined electron orbits.
5.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Outline how the electron was discovered.
- A3
-
Explain the basic principles of a mass spectrometer and indicate how such a device can be used to measure the masses of ions.
- A4
-
Explain how a mass spectrometer indicates the existence of isotopes.
- A5
-
Calculate the relative atomic mass of a mixture of isotopes given their relative abundance.
- A6
-
Explain the importance of α–scattering data in elucidating the structure of the atom.
- A7
-
Outline how the neutron was discovered.
- A8
-
Deduce the constituents, nuclear charge and overall charge of an atom given its atomic number, its mass number and its state of ionization.
- A9
-
Quote rough order of magnitude estimates (i.e. typical ‘scales’) for the mass, diameter and electric charge of atoms and nuclei.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
5.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions each of which tests one or more of the Achievements.
| Particle | Mass number | Net charge/e |
|---|---|---|
| proton | 1 | +1 |
| neutron | ||
| hydrogen atom | ||
| α–particle | ||
| electron |
Question E1 (A9)
Complete Table 3. You may assume that on the relative atomic mass scale, the mass of an electron is zero. Remember that the α–particle is a helium nucleus. Comment on the typical size of each of the listed particles.
| Particle | Mass number | Net charge/e |
|---|---|---|
| proton | 1 | +1 |
| neutron | ~1 | 0 |
| hydrogen atom | 1 | 0 |
| α–particle | 4 | +2 |
| electron | 0 | −1 |
Answer E1
The completed table is given in Table 4.
It is not particularly meaningful to associate a definite size with any of these particles unless that diameter is carefully defined. However, in general terms, the size scale associated with the atom is about 10−10 m, and that of the α–particle (a ${}^4_2{\rm He}$ nucleus) is about 10−14 m. The proton is also a nucleus (of ${}^1_1{\rm H}$) so it too can be associated with a size of order 10−14 m (though 10−15 m might be more appropriate in this case), and similar comments apply to the size of the neutron. There is as yet no indication that the electron has any finite size; it is certainly less than the nuclear scale (10−15 m say) but that does not mean it is necessarily zero.
(Reread Subsections 2.2, 2.3, 4.1, 4.2 and 4.3 if you had difficulty with this question.)
Question E2 (A2)
The (temporary) failure to observe which of the following properties of cathode rays led many physicists to think that they were not composed of charged particles: (a) motion in straight lines, (b) deflection by an electric field, (c) deflection by a magnetic field.
Answer E2
It was the apparent absence of deflection by an electric field.
(Reread Subsection 2.3 if you had difficulty with this question.)
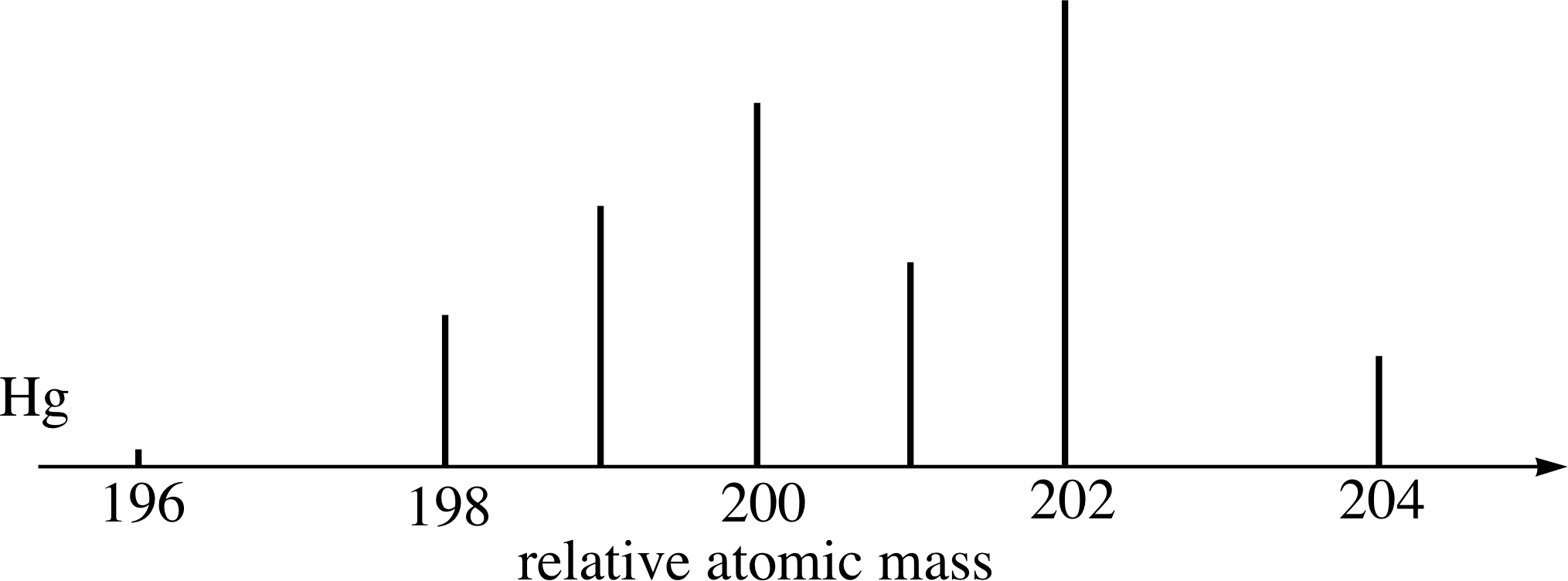
Figure 14 See Questions E3 and E4.
Question E3 (A4)
The mass spectrum of mercury is shown in Figure 14. Why are several peaks observed in the spectrum?
Answer E3
Mercury has several isotopes. The seven peaks in the mass spectrum indicate that naturally–occurring mercury has seven isotopes. A mass spectrometer separates a mixture of ionized atoms according to their mass-to-charge ratio. The appearance of several peaks in the mass spectrum shows that the sample, in this case mercury, consists of several types of mercury atom, which can be distinguished only by their mass.
(Reread Subsection 2.3 if you had difficulty with this question.)
Question E4 (A5)
(a) Write symbols for each of the isotopes of mercury which give rise to the peaks in the mass spectrum in Figure 14.
(b) If the relative abundances of these isotopes are as follows, calculate the relative atomic mass of this mixture:
(from left to right) 40.20%, 10.0%, 16.8%, 23.1%, 13.2%, 29.8%, 6.9%
Answer E4
(a) The symbols for the isotopes present are:
$19680Hg, 19880Hg, 19980Hg, 20080Hg, 20180Hg, 20280Hg}, 20480Hg
Isotopes are denoted by the symbol for the element, accompanied by a superscript to show the mass number of the atom of that isotope. For example, the lightest isotope present appears to have a relative atomic mass very close to 196: hence its mass number is 196. The symbol for this isotope is therefore 19680Hg
(b) The relative atomic mass for this mixture of isotopes is:
Ar = 196 × 0.002 + 198 × 0.100 + 199 × 0.168 + 200 × 0.231 + 201 × 0.132 + 202 × 0.298 + 204 × 0.069 = 200.63
(Reread Subsection 3.2 if you had difficulty with this question.)
Question E5 (A8)
What do the symbols 11H, 21H and 31H each represent? Identify the constituents of each isotope.
Answer E5
The symbols represent three isotopes of hydrogen. Each isotope contains one proton (this number is equal to the atomic number of hydrogen, which is specified by the subscript before the chemical symbol H). Each isotope, however, contains a different number of neutrons; this number can be obtained by subtracting the atomic number (the subscript) from the mass number (the superscript).
- ${}^1_1{\rm H}$ represents an isotope containing 1 − 1 = 0 neutrons;
- ${}^2_1{\rm H}$ (known as deuterium) represents an isotope containing 2 − 1 = 1 neutron;
- ${}^3_1{\rm H}$ (known as tritium) represents an isotope containing 3 − 1 = 2 neutrons.
(Reread Subsections 3.2 and 4.3 if you had difficulty with this question.)
Question E6 (A6)
Describe one piece of experimental evidence that can be explained by Rutherford’s model but not by Thomson’s model. State one feature of Rutherford’s model that is unsatisfactory.
Answer E6
The scattering of α–particles can be explained by Rutherford’s model but not by Thomson’s, which predicted that the particles would be scattered only through very small angles. Geiger and Marsden’s experiment showed that most α–particles were deflected through small angles, but some (roughly 1 in 104) were deflected through very large angles – back in the direction from which they came. This could not be explained using Thomson’s model, but could be explained by postulating that there is a very small positively charged nucleus at the centre of the atom that accounted for most of the atom’s mass. If the α–particle approaches closely to the massive nucleus, the repulsive electrostatic force can be sufficiently strong to deflect the α–particle through 180°.
One limitation of the Rutherford model is that it cannot explain the stability of the atom. According to classical physics, the orbiting electrons should continuously emit electromagnetic radiation, thus losing energy and rapidly spiralling into the nucleus. This problem was later solved by quantum theory, which says that the classical picture of the motion of the electrons is fundamentally incorrect.
(Reread Subsections 4.2 and 4.4 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 5Closing items.