PHYS 9.2: Radioactive decay |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
Towards the end of the 19th century, it was found that some nuclei are unstable – they spontaneously emit energetic radiation and sometimes change their chemical nature in the process. This phenomenon is known as radioactive decay or radioactivity, and is the subject of this module. In radioactive decay a radioactive nucleus or radionuclide emits alpha, beta or gamma radiation. In Section 2 we look at the properties of these types of ionizing radiation, and consider the processes by which nuclei decay and the relationship between the parent nucleus and the resulting daughter nucleus. This discussion includes an introduction to the positron and the neutrino, and shows how the penetration of matter by gamma–radiation can be described in terms of an attenuation coefficient. We conclude this discussion by taking a look at the four naturally–occurring decay chains.
Next, in Section 3, we see how a sample of radioactive material can be characterized by its activity and by its half-life, and hence introduce the radioactive decay constant and radioactive decay law. We then explain the use of radioactivity as a natural ‘clock’, and finish by discussing one of its applications – the dating of archaeological and geological materials by radiocarbon and potassium/argon dating.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Section 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Section 4.1Module summaryand the Section 4.2Achievements. If you are sure that you can meet each of these achievements, try the Section 4.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
Radionuclides decay by emission of α–, β– or γ–radiation. What do these radiations consist of?
Answer F1
α– and β–radiation consist of α– and β–particles. An α–particle is the nucleus of the helium isotope 42He. There are two types of β–particle. A β−–particle is an electron, a β+–particle is a positron (the antiparticle of the electron).
γ–radiation is electromagnetic radiation of very short wavelength.
Question F2
The nucleus 23292U decays as follows:
23292U → 22890Th + α + 5.4 MeV
What physical principles determine how much of the 5.4 MeV is carried away as the kinetic energy of the α–particle? (Do not attempt to calculate a numerical value.)
Answer F2
The two principles are: the conservation of linear momentum and the conservation of (relativistic) energy.
Question F3
Write down the equation for the β−–decay of 13755Cs. Which conservation principles does the equation illustrate, and how does it do so? (It doesn’t matter if you can’t name the daughter nucleus.)
Answer F3
The equation is:
13755Cs → 13756Ba + e− + ν−
The equation exhibits the conservation of nucleon number; there are 137 nucleons on each side. It also exhibits conservation_of_chargecharge conservation; there is a charge of +55e from the 55 protons before decay, and (+56 − 1)e from the 56 protons and one electron afterwards. β−–decay always involves the emission of an antineutrino, as well as an electron, which carries some of the energy released in the decay.
Question F4
A certain radionuclide has a half–life of 8 min. How long will it take for the activity of a sample to decay to 1% of its initial value?
Answer F4
The equation for the decay of a radionuclide is:
N (t) = N0e−λt
The decay constant λ is related to the half–life by:
$\lambda = \dfrac{\loge 2}{\tau} = \dfrac{0.693}{\tau}$
The activity is proportional to N, the number of nuclei present. The time T for N (t) to drop from N0 to N0/100, and hence for the activity to drop to 1% of its initial value, is given by:
${\rm e}^{\lambda T} = \dfrac{N_0}{N(T)} = 100$
Therefore$T = \dfrac{\loge 100}{\lambda} = \dfrac{\loge 100}{\loge 2}\tau = \rm \dfrac{4.605}{0.693}\times8\,min$
which gives T = 53 min.
1.3 Ready to study?
Study comment In order to begin to study this module you will need to be familiar with the following terms: atomic mass number A, atomic mass unit, atomic number Z, binding_energy_of_a_nucleusbinding energy, charge, Einstein’s mass–energy equation, electromagnetic radiation, electromagnetic wave, electron, ionization, isotope, neutron, nucleon, photon, proton, rest energy and rest mass. You should be familiar with the energy unit eV, and with masses expressed in atomic mass units (u) and in MeV/c2. You should be able to use conventional symbols to represent nuclides and apply the conservation principles of conservation_of_energyenergy, conservation_of_momentumlinear momentum and conservation_of_chargeelectric charge. You will also need to be familiar with calculus notation, exponential functions, natural logarithms (i.e. loge) and the relationship between them. If you are uncertain about any of these terms then you can review them by reference to the Glossary, which will also indicate where in FLAP they are developed. The following Ready to study questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
For the radium nucleus 22288Ra, write down the number of protons and neutrons in the nucleus.
Answer R1
In 22288Ra the mass number A = 222 and the atomic number Z = 88, so there are Z = 88 protons and (A − Z) = (222 − 88) = 134 neutrons.
Question R2
The mass of the proton is 1.672 × 10−27 kg. What is the energy equivalent of this mass?
Express the mass of the proton in MeV/c2.
(Use e = 1.602 × 10−19 C and c = 2.998 × 108 m s−1).
Answer R2
The mass of the proton is 1.672 × 10−27 kg. According to the Einstein’s mass–energy equation E = mc2 its energy equivalent is
1.672 × 10−27 kg × (2.998 × 108 m s−1)2 = 1.5028 × 10−10 J
Since 1 eV = 1.602 × 10−19 J, the mass energy of the proton is 1.503 × 10−10 J/1.602 × 10−19 J (eV)−1
= 938.1 MeV. The mass of the proton is therefore 938.1 MeV/c2.
Question R3
If y = eax, write down expressions for x and dy/dx in terms of y and a.
Answer R3
y = eax, so ax = loge y and hence $x = \dfrac1a\loge y$.
$\dfrac{dy}{dx} = \dfrac{d}{dx}({\rm e}^{ax}) = a{\rm e}^{ax}$
(The maths strand of FLAP gives further discussion of logarithmic_functionlogarithms, exponential functions and derivatives.)
2 Decay processes in unstable nuclei
2.1 Introduction to radioactive decay
There are many possible combinations of protons and neutrons, but only a few correspond to completely stable nuclei. Most naturally–occurring isotopes are stable, but many are not. i Unstable nuclei spontaneously emit energetic radiation, and may change their chemical nature. This phenomenon is called radioactive decay or radioactivity. An unstable nucleus decays into another nucleus, with the emission of alpha-, beta- or gamma- (α–, β– or γ–) radiation. The names α–, etc. were given to the three distinctive types of emission from radioactive materials at the time of their discovery (the late 19th century) before their natures were known. The initial nucleus is referred to as the parent nucleus (or parent isotope), the subsequent one as the daughter nucleus (or daughter isotope). i The decay of a parent nucleus, P, to a daughter nucleus, D, generally involves the emission of other decay products and can be represented symbolically by
P → D + other products + Q
The quantity Q (which is sometimes omitted) represents the energy required to balance this process; its value can be determined by applying the conservation of (relativistic) energy to the process. That is to say, Q can be found by requiring that the total energy immediately before the decay is equal to the total energy immediately after the decay, where the term ‘total energy’ is taken to include the energy equivalent of any (rest) masses involved i (as given by Einstein’s mass–energy equation, E = mc2) as well as the relativistic kinetic energy of the particles. i The energy represented by Q appears as the kinetic energy shared between the daughter nucleus, D, and other products. When Q is positive the decay is energetically allowed, whereas for negative Q it is energetically forbidden. The term nuclide is used to distinguish between nuclei that differ in their composition and/or internal energy, and unstable nuclei (i.e. those that undergo radioactive decay) are often referred to as radionuclides or radioisotopes.
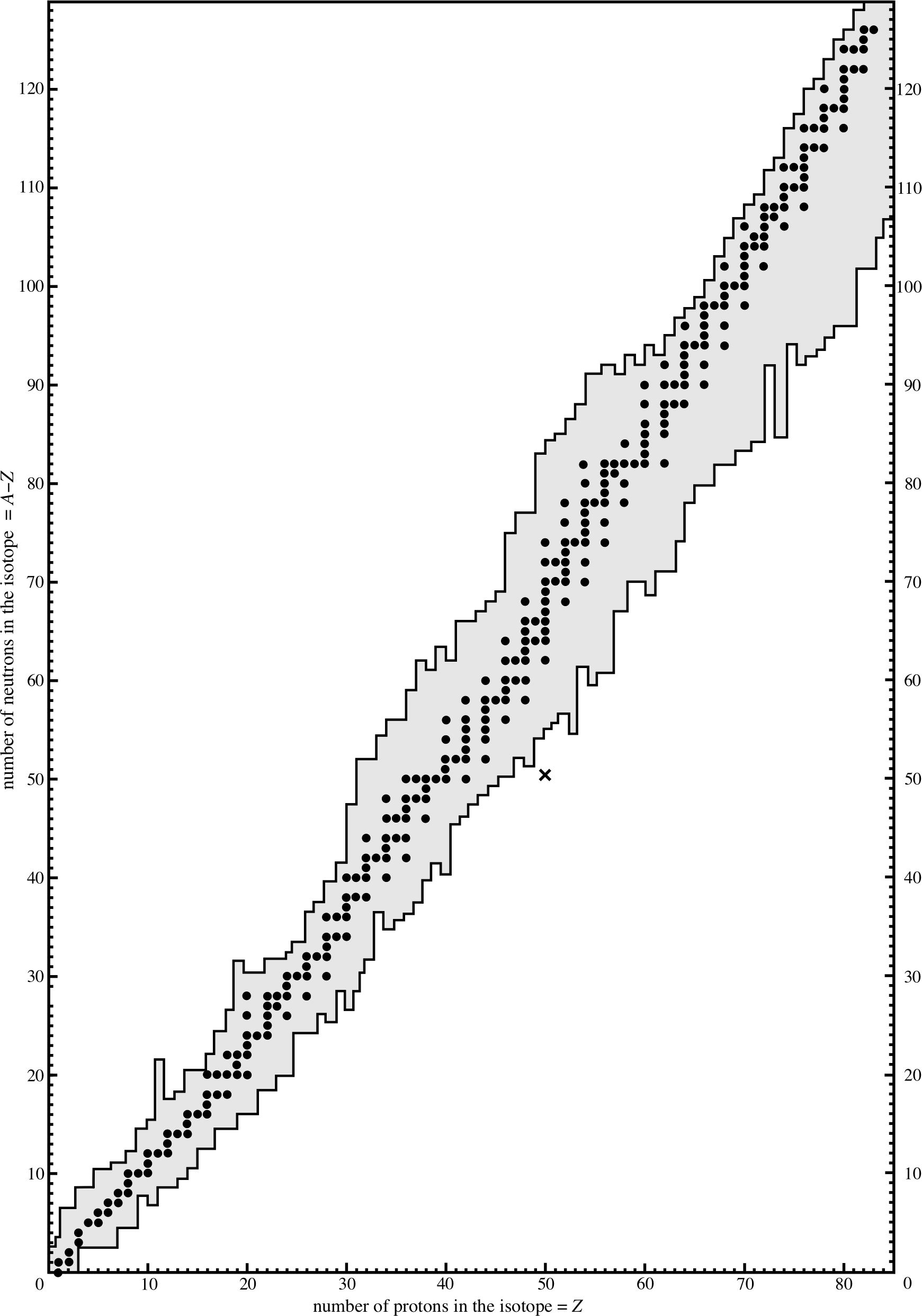
Figure 1 The number of neutrons in nuclei with Z < 83 plotted against the number of protons that the nuclei contain. Stable nuclei are shown as filled circles. The lines either side of the circles indicate the range within which the known unstable nuclei fall. The cross represents the latest isotope of tin to be found.
Figure 1 is a plot of the number of neutrons, N (where N = A − Z), against the numbers of protons, Z, for stable nuclides with mass number A. All stable nuclei lie on, or very near to, the stability line which corresponds approximately to N = Z for light nuclei, but has N > Z for heavier nuclei. i
A nucleus represented by a point some way from the stability line is unstable. This nucleus will decay into a daughter nucleus. If the point on the graph representing the daughter is near the stability line, then the daughter is likely to be stable and no further decay takes place. If however the point representing the daughter nucleus is not sufficiently near the line, then the daughter becomes the parent nucleus for a further decay, and so on until the stability line is reached.
We may therefore regard the ‘purpose’ of the decay as the approach to stability; each decay should bring the daughter closer to the stability line than the parent nucleus. To approach the stability line, the ratio N/Z of the neutron number to the proton number must be adjusted. Later in this section we will see how this may be achieved.
Table 1 summarizes the properties of the three types of emission from radioactive nuclei. All three radiations interact with matter electromagnetically.
| Type | Nature | Charge | Penetrating power |
|---|---|---|---|
| α | helium nucleus | +2 | low |
| β− | electron | −e | fairly high |
| β+ | positron | +e | fairly high |
| γ | electromagnetic radiation | zero | very high |
In α– and β–radiation the emitted particles are themselves charged and so interact powerfully with the charged particles (mainly the electrons) in matter. γ–radiation is a form of electromagnetic radiation and is therefore uncharged, though it too interacts with the electrons in matter, mainly through the electric field of the corresponding electromagnetic wave. Table 1 also indicates the radiation’s penetrating power – because the charged particles interact much more powerfully than γ–radiation they lose their energy rapidly and penetrate very little. In contrast, γ–radiation interacts only feebly and is therefore more highly penetrating.
The energies of radioactive emissions are at least of the order of hundreds of keV, whereas the binding energies of electrons within atoms are of the order of tens of eV.
✦ What is the likely result of the interaction between α–, β– or γ–radiation and an atomic electron?
✧ Because of the difference in energies, the atomic electron will be ejected from the atom which, as a result, will become a positive ion.
This ability to ionize leads to a more general descriptive name for the radioactive emissions – ionizing radiation. i
Decays are classified, according to the type of emission produced, as α–, β– or γ–decay. In each type of decay, (relativistic) energy and electric charge are conserved, as is the quantity N + Z that represents the total number of nucleons (i.e. neutrons and protons taken together). In the remainder of this section, we take a look at each of these types of decay in turn.
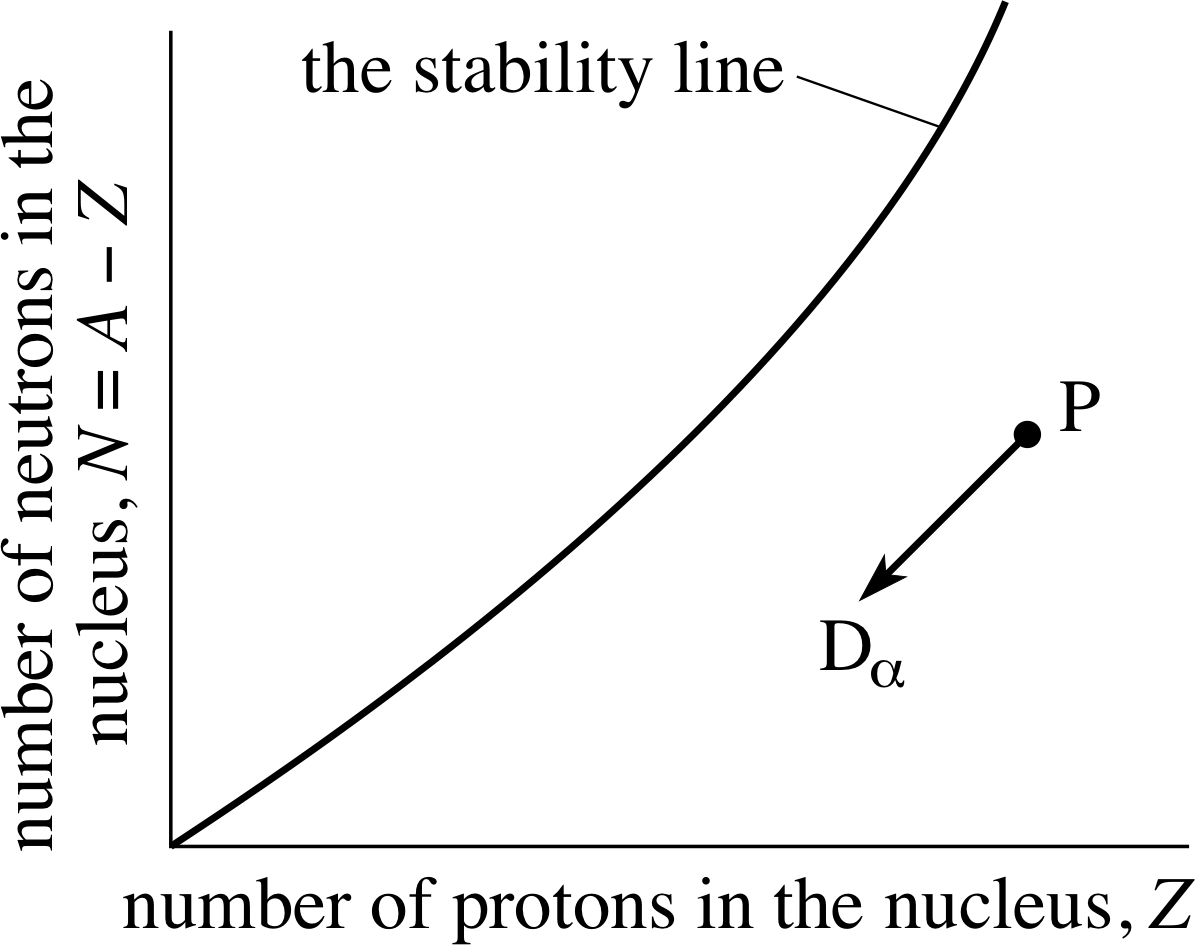
Figure 2 Alpha–decay of an unstable nucleus P.
2.2 Alpha-decay
In alpha_decayα–decay (alpha-decay) the parent nucleus emits a helium nucleus, known as an alpha_particleα–particle in this context, which has a charge +2e and a mass of approximately 4 u. i Thus for a parent nucleus, ZAP:
In α–decay ZAP → A−4Z−2D + 42α + Q(1)
The parent nucleus is usually fairly heavy and has N > Z.
The daughter nucleus has two protons and two neutrons fewer than the parent. On the stability plot of Figure 2 the ‘decay line’ P → Dα is therefore from right to left downwards at 45° to the horizontal.
✦ In α–decay two protons and two neutrons are emitted. How can the emission of an equal number of each particle change the ratio N/Z of the neutron number to the proton number and cause the daughter nucleus to be closer to the stability line than the parent nucleus?
✧ It does so because originally there are more neutrons than protons in the heavy nuclei that are potential α–decay candidates. The loss of two protons is proportionally a larger change than the loss of two neutrons and therefore emitting an α–particle increases the ratio of neutron number to proton number and thus increases the stability.
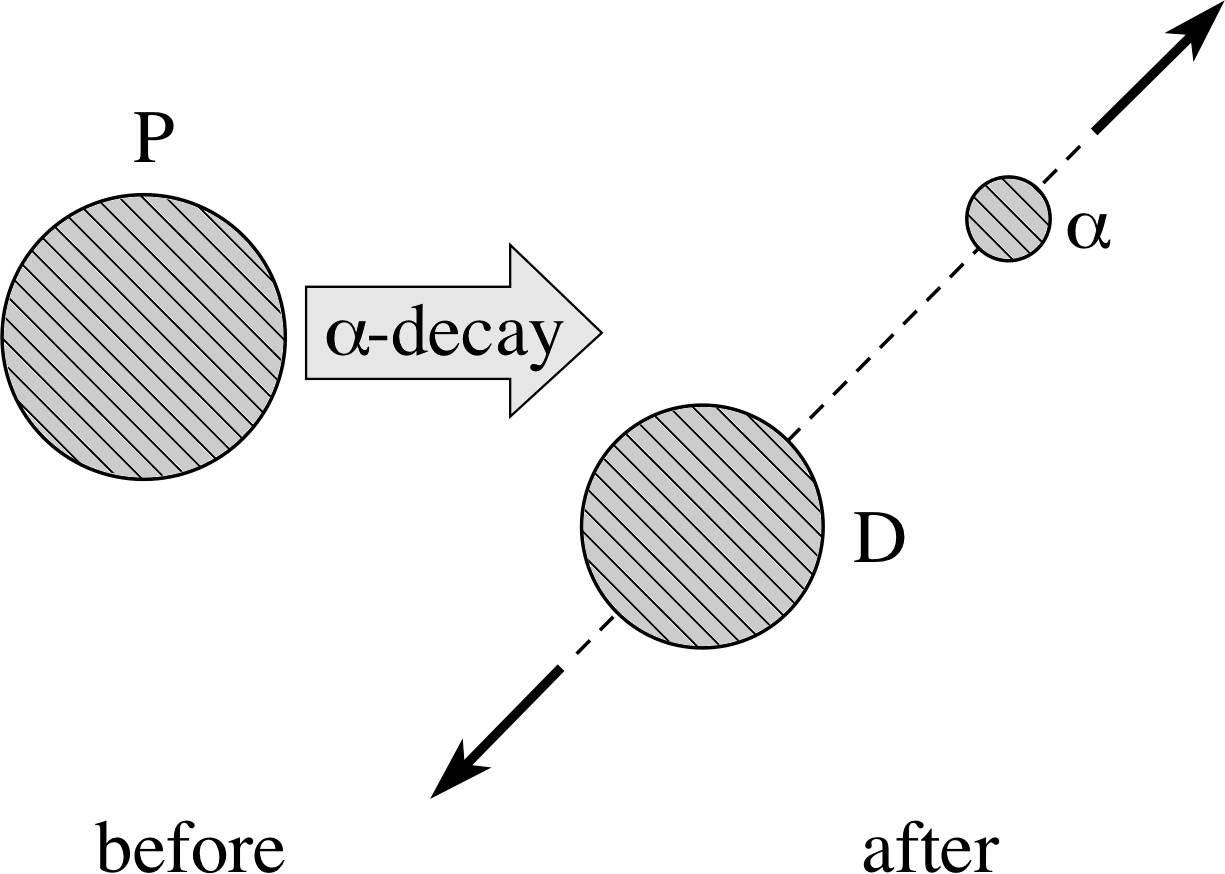
Figure 3 Schematic representation of the α–decay of 21084Po (polonium).
The emission of an α–particle from a heavy nucleus leads to an overall increase in nuclear binding_energy_of_a_nucleusbinding energy, i and allows some of the rest energy of the parent nucleus to supply the kinetic energy of the daughter nucleus and the α–particle. Typically, the energy released in an α–decay is a few MeV and this energy is divided between the daughter nucleus and the α–particle.
To see exactly how the energy is divided between the decay products we will look at a specific example, the α–decay of 21084Po (polonium):
21084Po → 20682Pb + 42He + Q
where Q represents the total kinetic energy of the 20682Pb (lead) and 42He (helium) nuclei. The decay is shown schematically in Figure 3.
We will estimate the kinetic energy of the α–particle on the assumption that the original polonium nucleus is at rest and that in this case the kinetic energy is given by the Newtonian formula, K = ½ mυ2. i We use Kα and KPb to represent the kinetic energy of the α–particle and lead nucleus, respectively. i
- atomic mass of 21084Po = 209.982 876 u
- atomic mass of 20682Pb = 205.974 455 u
- atomic mass of 24He = 4.002 603 u
The difference in mass between the parent nucleus and the decay products is therefore:
209.982 876 u − (205.974 455 + 4.002 603) u = 0.005 818 u
This is the mass equivalent of the increase in binding energy and implies a Q–value of 5.42 MeV since 1 u = 931.5 MeV/c2. To see how the kinetic energy Kα + KPb = 5.42 MeV is shared between the two particles, we use the fact that there is no external force acting on the decaying nucleus, so linear momentum, p, is conserved. i Since the parent nucleus is at rest, 0 = pPb + pα. The implication of this is that the momentum vectors of the α–particle and the lead nucleus must have equal magnitude and be in opposite directions, so their magnitudes are equal, i.e. pPb = pα.
To see what this implies for the kinetic energy note that:
$K_\alpha + K_{\rm Pb} = K_\alpha\left(1 + \dfrac{K_{\rm Pb}}{K_\alpha}\right)$
so$K_\alpha + K_{\rm Pb} = K_\alpha\left(1 + \dfrac{m_{\rm Pb}\upsilon_{\rm Pb}^2}{m_\alpha\upsilon_\alpha^2}\right) = K_\alpha\left(1+\dfrac{m_\alpha}{m_{\rm Pb}}\dfrac{m_{\rm Pb}^2\upsilon_{\rm Pb}^2}{m_\alpha^2\upsilon_\alpha^2}\right)$
Now, using the Newtonian formula, p = mυ i
$K_\alpha + K_{\rm Pb} = K_\alpha\left(1+\dfrac{m_\alpha}{m_{\rm Pb}}\dfrac{p_{\rm Pb}^2}{p_\alpha^2}\right)$
Since momentum conservation ensures that pPb = pα, we have, using the mass data given above:
$K_\alpha + K_{\rm Pb} = K_\alpha\left(1+\dfrac{m_\alpha}{m_{\rm Pb}}\right) = 1.019\,43\,K_\alpha$
But we know that Kα + KPb = 5.42 MeV, so 1.019 43Kα = 5.42 MeV. The kinetic energy of the α–particle is therefore 5.32 MeV and that of the lead nucleus 0.10 MeV. So, following the decay of 21084Po, the 20682Pb and 24He nuclei are emitted in opposite directions, the α–particle with an energy of 5.32 MeV and the lead nucleus with an energy of 0.10 MeV. Notice that the α–particle carries away most of the available kinetic energy; this is because its mass is much less than that of the daughter nucleus so it has to travel considerably faster to balance momentum, and its kinetic energy increases with the square of its speed.
This example suggests that for the general decay
P → D + α + Q
we have$Q = K_\alpha + K_{\rm D} = K_\alpha\left(1+\dfrac{m_\alpha}{m_{\rm D}}\right)$
or$Q \approx K_\alpha\left(1+\dfrac{4}{A_{\rm p}-4}\right) = K_\alpha\left(\dfrac{A_{\rm p}}{A_{\rm p}-4}\right)$ i
where AP is the mass number of the parent nucleus and we have made the approximation that mα = 4 u, mP = AP u and mD = (AP − 4) u.
Thus the kinetic energy division of the available energy Q is given approximately by:
$K_{\unicode[Times New Roman]{945}} \approx Q\left(1-\dfrac{4}{A_{\rm p}}\right)$(2)
and$K_{\rm D} \approx Q\left(\dfrac{4}{A_{\rm p}}\right)$(3)
Notice that the kinetic energy of the α–particle depends only on the Q–value and on the mass of the parent nucleus. This means that all α–particles emitted in this particular decay have the same kinetic energy.
Question T1
The α–decay of the uranium isotope 23892U is:
23892U → 23490Th + 42He + 4.30 MeV
Calculate the kinetic energies of the 23490Th and 42He nuclei.
Answer T1
For the decay 23892U → 23490Th + 42He + 4.30 MeV
we may use Equations 2 and 3:
$K_{\unicode[Times New Roman]{945}} \approx Q\left(1-\dfrac{4}{A_{\rm p}}\right)$(Eqn 2)
$K_{\rm D} \approx Q\left(\dfrac{4}{A_{\rm p}}\right)$(Eqn 3)
The kinetic energies are therefore:
$K_{\unicode[Times New Roman]{945}} \approx \rm 4.30\left(1-\dfrac{4}{238}\right)\,MeV = 4.23\,MeV$
and$K_{\rm D} \approx \rm 4.30\left(\dfrac{4}{238}\right)\,MeV = 0.07\,MeV$
When passing through a material, an α–particle ionizes atoms and molecules of the material by knocking out electrons, losing some of its own energy on each occasion. The mass of the α–particle is very large compared with that of the electron and so collisions with atomic electrons do not cause the α–particle to change direction substantially. i Since collision with a nucleus is unlikely, the α–particle usually continues in an almost straight line in the material until all its energy is lost. This loss involves a large number of collisions and is a statistical process, ensuring that the α–particle has a reasonably well defined range in any particular material. The range is the total distance travelled by the α–particle before it is brought to rest. It depends on the initial energy of the α–particle and on the medium through which it is passing. A range of a few centimetres in air at atmospheric pressure is typical. In solid materials the range is very small, of the order of tens of micrometres. i
Question T2
What would be the range of α–particles in a perfect vacuum?
Answer T2
In a perfect vacuum, α–particles would have infinite range. The absence of matter means that they would travel unimpeded, with no loss of energy.
2.3 Beta-decay
Beta–decay (β–decay) is rather more complicated than α–decay. β–decay involves the emission of a particle – named the beta_particleβ–particle – which is a high kinetic energy electron. The basic process is:
AZP → AZ+1Dβ + 0−1e + ...
Notice that, in order to conserve charge, β–decay must produce a daughter with a higher Z than the parent. In the mid 20th century it was established that this electron was also accompanied by another, neutral, particle (which we will discuss later).
A second type of β–decay can be observed:
AZP → AZ−1Dβ + 0+1e + ...
The particle emitted here has the same mass as the electron but it has the opposite charge of +e and has been named the positron. The β+–particle (or positron, e+) is the antiparticle of the electron. Each class of fundamental particles, protons, neutrons, electrons, etc. is thought to imply the existence of a corresponding class of antiparticles; electrons and positrons are simply one such pair of classes. Any antiparticle has the same mass as its partner particle but some of its other attributes, for example its charge, will have the opposite sign. In order to distinguish the two types of β–decay, emission of electrons is called β−–decay and emission of positrons β+–decay. β−–particles are electrons, and β+–particles are positrons. β+–decay is rarer than β−–decay, as you will see later.
There is a fundamental difference between β−–decay and α–decay. In α–decay the total number of protons (and also neutrons) before and after decay is the same. In β−–decay, however, the number of protons after decay has increased by one and the number of neutrons has decreased by one. The implication of this is that there must be some process which leads neutrons to change into protons:
n → p+ + e− + ...
This process is fundamentally responsible for β−–decay and it must be caused by something other than the strong interaction that holds the protons and neutrons together in the nucleus, and the electromagnetic interaction that is responsible for the electrical attraction and repulsion of charged particles. We call this new interaction the weak interaction, i since its intrinsic strength is less than that of the other two interactions. We will not discuss the weak interaction in any more detail here, except to say that because it is different from the interactions that produce the familiar ‘everyday’ forces of gravity and electromagnetism, and because it also differs from the strong interaction between nucleons, it is the fourth fundamental ‘force’ of nature.
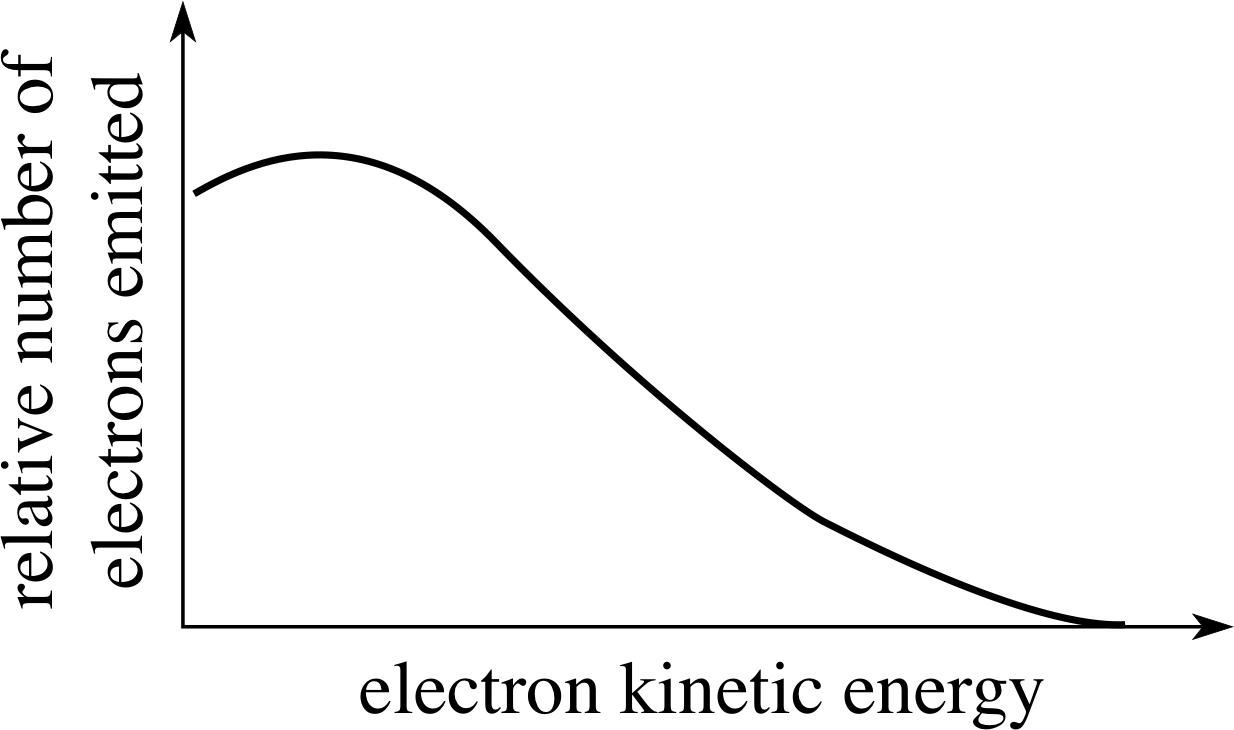
Figure 4 A typical spectrum of β−–particle kinetic energies emitted in β−–decay.
We said earlier that β−–decay involved the emission of another particle in addition to the electron. How do we know this? Why can we not simply have:
AZP → AZ+1Dβ− + 0−1e + ... ?
The main piece of evidence is this; when we study the kinetic energies of the β−–particles emitted in a particular β−–decay we find that, unlike α–decay, there is not a single unique kinetic energy for the β−–particle. All possible β−–particle (i.e. electron) kinetic energies are observed from zero up to some upper limit, which depends on the particular decay; this is shown in Figure 4.
✦ Why does this observation suggest that in β−–decay there is an additional particle produced in the decay, to accompany the daughter nucleus and the β−–particle (the electron)?
✧ If there were just two particles as products of the decay then the argument would parallel that for α–decay. Since the masses of the β−–particle and the daughter nucleus are fixed, the available energy (the Q–value) would split in a definite proportion between the two and only one definite kinetic energy for the β−–particle would be possible. If there is an additional third particle involved then the energy can be split between the three in an infinite number of ways, limited only by the total energy available – and all kinetic energies for the β−–particle, up to some maximum (total energy available), become possible.
The maximum β−–particle kinetic energy corresponds to those decays in which the β−–particle takes almost all the available energy with the third particle having a negligible amount – but the converse can also happen, with the β−–particle having little or no kinetic energy. All values of β−–particle kinetic energy between these two extremes are possible.
The observation of a continuous range of β−–particle kinetic energies in a given β−–decay process is now regarded as direct evidence of the involvement of a third particle. We say that β−–decay is a three-body process. However, when β−–decay was first observed this third particle was unknown and the continuous range of β− energies a complete mystery. Indeed, so profound was the mystery that it was even suggested that the principles of energy conservation and momentum conservation might not apply to β−–decay. The position changed however in 1930 when Wolfgang Pauli (1900–1958) proposed the existence of a hitherto unobserved class of particles which he called neutrinos. If every β−–decay involved a particle belonging to this class, the mystery could be resolved. Subsequent studies not only confirmed the existence of Pauli’s particles, they also established the existence of a family of neutrino–type particles. The current view is that there are six members of this family. The neutrino involved in β−–decay is now called the electron antineutrino and is represented by the symbol ν−e, i so the full statement of β−–decay becomes:
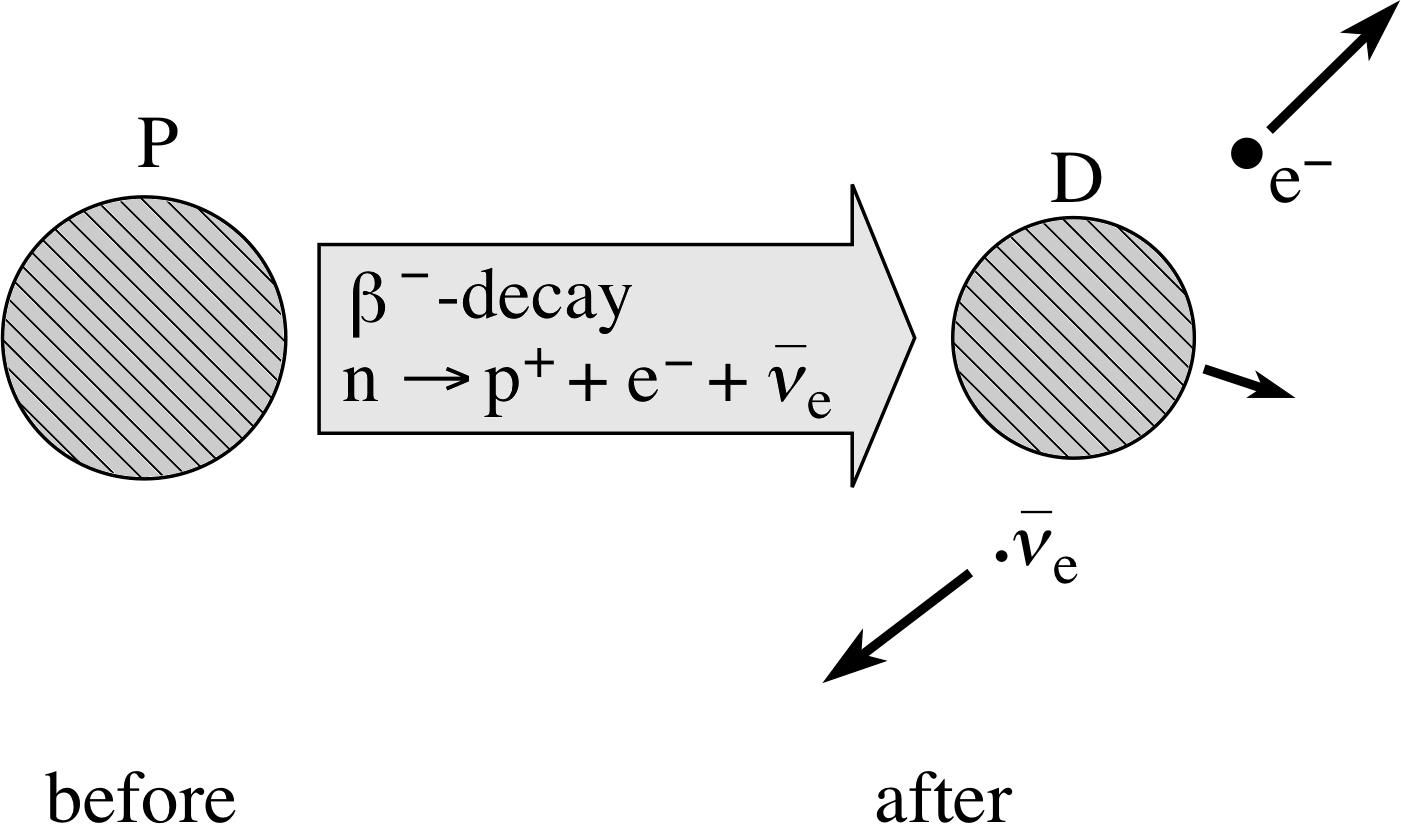
Figure 5 Schematic representation of β−–decay.
β−–decay involves$n\to p^+ + \underbrace{{\rm e}^- + \bar{\unicode[Times New Roman]{957}}_{\rm e}}_{\color{purple}{\large\rm{ejected}}}$(4)
and β−–decay itself is${}^A_Z{\rm P}\to{}^{\phantom{+1}A}_{Z+1}{\rm D}_{\unicode[Times New Roman]{946}^-} + {\rm e}^- + \bar{\unicode[Times New Roman]{957}}_{\rm e}$(5)
If the electron carries off less than its maximum energy, the energy of the antineutrino accounts for the balance. The β−–decay is represented schematically in Figure 5. The energy released in β−–decay is of the order of MeV in magnitude. It is carried away predominantly by the electron and antineutrino. The electrons emitted in β−–decay have energies ranging from about 0.02 MeV to about 3 MeV.
What properties must the antineutrino be postulated to have? It has no charge (if it did, charge would not be conserved in β−–decay). Energy conservation requires that the new particle, like all other neutrinos, has little or no rest mass. Without charge or rest mass and with no tendency to interact via the strong or electromagnetic interactions, the interaction of all neutrinos with matter is exceedingly feeble – in fact they can interact appreciably only via the weak nuclear interaction and cannot ionize matter. Neutrinos pass through matter with hardly any effect. They are able to pass entirely through the Earth with only a small chance of interaction! Trillions of them, coming from the Sun, pass through you every second! Their extraordinary powers of penetration make electron antineutrinos very difficult to detect, indeed, it was not until 1956 that particle detection technology was adequate for such a weakly interacting particle. Subsequently the other five neutrino family members have also been detected. i
Let us now return to the β−–particle itself (i.e. the electron), and investigate how it interacts with matter.
A β−–particle is much lighter than an α–particle, and so it is affected by its collisions with the atomic electrons in matter rather differently. In an interaction with an atomic electron it is deflected considerably and loses a substantial fraction of its kinetic energy. This means that an individual β−–particle does not travel in a straight line with a well–defined range, although it is carried in a generally ‘forward’ direction by its initial momentum. Despite this, the many β−–particles coming from a radioactive sample can be assigned a characteristic ‘range’ although it is not as well–defined as that of α–particles. Thus we can say that β−–particles are more penetrating than α–particles – for instance 100 keV β−–particles have a range of the order of 30 μm in aluminium.
β+–decay
We mentioned earlier that β+–decay had been observed to have the general form:
${}^A_Z{\rm P}\to{}^{\phantom{-1}A}_{Z-1}{\rm D}_{\unicode[Times New Roman]{946}^+} + {\rm e}^+ + \dots$
In this case the daughter nucleus has one proton fewer than the parent although the total number of nucleons remains the same. There must be some process involved which makes protons change into neutrons. Such a process is:
p+ → n + e+ + ...
In β+–decay the positron is found to have a continuous range of kinetic energies up to some maximum value for a given decay and so we know that a third particle is involved. Once again the new particle is a neutrino, in this case the electron neutrino. The electron neutrino and the electron antineutrino are particle and antiparticle and the electron neutrino is our second member of the family of six neutrino types.
The full description of β+–decay is then:
β+–decay involves$p^+\to n + \underbrace{{\rm e}^+ + \unicode[Times New Roman]{957}_{\rm e}^+}_{\color{purple}{\large\rm{ejected}}}$(6)
and β+–decay itself is${}^A_Z{\rm P}\to{}^{\phantom{-1}A}_{Z-1}{\rm D}_{\unicode[Times New Roman]{946}^+} + {\rm e}^+ + \unicode[Times New Roman]{957}_{\rm e}$(7)
If we compare Equations 4 and 6 (for β−–decay and β+–decay)
β−–decay involves$n\to p^+ + \underbrace{{\rm e}^- + \bar{\unicode[Times New Roman]{957}}_{\rm e}}_{\color{purple}{\large\rm{ejected}}}$(Eqn 4)
and remember that the neutron mass (1.008 665 u) exceeds the proton mass (1.007 825 u) it is apparent that it is energetically possible for a neutron to spontaneously decay into a proton, but not vice versa, i.e. the Q–value for Equation 4 may be positive but that for Equation 6 must be negative. For this reason an isolated neutron (outside the nucleus) will decay into a proton (the neutron half-life is about 10.6 min) i but an isolated proton will not decay into a neutron – it is a stable particle. i
✦ Why do you think β+–decay, a process which is energetically unfavoured, can nonetheless occur inside the nucleus?
✧ Changes in the neutron/proton ratio within the nucleus result in changes in the nuclear binding energy. In β+–decay the net positive charge on the nucleus decreases and so the electrostatic repulsion is reduced and this tends to increase the binding energy. So there can still be a net gain in nuclear binding in β+–decay despite the required increase in the rest mass of the nuclear constituents as a proton becomes a neutron.
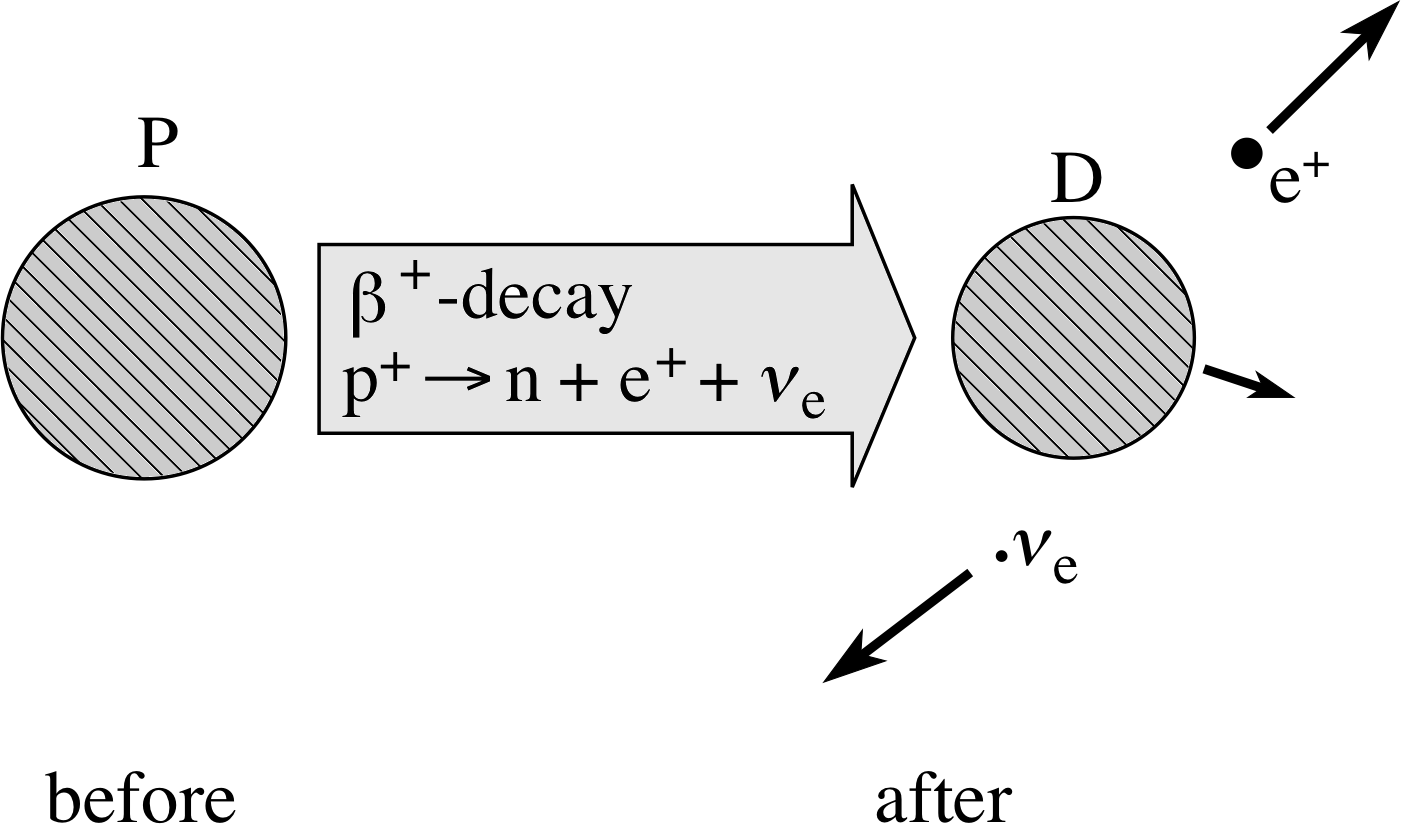
Figure 6 Schematic representation of β+–decay.
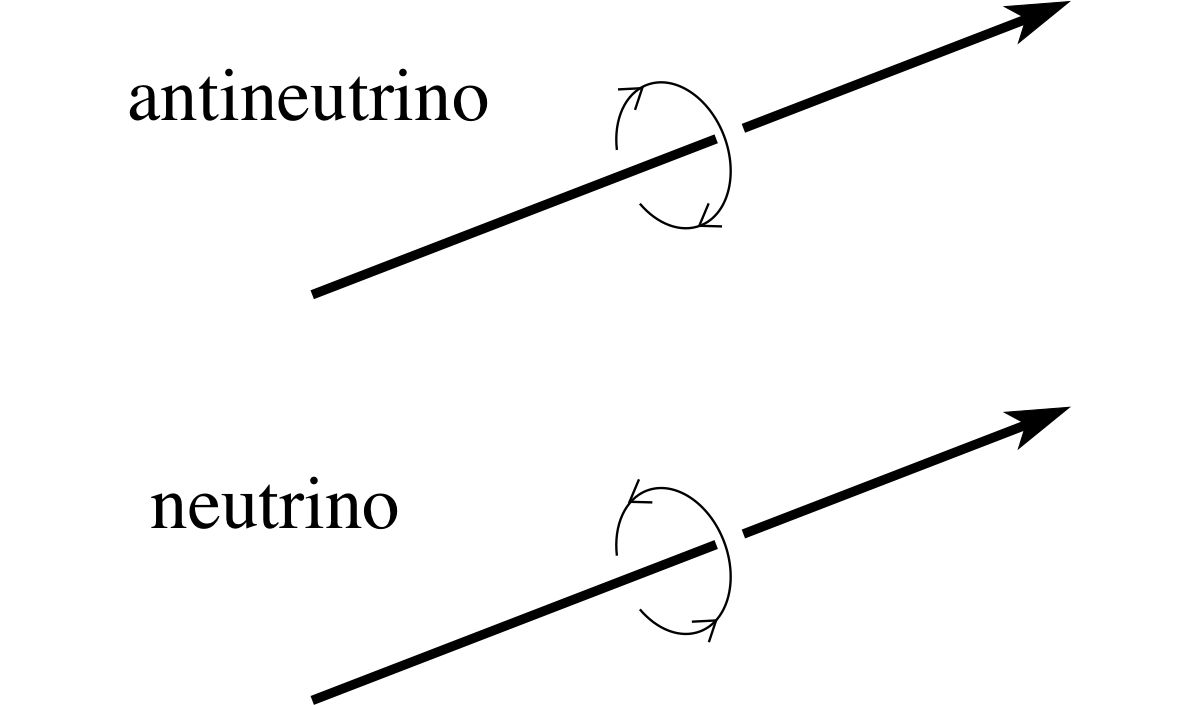
Figure 7 The spin directions of neutrinos and antineutrinos.
The β+–decay is represented schematically in Figure 6. The energy released in β+–decay is of the order of MeV in magnitude. It is carried away predominantly by the positron and the neutrino.
Aside Since neither the electron neutrino nor the electron antineutrino has any electric charge you may wonder what it means to say they are particle and antiparticle. One fundamental difference between them involves a property known as spin. Many particles, including electrons, protons and all types of neutrinos have spin. i It is actually a subtle quantum phenomenon, but for our purposes it can be crudely thought of as something like the spin of a ball about an axis. If we take the direction of motion of a neutrino or antineutrino as a suitable axis about which to measure the spin an interesting result emerges. An electron antineutrino approaching an observer always appears to spin in an anticlockwise sense, while an approaching electron neutrino always appears to spin in a clockwise sense (see Figure 7). This difference is symptomatic of the deeper difference that exists between the neutrino and the antineutrino.
Positrons can interact destructively with electrons by what is called pair annihilation. This is a common property of a particle and its partner antiparticle. The interaction is:
e+ + e− → 2γ
The total energy (rest energy + kinetic energy) of the electron–positron pair is converted into the electromagnetic energy of the gamma_radiationγ–radiation. Since electrons are plentiful in matter, positrons are absorbed very rapidly in matter via this process. The parent nucleus involved is usually fairly heavy and has N > Z.

Figure 2 Alpha–decay of an unstable nucleus P.
Question T3
On a sketch of Figure 2, indicate the position of the daughter nuclei produced if P undergoes β+– or β−–decay. Which side of the stability line must P lie if the nucleus is to achieve greater stability by undergoing β+–decay?
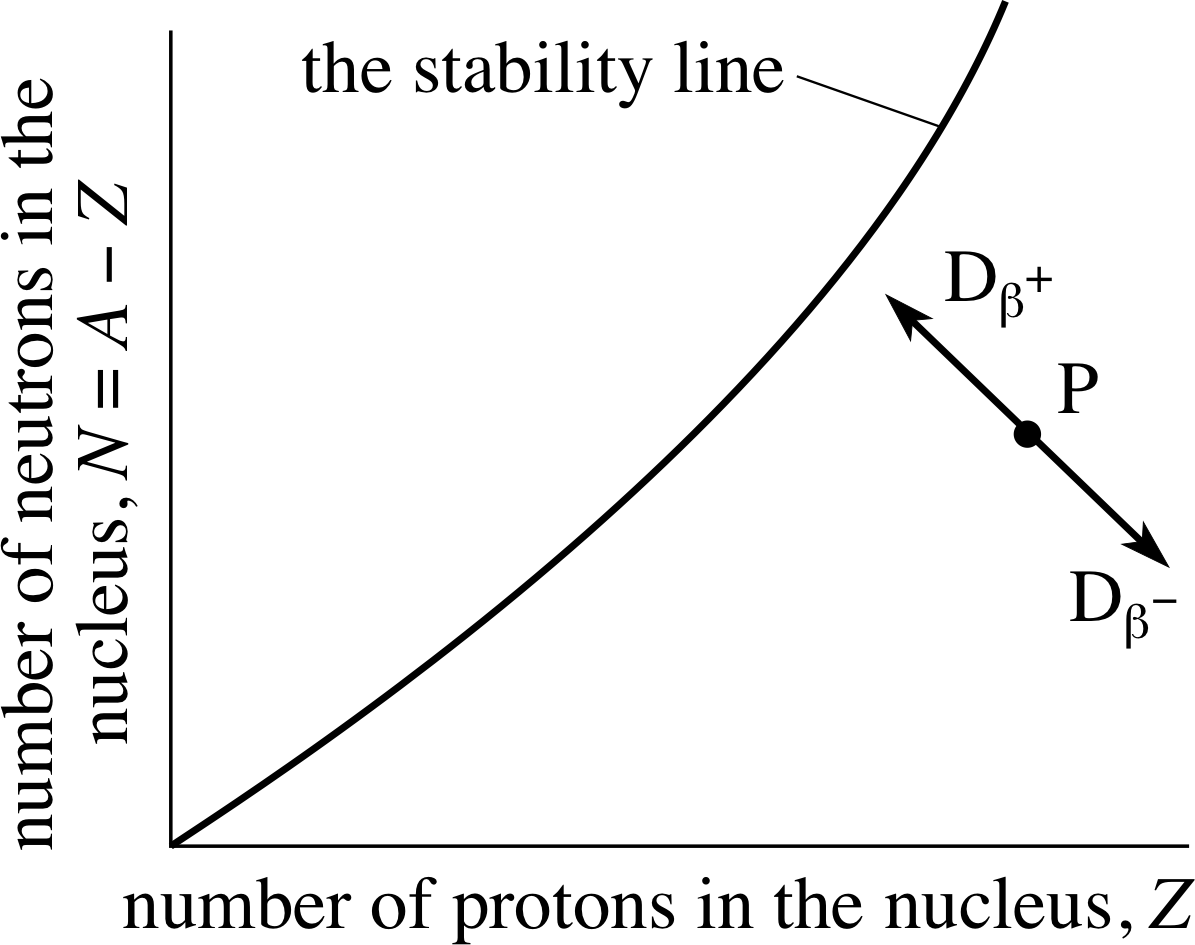
Figure 13 See Answer T3.
Answer T3
The ‘decay line’ P → Dβ− is from left to right downwards at 45° to the horizontal, and the ‘decay line’ P → Dβ+ is from right to left upwards at 45° to the horizontal. They are shown in Figure 13. Only a nucleus below the stability line, say at P, can achieve greater stability via β+–decay (whereas one above the line can achieve greater stability by β−–decay).
2.4 Q–values for β–decay
In Subsection 2.2 we considered the energy balance in the α–decay of 21084Po and we were able to calculate the Q–value for the decay from the atomic masses of the participants. If we now extend this idea to the calculation of Q–values in β–decay we must take care to remember that the atomic masses used in the calculations include the masses of the atomic electrons and we are therefore effectively overestimating the mass of each proton by an amount equal to the mass of an electron. For α–decay we need not be concerned about this since the number of protons present before and after the decay is the same; so when we subtract the initial and final mass energies to find Q, the overestimate cancels out. We may therefore safely use atomic masses and still obtain the correct energy balance.
The situation in β–decay is different since electrons or positrons (which have the same mass as electrons) are produced in the process and the number of protons does change. We must take account of both these effects when we use atomic masses to calculate Q. We can however ignore the neutrinos since their masses are negligible or zero.
In β−–decay the daughter nucleus has one additional proton and the atomic mass will assume the presence of one additional electron – which is equivalent to the rest mass of the emitted β−–particle. Thus, in using atomic masses in the calculation we need not worry about the rest energy of the β−–particle, and the Q–value found is the total energy which may appear distributed as the kinetic energy of the products.
In β+–decay the daughter nucleus has one fewer proton and the atomic mass will assume the presence of one fewer electron. In fact the decay must still produce one additional electron rest energy (the rest energy of the emitted positron) and so our calculation using atomic masses will overestimate the available Q–value by an amount equal to twice the rest energy of an electron, which is 2mec2.
Question T4
Calculate the rest mass of an electron in atomic mass units and in MeV/c2 given its rest mass is 9.11 × 10−31 kg, 1 eV = 1.60 × 10−19 J, the speed of light in vacuum is 3.00 × 108 m s−1 and 1 u = 1.66 × 10−27 kg.
Answer T4
In atomic mass units the electron mass is
$\rm \dfrac{9.11\times10^{-31}\,kg}{1.66\times10^{-27}\,kg\,u^{-1}} = 5.49\times10^{-4}\,u$
Using Einstein’s mass–energy equation E = mc2 with m = 9.11 × 10−31 kg gives electron rest energy E as
$E = \rm 9.11\times10^{-31}\,kg\times(3.00\times10^8\,m\,s^{-1})^2 = 8.20\times10^{-14}\,J\\ \phantom{E }= \dfrac{8.20\times10^{-14}\,J}{1.60\times10^{-19}\,J\,(eV)^{-1}} = 0.512\,MeV$
Electron rest mass is 0.512 MeV/c2.
Question T5
For the β−– and β+–decays below, calculate the energy balances Q1 and Q2 i
β−–decay:146C → 147Cβ− + e− + ν−e + Q1
β+–decay:137N → 136Nβ+ + e− + ν−e + Q2
given the following atomic masses:
136C = 13.003 355 u, 146C = 14.003 242 u, 137N = 13.005 739 u, 147N = 14.00 074 u and 1 u = 931.5 MeV/c2.
Answer T5
For β−–decay we can calculate Q directly from the atomic masses. From the data, the missing mass is
∆m = (14.003 242 − 14.003 074) u = 1.68 × 10−4 u
soQ1 = (1.68 × 10−4 × 931.5) MeV = 0.156 MeV
For β+–decay we need to subtract two electron rest energies when we calculate Q2 from the atomic masses. Using the result from the answer to Question T4, the electron rest energy is 0.512 MeV and we find from the data,
Q2 = 931.5 (13.005 739 − 13.003 355) MeV – 2(0.512) MeV
Q2 = 2.22 MeV − 1.02 MeV = 1.20 MeV
2.5 Gamma-decay
The third sort of radioactive decay, gamma_decayγ–decay, produces γ–radiation (or γ–rays), which is electromagnetic radiation of very short wavelength (λ < 50 pm). i It is emitted when a nucleus in an excited (higher energy) state loses energy. i The process is a nuclear analogue to the emission of light by an excited atom, but in the nuclei the energy changes are typically a million times greater than in atoms (roughly of order MeV in nuclei compared with a few eV in atoms) and this causes γ–radiation to be of much shorter wavelength than visible light. The excited nucleus is often the outcome of a previous α– or β–decay which has resulted in the daughter nucleus being left in an excited state rather than in its ground state. γ–radiation is uncharged and its emission leaves the number of nucleons unchanged, so the initial and final nuclides differ only in their energy and hence must have the same chemical symbol. The excited state nucleus is denoted by an asterisk (*); so the full process is:
In γ–decay${}^Z_A{\rm D}^*_{\unicode[Times New Roman]{947}}\to{}^Z_A{\rm D}_{\unicode[Times New Roman]{947}} + \unicode[Times New Roman]{947}$

Figure 13 See Answer T3.
γ–decay does not change the position of the point representing the nucleus on Figure 13 (see answer to Question T3).
γ–radiation has the same fundamental nature as any other form of electromagnetic radiation, such as light or X–rays. It can be thought of either as a stream of particles called photons i or as a train of electromagnetic waves. The photons are characterized by their energy E;
the waves by their wavelength λ or their frequency f (in a vacuum the γ–rays travel at the speed of light c = f λ).
Regarded as electromagnetic waves, the very short wavelength of γ–rays (λ < 50 pm = 0.05 nm) and correspondingly high frequency ( f > 6 × 1018 Hz) contrast strongly with the properties of visible light which has much longer wavelengths (roughly 400 nm to 700 nm) and much lower frequencies (roughly 4.3 × 1014 Hz to7.5 × 1014 Hz). Indeed, γ–rays are generally much closer in character to X–rays which are typically regarded as having wavelengths in the range 0.03 nm to 3 nm and frequencies in the range 1017 Hz to 1019 Hz.
When electromagnetic radiation, characterized by a frequency f, is regarded as a stream of particle–like photons, the energy E of each individual photon is given by:
Planck’s equation: E = hf(8)
where Planck’s constant h = 6.626 × 10−34 J s = 4.136 × 10−15 eV s. i The range of energies for visible light photons is from about 1.8 eV to 3.1 eV, while γ–ray photons have typical energies above 25 keV. It is customary to talk about γ–ray emissions in terms of the energies of the photons rather than in terms of the wavelength or frequency of the radiation.
Question T6
A photon of γ–radiation has an energy of 1 MeV. What is the frequency corresponding to this energy?
Answer T6
If we substitute numerical values into Planck’s formula (Equation 8) we get:
$f = \dfrac Eh = \rm \dfrac{10^6\,eV\times1.602\times10^{-19}\,J\,(eV)^{-1}}{6.626\times10^{-34}\,J\,s}\\ \phantom{f }= 2.418\times10^{20}\,s^{-1} = 2.418\times10^{20}\,Hz$
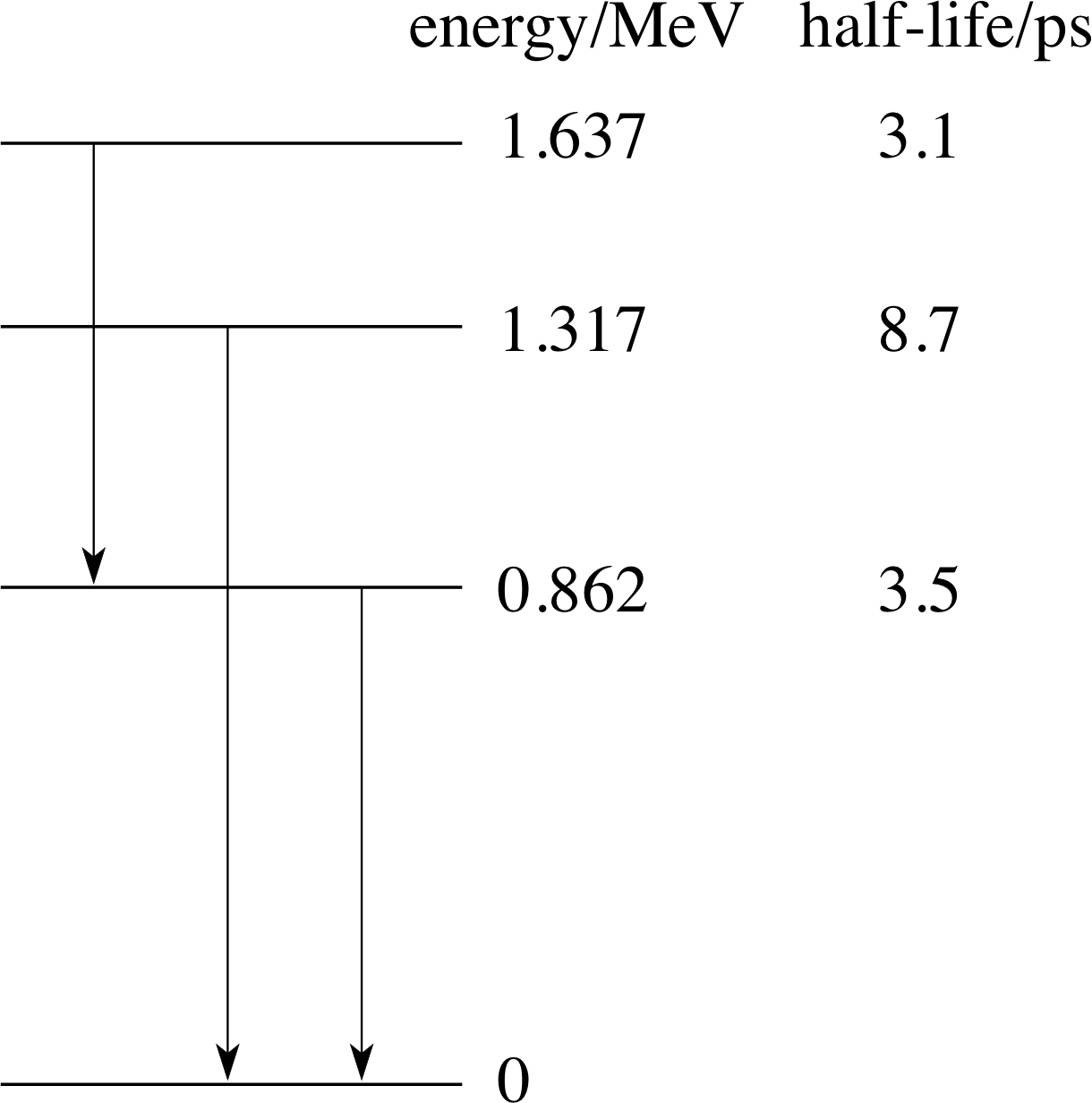
Figure 8 Part of the energy level diagram of 7234Se showing possible γ–decays and the half–lives of individual states. Each vertical arrow represents a strong transition leading to the emission of a γ–ray. The half-life here is equal to the time for half a sample of excited state nuclei to leave the excited state by decay to a lower state. The meaning of half–life will be discussed more fully in Section 3 of this module.
When a nucleus reduces its energy by an amount ∆E, by making a transition from an excited state to a state of lower energy, the emitted γ–ray photon carries away this energy ∆E and so the photon frequency is given by Planck’s formula (Equation 8) as:
$f = \dfrac{\Delta E}{h}$(9)
By observing such photons it is possible to determine the energies of transitions that gave rise to them. An energy level diagram (for 7234Se) showing the energy associated with various states of the nucleus is given in Figure 8. The strongest γ–ray emitting transitions are also shown on the figure. As with atomic energy states, the lowest nuclear energy state is called the ground state. De–excitation from a higher energy state may result in the emission of one or more γ–rays. For example, the decay of the state at 1.637 MeV to the ground state can proceed via two γ–rays through the state at 0.862 MeV.
Question T7
Use the information in Figure 8 to determine the energies (in MeV) and frequencies of the γ–ray photons for the transitions depicted by the vertical arrows.
Answer T7
We will denote the three transitions L(left), C(centre) and R(right) according to their position in Figure 8. The values of the energies and frequencies of the γ–ray photons are:
(i) EL = (1.637 − 0.862) MeV = 0.775 Me
$f_{\rm L} = \rm \dfrac{0.775\,MeV\times1.602\times10^{-13}\,J\,(MeV)^{-1}}{6.626\times10^{-34}\,J\,s} = 1.87\times10^{20}\,Hz$
(ii) EC = (1.317 − 0) MeV = 1.317 MeV; fC = 3.18 × 1020 Hz
(iii) ER = (0.862 − 0) MeV = 0.862 MeV; fR = 2.08 × 1020 Hz
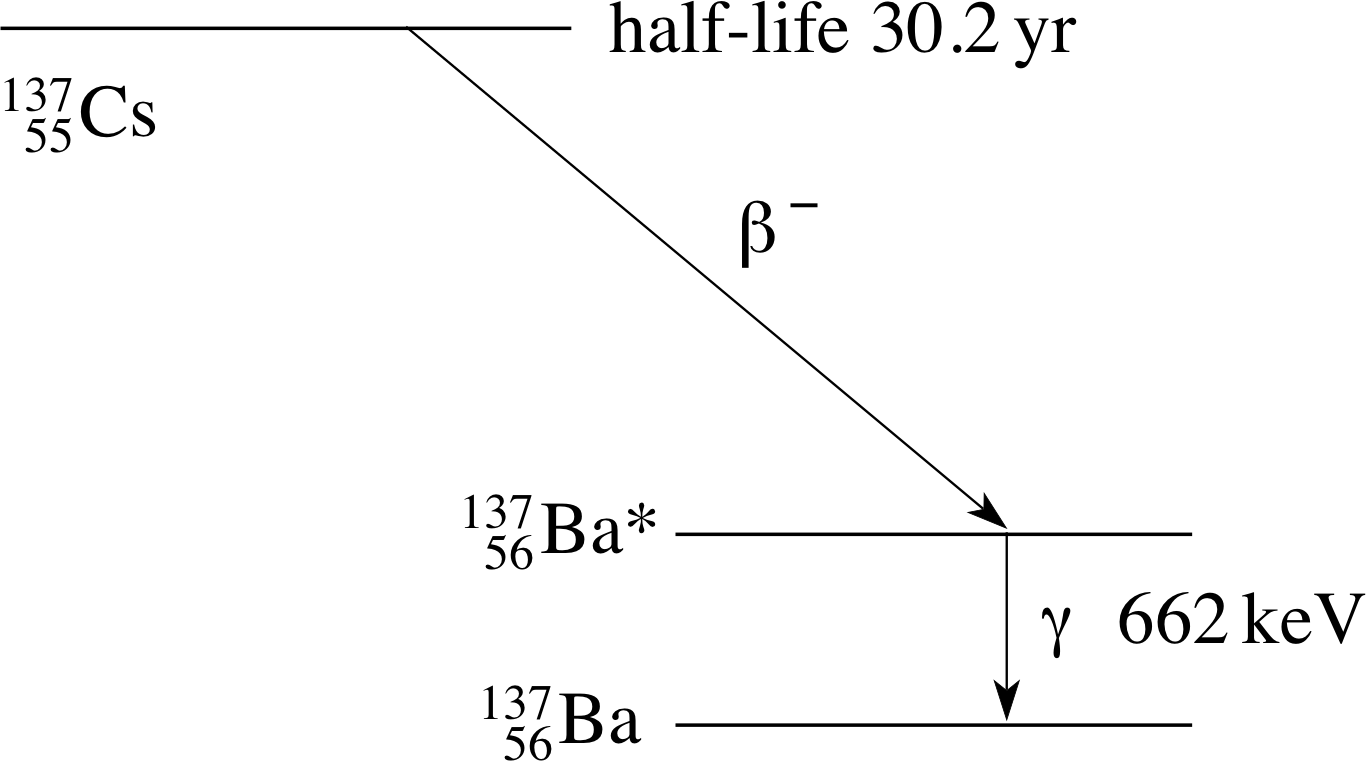
Figure 9 The decay sequence for a 13755Cs γ–ray.
We mentioned earlier that a radioactive decay sometimes produces a daughter nucleus in an excited state which then decays with the emission of a γ–ray. Figure 9 shows part of the energy level diagrams for 13755Cs and 13756Ba which indicates that 13755Cs may decay to an excited state of 13756Ba according to:
β−–decay:13755Cs → 13756Ba* + e− + ν−e
followed, almost immediately, by the γ–transition
γ–decay:13756Ba* → 13756Ba + γ
This illustrates another common feature of radioactive decay – the presence of γ–emission accompanying other emissions such as β– or α–decay. Figure 8 gives the fairly typical γ–decay half–lives of picoseconds whereas β–decay half–lives may be much longer – from seconds to many years.
This difference is due to the different interactions responsible for the two decay processes. γ–decay is electromagnetic in origin (with photons emitted) whereas β–decay is driven by the nuclear weak interaction (as discussed earlier). The different timescales involved give rise to the convention for the naming of the γ–rays from various nuclides.
To produce a source of the γ–rays shown in Figure 9 we would first need to produce radioactive caesium (13755Cs) (with a half–life of 30.2 yr) so that in the decay sequence the excited state of barium (13756Ba*) is produced which will then emit the required γ–ray. (If we tried to produce the excited barium directly we would have only a few picoseconds to deliver it to the user!)
For this reason the γ–ray in Figure 9 is usually (but rather loosely) described as a 13755Cs γ–ray, even though it is produced by 13756Ba. This convention for the naming of γ–rays is in common use.
γ–rays are much more penetrating than α- or β–particles. They are absorbed via processes which lead to the ionization of atoms in the material through which the γ–rays are passing. For the most part, the absorption of γ–rays in matter is attributable to their interaction with the electrons in the atoms of the material. However, it makes little difference which electrons are involved or to which atoms they are bound. This is because the energy of typical γ–rays (~ MeV) far exceeds the binding energies of electrons in atoms (~eV) and so the electrons act effectively as free particles. The effectiveness of a material as an absorber of γ–rays is determined simply by how many electrons are contained per unit volume. Since in neutral matter each electron is accompanied by a much more massive proton, the density of a material is a good indicator of the electron content – i.e. good γ–ray absorbers are dense materials. It is this property that makes lead a common choice as an absorber on a small scale, but due to cost, dense concrete shielding is used on a large scale.
The energy carried per second per unit area of cross section of a γ–ray beam (i.e. its intensity I) falls exponentially i with the thickness x of the absorber traversed according to the following expression, where I0 is the initial intensity of the γ–ray beam before it entered the material:
I (x) = I0 e−μx(10)
The coefficient μ, called the attenuation coefficient, describes how effectively the γ–ray beam is absorbed per unit thickness. The value of this coefficient depends both on the material and on the energy of the γ–ray photons. The product μx must be a dimensionless number, so the dimensions of μ are the reciprocal of length and will be related to the units of x. For instance, μ for lead with 10 MeV γ–ray photons is about 0.060 mm−1 but for 2 MeV γ–ray photons it is about 0.055 mm−1 – a small but significant difference. μ for water with 2 MeV γ–ray photons is about 5 m−1 (i.e. 0.005 mm−1).i) γ–rays are able to penetrate significantly through several centimetres of lead.
Question T8
For the 2 MeV γ–ray photons referred to above, what thickness of lead is needed to reduce the intensity to (a) 10% and (b) 1% of its initial value? (c) What thickness of water would give the reduction to 10% of the initial value?
Answer T8
(a) The thickness x necessary to reduce the intensity to 10% of its initial value may be obtained from Equation 10,
I (x) = I0 e−μx(Eqn 10)
with I = I0/10: I0/10 = I0e−μx. If both sides are divided by I0 and reciprocals are taken, we find eμx = 10.
Then if natural logs are taken of both sides and then divided by μ we have $x = \dfrac{\loge 10}{\mu}$.
If we now substitute μ = 0.055 mm−1 (as given in the text) we find x = 42 mm.
(b) If we repeat the calculation for 1% we find $x = \dfrac{\loge 100}{\mu}$, so x = 84 mm.
(c) For water, the value of μ is much smaller (0.055 mm−1) and the value of x proportionately larger (i.e. 0.055 mm−1/0.005 mm−1 = 11 times larger) than the value in (a) for lead, so the thickness of water is 11 × 42 mm = 0.46 m.
2.6 Decay chains
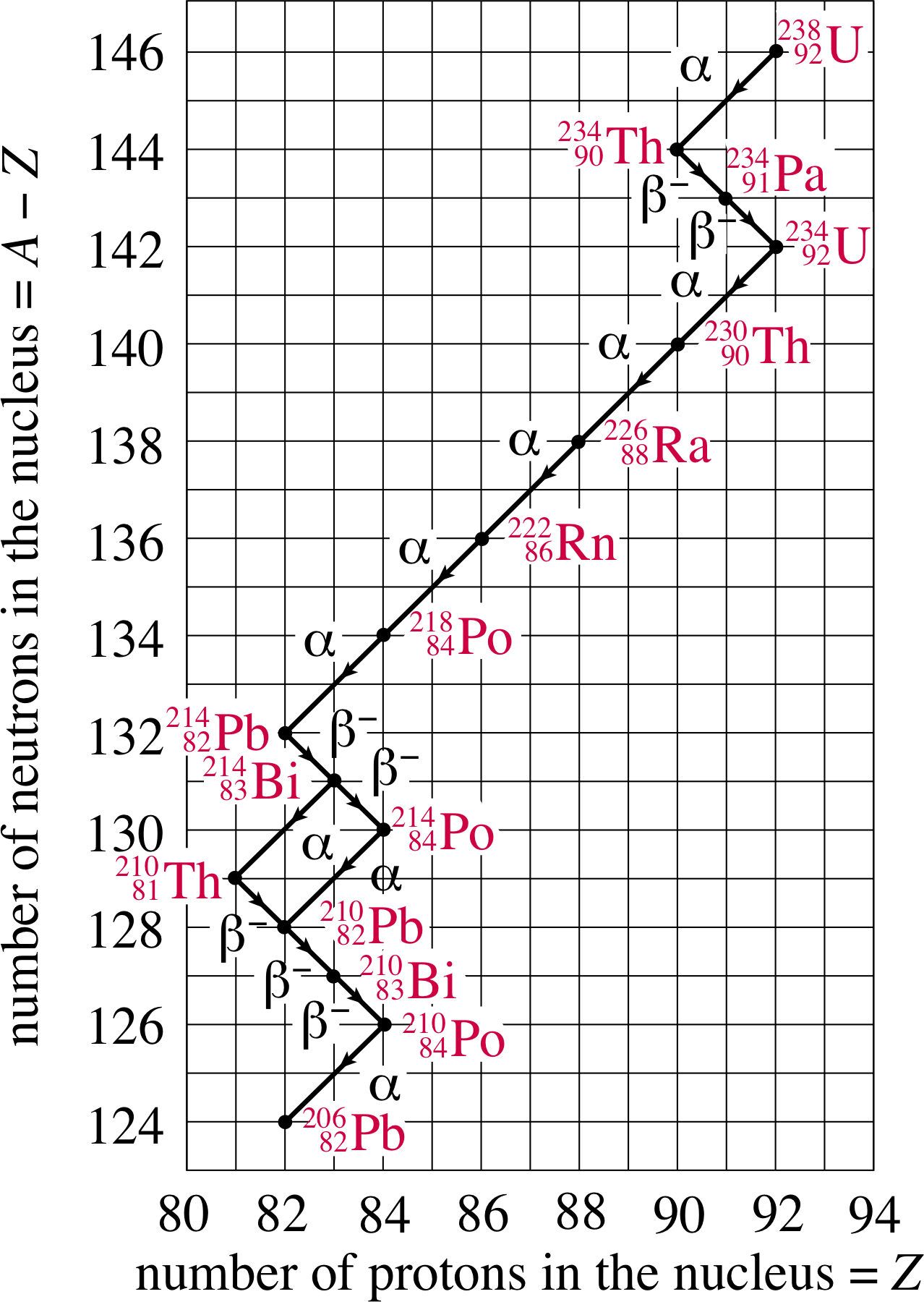
Figure 10 The decay chain 23892U → 20682Pb
Most unstable nuclei do not achieve stability in a single decay. For any decay, the daughter nucleus itself may be unstable – it becomes the parent for a further radioactive decay, and so on ...
For example, consider the decay of the uranium nucleus 23892U. It decays through a series of steps, in a nuclear decay chain, until a stable nucleus is reached – namely the lead isotope 20682Pb, as shown in Figure 10. i Have a look at the various links in the chain. You will see for instance that the 23892U nucleus decays first by α–decay to the nucleus 23490Th nucleus, which then undergoes β−–decay to a 23491Th nucleus. The chain continues until eventually it ends with 20682Pb, which is stable.
One interesting feature of this nuclear decay chain occurs at 21483Bi. Here the chain forks. This bismuth isotope may decay either into 21081Tl by α–decay or into 21484Po by β−–decay. 21483Bi is said to have two nuclear decay channels. There are four naturally–occurring nuclear decay chains – also called the natural radioactive series. They are called the thorium, neptunium, uranium and actinium series.
Why are there only four series? The reason is related to the mass number A of the nuclei in a series. As with the uranium series shown in Figure 10, the decays may be by α–decay, by β−–decay and, additionally but less commonly, by β+–decay. (γ–decay may also occur but this does not involve a change of isotope and so is not usually shown.)
An α–decay reduces A by 4; a β−– or β+–decay leads to no change in A between the parent and daughter nucleus. Therefore when A reduces in a series it must do so in units of four; there can therefore only be four independent series to include all values of A.
| Name of series | A (n = an integer) |
Final stable nucleus |
Longest lived nucleus |
Half-life of longest lived intermediate nucleus/Gyr |
|---|---|---|---|---|
| thorium | 4n | 20882Pb | 23290Th | 14 |
| neptunium | 4n + 1 | 20983Bi | 23793Np | 0.0021 |
| uranium | 4n + 2 | 20682Pb | 23892U | 4.5 |
| actinium | 4n + 3 | 20782Pb | 23592U | 0.70 |
Suppose, for instance, that a nucleus in a series has a mass number, A, that is a multiple of four; AParent = 4n, where n is an integer. This nucleus, if it decays by β−– or β+–decay gives ADaughter = 4n; if it decays by α–decay it leads to ADaughter = 4(n−1). In both cases both parent and daughter nuclei have a mass number that is a multiple of four, as will all nuclei in this series. Other numbers series will also link nuclei with mass changing by four or zero but with a difference of 1, 2 or 3 from the multiples of 4 we have just discussed. There are therefore just four series as is illustrated in Table 2, each of which consists of decays that either leave A unchanged or reduce its value by 4.
Question T9
21785At (astatine) decays to 20983Bi (bismuth) by a succession of α– and β−–decays. (a) To which natural series does this decay belong? (b) How many steps of each type must there be in this part of the decay chain? (Note that you are not asked for the order of the various steps.)
Answer T9
(a) It is part of the neptunium series, because A = 4n + 1.
(b) The mass number A changes by 8. As only α–decay can change A and each α–decay reduces A by 4, there must be two α–decays. However, each α–decay also reduces the atomic number Z by 2, so two α–decays alone would reduce Z by 4, but we want only to reduce it by 2. Each β−–decay increases Z by 1, so there must be two β−–decays. Therefore in total, there are two α–decays and two β−–decays.
3 Radioactive half–life and radioactive dating
3.1 The properties of radioactive materials
So far we have been concerned with the particles emitted as a result of radioactive decay and the changes to individual nuclei. We now turn to the large–scale properties of radioactive materials and how they change with time. The activity of a sample is defined as the average number of nuclear decays per second. The SI unit of activity is named after the French physicist Anton Henri Becquerel (1852–1908), the first person to observe radioactivity:
1 becquerel = 1 Bq = 1 nuclear decay per second
For commonly occurring radioactive samples, activities are often measured in gigabecquerels (GBq,
1 GBq = 109 Bq) because the Bq is a very small unit. The historical unit, the curie (Ci) was originally defined as the activity of 1 g of the radium isotope 22688Ra. i Improved methods of measurement caused the numerical value of this unit to be changed from time to time as more accurate determinations were made. To avoid such changes in the future the curie is now defined to have precisely the value:
1 Ci = 3.70 × 1010 decays per second = 37.0 GBq
Using this modern definition, the measured activity of 1 g of 22688Ra is a few per cent smaller than 1 Ci.
It is important to realize that radioactive decay is a random process – it is impossible to predict exactly when a particular nucleus will decay. Only the probability that it will have decayed after a certain time can be predicted. i We work in terms of the average (mean) number of decays per second because measurements of the actual number of decays in any one second will fluctuate randomly about the average. If the activity is large, these fluctuations will be only a small percentage of the average, but for low activities, the fluctuations become significant in comparison with the average.
For a sample containing a single radionuclide, the activity is proportional to the number of unstable nuclei present. i It depends only on the identity and number of nuclei, and is not affected by any external factors such as temperature or pressure, nor does it depend on whether the radioactive nuclei are in single atoms or combined in a chemical compound. These results are not surprising when we remember that radioactivity is a nuclear process, not an atomic (electron) process, and the conditions within a nucleus are not affected by external influences or by chemical processes.
If N (t) is the number of unstable nuclei present in the sample, and R (t) the activity of the sample at time t, then
R (t) = λN (t)(11)
where λ, the decay constant, is a characteristic property of the particular radionuclide. i
✦ What are the SI units of λ?
✧ The activity R (t) is the number of decays per second and the number of nuclei N (t) is dimensionless, so λ will have the unit s−1. i
One way of interpreting λ = R (t)/N (t) is to say that at any time t, when N (t) nuclei are present, λ is numerically equal to the fraction of nuclei that will decay in the next second. Alternatively, λ can be viewed as the probability that any given remaining nucleus will decay during the next second. However, both these interpretations of λ are strictly only applicable when N (t) can be taken as a constant over the one–second period, i.e. when λ ≪ 1 s−1.
More rigorously, if over a short time interval ∆t the average activity is $\langle R(t)\rangle$ and the average number of parent nuclei present is $\langle N(t)\rangle$ then the small change in N (t) over the period is ∆N (t) where:
$\Delta N(t) = -\langle R(t)\rangle\Delta t = -\lambda \langle N(t)\rangle\Delta t$
or$\langle R(t)\rangle = \dfrac{\langle N(t)\rangle}{\Delta t}\quad\text{and}\quad\dfrac{\langle N(t)\rangle}{\Delta t} = -\lambda\langle N(t)\rangle$
If we take the limit of these expressions as ∆t → 0, using the standard calculus notation i
$\lim_{\Delta t\to 0}\left[\dfrac{\langle N(t)\rangle}{\Delta t}\right] = \dfrac{dN(t)}{dt}$, we find:
$R(t) = -\dfrac{dN(t)}{dt}$(12)
and$\dfrac{dN(t)}{dt} = \lambda N(t)$(13)
We now see that λ is the constant of proportionality relating N (t) to the rate of change of N (t). Since we are using the instantaneous rate of change, this interpretation includes situations where N (t) (and hence the rate of decay R (t)) change significantly during one second.
Now let us look more closely at how the activity of a sample of radioactive material changes with time.
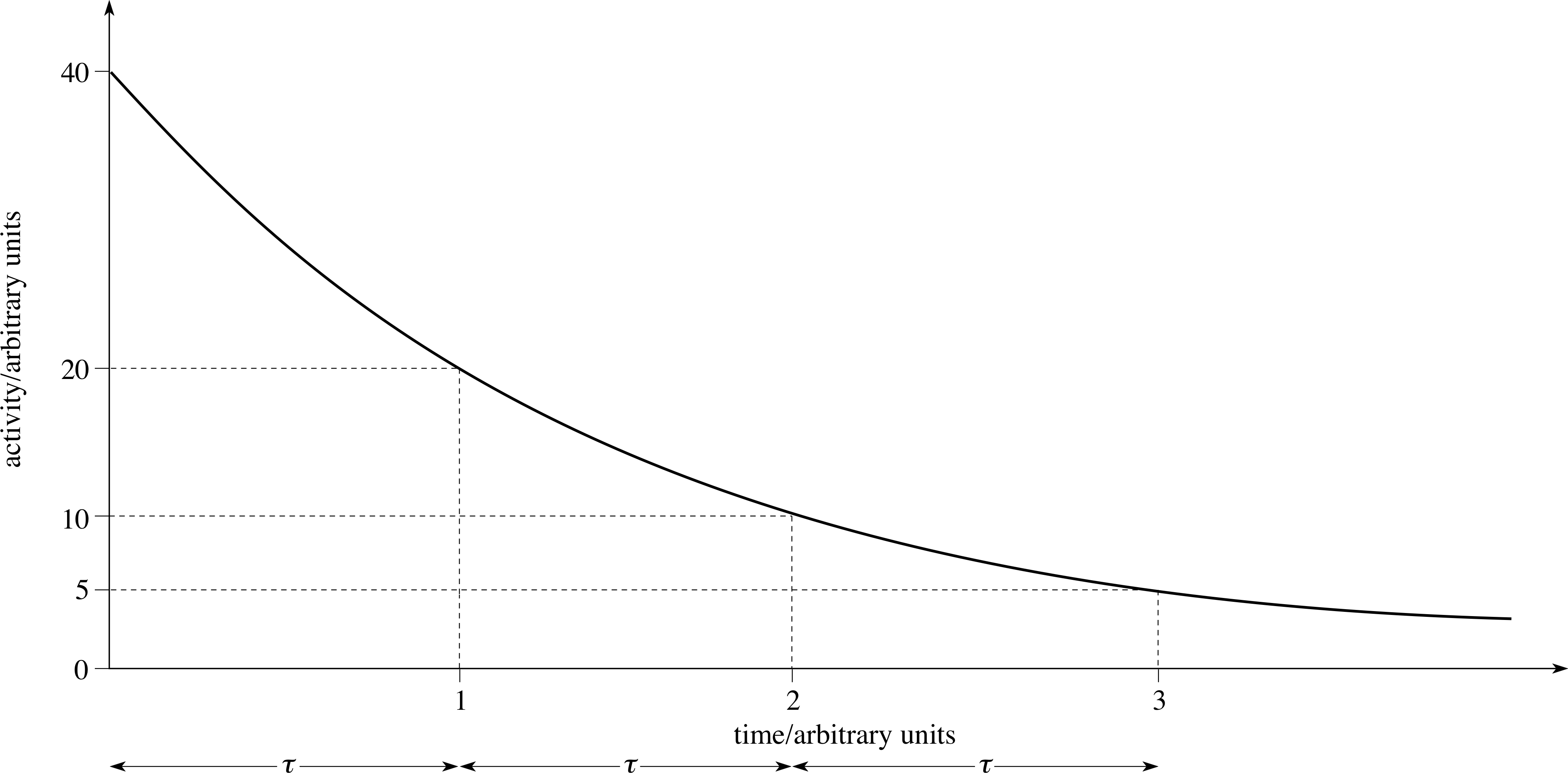
Figure 11 A graph of the activity of a radioactive sample against time.
Figure 11 shows a plot of activity, R (t), against time for a typical case. The time axis is marked off in equal intervals, each of duration τ, during which the activity decreases by a factor of two, i.e. τ is the time taken for half the radioactive sample to decay.
The time τ after which the activity has diminished to one–half of its initial value is called the half–life of the radionuclide.
The value of τ is a characteristic of the radionuclide, and is not affected by external conditions. i It does not depend on the initial activity of the sample. You can check this by choosing any point on Figure 11 and finding the time for the activity to fall to half your chosen value.
✦ What would be the shape of the graph of N (t) plotted against time for the same sample?
✧ R (t) is directly proportional to N (t), so the graph would have the same shape (though the scales on the vertical axes would differ by a factor of λ).
✦ How does N (t) change during a time interval τ?
✧ N (t) decreases to one–half its initial value. If R (t) halves in a given time interval, then Equation 11,
R (t) = λN (t)(Eqn 11)
shows that N (t) will also halve in this same time interval.
We could also define the half–life as the time τ over which the number of radioactive nuclei present falls to half its initial value.
Equation 13,
$\dfrac{dN(t)}{dt} = \lambda N(t)$(Eqn 13)
is an example of a differential equation.
To solve this equation we need to find N (t) such that its derivativefirst derivative with respect to t reproduces the original function N (t) with a numerical multiplier (−λ). It is shown elsewhere in FLAP that the solution involves an exponential function of time. i
In fact it has the following form:
The radioactive decay law N (t) = N0 e−λt(14)
since we then have
$\dfrac{dN(t)}{dt} = -\lambda N_0{\rm e}^{-\lambda t} = -\lambda N(t)$
as required by Equation 13.
Also, at t = 0 the value of N (0) becomes N0 according to Equation 14, so N0 is the number of radioactive nuclei present at t = 0.
From Equations 12,
$R(t) = -\dfrac{dN(t)}{dt}$(Eqn 12)
13 and 14, the activity $R(t) = -\dfrac{dN(t)}{dt} = \lambda N(t) = \lambda N_0{\rm e}^{\lambda t}$
We can therefore write:
The activity law R (t) = R0 e−λt(15)
where R0 = λN0, the initial activity at t = 0.
Equation 13 asserts the independence of each radioactive nucleus – each nucleus of a given type has the same probability of decay in a given time, and so the total decay rate must be proportional to the total number of participating nuclei. This aspect of independence is at the heart of the many exponential processes in physics – including those in Equations 14 and 15.
Equation 14 (the radioactive decay law) and Equation 15 (the activity law) express the fact that in a sample composed of nuclei of a given type both the activity and the number of radioactive nuclei fall exponentially with time, with the same decay constant. Of course the activity can be readily observed and so this is the usual method of measuring the decay constant.
Radioactive decay can be described either in terms of the decay constant λ (with units of s−1) or the half–life τ (with units of s). We can see how these two are related if we substitute t = τ in Equation 15, remembering that $R(\tau) = \frac12R_0$, we find
$\frac12R_0 = R_0{\rm e}^{-\lambda\tau}$
If we divide both sides of this equation by R0, it cancels from the equation. This confirms that τ is independent of the initial activity R0. If we then take the reciprocal of each side of the equation, we find
eλt = 2
Taking natural logarithms of each side gives us
λτ = loge 2
This leads us to the following relationship between decay constant and half-life:
$\lambda = \dfrac{\loge 2}{\tau} = \dfrac{0.693}{\tau}$(16)
Therefore either the half–life or the decay constant gives a complete description of how the activity of a sample of radionuclide changes with time. It is in fact more usual to quote the half–life (see, for example, Table 2). Some half–lives are very long, so it is customary to quote their values in suitable units of time – minutes, days, years, or even multiples of years.
It is then usual to give λ in the equivalent reciprocal unit, using Equation 16. For example, if τ = 2.5 min, then λ = 0.693/(2.5 min) = 0.28 min−1.
Question T10
The half–life of 13153I is 8.0 days. Calculate, (a) the decay constant of this isotope, and (b) the time for the activity of a sample to decrease by a factor of 10.
Answer T10
(a) The decay constant is given by Equation 16,
$\lambda = \dfrac{\loge 2}{\tau} = \dfrac{0.693}{\tau}$(Eqn 16)
$\lambda = \rm \dfrac{0.693}{8.0\,day} = 0.087\,day^{-1}$
Alternatively, $\lambda = \rm \dfrac{0.693}{8.0\times24\times3600\,s} = 1.0\times10^{-6}\,s^{-1}$
(b) We have R (t) = R0/10, and the algebra is the same as in Question T8. The time taken is therefore:
$t = \dfrac{\loge 10}{\lambda} = \rm \dfrac{2.303}{0.087\,day^{-1}} = 26.5\,days$
Alternatively, $t = \rm \dfrac{2.303}{1.0\times10^{-6}\,s^{-1}} = 2.3\times10^6\,s$
Note that the time for the activity to decrease by a factor of 10 is also independent of the actual activities. The time taken to change by any chosen factor depends only on the particular factor chosen – this is a characteristic of all exponential changes.
We are now able to calculate the activity of any sample of radionuclide. For example, suppose we wish to calculate the initial activity of a 1 μg i sample of 6027Co, with a half–life of 5.3 years. We can find this by using R0 = λN0, once we know λ and N0. The decay constant λ of 6027Co (from Equation 16) is:
$\lambda = \dfrac{0.693}{\tau} = \rm \dfrac{0.693}{5.3\times365\times24\times60\times60\,s} = 4.15\times10^{-9}\,s^{-1}$
The number of nuclei N0 in 1 μg of 6027Co is approximately given by: i
$N_0 = \rm \dfrac{1.00\times10^{-9}\,kg}{(60\,u)\times(1.66\times10^{-27}\,kg\,u^{-1})} = 1.00\times10^{16}$ i
So, the activity is
R0 = λN0 = (4.15 × 10−9 s−1) × 1.00 × 1016 = 4.15 × 107 s−1 = 41.5 MBq i
Question T11
The half–life of 13153I is 8.0 days. Calculate the activity of 1 μg of the isotope.
[Hint: Use the answer to part a of Question T10.]
Answer T11
From the answer to part a of Question T10:
λ = 1.0 × 10−6 s−1
As in the example in the text, we can estimate N0 as we know the mass number to be 131:
$N_0 = \rm \dfrac{1.00\times10^{-9}\,kg}{(13\,u)\times(1.66\times10^{-27}\,kg\,u^{-1})} = 4.60\times10^{15}$
Therefore R0 = λN0 = (1.0 × 10−6 s−1) × 4.60 × 1015 = 4.6 × 109 s−1 = 4.6 GBq = 0.12 Ci.
3.2 Radiocarbon dating
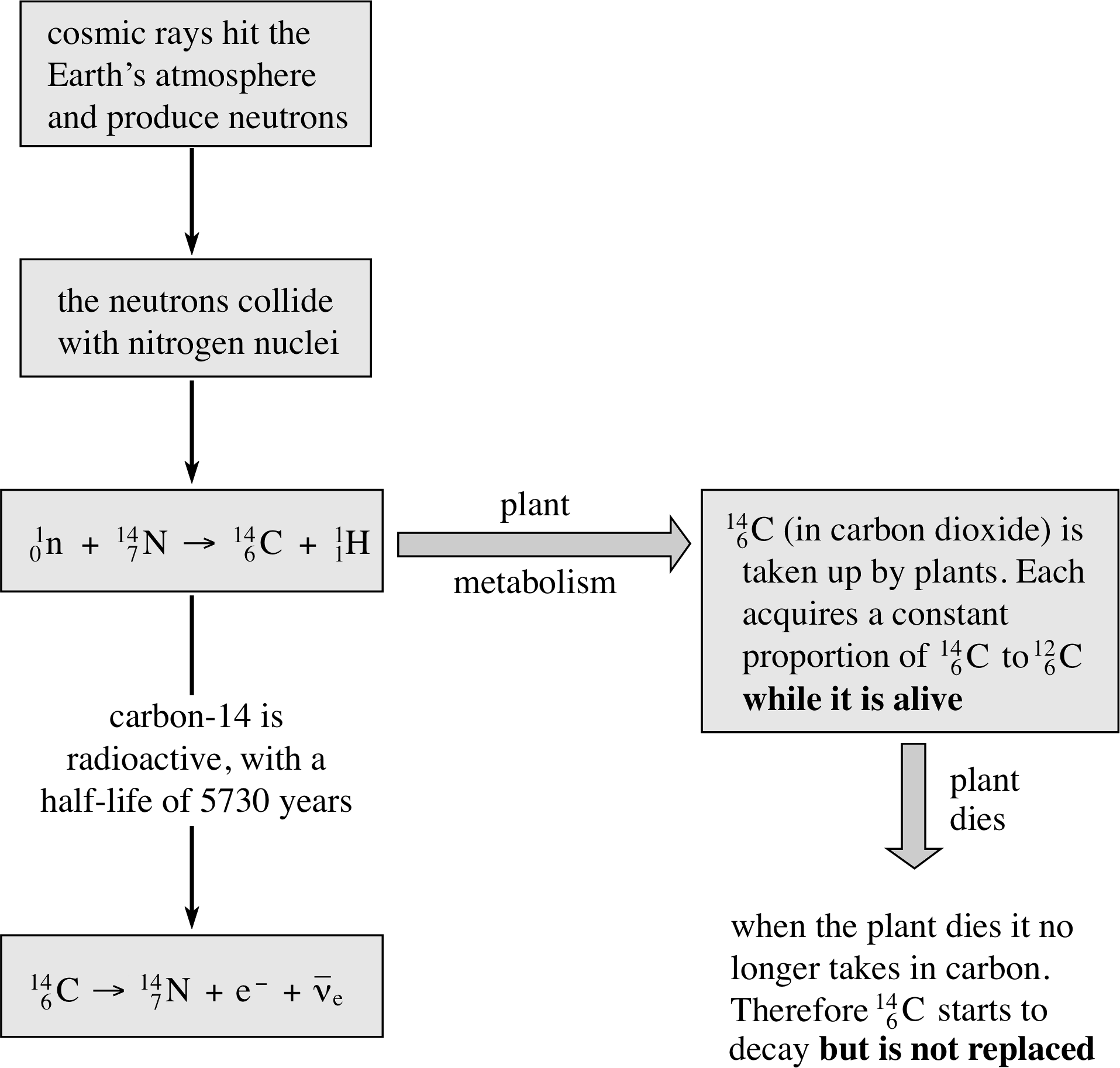
Figure 12 The basic principles behind radiocarbon dating.
We have already mentioned that the decay constant (and half-life) of a nuclide is unaffected by temperature and pressure, and is independent of the chemical environment, for example, whether the nucleus is part of the atom in a molecule or not. Radioactive nuclei can therefore be used as a ‘clock’ that is unaffected by changes in conditions. This is most useful when attempting to measure very long periods of time, for example in dating archaeological samples. One isotope that can be used in this way is 146C (known as carbon-14).
Carbon-14 decays by β−–emission to nitrogen-14, with a half–life of 5730 years. As it is a light element, it is not produced in any of the natural radioactive decay chains. You might expect therefore that the amount of 146C on Earth would long ago have been reduced to zero. However, it is found that the proportion of 146C to the stable isotope 126C is remarkably constant at about 1 : 1012. This is because 146C is constantly being produced in the upper atmosphere due to bombardment by cosmic rays. i Plants, for example, take in carbon (as carbon dioxide) from the atmosphere and incorporate it in their living tissue. The tissue will have the same ratio of 146C to 126C ratio as the atmosphere while carbon dioxide is being absorbed. However, when the plant dies it ceases to take in carbon from the atmosphere. From that moment the proportion of 146C will start to decrease with the characteristic half–life of the unstable 146C (the amount of the stable isotope 126C will, of course, remain constant).
The proportion of 146C in once–living material is therefore a measure of its age. This is the principle behind radiocarbon dating, summarized in Figure 12.
The activity per unit mass of a specimen is called the specific activity of the specimen. The strict SI unit for this quantity would be Bq kg−1 but other units, such as Bq g−1 or mCi g−1, are often used.
✦ A live piece of wood has an average specific activity of 15 Bq g−1 due to the β−–decay of 146C. Assuming that the average specific activity of live wood has been constant for at least the past 6000 years, what average specific activity would you expect from a piece of wood ‘harvested’ 5730 years ago?
✧ Since 5730 years is the half–life of 146C, you would expect the average specific activity to be 7.5 Bq g−1.
So, a measurement of the specific activity R i of a plant specimen indicates the time since its death providing we know its specific activity R0 when it was alive. It is useful to have a general formula relating the present specific activity of a sample to its age in terms of the half-life. From Equation 15,
The activity law R (t) = R0 e−λt(Eqn 15)
R0/R (t) = eλt, so λt = loge (R0/R) and hence:
$t = \dfrac{\loge(R_0/R)}{\lambda}$(17)
Using Equation 16,
$\lambda = \dfrac{\loge 2}{\tau} = \dfrac{0.693}{\tau}$(Eqn 16)
to eliminate λ we obtain:
$t = \tau\left[\dfrac{\loge (R_0/R)}{\loge 2}\right]$(18)
where τ is the half-life.
Question T12
A sample of cedar wood taken from the Egyptian pyramid of Sneferu has a specific activity from 146C decay corresponding to 55% of the present natural level. How old is the sample? (You should assume that the natural level has been constant over the time concerned.)
Answer T12
The age in terms of half–lives of 146C is given by Equation 18,
$t = \tau\left[\dfrac{\loge (R_0/R)}{\loge 2}\right]$(Eqn 18)
i.e.
$t = \rm 5730\left(\dfrac{loge(100/55)}{\loge 2}\right)\,years = 4942\,years$
We should always be concerned about the reliability of any physical measurement. One limiting factor in this case is our ability to measure the very low activities that the very old specimens show. As a rough measure, after about ten half–lives have elapsed the activity will be too weak to measure accurately. This gives an upper time limit of the order of 50 thousand years beyond which it would be unwise to rely on radiocarbon dating.
The primary limitation, though, concerns our knowledge of R0 and relates to the assumption that the proportion of 146C in the atmosphere has been constant over a very long period. We can check this by comparing the radiocarbon dates of suitable objects with dates found by other, independent, means. For example, the objects being dated may be paper or papyrus documents whose dates are known, or there may be documentary evidence for the dates of other artefacts. Broadly speaking, such checks support the acceptance of a fairly uniform level of 146C and thus indicate a fairly constant flux of cosmic rays.
There is, however, a lower age limit to the use of carbon dating because of human intervention. The burning of fossil fuels in much larger amounts since about the middle of the 18th century has significantly reduced the proportion of 146C in the atmosphere. This is because these fuels contain negligible amounts of 146C, containing 126C almost exclusively. Also, the testing of nuclear weapons in the atmosphere in the 1950s and 1960s approximately doubled the rate of production of 146C during these decades.
3.3 Potassium/argon dating
As we noted above, there is an upper age limit of about 50 thousand years for radiocarbon dating. To a geologist wishing to date a rock sample this is a very short time! Fortunately there are other decays with much longer half–lives that may be used for dating geological samples. One is the β+–decay of potassium-40 to argon-40:
4019K → 4018Ar + e+ + νe
which has a half–life of 1.3 × 109 years. Another is the β−–decay of rubidium-87 to strontium-87:
8737K → 8738Ar + e− + ν−e
which has a half–life of 4.8 × 1010 years. In either case, the ratio of daughter nuclei to parent nuclei in a sample of rock gives a measure of its age. The method relies on four assumptions:
- when the rock solidified (which we shall call time t = 0) a certain number of parent nuclei, NP(0), were trapped;
- at that time there were no daughter nuclei present, i.e. ND(0) = 0;
- no parent or daughter nuclei have escaped from the sample since;
- daughter nuclei have been created within the sample only by the one decay process and not as a result of some other radioactive decay.
If all the above conditions are satisfied, then for times t > 0,
NP(0) = NP(t) + ND(t)
since the decay of a parent nucleus (4019K, for instance) leads to the creation of a daughter nucleus (4018Ar in this case), i.e. the number of parent plus daughter nuclei is constant. We also know, from Equation 14, that NP(t) = NP(0)e−λt. This allows us to find a relationship between time t and the ratio ND/NP. Combining our two expressions we find:
NP(t) = NP(0) e−λt = [NP(t) + ND(t)] e−λt
i.e.NP(t) eλt = [NP(t) + ND(t)]
and hence
${\rm e}^{\lambda t} = \left[1 + \dfrac{N_{\rm D}(t)}{N_{\rm P}(t)}\right]$
If we take natural logarithms of both sides and then divide by λ, we find
$t = \dfrac1\lambda\left[1 + \dfrac{N_{\rm D}(t)}{N_{\rm P}(t)}\right]$
Using Equation 16,
$\lambda = \dfrac{\loge 2}{\tau} = \dfrac{0.693}{\tau}$(Eqn 16)
to substitute for λ, we obtain the age in terms of the half–life of the parent nucleus:
$t = \dfrac{\tau}{\loge 2}\left[1 + \dfrac{N_{\rm D}(t)}{N_{\rm P}(t)}\right]$(19)
Question T13
A sample of rock is thought by geologists to be 3.5 billion (3.5 × 109) years old. What argon/potassium ratio is expected for the sample?
Answer T13
We substitute the expected age into Equation 19,
$t = \dfrac{\tau}{\loge 2}\left[1 + \dfrac{N_{\rm D}(t)}{N_{\rm P}(t)}\right]$(Eqn 19)
and put X = ND/NP.
$3.5\times10^9 = \dfrac{1.3\times10^9}{\loge 2}\loge(1+X)$
orloge (1 + X) = 3.5 × 0.693/1.3 = 1.87.
So1 + X = e1.87 = 6.5, so X = 5.5 and ND/NP = 5.5.
4 Closing items
4.1 Module summary
- 1
-
Unstable (radioactive) nuclei undergo alpha-decayα–, beta-decayβ– or gamma-decayγ–decay. alpha-particleα–particles are $\rm^2_4He$ nuclei; beta minus-particleβ−–particles are electrons, beta plus-particleβ+–particles are positronpositrons; gamma-rayγ–rays are energetic photons of electromagnetic radiation.
- 2
-
The position of an unstable nucleus with respect to the nuclear stability line determines its likely mode(s) of decay.
- 3
-
Any given β–decay produces β–particles with a continuous range of energies up to a maximum. This implies that another particle is emitted during β–decay. The neutrino was postulated (and later confirmed experimentally) to fulfil this role.
- 4
-
β–decay arises from the ‘decay’ of a neutron to a proton (β−–decay) or vice versa (β+–decay) within a nucleus. In addition to the daughter nucleus and the β–particle a neutrino (β+–decay) or an antineutrino (β−–decay) is emitted during the decay of the parent nucleus.
- 5
-
An antiparticle has the same mass as its corresponding particle, but is opposite in other respects (e.g. its charge has the same magnitude but opposite sign).
- 6
-
An excited nucleus can exist in a number of different states, each characterized by its own particular energy. These energies can be displayed on an energy level diagram. γ–decay is the result of a transition from an excited state of the nucleus to a state of lower energy. The energy of a γ–ray emitted in such a transition is given by the energy difference between the two nuclear states involved and is related to the frequency of the γ–radiation through the Planck formula E = hf.
- 7
-
α–, β– and γ–rays are all ionizing radiationionizing radiations. α–radiation most readily loses energy via ionization so it has the shortest range in matter, γ–radiation is absorbed most weakly and has the greatest range in matter, with the intensity in a beam falling exponentially with distance travelled.
- 8
-
The daughter nuclei arising from the decay of heavy parent nuclei are usually themselves unstable. A decay chain continues until a stable daughter nucleus is produced. There are four naturally–occurring decay chains.
- 9
-
Both the activity and the number of parent nuclei in a sample of a radioactive isotope decay exponentially with time:
N (t) = N0 e−λt(Eqn 14)
R (t) = R0 e−λt(Eqn 15)
- 10
-
The time τ for activity or number of radionuclei to fall to one–half of the initial value is called the half-life of the radionuclide. The half–life is independent of the initial value of activity or number of nuclei:
$\tau = \dfrac{\loge }{\lambda}$
- 11
-
Any radioactive decay can be characterized either by its half–life or its decay constant. These two values are related to each other and are unaffected by the physical or chemical environment of the radionuclide.
- 12
-
Radioactive decay can be used to date objects of organic origin (radiocarbon dating) or geological specimens (potassium/argon dating).
4.2 Achievements
- A1
-
Having completed this module, you should be able to:
Define the terms that are emboldened and flagged in the margins of this module.
- A2
-
State the properties of α–, β– and γ–radiation and state how α–, β– and γ–decay changes the mass number and atomic number of a nucleus.
- A3
-
Calculate the kinetic energies of the products of α–decay from a stationary nucleus and describe the physical principles underlying the calculation.
- A4
-
Describe the underlying β−– and β+–decay processes and explain why the neutrino (or antineutrino) was postulated.
- A5
-
State how a particle differs from its partner antiparticle.
- A6
-
Calculate the energy of a γ–ray photon given its frequency, or vice versa.
- A7
-
Give a general account of the absorption of α–, β– and γ–radiation in matter.
- A8
-
Calculate the reduction in intensity of a γ–ray beam by a specified thickness of a material, given the attenuation coefficient.
- A9
-
Use the activity law to calculate the activity of a radioactive sample after given times.
- A10
-
Calculate the activity of a given mass of a radionuclide of known half-life.
- A11
-
State the basic principles underlying the techniques of radiocarbon dating and potassium/argon dating, and state the main limitations of each technique.
- A12
-
Calculate sample ages using radiocarbon and potassium/argon dating information.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
4.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions each of which tests one or more of the Achievements.
Question E1 (A2)
State the possible types of decay of unstable nuclei. For each, say what is produced in addition to the daughter nucleus.
Answer E1
α–decay: the emission of a 42He nucleus (see Subsections 2.1 and 2.2).
β−–decay: the emission of an electron and an electron antineutrino.
β+–decay: the emission of a positron and an electron neutrino (see Subsections 2.1 and 2.3).
γ–decay: emission of a high energy photon of electromagnetic radiation (see Subsections 2.1 and 2.5).
Question E2 (A3)
For the α–decay of 21686Rn the Q–value is 8.16 MeV. What is the initial kinetic energy of the daughter polonium nucleus?
Answer E2
From Equation 3,
$K_{\rm D} \approx Q\left(\dfrac{4}{A_{\rm p}}\right)$(Eqn 3)
the fraction of the Q–value carried away by the daughter nucleus when AP = 216 is 4/216 and:
$K_{\rm D} = \rm 8.16\left(\dfrac{4}{216}\right)\,MeV = 0.15\,MeV = 15\,keV$
(Reread Subsection 2.2 if you had difficulty with this question.)
Question E3 (A4)
Write down the processes underlying both types of β–decay. What features of the decay lead to the postulation of the neutrino (or antineutrino)?
Answer E3
The underlying process for β−–decay is n → p + e− + ν−e; for β+–decay it is p → n + e+ + νe.
The neutrino (or antineutrino) is postulated since the positron (or electron) from a given decay has a range of energies – it does not have the unique energy characteristic of a two–body decay. Also, neither energy nor momentum would be conserved without the postulation of the neutrino.
(Reread Subsection 2.3 if you had difficulty with this question.)
Question E4 (A5)
A certain particle called a pion is denoted π+. Suggest a suitable symbol for its antiparticle (other than π+ ). Give a reason for your suggestion. What will be the relationship between the masses of the π+ and its antiparticle?
Answer E4
The antiparticle of the π+ (which has positive charge) is the π− (which has negative charge of equal magnitude). The particle and antiparticle have equal masses.
(Reread Subsection 2.3 if you had difficulty with this question.)
Question E5 (A6)
What is the frequency corresponding to a 10 MeV γ–ray photon?
Answer E5
The frequency f is given by the Planck formula, E = hf.
Therefore$f = \rm \dfrac{10\,MeV\times1.6\times10^{-13}\,J\,(MeV)^{-1}}{6.626\times10^{-34}\,J\,s} = 2.41\times10^{21}\,Hz$
(Reread Subsection 2.5 if you had difficulty with this question.)
Question E6 (A2 and A7)
How is energy transferred from α–, β−– and γ–radiation to matter? What, in general terms, determines the rate of absorption?
Answer E6
All the radiations interact with the (negatively charged) electrons in the material through which they are passing and cause ionization.
The α–particle has two units of positive charge and a mass comparable to atoms. A typical α–particle readily transfers energy but is deflected little by collisions with electrons and so has a well–defined but very short range, of the order of a few micrometres.
A β−–particle is much less massive than an α–particle and so is more readily deflected by collisions with electrons and has a less well–defined range; it transfers energy less readily than an α–particle and so has greater range in matter, of the order of a few tens of micrometres.
γ–ray photons are least efficient at causing ionization so lose energy at the lowest rate and have the greatest range; γ–rays may penetrate several tens of centimetres of matter.
(Reread Subsections 2.2, 2.3 and 2.5 if you had difficulty with this question.)
Question E7 (A8)
What thickness of lead will halve the intensity of a 10 MeV beam of γ–rays? The attenuation coefficient is 0.06 mm−1.
Answer E7
Use Equation 10,
I (x) = I0 e−μx(Eqn 10)
with $I = \frac12I_0$:
$x = \dfrac{\loge 2}{\mu} = \rm \dfrac{0.693}{0.06\,mm^{-1}} = 12\,mm$
(Reread Subsection 2.5 if you had difficulty with this question.)
Question E8 (A9)
The half–life of 21283Bi is 60.6 min. How long will it be before the activity of a 3.0 GBq source has decreased to 0.30 MBq?
Answer E8
Use Equations 15 and 16:
The activity law R (t) = R0 e−λt(Eqn 15)
$\lambda = \dfrac{\loge 2}{\tau} = \dfrac{0.693}{\tau}$(Eqn 16)
R (t) = R0 e−λt and λ = loge 2/τ
$\lambda t = \loge\left(\dfrac{3.0\times10^9}{3.0\times10^5}\right) = 9.21$
and$\lambda = \rm \dfrac{0.693}{60.6\,min} = 0.0114\,min^{-1}$
so$t = \rm \dfrac{9.21}{0.0114\,min^{-1}} = 808\,min = 13.5\,h$
(Reread Subsection 3.1 if you had difficulty with this question.)
Question E9 (A10)
Estimate the activity, in Bq and in Ci, of 0.1 μg of 21684Po. The half–life is 0.15 s.
(Use 1 u = 1.66 × 10−27 kg and 1 Ci = 37.0 GBq.)
Answer E9
From Equation 16,
$\lambda = \dfrac{\loge 2}{\tau} = \dfrac{0.693}{\tau}$(Eqn 16)
the decay constant for the polonium isotope is:
$\lambda = \rm \dfrac{\loge 2}{0.15\,s} = 4.62\,s^{-1}$
0.1 μg = 10−7 g = 10−10 kg, so the number of nuclei in the sample is
$N_0 = \rm \dfrac{10^{-10}\,kg}{(216\,u)\times1.66\times10^{-27}\,kg\,u^{-1}} = 2.79\times10^{14}$
From Equation 11,
R (t) = λN (t)(Eqn 11)
with t = 0, the activity is
R0 = λΝ0 = 4.62 × 2.79 × 1014 s−1 = 1.29 × 106 GBq = 34.9 kCi
(Reread Subsection 3.1 if you had difficulty with this question.)
Question E10 (A11 and A12)
The activity of a sample of charcoal from an ancient fire is found to be 15% of that from freshly made charcoal. Estimate the age of the sample. On what assumptions does the estimate depend?
(The half–life of 146C is 5730 years.)
Answer E10
The age in terms of half–lives of 146C is given by Equation 18:
$t = \tau\left[\dfrac{\loge (R_0/R)}{\loge 2}\right]$(Eqn 18)
$t = \rm 5730\left(\dfrac{\loge(100/15)}{\loge 2}\right)\,years = 1.6\times10^4\,years$
This estimate rests on the assumption that the ratio of 146C to 126C in the atmosphere has remained constant.
(For a sample of this age the validity of this assumption cannot be tested. With changes known to have been caused by humans in the last one hundred or so years, it would be wise to cross check against an old sample of known age rather than a sample of freshly made charcoal.)
(Reread Subsection 3.2 if you had difficulty with this question.)
Question E11 (A12)
In a specimen of rock the argon/potassium ratio is 2.70. Estimate the age of the rock.
(The half–life of 4019K is 1.3 × 109 years.)
Answer E11
The relationship between the age t and the argon/potassium ratio X is given by Equation 19,
$t = \dfrac{\tau}{\loge 2}\left[1 + \dfrac{N_{\rm D}(t)}{N_{\rm P}(t)}\right]$(Eqn 19)
$t = \rm \dfrac{1.3\times10^9}{\loge 2}\loge(3.7)\,years = 2.5\times10^9\,years$
(Reread Subsection 3.3 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 4Closing items.