1. Theory
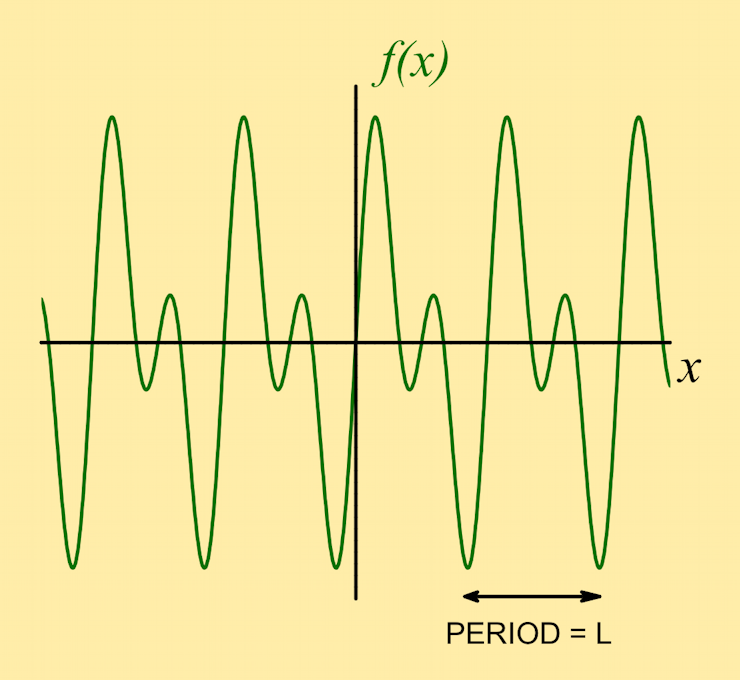
A graph of periodic function ƒ(x), that has period L, exhibits the same pattern every L units along the x-axis, so that f(x + L) = f(x) for every value of x. If we know what the function looks like over one complete period, we can thus sketch a graph of the function over a wider interval of x (that may contain many periods). This property of repetition defines a fundamental spatial frequency k = 2π ⁄ L that can be used to give a first approximation to the periodic patternƒ(x):
ƒ(x) ≃ c1 sin(kx + α1)
= a1 cos(kx) + b1 sin(kx)
- where symbols with subscript 1 are constants that determine the amplitude and phase of this first approximation. |
 |
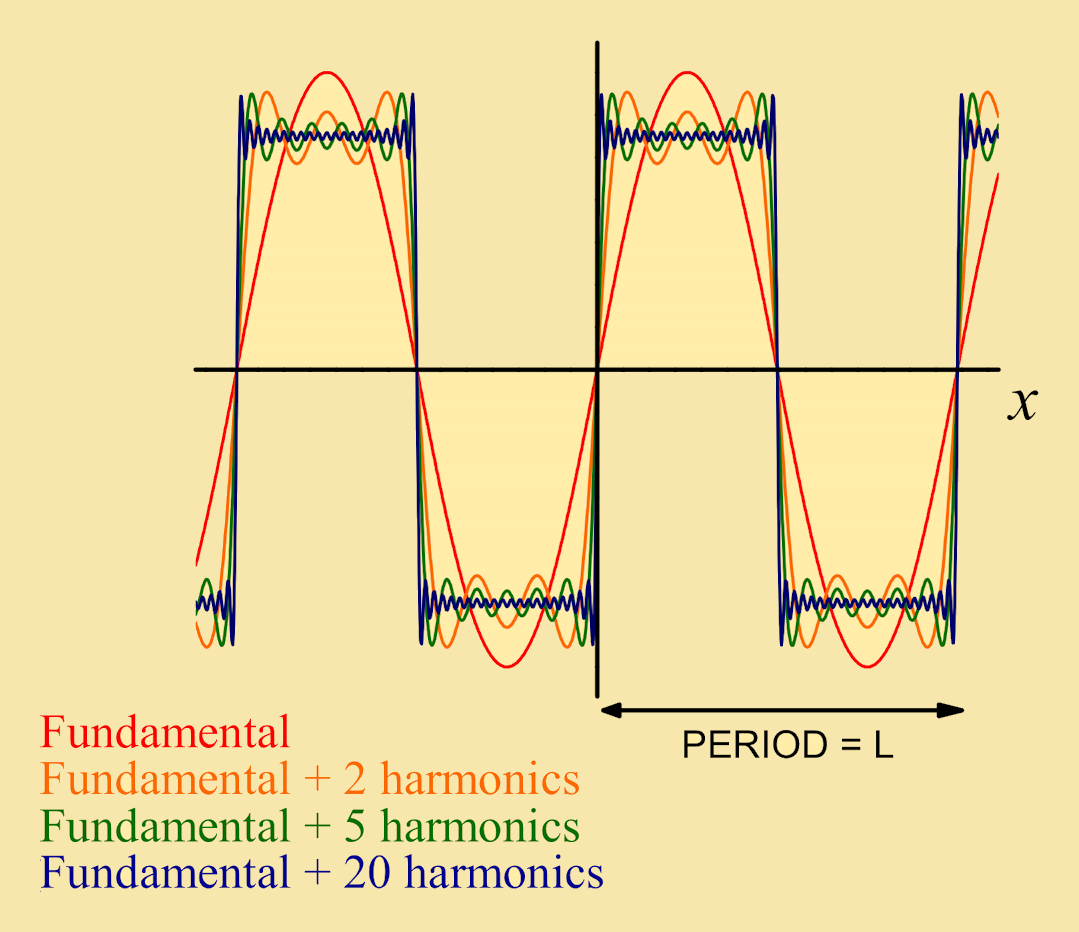 |
A much better approximation of the periodic pattern ƒ(x) can be built up by adding an appropriate combination of harmonics to this fundamental (sine-wave) pattern. For example, adding: c2 sin(2kx + α2) = a2 cos(2kx) + b2 sin(2kx) (the 2nd harmonic) c3 sin(3kx + α3) = a3 cos(3kx) + b3 sin(3kx) (the 3rd harmonic) Here, symbols with subscripts are constants that determine the amplitude and phase of each harmonic contribution. One can even approximate a square-wave pattern with a suitable sum that involves a fundamental sine-wave plus a combination of harmonics of this fundamental frequency. Such sums are called Fourier series. |
In this Tutorial, we consider working out Fourier series for functions f(x) with period L = 2π. Their fundamental frequency is then k = 2πL = 1, and their Fourier series representations involve terms like:
| a1cos x | , | b1sin x |
| a2cos 2x | , | b2sin 2x |
| a3cos 3x | , | b3sin 3x |
We also include a constant term a0 ⁄ 2 in the Fourier series. This allows us to represent functions that are, for example, entirely above the x−axis.
The higher the number of harmonics included, the closer our series represents the function ƒ(x):
| ƒ(x) = a0 ⁄ 2 | + a1cos x + a2cos 2x + a3cos 3x + ... |
| + b1sin x + b2sin 2x + b3sin 3x + ... |
A more compact way of writing the Fourier series of a function ƒ(x), with period 2π, uses the variable subscript n = 1, 2, 3, ...
We need to work out the Fourier coefficients (a0, an and bn) for given functions f(x). This process is broken down into three steps:
| STEP ONE | Compute constant coefficient: | a0 = 1π ∫2πƒ(x) dx | |
| STEP TWO | Compute cosine coefficients: | an = 1π ∫2πƒ(x) cos nx dx | |
| STEP TWO | Compute sin coefficients: | bn = 1π ∫2πƒ(x) sin nx dx |
- where integrations are over a single interval in x of L = 2π.
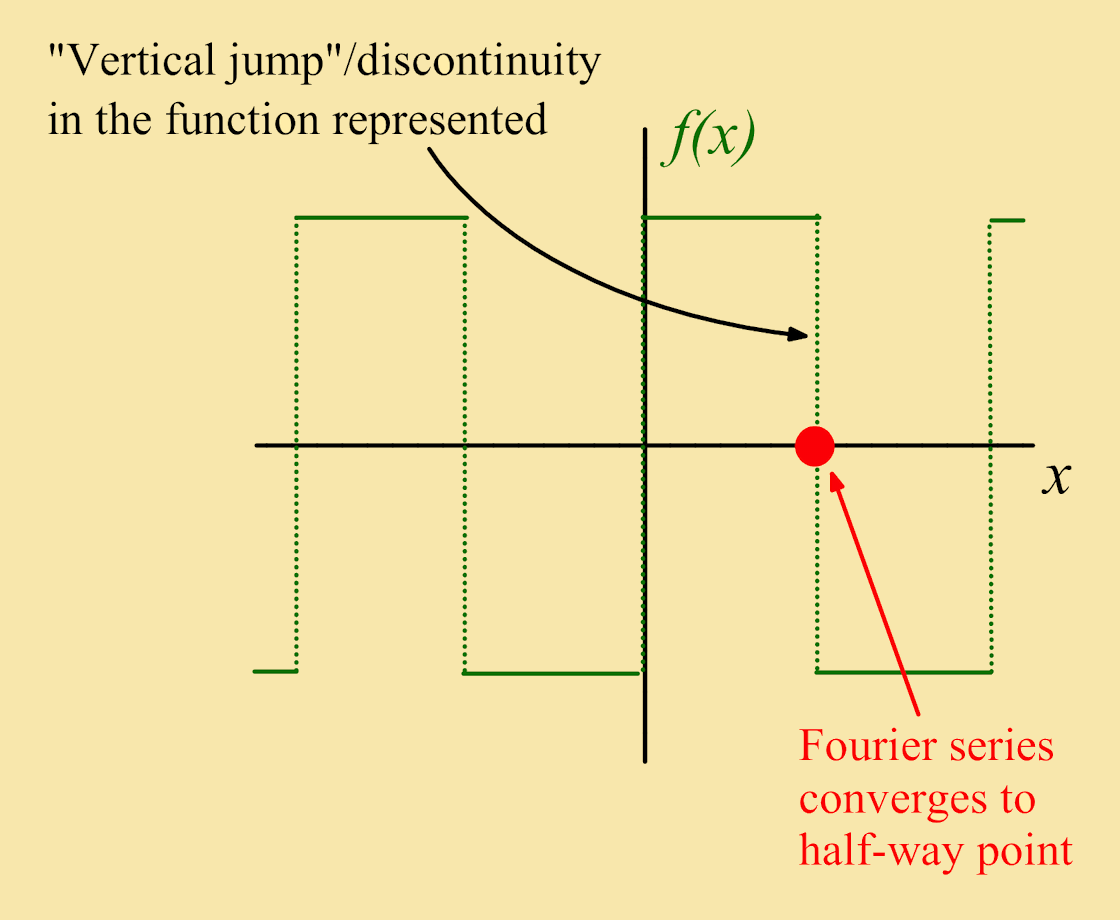
Finally, specifying a particular value of x = x1 in a Fourier series, gives a series of constants that should equal f(x1). However, if f(x) is discontinuous at this value of x, then the series converges to a value that is half-way between the two possible function values, as the figure on the right shows. |
 |
2. Exercises
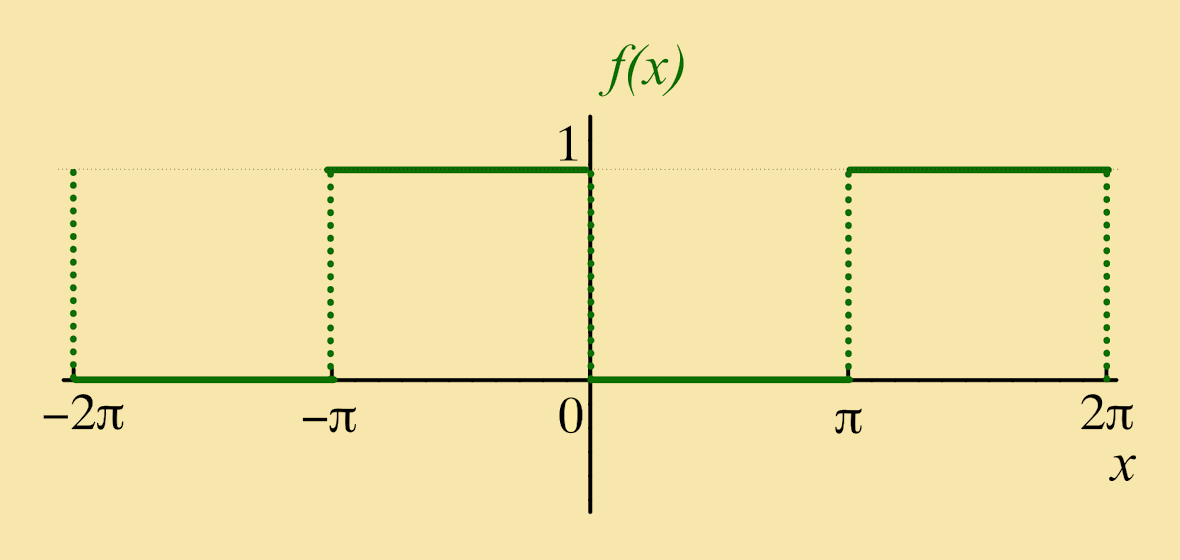
Exercise 1: Let ƒ(x) be a function of period 2π such that:
| ƒ(x) = { | 1: −π < x < 0 0: 0 < x < π |
Solution:
Solution:
STEP ONE| a0 = 1π π ∫ −π ƒ(x) dx | = | 1π 0 ∫ −π ƒ(x) dx + 1π π ∫ 0 ƒ(x) dx |
| = | 1π 0 ∫ −π 1⋅dx + 1π π ∫ 0 0⋅dx | |
| = | 1π 0 ∫ −π dx | |
| = | 1π [x]0−π dx | |
| = | 1π (0 − (−π)) | |
| = | 1π ⋅(π) | |
| i.e. a0 | = | 1 |
STEP TWO
| an = 1 π π ∫ π ƒ(x) cos nx dx | = | 1π 0 ∫ −π ƒ(x) cos nx dx + 1π π ∫ 0 ƒ(x) cos nx dx |
| = | 1π 0 ∫ −π 1⋅cos nx dx + 1 π π ∫ 0 0⋅cos nx dx | |
| = | 1π 0 ∫ −π cos nx dx | |
| = | 1π [ sin nxn ] 0 −π = 1nπ [sin nx]0−π | |
| = | 1π (sin 0 − sin (−nπ)) | |
| = | 1π (0 + sin nπ) | |
| i.e. an | = | 1π (0 + 0) = 0 |
STEP THREE
| bn = 1 π π ∫ π ƒ(x) sin nx dx | = | 1π 0 ∫ −π ƒ(x) sin nx dx + 1π π ∫ 0 ƒ(x) sin nx dx | ||||
| = | 1π 0 ∫ −π 1⋅sin nx dx + 1 π π ∫ 0 0⋅sin nx dx | |||||
| i.e. bn | = | 1π 0 ∫ −π sin nx dx = 1π [ − cos nxn ] 0 −π | ||||
| = | − 1nπ [cos nx]0−π = − 1nπ (cos 0 − cos (−nπ)) | |||||
| = | − 1nπ (1 − cos (nπ)) = − 1nπ (1 − (−1)n) see TRIG | |||||
| i.e. bn | = | { | 0: n even − 2nπ: nodd |
since (−1)n = { | 1: n even −1: odd |
|
We now have that ƒ(x) = a02 + ∞ Σ n=1 [ ancos nx + bnsin nx ]
with the three steps giving:
| a0 = 1, an = 0 and and bn = { | 0: n even − 2nπ: nodd |
It may be helpful to construct a table of values of bn:
| n | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| bn | − 2π | 0 | − 2π (13) | 0 | − 2π (15) |
Substituting our results now gives the required series:
Solution: Comparing the given series with:
we clearly require sin x = 1, sin 3x = −1, sin 5x = 1, sin 7x = −1, etc.
The first condition sin x = 1 suggests trying x = π 2. This choice gives:
| sin π2 | + | 1 3 sin 3π 2 | + | 1 5 sin 5π 2 | + | 1 7 sin 7π 2 | |
| i.e. | 1 | − | 1 3 | + | 1 5 | − | 1 7 |
From the figure we see that ƒ(π 2) = 0.
Picking x = π 2 this gives:
| 0 | = | 12 − 2 π [ | sin π2 | + | 13 sin 3π2 | + | 15 sin 5π2 | − | 17 sin 7π2 | + ... ] | |
| i.e. | 0 | = | 12 − 2 π [ | 1 | − | 13 | + | 15 | − | 17 | + ... ] |
A little manipulation then gives the series representation of π4:
Click on questions to reveal their solution
Exercise 2: Let ƒ(x) be a function of period 2π such that:
| ƒ(x) = | { | 0: −π < x < 0 x: 0 < x < π |
Solution:
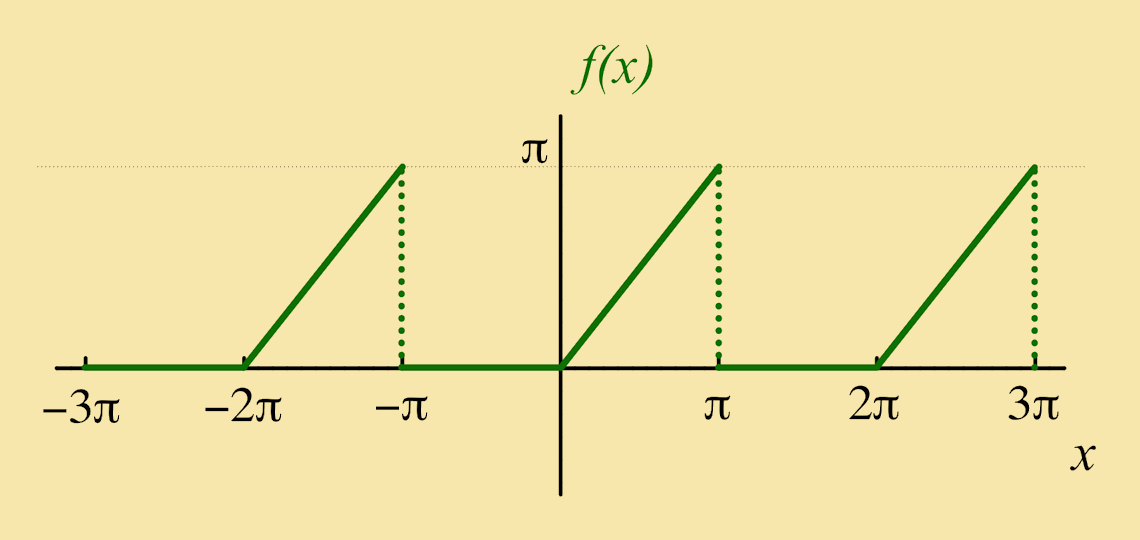
Solution:
STEP ONE| a0 = 1π π ∫ π ƒ(x) dx | = | 1π 0 ∫ −π ƒ(x) dx + 1π π ∫ 0ƒ(x) dx |
| = | 1π 0 ∫ −π0⋅dx + 1π π ∫ 0x dx | |
| = | 1π [ x22 ] π 0 | |
| = | 1π ( π22 − 0 ) | |
| i.e. a0 | = | π2 |
STEP TWO
| an = 1 π π ∫ −π ƒ(x) cos nx dx | = | 1π 0 ∫ −π ƒ(x) cos nx dx + 1π π ∫ 0 ƒ(x) cos nx dx | ||
| = | 1π 0 ∫ −π0⋅cos nx dx + 1 π π ∫ 0x cos nx dx | |||
| i.e. an = 1 π π ∫ −0 x cos nx dx | = | 1π {[ x sin nxn ] π 0 − π∫ 0sin nxn dx} - using integration by parts | ||
| i.e. an | = | 1π {( π sin nxn − 0 ) − 1n [ − cos nxn ] π 0 } | ||
| = | 1π { (0 − 0) + 1n2 [cos nx] π0 } | |||
| = | 1πn2 {cos nπ − cos 0} = 1πn2 {(−1)n − 1} | |||
| i.e. an | = | { | 0: n even − 2πn2: nodd; |
see TRIG |
STEP THREE
| bn = 1 π π ∫ π ƒ(x) sin nx dx | = | 1π 0 ∫ −π ƒ(x) sin nx dx + 1π π ∫ 0 ƒ(x) sin nx dx | |||
| = | 1π 0 ∫ −π0⋅sin nx dx + 1 π π ∫ 0x sin nx dx | ||||
| i.e. bn = 1π π ∫ 0x sin nx dx | = | 1π {[ x(− cos nxn) ] π 0 − π∫ 0(−cos nxn dx} - using integration by parts | |||
| = | 1π { − 1n [x cos nx] π0 + 1n π∫ 0cos nx dx } | ||||
| = | 1π { − 1n (π cos nx − 0) + 1n [ sin nxn ] π 0 } | ||||
| = | − 1n (−1)n + 1πn2(0 − 0) - see TRIG | ||||
| = | − 1n (−1)n | ||||
| i.e. bn | = | { | − 1n : n even + 1n: nodd |
||
We now have ƒ(x) = a02 + ∞ Σ n=1 [ ancos nx + bnsin nx ]
| - where: a0 = π2, an = { | 0: n even − 2πn2: nodd |
and bn = { | − 1n : n even + 1n: nodd |
Constructing a table of values gives:
| n | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| an | − 2π | 0 | − 2π⋅132 | 0 | − 2π⋅152 |
| bn | 1 | − 12 | 13 | − 14 | 15 |
This table of coefficients gives:
+ sin x − 1 2 sin 2x + 1 3 sin 3x − ...
and we have found the required series.
Solution:
(i) Comparing the given series with:
we see that the required series of constants does not involve terms like 132, 152, 172, ... so we need to pick a value of x that sets the cos nx terms to zero. The Trig section shows that cos nπ = 0 when n is odd, and we note also that the cos nx terms in the Fourier series all have odd n:
i.e. cos π2 = cos 3π2 = cos 5π2 = ... = 0
Setting x = π 2 in the series for ƒ(x) gives:
| ƒ(π 2) | = | π 4 − 2 π [ cos π2 + 1 32 cos 3π2 + 1 52 cos 5π2 + ...] |
| + [ sin π2 − 1 2 sin 2π2 + 1 3 sin 3π2 − 1 4 sin 4π2 + 1 5 sin 5π2 − ... ] | ||
| = | π 4 − 2 π [ 0 + 0 + 0 + ... ] | |
| + [ 1 − 1 2 sin π + 1 3(−1) − 1 4 sin 2π + 1 5(1) − ... ] |
From the figure we see that ƒ (π 2) = π 2 , so that:
| π2 | = | π4 + 1 − 13 + 15 − 17 + ... | |
| i.e. | π4 | = | 1 − 13 + 15 − 17 + ... |
(ii) Compare the given series with:
This time, we want to use the coefficients of the cos nx terms, and the same choice of x needs to set the sin nx terms to zero.
Picking x = 0 gives:
We also note from the figure that ƒ(x) = 0 when x = 0.
Setting x = 0 gives:
| 0 | = | π 4 − 2 π [ cos 0 + 1 32 cos 0 + 1 52 cos 0 + 1 72 cos 0 + ... ] + 0 − 0 + 0 − 0 − ... |
We then find that:
| 2π [ 1 + 132 + 152 − 172 + ... ] | = | π 4 |
| and 1 + 132 + 152 − 172 + ... ] | ||
| = | π2 8 |
Click on questions to reveal their solution
Exercise 3: Let ƒ(x) be a function of period 2π such that:
| ƒ(x) = | { | x: 0 < x < π π: π < x < 2π |
Solution:
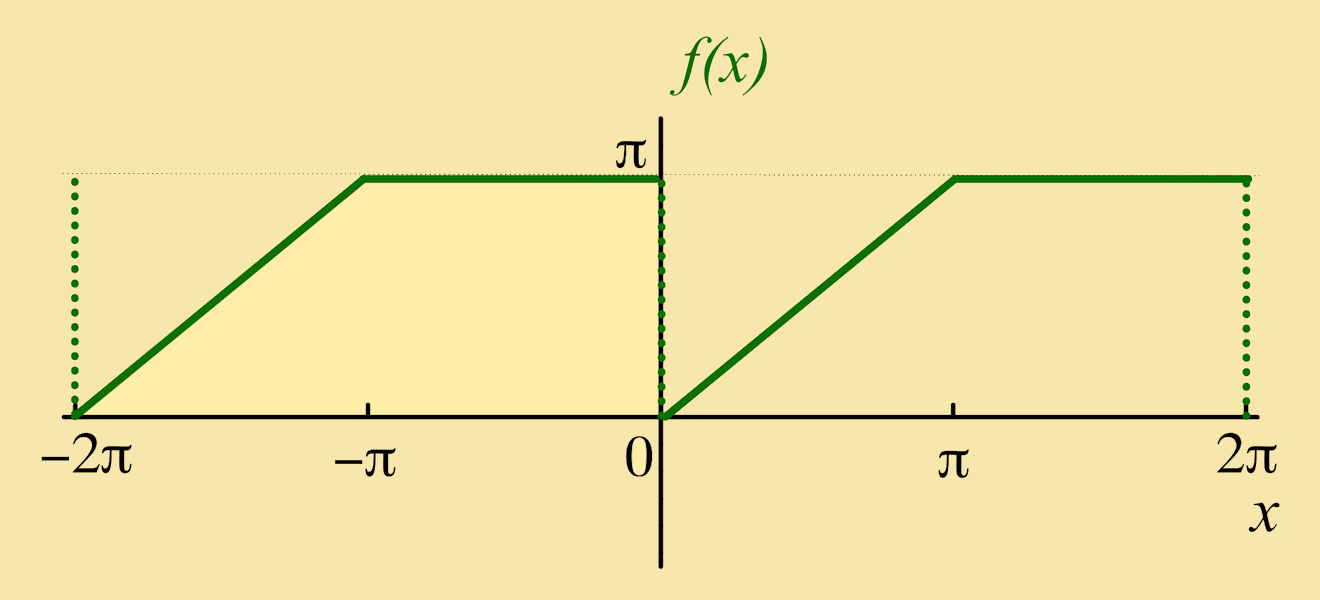
Solution:
STEP ONE| a0 = 1π 2π ∫ 0 ƒ(x) dx | = | 1π π ∫ 0 ƒ(x) dx + 1π 2π ∫ πƒ(x) dx |
| = | 1π π ∫ 0x dx + 1π 2π ∫ ππ dx | |
| = | 1π [ x22 ] π 0 + ππ [x] 2π π | |
| = | 1π ( π22 − 0) + (2π − π) | |
| = | π2 + π | |
| i.e. a0 | = | 3π2 |
STEP TWO
| an | = | 1π π ∫ 0 ƒ(x) cos nx dx | |
| = | 1π π ∫ 0 x cos nx dx + 1π 2π ∫ π π cos nx dx - use integration by parts on 1st part | ||
| = | 1π { [ x sin nxn ] π 0 − π∫ 0 sin nxn dx } + ππ [ sin nxn ] 2π π | ||
| = | 1π [ 1n ( π sin nx − 0⋅sin n0 ) − [ − cos nxn2 ] π 0 + 1n (sin n2π − sin nπ) | ||
| i.e. an | = | 1π [ 1n (0 − 0) + ( cos nxn2 − cos 0n2 ] + 1n (0 − 0) | |
| = | 1n2π (cos nπ − 1) - see TRIG | ||
| = | 1n2π ((−1)n − 1) | ||
| i.e. an | = | { | 1n2π: n odd 0: neven; |
STEP THREE
| bn | = | 1π π ∫ 0 ƒ(x) sin nx dx | |
| = | 1π π ∫ 0 x sin nx dx + 1π 2π ∫ π π sin nx dx - use integration by parts on 1st part | ||
| = | 1π { [ x ( −cos nxn ) ] π 0 − π∫0 ( − cos nxn ) dx } + ππ [ − cos nxn ] 2π π | ||
| = | 1π { ( −π cos nπn + 0 ) + [ sin nxn2 ] π 0 } − 1n (cos 2nπ − cos nπ) | ||
| = | 1π [ −π(−1)nn + ( sin nπ − sin 0 n2 ) ] − 1n (1 − (−1)n) | ||
| = | − 1n (−1)n + 0 − 1n (1 − (−1)n) | ||
| = | − 1n (−1)n − 1n + 1n (−1)n | ||
| i.e. bn | = | − 1n | |
We now have ƒ(x) = a02 + ∞ Σ n=1 [ ancos nx + bnsin nx ]
| - where: a0 = 3π2, an = { | 0: n even − 2πn2: nodd |
and bn = − 1n |
Constructing a table of values gives:
| n | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| an | − 2π | 0 | − 2π⋅132 | 0 | − 2π⋅152 |
| bn | −1 | −12 | −13 | −14 | −15 |
This table of coefficients gives:
| ƒ(x) | = | 1 2 ( 3π 2 ) | + | ( − 2 π ) | [ cos x + 0⋅cos 2x + 1 32 cos 3x + ... ] |
| + | ( −1 ) | [ sin x + 1 2 sin 2x + 1 3 sin 3x + ... ] | |||
| = | 3π 4 | − | 2 π | [ cos x + 1 32 cos 3x + 1 52 cos 5x + ... ] | |
| − | [ sin x + 1 2 sin 2x + 1 3 sin 3x + ... ] |
and we have found the required series.
Solution:
(i) Compare the given series with:
Here, we want to set the cos nx terms to zero (since their coefficients are 1, 132, 152, ... ). Since cos n π2 = 0 when n is odd, we try setting x = π2 in the series. Note also that ƒ(π2) = π2.
This gives:
(ii) Here, we want zero sin nx terms and to use the coefficients of cos nx. Setting x = 0 eliminates the sin nx terms from the series, and also gives:
The graph of ƒ(x) shows a discontinuity (a "vertical jump") at x = 0. The Fourier series converges to a value that is half-way between the two values of ƒ(x) around this discontinuity, that is, the series will converge to π 2 at x = 0:
Re-arranging the terms, we finally get:
Click on questions to reveal their solution
Exercise 4: Let ƒ(x) be a function of period 2π such that:
Solution:
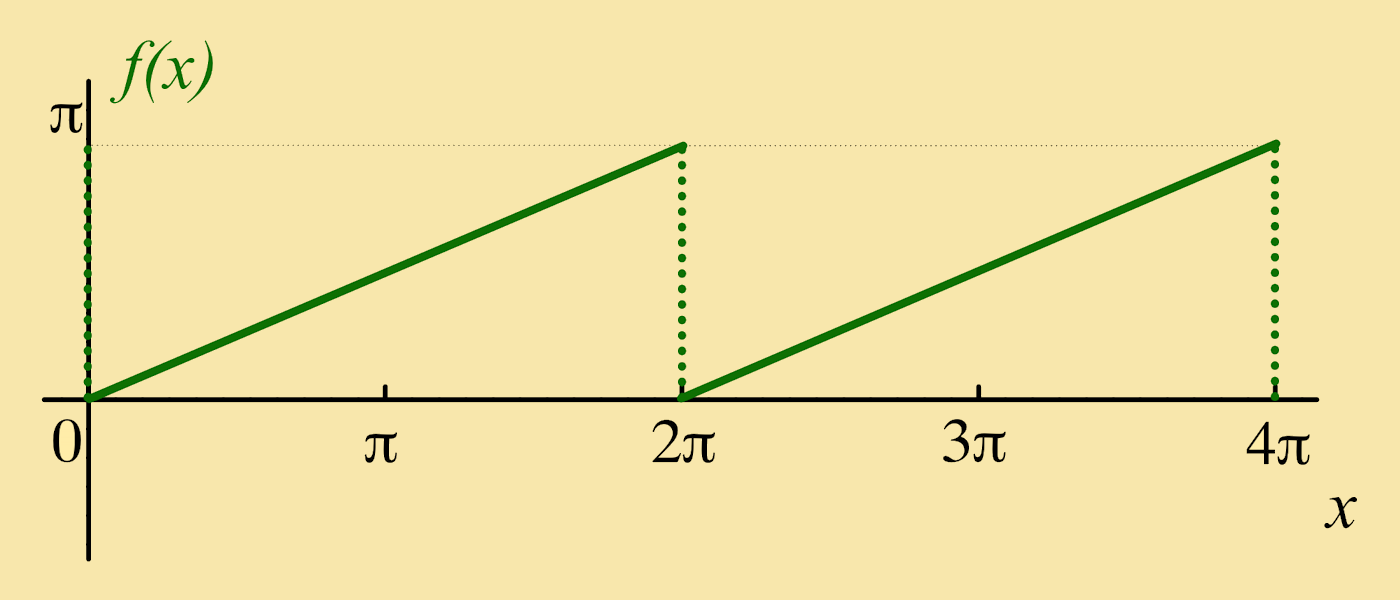
Solution:
STEP ONE| a0 | = | 1π 2π ∫ 0 ƒ(x) dx |
| = | 1π 2π ∫ 0x2 dx | |
| = | 1π [ x24 ] 2π 0 | |
| = | 1π [ (2π)24 − 0] | |
| i.e. a0 | = | π |
STEP TWO
| an | = | 1π 2π ∫ 0 ƒ(x) cos nx dx | |
| = | 1π 2π ∫ 0 ( x2 ) cos nx dx | ||
| = | 12π { [ x sin nxn ] 2π 0 − 1n 2π∫ 0 sin nx dx } - using integration by parts | ||
| = | 12π { ( 2π sin n2πn − 0⋅sin n⋅0n ) − 1n ⋅0} | ||
| = | 12π { (0 − 0) − 1n ⋅0} (see Trig section) | ||
| i.e. an | = | 0 | |
STEP THREE
| bn | = | 1π 2π ∫ 0 ƒ(x) sin nx dx | |
| = | 1π 2π ∫ 0 ( x2 ) sin nx dx = 12π 2π ∫ 0 x sin nx dx | ||
| = | 12π { [ x −cos nxn ] 2π 0 − 1n 2π∫ 0 ( −cos nxn ) dx } - using integration by parts | ||
| = | 12π { 1n (−2π cos n2π + 0) + 1n⋅0 } (see Trig section) | ||
| = | −2π2πn cos n2π | ||
| = | − 1n cos n2π | ||
| i.e. bn | = | − 1n - since 2n is even (see Trig section) | |
We now have ƒ(x) = a02 + ∞ Σ n=1 [ ancos nx + bnsin nx ]
- where: a0 = π2, an = 0 and bn = − 1n
These Fourier coefficients give:
| ƒ(x) | = | π 2 + ∞ Σ n=1 (0 − 1n sin nx) |
| i.e. ƒ(x) | = | π 2 − [ sin x + 1 2 sin 2x + 1 3 sin 3x + ... ] |
Solution:
Setting x = π2 gives ƒ(x) = π4 and:
| π4 | = | π2 − [ 1 + 0 − 13 + 0 + 15 + 0 − ... ] |
| π4 | = | π2 − [ 1 − 13 + 15 − 17 + 19 − ... ] |
| re-arrange: π4 | = | [ 1 − 13 + 15 − 17 + 19 − ... − ] |
| ∴ π4 | = | 1 − 13 + 15 − 17 + 19 − ... |
Click on questions to reveal their solution
Exercise 5: Let ƒ(x) be a function of period 2π such that:
| ƒ(x) = | { | π − x: 0 < x < π 0: π < x < 2π |
Solution:
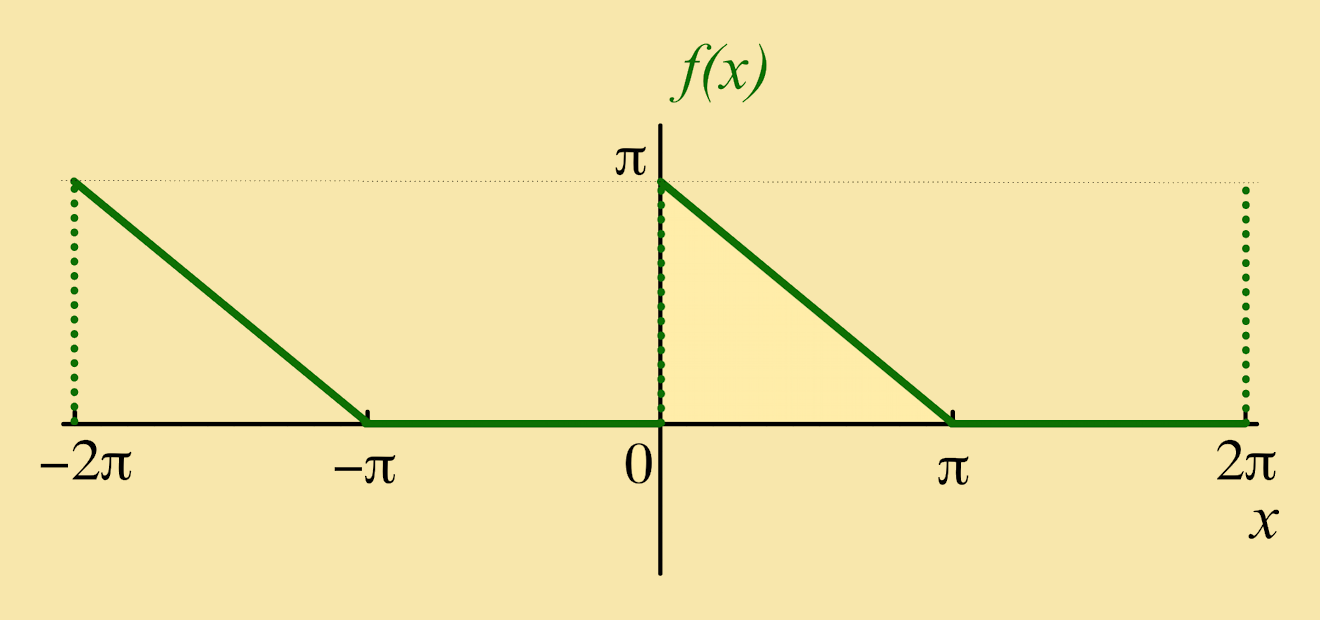
Solution:
STEP ONE| a0 | = | 1π 2π ∫ 0 ƒ(x) dx |
| = | 1π π ∫ 0(π − x) dx + 1π 2π ∫ π0⋅dx | |
| = | 1π [ πx − 12x2 ] π 0 + 0 | |
| = | 1π [ π2 − 12π2 − 0 ] | |
| i.e. a0 | = | π2 |
STEP TWO
| an | = | 1π 2π ∫ 0 ƒ(x) cos nx dx | |
| = | 1π π ∫ 0 (π − x) cos nx dx + 1π 2π ∫ π 0⋅dx - use integration by parts on 1st part | ||
| = | 1π { [ (π − x) sin nxn ] π 0 − π∫ 0 (−1) sin nxn dx } + 0 | ||
| = | 1π { (0 − 0) + π∫ 0 sin nxn dx } (see Trig section) | ||
| = | 1πn [ −cos nxn ] π 0 | ||
| = | 1πn2 (cos nx − cos 0) | ||
| = | 1πn2 ((−1)n − 1) (see Trig section) | ||
| i.e. an | = | { | 0: neven; 2πn2: n odd |
STEP THREE
| bn | = | 1π 2π ∫ 0 ƒ(x) sin nx dx | |
| = | 1π π ∫ 0(π − x sin nx dx + 1π 2π ∫ π 0⋅dx | ||
| = | 1π { [ (π − x)( −cos nxn ) ] π 0 − π∫0 (−1)⋅(− cos nxn ) dx } + 0 | ||
| = | 1π { [ 0 − ( −πn ) ] − 1n⋅0 } (see Trig section) | ||
| i.e. bn | = | 1n | |
In summary, a0 = π2, and the other Fourier coefficients are:
| n | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| an = 2πn2 (for n odd, 0 otherwise) | − 2π | 0 | − 2π⋅132 | 0 | − 2π⋅152 |
| bn = 1n | −1 | −12 | −13 | −14 | −15 |
| ∴ ƒ(x) | = | a02 | + | ∞ Σ n=1 [an cos nx + bn sin nx] |
| = | π 4 | + | 2 πcos x + 2 π 1 32 cos 3x + 2 π 1 52 cos 5x + ... | |
| + | sin x + 1 2 sin 2x + 1 3 sin 3x + 1 4 sin 4x + ... | |||
| i.e. ƒ(x) | = | π 4 | + | 2 π[ cos x + 1 32 cos 3x + 1 52 cos 5x + ... ] |
| + | sin x + 1 2 sin 2x + 1 3 sin 3x + 1 4 sin 4x + ... |
Solution:
Note that, as x → 0, the series converges to the half-way value of π2,
| and then: | π2 | = | π4 + 2π ( cos 0 + 132 cos 3⋅0 + 152 cos 5⋅0 + 172 cos 7⋅0 + ... ) |
| + sin 0 + 12sin 2⋅0 + 13sin 3⋅0 + 14sin 4⋅0 + ... | |||
| π2 | = | π4 + 2π (1 + 132 + 152 + 172+ ...) | |
| re-arranging: | π4 | = | 2π (1 + 132 + 152 + 172 + ...) |
| giving: | π28 | = | 1 + 132 + 152 + 172 + ... |
Click on questions to reveal their solution
Exercise 6: Let ƒ(x) be a function of period 2π such that:
Solution:
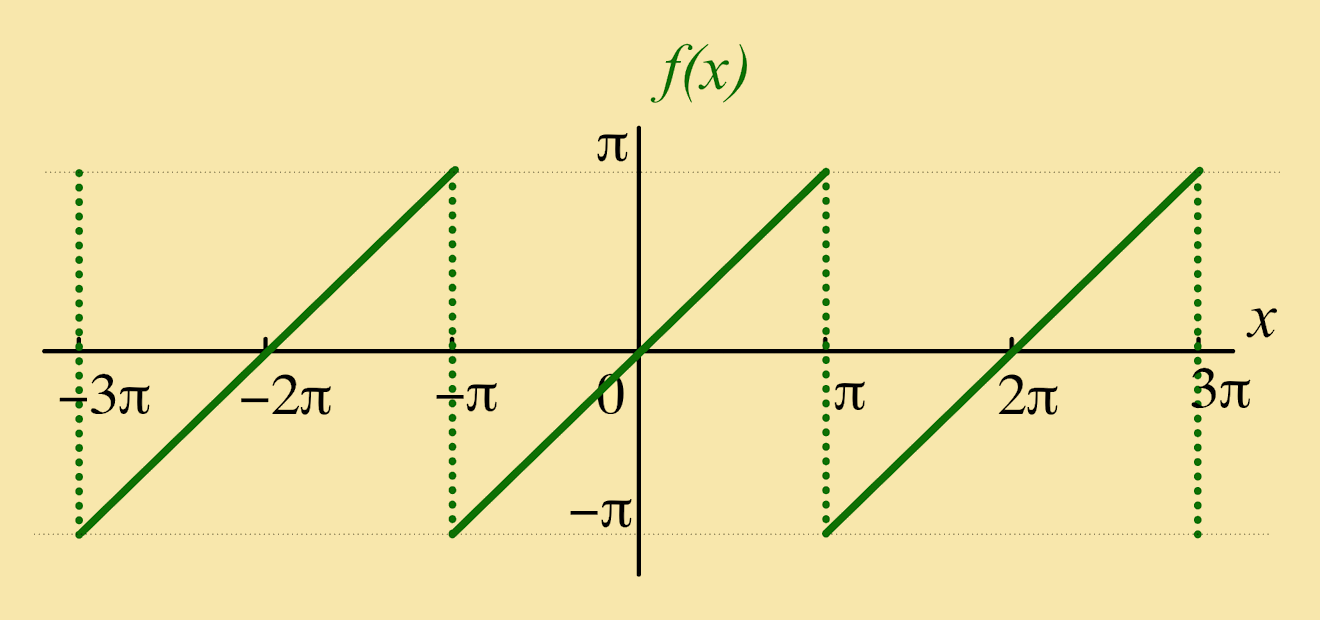
Solution:
STEP ONE| a0 | = | 1π π ∫ −π ƒ(x) dx |
| = | 1π π ∫ −πx dx | |
| = | 1π [x22]π −π | |
| = | 1π ( π22 − π22 ) | |
| i.e. a0 | = | 0 |
STEP TWO
| an | = | 1π π ∫ −π ƒ(x) cos nx dx | |
| = | 1π π ∫ −π x cos nx dx - use integration by parts | ||
| = | 1π { [ x sin nxn ] π −π − π∫ −π (sin nxn) dx } | ||
| = | 1π { 1n (π sin nπ − (−π) sin (−nπ)) − 1n π∫ −πsin nx dx} | ||
| = | 1π { 1n(0 − 0) − 1n⋅0 } - since sin nπ and ∫ 2π sin nx = 0 | ||
| i.e. an | = | 0 | |
STEP THREE
| bn | = | 1π π ∫ −π ƒ(x) sin nx dx | |
| = | 1π π ∫ −πx sin nx dx | ||
| = | 1π { [ −x cos nxn ] π −π − π∫−π (− cos nxn ) dx} | ||
| = | 1π { − 1n [x cos nx] π−π + 1n π∫−π cos nx dx } | ||
| = | 1π { − 1n (π cos nπ − (−π) cos (−nπ)) + 1n⋅0 } | ||
| !! | = | − πnπ (cos nπ + cos nπ) | |
| = | −1n 2 (cos nπ) | ||
| i.e. bn | = | −2n (−1)n | |
We thus have:
with a0 = 0, an = 0, bn = −2n(−1)n and:
| n | 1 | 2 | 3 |
|---|---|---|---|
| bn | 2 | −1 | 23 |
Therefore:
| ƒ(x) | = | b1 sin x + b2 sin 2x + b3 sin 3x + ... |
| i.e. ƒ(x) | = | 2 [ sin x − 1 2 sin 2x + 1 3 sin 3x − ... ] |
and we have found the required Fourier series.
Solution:
Putting x = π2 gives ƒ(x) and:
| π2 | = | 2 [ sin π2 − 12 sin 2π2 + 13 sin 3π2 − 14 sin 4π2 + 15 sin 5π2 − ... ] | |
| this gives: | π2 | = | 2 [ 1 + 0 + 13⋅(−1) − 0 + 15⋅(1) − 17⋅(−1) + ... ] |
| π2 | = | 2 [ 1 − 13 + 15 − 17 + ... ] | |
| i.e. | π4 | = | 1 − 13 + 15 − 17 + ... |
Click on questions to reveal their solution
Exercise 7: Let ƒ(x) be a function of period 2π such that:
Solution:
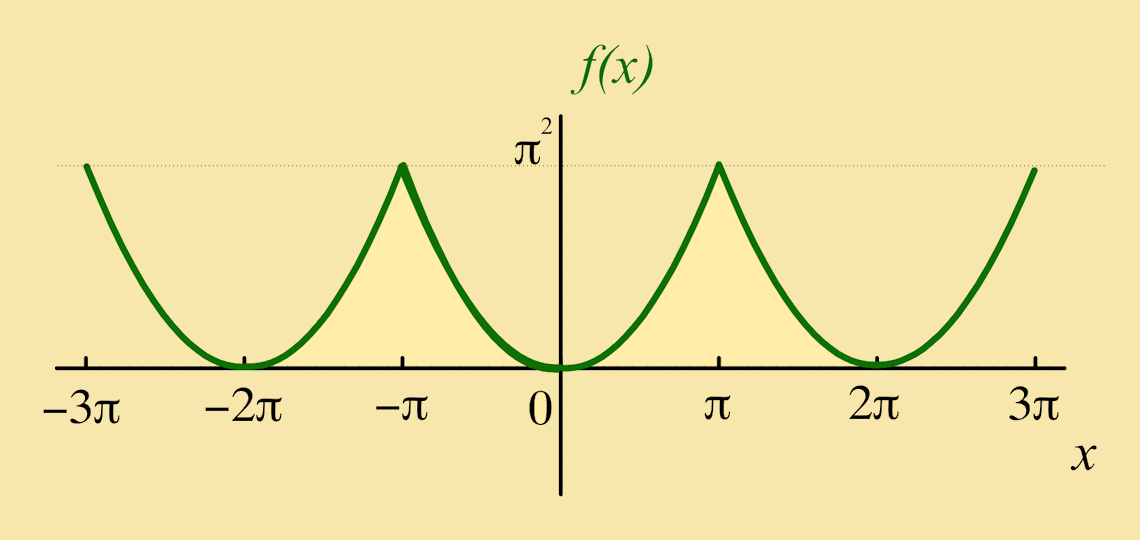
Solution:
STEP ONE| a0 | = | 1π π ∫ −π ƒ(x) dx |
| = | 1π π ∫ −πx2 dx | |
| = | 1π [x33]π −π | |
| = | 1π ( π33 − (π33 )) | |
| = | 1π ( 2π33) | |
| i.e. a0 | = | 2π23 |
STEP TWO
| an | = | 1π π ∫ −π ƒ(x) cos nx dx | |
| = | 1π π ∫ −π x2 cos nx dx - use integration by parts | ||
| = | 1π { [ x2 ( sin nxn ) ] π −π − π∫ −π2x ( sin nxn) dx } | ||
| = | 1π { 1n (π2 sin nπ − π2 sin (−nπ)) − 2n π∫ −πx sin nx dx} | ||
| = | 1π { 1n (0 − 0) − 2n π∫ −πx sin nx dx} TRIG | ||
| = | −2nπ π∫ −πx sin nx dx - use integration by parts | ||
| = | −2nπ { [ x ( − cos nxn ) ] π −π − π∫ −π ( − cos nxn ) dx } | ||
| = | −2nπ { −1n [x cos nx] π−π + 1n π∫ −πcos nx dx } | ||
| = | −2nπ { −1n ( π cos nπ − (−π) cos (−nπ) ) + 1n⋅0 } | ||
| = | −2nπ { −1πn ( π(−1)n + π(−1)n ) } | ||
| = | −2nπ { −2πn (−1)n } | ||
| = | 4n2 (−1)n | ||
| i.e. n | = | { | 4n2: neven; −4n2: n odd |
STEP THREE
| bn | = | 1π π ∫ −π ƒ(x) sin nx dx | |
| = | 1π π ∫ −π x2 sin nx dx - use integration by parts | ||
| = | 1π { [ x2 ( − cos nxn ) ] π −π − π∫ −π2x ( − cos nxn) dx } | ||
| = | 1π { −1n [x2 cos nπ] π−π + 2n π∫ −πx cos nx dx} | ||
| = | 1π { −1n (π2 cos nπ − π2 cos (−nπ)) + 2n π∫ −πx cos nx dx} | ||
| = | 1π { −1n (π2 cos nπ − π2 cos nπ) + 2n π∫ −πx cos nx dx} | ||
| = | 2πn π∫ −πx cos nx dx - use integration by parts | ||
| = | 2nπ { [ x ( sin nxn ) ] π −π − π∫ −π ( sin nxn ) dx } | ||
| = | 2nπ { 1n (π sin nx − (−π) sin (−nπ)) − 1n π∫ −πsin nx dx } | ||
| = | 2nπ { 1n (0 + 0) − 1n π∫ −πsin nx dx } | ||
| = | −2nπ2 π∫ −πsin nx dx | ||
| i.e. bn | = | 0 | |
| - where: a0 = 2π23, an = { | 4πn2: n even − −4πn2: nodd |
and bn = 0 |
| n | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| an | −4(1) | 4(122) | −4(132) | 4(142) |
| i.e. ƒ(x) | = | 12 ( 2π23 ) −4 [ cos x − 122 cos 2x + 132 cos 3x − 142 cos 4x + ... ] + [ 0 + 0 + 0 + ...] |
| i.e. ƒ(x) | = | π23 −4 [ cos x − 122 cos 2x + 132 cos 3x − 142 cos 4x + ... ] |
Solution:
| Set x = π and use the fact that cos nπ = { | 1: n even −1: nodd |
| i.e. | cos x | − | 122 cos 2x + 132 cos 3x − 142 cos 4x + ... |
| gives: | cos π | − | 122 cos 2π + 132 cos 3π − 142 cos 4π + ... |
| i.e. | (−1) | − | 122⋅(1) + 132⋅(−1) − 142⋅(1) + ... |
| i.e. | −1 | − | 122 − 132 − 142 − ... |
- where the term in round brackets is the desired series.
The graph of ƒ(x) gives that ƒ(π) = π2 and the series converges to this value.
Setting x = π in the Fourier series thus gives:
| π2 | = | π23 − 4 ( cos π − 122 cos 2π + 132 cos 3π − 142 cos 4π + ...) |
| π2 | = | π23 − 4 ( −1 − 122 − 132 − 142 − ...) |
| π2 | = | π23 + 4 ( 1 + 122 + 132 + 142 + ...) |
| 2π23 | = | 4 ( 1 + 122 + 132 + 142 + ...) |
| ∴ π26 | = | 1 + 122 + 132 + 142 + ... |
Click on questions to reveal their solution
3. Standard Integrals
Formula for integration by parts: b ∫ audv dx dx = [uv] ba − b ∫ adu dx v dx
| ƒ(x) | ∫ƒ(x) dx | ƒ(x) | ∫ƒ(x) dx | |
|---|---|---|---|---|
| xn | xn+1 n+1 (n ≠ −1) | [g(x)]n g'(x) | [g(x)]n+1 n+1 (n ≠ −1) | |
| 1x | ln x | g'(x)g(x) | ln g(x) | |
| ex | ex | ax | axln a (a > 0) | |
| sin x | −cos x | sinh x | cosh x | |
| cos x | sin x | cosh x | sinh x | |
| tan x | − ln cosx | tanh x | ln cosh x | |
| cosec x | ln tan x2 | cosech x | ln tanh x2 | |
| sec x | ln sec x + tan x | sec x | 2 tan−1ex | |
| sec2 x | tan x | sec2 x | tanh x | |
| cot x | ln sin x | cot x | ln sinh x | |
| sin2 x | x2 − sin 2x4 | sinh2 x | sinh 2x4 − x2 | |
| cos2 x | x2 + sin 2x4 | cosh2 x | sinh 2x4 + x2 | |
| 1 a2 + x2 | 1 a tan −1 x a (a > 0) | √a2 + x2 | a2 2 [ sinh−1( x a ) + x √a2−x2 a2 ] | |
| 1 a2 − x2 | 1 2a ln a + x a − x (0 < x < a) | √a2−x2 | a2 2 [ sin−1( x a ) + x √a2−x2 a2 ] | |
| 1 x2 − a2 | 1 2a ln x − a x + a (x > a > 0) | √x2 − a2 | a2 2 [−cosh−1( x a ) + x √x2−a2 a2 ] | |
| 1 √ a2 + x2 | ln x + √a2 + x2 a (a > 0) | |||
| 1 √ a2 − x2 | sin−1 x a (−a < x < a) | 1 √ x2 − a2 | ln x + √x2 − a2 a (x > a > 0) |
4. Useful Trig Results
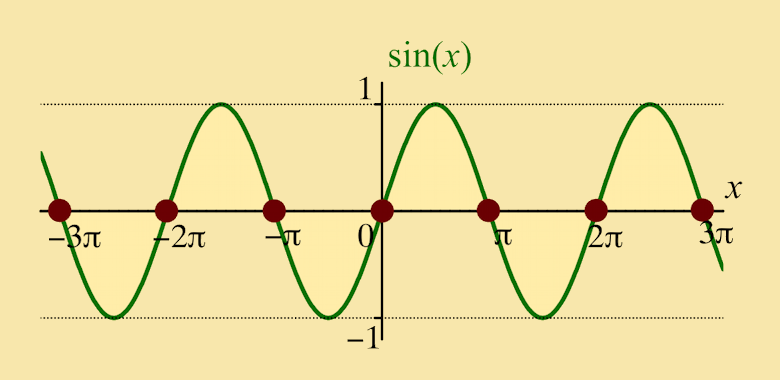
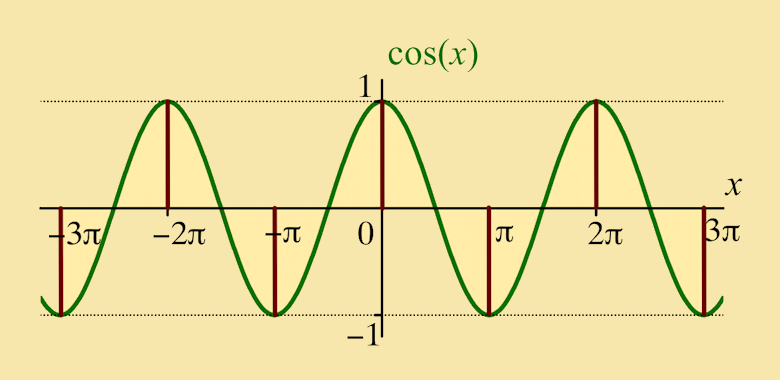
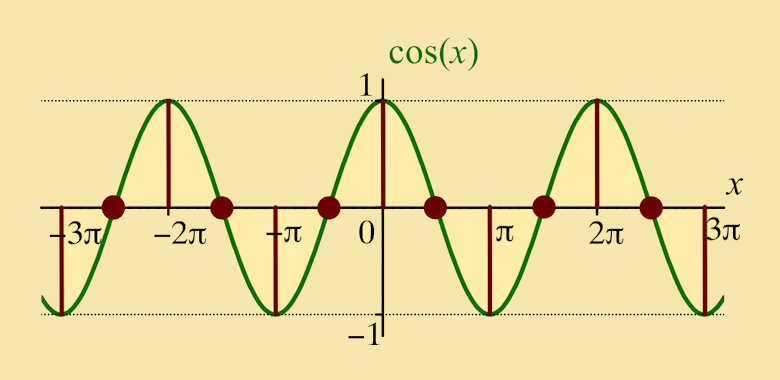
When calculating the Fourier coefficients an and bn, for which n = 1, 2, 3, ..., the following trig. results are useful. Each of these results, which are also true for n = 0, −1, −2, −3, ..., can be deduced from the graph of sin x or that of cos x:
 |
 |
|
| sin nπ | cos nπ = (−1)n |
 |
 |
|||
| sin n π2 = { | 0 : n even 1 : n = 1, 5, 9, ... −1 : n = 3, 7, 11, ... |
cos n π2 = { | 0 : n odd 1 : n = 0, 4, 8, ... −1 : n = 2, 6, 10, ... |
|
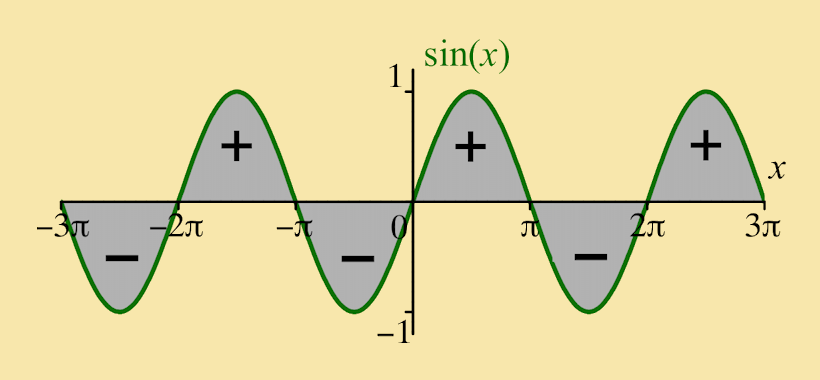
Areas cancel when integrating over whole periods: ∫ 2π sinx dx = 0 ∫ 2π cosx dx = 0 |
 |
5. Alternative Notation
For a waveform ƒ(x) with period L = 2πk
the corresponding Fourier coefficients are:
| STEP ONE | a0 | = | 2L ∫Lƒ(x) dx |
| STEP TWO | an | = | 2L ∫Lƒ(x) cos nx dx |
| STEP TWO | bn | = | 2L ∫Lƒ(x) sin nx dx |
- where integrations are over a single interval in x of L
For a waveform ƒ(x) with period 2L = 2πk, we have: k = 2π2k = πk and nkx = nπxL.
the corresponding Fourier coefficients are:
| STEP ONE | a0 | = | 1L ∫2Lƒ(x) dx |
| STEP TWO | an | = | 1L ∫2Lƒ(x) cos nπxL dx |
| STEP TWO | bn | = | 1L ∫2Lƒ(x) sin nπxL dx |
- where integrations are over a single interval in x of 2L
For a waveform ƒ(t) with period T = 2πω
The corresponding Fourier coefficients are:
| STEP ONE | a0 | = | 2T ∫Lƒ(x) dx |
| STEP TWO | an | = | 2T ∫Lƒ(x) cos nωt dx |
| STEP TWO | bn | = | 2T ∫Lƒ(x) sin nωt dx |
- where integrations are over a single interval in t of T
