1. Introduction (Vectors)

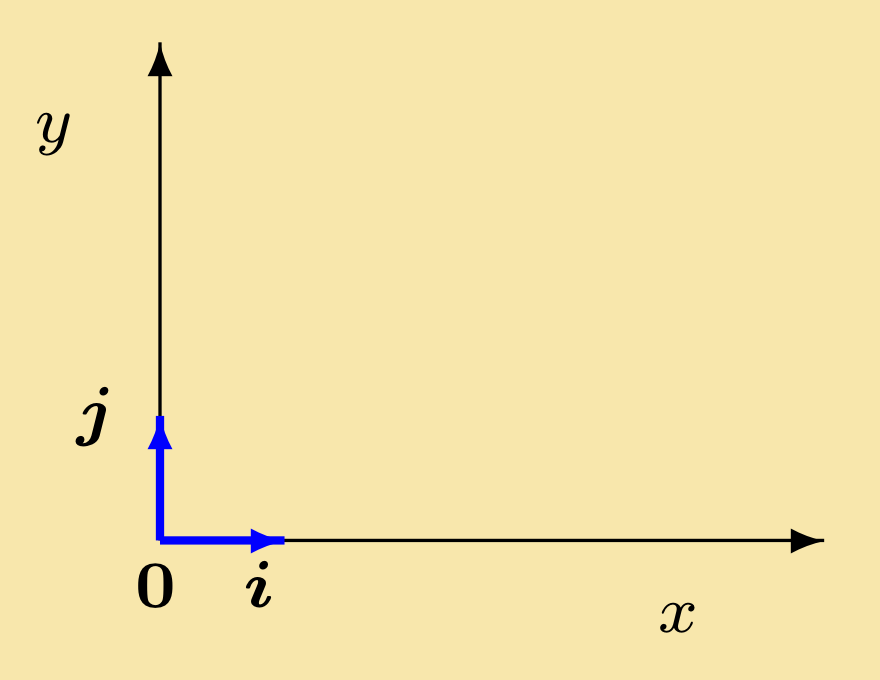
The base vectors in two dimensional Cartesian coordinates are the unit vector i in the positive direction of the x-axis and the unit vector j in the y direction (see figure bottom left). In three dimensions we also require k, the unit vector in the z direction.

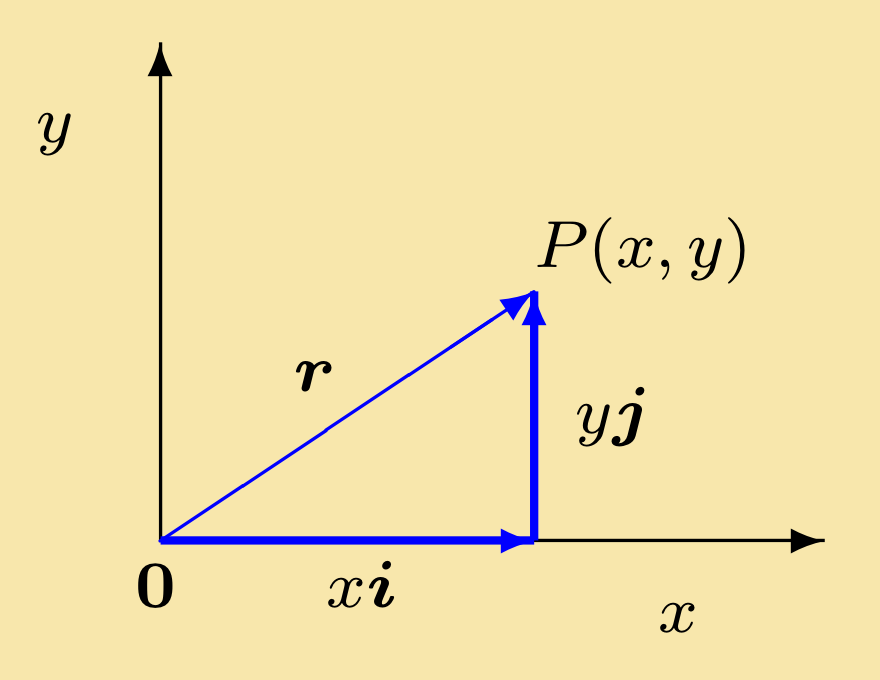
The position vector of a point P (x, y) in two dimensions is xi + yj. We will often denote this important vector by r (see figure bottom right). In three dimensions the position vector is r = xi + yj + zk.

The vector differential operator ∇, called 'del' or 'nabla', is defined in three dimensions to be:

∇ = ∂/∂xi + ∂/∂yj + ∂/∂zk

- note that these are partial derivatives!

This vector operator may be applied to (differentiable) scalar functions (scalar fields) and the result is a special case of a vector field, called a gradient vector field.

Here are two warming up exercises on partial differentiation:

Quiz 1: Select the following partial derivative: ∂/∂z(xyz^x):

(a) x²yz^x−1 Correct - well done!

(b) 0 Incorrect - please try again!

(d) yz^x−1 Incorrect - please try again!

Solution:The partial derivative of xyz^x with respect to the variable z is:

∂/∂z (xyz^x) = xy × ∂/∂z (z^x) = xy × x × z^x−1 = x²yz^x−1

Quiz 2: Choose the following partial derivative ∂/∂x(x cos (y) + y):

(a)cos (y) Correct - well done!

(b)cos (y) − x sin (y) + 1 Incorrect - please try again!

(d)−sin (y)

Solution: Consider the function ƒ (x,y) = x cos (y) + y. Its derivative with respect to the variable x is:

∂/∂x ƒ (x,y)	=	∂/∂x cos (y) + y
	=	∂/∂x (x) × cos (y) + ∂/∂x y
	=	1 × cos (y) + 0 = cos (y)

2. Gradient (Grad)

The gradient of a function, ƒ (x,y), in two dimensions is defined as:

grad ƒ (x,y) = ∇ƒ (x,y) = ∂ƒ/∂x i + ∂ƒ/∂y j

The gradient of a function is a vector field. It is obtained by applying the vector operator ∇ to the scalar function ƒ (x,y). Such a vector field is called a gradient (or conservative) vector field.

Example 1: The gradient of the function ƒ (x,y) = x + y² is given by:

∇ƒ (x,y)	=	∂ƒ/∂x i + ∂ƒ/∂y j
	=	∂/∂x (x + y²)i + ∂/∂y (x + y²)j
	=	(1 + 0)i + (0 + 2y)j
	=	i + 2yj

Quiz 3: Choose the gradient of ƒ (x,y) = x²y³:

(a) 2xi + 3y²j Incorrect - please try again!

(b) x²i + y³j Incorrect - please try again!

(d) y³i + x²j

Solution: The gradient of the function ƒ (x,y) =x²y³ is given by:

∇ƒ (x,y)	=	∂ƒ/∂x i + ∂ƒ/∂y j
	=	∂/∂x (x²y³)i + ∂/∂y (x²y³)j
	=	∂/∂x (x²) × y³i + x² × ∂/∂y (y³)j
	=	2x²⁻¹ × y³i + 3x² × y³⁻¹j
	=	2xy³i + 3x²y²j

The definition of the gradient may be extended to functions defined in three dimensions ƒ (x,y,z):

∇ ƒ (x,y,z) = ∂ƒ/∂x i + ∂ƒ/∂y j + ∂ƒ/∂z k

Exercise 1: Calculate the gradient of the following functions:

(a)ƒ (x,y) = x + 3y²

Solution: The function ƒ (x,y) = x + 3y² has gradient:

∇ƒ (x,y)	=	∂ƒ/∂x i + ∂ƒ/∂y j
	=	∂/∂x (x + 3y²)i + ∂/∂y (x + 3y²)j
	=	(1 + 0)i + (0 + 3 × 2y²⁻¹)j
	=	i + 6yj

(b)ƒ (x,y) = √x² + y²

Solution: The gradient of the function ƒ (x,y) = √x² + y² = (x² + y²)^½ is given by:

∇ƒ (x,y)	=	∂ƒ/∂x i + ∂ƒ/∂y j = ∂/∂x (x² + y²)^½i + ∂/∂y (x² + y²)^½j
	=	1/2 (x² + y²)^½−1 × ∂/∂x (x²)i + 1/2 (x² + y²)^½−1 × ∂/∂y (y²)j
	=	1/2 (x² + y²)^−½ × 2x²⁻¹i + 1/2 (x² + y²)^−½ × 2y²⁻¹j
	=	(x² + y²)^−½xi + (x² + y²)^−½yj
	=	x/ √x² + y²i + y/ √x² + y²j

Solution: The gradient of the function ƒ (x,y,z) = 3x²√y + cos (3z) = 3x²y^½ + cos (3z) is given by:

∇ƒ (x,y,z)	=	∂ƒ/∂xi + ∂ƒ/∂yj + ∂ƒ/∂z k
	=	3y^½∂/∂x (x²)i + 3x²∂/∂y (y^½)j + ∂/∂y (cos (3z))k
	=	3y^½ × 2x²⁻¹i + 3x² × 1/2y^½−1 j − 3 sin (3z)k
	=	6y^½xi + 3/2x²y^−½ j − 3 sin (3z)k
	=	6x√yi + 3/2 x²/ √yj − 3 sin (3z)k

(d) ƒ (x,y,z) =1/ √x² + y² + z²

Solution: The partial derivative of the function ƒ (x,y,z) = 1/ √x² + y² + z² = (x² + y² + z²)^½ with respect to the variable x is:

∂ƒ/∂x = − (x² + y² + z²)^½−1 × ∂(x²)/∂x = − x/ (x² + y² + z²)^{3 ⁄ 2}

Similarly, the derivatives ∂ƒ/∂y and ∂ƒ/∂z are:

∂ƒ/∂y = y/ (x² + y² + z²)^{3 ⁄ 2} and z/ (x² + y² + z²)^{3 ⁄ 2} respectively.

Therefore the gradient is:

∇ƒ (x,y,z) = − xi + yj + zk / (x² + y² + z²)^{3 ⁄ 2}

(e) ƒ (x,y) 4y/ (x² + 1)

Solution: The gradient of the function ƒ (x,y) 4y/ (x² + 1) = 4y(x² + 1)⁻¹ is:

∇ƒ (x,y)	=	4y × ∂/∂x (x² + 1)⁻¹i + (x² + 1)⁻¹ × ∂/∂y 4yj
	=	4y × (−1)(x² + 1)⁻¹⁻¹ ∂/∂x (x² + 1)²i + 4(x² + 1)⁻¹j
	=	−4y(x² + 1)⁻² × 2xi + 4(x² + 1)⁻¹j
	=	− 8xy/ (x² + 1)²i + 4/ (x² + 1)j

(f) ƒ (x,y,z) = sin (x) e^y ln(z)

Solution: The partial derivatives of the function ƒ (x,y,z) = sin (x) e^y ln(z) are:

∂ƒ/∂x	=	∂/∂x (sin (x)) e^y ln(z) = cos (x) e^y ln(z)
∂ƒ/∂y	=	sin (x)∂/∂y (e^y) ln(z) = sin (x) e^y ln(z)
∂ƒ/∂z	=	sin (x) e^y ∂/∂z (ln(z)) = sin (x) e^y 1/z

Therefore the gradient is:

∇ƒ (x,y,z) = cos (x) e^y ln(z)i + sin (x) e^y ln(z)j + sin (x) e^y 1/z k

3. Directional Derivatives

To interpret the gradient of a scalar field

∇ƒ (x,y,z) = ∂ƒ/∂x i + ∂ƒ/∂y j + ∂ƒ/∂z k

we note that its component in the i direction is the partial derivative of ƒ with respect to x. This is the rate of change of ƒ in the x direction since y and z are kept constant. In general, the component of ∇ƒ in any direction is the rate of change of ƒ in that direction.

Example 2: Consider the scalar field ƒ (x,y) = 3x + 3 in two dimensions. It has no y dependence and it is linear in x. Its gradient is given by:

∇ƒ	=	∂/∂x (3x + 3)i + ∂/∂y (3x + 3)j
	=	3i + 0j

As would be expected the gradient has zero component in the y direction and its component in the x direction is constant (3).

Quiz 4: Select a point from the answers below at which the scalar field ƒ(x,y,z) = x²yz − xy²z decreases in the y direction.

(a)(1, −1, 2) Incorrect - please try again!

(b)(1, 1, 1) Correct - well done!

(c)(−1, 1, 2) Incorrect - please try again!

(d)(1, 0, 1) Incorrect - please try again!

Solution: The partial derivative of the scalar function ƒ(x,y,z) = x²yz − xy²z with respect to y is:

∂ƒ/∂y (x,y,z) = x²z − 2xyz

Evaluating it at the point (1, 1, 1) gives:

∂ƒ/∂y(1, 1, 1) = 1² × 1 − 2 × 1 × 1 × 1 = 1 − 2 = −1

This is negative and therefore the function ƒ decreases in the y direction at this point.

It may be verified that the function does not decrease in the y direction at any of the other three points.

Definition: if is a unit vector, then ⋅ ∇ƒ is called the directional derivative of ƒ in the direction . The directional derivative is the rate of change of ƒ in the direction .

Example 3: Find the directional derivative of ƒ (x,y,z) = x²yz in the direction 4i − 3k at the point (1, −1, 1).

Solution: The vector 4i − 3k has magnitude √4² + (−3)² = √25 = 5. The unit vector in the direction 4i− 3k is thus 1/5(4i −3k).

The gradient of ƒ is:

∇ƒ	=	∂/∂x (x²yz)i + ∂/∂y (x²yz)j + ∂/∂z (x²yz)k
	=	2xyzi + x²zj + x²yk

and so the required directional derivative is:

⋅ ∇ƒ	=	1/5 (4i − 3k) ⋅ (2xyzi + x²zj + x²yk)
	=	1/5 [4 × 2xyz + 0 − 3 × x²y]

At the point (1, −1, 1) the desired directional derivative is thus:

⋅ ∇ƒ = 1/5 [8 × (−1) − 3 × (−1)] = −1

Exercise 2: Calculate the directional derivative of the following functions in the given directions and at the stated points:

(a)ƒ = 3x² − 3y² in the direction j at (1, 2, 3).

Solution: The directional derivative of the function ƒ = 3x² − 3y² in the unit vector j direction is given by the scalar product j ⋅ ∇.

The gradient of the function ƒ is

∇ƒ = 6xi − 6yj

Therefore the directional derivative in the unit vector j direction is:

j ⋅ ∇ƒ = j ⋅ (6xi − 6yj) = −6y

and at the point (1, 2, 3) it has the value −6 × 2 = −12.

(b)ƒ = √x² + y² in the direction 2i + 2j + k at (0, −2, 1).

Solution: The directional derivative of the function ƒ = √x² + y² in the direction defined by the vector 2i + 2j + k is given by the scalar product ⋅ ∇ƒ, where the unit vector is:

= 2i + 2j + k / √2² + 2² + 1² = 2i + 2j + k / √9 = 2/3i + 2/3j + 1/3k

The gradient of the function ƒ is:

∇ƒ = x/ √x² + y² i + y/ √x² + y² j + 0k = xi + yi/ √x² + y²

Therefore the required directional derivative is:

⋅ ∇ƒ = ( 2/3i + 2/3j + 1/3k ) ⋅ ( xi + yi/ √x² + y² ) = 2/3 x + y/ √x² + y²

At the point (0, −2, 1) it is equal to:

2/3 0 − 2/ √0² + (−2)² = 2/3 × −2/2 = − 2/3

(c)ƒ = sin (x) + cos (y) + sin (z) in the direction πi + πj at (π, 0, π).

Solution: The directional derivative of the function ƒ = sin (x) + cos (y) + sin (z) in the direction defined by the vector πi + πj is given by the scalar product ⋅ ∇ƒ, where the unit vector is:

= πi + πj / √π² + π² = i + j / √2

The gradient of the function ƒ is:

∇ƒ = cos (x)i − sin (y)j + cos (z)k

Therefore the directional derivative is:

⋅ ∇ƒ = ( i + j / √2 ) ⋅ [cos (x)i − sin (y)j + cos (z)k] = cos (x) − sin (y) / √2

and at the point (π, 0, π) it becomes cos (π) − sin (0) / √2 = − 1 / √2

We now state, without proof, two useful properties of the directional derivative and gradient:

The maximal directional derivative of the scalar field ƒ (x,y,z) is in the direction of the gradient vector ∇ƒ.
If a surface is given by ƒ (x,y,z) = c where c is a constant, then the normals to the surface are the vectors ±∇ƒ.

Example 4: Consider the surface xy³ = z + 2. To find its unit normal at (1, 1, −1), we need to write it as : ƒ = xy³ −z = 2 and calculate the gradient of ƒ:

∇ƒ = y³i + 3xy²j − k

At the point (1, 1, −1) this is ∇ƒ = i + 3j − k. The magnitude of this maximal rate of change is √1² + 3³ + (−1)² = √11

Thus the unit normals to the surface are: 1/√11(i + 3j − k).

Quiz 5: Which of the following vectors is normal to the surface x²yz = 1 at (1, 1, 1)?

(a) 4i + j + 17k Incorrect - please try again!

(b) 2i + j + 2k Incorrect - please try again!

(d) −2i − j − k Correct - well done!

Explanation: The surface is defined by the equation:

x²yz = 1

To find its unit normal at (1, 1, 1) we need to evaluate the gradient of the function ƒ (x,y,z) = x²yz:

∇ƒ = 2xyzi + x²zj + x²yk

At the point (1, 1, 1) this is:

∇ƒ = i + j + k

Thus the required normals to the surface are ±(i + j + k). Hence (d) is a normal vector to the surface.

Quiz 6: Which of the following vectors is a unit normal to the surface cos (x)yz = −1 at (π, 1, 1)?

(a) − 1/ √2j + 1/ √2k Incorrect - please try again!

(b) πi + j + 2/ √πk Incorrect - please try again!

(d) − 1/ √2j − 1/ √2k Correct - well done!

Explanation: The surface is defined by the equation:

cos (x)yz = −1

To find its unit normal at the point (π, 1, 1), we need to evaluate the gradient of ƒ = cos (x)yz:

∇ƒ = −sin (x)yzi + cos (x)zj + cos (x)yk

At the point (π, 1, 1) this is:

∇ƒ = 0i + (−1)j + (−1)k = −j −k

The magnitude of this vector is:

√(−1)² + (−1)² = √2

Therefore the unit normal is:

= − 1/ √2 j − 1/ √2 k

Quiz 7: Select a unit normal to the (spherically symmetric) surface at x² + y² + z² = 169 at (5, 0, 12):

(a) i + 1/6 j − 1/6 k Incorrect - please try again!

(b) 1/3 i + 1/3 j + 1/3 k Incorrect - please try again!

(d) − 5/13 i + 12/13 k Incorrect - please try again!

Explanation: The surface is defined by the equation:

x² + y² + z² = 169

To find its unit normal at point (5, 0, 12) we need to evaluate the gradient of ƒ = x² + y² + z²:

∇ƒ = 2xi + 2yj + 2zk

At the point (5, 0, 12) this is:

∇ƒ = 2 × 5i + 0 × j + 2 × 12k = 10i + 24k

The magnitude of this vector is:

√(2 × 5)² + (2 × 12)² = √4 × (25 + 144) = 2 √169 = 2 × 13

Therefore the unit normal is:

= 5/13 j + 12/13 k

5. Quiz on Gradients and Directional Derivatives

Choose the solutions from the options given

1. What is the gradient of ƒ (x, y, z) = xyz⁻¹?

(a) i + j + z⁻²k

(b) y/zi + x/zj − xy/z²k

(d) − 1/z²

2.If n is a constant, choose the gradient of ƒ (r) = 1 ⁄ rⁿ, where r = |r| and r = xi + yj + zk.

(a)0

(b)− n/2 i + j + k/rⁿ⁺¹

(d) − n/2 r/rⁿ⁺²

3.Select the unit normals to the surface of revolution, z = 1/2x² + 1/2y², at the point (1, 1, 4)

(a) ±1/ √3 (i + j − k)

(b) ±1/ √3 (i + j + k)

(d) ±1/ √2 (2i + 2j − 4k)

Gradients and Directional Derivatives

PPLATO / Basic Mathematics

Gradients and Directional Derivatives

1. Introduction

2. Gradient (Grad)

3. Directional Derivatives

4. Quiz on Gradients and Directional Derivatives

1. Introduction (Vectors)

2. Gradient (Grad)

3. Directional Derivatives

5. Quiz on Gradients and Directional Derivatives

PPLATO material © copyright 2004, Plymouth University