1. Introduction
Differentiation is concerned with the rate of change of one quantity with respect to another quantity.
Example 1: If a ball is thrown vertically upward with a speed of 10m s−1 then the height of the ball, in metres, after t seconds is approximately:
Find the average speed of the ball during the following time intervals:
(a) From t = 0.25s to t = 1s
Solution: Average speed is vaverage = distance travelledtime taken
So, the average speed from t = 0.25s to t = 1s is:
| h(1) − h(0.25)1 − 0.25 | = | (10 × 1 − 5 × 12) − (10 × 0.25 − 5 × 0.252)1 − 0.25 |
| = | 5 − 2.18750.75 = 3.75m s−1 |
(b) From t = 0.25s to t = 0.5s
Solution: Average speed is vaverage = distance travelledtime taken
So, the average speed from t = 0.25s to t = 0.5s is:
| h(0.5) − h(0.25)0.5 − 0.25 | = | (10 × 0.5 − 5 × 0.52) − (10 × 0.25 − 5 × 0.252)0.5 − 0.25 |
| = | 3.75 − 2.18750.25 = 6.25m s−1 |
Exercise 1: For the ball in Example 1, find the average speed of the ball during the following time intervals.
Solution: The average speed from t = 0.25s to t = 0.375s is:
| h(0.375) − h(0.25)0.375 − 0.25 | = | (10×0.375 − 5×0.3752) − (10×0.25 − 5×0.252)0.375 − 0.25 |
| = | 3.047 − 2.18750.125 = 6.875m s−1 |
Solution: The average speed from t = 0.25s to t = 0.3125s is:
| h(0.3125) − h(0.25)0.3125 − 0.25 | = | (10×0.3125 − 5×0.31252) − (10×0.25 − 5×0.252)0.3125 − 0.25 |
| = | 2.637 − 2.18750.0625 = 7.1875m s−1 |
Solution: The average speed from t = 0.25s to t = 0.251s is:
| h(0.251) − h(0.25)0.251 − 0.25 | = | (10×0.251 − 5×0.2512) − (10×0.25 − 5×0.252)0.251 − 0.25 |
| = | 2.195 − 2.18750.001 = 7.495m s−1 |
Solution: The average speed from t = 0.25s to t = 0.2501s is:
| h(0.2501) − h(0.25)0.2501 − 0.25 | = | (10×0.2501 − 5×0.25012) − (10×0.25 − 5×0.252)0.2501 − 0.25 |
| = | 2.1882 − 2.18750.0001 = 7.4995m s−1 |
Click on questions to reveal their solutions
Quiz 1: For the ball in Example 1, which of the following is a good choice for the speed of the ball when t = 0.25s?
Explanation: The table below shows the details of the calculations that were done in Example 1 and Exercise 1.
| Times distance measured (s) | Time inverval (s) | Average speed (m s−1) |
|---|---|---|
| t = 0.25 to t = 1 | 0.75 | 3.75 |
| t = 0.25 to t = 0.5 | 0.25 | 6.25 |
| t = 0.25 to t = 0.375 | 0.125 | 6.875 |
| t = 0.25 to t = 0.3125 | 0.0625 | 7.1875 |
| t = 0.25 to t = 0.251 | 0.001 | 7.495 |
| t = 0.25 to t = 0.2501 | 0.0001 | 7.4995 |
The difference in speeds is measured over decreasing intervals of time starting at t = 0.25s. As this interval decreases, so the average speed tends towards 7.5m s−1. This is then taken to be the speed of the ball when t = 0.25s. This limiting process, taking averages over smaller and smaller intervals, is at the heart of differentiation.
2. Rates of Change
In the previous section, the speed of the ball was found at t = 0.25s. The next example gives the general solution to this problem.
Example 2: If, as in Example 1, the height of a ball at time t is given by h(t) = 1 − t − 5t2, then find the following:
(a) The average speed of the ball over the time interval from t to t + δt
Solution: The height at time t + δt is h(t + δt). The difference in heights is h(t + δt) − h(t) and the time interval is δt.
| h(t+δt) − h(t) | = | [10(t+δt) − 5(t+δt2)] − [10t − 5t2] |
| = | [10t + 10δt − 5(t2 + 2tδt + (δt)2)] − [10t − 5t2] | |
| = | 10δt − 10tδt − 5(δt)2 | |
| = | δt(10 − 10t − 5δt) |
The required average speed of the ball at time t is thus
| h(t+δt) − h(t)δt | = | δt(10 − 10t − 5δt)δt |
| = | 10 − 10t − 5δt |
- after cancelling the δt.
(b) The limit of this average as δt → 0.
Solution: As δt gets smaller, i.e. δt → 0, the last term becomes negligible and the instantaneous speed at time t is v(t), where v(t) = 10 − 10t is the speed of the ball at time t.
Exercise 2:
Solution: The speed is found by putting t = 0.25s into v(t) = 10 − 10t. The resulting speed is:
This was precisely the value chosen in Quiz 1, confirming that the function v(t) = 10 − 10t is indeed the speed of the ball at any time t.
Click on question to reveal the solution
To recap, the speed v(t) is obtained from the height h(t) as:
3. The Derivative as a Limit
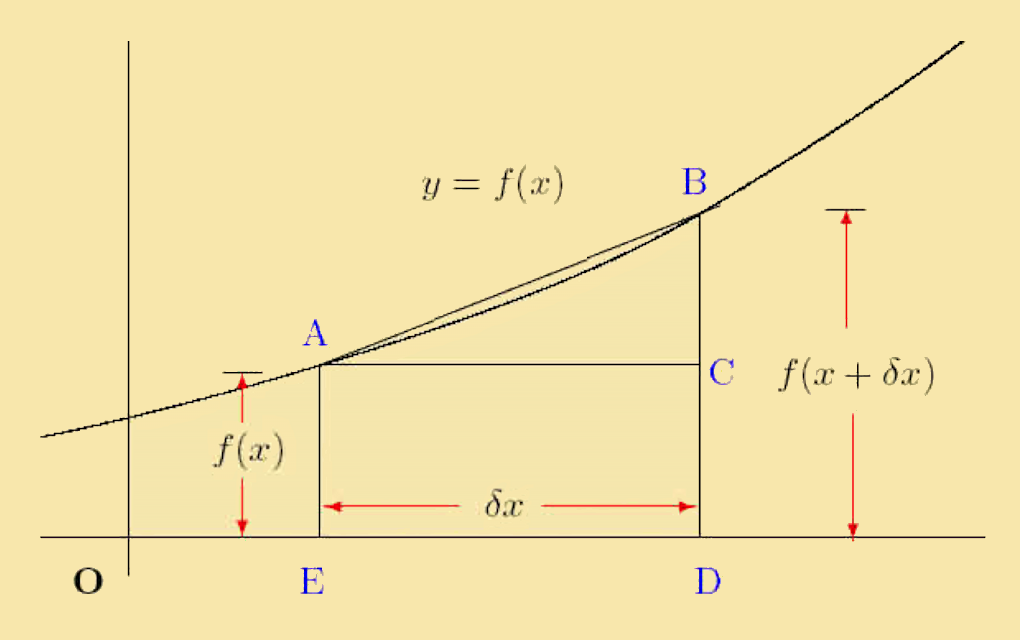
The diagram shows a function y = (x). The straight line AB has the gradient BC ⁄ CA. As the point B moves along the curve towards A, the straight line AB tends toward the tangent to the curve at A. At the same time, the gradient BC ⁄ CA tends towards the gradient of the tangent to the curve at A. From the figure we have:
BCCA = ƒ(x + δx) − ƒ(x)δx
Thus we define:
dydx = limδx → 0BCCA = ƒ(x+δx) − ƒ(x)δx
|
|
The limit, dydx is called the derivative of the function ƒ(x). Its value is the gradient of the tangent to the curve at the point A(x,y).
Example 3: Find the derivative of the function y = x3.
Solution: For this problem, y = ƒ(x) = x3, so the derivative is
The numerator of this is:
| (x+δx)3 − (x)3 | = | (x3 + 3x2δx + 3xδx2 + δx3) − x3 |
| = | 3x2δx + 3xδx2 + δx3 | |
| = | δx(3x2 + 3xδx + δx2) |
Then:
| dydx | = | limδx → 0δx(3x2 + 3xδx + δx2)δx |
| = | limδx → 0 (3x2 + 3xδx + δx2) |
The derivative is thus dydx = 3x2.
Exercise 3: For each of the following functions, using the technique as shown in Example 3, find the derivative of the function.
Solution: The derivative of y = ƒ(x) = x is
| dydx | = | limδx → 0ƒ(x+δx) − ƒ(x)δx |
| = | limδx → 0(x+δx) − xδx | |
| = | limδx → 0δxδx = 1 |
The derivative is thus:
This can also be deduced from the fact that y = x represents a straight line with gradient 1.
Solution: The derivative of y = ƒ(x) = x2 is
| dydx | = | limδx → 0ƒ(x+δx) − ƒ(x)δx |
| = | limδx → 0(x + δx)2 − x2δx | |
| = | limδx → 0x2 + 2xδx + (δx)2 − x2δx | |
| = | limδx → 02xδx + (δx)2δx | |
| = | limδx → 0(2x + δx)δxδx | |
| = | limδx → 0 (2x + δx) = 2x |
The derivative is thus:
Solution: The derivative of y = ƒ(x) = 1 is:
| dydx | = | limδx → 0ƒ(x + δx) − ƒ(x)δx |
| = | limδx → 01 − 1δx | |
| = | limδx → 00δx | |
| = | limδx → 0 (0) = 0 |
The derivative of y = 1 is thus:
This is a special case of the rule that the derivative of a constant is always zero.
Click on questions to reveal their solutions
Example 4: Find the gradient of the tangent to the curve y = x3 at the point on the curve when x = 2.
Solution: From Example 3, the derivative of this function is:
The gradient of the tangent to the curve when x = 2 is:
- where the expression dydx is the function evaluated at x = 2.
Exercise 4: Find the gradient of the tangent to each of the following functions at the indicated points.
Solution: According to Exercise 3, the derivative of the function y = x is:
Therefore, the gradient of the tangent to the curve at the point with coordinates (2, 2), i.e. when x = 2, is:
This is the gradient of the straight line y = x.
Solution: According to Exercise 3, the derivative of the function y = x2 is:
Therefore the gradient of the tangent to the curve at the point with coordinates (3,9), i.e. when x = 3, is:
Solution: According to Exercise 3, the derivative of the constant function y = 1 is:
Therefore the gradient of the tangent to the curve at the point with coordinates (27,1), is zero, i.e.
Click on questions to reveal their solutions
Quiz 2: Referring to Example 3 and Exercise 3, which of the following is the most likely choice for the derivative of the function y = x4
Explanation: The table below shows the details of the calculations that were done in Example 3 and Exercise 3:
| Function | Derivative |
|---|---|
| y = x3 | dy/dx = 3x2 |
| y = x2 | dy/dx = 2x (= 2 x1 = 2x2 − 1) |
| y = x | dy/dx = 1 (= x0 = 1x1 − 1) |
| y = 1 | dy/dx = 0 (= 0x0 − 1) |
The general form, given without proof, is:
If y = xn, then dydx = nxn−1
Thus, if y = x4, then dydx = 4x3.
Although the derivative of a function has been described in terms of a limiting process, it is not necessary to proceed in this fashion for each function. The derivatives for certain standard functions, and the rules of differentiation, are well known. The application of these rules, which is part of the discipline known as calculus, is the subject of the rest of this module.
4. Differentiation
The following table lists, without proof, the derivatives of some well known functions. Throughout, a is a constant.
| y | axn | sin (ax) | cos (ax) | eax | ln (ax) |
| dydx | naxn−1 | a cos (ax) | −a sin (ax) | a eax | 1x |
Here are two more useful rules of differentiation. They follow from the definition of differentiation but are stated here without proof:
If u, v are two functions of xand a is a constant, then:
| ddx (u+v) | = | dudx + dvdx | |
| and: | ddx (au) | = | a dudx |
The use of these rules is illustrated in Example 5.
Example 5: For each of the following functions, find dydx:
(a)y = x2 + 4x3
Solution: Using the rules of differentiation:
| y | = | x2 + 4x3 |
| dydx | = | ddx(x2) + dydx(4x3) |
| = | 2x + 3 × 4x2 = 2x + 12x2 |
(b)y = 5x2 + 1 ⁄ x
Solution: Before proceeding, first note that 1 ⁄ x = x−1 (see the module on Powers). The function may now be written as y = 5x2 + x−1 .
| y | = | 5x2 + x−1 |
| dydx | = | ddx(5x2) + dydx(x−1) |
| = | 2 × 5x + (−1)x−2 | |
| = | 10x − 1 ⁄ x2 |
(c)y = 5√x + 3x2 − 6x
Solution: From the module on Powers, √x = x1 ⁄ 2, so
| y | = | 5x1 ⁄ 2 + 3x−2 − 6x |
| dydx | = | ddx(5x1 ⁄ 2) + dydx(3x−2) − dydx(6x) |
| = | 1 ⁄ 2 × 5x−1 ⁄ 2 + (−2) × 3(x−3) − 6 | |
| = | 5 ⁄ 2 x−1 ⁄ 2 − 6x−3 − 6 | |
| = | 5(2x1 ⁄ 2) − 6(x3) − 6 |
Exercise 5: Find dy ⁄ dx for each of the following functions.
Solution: Using the rules of differentiation
| y | = | 3x4 + 4x5 |
| dydx | = | ddx(3x4) + ddx(4x5) |
| = | 4 × 3x(4−1) + 5 × 4x(5−1) | |
| = | 4 × 3x3 + 5 × 4x4 | |
| = | 12x3 + 20x4 |
Solution: From the module on Powers, 2 √x = 2x1 ⁄ 2 , so using the rules of differentiation
| y | = | 2x1 ⁄ 2 |
| dydx | = | ddx(2x1 ⁄ 2) |
| = | 12 × 2x(1 ⁄ 2 − 1) | |
| = | x−1 ⁄ 2 | |
| = | 1√x |
Solution: The function may be rewritten (see the module on Powers) as
Using the rules of differentiation:
| y | = | 4x−3 − 3x1 ⁄ 3 |
| dydx | = | ddx(4x−3) + ddx(3x1 ⁄ 3) |
| = | (−3) × 4x(−3−1) + (1 ⁄ 3) × 3x(1 ⁄ 3 −1) | |
| = | −12x−4 − x−2 ⁄ 3 | |
| = | −12x4 − 1x2 ⁄ 3 | |
| = | −12x4 − 13√x2 |
Click on questions to reveal their solutions
Example 6: Find dy ⁄ dw if y = 2 sin (3w) − 3 cos (4w) + e4w.
Solution: Using the rules:
| dydw | = | 2ddw(sin (3w)) − 3ddw(cos (4w)) + ddw(e4w) |
| = | 2(3 cos (3w)) − 3(−4 sin (4w)) + 4 e4w | |
| = | 6 cos (3w) + 12 sin (4w) + 4 e4w |
Exercise 6: Find the derivative with respect to z, i.e. dy ⁄ dz of each of the following functions:
Solution: Using the rules of differentiation and the table of derivatives:
| dydz | = | 2ddz(sin (z ⁄ 2)) |
| = | 2 × 1 ⁄ 2 cos (z ⁄ 2) | |
| = | sin (z ⁄ 2) |
Solution: Rewriting the function y = 4 ⁄ z − 3 ln (4z) as
y = 4z−1 − 3 ln (4z)
and using the table of derivatives:
| dydz | = | ddz(4z−1) − 3ddz(ln (4z)) |
| = | (−1) × 4z−1−1 − 3 × 1 ⁄ z | |
| = | −4z−2 − 3 ⁄ z | |
| = | −4 ⁄ z2 − 3 ⁄ z |
Solution: Using the rules of differentiation and the table of derivatives
| dydz | = | 2ddz(ln (7z)) + 3ddz(cos (2z)) |
| = | 2 × 1 ⁄ z + 3×(−2 sin (2z)) | |
| = | 2 ⁄ z − 6 sin (2z) |
Solution: Since ddz(e(az)) = aeaz
| dydz | = | ddz(e3z) − 3ddz(ez) |
| = | 3e3z − 3ez | |
| = | 3(e3z − ez) |
Click on questions to reveal their solutions
5. Quiz on Differentiation
Choose dydx for each of the following functions:
