1. Rules of Differentiation
Throughout this module the following rules of differentiation will be assumed. (In the table of derivatives below, a is an arbitrary, non-zero constant.) [what is n? integer?]
| y | axn | sin (ax) | cos (ax) | eax | ln (ax) |
|---|---|---|---|---|---|
| dydx | naxn − 1 | a cos (ax) | −a sin (ax) | a eax | 1x |
If a is any constant and u, v are two functions of x, then:
| ddx(u + v) | = | dudx + dvdx |
|---|---|---|
| ddx(au) | = | a dudx |
The stationary points of a function are those points where the gradient of the tangent (the derivative of the function) is zero.
Example 1: Find the stationary points of the functions:
Solution: The derivative is: dydx = 3 × 2x2−1 + 2 = 6x + 2
The stationary points are found by solving the equation:
In this case there is only one solution, x = −3. Substituting this into the equation for ƒ(x), the corresponding y value is then:
| y | = | 3(−3)2 + 2(−3) − 9 |
|---|---|---|
| = | 12 |
The stationary point is thus the point with coordinates (−3, 12).
Solution: The derivative is: dydx = 3x2 − 12x + 9
The stationary points are found by solving: 3x2 - 12x + 9 = 0. This is a quadratic equation (see the package on quadratic equations) and may be solved by factorising:
| 0 | = | 3x2 − 12x + 9 | = | 3(x2 − 4x + 3) |
| = | 3(x − 3) (x − 1) |
There are two solutions in this case, x = 3 and x = 1. If these are substituted into the function, the two stationary points will be found to be (3, −2) and (1, 2).
Exercise 1: Find the stationary points of the following functions:
Solution: The derivative is: dydu = −6 − 2u.
The stationary points are found by solving the linear equation:
In this case there is only one solution u = −6 ⁄ 2 = −3. Substituting this into the expression for the function ƒ(u) = 16 − 6u − u2, we find the corresponding y value:
The stationary point is thus the point with coordinates (−3, 25).
Solution:The derivative is: dydx = 6x − 4.
The stationary points are found by solving the linear equation:
In this case there is only one solution x = 4 ⁄ 6 = 2 ⁄ 3. Substituting this this into the expression for the function ƒ(x) = 3x2 − 4x + 7, we find the corresponding y value:
y = 3 × (2 ⁄ 3)2 − 4 × 2 ⁄ 3 + 7 = 4 ⁄ 3 - 8 ⁄ 3 + 7 = 17 ⁄ 3
Therefore the function y = 3x2 − 4x + 7 has only one stationary point (2 ⁄ 3, 17 ⁄ 3).
Solution:The derivative is: dydx = x2 − 2x − 3.
The stationary points are found by solving the quadratic equation x2 − 2x − 3 = 0. Factorisation of this equation gives:
This yields two solutions, x = −1 and x = 3.
Substituting x = −1 into the function ƒ(x), the corresponding y value is:
Similarly, substituting x = 3:
y = 1 ⁄ 3 (3)3 − (3)2 − 3(3) + 2 = 9 − 9 + 9 + 2 = −7
The two stationary points are thus (−1, 11 ⁄ 3) and (3, −7).
Solution:The derivative is: dydx = 3 x2 − 12x − 15.
The stationary points are found by solving the quadratic equation 3x2 − 12x − 15 = 0. Factorising it:
We obtain two solutions, x = *minus;1 and x = 5.
Substituting x = −1 into the function ƒ(x), the corresponding y value is:
Similarly, substituting x = 5:
y = (5)3 − 6 × (5)2 − 15 × (5) + 16 = −1 − 6 + 15 + 16 = −84
The two stationary points are thus (−1, 24) and (5, −84).
Click on questions to reveal solutions
2. Derivatives of Order 2 (and Higher)
In the package on Introductory Differentiation the height, h(t), in metres, of a ball thrown vertically at 10m s−1, was given by:
The velocity of the ball, vm s−1, after t seconds, was given by:
The rate of change of velocity with time, which is the acceleration, is then given by a(t), where:
Since the acceleration was derived from h(t) by two successive differentiations, the resulting function, which in this case is a(t), is called the second derivative of h(t) with respect to t. In symbols:
Example 2: Find the first, second and third derivatives of the function: y = 3x6 − 2x + 1:
Solution:
The first derivative is given by:
The second derivative is given by:
The third derivative is given by:
Exercise 2: Find the first, second and third derivatives of the following functions:
Solution:
The first derivative is given by:
The second derivative is given by:
The third derivative is given by:
Solution:
The first derivative is given by:
The second derivative is given by:
The third derivative is given by:
Click on questions to reveal solutions
3. Maxima and Minima
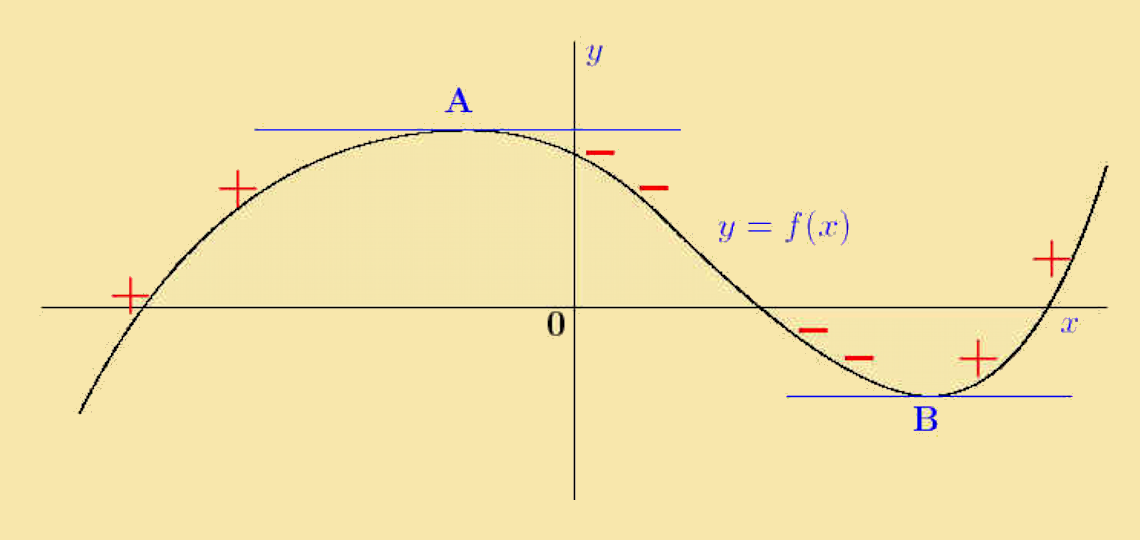
The figure on the right shows part of a function y = ƒ(x). The point A is a local maximum and the point B is a local minimum. At each of these points the tangent to the curve is parallel to the x-axis so the derivative of the function is zero. Both of these points are therefore stationary points of the function. The term local is used since these points are the maximum and minimum in this particular region, and there may be others outside this region. |

|
Further observations on the gradients of tangents to the curve are: to the left of A the gradients are positive (+) between A and B the gradients are negative (−) to the right of B the gradients are positive (+) About the local maximum point A the gradient changes from positive, to zero, to negative. The gradient is therefore decreasing. About the local minimum point B the gradient changes from negative, to zero, to positive. The gradient is therefore increasing. |
|
The rate of change of a function is measured by its derivative. When the derivative is positive, the function is increasing, when the derivative is negative, the function is decreasing. Thus the rate of change of the gradient is measured by its derivative, which is the second derivative of the original function. In mathematical notation this is as follows:
At the point (a, b):
| If | dydx | = | 0 | If | dydx | = | 0 |
|---|---|---|---|---|---|---|---|
| and | d2ydx2 | < | 0 | and | d2ydx2 | < | 0 |
| then the point (a, b) is a | then the point (a, b) is a | ||||||
| local maximum | local minimum | ||||||
Example 3: Find the stationary point of the function y = x2 − 2x + 3 and hence determine the nature of this point.
Solution:
If y = x2 − 2x + 3 then dydx = 2x − 2 and d2ydx2 = 2 Now dydx = 2x − 2 = 0 when x = 1. Since d2ydx2 = 2 > 0 for all values of x, this stationary point is a local minimum. Thus the function y = x2 − 2x + 3 has a local minimum at the point (1, 2). The figure on the right shows the function y = x2 − 2x + 3, with the local minimum point at (1,2) clearly visible. |

|
Exercise 3: Determine the nature of the stationary points of the following functions:
Solution: From the given function we have:
There is one stationary point when u = −3, which is obtained from the equation:
At this point y = 16 − 6 × (−3) − (−3)2 = 25. Since d2ydu2 = −2 < 0 for all values of u, this stationary point is a local maximum. Thus the function y = 16 − 6u − u2 has a local maximum at the point (−3, 25).
Solution: From the given function we have:
There is one stationary point when x = 2 ⁄ 3, which is the solution to the equation:
At this point y = 3 × (2 ⁄ 3)2 − 4 × (2 ⁄ 3) + 7 = 17 ⁄ 3. Since d2ydx2 = 6 > 0 for all values of x, this stationary point is a local minimum. Thus the function y = 3x2 4x + 7 has a local minimum at the point (2 ⁄ 3, 17 ⁄ 3).
Click on questions to reveal solutions
Quiz 1: Which of the following points is a local maximum of the function y = 2x3 − 15x2 − 36x + 6?
Explanation:
There are two stationary points x = −1 and x = 6 which are obtained from solving the equation:
At the point x = −1 the function value is y = 25 and its second derivative is:
Therefore, the point (−1, 25) is a local maximum.
For the second stationary point, at x = 6, the second derivative is:
and y = −318. The point (6,−318) is therefore a local minimum.
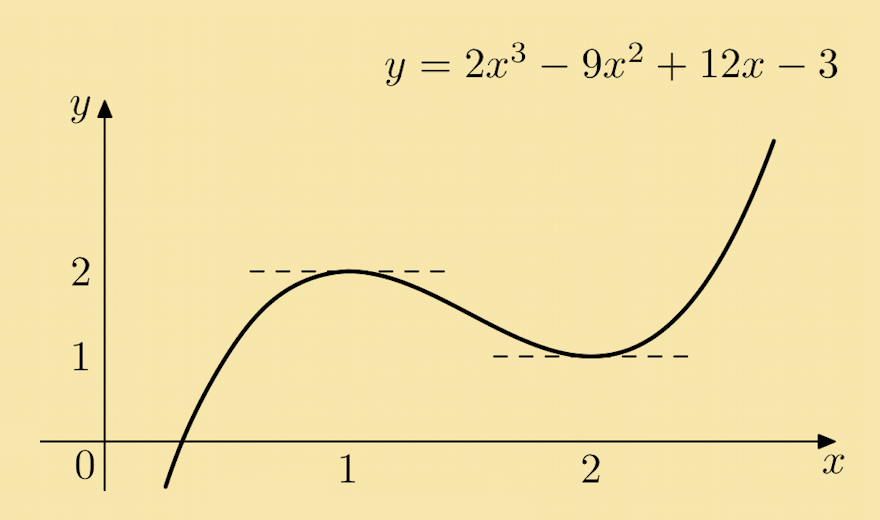
Example 4: Find the stationary point of the function y = 2x3 − 9x2 + 12x − 3 and determine their nature.
Solution: From the given function we have:
The stationary points are found by solving:
Now 6x2 − 18x + 12 = 6 (x2 − 3x + 2), so the solution is found by solving x2 − 3x + 2 = 0, i.e. x = 1 and x = 2 (see the module on Quadratics). Note that when x = 1, y = 2 and when x = 2, y = 1.
When x = 1, d2ydx2 = 12(1) − 18 = −6 < 0, so (1, 2) is a local maximum. When x = 2, d2ydx2 = 12 (2) − 18 = 6 > 0, so (2, 1) is a local minimum. The local maximum point at (1, 2) and the local minimum point at (2, 1) are clearly visible in the graph of the given function. |
|
Exercise 4: Determine the nature of the stationary points of the following functions:
Solution: From the given function we have:
There is one stationary point when u = −3 which is obtained from the equation:
At this point y = 16 − 6 × (−3) − (−3)2 = 25. Since d2ydu2 = −2 < 0 for all values of u, this stationary point is a local maximum. Thus the function y = 16 − 6u − u2 has a local maximum at the point (−3, 25).
Solution: We have:
There is only one stationary point, when s = 18, which is obtained from the equation:
When s = 18 the function ƒ(s) takes the value y = −76. Since its second derivative d2yds2 = 23 is positive for all values of s, the stationary point (18, −76) is a local minimum.
Solution: We have:
There are two stationary points x = −1 and x = 5, which are obtained from solving the quadratic equation:
When x = −1 the function value is y = 24 and its second derivative d2ydx2 = 6 × (−1) − 12 = −18 < 0. The point (−1, 24) is a local maximum.
At the second point, x = 5, the function value is y = −84 and the second derivative d2ydx2 = 6 × (5) − 12 = 18 > 0. The point (5, −84) is a local minimum.
Solution: We have:
There are two stationary points x = −2 and x = 2, which are obtained from solving the equation:
When x = −2 the function value is y = 28 and its second derivative d2ydx2 = 6 × (−2) = −12 < 0. The point (−2, 28) is a local maximum.
At the second point, x = 2, the function value is y = −4 and the second derivative d2ydx2 = 6 × (2) = 12 > 0. The point (2, −4) is a local minimum.
Quiz 2: Given the function y = x + 1 + 1 ⁄ x, which of the following statements is true?
Explanation:
The stationary points are found from the equation:
and this is zero when 1 − x2 = 0. There are two solutions in this case, x = −1 and x = 1.
When x = 1 the function value is y = 1 and its second derivative is d2ydx2 = 2(−1)3 = −2 < 0. The point (−1, −1) is a local maximum.
When x = 1 the function value is y = 3 and the second derivative is d2ydx2 = 2(1)3 = 2 > 0. The point (1, 3) is a local minimum.
Quiz 3: Given the function y = x22 − cos (x), which of the following statements is true?
Explanation:
The stationary points are found from the equation:
Since sin (0) = 0, a solution to this equation is x = 0. At this point the function value is:
Its second derivative when x = 0 is:
The point (0, −1) is therefore a local minimum of the given function.
4. Quiz on Maxima and Minima
In each of the following cases, choose the correct option:
