1. Introduction
A general linear function has the form y = mx + c , where m and c are constants.
Example 1:
If x is the temperature in °C and y the temperature in °F then there is a simple rule relating the values of x and y. The table below illustrates this rule for various values of x and y.
The general rule is:
y = 95 x + 32
- so that m = 9 ⁄ 5 and c = 32 in this case. |
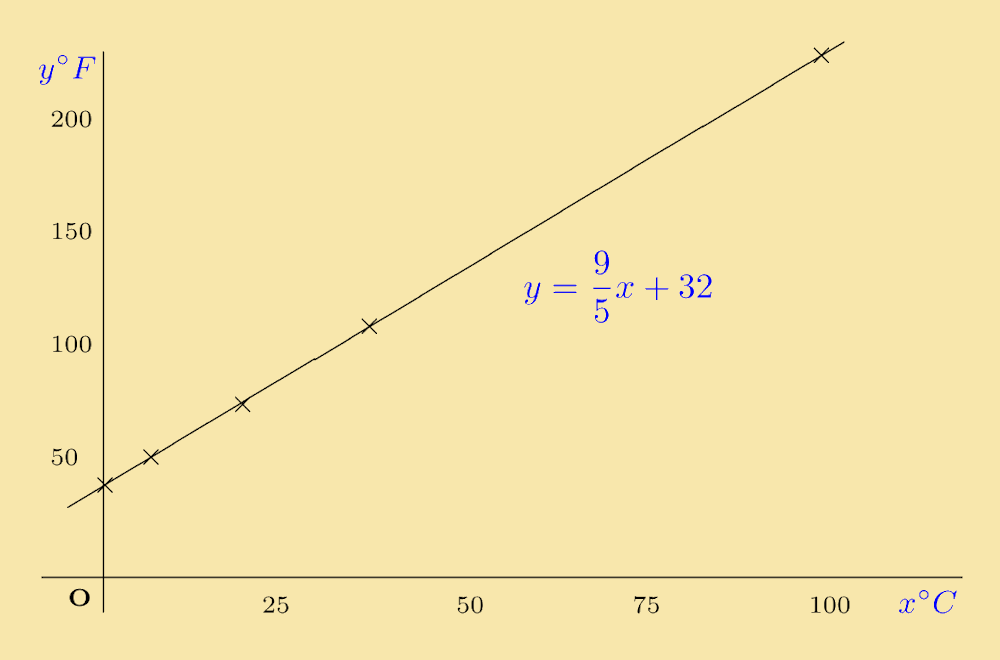
Graph of the relationship between Celsius and Fahrenheit temperature scales. |
Example 2: A straight line passes through the two points P(x,y) and Q(x,y) with coordinates P(0, 2) Q(1, 5). Find the equation of this straight line.
Solution: The general equation of a straight line is y = mx + c. Since the line passes through the points P, with coordinates x = 0, y = 2, and Q, with coordinates x = 1, y = 5, these coordinates must satisfy this equation, i.e. :
| 2 | = | m × 0 + c |
| 1 | = | m × 5 + c |
(See the module on Simultaneous Equations.) Solving these equations gives c = 2 and m = 3, i.e. the equation of the line is:
Exercise 1: In each of the following, find the equation of the straight line through the given pairs of points:
Solution: The general equation of a straight line is y = mx + c. Since the line passes through the points P and Q, the coordinates of both points must satisfy this equation. The point P has coordinates x = 0, y = −3 and the point Q has coordinates x = 2, y = 1. These satisfy the pair of simultaneous equations:
| −3 | = | m × 0 + c |
| 1 | = | m × 2 + c |
Solving these equations gives c = −3 and m = 2, i.e. the equation of the line is:
Solution: The general equation of a straight line is y = mx + c. Since the line passes through the points P and Q, the coordinates of both points must satisfy this equation. The point P has coordinates x = 0, y = 4 and the point Q has coordinates x = 1, y = 3. These satisfy the pair of simultaneous equations:
| 4 | = | m × 0 + c |
| 3 | = | m × 1 + c |
Solving these equations gives c = 4 and m = −3, i.e. the equation of the line is:
Click on questions to reveal solutions
2. Gradient of a Straight Line
The gradient of a straight line is defined as follows: Suppose that two points P, Q, on the line have coordinates P(x1, y1) and Q(x2, y2) (see figure on the right). The gradient of the line is given by:
gradient = RQPR = y2 − y1x2 − x1
|
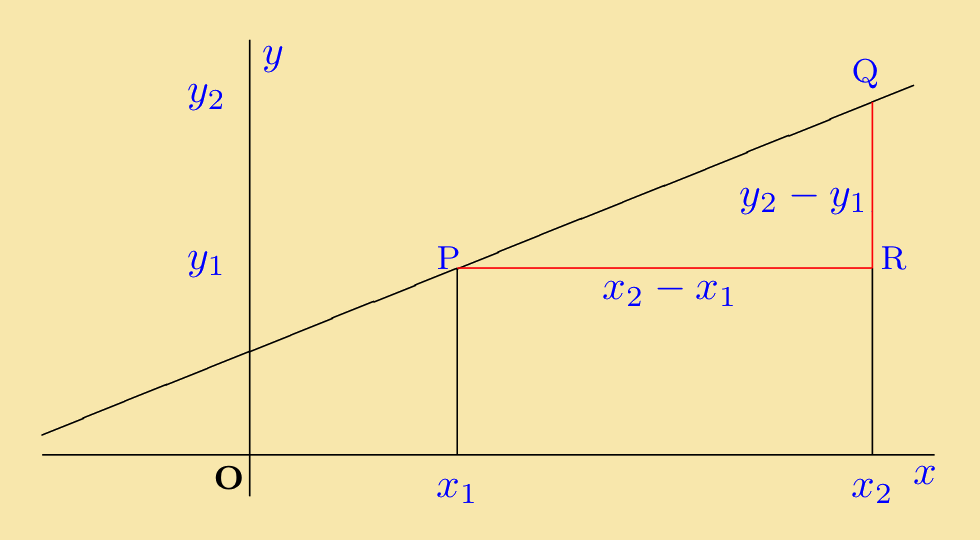
|
Example 3: From the table given in Example 1, find the gradient of the line giving the relationship between x (◦C) and y (◦F).
Solution: The boiling point, Q, of water is 100°C or 212°F, i.e. Q(100, 212). The freezing point of water is 0°C or 32°F , i.e. P(0, 32). The gradient is therefore:
The equation of the line is y = (9 ⁄ 5)x + 32. Comparing this with the general equation y = mx + c shows that m is the value of the gradient.
Exercise 2: Find the gradient of the line through the points P, Q with the following coordinates:
Solution:
| gradient | = | y2 − y1 x2 − x1 |
| = | 3 − 92 − 3 | |
| = | −6−1 | |
| = | 6 |
So that m = 6 in this case.
Solution:
| gradient | = | y2 − y1 x2 − x1 |
| = | −1 − 22 − (−1) | |
| = | −1 |
So that m = −1 in this case. We shall interpret the negative gradient later in this module.
Solution:
| gradient | = | y2 − y1 x2 − x1 |
| = | 3 − 24 − 1 | |
| = | 13 |
So that m = 1 ⁄ 3 in this case.
Click on questions to reveal solutions
3. Intercepts of a Straight Line
By putting x = 0 into the equation y = mx + c, the point where the straight line crosses the y axis is found to be y = c. This is known as the intercept on the y axis. The intercept on the x axis, i.e. when y = 0, is at:
The intercepts are shown in the figure to the right. |
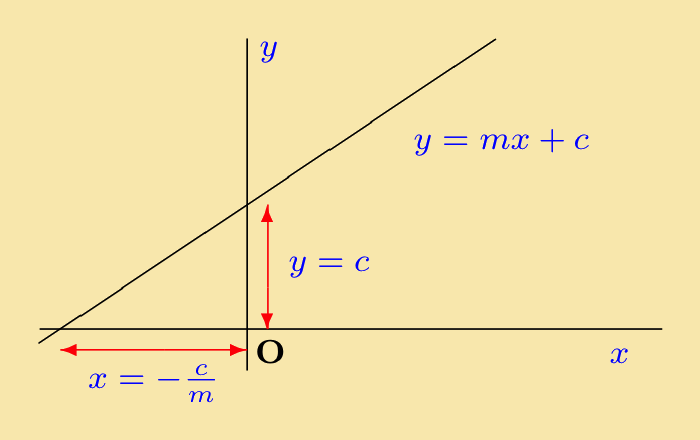
|
Example 3: By rearranging the equation 2y − 3x − 5 = 0, show that it is a straight line and find its gradient and intercept. Sketch the line.
Solution:
Rearranging the equation:
|
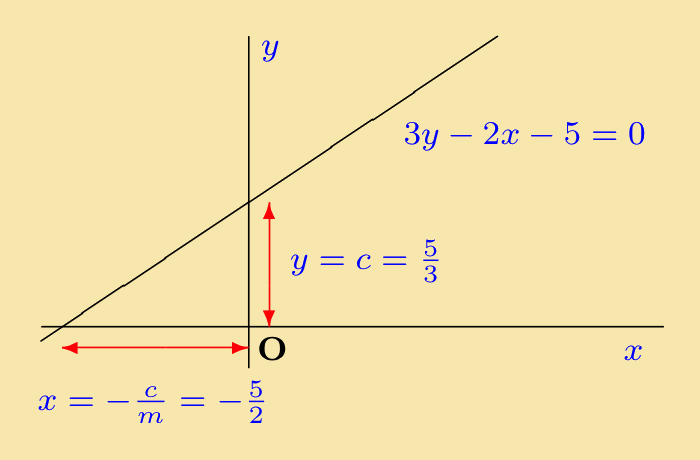
|
Exercise 3: Each of the following equations represent straight lines. By rearranging each of them find their gradient and the intercepts on the y and x axis. Sketch the straight lines they represent.
Solution:
So that m = 1 and c = −3 ⁄ 2 The intercept on the x-axis is:
−c ⁄ m = −(−3 ⁄ 2) ⁄ 1 = 3 ⁄ 2
|
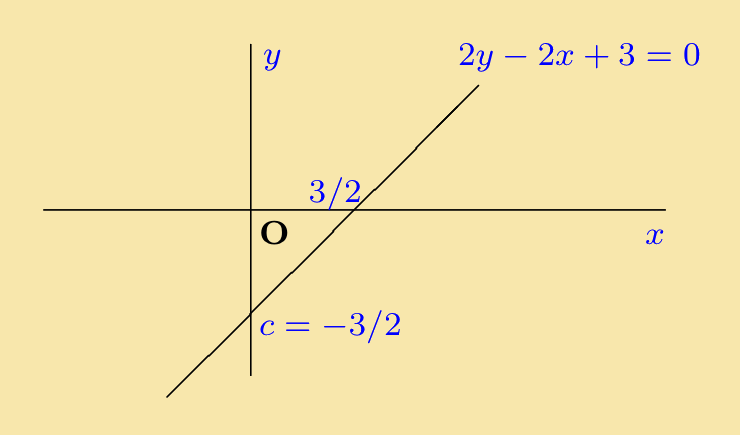
|
Solution:
So that m = 15 ⁄ 3 and c = −2 The intercept on the x-axis is:
−c ⁄ m = −(−2 ⁄ 2) ⁄ (5 ⁄ 3) = 6 ⁄ 5
|
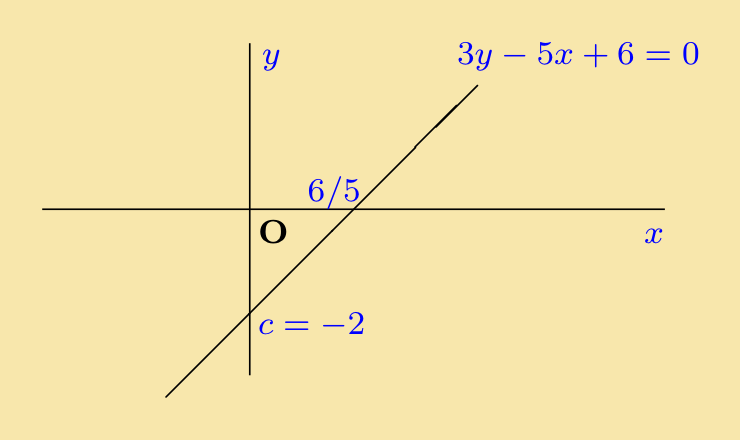
|
Solution:
So that m = −2 and c = −3 ⁄ 2 The intercept on the x-axis is:
−c ⁄ m = −(−3 ⁄ 2) ⁄ (−2) = −3 ⁄ 4
|
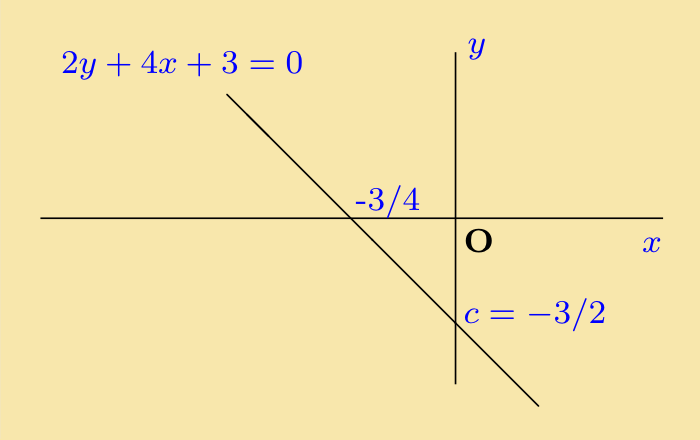
|
Click on questions to reveal solutions
Quiz 1: A straight line has the equation 3x + y + 3 = 0. If P is the point where the line crosses the x axis and Q is the point where it crosses the y axis, which of the following pair is P, Q?
The line crosses the x-axis when y = 0. Putting this into the equation of the line, 3x + y + 3 = 0, gives:
| 3x + 0 + 3 | = | 0 |
| 3x | = | −3 |
| x | = | −1 |
Thus P(−1,0) is the first point.
The line crosses the y-axis when x = 0. Putting this into the equation of the line:
| 3(0) + y + 3 | = | 0 |
| y + 3 | = | 0 |
| y | = | −3 |
Thus, Q(0,−3) is the second point.
Quiz 2: If the straight line 6x + 2y = 3 is written in the form y = mx + c, which of the following is the correct set of values for m and c?
The equation is rearranged as follows:
| 6x + 2y | = | 3 |
| 2y | = | −6x + 3 |
| y | = | -3x + 3 ⁄ 2 |
So m = −3 and c = 3 ⁄ 2
4. Positive and Negative Gradients
If a line has gradient m = 1 then, providing that the scales are the same for both axes, it makes an angle of 45° with the positive x-axis. If m > 1 then the gradient is steeper. If 0 < m < 1 then the line makes an angle between 0° and 45° with the positive x-axis. This is illustrated in the figure to the right.
|
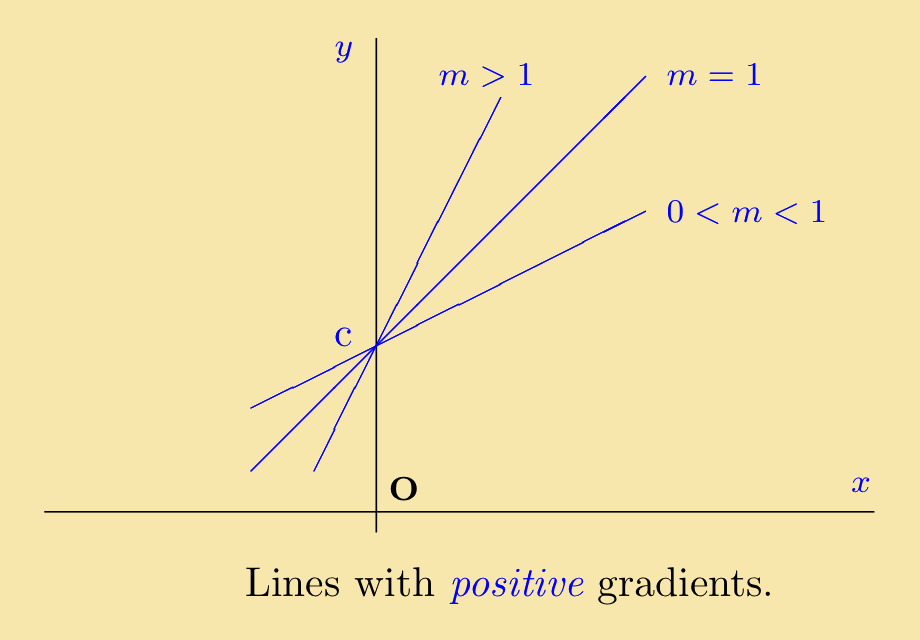
|
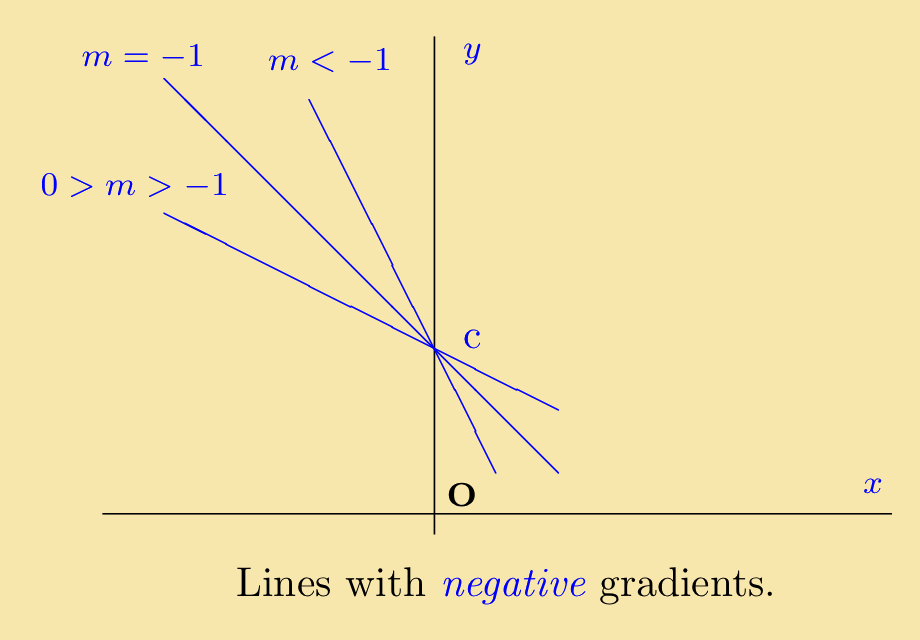 |
The figure on the left illustrates lines similar to those of the previous figure, except with negative gradients. They are the mirror images of the straight lines shown above, with the y axis acting as the mirror. |
Exercise 4: In each of the following either the coordinates of two points, P, Q are given, or the coordinates of a single point R and a gradient m. In each case, find the equation of the line:
Solution: Let the line be y = mx + c. Since both P (1, 1) and Q(2,−1) lie on the line, both sets of coordinates must satisfy the equation. Thus we have:
| 1 | = | m × 1 + c | ⇐ using the coordinates of P | |
| −1 | = | m × 2 + c | ⇐ using the coordinates of Q | |
| or: | m + c | = | 1 | |
| 2m + c | = | −1 |
This is a set of simultaneous equations which can be solved to give m = −2 and c = 3. (See the module on simultaneous equations for the technique for solving them.) The required equation is thus:
Substituting the coordinates for P and then Q into this equation will confirm that this line passes through both of these points.
Solution: Since m = 2, the equation must have the form y = 2x + c and only the value of c remains to be found. The line passes through R(1, 2) so the coordinates of this point must satisfy the equation. Thus:
| y | = | 2x + c | |
| 2 | = | 2 × 1 + c | ⇐ using the coordinates of R |
- giving c = 0. The equation of the line is now:
Solution: Let the line be y = mx + c . Since both P(−1, 2) and Q(1, −3) lie on the line, both sets of coordinates must satisfy the equation. Thus we have:
| 2 | = | m × (−1) + c | ⇐ using the coordinates of P | |
| −3 | = | m × 1 + c | ⇐ using the coordinates of Q | |
| or: | −m + c | = | 2 | |
| m + c | = | −3 |
This is a pair of simultaneous equations which can be solved to give m = −5 ⁄ 2 and c = −1 ⁄ 2. (See the module on simultaneous equations for the technique for solving them.) The required equation is thus:
Substituting the coordinates for P and then Q into this equation will confirm that this line passes through both of these points.
Solution: Since m = 4, the equation must have the form y = 4x + c and only c remains to be found. The line passes through R(−2, 1) so the coordinates of this point must satisfy the equation. Thus:
| y | = | 4x + c | ||
| 1 | = | 4 × (−2) + c | ⇐ using the coordinates of R | |
| or: | −8 + c | = | 1 | |
| c | = | 9 |
and the equation of the line is :
Solution: Let the line be y = mx + c. The coordinates P(−1, 2) and Q(−3, 3) both lie on the line so both sets of coordinates must satisfy the equation. We have:
| 2 | = | m × (−1) + c | ⇐ using the coordinates of P | |
| 3 | = | m × (−3) + c | ⇐ using the coordinates of Q | |
| or: | −m + c | = | 2 | |
| −3m + c | = | 3 |
This set of simultaneous equations can be solved to give m = −1/2 and c = 3/2. (See the module on simultaneous equations for the technique for solving them.) The required equation is thus:
Substituting the coordinates for P and then Q into this equation will confirm that this line passes through both of these points.
Solution: Let the line be y = mx + c . Both P(1, 2) and Q(−4, 7) both lie on the line so both sets of coordinates must satisfy the equation. We have:
| 2 | = | m × (1) + c | ⇐ using the coordinates of P | |
| 7 | = | m × (−4) + c | ⇐ using the coordinates of Q | |
| or: | m + c | = | 2 | |
| −4m + c | = | 7 |
The solution to this set of simultaneous equations is m = −1 and c = 3. (See the module on simultaneous equations for the technique for solving them.) The equation of the line is thus:
Substituting the coordinates for P and then Q into this equation will confirm that this line passes through both of these points.
Example 5: Two lines are described as follows: the first has gradient −1 and passes through the point R(2, 1); the second passes through the two points with coordinates P(2, 0) and Q(0, 4). Find the equation of both lines and find the coordinates of their point of intersection.
Solution: The first line has gradient m = −1 so it must be y = (−1)x + c, i.e. y = −x + c, for some c. Since the line passes through the point R(2, 1) these values of x, y must satisfy the equation. Thus 2 = −(1) + c so c = 3. The first line therefore has equation y = −x + 3. For the second case both points lie on the line and so satisfy the equation. If the equation is y = mx + c then putting these values into the equation gives:
| y | = | mx + c | |
| 0 | = | 2m + 3 | ⇐ using the coordinates of P |
| 4 | = | c | ⇐ using the coordinates of Q |
These equations yield m = −2 and c = 4. The second line thus has the equation y = −2x + 4. The equations of the two lines can now be rewritten as:
| y + x = 3 | (1) |
| y + 2x = 4 | (2) |
5. Some Useful Facts
- Parallel lines have the same gradient. Thus, for example, the lines with equations y = 3x + 7 and y = 3x − 2 are parallel.
- Lines parallel to the x-axis have equations of the form y = k, for some constant, k.
- Lines parallel to the y-axis (when m = 0) have equations of the form x = k, for some constant, k.
- The larger the absolute value of m, the ‘steeper’ the slope of the line.
- If two lines intersect at right angles then the product of their gradients is −1. The lines y = −7x + 4 and y = (1 ⁄ 7)x + 5, for example, intersect each other at right angles.
6. Quiz on Straight Line Graphs
In each of the following, choose the solution from the options given:
1. What is the equation of the straight line through P (−5, 4) and Q(2, −3) ?
2. What are the gradient m and intercept c of −2x + 3y + 6 = 0 ?
3. What is the equation of the straight line with gradient m = −3 passing through R(−1, 3) ?
4. What is the point of intersection of the lines 2x + y = 1 and 3x − 2y = 5 ?
