Functions
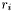 and the Jacobian matrix.
and the Jacobian matrix. 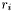 .
. 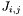 with a new parameter.
with a new parameter. stderr. These robust routines are implemented using the GNU Scientific Library. The user can choose which of the two Levenberg-Marquardt algorithms available in the GSL to use.
Functions | |
| int | lstsq_main (void *void_gsl_fit_struct) |
| The main function for performing method of least squares fitting. | |
| int | lstsq_fdf (const gsl_vector *parameters, void *void_gsl_fit_struct, gsl_vector *r, gsl_matrix *J) |
A routine which calculates the residuals 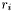 and the Jacobian matrix. and the Jacobian matrix. | |
| int | lstsq_f (const gsl_vector *parameters, void *void_gsl_fit_struct, gsl_vector *r) |
A routine which calculates the residuals 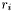 . . | |
| int | lstsq_df (const gsl_vector *parameters, void *void_gsl_fit_struct, gsl_matrix *J) |
| A routine which calculates the Jacobian matrix. | |
| double | lstsq_derivatives (double p, void *void_gsl_fit_struct) |
A routine which calculates 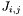 with a new parameter. with a new parameter. | |
| int | lstsq_status (gsl_fit *gft, int iteration, gsl_multifit_fdfsolver *s, gsl_matrix *c) |
A fitting status update printed to stderr. | |
| int lstsq_main | ( | void * | void_gsl_fit_struct | ) |
| void_gsl_fit_struct | A void pointer, expected to be a gsl_fit. |
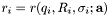 , with respect to a set of parameters
, with respect to a set of parameters ![$\mathbf{a}=[a_1, a_2, \ldots]$](form_14.png) . The function to be minimized is given by,
. The function to be minimized is given by,
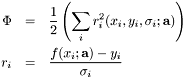
where the sum is over the data points 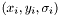 .
.
The iteration can be stopped by an error, or by successful completion. There are two stopping criterion, and the iteration stops on the success of either one. The first is when the gradient falls below a tolerance level. The test can be summarized as,
![\[ \left|\frac{\partial\Phi}{\partial a_i}\right| \leq \epsilon. \]](form_17.png)
The second stop test compares the residuals, 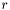 , of the last step with the residuals of the current step according to,
, of the last step with the residuals of the current step according to,
![\[ |r^{i-1}| \leq \epsilon_{\mathrm{absolute}} + \epsilon_{\mathrm{relative}}|r^i| \]](form_19.png)
Perhaps a later version will allow user configuration of the tolerances.
As in the other fitting methods, the GSL library takes a (void *) struct as the fitting parameters, so this is set to be the gsl_fit struct. In this way the data is totally accessible. The parameters are overwritten with this technique, however, since the gsl_fit struct is used as workspace.
Definition at line 10 of file gsl_lstsq.c.
00011 { 00012 unsigned int count, i; 00013 int stop1, stop2; 00014 gsl_vector *guess; 00015 gsl_vector *gradt; 00016 gsl_matrix *covar; 00017 gsl_multifit_function_fdf lstsq_func; 00018 gsl_multifit_fdfsolver *solvr; 00019 gsl_fit *gft; 00020 00021 gft = (gsl_fit *)void_gsl_fit_struct; 00022 00023 /* Inital guess is the paramters as they were passed into here */ 00024 guess = gsl_vector_alloc(gft->para.num); 00025 for (i=0; i<gft->para.num; i++) 00026 { 00027 gsl_vector_set(guess, i, gft->para.par[i]); 00028 } 00029 00030 /* count the number of data points */ 00031 count = 0; 00032 for (i=0; i<gft->numd; i++) count += gft->data[i].num; 00033 00034 /* need this vector for stop test #2 */ 00035 gradt = gsl_vector_alloc(gft->para.num); 00036 00037 /* covariant matrix */ 00038 covar = gsl_matrix_alloc(gft->para.num,gft->para.num); 00039 00040 lstsq_func.f = &lstsq_f; 00041 lstsq_func.df = &lstsq_df; 00042 lstsq_func.fdf = &lstsq_fdf; 00043 lstsq_func.n = count; /* number of data points */ 00044 lstsq_func.p = gft->para.num; /* number of paramters */ 00045 lstsq_func.params = (void *)gft; /* pass the full gsl_fit struct */ 00046 00047 solvr = gsl_multifit_fdfsolver_alloc(gft->meth.lstsq_type, \ 00048 lstsq_func.n, lstsq_func.p); 00049 00050 /*==================================================*/ 00051 count = 0; 00052 gsl_multifit_fdfsolver_set(solvr, &lstsq_func, guess); 00053 gsl_multifit_covar(solvr->J, 0.0, covar); 00054 lstsq_status(gft, count, solvr, covar); 00055 00056 do 00057 { 00058 count++; 00059 stop1 = gsl_multifit_fdfsolver_iterate(solvr); 00060 gsl_multifit_covar(solvr->J, 0.0, covar); 00061 lstsq_status(gft, count, solvr, covar); 00062 00063 if (stop1) 00064 { 00065 fprintf(stderr,"STATUS: %s\n", gsl_strerror(stop1)); 00066 break; 00067 } 00068 00069 /* Stop test #1 */ 00070 stop1 = gsl_multifit_test_delta(solvr->dx, solvr->x, 1e-6, 1e-6); 00071 00072 /* Stop test #2 */ 00073 gsl_multifit_gradient(solvr->J, solvr->f, gradt); 00074 stop2 = gsl_multifit_test_gradient(gradt, 1e-6); 00075 00076 if ((stop1==GSL_SUCCESS) && (stop2==GSL_SUCCESS)) 00077 { 00078 fprintf(stderr,"STATUS: %s\n", gsl_strerror(stop1)); 00079 } 00080 00081 } while (((stop1 == GSL_CONTINUE) || (stop2 == GSL_CONTINUE)) \ 00082 && (count < gft->maxi)); 00083 00084 /*==================================================*/ 00085 gsl_multifit_covar(solvr->J, 0.0, covar); 00086 lstsq_status(gft, -1, solvr, covar); 00087 00088 /*==================================================*/ 00089 00090 gsl_multifit_fdfsolver_free(solvr); 00091 gsl_matrix_free(covar); 00092 gsl_vector_free(guess); 00093 gsl_vector_free(gradt); 00094 00095 return GSL_SUCCESS; 00096 }
| int lstsq_fdf | ( | const gsl_vector * | parameters, | |
| void * | void_gsl_fit_struct, | |||
| gsl_vector * | r, | |||
| gsl_matrix * | J | |||
| ) |
| parameters | A gsl_vector containing the trial parameters | |
| void_gsl_fit_struct | A void pointer, expected to be a gsl_fit. | |
| r | A gsl_vector containing the residuals 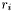 , defined above. , defined above. | |
| J | A gsl_matrix containing the Jacobian matrix. |
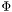 with respect to the parameters. This function does nothing but call the functions
with respect to the parameters. This function does nothing but call the functions lstsq_f and lstsq_df to do the work.
Definition at line 100 of file gsl_lstsq.c.
00103 { 00104 lstsq_f (parameters, void_gsl_fit_struct, r); 00105 lstsq_df(parameters, void_gsl_fit_struct, J); 00106 return GSL_SUCCESS; 00107 }
| int lstsq_f | ( | const gsl_vector * | parameters, | |
| void * | void_gsl_fit_struct, | |||
| gsl_vector * | r | |||
| ) |
| parameters | A gsl_vector containing the trial parameters | |
| void_gsl_fit_struct | A void pointer, expected to be a gsl_fit. | |
| r | A gsl_vector containing the residuals 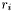 , defined above. , defined above. |
![\[ r_i = \frac{f(x_i;\mathbf{a}) - y_i}{\sigma_i} \]](form_22.png)
The length of the vecotr f is 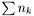 , where
, where 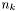 is the number of data points in data set
is the number of data points in data set 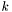
Definition at line 111 of file gsl_lstsq.c.
00114 { 00115 int i, j, k; 00116 int r_index; 00117 double tmp; 00118 gsl_fit *gft; 00119 00120 gft = (gsl_fit *)void_gsl_fit_struct; 00121 /* 00122 ** Load the params back into the parameter array. 00123 ** Why should we do this step? 00124 ** We could say below that p = params.data + d->func[j].idx 00125 */ 00126 for(i=0; i<gft->para.num; i++) 00127 { 00128 gft->para.par[i] = gsl_vector_get(parameters, i); 00129 } 00130 /* 00131 ** Loop over the data sets with index k. 00132 */ 00133 r_index = 0; 00134 for (k=0; k<gft->numd; k++) 00135 { 00136 /* 00137 ** Loop over the data points with index i 00138 */ 00139 for (i=0; i<gft->data[k].num; i++) 00140 { 00141 /* 00142 ** Loop over the functions with index j 00143 */ 00144 tmp = 0.0; 00145 for (j=0; j<gft->numf; j++) 00146 { 00147 if (gft->type==MULTIPLE) 00148 { 00149 tmp += gft->func[j].fun_m(gft->data[k].xpt[i], \ 00150 gft->para.par + gft->func[j].idx, \ 00151 k, j); 00152 } 00153 else 00154 { 00155 tmp += gft->func[j].fun_s(gft->data[k].xpt[i], \ 00156 gft->para.par + gft->func[j].idx); 00157 } 00158 } 00159 tmp = (tmp - gft->data[k].ypt[i]) / gft->data[k].sig[i]; 00160 gsl_vector_set(r, r_index, tmp); 00161 r_index++; 00162 } 00163 } 00164 return GSL_SUCCESS; 00165 }
| int lstsq_df | ( | const gsl_vector * | parameters, | |
| void * | void_gsl_fit_struct, | |||
| gsl_matrix * | J | |||
| ) |
| parameters | A gsl_vector containing the trial parameters | |
| void_gsl_fit_struct | A void pointer, expected to be a gsl_fit. | |
| J | A gsl_matrix containing the Jacobian matrix. |
![\[ J_{i,j} = \frac{\mathrm{d}r_i}{\mathrm{d}a_j} \]](form_26.png)
where the residuals 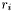 are given by
are given by
![\[ r_i = \frac{f(x_i;\mathbf{a}) - y_i}{\sigma_i} \]](form_22.png)
The number of rows of the Jacobian is 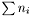 , where
, where 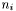 is the number of data points in data set
is the number of data points in data set 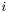 . The number of columns is
. The number of columns is 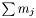 , where
, where 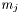 is the number of parameters in function
is the number of parameters in function 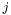
It uses gsl_deriv_central as a numerical method to calculate the derivatives. In order for this to work, we need a sub-fucntion that calculates 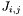 with the new parameter. This is what
with the new parameter. This is what lstsq_derivatives does. In order for lstsq_derivatives to know which parameter is currently being tested, the index gfc->para.idx is set. To know which data point is being tested, the data set index gfc->idx and the data point gfc->data[gfc->idx].idx are both set.
If a parameter is to be held fixed, then 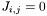 .
.
Definition at line 169 of file gsl_lstsq.c.
00172 { 00173 int i, j, k; 00174 int r_index; 00175 double res, err; 00176 gsl_function F; 00177 gsl_fit *gft; 00178 00179 gft = (gsl_fit *)void_gsl_fit_struct; 00180 /* 00181 ** Load the params back into the parameter array. 00182 ** Why should we do this step? 00183 ** We could say below that p = params.data + d->func[j].idx 00184 */ 00185 for(i=0; i<gft->para.num; i++) 00186 { 00187 gft->para.par[i] = gsl_vector_get(parameters,i); 00188 } 00189 00190 F.params = void_gsl_fit_struct; 00191 F.function = &lstsq_derivatives; 00192 00193 /* 00194 ** Loop over the data sets with index k. 00195 */ 00196 r_index = 0; 00197 for (k=0; k<gft->numd; k++) 00198 { 00199 gft->indx = k; 00200 /* 00201 ** The jacobian mtirx J_ij = d(r_i)/d(a_j) 00202 ** => i is the data index of residual r 00203 ** => j is the parameter index 00204 */ 00205 /* 00206 ** Loop over the data points with index i 00207 */ 00208 for (i=0; i<gft->data[k].num; i++) 00209 { 00210 gft->data[k].idx = i; 00211 /* 00212 ** Loop over the parameters with index j 00213 */ 00214 00215 for (j=0; j<gft->para.num; j++) 00216 { 00217 gft->para.idx = j; 00218 /* 00219 ** If fixed, J_ij = 0 00220 */ 00221 if (gft->para.fix[j]) res=0.0; 00222 else gsl_deriv_central(&F, gft->para.par[j], 1e-4, &res, &err); 00223 gsl_matrix_set(J, r_index, j, res); 00224 } 00225 r_index += 1; 00226 } 00227 } 00228 00229 return GSL_SUCCESS; 00230 }
| double lstsq_derivatives | ( | double | p, | |
| void * | void_gsl_fit_struct | |||
| ) |
| p | The new parameter to evaluate 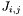 with with | |
| void_gsl_fit_struct | A void pointer, expected to be a gsl_fit. |
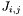 .
.
This routine is called repeatedly by gsl_deriv_central which is a numerical method to calculate the derivative. Each time this function is called, it is with a slightly changing parameter 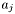
In order for lstsq_derivatives to know which parameter is currently being tested, the index gfc->para.idx is set. To know which data point is being tested, the data set index gfc->idx and the data point index gfc->data[_gfc->idx].idx are set.
Definition at line 234 of file gsl_lstsq.c.
00235 { 00236 int i, j; 00237 double tmp; 00238 gsl_fit *gft; 00239 00240 gft = (gsl_fit *)void_gsl_fit_struct; 00241 /* 00242 ** We need a complete set of paramters 'tmp', 00243 ** with the derivative parameter 'p' 00244 ** replacing the parameter at index 'd->para.idx'. 00245 */ 00246 for(i=0; i<gft->para.num; i++) gft->para.tmp[i] = gft->para.par[i]; 00247 gft->para.tmp[gft->para.idx] = p; 00248 00249 tmp = 0.0; 00250 i = gft->data[gft->indx].idx; 00251 for (j=0; j<gft->numf; j++) 00252 { 00253 if (gft->type == MULTIPLE) 00254 { 00255 tmp += gft->func[j].fun_m(gft->data[gft->indx].xpt[i], \ 00256 gft->para.tmp+gft->func[j].idx, \ 00257 gft->indx, j); 00258 } 00259 else 00260 { 00261 tmp += gft->func[j].fun_s(gft->data[gft->indx].xpt[i], \ 00262 gft->para.tmp+gft->func[j].idx); 00263 } 00264 } 00265 tmp = (tmp - gft->data[gft->indx].ypt[i]) / gft->data[gft->indx].sig[i]; 00266 return tmp; 00267 }
| int lstsq_status | ( | gsl_fit * | gft, | |
| int | iteration, | |||
| gsl_multifit_fdfsolver * | s, | |||
| gsl_matrix * | c | |||
| ) |
| gft | A gsl_fit. | |
| iteration | The current iteration of the fitting method | |
| s | A gsl_multifit_fdfsolver containing the current state of the fit. | |
| c | A gsl_matrix conatining the covarient matrix. |
stderr. The covarant matrix is used to determine the error in the fitted paramters.
Definition at line 271 of file gsl_lstsq.c.
00275 { 00276 int j; 00277 double chisq; 00278 00279 if (iteration >= 0) 00280 { 00281 fprintf(stderr,"ITERATION:%3u ", iteration); 00282 fprintf(stderr,"===================\n"); 00283 } 00284 else 00285 { 00286 fprintf(stderr,"COMPLETE "); 00287 fprintf(stderr,"===================\n"); 00288 } 00289 chisq = gsl_blas_dnrm2(s->f)/(double)((gft->numd)-(gft->para.num)); 00290 fprintf(stderr,"ChiSq: %12.6e\n", chisq); 00291 00292 for (j=0; j<gft->para.num; j++) 00293 { 00294 fprintf(stderr,"%3d: %12.6f +/- %8.6f\n", 00295 j, 00296 gsl_vector_get(s->x, j), 00297 sqrt(gsl_matrix_get(c, j, j))); 00298 } 00299 fprintf(stderr,"\n"); 00300 00301 if (iteration < 0) 00302 { 00303 for (j=0; j<gft->para.num; j++) 00304 { 00305 gft->para.par[j] = gsl_vector_get(s->x, j); 00306 gft->para.err[j] = sqrt(gsl_matrix_get(c, j, j)); 00307 } 00308 gft->chis = chisq; 00309 } 00310 00311 return GSL_SUCCESS; 00312 }
 1.4.7
1.4.7