| int lstsq_main | ( | Parratt * | d | ) |
The method minimizes the sum of residuals 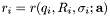 , with respect to a set of parameters
, with respect to a set of parameters ![$\mathbf{a}=[a_1, a_2, \ldots]$](form_6.png) , which define the layered structure. The function to be minimized is given by,
, which define the layered structure. The function to be minimized is given by,
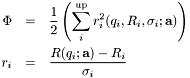
where the sum is over the data points 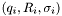 .
.
The iteration can be stopped by an error, or by successful completion. There are two stopping criterion, and the iteration stops on the success of either one. The first is when the gradient falls below a tolerance level. The test can be summarized as,
![\[ \left|\frac{\partial\Phi}{\partial a_i}\right| \leq \epsilon. \]](form_9.png)
The second stop test compares the residuals, 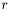 , of the last step with the residuals of the current step according to,
, of the last step with the residuals of the current step according to,
![\[ |r^{i-1}| \leq \epsilon_{\mathrm{absolute}} + \epsilon_{\mathrm{relative}}|r^i| \]](form_10.png)
Perhaps a later version will allow user configuration of the tolerances.
As in the other fitting methods, the GSL library takes a (void *) struct as the fitting parameters, so this is set to be the Parratt struct. In this way the data is totally accessible. The parameters are overwritten with this technique, however, since the Parratt struct is used as workspace.
The code requires one external function, calcReflectivity(), which takes the form
double calcReflectivity(double q, double *a, Parratt *p)
- Parameters:
-
q The 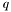 value to evaluate
value to evaluate 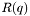 .
. a The set of all adjustable parameters in one array. p The Parratt struct containing all the other information necessary for calculation of 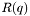 .
.
- Returns:
- The reflectivity
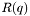 .
.
00023 { 00024 unsigned int iter; 00025 int status, status2, ndat; 00026 gsl_vector *guess; 00027 gsl_vector *gradt; 00028 gsl_matrix *covar; 00029 gsl_multifit_function_fdf my_func; 00030 gsl_multifit_fdfsolver *solv; 00031 00032 /* Initial guess */ 00033 guess = gsl_vector_alloc(d->m.num); 00034 for (iter=0; iter<d->m.num; iter++) 00035 { 00036 gsl_vector_set(guess, iter, d->m.par[iter]); 00037 } 00038 00039 /* Need for stop test #2 */ 00040 gradt = gsl_vector_alloc(d->m.num); 00041 00042 /* Co-variant matrix */ 00043 covar = gsl_matrix_alloc(d->m.num,d->m.num); 00044 00045 my_func.f = &lstsq_f; 00046 my_func.df = &lstsq_df; 00047 my_func.fdf = &lstsq_fdf; 00048 /* Number of data points */ 00049 if (d->s.pntp == POLARIZED) ndat = d->d1.num + d->d2.num; 00050 else ndat = d->d1.num; 00051 my_func.n = ndat; 00052 /* Number of parameters */ 00053 my_func.p = d->m.num; 00054 my_func.params = (void *)d; 00055 00056 solv = gsl_multifit_fdfsolver_alloc(fit_method.lstsq_type, \ 00057 ndat, d->m.num); 00058 00059 /*==================================================*/ 00060 iter = 0; 00061 gsl_multifit_fdfsolver_set(solv, &my_func, guess); 00062 gsl_multifit_covar(solv->J, 0.0, covar); 00063 lstsq_status(iter, solv, covar, d); 00064 00065 do 00066 { 00067 iter++; 00068 status = gsl_multifit_fdfsolver_iterate(solv); 00069 gsl_multifit_covar(solv->J, 0.0, covar); 00070 lstsq_status(iter, solv, covar, d); 00071 00072 if (status) 00073 { 00074 fprintf(stderr,"STATUS: %s\n", gsl_strerror(status)); 00075 break; 00076 } 00077 00078 /* Stop test #1 */ 00079 status = gsl_multifit_test_delta(solv->dx, solv->x, 1e-7, 1e-7); 00080 00081 /* Stop test #2 */ 00082 gsl_multifit_gradient(solv->J, solv->f, gradt); 00083 status2 = gsl_multifit_test_gradient(gradt, 1e-7); 00084 00085 if ((status==GSL_SUCCESS) || (status2==GSL_SUCCESS)) 00086 { 00087 fprintf(stderr,"STATUS1: %s\n", gsl_strerror(status)); 00088 fprintf(stderr,"STATUS2: %s\n", gsl_strerror(status2)); 00089 } 00090 00091 } while ((status == GSL_CONTINUE) && \ 00092 (status2 == GSL_CONTINUE) && \ 00093 (iter < MAX_ITER)); 00094 00095 /*==================================================*/ 00096 gsl_multifit_covar(solv->J, 0.0, covar); 00097 lstsq_status(-1, solv, covar, d); 00098 00099 /*==================================================*/ 00100 00101 gsl_multifit_fdfsolver_free(solv); 00102 gsl_matrix_free(covar); 00103 gsl_vector_free(guess); 00104 gsl_vector_free(gradt); 00105 00106 return GSL_SUCCESS; 00107 }
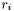 .
. ![\[ J_{ij} = \partial r_i/\partial a_j. \]](form_13.png)
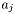 .
. 1.4.7
1.4.7