Functions
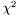 .
. 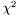 .
. 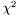 .
. 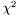 .
. stdout. 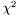 with respect to the parameters to choose the direction of minimization.
with respect to the parameters to choose the direction of minimization.
The routine is implemented using the GNU Scientific library. By using the fit_method struct, the user can choose which of the four complex conjugate algorithms available in the GSL to use. None of the routines, however, are quite as robust as the least squares method.
Functions | |
| int | mdmin_main (Parratt *d) |
| The main function for multidimensional minimization. | |
| void | mdmin_fdf (const gsl_vector *params, void *data, double *f, gsl_vector *df) |
| Called by the solver. | |
| double | mdmin_f (const gsl_vector *params, void *data) |
Calculates 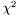 . . | |
| void | mdmin_df (const gsl_vector *params, void *data, gsl_vector *df) |
Calculates the gradient of 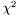 . . | |
| double | mdmin_derivatives (double p, void *data) |
Help calculate the gradient of 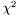 . . | |
| double | mdmin_chisq (double *p, Parratt *d) |
Calculates 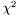 . . | |
| void | mdmin_status (int i, gsl_multimin_fdfminimizer *s, Parratt *d) |
Updates the fit to stdout. | |
| int mdmin_main | ( | Parratt * | d | ) |
The method minimizes 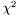 , with respect to a set of parameters
, with respect to a set of parameters ![$\mathbf{a}=[a_1,a_2,\ldots]$](form_16.png) , which define the layered model structure. The function
, which define the layered model structure. The function 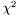 is given by,
is given by,
![\[ \chi^2 = \frac{1}{n-p} \sum_{i} \left(\frac{R(q_i;\mathbf{a}) - R_i}{\sigma_i}\right)^2 \]](form_17.png)
where the sum is over the data points 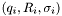 ,
, 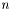 is the number of data points, and
is the number of data points, and 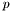 the total number of parameters. This is not exactly correct, since
the total number of parameters. This is not exactly correct, since 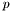 should be the number of parameters not being held fixed.
should be the number of parameters not being held fixed.
The iteration can be stopped by an error, or by successful completion. The stopping criterion is the gradient falls below a tolerance level. The test can be summarized as,
![\[ \left|\frac{\partial\chi^2}{\partial a_i}\right| \leq \epsilon \]](form_20.png)
As in the other fitting methods, the GSL library takes a (void *) struct as the fitting parameters, so this is set to be the Parratt struct. In this way the data is totally accessible. The parameters are overwritten with this technique, however, since the Parratt struct is used as workspace.
One difficulty is the initial step size, since there is only one that must be shared among all the variables. When the SLD and background is given in the scale of 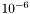 , then all variables hopefully are of the similar order of magnitude, and can be varied by a similar step size.
, then all variables hopefully are of the similar order of magnitude, and can be varied by a similar step size.
The code requires one external function, calcReflectivity(), which takes the form
double calcReflectivity(double q, double *a, Parratt *p)
| q | The 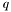 value to evaluate value to evaluate 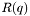 . . | |
| a | The set of all adjustable parameters in one array. | |
| p | The Parratt struct containing all the other information necessary for calculation of 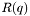 . . |
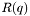 .
. 00023 { 00024 int iter; 00025 int status; 00026 gsl_vector *guess; 00027 gsl_multimin_function_fdf my_func; 00028 gsl_multimin_fdfminimizer *solv; 00029 00030 /* Initial guess */ 00031 guess = gsl_vector_alloc(d->m.num); 00032 for (iter=0; iter<d->m.num; iter++) 00033 { 00034 gsl_vector_set(guess, iter, d->m.par[iter]); 00035 } 00036 00037 my_func.f = &mdmin_f; 00038 my_func.df = &mdmin_df; 00039 my_func.fdf = &mdmin_fdf; 00040 my_func.n = d->m.num; 00041 my_func.params = (void *)d; 00042 00043 solv = gsl_multimin_fdfminimizer_alloc(fit_method.mdmin_type, d->m.num); 00044 00045 /*==================================================*/ 00046 iter = 0; 00047 gsl_multimin_fdfminimizer_set(solv, &my_func, guess, 0.001, 1e-6); 00048 mdmin_status(iter, solv, d); 00049 00050 do 00051 { 00052 iter++; 00053 status = gsl_multimin_fdfminimizer_iterate(solv); 00054 mdmin_status(iter, solv, d); 00055 00056 if (status) 00057 { 00058 fprintf(stderr,"STATUS: %s\n", gsl_strerror(status)); 00059 break; 00060 } 00061 00062 status = gsl_multimin_test_gradient(solv->gradient, 1e-7); 00063 00064 if (status==GSL_SUCCESS) 00065 { 00066 fprintf(stderr,"STATUS: %s\n", gsl_strerror(status)); 00067 } 00068 00069 } while ((status == GSL_CONTINUE) && (iter < MAX_ITER)); 00070 00071 mdmin_status(-1, solv, d); 00072 00073 gsl_multimin_fdfminimizer_free(solv); 00074 gsl_vector_free(guess); 00075 return GSL_SUCCESS; 00076 }
| void mdmin_fdf | ( | const gsl_vector * | params, | |
| void * | data, | |||
| double * | f, | |||
| gsl_vector * | df | |||
| ) |
| double mdmin_f | ( | const gsl_vector * | params, | |
| void * | data | |||
| ) |
This uses mdmin_chisq() for the given parameters to return 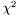 . This is a required function by the GSL , so it is essentially a do-nothing function.
. This is a required function by the GSL , so it is essentially a do-nothing function.
00086 { 00087 int i; 00088 double tmp; 00089 Parratt *d; 00090 00091 d = (Parratt *)data; 00092 00093 /* put the parameters back into the fit struct */ 00094 for (i=0; i<d->m.num; i++) 00095 { 00096 d->m.par[i] = gsl_vector_get(params,i); 00097 } 00098 00099 tmp = mdmin_chisq(d->m.par, (Parratt *)data); 00100 return tmp; 00101 }
| void mdmin_df | ( | const gsl_vector * | params, | |
| void * | data, | |||
| gsl_vector * | df | |||
| ) |
Calculates the vector df, which is defined as 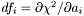 , for the given parameters, using numerical derivatives. If the parameter is to be held fixed, then the gradient is set to zero.
, for the given parameters, using numerical derivatives. If the parameter is to be held fixed, then the gradient is set to zero.
00104 { 00105 int i, j; 00106 gsl_function F; 00107 double res, err; 00108 Parratt *d; 00109 00110 d = (Parratt *)data; 00111 00112 for (i=0; i<d->m.num; i++) 00113 { 00114 d->m.par[i] = gsl_vector_get(params,i); 00115 } 00116 00117 F.params = data; 00118 F.function = &mdmin_derivatives; 00119 00120 for (j=0; j<d->m.num; j++) 00121 { 00122 d->m.idx = j; 00123 if (d->m.fix[j]) res=0.0; 00124 else gsl_deriv_central(&F, d->m.par[j], 1e-4, &res, &err); 00125 gsl_vector_set(df, j, res); 00126 } 00127 00128 return; 00129 }
| double mdmin_derivatives | ( | double | p, | |
| void * | data | |||
| ) |
This function is needed by gsl_deriv_central to return the value of the 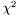 at slightly changing values of one of the parameters.
at slightly changing values of one of the parameters.
In order for this trick to work, the parameter that the derivative is with respect to is flagged by d->m.idx . The value of the other parameters, which are held fix as gsl_deriv_central figure the derivatives were put back into d->m.par in the function mdmin_df(), so are available here.
00132 { 00133 int i; 00134 double tmp, a[MAX_PARAM]; 00135 Parratt *d; 00136 00137 for (i=0; i<MAX_PARAM; i++) a[i]= 0.0; 00138 00139 d = (Parratt *)data; 00140 00141 for (i=0; i<d->m.num; i++) 00142 { 00143 if (d->m.idx==i) a[i] = p; 00144 else a[i] = d->m.par[i]; 00145 } 00146 00147 tmp = mdmin_chisq(a, (Parratt *)data); 00148 return tmp; 00149 }
| double mdmin_chisq | ( | double * | p, | |
| Parratt * | d | |||
| ) |
This function does the work of calculating 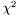 Although the
Although the Parratt struct is passed in, we must use the parameter set provided by the passed parameter p. The purpose of using Parratt is to have access to the raw data and the number of layers.
00152 { 00153 int i; 00154 double tmp, tmp1; 00155 double sum1 = 0.0; 00156 double sum2 = 0.0; 00157 00158 d->g.plz = POLARIZED_UP; 00159 for (i=0; i<d->d1.num; i++) 00160 { 00161 tmp = calcReflectivity(d->d1.xpt[i], p, (Parratt *)d); 00162 tmp1 = (tmp - d->d1.ypt[i]) / (d->d1.sig[i]); 00163 sum1 += (tmp1 * tmp1); 00164 sum2 = (double)(d->d1.num - d->m.num); 00165 } 00166 00167 if (d->s.pntp == POLARIZED) 00168 { 00169 d->g.plz = POLARIZED_DOWN; 00170 for (i=0; i<d->d2.num; i++) 00171 { 00172 tmp = calcReflectivity(d->d2.xpt[i], p, (Parratt *)d); 00173 tmp1 = (tmp - d->d2.ypt[i]) / (d->d2.sig[i]); 00174 sum1 += (tmp1 * tmp1); 00175 } 00176 sum2 +=(double)d->d2.num; 00177 } 00178 00179 tmp = sum1 / sum2; 00180 return tmp; 00181 }
| void mdmin_status | ( | int | i, | |
| gsl_multimin_fdfminimizer * | s, | |||
| Parratt * | d | |||
| ) |
| i | Current iteration | |
| s | Current state of the solution |
00184 { 00185 int j; 00186 double chisq; 00187 00188 if (i >= 0) 00189 { 00190 fprintf(stderr,"ITER:%3u ", i); 00191 fprintf(stderr,"===================\n"); 00192 } 00193 else 00194 { 00195 fprintf(stderr,"RESULT "); 00196 fprintf(stderr,"===================\n"); 00197 } 00198 00199 /* 00200 * Chisq 00201 */ 00202 chisq = mdmin_chisq(d->m.par, d); 00203 00204 /* 00205 * Report results 00206 */ 00207 fprintf(stderr,"ChiSq: %12.6e\n", chisq); 00208 for (j=0; j<d->m.num; j++) 00209 { 00210 if (d->m.fix[j] == 0) 00211 { 00212 fprintf(stderr,"%03d: %12.6f\n", j, gsl_vector_get(s->x, j)); 00213 d->m.par[j] = gsl_vector_get(s->x, j); 00214 } 00215 } 00216 fprintf(stderr,"\n"); 00217 00218 return; 00219 }
 1.4.7
1.4.7