Calculating the reflectivity

For a set of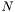 $N$

slabs, that run from the front layer that the neutrons enter, ( $i=0$

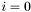), to the bulk layer at the back, ( $i=N+1$

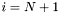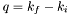), reflectivity can be calculated by the Parratt formalism. The measured wavevector transfer $q=k_f-k_i$

value is determined at scan time by the angle of the scan and the wavelength: 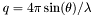$q=4\pi\sin(\theta)/\lambda$ . The incident wavevector normal to the surface in a layer ( $k_i$

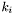) is related to that in vacuum ( $k_v$

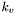) by

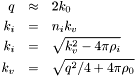
$\begin{eqnarray*} q &\approx& 2k_0 \\ k_i &=& n_ik_v \\ k_i &=& \sqrt{k_v^2-4\pi\rho_i} \\ k_v &=& \sqrt{q^2/4+4\pi\rho_0} \end{eqnarray*}$

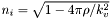where $n_i=\sqrt{1-4\pi\rho/k_v^2}$ is the index of refraction for a layer with total scattering length density $\rho$ .

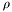The Fresnel reflectiviy between any two layers is given by

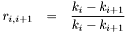
$\begin{eqnarray*} r_{i,i+1} &=& \frac{k_i - k_{i+1}} {k_i - k_{i+1}} \end{eqnarray*}$

The total reflectivity is calculated from back to front assuming there is no refelctivity from the backmost (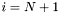 $i=N+1$ ) layer ( 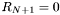$R_{N+1}=0$ ) since it is infinite in extent.

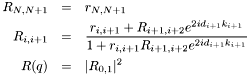
$\begin{eqnarray*} R_{N,N+1} &=& r_{N,N+1} \\ R_{i,i+1} &=& \frac{r_{i,i+1}+R_{i+1,i+2}e^{2id_{i+1}k_{i+1}}} {1+r_{i,i+1}R_{i+1,i+2}e^{2id_{i+1}k_{i+1}}} \\ R(q) &=& |R_{0,1}|^2 \end{eqnarray*}$

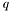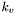The reflectivity of the entire system is given by the reflectivity from the top surface, and is shown in the last line above. Here, $q$ and $k_v$ are real valued, and everything else, including 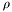$\rho$ , is complex.