Building Guitar Chords : Worked example
Local copy, original at www.phonature.com
Introduction
The fingering for different guitar chords is one of the biggest mysteries in
guitar playing. Even with a chord dictionary of a thousand chords, you might
still fail to find certain chords. The spiral shaped Mathematical Cochlea
scale gives the whole picture of which string is responsible for which tones.
The basic concept of the Mathematical Cochlea is to represent an octave by a
circle which is divided into 12 semi-tones like a clock face. Then for each
chord, we can easily find its variation by choosing notes from different
octaves. How it helps us work out chord fingering becomes clear with the
help of subsequent worked example.
Relating the fretboard to the Mathematical Cochlea
For convenience of discussion, we shall use the standard E guitar tuning in our worked example.
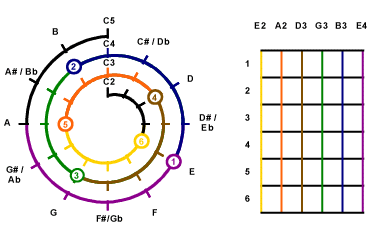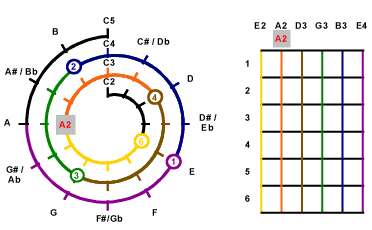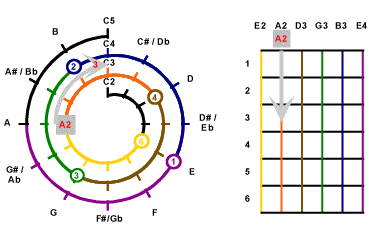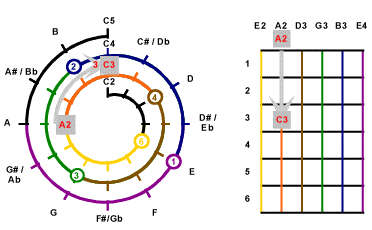
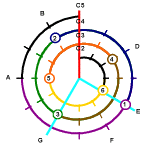
Now let us examine the Mathematical Cochlea scale in more detail.
The normal form is a spiral of 3 revolutions. The inner end at
12 O'clock position is C2 and spirals out in clockwise direction.
So 1 O'clock is C2#, 2 O'clock is D2 and so on. One revolution
from C2 is the second layer of the spiral which is at 12 O'clock
directly above C2, representing C3.
|

|
Now let us examine the Mathematical Cochlea scale in more detail.
The location of the various keys C-D-E-F-G-A-B are labelled around the
outer rim of the spiral. The keys that the 6 strings of a guitar should be
tuned to depends on the tuning. For Standard E tuning, the keys should
be E2-A2-D3-G3-B3-E4. They are marked them as small circles at their
proper locations in the Mathematical Cochlea scale. A number inside
the circle shows which string this tone belongs to. These are target
marks for tuning with the Mathematical Cochlea scale.
|
|
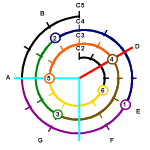
Now let us examine the Mathematical Cochlea scale in more detail.
Now the important thing : To determine how a note should be made,
we can do by simply counting anti-clockwise the number of
semi-tones (1 hour intervals on the clock face) from the nearest
tuning mark. For example, to create the C3 tone, we count
anti-clockwise from the 12 O'clcok position of the inner 2nd layer
of the spiral. At the 9 O'clock position, we find A2 which is
associated with the 5th string. Since 9 O'clock and 12 O'clock is
3 hours interval apart, it means we can play the C3 tone by
pressing the 3 fret position of the 5th string.
|
|
The chord types and spelling
A natural extension of the Pentatonic scale is to further subdivide the wider gaps.
One tone is 8/9 times of the 12 unit tone and another is 9/8 times of the 13.5 unit
tone. If we write the ratios with the lowest tone, we get 1/1, 9/8, 81/64, 4/3, 3/2, 27/16, 243/128, 2/1
respectively.
Now we get back to understanding the meaning of chords and how they are
specified. Basically, the chord type specifies the relative pitch of the
notes, and its name suggests what they are. So let's first get familiar with
the names of the different intervals. Every interval can be written as
a multiple of half tones, which is the smallest interval. A halftone is
represented as 1 hour interval in the Mathematical Cochlea scale. The names
of the interval, and the multiple of half-tone intervals it represents are
tabulated below.
| Semitone Count |
Interva Number |
Name |
| 0 |
1 |
unison |
| 1 |
2b |
diminished 2nd |
| 2 |
2 |
2nd |
| 3 |
3b |
minor 3rd |
| 4 |
3 |
3rd |
| 5 |
4 |
4th or suspended third |
| 6 |
5b 4# |
diminished 5th or augmented fourth |
| 7 |
5 |
5th |
| 8 |
5# 6b |
augmented 5th or minor 6th |
| 9 |
6 or 7bb |
6th or diminished 7th |
| 10 |
7b |
minor 7th |
| 11 |
7 |
major 7th |
| 12 |
8 |
octave |
| 14 |
9 |
9th |
| 17 |
11 |
11th |
| 21 |
13 |
13th |
In addition, the major triad composed of intervals unison, the 3rd and 5th is
the basic chord which is often not named. The chord type highlights variation
from this basic structure or the additional intervals for chords with more
than 3 notes. So in suspended 4th, the 3rd of the major triad is
"suspended" by raising to the 4th. And the minor 7th is based on the
triad with a minor third and the addition of the minor 7th interval. So from
the name and the above interval name table, we can write minor 7th as
1-3b-5-7b to represent the chord structure. This is the spelling of the
chord in interval terms. Or written as pure multiples of semi-tones 0,3,7,10.
Likewise, major 7th is 1-3-5-7 with multiples of semi-tones 0,4,7,11.
Chord Structure and Semitone Structure
| Chord Name |
Chord Structure |
Semitone Structure |
| Major |
1, 3, 5 |
0,4,7 |
| Minor |
1, 3b, 5 |
0, 3, 7 |
| Diminished |
1, 3b, 5b |
0, 3, 6 |
| Diminished 7th |
1, 3b, 5b, 7bb |
0,3,6,9 |
| Half diminished |
1, 3b, 5b, 7b |
0, 3, 6, 10 |
| Augmented |
1, 3, 5# |
0, 4, 8 |
| 5th |
1, 5 |
0, 7 |
| 7th |
1, 3, 5, 7b |
0, 4, 7, 10 |
| Minor 7th |
1, 3b, 5, 7b |
0, 3, 7, 10 |
| Major 7th |
1, 3, 5, 7 |
0, 4, 7, 11 |
| Minor / Major 7th |
1, 3b, 5, 7 |
0, 3, 7, 11 |
| Suspended 4th |
1, 4, 5 |
0, 5, 7 |
| Suspended 2nd |
1, 2, 5 |
0, 2, 7 |
| 7th suspended 4th |
1, 4, 5, 7b |
0, 5, 7, 10 |
| 7th suspended 2nd |
1, 2, 5, 7b |
0, 2, 7, 10 |
| Add 2nd |
1, 2, 3, 5 |
0, 2, 4, 7 |
| Added 9th |
1, 3, 5, 9 |
0, 4, 7, 14 |
| Added 4th |
1, 3, 4, 5 |
0, 4, 5, 7 |
| 6th |
1, 3, 5, 6 |
0, 4, 7, 9 |
| Minor 6th |
1, 3b, 5, 6 |
0, 3, 7, 9 |
| 9th |
1, 3, 5, 7b, 9 |
0, 4, 7, 10, 14 |
| Minor 9th |
1, 3b, 5, 7b, 9 |
0, 3, 7, 10, 14 |
| Major 9th |
1, 3, 5, 7, 9 |
0, 4, 7, 11, 14 |
The key and spelling of a chord
The key specifies the base note of the chord. That is, where to begin the
counting. So a major 7th in C becomes C Major 7th, and includes notes C,
and those that are 4, 7, and 11 semi-tones above C. From the Mathematical
Cochlea scale, it represents the notes at 12, 4, 7, 11 O'clcok positions,
which are C, E, G, B respectively. Likewise, for D Major 7th, we have to
add 2 hour intervals to read as 2, 6, 9, and 1 O'clock positions, which are
D, F#, A, C# respectively. The combination of these notes spells out clearly the
composition of the chord, so is the "spelling" for the chord.
Since the guitar has 6 strings, sometimes, it is possible to have a note
and another that is 1 octave higher to be strummed together. The result is
the same chord. And the variations are the different "voices".
The voices also distinguish different "inversions" of the
same chord.
Graphic Example for Major
|
Sep 1
|
Check: Chord Name
|
Example = Major
|
|
Sep 2
|
Check: Chord Structure
|
= 1, 3, 5
|
|
Sep 3
|
Check: Semitone Structure
|
= 0,4,7
|
|
Sep 4
|
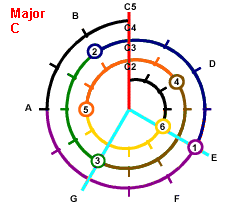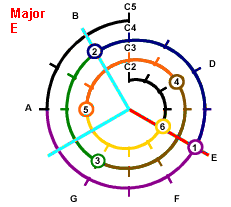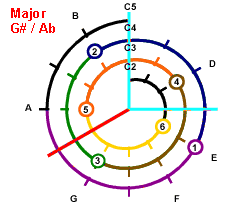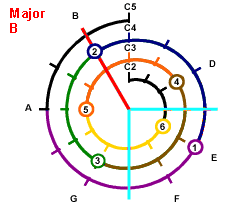
If Root is C, then draw on the Mathematical Cochlea
|
Red is root note
and Light Blue is other notes
of the chord
|
C Major:
Spelling : C, E, G
|
|
|
Sep 4
|
If Root is C#, then draw on the Mathematical Cochlea
|

Red is root note
and Light Blue is other notes
of the chord
|
C# Major:
Spelling : C#, E#, G#
|
|
|
Sep 4
|
If Root is D, then draw on the Mathematical Cochlea
|
Red is root note
and Light Blue is other notes
of the chord
|
D Major:
Spelling : D, F, A
|
|
|
All Major Chord Structures
|
|
Red is root note
and Light Blue is other notes
of the chord
|
|
|
|
From spelling to fret positions
After getting the spelling of a chord, it becomes easy to locate them
in the Mathematical Cochlea scale, then identify the string and fret
position to get the various notes. If two notes need to use the same
string, the note that can be handled by another string gives way to the
one that can only use that string. In complex chords, certain notes are
considered less important and so can be dropped. Now let's use again
the C Major 7th as our example. The spelling is C-E-G-B at 12, 4, 7, 11 O'clock
positions. C2 is too low to be handled by any string. But if we begins
from C4, then we soon go to the highest pitch string and can't complete
the chord unless we move very low down the fretboard. So we begins from
C3. It can be made by pressing the 3rd fret position of the 5th string.
Similarly, E is made by pressing the 2nd fret position of the 4th string.
G and B are the open positions of the 3rd and 2nd string. We can make C4
if a string is available. But the 2nd string that can make C4 is already
used by B note ofthe chord. Finally, we continue to find the next possible
note which is E4. It just happens to be the open fret note of the 1st
string. That completes the translation for one possible fingering. See
if you can work out other possibilities using the Mathematical Cochlea ?
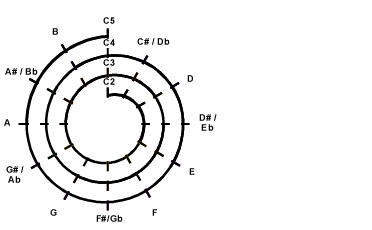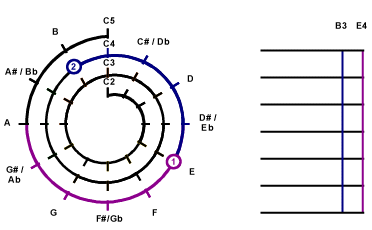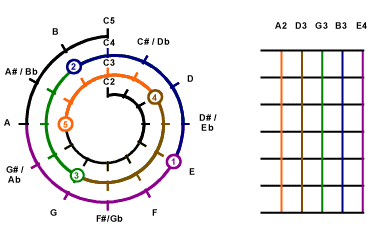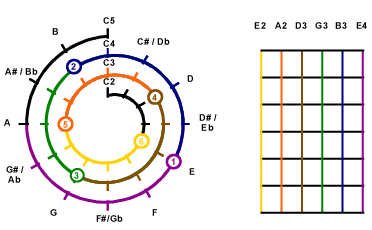
Graphic Example for B Major
(We do not consider the fingering at this moment)
|
Sep 1
|
Example =
|
B Major
|
|
Sep 2
|
Check: Chord Structure ---> Semitone Structure
|
= 1, 3, 5 ---> 0, 4, 7
|
|
Sep 3
|
Draw on Mathematical Cochlea
|
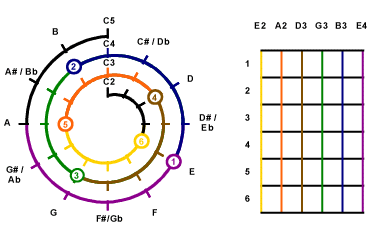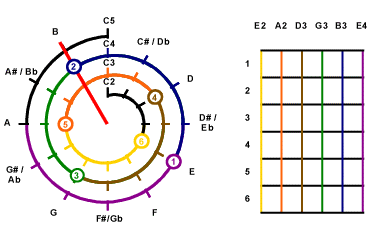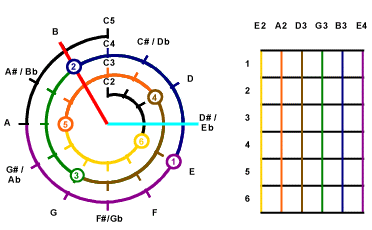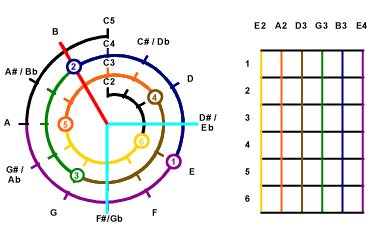
|
|
Sep 4
|
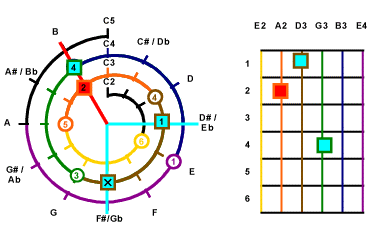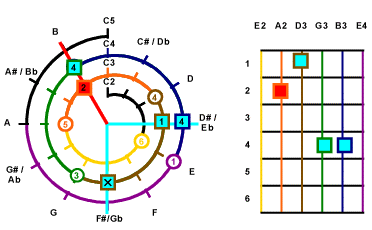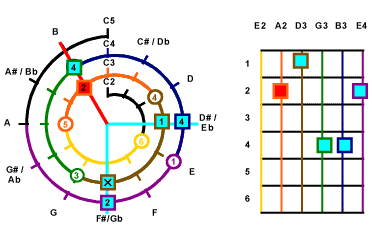
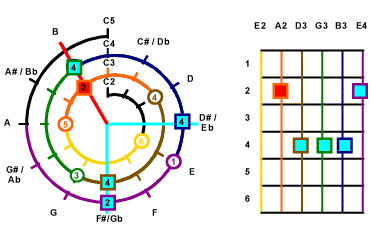
Look for Root Key.
Since the lowest key is E2 so the loweest root for B Major should be B2,
and the 6th String will not be used.
So we begins from B2. From the Mathematical Cochlea,
B2 is 2 semitones clockwise from A2. So you can see
 . .
The border color represents the number of the string, red background means root,
the number represents the counting clockwise from the starting note of the string.
 represents on 5th String,
count 2 from A2 clockwise. We now get B2.
Check also the Fret Positioning is also counting 2 downward on
the 5th String.
represents on 5th String,
count 2 from A2 clockwise. We now get B2.
Check also the Fret Positioning is also counting 2 downward on
the 5th String.
|
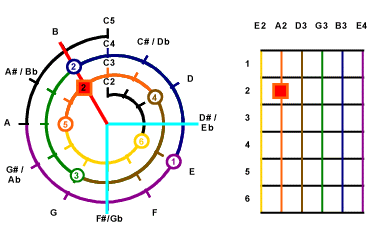
|
|
Sep 5
|
Then look for the 2nd note of the chord.
On the Mathematical Cochlea, the next note D#3 aligns with the
4th String and
the Light Blue Line. A square mark is marked on the spot of D#3.
The border color of this mark represents the number of the string, the
light blue background means non-root key of the chord, the number represents
the counting clockwise from the starting note of the string.
|
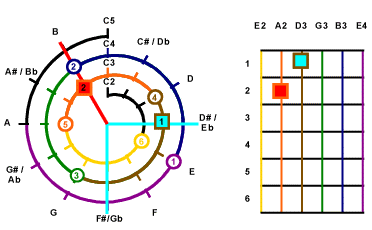
|
|
Sep 6
|
Then look for the next key of the chord.
On the Mathematical Cochlea, the next key which is also
covered by the 4th String
and that is F#3. Since one string cannot handle 2 keys at the same time.
So we have to make the selection on use either D#3 or F#3. The
decision depends on the structure of the music and figuring. This time, we pick
D#3 for example.
|
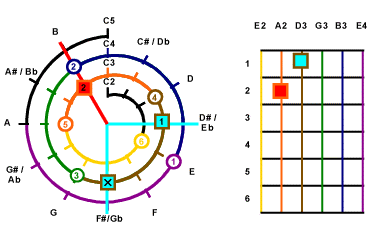
|
|
Sep 7
|
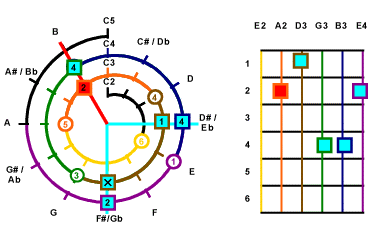
The next one can be handled by the 3rd string
or 2nd string. We
pick up the one on 3rd string this time.
|
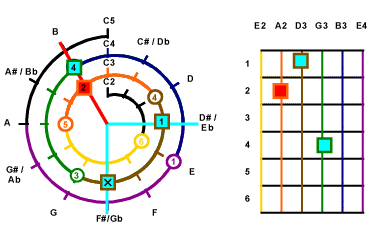
|
|
Sep 8
|
So easy to find the rest of them. D#4 on 2nd String, count 4 clockwise from
the starting noe of 2nd string.
F#4 on 1st String,
count 2 clockwise from the starting note of 1st String.
|
|
|
Sep 9
|
Now, we get this B Major Chord combination -
B, D#, B, D#,F#
on both Mathematical Cochlea and Fretboard.
|
|
There are many kinds of chord combination for one root, and they can
easily be found by Mathematical Cochlea. Which chord should be picked
depends on the whole Structure of music and the figuring. Like the example of
B Major, the most common chord is actually the one below (B, F#, B, D#, F#).
|
|
|








 .
.






