MATH 3.1: Introducing complex numbers |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
This module concerns the special symbol i, which is defined to have the property that i × i = −1. Expressions involving i, such as 3 + 2i, are known as complex numbers, and they are used extensively to simplify the mathematical treatment of many branches of physics, such as oscillations, waves, a.c. circuits and optics. Complex numbers arise in a very natural fashion in the solutions of certain mathematical problems, indeed some branches of mathematics would be incomplete, and some mathematical problems impossible to solve, without them; but they are also widely used as a practical calculating aid in many branches of science and engineering. For a physicist, complex numbers are certainly valuable as an aid to calculation, but later we will see that they play an essential role in one of the most important developments of 20th century physics: quantum theory.
In Subsection 2.1 we give the mathematical motivation for introducing complex numbers and follow this by discussing imaginary numbers (those consisting of i multiplied by a real number). We then introduce complex numbers in Subsection 2.3 and give an explanation of how to perform standard operations, such as addition and multiplication, on complex numbers. Subsection 2.6 gives, without proof, the fundamental theorem of algebra; this theorem tells us that the roots (i.e. solutions) of any polynomial equation can be given in terms of complex numbers, and that the number of roots is equal to the degree of the polynomial. An important graphical technique (known as the Argand diagram) for interpreting complex numbers is introduced in Subsection 2.7.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 3.1Module summary and the Subsection 3.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 3.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
State the fundamental theorem of algebra. How many roots does the equation x2 + 5ix − 6 = 0 have? Find these roots.
Answer F1
The fundamental theorem of algebra states that each polynomial with complex number coefficients and of degree n has, counting multiple roots an appropriate number of times, exactly n complex roots. Therefore the equation given has two roots, and it can be solved by using the well known formula
$x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$
with a = 1, b = 5i and c = −6. This gives us
$x=\dfrac{-5i\pm\sqrt{-25-4(-6)\os}}{2} = \dfrac{-5i\pm i}{2}$
Therefore the roots are −2i and −3i. Since the coefficient of x is imaginary, both roots are likely to be imaginary. The factors of 6 are 2 and 3, so we could try
(x + 2i)(x + 3i) = x2 + (2i + 3i)x + 2i × 3i = x2 + 5ix − 6
The roots of x2 + 5ix − 6 are therefore −2i and −3i.
Question F2
What is an Argand diagram? Plot the following points on an Argand diagram
−1 + $\sqrt{3\os}$ i, 1 −$\sqrt{3\os}$ i, $\sqrt{3\os}$ + i i
What is the exact distance of these points from the origin?
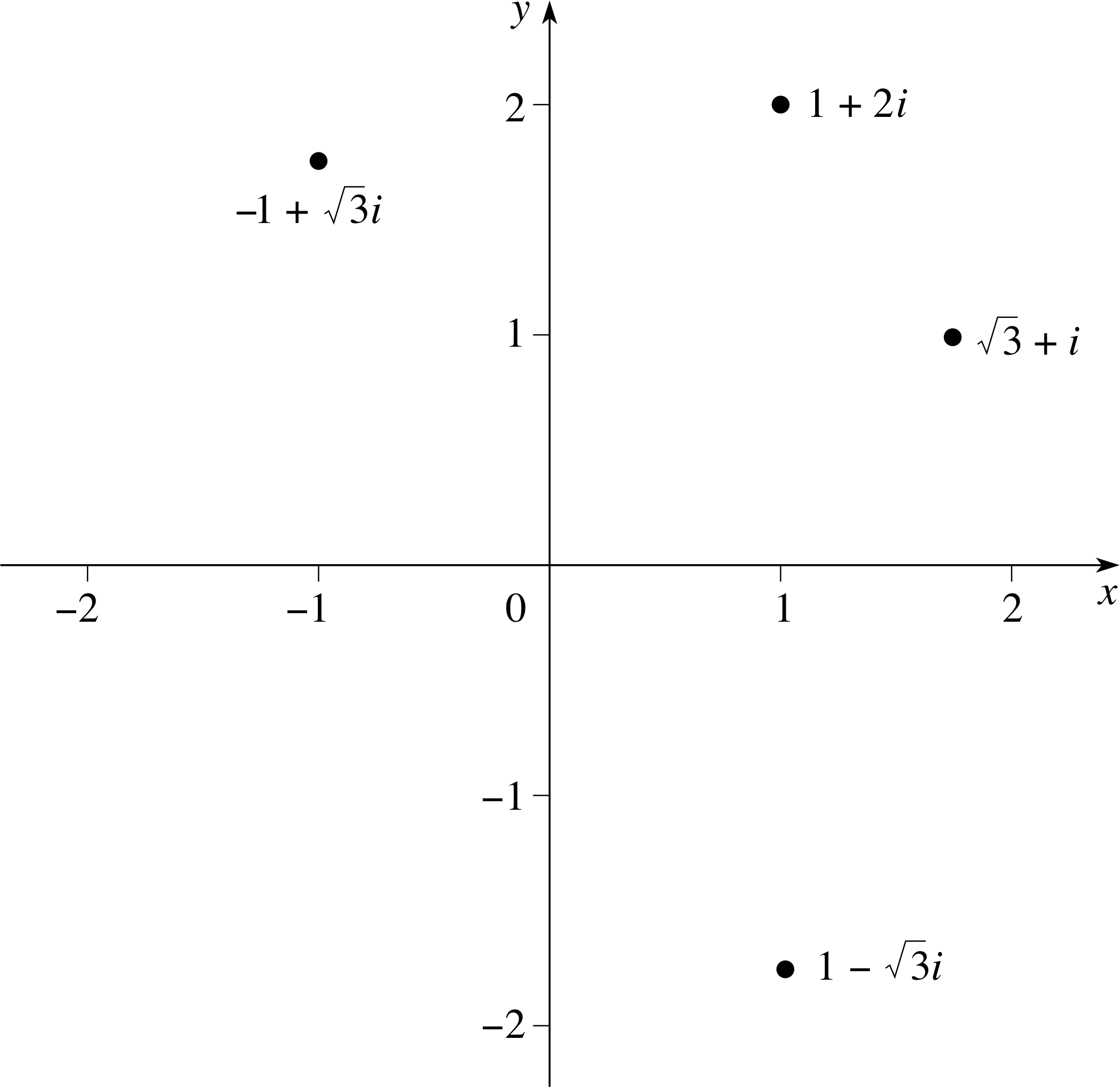
Figure 6 See Answer F2.
Answer F2
For any complex number, z = x + iy, the real numbers, x and y, can be used as the coordinates of a point on a graph, as shown in Figure 6. Such a graph is known as an Argand diagram. Any complex number corresponds to a point on the Argand diagram and, as an example, the number, 1 + 2i, is plotted in Figure 6. Conversely, any point on the Argand diagram corresponds to a unique complex number.
The positions of the points, −1 + $\sqrt{3\os}$i, 1 − $\sqrt{3\os}$ i, $\sqrt{3\os}$ + i, are shown on the Argand diagram in Figure 6. The exact distance of each point from the origin is | z |. This is given by the positive root of $\sqrt{(\sqrt{3\os})^2+1^2}$ = 2.
Question F3
A particular complex number, z, is given by
$z = \dfrac{1+i}{(1-i)(3+i)}$
Find the following and reduce them to their simplest forms:
(a) Re(z), the real part of z, and Im(z), the imaginary part of z
(b) z*, the complex conjugate of z (sometimes written as z)
(c) | z |, the modulus of z.
Answer F3
(a) First we simplify the denominator
(1 − i)(3 + i) = (3 + 1) + i (−3 + 1) = 4 − 2i
So we have
$z = \dfrac{(1+i)}{2(2-i)} = \dfrac{(1+i)(2+i)}{2(2^2+1)} = \dfrac{(2-1)+i(2+1)}{10} = \dfrac{1+3i}{1-}$
and therefore Re(z) = 1/10 and Im(z) = 3/10.
(b) $z^* = \dfrac{1-3i}{10}$
(c) | z | = $\dfrac{\sqrt{1+3^2}}{10} = \dfrac{1}{\sqrt{10\os}}$
1.3 Ready to study?
Study comment To begin the study of this module you need to be familiar with the basic ideas of arithmetic and algebra. In particular, you should be able to give clear definitions and be able to use the following terms: polynomial_functionpolynomial of degree n, quadratic equation, quotient, roots of an equation, set, simultaneous_linear_equationssolution of simultaneous equations, square root and polynomial_equationzeros of a polynomial. You should also be able to plot simple graphs and be familiar with the idea of the Cartesian coordinates of a point on a graph. If you are uncertain about any of these terms, review them by reference to the Glossary, which will indicate where in FLAP they are developed. The following questions will help you to establish whether you need to review some of the above topics before embarking on this module. i
Question R1
Write $\dfrac{\sqrt{2\os}+1}{\sqrt{2\os}-1}$ in the form $a + b\sqrt{2\os}$ by multiplying the numerator (the top) and the denominator (the bottom) of the fraction by $\sqrt{2\os}+1$.
Answer R1
$\dfrac{\sqrt{2\os}+1}{\sqrt{2\os}-1} = \dfrac{\sqrt{2\os}+1}{\sqrt{2\os}-1} \times \dfrac{\sqrt{2\os}+1}{\sqrt{2\os}+1} = 3 + 2\sqrt{2\os}$
Question R2
Explain what is meant by a quadratic equation and give the general solution for such an equation.
Answer R2
A quadratic equation is an equation of the form ax2 + bx + c = 0 where a is non-zero. The solutions of such equations are given by
$x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$
Question R3
Use a Cartesian coordinate system to plot the points A, B, C and D specified, respectively, by the following coordinate pairs:
(a) x = 1, y = 0, (b) x = 0, y = −1, (c) x = $\sqrt{2\os}$, y = −$\sqrt{2\os}$, (d) x = −$\sqrt{3\os}$, y = $\sqrt{3\os}$.
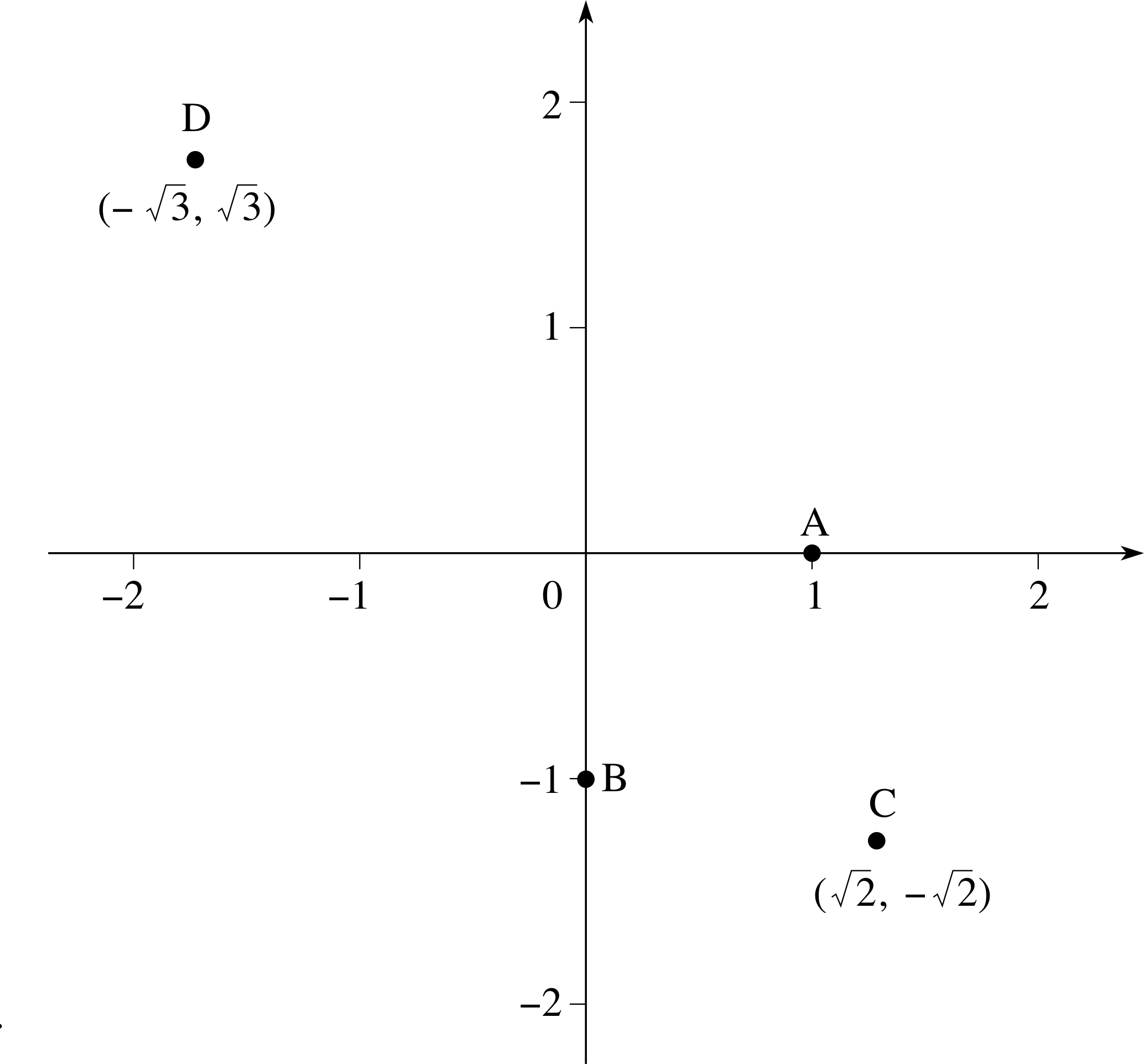
Figure 7 See Answer R3.
Answer R3
The points are plotted on the Cartesian coordinate system shown in Figure 7.
Question R4
Which of the following are polynomials in x? State the degree of those that are.
(a) x−3 + x−2 + x−1 + 1
(b) (x − 1)3 + (x − 1)2 + 1
(c) (sin x)2 + sin x + 3
(d) 1 + x5 + x − x3
What is meant by a zero of a polynomial?
Answer R4
A polynomial_equationpolynomial of degree n is an expression that can be rewritten in the same form as the left–hand side of Equation 21,
anx n + an−1x n−1 + an−2x n−2 + ... + a0 = 0(Eqn 21)
with an ≠ 0.
(a) not a polynomial
(b) polynomial of degree 3
(c) not a polynomial in x (some authors might describe this as a polynomial in sin x)
(d) polynomial of degree 5
A zero of a polynomial is a value x that satisfies Equation 21. This value is also known as a root_of_an_equationroot of the equation.
(If you are unsure about any of the answers to Questions R1 to R4, consult the relevant terms in the Glossary.)
2 Complex numbers i
2.1 Quadratic equations and the square roots of negative numbers
Historically, complex numbers were first introduced in 1545 when the mathematician, Gerolamo Cardano (1501–1576), was trying to solve a certain quadratic equation. Finding the roots of quadratic equations is a common mathematical problem, which occurs throughout physics and many other branches of science and engineering. It is straightforward to verify that the simple quadratic equation
x2 − 1 = 0(1)
has solutions x = ±1. However, the solution of the equally simple equation
x2 + 1 = 0(2)
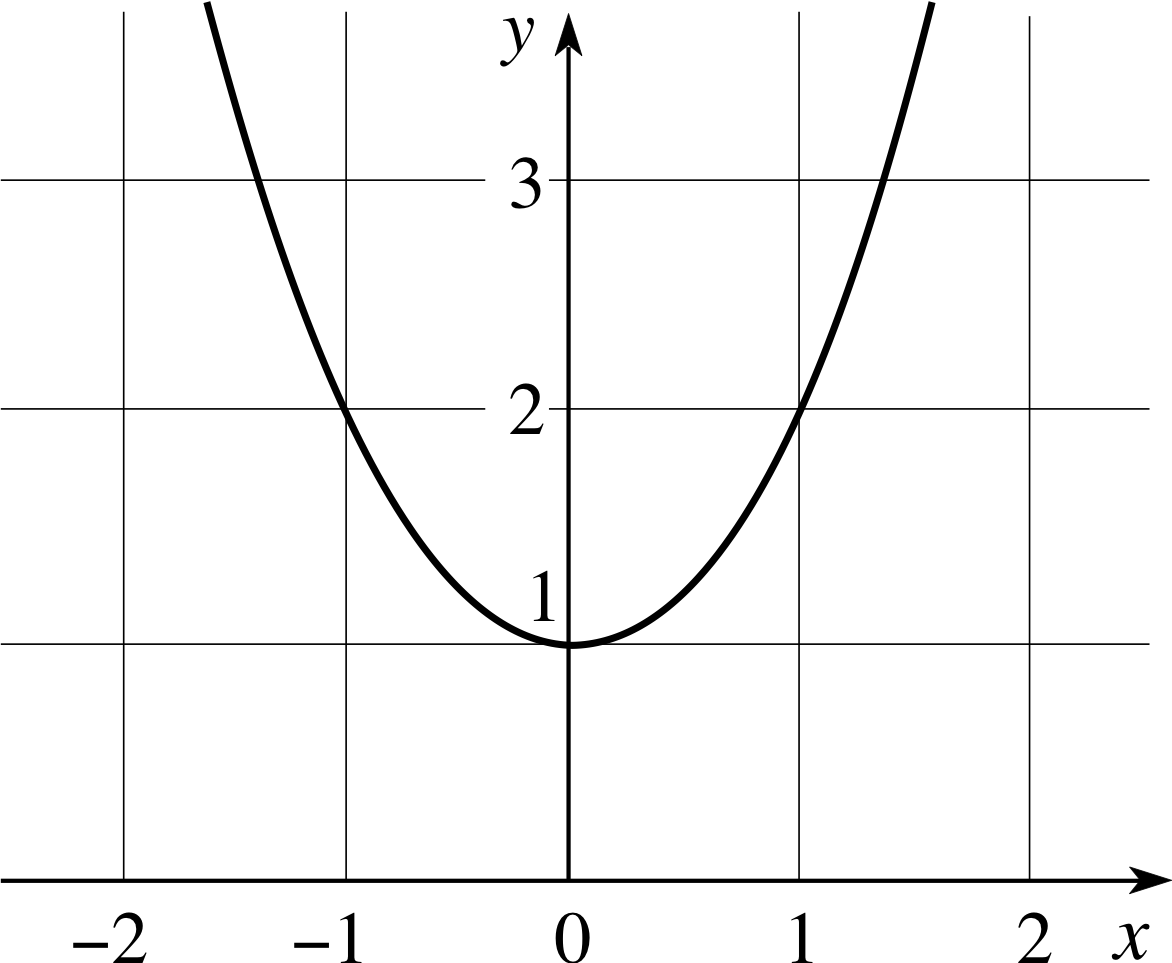
Figure 1 The graph of y = x2 + 1.
is much more problematic. The equation can be written as x2 = −1, so it would seem that we need to find a number, or numbers, whose square is −1. Such a number certainly cannot be an integer, a rational number or indeed a real number since any such numbers produce a positive result when squared.
We can illustrate the difficulty by referring to the graph of y = x2 + 1 shown in Figure 1. i
The real number solutions to the equation x2 + 1 = 0 should correspond to the points where the graph meets the x–axis. But the curve does not meet the x–axis. Does this mean that there are no numbers that solve the equation? Well that depends on what you mean by a ‘number’; certainly there are no real number solutions, but if we extend our notion of the meaning of ‘number’ we will be able to find solutions of such equations. This is our motivation for defining the symbol i by the relation,
i2 = −1(3) i
The solution to the equation, x2 + 1 = 0, is then i or −i, which we can write more compactly as ±i i (because i × i + 1 = −1 + 1 = 0 and (−i) × (−i) + 1 = −1 + 1 = 0).
You may well object to this sleight of hand and, if so, you are in very good company; over the centuries, many distinguished mathematicians, including René Descartes (1596–1650) and Sir Isaac Newton (1642–1727), had deep reservations about the meaning of i. Later mathematicians, such as Karl Friedrich Gauss (1777–1855) and Sir William Rowan Hamilton (1805–1865) realized that such reservations are ill-founded, but for the moment you should accept that i is simply an algebraic symbol which obeys the ‘strange’ rule that when squared it gives the result of minus one. However, one thing is certain; i cannot represent any of our familiar real numbers.
The symbol, i, obeys the usual rules of algebra, such as
i + i = 2i and i − i = 0
and this enables us to solve those quadratic equations which are insoluble in terms of real numbers. Consider the general form of a quadratic equation in x
ax2 + bx + c = 0
where for the moment we assume that a, b and c represent real numbers (that is, they do not involve i).
The two solutions of this equation are given by
$x = \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$
For the following example (Cardano’s original problem)
x2 − 10x + 40 = 0(4)
this leads to the solutions
$x = \dfrac{10\pm\sqrt{10^2-4\times 1\times 40}}{2} = \dfrac{10\pm\sqrt{-60\os}}{2}$
We can write
$\sqrt{-60\os} = \sqrt{60\times(-1)\os} = \sqrt{60\os} \times \sqrt{-1\os} = \left(\sqrt{60\os}\right)i = \left(\sqrt{4\times 15\os}\right)i = 2\left(\sqrt{15\os}\right)i$
by replacing −1 by i.
The solutions for x are therefore given by
$x = \dfrac{10\pm i\sqrt{60\os}}{2} = 5\pm i\sqrt{15\os}$
✦ If α = 5 + i$\sqrt{15\os}$ and β = 5 − i$\sqrt{15\os}$, show that α + β = 10 and αβ = 40.
✧ α + β = $5 + i\sqrt{15\os} + 5 - i\sqrt{15\os}$ = 10
αβ = $\left(5 + i\sqrt{15\os}\right)\left(5-i\sqrt{15\os}\right) = 5^2-\left(i\sqrt{15\os}\right)^2 = 25-15i^2 = 25+15 = 40$
Question T1
Use explicit substitution to verify that $x = 5 \pm i\sqrt{15\os}$ are solutions to the equation x2 − 10x + 40 = 0.
[Hint: You may assume that the normal rules of algebra apply to expressions involving i.]
Answer T1
Substituting x = 5 + i $\sqrt{15\os}$ into the left–hand side of the equation we have
$x^2-10x+40 = \left(5+i\,\sqrt{15\os}\right)^2-10\left(5+i\,\sqrt{15\os}\right) + 40$
$\phantom{x^2-10x+40 }= \left[25+10i\,\sqrt{15\os}+i^2\,\left(\sqrt{15\os}\right)^2\right]+\left(-50-10i \,\sqrt{15\os}\right)+40$
$\phantom{x^2-10x+40 }= \left(25-15-50+40\right)+i\,\left(10\sqrt{15\os}-10\sqrt{15\os}\right) = 0$
For x = 5 − i$\sqrt{15\os}$ the calculation is very similar
$x^2-10x+40 = \left(5-i\,\sqrt{15\os}\right)^2-10\left(5-i\,\sqrt{15\os}\right) + 40$
$\phantom{x^2-10x+40 }= \left[25-10i\,\sqrt{15\os}+i^2\,\left(\sqrt{15\os}\right)^2\right]+\left(-50+10i \,\sqrt{15\os}\right)+40$
$\phantom{x^2-10x+40 }= \left(25-15-50+40\right)+i\,\left(-10\sqrt{15\os}+10\sqrt{15\os}\right) = 0$
Notice that we treat i as an algebraic symbol, with the additional property that i2 = −1.
In Question T1 you have merely verified that the given expressions are indeed solutions of the equation. The process of determining such solutions is a different matter and requires a better understanding of how to perform arithmetic for expressions involving i. We now consider such arithmetic in more detail.
2.2 Imaginary numbers
An imaginary number has the form iy where y is a real number.
The following are examples of imaginary numbers: 3i, −7i, 3.1734i and ia (where a is an algebraic symbol representing a real number). Notice that we commonly write iy but 3i; the order doesn’t really matter, but this is the standard convention.
Addition and subtraction of imaginary numbers is simple, for example
2i + 3i = 5i, $\dfrac{2i}{3} + \dfrac12 = \dfrac{7i}{6}$ i
and1.7i − 0.2i = 1.5i
but in order to solve equations we also need to know how to multiply and divide imaginary numbers.
Multiplication and positive integer powers
The fundamental idea is that we should treat imaginary numbers as if we were carrying out ordinary algebraic operations, with the additional feature that i2 = −1. Consequently an imaginary number has the important property
(iy)2 = −y2(5)
where y represents an arbitrary real number. This means that (iy)2 must be less than or equal to zero, with zero
only possible if y is zero. For example
(5i)2 = 52i2 = −25
Any two imaginary numbers can be multiplied together since (if y and b are real numbers) we find
(ib)(iy) = i2yb = −yb
i.e. a real number.
We find the same result if the factors are multiplied in the reverse order i
(ib)(iy) = (iy)(ib) = −yb(6)
Positive integer powers of an imaginary number are interpreted as in conventional algebra, so that, for example, i3 = i × i × i.
✦ Simplify the following:
(a) (3i)(2i), (b) i (3i), (c) (i)(4i), and (d) i4.
✧ (a) (3i)(2i) = 3 × i × 2 × i = 3 × 2 × i × i = 3 × 2 × (−1) = −6
(b) i (3i) = −1 × 3 = −3
(c) (i)(4i) = 0 × i × 4 × i = 0 × 4 × i × i = 0 × 4 × (−1) = 0
(d) i4 = (i × i) × (i × i) = −1 × −1 = 1
If a and y are any real numbers then i
a (iy) = i (ay)(7)
Therefore multiplication of an imaginary number by a real number produces an imaginary number.
✦ Simplify the following: (a) 3 (2i), (b) 2.1 (−3.6i).
✧ (a) 3 (2i) = 6i
(b) 2.1 (−3.6i) = −7.56i
Question T2
Simplify the following: (a) (−3.4i)(2i), (b) (−2i)(2i), (c) −3.4 (2i), (d) 2 (2i), (e) (ix)(−ix), (f) (iy)3, where x and y are real numbers. i
Answer T2
(a) (−3.4i)(2i) = −3.4 × 2i2 = 6.8
(b) (−2i)(2i) = −2 × 2i2 = 4
(c) −3.4 (2i) = −3.4 × 2i = −6.8i
(d) 2 (2i) = 2 × 2i = 4i
(e) (ix)(−ix) = −(−1) × x2 = −(−x2) = x2
(f) (iy)3 = iy × iy × iy = −iy2
Parentheses
Brackets are used, as in normal algebra, to determine the order in which operations are performed, in particular
iy + ib = i (y + b)(8)
iy − ib = i (y − b)(9)
For example,
2i + 3i = (2 + 3) i = 5i, 2.4i − 4i = (2.4 − 4) i = −1.6i and 3i (5i + 2i) = −21
✦ Simplify i5 − 5 (i + i3) + (3i)3 − i.
✧ i5 − 5 (i + i3) + (3i)3 − i = i − 5 (0) − 27i − i = −27i.
Division
Dividing an imaginary number by a real number is straightforward, for example 7i ÷ 2 = 7i/2 = 3.5i.
To divide one imaginary number by another, for example 10i/5i, we may cancel 5i to obtain the value 2 as we would do in ordinary algebra. In fact we can justify such an operation by multiplying both numerator and denominator by i to obtain
$\dfrac{10i}{5i} = \dfrac{10i\times i}{5i\times i} = \dfrac{-10}{-5} = 2$ i
The same trick will allow us to divide a real number by an imaginary number, say 3/4i. Multiplying the numerator and denominator by i we have
$\dfrac{3}{4i} = \dfrac{3\times i}{4i\times i} = \dfrac{3i}{-4} = -0.75i$
✦ Simplify (i + 1/i)7. i
✧ $(i+1/i)^7 = \left(1+\dfrac{i}{1\times i}\right)^7 = (i-i)^7 = 0$
Question T3
Simplify the following expressions: (a) −2i + 3.4i + 7i − 4i, (b) (i − 3i)2 + (i + 3i)2, (c) 2/i, (d) (i − 1/i)2/(1/i), $\dfrac{2}{3i} + \dfrac i2$
Answer T3
(a) −2i + 3.4i + 7i − 4i = (−2 + 3.4 + 7 − 4) i = 4.4i
(b) (i − 3i)2 + (i + 3i)2 = (−2i)2 + (4i)2 = −04 − 16 = −20
(c) 2/i = −2i
(d) (i − 1/i)2/(1/i) = (2i)2/(−i) = 4/i = −4i
(e) $\dfrac{2}{3i}+\dfrac i2 = -\dfrac{2i}{3}+\dfrac i2 = -\dfrac{4i}{6}+\dfrac{3i}{6}=-i/6$
2.3 Real and imaginary parts of a complex number
A complex number is an expression of the form x + iy, where x and y are real numbers. i
The following are examples of complex numbers: 3 + 2i and −1.6 + 3.7i. Either x and/or y may be zero, so that 3, 4.2i and 0 are also complex numbers, but we would not normally bother to write 3 + 0i, 0 + 4.2i or 0 + 0i. It follows that the real numbers and the imaginary numbers are both just special classes of complex numbers.
It is conventional to use a single algebraic symbol z to represent an arbitrary complex number x + iy where x and y are real numbers. i
Given a complex number in the form z = x + iy, i the real number x is known as the real part of z and the real number y is known as the imaginary part of z. For example, if z = −1.6 + 3.7i, then the real part of z is −1.6 and the imaginary part is 3.7. i
Writing ‘the real part of z’ or ‘the imaginary part of z’ can be a little tedious and so we introduce the following notation. Re i is an abbreviation for ‘take the real part of the complex quantity that is immediately to the right’, as in
Re(−1.6 + 3.7i) = −1.6
In a similar way, Im means ‘take the imaginary part of the complex quantity that is immediately to the right’, as in
Im(−1.6 + 3.7i) = 3.7
Notice that we have used parentheses in the above expressions since Re and Im are actually functions; indeed they are functions that associate a unique real number with any given complex number, i.e. their domain is the set of complex numbers and their codomain is the set of real numbers. If we feed the complex number z = x + iy into the function Re, the output will be x; and similarly if we feed the complex number z into the function Im the output will be y. In other words:
Ifz = x + iy then Re(z) = x and Im(z) = y(10)
If you are asked to ‘simplify’ or to ‘evaluate’ an expression involving complex numbers it usually means that you are required to express your answer in the form x + iy, where x and y are real.
✦ Evaluate the following expressions: (a) Re(3 − i), (b) Im(5i − 1), (c) Re(i (i − 1)), (d) Im((a + ib)(a − ib)), where a and b are real.
✧ (a) Re(3 − i) = 3
(b) Im(5i − 1) = 5
(c) Re(i (i −1)) = Re(−1 − i) = −1
(d) Im((a + ib)(a − ib)) = Im(a2 + b2) = 0
Question T4
Evaluate the following expressions: (a) Re(3i), (b) Im(3i), (c) Re(4 + 8i), (d) Im(3 + 7i + 7i3).
Answer T4
(a) Re(3i) = 0
(d) Im(3i) = 3
(c) Re(4 + 8i) = 4
(d) Im(3 + 7i + 7i2) = Im(3 + 7i − 7i) = Im(3) = 0
It is worth pointing out here that some textbooks call a complex number with no real part a ‘pure imaginary number’. We do not use this terminolgy in FLAP since we call such numbers ‘imaginary’ as in Subsection 2.2. You should also notice that there is a tradition (which we attempt to follow) of using symbols such as z (and w) to denote complex quantities and x and y (or a and b) to denote real quantities.
Two complex numbers can only be equal if both their real and imaginary parts are equal, in other words, if x + iy = a + ib then x = a and y = b. This apparently trivial remark is actually the basis of a useful technique known as equating real and imaginary parts which we will meet later.
2.4 Sums, products, quotients, conjugate and modulus
Addition and subtraction
To add (or subtract) two complex numbers we simply add (or subtract) their real parts and then their imaginary parts. So we can write:
(a + ib) + (x + iy) = (a + x) + i (b + y)(11)
and(a + ib) − (x + iy) = (a − x) + i (b − y)(12)
where a, b, x and y are all arbitrary real numbers.
✦ Simplify the following expressions: (a) (2 + 3i) + (4 + i), (b) (3 − 2.5i) + (7 + 0.1i), (c) (3.4 − 2i) − (0.4 + i), (d) (−1 + i) − (−1 − i).
✧ (a) (2 + 3i) + (4 + i) = 6 + 4i
(b) (3 − 2.5i) + (7 + 0.1i) = 10 − 2.4i
(c) (3.4 − 2i) − (0.4 + i) = 3 − 3i
(d) (−1 + i) − (−1 − i) = 2i
Question T5
Evaluate the following expressions: (a) 2i + (7 + 3i) + 3, (b) (3 + 2i) + (3 − 2i), (c) (3 + 2i) − (3 − 2i).
Answer T5
(a) 2i + (7 + 3i) + 3 = (7 + 3) + i (2 + 3) = 10 + 5i
(b) (3 + 2i) + (3 − 2i) = (3 + 3) + i (2 − 2) = 6
(c) (3 + 2i) − (3 − 2i) = (3 − 3) + i (2 + 2) = 4i
Multiplication and positive integer powers
To multiply two complex numbers we use the ordinary rules of algebra, together with the fact that i2 = −1. For example, to multiply 2 + 3i by 4 + 5i, we write
(2 + 3i)(4 + 5i) = 2 × 4 + 2 × 5i + 3i × 4 + 3i × 5i
(2 + 3i)(4 + 5i) = 8 + 10i + 12i + 15i2 = 8 + 22i − 15
(2 + 3i)(4 + 5i) = −7 + 22i
In general, if a, b, x and y represent arbitrary real numbers we have i
(a + ib)(x + iy) = (ax − by) + i (ay + bx)(13)
Positive integer powers, for example (2 + 3i)3, are interpreted in exactly the same way as in conventional algebra, in this case as (2 + 3i)(2 + 3i)(2 + 3i).
If you need to multiply more than two complex numbers then it is probably easiest to multiply pairs of complex numbers in turn, replacing any occurrence of i2 by −1 as you go along.
Once again, we emphasize that the algebra of complex numbers is simply standard algebra with the additional feature that whenever you see i2 you should replace it by −1.
✦ Simplify the following expressions: (a) (2 + 3i) (4 + i), (b) 5i (7 − 3i), (c) 2 (5 + 3i), (d) 2i (1 − i)2.
✧ (a) (2 + 3i) (4 + i) = 2 × 4 + 3i × i + 3i × 4 + 2 × i = 5 + 14i
(b) 5i (7 − 3i) = 5i × 7 + (5i ) × (−3i) = 15 + 35i
(c) 2 (5 + 3i) = 10 + 6i
(d) 2i (1 − i)2 = 2i (1 − i)(1 − i) = 2i (1 − i − i + i02) = 2i (−2i) = 4
✦ Simplify the expression (1 + i)(2 + i)(3 + i)(4 + i).
✧ We simplify the product of the first two brackets (1 + i)(2 + i) = 1 + 3i then the product of the last two brackets
(3 + i)(4 + i) = 11 + 7i
Then we multiply these two together
(1 + 3i)(11 + 7i) = −10 + 40i
Question T6
Simplify the following expressions: (a) (1 + 2i)(3 + 4i), (b) (3 + 2i)(1 − 4i), (c) 7 (2 + 3i), (d) 3i (2 + 3i), (e) (1 + z2)2, where z = 1 + i
Answer T6
(a) (1 + 2i)(3 + 4i) = (1 × 3 − 2 × 4) + i (2 × 3 + 1 × 4) = −5 + 10i
(b) (3 + 2i)(1 − 4i) = 3 × 1 − 2 × (−4) + i [2 × 1 + 3 × (−4)] = 11 − 10i
(c) 7 (2 + 3i) = 7 × 2 + 7 × 3i = 14 + 21i
(d) 3i (2 + 3i) = 3 × 2i + 3 × 3i2 = 6i − 9
(e) z2 = (1 + i)2 = 2i, so that (1 + z2)2 = (1 + 2i)2 = −3 + 4i
Question T7
Simplify (2 + i)(3 + i)(2 − i)(3 − i).
Answer T7
(2 + i)(3 + i) = 5 + 5i and (2 − i)(3 − i) = 5 − 5i, so that
(2 + i)(3 + i)(2 − i)(3 − i) = (5 + 5i)(5 − 5i) = 50
Notice that the final result is real.
(We consider a quicker way of simplifying this expression in Question T12).
The complex conjugate
Pairs of complex numbers such as 3 + 2i and 3 − 2i have the interesting property that both their sum and their product are real. This motivates us to make the following definition: Given a complex number z = x + iy, then the complex number x − iy is known as the complex conjugate (often abbreviated to conjugate) of z and is written as z* (pronounced ‘z star’), i so we have
(x + iy)* = (x − iy)(14)
The fundamental rule for obtaining the complex conjugate of any expression involving complex numbers is to replace i by −i throughout.
✦ Simplify the following expressions: (a) (3 + 4i)*, (b) (2.5 − 7.3i)*, (c) (z*)*.
✧ (a) (3 + 4i)* = 3 − 4i
(b) (2.5 − 7.3i)* = 2.5 + 7.3i
(c) (z*)* = z
Question T8
Simplify the following expressions: (a) (3i)*, (b) (−3.5 + 2i)*, (c) z + z* and z − z* given that z = 2 + 5i.
Answer T8
(a) (3i)* = −3i
(b) (−3.5 + 2i)* = −3.5 − 2i
(c) z + z2 = (2 + 5i) + (2 − 5i) = 4, and z − z2 = (2 + 5i) − (2 − 5i) = 10i
Part (c) of Question T8 is an example of a general property of complex conjugates.
The sum of a complex number z and its complex conjugate is twice the real part of z, and their difference is 2i times the imaginary part, so that, using the notation of Subsection 2.3, i
z + z* = 2Re(z)(15)
z − z* = 2iIm(z)(16)
For example:(3 + 4i) + (3 + 4i)* = 2 × 3 = 6; (3 + 4i) − (3 + 4i)* = 2 × 4i = 8i;
and5i + (5i)* = 2 × 0 = 0; 5i − (5i)* = 2 × 5i = 10i
Question T9
Evaluate z + w + (z + w)*, where z = 1 + 3i and w = 2 + 4i.
Answer T9
z + w + (z + w)* = 2 Re(z + w) = 2 (1 + 2) = 6
Question T10
Evaluate (z + v + w) − (z + v + w)*, where z = 2i, v = 3 + 4i and w = 1 + i.
Answer T10
(z + v + w) − (z + v + w)* = 2i Im(z + v + w) = 2i (2 + 4 + 1) = 14i
The conjugate of the product of two complex numbers is equal to the product of the conjugates, in other words, for any two complex numbers z and w,
(zw)* = z*w*(17)
✦ Prove that (zw)* = z*w*.
✧ Let z = x + iy and w = u + iv
then zw = (xu − yv) + i (xv + yu)
and (zw)* = (xu − yv) − i (xv + yu)
also z*w* = (x − iy)(u − iv) = (xu − yv) − i (xv + yu)
✦ Show that for any two complex numbers z and w, the expression z*w + zw* is real. i
✧ Using Equation 17,
(zw)* = z*w*(Eqn 17)
we have
(z*w)* = (z*)*w* = zw*
and it follows that
z*w + zw*
is the sum of a complex number (z*w) and its conjugate (zw*), and from Equation 15 this must be real.
If we multiply z = x + iy by its complex conjugate we get a real quantity
z z* = (x + iy)(x − iy) = (x2 + y2) + i (yx − xy) = x2 + y2
and so we have the important result
z z* = z*z = x2 + y2 = [Re(z)]2 + [Im(z)]2(18)
This means that z z* is a non–negative real number, and it can only be equal to zero if z is zero (that is, if both Re(z) and Im(z) are zero). This simple property is of great significance in quantum theory, i where many of the mathematical quantities are essentially complex in character, and yet the quantities that we measure are always real. A quick glance at any book on quantum mechanics will show you that it is full of expressions such as ψ ψ*.
✦ Evaluate the following expressions: (a) (3 + 4i)(3 + 4i)*, (b) (1 + i)*(1 + i), (c) i*i.
✧ (a) (3 + 4i)(3 + 4i)* = 32 + 42 = 25
(b) (1 + i)*(1 + i) = 12 + 12 = 2
(c) i*i = 12 = 1
Question T11
Evaluate zz* for the following: (a) z = 1 − i, (b) z = 4i, (c) z = 2.
Answer T11
(a) (1 − i)(1 + i) = 12 + 12 = 2
(b) 4i (−4i) = 42 = 16
(c) 2 (2) = 22 = 4
Question T12
Given that z = 2 + i and w = 3 − i, evaluate zz* and ww* then use your result to simplify (2 + i)(3 + i)(2 − i)(3 − i).
Answer T12
zz* and ww* are as follows:
zz* = (2 + i)(2 + i)* = 22 + 12 = 5
ww* = (3 − i)(3 − i)* = 32 + 12 = 10
Therefore
(2 + i)(3 + i)(2 − i)(3 − i) = (2 + i)(2 + i)* (3 + i)(3 + i)* = 5 × 10 = 50
You should compare this method with the answer to Question T7.
The modulus of a complex number
Expressions such as (x + iy)(x − iy) occur so frequently in both mathematics and physics that it is worth introducing the following definition. For a complex number, z = x + iy, the modulus_of_a_complex_numbermodulus of z is the positive square root of x2 + y2. The standard notation for the modulus of z is | z |, read as ‘mod z’, so we have the result
$\lvert\,z\,\rvert = \sqrt{[{\rm Re}(z)]^2 + {[{\rm Im}(z)]^2}} = \sqrt{x^2+y^2}$(19)
✦ Evaluate the following expressions: (a) | 3 + 4i |, (b) | 2 + i |, (c) | 3 − 4i |, (d) | −4 |, (e) | 2i |, (f) | 0 |.
✧ (a) | 3 + 4i | = $\sqrt{3^2+ 4^2} = \sqrt{25\os} = 5$
(b) | 2 + i | = $\sqrt{2^2 +1^2} = \sqrt{5\os}$
(c) | 3 − 4i | = $\sqrt{3^2+ 4^2} = \sqrt{25\os} = 5$
(d) | −4 | = $\sqrt{4^2} = 4 $
(e) | 2i | = $\sqrt{2^2} = \sqrt{4\os} = 2$
(f) | 0 | = $\sqrt{0^2+ 0^2} = 0$
Notice that in the case of a real number, the modulus reduces to the absolute value. Another consequence of the definition is that the modulus of any complex number, z, is greater than or equal to zero, with equality only occurring if both the real and imaginary parts of z are zero.
Question T13
Two complex numbers z1 and z2 are given by z1 = 8 + 6i and z2 = 12 + 5i.
Calculate the following: (a) | z1 |, (b) | z2 |, (c) | z1 + z2 |, (d) | z1 | + | z2 |.
Answer T13
(a) | z1 | = | 8 + 6i | = $\sqrt{8^2+6^2} = 10$
(b) | z2 | = | 12 + 5i | = $\sqrt{12^2+5^2} = 13$
(c) | z1+ z2 | = | 20 + 11i | = $\sqrt{20^2+11^2}= \sqrt{521\os}$
(d) | z1 | + | z2 | = 10 + 13 = 23
The modulus of a complex number is related to its complex conjugate by the following relation
zz* = | z |2(20)
We can easily check this by substituting z = x + iy (with x and y, as always, representing real numbers) into Equation 20,
zz* = (x + iy)(x + iy)* = (x + iy)(x − iy) = x2 + y2 = | z |2
✦ Given that w = 3 + 2i and that z = x + iy are complex numbers, such that wz = 1, find the values of x and y.
✧ Since wz = (3 + 2i)(x + iy) = (3x − 2y) + (2x + 3y) i
we have
(3x − 2y) + (2x + 3y) i = 1
The right–hand side of this equation is real, so that, equating real and imaginary parts, we obtain the pair of simultaneous equations
3x − 2y = 1
2x + 3y = 0
Solving these equations (by the techniques of ordinary algebra) we obtain
x = 3/13 and y = −2/13
From the above exercise it follows that $z = \dfrac1w = \dfrac{1}{3+2i} = \dfrac{3}{13} - \dfrac{2}{13}i$
The quotient of complex numbers
Dividing a complex number by a real number presents us with no difficulty, for example, (1 + 3i)/2 = 1/2 + (3/2)i. We could proceed in this way in order to evaluate an expression such as $\dfrac{1}{3+2i}$, but the simplest method is to multiply both numerator and denominator by 3 − 2i, the conjugate of 3 + 2i. i This will give us
$\dfrac{1}{3+2i} = \dfrac{1}{3+2i}\times \dfrac{3-2i}{3-2i} = \dfrac{3-2i}{13} = \dfrac{3}{13} - \dfrac{2}{13}i$
Notice how multiplying the denominator by its conjugate produces the real number 13. The same method will work more generally, as we ask you to show in the following question.
Question T14
Show that $\dfrac1z = \dfrac{z^*}{\lvert\,z\,\rvert^2}$ for any complex number, z ≠ 0.
Answer T14
We know that zz* = | z | 2 so we have
$\dfrac1z = \dfrac{z^*}{zz^*} = \dfrac{z^*}{\lvert\,z\,\rvert^2}$
Notice that if z = 0 then | z |2 = 0 and so 1/z is not defined.
Negative indices are used for complex numbers exactly as they are for real numbers, so we may write $\dfrac1z = z^{-1}$, or, more generally, $\dfrac{1}{z^n} = z^{-n}$ for any integer n.
✦ Multiply the numerator and denominator of the quotient
$\dfrac{3 + 4i}{2+i}$
by the conjugate of 2 + i (the denominator) and hence express it as a complex number in the form x + iy.
✧ $\dfrac{3+4i}{2+i} = \dfrac{3+4i}{2+i} \times \dfrac{2-i}{2-i} = \dfrac{6+4+8i-3i}{5} =2+i$
In general, the quotient of two complex numbers can be written as x + iy
$\dfrac{x + iy}{a+ib}$
where x, y, a and b are all real.
We can use the same technique as just described to evaluate such expressions. This process is known as rationalizing a (complex) quotient
$\dfrac{x + iy}{a+ib} = \dfrac{x + iy}{a+ib} \times \dfrac{a-ib}{a-ib} = \dfrac{(x + iy)(a+ib)}{a^2+b^2} = \dfrac{(xa + yb) + i(ya-xb)}{a^2+b^2}$
The above calculation is valid provided that a and b are not both zero, in other words, provided that a + ib ≠ 0. Just as for real numbers, we are not allowed to divide by zero.
For more complicated expressions, such as
$\dfrac{1 + i}{(2+i)(1-3i)}$
the best approach is to first simplify the denominator, in this case
(2 + i)(1 − 3i) = (2 + 3) + i (1 − 6) = 5 − 5i = 5 (1 − i)
We can then continue as in the previous example
$\dfrac{1 + i}{(2+i)(1-3i)} = \dfrac{1+i}{5(1-i)} = \dfrac{(1+i)(1+i)}{5(1-i)(1+i)} = \dfrac{(1+i)(1-i)}{10} = \dfrac{(1-1)+i(1+1)}{10} = \dfrac i5$
Question T15
Simplify the following expressions: (a) $\dfrac{2+i}{3-4i}$, (b) $\dfrac{1-i}{6+8i}$, (c) $\dfrac{3+i}{(2+i)(1-i)}$.
Answer T15
(a) $\dfrac{2+i}{3-4i} = \dfrac{(2+i)(3+4i)}{(3-4i)(3+4i)} = \dfrac{(2\times 3-1\times 4)+i(1\times 3+2\times 4)}{25} = \dfrac{2+11i}{25}$
(b) $\dfrac{1-i}{6+8i} = \dfrac{(1-i)(6-8i)}{6^2+8^2} = \dfrac{(6-8)+i(-6-8)}{100} = \dfrac{-1-7i}{50}$
(c) $\dfrac{3+i}{(2+i)(1-i)} = \dfrac{3+i}{3-i} = \dfrac{3+i}{3-i} \times \dfrac{3+i}{3+i} = \dfrac{8+6i}{10} = \dfrac45 + \dfrac35i$
Question T16 i
Solve each of the following equations for the complex number z, expressing your answer in the form x + iy:
(a) 5z = 2 + 8i, (b) $\dfrac{z}{2-i} = (3-i)(5+i)$, (c) iz = 4 + 3i, (d) 3z + i = 1 − iz,
(e) (2 + i)z = i, (f) (3 + i)(z + 2i) = 1 − i, (g) | 2z + 3 − i | = 0, (h) z + 2z* = 1 + i,
(i) 2 (5 − i) = (1 + i)/z, (j) (2 + i)2z = 1 + (1 − i)−1.
Answer T16
(a) z = 0.4 +1.6i
(b) z = 30 − 20i
(c) z = 3 − 4i
(d) z = 0.2 − 0.4i
(e) z = 0.2 + 0.4i
(f) z = 0.2 − 2.4i
(g) z = −1.5 + 0.5i (| 2z + 3 − i | = 0 implies 2z + 3 − i = 0)
(h) Rewrite z and z* in terms of x and y, then equate real and imaginary parts to obtain x = 1/3 and y = −1.
(i) $z = \dfrac{1}{13} + \dfrac{3i}{26}$
(j) z = 13/50 − 9i/50
2.5 The development of complex numbers
Now that you have a good working knowledge of complex arithmetic it is worth putting the subject into perspective by briefly reviewing the history of numbers. In this discussion we will find it helpful to use the (modern) mathematicians’ concept of a set, which merely means a collection of objects with a common defining property.
The earliest use of numbers was probably similar to the simple systems that exist to the present day in which the counting sequence is: ‘one’, ‘two’, ‘three’, ‘many’. Although the details are lost in pre-history, the need for a more specific means of tallying cattle, and such like, must have eventually led to the ‘counting’ or ‘natural’ numbers which today we write as 1, 2, 3, and so on (although many different systems of writing these numerals were invented). We may categorize the subsequent development of numbers in five stages as follows:
- 1
-
The set of natural numbers 1, 2, 3, ...i is often denoted by $\mathbb{N}$. Such numbers enable us to:
(a) count objects (such as the number of apples in a box)
(b) add objects (3 apples and 2 apples gives 5 apples)
(c) subtract objects (removing 2 apples from 5 apples leaves 3)
(d) multiply objects (2 lots of 3 apples gives 6 apples)
(e) solve equations such as 3x − 6 = 0.
However, the set $\mathbb{N}$ would not be sufficient for our modern decimal system in which the concept of zero is an essential ingredient. The symbol 0 is needed to indicate ‘place value’, e.g. to distinguish 50 from 5; and so we need to add one further element to our collection of numbers to form the set of non–negative integers 0, 1, 2, 3, ... often denoted by $\mathbb{Z}^{+}$. i The processes of arithmetic would soon lead to the conclusion that this set is also ‘incomplete’, since it does not allow calculations such as 5 − 10, nor does it contain the solutions of equations such as 3x + 6 = 0
- 2
-
We can extend the number system by introducing the set of integers with elements ... −3, −2, −1, 0, 1, 2, 3, ... . This set, which is usually denoted by $\mathbb{Z}$, is difficult to interpret in terms of objects such as apples, and still causes great confusion among schoolchildren. (For example, try drawing −2 apples or consider what −2 lots of 3 apples means!)

Figure 2 The set of integers, $\mathbb{Z}$.
However this set is easy to interpret as a collection of points on an infinitely long line, where only integer positions are allowed. Part of such a line is shown in Figure 2. Using negative numbers, we can solve equations such as 3x + 6 = 0 (which has the solution x = −2).
However, our set of numbers is still not complete since it does not contain the solutions of equations such as 2x + 3 = 0.

Figure 3 Elements from the set of rational numbers, $\mathbb{Q}$.
- 3
-
The next extension is to introduce the rational numbers, defined as the set of all ratios of integers, such as 2/3, −3/2 and 7/8. For instance, we can define 2/3 as the solution of the equation 3x = 2. This set is usually denoted by the symbol, $\mathbb{Q}$. Again, it is possible to interpret the members of this set as points on a ‘line’, as we have attempted to show in Figure 3. (It is impossible to draw this figure accurately as the dots representing rational numbers may be arbitrarily close together.)
Rational numbers certainly enable us to solve equations such as 2x + 3 = 0 (the result is −3/2), but there are quite simple equations whose solutions do not lie in this set. For example the equation x2 − 2 = 0 does not have rational solutions. This is because there are in fact ‘gaps’ in the line, although these are not shown in Figure 3; in other words it is possible to show that $\sqrt{2\os}$ is not a rational number (although this is certainly not obvious). The numbers e and π are not rational numbers.
- 4
-
We can extend the rational numbers by introducing the real numbers, which in decimal notation consist of a string of digits, followed by a decimal point and then a second string of digits. The real numbers that are not rational numbers are said to be irrational numbers. In some cases, and always for irrational numbers, the string of digits following the decimal point does not terminate. Some of these non–terminating decimals do not have a recurring pattern of digits, and it is this property that distinguishes the set of real numbers.

Figure 4 The real line, $\mathbb{R}$.
This set is usually denoted by $\mathbb{R}$ and is sometimes known as the real line. i The reason for this is that all real numbers correspond to points on a infinite line, as shown in Figure 4. The converse is also true; every point on the real line corresponds to a real number. In other words, there are no ‘gaps’ in the real line. Using the real numbers, we can solve equations such as x2 − 2 = 0 (the solution is $\pm\sqrt{2\os}$) or sin(x) = 0 (the solutions are integer multiples of π). However, we cannot solve equations such as x2 + 2 = 0, which is where the ideas presented in this module make their appearance. Notice that each extension of the number system appears to be motivated by the need to solve a further class of equations, and from this point of view the complex numbers are the next step.
- 5
-
The next extension is to introduce complex numbers of the form z = x + iy, where x and y are real numbers and i2 = −1. The set of complex numbers is often denoted by $\mathbb{C}$ and such numbers allow us to solve equations such as x2 + 2 = 0. (The solution is $\pm\sqrt{2\os}\,i$).
This is the story of the development of numbers over thousands of years. i But we still haven’t answered two obvious questions:
- Is this the end of the road? (In other words, do the solutions of any algebraic equation, for example x3 + 2x2 + 3x + 1 = 0 or x4 + 7x2 + 2 = 0, lie in the set $\mathbb{C}$?)
- Can we represent complex numbers by a diagram? i The answer is ‘yes’ to both questions as we shall see later in this module. The first question is discussed in the following subsection and the second in Subsection 2.7.
2.6 The fundamental theorem of algebra
The following examples are intended to set the scene for one of the most important results in mathematics.
- 1
-
An equation of the form ax + b = 0 has just one solution if a ≠ 0 (i.e. x = −b/a). This is a polynomial equation of degree one. i
- 2
-
Many quadratic equations have two real roots, for example
x2 + 3x + 2 = 0
-
has two real roots. Some quadratic equations, such as
x2 + 2x + 1 = 0
-
only appear to have one real root; but if we rewrite the equation in the form (x + 1)2 = 0 we can see that the root (x = − 1) occurs with multiplicity two (corresponding to the power two), so in a sense it occurs twice, and from this point of view this equation can also be said to have two solutions rather than one. i
The equation
-
x2 + 2 = 0
has no real roots, but it has two complex solutions 2i and − 2i, so, provided we allow for complex numbers, this equation can also be said to have two solutions. In fact, all polynomial equations of degree two have two solutions if we include complex solutions and take due account of the multiplicity of repeated solutions.
- 3
-
A cubic equation such as
x3 − 4x2 + 5x − 2 = 0
-
which can be rewritten in the form
(x − 1)2 (x − 2) = 0
-
has three solutions if we count the root x = 1 twice, while the equation
(x − 4)3 = 0
-
has three solutions if we count the root x = 4 three times (i.e. according to its multiplicity). These are
polynomial equations of degree three.
A polynomial equation of degree n is of the form
anx n + an−1x n−1 + an−2x n−2 + ... + a0 = 0(21) i
where an ≠ 0, and n is a positive integer. Remember that the left–hand side of this equation is known as a polynomial of degree n and the numbers ai (for i = 0 to n) are called its coefficients.
It would appear that a polynomial equation of degree one has one root i, while (if we count them appropriately) a polynomial equation of degree two has two roots, and a polynomial equation of degree three has three roots. Naturally we are led to suspect that a polynomial equation of degree n will have n roots, and this is indeed the case provided that we count the roots according to their multiplicity. i
The fundamental theorem of algebra states that each polynomial with complex number coefficients and of degree n has, counting multiple roots an appropriate number of times, exactly n complex roots. i
The proof of this theorem was given by Gauss in 1799, but it is not easy, so we ask you to take it on trust for this module.
One obvious limitation of the fundamental theorem of algebra is that although the theorem tells us how many roots an equation must have, it tells us nothing about how to go about finding them. Finding the root of a polynomial equation of degree one is straightforward and simply consists of rearranging the terms in the equation.
To find the roots of a quadratic equation
ax2 + bx + c = 0
(with a ≠ 0) we can use the well–known formula
$x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$(22) i
This equation is valid even if a, b and c are complex. There are also similar, but much more complicated, formulae for polynomial equations of degree three and four. Surprisingly, it can be shown that no formulae exist for solving general equations of degree higher than four; however, there are numerical techniques for finding the approximate roots of polynomial equations of any degree and such techniques form the basis of many computer programs.
Another important result which we state, but do not prove, is that any complex zeros of a polynomial with real coefficients always occur as complex conjugate pairs. For example, the complex zeros of z2 − 2z + 2 (i.e. the roots of the equation z2 − 2z + 2 = 0) are 1 − i and 1 + i, a conjugate pair of complex numbers. We can see that this is generally true for a quadratic equation with a, b and c all real because the imaginary part comes from b2 − 4ac < 0 in Equation 22.
Question T17
From the fundamental theorem of algebra the polynomial equation x2 − ix + 2 = 0 must have two roots. Use Equation 22 to find the roots and hence, factorize the polynomial x2 − ix + 2 = 0.
Answer T17
From Equation 22,
$x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$(Eqn 22)
$x = \dfrac{i\pm\sqrt{-1-8\os}}{2} = \dfrac{i\pm\sqrt{-9\os}}{2} = \dfrac{i\pm 3i}{2}$
Therefore the roots are −i and 2i, hence
x2 − ix + 2 = (x + i)(x − 2i).
2.7 The Argand diagram
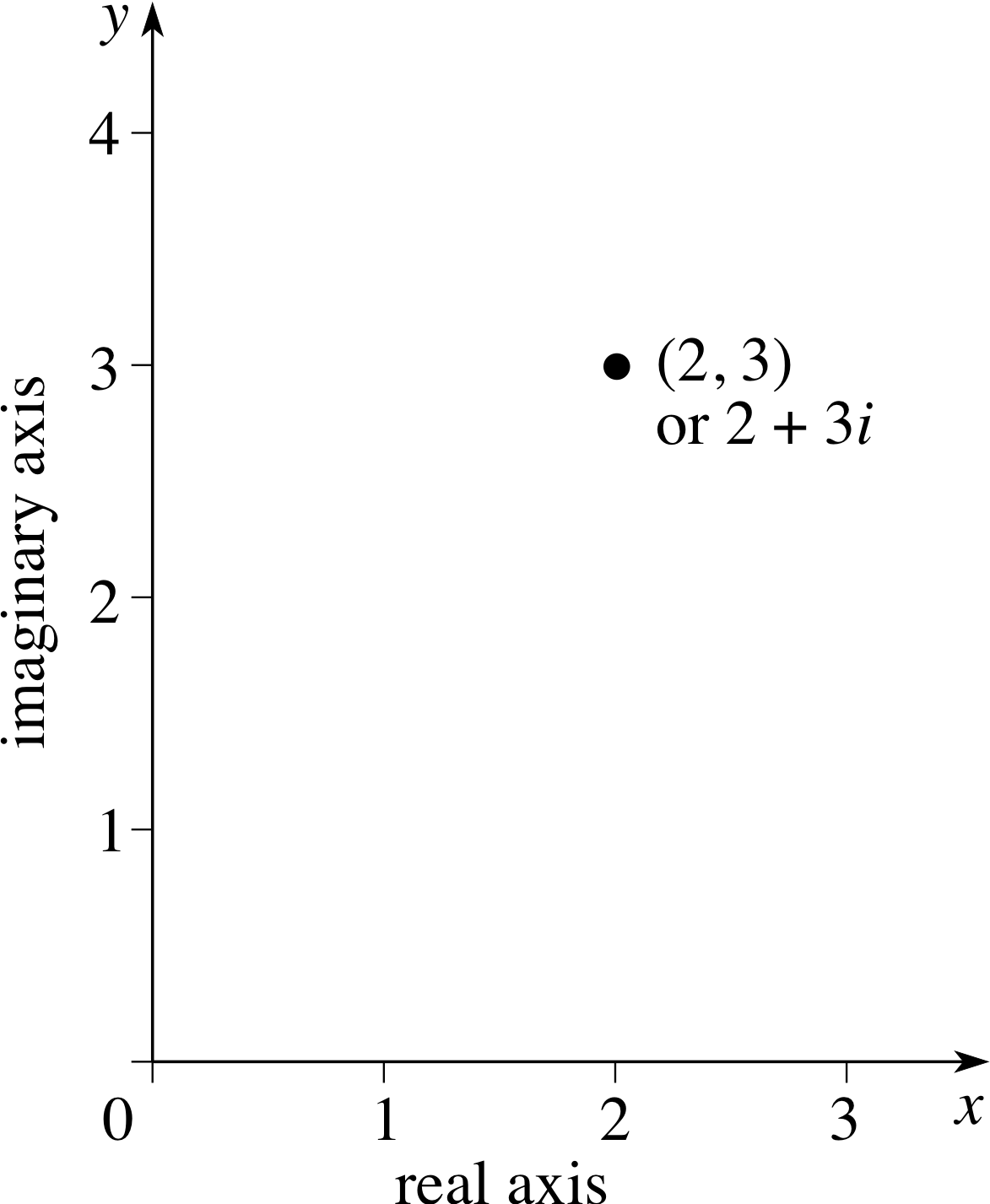
Figure 5 The complex number, 2 + 3i, plotted on an Argand diagram.
A complex number, z = x + iy, is completely determined by the pair of real numbers, x and y. In 1831 Gauss suggested using x and y as the coordinates of a point on a graph. Such a graph is known as an Argand diagram, after the French mathematician Jean Robert Argand (1768–1822) who described a similar idea in 1806. Any complex number corresponds to a point on the Argand diagram and, as an example, the number, 2 + 3i, is plotted in Figure 5. Conversely, any point on the Argand diagram corresponds to a unique complex number.
In Figure 5 we have plotted an arbitrary point z = x + iy, and we have labelled the horizontal axis as the x–axis and the vertical axis as the y–axis. The horizontal and vertical axes in an Argand diagram are known as the real axis and the imaginary axis, respectively. i We will not usually label the axes since we may wish to plot arbitrary points such as x + iy, p + iq or u + iv on the same Argand diagram.
The distance from the origin of a point with coordinates x and y is $\sqrt{x^2 + y^2}$. But since this is also the expression for the modulus of a complex number, z = x + iy it follows that the distance of the point from the origin is | z |.
Question T18
If z = 3 + 4i, plot z and z* on an Argand diagram.
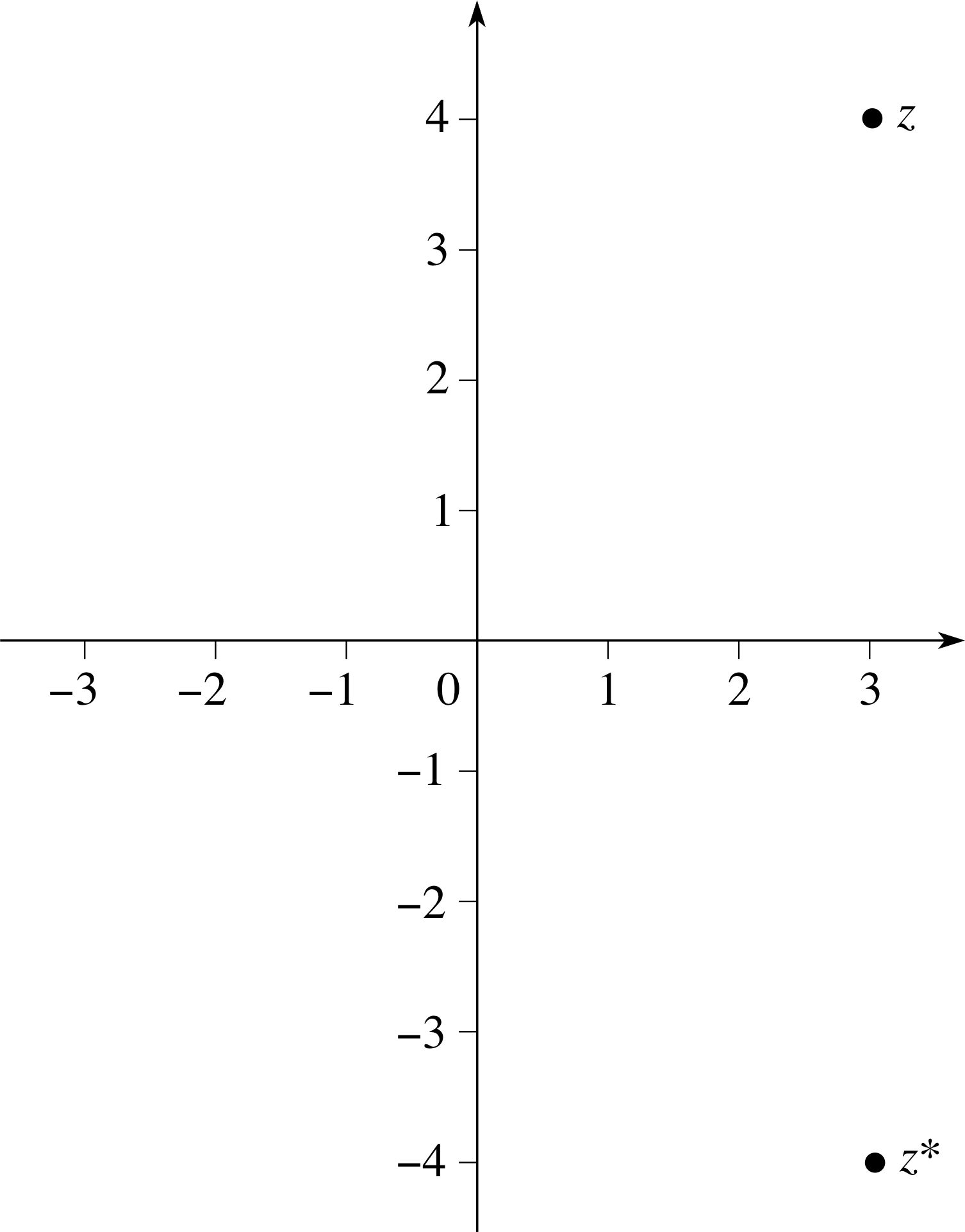
Figure 8 See Answer T18.
Answer T18
The complex numbers, z and z*, plotted on an Argand diagram for z = 3 + 4i are given in Figure 8.
The Argand diagram is the answer to our earlier question (at the end of Subsection 2.5) about how to extend the real line so that we can represent a complex number graphically; instead of a line we use a plane. It is an important tool in the application of complex numbers and is developed further elsewhere within FLAP.
In fact the Argand diagram is often known as the complex plane. i The set of real numbers is sometimes referred to as the real line, and similarly the set of all complex numbers, $\mathbb{C}$, is often known as the complex plane, even when no Argand diagram is actually drawn.
Question T19
Plot the following complex numbers on the same Argand diagram:
i, $\dfrac{1+i}{\sqrt{2\os}}$, $\dfrac{1-i}{\sqrt{2\os}}$, 1, −i, $\dfrac{-1-i}{\sqrt{2\os}}$, −1, $\dfrac{-1+i}{\sqrt{2\os}}$.
What significant features does this collection of points have?
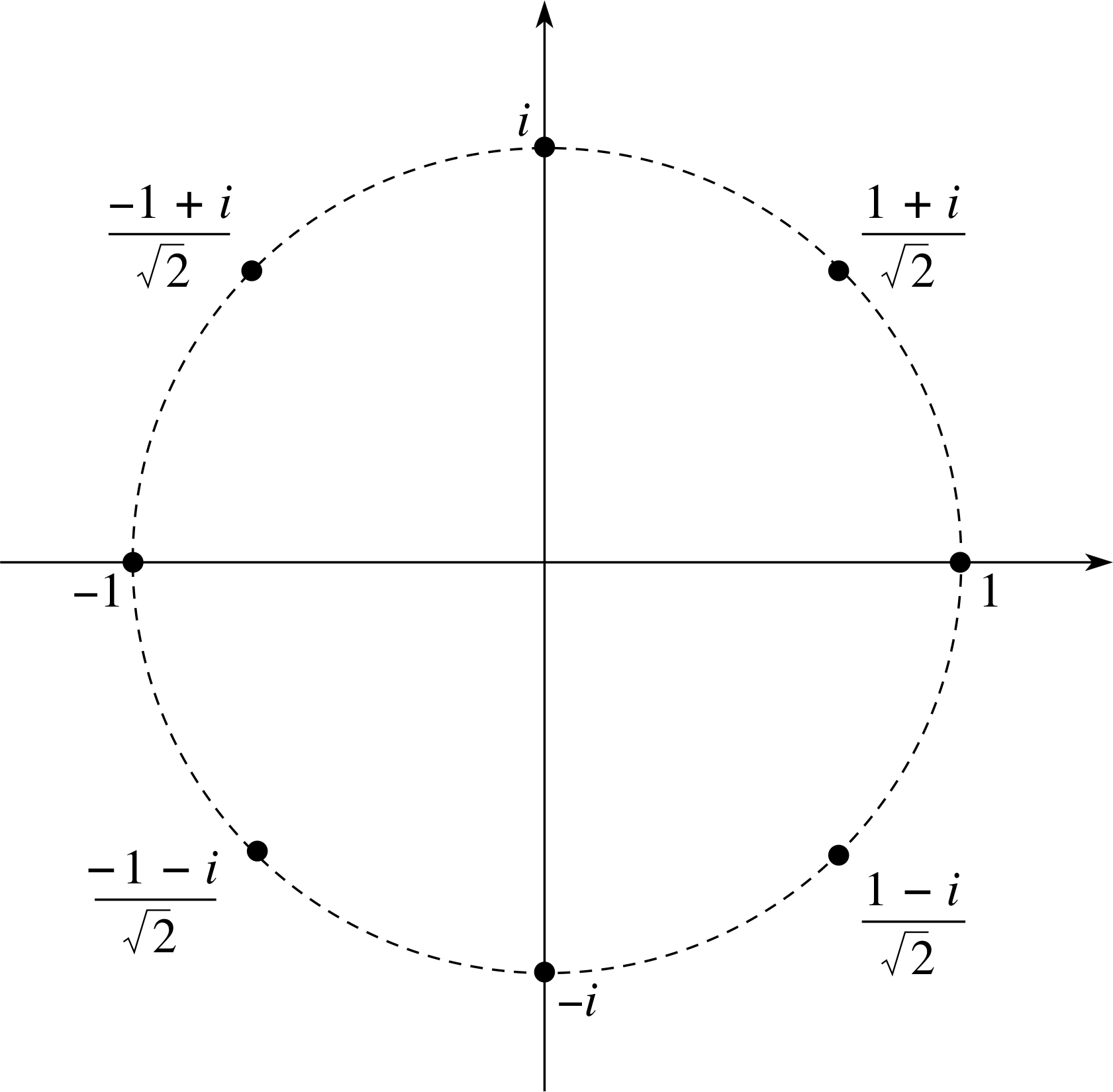
Figure 9 See Answer T19.
Answer T19
An Argand diagram showing the points
i, $\dfrac{1+i}{\sqrt{2\os}}$, $\dfrac{1-i}{\sqrt{2\os}}$, 1, −i, $\dfrac{-1-i}{\sqrt{2\os}}$, −1, $\dfrac{-1+i}{\sqrt{2\os}}$
is given in Figure 9. From Figure 9 we can see the following features:
- All points lie on a circle of radius 1; this is because each of the numbers has modulus 1. For example
$\left\lvert\,\dfrac{1-i}{\sqrt{2\os}}\,\right\rvert = \sqrt{\dfrac{1^2+1^2}{2}} = 1$
- The points are symmetrically placed on this circle at intervals of 45° (or π/4 radians).
- The points either occur in complex conjugate pairs, such as
$\dfrac{1\pm i}{\sqrt{2\os}}$ or are real.
2.8 Applications of complex arithmetic
We now look at some examples of complex arithmetic. The formulae and exercises are useful in general, but (with our choice of symbols) they are particularly relevant to the analysis of a.c. i circuits. In this subsection the symbols ω, R, X, L and C represent dimensionless real numbers while Z represents a dimensionless complex number, which ensures that you need to know nothing about electricity in order to understand the exercises; but apart from this, the calculations are typical of those you may meet in a practical context. You may be interested to know that, in the theory of a.c. circuits, the following meanings and SI units are usually given to these symbols:
| ω | angular frequency (s−1) | R | resistance (ohm) | |
| X | reactance (ohm) | L | inductance (henry) | |
| C | capacitance (farad) | Z | impedance (ohm) | i |
Example 1
Simplify $\dfrac{1}{\cfrac{1}{2+3i}+4i}$
Solution
If we express the denominator as a single fraction we have
$\dfrac{1}{2+3i}+4i = \dfrac{2-3i}{(2+3i)(2-3i)}+4i = \dfrac{2}{13} -\dfrac{3}{13}i+4i = \dfrac{2+49i}{13}$
and it follows that
$\dfrac{1}{\cfrac{1}{2+3i}+4i} = \dfrac{13}{2+49i} = \dfrac{13(2-49i)}{(2+49i)(2-49i)} = \dfrac{2-49i}{185}$
As an alternative method, we could have multiplied both numerator and denominator of the original expression by 2 + 3i to obtain
$\dfrac{1}{\cfrac{1}{2+3i}+4i} = \dfrac{2+3i}{1+4i(2+3i)} = \dfrac{2+3i}{-11+8i} = \dfrac{(2+3i)}{(-11+8i)}\dfrac{(-11-8i)}{(-11-8i)} = \dfrac{2-49i}{185}$
Further examples are given below to illustrate the usefulness of the methods of complex arithmetic covered in this module. i
Example 2
Complex numbers Z1 and Z2 are given by:
Z1 = R1 + iX1
Z2 = R2 + iX2
where R1, R2, X1 and X2 are real.
If R1 = 2, R2 = 4, X1 = 1, X2 = 3 and
Z = Z1 + Z2(23)
find: (a) Re(Z), (b) Im(Z) and (c) | Z |.
Solution
We have
Z = Z1 + Z2 = (2 + i) + (4 + 3i) = 6 + 4i
and therefore Re(Z) = 6 and Im(Z) = 4.
| Z | is given by
| Z |= $\sqrt{6^2+4^2} = \sqrt{52\os}$ i
Example 3
Repeat the previous example, where
Z1 = R1 + iX1
Z2 = R2 + iX2
but replace Equation 23 by
$\dfrac1Z = \dfrac{1}{Z_1} + \dfrac{1}{Z_2}$(24)
Solution
It is probably easier to do this example by working directly with the given numbers, rather than to try to obtain a general algebraic expression for Z first, so we have
$\dfrac1Z = \dfrac{1}{2+i}+\dfrac{1}{4+3i} = \dfrac{(4+3i)+(2+i)}{(2+i)(4+3i)} = \dfrac{6+4i}{5+10i}$
and therefore
$Z = \dfrac{5+10i}{6+4i} = \dfrac{5+10i}{2(3+2i)} = \dfrac{(5+10i)(3-2i)}{2(3+2i)(3-2i)} = \dfrac{(15+20)+i(30-10)}{26} = \dfrac{35+20i}{26}$
This gives:
Re(Z) = $\dfrac{35}{26}$
Im(Z) = $\dfrac{20}{26} = \dfrac{10}{13}$
| Z | = $\dfrac{\sqrt{\smash[b]{(35)^2+(20)^2}}}{26} \approx 1.55$
Example 4
Given that R1 = 1, R2 = 2, ωL = 3, ωC = 4 and
$Z = R_1 + \dfrac{1}{\cfrac{1}{R_2+i\omega L}+\cfrac{1}{1/(i\omega C)}}$(25)
find Re(Z) and Im(Z).
Solution
Substituting the given values we have
$Z = 1 + \dfrac{1}{\cfrac{1}{2+3i}+\cfrac{1}{1/(4i)}} = 1 + \dfrac{1}{\cfrac{1}{2+3i}+4i} = 1+\dfrac{2-49i}{185}$ (see Example 1)
$\phantom{Z} =\dfrac{187-49i}{185}${2\os}
and therefore Re(Z) = 187/185 and Im(Z) = −49/185.
Question T20
Given that R1 = 1.5, R2 = 2.5, ωL = 1.0, ωC = 2.0 and
$Z = R_1 + \dfrac{1}{\cfrac{1}{R_2+i\omega L}+\cfrac{1}{1/(i\omega C)}}$
find Re(Z) and Im(Z).
Answer T20
$Z = 1.5 + \dfrac{1}{\cfrac{1}{2.5+i}+\cfrac{1}{1/(2i)}} = \dfrac{83}{52}-\dfrac{27}{52}i\approx 1.60 - 0.519i$
3 Closing items
3.1 Module summary
- 1
-
Any Section 2complex number, z, can be written as z = x + iy where x and y are real numbers and i satisfies i2 = −1.
- 2
-
If z = x + iy (with x and y real) then x is known as the Subsection 2.3real part of z, written as Re(z) and y is known as the Subsection 2.3imaginary part of z, written as Im(z). i
- 3
-
An Subsection 2.2imaginary number has a zero real part and therefore takes the form, z = iy, where y is real.
- 4
-
Complex numbers obey the rules of normal algebra with the additional rule that that i2 can be replaced by −1.
- 5
-
The complex conjugate of z (written z*) is defined by:
z* = Re(z) − i Im(z)
- 6
-
The modulus of z = x + iy (written as | z |) is defined by
$\lvert\,z\,\rvert = \sqrt{[{\rm Re}(z)]^2 + {[{\rm Im}(z)]^2}} = \sqrt{x^2+y^2}$(Eqn 19)
and satisfies
| z | = zz*(Eqn 20)
- 7
-
To rewrite a quotient of complex numbers as a single complex number, multiply the numerator and
denominator by the complex conjugate of the denominator, as in
$\dfrac{x + iy}{a+ib} = \dfrac{(x + iy)(a-ib)}{a^2+b^2}$
This process is known as rationalizing a complex quotient.
- 8
-
The Subsection 2.6fundamental theorem of algebra states that each polynomial with complex number coefficients and of degree n has, counting multiple roots an appropriate number of times, exactly n complex roots.
- 9
-
Any complex number, z = x + iy (with x and y real), can be represented by a point with coordinates (x, y) on an Subsection 2.7Argand diagram. Conversely, any point on an Argand diagram corresponds to a unique complex number. The set of complex numbers is often denoted by the symbol $\mathbb{C}$.
3.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define and use the terms that are emboldened and flagged in the margins of the module.
- A2
-
State and apply the fundamental theorem of algebra.
- A3
-
Perform complex arithmetic, including addition, subtraction and multiplication and the use of conjugates and modulus.
- A4
-
Convert a quotient of complex numbers into the sum of a real and an imaginary part.
- A5
-
Plot complex numbers as points on an Argand diagram.
Study comment You may now wish to take the Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
3.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions, each of which tests one or more of the Achievements.
Question E1 (A3)
A complex number, z, is defined by
z = (2 + 3i)2 − | 3 + 4i | + 2 − 6i
Find Re(z), Im(z), z* and | z |.
Answer E1
Use the result
| 3 + 4i | = $\sqrt{3^2+4^2}$ = 5
and expand (2 + 3i)2 to find
z = 4 + 12i − 9 − 5 + 2 − 6i = −8 + 6i
This expression for z gives the results
Re(z) = −8 Im(z) = 6
z* = −8 − 6i | z | = $\sqrt{8^2+6^2}$ = 10
(Reread Subsection 2.3Subsections 2.3 and Subsection 2.42.4 if you had difficulty with this question.)
Question E2 (A3 and A4)
Express $\dfrac{1}{3+i} + \dfrac{2-i}{i+\cfrac{3}{1+i}}${2\os} in the form x + iy.
Answer E2
$\dfrac{1}{3+i} + \dfrac{2-i}{i+\cfrac{3}{1+i}} = \dfrac{17}{10} - \dfrac{3}{10}\,i${2\os}
(Reread Subsection 2.4Subsections 2.4 and Subsection 2.82.8 if you had difficulty with this question.)
Question E3 (A2 and A3)
State the fundamental theorem of algebra. Verify that two of the roots of
z3 + 2z2 + z + 2 = 0
are i and −2. Find any remaining roots. [Hint: The coefficients in the equation are real.]
Answer E3
The fundamental theorem of algebra states that each polynomial with complex number coefficients and of degree n has, counting multiple roots an appropriate number of times, exactly n complex roots.
Substituting z = i in the left–hand side of the equation we find
z3 + 2z2 + z + 2 = i3 + 2i2 + i + 2 = −i − 2 + i + 2 = 0
Similarly, substituting z = −2 in the left–hand side of the equation gives us
z3 + 2z2 + z + 2 = − 23 + 2 (−2)2 − 2 + 2 = −8 + 8 − 2 + 2 = 0
The equation is of degree 3 and therefore has three roots. Since all coefficients in the equation are real, any complex roots must be in complex conjugate pairs. The remaining root is therefore −i.
(Reread Subsection 2.6 if you had difficulty with this question.)
Question E4 (A3, A4 and A5)
Plot the complex numbers
$\dfrac{1}{1+i},~\dfrac{1}{1-i},~\dfrac{1}{-1+i},~\dfrac{1}{-1-i}$
as labelled points on an Argand diagram.
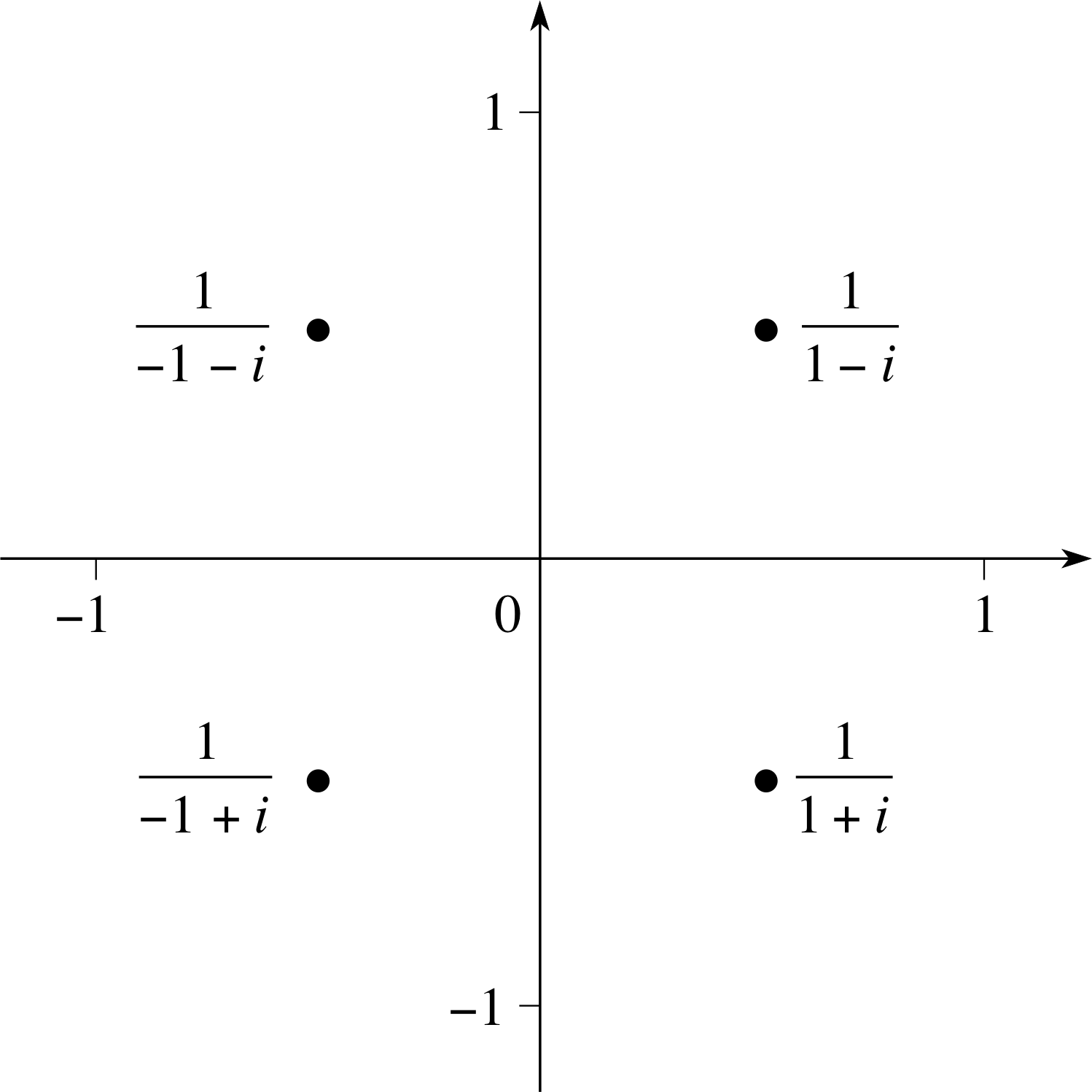
Figure 10 See Answer E4.
Answer E4
Multiplying the numerator and denominator in each expression by the complex conjugate of the denominator we obtain
$\dfrac{1}{1+i} = \dfrac{1-i}{2}$, $\dfrac{1}{1-i} = \dfrac{1+i}{2}$
$\dfrac{1}{-1+i} = \dfrac{-1-i}{2}$, $\dfrac{1}{-1-i} = \dfrac{-1+i}{2}$
These complex numbers are plotted on the Argand diagram shown in Figure 10.
(Reread Subsection 2.4Subsections 2.4 and Subsection 2.72.7 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 3Closing items.