MATH 3.2: Polar representation of complex numbers |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
The symbol i is defined to have the property that i × i = −1. Expressions involving i, such as 3 + 2i, are known as complex numbers, and they are used extensively to simplify the mathematical treatment of many branches of physics, such as oscillations, waves, a.c. circuits, optics and quantum theory. This module is concerned with the representation of complex numbers in terms of polar coordinates, together with the related exponential representation. Both representations are particularly useful when considering the multiplication and division of complex numbers, and are widely used in physics.
In Subsection 2.1 we review the Cartesian representation of complex numbers and show how any complex number can be represented as a point on an Argand diagram (the complex plane). We also show how complex numbers can be interpreted as an ordered pair of real numbers. Points in a plane are often specified in terms of their Cartesian coordinates, x and y, but they can equally well be defined in terms of polar coordinates r and θ. It will transpire that, while addition and subtraction of complex numbers is easy for complex numbers in Cartesian form, multiplication and division are usually simplest when the numbers are expressed in terms of polar coordinates. Subsection 2.2 and the subsequent two subsections are concerned with the polar representation of complex numbers, that is, complex numbers in the form r (cos θ + i sin θ). Subsection 2.5 introduces the exponential representation, r eiθ. Section 3 is devoted to developing the arithmetic of complex numbers and the final subsection gives some applications of the polar and exponential representations which are particularly relevant to physics.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 4.1Module summary and the Subsection 4.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 4.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
The complex number z is defined by z = 1 + i. Find the following in their simplest representations: z, | z |, arg(z), z* and z−1.
Answer F1
We can write z as
$z = 1 + i = \sqrt{2\os}\left(\dfrac{1}{\sqrt{2\os}}+i\dfrac{1}{\sqrt{2\os}}\right)$
But we also know that
$\cos(\pi/4) = \dfrac{1}{\sqrt{2\os}}$ and $\sin(\pi/4) = \dfrac{1}{\sqrt{2\os}}$
and therefore
z = 2 [cos(π/4) + i sin(π/4)]
which is the polar representation of z.
The modulus of z is given by | z | = $\sqrt{2\os}$. The argument of z is given by arg(z) = π/4. (The argument is undefined up to an additive term of 2πn, where n is any integer.)
The complex conjugate of z is given by
$z\cc = \sqrt{2\os}[\cos(\pi/4) - i\sin(\pi/4)]$
The reciprocal of z is given by
$z^{-1}= \dfrac{1}{\sqrt{2\os}}[\cos(\pi/4) - i\sin(\pi/4)]$
because $z^{-1} = \dfrac{z\cc}{\lvert\,z\,\rvert^2}$
Question F2
The complex numbers z and w are defined by z = 3 eiπ/10 and w = 4 eiπ/5. Find the simplest exponential representations of zw and z/w.
Answer F2
zw = 3 eiπ/10 × 4 eiπ/5 = 3 × 4 ei (π/10 + π/5) = 12 e3iπ/10
$\dfrac{z}{w} = \dfrac{3{\rm e}^{i\pi/10}}{4{\rm e}^{i\pi/5}} = \dfrac{3}{4}{\rm e}^{i(\pi/10-\pi/5)} = \dfrac{3}{4}{\rm e}^{-i\pi/10}$
Question F3
Suppose that a complex quantity, z, is known to satisfy
z = 2 + i + eiθ
where θ can take any real value. Sketch a curve on an Argand diagram giving the position of all possible points representing z.
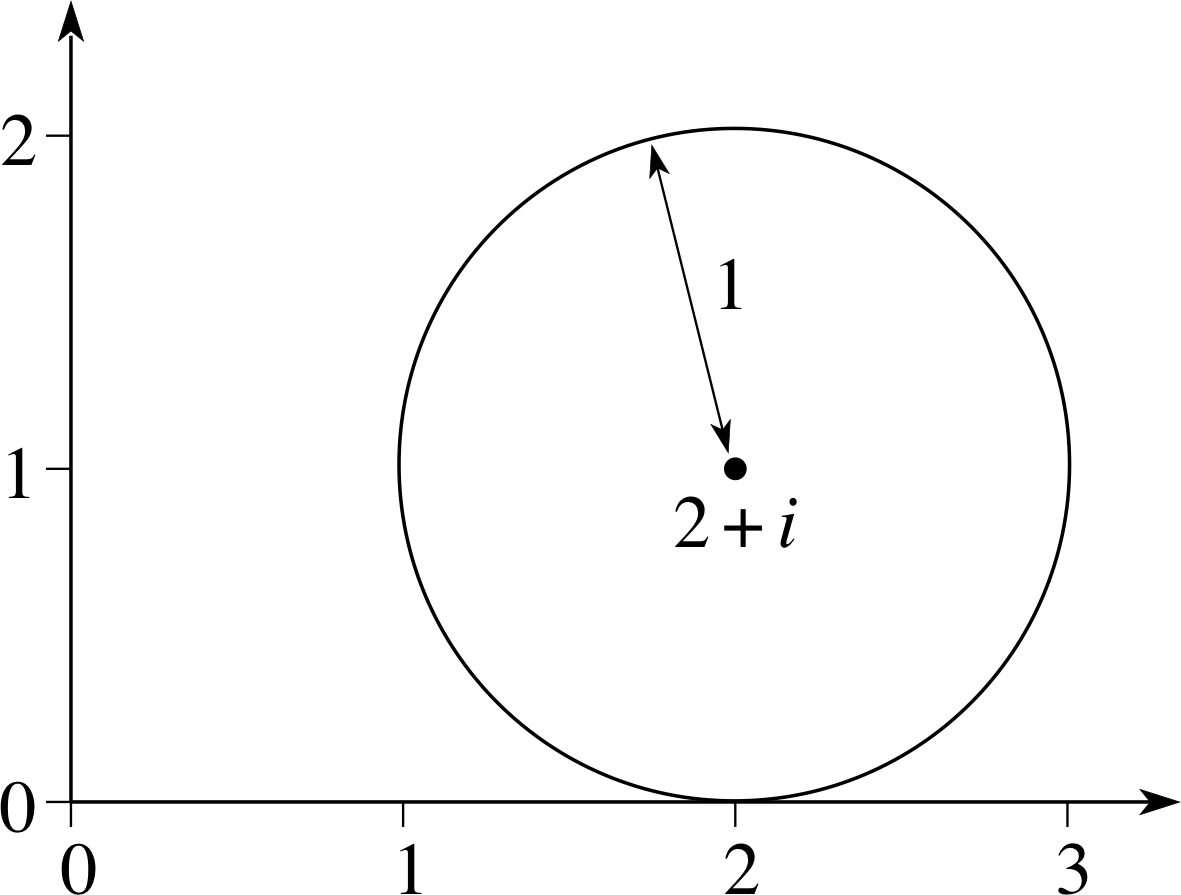
Figure 13 See Answer F3.
Answer F3
All complex numbers which satisfy z = eiθ lie on a circle of radius 1, centre the origin, on an Argand diagram. The additional terms, 2 + i, have the effect of moving the centre to the point representing 2 + i, so the curve on which z = 2 + i + eiθ must lie is shown in Figure 13.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection. Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 4Closing items.
1.3 Ready to study?
Study comment To begin the study of this module you need to be familiar with the following topics: the arithmetic of complex numbers in the form, z = x + iy, where i2 = −1. You should know how to add, subtract and multiply such numbers, be able to reduce the quotient of two complex numbers to rationalizing_a_complex_quotientrational form, to find the modulus_of_a_complex_numbermodulus, complex conjugate, real part and imaginary part of a complex number, and you should know how to plot a complex number on an Argand diagram.
You should be familiar with the addition of two–dimensional vectors by means of a diagram and by adding their components_of_a_vectorcomponents. You should also be familiar with Pythagoras’s theorem, the definition of sine, cosine and tangent, the measurement of angles in terms of radians and the following trigonometric identities
sin(α + β) = cos α sin β + sin α cos β(1)
cos(α + β) = cos α cos β − sin α sin β(2)
You should also know that (n factorial) n! = n (n − 1) ... 3, 2, 1, and 0! = 1. We will need to refer to the following power series for ex, sin x and cos x:
$\displaystyle {\rm e}^x = \sum_{n=0}^{\infty} \dfrac{x^n}{n!} = 1 + \dfrac{x}{1!} + \dfrac{x^2}{2!} + \dfrac{x^3}{3!} + \dots$(3)
$\displaystyle \sin x = \sum_{n=0}^{\infty} \dfrac{(-1)^n x^{2n+1}}{(2n+1)!} = x - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + \dots$(4)
$\displaystyle \cos x = \sum_{n=0}^{\infty} \dfrac{(-1)^n x^{2n}}{(2n)!} = 1 - \dfrac{x^2}{2!} + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + \dots$(5)
You will need to be familiar with the following properties of power_mathematicalpowers (i.e. indices)
u au b = u(a + b), (uv) a = u av a, (u a) b = u ab(6)
also to know that the nth root of u can be written as u1/n and to be able to use inverse trigonometric functions to solve an equation such as sin θ = 0.5 for θ (and to use the graph of sin θ, or otherwise, to find all the solutions). If you are unfamiliar with any of these topics you can review them by referring to the Glossary, which will indicate where in FLAP they are developed. The following questions will help you to establish whether you need to review some of the above topics before embarking on this module.
Throughout this module $\sqrt{x\os}$ means the positive square root, so that $\sqrt{4\os} = 2$.
Question R1
Rationalize the expression $z = \dfrac{3 + 2i}{1+2i}$ (i.e. express z in the form x + iy, finding the values of the real numbers x and y). What are the real and imaginary parts of z? Also find the complex conjugate and the modulus of z.
Answer R1
To rationalize the expression we multiply the denominator and the numerator by the complex conjugate of the denominator
$z = \dfrac{3 + 2i}{1 + 2i} = \dfrac{3 + 2i}{1 + 2i} \times \dfrac{1 - 2i}{1 - 2i}$
$\phantom{z }= \dfrac{(3\times 1 + 2\times 2)+i\,(-2\times 3 + 2\times 1)}{1^2+2^2} = \dfrac{7-4i}{5}$
The real part of z (often written as Re(z)) is 7/5 and the imaginary part of z (often written as Im(z)) is −4/5. Notice that Im(z) is not equal to −4i/5.
The complex conjugate of z = x + iy (sometimes written as $\bar{z}$ but as z* in FLAP) is equal to x − iy and so in this case we have
$z\cc = x - iy = \dfrac{7+4i}{5}$
The modulus of z = x + iy (usually written as | z |) is defined by | z | = $\sqrt{x^2+y^2}$ and therefore we have
$\lvert\,z\,\rvert = \sqrt{x^2+y^2} = \dfrac{\sqrt{7^2+4^2}}{5} = \dfrac{\sqrt{65\os}}{5} = \sqrt{13/5\os} \approx 1.612$
Note that the modulus of a complex number cannot be negative, i.e. | z | ≥ 0.
Consult the relevant terms in the Glossary for further information.
Question R2
Draw and label the points representing the complex numbers −2 + i, −2 − i and −3i on an Argand diagram.
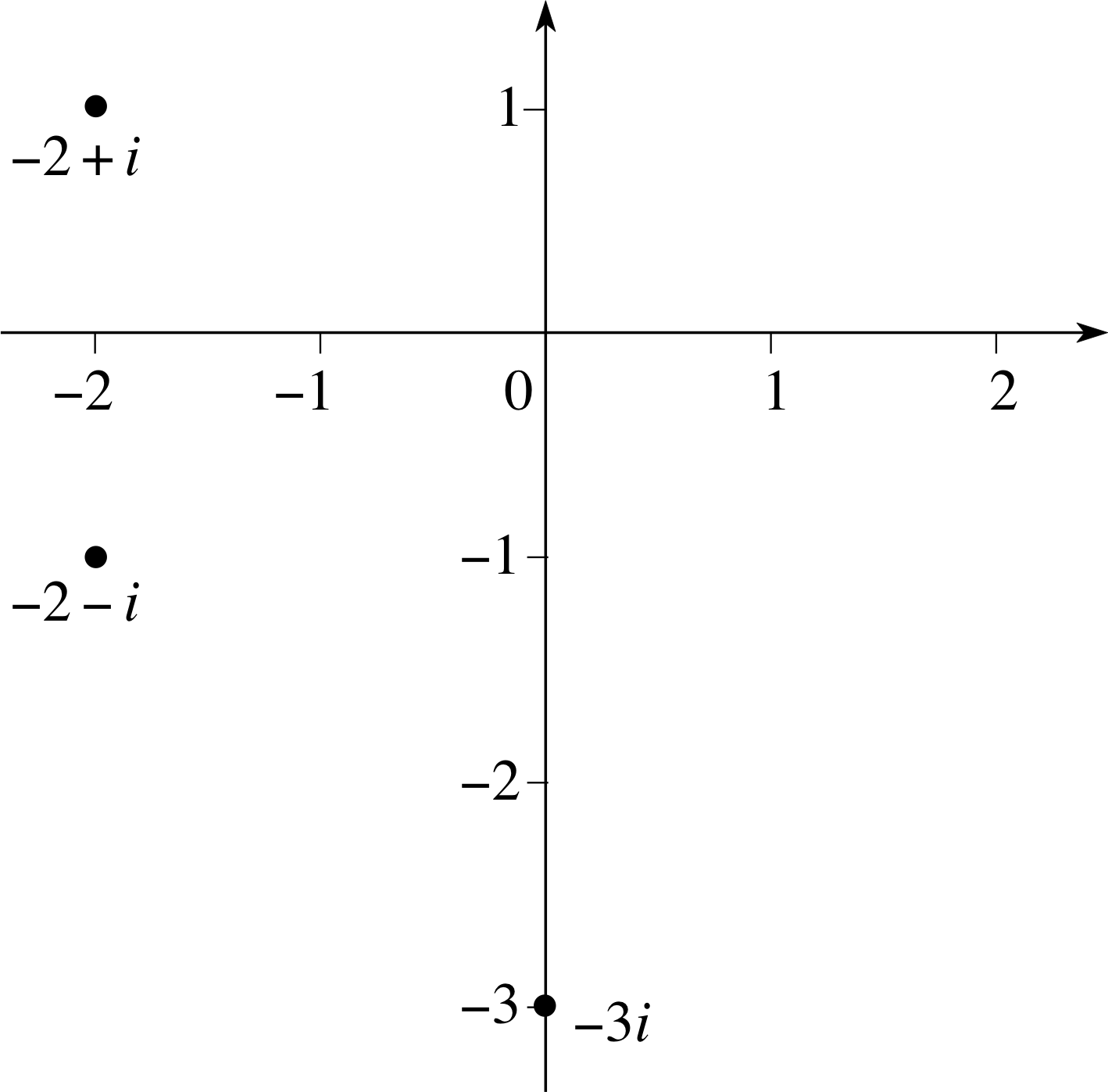
Figure 14 See Answer R2.
Answer R2
The points representing the complex numbers −2 + i, −2 − i and −3i are shown on the Argand diagram in Figure 14.
Consult Argand diagram in the Glossary for further information.
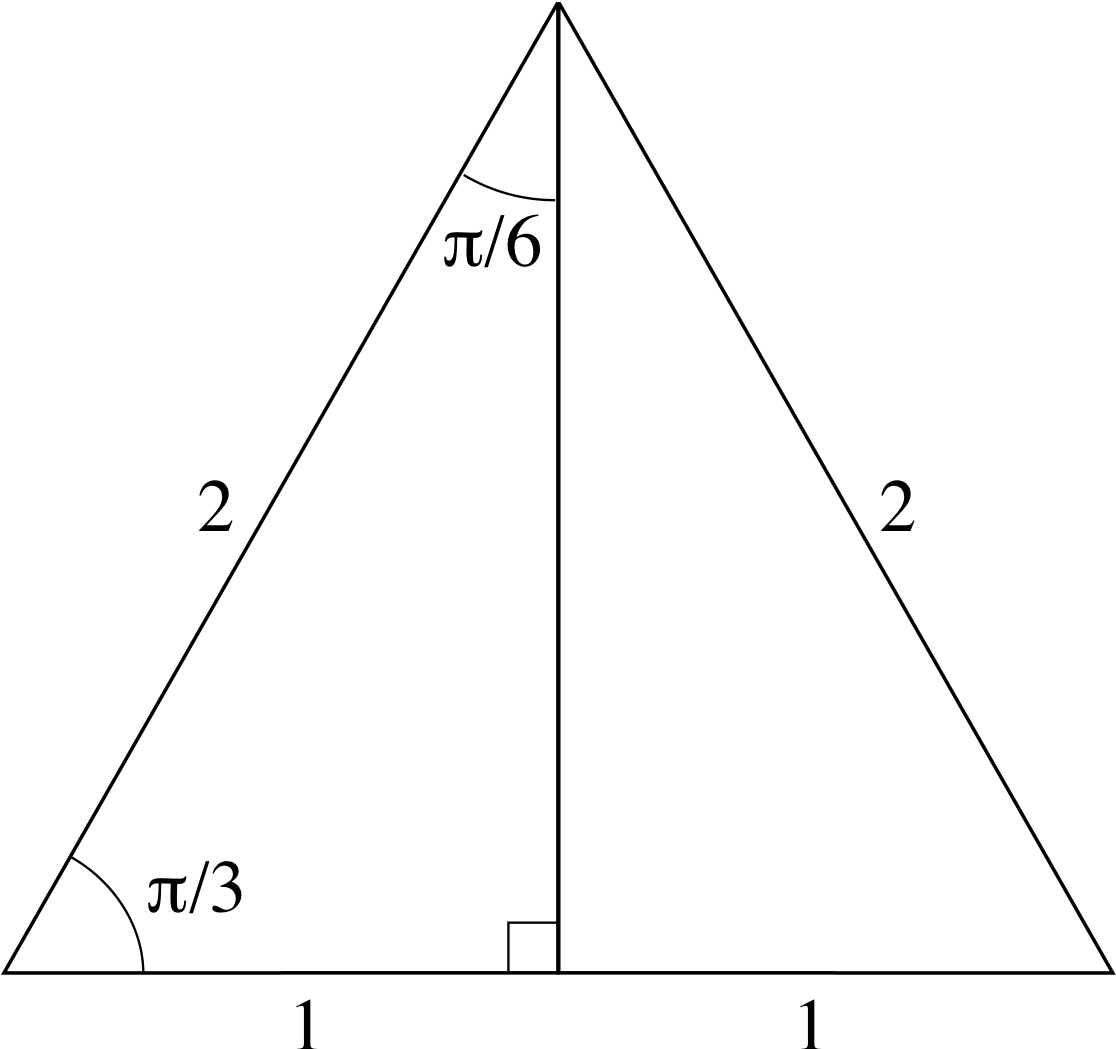
Figure 1 See Question R3.
Question R3 i
The equilateral triangle shown in Figure 1 has a perpendicular drawn from one vertex to the opposite side. Use the triangle in Figure 1 to find the values of cos(π/3), sin(π/3), tan(π/3), cos(π/6), sin(π/6) and tan(π/6).
Answer R3
By Pythagoras’s theorem the length of the perpendicular in Figure 1 is $\sqrt{2^2-1^2} = \sqrt{3\os}$, so we have
cos(π/3) = 1/2, sin(π/3) = $\sqrt{3\os}$/2, tan(π/3) = $\sqrt{3\os}/1 = \sqrt{3\os}$
cos(π/6) = $\sqrt{3\os}$/2, sin(π/6) = 1/2, tan(π/6) = 1/$\sqrt{3\os}$
Consult Pythagoras’s theorem and trigonometric functions in the Glossary for further information.
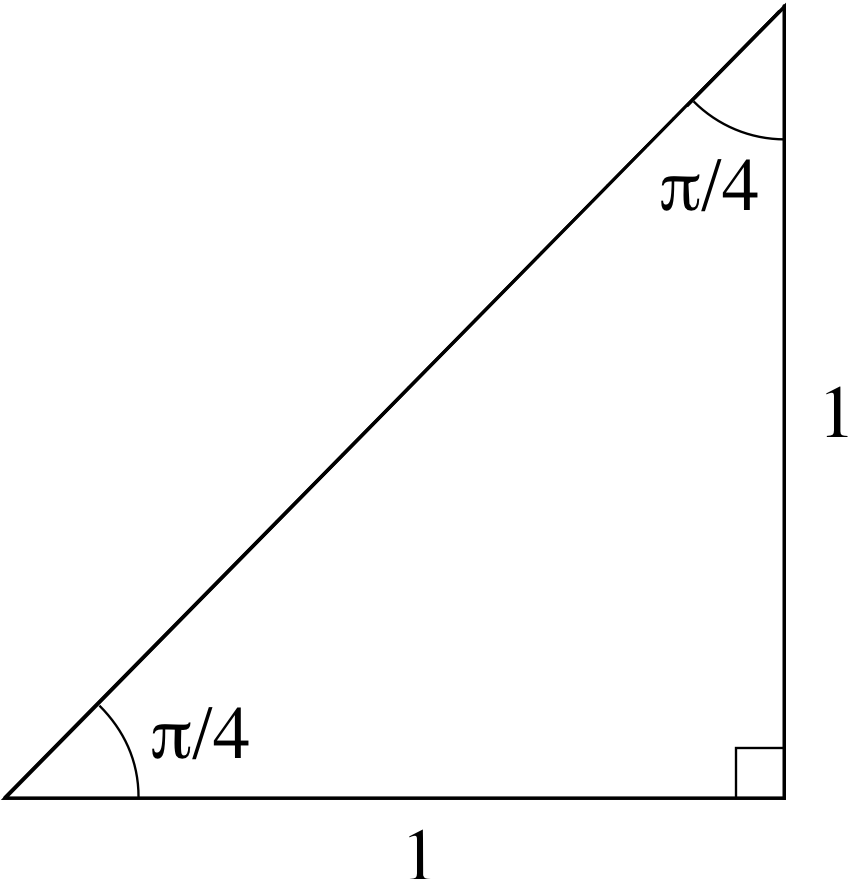
Figure 2 See Question R4.
Question R4 i
Use the right–angled triangle with two sides equal, shown in Figure 2 to find the values of cos(π/4), sin(π/4) and tan(π/4).
Answer R4
By Pythagoras’s theorem the length of the hypotenuse in Figure 2 is $\sqrt{1^2+1^2} = \sqrt{2\os}$ so we have
cos(π/4) = 1/$\sqrt{2\os}$, sin(π/4) = 1/$\sqrt{2\os}$, tan(π/4) = 1/1 = 1
Consult inverse trigonometric functions in the Glossary for further information.
Question R5
Two two–dimensional vectors, u and v, are specified in component form as (2, 3) and (1, −4), respectively. Find u + v by (a) drawing a suitable diagram and (b) adding the components directly.
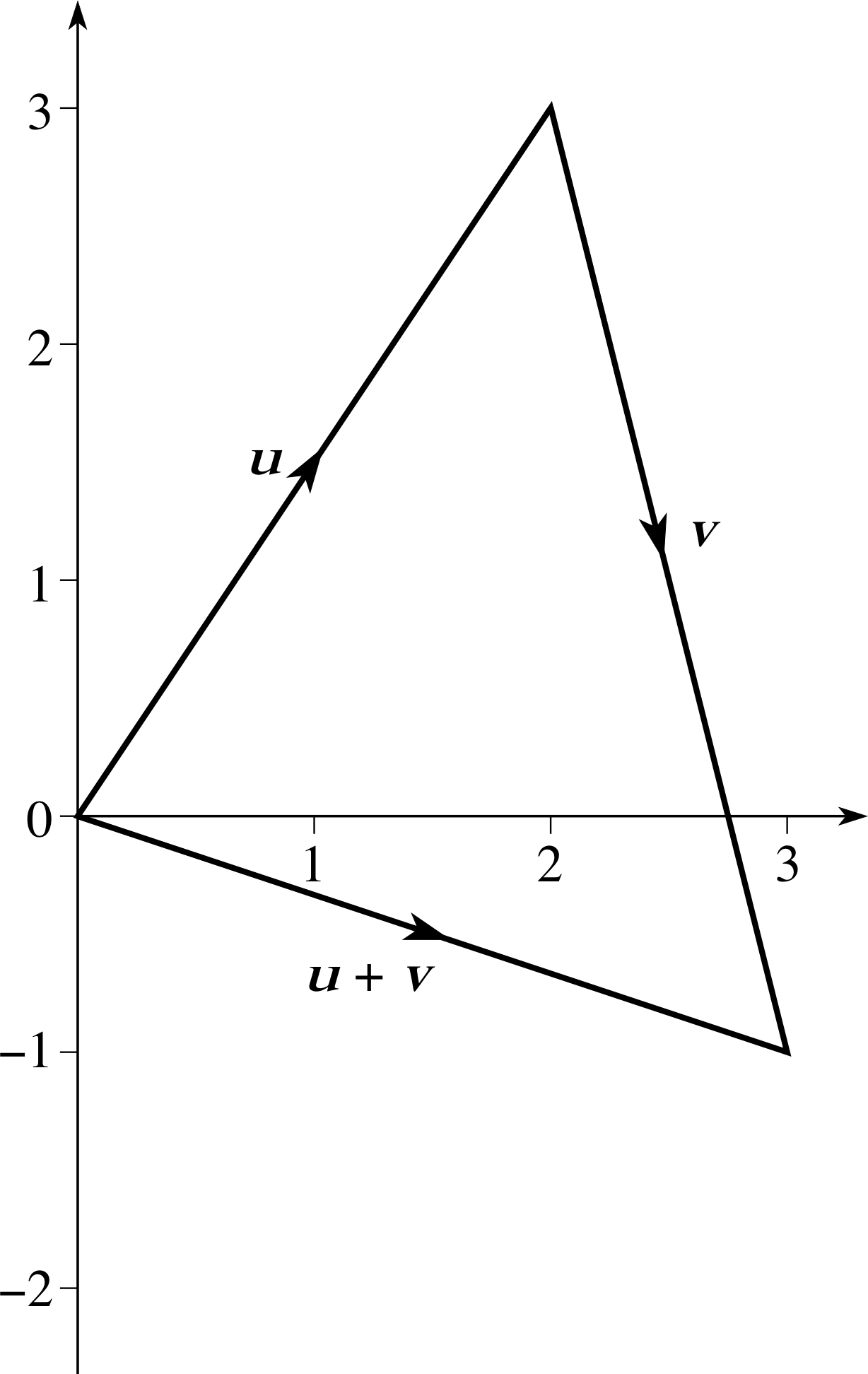
Figure 15 See Answer R5.
Answer R5
(a) The two vectors are shown in Figure 15 and their sum is represented by the third side of the triangle.
(b) The sum of the vectors can also be obtained by adding their components,
(2, 3) + (1, −4) = (2 + 1, 3 −4) = (3, −1)
Consult vector addition in the Glossary for further information.
Question R6
Solve the equation tan θ = 1.
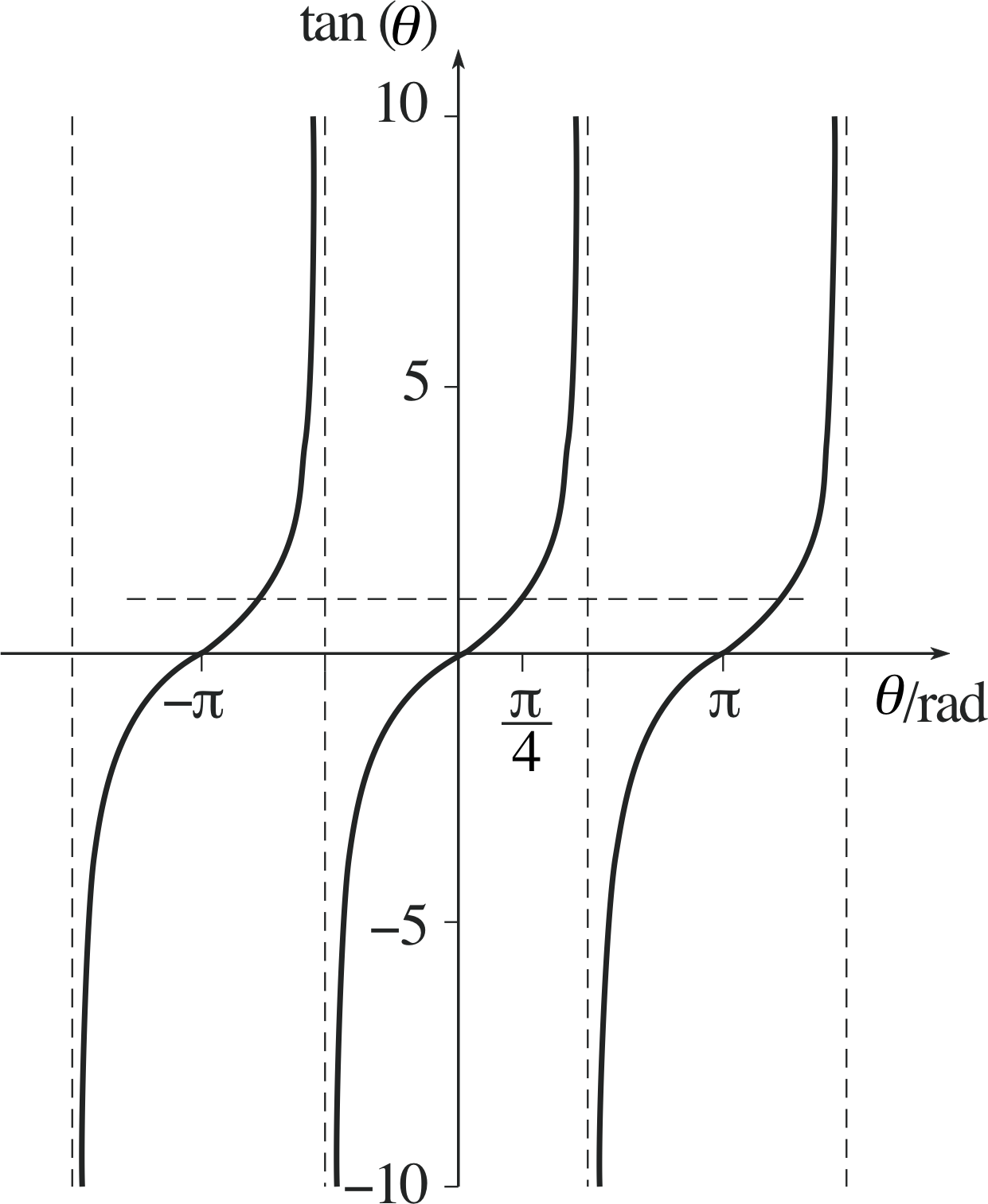
Figure 16 See Answer R6.
Answer R6
From Answer R4 we know that θ = π/4 is one solution of the equation tan θ = 1.
However, from the graph of y = tan θ (see Figure 16) it is easy to see that π/4 ± nπ is also a solution for any integer n.
Consult inverse trigonometric functions in the Glossary for further information.
Question R7
Express $\left.\sqrt{{\rm e}^{3x}}\middle /{\rm e}^x\right.$ in the form ekx (for some value of k) and hence write down the first three terms of its power series expansion.
Answer R7
$\left.\sqrt{{\rm e}^{3x}}\middle /{\rm e}^x\right. = {\rm e}^{3x/2} \times {\rm e}^{-x} = {\rm e}^{x/2} = 1 + x/2 + x^2/8 + \dots$
where the power series has been obtained by substituting y = x/2 into the general power series
${\rm e}^y = 1 + y + \dfrac{y^2}{2!} + \dfrac{y^3}{3!} + \dots$
Consult power series in the Glossary for further information.
2 Representing complex numbers
2.1 Complex numbers and Cartesian coordinates
A complex number, z, can be written as z = x + iy where x and y are real numbers and i2 = −1. Some examples of complex numbers are 2 + 3i, 7i and 2.4. i
Such numbers satisfy straightforward rules for addition and subtraction, which essentially mean that the real and imaginary parts are treated separately, so that, for example,
(3 + 4i) + (2 − i) − (−2 − 3i) = (3 + 2 + 2) + (4i − i + 3i) = 7 + 6i
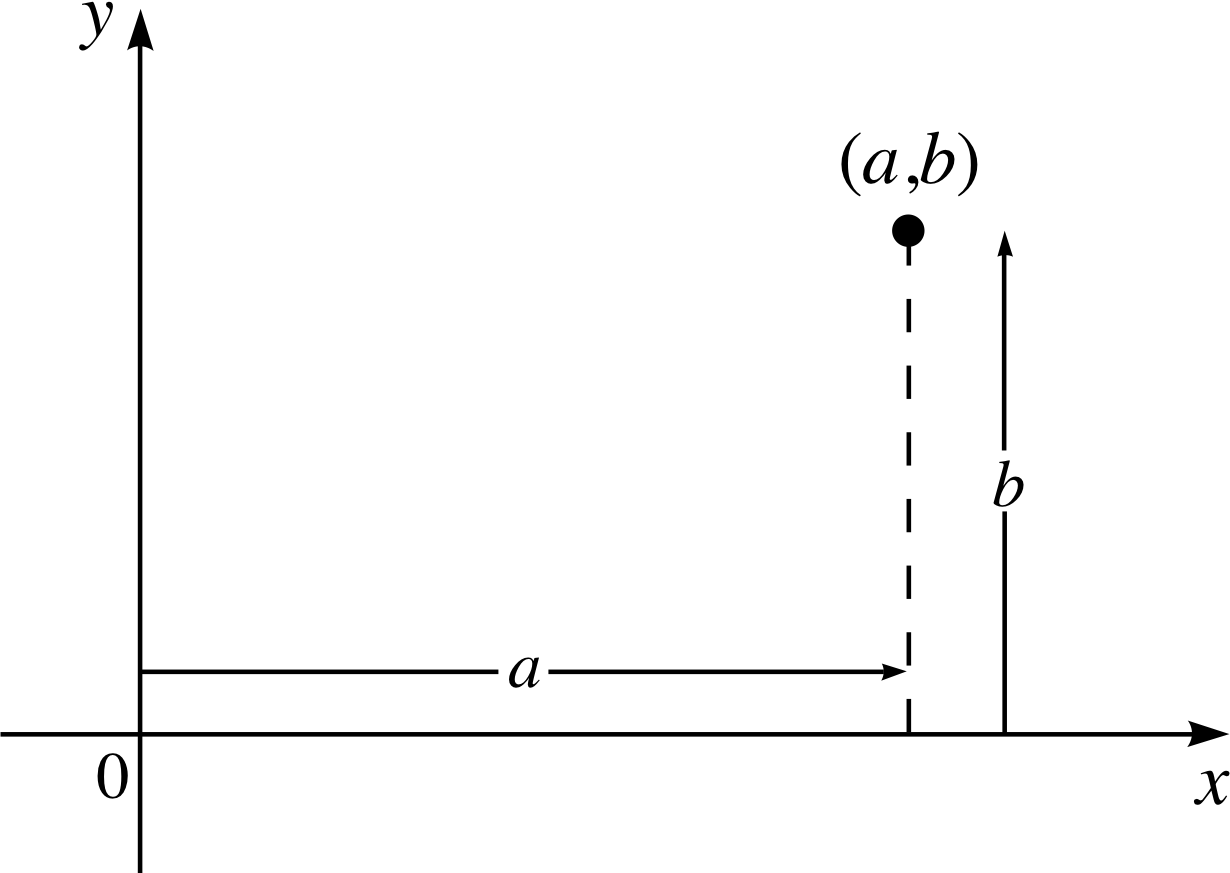
Figure 3 An Argand diagram showing the point corresponding to a complex number, z = a + ib.

Figure 4 An Argand diagram showing the addition of 3 + 2i and 1 + 3i.
Multiplication is quite simple provided that we remember to replace every occurrence of i × i by −1, although a mathematician would probably prefer a formal statement that the product of two complex numbers (a + ib) and (x + iy) is given by
(a + ib)(x + iy) = (ax − by) + i (ay + bx)(7)
For a long time the meaning of the symbol i gave many famous mathematicians cause for concern. However, in 1833 Sir William Rowan Hamilton (1805–1865) realized that the i and + sign in z = x + iy are both unnecessary sources of confusion. The role of the i is really to keep the x and y separate, while the + sign is there to tell us that x and y are part of a single entity; it does not mean addition in the sense that we might, for example, add 2 apples to 3 apples to get 5 apples. In fact, the x and y in z = x + iy are very much like the (ordered) pairs of numbers used as Cartesian coordinates. Hamilton’s ideas are closely linked to the those of Robert Argand (1768–1822) and Karl Friedrich Gauss (1777–1855) who both suggested representing a complex number by a point in a plane. As an example, the complex number a + ib is shown on an (x, y) coordinate system in Figure 3; notice that it is conventional that the number multiplying the i corresponds to the y–value. A figure in which the real and imaginary parts of complex numbers are used as Cartesian coordinates is known as an Argand diagram or the complex plane. An expression such as a + ib, where a and b are real numbers, is said to be the cartesian_form_of_a_complex_numberCartesian form (or cartesian_representation_of_a_complex_numberCartesian representation) of a complex number.
In some mathematics textbooks the authors avoid the problem of the meaning of the symbol i entirely – by not mentioning it – and they introduce the complex numbers as a set of ordered pairs of real numbers (x, y) with certain operations defined on them. Such a treatment has the advantage that complex numbers can immediately be seen to have much in common with vectors. The addition of two complex numbers is then defined by
(x, y) + (a, b) = (x + a, y + b)(8)
which is just the same as the rule that defines the addition of two vectors. An example is shown in Figure 4 where the addition of z = 3 + 2i and w = 1 + 3i is performed graphically on an Argand diagram or, equivalently
z + w = (3, 2) + (1, 3) = (4, 5)
Question T1
If z = 4 + 8i and w = 15 − 12i, use an Argand diagram to find the sum, z + w. Check your answer by means of vector addition using the (x, y) notation.
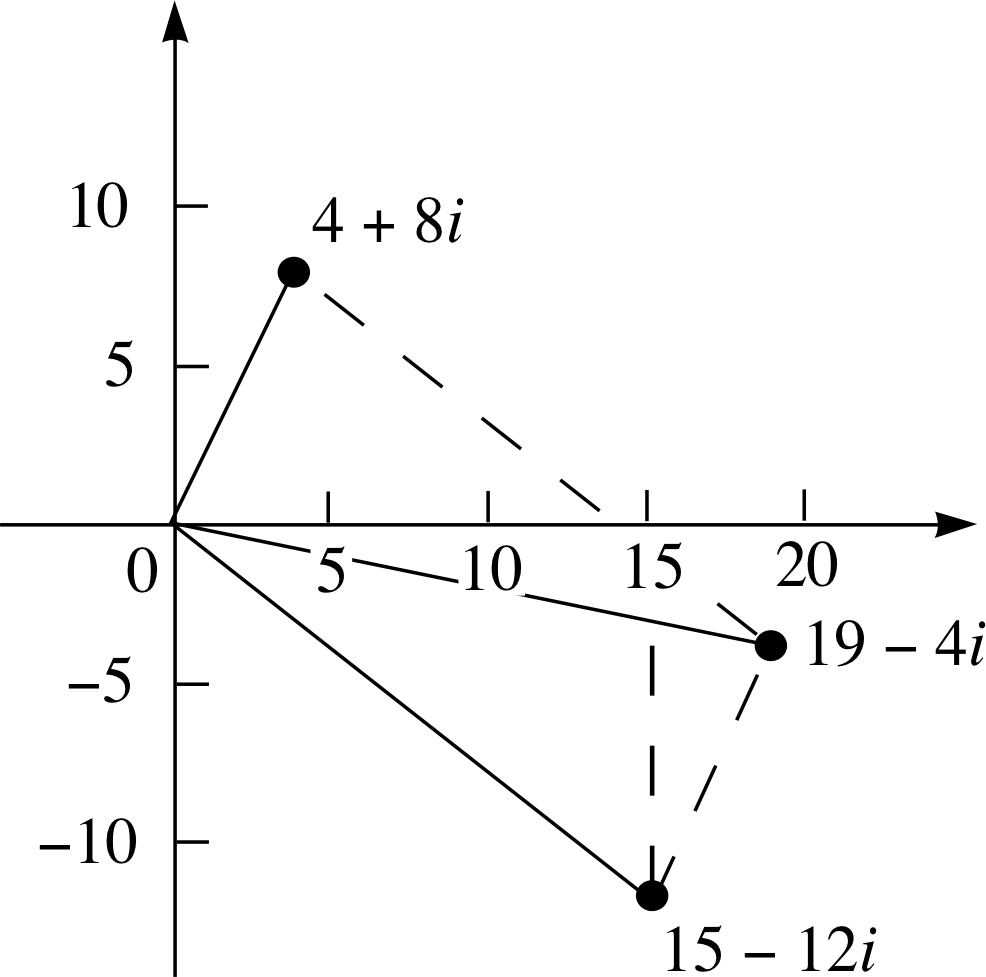
Figure 17 See Answer T1.
Answer T1
The points representing w and z are plotted on the Argand diagram in Figure 17. Lines drawn from the origin to these points can be considered as vectors which define the sides of a parallelogram and the sum of these vectors is a diagonal of this parallelogram. From the diagram we find that z + w is 19 − 4i. This can be checked numerically
(4, 8) + (15, −12) = (19, −4)
Although complex numbers behave like vectors as far as addition is concerned, when it comes to multiplication and division the two topics diverge. In terms of ordered pairs of real numbers, multiplication of complex numbers can be defined by i
(a, b) × (x, y) = [(ax − by), (ay + bx)](9)
Although one can introduce complex numbers by this route, which is entirely independent of the symbol i, it must be admitted that Equation 9 looks as though it came out of thin air. In practice i is a very useful notational convenience which makes Equation 9 look much more natural. The i notation is used throughout science and engineering, and even by the purest of pure mathematicians. It is a practice which we follow in FLAP.
2.2 Polar coordinates
We have seen how it is straightforward to interpret complex addition as vector addition on an Argand diagram. In order to investigate the effect of complex multiplication, try the following question.
Question T2
(a) Plot the numbers, 1, 2i, −3 −i and 2 − i on an Argand diagram.
(b) Multiply each of the numbers in part (a) by 2 and plot the resulting points on the same diagram. Suggest a geometric interpretation of multiplication by 2 and check your conjecture by finding the effect of multiplying −1 − i by 2.
(c) Repeat parts (a) and (b), but multiply by i instead of 2.
(d) Repeat parts (a) and (b), but multiply by 2i.
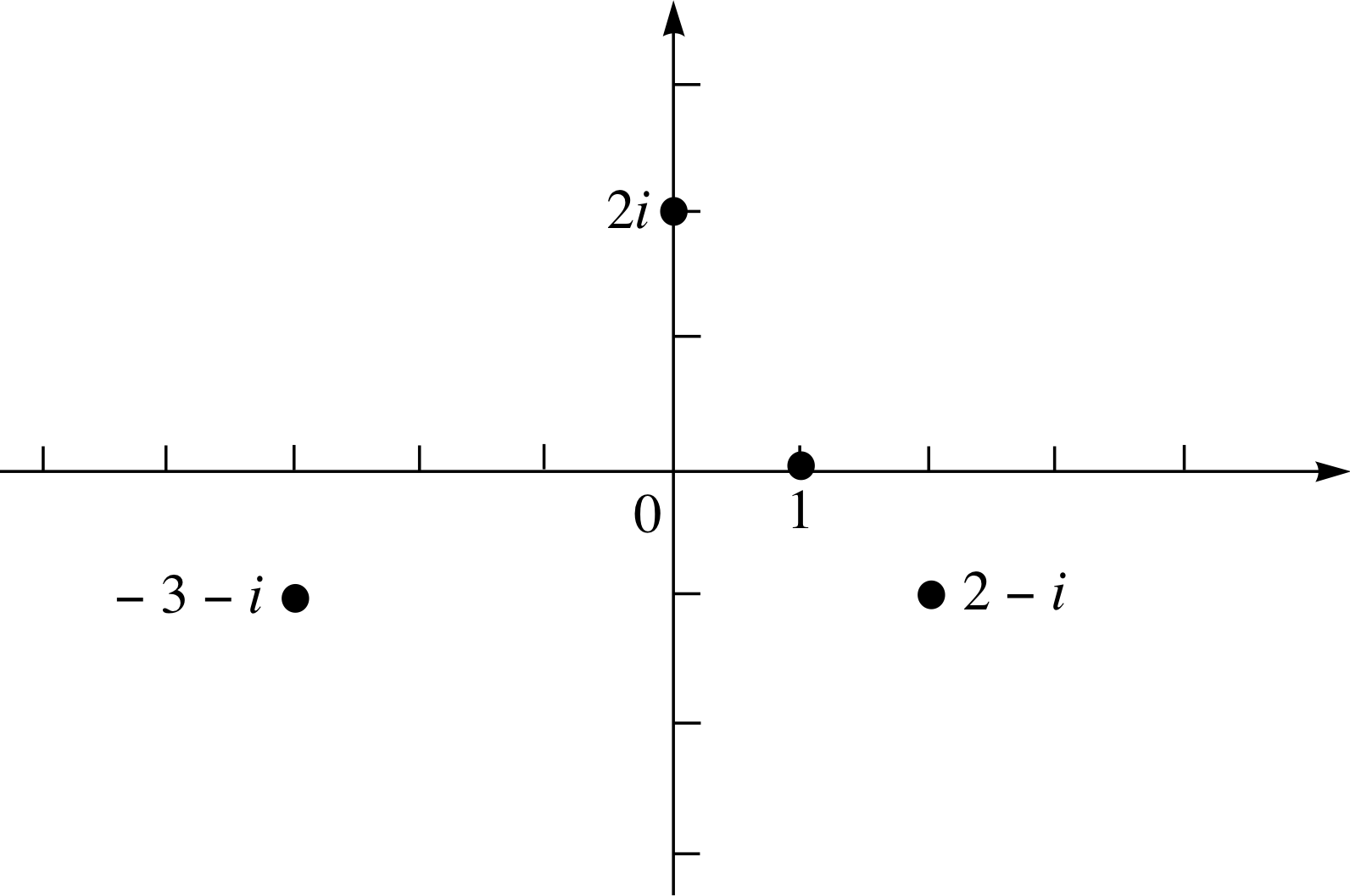
Figure 18 See Answer T2(a).
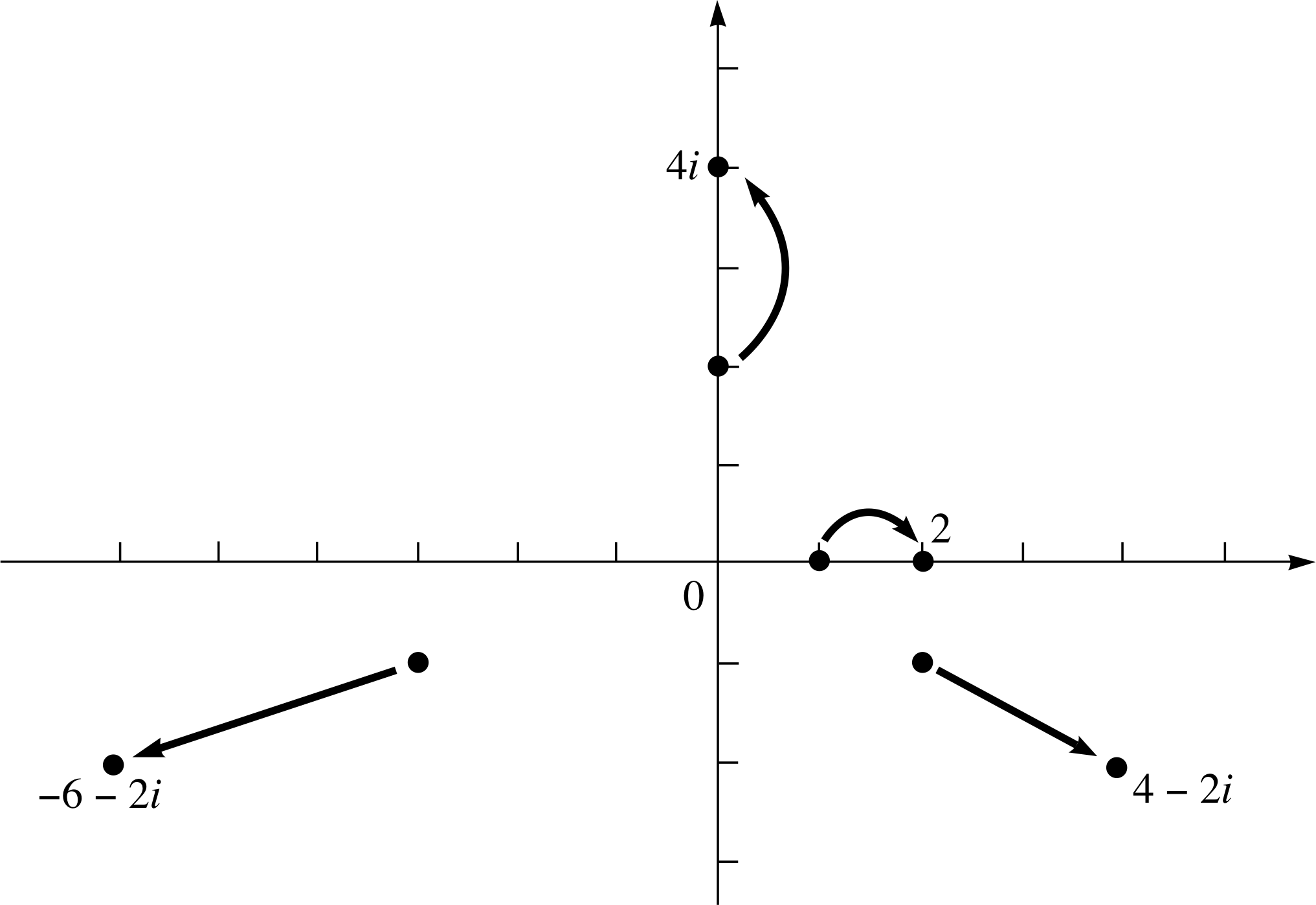
Figure 19 See Answer T2(b).
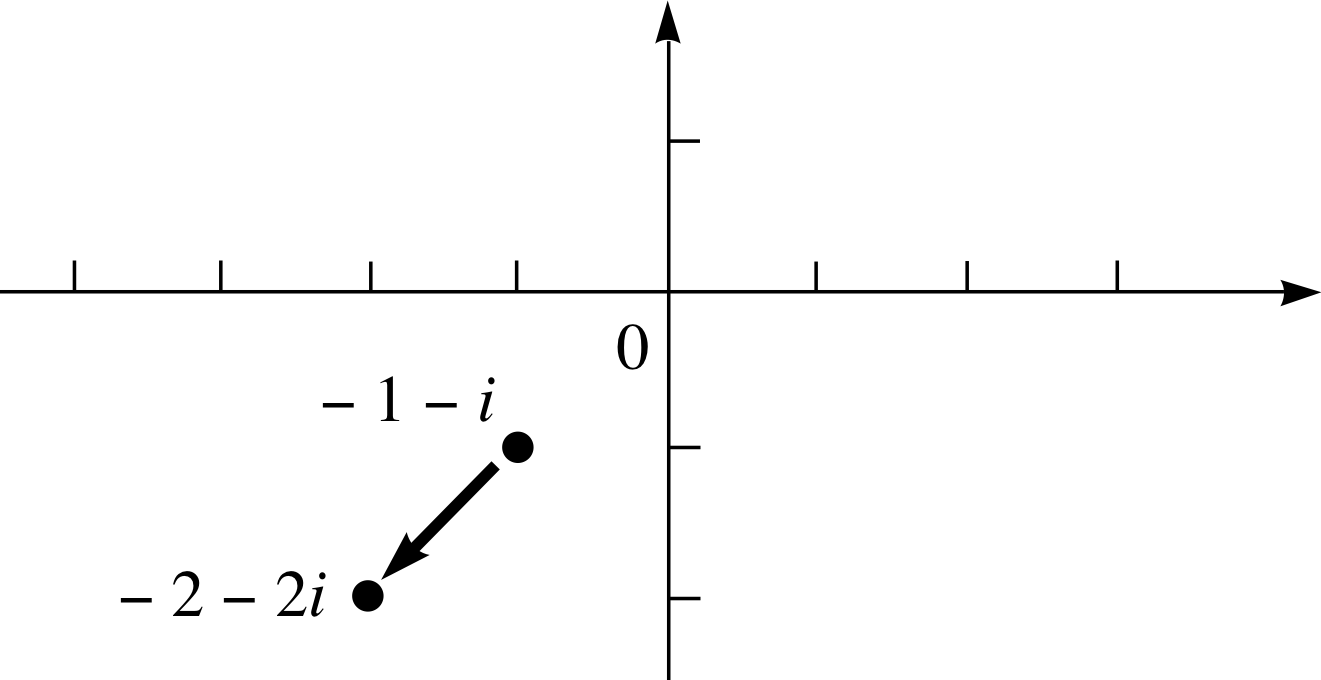
Figure 20 See Answer T2(b).
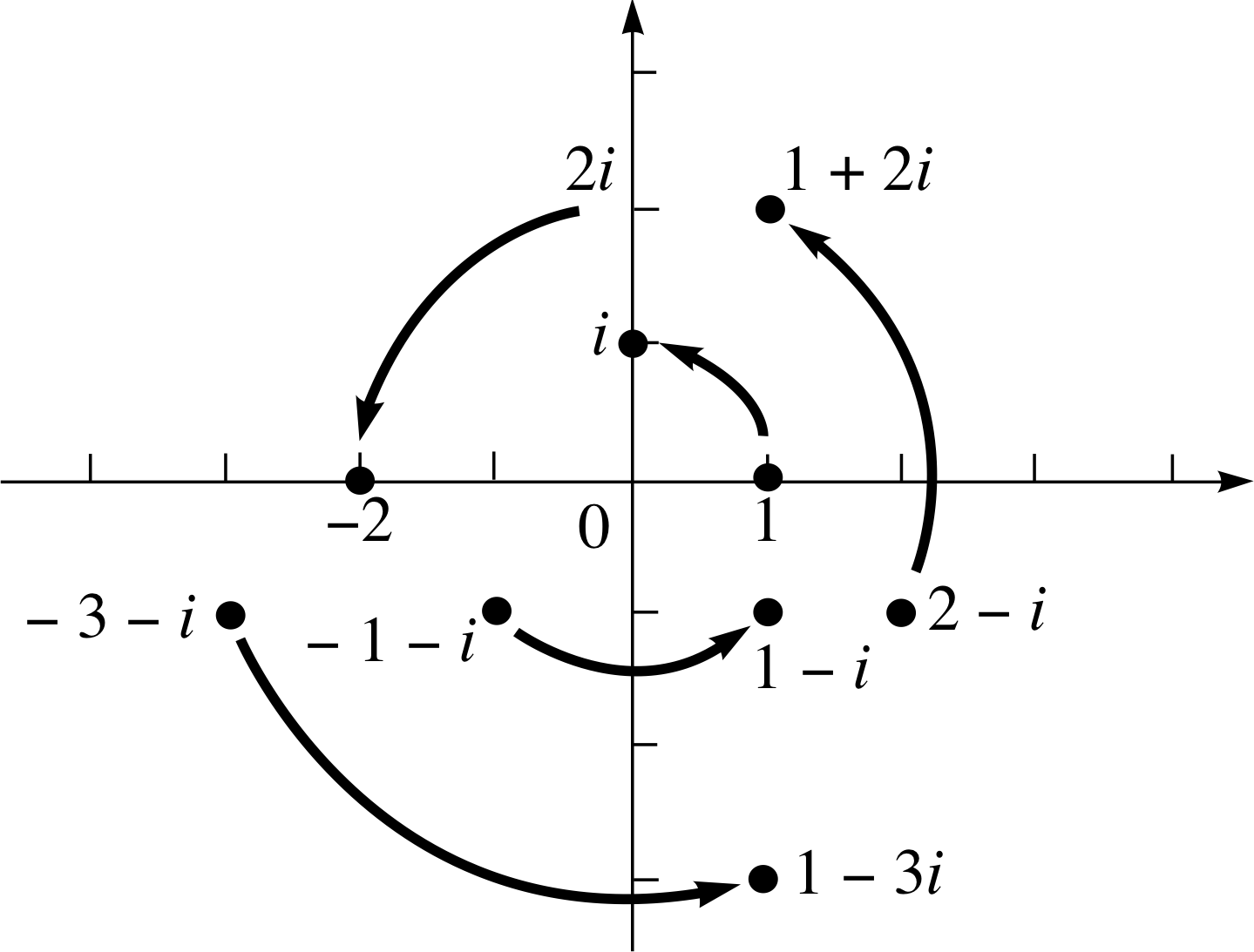
Figure 21 See Answer T2(c).
Answer T2
(a) The points are plotted on the Argand diagram in Figure 18.
(b) Multiplying each number by 2 gives us
1 × 2 = 2,
2i × 2 = 4i
(−3 −i) × 2 = −6 − 2i,
(2 − i) × 2 = 4 − 2i
These results are plotted in Figure 19.
You can see that all points move along a line through the origin to a position twice as far from the origin.
If we multiply −1 −1i by 2 we find
(−1 −1i) × 2 = −2 − 2i
This point is plotted in Figure 20 and confirms this conclusion.
(c) Multiplying each number by i we find:
1 × i = i,
2i × i = −2,
(−3 − i) × i = 1 − 3i,
(2 − i) × i = 1 + 2i
Looking at Figure 21 we see that multiplication by i produces a rotation of (π/2) rad in an anticlockwise direction about the origin. This observation is consistent with
(−1 − i) × i = 1− i
which is also shown on Figure 21.
(d) Multiplying each number by 2i we obtain:
1 × 2i = 2i,
2i × 2i = −4,
(−3 − i) × 2i = 2 − 6i,
(2 − i) × 2i = 2 + 4i
Looking at Figure 22 we see that multiplication by 2i produces a rotation of (π/2) rad in an anticlockwise direction about the origin. There is also an increase by a factor of 2 in the distance of the points from the origin.
This observation is consistent with
(−1 − i) × 2i = 2 − 2i
which is also shown on Figure 22.
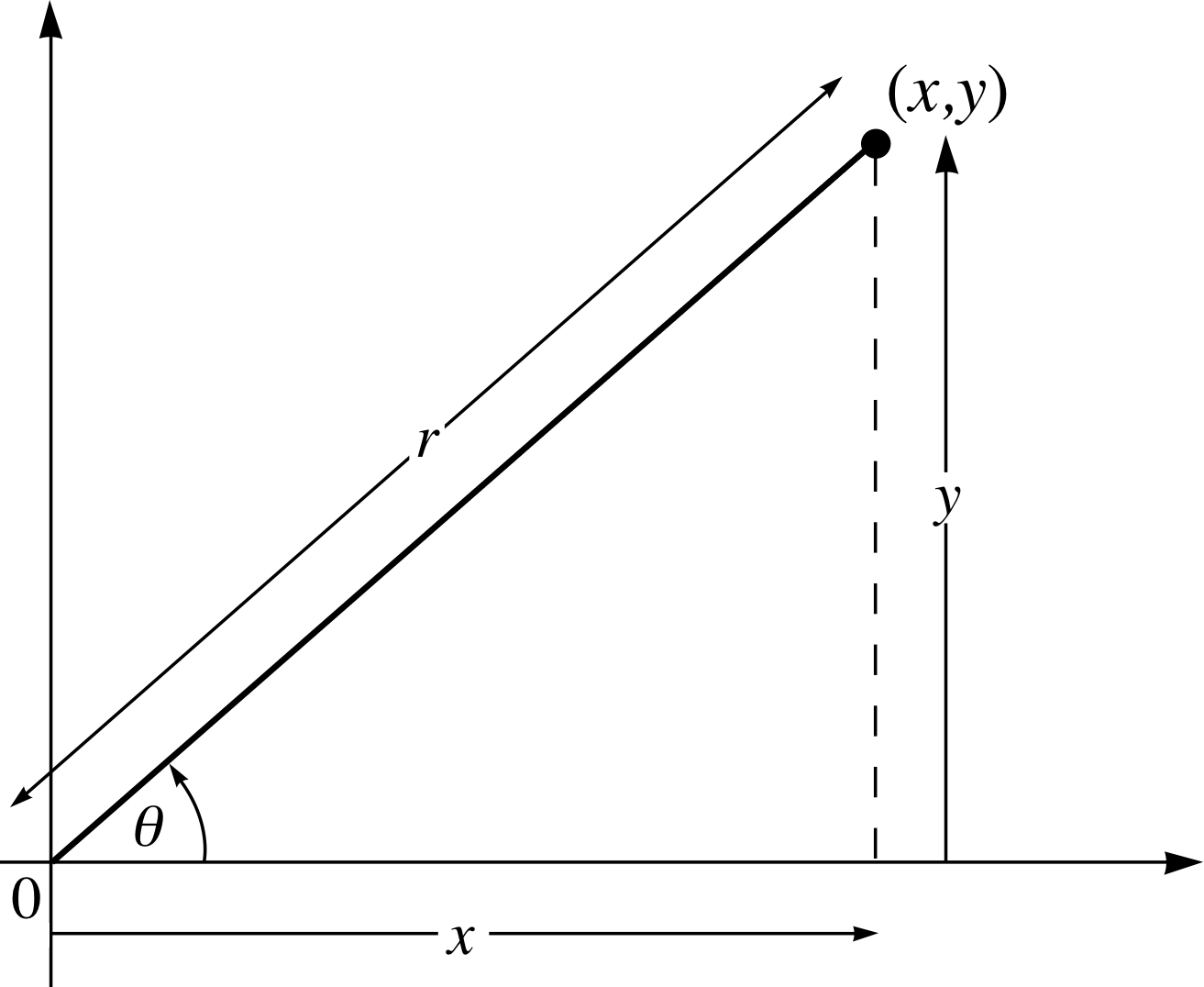
Figure 5 Polar coordinates, r, θ.
The solution to this problem suggests that the geometric interpretation of complex multiplication may involve both a rotation and a change in the distance from the origin, but this is not easy to see if we write complex numbers in the Cartesian form x + iy.
However, the geometric properties of complex multiplication are quite evident when the complex numbers are expressed in terms of polar coordinates. Figure 5 shows a point specified by means of polar coordinates; we can see that the ‘distance’ of the point from the origin is called r and θ is the angle between the line from the point to the origin and the x–axis. Notice that r is (by definition) non–negative and that θ is conventionally measured anticlockwise. i
Standard results from trigonometry enable us to express the Cartesian coordinates (x and y) in terms of polar coordinates (r and θ )
x = r cos θ(10)
y = r sin θ(11)
This means that we can write a complex number, z = x + iy, in the form
z = r (cos θ + i sin θ)(12)
which is known as the polar_form_of_a_complex_numberpolar form (or polar_representation_of_a_complex_numberpolar representation) of the complex number, z. Examples of complex numbers in polar form are:
2 [cos(π/4) + i sin(π/4)]
3.5 [cos(π/16) + i sin(π/16)]
and0.025 [cos(1.05) + i sin(1.05)]
To convert a complex number from polar to Cartesian form we can again use Equations 10 and 11.
For example, z = 3 [cos(π/4) + i sin(π/4)] has r = 3 and θ = π/4. If we substitute these values into Equations 10 and 11, we find
x = r cos θ = 3 cos(π/4) = $\dfrac{3}{\sqrt{2\os}}$ and y = r sin θ = 3 sin(π/4) = $\dfrac{3}{\sqrt{2\os}}$
i.e.$z = \dfrac{3}{\sqrt{2\os}} + \dfrac{3}{\sqrt{2\os}}\,i = \dfrac{3}{\sqrt{2\os}}(1+i)$
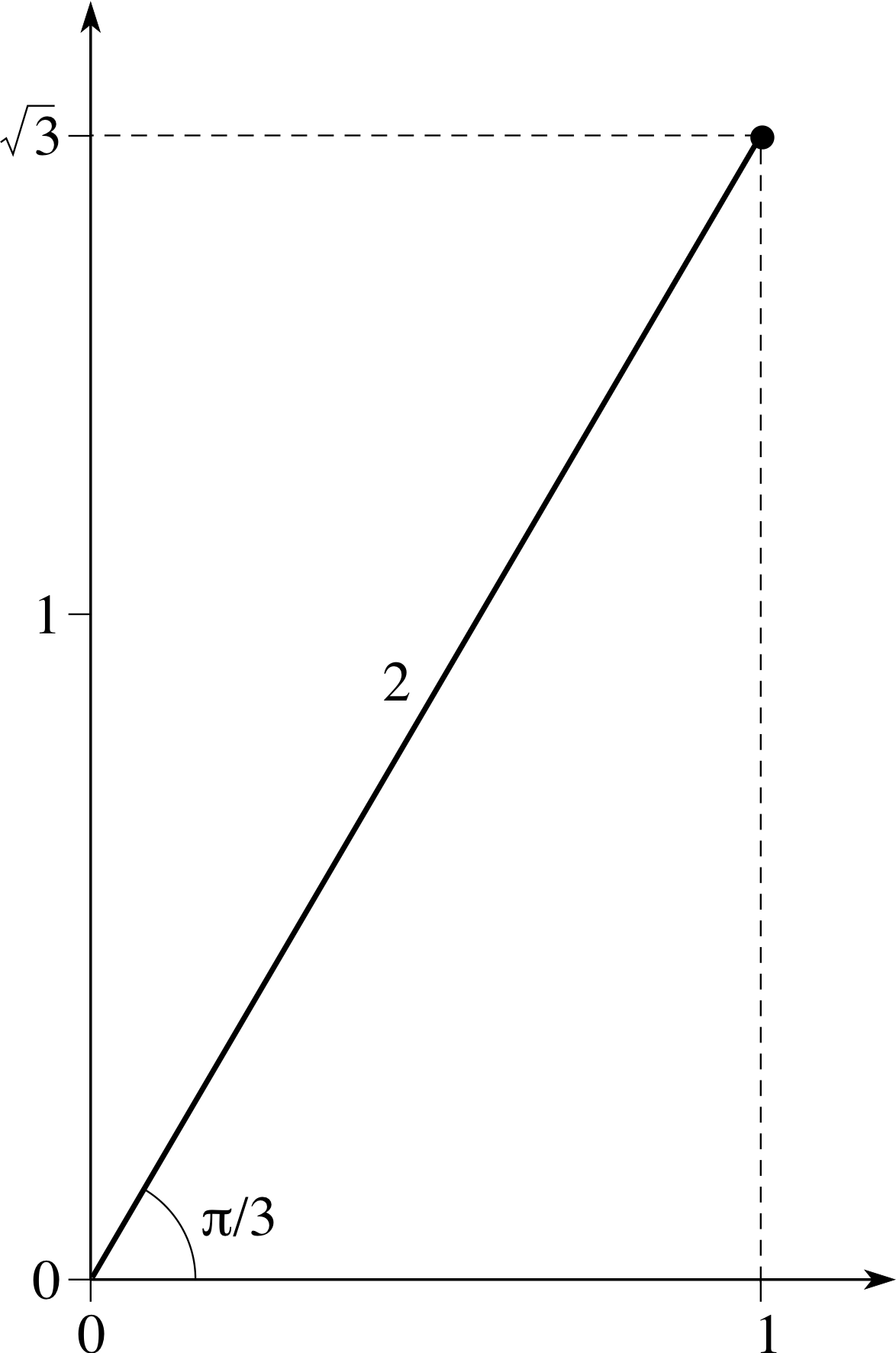
Figure 6 The complex number, $z = 1 + \sqrt{3\os}\,i$, in terms of polar coordinates.
It is also straightforward to convert from Cartesian to polar form since the length, r, is given by i
$r = \sqrt{x^2+y^2}$(13)
and the angle, θ, is such that
$\cos\theta = \dfrac{x}{\sqrt{x^2+y^2}}$(14)
$\cos\theta = \dfrac{y}{\sqrt{x^2+y^2}}$(15)
For example, the complex number, $z = 1 + \sqrt{3\os}\,i$ which has x = 1 and $y = \sqrt{3\os}$, can be represented in terms of polar coordinates by
$r = \sqrt{x^2+y^2} = \sqrt{1+3\os} = 2$
and since sin(θ) = $\dfrac{3}{\sqrt{2\os}}$ and cos(θ) = 1/2 we have θ = (π/3) rad. The position of the number $1 + \sqrt{3\os}\,i$ on an Argand diagram is shown in terms of polar coordinates in Figure 6.
✦ The polar coordinates of three points A, B and C are, respectively,
r = 2 θ = (π/4) rad
r = 3 θ = (−π/3) rad
r = 4 θ = (5π/6) rad
Express the points in Cartesian coordinates.
✧ We can use Equations 10 and 11
x = r cos θ(Eqn 10)
y = r sin θ(Eqn 11)
to convert from polar coordinates to Cartesian coordinates
For A we have
$x = r\cos\theta = 2\cos(\pi/4) = 2\times 1/\sqrt{2\os} = \sqrt{2\os}$
and$x = r\sin\theta = 2\sin(\pi/4) = 2\times 1/\sqrt{2\os} = \sqrt{2\os}$
For B
$x = r\cos\theta = 3\cos(\pi/3) = 3\times 1/2 = 3/2$
and$x = r\sin\theta = -3\sin(\pi/3) = -3\times \sqrt{3\os}/2 = -3\sqrt{3\os}/2$
For C
$x = r\cos\theta = 4\cos(5\pi/6) = -4\cos(\pi/6) = -4\times \sqrt{3\os}/2 = -2\sqrt{3\os} $
and$x = r\sin\theta = 4\sin(5\pi/6) = 4\sin(\pi/6) = 4\times 1/2 = 2$
One big advantage of the polar representation is that the multiplication of complex numbers is easy when they are expressed in this form. To see this, consider two complex numbers, z = x + iy and w = a + ib for which
x = r cos θ and y = r sin θ
a = ρ cos ϕ and b = ρ sin ϕ
Recalling two results from trigonometry:
sin(α + β) = cos α sin β + sin α cos β(Eqn 1) i
cos(α + β) = cos α cos β − sin α sin β(Eqn 2)
we see that the real part of the product zw (see Equation 7) is given by
Re(zw) = ax − by = ρ cos ϕ × r cos θ − ρ sin ϕ × r sin θ
Re(zw) = ρr (cos θ cos ϕ − sin θ sin ϕ)
Re(zw) = ρr cos(θ + ϕ)
and the imaginary part is given by
Im(zw) = ay + bx = ρ cos ϕ × r sin θ + ρ sin ϕ × r cos θ
Im(zw) = ρr (cos ϕ sin θ + sin ϕ cos θ)
Im(zw) = ρr sin(θ + ϕ)
We can summarize these two results by the following rule for multiplying complex numbers in polar form:
r (cos θ + i sin θ) × ρ (cos ϕ + i sin ϕ) = ρr [cos(θ + ϕ) + i sin(θ + ϕ)](16)
So, multiplying a complex number, w say, by a complex number with a polar representation r (cos θ + i sin θ), produces a new complex number which corresponds to the line from the origin to the point representing w being first scaled by a factor r, then the resulting line being rotated anticlockwise about the origin through an angle θ.
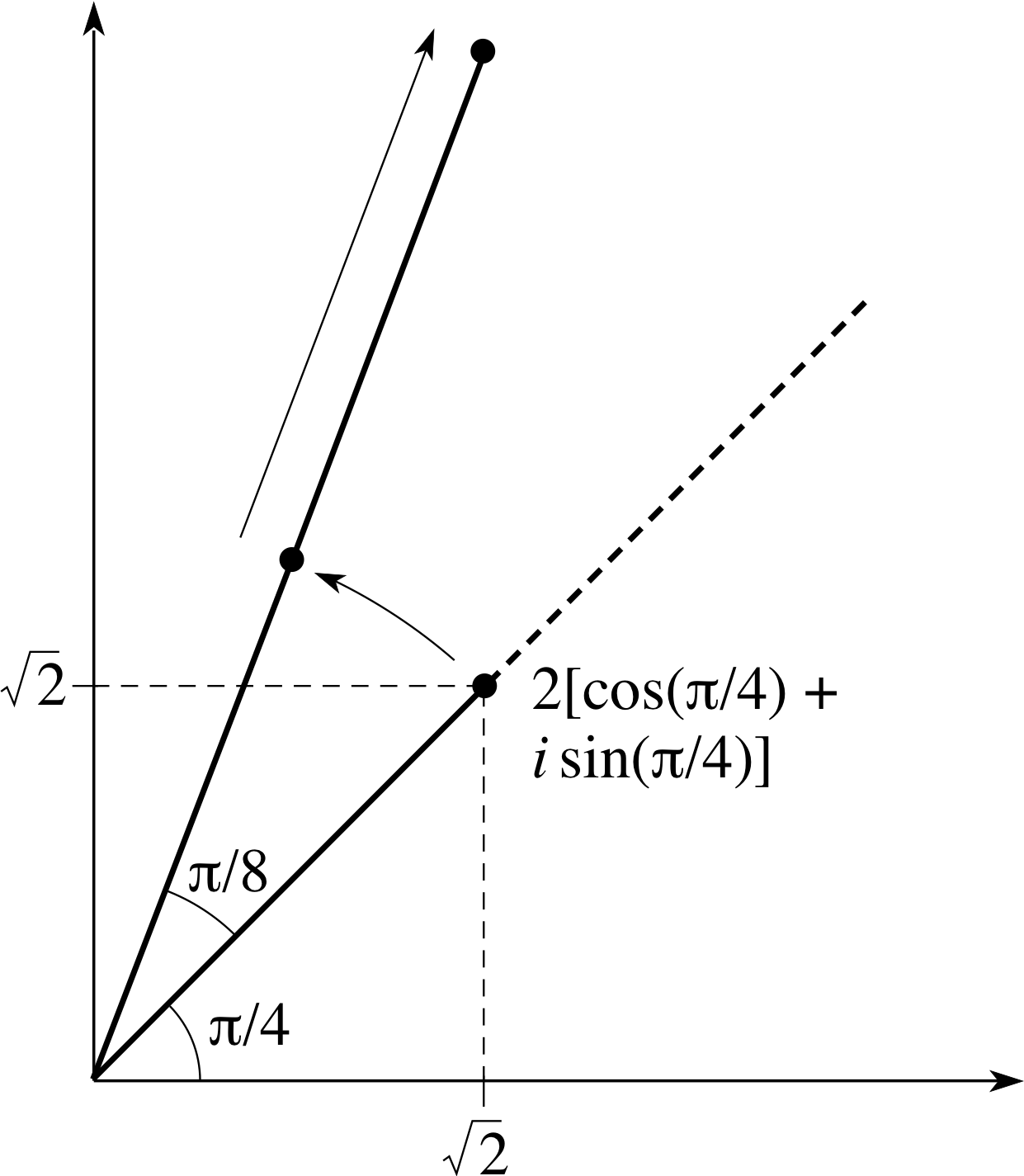
Figure 9 Complex multiplication causing a rotation and a change in distance from the origin.
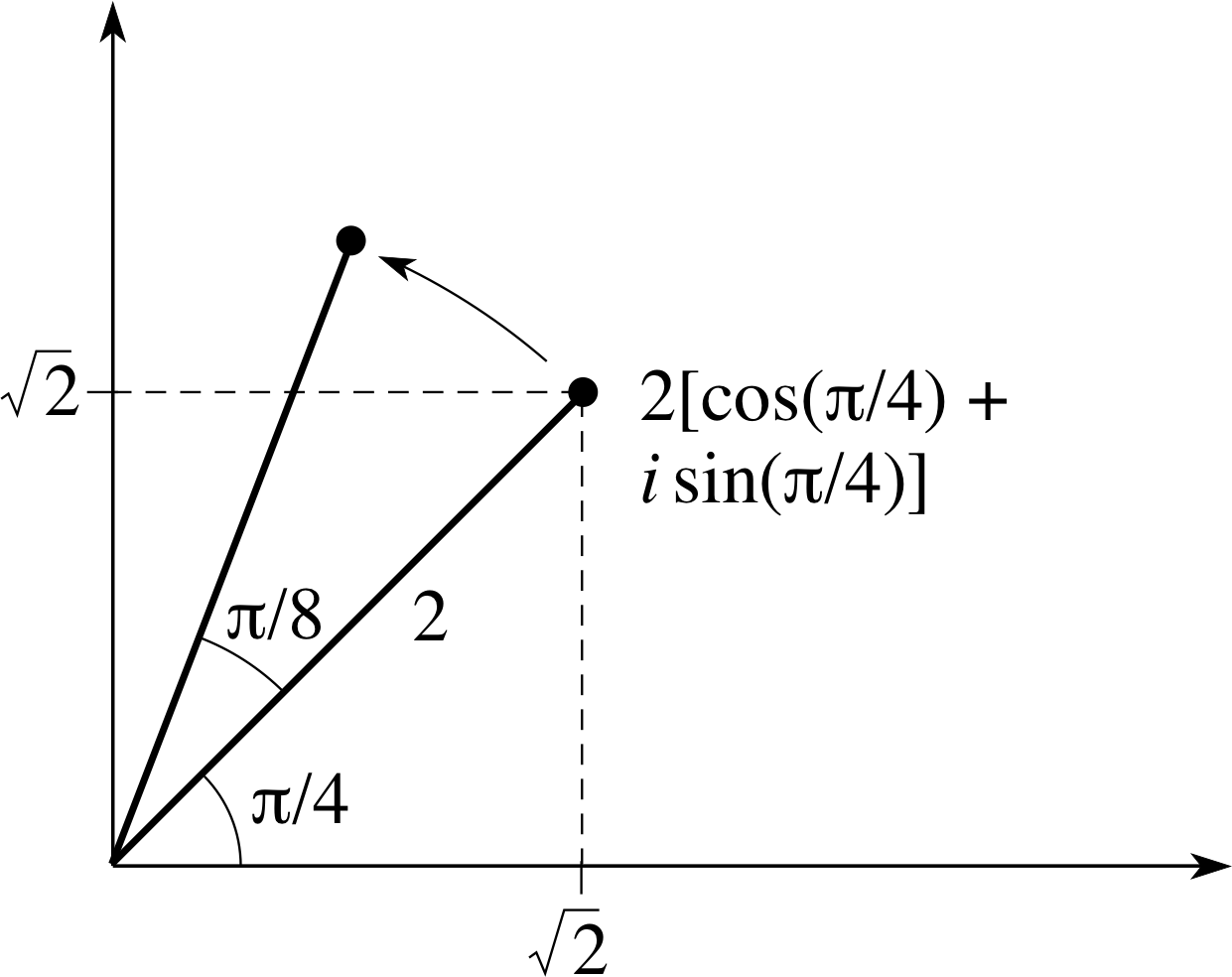
Figure 8 Complex multiplication causing a rotation.
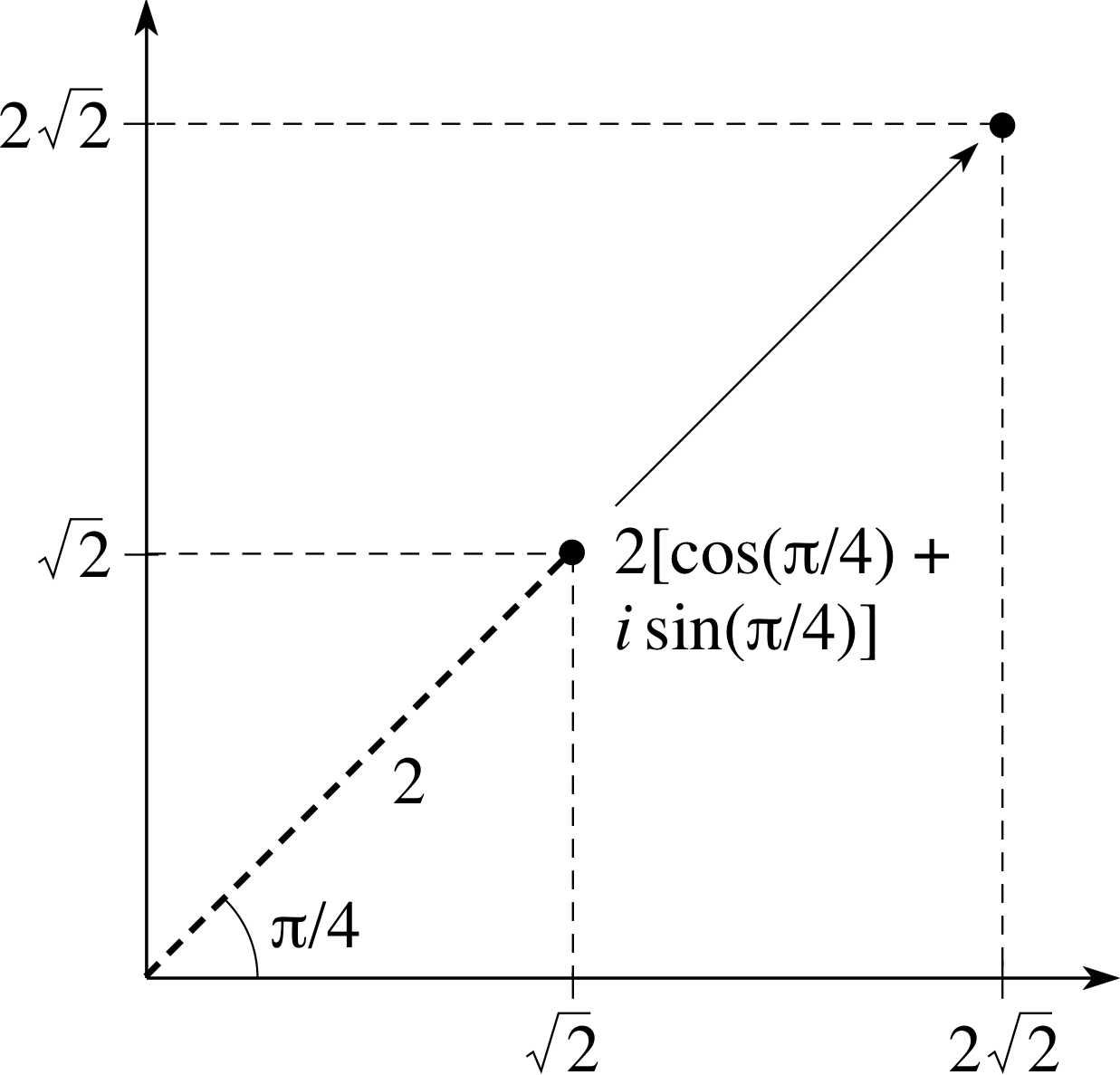
Figure 7 Complex multiplication resulting in a change in distance from the origin.
As an illustration we will start with the complex number w = 2 [cos(π/4) + i sin(π/4)] and first multiply it by 2 in Figure 7, then by [cos(π/8) + i sin(π/8)] in Figure 8, and finally by 2 [cos(π/8) + i sin(π/8)] in Figure 9.
Notice that in Figure 9 the line from the origin to the original point is rotated through an angle of (π/8) and the distance from the origin is doubled.
2.3 The modulus of a complex number
Given a complex number, z = x + iy, the modulus_of_a_complex_numbermodulus of z is defined by
$\lvert\,z\,\rvert = \sqrt{x^2+y^2}$(17)
In polar coordinates, where x = r cos θ and y = r sin θ, we have
x2 + y2 = r2 cos2 θ + r2sin2 θ = r2 (because cos2 θ + sin2 θ = 1)
So in polar coordinates, the modulus of a complex number is simply the distance from the origin of a point on an Argand diagram. This distance is clearly a non–negative real number.
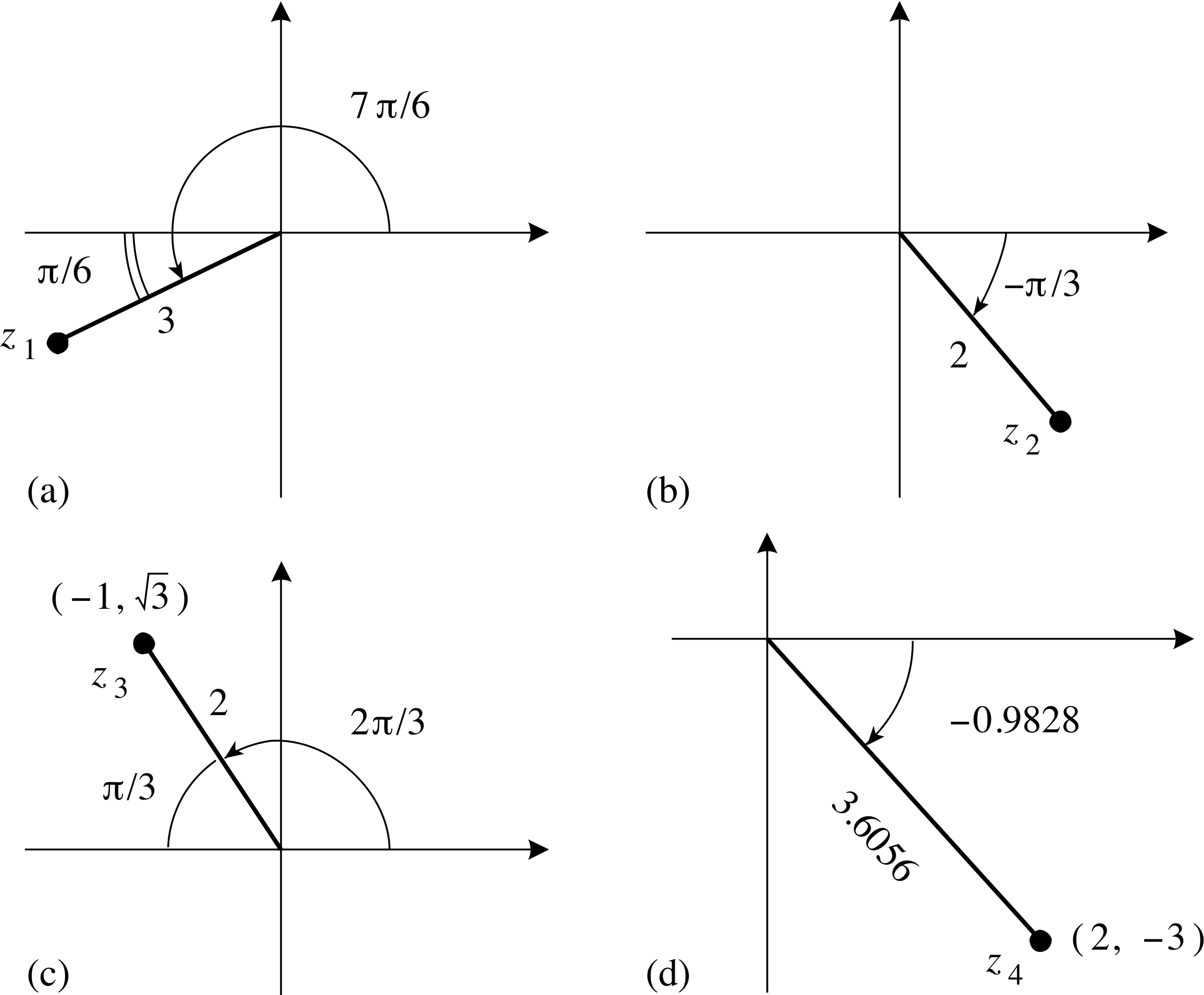
Figure 10 See Question T3.
Question T3
(a) Figures 10a and 10b show two complex numbers z1 and z2, respectively. Write z1 and z2 in the x + iy form.
(b) Figures 10c and 10d show two complex numbers z3 and z4, respectively. Calculate the modulus of the complex numbers z3z4.
Answer T3
(a) z1 = 3 [cos(7π/6) + i sin(7π/6)] = $3\left(-\dfrac{\sqrt{3\os}}{2}-\dfrac{i}{2}\right) = -\dfrac{3}{2}\left(\sqrt{3\os} + i\right)$
z2 = 2 [cos(−π/3) + i sin(−π/3)] = $2\left(\dfrac{1}{2}-\dfrac{i\sqrt{3\os}}{2}\right) = 1 - i\sqrt{3\os}$
(b) | z3z4 | = 2 × 3.6056 = 7.2112
(by putting ρ = 2 and r = 3.6056 into Equation 16),
r (cos θ + i sin θ) × ρ (cos ϕ + i sin ϕ) = ρr [cos(θ + ϕ) + i sin(θ + ϕ)](Eqn 16)
2.4 The argument of a complex number

Figure 6 The complex number,

Figure 5 Polar coordinates, r, θ.
If a complex number is written in polar form as z = r (cos θ + i sin θ), then θ is known as the argument of z and is denoted by argument_of_a_complex numberarg(z). For example, if z = 4 [cos(π/15) + i sin(π/15)] then arg(z) is (π/15) rad which can be interpreted geometrically as follows. Consider a typical point representing a complex number, z, on an Argand diagram such as in Figure 5. Then the angle θ made by the line joining the point to the origin with the positive real axis is the argument. Notice that by convention the angle is measured anticlockwise (so that a negative angle would be measured in a clockwise direction). If z = 1 + $\sqrt{3\os}$i then arg(z) is (π/3) rad, as shown in Figure 6.
There is a slight complication in the definition of the argument since a point, z, on an Argand diagram does not correspond to a single value of arg(z) because we can always add any integer multiple of 2π to the value of θ; in other words, if we rotate the point about the origin through any number of complete turns we always get back to the same point (see Figure 11). i
Figure 11 The non–uniqueness of arg(z) (shown here as θ).
However, if we impose the condition that −π < θ ≤ π i then θ is uniquely determined, and with this condition θ is known as the principal value of the argument of z. Notice that whereas the lower limit is greater than −π, the upper limit is less than or equal to π. i
If we have a complex number, z = x + iy, where x and y are not both zero, then the argument, θ, is given by the solution to the following pair of equations
$\cos\theta = \dfrac{x}{\sqrt{x^2+y^2}}$(18)
$\sin\theta = \dfrac{y}{\sqrt{x^2+y^2}}$(19)
From Equations 18 and 19 we obtain
tan θ = y/x(20)
and while it is possible to use Equation 20 to find the angle θ, this must be done with some care as the following example shows. (Alternatively we can use the Equations 18 and 19, see Solution B to Example 1).
Example 1
Find the principal value of the argument of the complex number z = −1 + i.
Solution A
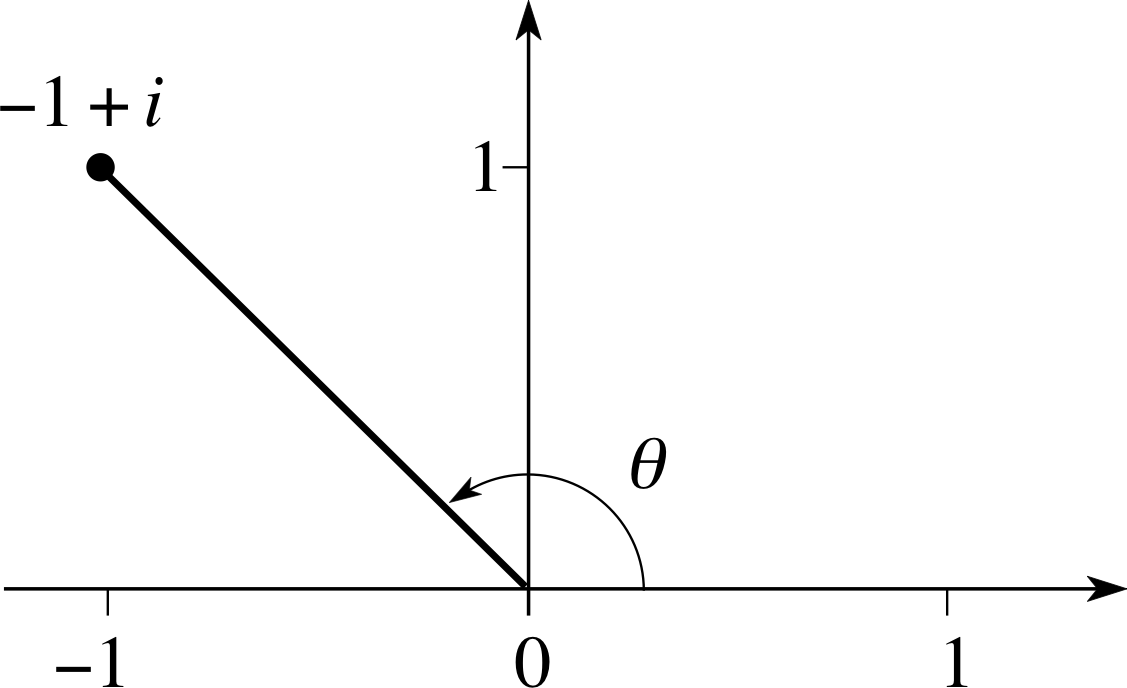
Figure 12 The complex number, z = −1 + i, plotted on an Argand diagram.
In this case x = −1 and y = 1, and from Equation 20 we have tan θ = −1. In order to find θ your first thought might be to set your calculator to radian mode and to evaluate arctan(−1), which will give you the approximate value −0.785 398 rad for θ.
However, this is not a value of the argument, and certainly not the principal value, as you can easily see if you plot the point −1 + i on an Argand diagram, see Figure 12. The correct answer is approximately 2.356 194 rad (or more precisely (3π/4) rad).
The essential point to realize here is that Equation 20 does not determine the angle θ uniquely because there are generally two angles in the range −π < θ ≤ π that correspond to a given value of the tangent, and these angles differ by π radians. The difficulty is quite easy to resolve if we always draw a diagram (such as Figure 12) when calculating a value for arg(z). In this case we would obtain the value −00.785 398 rad from the calculator as before, then we see from the diagram that we must add π radians to obtain the principal value
arg(z) ≈ −0.785 0398 + 3.141 1593 = 2.356 0194 rad
For this particular value of z you may be able to avoid the use of the calculator if you can see that arg(z) = (3π/4) rad directly from the figure.
Solution B
Alternatively we can use Equations 18 and 19 to obtain $\cos\theta = -1/\sqrt{2\os} \quad\text{and}\quad\sin\theta = -1/\sqrt{2\os}$. The only angles in the range −π < θ ≤ π that satisfy the first equation are θ = (3π/4) rad or θ = (−3π/4) rad, while the only angles that satisfy the second equation are θ = (π/4) rad or θ = (3π/4) rad. Thus the required angle is θ = (3π/4) rad.
Notice that the argument of z = x + iy is not defined when x and y are both zero; in other words, the argument of z = 0 is not defined.
The polar representation of a complex number is not unique. For example, both $\sqrt{2\os}[\cos(\pi/4) + i\,\sin(\pi/4)]\;\text{and}\;\sqrt{2\os}[\cos(9\pi/4) + i\,\sin(9\pi/4)]$ represent the same complex number 1 + i. We can, however, make the representation unique if we insist that the argument takes its principal value. Notice that $-2[\cos(\pi/)3 + i\,\sin(\pi/3)]$ is not in polar form. In fact from Equation 16,
r (cos θ + i sin θ) × ρ (cos ϕ + i sin ϕ) = ρr [cos(θ + ϕ) + i sin(θ + ϕ)](Eqn 16)
−2 [cos(π/3) + i sin(π/3)] = 2 (cos π + i sin π)[cos(π/3) + i sin(π/3)] = 2 [cos(4π/3) + i sin(4π/3)]
and this final result is in polar form.

Figure 1 See Question R3.
Question T4
For each of the following complex numbers, find the principal value of the argument:
(a) $-1 + \sqrt{3\os}\,i$, (b) 1 - $\sqrt{3\os}\,i$, (c) $\sqrt{3\os} + i$, (d) 3 + 2i.
[Hint: You may find Figure 1 helpful.]
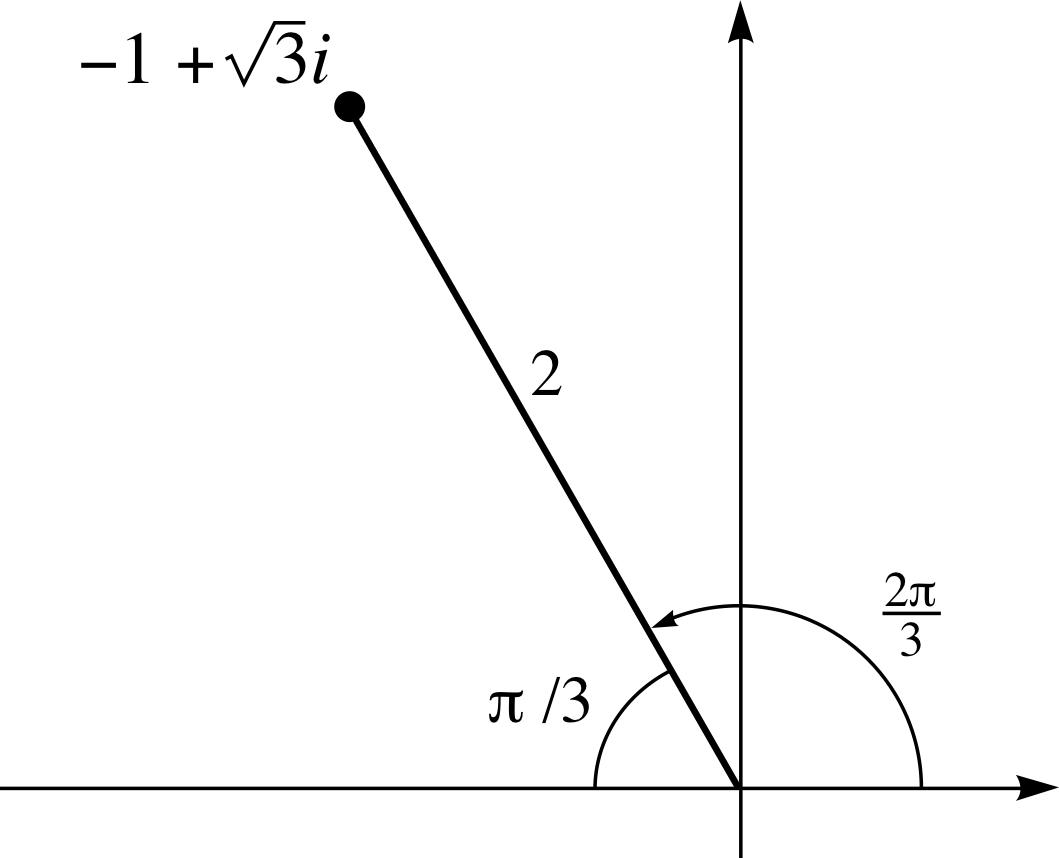
Figure 23 See Answer T4(a).
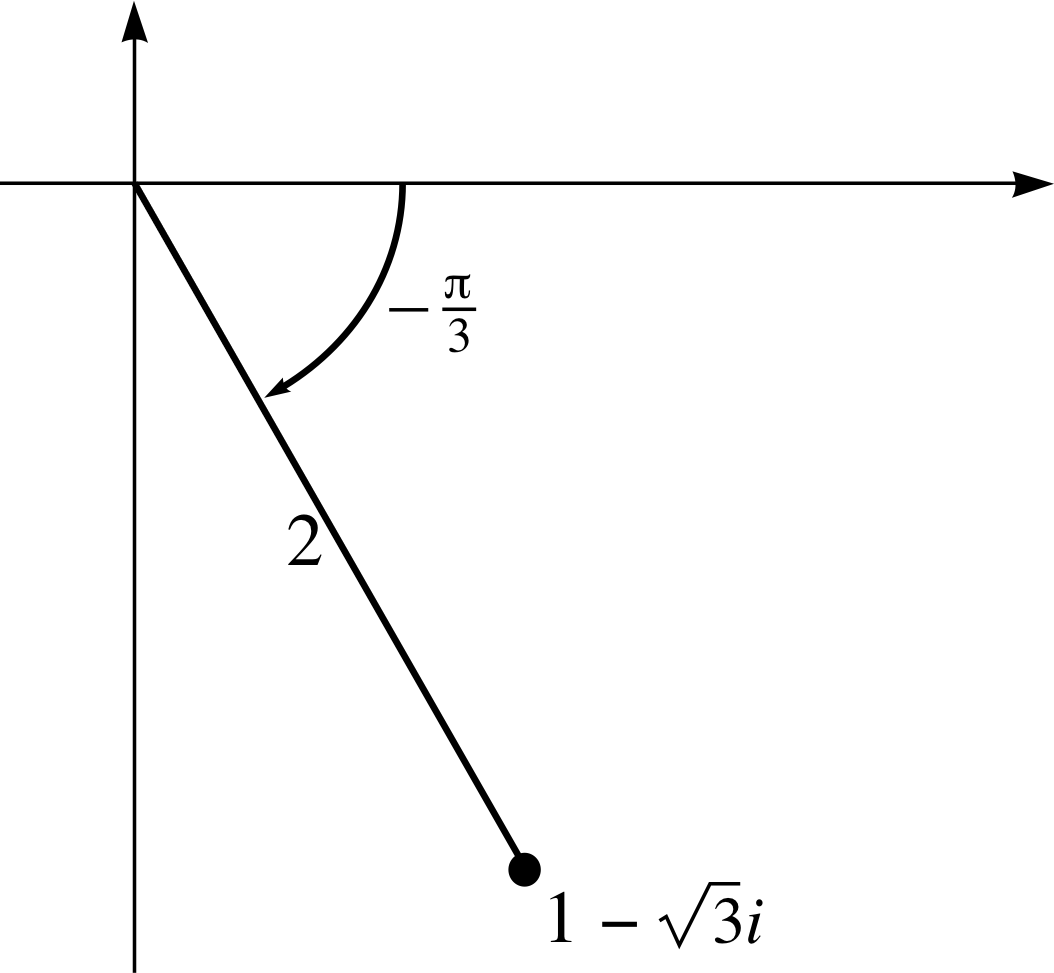
Figure 24 See Answer T4(b).
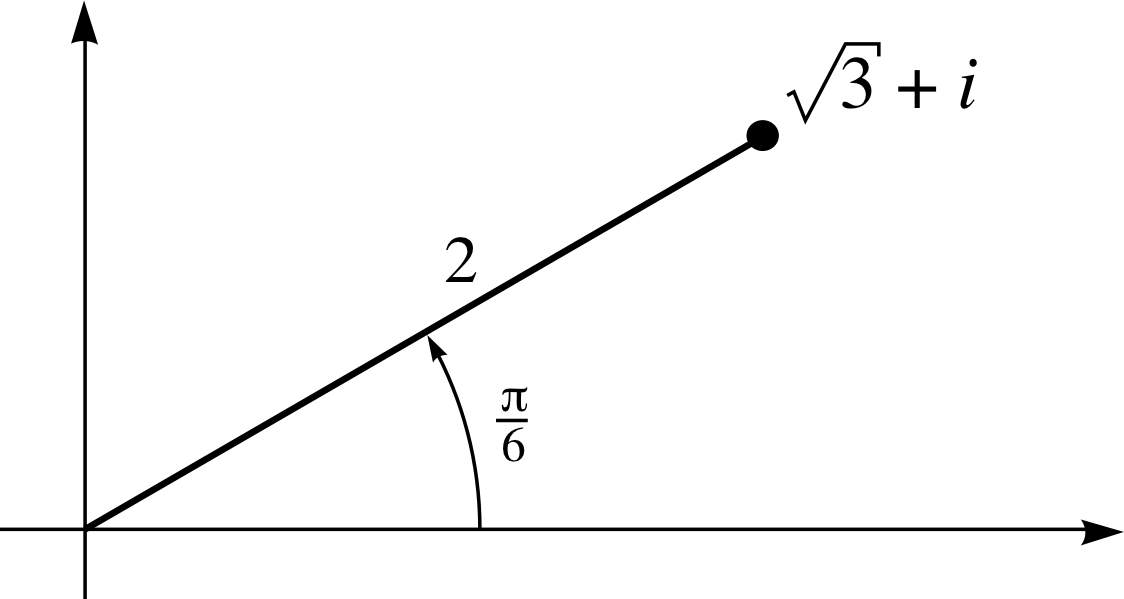
Figure 25 See Answer T4(c).
Answer T4
You will find it is useful to draw an Argand diagram for such problems.
(a) The position of the point representing $-1 + \sqrt{3\os}\,i$ on an Argand diagram is shown in Figure 23. The angle made by the line joining the point to the origin with the negative real axis is (π/3) rad since cos(π/3) = 1/2. The principal value of arg(z) is the angle made with the positive real axis which we can see from the diagram to be (2π/3) rad.
(b) The position of the point representing $1 - \sqrt{3\os}\,i$ on an Argand diagram is shown in Figure 24. The angle made by the line joining the point to the origin with th positive real axis is (π/3) rad since cos(π/3) = 1/2. The principal value of arg(z) is −π/3 since the angle is measured anticlockwise.
(c) The position of the point representing $\sqrt{3\os} + i$ on an Argand diagram is shown in Figure 25. The angle made by the line joining the point to the origin with the positive real axis is (π/6) rad since cos(π/6) = $\sqrt{3\os}$/2. This is the principal value of arg(z).
(d) A sketch shows that the complex number 3 + 2i lies in the first
quadrant and, from Equation 20,
tan θ = y/x(Eqn 20)
tan θ = 2/3. It therefore follows that θ ≈ 0.5880 rad.
2.5 The exponential form
You should be familiar with the following functions, and their series expansions i
$\displaystyle {\rm e}^x = \sum_{n=0}^{\infty} \dfrac{x^n}{n!} = 1 + \dfrac{x}{1!} + \dfrac{x^2}{2!} + \dfrac{x^3}{3!} + \dots$(Eqn 3) i
$\displaystyle \sin x = \sum_{n=0}^{\infty} \dfrac{(-1)^n x^{2n+1}}{(2n+1)!} = x - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + \dots$(Eqn 4)
$\displaystyle \cos x = \sum_{n=0}^{\infty} \dfrac{(-1)^n x^{2n}}{(2n)!} = 1 - \dfrac{x^2}{2!} + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + \dots$(Eqn 5)
Each of these functions may be extended so that they apply to a complex variable z (rather than the real variable x), but, since real numbers are just a special case of complex numbers, the new functions must agree with the old ones in the special case when z is real. For example, in order to define ez we simply replace x by z in Equation 3,
$\displaystyle {\rm e}^z = \sum_{n=0}^{\infty} \dfrac{z^n}{n!} = 1 + \dfrac{z}{1!} + \dfrac{z^2}{2!} + \dfrac{z^3}{3!} + \dots$(21) i
Now let us consider the special case of z = iθ, where θ is real and therefore z is imaginary
$\displaystyle {\rm e}^{i\theta} = 1 + \dfrac{{i\theta}}{1!} + \dfrac{({i\theta})^2}{2!} + \dfrac{({i\theta})^3}{3!} + \dfrac{({i\theta})^4}{4!} + \dfrac{({i\theta})^5}{5!} + \dots$
This expression can be simplified by using i2 = −1 to give
$\displaystyle {\rm e}^{i\theta} = 1 + \dfrac{{i\theta}}{1!} - \dfrac{\theta^2}{2!} + \dfrac{i\theta^3}{3!} - \dfrac{\theta^4}{4!} + \dfrac{i\theta^5}{5!} - \dots$
We can see that the terms are alternately real and imaginary, so it is useful to split the series into two
$\displaystyle {\rm e}^{i\theta} = \left(1 - \dfrac{\theta^2}{2!} + \dfrac{\theta^4}{4!} - \dfrac{\theta^6}{6!} + \dots\right) + i\left(\dfrac{{\theta}}{1!} - \dfrac{\theta^3}{3!} + \dfrac{\theta^5}{5!} - \dfrac{\theta^7}{7!} + \dots\right)$
If we compare the right–hand side of this equation with the series for sin θ and cos θ we see that eiθ can be written as
eiθ = cos θ + i sin θ (Euler’s formula)(22)
This important formula, known as Euler’s formula, gives us the real and imaginary parts of eiθ. i
Question T5
Plot einπ/8 on an Argand diagram for n = 0, 1, 2, ... 15. What geometrical shape do you think would describe the position of the points representing z = eiθ where θ can take any real value?
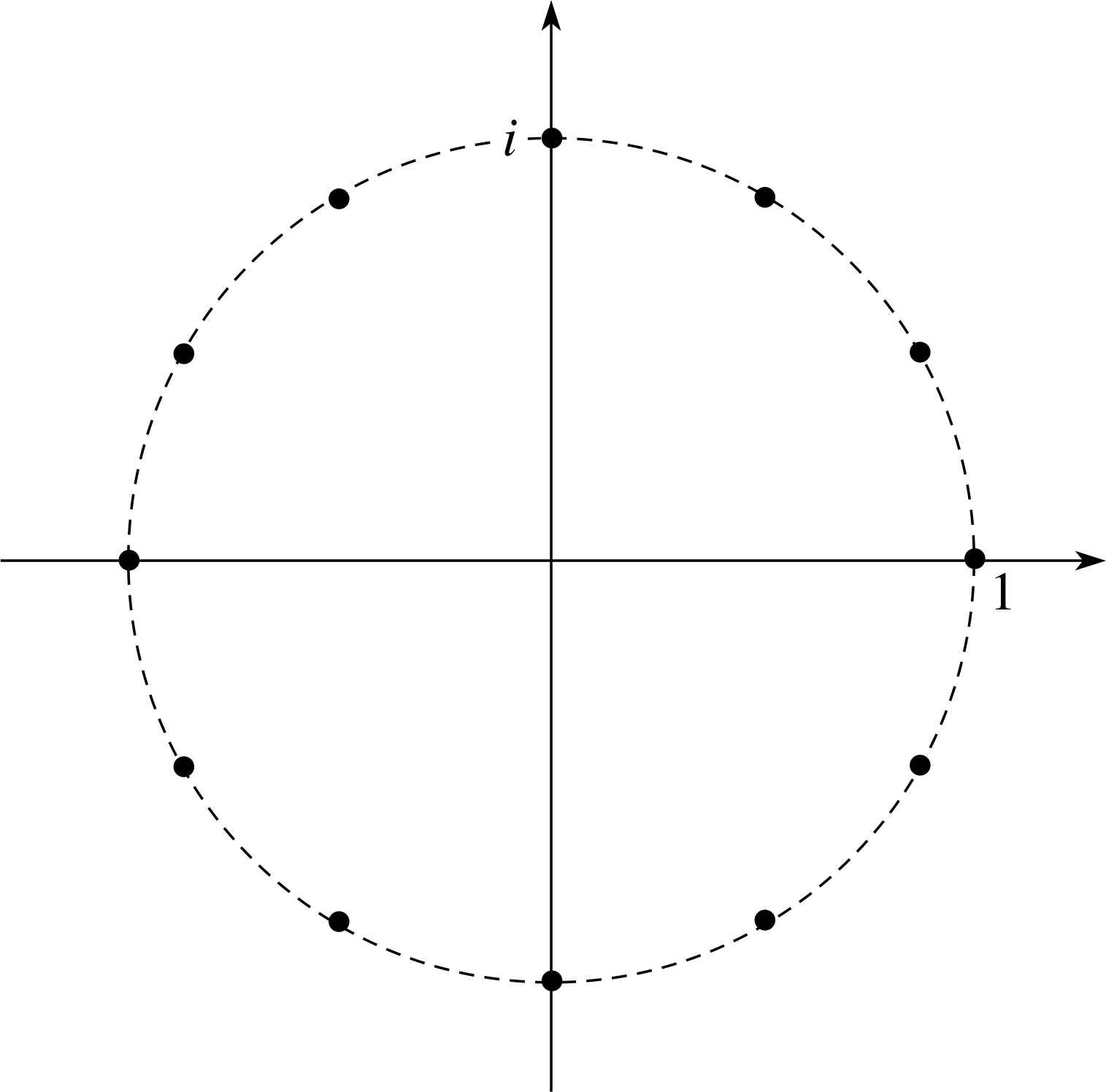
Figure 26 See Answer T5.
Answer T5
There are two ways to answer this question.
(a) Euler’s formula enables us to write
z = enπi/8 = cos(nπ/8) + i sin(nπ/8)
Then use a calculator to evaluate the sine and cosine for n = 0, 1, 2, ... 15 and plot the points on an Argand diagram, as in Figure 26. Notice that the points all lie on a circle of radius, 1, with the origin as the centre.
The following alternative method is somewhat easier.
(b) Notice that if we compare
z = enπi/8 = cos(nπ/8) + i sin(nπ/8)
with the polar form
z = r (cos θ + i sin θ)
then we have r = 1 and arg(z) = nπ/8. The value of r tells us that all points are a distance of 1 from the origin; that is all points lie on a circle of radius 1 centred on the origin. The θ coordinate is the value of arg(z) for each n and points can therefore be plotted directly on the Argand diagram.
The second approach also shows that all points representing z = eiθ, where θ takes any real value, lie on a circle of radius 1, whose centre is the origin. (This circle is sometimes known as the unit circle.)
If we put θ = π in Euler’s formula then, since cos(π) = −1 and sin(π) = 0, we find i
eiπ = −1(23)
This identity is quite remarkable since it relates:
- the numerical constant e, which originates from problems of growth and decay;
- the numerical constant π, which originates from the ratio of the circumference to the diameter of a circle;
- the number 1, which has the special property that 1 × n = n for any number n;
- the symbol i, which has the property i2 = −1 and was originally introduced in order to solve equations such as x2 + 1 = 0.
Question T6
Use Euler’s formula to prove the following important relations (Equations 24 and 25):
$\sin\theta = \dfrac{{\rm e}^{i\theta} - {\rm e}^{-i\theta}}{2i}$(24)
$\cos\theta = \dfrac{{\rm e}^{i\theta} + {\rm e}^{-i\theta}}{2}$(25)
Answer T6
We can use Euler’s formula and the fact that cos(−θ) = cos θ and sin(−θ) = −sin θ to obtain
eiθ = cos θ + i sin θ
e−iθ = cos θ − i sin θ
Addition of the two identities gives eiθ + e−iθ = 2 cos θ
and therefore
$\cos\theta = \dfrac{{\rm e}^{i\theta}+{\rm e}^{-i\theta}}{2}$
Subtraction of the two identities gives eiθ − e−iθ = 2i sin θ
$\sin\theta = \dfrac{{\rm e}^{i\theta}-{\rm e}^{-i\theta}}{2i}$
Now let us consider a general complex number, z = x + iy, and write it in terms of polar coordinates by substituting x = r cos θ and y = r sin θ
z = x + iy = r cos θ + ir sin θ = r (cos θ + i sin θ)
which can be written more compactly, using Euler’s equation, to obtain
z = r eiθ(26)
which is known as the exponential_form_of_a_complex_numberexponential form (or exponential_representation_of_a_complex_numberexponential representation) of a complex number. Notice that r is (by definition) non-negative.
Question T7
Find the exponential representation for the following complex numbers:
(a) $\sqrt{2\os}(1+ i)$, (b) $3(1+ i\sqrt{3\os})$, (c) $2(\sqrt{3\os} + i)$, (d) 0.2 + 2.3i.

Figure 1 See Answer T7.
Answer T7
Initially we want to write each number in the form
z = r (cos θ + i sin θ)
and we can do this by ensuring that the sum of the squares of the real and imaginary parts within the parentheses is 1. This can be achieved in each case by dividing the complex number in parentheses by its modulus; for example, the complex number (1 + i) has modulus $\sqrt{2\os}$ and we therefore write (1 + i) = $\sqrt{2\os}\left(\dfrac{1}{\sqrt{2\os}}+\dfrac{i}{\sqrt{2\os}}\right)$
(a) $\sqrt{2\os}(1+i) = 2\left(\dfrac{1}{\sqrt{2\os}}+\dfrac{i}{\sqrt{2\os}}\right)$
The value of r is 2 and θ is π/4 rad since cos(π/4) = 1/$\sqrt{2\os}$ and sin(π/4) = 1/$\sqrt{2\os}$. To check these values either use a calculator or, much better, consider a right–angled triangle with two sides of equal length, as in Question R4. So the exponential form is 2 eiπ/4.
(b) $3(1+i\sqrt{3\os}) = 6\left(\dfrac{1}{2}+\dfrac{i\sqrt{3\os}}{2}\right)$
The value of r is 6. To obtain θ we need to solve the equations cos θ = 1/2 and sin θ = $\sqrt{3\os}$/2, and from Figure 1 (see Question R3) we see that the result is θ = (π/3) rad. So the exponential form is 6 eiπ/3.
(c) $2(\sqrt{3\os}+i) = 4\left(\dfrac{\sqrt{3\os}}{2}+\dfrac{i}{2}+\right)$
We have r = 4 and θ is the solution of cos θ = $\sqrt{3\os}$/2 and sin θ = 1/2. From Figure 1 (see Question R3) we get θ = (π/6) rad and therefore the exponential form is 4 eiπ/6.
(d) The modulus of 0.2 + 2.3i is $\sqrt{(0.2)^2+(2.3)^2} \approx 2.309$ and since the point lies in the first quadrant its argument is arctan(2.3/0.2) ≈ 1.484 rad. Hence 0.2 + 2.3i ≈ 2.309 e1.484i.
✦ Express the complex numbers i and 2 in exponential form.
✧ From Euler’s formula i = eiπ/2 (because sin(π/2) = 1 and cos(π/2) = 0) and 2 = 2 × 1 = 2 ei0 (because sin(0) = 0 and cos(0) = 1).
3 Arithmetic of complex numbers
3.1 Products and quotients
Multiplication of complex numbers in exponential form is very easy, however in this form addition is more difficult.
Products
One important property of real powers of any real quantity is the identity
a sa t = a s + t(27) i
which we will assume is also true if any (or all) of the quantities a, s and t are complex. This identity allows us to multiply complex numbers easily in exponential form since, if z = r eiθ and w = ρ eiϕ, then the product is given by
r eiθ × ρ eiϕ = rρ ei (θ + ϕ)(28)
which is closely related to the result quoted in Equation 16,
r (cos θ + i sin θ) × ρ (cos ϕ + i sin ϕ) = ρr [cos(θ + ϕ) + i sin(θ + ϕ)](Eqn 16)
Notice that in Equation 28 the moduli i of the two complex numbers are multiplied whereas the arguments are added (as in Equation 16).
Question T8
Find zw in exponential form (choosing the principal value of the argument in each case) for each of the following:
(a) z = 2 eiπ/4 w = 2 eiπ/4
(b) z = 3 eiπ w = 2 eiπ/4
(c) z = 2 eiπ/16 w = ½ e−iπ/16
Answer T8
(a) zw = 2 eiπ/4 × 2 eiπ/4 = 4 eiπ/2
(b) zw = 3 eiπ × 2 eiπ/4 = 6 e5iπ/4 = 6 e5iπ/4 × e−2iπ = 6 e−3iπ/4
Notice that we have used the result e−2iπ = 1 to make the argument of zw consistent with the range −π < arg(zw) ≤ π.
(c) zw = 2 eiπ/16 × ½ e−iπ/16 = e0 = 1
Quotients
For real numbers we have the general result that $\dfrac{a^m}{b^n} = a^mb^{-n}$ where b is non-zero.
Extending this result to complex numbers, we find that simplifying a quotient of two complex numbers in exponential form is a straightforward variation of multiplication. So if z = r eiθ and w = ρ eiϕ, then z/w is given by $\dfrac{z}{w} = \dfrac{r{\rm e}^{i\theta}}{\rho{\rm e}^{i\phi}} = \dfrac{r}{\rho}{\rm e}^{i(\theta-\phi)}$ that is, we divide the moduli and subtract the arguments.
Question T9
Find z/w in exponential form (choosing the principal value of the argument in each case) for each of the following:
(a) z = 2 eiπ/4 w = 4 e−iπ/8
(b) z = 3 eiπ/4 w = 2 eiπ/2
(c) z = 2 e−iπ/16 w = 2 eiπ/16
Answer T9
(a) $\dfrac{z}{w} = \dfrac{2{\rm e}^{i\pi/4}}{4{\rm e}^{-i\pi/8}} = \dfrac{1}{2}{\rm e}^{3i\pi/8}$
(b) $\dfrac{z}{w} = \dfrac{3{\rm e}^{i\pi/4}}{2{\rm e}^{i\pi/2}} = \dfrac{3}{2}{\rm e}^{-i\pi/4}$
(c) $\dfrac{z}{w} = \dfrac{2{\rm e}^{-i\pi/16}}{2{\rm e}^{i\pi/16}} = {\rm e}^{-i\pi/8}$
3.2 Sums and differences
Suppose that we are given two complex numbers in exponential form, a eiα and b eiβ, we can certainly write their sum in exponential form
a eiα + b eiβ = c eiγ(29) i
but it is not particularly easy to find the values of c and γ directly. First we will show you a direct method of finding the sum, then an alternative method which is often easier.
Method 1
To find c we can write
c2 = (c eiγ)(c e−iγ) = (a eiα + b eiβ)(a e−iα + b e−iβ)
c2 = a2 + b2 + ab [ei (α − β) + e−i (α − β)]
c2 = a2 + b2 + 2ab cos(α − β)
So we have an equation for c
$c= \sqrt{\smash[b]{a^2+b^2+2ab\cos(\alpha-\beta)}}$(30) i
To find γ we can use Euler’s formula to write eiα, eiβ and eiγ in polar form, and Equation 29 then becomes
a (cos α + i sin α) + b (cos β + i sin β) = c (cos γ + i sin γ)
and equating real and imaginary parts gives us:
$\cos\gamma = \dfrac{a\cos\alpha + b\cos\beta}{c}$
$\sin\gamma = \dfrac{a\sin\alpha + b\sin\beta}{c}$
So if we are given a, b, α and β we can first find c, then cos γ and sin γ. Then the condition, −π < γ ≤ π uniquely fixes γ.
✦ Given that z = a eiα = e2iπ/3 and w = b eiβ = eiπ/3, find z + w in exponential form.
✧ If z + w = c eiγ
then c2 = a2 + b2 + 2ab cos(α −β)
then c2 = 12 + 12 + 2 × 1 × 1 × cos(2π/3 − π/3)
then c2 = 12 + 12 + 2 × 1 ×1 × cos(π/3) = 3
which gives $c = \sqrt{3\os}$.
The angle, γ, can be obtained from
$\cos\gamma = \dfrac{a\cos\alpha+b\cos\beta}{c}$
$\phantom{\cos\gamma }= \dfrac{\cos(2\pi/3)+\cos(\pi/3)}{\sqrt{3\os}}$
$\phantom{\cos\gamma }= \dfrac{1}{\sqrt{3\os}}\left(-\dfrac{1}{2}+\dfrac{1}{2}\right) = 0$
and$\sin\gamma = \dfrac{a\sin\alpha+b\sin\beta}{c}$
$\phantom{\cos\gamma }= \dfrac{\sin(2\pi/3)+\sin(\pi/3)}{\sqrt{3\os}}$
$\phantom{\cos\gamma }= \dfrac{1}{\sqrt{3\os}}\left(\dfrac{\sqrt{3\os}}{2}+\dfrac{\sqrt{3\os}}{2}\right) = 1$
The only angle γ in the range −π < γ ≤ π for which cos γ = 0 and sin γ = 1 is γ = π/2 and therefore
e2iπ/3 + eiπ/3 = 3 eiπ/24
Method 2
The alternative method of finding the sum in exponential form relies on the fact that addition in Cartesian form is very straightforward. So if z and w are given in exponential form, we first convert them into Cartesian form, then find the sum, and finally convert the answer back into exponential form. We can use the previous example to illustrate the method.
Given that z = e2iπ/3 and w = eiπ/3, we can use Euler’s formula (Equation 22)
eiθ = cos θ + i sin θ(Eqn 22)
to write z and w in Cartesian form
$z = \dfrac{-1+i}{\sqrt{3\os}}{2}$ and $w = \dfrac{1+i}{\sqrt{3\os}}{2}$
from which it is straightforward to find the sum
$z + w = \dfrac{-1+i}{\sqrt{3\os}}{2} +\dfrac{1+i}{\sqrt{3\os}}{2} = i\sqrt{3\os}$
Since $i\sqrt{3\os} = \sqrt{3\os}\,{\rm e}^{i\pi/2}$ this result for z + w agrees with our previous result, but you should now be convinced that addition (and subtraction) are much easier using the Cartesian rather than exponential form of complex numbers.
Question T10
Express eiπ − eiπ/2 in exponential form.
Answer T10
${\rm e}^{i\pi} - {\rm e}^{i\pi/2} = -1 - i = \sqrt{2\os}{\rm e}^{-3i\pi/4}$
Question T11
Use the exponential representation to show that for any complex numbers z1 and z2
| z1 | + | z2 | ≥ | z1 + z2 | i
[Hint: Use Equation 30 and the fact that the cosine of any angle is less than or equal to one.]
$c= \sqrt{\smash[b]{a^2+b^2+2ab\cos(\alpha-\beta)}}$(Eqn 30)
Answer T11
We write z1 and z2 in exponential form as z1 = a eiα and z2 = b eiβ, so we immediately have | z1 | + | z2 | = a + b. Now let z1 + z2 = c eiγ, then, from Equation 30, we have
$c = \sqrt{\smash[b]{a^2+b^2+2ab\cos(\alpha-\beta)}}$(Eqn 30)
But cos(α − β) ≤ 1, so we have
| z1 + z2 | = c ≤ $\sqrt{a^2+b^2+2ab}$ = a + b = | z1 | + | z2 |
and therefore | z1 | + | z2 | ≥ | z1+ z2 |.
3.3 Powers, roots and reciprocals
The meaning of an expression such as (1 + 2i)3 is clear enough, i however the meaning of an expression such as (1 + 2i) π is by no means obvious. In this subsection we will attempt to attach a sensible meaning to such expressions. The following results are certainly true for real numbers a and b
(uv) a = u av a and (u a) b = u ab
and we assume that they also hold for complex numbers. So to raise the complex number z = r eiθ to the power α we have
z = (r eiθ) α = r α eiαθ(31)
For example, if z = 2 eiπ/4 then
z2 = 4 eiπ/2 = 4 [cos(π/2) + i sin(π/2)] = 4i
We can check this result by first putting z into Cartesian form
z = 2 eiπ/4 = 2 [cos(π/4) + i sin(π/4)] = $\dfrac{2}{\sqrt{2\os}}(1 + i) = \sqrt{2\os}(1+i)$
and then evaluating z2 to give z2 = 2 (1 + 2i + i2) = 4i.
Question T12
Find z2 and z3, where z = 2 eiπ/3. Plot z and z2 and z3 on an Argand diagram and use it to explain the movement of the point representing z n for successive integer values of n.
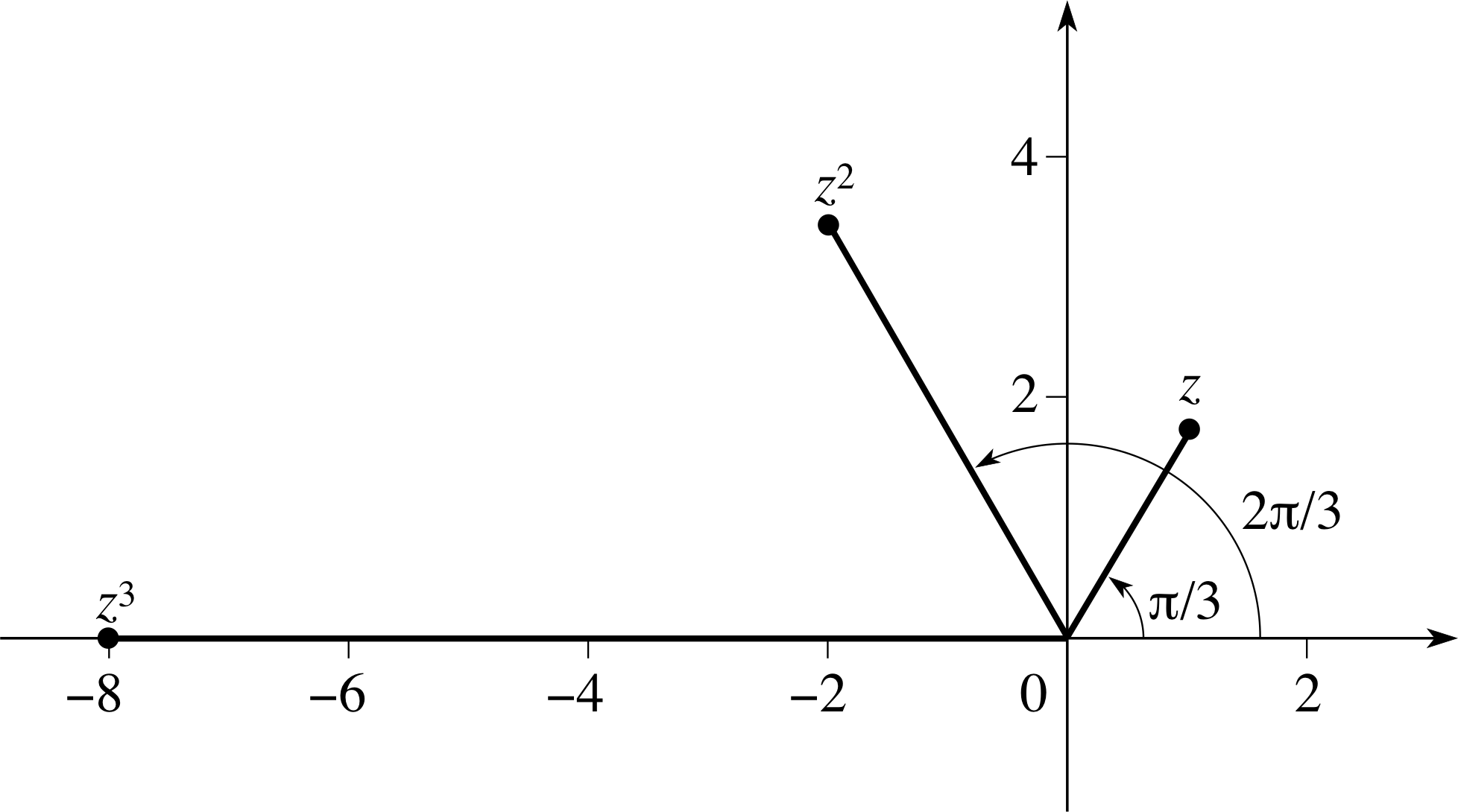
Figure 27 See Answer T12.
Answer T12
z2 = (2 eiπ/3)2 = 22e2iπ/3 = 4 e2iπ/3
z3 = (2 eiπ/3)3 = 23e3iπ/3 = −8 e3iπ/3 = −8 (since eiπ = −1)
If we plot the result of multiplying any complex number by z on an Argand diagram, then the distance from the origin will increase by a factor of 2 and the point will rotate about the origin through an angle of (π/3) rad. Therefore multiplying by z2 will increase the distance by a factor of 4 and rotate the point through an angle of (2π/3) rad. This is confirmed by Figure 27.
It is certainly possible to calculate powers of a complex number in Cartesian form, but it must be done with some care if we are to keep the algebra under control.
✦ Express (1 + i)8 in Cartesian form.
✧ (1 + i)2 = (1 + 2i + i2) = 2i
so that(1 + i)4 = (2i)2 = −4
and(1 + i)8 = (−4)2 = 16.
Very often a better method would be to express the complex number in exponential form, then raise it to the power, and finally convert the answer back into Cartesian form. Using this approach to evaluate (1 + i)8 we have
$(1 + i) = \sqrt{2\os}\,{\rm e}^{i\pi/4}$ so that $(1 + i)^8 = (\sqrt{2\os}\,{\rm e}^{i\pi/4})^8 = (\sqrt{2\os})^8\,{\rm e}^{2\pi i} = 16$
Question T13
Evaluate i $(1 + \sqrt{3\os}\,i)^3$ and hence express $(1 + \sqrt{3\os}\,i)^{10}$ in Cartesian form. Also express $z = 1 + \sqrt{3\os}\,i$ in exponential form and use this result to evaluate $(1 + \sqrt{3\os}\,i)^{10}$.
Answer T13
First we have $(1 + \sqrt{3\os}\,i)^2 = (1 - 3 + 2\sqrt{3\os}\,i) = -2 + \sqrt{3\os}\,i$
We then use the result to calculate $(1 + \sqrt{3\os}\,i)^3$
$(1 + \sqrt{3\os}\,i)^3 = (-2 + 2\sqrt{3\os}\,i)(1+ 3i) = -2\times 1- 2\times 3+i\,(-2\times 3 + 2\sqrt{3\os}\,i\times 1) = -8$
So we have
$(1 + \sqrt{3\os}\,i)^{10} = (1 + \sqrt{3\os}\,i)^9(1 + \sqrt{3\os}\,i) = (-8)^3(1 + \sqrt{3\os}\,i) = -512(1 + \sqrt{3\os}\,i)$
Now compare this calculation with the following which uses the exponential form of a complex number.
Using cos(π/3) = 1/2 and sin(π/3) = $\sqrt{3\os}$/2 we have
$z = 1+\sqrt{3\os} = {\rm e}^{i\pi/3}$
and therefore
$z^{10} = 2^{10}{\rm e}^{10i\pi/3} = 2^{10}{\rm e}^{-2i\pi/3} = 2^{10}[\cos(2\pi/3) -i\sin(2\pi/3)]$
$\phantom{z^{10} }= 2^{10}(-1/2-i\sqrt{3\os}/2) = -512(1 + \sqrt{3\os}\,i)$
This is consistent with the previous method but is a little easier.
Question T14
The complex number, u, is defined by
u = (1.1) e2πi/15
Use an Argand diagram to plot u n for n = 1, 2, 3, ... 15. What sort of curve would you expect to get if larger (integer) values of n were plotted and the points joined by a smooth curve?
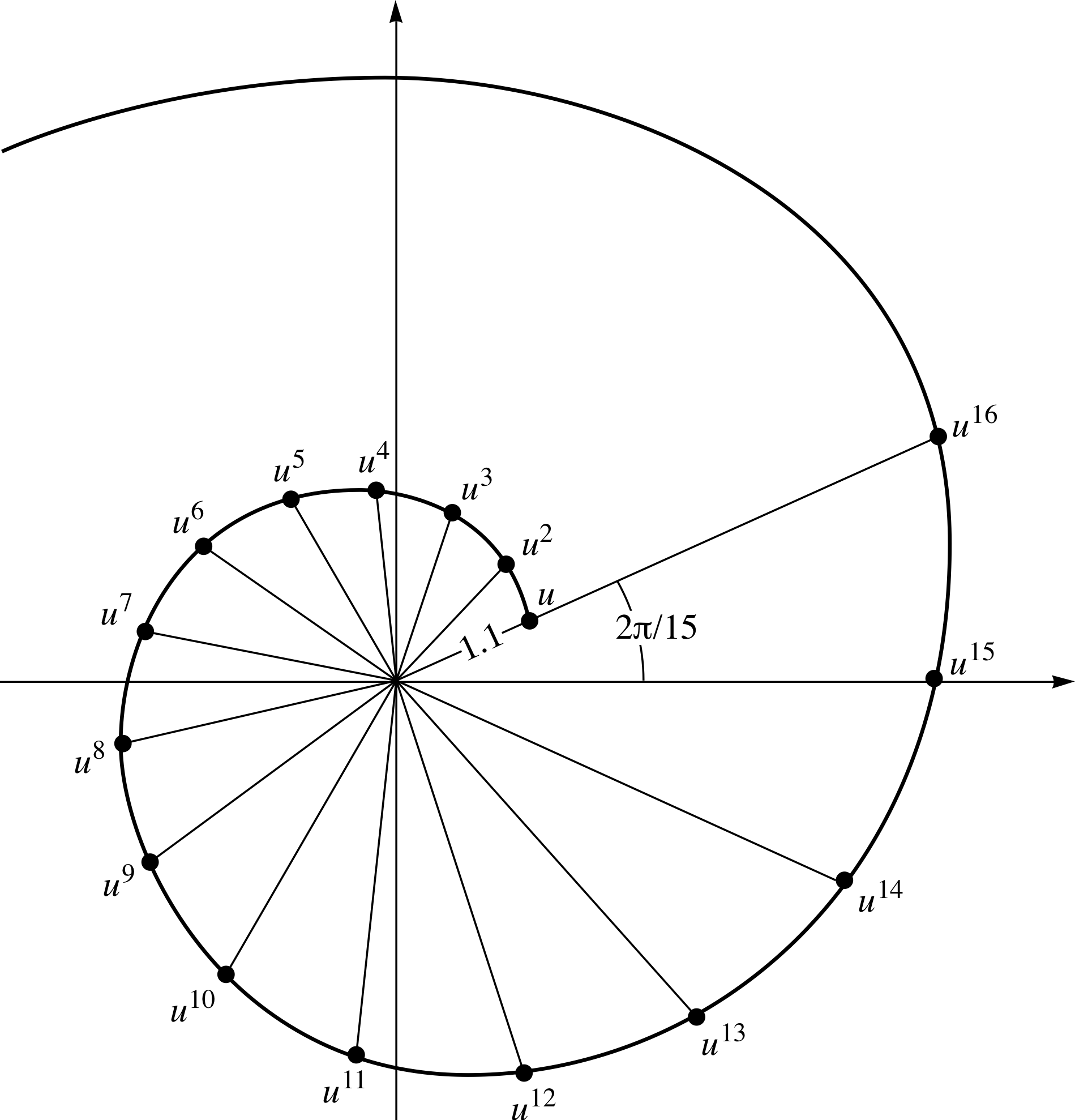
Figure 28 See Answer T14.
Answer T14
The argument of u n is 2πn/15. The point representing u n for n = 1 lies on a line from the origin which makes an angle of (2π/15) rad with the positive real axis. For any integer n this angle increases to (2nπ/15) rad.
For n = 1, the distance of the point from the origin is 1.1, and in general the distance is (1.1) n. The result is the series of points shown in Figure 28. Notice that the points lie on a spiral curve.
The following example illustrates an area of physics that uses complex numbers.
✦ The propagation constant of a cable carrying an alternating current of angular frequency ω is given by
$\sigma = \sqrt{(R+i\omega L)(G+i\omega C)\os}$ i
where R, L, G and C are, respectively, the resistance, inductance, conductance and capacitance of the cable i
Evaluate σ if R = 90 Ω, L = 0.002 H, G = 5 × 10−5 S, C = 0.05 × 10−6 F and ω = 5000 s−1.
✧ R + iω L = 90 Ω + [(5000) × (0.002)i] Ω = (90 + 10i) Ω
G + iωC = [5 × 10−5 + (5000) × (0.05 × 10−6)i] S = (5 + 25i) × 10−5 S
It follows that
(R + iωL)(G + iωC) = (90 + 10i) Ω × (5 + 25i) × 10−5 Ω−1
(R + iωL)(G + iωC) = (0.2 + 2.3i) × 10−2 ≈ (2.309) e1.484i × 10−2 (see Question T7(d))
Therefore$\sigma = \sqrt{(R+i\omega L)(G+i\omega C)}$ ≈ [(2.309) e1.484 i]1/2 × 10−1 ≈ (0.1519) e0.742 i
Complex powers
The meaning of a complex power of a complex number becomes clear if we use the exponential, rather than Cartesian, form. For example
z = (eiπ/4) i = e−π/4
Question T15
Use suitable exponential representations to reduce the following to simpler (or at least, more familiar) expressions:
(a) ii, (b) $\left(\dfrac{1+\sqrt{3\os}\,i}{2}\right)^i$, (c) $\left(\dfrac{1+\sqrt{3\os}\,i}{2}\right)^{i+1}$.
Answer T15
(a) Using eiπ/2 = cos(π/2) + i sin(π/2) = i we obtain
i i = (eiπ/2) i = e−π/2
Comment There is a deeper side to this question. Since e2πin = 1 for any integer, n, we also have
i i = (eiπ/2e2πin) i = e−π/2−2πn
So i i takes an infinity of values. You may find this surprising, but the nature of the result is similar to the fact that the square root of any positive number takes two values. A complete understanding of such results would take us far beyond the scope of this module and into a subject area known as complex analysis.
(b) Using $1+\sqrt{3\os}\,i = 2{\rm e}^{i\pi/3}$ we obtain
$\left(\dfrac{1+\sqrt{3\os}\,i}{2}\right)^i = \left({\rm e}^{i\pi/3}\right)^i = {\rm e}^{-\pi/3}$
Again, introducing a factor of e2πin would show that there is an infinity of possible results.
(c) $\left(\dfrac{1+\sqrt{3\os}\,i}{2}\right)^{i+1} = \left({\rm e}^{i\pi/3}\right)^{i+1} = {\rm e}^{-\pi/3}{\rm e}^{i\pi/3} = {\rm e}^{-i\pi/3}[\cos(\pi/3)+i\sin(\pi/3) = \frac12{\rm e}^{-\pi/3}(1+\sqrt{3\os}\,i)$
Roots
The exponential form is also convenient for working out roots of complex numbers since roots are fractional powers. As an example, if we require z1/2, where z = 2 eiπ/2, then we can write
$z^{1/2} = 2^{1/2}{\rm e}^{i\pi/4} = \dfrac{\sqrt{2\os}\,(1+i)}{\sqrt{2\os}} = 1+i$ i
This result can be checked by realizing that
z = 2 eiπ/2 = 2 [cos(π/2) + i sin(π/2)] = 2i
and that(z1/2)2 = (1 + i)2 = 1 + 2i + i2 = 2i
Question T16
Use a suitable exponential representation to express i1/2 in Cartesian form. Check your answer by means of explicit multiplication.
Answer T16
Using $i = {\rm e}^{i\pi/2}$ we find
$i^{1/2} = \left({\rm e}^{i\pi/2}\right)^{1/2} = {\rm e}^{i\pi/4} = \dfrac{1+i}{\sqrt{2\os}}$
and we can check this result by means of explicit multiplication
$\left(\dfrac{1+i}{\sqrt{2\os}}\right)^2 = \dfrac{1+2i-1}{2} = i$
Because ${\rm e}^{2\pi in} = 1$ for any integer n, there is also another root. Taking n = 1, we have
$i^{1/2} = \left({\rm e}^{\pi i/2}{\rm e}^{2\pi i}\right)^{1/2} = {\rm e}^{5i\pi/4} = \cos(5\pi/4)+i\sin(5\pi/4) = \dfrac{-1-i}{\sqrt{2\os}}$
This is clearly the previous solution multiplied by −1 and therefore squaring will again give i. It can be shown that other values of n in ${\rm e}^{2\pi in}$ do not lead to any new values for i1/2 so that, as one would expect, there are just two distinct values.
Reciprocals
The reciprocal i of a complex number is a special case of a power, so, if z = r eiθ with r non-zero, we have
$z^{-1} = (r\,{\rm e}^{i\theta})^{-1} = \dfrac{{\rm e}^{-i\theta}}{r}$
For example, if z = eiπ/3 then z−1 = e−iπ/3. We can compare this result with the equivalent calculation using the Cartesian form for z.
Sincez = eiπ/3 = $\dfrac{1+\sqrt{3\os}\,i}{2}$
$z^{-1} = \dfrac{2}{1+\sqrt{3\os}} = \dfrac{2(1-\sqrt{3\os})}{(1+\sqrt{3\os})(1-\sqrt{3\os})} = \dfrac{2(1-\sqrt{3\os})}{1+3} = \dfrac{1-\sqrt{3\os}}{2} = {\rm e}^{-i\pi/3}$
As you can see, the exponential form provides a somewhat easier method of calculating reciprocals than does the Cartesian form.
Question T17
If z = 2 e(i + 1)π/4 what are the exponential and Cartesian forms of z−1?
Answer T17
If $z = 2{\rm e}^{(i+1)\pi/4}$ then
$z^{-1} = \left[2{\rm e}^{(i+1)\pi/4}\right]^{-1} = \dfrac{1}{2{\rm e}^{\pi/4}}{\rm e}^{-i\pi/4}$ (exponential form)
$\phantom{z^{-1} }= \dfrac{1}{2{\rm e}^{\pi/4}}\dfrac{(1-i)}{\sqrt{2\os}} = \dfrac{\sqrt{2\os}}{4{\rm e}^{\pi/4}}(1-i)$ (Cartesian form)
3.4 Complex conjugates
The rule for finding the complex conjugate is to change i to −i, as in
(2 + 3i)* = 2 − 3i
so for any complex number in exponential form, z = r eiθ, we have
z* = r e−iθ(33)
From this result we see that the product of any complex number with its complex conjugate is real
zz* = r eiθ × r e−iθ = r2
But from Subsection 2.3 we know that r is actually the modulus of z, i.e. | z | and so we have the identity
zz* = | z |2 (34)
and therefore, for non–zero values of r, we have
$z^{-1} = r^{-1}\,{\rm e}^{-i\theta} = \dfrac{r\,{\rm e}^{-i\theta}}{r^2}$
so that
$z^{-1} = \dfrac{z\cc}{\lvert\,z\,\rvert^2}$(35) i
Equation 34 can often be useful if you wish to check that a complicated expression is real and positive (which is often the case in quantum mechanics, for example), for you simply need to recognize that the complicated expression is a product of a complex number with its conjugate. It can also be useful if you wish to establish a result involving moduli (as in the following example).
✦ Show that for any two complex numbers z and w
| z + w |2 + | z − w |2 = 2| z |2 + 2| w |2
✧ From Equation 34,
zz* = | z |2(Eqn 34)
| z + w |2 = (z + w)(z* + w*) = zz* + ww* + wz* + zw* | z − w |2
| z + w |2 = (z − w)(z* − w*) = zz* + ww* − wz* − zw*
and therefore
| z + w |2 + | z − w |2 = 2zz* + 2ww* = 2 | z |2 + 2 | w |2
The next question establishes some results which you have probably already assumed to be true.
Question T18
For any complex numbers z and w show that:
(a) (zw)* = z*w*, (b) | z−1 | = | z |−1, (c) | z w | = | z | | w |.
Answer T18
(a) It is certainly possible to establish this result by expressing the complex numbers in Cartesian form as follows:
(zw)* = [(x + iy)(u + iv)]* = [(xu − yv) + i (yu + xv)]* = [(xu − yv) − i (yu + xv)] = [(x − iy)(u − iv)] = z*w*
However, it is slightly easier to write z = r eiθ and w = ρ eiϕ, then we can write
(zw)* = (r eiθρ eiϕ)* = [rρ ei (θ + ϕ)]* = [rρ e−i (θ + ϕ)] = r e−iθρ e−iϕ = z*w*
(b) If we write z = r eiθ then we find
| z−1 | = | r−1 e−iθ | = r−1
and| z |−1 = r−1
and therefore | z−1 | = | z |−1
Alternatively, using Equation 35,
$z^{-1} = \dfrac{z\cc}{\lvert\,z\,\rvert^2}$(Eqn 35)
and the fact that | z* | = | z |
$\lvert\,z^{-1}\,\rvert = \dfrac{z\cc}{\lvert\,z\,\rvert^2} = \dfrac{\lvert\,z\,\rvert}{\lvert\,z\,\rvert^2} = \lvert\,z\,\rvert^{-1}$
(c) We write z and w in exponential form as r eiθ and w = ρ eiϕ, where r, ρ, θ and ϕ are all real. This means that | z | = r and | w | = ρ, which enables us to write
| zw | = | r eiθ ρ eiϕ | = | rρ ei (θ + ϕ) | = rρ = | z | | w |
Alternatively:
| zw |2 = (zw)(zw)* = (zz*)(ww*) = | z |2 | w |2
and the result follows (because the moduli are positive).
3.5 Applications
In this subsection we consider some applications of the polar and exponential representations which are of particular relevance to physics. You do not need to be familiar with the physics involved.
Example 2
Two complex numbers, Z1 and Z2 are
Z1 = 2 + 2i
Z2 = 1 + 2i
If Z = Z1 + Z2 find | Z | and the principal value of arg(Z). i
Solution
Z = (2 + 2i) + (1 + 2i) = 3 + 4i
$\lvert\,Z\,\rvert = \sqrt{3^2+4^2} = 5$
If θ = arg(Z), then sin θ = 4/5 and cos θ = 3/5 which implies that θ ≈ 0.927 rad.
Example 3
Repeat Example 2 with Z1 and Z2 as before, but this time suppose that Z is given by
$\dfrac{1}{Z} = \dfrac{1}{Z_1} + \dfrac{1}{Z_2}$ i
Solution
$Z = \dfrac{Z_1 Z_2}{Z_1 + Z_2} = \dfrac{(2+2i)(1+2i)}{3+4i} = \dfrac{(2-4) +i(2+4)}{3+4i}$
$\phantom{Z}= \dfrac{(-2+6i)(3-4i)}{25} = \dfrac{18+26i}{25}$
$\lvert\,Z\,\rvert = \dfrac{\sqrt{(18)^2+(26)^2}}{25} \approx 1.26$
If θ = arg(Z), then
$\sin\theta = \dfrac{26}{\sqrt{(18)^2+(26)^2}}$ and $\sin\theta = \dfrac{18}{\sqrt{(18)^2+(26)^2}}$
which implies that θ ≈ 0.965 rad.
Example 4
The function
f (ϕ) = eimϕ(36)
where ϕ is an angle (and therefore real) and m is a real number, occurs in quantum theory. What are the possible values of m, if we require that for every value of ϕ:
f (ϕ) = f (ϕ + 2π)
Solution
If f (ϕ) = f (ϕ + 2π) then
eimϕ = eim (ϕ + 2π) = eimϕ e2mπi
We can cancel the factor eimϕ (since it is non-zero) giving
e2imϕ = 1
Using Euler’s formula, this can be written as
cos(2πm) + i sin(2πm) = 1
so thatcos(2πm) = 1 and sin(2πm) = 0
We recall that cos θ = 1 if θ = 0, ±2π, ±4π, ... and sin θ = 0 if θ = 0, ±π, ±2π, ...
and, since both conditions must apply simultaneously, we have:
2πm = 0, ±2π, ±4π, ...
it therefore follows that:
m = 0, ±1, ±2, ±3, ...
In other words, the condition f (ϕ) = f (ϕ + 2π) ensures that only integer values of m are acceptable.
Example 5
Given that $a = \dfrac{{\rm e}^{-i\phi t}-1}{\phi}$, with ϕ and t real, show that
$\lvert\,a\,\rvert^2 = \dfrac{4}{\phi^2}\sin^2\left(\dfrac{\phi t}{2}\right)$ i
Solution
We could certainly calculate | a |2 by using Equation 35,
$z^{-1} = \dfrac{z\cc}{\lvert\,z\,\rvert^2}$(Eqn 35)
and writing
$\lvert\,a\,\rvert^2 = \dfrac{({\rm e}^{-i\phi t}-1)({\rm e}^{i\phi t}-1)}{\phi^2}$
and then simplifying the result (using various trigonometric identities); however if you notice that the required expression for | a |2 involves only (ϕt/2) then you might think of the following (more elegant) method.
We force the expression for a to involve terms in (ϕt/2) by extracting a factor e−iϕt/2, so that
$a = \dfrac{{\rm e}^{-i\phi t/2}}{\phi}\left({\rm e}^{-i\phi t/2} - {\rm e}^{i\phi t/2}\right) = \dfrac{{\rm e}^{-i\phi t/2}}{\phi}\left[-2i\sin\left(\dfrac{\phi t}{2}\right)\right] = (-2i)\left[\dfrac{\sin(\phi t/2)}{\phi}{\rm e}^{-i\phi t/2}\right]$
In the right–hand expression, −2i has a modulus of 2, while the term in square brackets is in exponential form
r eiθ with $r = \dfrac{\sin(\phi t/2)}{\phi}$, so it follows that
$\lvert\,a\,\rvert^2 = \left[\dfrac{2}{\phi}\sin\left(\dfrac{\phi t}{2}\right)\right]^2 = \dfrac{4}{\phi^2}\sin^2\left(\dfrac{\phi t}{2}\right)$ i
4 Closing items
4.1 Module summary
- 1
-
A complex number is equivalent to an ordered pair of real numbers, (x, y). The addition and subtraction of complex numbers obey the same rules as of two–dimensional vectors
(x, y) + (a, b) = (x + a, y + b)(Eqn 8)
Multiplication of two complex numbers obeys the rule
(a, b) × (x, y) = [(ax − by), (ay + bx)](Eqn 9)
In practice, a complex number is more usually written as x + iy with i having the property that i2 = −1.
- 2
-
A complex number, z = x + iy, is said to be in Cartesian form or a Cartesian representation.
- 3
-
A complex number, z = r (cos θ + i sin θ) is said to be in Subsection 2.2polar form or a Subsection 2.2polar representation.
The polar form r (cos θ + i sin θ) of a given complex number z is not unique. However, we can make it so by chosing the principal value of the argument of z, i.e. if −π < θ ≤ π. (Note that r = | z | ≥ 0).
- 4
-
We can convert from Cartesian into polar form by using
$r = \sqrt{x^2+y^2}$(Eqn 13)
$\cos\theta = \dfrac{x}{\sqrt{x^2+y^2}}$(Eqn 14)
$\cos\theta = \dfrac{y}{\sqrt{x^2+y^2}}$Eqn (15)
and from polar to Cartesian form by means of x = rcosθ
x = r cosθ(Eqn 10)
y = r sin θ(Eqn 11)
- 5
-
A complex number can be represented by a point on an Argand diagram by using (x, y) as the Cartesian coordinates or (r, θ) as the Subsection 2.2polar coordinates of the point. By convention, θ is measured anticlockwise from the positive real axis.
- 6
-
If a complex number is represented by a point on an Argand diagram, then multiplication by z = r (cos θ + i sin θ) corresponds to a change in the distance of the point from the origin by a factor of r, together with an anticlockwise rotation through an angle θ.
- 7
-
If a complex number, z, is represented in polar form by z = r (cos θ + i sin θ) then the modulus of z is given by | z | = r, and θ is known as the Subsection 2.4argument of z (written as arg(z) ). If z is represented by a point on an Argand diagram then r is the ‘distance’ of the point from the origin and θ is the angle made by a line from the point to the origin with the positive real axis. If θ satisfies −π < θ ≤ π, then θ is known as the principal value of the argument of z.
- 8
-
Euler’s formula states that
eiθ = cos θ + i sin θ(Eqn 22)
- 9
-
9 If a complex number, z, is written as z = r eiθ, with r ≥ 0, then z is said to be in exponential form or exponential representation. Euler’s formula provides a direct connection between the polar and exponential forms since
r eiθ = r (cos θ + i sin θ)
- 10
-
The following operations can be carried out on complex numbers in exponential form:
multiplication
r eiθ × ρ eiϕ = rρ ei (θ + ϕ)
simplifying quotients
$\dfrac{r\,{\rm e}^{i\theta}}{\rho\,{\rm e}^{i\phi}} = \dfrac{r}{\rho}{\rm e}^{i(\theta-\phi)}$
finding real powers
(r eiθ) α = r α eiαθ
finding reciprocals
(r eiθ)−1 = r−1 e−iθ
finding complex conjugates
(r eiθ)* = r e−iθ
We may also calculate complex powers of a complex number. The same values apply as for real powers, i.e.
z az b = z ab and (z a) b = z ab
for complex numbers a, b and z.
- 11
-
The addition and subtraction of complex numbers in either exponential or polar form are complicated in comparison to the same operations on complex numbers in the Cartesian form. Specifically, the sum of a eiα and b eiβ can be written as
a eiα + b eiβ = c eiγ(Eqn 29)
where$c = \sqrt{\smash[b]{a^2+b^2+2ab\cos(\alpha-\beta)}}$(Eqn 30)
$\cos\gamma = \dfrac{a\cos\alpha + b\cos\beta}{c}$
$\sin\gamma = \dfrac{a\sin\alpha + b\sin\beta}{c}$
Where possible, it is better to use the Cartesian form for addition and subtraction.
4.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Convert a complex number between the Cartesian, polar and exponential forms.
- A3
-
Represent a complex number (in either Cartesian, exponential or polar form) by means of a point on an Argand diagram, and describe geometrically the effect of complex addition or multiplication.
- A4
-
Find the modulus, argument and complex conjugate of complex numbers.
- A5
-
Find powers and reciprocals of complex numbers.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
4.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions, each of which tests one or more of the Achievements.
Question E1 (A2)
If Re(z) = 1 and Im(z) = − 3, express z in (a) Cartesian form, (b) polar form using the principal value of the argument, (c) exponential form.
Answer E1
(a) $z = 1 - i\sqrt{3\os}$
(b) We have $r = \sqrt{1+3\os} = 2$. We also have cos θ = 1/2 and sin θ = −$\sqrt{3\os}$/2 and therefore θ = −(π/3) rad.
So in polar form we have
z = 2 [cos(−π/3) + i sin(−π/3)]
(c) Using the answer to part (b), together with Euler’s formula, we have z = 2 e−iπ/3.
(Reread Section 2 if you had difficulty with this question.)
Question E2 (A2, A4 and A5)
Express $z = 1 - i\sqrt{3\os}$ and w =1 + i in exponential form and use your results to express R in exponential form, where R is given by
$R = \dfrac{1}{w}\left(\dfrac{z}{2}\right)^{12}$
Make sure that you give the principal value of arg(R).
[Hint: You may find the answers to Questions Question F1F1 and E1 helpful.]
Answer E2
We have
$z = 1 - i\sqrt{3\os} = 2{\rm e^{-i\pi/3}}$
$w = 1 + i = \sqrt{2\os}{\rm e}^{+i\pi/4}$
$R = \dfrac{1}{w}\left(\dfrac{z}{2}\right)^{12} = \dfrac{1}{\sqrt{2\os}{\rm e}^{i\pi/4}}\left({\rm e}^{-i\pi/3}\right)^{12} = \dfrac{{\rm e}^{-i 12\pi/3}}{\sqrt{2\os}}\rm e{^{i\pi/4}} = \dfrac{1}{\sqrt{2\os}}{\rm e}^{-4/pi i}{\rm e}^{-i/pi} = \dfrac{1}{\sqrt{2\os}}{\rm e}^{-i\pi/4}$
Notice that we can factor out multiples of e2πi (since e2πi = 1) in order to ensure that −π < θ ≤ π and so obtain the principal value of the argument.
(Reread Subsection 2.4Subsections 2.4, Subsection 2.52.5, Subsection 3.13.1 and Subsection 3.33.3 if you had difficulty with this question.)
Question E3 (A3)
If z is given by
$z = \dfrac{{\rm e}^{i\theta}}{1+\theta}$
where θ can take any non–negative real value, sketch the curve on which any point corresponding to z must lie on an Argand diagram. Justify the main features of the curve.

Figure 29 See Answer E3.
Answer E3
For θ = 0, we have z = 1. As θ increases, the point representing z on an Argand diagram rotates anticlockwise about the origin, with one complete rotation for every change of 2π in θ. The distance of the point from the origin is | z | = (1 + θ)−1, so as θ increases from zero, this distance decreases from 1. As θ becomes very large, the point representing z spirals towards the origin and the resulting curve is shown in Figure 29.
(Reread Subsection 2.2Subsections 2.2 and Subsection 2.42.4 if you had difficulty with this question.)
Question E4 (A3)
(a) Show how the addition of complex numbers z = 1 + i and w = 2 + 4i can be considered as vector addition on an Argand diagram.
(b) A complex number z is defined by z = e2πi/n for some fixed positive integer value of n. Show (giving a sketch) how the series
$\displaystyle S = \sum_{k=1}^n z^k$
can be considered as the sum of n vectors on an Argand diagram. Hence determine the value of S.

Figure 31 See Answer E4(b).
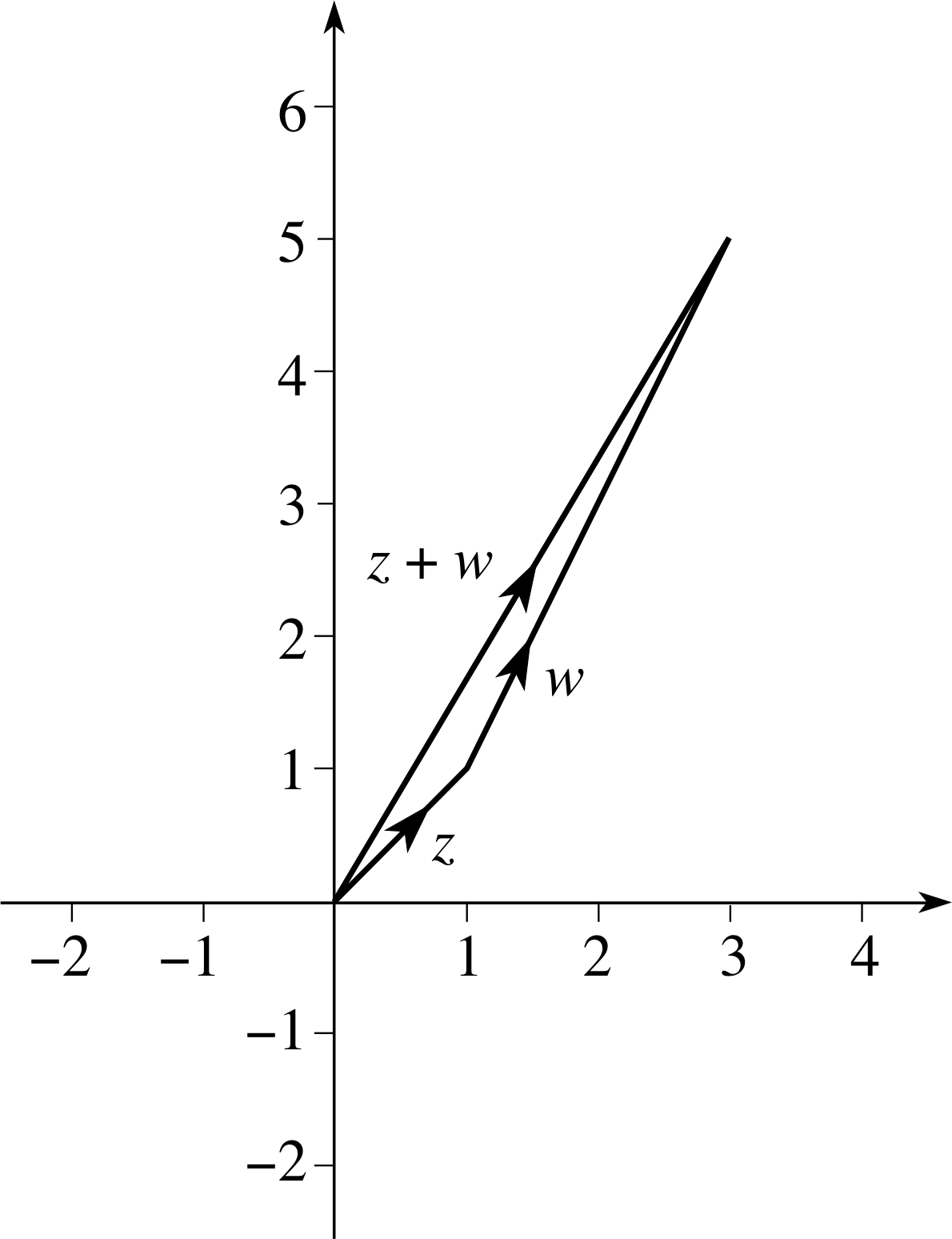
Figure 30 See Answer E4(a).
Answer E4
(a) The vector addition of z + w is given on the Argand diagram shown in Figure 30. Therefore we have z = 3 + 5i.
(b) If z = e2πi/n then z k = e2πki/n which is a complex number with modulus 1 and argument 2πk/n. If we define ϕ = 2π/n, then as we add each successive vector it makes an angle, ϕ, with the previous one. Since there are n such vectors, and each is of length 1, we proceed round the sides of a regular polygon, ending back where we started! The result for S is therefore zero. Figure 31 shows the result of adding vectors defined by z k = e2πki/n for the case n = 9. This result can also be shown algebraically since the right–hand side is a geometric series and
$\displaystyle S = \sum_{k=1}^n z^k = z + z^2 + \dots + z^n = \dfrac{z(1-z^n)}{1-z} = 0$
because zn = e2πi = 1.
(Reread Subsection 3.2 if you had difficulty with this question.)
Question E5 (A2)
Show that (−1) n = einπ, where n is any integer.
Answer E5
Using Euler’s formula we can write
einπ = cos(nπ) + i sin(nπ)
But sin(ϕ) = 0 for ϕ = 0, ±π, ±2π, ... and so sin(nπ) = 0 for n = 0, ±1, ±2, ... . This means that the imaginary part of einπ is zero. We also have cos θ = 1 for θ = 0, ± 2π, ± 4π, ... and cos θ = −1 for θ = 0, ±π, ±3π, ±5π, ... , which shows that cos(nπ) = (−1) n. Putting these results together we find (−1) n = einπ.
(Reread Subsection 2.4Subsections 2.4, Subsection 2.52.5 and Subsection 3.33.3 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to Ready to study? in Subsection 1.3.