MATH 4.3: Further differentiation |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
Applications of differentiation are widespread throughout physics. For example, given the displacement from the origin of a moving object as a function of time, the corresponding velocity can be found by differentiating that function. Or, given a simple electrical circuit consisting of a resistor and an inductor connected in series with a charged capacitor and a switch (i.e. an LCR circuit), the potential differences across the inductor and resistor are, respectively, $L\dfrac{dI}{dt}$ and RI (t) where I (t) is the current in the circuit at time t after the switch is closed and L and R are constants. It is also the case that in such a circuit $I(t) = \dfrac{dq}{dt}(t)$ where q (t) is the charge on the capacitor at time t. Because the need to differentiate arises so often in physics it is essential that you should be able to differentiate readily a wide variety of functions. The techniques of basic differentiation should enable you to differentiate certain standard functions such as powers, trigonometric functions, exponentials and logarithms, or certain combinations of those standard functions such as sums, constant multiples, products and quotients. This module goes further in that it introduces techniques that, when combined with those of basic differentiation, will allow you to differentiate almost all the functions of a single variable that you are likely to meet.
It is often the case that a physical quantity can be represented by a function of a variable that is itself a function of another variable. For example, the displacement from equilibrium of a one–dimensional simple harmonic oscillator may be represented by x = Acos(ωt + ϕ), but (ωt + ϕ) is itself a function of t, so we might write θ (t) = (ωt + ϕ), in which case we can write x = Acos(θ (t)). Such an expression makes it clear that x is a function of a function of t, and that to find the velocity of such an oscillator we need to be able to differentiate a function of a function of t. Section 2 of this module describes functions of a function in more detail and introduces (in Subsection 2.2) the chain rule for their differentiation. The chain rule is one of the most useful techniques of calculus; among other things it enables us to differentiate implicit functions, inverse functions and parametric functions, all of which are discussed in Subsection 2.3Subsections 2.3, Subsection 2.42.4 and Subsection 2.52.5.
If we want to find the acceleration of an object given its position then we must proceed via its velocity; the acceleration is the rate of change of the velocity, which is itself the rate of change of the position. Hence the process requires two successive differentiations. We say that the acceleration is the second derivative of the position of the object. Similarly, the potential difference across the inductor in the series LCR circuit mentioned earlier is proportional to dI/dt but I = dq/dt, so the potential difference is proportional to the second derivative of the charge. Clearly, second (and higher) derivatives are also of interest to physicists, so they form the second major theme of this module, discussed in Section 3.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 5.1Module summary and the Subsection 5.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 5.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
Find the first four derivatives of the following functions:
(a) F (x) = 3 sin x + 4 cos x
(b) y = loge x x > 0 i
Answer F1
(a) f ′ (x) = 3 cosx − 4 sin x
f ′′ (x) = −3 sin x − 4 cosx
f ′′′ (x) = −3 cos x + 4 sin x
F(iv)(x) = 3 sin x + 4 cos x
(b) $\dfrac{dy}{dx} = \dfrac1x,~~~\dfrac{d^2y}{dx^2} = \dfrac{-1}{x^2},~~~\dfrac{d^3y}{dx^3} = \dfrac{2}{x^3},~~~\dfrac{d^4y}{dx^4} = \dfrac{-6}{x^4}$
Comment The two notations used in parts (a) and (b) are equivalent, i.e. f ′ (x) is equivalent to dy/dx.
Question F2
If x = a (θ − sin θ) and y = a (1 − cos θ), where a is a constant, find $\dfrac{dy}{dx}~\text{and}~\dfrac{d^2y}{dx^2}$.
Answer F2
$\dfrac{dx}{d\theta} = a(1-\cos\theta)\quad\text{and}\quad\dfrac{dy}{d\theta} = a\sin\theta$
so$\dfrac{dy}{dx} = \dfrac{dy}{d\theta} \times \dfrac{d\theta}{dx} = \dfrac{dy}{d\theta}\left/\dfrac{dx}{d\theta}\right. = \dfrac{a\sin\theta}{a(1- \cos\theta)} = \dfrac{\sin\theta}{(1- \cos\theta)}\quad\text{i.e.}\quad\dfrac{dy}{dx} = \dfrac{\sin\theta}{(1- \cos\theta)}$
Also$\dfrac{d^2y}{dx^2} = \dfrac{d}{dx}\left(\dfrac{\sin\theta}{1-\cos\theta}\right) = \dfrac{d}{d\theta} \left(\dfrac{\sin\theta}{1-\cos\theta}\right)\times\dfrac{d\theta}{dx}$
so$\dfrac{d^2y}{dx^2} = \left[\dfrac{(1-\cos\theta)\cos\theta -\sin\theta(+\sin\theta)}{(1-\cos\theta)^2}\right]\times\dfrac{d\theta}{dx} d\theta$
i.e.$\dfrac{d^2y}{dx^2} = \left.\left[\dfrac{\cos\theta-\cos^2\theta-\sin^2\theta}{(1-\cos\theta)^2}\right]\right/\dfrac{dx}{d\theta}$
$\phantom{\dfrac{d^2y}{dx^2}} = \left[\dfrac{\cos\theta-1}{(1-\cos\theta)^2}\right]\times\dfrac{1}{a(1-\cos\theta)} = \dfrac{-1}{a(1-\cos\theta)^2}$
Question F3
Find the first and second derivatives of the following functions:
(a) F (t) = exp[αt + sin(ωt)] with respect to t, where α and ω are constants
(b) F (x) = 5 loge(sin2x + 1) with respect to x
(c) F (x) = arcsin(5x) with respect to x i
Answer F3
- (a)
-
Put u = αt + sin(ωt) and F (u) = eu
then$\dfrac{du}{dt} = \alpha + \omega\cos(\omega t)$ and f ′ (u) = eu
Hence, by the chain rule
$\dfrac{dF}{dt} = \dfrac{dF}{du}\times\dfrac{du}{dt} = {\rm e}^u \times[\alpha+\omega\cos(\omega t)] = [\alpha+\omega\cos(\omega t)]{\rm e}^u = [\alpha+\omega\cos(\omega t)]\times{\rm {exp}}[\alpha t+\omega\sin(\omega t)]$
i.e.$\dfrac{dF}{dt} = [\alpha+\omega\cos(\omega t)]\times{\rm {exp}}[\alpha t+\omega\sin(\omega t)]$
By the product rule
$\dfrac{d^2F}{dt^2} = [\alpha + \omega\cos(\omega t)]\times\dfrac{d}{dt}\{{\rm exp}[\alpha t + \omega\sin(\omega t)]\} + [-\omega^2\sin(\omega t)]\times{\rm exp}[\alpha t + \omega\sin(\omega t)]$
i.e.$\dfrac{d^2F}{dt^2} = [\alpha + \omega\cos(\omega t)]\times[\alpha + \omega^2\cos(\omega t)]\times\{{\rm exp}[\alpha t + \omega\sin(\omega t)]\} - \omega^2\sin(\omega t)\times{\rm exp}[\alpha t + \omega\sin(\omega t)]$
so$\dfrac{d^2F}{dt^2} = \{[\alpha + \omega\cos(\omega t)]\times[\alpha + \omega^2\cos(\omega t)] - \omega^2\sin(\omega t)]\}\times{\rm exp}[\alpha + \omega\sin(\omega t)]\}$
- (b)
-
Put u = sin2x + 1 and F (u) = 5 loge u
then, using either the product rule (sin2x = sin x × sin x) or the chain rule, we find
$\dfrac{du}{dx} = 2\sin x\cos x$ and $F'(u) = \dfrac5u$
$\dfrac{dF}{dx} = \dfrac{dF}{du} \times\dfrac{du}{dx} = \dfrac5u \times (2\sin x\cos x) = \dfrac{5 \times2\sin x\cos x}{\sin^2x+1} = \dfrac{10\times\sin x\cos x}{\sin^2x+1}$
Applying the quotient rule we find
$\dfrac{d^2F}{dx^2} = [(\sin^2x+1)\times\dfrac{d}{dx}(10\sin x\cos x)-10\sin x\cos x(2\sin x\cos x)]/(\sin^2 x+1)^2$
$\phantom{\dfrac{d^2F}{dx^2} }= \{(\sin^2 x+1)[10\cos x\times\cos x+10\sin x\times(-\sin x)]-10\sin x\cos x(2\sin x\cos x)\}\left/(\sin^2 x+1)^2\right.$
$\phantom{\dfrac{d^2F}{dx^2} }= \dfrac{10(\sin^2 x+1)(\cos^2 x-\sin^2x)-2\sin^2 x\cos^2 x}{(\sin^2 x+1)^2}$
- (c)
-
Let y = arcsin(5x) then sin y = 5x.
Hence, differentiating implicitly with respect to x, we find
$\cos y\dfrac{dy}{dx} = 5$
so$\dfrac{dy}{dx} = \dfrac{5}{\cos y} = \dfrac{5}{\sqrt{1-25x^2}}$
Now put
$\dfrac{dy}{dx} = dfrac{5}{\sqrt{1-25x^2}} = 5(1-25x^2)^{-1/2} = G(x)$
letu = 1 − 25x2 and g (u) = 5u−1/2
so$\dfrac{du}{dx} = -50x$ and $\dfrac{dg}{du} = -\dfrac12\times5u^{-3/2} = \dfrac{-5}{2u^{3/2}}$
Hence, by the chain rule
$\dfrac{d^2F}{dx^2} = \dfrac{dG}{dx} = \dfrac{dg}{du}\times\dfrac{du}{dx} = \dfrac{-5}{2u^{3/2}}\times(-50x) = \dfrac{125x}{(1-25x^2)^{3/2}}$
1.3 Ready to study?
Study comment In order to study this module you should be familiar with the following terms: derivative, differentiate, domain, function and inverse function. You will need to be familiar with the following specific types of function: exponential functions, logarithmic functions, power_mathematicalpower functions, trigonometric functions (cosine, sine, tangent, cosec, sec, cot) and inverse trigonometric functions (arccos, arcsin, arctan). You should also know the meaning of the term radian and be aware of the need to express angles in radians when using them in the arguments of trigonometric functions. You should be able to differentiate power_mathematicalpowers, exponential functions, logarithmic functions and trigonometric functions, and to use the sum_rule_of_differentiationsum rule, constant_multiple_rule_of_differentiationconstant multiple rule, product_rule_of_differentiationproduct rule and quotient_rule_of_differentiationquotient rule of differentiation. If you are unsure of any of these terms then you can review them by referring to the Glossary, which will also indicate where in FLAP they are developed. The following questions will let you establish whether you need to review some of these topics before working through this module.
Question R1
Which of the following formulae can be used to define a function of x? What restrictions are there on the admissible values of x?
(a) f (x) = x5, (b) y = arcsin x (i.e. sin y = x), (c) y2 = 4x2.
Answer R1
- (a)
-
f (x) is an acceptable function of x and there are no restrictions on the value of x. Each value of x corresponds to a single value of y.
- (b)
-
y is an acceptable function of x, provided x is in the range −1 ≤ x ≤ 1 (this defines the domain of the function). There are many different values of y that could correspond to a given value of x, so to ensure that each admissible value of x corresponds to only a single value of y it is also necessary to impose restrictions on y in this case. Conventionally, y is required to be in the range −π/2 ≤ y ≤ +π/2, i.e. −90° ≤ y ≤ +90° (this defines the codomain of the function).
- (c)
-
y is not a function of x since the given formula implies that y = ±2x, so it is not the case that a single value of y corresponds to each value of x.
Question R2
For each of the following, express x as a function of y:
(a) y = 9x3, (b) y = tan x, (c) y = e2x, (d) y = loge(3x).
Answer R2
(a) x = (y/9)1/3 (b) x = arctan y (c) 2x = loge y so, x = (loge y)/2 (d) 3x = ey, so x = ey/3
(If you are unsure of the answers to Questions R1 or R2, consult the entries on functions, trigonometric functions, exponential functions, logarithmic functions and inverse functions in the Glossary.)
Question R3
Define the derivative of a function f (x) at x = a.
Answer R3
If the expression $\dfrac{f(a + h) - f(a)}{h}$ approaches a unique limiting value as h approaches zero, then that limiting h value is called the derivative of f (x) at x = a and is written f ′ (a).
Question R4
For each of the functions f (x) below find the derivative f ′ (x):
(a) 8x6 + 6x3 − 5x2 − 2, (b) 3 sin x + 4 cos x.
Answer R4
(a) f ′ (x) = 48x5 + 18x2 − 10x (differentiation of power_mathematicalpowers).
(b) f ′ (x) = 3 cos x − 4 sin x (differentiation of trigonometric functions)
Question R5
Find dy/dx for each of the following:
(a) y = 6ex, (b) y = x2 −5 loge x.
Answer R5
(a) $\dfrac{dy}{dx} = 6\,{\rm e}^x$ (differentiation of exponential functions)
(b) $\dfrac{dy}{dx} = 2x - \dfrac5x$ (differentiation of logarithmic functions)
Question R6
Differentiate the following functions of x:
(a) x2ex, (b) x3sin x, (c) excos x, (d) $\dfrac{\log_{\rm e}x}{3x^2+x}$ x > 0, (e) $\dfrac{3\cos x}{2+\sin x}$, (f) $\dfrac{x}{2+\cos x}$.
Answer R6
(a) x2 × ex + 2x ex = (x2 + 2x) ex (product_rule_of_differentiationproduct rule)
(b) x3 cos x + 3x2 sin x (product_rule_of_differentiationproduct rule)
(c) ex × (−sin x) + (ex) × cos x = ex (−sin x + cos x) (product_rule_of_differentiationproduct rule)
(d) $\dfrac{(3x^2+x)\left(\dfrac1x\right) - \log_{\rm e}x\times(6x+1)}{(3x^2+x)^2} = \dfrac{(3x+1) - \log_{\rm e}x\times(6x+1)}{(3x^2+x)^2}$ (quotient_rule_of_differentiationquotient rule)
(e) $\dfrac{(2 + \sin x) \times (-3\sin x) - 3\cos x \times (\cos x)}{(2 + \sin x)^2} = \dfrac{-6\sin x - 3\sin^2 x - 3\cos^2 x}{(2 + \sin x)^2} = \dfrac{-3(2\sin x+1)}{(2 + \sin x)^2}$ (quotient_rule_of_differentiationquotient rule)
(f) $\dfrac{(2+\cos x)\times(1)-x\times(-\sin x)}{(2+\cos x)^2} = \dfrac{\cos x+2+x\sin x}{(2+\cos x)^2}$ (quotient_rule_of_differentiationquotient rule)
(If you are unsure of the answers to Questions R3 or R6, consult the relevant entries in the Glossary.)
A special note about $\boldsymbol{\sqrt{x\os}}$ Generally in FLAP we follow the convention that $\sqrt{x\os}$ may be positive or negative. Thus $\sqrt{4\os}$ = ±2. A consequence of this convention is that $f(x) = \sqrt{x\os}$ does not define a function since it does not associate a unique value of f (x) with each value of x. This would be an exceptionally inconvenient convention to follow in this module so instead we adopt the convention that $\sqrt{x\os}$ is positive. Of course, it remains true that the square roots of $\sqrt{x\os}$ may be positive or negative, $\sqrt{x\os}$ or −$\sqrt{x\os}$, so within this convention we will call $\sqrt{x\os}$ the positive square root of x, and not simply the square root. In a similar spirit x1/2 = $\sqrt{x\os}$ will also be a positive quantity.
2 Derivatives of composite functions
2.1 A function of a function
In this subsection, we introduce the concept and notation of a function of a function i by considering the example of a simple harmonic oscillator, i such as a (frictionless) simple pendulum or a weight on an (ideal) spring. At time t the displacement x of such a simple harmonic oscillator from its equilibrium position (x = 0) is given by
x = A cos(ωt + ϕ)(1)
where A is the amplitude of the oscillation, ω the angular frequency and ϕ the phase constant. The expression inside the brackets, ωt + ϕ, is called the phase; it is a function of time, and its value determines the stage the oscillator has reached in its cycle of motion. The oscillator returns to the same position each time the phase increases by 2π. i Now, suppose that A = 5.00 cm, ω = 0.60 s−1 and ϕ = π, and that you are asked to calculate the displacement of the oscillator at t = 10 s. To answer this question you would first need to evaluate the phase when t = 10 s. This is given by
ωt + ϕ = 0.60 s−1 × 10 s + π = 9.144 (to two decimal places)
and then substitute this value into Equation 1 to find
x = 5.00 cm × cos(9.14) = − 4.94 cm i

Figure 1 Box representation of a function.
In this example, x is a function of the expression (ωt + ϕ), which is itself a function of t. For this reason x is said to be a function of a function of t, or a composite function of t.
In Subsection 2.2 we will see how to differentiate such expressions, but for the moment we concentrate on reviewing the concept of and notation for a function of a function.
The use of boxes to represent the action of functions is helpful here. Figure 1 shows, in this form, the three functions f (t) = 5t + 1, f (t) = t6, f (t) = sin t.
In each case the function converts an input value (the argument of the function) into an output value of the function. It is an inherent property of functions that a single output value corresponds to each valid input.
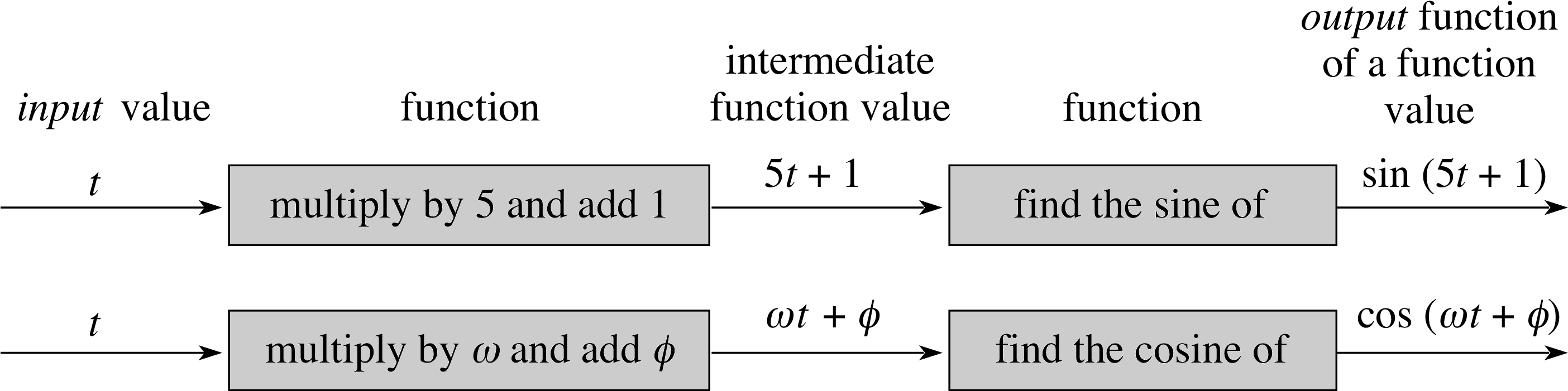
Figure 2 Composite functions.
For the function of a function we use two boxes in series. Figure 2 shows the action of the two composite functions sin(5t + 1) and cos(ωt + ϕ).
In each case the output from the first box is used as the input for the second box.
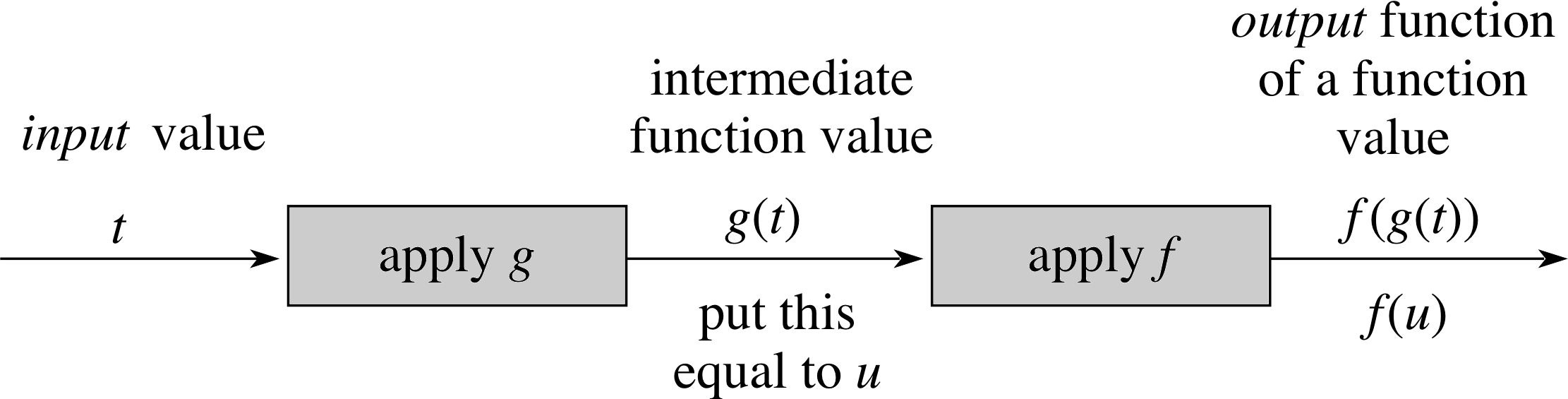
Figure 3 General composite function.
In general, we can consider a composite function f (g (t)) as depicted in Figure 3. f (g (t)) is read as ‘f of g of t’. The composite function can be made more user–friendly by writing u = g (t) so that the output is f (u). Hence, if we consider the composite function sin(5t + 1), we can write g (t) = 5t + 1 so that f (g (t)) = sin(g (t)) and we can denote g (t) by u so that f (u) = sin u where, in this case, u = 5t + 1. i
Question T1
Draw a box representation of the following functions:
(a) cos(3t − 4), (b) (t4 + 2)3.
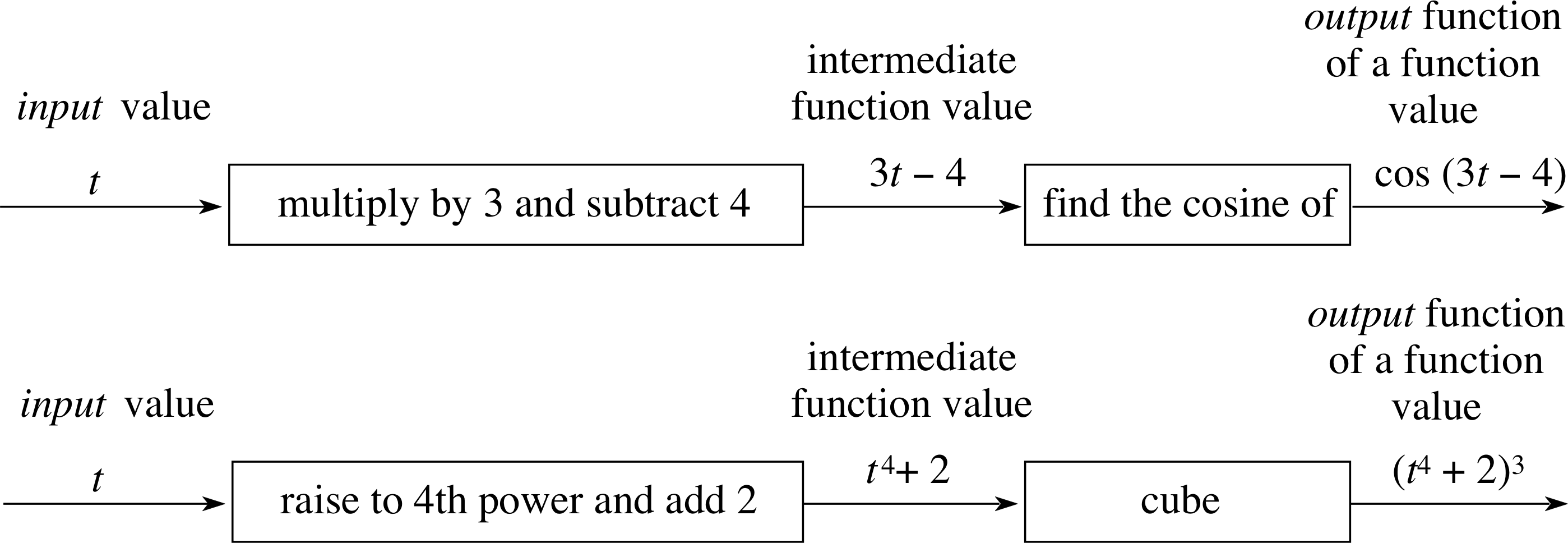
Figure 8 See Answer T1.
Answer T1
The box representations of the functions are shown in Figure 8.
There are two observations that you may find useful when trying to determine whether or not a function is a composite. First, decide if the function definition can be read naturally by using the word ‘of’. For example, in
h (x) = loge(x2) (x ≠ 0) i
the right–hand side can be read as ‘log to base e of (x squared)’, which helps to identify h (x) as a composite f (g (x)), i where
f (x) = loge x
andg (x) = x2
Second, think about how you would calculate function values on a calculator. For h (x) = loge(x2), you would proceed as follows:
first enter the value of x and square it, then find the natural logarithm loge of the result.
| Composite function | Read as ... | First ... | then ... |
|---|---|---|---|
| tan(3x) | ‘tan of 3x’ | find 3x | take tan (of the result) |
| loge(1/x) | ‘loge of 1/x’ | find 1/x | take loge (of the result) |
| esin x | ‘exp of sin x’ | find sin x | take exp (of the result) |
A function of a function always involves applying first one process, then another to the result of the first. Table 1 shows some examples of composite functions.
The following is a very important question. Make sure that you understand it before continuing.
Question T2
For each of the following functions, decide whether F (x) is a composite function. If F (x) is composite, express F in the form f (g (x)), by writing down explicit expressions for u = g (x) and f (u).
(a) F (x) = e2x
(b) F (x) = exsin x
(c) F (x) = loge(x3)
(d) F (x) = sin(x2 + 2x + 1)
(e) F (x) = sin2x (Remember that sin2x means (sin x)2)
(f) F (x) = sin3x
(g) F (x) = (cos x)0.5
Answer T2
(a) Composite; g (x) = u = 2x, f (u) = ex
(b) Not composite; F is a product
(c) Composite; the log of x cubed
u = g (x) = x3, f (u) = loge u
(d) Composite; u = g (x) = x2 + 2x + 1, f (u) = sin u
(e) Composite; the square of sin x
u = g (x) = sin x, f (u) = u2. (It is also a product.)
(f) Composite; u = g (x) = sin x, f (u) = u3 (It is also a product)
(g) Composite; u = g (x) = cos x, f (u) = u0.5
Comment Two points are worthy of comment to save you from possible errors. In general f (g (x)) ≠ g (f (x)). The order in which the functions are applied is important. i
This is easily illustrated by the following example. When f is the function ‘add 3’ and g is the function ‘square’ then g (f (x)) = (x + 3)2 but f (g (x)) = x2 + 3. The only value of x for which (x + 3)2 = x2 + 3 is x = −1, as you can verify, so it is generally true that f (g (x)) ≠ g (f (x)). There are some pairs of functions for which f (g (x)) = g (f (x)); for example if g is ‘cube’ and f is ‘square’ then f (g (x)) = (x3)2 = x6 and g (f (x)) = (x2)3 = x6, also. These are exceptions, however.
✦ Does f (g (x)) = g (f (x)) for the functions g (x) = 2x + 1, f (x) = 3x + 2?
✧ f (g (x)) = f (u) = 3u + 2 = 3 (2x + 1) + 2 = 6x + 3 + 2 = 6x + 5
g (f (x)) = g (u) = 2u + 1 = 2 (3x + 2) + 1 = 6x + 4 + 1 = 6x + 5
Hence f (g (x)) = g (f (x)) in this case.
Comment When dealing with a composite function f (g (x)), care must be taken to ensure that the function is only applied to admissible values of x, i.e. to values of x that are within the domain of the composite function.
Consider the following three examples.
- 1
-
g (x) = x2 + 1, f (x) = loge(x)
Here f (g (x)) = loge(x2 + 1). The logarithmic function loge(x) is defined only if x > 0, that is, only if the input to the function is positive.
However, in this case x2 + 1 > 0 for all x, so the composite function is well defined for all (real) values of x.
- 2
-
g (x) = x2 −1, f (x) = x1/2
Here f (g (x)) = (x2 −1)1/2.
Any input value x will lead to a value of g (x), but the input to the function f must be non-negative. Hence values of x that satisfy x ≥ 1 or x ≤ −1 are admissible, but values such that −1 < x < 1 are excluded from the domain of f (g (x)).
- 3
-
g (x) = sin(x), f (x) = loge(x)
Here f (g (x)) = loge(sin(x)).
The values of x for which sin(x) ≤ 0 are not admissible since they provide an unacceptable input for the loge function. i

Figure 4 The function loge(sin(x)).
The box diagram presents a useful check. In Figure 4 we show the function loge(sin(x)).
✦ What are the entry requirements for each box in Figure 4?
✧ The input to the first box can be any real number but the input to the second box must be positive. Therefore, only those values of x which lead to a positive value of sin x are acceptable and will allow a successful evaluation of loge(sin(x)).
Question T3
If f (x) = (x + 1)1/2 and g (x) = loge x what are the restrictions on x in order that we may define f (g (x)) and g (f (x))?
Answer T3
f (x) is defined only for x ≥ −1; g (x) is defined only for x > 0
f (g (x)) defined only for those x for which loge x > −1, i.e. x > 1/e
g (f (x)) always defined if x > −1, for then f (x) > 0
2.2 The chain rule
It is often necessary to differentiate a function of a function. This can sometimes be achieved by using basic differentiation techniques. Here, we will consider two special cases where this is possible, and then we will generalize the results to provide a powerful general rule (the chain rule) that can be used to differentiate any function of a function.
Using the product rule
Consider the function sin2x.
This can be regarded as a function of a function, for if we write g (x) = sin(x) and f (x) = x2
thenf (g (x)) = (sin x)2 = sin2x
However, it can also be regarded as a product since sin2x = sin x × sin x, so it can be differentiated by means of the product rule to give
$\dfrac{d}{dx}(\sin^2 x) = \dfrac{d}{dx}(\sin x\times\sin x) = (\cos x\times\sin x) + (\sin x\times\cos x)$
i.e.$\dfrac{d}{dx}(\sin^2 x) = 2\sin x\cos x$
Now, the derivative of a function does not depend on how we choose to ‘regard’ the function. So, in this particular case, we have been able to use the product rule to find the derivative of a function of a function.
Similarly, the function cos2x can be considered as a product, so
$\dfrac{d}{dx}(\cos^2 x) = \dfrac{d}{dx}(\cos x\times\cos x) = (-\sin x\times\cos x) + [(\cos x\times(-\sin x)] = -2\cos x\sin x$
and$\dfrac{d}{dx}(x^3+ 4)^2 = \dfrac{d}{dx}[(x^3+4)\times(x^3+4)] = 3x^2(x^3+ 4) + (x^3+ 4)\times 3x^2 = 2(x^2+4)\times 3x^2$
In each of these three cases the pattern is the same; we start with an expression of the form:
q (x) = (function of x)2
and we find that:
$\dfrac{dq}{dx}$ = 2 (function of x) × (derivative of function)
So, ifq (x) = [p (x)]2
thenq ′ (x) = 2p (x) × p ′ (x)
Question T4
Find the derivatives of the following composite functions:
(a) q (x) = (2x − 3)2, (b) q (x) = (3x4 + 1)2, (c) q (x) = (x + sin x)2.
Answer T4
(a) dq/dx = 2 (2x − 3) × 2 = 4 (2x − 3) (b) dq/dx = 2 (3x4 + 1) × 12x3 = 24x3(3x4 + 1) (c) dq/dx = 2 (x + sin x) × (1 + cos x)
Using the properties of the logarithmic function
The function loge(x3) can be regarded as a function of a function, but thanks to the special properties of logarithmic functions it can also be written as 3 loge x, and it then follows from the constant multiple rule that
$\dfrac{d}{dx}[\log_{\rm e}(x^3)] = 3 \times \dfrac{d}{dx}[\log_{\rm e}(x)] = 3 \times \dfrac1x = \dfrac3x$
So, once again, we have been able to use a technique of basic differentiation to find the derivative of a function of a function. In this case it would have been tempting to have taken the result that the derivative of loge(x) is 1/x and to have concluded that the derivative of loge x3 is 1/x3. But this is clearly wrong. In fact, the correct answer, $\dfrac3x = \dfrac{1}{x^3} \times 3x^2$ and the ‘correction factor’ of 3x2 is the derivative of the function x3.
✦ What is the derivative of loge(x5)?
✧ loge (x5) = 5 loge x and the derivative is 5/x. (Once again it is worth noticing that this answer may be written as 1 ×(5x4)x5 where the final factor (5x4) is the derivative of the ‘inner’ function x5).
We can summarize this result as follows:
ifq (x) = loge [p (x)]
then$q'(x) = \dfrac{1}{p(x)}\times p'(x)$
The general case – the chain rule
The two boxed results given above are special cases of a general rule for differentiating functions of functions.
That general rule is known as the chain rule.
The chain rule
Ifq (x) = f (g (x))
thenq ′ (x) = f ′ (g (x)) × g ′ (x)(2a)
Alternatively, if we write
u = g (x) and q = f (u)
then we can express the chain rule in the form
$\dfrac{dq}{dx} = \dfrac{dq}{du}\times\dfrac{du}{dx}$(2b)
The chain rule, expressed in either of these equivalent forms is also known as the function of a function rule.
You will also see the rule written in various ‘mixed’ notations such as $\dfrac{dq}{dx} = f'(u)\times\dfrac{du}{dx}$.
When we use the chain rule in the form of Equation 2b it is almost as if we are multiplying together two fractions, dq/du and du/dx, and cancelling the du terms to leave dq/dx. We most definitely are not doing this, but it must be admitted that the idea makes the rule easier to remember!
All of the results obtained earlier in this subsection using the product rule, or the special properties of logarithmic functions, can also be obtained from the chain rule. For example, if we look again at the function q (x) = sin2x but we now identify g (x) = u = sin x and q = u2, the chain rule tells us that
$q'(x) = \dfrac{dq}{du} \times \dfrac{du}{dx} = 2u\times\cos x = 2\sin x\cos x$
Similarly, in the second example, if q (x) = (x3 + 4)2 and we identify u = x3 + 4 and q = u2 then
$q'(x) = \dfrac{dq}{du} \times \dfrac{du}{dx} = 2u \times (3x^2) = 2(x^3+ 4) \times 3x^2= 6x^2(x^3+ 4)$
Also, if q (x) = loge(x3) and we identify u = x3 and q = loge u then
$q'(x) = \dfrac{dq}{du} \times \dfrac{du}{dx} = \dfrac1u \times (3x^2) = \dfrac{3x^2}{x^3} = \dfrac3x$
Moreover, the chain rule can be applied to many other composite functions that could not be differentiated using more elementary techniques. We can summarize the steps involved in applying the chain rule as follows:
To differentiate a function of a function q(x) = f (g (x)) using the chain rule:
1 Identify u = g (x) and q = f (u)
2 Differentiate to find $\dfrac{du}{dx}\quad\text{and}\quad\dfrac{dq}{du}$.
3 Multiply the last two expressions to find $\dfrac{dq}{dx}$
4 Rewrite u in terms of x and simplify. i
Here are some worked examples to show how this procedure works in practice.
Example 1
Find the derivative of esin x.
Solution
Letu = sin x and q = eu
then$\dfrac{du}{dx} = \cos x,~~~\dfrac{dq}{du} = {\rm e}^u$
so$\dfrac{dq}{dx} = \dfrac{dq}{du}\times\dfrac{du}{dx} = {\rm e}^u\times\cos x$
thus$\dfrac{dq}{dx} = {\rm e}^{\sin x} \times \cos x = {\rm e}^{\sin x}\,\cos x$
Example 2
Find the derivative of sin(x2 + 1).
Solution
Letu = x2 + 1 and q = sin u
then$\dfrac{du}{dx} = 2x,~~~\dfrac{dq}{du} = \cos u$
so$\dfrac{dq}{dx} = \cos u \times 2x$
thus$\dfrac{dq}{dx} = \cos(x^2+1)\times 2x = 2x\cos(x^2+1)$
Question T5
Using the chain rule, find the derivatives of the following functions:
(a) e2x, (b) exp(x2), (c) (x2 + 1)5, (d) sin(6x), (e) cos(3x), (f) loge(ex), (g) loge(1 + x2), (h) cos(ωt + ϕ).
Answer T5
(a) 2e2x
(b) 2x exp(x2)
(c) 5 (x2 + 1)4 × 2x = 10x (x2 + 1)4
(d) 6 cos(6x)
(e) −3 sin(3x)
(f) $\dfrac{1}{{\rm e}^x}\times{\rm e}^x= 1$
(g) 2x/(1 + x2)
(h) −ω sin(ωt + ϕ)
In practice you may have to deal with much nastier functions, and they may include functions of functions of functions or worse! This is where the chain rule really justifies its name since we can go on applying it as though adding links to a chain. For example, if q = f (g (h (x))) then we can let v = h (x), u = g (v) and q = f (u) and use the chain rule to obtain
$\dfrac{dq}{dx} = \dfrac{dq}{du} \times \dfrac{du}{dv} \times {dv}{dx} = f'(u)\times g'(v)\times h'(x)$
In practice, when faced with this kind of problem, it is often easier to just repeatedly apply the usual two–step form of the chain rule. Part (c) of the next question will give you the chance to try this for yourself.
✦ Differentiate the following composite functions, which all arise in physical problems, with respect to the indicated variable.
(a) The gaussian_integralGaussian function, $y = \dfrac{1}{\sigma\sqrt{2\pi\os}}{\rm exp}[-(x-m)^2/(\sigma^2)]$ with respect to x, where σ, m and π are constants.
(b) The Boltzmann factor, y = e−E/kT with respect to T, where E and k are constants.
(c) The plancks_functionPlanck function $y = \dfrac{2hc^2}{\lambda^5} \dfrac{1}{(e^{hc/\lambda kT} - 1)}$ with respect to λ, where h, c, k and T are all constants.
✧ (a) $\dfrac{dy}{dx} = \dfrac{1}{\sigma\sqrt{2\pi\os}}{\rm{exp}}[-(x-m)^2/(2\sigma^2)]\times \dfrac{d}{dx}\left[\dfrac{-(x-m)^2}{2\sigma^2}\right]$
(a) $\phantom{\dfrac{dy}{dx} }= \dfrac{1}{\sigma\sqrt{2\pi\os}}{\rm{exp}}[-(x-m)/(2\sigma^2)]\times\left[\dfrac{-2(x-m)}{2\sigma^2}\right]$
(a) $\phantom{\dfrac{dy}{dx} }= \dfrac{-(x-m)}{\sigma^3\sqrt{2\pi\os}}{\rm{exp}}[-(x-m)/(2\sigma^2)]$
(b) $\dfrac{dy}{dT} = {\rm e}^{-E/kT}\times\dfrac{d}{dT}\left(\dfrac{-E}{kT}\right) = \dfrac{E}{kT^2}{\rm e}^{-E/kT}$
(c) Using the product rule, we obtain:
$\dfrac{dy}{d\lambda} = \dfrac{d}{d\lambda}\left(\dfrac{2hc^2}{\lambda^5}\right)\times\dfrac{1}{({\rm e}^{hc/\lambda kT}-1)} + \dfrac{2hc^2}{\lambda^5}\times\dfrac{d}{d\lambda}\left[\dfrac{1}{({\rm e}^{hc/\lambda kT}-1)}\right]$
$\phantom{\dfrac{dy}{d\lambda} }= \dfrac{-10hc^2}{\lambda^6}\times\dfrac{1}{({\rm e}^{hc/\lambda kT}-1)} + \dfrac{2hc^2}{\lambda^5}\times\dfrac{d}{d\lambda}\left[({\rm e}^{hc/\lambda kT}-1)^{-1}\right]$
Now, applying the chain rule to the final term, we find:
$\dfrac{dy}{d\lambda} = \dfrac{-10hc^2}{\lambda^6}\times\dfrac{1}{({\rm e}^{hc/\lambda kT}-1)} + \dfrac{2hc^2}{\lambda^5}\times\left[-({\rm e}^{hc/\lambda kT}-1)^{-2}\right]\times\dfrac{d}{d\lambda}({\rm e}^{hc/\lambda kT}-1)$
Applying the chain rule again, to the new final term:
$\dfrac{dy}{d\lambda} = \dfrac{-10hc^2}{\lambda^6}\times\dfrac{1}{({\rm e}^{hc/\lambda kT}-1)} + \dfrac{2hc^2}{\lambda^5}\times\left[\dfrac{-1}{({\rm e}^{hc/\lambda kT}-1)^{2}}\right] \times{\rm e}^{hc/\lambda kT}\dfrac{d}{d\lambda}\left(\dfrac{hc}{\lambda kT}\right)$
$\phantom{\dfrac{dy}{d\lambda} }= \dfrac{-10hc^2}{\lambda^6}\times\dfrac{1}{({\rm e}^{hc/\lambda kT}-1)} + \dfrac{2hc^2}{\lambda^5}\times\left[\dfrac{-1}{({\rm e}^{hc/\lambda kT}-1)^{2}}\right] \times{\rm e}^{hc/\lambda kT}\left(\dfrac{-hc}{\lambda^2 kT}\right)$
$\phantom{\dfrac{dy}{d\lambda} }= \dfrac{2hc^2}{\lambda^6({\rm e}^{hc/\lambda kT}-1)}\left[\dfrac{hc}{\lambda kT}\dfrac{{\rm e}^{hc/\lambda kT}}{({\rm e}^{hc/\lambda kT}-1)}-5\right]$
2.3 Differentiating implicit functions
Functions are often specified explicitly in terms of equations or formulae such as f (x) = ax2 or θ (t) = ωt + ϕ, where the dependent variable is isolated on the left–hand side as the subject of the equation. However, it is also possible to specify a function implicitly by means of a formula that relates the dependent and independent variables, but does not isolate the dependent variable as the subject. For instance, the formula
$\sqrt{\dfrac ya}-x = 0$(3)
implicitly defines y as a function of x, even though it does not do so explicitly. In this particular case a little
algebraic manipulation soon leads to the explicit relationship y = ax2, but there are also cases where an implicitly defined function has no explicit representation at all. i In general, a dependent variable y will be defined implicitly as a function of an independent variable x if x and y are related by an equation of the form
F (x, y) = 0
where F (x, y) is a function of both x and y. A function y (x) defined in this way is called an implicit function.
The chain rule makes it possible to differentiate implicit functions by means of a technique known as implicit differentiation. As a simple example, suppose that y is defined as an implicit function of x by the equation
y3 = x5
Differentiating both sides of this equation (with respect to x) gives us
$\dfrac{d}{dx}(y^3) = 5x^4$
But, if we put u = y3 and use the chain rule $\dfrac{du}{dx} = \dfrac{du}{dy}\times \dfrac{dy}{dx}$ we find
$\dfrac{d}{dx}(y^3) = 3y^2\dfrac{dy}{dx}$
thus$3y^2\dfrac{dy}{dx} = 5x^4$ and hence $\dfrac{dy}{dx} = \dfrac{5x^4}{3y^2}$
We can now use the original relationship between x and y to express the right–hand side entirely in terms of x. In this case, y2 = x10/3
so$\dfrac{dy}{dx} = \dfrac53x^{2/3}$
In physics, implicit differentiation often arises in proofs and derivations, and frequently involves functions that have no exact explicit representation.
Question T6
Use the technique of implicit differentiation to find dy/dx if y5 = sin x. Leave your answer as an expression in both x and y.
Answer T6
$5y^4\dfrac{dy}{dx} = \cos x$, so $\dfrac{dy}{dx} = (\cos x)/5y^4$
2.4 Differentiating inverse functions
This subsection shows how the chain rule can be used to differentiate inverse functions such as the inverse trigonometric function arcsin x. However, before introducing the general method for differentiating such functions we consider a simple problem that illustrates a useful ancillary rule.
✦ If y = x1/2, write down dy/dx. i Then write down an expression for x in terms of y, and hence find dx/dy as a function of y. Finally, express dx/dy in terms of x.
✧ Using the rule for differentiating powers:
$\dfrac{dy}{dx} = \dfrac12x^{-1/2} = \dfrac{1}{2\sqrt{2}}$
$x = y^2$, so $\dfrac{dy}{dx} = 2y$.
In terms of x, $\dfrac{dx}{dy} = 2\sqrt{x}$
Notice that the expression for $\dfrac{dy}{dx}$ in the last question is the reciprocal of that for $\dfrac{dx}{dy}$. This is illustrative of a very useful general rule, the inversion rule:
the inversion rule: $\dfrac{dy}{dy} = 1\left/\left(\dfrac{dy}{dx}\right)\right.$(4) i
This looks as if we are finding the reciprocal of a fraction dy/dx. That is definitely not what we are doing, but it does make the rule easy to remember.
In a few cases the inversion rule is sufficiently powerful on its own to enable us to differentiate some inverse functions. For instance, using the inversion rule we can differentiate loge x, the inverse function of ex. If y = loge x, then x = ey and dx/dy = ey. Now, using this result together with the inversion rule,
$\dfrac{d\log_{\rm e}x}{dx} = \dfrac{dy}{dx} = 1\left/\left(\dfrac{dx}{dy}\right)\right. = \dfrac{1}{{\rm e}^y} = \dfrac1x$
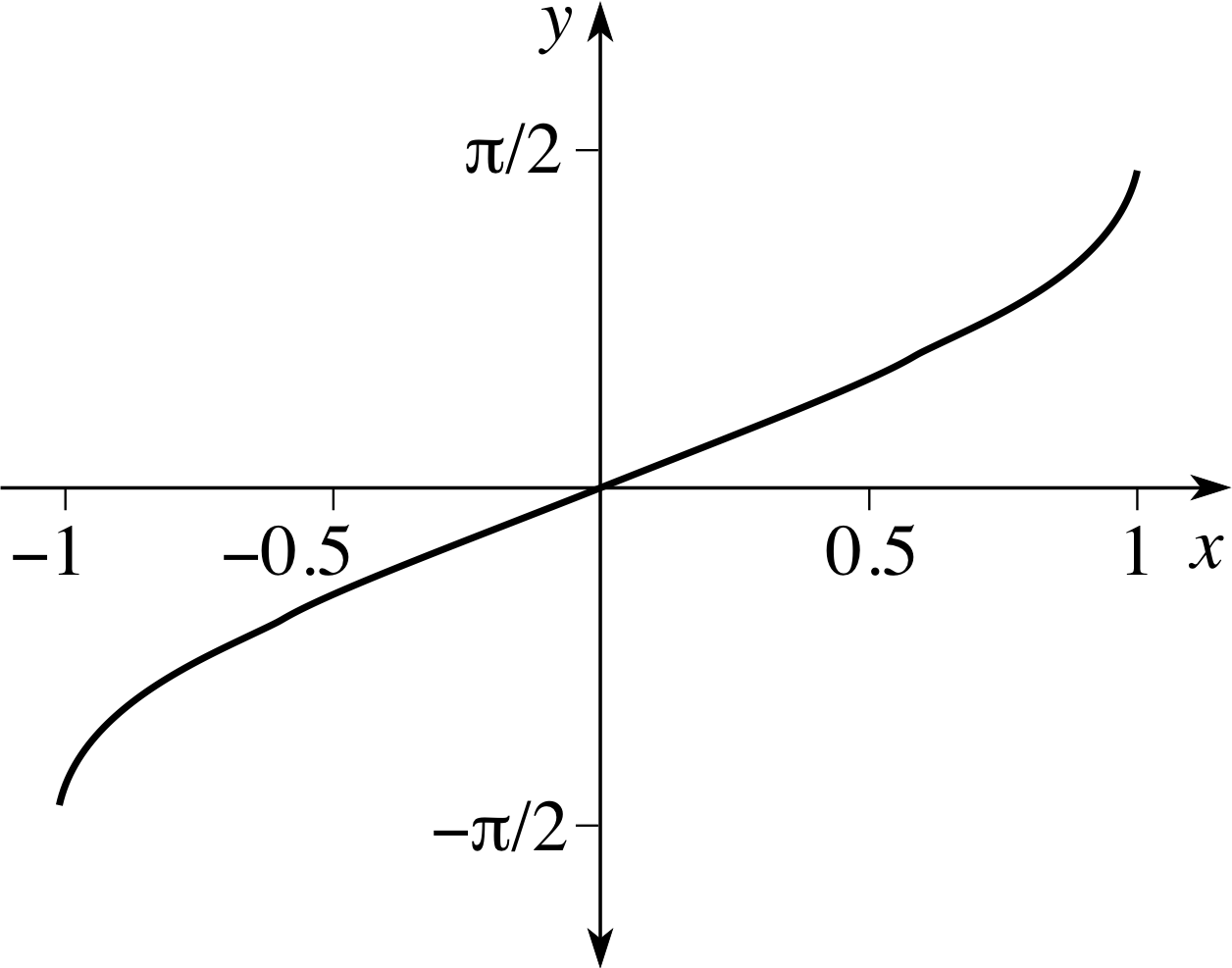
Figure 5 The graph of y = arcsin x.
Often, though, the inversion rule is not enough and we have to use the chain rule to differentiate inverse functions. As an example, consider the problem of finding the derivative dy/dx when
y = arcsin x i
The graph of this function is shown in Figure 5. Taking the sine of both sides gives us
sin y = sin(arcsin x) = x
Now differentiate both the right and left–hand sides of this equation with respect to x. The right–hand side is simply 1, but to differentiate the left–hand side we have to apply the chain rule.
If we let z = sin y, $\dfrac{dz}{dx} = \dfrac{dz}{dy}\times\dfrac{dy}{dx} = \cos y\times\dfrac{dy}{dx}$
Hence, the result of differentiating both sides of the equation sin y = x is
| f (x) | f ′ (x) |
|---|---|
| arcsin x | $\dfrac{1}{\sqrt{1-x^2}}$ |
| arccos x | $-\dfrac{1}{\sqrt{1-x^2}}$ |
| arctan x | $\dfrac{1}{1+x^2}$ |
| arcsec x | $\dfrac{1}{x\sqrt{x^2-1}}$ |
| arccosec x | $\dfrac{-1}{x\sqrt{x^2-1}}$ |
| arccot x | $\dfrac{-1}{1+x^2}$ |
$\cos y\times\dfrac{dy}{dx} = 1$
so that$\dfrac{dy}{dx} = \dfrac{1}{\cos y}$
All that remains is to express the right–hand side in terms of x. To do this note that cos2y = 1 − sin2y = 1 − x2, so $\cos y = \pm\sqrt{1-x^2}$.
Now, an examination of Figure 5 shows that the graph of y = arcsin x has a positive gradient throughout its domain of definition, so only positive values of cos y are admissible and hence we must use the positive square root when writing the final answer.
Thus$\dfrac{dy}{dx} = \dfrac{1}{\sqrt{1-x^2}}$
Table 2 records this result together with the derivatives of some other inverse functions.
Finally, let us look at a more complicated example that uses both the chain rule and the inversion rule.

Figure 6 Motion of an object released from an aircraft.
Example 3
Figure 6 shows the trajectory of a falling object released at point O from an aircraft moving horizontally with a constant speed u. The tangent at any point on the trajectory is inclined at an angle θ to the horizontal as shown, and this angle increases throughout the fall. What is the rate of change of θ with time?
Solution
Assuming that air resistance may be neglected, and using the coordinate system shown in Figure 6, in which x increases to the right and y increases downwards, the components of velocity in the horizontal and vertical direction will be
$\dfrac{dx}{dt} = u\quad\text{and}\quad\dfrac{dy}{dt} = gt$
where g is the magnitude of the acceleration due to gravity.
Now, you should be able to see from Figure 6 that tan θ = dy/dx. Bur using the chain rule and the inversion rule we find
$\dfrac{dy}{dx} = \dfrac{dy}{dt}\times\dfrac{dt}{dx} = \dfrac{dy}{dt}\left/\dfrac{dx}{dt}\right. = \dfrac{gt}{u}$
Thus,$\tan\theta = \dfrac{gt}{u}$
and from this we obtain $\theta = \arctan\left(\dfrac{gt}{u}\right)$
So, to find the rate of change of θ with t, i.e. $\dfrac{d\theta}{dt}$, we need to differentiate the inverse function $\arctan\left(\dfrac{gt}{u}\right)$.
To do this we first take the tangent of both sides:
$\tan\theta = \tan\left[\arctan\left(\dfrac{gt}{u}\right)\right] = \dfrac{gt}{u}$
and then differentiate with respect to t. The right–hand side gives g/u, so applying the chain rule to the left-hand
side we obtain
$\sec^2\theta \times \dfrac{d\theta}{dt} = \dfrac gu$
so$\dfrac{d\theta}{dt} = \dfrac{g}{u\sec^2\theta}$
Now we only need to express sec2θ in terms of t, and we can do this using a standard trigonometric identity i and the expression for tan θ we obtained earlier: $\sec^2\theta = 1 + \tan^2\theta = 1 + \dfrac{g^2t^2}{u^2}$
Thus$\dfrac{d\theta}{dt} = \dfrac gu\times \dfrac{1}{\left(1+\cfrac{g^2t^2}{u^2}\right)} = \dfrac{gu}{u^2+g^2t^2}$
A word of caution If you differentiate the function θ = arctan(t) then, as Table 2 indicates, you should find that $\dfrac{d\theta}{dt} = \dfrac{1}{1+t^2}$. It would be quite wrong to conclude from this that the process of differentiating $\theta = \arctan\left(\dfrac{gt}{u}\right)$ can be accomplished by simply replacing t on the right–hand side by gt/u. You can obtain the right answer by replacing t by gt/u on both sides, but the safest way is to go through the full method as we have just done.
Question T7
Find the derivative of each of the following functions:
(a) arcsin(x2), (b) arccos(x2 + 4), i (c) arctan(3 − x).
Answer T7
- (a)
-
y = arcsin(x2), so sin y = x2
so, differentiating both sides gives us
$\cos y\dfrac{dy}{dx} = 2x$
$\dfrac{dy}{dx} = \dfrac{2x}{\cos y} =\dfrac{2x}{\sqrt{1-\sin^2 y}} = \dfrac{2x}{\sqrt{1-x^4}}$
Note that we have taken the positive square root expression for cos y, as in the text, to ensure that dy/dx has the required sign.
- (b)
-
There are no (real) values of x for which arccos(x2 + 4) is meaningful. The function arccos u is only defined when its argument u is in the range −1 ≤ u ≤ 1. No x will produce an argument in this range. Moral: don’t just differentiate without thinking first!
- (c)
-
y = arctan(3 − x), tan y = 3 − x
therefore $\sec^2 y \dfrac{dy}{dx} = −1$
therefore$\dfrac{dy}{dx} = \dfrac{-1}{\sec^2 y} = \dfrac{-1}{1+\tan^2 y} = \dfrac{-1}{1+(3-x)^2} = \dfrac{-1}{10-6x+x^2}$
2.5 Differentiating parametric functions
It is sometimes useful to express two variables x and y each in terms of a third variable called a parameter. For example, in coordinate geometry i the equation that represents a circle of radius a, centred on the origin, is usually written in the form
x2 + y2 = a2
However, thanks to the trigonometric identity cos2θ + sin2θ = 1, the same circle can also be represented in terms of the parameter θ by the pair of equations
x = a cos θ(5a)
y = a sin θ(5b)
where θ may take any value in the range 0 to 2π.
Eliminating θ from Equations 5a and 5b (by squaring and adding the two equations) immediately yields the usual equation of the circle. Equations 5a and 5b are called the parametric equations of the circle. Functions defined in terms of parametric equations are called parametric functions. Whenever we describe the motion of a moving object by specifying its position coordinates x, y and z as functions of time, we are really writing down the parametric equations of the object’s pathway, with time t as the parameter.
Returning to the case of the circle x2 + y2 = a2, if we want to find dy/dx, the gradient of the tangent at a point on the circle, we can use the parametric equations and employ a variation of the chain rule, namely
$\dfrac{dy}{dx} = \dfrac{dy}{d\theta}\times\dfrac{d\theta}{dx} = \dfrac{dy}{d\theta}\left/\dfrac{dx}{d\theta}\right.$(6)
Now, $\dfrac{dy}{dx} = a\cos\theta$ and $\dfrac{dx}{d\theta} = -a\sin\theta$
so we obtain $\dfrac{dy}{dx} = \dfrac{a\cos\theta}{a\sin\theta} = -\cot\theta$
This is an example of parametric differentiation. i
Figure 7 Trajectory of a projectile.
Example 4
As illustrated in Figure 7, a projectile is fired into the air at an angle of 60° to the horizontal with a speed of u = 6 m s−1, so its initial horizontal velocity is ux = u cos(60°) = 3 m s−1, and its initial vertical velocity is uy = u sin(60°) = $3\sqrt{3\os}$ m s−1. What is the flight time for the projectile to reach the top of its trajectory (i.e. how long does it take to reach the O point at which the tangent to the trajectory is horizontal)?
Solution
If we neglect air resistance, and take upwards as the positive y–direction, the equations describing its trajectory are i
x = uxt and y = uyt − ½ gt2
where x and y are, respectively, the horizontal and vertical displacements from the point of projection at time t, and g is the magnitude of the acceleration due to gravity. The horizontal and vertical components of the velocity are given by
$\dfrac{dx}{dt} = u_x\quad\text{and}\quad\dfrac{dy}{dt} = u_y-gt$
At the top of the trajectory the tangent to the trajectory is horizontal, therefore $\dfrac{dy}{dt} = 0$ but, using the chain rule and the inversion rule
$\dfrac{dy}{dx} = \dfrac{dy}{dt}\times\dfrac{dt}{dx} = \dfrac{dy}{dt}\left/\dfrac{dx}{dt}\right. = \dfrac{u_y-gt}{u_x}$
so at the top of the trajectory $\dfrac{u_y-gt}{u_x}= 0$, i.e. $t = \dfrac{u_y}{g}$
Question T8
Find the derivative dy/dx for each of the following pairs of parametric equations:
(a) x = a cos θ, y = b sin θ, (b) x = at2; y = 2at, (c) x = ct, y = c/t.
Answer T8
(a) $\dfrac{dx}{d\theta} = -a\sin\theta, \dfrac{dy}{d\theta} = b\cos\theta$
so, $\dfrac{dy}{d\theta} = \dfrac{dy}{d\theta}\times\dfrac{d\theta}{dx} = \dfrac{dy}{d\theta}\left/\dfrac{dx}{d\theta}\right. = \dfrac{-b\cos\theta}{a\sin\theta} = \dfrac{-b}{a}\cot\theta$
(b) $\dfrac{dx}{dt} = 2at, \dfrac{dy}{dt} = 2a, \dfrac{dy}{dx} = \dfrac{2a}{2at} = \dfrac1t$
(c) $\dfrac{dx}{dt} = c, \dfrac{dy}{dt} = \dfrac{-c}{t^2}, \dfrac{dy}{dx} = \dfrac{-1}{t^2}$
3 Second and higher derivatives
3.1 The derivative of a derivative
In the same way that we can differentiate a function f (x) to obtain its derivative (or derived function) f ′ (x), so we can differentiate the function f ′ (x) to obtain its derivative which is denoted f ′′ (x). This is called the second derivative of f (x).
Hence iff (x) = 4x3 + 7x2 + 6x − 8 it follows that
f ′ (x) = 12x2 + 14x + 6
andf ′′ (x) = 24x + 14 i
If we write y = f (x) and denote its derivative (sometimes called its first derivative in this context) by dy/dx, then an alternative notation for the second derivative is $\dfrac{d^2y}{dx^2}$.i For example, if y = 4 sin(2x) + e3x, then the first derivative is
$\dfrac{dy}{dx} = 8\cos(2x) + 3{\rm e}^{3x}$
and the second derivative is
$\dfrac{dy}{dx}\left(\dfrac{dy}{dx}\right) = \dfrac{d^2y}{dx^2} = 8\times\left[-2\sin(2x)\right] + 3\times(3{\rm e}^{3x})$
i.e.$\dfrac{d^2y}{dx^2} = -16\sin(2x) + 9{\rm e}^{3x}$
Notice that the notation $\dfrac{d^2y}{dx^2}$ is a rather natural one since it suggests that the operation of differentiation has been repeated twice. Indeed, the symbol $\dfrac{d}{dx}$ is sometimes referred to as a differential operator since it conveys the instruction to differentiate whatever appears immediately to its right. Also notice the precise position of the superscript 2s in the second derivative symbol; it is the differential operator that is ‘squared’, not the independent variable y.
Some important physical quantities are often thought of as second derivatives. For instance, in kinematics – the study of motion – velocity is defined as the rate of change of position, so $v_x = \dfrac{dx}{dt}$ for example, but acceleration is defined as the rate of change of velocity, so $a_x = \dfrac{dv_x}{dt}$ and consequently we can regard acceleration as a second derivative, with $ax = \dfrac{d^2x}{dt^2}$. Indeed, derivatives with respect to time arise so often in physics that you will often see them denoted by a special notation that uses a dot to indicate differentiation; thus $v_x =\overset{.}{x}(t)\text{ and }a_x= \overset{..}{x}(t)$.
Question T9
Find f ′′ (x) for each of the following functions:
(a) f (x) = x6 − 2x2 + 7
(b) f (x) = ax + b, where a and b are constants
(c) f (x) = a sin x + b cos x
(d) f (x) = e3x
(e) f (x) = loge(x2 + 1)
(f) Rewrite your answers to parts (a) to (e) using $\dfrac{d^2y}{dx^2}$ notation.
Answer T9
(a) f ′ (x) = 6x5 − 4x, f ′′ (x) = 30x2 − 4
(b) f ′ (x) = a, f ′′ (x) = 0
(c) f ′ (x) = a cos x − b sin x, f ′′ (x) = −a sin x − b cos x (Note that f ′′ (x) = −f (x), in this example)
(d) f ′ (x) = 3 e3x f ′′ (x) = 9 e3x
(e) $f'(x) = \dfrac{2x}{x^2+1}, f''(x) = \dfrac{(x^2+1)\times 2-2x\times(2x)}{(x^2+1)^2} = \dfrac{2-2x^2}{(x^2+1)^2}$
(f) This is exactly the same as parts (a) to (e) except that f ′ (x) is replaced by dy/dx and f ′′ (x) is replaced by $\dfrac{dy}{dx}$ in each case.
Question T10
(a) If the x–coordinate of a moving object is given as a function of time by x (t) = pt + qt2, find expressions for the components of velocity and acceleration in the x–direction.
(b) Find $\overset{..}x(t)$ when x (t) = A sin(ωt) and when x (t) = B cos(ωt).
Answer T10
- (a)
-
v (t) = dx/dt = p + 2qt, i.e. $\overset{.}{x}(t)$ = p + 2qt; a (t) = d2x/dt2 = 2q, i.e. $\overset{..}{x}(t)$ = 2q
- (b)
-
When x (t) = Asin(ωt), $\overset{.}{x}(t)$ = Aω cos(ωt) and $\overset{..}{x}(t)$ = −Aω2 sin(ωt).
When x (t) = B cos(ωt), $\overset{.}{x}(t)$ = −Bω sin(ωt) and $\overset{..}{x}(t)$ = −Bω cos(ωt)
Note that both these expressions for x satisfy the equation $\overset{.}{x}(t)$ = −ω2x.
3.2 Higher derivatives
Assuming that the necessary derivatives exist, we can differentiate a function y = f (x) as many times as we want. The third derivative is the derivative of the second derivative, the fourth derivative is the derivative of the third derivative and so on. All these are known collectively as higher derivatives, and we define them by
$\dfrac{d^3y}{dx^3} = \dfrac{d}{dx}\left(\dfrac{d^2y}{dx^2}\right), \dfrac{d^4y}{dx^4} = \dfrac{d}{dx}\left(\dfrac{d^3y}{dx^3}\right)$, and so on.
In general, the nth derivative is defined by $\dfrac{d^ny}{dx^n} = \dfrac{d}{dx}\left(\dfrac{d^{n-1}y}{dx^{n-1}}\right)$(7) i
To be consistent with this notation we should write $\dfrac{dy}{dx}$ as $\dfrac{d^1y}{dx^1}$ but this is never done in practice.
In the alternative functional notation, derivatives higher than the third are usually denoted by lower case Roman numerals: f ′ (x), f ′′ (x), f ′′′ (x), f (iv)(x) ..., but the nth derivative is usually denoted f (n)(x). i
Example 5
Find the first three derivatives of $y=\dfrac{1}{x^3}$.
Solution
$\dfrac{dy}{dx} = \dfrac{-3}{x^4}$, $\dfrac{d^2y}{dx^2} = \dfrac{+12}{x^5}$, $\dfrac{d^3y}{dx^3} = \dfrac{-60}{x^6}$
✦ Find the first three derivatives of x n, where n ≥ 3. What happens if n = 2?
✧ $\dfrac{dy}{dx} = nx^{n-1}$
$\dfrac{d^2y}{dx^2} = n(n-1)x^{n-2}$
$\dfrac{d^3y}{dx^3} = n(n-1)(n-2)x^{n-3}$
If n = 2 the derivatives are 2x, 2, and 0.
Example 6
Find the first four derivatives of f (x) = 3x4 − 8x3 + 5x2 − 6.
Solution
f ′ (x) = 12x3 − 24x2 + 10x
f ′′ (x) = 36x2 − 48x + 10
f ′′′ (x) = 72x − 48
f (iv)(x) = 72 i
Example 7
Find the nth derivative of f (x) = e3x.
Solution
The first, second and third derivatives are:
f ′ (x) = 3e3x, f ′′ (x) = 3 × 3e3x = 32e3x, and f ′′′ (x) = 32 × 3e3x = 33e3x.
It is clear from these that in general, the nth derivative is given by
f (n)(x) = 3ne3x
Question T11
Find the first four derivatives and the nth derivative of the following functions:
(a) y = f (x) = 4 e5x
(b) y = 3x3
(c) y = A cos(2x) + B sin(2x) where A and B are constants.
(d) y = loge x where x ≠ 0
Answer T11
(a) $\dfrac{dy}{dx} = f'(x) = 20{\rm e}^{5x}, \dfrac{d^2y}{dx^2} = f''(x) = 100{\rm e}^{5x}$
(a) $\dfrac{d^3y}{dx^3} = f'''(x) = 500{\rm e}^{5x}, \dfrac{d^4y}{dx^4} = f^{({\rm iv})}(x) = 2500{\rm e}^{5x}$
(a) $\dfrac{d^ny}{dx^n} = f^{(n)}(x) = 4\times5^n\times{\rm e}^{5x}$
(b) $\dfrac{dy}{dx} = 9x^2, \dfrac{d^2y}{dx^2} = 18x, \dfrac{d^3y}{dx^3} = 18$
(b) $\dfrac{d^4y}{dx^4} = 0, \dfrac{d^ny}{dx^n} = 0$ for n ≥ 4
(c) $\dfrac{dy}{dx} = -2A\sin(2x) + 2B\cos(2x), \dfrac{d^2y}{dx^2} = -4A\cos(2x)-4B\sin(2x)$
(c) $\dfrac{d^3y}{dx^3} = 8A\sin(2x) - 8B\cos(2x), \dfrac{d^4y}{dx^4} = 16A\cos(2x)+16B\sin(2x)$
(c) Note that $\dfrac{d^2y}{dx^2} = -2^2y\quad\text{and that}\quad\dfrac{d^4y}{dx^4} = 2^4y$
(c) If n is even $\dfrac{d^ny}{dx^n} = (-1)^{n/2}(2)^ny$, if n is odd $\dfrac{d^ny}{dx^n} = (-1)^{(n-1)/2}(2)^{n-1}\dfrac{dy}{dx}$
(d) $\dfrac{dy}{dx} = \dfrac1x, \dfrac{d^2y}{dx^2} = \dfrac{-1}{x^2}, \dfrac{d^3y}{dx^3} = \dfrac{2}{x^3}$
(d) $\dfrac{d^4y}{dx^4} = \dfrac{-6}{x^2}, \dfrac{d^ny}{dx^n} = \dfrac{(-1)^{n-1}(n-1)(n-2)\dots 2}{x^n}$
3.3 Second derivatives of implicit and parametric functions
The techniques we have accumulated so far to obtain f ′ (x) from f (x) can, in most cases, be applied to f ′ (x) to obtain f ′′ (x) with no major difficulties. There are, however, two points which need great care. First is the fact that
$\dfrac{dx}{dy} = 1\left/\left(\dfrac{dy}{dx}\right)\right.$ is an exception
$\dfrac{d^2x}{dy^2}$ and $1\left/\left(\dfrac{d^2y}{dx^2}\right)\right.$ are not generally equal.
Consider, for example the relationship
$y = \dfrac1x$
Differentiating this expression twice we obtain
$\dfrac{dy}{dx} = -\dfrac{1}{x^2}$ and $\dfrac{d^2y}{dx^2} = +\dfrac{2}{x^3}$
Now, if $x = \dfrac1y$, $\dfrac{dx}{dy} = -\dfrac{1}{y^2}$ and $\dfrac{d^2x}{dy^2} = +\dfrac{2}{y^3}$
So, while it is true that $\dfrac{dx}{dy} = -\dfrac{1}{y^2} = -x^2 = 1\left/\left(\dfrac{dy}{dx}\right)\right.$
it is also the case that $\dfrac{d^2x}{dy^2} \ne 1\left/\left(\dfrac{d^2y}{dx^2}\right)\right.$ i
since$\dfrac{d^2x}{dy^2} = \dfrac{2}{y^3} = 2x^3$, whereas $1\left/\left(\dfrac{d^2y}{dx^2}\right)\right. = 1\left/\left(\dfrac{2}{x^3}\right)\right. = \dfrac{x^3}{2}$
We also need to take great care over parametric differentiation. We have seen that for the pair of equations
x = a cos θ and y = a sin θ
$\dfrac{dy}{dx} = \dfrac{dy}{d\theta}\times\dfrac{d\theta}{dx} = \dfrac{dy}{d\theta}\left/\dfrac{dx}{d\theta}\right. = \dfrac{a\cos\theta}{-a\sin\theta} = -\cot\theta$
But to obtain $\dfrac{d^2y}{dx^2}$ we need to determine $\dfrac{d^2y}{dx^2} = \dfrac{d}{dx}(-\cot\theta)$.
This can be done with the aid of the chain rule, either by writing z = −cot θ and using
$\dfrac{dz}{dx} = \dfrac{dz}{d\theta}\times\dfrac{d\theta}{dx}$
or more directly, by writing
$\dfrac{d}{dx}(-\cot\theta) = \dfrac{d}{d\theta}(-\cot\theta)\times\dfrac{d\theta}{dx}$
In either case we use the inversion rule to replace dθ/dx by the reciprocal of dx/dθ and hence obtain
$\dfrac{d^2y}{dx^2} = \dfrac{d}{d\theta}(-\cot\theta)\left/\dfrac{dx}{d\theta}\right. = \dfrac{+\cosec^2\theta}{-a\sin\theta} = -\dfrac1a\cosec^3\theta$
Example 8
If x = at2 and y = 2at, determine $\dfrac{d^2y}{dx^2}$
Solution
$\dfrac{dx}{dt} = 2at\quad\text{and}\quad\dfrac{dy}{dt} = 2a$
so$\dfrac{dy}{dx} = \dfrac{dy}{dt}\times\dfrac{dt}{dx} = \dfrac{dy}{dt}\left/\dfrac{dx}{dt}\right. = \dfrac{2a}{2at} = \dfrac1t$
hence$\dfrac{d^2y}{dx^2} = \dfrac{d}{dx}\left(\dfrac{dy}{dx}\right) = \dfrac{d}{dx}\left(\dfrac1t\right)$
using the chain rule, we find
$\dfrac{d^2y}{dx^2} = \dfrac{d}{dt}\left(\dfrac1t\right)\times\dfrac{dt}{dx} = -\dfrac{1}{t^2}\times\dfrac{dt}{dx}$
and using the inversion rule, we find
$\dfrac{d^2y}{dx^2} = -\dfrac{1}{t^2}\left/\dfrac{dx}{dt}\right. = -\dfrac{1}{t^2}\dfrac{1}{2at} = \dfrac{-1}{2at^3}$
It is worth observing that implicit differentiation provides an alternative way of dealing with this example. To adopt this approach start by noting that y2 = 4a2t2 = 4a × at2 = 4ax.
So implicit differentiation of this with respect to x gives us
$2y\dfrac{dy}{dx} = 4a$
A second implicit differentiation, in which $y\dfrac{dy}{dx}$ is treated as a product, gives
$2y\dfrac{d^2y}{dx^2} + 2y\dfrac{dy}{dx}\times\dfrac{dy}{dx} = 0$
so$2\times2at\times\dfrac{d^2y}{dx^2} + 2\dfrac1t\times\dfrac1t = 0$
i.e.$4at\dfrac{d^2y}{dx^2}+\dfrac{2}{t^2} = 0$
hence, as before $\dfrac{d^2y}{dx^2} = \dfrac{-2}{t^2}\times\dfrac{1}{4at} = \dfrac{-1}{2at^3}$
Question T12
Find $\dfrac{d^2y}{dx^2}$ for each of the following pairs of parametric equations:
(a) x = cos θ; y = sin θ, (b) x = a cos θ; y = b sin θ, (c) x = ct, y = c/t.
Answer T12
(You may wish to look back at Answer T8 for some of the results used in this answer.)
(a) $\dfrac{dx}{d\theta} = -\sin\theta, \dfrac{dy}{d\theta} = \cos\theta$, therefore
(a) $\dfrac{dy}{dx} = -\dfrac{\cos\theta}{\sin\theta} = -\cot\theta$
(a) $\dfrac{d^2y}{dx^2} = \dfrac{d}{d\theta}(-\cot\theta)/(-\sin\theta) = \cosec\theta/(-\sin\theta) = \dfrac{1}{\sin^2\theta}\times\left(-\dfrac{1}{\sin\theta}\right) = -\dfrac{1}{\sin^3\theta} = -\cosec^3\theta$
(b) $\dfrac{dx}{d\theta} = -a\sin\theta, \dfrac{dy}{d\theta} = b\cos\theta$, therefore
(b) $\dfrac{dy}{dx} = \dfrac{-b\cos\theta}{a\sin\theta} = \dfrac{-b}{a}\cot\theta$
(b) $\dfrac{d^2y}{dx^2} = \left.\dfrac{d}{d\theta}\left(-\dfrac ba\cot\theta\right)\right/(-a\sin\theta) = \dfrac ba\cosec\theta\left/(-a\sin\theta)\right. = \dfrac ba\dfrac{1}{\sin^2\theta}\times\left(-\dfrac{1}{a\sin\theta}\right) = -\dfrac{b}{a^2\sin^3\theta} = \dfrac{-b}{a^2}\cosec^3\theta$
(c) $\dfrac{dx}{dt} = c, \dfrac{dy}{dt} = -\dfrac{c}{t^2}$ therefore $\dfrac{dy}{dx} = -\dfrac{1}{t^2}$
(c) $\dfrac{d^2y}{dx^2} = \left.\dfrac{d}{dt}\left(-\dfrac{1}{t^2}\right)\right/c = +\dfrac{2}{ct^3}$
4 A further example
We will end by tackling a set of related electrical problems – all of which involve a circuit containing an inductor and capacitor (an LC circuit). Working through each of the steps in these problems for yourself will help you to review what you have learned in this module.
4.1 An example from electrical circuits
In a series LCR circuit the charge q (t) on the capacitor at time t > 0 satisfies the equation
$L\dfrac{d^2q}{dt^2} + \dfrac1Cq = 0$(8) i
where L and C are constants, known as the inductance and capacitance, respectively.
The first problem we consider is that of showing that
$q(t) = A\cos\left(\dfrac{t}{\sqrt{LC\os}}\right) + B\sin\left(\dfrac{t}{\sqrt{LC\os}}\right)$(9)
satisfies Equation 8 for arbitrary values of the constants A and B.
To do this we need to deduce an expression for d2q/dt2 from Equation 9 and substitute it into Equation 8. The first step is to find dq/dt from Equation 9. Now, q (t) is the sum of two terms, each of which is a function of a function. Taking just the second term and calling it y we have $y = B\sin\left(\dfrac{t}{\sqrt{LC\os}}\right)$ and if we put $u = \dfrac{t}{\sqrt{LC\os}}$
we find y = B sin u. From this, we see
$\dfrac{du}{dt} = \dfrac{1}{\sqrt{LC\os}}\quad\text{and}\quad\dfrac{dy}{du} = \cos u$
if we then use the chain rule, we find
$\dfrac{dy}{dt} = \dfrac{dy}{du}\times\dfrac{du}{dy} = B\cos u\times\dfrac{1}{\sqrt{LC\os}} = \dfrac{B}{\sqrt{LC\os}}\cos u = \dfrac{B}{\sqrt{LC\os}}\cos\left(\dfrac{1}{\sqrt{LC\os}}\right)$
✦ If we now repeat the process for the first term in Equation 9, what is its derivative?
✧ If we put $y = A\cos u$, where $u=\dfrac{t}{\sqrt{LC\os}}$, it follows from the chain rule that:
$\dfrac{dy}{dt}=\dfrac{dy}{du}\times\dfrac{du}{dt} = -A\sin \times\dfrac{1}{\sqrt{LC\os}} = -\dfrac{A}{\sqrt{LC\os}}\sin\left(\dfrac{t}{\sqrt{LC\os}}\right)$
✦ From the above discussion, what is dq/dt from Equation 9?
✧ $\dfrac{dq}{dt} = \dfrac{-A}{\sqrt{LC\os}}\sin\left(\dfrac{t}{\sqrt{LC\os}}\right) + \dfrac{B}{\sqrt{LC\os}}\cos\left(\dfrac{t}{\sqrt{LC\os}}\right)$
So we now know dq/dt. We now need to find $\dfrac{d^2q}{dt}$.
✦ What is the derivative of $y = \dfrac{-A}{\sqrt{LC\os}}\sin\left(\dfrac{t}{\sqrt{LC\os}}\right)$?
✧ Putting $y = \dfrac{-A}{\sqrt{LC\os}}\sin u$, where $u=\dfrac{t}{\sqrt{LC\os}}$, we find using the chain rule:
$\dfrac{dy}{dt}=\dfrac{dy}{du}\times\dfrac{du}{dt} = \dfrac{-A}{\sqrt{LC\os}}\cos u\times\dfrac{1}{\sqrt{LC\os}} = \dfrac{-A}{LC}\cos\left(\dfrac{t}{\sqrt{LC\os}}\right)$
✦What is the derivative of $y = \dfrac{B}{\sqrt{LC\os}}\cos\left(\dfrac{t}{\sqrt{LC\os}}\right)$?
✧ Using the same method we find:
$\dfrac{dy}{dt} = \dfrac{-B}{LC}\sin\left(\dfrac{t}{\sqrt{LC\os}}\right)$
✦ What is $\dfrac{d^2q}{dt}$?
✧ $\dfrac{d^2q}{dt^2} = \dfrac{-A}{LC}\cos\left(\dfrac{t}{\sqrt{LC\os}}\right)-\dfrac{B}{LC}\sin\left(\dfrac{t}{\sqrt{LC\os}}\right)$
Therefore, if we substitute this result (and Equation 9) into Equation 8,
$q(t) = A\cos\left(\dfrac{t}{\sqrt{LC\os}}\right) + B\sin\left(\dfrac{t}{\sqrt{LC\os}}\right)$(Eqn 9)
$L\dfrac{d^2q}{dt^2} + \dfrac1Cq = 0$(Eqn 8)
we find
$L\dfrac{d^2q}{dt^2} + \dfrac1Cq = L\left[\dfrac{-A}{LC}\cos\left(\dfrac{t}{\sqrt{LC\os}}\right) - \dfrac{B}{LC}\sin\left(\dfrac{t}{\sqrt{LC\os}}\right)\right] + \dfrac1C\left[A\cos\left(\dfrac{t}{\sqrt{LC\os}}\right) + B\sin\left(\dfrac{t}{\sqrt{LC\os}}\right)\right]$
$\phantom{L\dfrac{d^2q}{dt^2} + \dfrac1Cq }= \dfrac{-A}{C}\cos\left(\dfrac{t}{\sqrt{LC\os}}\right) - \dfrac BC\sin\left(\dfrac{t}{\sqrt{LC\os}}\right) + \dfrac AC\cos\left(\dfrac{t}{\sqrt{LC\os}}\right) + \dfrac BC\sin\left(\dfrac{t}{\sqrt{LC\os}}\right) = 0$
Thus the given expression (Equation 9) does satisfy the equation $L\dfrac{d^2q}{dt^2} + \dfrac1Cq = 0$, irrespective of the values of A and B.
Now we can consider a related problem. Given that Equation 9 provides a solution to Equation 8 for any values of A and B, what are the specific choices of A and B needed to ensure that at time t = 0 the charge on the capacitor has the value q0 and the rate of flow of charge in the circuit is zero? In other words, what choices of A and B ensure that
q (0) = q0 and $\dfrac{dq}{dt}(0) = 0$
To satisfy the second of these conditions we require
$-\dfrac{A}{\sqrt{LC\os}}\sin(0) + \dfrac{B}{\sqrt{LC\os}}\cos(0) = 0$
i.e.$\dfrac{B}{\sqrt{LC\os}} = 0$
We must therefore choose B = 0, so $q = A\cos\left(\dfrac{t}{\sqrt{LC\os}}\right)$
To satisfy the additional condition that q (0) = q0 we require
A cos(0) = q0 i.e. A = q0
so the solution satisfying both the given initial conditions is $q(t) = q_0\cos\left(\dfrac{t}{\sqrt{LC\os}}\right)$
5 Closing items
5.1 Module summary
- 1
-
A function of a function produces an output by applying first one process, then another to an input. In general f (g (x)) ≠ g (f (x)). The order in which the functions are applied is important.
- 2
-
When dealing with a composite function f (g (x)), care must be taken to ensure that the function is only applied to admissible values of x, i.e. to values of x that are within the domain of the composite function.
- 3
-
A function of a function can be differentiated using the Subsection 2.2chain rule, which states that if u = g (x) and q = f (u), then
$\dfrac{dq}{dx} = \dfrac{dq}{du} \times \dfrac{du}{dx} = f'(u) \times g'(x)$(Eqn 2)
- 4
-
An implicit function is a function that is defined by means of a relation such as F (x, y) = 0.
- 5
-
The chain rule makes it possible to differentiate implicit functions by the technique of implicit differentiation.
e.g. ify3 = x5 then $3y^2\dfrac{dy}{dx} = 5x^4$, so $\dfrac{dy}{dx} = \dfrac{5x^4}{3y^2} = \dfrac53x^{2/3}$
- 6
-
According to the Subsection 2.4inversion rule
$\dfrac{dy}{dx} = 1\left/\left(\dfrac{dx}{dy}\right)\right.$(Eqn 4)
- 7
-
Subsection 2.4Inverse functions can be differentiated by applying the inversion rule and the chain rule.
- 8$\vphantom{\dfrac{dy}{dx}}$
-
If x and y are both defined in terms of a parameter θ, then the derivative $\dfrac{dy}{dx}$ may be determined by the technique of parametric differentiation
$\dfrac{dy}{dx} = \dfrac{dy}{d\theta}\times\dfrac{d\theta}{dx} = \dfrac{dy}{d\theta}\left/\dfrac{dx}{d\theta}\right.$(Eqn 6)
- 9
-
If y = f (x), then the Subsection 3.2nth derivative of y is defined by
$\dfrac{d^ny}{dx^n} = \dfrac{d}{dx}\left(\dfrac{d^{n-1}y}{dx^{n-1}}\right)$(Eqn 7)
The first four derivatives of f (x) may also be represented by f ′ (x), f ′′ (x), f ′′′ (x), f (iv)(x), and the nth derivative by f (n)(x).
5.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Identify a function of a function.
- A3
-
Use the chain rule to find the derivative of a function of a function.
- A4
-
Find the derivative of an inverse function.
- A5
-
Find the derivative of a function defined parametrically or implicitly.
- A6
-
Find the second derivative of a function of a function.
- A7
-
Find the second derivative of an inverse function.
- A8
-
Find the second derivative of a function defined parametrically or implicitly.
- A9
-
Find the nth derivative of a function.
- A10
-
Recognize and use the different notations for higher derivatives.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
5.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions, each of which tests one or more of the Achievements.
Question E1 (A2)
Which of the following is a function of a function? If it is necessary to restrict the values of x, then say so.
(a) F (x) = sin(3x) (b) F (x) = loge(1 − x2) (c) y3 = x
Answer E1
(a) Function of a function; read as ‘sin of 3x’.
(b) Function of a function; read as ‘log of (1 − x2)’. We require that
1 − x2 > 0 so that x2 < 1, i.e. −1 < x < 1.
(c) If it is rewritten as y = x1/3; it is a function, read as cube root of x so not a function of a function.
(Reread Subsection 2.1 if you had difficulty with this question.)
Question E2 (A2 and A3)
Find the derivative of:
(i) each of the functions in Question E1
(ii) f (g (x)) and g (f (x)), where u = g (x) = x3 + 2 and f (x) = 5x + 4.
Answer E2
(i) (a) 3 cos(3x) (b) $\dfrac{-2x}{1-x^2}$ (c) $\dfrac{1}{3x^{2/3}}$
(ii) f (g (x)) = 5 (x3 + 2) + 4 = 5u + 4
$\dfrac{du}{dx} = 3x^2$, f ′ (u) = 5, therefore using the chain rule, the derivative $\dfrac{df}{du}$ is
5 × 3x2 = 15x2
g (f (x)) = (5x + 4)3 + 2, therefore the derivative is
$\dfrac{dg}{dx} = 3(5x + 4)^2 × 5 = 15(5x + 4)^2$
(Reread Subsection 2.2 if you had difficulty with this question.)
Question E3 (A2, A3 and A4)
Find the derivative dy/dx of y = arccos(3x − 2).
Answer E3
cos y = 3x − 2, $-\sin y\dfrac{dy}{dx} = 3$
so$\dfrac{dy}{dx} = \dfrac{-3}{\sin y} = \dfrac{-3}{\sqrt{1-\cos^2 y}} = \dfrac{-3}{\sqrt{\smash[b]{1-(3x-2)^2}}} = \dfrac{-3}{\sqrt{-9x^2+12x-3}}$
Note that we have expressed sin y in terms of a positive square root to ensure that dy/dx is negative, as is required of the arccos function.
(Reread Subsection 2.3 if you had difficulty with this question.)
Question E4 (A2, A3 and A5)
Find the derivative dy/dx when $x = 2 + 3\sqrt{2\os}t$ and $y = 1 + 3\sqrt{2\os}t-4.9t^2$
Answer E4
$\dfrac{dx}{dt} = 3\sqrt{2\os}$, $\dfrac{dy}{dt} = 3\sqrt{2\os} - 9.8t$
therefore$\dfrac{dy}{dx} = \dfrac{3\sqrt{2\os} - 9.8t}{3\sqrt{2\os}}$
(Reread Subsection 2.4 if you had difficulty with this question.)
Question E5 (A2 to A8)
Find the second derivatives of the functions in Questions E1, E3 and E4. If it is necessary to restrict the values of x, then say so.
Answer E5
y = sin(3x), $\dfrac{dy}{dx} = 3\cos(3x)$
therefore$\dfrac{d^2y}{dx^2} = −9\sin(3x)$ and 1 ≥ 3x ≥ −1
y = loge(1 − x2), $\dfrac{dy}{dx} = \dfrac{-2x}{1-x^2}$
therefore$\dfrac{d^2y}{dx^2} = \dfrac{(1-x^2)(-2) - (-2x)(-2x)}{(1-x^2)^2} = \dfrac{-2(1-x^2+ 2x^2)}{(1-x^2)^2} = \dfrac{-2(1+ x^2)}{(1-x^2)^2}$ and (1 − x2) ≥ 0 so | x | ≤ 1
$y = x^{1/3}$, $\dfrac{dy}{dx} = \dfrac13x^{-2/3}$
therefore$\dfrac{d^2y}{dx^2} = \dfrac{-2}{9x^{5/3}}$
cos y = 3x − 2, $\dfrac{dy}{dx} = \dfrac{-3}{(-9x^2+12x-3)^{1/2}} = f(g(x))$ and 1 ≥ 3x + 2 ≥ −1
where g (x) = u = −9x2 + 12x − 3, $f(u) = \dfrac{-3}{u^{1/2}}$
$\dfrac{du}{dx} = -18x+12$, $f'(u) = \dfrac{3}{2u^{3/2}}$
$\dfrac{d^2y}{dx^2} = \dfrac{3}{2(-9x^2+12x-3)^{3/2}}\times(-18x+12) = \dfrac{-27x+18}{(9x^2+12x-3)^{3/2}}$
$x = 2 + 3\sqrt{2\os}t$, $y = 1 + 3\sqrt{2\os}t - 4.9t^2$
$\dfrac{dy}{dx} = \dfrac{3\sqrt{2\os} - 9.8t}{3\sqrt{2\os}}$, $\dfrac{d^2y}{dx^2} = \left.\dfrac{d}{dt}\left(\dfrac{3\sqrt{2\os} - 9.8t}{3\sqrt{2\os}}\right)\right/3\sqrt{2\os} = \dfrac{-9.8}{3\sqrt{2\os}}\times\dfrac{1}{3\sqrt{2\os}} = \dfrac{-9.8}{18}$
(Reread Subsections 3.1 and 3.3 if you had difficulty with this question.)
Question E6 (A6 and A9)
Find the first five derivatives and the nth derivative of the following functions:
(a) f (x) = x6 − 2x4 − x3 + 6x (b) f (x) = x ex
Answer E6
(a) f ′ (x) = 6x5 − 8x3 − 3x2 + 6
f ′′ (x) = 30x4 − 24x2 − 6x
f ′′′ (x) = 120x3 − 48x − 6
f (iv)(x) = 360x2 − 48
f (v)(x) = 720 x
f (n)(x) = 0, 3n > 6
(b) f ′ (x) = x ex + 1ex = (x + 1) ex
f ′′ (x) = (x + 1) ex + 1ex = (x + 2) ex
f ′′′ (x) = (x + 2) ex + 1ex = (x + 3) ex
f (iv)(x) = (x + 4) ex
f (v)(x) = (x + 5) ex
f (n)(x) = (x + n) ex, for all n.
(Reread Subsection 3.2 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so. If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 5Closing items.