MATH 4.6: Hyperbolic functions and differentiation |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction

Figure 1 A heavy cable suspended between two pylons.
Figure 1 shows a situation that you have certainly seen countless times, a heavy cable suspended between two pylons. We all know that the cable sags in the middle, but is there a mathematical function which describes the shape of this curve? It turns out that there is such a function, and it is particularly relevant to this module because it is one of the so–called hyperbolic functions.
The hyperbolic functions: sinh(x), cosh(x), tanh(x), sech(x), arctanh(x) and so on, which have many important applications in mathematics, physics and engineering, correspond to the familiar trigonometric functions: sin(x), cos(x), tan(x), sec(x), arctan(x), etc.
In Section 2 of this module we begin by defining the basic hyperbolic functions sinh(x), cosh(x) and tanh(x), and show how the infinite series for these functions are related to those of the corresponding trigonometric functions. We also show how these two sets of functions are related through the introduction of the complex number, i (where i2 = −1). Section 2 concludes with a description of how the first few terms of the infinite series for the basic hyperbolic functions can be used to provide approximations to the functions for small values of their arguments.
In Section 3 we go on to consider more advanced aspects of hyperbolic functions, including the reciprocal and inverse functions. Section 4 lists some useful identities which are analogous to those listed elsewhere in FLAP for the trigonometric functions. We end, in Section 5, by finding derivatives of some of the hyperbolic functions, which also provides practice in using differentiation techniques. The final example given in Section 5 leads to the function that describes the shape of a heavy cable suspended between two pylons (illustrated in Figure 1).
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 6.1Module summary and the Subsection 6.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 6.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
Define sinh(x), cosh(x) and tanh(x) in terms of the exponential function, exp(x) = ex.
Answer F1
$\sinh(x) = \dfrac{{\rm e}^x-{\rm e}^{-x}}{2}$, $\cosh(x) = \dfrac{{\rm e}^x+{\rm e}^{-x}}{2}$ and $\tanh(x) = \dfrac{{\rm e}^x-{\rm e}^{-x}}{{\rm e}^x+{\rm e}^{-x}}$
Question F2
First define sech(x) and coth(x), and then use your answer to the previous question to show that
sech(x) = sec(ix) and coth(x) = icot(ix)
Answer F2
$\sech(x) = \dfrac{1}{\cosh(x)}$, and $\coth(x) = \dfrac{1}{\tanh(x)}$ provided x ≠ 0.
Using the expression for cosh(x) given in Answer F1 we have
$\sech(x) = \dfrac{1}{\cosh(x)} = \dfrac{2}{{\rm e}^x+{\rm e}^{-x}}$
However$\sec(x) = \dfrac{1}{\cos(x)} = \dfrac{2}{{\rm e}^{ix}+{\rm e}^{-ix}}$ and therefore
$\sec(ix) = \dfrac{2}{{\rm e}^{-x}+{\rm e}^{x}} = \sech(x)$
In a similar way, using the expressions for sinh(x) and cosh(x) given in Answer F1 we have
$\coth(x) = \dfrac{\cosh(x)}{\sinh(x)} = \dfrac{{\rm e}^{x}+{\rm e}^{-x}}{{\rm e}^{x}-{\rm e}^{-x}}$
However$\cot(x) = \dfrac{\cos(x)}{\sin(x)} = i\dfrac{{\rm e}^{ix}+{\rm e}^{-ix}}{{\rm e}^{ix}-{\rm e}^{-ix}}$
and therefore
$i\cot(ix) = i\times i\dfrac{{\rm e}^{-x}+{\rm e}^{x}}{{\rm e}^{-x}-{\rm e}^{x}} = \dfrac{{\rm e}^{x}+{\rm e}^{-x}}{{\rm e}^{x}-{\rm e}^{-x}} = \coth(x)$
Question F3
Show that
$\arccoth(x) = \dfrac12\loge\left(\dfrac{x+1}{x-1}\right)$ for | x | > 1
Use the fact that $\loge(1-x) = -\left(x + \dfrac{x^2}{2} + \dfrac{x^3}{3} + \dots\right)$ for | x | < 1 to find a series for arccoth(1/s) valid for | s | < 1, and then use this series to estimate the value of arccoth(10).
Use the logarithmic form for arccoth(x) given above, and your calculator, to check your estimate for arccoth(10).
Answer F3
Let y = arccoth(x) then
$x = \coth(y) = \dfrac{\cosh(y)}{\sinh(y)} = \dfrac{{\rm e}^{y}+{\rm e}^{-y}}{{\rm e}^{y}-{\rm e}^{-y}}$
which can be rearranged as follows:
xey − xe−y = ey + e−y
ey(x − 1) = ey(x + 1)
${\rm e}^{2y} = \left(\dfrac{x+1}{x-1}\right)$
Taking the logarithm of both sides gives us
$2y = \loge\left(\dfrac{x+1}{x-1}\right)$
and therefore $\arccoth(x) = y = \dfrac12\loge\left(\dfrac{x+1}{x-1}\right)$
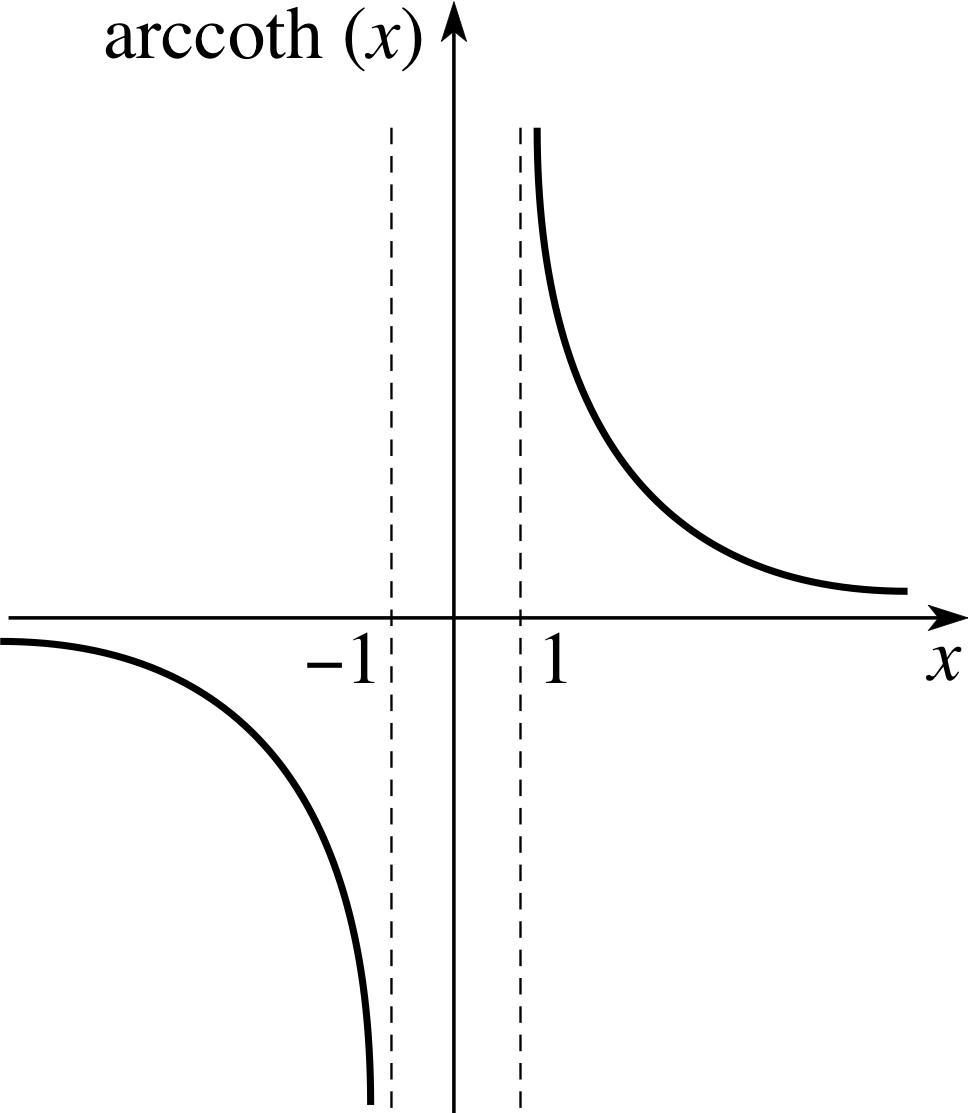
Figure 14 Graph of arccoth(x).
The condition | x | > 1 is necessary so that the argument of the logarithmic function is positive (and this is consistent with Figure 14).
$\begin{align} \arccoth(1/s) & = \dfrac12\loge\left(\dfrac{1/s+1}{1/s-1}\right) = \loge\left(\dfrac{1+s}{1-s}\right)\\ & = \dfrac12\left[\loge(1+s) - \loge(1-s)\right]\\ & = \dfrac12\left[\left(s-\dfrac{s^2}{2}+\dfrac{s^3}{3}-\dfrac{s^4}{4}+\dots\right) + \left(s+\dfrac{s^2}{2}+\dfrac{s^3}{3}+\dfrac{s^4}{4}+\dots\right)\right]\\ & = s + \dfrac{s^3}{3}+\dfrac{s^5}{5}+\dots\end{align}$
which is valid for | s | < 1 (since the series for loge(1 − s) and loge(1 + s) are valid for | s | < 1).
From this series (putting s = 0.1) we have
$\arccoth(10) \approx 0.1 + \dfrac{(0.1)^3}{3} + \dfrac{(0.1)^5}{5} \approx 0.100\,335\,33 $
From my calculator
$\arccoth(10) = \dfrac12\log{\rm e}\left(\dfrac{10+1}{10-1}\right) = \loge(11/9) \approx 0.100\,335\,35$
Question F4
Use the logarithmic expression for arccoth(x) (see Question F3) to find $\dfrac{d}{dx}\arccoth(x)$.
Answer F4
$\dfrac{d}{dx}\arccoth(x) = \dfrac{d}{dx}\left[\dfrac12\loge\left(\dfrac{x+1}{x-1}\right)\right] = \dfrac12\dfrac{d}{dx}\left[\loge(x+1)-\loge(x-1)\right] = \dfrac12\left(\dfrac{1}{x+1}-\dfrac{1}{x-1}\right) = \dfrac{1}{1-x^2}$
1.3 Ready to study?
Study comment To begin the study of this module you need to be familiar with the following: the definition of a function and the general formula for the solution of a quadratic equation; also the exponential function, ex, including its taylor_expansion_or_seriesTaylor series expansion about x = 0 and the main features of its graph (the function ex is often written as exp(x)), plus the trigonometric functions, including their graphs, series, identities, reciprocal and inverse functions. You will also need to have some skill at differentiation (including the quotient_rule_of_differentiationquotient rule and chain rule), and have some familiarity with complex numbers (including productmultiplication and sumaddition of such numbers, and the use of Euler’s formula eiθ = cos θ + i sin θ). It would also be helpful, though not essential, if you have met odd_functionodd and even_functioneven functions, and factorials. If you are unfamiliar with any of these terms, refer to the Glossary, which will indicate where they are developed in FLAP. The following questions will help you to establish whether you need to review some of the above topics before embarking on this module. i
Question R1
(a) Write down the taylor_expansion_or_series_for_fx_near_x_0Taylor expansion of ex about x = 0.
(b) Write down the solutions of the quadratic equation x2 − ax + 1 = 0 where a ≥ 2. Hence write down the solutions of the equation e2w − aew + 1 = 0.
Answer R1
(a) $\displaystyle {\rm e}^x = \sum_{n=0}^\infty\dfrac{x^n}{n!} = 1 + \dfrac{x}{1!} +\dfrac{x^2}{2!} +\dfrac{x^3}{3!} + \dots$
(b) Using the general formula for the solution of a quadratic equation we have $x = \dfrac{a \pm \sqrt{a^2-4}}{2}$ and since a ≥ 2 we see that both roots will be real. The solutions of the equation e2w − aew + 1 = 0 are
$w = \loge(a\pm\sqrt{a^2-4)}-\loge2$
Consult taylor_expansion_or_series_for_fx_near_x_0Taylor expansion in the Glossary for further information.
Question R2
Use your calculator to find the values of:
(a) arcsin(1/3) and $\dfrac{1}{\sin(1/3)}$, (b) sin[sin(1/3)] and sin2(1/3). i
Answer R2
(a) arcsin(1/3) ≈ 0.3398 and $\dfrac{1}{\sin(1/3)} \approx 3.06$
Notice that these results are not the same. Whereas arcsin(x) is the inverse of the sine function, $\dfrac{1}{\sin(x)}$ is the reciprocal of the sine function.
(b) sin[sin(1/3)] ≈ 0.321 and sin2(1/3) ≈ 0.107
Notice again that these results are not the same. This is because the expression sin[sin(x)] means ‘take the sine of x and then take the sine of the result’. By contrast, sin2(x) means sin(x) × sin(x), i.e. the square of sin(x).
Consult trigonometric functions in the Glossary for further information.
Question R3
If s (x) and c (x) are defined by:
$s(x) = \dfrac{{\rm e}^{ix}-{\rm e}^{-ix}}{2i}\quad\text{and}\quad c(x) = \dfrac{{\rm e}^{ix}+{\rm e}^{-ix}}{2}$
show that:
(a) s (x) × s (x) + c (x) × c (x) = 1
(b) Use Euler’s formula to express s (x) and c (x) in more familiar form.
Answer R3
(a) We have
$s(x) \times s(x) = \left(\dfrac{{\rm e}^{ix}-{\rm e}^{-ix}}{2i}\right)^2 = -\dfrac14\left({\rm e}^{2ix}-2{\rm e}^{-2ix}\right)$
and$c(x) \times c(x) = \left(\dfrac{{\rm e}^{ix}+{\rm e}^{-ix}}{2}\right)^2 = \dfrac14\left({\rm e}^{2ix}+2{\rm e}^{-2ix}\right)$
Adding these two results gives
s (x) × s (x) + c (x) × c (x) = 1
(b) From Euler’s formula eix = cos(x) +i sin(x)
we have
$s(x) = \dfrac{{\rm e}^{ix}-{\rm e}^{-ix}}{2i} = \dfrac{\cos(x)+i\sin(x)-[\cos(x)-i\sin(x)]}{2i} = \sin(x)$
and
$c(x) = \dfrac{{\rm e}^{ix}+{\rm e}^{-ix}}{2} = \dfrac{\cos(x)+i\sin(x)+[\cos(x)-i\sin(x)]}{2} = \cos(x)$
Consult Euler’s formula in the Glossary for further information.
Question R4
Express $\dfrac{d}{dx}\left(\dfrac{u(x)}{v(x)}\right)$ and $\dfrac{d}{dx}g\left(f(x)\right)$ in terms of derivatives of u, v, g and f.
Answer R4
$\dfrac{d}{dx}\left(\dfrac{u(x)}{v{x}}\right) = \dfrac{1}{v(x)}\dfrac{du(x)}{dx} - \dfrac{u(x)}{v(x)^2}\dfrac{dv(x)}{dx} = \dfrac{v(x)\dfrac{du(x)}{dx}-u(x)\dfrac{dv(x)}{dx}}{v(x)^2}$
and$\dfrac{d}{dx}g\left(f(x)\right) = \dfrac{dg}{df}\times\dfrac{df}{dx}$
Consult quotient_rule_of_differentiationquotient rule and chain rule in the Glossary for further information.
2 Basic hyperbolic functions
2.1 Defining sinh, cosh and tanh
It follows from Euler’s formula (see Question R3) that the trigonometric functions sine and cosine can be expressed in terms of the exponential function as
$\sin(x) = \dfrac{{\rm e}^{ix}-{\rm e}^{-ix}}{2i}$(1)
and$\sin(x) = \dfrac{{\rm e}^{ix}+{\rm e}^{-ix}}{2}$(2)
Since analogous combinations of ex and e−x occur frequently in mathematics and physics, it is useful to define the hyperbolic functions, sinh(x) and cosh(x), i by
$\sinh(x) = \dfrac{{\rm e}^x-{\rm e}^{-x}}{2}$(3)
$\cosh(x) = \dfrac{{\rm e}^x+{\rm e}^{-x}}{2}$(4)
These functions are given their particular names because they have much in common with the corresponding trigonometric functions, but we leave a discussion of this until later.
✦ Write down (without using your calculator) the values of sinh(0) and cosh(0).
✧ Since e0 = 1 we have sinh(0) = 0 and cosh(0) = 1.
Question T1
Use the basic definitions of cosh(x) and sinh(x) in terms of exponentials to show that
(a) sinh(x) is an odd function while cosh(x) is an even function i
(b) ex = cosh(x) + sinh(x)
(c) cosh2(x) − sinh2(x) = 1 i
Answer T1
(a) $\sinh(-x) = \dfrac{{\rm e}^{-x}-{\rm e}^x}{2} = -\dfrac{{\rm e}^{x}-{\rm e}^{-x}}{2} = -\sinh(x)$, therefore it is an odd_functionodd function
and $\cosh(-x) = \dfrac{{\rm e}^{-x}+{\rm e}^x}{2} =\cosh(x)$, therefore it is an even_functioneven function.
(b) Adding the expressions for sinh(x) and cosh(x)
$\sinh(x) + \cosh(x) = \dfrac{{\rm e}^{x}-{\rm e}^{-x}}{2} + \dfrac{{\rm e}^{x}+{\rm e}^{-x}}{2} = {\rm e}^{x}$
(c) $\cosh^2(x) - \sinh^2(x)= \left(\dfrac{{\rm e}^{x}-{\rm e}^{-x}}{2}\right)^2 - \left(\dfrac{{\rm e}^{x}+{\rm e}^{-x}}{2}\right)^2 = \dfrac14\left({\rm e}^{2x}+2+{\rm e}^{-2x}\right) - \dfrac14\left({\rm e}^{2x}-2+{\rm e}^{-2x}\right) = 1$
It is also convenient to define a third hyperbolic function, tanh(x), by
$\tanh(x) = \dfrac{\sinh(x)}{\cosh(x)}$(5)
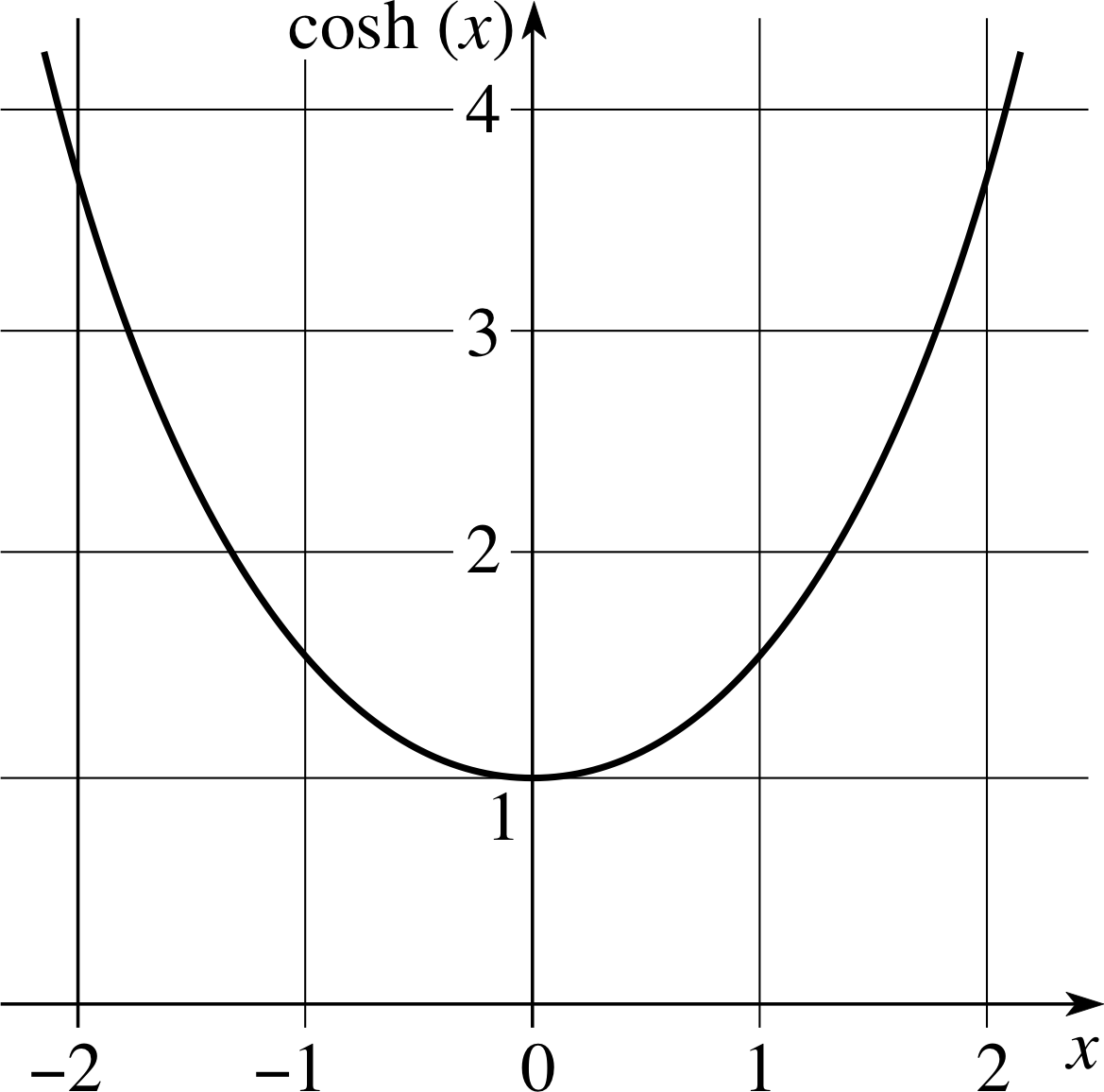
Figure 3 Graph of cosh(x).
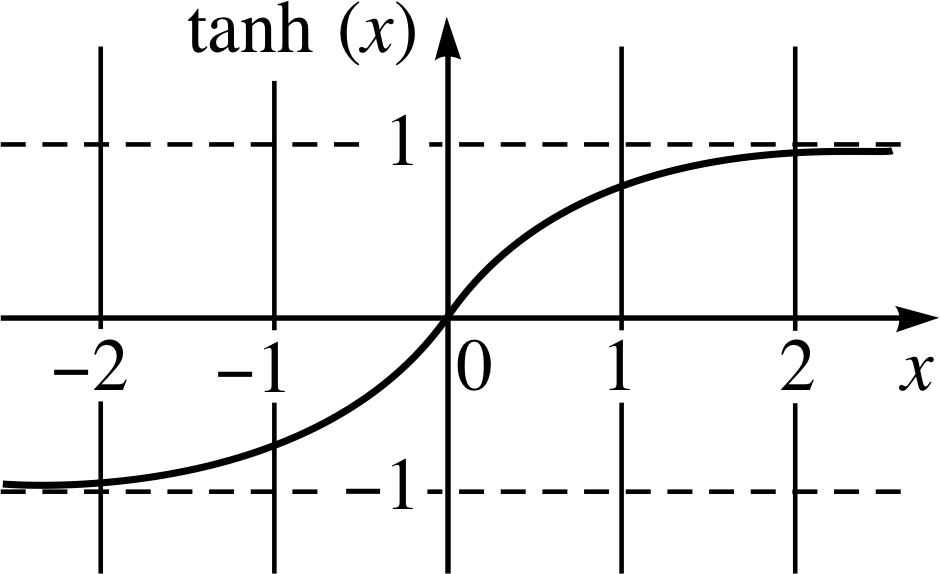
Figure 4 Graph of tanh(x).
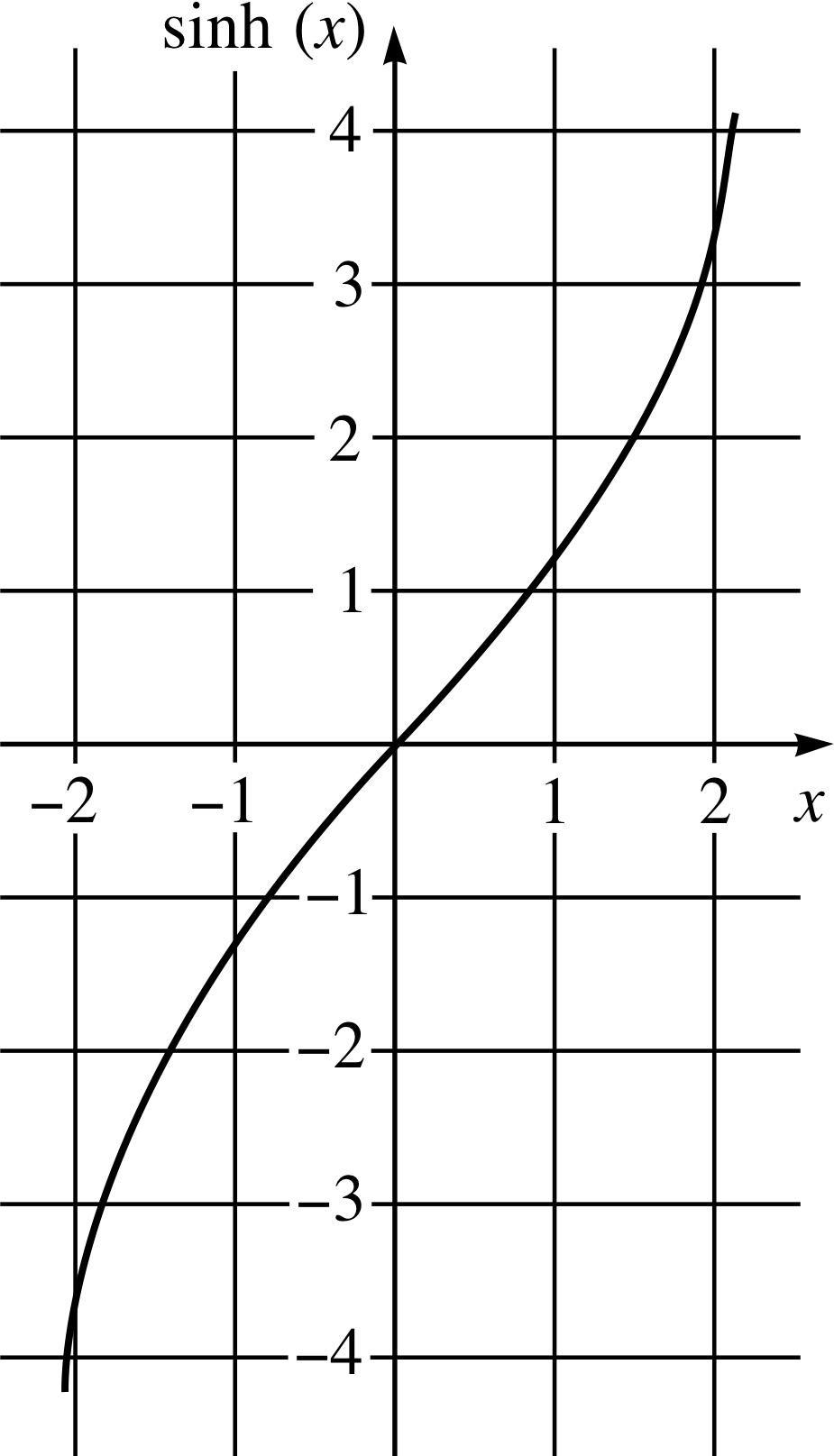
Figure 2 Graph of sinh(x).
✦ What is the value of tanh(0)?
✧ tanh(0) = 0 since (as we saw before) sinh(0) = 0 and cosh(0) = 1.
The graphs of these three basic hyperbolic functions are given in Figures 2 to 4. Notice in Figure 3 that cosh(x) ≥ 1. In Figures 2 and 3 we see that sinh(x) and cosh(x) are very close in value when x is large and positive, but sinh(x) < cosh(x) for other values of x. From Figure 4 we see that tanh(x) is approximately 1 when x is large and positive, and approximately −1 when x is large and negative, and that −1 < tanh(x) < 1.
Why are they called hyperbolic functions? To answer this question, we define variables x and y by
x = a cosh(s)(6)
y = b sinh(s)(7)
Note The equations for x and y in terms of s are known as parametric equations since s is a parameter which specifies a point on a curve (in this case, a hyperbola).
Then use the result from part c of Question T1
cosh2(x) − sinh2(x) = 1
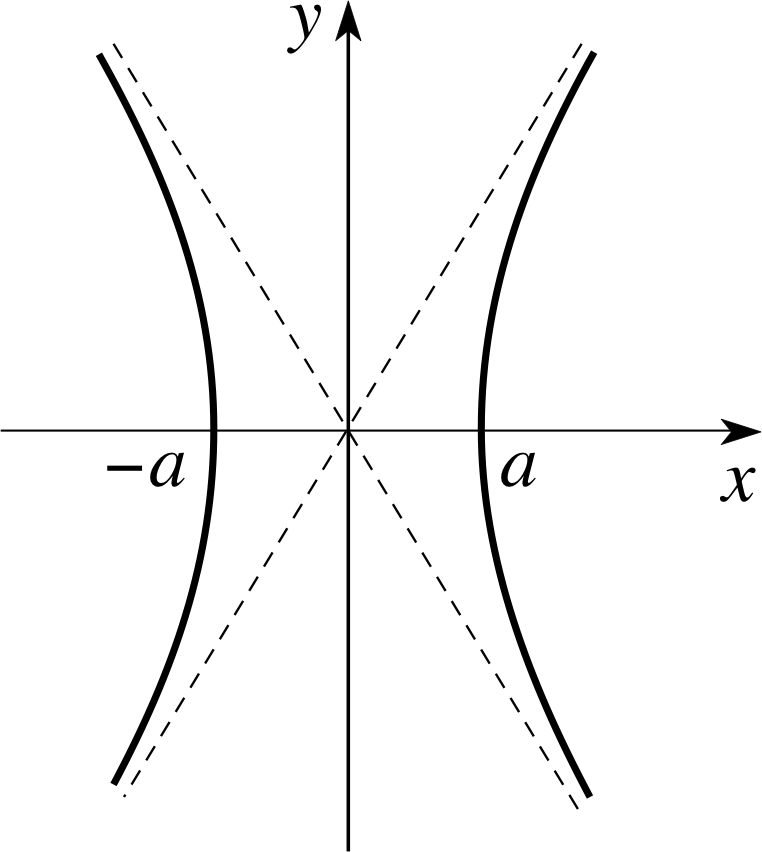
Figure 5 The hyperbola corresponding to x2/a2 − y2/b2 = 1.
to obtain
$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} = \cosh(s) - \sinh(s) = 1$(8)
which is the equation for a hyperbola, as shown in Figure 5. Thus Equations 6 and 7 are the parametric equations of a hyperbola, and this is the reason why sinh and cosh are known as hyperbolic functions.
As we shall see, there are many other functions (such as tanh) which can be defined in terms of sinh and cosh and these are all collectively known as hyperbolic functions.
Notice that, unlike the corresponding trigonometric functions, the sinh, cosh and tanh functions are not periodic. Moreover, sinh(x) and cosh(x) may take very large values (unlike sin(x) and cos(x)).
✦ Use the exponential function on your calculator to find sinh(1), cosh(1) and tanh(1). From these results calculate cosh2(1) − sinh2(1).
✧ $\sinh(1) = \dfrac{{\rm e} - {\rm e}^{-1}}{2} \approx \dfrac{2.718\,28 - 0.367\,88}{2} \approx 1.175$
$\cosh(1) = \dfrac{{\rm e} + {\rm e}^{-1}}{2} \approx \dfrac{2.718\,28 + 0.367\,88}{2} \approx 1.543$
$\tanh(1) = \dfrac{\sinh(1)}{\cosh(1)} \approx \dfrac{1.175}{1.543} \approx 0.762$
and
$\cosh^2(1) - \sinh^2(1) = (1.543)^2 - (1.175)^2 \approx 1.000\,22$
Note A more accurate result for this calculation (and also for the calculation of tanh(1)) could be obtained by retaining as many decimal places as possible in the intermediate steps. In fact, from Question T1(c) we know that the result for cosh2(1) − sinh2(1) should be exactly 1.
Question T2
The speed of waves in shallow water is given by the following equation
$v^2 = A\lambda\tanh\left(\dfrac{6.3d}{\lambda}\right)$
where λ is the wavelength and d is the depth of the water. Find the speed, v when d = 6 m, λ = 18.9 m and
A = 1.8 m s−2.
Answer T2
$v= \sqrt{A\lambda\tanh\left(\dfrac{6.3d}{\lambda}\right)} = \sqrt{(1.8\,{\rm m\,s^{-2}})\times 18.9\,{\rm m}\times\tanh\left(\dfrac{6.3\times6\,{\rm m}}{18.9\,{\rm m}}\right)} \approx 5.73\,{\rm m\,s^{-1}}$
2.2 Series for sinh, cosh and tanh
So far we have defined the three basic hyperbolic functions in terms of the exponential function, ex, which in turn can be defined in terms of an infinite series:
$\displaystyle {\mathrm e}^x = \sum_{n=0}^\infty\dfrac{x^n}{n!} = 1 + \dfrac{x}{1!} +\dfrac{x^2}{2!} +\dfrac{x^3}{3!} + \dots$(9) i
Replacing x with −x this equation gives us
$\displaystyle {\mathrm e}^{-x} = \sum_{n=0}^\infty\dfrac{(-x)^n}{n!} = 1 - \dfrac{x}{1!} +\dfrac{x^2}{2!} - \dfrac{x^3}{3!} + \dots$(10)
and hence Equation 3,
$\sinh(x) = \dfrac{{\rm e}^x-{\rm e}^{-x}}{2}$(Eqn 3)
gives
$\displaystyle \sinh(x) = \sum_{n=0}^\infty\dfrac{x^{2n+1}}{(2n+1)!} = \dfrac{x}{1!} +\dfrac{x^3}{3!} +\dfrac{x^5}{5!} +\dfrac{x^7}{7!} + \dfrac{x^9}{9!} + \dots$(11)
Comparing Equation 11 with the series for sin(x)
$\displaystyle \sin(x) = \sum_{n=0}^\infty\dfrac{(-1)^nx^{2n+1}}{(2n+1)!} = \dfrac{x}{1!} -\dfrac{x^3}{3!} +\dfrac{x^5}{5!} -\dfrac{x^7}{7!} + \dfrac{x^9}{9!} - \dots$(12)
we see that both series contain only odd powers (they are both odd functions) and the only difference is that the signs do not alternate for the sinh series. Likewise, from Equation 4,
$\cosh(x) = \dfrac{{\rm e}^x+{\rm e}^{-x}}{2}$(Eqn 4)
we find that the series for cosh(x) consists of the even terms in the series for ex; that is
$\displaystyle \cosh(x) = \sum_{n=0}^\infty\dfrac{x^{2n}}{(2n)!} = 1 + \dfrac{x^2}{2!} + \dfrac{x^4}{4!} + \dfrac{x^6}{6!} + \dfrac{x^8}{8!} + \dots$(13)
and comparing this with the series for cos(x)
$\displaystyle \cos(x) = \sum_{n=0}^\infty\dfrac{(-1)^nx^{2n}}{(2n)!} = 1 - \dfrac{x^2}{2!} +\dfrac{x^4}{4!} - \dfrac{x^6}{6!} +\dfrac{x^8}{8!} - \dots$(14)
we again see that they both contain even powers (both are even functions) and the only difference is that the signs do not alternate for the cosh function. There is a similar relationship between tan(x) and tanh(x) since it can be shown that
$\tanh(x) = x - \dfrac{x^3}{3} + \dfrac{2x^5}{15} - \dfrac{17x^7}{315} + \dots$(15) i
$\tan(x) = x + \dfrac{x^3}{3} + \dfrac{2x^5}{15} + \dfrac{17x^7}{315} + \dots$(16)
We can now appreciate the motivation for giving the hyperbolic functions their names; in each case the ‘h’ is added to give the ‘hyperbolic’ version of the related trigonometric function.
You are probably familiar with the many trigonometric functions that can be defined in terms of the sine and cosine functions, and, as you might expect, a large number of hyperbolic functions can be similarly defined in terms of sinh and cosh(as we will see in Section 3).
✦ Write down and simplify the Taylor expansions about x = 0 for
(a) sinh(x) + sin(x), and (b) cosh(x) − cos(x).
✧ (a) Using Equation 11,
$\displaystyle \sinh(x) = \sum_{n=0}^\infty\dfrac{x^{2n+1}}{(2n+1)!} = \dfrac{x}{1!} + \dfrac{x^3}{3!} + \dfrac{x^5}{5!} + \dfrac{x^7}{7!} + \dfrac{x^9}{9!} + \dots$(Eqn 11)
and Equation 12,
$\displaystyle \sin(x) = \sum_{n=0}^\infty\dfrac{(-1)^nx^{2n+1}}{(2n+1)!} = \dfrac{x}{1!} - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + \dfrac{x^9}{9!} + \dots$(Eqn 12)
we have
$\begin{align} \sinh(x) + \sin(x) & = \dfrac{x}{1!} + \dfrac{x^3}{3!} + \dfrac{x^5}{5!} + \dfrac{x^7}{7!} + \dfrac{x^9}{9!} + \dots + \left[\dfrac{x}{1!} - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + \dfrac{x^9}{9!} + \dots\right]\\ & = 2\left[\dfrac{x}{1!} + \dfrac{x^5}{5!} + \dfrac{x^9}{9!} + \dots\right] = 2\sum_{n=0}^\infty\dfrac{x^{4n+1}}{(4n+1)!}\end{align}$
(b) Similarly from Equation 13,
$\displaystyle \cosh(x) = \sum_{n=0}^\infty\dfrac{x^{2n}}{(2n)!} = 1 + \dfrac{x^2}{2!} + \dfrac{x^4}{4!} + \dfrac{x^6}{6!} + \dfrac{x^8}{8!} + \dots$(Eqn 13)
and Equation 14,
$\displaystyle \cos(x) = \sum_{n=0}^\infty\dfrac{(-1)^{2n}x^{2n}}{(2n)!} = 1 - \dfrac{x^2}{2!} + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + \dfrac{x^8}{8!} + \dots$(Eqn 14)
we have
$\begin{align} \cosh(x) - \cos(x) & = 1 + \dfrac{x^2}{2!} + \dfrac{x^4}{4!} + \dfrac{x^6}{6!} + \dfrac{x^8}{8!} + \dots - \left[1 - \dfrac{x^2}{2!} + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + \dfrac{x^8}{8!} - \dots\right]\\ & = 2\left[\dfrac{x^2}{2!} + \dfrac{x^6}{6!} + \dfrac{x^{10}}{10!} + \dots\right] = 2\sum_{n=0}^\infty\dfrac{x^{4n}}{(4n+2)!}\end{align}$
Question T3
Use the series for sinh(x) and cosh(x) to show that
$\dfrac{d}{dx}\sinh(x) = \cosh(x)$(17)
$\dfrac{d}{dx}\cosh(x) = \sinh(x)$(18)
Answer T3
$\displaystyle \dfrac{d}{dx}\sinh(x) = \sum_{n=0}^\infty\dfrac{1}{(2n+1)!}\dfrac{d}{dx}x^{2n+1} = \sum_{n=0}^\infty\dfrac{1}{(2n+1)!}(2n+1)x^{2n} = \sum_{n=0}^\infty\dfrac{1}{(2n)!}x^{2n} = \cosh(x)$
Also $\displaystyle \dfrac{d}{dx}\cosh(x) = \sum_{n=0}^\infty\dfrac{1}{(2n)!}\dfrac{d}{dx}x^{2n} = \sum_{n=0}^\infty\dfrac{1}{(2n)!}(2n)x^{2n-1} = \sum_{n=0}^\infty\dfrac{1}{(2n-1)!}x^{2n-1}$
and since there is no n = 0 term in this series, it is convenient to change the summation variable by setting m = n − 1. At the lower limit n = 1 corresponds to m = 0, and therefore
$\displaystyle \sum_{n=0}^\infty\dfrac{1}{(2n-1)!}x^{2n-1} = \sum_{m=0}^\infty\dfrac{1}{(2m+1)!}x^{2m+1} = \sinh(x)$
2.3 Connection with sine, cosine and tangent via complex numbers
The study of complex numbers (that is, numbers involving i where i2 = −1) leads to the following important result, known as Euler’s formula, which connects the exponential, sine and cosine functions
eix = cos(x) + i sin(x)(19)
By replacing x by −x we have
e−ix = cos(x) − i sin(x)
from which we can obtain concise expressions for cos(x) and sin(x) which resemble the definitions of cosh(x)
and sinh(x) given in Subsection 2.1.
$\cos(x) = \dfrac{{\rm e}^{ix}+{\rm e}^{-ix}}{2}$(20)
$\sin(x) = \dfrac{{\rm e}^{ix}-{\rm e}^{-ix}}{2i}$(21)
This suggests that identities should exist which relate the hyperbolic and trigonometric functions. Such identities can be obtained if we replace x by ix in the basic definitions of cosh(x) and sinh(x)
$\cosh(ix) = \dfrac{{\rm e}^{ix}+{\rm e}^{-ix}}{2}$
$\sinh(ix) = \dfrac{{\rm e}^{ix}-{\rm e}^{-ix}}{2}$
and then write these expressions in terms of cos(x) and sin(x).
sinh(ix) = i sin(x)(22)
cosh(ix) = cos(x)(23)
Question T4
Use the expressions for the sine and cosine functions in terms of the exponential function to relate
(a) sin(ix) to sinh(x), and (b) cos(ix) to cosh(x).
Answer T4
(a) $\sin(ix) = \dfrac{{\rm e}^{i(ix)}-{\rm e}^{-i(ix)}}{2i} = -\dfrac1i\left(\dfrac{{\rm e}^x-{\rm e}^{-x}}{2}\right) = -\dfrac1i\sinh(x) = i\sinh(x)$
implying that sin(ix) = i sinh(x)
(b) $\cos(ix) = \dfrac{{\rm e}^{i(ix)}+{\rm e}^{-i(ix)}}{2} = \dfrac{{\rm e}^x+{\rm e}^{-x}}{2} = \cosh(x)$
implying that cos(ix) = cosh(x)
The connection between the hyperbolic and trigonometric functions can also be seen from their series. For example
$\begin{align} \sinh(x) & = \dfrac{ix}{1!} + \dfrac{(ix)^3}{3!} + \dfrac{(ix)^5}{5!} + \dfrac{(ix)^7}{7!} + \dfrac{(ix)^9}{9!} + \dots\\& = \dfrac{ix}{1!} - i\dfrac{x^3}{3!}+ i\dfrac{x^5}{5!} - i\dfrac{x^7}{7!} + i\dfrac{x^9}{9!} - \dots\\& = i\left[\dfrac{x}{1!} - \dfrac{x^3}{3!}+ \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + \dfrac{x^9}{9!} - \dots\right] = i\sin(x)\end{align}$
Question T5
Use the series for cos(x) and cosh(x) to show that cos(ix) = cosh(x).
Answer T5
Since the series for cos(x) and cosh(x) are
$\displaystyle \cos(x) = \sum_{n=0}^\infty\dfrac{(-1)^nx^{2n}}{(2n)!} = 1 - \dfrac{x^2}{2!} + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + \dfrac{x^8}{8!} - \dots$
$\displaystyle \cosh(x) = \sum_{n=0}^\infty\dfrac{x^{2n}}{(2n)!} = 1 + \dfrac{x^2}{2!} + \dfrac{x^4}{4!} + \dfrac{x^6}{6!} + \dfrac{x^8}{8!} + \dots$
we have $\displaystyle \cos(ix) = \sum_{n=0}^\infty\dfrac{(-1)^n(ix)^{2n}}{(2n)!} = \sum_{n=0}^\infty\dfrac{x^{2n}}{(2n)!} = \cosh(x)$
2.4 Small argument approximations
Since the infinite series for sinh(x) and cosh(x) given in this module are Taylor expansions about x = 0, we would expect the first few terms in the series to provide reasonable approximations to the functions for values of x ‘close’ to zero. The following example provides an illustration.
Example 1
Use Equation 11,
$\displaystyle \sinh(x) = \sum_{n=0}^\infty\dfrac{x^{2n+1}}{(2n+1)!} = \dfrac{x}{1!} +\dfrac{x^3}{3!} +\dfrac{x^5}{5!} +\dfrac{x^7}{7!} + \dfrac{x^9}{9!} + \dots$(Eqn 11)
to evaluate sinh(0.2) to three places of decimals. i
Solution
From Equation 11 we have
$\sinh(0.2) = 0.2 + \dfrac{0.008}{3!} + \dfrac{0.000\,32}{5!} + ... = 0.2 + 0.0013 + ... \approx 0.201$
This is consistent with my calculator which gives a value of 0.201 336.
Question T6
Use the series given in Equation 15,
$\tanh(x) = x - \dfrac{x^3}{3} + \dfrac{2x^5}{15} - \dfrac{17x^7}{315} + \dots$(Eqn 15)
to find tanh(0.4) to three places of decimals. Check the result with your calculator. i
Answer T6
Using the series for tanh(x)
$\tanh(x) = x - \dfrac{x^3}{3} + \dfrac{x^5}{15} - \dfrac{17x^7}{315} + \dots$
we obtain
$\begin{align} \tanh(0.4) & = 0.4 - \dfrac{(0.4)^3}{3} + \dfrac{(0.4)^5}{15} - \dfrac{17(0.4)^7}{315} + \dots\\\\[0.5em] & = 0.4 - 0.021\,333 + 0.001\,365 - 0.000\,088 + \dots \approx 0.380\end{align}$
To check the result on a calculator (which doesn’t have a tanh button) we can use
$\tanh(0.4) = \dfrac{{\rm e}^{0.4}-{\rm e}^{-0.4}}{{\rm e}^{0.4}+{\rm e}^{-0.4}} \approx 0.379\,949 \approx 0.380$
3 More advanced hyperbolic functions
3.1 Reciprocal hyperbolic functions
The reciprocal_trigonometric_functionsreciprocals of the basic hyperbolic functions occur fairly frequently and so are given special names cosech, sech and coth: i
$\cosech(x) = \dfrac{1}{\sinh(x)}$ provided x ≠ 0(24)
$\sech(x) = \dfrac{1}{\cosh(x)}$ for all x(25)
$\coth(x) = \dfrac{1}{\tanh(x)}$ provided x ≠ 0(26)

Figure 3 Graph of cosh(x).
Notice that cosech(x) is the reciprocal of sinh(x) and that sech(x) is the reciprocal of cosh(x). As in the case of trigonometric functions, this terminology may seem rather odd, but it is easily remembered by recalling that each reciprocal pair – (sinh, cosech), (cosh, sech), (tanh, coth) – involves the letters ‘co’ just once. In other words, there is just one ‘co’ between each pair. Also notice that the cosech and coth functions are undefined when their partner functions are zero. By contrast, sech(x) is defined for all real x since cosh(x) is never zero, see Figure 3.
The reciprocal functions can be written in terms of ex as
$\cosech(x) = \dfrac{2}{{\rm e}^x - {\rm e}^{-x}}$(27)
$\sech(x) = \dfrac{2}{{\rm e}^x + {\rm e}^{-x}}$(28)
$\coth(x) = \dfrac{{\rm e}^x + {\rm e}^{-x}}{{\rm e}^x - {\rm e}^{-x}}$(29)
Graphs of these functions are given in Figures 6 to 8, respectively.
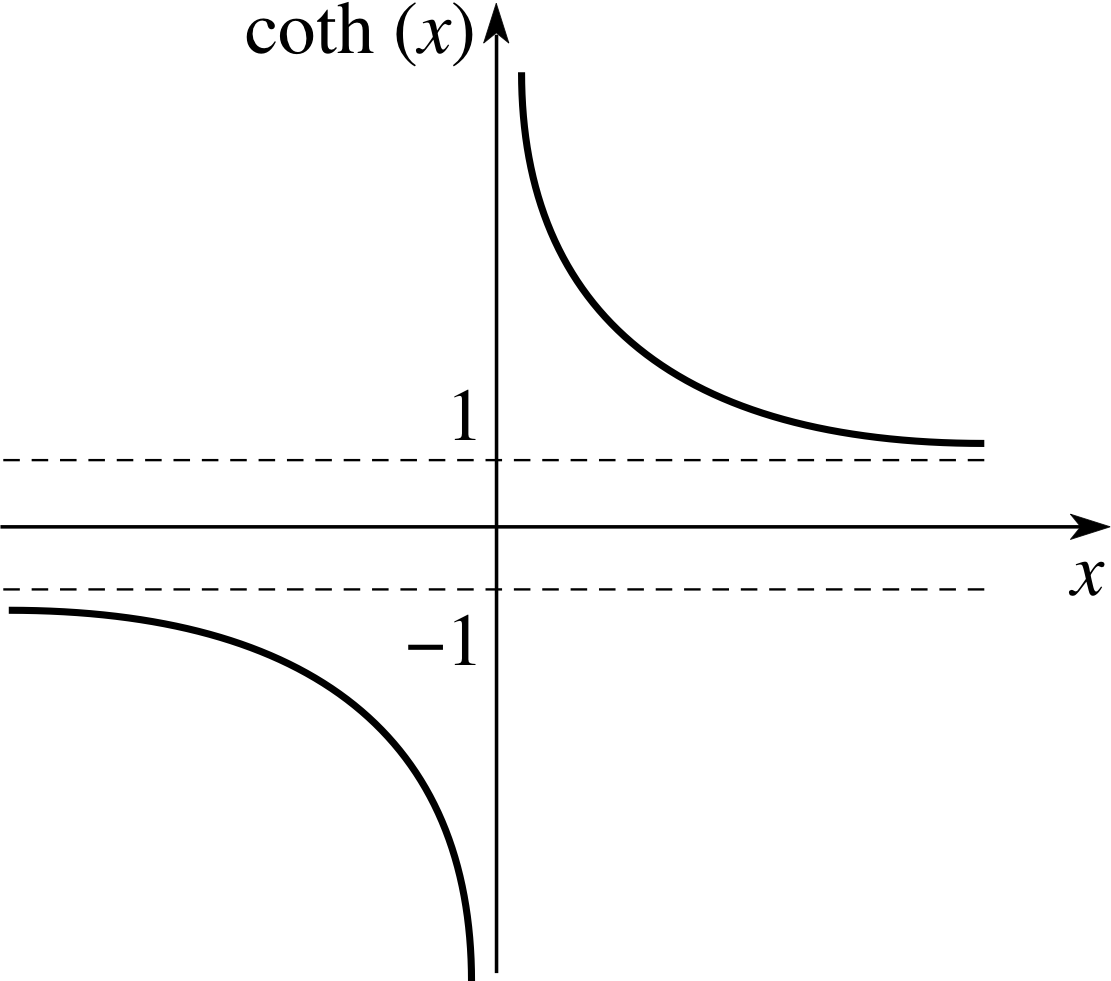
Figure 8 Graph of coth(x).
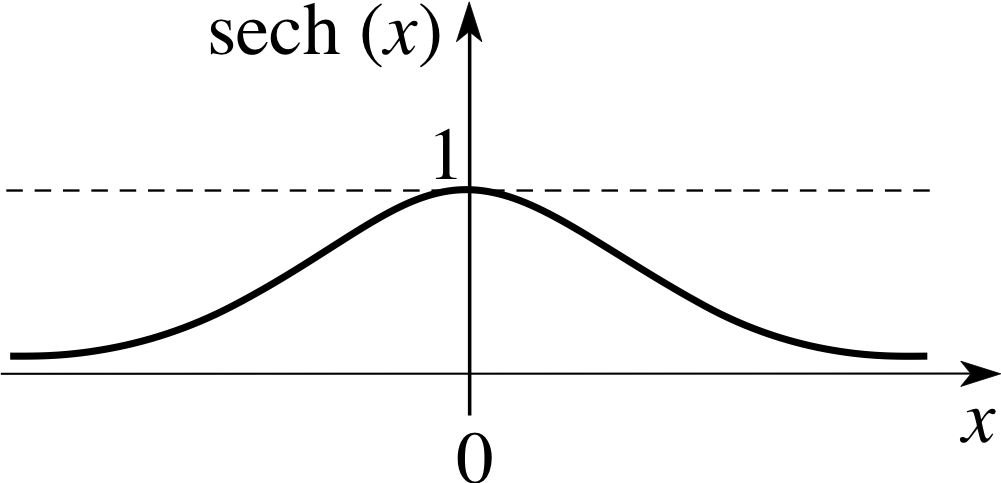
Figure 7 Graph of sech(x).
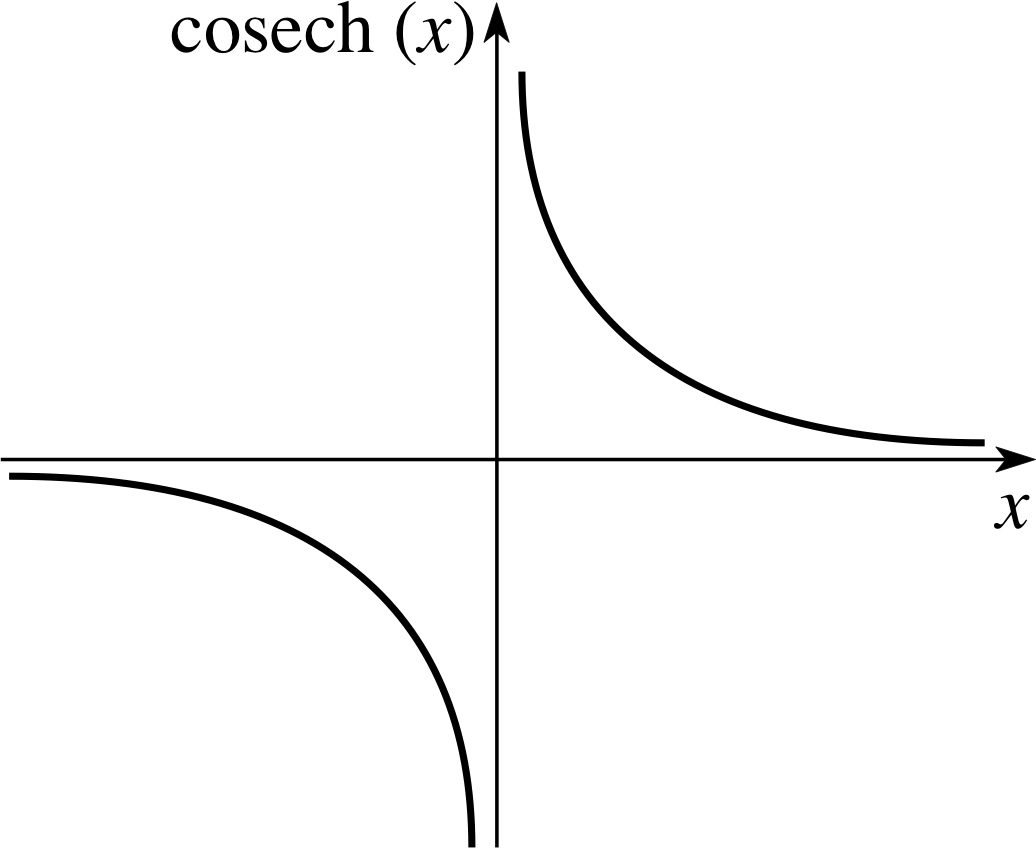
Figure 6 Graph of cosech(x).
Question T7
Show that coth2(x) − cosech2(x) = 1.
Answer T7
Dividing the identity cosh2(x) − sinh2(x) = 1, given in Question T1(c), by sinh2(x) gives
$\dfrac{\cosh^2(x)}{\sinh^2(x)} - 1 = \dfrac{1}{\sinh^2(x)}$
and therefore
coth2(x) − 1 = cosech2(x), i.e. coth2(x) − cosech2(x) = 1.
3.2 Inverse hyperbolic functions (and logarithmic forms)
A common problem is to find what argument gives rise to a particular value of some hyperbolic function. For example, if sinh(x) = 3.6, what is the value of x? We can get an approximate value of x by looking at Figure 2.
✦ Use Figure 2 to find the (approximate) value of x that corresponds to sinh(x) = 3.6?
✧ x is approximately 2.0.
To answer such questions more precisely we need to know the inverse hyperbolic functions which ‘undo’ the effect of the hyperbolic functions. These new functions are known as arcsinh, arctanh and arccosh, and the first two functions are defined by
arcsinh[sinh(x)] = x(30)
arctanh[tanh(x)] = x(31)
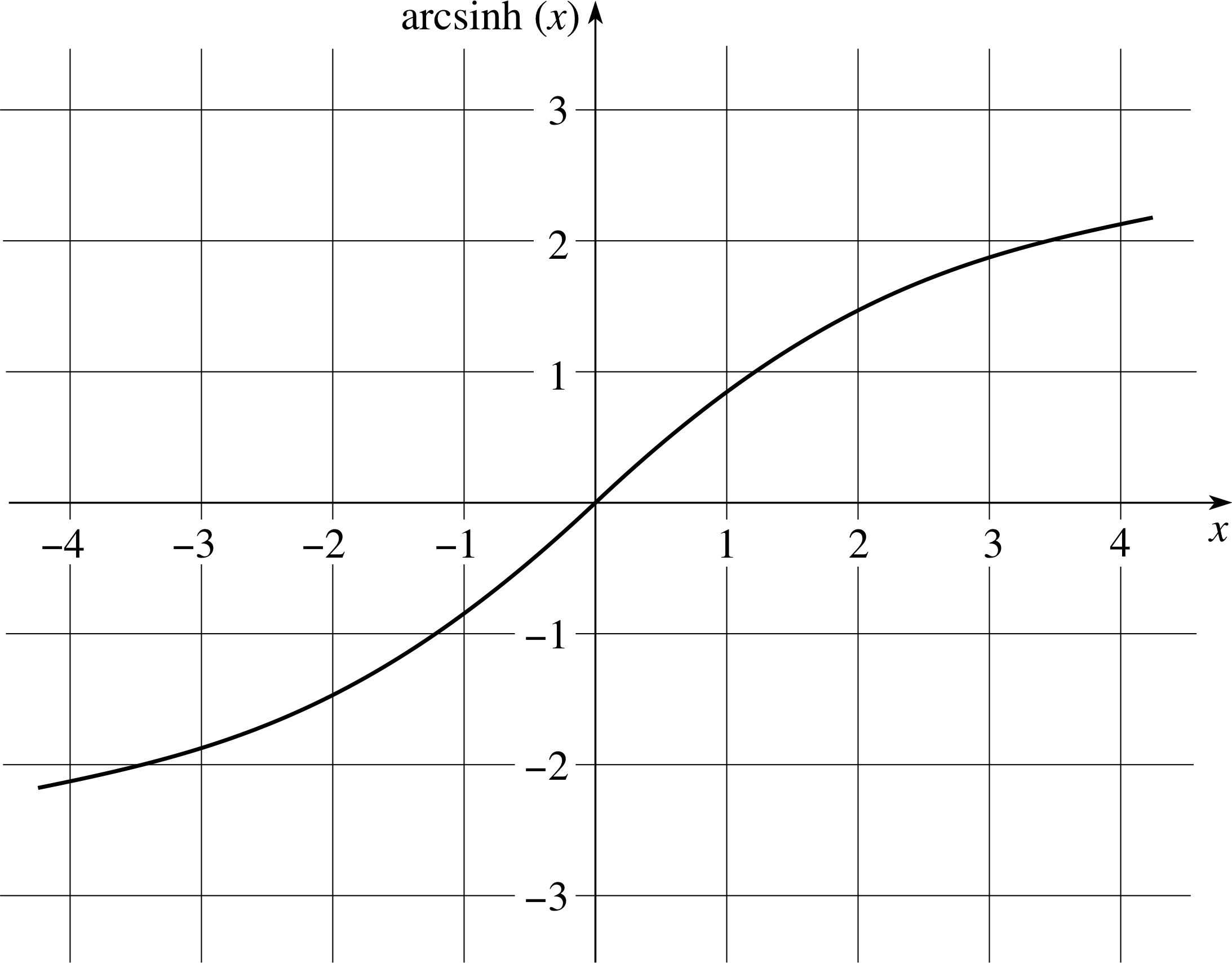
Figure 9 Graph of arcsinh(x).
Graphs of these functions are given in Figures 9 and 10, respectively. Notice that the domain of arctanh(x) is −1 < x < 1.
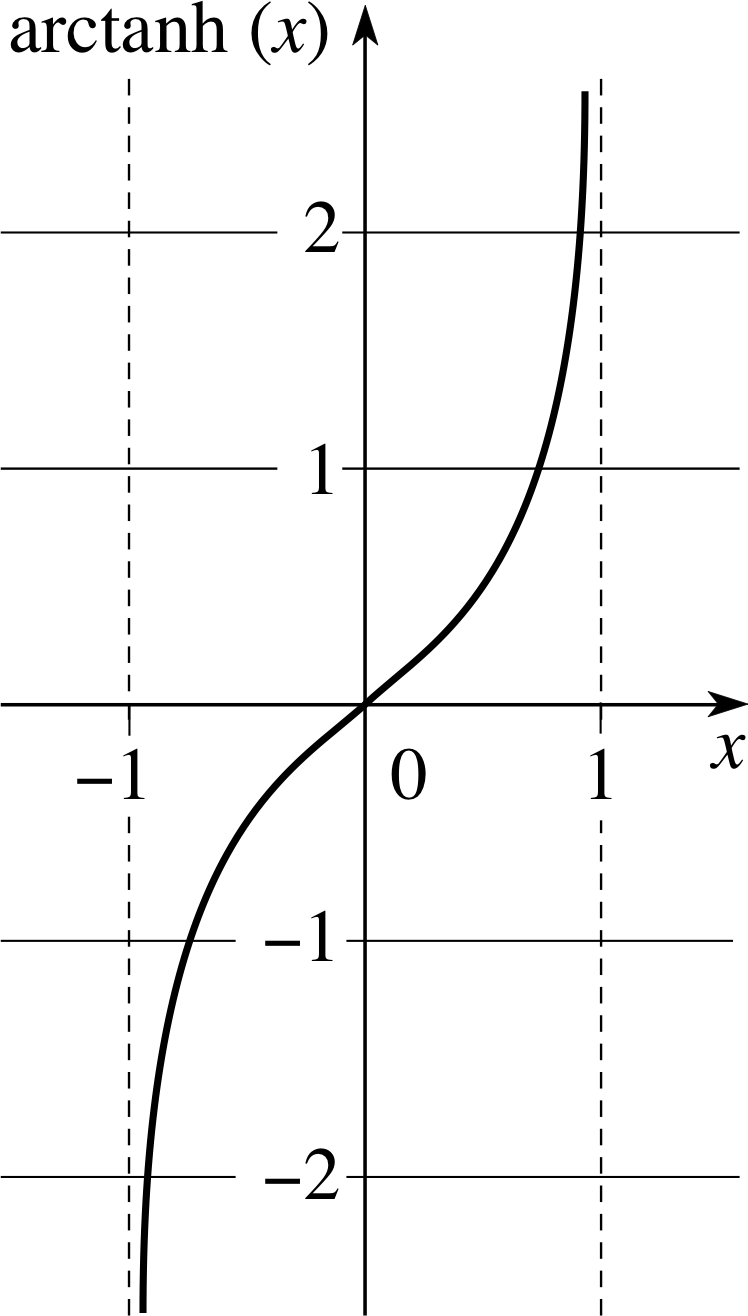
Figure 10 Graph of arctanh(x).
✦ From Figure 3, estimate values of x that correspond to cosh(x) = 1, 2 and 3.
✧ The values of x are approximately 0, ±1.3 and ±1.8.
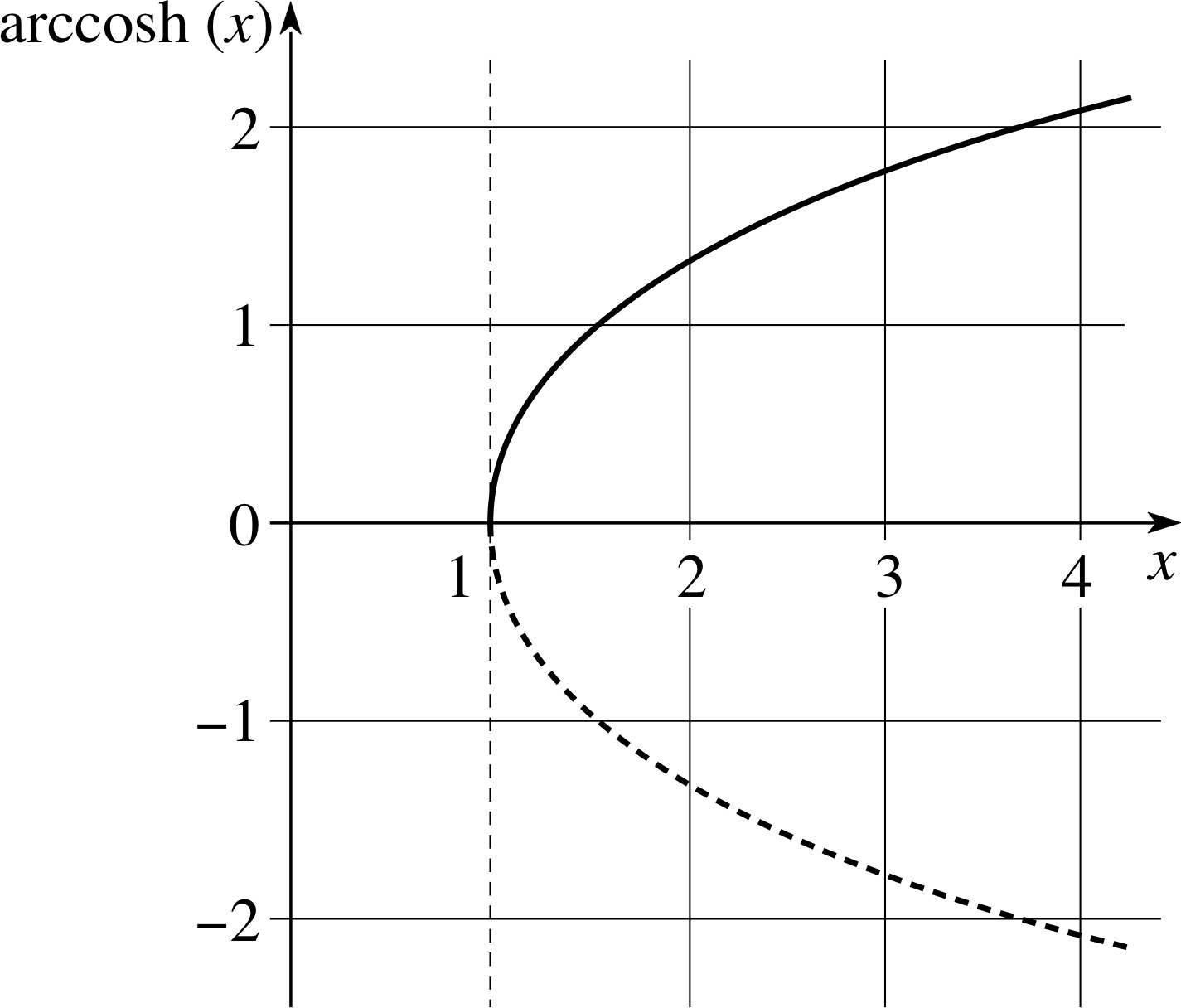
Figure 11 Graph of arccosh(x). Note that only the solid line is involved in the definition.

Figure 3 Graph of cosh(x).
From Figure 3, we see that for any given value of cosh(x) > 1 there are two corresponding values of x ; in other words, the equation cosh(x) = a > 1 has two solutions. Consequently, in order for arccosh to be a function, we must impose a condition which picks out just one value (i.e. x ≥ 0).
Figure 11 shows the graph of the inverse function (the continuous line), and as you can see we choose the positive value for arccosh(x), i which gives
cosh[arccosh(x)] = x for x ≥ 1(32a)
✦ (a) Simplify $\sqrt{x^2}$ and $\left(\sqrt{x\os}\right)^2$. Do you need to place any restrictions on the values of x in either case?
(b) Simplify arccosh[cosh(x)] and cosh[arccosh(x)]. Do you need to place any restrictions on the values of x in either case?
✧ (a) In this module we always use the positive square root, so that $\sqrt{x^2} = \vert\,x\,\vert$ and there are no restrictions on the value of x. On the other hand, $\sqrt{x^\os}$ only makes sense if x ≥ 0, in which case $\left(\sqrt{x^2}\right) = x$.
(b) arccosh always gives rise to a positive value, and cosh(x) is defined for all values of x, so that arccosh[cosh(x)] = | x | for all x. On the other hand, arccosh(x) only makes sense if x ≥ 1, in which case cosh[arccosh(x)] = x.
If we agree to restrict ourselves to positive values of x, so that we can be sure that | x | = x, there is no problem with the inverse of cosh(just as there is no problem with the inverse of ‘squaring’ if we restrict ourselves to positive numbers) for then we have
arccosh[cosh(x)] = x for x ≥ 0(32b)
✦ From Figure 3, what are the approximate values of arccosh(2) and arccosh(3)?
✧ We find arccosh(2) ≈ 1.3 and arccosh(3) ≈ 1.8. These values are consistent with Figure 11.
✦ Find all solutions of the equation cosh(x) = 2.
✧ Our first thought might be that we have just shown that arccosh(2) ≈ 1.3 and therefore the solution is approximately 1.3. However, from Figure 3 we know that there are two solutions of the equation cosh(x) = 2. These solutions are given by x = ± arccosh(2) ≈ ±1.3
As in the case of trigonometric functions, an alternative notation is sometimes used to represent the inverse hyperbolic functions:
sinh−1(x) for arcsinh(x)
cosh−1(x) for arccosh(x)
tanh−1(x) for arctanh(x)
Notice that there is no connection with the positive index notation used to denote powers of the hyperbolic functions, for example, using sinh2(x) to represent [sinh(x)]2. Also notice that, although this notation might make it appear otherwise, there is still a clear distinction between the inverse hyperbolic functions and the reciprocal hyperbolic functions. So
sinh−1[sinh(x)] = arcsinh[sinh(x)] = x
but$\cosech(x) \times \sinh(x) = \dfrac{1}{\sinh(x)} \times \sinh(x) = 1$
More inverse hyperbolic functions
There are three more inverse hyperbolic functions which we have not mentioned yet; these are arccosech(x), arcsech(x) and arccoth(x). As you might expect, they are defined so that
arccosech[cosech(x)] = x(33)
arcsech[sech(x)] = x(34)
arccoth[coth(x)] = x(35)

Figure 14 Graph of arccoth(x).
Figure 13 Graph of arcsech(x).
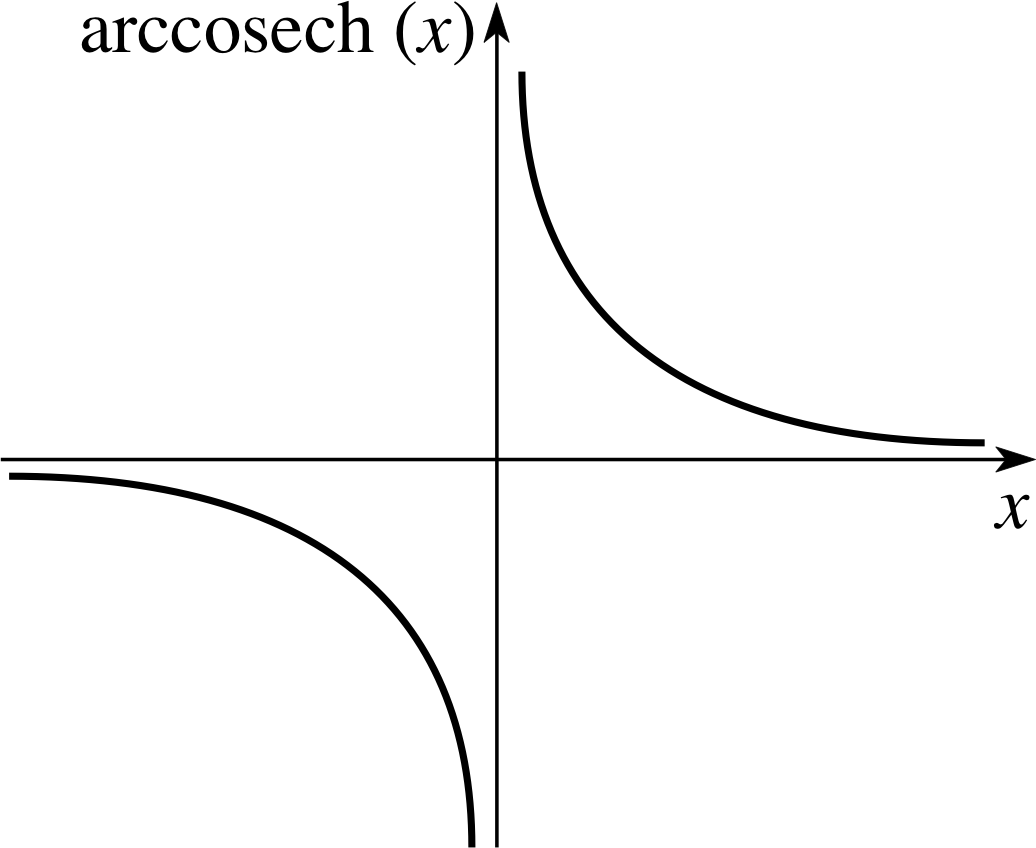
Figure 12 Graph of arccosech(x).
Graphs of these functions are given in Figures 12 to 14, respectively, and the following exercise leads to some useful identities.
Question T8
Show that (a) arccosech(x) = arcsinh(1/x), (b) arcsech(x) = arccosh(1/x), and (c) arccoth(x) = arctanh(1/x).
Answer T8
(a) Let x = cosech(y), then sinh(y) = 1/x, and therefore y = arcsinh(1/x).
However, from the definition of the arccosech function, we have
arccosech(x) = y = arcsinh(1/x)
(b) Let x = sech(y), then cosh(y) = 1/x, so that y = arccosh(1/x).
However, from the definition of the arcsech function, we have
arcsech(x) = y = arccosh(1/x)
(c) Let x = coth(y), then tanh(y) = 1/x, so that y = arctanh(1/x).
However, from the definition of the arccoth function, we have
arccoth(x) = y = arctanh(1/x)
Connection with logarithmic function
Given the relationship between the exponential and logarithmic functions, and the fact that the hyperbolic functions are defined in terms of the exponential function, it might be expected that the inverse hyperbolic functions can be expressed in terms of the logarithmic function. This is indeed the case, and it can be shown that the three basic hyperbolic functions can be written as
$\arcsinh(x) = \loge\left(x + \sqrt{x^2 + 1}\right)$(36)
$\arccosh(x) = \loge\left(x + \sqrt{x^2 - 1}\right)$ for x ≥ 1(37)
$\arctanh(x) = \dfrac12\loge\left(\dfrac{1+x}{1-x}\right)$ for −1 < x < 1(38)
As an example, we now prove the second of these identities.
We start by setting y = arccosh(x) i
which implies that $x = \cosh(y) = \dfrac{{\rm e}^y+{\rm e}^{-y}}{2}$, and we see that x ≥ 1. i
Multiplying the right– and left–hand sides of this last relationship by 2ey and rearranging, we obtain
e2y − 2xey + 1 = 0
a quadratic equation in ey which we can solve to obtain
${\rm e}^y = \dfrac{2x\pm\sqrt{4x^2-4}}{2} = x\pm\sqrt{x^2-1}$
The question now is whether either (or both) of the signs on the right–hand side of this equation are allowable. First we note that the right–hand side must be greater than or equal to one, because y = arcosh(x) ≥ 0, so ey ≥ 1.
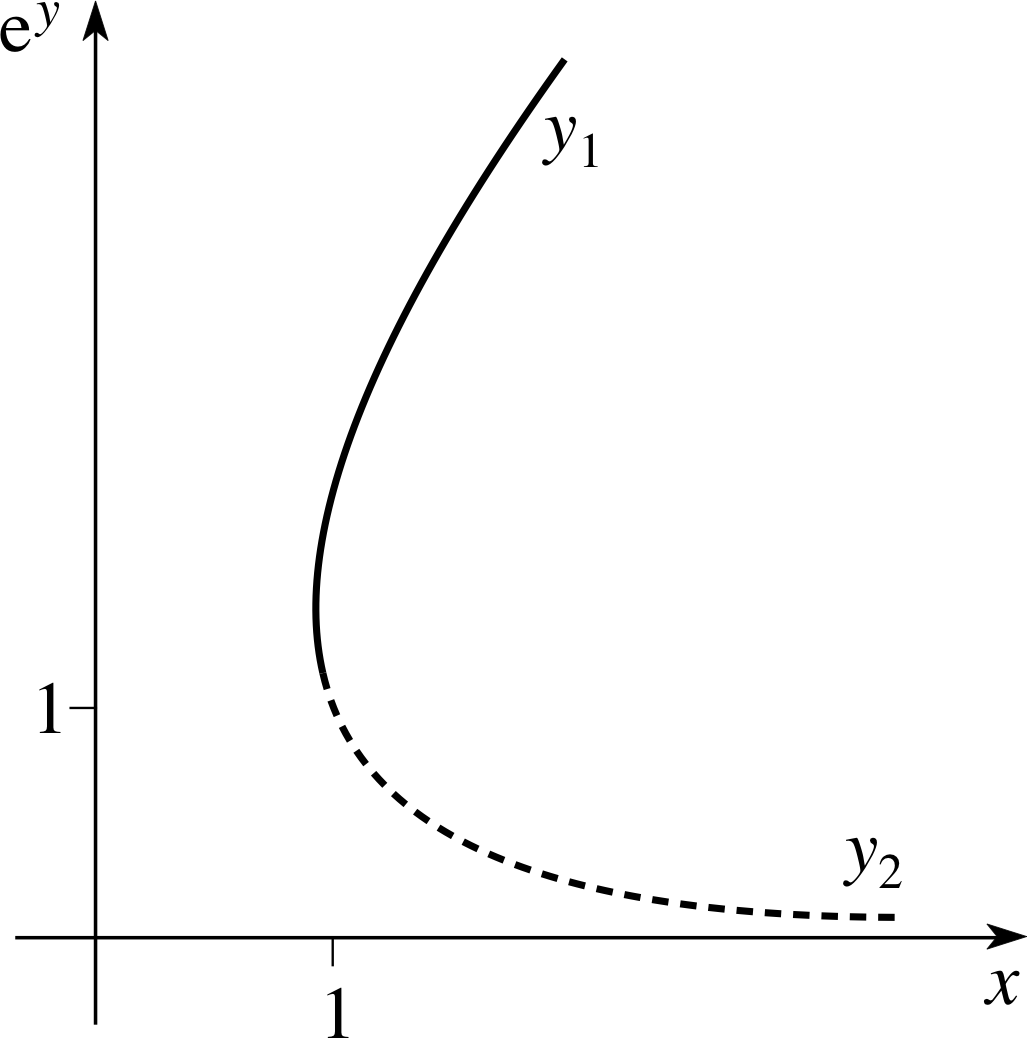
Figure 15 Graphs of Y1 = (x + x2 −1)(full line) and Y2 = (x − x2 −1)(dotted line) for x ≥ 1.
Then we can eliminate the negative sign as follows. i
We consider the graphs of $Y_1 = (x + \sqrt{x^2 - 1})\quad\text{and}\quad Y_2 = (x - \sqrt{x^2 -1})$ for x ≥ 1 (shown in Figure 15), and ask if it is possible for either Y1 or Y2 to be greater than or equal to 1 as required.
From the graphs it is clear that Y2 ≤ 1, which makes this choice impossible, and therefore the only acceptable solution is
${\rm e}^y = x + \sqrt{x^2-1}$
Taking the logarithm of this result gives us
$y = \loge(x + \sqrt{x^2-1})$
The remaining two identities can be proven in a similar way, as the following question demonstrates.
Question T9
Show that
$\arctanh(x) = \dfrac12\loge\left(\dfrac{1+x}{1-x}\right)$ for −1 < x < 1
Answer T9
Let y = arctanh(x), then $x = \tanh(y) = \dfrac{{\rm e}^y-{\rm e}^{-y}}{{\rm e}^y+{\rm e}^{-y}}$
and therefore ey(1 − x) = e−y(1 + x)
which gives ${\rm e}^{2y} = \left(\dfrac{1+x}{1-x}\right)$
The condition $\left(\dfrac{1+x}{1-x}\right) = {\rm e}^{2y} \gt 0$ ensures that −1 < x < 1, and taking logarithms of both sides gives
$2y = \loge\left(\dfrac{1+x}{1-x}\right)$, which gives the required result.
Expressing the inverse hyperbolic functions in terms of the logarithmic function can be a useful way of solving certain algebraic equations. For example, suppose we want the values of x which satisfy
sinh2(x) − 3 cosh(x) + 3 = 0
then we can use the identity
cosh2(x) − sinh2(x) = 1
to obtain an equation involving just cosh(x)
cosh2(x) − 3 cosh(x) + 2 = 0
This can be factorized to give
(cosh(x) − 2) (cosh(x) − 1) = 0
so, eitherx = ± arccosh(2) i
orx = ± arccosh(1)
Using$\arccosh(x) = \loge\left(x + \sqrt{x^2 - 1}\right)$
gives$x = \pm\arccosh(2) = \pm\loge\left(2+\sqrt{3\os}\right)$
orx = ± arccosh(1) = ± loge(1) = 0
(One advantage of this approach is that the logarithmic function is more likely to be available on a calculator.)
Question T10
Solve cosh2(x) + sinh(x) = 3, in terms of the logarithmic function.
Answer T10
Using the identity cosh2(x) − sinh2(x) = 1
we can write the equation as (sinh2(x) + 1) + sinh(x) = 3
which can be rearranged to give sinh2(x) + sinh(x) − 2 = 0
and then factorized to read (sinh(x) − 1)(sinh(x) + 2) = 0
This equation has the solutions
x = arcsinh(1) and x = arcsinh(−2)
Using $\arcsinh(x) = \loge(x + \sqrt{x^2+1})$ the two solutions can be written as
$x = \loge(1 + \sqrt{2^\os})$ and $x = \loge(\sqrt{5^\os} - 2)$
4 Identities
There are many identities involving trigonometric functions, and there are an equally large number of identities involving hyperbolic functions. In fact, since the trigonometric and hyperbolic functions are related (by, for example, sinh(ix) = i sin(x)) every trigonometric identity has an analogue for hyperbolic functions. The most important hyperbolic function identities i are listed below, and it is worth comparing them with their trigonometric partners which are given elsewhere in FLAP.
The symmetry relations: i
sinh(−x) = −sinh(x)(39)
cosh(−x) = cosh(x)(40)
tanh(−x) = −tanh(x)(41)
The basic identities:
$\tanh(x) = \dfrac{\sinh(x)}{\cosh(x)}$(42)
cosh2(x) − sinh2(x) = 1(43)
$\coth(x) = \dfrac{\cosech(x)}{\sech(x)}$ for x ≠ 0(44)
1 − tanh2(x) = sech2(x)(45)
The addition identities: i
sinh(x + y) = sinh(x) cosh(y) + cosh(x) sinh(y)(46)
cosh(x + y) = cosh(x) cosh(y) + sinh(x) sinh(y)(47)
$\tanh(x + y) = \dfrac{\tanh(x) + \tanh(y)}{1+ \tanh(x)\tan(y)}$(48)
The double–argument identities: i
sinh(2x) = 2 sinh(x) cosh(x)(49)
cosh(2x) = cosh2(x) + sinh2(x)(50)
cosh(2x) = 1 + 2 sin h2(x)(51)
cosh(2x) = 2 cosh2(x) − 1(52)
$\tanh(2x) = \dfrac{2\tanh(x)}{1 + \tanh^2(x)}$(53)
The half–argument identities: i
$\cosh^2\left(\dfrac x2\right) = \dfrac12[1+\cosh(x)]$(54)
$\sinh^2\left(\dfrac x2\right) = \dfrac12[-1+\cosh(x)]$(55)
and if t = tanh(x/2) then
$\sinh(x) = \dfrac{2t}{1-t^2}$(56)
$\cosh(x) = \dfrac{1+t^2}{1- t^2}$(57)
$\tanh(x) = \dfrac{2t}{1+t^2}$(58)
The sum identities:
$\sinh(x) + \sinh(y) = 2\sinh\left(\dfrac{x + y}{2}\right)\cosh\left(\dfrac{x-y}{2}\right)$(59)
$\sinh(x) - \sinh(y) = 2\cosh\left(\dfrac{x + y}{2}\right)\sinh\left(\dfrac{x-y}{2}\right)$(60)
$\cosh(x) + \cosh(y) = 2\cosh\left(\dfrac{x + y}{2}\right)\cosh\left(\dfrac{x-y}{2}\right)$(61)
$\cosh(x) - \cosh(y) = 2\sinh\left(\dfrac{x + y}{2}\right)\sinh\left(\dfrac{x-y}{2}\right)$(62)
The product identities:
2 sinh(x) cosh(y) = sinh(x + y) + sinh(x − y)(63)
2 cosh(x) cosh(y) = cosh(x + y) + cosh(x − y)(64)
2 sinh(x) sinh(y) = cosh(x + y) − cosh(x − y)(65)
All of these identities can be derived from the definitions of sinh(x) and cosh(x) in terms of ex as the following questions demonstrate. i
✦ Use the definitions of sinh(x) and cosh(x) in terms of ex to show that sinh(x + y) = sinh(x) cosh(y) + cosh(x) sinh(y).
✧ The left–hand side can be written as
$\dfrac12({\rm e}^{x+y} - {\rm e}^{-x-y})$
The right–hand side seems complicated but reduces to the left–hand side after some algebraic manipulation:
$\left(\dfrac{{\rm e}^x - {\rm e}^{-x}}{2}\right)\left(\dfrac{{\rm e}^y + {\rm e}^{-y}}{2}\right) + \left(\dfrac{{\rm e}^x + {\rm e}^{-x}}{2}\right)\left(\dfrac{{\rm e}^y - {\rm e}^{-y}}{2}\right)$
$= \dfrac14\left[({\rm e}^{x+y} + {\rm e}^{x-y} - {\rm e}^{-x+y} - {\rm e}^{-x-y}) + ({\rm e}^{x+y} - {\rm e}^{x-y} + {\rm e}^{-x+y} - {\rm e}^{-x-y})\right]$
$= \dfrac12({\rm e}^{x+y} - {\rm e}^{-x-y})$
Question T11
Use the definition of the hyperbolic functions in terms of the exponential function to show that sinh(2x) = 2 sinh(x) cosh(x).
Answer T11
$2\sinh(x)\cosh(x) = 2 \times \left(\dfrac{{\rm e}^x-{\rm e}^{-x}}{2}\right) \times \left(\dfrac{{\rm e}^x+{\rm e}^{-x}}{2}\right) = \left(\dfrac{{\rm e}^{2x}-{\rm e}^{-2x}}{2}\right) = \sinh(x)$
In many cases it is more convenient to derive identities from other identities rather than from the basic definitions. For example, by putting x = y in
sinh(x + y) = sinh(x) cosh(y) + cosh(x) sinh(y)
we obtain sinh(2x) = 2 sinh(x) cosh(x)
This is certainly more straightforward than using the basic definitions; the other double–argument identities follow from the addition identities in a similar fashion.
Question T12
Use the addition identities
sinh(x + y) = sinh(x) cosh(y) + cosh(x) sinh(y)(Eqn 46)
cosh(x + y) = cosh(x) cosh(y) + sinh(x) sinh(y)(Eqn 47)
$\tanh(x + y) = \dfrac{\tanh(x) + \tanh(y)}{1+ \tanh(x)\tan(y)}$(Eqn 48)
to show that
cosh(2x) = 2 cosh2(x) − 1 and $\tanh(2x) = \dfrac{2\tanh(x)}{1+\tanh^2(x)}$
Answer T12
(a) If we set y = x in the identity cosh(x + y) = cosh(x) cosh(y) + sinh(x) sinh(y)
we find cosh(2x) = cosh2(x) + sinh2(x)
But we also have the identity cosh2(x) − sinh2(x) = 1
and so, substituting for sinh(x) we obtain
cosh(2x) = 2 cosh2(x) − 1
(b) Setting y = x in the identity $\tanh(x + y) = \dfrac{\tanh(x) + \tanh(y)}{1+ \tanh(x)\tanh(y)}$
leads directly to
$\tanh(2x) = \dfrac{2\tanh(x)}{1+ \tanh^2(x)}$
5 Differentiating hyperbolic functions
Study comment This section contains some results that are important in their own right, but its main purpose is to give you further practice in using the techniques of differentiation.
As shown in Question T3, the derivatives of the basic hyperbolic functions are given by
$\dfrac{d}{dx}\sinh(x) = \cosh(x)$(Eqn 17)
$\dfrac{d}{dx}\cosh(x) = \sinh(x)$(Eqn 18)
These important results can be used to find the derivatives of other hyperbolic functions. Here we consider some specific examples.
Example 2
Show that $\dfrac{d^2}{dx^2}\sinh(3x) = 9\sinh(3x)$
Solution
$\dfrac{d}{dx}\sinh(3x) = 3\cosh(3x)$ i and $\dfrac{d}{dx}3\cosh(3x) = 9\sinh(3x)$
Example 3
Show that $\dfrac{d}{dx}\tanh(x) = \sech^2(x)$
Solution
We know that$\tanh(x) = \dfrac{\sinh(x)}{\cosh(x)}$
and using the quotient rule$\dfrac{d}{dx}\left(\dfrac uv\right) = \dfrac1v\dfrac{du}{dx} - \dfrac{u}{v^2}\dfrac{dv}{dx}$
we have$\dfrac{d}{dx}\tanh(x) = \dfrac{1}{\cosh(x)}\times \cosh(x) - \dfrac{\sinh(x)}{\cosh^2(x)}\times \sinh(x)$
so$\dfrac{\cosh^2(x)-\sinh^2(x)}{\cosh^2(x)} = \dfrac{1}{\cosh^2(x)} = \sech^2(x)$
Question T13
Use Equations 17 and 18
$\dfrac{d}{dx}\sinh(x) = \cosh(x)$(Eqn 17)
$\dfrac{d}{dx}\cosh(x) = \sinh(x)$(Eqn 18)
to show that $\dfrac{d}{dx}\coth(x) = -\cosech^2(x)$
Answer T13
$\begin{align} \dfrac{d}{dx}\coth(x) & = \dfrac{d}{dx}\left[\dfrac{\cosh(x)}{\sinh(x)}\right] = \dfrac{1}{\sinh(x)}\dfrac{d}{dx}\cosh(x) - \dfrac{\cosh(x)}{\sinh^2(x)}\dfrac{d}{dx}\sinh(x)\\\\[0.5em] & = \dfrac{1}{\sinh(x)}\times\sinh(x) - \dfrac{\cosh(x)}{\sinh^2(x)}\times\cosh(x) = \dfrac{\sinh^2(x) - \cosh^2(x)}{\sinh^2(x)}\\\\[0.5em] & = -\dfrac{1}{\sinh^2(x)} = -\cosech^2(x)\end{align}$
Example 4
Show that $\dfrac{d}{dx}\arcsinh(x) = \dfrac{1}{\sqrt{x^2+1}}$ i
Solution
There are two approaches:
(a) Let y = arcsinh(x) so that we have to find $\dfrac{dy}{dx}$.
We have x = sinh(y), and differentiating both sides of this equation with respect to x gives us
$1 = \dfrac{d}{dx}[\sinh(y)] = \dfrac{dy}{dx}\dfrac{d}{dx}[\sinh(y)]$ (from the chain rule)
and therefore$1 = \dfrac{dy}{dx}\cosh(y)$
which gives us$\dfrac{dy}{dx} = \dfrac{1}{\cosh(y)}$
We need the derivative in terms of x, so we use the identity of Equation 43,
cosh2(x) − sinh2(x) = 1(Eqn 43)
to write
$\cosh(y) = \sqrt{1 + \sinh^2(y)} = \sqrt{1+x^2}$
(Notice that the positive square root is taken in this expression because cosh(y) ≥ 1).
We can now see that $\dfrac{dy}{dx} = 1$ and therefore $\dfrac{d}{dx}\arcsinh(x) = \dfrac{1}{\sqrt{x^2+1}}$
(b) Differentiating the identity $\arcsin(x) = \loge(x + \sqrt{x^2 +1})$ with respect to x, and using the fact that $\dfrac{d}{dx}\loge(f(x)) = \dfrac{f'(x)}{f(x)}$, i we have
$\dfrac{d}{dx}\arcsin(x) = \dfrac{d}{dx}\loge(x + \sqrt{x^2 +1}) = \dfrac{1}{x+\sqrt{x^2+1}}\left(1+2x\times \dfrac12\times \dfrac{1}{\sqrt{x^2+1}}\right) = \dfrac{1}{\sqrt{x^2+1}}$
Question T14
Show that $\dfrac{d}{dx}\arctanh(x) = \dfrac{1}{1-x^2}$ by using:
(a) the known derivative of tanh(x);
(b) the identity for arctanh(x) in terms of the logarithmic function.
Answer T14
(a) Setting x = tanh(y) and differentiating both sides with respect to x we find
$1 = \dfrac{dy}{dx}\dfrac{d}{dy}\tanh(y) = \dfrac{dy}{dx}\sech^2(y)$
and therefore $\dfrac{dy}{dx} = \dfrac{d}{dx}\arctan(x) = \dfrac{1}{\sech^2(y)}$
Using the identity sech2(y) + tanh2(y) = 1 gives us
$\sech(y) = \sqrt{1-\tanh^2(y)} = \sqrt{1-x^2}$
and therefore $\dfrac{d}{dx}\arctanh(x) = \dfrac{1}{1-x^2}$
(b) Differentiating the identity $\arctanh(x) = \dfrac12\loge\left(\dfrac{1+x}{1-x}\right) = \dfrac12\left[\loge(1+x) - \loge(1-x)\right]$
with respect to x gives us $\dfrac{d}{dx}\arctanh(x) = \dfrac{1}{2(1+x)} + \dfrac{1}{2(1-x)} = \dfrac{1}{(1-x^2)}$
Example 5
Find $\dfrac{d}{dx}\sech(x)$
Solution
$\dfrac{d}{dx}\sech(x) = \dfrac{d}{dx}[\cosh(x)]^{-1} = -[\cosh(x)]^{-2}\dfrac{d}{dx}\cosh(x) = -\dfrac{\sinh(x)}{\cosh^2(x)} = -\sech(x)\tanh(x)$
Question T15
Find $\dfrac{d}{dx}\cosech(x)$
Answer T15
$\dfrac{d}{dx}\cosech(x) = \dfrac{d}{dx}\left[\sinh(x)\right]^{-1} = -\left[\sinh(x)\right]^{-2}\dfrac{d}{dx}\sinh(x) = -\dfrac{\cosh(x)}{\sinh^2(x)} = -\cosech(x)\coth(x)$
Example 6
Find $\dfrac{d}{dx}\sinh^3(2x)$
Solution
$\dfrac{d}{dx}\sinh^3(2x) = 3\sinh^2(2x)\dfrac{d}{dx}\sinh(2x) = 6\sinh^2(2x)\cosh^2(2x) = 3\sinh(2x)\sinh(4x)$
Question T16
Find $\dfrac{d}{dx}\cosh^5(3x)$
Answer T16
$\dfrac{d}{dx}\cosh^5(3x) = 5\cosh^4(3x)\dfrac{d}{dx}\cosh(3x) = 15\cosh^4(3x)\sinh(3x)$
Example 7
Find $\dfrac{d}{dx}[\sinh(x)\tanh(x)]$
Solution
$\begin{align} \dfrac{d}{dx}[\sinh(x)\tanh(x)] & = \left(\dfrac{d}{dx}\sinh(x)\right)\tanh(x) + \sinh(x)\dfrac{d}{dx}\tanh(x)\\ & = \cosh(x)\tanh(x) + \sinh(x)\sech^2(x)\\ & = \sinh(x)[1+\sech^2(x)]\end{align}$
Question T17
Find $\dfrac{d}{dx}[\cosh(x)\coth(x)]$
Answer T17
$\begin{align} \dfrac{d}{dx}[\cosh(x)\coth(x)] & = \dfrac{d \cosh(x)}{dx}\coth(x) + \cosh(x)\dfrac{d}{dx}\coth(x)\\\\[0.5em] & = \sinh(x)\coth(x) - \cosh(x)\cosech^2(x) = \cosh(x)(1 - \cosech^2(x))\end{align}$
Example 8
Find $\dfrac{d}{dx}\sinh(3x^2+1)$
Solution
$\dfrac{d}{dx}\sinh(3x^2+1) = \cosh(3x^2+1)\dfrac{d}{dx}(3x^2+1) = 6x\cosh(3x^2+1)$
Question T18
Find $\dfrac{d}{dx}\cosh(5x^4 +1)$
Answer T18
$\dfrac{d}{dx}\cosh(5x^4+1) = \sinh(5x^4+1)\dfrac{d}{dx}(5x^4+1) = 20x^3\sinh\left(5x^4+1\right) = 20x^3\sinh\left(5x^4+1\right)$
Example 9
Find $\dfrac{d}{dx}(\exp[\cosh(5x)])$
Solution
$\dfrac{d}{dx}(\exp[\cosh(5x)]) = \exp[\cosh(5x)]\dfrac{d}{dx}[\cosh(5x)] = 5\exp[\cosh(5x)]\sinh(5x)$
Question T19
Find $\dfrac{d}{dx}(\exp[\sinh^2(x)])$
Answer T19
$\begin{align} \dfrac{d}{dx}\left[\exp\left(\sinh^2(x)\right)\right] & = \exp\left(\sinh^2(x)\right)\dfrac{d}{dx}\sinh^2(x)\\ & = 2\sinh(x)\cosh(x)\exp\left(\sinh^2(x)\right) = \sinh(2x)\exp\left(\sinh^2(x)\right)\end{align}$
Example 10
Find $\dfrac{d}{dx}\loge[\cosh(x)]$
Solution
$\dfrac{d}{dx}\loge[\cosh(x)] = \dfrac{1}{\cosh(x)}\times \dfrac{d}{dx}\cosh(x) = \dfrac{\sinh(x)}{\cosh(x)} = \tanh(x)$
Question T20
Find $\dfrac{d}{dx}\loge[\sinh(x)]$
Answer T20
$\dfrac{d}{dx}\log\left[\sinh(x)\right] = \dfrac{1}{\sinh(x)}\dfrac{d}{dx}\sinh(x) = \dfrac{\cosh(x)}{\sinh(x)} = \coth(x)$
Example 11
Figure 16 A heavy cable suspended between two points (such as two pylons).
A heavy cable is suspended between two pylons of the same height, as shown schematically in Figure 16. i
It can be shown that the y–coordinate of the cable satisfies the (differential) equation
$\dfrac{d^2y}{dx^2} = \dfrac{\rho g}{T_0}\sqrt{1+\left(\dfrac{dy}{dx}\right)^2}$
where T0 is the tension in the cable at x = 0, ρ is the density per unit length of the cable, and g is the magnitude of the acceleration due to gravity.
Show that
$y = \dfrac{T_0}{\rho g}\cosh\left(\dfrac{\rho gx}{T_0}\right)$
is a solution to this equation.
Solution
If$y = \dfrac{T_0}{\rho g}\cosh\left(\dfrac{\rho gx}{T_0}\right)$
then$\dfrac{dy}{dx} = \sinh\left(\dfrac{\rho gx}{T_0}\right)$
and$\dfrac{d^2y}{dx^2} = \dfrac{\rho g}{T_0}\cosh\left(\dfrac{\rho gx}{T_0}\right)$ which is the left–hand side of the differential equation.
Using the identity cosh2(x) − sinh2(x) = 1
we see that the right–hand side of the differential equation can be written as
$\dfrac{\rho g}{T_0}\sqrt{1+\left(\dfrac{dy}{dx}\right)^2} = \dfrac{\rho g}{T_0}\sqrt{1+\sinh^2\left(\dfrac{\rho gx}{T_0}\right)} = \dfrac{\rho g}{T_0}\cosh\left(\dfrac{\rho gx}{T_0}\right)$
which verifies that $y = \dfrac{T_0}{\rho g}\cosh\left(\dfrac{\rho gx}{T_0}\right)$ is indeed a solution.
6 Closing items
6.1 Module summary
- 1
-
There are Section 2hyperbolic functions corresponding to all the trigonometric functions, and though they are similar in some respects they are very different in others. In particular, the hyperbolic functions are not periodic, and, sinh(x) and cosh(x) are not constrained to lie between −1 and 1. Hyperbolic functions are named by appending ‘h’ to the corresponding trigonometric function.
- 2
-
sinh(x) and cosh(x) are defined by
$\sinh(x) = \dfrac{{\rm e}^x-{\rm e}^{-x}}{2}$(Eqn 3)
$\cosh(x) = \dfrac{{\rm e}^x+{\rm e}^{-x}}{2}$(Eqn 4)
- 3
-
tanh(x) is defined by
$\tanh(x) = \dfrac{\sinh(x)}{\cosh(x)} = \dfrac{{\rm e}^x-{\rm e}^{-x}}{{\rm e}^x+{\rm e}^{-x}}$(Eqn 5)
- 4
-
A hyperbola can be defined by means of the parametric equations
x = a cosh(s)(Eqn 6)
y = b sinh(s)(Eqn 7)
- 5
-
The Subsection 2.2Taylor expansions of sinh(x) and cosh(x) about x = 0 are
$\displaystyle \sinh(x) = \sum_{n=0}^\infty\dfrac{x^{2n+1}}{(2n+1)!} = \dfrac{x}{1!} +\dfrac{x^3}{3!} +\dfrac{x^5}{5!} +\dfrac{x^7}{7!} + \dfrac{x^9}{9!} + \dots$(Eqn 11)
$\displaystyle \cosh(x) = \sum_{n=0}^\infty\dfrac{x^{2n}}{(2n)!} = 1 + \dfrac{x^2}{2!} + \dfrac{x^4}{4!} + \dfrac{x^6}{6!} + \dfrac{x^8}{8!} + \dots$(Eqn 13)
- 6
-
The first few terms of the Taylor expansion of tanh(x) about x = 0 are
$\tanh(x) = x - \dfrac{x^3}{3} + \dfrac{2x^5}{15} - \dfrac{17x^7}{315} + \dots$(Eqn 15)
- 7
-
The T3-questionderivatives of the two basic hyperbolic functions are
$\dfrac{d}{dx}\sinh(x) = \cosh(x)$(Eqn 17)
$\dfrac{d}{dx}\cosh(x) = \sinh(x)$(Eqn 18)
- 8
-
The trigonometric and hyperbolic functions are related by sinh(ix) = isin(x)
sinh(ix) = i sin(x)(Eqn 22)
cosh(ix) = cos(x)(Eqn 23)
sin(ix) = isinh(x)
cos(ix) = cosh(x)
- 9
-
Subsection 3.1Reciprocal hyperbolic functions are defined by
$\cosech(x) = \dfrac{1}{\sinh(x)}$ provided x ≠ 0(Eqn 24)
$\sech(x) = \dfrac{1}{\cosh(x)}$ for all x(Eqn 25)
$\coth(x) = \dfrac{1}{\tanh(x)}$ provided x ≠ 0(Eqn 26)
- 10
-
Subsection 3.1Inverse hyperbolic functions are defined by
arcsinh[sinh(x)] = x(Eqn 30)
arccosh[cosh(x)] = x for x ≥ 0(Eqn 32b)
arctanh[tanh(x)] = x(Eqn 31)
- 11
-
The inverse hyperbolic functions can be written in terms of the logarithmic function
$\arcsinh(x) = \loge\left(x + \sqrt{x^2 + 1}\right)$(Eqn 36)
$\arccosh(x) = \loge\left(x + \sqrt{x^2 - 1}\right)$ for x ≥ 1(Eqn 37)
$\arctanh(x) = \dfrac12\loge\left(\dfrac{1+x}{1-x}\right)$ for −1 < x < 1(Eqn 38)
- 12
-
There are a large number of Section 4hyperbolic function identities, such as
cosh2(x) − sinh2(x) = 1(Eqn 43)
The most important are listed in Section 4.
6.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of this module.
- A2
-
Relate the trigonometric and hyperbolic functions by means of the complex number, i.
- A3
-
Sketch graphs for the more common hyperbolic functions
- A4
-
Recognize the more common identities for the hyperbolic functions and use them to solve mathematical and physical problems.
- A5
-
Differentiate the hyperbolic functions.
- A6
-
Derive, identify and use the Taylor series for the hyperbolic functions.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
6.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions, each of which tests one or more of the Achievements.
Question E1 (A2)
Use the definitions of trigonometric and hyperbolic functions in terms of the exponential function to show that:
(a) tanh(x) = −itan(ix), (b) cosech(x) = i cosec(ix).
Answer E1
(a) We can write tanh(x) as $\tanh(x) = \dfrac{{\rm e}^x-{\rm e}^{-x}}{{\rm e}^x+{\rm e}^{-x}}$
andtan(x) as $\tan(x) = \dfrac{{\rm e}^{ix}-{\rm e}^{-ix}}{i({\rm e}^{ix}+{\rm e}^{-ix})}$ which means that
and$-i\,\tan(ix) = -\dfrac{{\rm e}^{-x}-{\rm e}^{x}}{{\rm e}^{-x}+{\rm e}^{x}} = \dfrac{{\rm e}^{x}-{\rm e}^{-x}}{{\rm e}^{x}+{\rm e}^{-x}} = \tanh(x)$
(b) Using the definitions of cosech(x) and cosec(x), we can write
$\cosech(x) = \dfrac{2}{{\rm e}^x-{\rm e}^{-x}}$ and $\cosech(x) = \dfrac{2i}{{\rm e}^{ix}-{\rm e}^{-ix}}$
so that$i\,\cosech(ix) = \dfrac{-2}{{\rm e}^{-x}-{\rm e}^{x}} = \dfrac{2}{{\rm e}^{x}-{\rm e}^{-x}} = \cosech(x)$
(Reread Subsection 2.1Subsections 2.1 and Subsection 2.32.3 if you had difficulty with this question.)
Question E2 (A4)
Use the double–argument identities to show that
(a) $\cosh^2\left(\dfrac x2\right) = \dfrac12[1+ \cosh(x)]$, (b) $\sinh^2x = \dfrac12[-1+\cosh(x)]$.
Answer E2
(a) Using the identity cosh(2x) = 2 cosh2(x) − 1 we find
$\cosh^2(x) = \dfrac12[1+\cosh(2x)]$
and therefore (replacing x by x/2)
$\cosh^2\left(\dfrac x2\right) = 1[1+\cosh(x)]$
(b) In a similar way, using the identity cosh(2x) = 1 + 2 sinh2(x) gives us
$\sinh^2(x) = \dfrac12[-1+\cosh(2x)]$
and therefore $\sinh^2\left(\dfrac x2\right) = \dfrac12[-1 +\cosh(x)]$
(Reread Section 4 if you had difficulty with this question.)
Question E3 (A5)
Show that y (t) = A sinh(ωt) + B cosh(ω t) is a solution of $\dfrac{d^2y(t)}{dt^2} = \omega^2t$.
If y (0) = 4 and y ′ (0) = 1, find A and B.
Answer E3
Using the standard results
$\dfrac{d}{dt}\sinh(\omega t) = \omega \cosh(\omega t)$ and $\dfrac{d}{dt}\cosh(\omega t) = \omega \sinh(\omega t)$
we obtain
$\dfrac{d}{dt}y(t) = \omega[A\cosh(\omega t) + B\sinh(\omega t)]$
and therefore
$\dfrac{d^2}{dt^2}y(t) = \omega^2[A\sinh(\omega t) + B\cosh(\omega t)] = \omega^2y(t)$
If we set y (0) = 4 we find
4 = A sinh(0) + B cosh(0) = B and therefore B = 4.
If we set y ′ (0) = 1, we find
1 = ω [A cosh(0) + B sinh(0)] = ωA
which implies that A = 1/ω.
(Reread Section 5 if you had difficulty with this question.)
Question E4 (A4)
Suppose that we are given the values of A and B. Use the identities given in Section 4 to find values of C and y (in terms of A and B) such that
A sinh(x) + B cosh(x) = C sinh(x + y)
Explain any restrictions on the possible values for A and B.
Answer E4
Using the identity
sinh(x + y) = sinh(x) cosh(y) + cosh(x) sinh(y)
we obtain $\dfrac AC = \cosh(y)$ and $\dfrac BC = \sinh(y)$
then using the identity cosh2(y) − sinh2(y) = 1 we obtain
A2 − B2 = C 2
which is only possible if | B | ≤ | A |. We then have $C = \pm\sqrt{A^2-B^2}$ with an apparent ambiguity in the sign of C. However, we know that $\dfrac AC = \cosh(y) \ge 1$ and therefore A and C must have the same sign.
Finally, y = arctanh(B/A), which is well–defined if | B | < | A |
The conclusion is that A sinh(x) + B cosh(x) can be written in the form
C sinh(x + y) with $C = \pm\sqrt{A^2-B^2}$ and y = arctanh(B/A) provided that | B | < | A |.
(Reread Section 4 if you had difficulty with this question.)
Question E5 (A3)
From the graphs given in this module, which hyperbolic functions would you expect to have a domain which excludes the point x = 0. Confirm your suspicions by looking at algebraic expressions for the functions that you have picked out. (You should include the reciprocal and inverse hyperbolic functions in your discussion.)
Answer E5
The functions are:
(a) coth(x) (see Figure 8), since $\coth(x) = \dfrac{{\rm e}^x+{\rm e}^{-x}}{{\rm e}^x-{\rm e}^{-x}}$ which, on setting x = 0, becomes $\dfrac{1+1}{1-1}$ which is undefined.
(b) cosech(x) (see Figure 6), since $\cosech(x) = \dfrac{2}{{\rm e}^x-{\rm e}^{-x}}$ which, on setting x = 0, becomes $\dfrac{2}{1-1}$ and this is again undefined.
(c) arccosh(x) (see Figure 11), is not defined at x = 0 (no value of x makes cosh(x) equal to zero).
(d) arccosech(x) (see Figure 12), is not defined at x = 0 (no value of x makes cosech(x) equal to zero).
(e) arcsech(x) (see Figure 13), is not defined at x = 0 (no value of x makes sech(x) equal to zero).
(f) arccoth( x) (see Figure 14), is not defined at x = 0 (no value of x makes coth(x) equal to zero).
(Reread Section 3 if you had difficulty with this question.)
Question E6 (A4)
Starting from the definition of sinh(x) in terms of the exponential function, show that
$\arcsinh(x) = \loge(x+\sqrt{x^2+1})$
Answer E6
Let y = arcsinh(x) then $x = \sinh(y) = \dfrac{{\rm e}^y-{\rm e}^{-y}}{2}$
which can be rearranged as e2y − 2xey − 1 = 0. This is a quadratic equation in ey and its two solutions are ${\rm e}^y = x ± \sqrt{x^2+1}$. We can reject the negative root because ey ≥ 0 would imply $x - \sqrt{x^2+1} \gt 0$, which would give x2 > x2 + 1, which is impossible. It follows that only the positive root is relevant, and taking the logarithm of both sides of the equation gives us, $\arcsinh(x) = \loge(x+\sqrt{x^2+1})$.
(Reread Subsection 3.2 if you had difficulty with this question.)
Question E7 (A5)
Use the known derivative of tanh(x) to express $\dfrac{d}{dx}\loge[\tanh(x)]$ in terms of hyperbolic functions.
Answer E7
See Example 3 for the derivation of the result
$\dfrac{d}{dx}\tanh(x) = \sech^2(x)$
We can use this to obtain
$\dfrac{d}{dx}\loge[\tanh(x)] = \dfrac{1}{\tanh(x)}\dfrac{d}{dx}\tanh(x) = \dfrac{\sech^2(x)}{\tanh(x)} = \dfrac{1}{\cosh(x)\sinh(x)} = \dfrac{2}{\sinh(2x)} = 2\cosech(2x)$
(Reread Section 5 if you had difficulty with this question.)
Question E8 (A5)
Find $\dfrac{d}{dx}\tanh^3(2x)$.
Answer E8
$\dfrac{d}{dx}\tanh^2(2x) = 3\tanh^2(2x)\dfrac{d}{dx}\tanh(2x) = 6\tanh^2(2x)\sech^2(2x)$
(Reread Section 5 if you had difficulty with this question.)
Question E9 (A4 and A6)
Use the series for sinh(x) and cosh(x) to find a first estimate for a solution of the equation
sinh(x) = 0.01 cosh(x)
then use the logarithmic form of tanh(x) to find a more accurate value for the solution.
Answer E9
From Equations 11 and 13
$\displaystyle \sinh(x) = \sum_{n=0}^\infty\dfrac{x^{2n+1}}{(2n+1)!} = \dfrac{x}{1!} +\dfrac{x^3}{3!} +\dfrac{x^5}{5!} +\dfrac{x^7}{7!} + \dfrac{x^9}{9!} + \dots$(Eqn 11)
$\displaystyle \cosh(x) = \sum_{n=0}^\infty\dfrac{x^{2n}}{(2n)!} = 1 + \dfrac{x^2}{2!} + \dfrac{x^4}{4!} + \dfrac{x^6}{6!} + \dfrac{x^8}{8!} + \dots$(Eqn 13)
we have
$\sinh x \approx x + \dfrac{x^3}{6}$ and $\cosh x \approx 1 + \dfrac{x^2}{2}$
so that the given equation becomes
$x + \dfrac{x^3}{6} \approx (0.01)\left(1+\dfrac{x^2}{2}\right)$
Ignoring the terms in x2 and x3 we obtain the rough estimate x ≈ 0.01 for the solution. We can obtain a better estimate for the solution if we observe that the given equation implies, tanh(x) = 0.01, so that using Equation 38 we have
$\arctanh(x) = \loge\left(\dfrac{1+0.01}{1-0.01}\right) \approx 0.010\,0003$.
(Reread Subsection 2.2Subsections 2.2, Subsection 2.42.4 and Subsection 3.23.2 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 6Closing items.