MATH 5.3: Techniques of integration |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
You should already know that obtaining the indefinite integral of a function f (x) amounts to finding a function F (x) whose derivative $\dfrac{dF}{dx}$ is equal to f (x), so that, for example, we know that ${\large\int}\cos x\,dx = \sin x + C$ precisely because $\dfrac{d}{dx}(\sin x + C) = \cos x$. Every time we manage to differentiate a specific function $\dfrac{dF}{dx}$ to obtain the answer $\dfrac{dF}{dx} = f(x)$ we automatically discover the solution to a corresponding problem in integration, namely ‘what is the indefinite integral ${\large\int}f(x)\,dx$?’ Integrals of simple functions, i.e. those that can be easily recognized as the derivatives of other functions, can quickly be found in this way. For example, to find ${\large\int}\cos(x)\,dx$, you might guess that the result was something like sin(2x) + C. On differentiating sin(2x) + C, you would find that the derivative was in fact 2 cos(2x). So your initial guess has to be adjusted by a factor of ½, and the answer is ${\large\int}\cos(2x)\,dx = \frac12\sin(2x)+C$.
Whereas there are simple rules that enable us to differentiate almost any function we meet, it is a sad fact of life that there are no such rules for integration. This is not to say that there aren’t methods for finding integrals, there are plenty; it is just that these methods do not always work, and, what is more, there are many simple looking integrals for which no method could possibly work. For example, it is not possible to express the integral ${\large\int}e^{x^2}\,dx$ in terms of the elementary functions, sine, cosine, exp and so on. The methods discussed in this module will enable you to find many useful integrals, but all integration methods ultimately amount to recognizing the integrand f (x) as the derivative of some function. Indeed, many simple integrals, such as ${\large\int}\cos(2x)\,dx$, can be found by making an intelligent guess at the function F (x), then differentiating your guess to see if it gives f (x), and, if not, adjusting it appropriately (this may involve, for example, multiplication by a constant). Of course there are many functions f (x) for which it would be very difficult to guess the form of the indefinite integral straight away. In this module, we discuss two standard methods of integration which can sometimes be used to manipulate an integral so as to bring it into a form where intelligent guesswork (or use of a table of standard integrals) will give you the final answer.
The first of these methods, integration by parts, is based on the product rule for differentiation, and is often useful when the function f (x) to be integrated is the product of two simpler functions. Thus, for example, it enables you to integrate functions like xex.
The second method, integration by substitution, involves rewriting the integral ${\large\int}f(x)\,dx$ in terms of a new variable y = g (x), and is based on the chain rule for differentiation. It will often enable you to turn a really unpleasant–looking integral – such as ${\large\int}x(1-x^2)^{5/2}\, dx$ – into one which can be evaluated more easily.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Subsection 1.2Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 5.1Module summary and the Subsection 5.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 5.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Note: In the answers to the following questions, C denotes a constant of integration.
Question F1
Find the indefinite integrals:
(a) ${\large\int}x^2{\rm e}^{-x}\,dx$ (b) ${\large\int}{\rm e}^{-x}\sin(3x)\,dx$
Answer F1
Both these integrals can be found using the formula for integration by parts,
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
(a) Let f (x) = e−x and g (x) = x2. Then F (x) = −e−x and $\dfrac{dg}{dx} = 2x$.
So${\large\int}x^2{\rm e}^{-x}dx = -x^2{\rm e}^{-x} + 2{\large\int}x{\rm e}^{-x}\,dx$(20)
Now consider ${\large\int}x{\rm e}^{-x}\,dx$. Let f (x) = e−x and g (x) = x. Then F (x) = −e−x and $\dfrac{dg}{dx} = 1$.
So${\large\int}x{\rm e}^{-x}\,dx = -x{\rm e}^{-x} + {\large\int}{\rm e}^{-x}\,dx = -x{\rm e}^{-x} - {\rm e}^{-x} + C$
Substituting this into Equation 20 gives us
${\large\int}x^2{\rm e}^{-x}dx = -x^2{\rm e}^{-x} - 2x{\rm e}^{-x} - 2{\rm e}^{-x} + C$
(b) Let f (x) = e−x and g (x) = sin(3x). Then F (x) = −e−x and $\dfrac{dg}{dx} = 3\cos(3x)$.
Hence ${\large\int}{\rm e}^{-x}\sin(3x)\,dx = -{\rm e}^{-x}\sin(3x) + 3{\large\int}{\rm e}^{-x}\cos(3x)\,dx$(21)
Now apply integration by parts to ${\large\int}{\rm e}^{-x}\cos(3x)\,dx$. Take f (x) = e−x and g (x) = cos(3x). Then F (x) = −e−x and $\dfrac{dg}{dx} = -3\sin(3x)$. Hence ${\large\int}{\rm e}^{-x}\cos(3x)\,dx = -{\rm e}^{-x}\cos(3x) - 3{\large\int}{\rm e}^{-x}\sin(3x)\,dx$
Substituting this result into Equation 21 gives us
${\large\int}{\rm e}^{-x}\sin(3x)\,dx = -{\rm e}^{-x}\sin(3x) - 3{\rm e}^{-x}\cos(3x) - 9{\large\int}{\rm e}^{-x}\sin(3x)\,dx$
Collecting the ${\large\int}{\rm e}^{-x}\sin(3x)\,dx$ terms on the left–hand side gives us
$10{\large\int}{\rm e}^{-x}\sin(3x)\,dx = -{\rm e}^{-x}\sin(3x) - 3{\rm e}^{-x}\cos(3x) + C$
i.e.${\large\int}{\rm e}^{-x}\sin(3x)\,dx= -\dfrac{1}{10}{\rm e}^{-x}\sin(3x) - \dfrac{3}{10}{\rm e}^{-x}\cos(3x) + C$
Question F2
Find the indefinite integral ${\large\int}\sin x (1+\cos x)^4\,dx$.
Answer F2
Make the substitution y = 1 + cos x, dy = − sin x dx. Then
${\large\int}\sin x(1+\cos x)^4\,dx = -{\large\int}y^4\,dy = -\dfrac15y^5 + C = -\dfrac15(1+\cos x)^5 + C$
Question F3
Evaluate the integral $\displaystyle \int_0^1\dfrac{1}{\sqrt{{1 + x}\os}}\,dx$ to three decimal places.
Answer F3
Make the substitution y = x + 1, so that x = y − 1, and dx = dy. Then the integrand becomes
$\dfrac{y-1}{\sqrt{y\os}} = \sqrt{y\os} - \dfrac{1}{\sqrt{y\os}}$
When x = 0, y = 1; and when x = 1, y = 2. Therefore
$\displaystyle \int_0^1\dfrac{x}{\sqrt{1+x\os}}\,dx = \int_1^2\left(\sqrt{\smash[b]{y\os}} - \dfrac{1}{\sqrt{\smash[b]{y\os}}}\right)\,dy = {\large\int}_1^2(y^{1/2} - y^{-1/2})\,dy = \left[\dfrac23y^{3/2} - 2y^{1/2}\right]_1^2 = 0.391$
1.3 Ready to study?
Study comment In order to study this module, you will need to be familiar with the following terms: chain rule, constant of integration, definite integral, derivative, function of a function, fundamental theorem of calculus, indefinite integral, integrand, inverse derivative, inverse trigonometric functions, product_rule_of_differentiationproduct rule, and trigonometric identities. If you are uncertain of any of these terms, you can review them now by referring to the Glossary which will indicate where in FLAP they are developed. In addition, you will need to have a good knowledge of differentiation (including the use of the product_rule_of_differentiationproduct and chain_rulechain rules). You should be able to recognize an indefinite integral as an inverse derivative, and you need to be familiar with the integrals of simple functions such as x n, sin x, cos x, ex. You should also be able to find integrals of functions like 3x and cos(2x) using intelligent guesswork, and you should be familiar with the procedure of evaluating definite integrals.
The following questions will allow you to establish whether you need to review some of these topics before embarking on this module.
Note In the answers to the following questions, C denotes an arbitrary constant of integration.
Question R1
Use the product_rule_of_differentiationproduct rule to find $\dfrac{dy}{dx}$ in each of the following cases: i
(a) y = x6 logex (b) y = ex cos(2x)
Answer R1
Here we use the product_rule_of_differentiationproduct rule: $\dfrac{d}{dx}[f(x)g(x)] = \dfrac{df}{dx}g(x) + f(x)\dfrac{dg}{dx}$.
(a) Taking f (x) = x6, g (x) = loge x, we have
$\dfrac{df}{dx} = 6x^5\quad\text{and}\quad\dfrac{dg}{dx} = \dfrac1x$
So$\dfrac{d}{dx}\left(x^6\log_{\rm e}x\right) = \left(6x^5\times\log_{\rm e}x\right) + \left(x^6\times \dfrac1x\right) = x^5(1 + 6\log_{\rm e}x)$
(b) Taking f (x) = ex, g (x) = cos(2x), we have
$\dfrac{df}{dx} = {\rm e}^x$ and $\dfrac{dg}{dx} = 2\sin(2x)$
So$\dfrac{d}{dx}\left[{\rm e}^x\cos(2x)\right] = {\rm e}^x\cos(2x) + {\rm e}^x\left[-2\sin(2x)\right] = {\rm e}^x\left[\cos(2x) - 2\sin(2x)\right]$
Question R2
Use the chain rule to find f ′ (x) when
(a) f (x) = cos(x4) (b) f (x) = loge(1 + x2)
Answer R2
Here we use the chain rule: $\dfrac{d}{dx}\left\{f\left[y(x)\right]\right\} = \dfrac{df}{dy}\dfrac{dy}{dx}$.
(a) Taking f (y) = cos y, y (x) = x2, we have
$\dfrac{df}{dy} = -\sin y, \dfrac{dy}{dx} = 4x^3$
So$\dfrac{d}{dx}\left[\cos(x^4)\right] = -4x^3\sin y = -4x^3\sin(x^4)$
(b) Taking f (y) = loge y, y (x) = 1 + x2, we have
$\dfrac{df}{dy} = \dfrac1y$ and $\dfrac{dy}{dx} = 2x$
So$\dfrac{d}{dx}\left[\log_{\rm e}(1+x^2)\right] = \dfrac{2x}{y} = \dfrac{2x}{1+x^2}$
Question R3
Differentiate the inverse trigonometric function arcsin(2x). Use your answer to find the indefinite integral of $\dfrac{1}{\sqrt{1-4x^2}}$
Answer R3
To differentiate arcsin(2x), write y = arcsin(2x). Since arcsin is the inverse function of sin, it follows that sin y = 2x. Now differentiate both sides of this equation with respect to x, using the chain rule to differentiate sin y. This gives $\cos y\dfrac{dy}{dx} = 2$, or $\dfrac{dy}{dx} = \dfrac{2}{\cos y}$. To express$\dfrac{dy}{dx}$ in terms of x, use the identity cos2 y + sin2 y = 1
or$\cos y = \sqrt{\smash[b]{1-\sin^2y}} = \sqrt{1-4x^2}$
Then $\dfrac{d}{dx}\left[\arcsin(2x)\right] = \dfrac{2}{\sqrt{1-4x^2}}$
This shows that $\dfrac{2}{\sqrt{1-4x^2}}$ has the inverse derivative arcsin(2x) + C, and so (dividing by 2), the inverse derivative of $\dfrac{1}{\sqrt{1-4x^2}}$ is $\dfrac12\arcsin(2x) + C$.
If you are having difficulty with any of the terms in these questions, don’t forget to consult the Glossary.
Question R4
Find the indefinite integrals of
(a) x−4/3, (b) sin(2x) + 3 cos x, (c) exp(x/4)
Answer R4
Note: C denotes an arbitrary constant of integration.
These integrals may all be found by making an intelligent guess at the form of the answer, then checking by differentiation. The answers are:
(a) −3x−1/3 + C
(b) $-\frac12\cos(2x) + 3\sin x + C$ (here, we also use the fact that an integral of a sum of terms is equal to the sum of the integrals of each term).
(c) 4 exp(x/4) + C.
Question R5
Evaluate the definite integral ${\Large\int}_1^2x^2\,dx$.
Answer R5
${\large\int}_1^2x^2\,dx = \left[\dfrac13x^3\right]_1^2 = \dfrac83 - \dfrac18 = \dfrac73 \approx 2.333$
Question R6
Without using a calculator, find the possible values of
(a) cos(x) if $\sin(x) = \dfrac13$, (b) tan(x) if sec(x) = $\sqrt{5\os}$
Answer R6
(a) Here we use the trigonometric identity: cos2 x + sin2 x = 1.
Thus, if sin x = 1/3 then $\cos^2x = 1 - \dfrac13 = \dfrac89$.
So$\cos x = \pm\dfrac{2\sqrt{2\os}}{3}$
(b) Here we use the trigonometric identity: 1 + tan2 x = sec2 x.
Thus, if $\sec x = \sqrt{5\os}$ then tan2 x = 5 − 1 = 4.
Sotan x = ± 2.
Question R7
If $f(x) = \dfrac{(x+1)^2}{x + 3}$ and y = x + 3, express f (x) in terms of y.
Answer R7
If y = x + 3, then x + 1 = y − 2.
So$\dfrac{(x+1)^2}{x + 3} = \dfrac{(y-2)^2}{y}$
Note: If you were unsure of any of the terms used in the above questions, consult the Glossary.
2 Integration by parts
2.1 The method deduced from the differentiation of a product
In this subsection, we shall look at the product rule for differentiation, and derive from it the important integration technique known as integration by parts. We begin with an example. i
Example 1
Find the integral ${\large\int}x\cos x\,dx$.
Solution
As you will see shortly, we can find this integral by looking at the derivative of the product x sin x, the reason being that the integrand x cos x, appears in this derivative. To be precise, on using the product_rule_of_differentiationproduct rule to differentiate x sin x, we find that
$\dfrac{d}{dx}(x\sin x) = \sin x + x\cos x\,dx$
An alternative way of expressing this result is to say that x sin x is the indefinite integral of (sin x + x cos x), so that we can write
${\large\int}(\sin x + x\cos x)\,dx = x\sin x + C$ i
where C is an arbitrary constant.
Using the rule for the sum of two integrals, it follows that
${\large\int}\sin x\,dx + {\large\int}x\cos x\,dx = x\sin x + C$
and a little rearrangement gives us
${\large\int}x\cos x\,dx = x\sin x - {\large\int}\sin x\,dx + C$
Using the fact that the indefinite integral of (− sin x) is cos x + C, we obtain the result
${\large\int}x\cos x\,dx = x\sin x + \cos x + C$ i
Thus, by looking at the derivative of the product x sin x, we have been able to find ${\large\int}x\cos x\,dx$, the indefinite
integral of another product. We will show you shortly how to generalize this method, but first you should try the following question.
Question T1
Find the derivative of the product xex, and use it to find ${\large\int}x{\rm e}^x\,dx$.
Answer T1
$\dfrac{d}{dx}(x{\rm e}^x) = {\rm e}^x+ x{\rm e}^x$ using the product_rule_of_differentiationproduct rule.
So$x{\rm e}^x = {\large\int}\left({\rm e}^x +x{\rm e}^x\right)\,dx = {\large\int}{\rm e}^x\,dx + {\large\int}x{\rm e}^x\,dx$
and therefore
${\large\int}x{\rm e}^x\,dx = x{\rm e}^x - {\large\int}{\rm e}^x\,dx = x{\rm e}^x - {\rm e}^x + C$
We have seen that looking at derivatives of products has enabled us to find some integrals that also involve products; however, you may feel that the method is rather ‘hit or miss’. The question is: What product should we differentiate in order to find the integral of a given product? In order to answer this question, we must first investigate the derivative of two arbitrary functions F (x) and g (x). From the product_rule_of_differentiationproduct rule, we have
$\dfrac{d}{dx}\left[F(x)g(x)\right] = \dfrac{dF(x)}{dx}g(x) + F(x)\dfrac{dg(x)}{dx}$(1)
which means that F (x)g (x) is an inverse derivative, or indefinite integral, of the function
$\dfrac{dF(x)}{dx}g(x) + F(x)\dfrac{dg(x)}{dx}$
on the right–hand side of Equation 1.
So we may write
$\displaystyle \int\left[\dfrac{dF(x)}{dx}g(x) + F(x)\dfrac{dg(x)}{dx}\right] = F(x)g(x) + C$ i
i.e.$\displaystyle \int\dfrac{dF(x)}{dx}g(x)\,dx + \int F(x)\dfrac{dg}{dx}\,dx = F(x)g(x) + C$
and, rearranging this equation (and absorbing the arbitrary constant C into the integrals), it follows that i
$\displaystyle \int\dfrac{dF(x)}{dx}g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$
When applying this equation, we are usually given the left–hand side, i.e. we are given $\dfrac{dF}{dx}$ and g (x), and for this reason it is normal to represent the function $\dfrac{dF}{dx}$ by f (x), so that the equation becomes
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(2) i
✦ Use Equation 2, with f (x) = cos x and g (x) = x, to find ${\large\int}x\cos x\,dx$.
✧ We know that g (x) = x.
Also we have $\dfrac{dF}{dx} = f(x) = \cos x\,dx$ so that we may choose F (x) = sin x.
Thus Equation 2 gives
${\large\int}x\cos x\,dx = {\large\int}\underbrace{(\cos x)}_{\color{purple}{\large f(x)}}\times \overbrace{x}^{\color{purple}{\large g(x)}}\,dx = \underbrace{(\sin x)}_{\color{purple}{\large F(x)}}\times \overbrace{x}^{\color{purple}{\large g(x)}} - {\large\int}\underbrace{(\sin x)}_{\color{purple}{\large F(x)}}\times \overbrace{1}^{\color{purple}{\large g'(x)}}\,dx$
as we saw in Example 1. i
As you can see, Equation 2 converts the problem of finding ${\large\int}f(x)g(x)\,dx$ into that of finding $\displaystyle \int F(x)\dfrac{dg}{dx}\,dx$.
In order for this equation to be useful in practice, there are clearly two necessary requirements:
- 1
-
We need to be able to find F (x), an indefinite integral of f (x).
- 2
-
The integral on the right–hand side of Equation 2, i.e. ${\Large\int}F(x)\dfrac{dg}{dx}\,dx$, should be easier to find than our original integral, ${\large\int}f(x)g(x)\,dx$.
The technique of using Equation 2 to find ${\large\int}f(x)g(x)\,dx$ is called the method of integration by parts. Some questions and examples should help to make this method clearer, and will also illustrate the importance of the two requirements just mentioned.
Example 2
Use Equation 2 to find the indefinite integral ${\large\int}x\sin x\,dx$.
Solution
We start by choosing functions f (x) and g (x) so that our integral ${\large\int}x\sin x\,dx$ is the integral ${\large\int}f(x)g(x)\,dx$ appearing on the left–hand side of Equation 2. There are two possibilities: we can either choose
f (x) = sin x and g (x) = x
orf (x) = x and g (x) = sin x
Since we know how to integrate both x and sin x, the requirement that f (x) should be a function that is easy to integrate does not help us in our choice. Let us, therefore, decide to take f (x) = sin x and g (x) = x, and see what happens. With this choice of f (x) and g (x), we have F (x) = − cos x and $\dfrac{dg}{dx} = 1$
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
Substituting our expressions for f (x), g (x), F (x) and $\dfrac{dg}{dx}$ into Equation 2, we obtain
$\int\overbrace{x}^{\color{purple}{\large g(x)}}\underbrace{\sin x}_{\color{purple}{\large f(x)}}\,dx = \overbrace{x}^{\color{purple}{\large g(x)}}\underbrace{(-\cos x)}_{\color{purple}{\large F(x)}} - \int\overbrace{1}^{\color{purple}{\large \frac{dg}{dx}}}\underbrace{(-\cos x)}_{\color{purple}{\large F(x)}}\,dx$
so that${\large\int}x\sin x\,dx = -x\cos x + {\large\int}\cos x\,dx$
and since we know that the integral of cos x is sin x + C, the final result is
${\large\int}x\sin x\,dx = -x\cos x + \sin x + C $(3) i
Let us see what would have happened in this example if we had chosen f (x) = x and $\dfrac{dg}{dx} = \sin x$.
In that case, F (x), the integral of x, is $\dfrac{x^2}{2}$ while $\dfrac{dg}{dx}$, the derivative of sin x, is cos x.
Substituting these expressions into Equation 2,
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
we obtain
$\int\underbrace{x}_{\color{purple}{\large f(x)}}\overbrace{\sin x}^{\color{purple}{\large g(x)}}\,dx = \underbrace{\dfrac{x^2}{2}}_{\color{purple}{\large F(x)}}\overbrace{(\sin x)}^{\color{purple}{\large g(x)}} - \int\underbrace{\dfrac{x^2}{2}}_{\color{purple}{\large F(x)}}\overbrace{(\cos x)}^{\color{purple}{\large\frac{dg}{dx}}}\,dx$(4)
As you can see, the integral appearing on the right–hand side of Equation 4 is no easier to find than the one we started with (in fact, it is harder!).
As we mentioned earlier, when we apply Equation 2, the choice of f (x) and g (x), in any particular situation, must be such that the integral $\displaystyle \int F(x)\dfrac{dg}{dx}\,dx$ is easier to find than the original integral, ${\large\int}f(x)g(x)\,dx$.
If, in using integration by parts, you find that you are left with a more complicated integral than the one you started with, this probably means that you have chosen f (x) and g (x) the wrong way round. Do not despair – simply change them over and start again.
✦ What would be the right choice of f (x) and g (x) to find the indefinite integral ${\large\int}x{\rm e}^{-x}\,dx$?
✧ If we choose f (x) = e−x, g (x) = x, then Equation 2 gives
${\large\int}x{\rm e}^{-x}\,dx = -x{\rm e}^{-x}+{\large\int}{\rm e}^{-x}\,dx$
leaving us with an easy integral to find. But if we choose f (x) = x, g (x) = e−x, then on applying Equation 2 we find
${\large\int}x{\rm e}^{-x}\,dx = \frac12x^2{\rm e}^{-x}+{\large\int}\frac12{\rm e}^{-x}\,dx$
which leaves us with a harder integral to find. Thus we should choose f (x) = e−x, g (x) = x.
Example 3
Use Equation 2,
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
to find ${\large\int}x\log_{\rm e}(x)\,dx$.
Solution
Here we could either choose
f (x) = x, and g (x) = loge x
orf (x) = loge x and g (x) = x
Remember that we need to be able to integrate f (x) in order to obtain F (x). It is much easier to integrate x than it
is to integrate loge x; so we choose f (x) = x and g (x) = logex. Then $F(x) = \dfrac12x^2$ and $\dfrac{dg}{dx} = \dfrac1x$. Substituting our expressions for f (x), g (x), F (x) and $\dfrac{dg}{dx}$ into Equation 2, we obtain:
$\displaystyle {\small\int}x\log_{\rm e}x\,dx = \dfrac12x^2\log_{\rm e}x - \int\left(\dfrac{x^2}{2}\right)\left(\dfrac1x\right)\,dx = \dfrac12x^2\log_{\rm e}x - \int\dfrac12 x\,dx$
Since the integral of $\dfrac12x$ is $\dfrac12\left(\dfrac12x^2\right) + C = \dfrac14x^2 + C$ we obtain as our final answer
$\displaystyle {\small\int}x\log_{\rm e}x\,dx = \dfrac12x^2\log_{\rm e}x -\dfrac14x^2 + C$
Question T2
Use Equation 2,
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
to find the indefinite integral ${\large\int}x^2\log_{\rm e}x\,dx$.
Answer T2
Take f (x) = x2, g (x) = logex. Then $F(x) = \dfrac13x^3$ and $\dfrac{dg}{dx} = \dfrac1x$.
Substituting these expressions in Equation 2,
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
we obtain
${\large\int}x^2\log_{\rm e}x\,dx = \dfrac13x^3\log_{\rm e}x - \dfrac13\displaystyle \int x^2\,dx = \dfrac13x^3\log_{\rm e}x - \dfrac19x^3 + C$
Definite integrals
So far, we have used integration by parts to find indefinite integrals, but the method can just as easily be used to evaluate definite integrals. Applying the fundamental theorem of calculus to Equation 1,
$\dfrac{d}{dx}\left[F(x)g(x)\right] = \dfrac{dF(x)}{dx}g(x) + F(x)\dfrac{dg}{dx}$(Eqn 1)
it quickly follows that
$\displaystyle \int_a^b\left[\dfrac{dF(x)}{dx}g(x) + F(x)\dfrac{dg}{dx}\right]\,{dx} = \left[F(x)g(x)\right]_a^b$
This can be rewritten as
$\displaystyle \int_a^b\dfrac{dF(x)}{dx}g(x)\,dx + \int_a^b F(x)\dfrac{dg}{x}\,{dx} = \left[F(x)g(x)\right]_a^b$
Rearranging this equation, and introducing again the notation f (x) for $\dfrac{dF}{dx}$, we arrive at the following formula:
$\displaystyle \int_a^bf(x)g(x)\,dx = \left[F(x)g(x)\right]_a^b + \int_a^b F(x)\dfrac{dg}{dx}\,{dx}$(5)
where $\dfrac{dF}{dx} = f(x)$
Example 4
Evaluate the integral ${\large\int_1^2}x{\rm e}^{2x}\,dx$, correct to four decimal places.
Solution
We use Equation 5, taking f (x) = e2x and g (x) = x, then $\dfrac{dg}{dx}$ = 1 and $F(x) = \dfrac12{\rm e}^{2x}$.
Substituting into Equation 5 we obtain
$\displaystyle \int_1^2x{\rm e}^{2x}\,dx = \left[\dfrac12x{\rm e}^{2x}\right]_1^2 - \dfrac12\int_1^2{\rm e}^{2x}\,dx = \left[\dfrac12x{\rm e}^{2x}\right]_1^2 - \dfrac12\left[\dfrac12{\rm e}^{2x}\right]_1^2$
$\displaystyle \phantom{\int_1^2x{\rm e}^{2x}\,dx }= (54.598150 - 3.698150) - \dfrac12(27.299075 - 3.694528) = 39.1013$
Question T3
Evaluate the integral ${\large\int}_0^1x{\rm e}^{3x}\,dx$, correct to four decimal places.
Answer T3
Take f (x) = e3x, g (x) = x. Then $F(x) = \dfrac13{\rm e}^{3x}$ and $\dfrac{dg}{dx} = 1$.
Substituting these expressions in Equation 5,
$\displaystyle \int_a^bf(x)g(x)\,dx = \left[F(x)g(x)\right]_a^b + \int_a^b F(x)\dfrac{dg}{dx}\,{dx}$(5)
we obtain
${\large\int}_0^1x{\rm e}^{3x}\,dx = \left[\dfrac13x{\rm e}^{3x}\right]_0^1 - \dfrac13{\large\int}_0^1{\rm e}^{3x}\,dx = \left[\dfrac13x{\rm e}^{3x}\right]_0^1 - \left[\dfrac19{\rm e}^{3x}\right]_0^1 \approx 4.5746$
2.2 Integrating by parts more than once
If you look back over the integrals appearing in Subsection 2.1, both in the text and in the Text questions, you
will see that many of them are of the form ${\large\int}xf(x)\,dx$ where f (x) is a function that is straightforward to
integrate, such as an exponential, a sine or cosine. These are, perhaps, the easiest integrals to find using integration by parts, and it is not hard to see why. Referring to Equation 2,
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
we see that if g (x) = x, then $\dfrac{dg}{dx} = 1$ and so an integral of this form becomes
${\large\int}xf(x)\,dx = xF(x) - {\large\int}F(x)\,dx$(6)
Provided that we can not only integrate f (x) to find F (x), but also integrate F (x) itself, then the right–hand side of Equation 6 is easy to find. This will certainly be the case if f (x) is an exponential function, a sine or cosine – for such functions can be integrated readily, to give functions of the same form which can also be integrated.
What would happen if instead of ${\large\int}xf(x)\,dx$, we had to find an integral of the form ${\large\int}x^2f(x)\,dx$?
Example 5
Find ${\large\int}x^2\cos x\,dx$.
Solution
We will try taking f (x) = cos x and g (x) = x2. (Remember that if this should prove unhelpful, we can always make the opposite choice, and see whether that works better.) With this choice, we have F (x) = sin x and $\dfrac{dg}{dx} = 2x$. Substituting these expressions into Equation 2, we find
${\large\int}x^2\cos x\,dx = x^2\sin x - {\large\int}2x\sin x\,dx = x^2\sin x - 2{\large\int}x\sin x\,dx$(7)
At first sight, the integral appearing on the right–hand side, i.e. ${\large\int}x\sin x\,dx$, may not look much better than the one we started with, ${\large\int}x^2\cos x\,dx$, but you may recognize it as an integral that you know how to do by integration by parts! In fact, we have already found it, in Example 2. Equation 3 tells us that
${\large\int}x\sin x\,dx = -x\cos x + \sin x + C$(Eqn 3)
and substituting this into Equation 7, we find
${\large\int}x^2\cos x\,dx = x^2\sin x - 2(-x\cos x + \sin x + C) = x^2\sin x + 2x\cos x - 2\sin x + C$ i
Any integral of the form ${\large\int}x^nf(x)\,dx$ containing the product of some positive integer power n of x and a function f (x) which is an exponential, or a sine or cosine (and so can easily be integrated as many times as is necessary), can be found by repeated application of the method of integration by parts. Note that – as our notation suggests – it is important to take x n to be g (x), for it is this that ensures that every time we integrate by parts, we are left with a similar integral, but one in which the power of x has been reduced by 1.
Question T4
Find the integral ${\large\int}x^2{\rm e}^{2x}\,dx$.
Answer T4
Take f (x) = e2x, g (x) = x2. Then $F(x) = \dfrac12{\rm e}^{2x}$ and $\dfrac{dg}{dx} = 2x$.
Substituting these expressions into Equation 2,
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
gives us
${\large\int}x^2{\rm e}^{2x}\,dx = \dfrac12x^2{\rm e}^{2x} - {\large\int}x{\rm e}^{2x}\,dx$(22)
Now apply integration by parts to the integral ${\large\int}x{\rm e}^{2x}\,dx$ taking f (x) = e2x, g (x) = x, giving $F(x) = \dfrac12{\rm e}^{2x}$ and $\dfrac{dg}{dx} = 1$. Thus
${\large\int}x{\rm e}^{2x}\,dx = \dfrac12x{\rm e}^{2x} - \dfrac12{\large\int}{\rm e}^{2x}\,dx = \dfrac12x{\rm e}^{2x} - \dfrac14{\rm e}^{2x} + C$
Substituting this result in Equation 22 gives us
${\large\int}x^2{\rm e}^{2x}\,dx = \dfrac12x^2{\rm e}^{2x} - \dfrac12x{\rm e}^{2x}\,dx + \dfrac14{\rm e}^{2x} + C$
2.3 Integrals of various functions, including loge x and ex sin x
You now know how to use integration by parts to find any integral of the form ${\large\int}x^nf(x)\,dx$, where f (x) is an exponential function, a sine or cosine function. In this subsection, we shall show you some clever tricks that will enable you to use integration by parts to find some other integrals. We will concentrate here on indefinite integrals, and so use Equation 2;
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
it is equally easy to use these methods to evaluate definite integrals, using Equation 5. i
$\displaystyle \int_a^bf(x)g(x)\,dx = \left[F(x)g(x)\right]_a^b + \int_a^b F(x)\dfrac{dg}{dx}\,{dx}$(Eqn 5)
The first trick simply involves the realization that the function f (x) in Equation 2 may be taken to be 1. This means that integration by parts, which is a technique that essentially applies to integrals of products, can in fact be applied to an integral of any function; we simply regard the integrand as the product of the original function and 1. This approach may often lead to integrals worse than the one we start with, but in some cases it is extremely useful, as in the following example.
Example 6
Find the integral ${\large\int}\log_{\rm e}x\,dx$.
Solution
Here we choose f (x) = 1, g (x) = logex. Then we have F (x) = x, $\dfrac{dg}{dx} = \dfrac1x$.
Substituting these expressions for f (x), g (x), F (x) and $\dfrac{dg}{dx} = g'(x)$ into Equation 2,
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
we obtain
$\int\underbrace{1}_{\color{purple}{\large f(x)}}\overbrace{\log_{\rm e} x}^{\color{purple}{\large g(x)}}\,dx = \underbrace{x}_{\color{purple}{\large F(x)}}\overbrace{\log_{\rm e}x}^{\color{purple}{\large g(x)}} - \int\underbrace{x}_{\color{purple}{\large F(x)}}\overbrace{1/x}^{\color{purple}{\large\frac{dg}{dx}}}\,dx = x\log_{\rm e}x - \int1\,dx = x\log_{\rm e}x - x + C$
So our final answer is
${\large\int}\log-{\rm e}x\,dx = x\log_{\rm e}x - x + C$
It is not always easy to know in advance whether this trick will work, but it is worth bearing it in mind as part of your repertoire of integration methods. Try applying it to the integral in the next question.
Question T5
Given that $\displaystyle \int\dfrac{x}{1+x^2}\,dx = \dfrac12\log_{\rm e}(1 + x^2) + C$ i
find the integral $\int \arctan x\,dx$.
Answer T5
Take f (x) = 1, g (x) = arctan 1x. Then F (x) = x and $\dfrac{dg}{dx} = \dfrac{1}{1+x^2}$
So Equation 2,
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
gives us
${\large\int}\arctan x\,dx = x\arctan x - \displaystyle \int\dfrac{x}{1+x^2}\,dx$
and, on using the result given in the question,
${\large\int}\arctan x\,dx = x\arctan x - \dfrac12\log_{\rm e}(1 + x^2) + C$
The second clever trick that you will often find useful involves applying Equation 2 twice,
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
this time in such a way as to obtain a simple algebraic equation for the unknown integral, which can then be solved. An example is the best way to present the method. We will let I denote the integral that we wish to evaluate, and for our example we will choose
$I = {\large\int}{\rm e}^x\sin(2x)\,dx$ i
If we take
f (x) = sin(2x) and g (x) = ex(8)
then $F(x) = -\dfrac12\cos(2x)$ and $\dfrac{dg}{dx} = {\rm e}^x$.
Equation 2 then gives us
$I = {\large\int}{\rm e}^x\sin(2x)\,dx = {\rm e}^x\left[-\dfrac12\cos(2x)\right] - {\displaystyle\int}\left[-\dfrac12\cos(2x)\right]{\rm e}^x\,dx$
i.e.$I = \dfrac12{\rm e}^x\cos(2x) + \dfrac12{\large\int}{\rm e}^x\cos(2x)\,dx$(9)
At this point, it may seem that integration by parts has failed; the integral remaining on the right–hand side of Equation 9 is no simpler than the one we started with. However, let us see what happens when we apply integration by parts to this integral, ${\large\int}{\rm e}^x\cos(2x)\,dx$.
We will take f (x) = cos(2x) and g (x) = ex. i
Then we have $F(x) = \dfrac12\sin(2x)$ and $\dfrac{dg}{dx} = {\rm e}^x$, so
$\displaystyle {\small\int}{\rm e}^x\cos(2x)\,dx = {\rm e}^x\left[\dfrac12\sin(2x)\right] - \int\left[\dfrac12\sin(2x)\right]{\rm e}^x\,dx = \dfrac12{\rm e}^x\sin(2x) - \dfrac12\underbrace{{\small\int}{\rm e}^x\sin(2x)\,dx}_{\color{purple}{\large{\text{This is the integral } I}}}$(10)
which contains the integral I with which we started!
Substituting Equation 10 into Equation 9 we obtain
$I = -\dfrac12{\rm e}^x\cos(2x) + \dfrac12\left[\dfrac12{\rm e}^x\sin(2x) - \dfrac12{\large\int}{\rm e}^x\sin(2x)\,dx\right]$
so that$I = -\dfrac12{\rm e}^x\cos(2x) + \dfrac14{\rm e}^x\sin(2x) - \dfrac14I$ i
We can now collect all the terms in I together on the left–hand side to give
$\dfrac54I = -\dfrac12{\rm e}^x\cos(2x) + \dfrac14{\rm e}^x\sin(2x) + C$
i.e.$I = \dfrac45\left[-\dfrac12{\rm e}^x\cos(2x) + \dfrac14{\rm e}^x\sin(2x) + C\right]$
or${\large\int}{\rm e}^x\sin(2x)\,dx = -\dfrac25{\rm e}^x\cos(2x) + \dfrac15{\rm e}^x\sin(2x) + C$ i
This method, using integration by parts twice and then solving the resulting equation to obtain the required integral, will work for any product of an exponential function with either a sine or cosine function. For such cases, it does not matter whether you choose the exponential function to be f (x) or g (x), as long as you make the same choice in both your integrations by parts. If you do not, your resulting equation will simply reduce to 0 = 0 – true, but not very useful!
Question T6
Find the integral ${\large\int}{\rm e}^{2x}\cos x\,dx$. (Start by taking f (x) = cos x and g (x) = e2x, then let $J = {\large\int}{\rm e}^{2x}\cos x\,dx$).
Answer T6
Taking f (x) = cos x and g (x) = e2x we have F (x) = sin x and $\dfrac{dg}{dx} = 2{\rm e}^{2x}$.
Then Equation 2,
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
gives us
$J = {\large\int}{\rm e}^{2x}\cos x\,dx = {\rm e}^{2x}\sin x - 2{\large\int}{\rm e}^{2x}\sin x\,dx$(23)
Now apply integration by parts to ${\large\int} {\rm e}^{2x}\sin x\,dx$ taking f (x) = sin x and g (x) = e2x. Then F (x) = − cos x and $\dfrac{dg}{dx} = 2{\rm e}^{2x}$.
Hence${\large\int}{\rm e}^{2x}\sin x\,dx = -{\rm e}^{2x}\cos x + 2{\large\int}{\rm e}^{2x}\cos x\,dx = -{\rm e}^{2x}\cos x + 2J$
Substituting this result into Equation 23 gives us
$J = {\rm e}^{2x}\sin x - 2(-{\rm e}^{2x}\cos x + 2J)$
and collecting all terms in ${\large\int}{\rm e}^{2x}\cos x\,dx$ on the left–hand side gives us
${\large\int}{\rm e}^{2x}\cos x\,dx = {\rm e}^{2x}\sin x + 2{\rm e}^{2x}\cos x + C$
so that$J = \dfrac15{\rm e}^{2x}\sin x + \dfrac25{\rm e}^{2x}\cos x + C$
It is sometimes possible to obtain a simple equation for your desired integral by integrating by parts just once, as in the next example.
Example 7
Find the integral ${\large\int}\cos 2x\,dx$.
Solution
If we let f (x) = cos x and g (x) = cos x then F (x) = sin x and $\dfrac{dg}{dx} = -\sin x$. Applying Equation 2 then gives us
${\large\int}\cos^2x\,dx = \sin x\cos x + {\large\int}\sin^2x\,dx$(11)
We can now use the trigonometric identity cos2 x + sin2 x = 1, so that sin2 x = 1 − cos2 x, in Equation 11, so that it becomes
${\large\int}\cos^2x\,dx = \sin x\cos x + {\large\int}(1-\cos^2x)\,dx = \sin x\cos x + {\large\int}1\,dx - {\large\int}\cos^2x\,dx$
Putting ${\large\int}1\,dx = x + C$ and collecting all ${\large\int}\cos^2x\,dx$ terms together on the left–hand side, we find
$2{\large\int}\cos^2x\,dx = \sin x\cos x + x + C$
or finally,
${\large\int}\cos^2x\,dx = \dfrac12\sin x\cos x + \dfrac12x + C$
Question T7
In the integral ${\large\int}\cos^4x\,dx$, take f (x) = cos x, g (x) = cos3 x, and show that
${\large\int}\cos^4 x dx = \dfrac14\sin x\cos^3x + \dfrac34{\large\int}\cos^2x\,dx$
[Hint: You will need to use the identity cos2 x + sin2 x = 1.]
Answer T7
With f (x) = cos x, g (x) = cos3 x we have F (x) = sin x and $\dfrac{dg}{dx} = -3\sin x\cos^2x$.
So Equation 2,
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
gives us
${\large\int} cos^4x\,dx = \sin x\cos^3x + 3{\large\int}\sin^2x\cos^2x\,dx$(24)
Writing sin2 x = 1 − cos2 x in the integral on the right–hand side of Equation 24 gives
${\large\int}\cos^4x\,dx = \sin x\cos^3x + 3{\large\int}\cos^2x(1 - \cos^2x)\,dx = \sin x\cos^2x + 3{\large\int}\cos^2x\,dx - 3{\large\int}\cos^4x\,dx$
Collecting together all terms in ${\large\int}\cos^4x\,dx$ on the left–hand side gives
$4{\large\int}\cos^4x\,dx = \sin x\cos^3x + 3{\large\int}\cos^2x\,dx$
or${\large\int}\cos^4x\,dx = \dfrac14\sin x\cos^3x + \dfrac34{\large\int}\cos^2x\,dx$
3 Integration by substitution
3.1 An introduction to the method of substitution
Evaluating an integral of the form ${\large\int}f(x)\,dx$ amounts to recognizing f (x) as the derivative of some function F (x). However, if F (x) is a rather complicated function of x, perhaps a function of a function of x, it may not be at all easy to spot that f (x) is its derivative.
✦ Use the chain rule to find the derivative of $\dfrac23(1+x)^{3/2}$.
✧ This function can be written as f [y (x)], where $f(y) = \dfrac23y^{3/2}$ and y (x) = 1 + x.
The chain rule tells us that $\dfrac{d}{dx}\left\{f\left[y(x)\right]\right\} = \dfrac{df(y)}{dy}\dfrac{dy(x)}{dx}$
and here, $\dfrac{df}{dy} = y^{1/2}$ and $\dfrac{dy}{dx} = 1$.
So we find
$\dfrac{d}{dx}\left[\dfrac23\left(1+x\right)^{3/2}\right] = (1+x)^{1/2}$
Since the derivative of $\dfrac23(1+x)^{3/2}$ is (1 + x)1/2, it follows that
${\large\int}(1+x)^{1/2}\,dx = \dfrac23(1+x)^{3/2} + C$(12)
This result is probably not one that would have been obvious to you if you had not first calculated the derivative of $\dfrac23(1+x)^{3/2}$. In this section, we explain an integration method that can often be used to bring integrals like ${\large\int}(1+x)^{1/2}\,dx$ into a much simpler form, such that you will probably be able to evaluate it by inspection, or by reference to a table of standard integrals.
We will first show you how the method works, by applying it to the integral that we have just found, i.e. ${\large\int}(1+x)^{1/2}\,dx$.
Our first step is to introduce a new variable y, equal to 1 + x. The integrand (1 + x)1/2, is then simply equal to y1/2. We must now decide what to do with the ‘dx’ inside the integral sign. Since y = 1 + x it follows that $\dfrac{dy}{dx} = 1$, and if $\dfrac{dy}{dx}$ could be regarded as the quotient of the two quantities dy and dx, we could rearrange this equation to read
dy = dx(13)
Strictly speaking, dy is not a quotient, and the symbols dy and dx have not been defined to have any meaning on their own. However the procedure that we outline here can certainly be justified (though a proof of its veracity lies outside the scope of FLAP and properly belongs in a course on mathematical analysis).
We use Equation 13 to transform the integral ${\large\int}(1+x){1/2}\,dx$ into another integral written just in terms of y, and putting dx = dy and (1 + x)1/2 = y1/2, we find that
${\large\int}(1+x)^{1/2}\,dx = {\large\int}y^{1/2}\,dy = \dfrac23y^{3/2} + C$ i
Finally, our answer must be written in terms of x, and so we replace y by (1 + x) on the right–hand side, to obtain
${\large\int}(1+x)^{1/2}\,dx = \dfrac23(1+x)^{3/2} + C$(14)
Although you may be worried by the use of Equation 13 in deriving Equation 14, you can see that the result is correct – it is exactly the same as Equation 12.
The method used here to find the integral ${\large\int}(1+x)^{1/2}\,dx$ is known as integration by substitution because we substitute the new variable y into our unknown integral to obtain another integral that we hope will be easier to evaluate.
Try the method that we used to derive Equation 14 on the next question.
Question T8
Find the integral ${\large\int}(x-2)^{4/3}\,dx$. Check your answer by differentiation.
Answer T8
Here, we make the substitution y = x − 2, and (since $\dfrac{dy}{dx} = 1$) we also write dy = dx. Then the integral becomes
${\large\int}(x - 2)^{4/3}\,dx = {\large\int}y^{4/3}\,dy$
We now evaluate this integral with respect to y
${\large\int}y^{4/3}\,dy = \dfrac37y^{7/3} + C$
and finally write y = x − 2 in this result, to obtain an answer in terms of x:
${\large\int}(x - 2)^{4/3}\,dx = \dfrac37(x - 2)^{7/3} + C$
To differentiate $\dfrac37(x - 2)^{7/3}$ we use the chain rule. This function can be written as f [y (x)], where
$f(y) = \dfrac37y^{7/3}$ and y = x − 2. So $\dfrac{df}{dx} = y^{4/3}$ and $\dfrac{dy}{dx} = 1$.
Substituting these results in the chain rule,
$\dfrac{d}{dx}\left\{f\left[y(x)\right]\right\} = \dfrac{df}{dy}\dfrac{dy}{dx}$
we find$\dfrac{d}{dx}\left(\dfrac37(x - 2)^{7/3}\right) = y^{4/3}\times 1 = (x - 2)^{4/3}$
which confirms the result obtained for the integral ${\large\int}(x - 2)^{4/3}\,dx$.
Here is a slightly harder example of integration by substitution:
Example 8
Find the integral ${\large\int}x^2\cos(x^3)\,dx$ by means of the substitution y = x3.
Solution
We note first that if y = x3, then $\dfrac{dy}{dx} = 3x^2$. Again, treating dy and dx as though they were ordinary algebraic quantities, we rewrite this equation as dy = 3x2 dx. We can rearrange this equation further if we want to, and at this point, it is convenient to notice that the ‘product’ x2 dx appears in the integral we are trying to find.
So we write $x^2\,dx = \dfrac13dy$ and we can also write cos(x3) = cos y so that, on making the substitution y = x3, we find that
${\large\int}x^2\cos(x^3)\,dx = \dfrac13{\large\int}\cos y\,dy = \dfrac13\sin y + C$
Finally, we substitute y = x3 into the right–hand side of this result, to obtain an answer for our integral in terms of x
${\large\int}x^2\cos(x^3)\,dx = \dfrac13\sin(x^3) + C$
You can easily check that this result is correct by differentiating it.
We will now list the steps involved in the method of substitution. As we do so, we shall show how we applied these to the integral in Example 8, and this will also show you how you can set your working out when you come to do problems of this sort.
| Method | Example: ${\large\int}x^2 \cos(x^3)\,dx$ | ||
|---|---|---|---|
| Step 1: | Decide what substitution y = g (x) to try. | We make the substitution y = x3. | |
| Step 2: | Calculate $\dfrac{dg}{dx}$ and write down the equation $dy = \dfrac{dg}{dx}\,dx$ It may be convenient to rearrange this equation. |
Here, $\dfrac{dg}{dx} = 3x^2$, so dy = 3x2 dx. We rearrange this equation into the form $x^2dx = \dfrac13dy$ |
|
| Step 3: | Make the substitution, to obtain an integral in terms of y. |
${\large\int}x^2\cos(x^3) = {\large\int}\underbrace{\cos(x^3)}_{\color{purple}{\large\cos y}}\times \underbrace{x^2\,dx}_{\color{purple}{\large{\frac13dy}}} = \dfrac13{\large\int}\cos y\,dy$ | |
| Step 4: | Integrate with respect to y. | $= \dfrac13\sin y + C$ | |
| Step 5: | Substitute g (x) for y in order to obtain a final answer that is a function of x. |
$= \dfrac13\sin(x^3) + C$ |
Question T9
Use integration by substitution to find the integrals:
(a) ${\large\int}x(5 + 2x^2)^{16}\,dx$, making the substitution y = 5 + 2x2
(b) ${\large\int}\cos^4(x)\sin(x)\,dx$, making the substitution y = cos x
Answer T9
(a) Step 1: We try the substitution y = g (x) = 5 + 2x2.
Step 2: Then $\dfrac{dg}{dx} = 4x$, so we write dy = 4x dx or, since the product x dx appears in the integral, $x\,dx = \dfrac14dy$.
Step 3: We now put (5 + 2x2)16 = y16 and $x\,dx = \dfrac14dy$ in the integral, to obtain
${\large\int}x(5+2x^2)^{16}\,dx = \dfrac14{\large\int}y^{16}\,dy$
Step 4: Now we integrate to obtain
$\dfrac14{\large\int}y^{16}\,dy = \dfrac14 \times \dfrac{1}{17}y^{17} + C = \dfrac{1}{68}y^{17} + C$
Step 5: Finally, we substitute y = 5 + 2x2 into the answer obtained in Step 4, to arrive at an answer which is a function of x:
${\large\int}x(5+2x)^{16}\,dx = \dfrac{1}{68}(5+2x^2)^{17} + C$
(b) Step 1: We try the substitution y = g (x) = cos x.
Step 2: Then $\dfrac{dg}{dx}= -\sin x$, so we write dy = − sin x dx or, since the product sin x dx appears in the integral, sin x dx = −dy.
Step 3: We now put y = cos x and sin x dx = −dy in the integral, to obtain
${\large\int}\cos^4x\sin x\,dx = -{\large\int}y^4\,dy$
Step 4: Now we integrate to obtain $-{\large\int}y\,dy = -\dfrac15y^5 + C$.
Step 5: Finally we substitute y = cos x into the answer obtained in Step 4, to arrive at an answer which is a function of x:
${\large\int}\cos^4x\sin x\,dx = -\dfrac15\cos^5x + C$
Much the hardest part of the method of integration by substitution is to know what substitution to make – after all, we begin with an integral that we cannot find, and the point of the method is to arrive in Step 3 at an integral which is easier, and this obviously depends on our choice of g (x). Skill at picking a suitable substitution will come with practice and experience, and in Subsection 3.2Subsections 3.2 and Subsection 3.33.3, we will present you with several examples of particular substitutions which will work for certain types of integrals.
3.2 Integrals of ‘a function and its derivative’
In this subsection, we shall introduce you to a particular class of integrals that can always be simplified by a suitable substitution. We will start with an example.
Example 9
Find the integral ${\large\int}x\sqrt{1+x^2}\,dx$. i
Solution
Step 1: We will try the substitution y = g (x) = 1 + x2.
Step 2: $\dfrac{dg}{dx} = 2x$, so dy = 2x dx. As x dx appears in the integral, we rearrange this equation to read $x\,dx = \dfrac12dy$.
Step 3: We also have $\sqrt{1+x^2} = y^{1/2}$. Substituting this, and $x\,dx = \dfrac12dy$ into the integral, we obtain
${\large\int}x\sqrt{1+x^2}\,dx = \dfrac12{\large\int}\sqrt{y\os}\,dy$
Step 4: Integrating with respect to y gives us $\dfrac12{\large\int}\sqrt{y\os}\,dy = \dfrac13y^{3/2} + C$
Step 5: Finally, we substitute y = 1 + x2 into the answer obtained in Step 4, to obtain
${\large\int}x\sqrt{1+x^2}\,dx = \dfrac13(1+x^2)^{3/2} + C$
Question T10
Find the integral ${\large\int}(\cos x){\rm e}^{\sin x}\,dx$ by making the substitution y = sin x.
Answer T10
(a) Step 1: We use the suggested substitution y = g (x) = sin x.
Step 2: Then $\dfrac{dg}{dx} = \cos x$ so we write dy = cos(x) dx
Step 3: We now put esin x = ey and dy = cos(x) dx in the integral, to obtain
${\large\int}(\cos x){\rm e}^{\sin x}\,dx = {\large\int}{\rm e}^y\,dy$
Step 4: Now we integrate: ${\large\int}{\rm e}^y\,dy = {\rm e}^y + C$
Step 5: Finally, we write y = sin x in the answer obtained in Step 4, to arrive at an answer which is a function of x:
${\large\int}(\cos x){\rm e}^{\sin x}\,dx = {\rm e}^{\sin x} + C$
You may have noticed that the integral in Example 9, ${\large\int}x(1+x^2)^{1/2}\,dx$, and that of Question T10, ${\large\int}(\cos x){\rm e}^{\sin x}\,dx$, have something in common. In both cases, the integrand is not simply a function of the suggested g (x) – instead it is a product of some function of g (x) and the derivative $g'(x) \left(=\dfrac{dg}{dx}\right)$.
For example, we can write the integrand x (1 + x2)1/2 as $2x \times \dfrac12(1+x^2)^{1/2}$ i.e. as a product of the function of a function $\dfrac12\left[g(x)\right]^{1/2}$ and the derivative g ′ (x) = 2x so that ${\large\int}x(1+x^2)^{1/2}\,dx ={\large\int}\underbrace{2x}_{\color{purple}{\large g'(x)}}\underbrace{\frac12(1+x^2)^{1/2}}_{\underbrace{\color{purple}{\large\frac12g(x)^{1/2}}}_{\color{purple}{\large\text{function of } g(x)}}}\,dx$
✦ Write (cos x) esin x in the form ‘g ′ (x) × [function of g (x)]’, where g (x) = sin x.
✧ Here g ′ (x) = cos x, so (cos x) esin x = eg (x) × g ′ (x)
✦ Write e2x(1 + e2x)3 in the form ‘g ′ (x) × [function of g (x)]’, where g (x) = e2x.
✧ Here g ′ (x) = 2e2x so that
e2x(1 + e2x)3 = 2 e2x × ½ (1 + e2x)3 = g ′ (x) × ½ (1 + e2x)3 = g ′ (x) × ½ [1 + g (x)]3
Integrals of the form ${\large\int}g'(x) p[g(x)]\,dx$ i, where the integrand is the product of some composite function p [g (x)] and the derivative g ′ (x), are sometimes called ‘integrals of a function and its derivative’. Such integrals can always be simplified by making the substitution y = g (x). Let us see why.
When we make this substitution in the integral
${\large\int}p[g(x)]g'(x)\,dx$
the expression p [g (x)] becomes simply p (y), and we can also write
dy = g ′ (x)dx
Thus the integral becomes
${\large\int}p(y)\,dy$
and so, if we know how to integrate the function p (y), the substitution y = g (x) will enable us to find the original integral ${\large\int}p[g(x)]g'(x)\,dx$.
Indeed, if we introduce the notation $P(y) = {\large\int}p(y)\,dy$, and remember that our final answer must be given as a function of x by writing y = g (x) in P (y), we can write down a neat formula for integrals of this sort:
${\large\int}p[g(x)]g'(x)\,dx = P[g(x)]$ where $P(y) = {\large\int}p(y)\,dy$(15)
Example 10
Find ${\large\int}{\rm e}^{2x}(1 + {\rm e}^{2x})^3\,dx$.
Solution
We make the substitution y = g (x) = e2x so that g ′ (x) = 2e2x.
The integral then becomes ${\large\int}g'(x)\times\frac12[1 + g(x)]^3\,dx$
so that in this case the function $p(y) = \frac12(1 + y)^3$.
The integral P (y) is therefore given by P (y) = ${\large\int}p(y)\,dy = {\large\int}\frac12(1 + y)^3\,dy$ which can be simplified to $P(y) = \frac18(1 + y)^4 + C$.
and this means that $P[g(x)] = \frac18(1+{\rm e}^{2x})^4 + C$
Finally Equation 15 becomes ${\large\int}{\rm e}^{2x}(1+{\rm e}^{2})^3\,dx = \frac18(1+{\rm e}^{2x})^4 + C$
Whenever you encounter an integral that you think requires a substitution, you should first check whether it is of the form given on the left–hand side of Equation 15. If it is, the substitution y = g (x) may well enable you to find it. There is no need to memorize Equation 15 though – the method is the important thing. Don’t forget that g ′ (x) may simply be a constant. Thus, for example, the integral ${\large\int}(3+2x)^{7/2}\,dx$ is of this form – we can write it as ${\large\int}\left[\frac12(3+2x)^{7/2}\right]\times 2\,dx$, observing that the derivative of g (x) = (3 + 2x) is simply 2.
Question T11
Find the integrals
(a)${\large\int}(2+\cos x)\sin x\,dx$ (b)$\displaystyle \int\dfrac{x}{x^2+1}\,dx$ i
Answer T11
(a) Step 1: Note first that the derivative of (2 + cos x) is (− sin x). So we can write the integrand in the form ‘p [g (x)] × g ′ (x)’, where g (x) = 2 + cos x. This suggests the substitution y = 2 + cos x.
Step 2: Then we write dy = − sin x dx
Step 3: Substituting (2 + cos x)2 and − sin x dx = dy in the integral, we obtain
${\large\int}\sin x(2 + \cos x)^7\,dx = -{\large\int}y^7\,dy$
Step 4: Now we integrate ${\large\int}(-y^7)\,dy = -\dfrac18y^8 + C$
Step 5: Finally, we write y = 2 + cos x, to arrive at an answer which is a function of x:
${\large\int}\sin x(2 + \cos x)^7\,dx = -\dfrac18(2 + \cos x)^8 + C$
(b) Step 1: Note first that the derivative of (x2 + 1) is 2x. So we can write the integrand in the form p [g (x)] × g ′ (x), where g (x) = x2 + 1. This suggests the substitution y = x2 + 1.
Step 2: Then dy = 2x dx, or $x\,dx = \dfrac12dy$.
Step 3: Substituting $\dfrac{1}{x^2+1} = \dfrac1y$ and $x\,dx = \dfrac12dy$ in the integral, we obtain
${\large\int}\dfrac{x}{x^2+1}\,dx = \dfrac12{\large\int}\dfrac1y\,dy$
Step 4: Now we integrate: $\dfrac12{\large\int}\dfrac1y\,dy = \dfrac1y\log_{\rm e}y + C$
Step 5: Finally, we write y = x2 + 1 to give an answer which is a function of x:
${\large\int}\dfrac{x}{x^2+1}\,dx = \dfrac12\log_{\rm e}(x^2 +1) + C$
As you gain more practice with integrals of a function and its derivative, you will probably find that you can write down the answer almost immediately, by intelligent guesswork.
3.3 More examples of integration by substitution
In this subsection, we will show you some other examples of integration by substitution. Each example will be followed by a similar Text question, which should help you to become familiar with the lines of attack likely to work with different types of integral.
Example 11
Find the integral $\displaystyle \int\dfrac{x}{(1+2x)^2}\,dx$.
Solution
Step 1: Here we will try the substitution y = g (x) = 1 + 2x
Step 2: Then $\dfrac{dg}{dx} = 2$, so dy = 2 dx, i.e. $dx = \frac12dy$.
Step 3: The integral can now be written in the form $\displaystyle \int\left[\dfrac{x}{(1+2x)^2}\right]\dfrac12\,dy$
The integrand, which is in square brackets, must be converted into a function of y, and in order to do this we need to invert the relation y = 1 + 2x to obtain x in terms of y. i This gives $x = \frac12(y - 1)$. Thus on making the substitution y = 1 + 2x, the integral becomes
$\displaystyle \dfrac{x}{(1+2x)^2}\,dx = \int\left[\dfrac{1}{y^2}\times\dfrac{(y-1)}{2}\right]\times\left(\dfrac12y\right) = \dfrac14\int\left(\dfrac1y-\dfrac{1}{y^2}\right)\,dy$
Step 4: Evaluating the integral with respect to y (on the right) gives
$\displaystyle \dfrac14\int\left(\dfrac1y-\dfrac{1}{y^2}\right)\,dy = \dfrac14\left(\log_{\rm e}y+\dfrac1y\right) + C$
Step 5: Substituting y = 1 + 2x in this result gives the final answer
$\displaystyle \int\dfrac{x}{(1+2x)^2}\,dx = \dfrac14\left(\log_{\rm e}(1+2x)+\dfrac{1}{1+2x}\right) + C$
This example illustrates the point that if a particular function of x, in this case (1 + 2x), features prominently in the integrand, it is worth trying that function as g (x).
Question T12
Find ${\large\int} x(1+x)^{5/2}\,dx$ by making the substitution y = 1 + x.
Answer T12
Step 1: We take y = 1 + x.
Step 2: Then dy = dx.
Step 3: To express the integrand as a function of y, we invert the relation y = 1 + x to obtain x = y − 1. Then x (1 + x)5/2 = (y − 1)y5/2, so we have
${\large\int}x(1+ x)^{5/2}\,dx = {\large\int}(y - 1)y^{5/2}\,dy$
Step 4: Integrate with respect to y
${\large\int}(y-1)y^{5/2}\,dy = {\large\int}y^{7/2}\,dy - {\large\int}y^{5/2}\,dy = \dfrac29y^{9/2} - \dfrac{2}7{}y^{7/2} + C$
Step 5: Express the result in terms of x
${\large\int}x(1+x)^{5/2}\,dx = \dfrac29(1+x)^{9/2} - \dfrac27(1+x)^{7/2} + C$
In Example 11 and Question T12, it was necessary at one stage to find x in terms of y. Sometimes it is simpler to start with x as a function of y, and write the substitution in the form x = h (y). In that case, we simply substitute h (y) into the integrand, and replace dx by $\dfrac{dh}{dy}dy$. The next example is of this type.
Example 12
Find the integral $\displaystyle \int\dfrac{1}{\sqrt{1-x^2}}\,dx$.
Solution
Step 1: The presence of $\sqrt{1-x^2}$ in the denominator suggests we should make use of the trigonometric relationship cos2 y = 1 − sin2 y.
So we try the substitution x = h (y) = sin y.
Step 2: Then $\dfrac{dh}{dy} = \cos y$, and so dx = cos y dy and the integral can be written in the form
$\displaystyle \int\left[\dfrac{1}{\sqrt{1-x^2}}\right](\cos y\,dy$)
where again the expression in square brackets must be converted into a function of y.
Step 3: With this substitution, $\sqrt{1-x^2} = \sqrt{\smash[b]{1-\sin^2y}}$ so the integral becomes i
$\displaystyle \int\dfrac{1}{\sqrt{1-x^2}}\,dx = \int\dfrac{\cos y}{\cos y}\,dy = {\small\int}1\,dy$
Step 4: The integral is easy: $\int 1\,dy = y + C$.
Step 5: Finally, we express the result in terms of x, using the fact that if x = sin y, then y = arcsin x, and so
$\displaystyle \int\dfrac{1}{\sqrt{1-x^2}}\,dx = {\small\int}1\,dy = y + C = \arcsin x + C$
You may already have known the integral in Example 12 – it appears in every table of standard integrals. The method used to find it in Example 12 opens the way to finding many other integrals of the same type. Consider, for example, the integral $\displaystyle \dfrac{1}{\sqrt{9-x^2}}\,dx$. What substitution might we make here?
The experience that we gained in Example 12 suggests that we want something like x = a sin y, where a is a suitable constant. We must choose a so that the identity cos2 y + sin2 y = 1 can be used to turn $\sqrt{9-x^2}$ into a multiple of cos y. Then this will cancel the cos y term in dx = a cos y dy, leaving us with a very simple integral. Putting x = a sin y into $\sqrt{9-x^2}$, it becomes $\sqrt{\smash[b]{9-a^2\sin^2y}}$, and if we choose a = 3 it will be equal to $\sqrt{\smash[b]{9-a^2\sin^2y}} = 3\cos y$. So the substitution x = 3 sin y can be used to simplify the integral. The following integral is of the same type; so try replacing x by a sin y for a suitable choice of the constant a.
Question T13
Find the integral $\displaystyle \dfrac{1}{\sqrt{16-x^2}}\,dx$
Answer T13
Step 1: We want to make a substitution of the form x = a sin y, which will ensure that $\sqrt{1-16x^2}$ is a multiple of cos y. However, 1 − 16a2 sin2 y = cos2 y if $a = \dfrac14$.
So we take $x = \dfrac14\sin y$.
Step 2: Then $dx = \dfrac14\cos y\,dy$.
Step 3: With $\sqrt{1-16x^2} = \cos y$ and $dx = \dfrac14\cos y\,dy$ the integral becomes
$\displaystyle \int\dfrac{1}{\sqrt{1-16x^2}}\,dx= \int\dfrac14\dfrac{\cos y}{\cos y}\,dy = \int \dfrac14\,dy$
Step 4: Integrate with respect to y: $\displaystyle \dfrac14\,dy = \dfrac14y + C$.
Step 5: If $x = \dfrac14\sin y$, y = arcsin(4x). So, expressing the result in terms of x gives us
$\displaystyle \int\dfrac{1}{\sqrt{1-16x^2}}\,dx = \arcsin(4x) + C$
The substitution x = sin y can also be used to find integrals where the integrand is some other function of $\sqrt{1-x^2}$ as in the next question.
Question T14
Find the integral ${\large\int}\sqrt{1-x^2}\,dx$.
[Hint: You will find the solution to Example 7 helpful here; you will also need to use the identity cos2 y + sin2 y = 1, both in making the substitution and in expressing the final answer in terms of x.]
Answer T14
Step 1: Take x = sin y.
Step 2: Then dx = cos y dy.
Step 3: The integrand $\sqrt{1 - x^2} = \cos y$ (using cos2 y + sin2 y = 1). So the integral becomes
${\large\int}\sqrt{1 - x^2}\,dx = {\large\int}\cos^2y\,dy$.
Step 4: The integral with respect to y was found in Example 7:
${\large\int}\cos^2y\,dy = \dfrac12\sin y\cos y + \dfrac12y + C$
Step 5: To express this answer in terms of x, we put sin y = x, so y = arcsin x. We must also express cos y in terms
of x; and, since cos2 y + sin2 y = 1, we have $\cos y = \sqrt{\smash[b]{1 - \sin^2y}} = 1 - x^2$.
So${\large\int}\sqrt{1 - x^2}\,dx = \dfrac12x\sqrt{1 - x^2} + \dfrac12\arcsin x + C$
Our next example is one of another class of integrals that can be found by means of a different trigonometric substitution.
Example 13
Find the integral $\displaystyle \int\dfrac{1}{1+x^2}\,dx$.
Solution
Step 1: Here, we will make the substitution x = h (y) = tan y.
Step 2: Then $\dfrac{dx}{dy} = \dfrac{dh}{dy} = \sec^2 y$, so dx = sec2 y dy.
Step 3: With this substitution, 1 + x2 = 1 + tan2 y. At this point, we use the trigonometric identity 1 + tan2 y = sec2 y. Thus the integrand is simply $\dfrac{1}{\sec^2y}$.
Using this, and dx = sec2 y dy, we find that the integral becomes
$\displaystyle \int\dfrac{1}{1+x^2}\,dx = \int \dfrac{\sec^2y}{\sec^2y}\,dy = {\small\int}1\,dy$
Step 4: $\int 1\,dy = y + C$
Step 5: If x = tan y, then y = arctan x, so the final answer is
$\displaystyle \int\dfrac{1}{1+x^2}\,dx = \arctan x + C$
The integral in Example 13 may also be one that you have seen before – but again, the point is that the method can be generalized to other integrals of the same form.
Consider $\displaystyle \int\dfrac{1}{4+x^2}\,dx$. Here, we might reason that a substitution of the form x = a tan y should work; we choose
the constant a so that the identity 1 + tan2 y = sec2 y can be used to transform (4 + x2) into a multiple of sec2 y. Putting x = a tan y into (4 + x2), it becomes (4 + a2 tan2 y); and if we choose a = 2, this becomes 4 (1 + tan2 y) = 4 sec2 y. So x = 2 tan y is the substitution we want here.
Question T15
Find the integral $\displaystyle \int\dfrac{1}{5+4x^2}\,dx$.
Answer T15
Step 1: We want a substitution of the form x = a tan y, such that (5 + 4x2) is a multiple of sec2 y.
We see that 5 + 4a2 tan2 y = 5 sec2 y if 4a2 = 5, i.e. if $a = \dfrac12\sqrt{5\os}$. So we take $x = \dfrac12\sqrt{5\os}\tan y$.
Step 2: Then $x = \dfrac12\sqrt{5\os}\sec^2 y\,dy$
Step 3: Since 5 + 4x2 = 5 sec2 y the integral becomes
$\displaystyle \int\dfrac{1}{5 + 4x^2}\,dx = \int\dfrac12\dfrac{\sqrt{5\os}\sec^2 y}{5\sec^2 y}\,dt = \int \dfrac{1}{2\sqrt{5\os}}\,dy$
Step 4: Integrating with respect to y gives us $\displaystyle \int\dfrac{1}{2\sqrt{5\os}}\,dy = \dfrac{1}{2\sqrt{5\os}}y + C$
Step 5: Expressing this result in terms of x, using $y = \arctan\left(\dfrac{2x}{\sqrt{5\os}}\right)$
gives us $\displaystyle \int\dfrac{1}{5 + 4x^2}\,dx = \dfrac{1}{2\sqrt{5\os}}\arctan\left(\dfrac{2x}{\sqrt{5\os}}\right) + C$
3.4 Definite integrals; transforming the limits
So far in this section, we have dealt exclusively with indefinite integrals. Of course, once you have found the appropriate indefinite integral, finding a definite integral is just a matter of putting in the limits of integration. For example, let us return to the integral of Example 8,
${\large\int}x^2\cos(x^3)\,dx = \dfrac13\sin(x^3) + C$
If, say, we want to evaluate the definite integral ${\large\int}_0^2x^2\cos(x^3)\,dx$, we simply put the limits in:
${\large\int}_0^2x^2\cos(x^3)\,dx = \left[\dfrac13\sin(x^3)\right]_0^2$
$\phantom{{\large\int}_0^2x^2\cos(x^3)\,dx }= \dfrac13\left(\sin(2^3) - \sin 0\right)$
$\phantom{{\large\int}_0^2x^2\cos(x^3)\,dx }= \dfrac13\sin 8 = 0.3298$ (to 4 decimal places)(16) i
However, there is sometimes slightly less work involved if we find the definite integral directly, in terms of the new variable y. This involves transforming the limits of the definite integral. To see how it works, let us go through the process of substituting y = x3 into the above integral.
As before, we write cos(x3) = cos y and $x^2\,dx = \dfrac13dy$. We must now note that if x ranges from 0 to 2, then y = x3 ranges from 03 to 23, i.e. between 0 and 8. So the limits of integration in the integral with respect to y are 0 and 8. Thus we obtain
${\large\int}_0^2x^2\cos(x^3)\,dx = \dfrac13{\large\int}_0^8\cos y\,dy = \dfrac13\left[\sin y\right]_0^8 = \dfrac13(\sin 8-\sin0) = \dfrac13\sin 8 = 0. 3298$ (to 4 decimal places)
as in Equation 16.
✦ In Example 9, you saw that the indefinite integral $\int_a^b x(1 + x^2)^{1/2}dx$ could be found by means of the substitution y = 1 + x2. If we want to evaluate the definite integral $\int_a^b x(1 + x)dx$ using this substitution, what are the limits in the integral with respect to y?
✧ When x = 1, y = 1 + 12 = 2; and when x = 3, 1 + 32 = 10.
So the lower limit is 2 and the upper limit is 10.
So, for definite integrals, when we make the substitution y = g (x), we have two ways of proceeding. We can either follow Steps 1–5 of Subsection 3.1, finding the indefinite integral first, and putting in the x limits of integration at the end of the calculation.
Alternatively, when carrying out Step 3 and writing the integral in terms of y, we can at the same time transform the x limits of integration (let us call the lower limit a and the upper limit b) into the corresponding y limits of integration, g (a) and g (b). Often this will save a little time because there is then no need to carry out Step 5. i Use the second procedure to answer the following question.
Question T16
Evaluate the integral ${\large\int}_0^4x\sqrt{4-x\os}\,dx$ by means of the substitution y = 4 − x.
Answer T16
Step 1: We take y = 4 − x.
Step 2: Then dy = −dx.
Step 3: If y = 4 − x, then x = 4 − y so the integrand $x\sqrt{4 - x\os}$ becomes $(4 - y)\sqrt{y\os}$.
When x = 0, y = 4, and when x = 4, y = 0. Thus the integral becomes
${\large\int}_0^4x\sqrt{4-x\os}\,dx = {\large\int}_4^0(4-y)\sqrt{y\os}(-dy) = -{\large\int}_4^04y^{1/2}\,dy + {\large\int}_4^0y^{3/2}\,dy$
Step 4: We now evaluate the definite integrals with respect to y:
$-{\large\int}_4^04\sqrt{y\os}\,dy + {\large\int}_4^0y^{3/2}\,dy = -\left[\dfrac83y^{3/2}\right]_4^0 + \left[\dfrac25y^{5/2}\right]_4^0 = -\dfrac83(0-4^{3/2}) + \dfrac25(0-4^{5/2}) \approx 8.5333$
An application to electricity and magnetism
We will end this subsection with an application of integration by substitution to electricity and magnetism. i
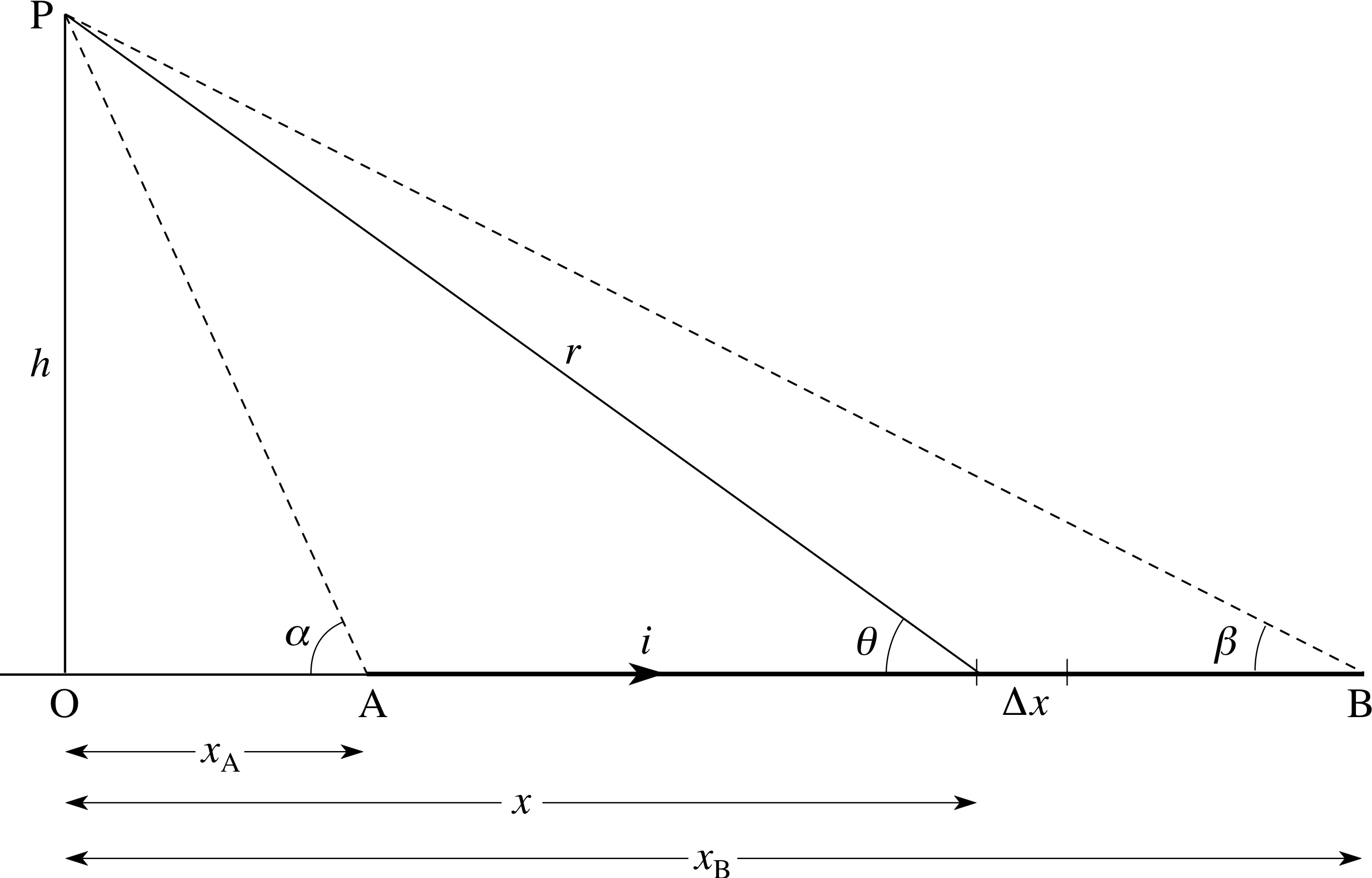
Figure 1 An electrical current through a segment of wire AB.
Example 14
Figure 1 shows a wire AB carrying a current I (denoted i on the figure).
Such a current produces a magnetic field around the wire, and each small element of the wire, ∆x say, makes a small contribution to this field. i The object of this example is to determine the magnitude B of the resulting field at P due to the contributions from all such elements from A to B.
Solution
First we need to know that the current through the element ∆x produces a contribution to the field at P perpendicular to the plane of the paper, and of magnitude $\dfrac{I\sin\theta\Delta x}{r^2}$. Thus the total magnitude B of the field at P is $\displaystyle \int_{x_A}^{x_B}\dfrac{I\sin\theta\Delta x}{r^2}\,dx$ and, since h = r sin θ while I and h are constants, we have
$\displaystyle B = \int_{x_A}^{x_B}\dfrac{I\sin\theta\Delta x}{r^2}\,dx = I\int_{x_A}^{x_B}\dfrac{h}{r^3}\,dx = I\int_{x_A}^{x_B}\dfrac{h}{(x^2+h^2)^{3/2}}\,dx$
In order to evaluate the integral on the right–hand side, we make the substitution x = h tan ϕ so that dx = h sec2 ϕ dϕ, and therefore
$\displaystyle I\int\dfrac{h}{(x^2+h^2)^{3/2}}\,dx = I\int\dfrac{h^2\sec^2\varphi}{(h^2\tan^2\varphi+h^2)^{3/2}}\,d\varphi = I\int\dfrac{h^2\sec^2\varphi}{h^3\sec^3\varphi}\,d\varphi = I\int\cos\varphi\,d\varphi = \dfrac Ih\sin\varphi + C$ (17)
In deriving this equation we have made use of the identity sec2 ϕ = 1 + tan2 ϕ. Now we substitute for ϕ in terms of x in Equation 17 using the fact that tan ϕ = x implies that sin ϕ = x, see Figure 2.
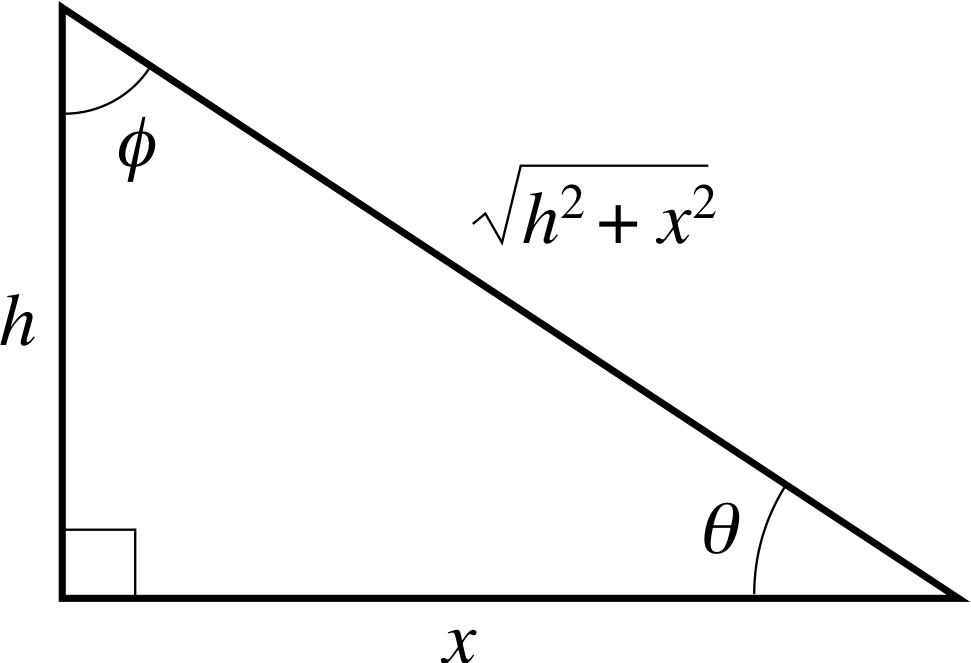
Figure 2 Geometrical meaning of the substitution x = h tan ϕ. Notice that sin ϕ = cos θ.
It follows that
$\displaystyle I\int\dfrac{h}{(x^2+h^2)^{3/2}}\,dx = \dfrac Ih\sin\varphi + C$(Eqn 17)
We can now evaluate the magnitude of the field at P, and write
$\displaystyle B = \int_{x_A}^{x_B}\dfrac{I\sin\theta\Delta x}{r^2}\,dx = \left[\dfrac{Ix}{h\sqrt{h^2+x^2}}\right]_{x_A}^{x_B} = \dfrac Ih\left[\dfrac{x_B}{\sqrt{\smash[b]{h^2+x_B^2}}} - \dfrac{x_A}{\sqrt{\smash[b]{h^2+x_A^2}}}\right]$
Using the angles α and β defined by Figure 1, we obtain the neat result
$B = \dfrac Ih(\cos\beta - \cos\alpha)$(18)
There is one circumstance that is of particular interest, namely when we wish to estimate the field at points close to a very long straight wire; in which case we can assume that the wire is of infinite length (since the contributions from distant sections of the wire are insignificant).
This corresponds to choosing α = π and β = 0, in Equation 18, and we then have the useful result
$B \approx \dfrac{2I}{h}$(19)
4 Which method to try?
In the Text questions you have done so far in this module, either you have been told what integration method to use, or it has been clear by comparison with what has gone immediately before. It is time for you now to start deciding for yourself what the best line of attack will be and, if you decide to use substitution, to choose for yourself what substitution to try. To help you with this, we shall list below some types of integrals and comment on the best methods of finding them. (As we are concerned here with the method of integration, we shall consider only indefinite integrals.)
4.1 Some helpful advice
1 Integrals of products of certain functions.
Integration by parts will always work if the integrand is a product of any two of: an integer power of x; a sine or cosine; an exponential. There are certain other products for which it works: for example, x loge x. However, integration by parts is certainly not applicable to all products (try applying it, for example, to ${\large\int}x^2\cos(x^3)\,dx$ and you will soon discover that it doesn’t work).
2 Integrals of the form ${\large\int}p[g(x)]g'(x)\,dx$.
Make the substitution y = g (x), which will transform the integral into ${\large\int}p(y)\,dy$
3 Integrals of the form $\displaystyle \int\dfrac{1}{A-Bx^2}\,dx$ or ${\large\int}\sqrt{A-Bx^2}\,dx$, where A and B are positive constants.
Use a substitution of the form x = a sin y, where a is chosen so that $\sqrt{A-Bx^2}$ turns into a multiple of cos y when you make the substitution. In this case, we can guarantee that this substitution will work.
4 Integrals of the form $\displaystyle \int\dfrac{1}{A+Bx^2}\,dx$ where A and B are positive constants.
Use a substitution of the form x = a tan y, where a is chosen so that A + Bx2 turns into a multiple of sec2 y when you make the substitution. Here too, a substitution of this sort will certainly work.
5 Integrals in which the integrand contains some particular function of x.
For example, in the integral ${\large\int}{\rm e}^{2x}(1 + {\rm e}^{2x})^3\,dx$ we might try g (x) = e2x. Of course, there may be several functions of x appearing in the integrand. However, if a particular function of x appears in the denominator, or is raised to some power, that is a good one to try as g (x).
4.2 Exercises
In the following question, all the integrals except one can be found using the methods introduced in this module; we leave it to you to choose which method to use. The exception is an integral that can be done in a very simple fashion, it doesn’t require integration by parts or the method of substitution.
Question T17
Find the indefinite integrals
(a) $\displaystyle \int\dfrac{(x+3)^2}{(x+5)^4}\,dx$ (b) ${\large\int}3x\cos\left(\frac12x\right)\,dx$ (c) $\displaystyle \int\dfrac{1}{\sqrt{2-x^2}}\,dx$ (d) $\displaystyle \int\dfrac{x}{\sqrt{2-x^2}}\,dx$ (e) ${\large\int}\sqrt{x\os}(1+x)\,dx$
Answer T17
(a) This integral can be found by a suitable substitution.
Step 1: Since (x + 5) appears in the denominator of the integral, the best substitution to try is y = x + 5.
Step 2: Then dx = dy.
Step 3: If y = x + 5, then x + 3 = y − 2. So the integral becomes
$\displaystyle \int\dfrac{(x+3)^2}{(x+5)^4}\,dx = \int\dfrac{(y-2)^2}{y^4}\,dy = \int\left(\dfrac{1}{y^2}-\dfrac{4}{y^3}+\dfrac{4}{y^4}\right)\,dy$
Step 4: Integrating with respect to y gives us $\displaystyle \int\dfrac{(y-2)^2}{y^4}\,dy = \int\left(\dfrac{1}{y^2}-\dfrac{4}{y^3}+\dfrac{4}{y^4}\right)\,dy = -\dfrac1y+\dfrac{2}{y^2}-\dfrac{4}{3y^3} + C$
Step 5: Expressing the result in terms of x gives us
$\displaystyle \int\dfrac{(x+3)^2}{(x+5)^4}\,dx = -\dfrac{1}{x+5}+\dfrac{2}{(x+5)^2}-\dfrac{4}{3(x+5)^3} + C$
(b) This integral can be found by integrating by parts. We take f (x) = cos(x/2), g (x) = 3x; then F (x) = 2 sin(x/2) and $\dfrac{dg}{dx} = 3$. Substituting into Equation 2,
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
gives us
$\displaystyle \int 3x\cos\dfrac x2\,dx = 6x\sin\dfrac x2 - 6\int \sin\dfrac x2 = 6x\sin\dfrac x2 + 12\cos\dfrac x2 + C$
(c) This integral can be found by means of a suitable substitution.
Step 1: We want a substitution of the form x = a sin y that will convert $\sqrt{2 - x^2}$ into a multiple of cos y.
This can be achieved if we take $x = \sqrt{2\os}\sin y$.
Step 2: Then $dx = \sqrt{2\os}\cos y\,dy$.
Step 3: Since $\sqrt{2 - x^2} = 2\cos y$ and $dx = \sqrt{2\os}\cos y\,dy$ the integral becomes simply ${\large\int}1\, dy$.
Step 4: Integrate with respect to y: ${\large\int}1\,dy = y + C$.
Step 5: Expressing the result in terms of x, using
$y = \arcsin\left(\dfrac{x}{2\os}\right)$ gives us
$\displaystyle \int\dfrac{1}{\sqrt{2-x^2}}\,dx = \arcsin\left(\dfrac{x}{2\os}\right) + C$
(d) This integral can be found by means of a suitable substitution.
Step 1: The integrand can be written as a product of a function of (2 − x2) and the derivative of (2 − x2), namely
−2x. So we make the substitution y = (2 − x2).
Step 2: Then dy = −2x dx, or $x\,dx = -\dfrac12\,dy$.
Step 3: As $\sqrt{2 - x^2} = \sqrt{y\os}$ the integral becomes
$\displaystyle \int\dfrac{x}{\sqrt{2-x^2}}\,dx = -\int\sqrt{\dfrac{1}{2\sqrt{y\os}}}\,dy$
Step 4: Integrating with respect to y gives us
$\displaystyle -\int \dfrac{1}{2\sqrt{y\os}}\,dy = -\sqrt{y\os} + C$
Step 5: Expressing the result in terms of x gives us
$\displaystyle \int \dfrac{x}{\sqrt{2-x^2}}\,dx = -\sqrt{2-x^2} + C$
Comment In part (d), you may have reasoned that as the integrand contains 2 − x2 then the substitution $x = \sqrt{2\os}\sin y$ would be suitable (as in part (c)). This will indeed work; the integral becomes $\sqrt{2\os}{\large\int}\sin y\,dy = -2\cos y + C = -\sqrt{2-x^2} + C$. Quite often, there is more than one substitution which will enable you to find a given integral.
(e) The integral ${\large\int}\sqrt{x\os}(1 + x)\,dx$ can be found by quite simple methods. Expanding the integrand ${\large\int}\sqrt{x\os}(1 + x)\,dx$ = ${\large\int}(x^{1/2} + x^{3/2})\,dx = \frac23x^{3/2} + \frac25x^{5/2} + C$. (The moral is to try the simplest method first.)
As you carry your study of mathematics and physics further, you will probably encounter more substitutions that can be used for certain classes of integral; you may also learn how to combine various types of substitution with clever algebraic manipulations, or crafty use of trigonometric identities, and this will enlarge your integration repertoire even more. However, the most important techniques of integration are the two that have been presented in this module: integration by parts and integration by substitution. Consequently, if you have mastered these (as we hope), you have, in a sense, nothing further to learn about integration; all that remains for you to do is to gain greater familiarity with the ingenious tricks that can be used to bring an even greater number of integrals under your control.
5 Closing items
5.1 Module summary
- 1
-
A product f (x)g (x) may often be integrated using the method of Section 2integration by parts, which is based on the formula
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
- 2
-
If this formula is to be useful, we must be able to integrate the function f (x) to obtain F (x); also, we want the integral on the right–hand side to be easier than the original integral. These considerations must be borne in mind when choosing f (x) and g (x) in any given case.
- 3
-
In the case of a definite integral, the formula becomes
$\displaystyle \int_a^bf(x)g(x)\,dx = \left[F(x)g(x)\right]_a^b + \int_a^b F(x)\dfrac{dg}{dx}\,{dx}$(Eqn 5)
- 4
-
It is sometimes necessary to apply the technique of integrating by parts more than once. This can either be because the remaining integral to be evaluated also requires the use of integration by parts; or, in the case of integrals like ${\large\int}{\rm e}^x\sin x\,dx$, by integrating by parts twice we can arrive at a simple equation involving the original integral, which can then be solved.
- 5
-
A small class of integrals can be found by taking the function f (x) to be 1.
- 6
-
Section 3Integration by substitution. An integral of the form ${\large\int}f(x)\,dx$ may often be transformed into a simpler integral by writing y = g (x) and $dy = \dfrac{dg}{dx}dx$, and substituting these relations into the integral to obtain an integral in terms of the new variable y which (if g (x) has been intelligently chosen) should be easy to find. Once it is found, the answer may then be expressed in terms of x by substituting y = g (x).
- 7
-
Integrals of a function and its derivative, of the form ${\large\int}p[g(x)]g'(x)\,dx$ may always be simplified by means of the substitution y = g (x).
- 8
-
If some function of x appears raised to some power, or as a denominator, in the integrand, that may be a good choice for g (x).
- 9
-
There are also certain types of substitution which work for particular classes of integrals; for example, a substitution of the form x = a sin y, where a is a suitable constant, can be used to find integrals of the form $\displaystyle \int\dfrac{1}{\sqrt{A-Bx^2}}\,dx$, where A and B are positive constants.
- 10
-
When a substitution y = g (x) is used to evaluate definite integrals, it is necessary to transform the limits of integration when writing down the integral with respect to y.
5.2 Achievements
Having completed this module, you should be able to:
- A1
-
A1 Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Use the method of integration by parts to find indefinite integrals involving products of simple functions, such as ${\large\int}x\sin x\,dx$ or ${\large\int}x^3\log_{\rm e}x\,dx$.
- A3
-
Apply integration by parts more than once to find indefinite integrals of the form ${\large\int}x^nf(x)\,dx$, where f (x) is an exponential, or a sine or cosine.
- A4
-
Apply integration by parts in such a way as to obtain a simple equation for the original unknown integral, which can then be solved, and recall that this method is particularly useful when the integrand is a product of an exponential function and a sine or cosine function.
- A5
-
Remember that, in the formula for integration by parts (Equation 2), the function f (x) may be taken to be 1, and use this trick to find certain integrals.
- A6
-
Use integration by parts to evaluate definite integrals.
- A7
-
Use a given substitution to transform a difficult indefinite integral into an easier one, and so find the original integral.
- A8
-
Recognize an integral of the form ${\large\int}p[g(x)]g'(x)\,dx$ and use the substitution y = g (x) to find it.
- A9
-
Use the method of substitution to evaluate definite integrals, remembering to transform the limits correctly.
- A10
-
Choose, for a given integral, a suitable substitution that will enable you to evaluate it.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
5.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions, each of which tests one or more of the Achievements.
Question E1 (A2 and A3)
Find the integral ${\large\int}x^2\sin(kx)\,dx$ where k is a constant.
Answer E1
Applying integration by parts, take f (x) = sin(kx), g (x) = x2. Then $F(x) = -\dfrac1k\cos(kx)$ and $\dfrac{dg}{dx} = 2x$.
Substituting these expressions in Equation 2,
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
gives us
$\displaystyle \int x^2\sin(kx)\,dx = -\dfrac1kx^2\cos(kx) + \dfrac2k\int x\cos(kx)\,dx$(25)
Now apply integration by parts again, to the integral $\int x\cos(kx)\,dx$. Taking f (x) = cos(kx) and g (x) = x, we have $F(x) = \dfrac1k\sin(kx)$ and $\dfrac{dg}{dx} = 1$.
So$\displaystyle \int x\cos(kx)\,dx = \dfrac1kx\sin(kx) - \dfrac1k\int\sin(kx)\,dx = \dfrac1kx\sin(kx) + \dfrac{1}{k^2}\cos(kx) + C$
Substituting this result in Equation 25 gives us
$\displaystyle \int x^2\sin(kx)\,dx = -\dfrac1kx^2\cos(kx)\,dx + \dfrac{2}{k^2}x\sin(kx) + \dfrac{2}{k^3}\cos(kx) + C$
(Reread Subsection 2.1Subsections 2.1 and Subsection 2.22.2 if you had difficulty with this question.)
Question E2 (A4)
Find the integral ${\large\int}{\rm e}^{3x}\cos(3x)\,dx$. [Hint: Start by taking f (x) = e3x and g (x) = cos(3x).]
Answer E2
Taking f (x) = e3x andg (x) = cos(3x), we have $F(x) = \dfrac13{\rm e}^{3x}$ and $\dfrac{dg}{dx} = -3\sin(3x)$.
Substituting these expressions in Equation 2,
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
gives us
$\displaystyle \int{\rm e}^{3x}\cos(3x)\,dx = \dfrac13{\rm e}^{3x}\cos(3x) + \int{\rm e}^{3x}\sin(3x)\,dx$(26)
We now apply integration by parts to ${\large\int}{\rm e}^{3x}\sin(3x)\,dx$ taking f (x) = e3x (as we did before – if you did not do this you may have run into difficulties!) and g (x) = sin(3x). Then $F(x) = \dfrac13{\rm e}^{3x}$ and $\dfrac{dg}{dx} = 3\cos(3x)$. So
$\displaystyle \int{\rm e}^{3x}\sin(3x)\,dx = \dfrac13{\rm e}^{3x}\sin(3x) - \int{\rm e}^{3x}\cos(3x)\,dx$
Substituting this into Equation 26 gives us
$\displaystyle \int{\rm e}^{3x}\cos(3x)\,dx = \dfrac13{\rm e}^{3x}\cos(3x) + \dfrac13{\rm e}^{3x}\sin(3x) - \int{\rm e}^{3x}\cos(3x)\,dx$
Collecting all terms in ${\large\int}{\rm e}^{3x}\cos(3x)\,dx$ on the left–hand side gives us
$\displaystyle 2\int{\rm e}^{3x}\cos(3x)\,dx = \dfrac13{\rm e}^{3x}\cos(3x) + \dfrac13{\rm e}^{3x}\sin(3x) + C$
i.e.$\displaystyle \int{\rm e}^{3x}\cos(3x)\,dx = \dfrac16{\rm e}^{3x}\cos(3x) + \dfrac16{\rm e}^{3x}\sin(3x) + C$
(Reread Subsection 2.3 if you had difficulty with this question.)
Question E3 (A6)
Evaluate the integral ${\large\int}_0^1x\cos(5x)\,dx$ to four decimal places.
Answer E3
We take f (x) = cos(5x) and g (x) = x. Then $F(x) = \dfrac15\sin(5x)\quad\text{and}\quad\dfrac{dg}{dx} = 1$.
Substituting these expressions into Equation 5,
$\displaystyle \int_a^bf(x)g(x)\,dx = \left[F(x)g(x)\right]_a^b + \int_a^b F(x)\dfrac{dg}{dx}\,{dx}$(Eqn 5)
gives
$\displaystyle \int_0^1 x\cos(5x)\,dx = \dfrac15\left[x\sin(5x)\right]_0^1 - \dfrac15\int_0^1\sin(5x)\,dx = \dfrac15\left[\sin(5x)\right]_0^1 + \dfrac{1}{25}\left[\cos(5x)\right]_0^1$
$\displaystyle \phantom{\int x\cos(5x)\,dx }= -0.1918 - 0.0287 = -0.2205$
(Reread Subsection 2.1 if you had difficulty with this question.)
Question E4 (A7)
Use the substitution y = x2 + 2 to find the integral ${\large\int}\left(x^2 +2\right)^6x^3\,dx$.
Answer E4
Step 1: Take y = g (x) = x2 + 2.
Step 2: Then dy = 2x dx, or $x\,dx = \dfrac12dy$.
Step3 Writing the integral as ${\large\int}\left[(x^2 + 2)^6x^2\right]x\,dx$, we put (x2 + 2)6 = y6, x2 = y − 2, and $x\,dx = \dfrac12dy$. So the integral becomes
$\displaystyle \int(x^2+2)^6x^3\,dx = \dfrac12\int y^6(y-2)\,dy = \dfrac12\int y^7\,dy - \int y^6\,dy$
Step 4: Integrate with respect to y: $\dfrac12\int y^7\,dy - \int y^6\,dy = \dfrac{1}{16}y^8 - \dfrac17y^7 + C$
Step 5: Expressing the result in terms of x gives us
$\displaystyle \int\left[(x^2 + 2)^6x^3\right]x\,dx = \dfrac{1}{16}(x^2+2)^8 - \dfrac17(x^2+2)^7 + C$
(Reread Subsection 3.1Subsections 3.1 and Subsection 3.23.2 – especially Example 11 – if you had difficulty with this question.)
Question E5 (A8)
Find the integrals
(a) $\displaystyle \int\dfrac{2}{3x+4}\,dx$, (b) ${\large\int}x\exp\left(x^2\right)\,dx$, i (c) ${\large\int}{\rm e}^{2x}\sin\left({\rm e}^{2x}\right)\,dx$.
Answer E5
(a) Step 1: The derivative of 3x + 4 is a constant, namely 3. Thus the integrand can be written as a function of g (x) = 3x + 4, multiplied by g ′ (x). So we make the substitution y = 3x + 4.
Step 2: Then dy = 3 dx, or $dx = \dfrac13dy$.
Step 3: Substituting y = 3x + 4 and $dx = \dfrac13dy$ into the integral, it becomes
$\displaystyle \int\dfrac{2}{3x+4}\,dx = \int\dfrac{2}{3y}\,dy$
Step 4: Integrating with respect to y gives us
$\displaystyle \int\dfrac{2}{3y}\,dy = \dfrac23\log_{\rm e}y + C$
Step 5: Expressing this result in terms of x gives us
$\displaystyle \int\dfrac{2}{3x+4}\,dx = \dfrac23\log_{\rm e}(3x+4) + C$
(b) Step 1: The integrand can be written as a function of x2 multiplied by the derivative of x2, namely 2x. So we make the substitution y = x2.
Step 2: Then dy = 2x dx, or $x\,dx = \dfrac12dy$.
Step 3: The integral then becomes
$\displaystyle \int x\exp\left(x^2\right)\,dx = \dfrac12{\rm e}^y\,dy$
Step 4: Integrating with respect to y gives us
$\displaystyle \dfrac12\int{\rm e}^y\,dy = \dfrac12{\rm e}^y\,dy + C$
Step 5: Expressing the result in terms of x gives us
$\displaystyle \int x\exp\left(x^2\right)\,dx = \dfrac12\exp\left(x^2\right) + C$
(c) Step 1: The integrand can be written as a function of e2x, multiplied by the derivative of e2x, namely 2e2x. So we make the substitution y = e2x.
Step 2: Then dy = 2 e2x dx, or ${\rm e}^{2x}\,dx = \dfrac12\,dy$.
Step 3: The integral then becomes
$\displaystyle \int{\rm e}^{2x}\sin\left({\rm e}^{2x}\right)\,dx = \dfrac12\int\sin y\,dy$
Step 4: Integrating with respect to y gives us
$\displaystyle \int\dfrac12\sin y\,dy = -\dfrac12\cos y + C$
Step 5: Expressing the result in terms of x gives us
$\displaystyle \int{\rm e}^{2x}\sin\left({\rm e}^{2x}\right)\,dx = -\dfrac12\cos\left({\rm e}^{2x}\right) + C$
(Reread Subsection 3.2 if you had difficulty with this question.)
Question E6 (A9 and A10)
Evaluate the integral ${\large\int}_1^2x(2 + x)^{3/2}\,dx$ to four decimal places.
Answer E6
Step 1: As the integrand contains (2 + x) raised to the power 3/2, try the substitution y = 2 + x (so that x = y − 2).
Step 2: Then dy = dx.
Step 3: The integrand x (2 + x)3/2 becomes (y − 2)y3/2.
When x = 1, y = 3, and when x = 2, y = 4. So the integral becomes
${\large\int}_1^2x(2+x)^{3/2}\,dx = {\large\int}_3^4(y-2)y^{3/2}\,dy = {\large\int}_3^4y^{5/2}\,dy - 2{\large\int}_3^4y^{3/2}\,dy$
Step 4: Evaluating the integral with respect to y gives us
${\large\int}_3^4y^{5/2}\,dy - 2{\large\int}_3^4y^{3/2}\,dy = \displaystyle \left[\dfrac27y^{7/2}\right]_3^4 - \left[\dfrac45y^{5/2}\right]_3^4 \approx 123.209\,894 - 13.129\,234 \approx 10.0807$
(Reread Subsection 3.4 if you had difficulty with this question.)
Question E7 (A5 and A8)
Find the integral $\int \arcsin x\,dx$. [Hint: Start by integrating by parts.]
Answer E7
We first integrate by parts, taking f (x) = 1, g (x) = arcsin x. Then F (x) = x and $\dfrac{dg}{dx} = \dfrac{1}{\sqrt{1-x^2}}$
So, using Equation 2,
$\displaystyle \int f(x)g(x)\,dx = F(x)g(x) - \int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 2)
${\large\int}\arcsin x\,dx = x\arcsin x - \displaystyle \int\dfrac{x}{\sqrt{1-x^2}}\,dx$(27)
The integral on the right–hand side can be found by a suitable substitution.
Step 1: The integrand can be written as a function of (1 − x2) multiplied by the derivative of (1 − x2) namely 2x. So we make the substitution y = 1 − x2.
Step 2: Then dy = −2x dx, or $x\,dx = -\dfrac12dy$.
Step 3: Since $\sqrt{1-x^2} = \sqrt{y\os}$ the integral becomes
$\displaystyle \int\dfrac{x}{\sqrt{1-x^2}}\,dx = -\int\dfrac{1}{2\sqrt{y\os}}\,dy$
Step 4: Integrating with respect to y gives us
$\displaystyle -\int\dfrac{1}{2\sqrt{y\os}}\,dy = -\sqrt{y\os} + C$
Step 5: Expressing the answer in terms of x gives us
$\displaystyle \int\dfrac{1}{2\sqrt{1-x^2}}\,dx = -\sqrt{1-x^2} + C$
Substituting this result in Equation 27 we finally have
${\large\int}\arcsin x\,dx = x\arcsin x + \sqrt{1-x^2} + C$
(Reread Subsection 2.3Subsections 2.3 and Subsection 3.23.2 if you had difficulty with this question.)
Question E8 (A10)
Find the integrals
(a) ${\large\int}\sec(3x)\tan(3x)\,dx$, (b) $\displaystyle \int\dfrac{1}{1+9x^2}\,dx$, (c) $\displaystyle \int\dfrac{x^5}{1+2x^3}\,dx$.
Answer E8
All these integrals can be found by appropriate substitutions
(a) Step 1: The integrand is a function of tan(3x), multiplied by the derivative of tan(3x), namely 3 sec2(3x).
So we make the substitution y = tan(3x).
Step 2: Then dy = 3 sec2(3x) dx, or $\sec^2(3x)\,dx = \dfrac13\,dy$
Step 3: Putting tan(3x) = y and $\sec^2(3x)\,dx = \dfrac13\,dy$ in the integral, it becomes
${\large\int}\sec^2(3x)\tan(3x)\,dx = \dfrac13\displaystyle \int y\,dy$
Step 4: Integrating with respect to y gives us
$\displaystyle \dfrac13\int y\,dy = \dfrac16y^2 + C$
Step 5: Expressing the answer in terms of x gives us
${\large\int}\sec^2(3x)\tan(3x)\,dx = \dfrac16\tan^2(3x) + C$
You should note that different methods may produce answers that appear to be very different. In this case
$\dfrac16\sec^2(3x) + C$
is an alternative answer that is equally correct; can you see why? If not, have a look at the trigonometric identity we used in Example 13.
(b) Step 1: We want a substitution of the form x = a tan y, such that (1 + 9x2) is a multiple of sec2 y. We see that 1 + 9a2 tan2 y = sec2 y if 9a2 = 1, i.e. if a = 1/3. So we take $x = \dfrac13\tan y$.
Step 2: Then $dx = \dfrac13\sec^2y\,dy$.
Step 3: Since 1 + 9x2 = sec2 y, the integral becomes
$\displaystyle \int\dfrac{1}{1+9x^2}\,dx = \int\dfrac13\dfrac{\sec^2y}{\sec^2y}\,dy = \int\dfrac13\,dy$
Step 4: Integrating with respect to y gives
$\displaystyle \int\dfrac13\,dy = \dfrac13y + C$
Step 5: Expressing this result in terms of x, using y = arctan(3x), gives us
$\displaystyle \int\dfrac{1}{1+9x^2}\,dx = \dfrac13\arctan(3x) + C$
(c) Step 1: As the function (1 + 2x3) appears as the denominator of the integrand, we try the substitution y = 1 + 2x3.
Step 2: Then dy = 6x2 dx or $x^2\,dx = \dfrac16dy$.
Step 3: Writing the integral as $\displaystyle \int\dfrac{x^3}{1+2x^3}x^2\,dx$, we put 1 + 2x3 = y from which it follows that $x^3 = \dfrac12(y - 1)$; we also put $x^2\,dx = \dfrac16dy$, to obtain
$\displaystyle \int\dfrac{x^5}{1+2x^3}\,dx = \int\dfrac{1}{1+2x^3}x^3x^2\,dx = \int\underbrace{\dfrac1y}_{\color{purple}{\large{1/(1+2x^3)}}} \times \underbrace{\dfrac12(y-1)}_{\color{purple}{\large x^3}} \times \underbrace{\dfrac16\,dy}_{\color{purple}{\large x^2\,dx}} = \dfrac{1}{12}\int\left(1-\dfrac1y\right)\,dy$
Step 4: Integrating with respect to y gives us
$\displaystyle \int\left(1-\dfrac1y\right)\,dy = \dfrac{1}{12}(y-\log_{\rm e}y) + C$
Step 5: Expressing the answer in terms of x gives us
$\displaystyle \int\dfrac{x^5}{1+2x^3}\,dx = \dfrac{1}{12}\left[1 + 2x^3 - \log_{\rm e}(1+2x^3)\right] + C$
(Reread Section 3 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 5Closing items.