MATH 5.5: Further integration |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
This module discusses in depth a range of techniques which will enable you to evaluate a wide range of integrals. Such a detailed treatment may not be relevant to your course of study, and you are therefore advised to consult your tutor before working through the module. You should be prepared to spend more time than for the other FLAP modules if you are advised to read all the material.
In Section 2 we discuss several ingenious tricks which you can combine with methods such as integration by parts and integration by substitution in order to evaluate a very wide range of integrals. Some of these tricks (partial fractions, completing the square and splitting the numerator) involve algebraic manipulation of the integrand, while others make use of trigonometric identities to simplify integrals of powers of trigonometric functions. We also discuss some particularly useful substitutions involving hyperbolic functions.
Subsection 3.1 deals with certain types of improper integral – those with an infinite upper or lower limit. We will explain there how to define and evaluate these. Subsection 3.2 discusses some integrals of this sort known as Gaussian integrals, which arise very often in physics (in quantum mechanics and in the kinetic theory of gases, for example). We show how these can all be evaluated in terms of the basic Gaussian integral $\Int_0^\infty\exp(-x^2)\,dx$ i
Finally, in Subsection 3.3, we introduce and explain the idea of a line integral – an integral of the form $\Int_{r_a}^{r_b}\bi{F}(\bi{r})\,{\boldsymbol\cdot}\,d\bi{r}$. Integrals of this sort arise in calculating the work done by a force, for example, or the electrostatic potential difference between two points in a region of space where there is an electric field. You may occasionally find that your answers to the exercises differ from ours. This may be because your answer is in a slightly different form; for example, you may have written $\sqrt{\loge x(x-1)\os}$ where we have written $\frac12\loge x - \frac12\loge(x-1)$. If you cannot tell if your expression for an indefinite integral is the same as ours, you can always check your answer by differentiating it.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 4.1Module summary and the Subsection 4.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 4.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
Find the integrals: (a) $\displaystyle \int\dfrac{x-1}{\sqrt{4x^2-1}}\,dx$, (b) $\displaystyle \int\dfrac{1}{\sqrt{1+8x-4x^2}}\,dx$
Answer F1
(a) We evaluate this integral by splitting it into two:
$\displaystyle \int\dfrac{x-1}{\sqrt{4x^2-1}}\,dx = \int\dfrac{x}{\sqrt{4x^2-1}}\,dx - \int\dfrac{1}{\sqrt{4x^2-1}}\,dx$
The first integral may be evaluated by the substitution u = 4x2 − 1; then du = 8x dx or $x\,dx = \dfrac18\,du$ and we have
$\displaystyle \int\dfrac{x}{\sqrt{4x^2-1}}\,dx = \int\dfrac{1}{8\sqrt{u\os}}\,du = \dfrac14\sqrt{u\os} + C = \dfrac14\sqrt{4x^2-1} + C$
The second may be found by the substitution 2x = cosh u, so that 4x2 − 1 = cosh2 u − 1 = sinh u and $dx = \dfrac12\sinh u\,du$; thus
$\displaystyle \int\dfrac{1}{\sqrt{4x^2-1}}\,dx = \int\dfrac{\frac12\sinh u}{\sinh u}\,du = \int\dfrac12\,du = \dfrac u2 + C = \dfrac12\arccosh(2x) + C$
So, finally,
$\displaystyle \int\dfrac{x-1}{\sqrt{4x^2-1}}\,dx = \dfrac14\sqrt{4x^2-1} - \dfrac12\arccosh(2x) + C$
(b) For convenience we write $\displaystyle I = \int\dfrac{1}{\sqrt{1+8x-4x^2}}\,dx$, then we write the quadratic expression in the denominator in completed square form:
1 + 8x − 4x2 = 1 − 4 (x2 − 2x) = 1 − 4 [(x − 1)2 − 1] = 5 − 4 (x − 1)2
Thus$\displaystyle I = \int\dfrac{1}{\sqrt{5-4(x-1)^2}}\,dx$
We now make the substitution y = x − 1, dy = dx, so that $\displaystyle I = \int\dfrac{1}{\sqrt{5-4y^2}}\,dy$
Next, we write $2y = \sqrt{5\os}\sin u$.
Then$\sqrt{5-4y^2} = \sqrt{5-5\sin^2u} = 5\cos u$ and $dy = -\dfrac{\sqrt{5\os}}{2}\cos u\,du$
so that$\displaystyle I = \int\dfrac{-(\sqrt{5/2\os})\cos u}{\sqrt{5\os}\cos u}\,du = -\int\dfrac{1}{\sqrt{2\os}}\,du = \dfrac{-1}{\sqrt{2\os}}u + C$
Finally, we express the integral in terms of x to obtain
$\displaystyle I = \dfrac{-1}{\sqrt{2\os}}u + C = \dfrac{-1}{\sqrt{2\os}}\arcsin\left(\dfrac{2y}{\sqrt{5\os}}\right) + C = \dfrac{-1}{\sqrt{2\os}}\arcsin\left[\dfrac{2(x-1)}{\sqrt{5\os}}\right] + C$
Question F2
Evaluate the definite integral: $\displaystyle \int_0^\infty\dfrac{x+3}{(x+2)^2(x+1)}\,dx$ i
Answer F2
We first split the integrand up into partial fractions; this gives
$\dfrac{x+3}{(x+2)^2(x+1)} = \dfrac{2}{x+1} - \dfrac{2}{x+2} -\dfrac{1}{(x+2)^2}$
So the integral becomes
$\displaystyle \int_0^\infty\dfrac{x+3}{(x+2)^2(x+1)} = \int_0^\infty\left(\dfrac{2}{x+1} - \dfrac{2}{x+2} -\dfrac{1}{(x+2)^2}\right)\,dx$
$\displaystyle \phantom{\int_0^\infty\dfrac{x+3}{(x+2)^2(x+1)}} = \left[2\loge(x+1) - 2\loge(x+2) + \dfrac{1}{x+2}\right]_0^\infty = \left[2\loge\left(\dfrac{x+1}{x+2}\right) + \dfrac{1}{x+2}\right]_0^\infty$
As x becomes very large, the ratio $\dfrac{x+1}{x+2}$ tends to 1, so its logarithm tends to zero; and $\dfrac{1}{x+2}$ also tends to zero.
So we find
$\displaystyle \int_0^\infty\dfrac{x+3}{(x+2)^2(x+1)} = 0 + 0 - 2\loge\left(\dfrac12\right) - \dfrac12 \approx 0.8863$
Question F3
Evaluate the definite integral $\Int_{-\infty}^\infty\exp(-3x^2+4x)\,dx$, given that $\Int_{-\infty}^\infty\exp(-y^2)\,dy = \sqrt{\pi\os}$
Answer F3
To evaluate $\Int_{-\infty}^\infty\exp(-3x^2+4x)\,dx$, we first complete the square in the exponent, and write
$-3x^2+4x = -3\left(x^2-\dfrac43x\right) = -3\left[\left(x-\dfrac23\right)^2-\dfrac49\right] = -3\left(x-\dfrac23\right)^2+\dfrac43$
Then $\Int_{-\infty}^\infty\exp(-3x^2+4x)\,dx = \exp\left(\dfrac43\right){\displaystyle \int}_{-\infty}^\infty\exp\left[-3\left(x-\dfrac23\right)^2\right]\,dx$
We now substitute $y = \sqrt{3\os}\left(x-\dfrac23\right)$; then $dx = \dfrac{dy}{\sqrt{3\os}}$. The limits of integration are still ∞ and −∞, so that
$\Int_{-\infty}^\infty\exp(-3x^2+4x)\,dx = \dfrac{1}{\sqrt{3\os}}\exp(4/3)\Int_{-\infty}^\infty\exp(-y^2)\,dy$
Using the given result $\Int_{-\infty}^\infty\exp(-y^2)\,dy = \sqrt{\pi\os}$, we obtain $\Int_{-\infty}^\infty\exp(-3x^2+4x)\,dx = \exp(4/3)\sqrt{\pi/3\os} \approx 3.882$
1.3 Ready to study?
Study comment In order to study this module, you will need to be familiar with the following terms: completing the square, definite integral, even function, hyperbolic function, improper integral, integrand, integration by parts, integration by substitution, inverse hyperbolic function, limits of integration, scalar product and vector. If you are uncertain of any of these terms, you can review them now by referring to the Glossary which will indicate where in FLAP they are developed. In addition, you will need to be familiar with standard integrals (such as $\Int x^n\,dx = \dfrac{x^{n+1}}{n+1} + C$ i and $\Int {\rm e}^{ax}\,dx = \dfrac{{\rm e}^{ax}}{a} + C$), and know how to evaluate definite and indefinite integrals by the integration_by_substitutionmethod of substitution, or by integration by parts. You will also need to be familiar with trigonometric identities, and with the analogous identities involving hyperbolic functions. The following questions will allow you to establish whether you need to review some of these topics before embarking on this module.
Question R1
The expression $\dfrac{1}{x-1} + \dfrac{2}{x+2}$ can be written as a single fraction by putting
$\dfrac{1}{x-1} + \dfrac{2}{x+2} = \dfrac{x+2}{(x-1)(x+2)} + \dfrac{2(x-1)}{(x-1)(x+2)} = \dfrac{(x+2)+2(x-1)}{(x-1)(x+2)} = \dfrac{3x}{(x-1)(x+2)}$
Use a similar method to express the following as single fractions:
(a) $\dfrac{1}{2(x-3)} - \dfrac{1}{2(x+3)}$, (b) $\dfrac{1}{2-x} + \dfrac{x}{3+x^2}$, (c) $\dfrac{5}{9(x-1)} - \dfrac{5}{9(x + 2)} - \dfrac{2}{3(x + 2)^2}$.
Answer R1
(a) $\dfrac{1}{2(x-3)} - \dfrac{1}{2(x+3)} = \dfrac{(x+3)-(x-3)}{2(x-3)(x+3)} = \dfrac{6}{2(x-3)(x+3)} = \dfrac{3}{x^2-9}$
(b) $\dfrac{1}{2-x} + \dfrac{x}{3+x^2} = \dfrac{(x+3)-(x-3)}{2(x-3)(x+3)} = (2x+3)/[(2-x)(3+x^2)]$
(c) $\dfrac{5}{9(x-1)\os} - \dfrac{5}{9(x+2)\os} - \dfrac{2}{3(x+2)^2} = \dfrac{5(x+2)^2 - 5(x-1)(x+2) - 6(x-1)}{9(x-1)(x+2)^2}$
(c) $\phantom{\dfrac{5}{9(x-1)\os} }= \dfrac{5(x^2+4x+4)-5(x^2+x-2)-6(x-1)}{9(x -1)(x + 2)^2} = \dfrac{9x+36}{9(x -1)(x + 2)^2} = \dfrac{x+4}{(x -1)(x + 2)^2}$
Question R2
Write the following quadratic functions in completed square form: (a) 3x2 − 12x + 16, (b) 3 − 4x − 2x2.
Answer R2
(a) 3x2 − 12x + 16 = 3 (x2 − 4x) + 16 = 3 [(x − 2)2 − 4] + 16 = 3 (x − 2)2 + 4
(b) 3 − 4x − 2x2 = 3 − 2 (x2 + 2x) = 3 − 2 [(x + 1 )2 − 1] = 5 − 2 (x + 1)2
Consult completing the square in the Glossary for further information.
Question R3
(a) If y = cos(2x), express sin4 x in terms of y
(b) If y = cosh(2x), express sinh4 x in terms of y.
Answer R3
(a) We use the identity cos(2x) = 1 − 2 sin2 x; re–arranging this gives
$\sin^2x = \dfrac12 [1-\cos(2x)] = \dfrac12(1-y)$
So$\sin^4x = \dfrac14(1-y)^2$
(b) We use the identity cosh(2x) = 1 + 2 sinh2 x; rearranging this gives us
$\sinh^2x = \dfrac12[\cosh(2x)-1] = \dfrac12(y-1)$
So$\sinh^4x = \dfrac14(y-1)^2$.
Consult hyperbolic functions in the Glossary for further information.
Question R4
Find the indefinite integrals: (a) $\displaystyle \int\dfrac{1}{2+3x}\,dx$, (b) $\displaystyle \int\dfrac{1}{4+9x^2}\,dx$, (c) $\displaystyle \int\dfrac{1}{\sqrt{25-4x^2}}\,dx$
Answer R4
(a) The integral $\displaystyle \int\dfrac{1}{2+3x}\,dx$ can be found by the substitution u = 2 + 3x; then du = 3 dx,
and the integral becomes $\displaystyle \dfrac13\int\dfrac1u\,du = \dfrac13\loge u + C$
So$\displaystyle \int\dfrac{1}{2+3x}\,dx = \dfrac13\loge(2+3x) + C$
(b) The integral $\displaystyle \int\dfrac{1}{4+9x^2}\,dx$ can be found using the substitution 3x = 2 tan u.
Then $dx = \dfrac23\sec^2u\,du$ and 4 + 9x2 = 4 + 4 tan2 u = 4 sec2 u
The integral becomes $\displaystyle \int\dfrac16\,du = \dfrac16u + C$. Since 3x = 2 tan u we have u = arctan(3x/2), and so
$\displaystyle \int\dfrac{1}{4+9x^2}\,dx = \dfrac u6 + C = \dfrac16\arctan\left(\dfrac{3x}{2}\right) + C$
(c) The integral $\displaystyle \int\dfrac{1}{\sqrt{25-4x^2}}\,dx$ can be found using the substitution 2x = 5 sin u so that
$dx = \dfrac52\cos u\,du\quad\text{and}\quad\sqrt{25-4x^2} = \sqrt{25-25\sin^2u} = 5\cos u$
The integral becomes $\displaystyle \int2\,du = \dfrac12u + C$. Writing u in terms of x gives u = arcsin(2x/5), so
$\displaystyle \int\dfrac{1}{\sqrt{25-4x^2}}\,dx = \dfrac12\arcsin(2x/5) + C$
Consult indefinite integrals in the Glossary for further information.
Question R5
Evaluate the definite integrals: (a) $\Int_0^\pi x\sin(3x)\,dx$, (b) $\Int_0^1x\sqrt{1+4x^2}\,dx$
Answer R5
(a) This integral can be evaluated by using the formula for integration by parts,
$\Int f(x)g(x)\,dx = F(x)g(x) - \Int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 13)
Taking f (x) = sin(3x) and g (x) = x, we have
$F(x) = -\dfrac13\cos(3x)\quad\text{and}\quad\dfrac{dg}{dx} = 1$
So$\Int_0^\pi x\sin(3x)\,dx = \left[-\dfrac13x\cos(3x)\right]_0^\pi + \dfrac13\Int_0^\pi\cos(3x)\,dx = \left[-\dfrac13x\cos(3x) + 9\sin(3x)\right]_0^\pi = \dfrac{\pi}{3} \approx 1.0472$
(b) This integral can be evaluated by the substitution u = 1 + 4x2. Then du = 8x dx, or $x\,dx = \dfrac18\,du$. When x = 0, u = 1; and when x = 1, u = 5. So
$\Int_0^1x\sqrt{1+4x^2}\,dx = \dfrac18\Int_1^5u\,du = \dfrac18\left[\dfrac23u^{3/2}\right]_1^5 = \dfrac{1}{12}(5^{3/2}-1) \approx 0.8484$
Consult definite integrals and integration by parts in the Glossary for further information.
Question R6
Define the hyperbolic functions cosh x and sinh x, and use your definitions to prove the identity cosh2 x − sinh2 x = 1.
Answer R6
$\cosh x = \dfrac{{\rm e}^x+{\rm e}^{-x}}{2}\quad\text{and}\quad\sinh x = \dfrac{{\rm e}^x-{\rm e}^{-x}}{2}$. So
$\cosh^2x-\sinh^2x = \dfrac14\left({\rm e}^{2x}+2+{\rm e}^{-2x}\right) - \dfrac14\left({\rm e}^{2x}-2+{\rm e}^{-2x}\right) = \dfrac14[2-(-2)] = 1$
Consult hyperbolic function in the Glossary for further information.
Question R7
(a) What are the derivatives of cosh x and sinh x? Use these derivatives, and the quotient_rule_of_differentiationquotient rule, to find the derivative of tanh x.
(b) Find the integrals $\Int\cosh(2x)\,dx$ and $\Int\sinh(x/3)\,dx$.
Answer R7
(a) $\dfrac{d}{dx}(\cosh x) = \sinh x\quad\text{and}\quad\dfrac{d}{dx}(\sinh x) = \cosh x$
So$\dfrac{d}{dx}(\tanh x) = \dfrac{d}{dx}\left(\dfrac{\sinh x}{\cosh x}\right) = \dfrac{\cosh^2x-\sinh^2x}{\cosh^2x} = \dfrac{1}{\cosh^2x} = \sech^2x$
(b) These integrals can be found by making an intelligent guess at the form of the answer, then checking by differentiation. The answers are
$\Int\cosh(2x)\,dx = \dfrac12\sinh(2x) + C$
and$\Int\sinh\left(\dfrac x3\right)\,dx = 3\cosh x + C$
Consult quotient_rule_of_differentiationquotient rule in the Glossary for further information.
Question R8
If r is the vector x i + y j + z k, a is the vector 2 i − k and b is the vector 2 i − 2 j + k, find an expression for (a ⋅ b)(b ⋅ r) in terms of x, y and z.
Answer R8
The scalar product (a ⋅ b) of a and b is (2 × 2) + (0 × −2) + (−1 × 1) = 3
The scalar product (b ⋅ r) of b and r is (2 × x) + (−2 × y) + (1 × z) = 2x − 2y + z
So(a ⋅ b)(b ⋅ r) = 6x − 6y + 3z
Consult scalar product in the Glossary for further information.
2 Further techniques of integration
2.1 Partial fractions
Suppose that we want to find the integral $\displaystyle \int\dfrac{1}{(x+1)(x+2)}\,dx$. The integrand does not seem to be a particularly complicated function of x. Yet this is not an integral that can immediately be related to a standard integral, nor will integration by parts work (as you will find if you try!), nor is it easy to find a substitution that will simplify the integral.
However, this integral can in fact be found quite easily if we first split the integrand into its partial fractions. i To do this, we write
$\dfrac{1}{(x+1)(x+2)} = \dfrac{a}{x+1} + \dfrac{b}{x+2}$(1)
where a and b are constants that we will need to find. Adding together the two fractions on the right–hand side of Equation 1 gives us
$\dfrac{1}{(x+1)(x+2)} = \dfrac{(a+b)x+2a+b}{(x+1)(x+2)}$
from which we deduce that a + b = 0 and 2a + b = 1, so that a = 1, b = −1. Thus we have the identity
$\dfrac{1}{(x+1)(x+2)} = \dfrac{1}{x+1} - \dfrac{1}{x+2}$ i
It follows that
$\displaystyle \int\dfrac{1}{(x+1)(x+2)}\,dx = \int\dfrac{1}{x+1}\,dx - \int\dfrac{1}{x+2}\,dx = \loge(x + 1) - \loge(x + 2) + C$ i
The method we have used here to find $\displaystyle \int\dfrac{1}{(x+1)(x+2)}\,dx$ can be applied to a wide variety of integrals of fractions whose denominators can be factorized. Here is a slightly more complicated example.
Example 1
Find $\displaystyle \int\dfrac{x}{x^2+x-6}\,dx$.
Solution
Since the denominator is not already factorized, we must first find its factors, which are (x − 2) and (x + 3). We now express $\dfrac{x}{x^2+x-6} = \dfrac{x}{(x-2)(x+3)}$ in partial fractions. We write
$\dfrac{x}{(x-2)(x+3)} = \dfrac{a}{x-2} + \dfrac{b}{x+3} = \dfrac{(a+b)x+3a-2b}{(x-2)(x+3)}$
from which we deduce that a + b = 1 and 3a − 2b = 0, i.e. a = 2/5 and b = 3/5.
Thus$\dfrac{x}{x^2+x-6} = \dfrac{2}{5(x-2)} + \dfrac{3}{5(x+3)}$
so that$\displaystyle \int\dfrac{x}{x^2+x-6}\,dx = \dfrac{2}{5}\int\dfrac{1}{x-2}\,dx + \dfrac{3}{5}\int\dfrac{1}{x+3}\,dx = \dfrac{2}{5}\loge(x-2) + \dfrac{3}{5}\loge(x+3) + C$
This example shows that using partial fractions to evaluate integrals generally involves three steps:
Step 1 Factorize the denominator of the integrand (if necessary).
Step 2 Express the integrand in terms of partial fractions.
Step 3 Integrate each partial fraction.
Practise these steps by doing the following question.
Question T1
Find the integral $\displaystyle \int\dfrac{1}{9-4x^2}\,dx$. i
Answer T1
First factorize the denominator:
9 − 4x2 = (3 − 2x)(3 + 2x),
then express $\dfrac{1}{(3-2x)(3+2x)}$ in terms of partial fractions:
$\dfrac{1}{(3-2x)(3+2x)} = \dfrac{a}{(3-2x)} + \dfrac{b}{(3+2x)} = \dfrac{2(a-b)x+3a+3b}{(3-2x)(3+2x)}$
so that a − b = 0 and 3a + 3b = 1, giving a = b = 1/6. So
$\dfrac{1}{9-4x^2} = \dfrac{1}{6(3-2x)} + \dfrac{1}{6(3+2x)}$
Integrating this, we obtain
$\displaystyle \int\dfrac{1}{9-4x^2} = \dfrac16\int\dfrac{1}{(3-2x)} + \dfrac16\int\dfrac{1}{(3+2x)} = -\dfrac{1}{12}\loge(3-2x)+\dfrac{1}{12}\loge(3+2x) + C$
The three steps described above apply equally well if there is a repeated factor in the denominator of the integrand. For example, consider the integral
$\displaystyle \int\dfrac{1}{x^3-2x^2+x}\,dx$
The denominator here is x3 − 2x2 + x = x (x2 − 2x + 1) = x (x − 1)2, which has a repeated factor (x –1).
We now write
$\dfrac{1}{x(x-1)^2} = \dfrac{a}{x\os} + \overbrace{\dfrac{b}{x-1\os}}^{\color{purple}{\large\substack{\text{A term for}\\[2pt](x-1)}}} + \overbrace{\dfrac{d}{(x-1)^2}}^{\color{purple}{\large\substack{\text{A term for}\\[1pt](x-1)^2}}} = \dfrac{(a+b)x^2+(d-2a-b)x+a}{x(x-1)^2}$
(notice that we have included a term for (x – 1) and a term for (x – 1)2)
so that a + b = 0, d − 2a − b = 0, and a = 1, i.e. a = 1, b = −1, d = 1.
So$\dfrac{1}{x^3-2x^2+x} = \dfrac{1}{x} - \dfrac{1}{x-1} + \dfrac{1}{(x-1)^2}$(2)
✦ Find $\displaystyle \int\dfrac{1}{x^3-2x^2+x}\,dx$.
✧ We integrate each term on the right–hand side of Equation 2,
$\dfrac{1}{x^3-2x^2+x} = \dfrac{1}{x} - \dfrac{1}{1-x} + \dfrac{1}{(x-1)^2}$(Eqn 2)
This gives
$\displaystyle \int\dfrac{1}{x^3-2x^2+x} = \loge x - \loge(x-1) - \dfrac{1}{x-1} + C$ i
Partial fractions can also often be used to integrate a fraction even if its denominator does not factorize completely into real linear factors, as in the following example.
Example 2
Find the integral $\displaystyle \int\dfrac{x+3}{(x-1)(x^2+1)}\,dx$.
Solution
We cannot factorize the quadratic factor (x2 + 1). So, to express the integrand in terms of partial fractions, we must first write it in the form
$\dfrac{x+3}{(x-1)(x^2+1)} = \dfrac{a}{x-1\os} + \overbrace{\dfrac{bx+d}{x^2+1}}^{\color{purple}{\large\substack{\text{Two constants for}\\[2pt]\text{the quadratic factor}}}} = \dfrac{(a+b)x^2+(d-b)x+a-d}{(x-1)(x^2+1)}$
(notice that the term corresponding to the factor (x2 + 1) includes two unknown constants)
from which it follows that a + b = 0, d − b = 1 and a − d = 3, i.e. a = 2, b = −2, d = −1.
So$\displaystyle \int\dfrac{x+3}{(x-1)(x^2+1)}\,dx = \int\dfrac{2}{x-1}\,dx - \int\dfrac{2x+1}{x^2+1}\,dx$(3)
The first integral on the right–hand side of Equation 3 is equal to 2 loge(x − 1) + C. To evaluate the second integral, we split it into two, and write it as $\displaystyle \int\dfrac{2x}{x^2+1}\,dx + \int\dfrac{1}{x^2+1}\,dx$. With the substitution u = x we quickly find that
$\displaystyle \int\dfrac{2x}{x^2+1}\,dx = \loge(x +1) + C$, while $\displaystyle \int\dfrac{1}{x^2+1}\,dx$ is a standard integral, equal to arctan x + C.
Substituting these results into Equation 3 gives us
$\displaystyle \int\dfrac{x+3}{(x-1)(x^2+1)}\,dx = 2\loge(x-1) - \loge(x^2+1) - \arctan x + C$ i
Question T2
Find the integral $\displaystyle \int\dfrac{3x^2+11}{(x-3)(2x^2+1)}\,dx$.
Answer T2
We first express the integrand in terms of partial fractions:
$\dfrac{3x^2+11}{(x-3)(2x^2+1)} = \dfrac{a}{x-3} + \dfrac{bx+d}{2x^2+1} = \dfrac{(2a+b)x^2+(d-3b)x+a-3d}{(x-3)(2x^2+1)}$
Therefore2a + b = 3, d − 3b = 0, a − 3d = 11, which gives a = 2, b = −1, d = −3
So$\dfrac{3x^2+11}{(x-3)(2x^2+1)} = \dfrac{2}{x-3} - \dfrac{x+3}{2x^2+1}$
and$\displaystyle \int\dfrac{3x^2+11}{(x-3)(2x^2+1)} = \int\dfrac{2}{x-3}\,dx - \int\dfrac{x}{2x^2+1}\,dx - \int\dfrac{3}{2x^2+1}\,dx$(42)
where we have split the second partial fraction into two terms. The first integral in Equation 42 is equal to 2 loge (x − 3) + C. The second integral can be found by the substitution u = 2x2 + 1 so that du = 4x dx and x dx = du/4, and the second integral becomes
$\dfrac14\Int\dfrac1u\,du = \dfrac14\loge u + C = \dfrac14\loge(2x^2+1) + C$
The third integral can be found using the substitution $\sqrt{2\os}x = \tan u$; then $dx = \dfrac{\sec^2u}{\sqrt{2\os}}\,du$ and 2x2 + 1 = sec2 u, which gives us
$\displaystyle \int\dfrac{3}{2x^2+1}\,dx = \int\left(\dfrac{3}{\sec^2u}\right)\left(\dfrac{\sec^2u}{\sqrt{2\os}}\,du\right) = \dfrac{3}{\sqrt{2\os}}\int1\,du = \dfrac{3}{\sqrt{2\os}} + C = \dfrac{3}{\sqrt{2\os}}\arctan\left(\sqrt{2\os}x\right) + C$
So finally, we have
$\displaystyle \int\dfrac{3x^2+11}{(x-3)(2x^2+1)}\,dx = 2\loge(x-3) - \dfrac14\loge(2x^2+1) - \dfrac{3}{\sqrt{2\os}}\arctan\left(\sqrt{2\os}x\right) + C$
The technique of splitting the integrand into partial fractions will enable you to find many integrals of the form $\displaystyle \int\dfrac{p(x)}{q(x)}\,dx$, where p (x) and q (x) are both polynomials in x. However, it clearly will not be of any use unless q (x) factorizes, at least partly. What can we do if q (x) does not factorize at all? This case is discussed in the next two subsections.
2.2 Completing the square
If you are asked to find the integral $\displaystyle \int\dfrac{1}{x^2+4x+8}\,dx$, your response may now be to try writing the integrand in terms of partial fractions. If you try this, you will quickly find that the quadratic equation x2 + 4x + 8 = 0 has no real roots, so that we cannot factorize the integrand, and partial fractions are of no use. i
To see how to proceed with an integral of this sort, recall that there are integrals similar to this which you do know how to evaluate; for example, the integral $\displaystyle \int\dfrac{1}{x^2+4}\,dx$. This also has the property that its integrand does not factorize. However it can be quickly evaluated by means of the substitution x = 2 tan u. Then x2 + 4 = 4 sec2 u, and dx = 2 sec2 u du, so that the integral becomes
$\Int\frac12\,du = \frac12 u + C = \frac12\arctan(x/2) + C$
We can make the integral $\displaystyle \int\dfrac{1}{x^2+4x+8}\,dx$ look very much like the integral $\displaystyle \int\dfrac{1}{x^2+4}\,dx$ by the trick known as completing the square, in which we write the denominator as the sum of two squared terms, one involving x and the other a constant. In the case under consideration, it works as follows.
We notice that x2 + 4x = (x + 2)2 − 4, so that x2 + 4x + 8 = (x + 2)2 + 4.
Thus we have $\displaystyle \int\dfrac{1}{x^2+4x+8}\,dx = \int\dfrac{1}{(x+2x)^2+4}\,dx$
We now make the change of variables y = x + 2, so as to obtain
$\displaystyle \int\dfrac{1}{x^2+4x+8}\,dx = \int\dfrac{1}{y^2+4}\,dy$
We have just evaluated the integral on the right–hand side here; it is equal to $\frac12\arctan(x/2) + C$. Replacing y by x + 2, we finally find that
$\displaystyle \int\dfrac{1}{x^2+4x+8}\,dx = \frac12\arctan[(x+2)/2] + C$
Here is a slightly more complicated example, which we will set out as a series of steps; you can follow these when you do similar problems.
Example 3
Find the integral $\displaystyle I = \int\dfrac{1}{2x^2+6x+5}\,dx$ i
Solution
Step 1 First, write the denominator in completed square form.
2x2 + 6x + 5 = 2 (x2 + 3x) + 5 = 2 (x + 3/2)2 − 9/4 + 5 = 2 (x+3/2)2 + 1/2
So$\displaystyle I = \int\dfrac{1}{2[x + (3/2)]^2 + 1/2}\,dx$
Step 2 Make the substitution y = x + 3/2, then $\displaystyle I = \int\dfrac{1}{2y^2+(1/2)}\,dy$
Step 3 Make the substitution $y = \frac12\tan u$, then $2y^2 + \frac12 = \frac12\sec^2 u$ and $dy = \frac12\sec^2u\,du$. So
$I = {\displaystyle\int}\dfrac{1/2}{1/2}\,du = \Int1\,du = u + C$. i
Step 4 Finally, express the integral in terms of x (using the fact that $x + \frac23 = \frac12\tan u$),
$I = u + C = \arctan(2y) + C = \arctan(2x + 3) + C$
Question T3
Find the integral $\displaystyle I = \int\dfrac{1}{3x^2-6x+7}\,dx$.
Answer T3
Step 1 Write the denominator in completed square form:
3x2 − 6x + 7 = 3 (x2 − 2x ) + 7 = 3 [(x − 1)2 − 1] + 7 = 3 (x − 1)2 + 4
So$\displaystyle I = \int\dfrac{1}{3(x-1)^2+4}\,dx$
Step 2 Substitute y = x − 1, to obtain $\displaystyle I = \int\dfrac{1}{3y^2+4}\,dy$
Step 3 Make the substitution $\sqrt{3\os}y = 2\tan u$. The denominator 3y2 + 4 becomes 4 sec2 u, and $dy = \dfrac{2}{\sqrt{3\os}}\sec^2u\,du$.
So$\displaystyle I = \int\dfrac{1}{2\sqrt{3\os}}\,du = \dfrac{1}{2\sqrt{3\os}}u + C$
Step 4 Finally, write the integral I in terms of x:
$I = \dfrac{1}{2\sqrt{3\os}}u + C = \dfrac{1}{2\sqrt{3\os}}\arctan3y + C = \dfrac{1}{2\sqrt{3\os}}\arctan\left(\dfrac{\sqrt{3\os}(x-1)}{2}\right) + C$
The technique of completing the square can also be used in conjunction with a substitution of the form
x = a sin u, where a is a constant; this enables us to find integrals such as $\displaystyle I = \int\dfrac{1}{\sqrt{3-2x-x^2}}\,dx$. To evaluate this integral, we first write the quadratic expression appearing under the square root sign in completed square form.
✦ Write 3 − 2x − x2 in completed square form.
✧ 3 − 2x − x2 = 3 − (x2 + 2x) = 3 − [(x + 1)2 − 1] = 4 − (x + 1)2
So $\displaystyle I = \int\dfrac{1}{\sqrt{3-2x-x^2}}\,dx = \int\dfrac{1}{\sqrt{\smash[b]{4-(x+1)^2}}}\,dx$. We now make the substitution y = x + 1; then the integral becomes $\displaystyle I = \int\dfrac{1}{\sqrt{4-y^2}}\,dy$. This integral can easily be found by the substitution y = 2 sin u, so that dy = 2 cos u du, then
${\displaystyle\int}\dfrac{1}{\sqrt{4-y^2}}\,dy = {\displaystyle\int}\dfrac{1}{\sqrt{\smash[b]{4-(2\sin u)^2}}}(2\cos u\,du)$
$\phantom{{\displaystyle\int}\dfrac{1}{\sqrt{4-y^2}}\,dy}= {\displaystyle\int}\dfrac{1}{2\cos u}(2\cos u\,du) = \Int 1\,du = u + C = \arcsin(y/2) + C$
Replacing y by x + 1, we finally have
$\displaystyle I = \int\dfrac{1}{\sqrt{3-2x-x^2}}\,dx = \arcsin\left(\dfrac{x+1}{2}\right) + C$
Here is another example, which again we will set out as a series of steps.
Example 4
Find the integral $\displaystyle I = \int\dfrac{1}{6x-x^2}\,dx$.
Solution
Step 1 Write 6x − x2 in completed square form:
6x − x2 = − (x2 − 6x) = −[(x − 3)2 − 9] = 9 − (x − 3)2
so $\displaystyle I = \int\dfrac{1}{\sqrt{9-(x-3)^2}}\,dx$
Step 2 Make the substitution y = x – 3; then $\displaystyle I = \int\dfrac{1}{\sqrt{9-y^2}}\,dy$
Step 3 Make the substitution y = 3 sin u; then $\sqrt{9 - y^2} = 3\cos u$ and
dy = 3 cos u du. So $I = \Int 1\,du = u + C$
Step 4 Express I in terms of x:
$I = u + C = \arcsin\left(\dfrac{y}{3}\right) + C = \arcsin\left(\dfrac{x-3}{3}\right) + C$
Question T4
Find the integral $\displaystyle I = \int\dfrac{1}{\sqrt{9+8x-2x^2}}\,dx$.
Answer T4
Step 1 Write the quadratic expression under the square root sign in completed square form:
9 + 8x − 2x2 = 9 − 2(x2 − 4x) = 9 − 2[(x − 2)2 − 4] = 17 − 2 (x − 2)2
So$\displaystyle I = \int\dfrac{1}{17-2(x-2)^2}\,dx$
Step 2 Substitute y = x − 2, to obtain $\displaystyle I = \int\dfrac{1}{17-2y^2}\,dy$
Step 3 Substitute $\sqrt{2\os}y = \sqrt{17\os}\sin u$. The denominator becomes $\sqrt{17\os}\cos u$, and $dy = \dfrac{\sqrt{17\os}}{\sqrt{2\os}}\cos u\,du$.
So $\displaystyle I =\int\dfrac{1}{\sqrt{2\os}}\,du = \dfrac{1}{\sqrt{2\os}}u + C$
Step 4 Finally, write the integral I in terms of x:
$I = \dfrac{1}{\sqrt{2\os}}u + C = \dfrac{1}{\sqrt{2\os}}\arcsin\left(\dfrac{\sqrt{2\os}}{\sqrt{17\os}}y\right) + C = \dfrac{1}{\sqrt{2\os}}\arcsin\left(\dfrac{\sqrt{2\os}(x-2)}{\sqrt{17\os}}\right) + C$
In this subsection, we have so far discussed only indefinite integrals. However the techniques presented here can just as easily be used to evaluate definite integrals. You need only remember to transform the limits of integration appropriately in each of Steps 2 and 3; if you do this, there will be no need for Step 4.
Question T5
Evaluate $\displaystyle \int_3^7\dfrac{1}{x2-6x+25}\,dx$.
Answer T5
Step 1 First write the denominator in completed square form:
x2 – 6x + 25 = [(x − 3)2 − 9] + 25 = (x − 3)2 + 16
So the integral to be evaluated becomes $\displaystyle \int_3^7\dfrac{1}{(x-3)^2+16}\,dx$
Step 2 Make the substitution y = x − 3. The new limits of integration are y = 0 and y = 4. So now we are left with
$\displaystyle \int_0^4\dfrac{1}{y^2+16}\,dy$ to evaluate.
Step 3 Make the substitution y = 4 tan u. The denominator becomes 16 sec2 u and dy = 4 sec2 u du. The limits of
integration are u = 0 (the lower limit) and u = π/4 (the upper limit). Thus the definite integral becomes
$\displaystyle \int_0^{\pi/4}\dfrac13\,du = \left[\dfrac14u\right]_0^{\pi/4} = \dfrac{\pi}{16}$
2.3 Splitting the numerator
In the previous subsection, you learnt how to find integrals where the integrand had a quadratic denominator that did not factorize, and had a constant in the numerator. Suppose the integrand had an expression linear in x in the numerator, instead of a constant; for example, suppose you were required to integrate $\dfrac{2x+3}{x^2-4x+10}$. How would you proceed here?
To see what to do in such a case, notice that we in fact already encountered an integral of this sort in Example 2, where we had to find the integral $\displaystyle \int\dfrac{x+3}{(x-1)(x^2+1)}\,dx$. We evaluated it by writing it as the sum of the two integrals:
$\displaystyle \int\dfrac{2}{x-1}\,dx$ and $\displaystyle \int\dfrac{2x+1}{x^2+1}\,dx$. The first of these integrals could be easily evaluated, since the numerator is equal to the derivative of the denominator; thus the substitution y = x2 + 1 enabled us to find it. The second could also be found, using the substitution x = tan y.
We can apply the same idea to an integral such as $\dfrac{2x+3}{x^2-4x+10}$. We write the numerator as the sum of two terms, one which is a multiple of the derivative of the denominator and the other a constant. In the present case, this is easy to do. The derivative of x2 − 4x + 10 is 2x − 4, and clearly the numerator of our integral, 2x + 3, is equal to (2x − 4) + 7. So we write the integral as the sum of two integrals:
$\displaystyle \int\dfrac{2x+3}{x^2-4x+10}\,dx = \int\dfrac{2x-4}{x^2-4x+10}\,dx + \int\dfrac{7}{x^2-4x+10}\,dx$(4)
The first integral on the right–hand side of Equation 4 can be found by means of the substitution y = x2 – 4x + 10, and since dy = (2x − 4) dx, the integral becomes $\displaystyle \int 1\,dy = \loge y + C = \loge(x^2-4x+10) + C$.
The second integral on the right–hand side of Equation 4 is of the sort you learnt to evaluate in Subsection 2.2.
The trick of writing
numerator = multiple of derivative of denominator + constant
is known as splitting the numerator. It involves only very simple algebra, as the following example shows.
Example 5
Split the numerator in the integral $\displaystyle \int\dfrac{2x+1}{3x^2+4x+2}\,dx$.
Solution
The derivative of the denominator is $\dfrac{d}{dx}(3x^2+4x+2) = 6x + 4$. So we write 2x + 1 = a (6x + 4) + b.
Equating the coefficients of x on both sides we find 2 = 6a, i.e. a =1/3, then equating the constant terms we find 1 = 4a + b, so that b = −1/3.
Thus$\displaystyle \int\dfrac{2x+1}{3x^2+4x+2}\,dx = \dfrac{1}{3}\int\dfrac{6x+4}{3x^2+4x+2}\,dx - \dfrac{1}{3}\int\dfrac{1}{3x^2+4x+2}\,dx$
✦ Split the numerator in the integral $\displaystyle \int\dfrac{4-x}{x^2-x+3}\,dx$.
✧ The derivative of the denominator of $\displaystyle \dfrac{4-x}{x^2-x+3}\,dx$ is 2x − 1.
So we write 4 − x = a (2x − 1) + b. Thus 2a = −1, i.e. a = −1/2 and 4 = −a + b, so b = 7/2. Hence
$\displaystyle \dfrac{4-x}{x^2-x+3}\,dx = -\dfrac{1}{2}\int\dfrac{2x-1}{x^2-x+3}\,dx +\dfrac{7}{2}\int\dfrac{1}{x^2-x+3}\,dx$
The technique of splitting the numerator can also be used to find integrals such as $\displaystyle \int\dfrac{1-x}{\sqrt{5-2x-x^2}}\,dx$ where the integrand has the square root of a quadratic function of x in the denominator, and a linear function of x in the numerator. To find this integral, we again write the numerator as a multiple of the derivative of the quadratic function in the denominator [in this case $\dfrac{d}{dx}(5-2x-x^2 ) = -2-2x$], plus a constant; so that for this example we have:
$\overbrace{1-x}^{\color{purple}{\large\text{numerator}}} = a\overbrace{(-2-2x)}^{\color{purple}{\large\substack{\text{derivative of}\\[2pt]\text{ quadratic}}}}+\overbrace{~b~}^{\color{purple}{\large\text{constant}}}$
Equating the coefficient of x, and the constant terms, on each side of this equation, we find a = 1/2, b = 2.
So$\displaystyle \int\dfrac{1-x}{\sqrt{5-2x-x^2}}\,dx = \dfrac{1}{2}\int\dfrac{-2-2x}{\sqrt{5-2x-x^2}}\,dx + 2\int\dfrac{1}{\sqrt{5-2x-x^2}}\,dx$
The first integral on the right–hand side here can be found by the substitution y = 5 − 2x − x2, so that dy = (−2 − 2x) dx, and we have
$\displaystyle \dfrac{1}{2}\int\dfrac{-2-2x}{\sqrt{5-2x-x^2}}\,dx = \dfrac{1}{2}\int\dfrac{1}{\sqrt{y\os}}\,dy = \sqrt{y\os} + C = \sqrt{5-2x-x^2} + C$
The second integral is one of those that you learnt to evaluate in Subsection 2.2. We complete the square in the denominator, to obtain
$\displaystyle \int\dfrac{1}{\sqrt{5-2x-x^2}}\,dx = \dfrac{1}{\sqrt{\smash[b]{6-(x+1)^2}}}\,dx$
and make the substitution y = x + 1, followed by the substitution $y = \sqrt{6\os}\sin u$ to obtain i
$\displaystyle \int\dfrac{1}{\sqrt{5-2x-x^2}}\,dx = \arcsin\left(\dfrac{x+1}{\sqrt{6\os}}\right) + C$
So, finally, $\displaystyle \int\dfrac{1-x}{\sqrt{5-2x-x^2}}\,dx = \sqrt{5-2x-x^2} + 2\arcsin\left(\dfrac{x+1}{\sqrt{6\os}}\right) + C$
Question T6
Find the integral $\displaystyle t = \int \dfrac{r}{\sqrt{ar^2+br-c}}\,dr$, where a, b and c are constants, for the case a = − 1, b = 4 and c = 3.
(Such integrals arise in physics when the motion of an object that is moving under an inverse_square_lawinverse square law of force is considered. Its distance r from the centre of force will be related to time t by such an integral.)
Answer T6
We are required to find $\displaystyle \int\dfrac{r}{\sqrt{4r-r^2-3}}\,dr$, and we start by splitting the numerator. The derivative $\dfrac{d}{dr}(4r-r^2-3) = 4-2r$, so we write r = P (4 − 2r) + Q (where P and Qare constants), from which we see that −2P = 1 and 4P + Q = 0, which gives P = −1/2 and Q = 2. Then
$\displaystyle \int\dfrac{r}{\sqrt{4r-r^2-3}}\,dr = -\dfrac12\int{4-2r}{\sqrt{4r-r^2-3}}\,dr + 2\int{1}{\sqrt{4r-r^2-3}}\,dr$
We find the first integral using the substitution y = 4r − r2 − 3, dy = (4 − 2r) dr and then
$\displaystyle -\dfrac12\int{4-2r}{\sqrt{4r-r^2-3}}\,dr = -\dfrac12\int\dfrac{1}{\sqrt{y\os}}\,dy = -\sqrt{y\os} + C = -\sqrt{4r-r^2-3} + C$
To find the second integral, we first complete the square in the denominator and write 4r − r2 − 3 = −3 − (r2 − 4r) = −3 − [(r − 2)2 − 4] = 1 − (r − 2)2, then
$\displaystyle 2\int\dfrac{1}{\sqrt{4r-r^2-3}}\,dr = 2\int\dfrac{1}{\sqrt{\smash[b]{1-(r-1)^2}}}\,dr$
We now make the substitution y = r − 2, so that this integral becomes $\displaystyle 2\int\dfrac{1}{\sqrt{1-y^2}}\,dy$, which is a standard integral, equal to 2 arcsin y + C = 2 arcsin(r − 2) + C. So, finally,
$\displaystyle \int\dfrac{r}{\sqrt{4r-r^2-3}}\,dr = -\sqrt{4r-r^2-3} + 2\arcsin(r-2) + C$
2.4 Substitutions involving hyperbolic functions
You should know how to evaluate integrals of the form: i
- $\displaystyle \int \dfrac{1}{\sqrt{1-x^2}}\,dx$ by means of the substitution x = sin u i
- $\displaystyle \int \dfrac{1}{x^2+1}\,dx$ by means of the substitution x = tan u i
- $\displaystyle \int \dfrac{1}{x^2-1}\,dx$ using partial fractions. i
Looking at this list, it may occur to you that there are two integrals which are missing from it, although they are very similar to the integrals that do appear there: we have in mind the integrals
$\displaystyle \int \dfrac{1}{\sqrt{x^2+1}}\,dx\quad\text{and}\quad\int \dfrac{1}{\sqrt{x^2-1}}\,dx$
In this subsection, we will show how to find these integrals (and many more which are related to them).
The integral $\displaystyle \int \dfrac{1}{\sqrt{1-x^2}}\,dx$ is equal to arcsin x + C; and one way to prove this is to make the substitution x = sin u. This substitution gets rid of the square root in the denominator, by virtue of the trigonometric identity cos2 u + sin2 u = 1; $\sqrt{1-x^2}$ becomes $\sqrt{1-\sin^2u} = \cos u$, and this gives us a clue as to how to proceed with the integral $\displaystyle \int \dfrac{1}{\sqrt{1+x^2+1}}\,dx$. We recall that the hyperbolic functions cosh and sinh satisfy an identity very similar to the one satisfied by cos and sin, but with a minus sign present, i.e. instead of cos2 u + sin2 u =1, we have cosh2 u – sinh2 u =1. Thus we can get rid of the square root in $\sqrt{1+ x^2}$ if we make the substitution x = sinh u, which gives $\sqrt{1+ x^2} = \sqrt{1+\sinh^2u} = \cosh u$. Since $\dfrac{d}{du}(\sinh u) = \cosh u$, we also have dx = cosh u du.
So, with the substitution x = sinh u, the integral $\displaystyle \int \dfrac{1}{\sqrt{1+x^2}}\,dx$ becomes very easy, and specifically we have
$\displaystyle \int \dfrac{1}{\sqrt{x^2+1}}\,dx = \int\left(\dfrac{1}{\cosh u}\right)\cosh u\,du = u + C$
If x = sinh u then u = arcsinh x. Thus finally we have the result
$\displaystyle \int \dfrac{1}{\sqrt{x^2+1}}\,dx = \arcsinh x + C$(5) i
We can also exploit the identity cosh2 u − sinh2 u = 1 to evaluate the integral $\displaystyle \int \dfrac{1}{\sqrt{x^2-1}}\,dx$. The identity can be rewritten in the form $\sinh u = \sqrt{\cosh^2 u-1}$, which suggests that we make the substitution x = cosh u.
✦ What does the integral $\displaystyle \int \dfrac{1}{\sqrt{x^2-1}}\,dx$ become if we make the substitution x = cosh u?
✧ $\sqrt{x^2-1} = \cosh^2u-1 = \sinh u$; and dx = sinh u du.
So $\displaystyle \int\dfrac{1}{\sqrt{ x^2-1}}\,dx = \int\left(\dfrac{1}{\sinh u}\right)(\sinh u\,du) = \int 1\,du = u + C$
If x = cosh u then u = arccosh x, so that
$\displaystyle \int \dfrac{1}{\sqrt{x^2-1}}\,dx = \arccosh x + C$(6) i
Now that you know how to find the basic integrals $\displaystyle \int \dfrac{1}{\sqrt{x^2+1}}\,dx\quad\text{and}\quad\int\dfrac{1}{\sqrt{x^2-1}}\,dx$, you should not find it hard to adapt the method to find integrals involving similar square roots. Here is an example.
Example 6
Find the integral $\displaystyle \int\dfrac{1}{\sqrt{4+9x^2}}\,dx$.
Solution
The experience that we gained in deriving Equation 5 suggests that we need to make a substitution of the form x = a sinh u, where a is a suitably chosen constant. We choose a so that the identity cosh2 u − sinh2 u = 1 can be used to turn $\sqrt{4 + 9x^2}$ into a multiple of cosh u. If we substitute x = a sinh u into $\sqrt{4 + 9x^2}$, it becomes $\sqrt{4 + 9a^2\sinh^2 u}$ which is equal to 2 cosh u if we choose 9a2 = 4, i.e. a = 2/3. So the required substitution is x = (2/3) sinh u. We then have dx = (2/3) cosh u du, and the integral becomes
$\displaystyle \int\dfrac{1}{\sqrt{4+9x^2}}\,dx = \int\dfrac{1}{2\cosh u}(2/3)\cosh u\,du = \int\dfrac{1}{3}\,du = \dfrac{1}{u} + C$
Since x = (2/3) sinh u we have u = arcsinh(3x/2) and so finally we obtain
$\displaystyle \int\dfrac{1}{\sqrt{4+9x^2}}\,dx = \dfrac{1}{3}\arcsinh\left(\dfrac{3x}{2}\right) + C$
When you have to evaluate integrals of the form $\displaystyle \int\dfrac{1}{\sqrt{a+bx^2}}\,dx$ or $\displaystyle \int\dfrac{1}{\sqrt{bx^2-a}}\,dx$
where a and b are positive constants, you should start by asking yourself ‘What substitution will get rid of the square root in the denominator when I use the identity cosh2 u – sinh2 u = 1?’ If you make this your goal, you will be able to decide whether you need to make a substitution of the form x = a sinh u or of the form x = a cosh u, and you will also be able to determine the required value of the constant a. Use this approach in answering the following question.
Question T7
Find the integrals: (a) $\displaystyle \int\dfrac{2}{\sqrt{4x^2-1}}\,dx$, (b) $\displaystyle \int\dfrac{1}{\sqrt{8x^2+3}}\,dx$.
Answer T7
(a) To find $\displaystyle \int\dfrac{2}{\sqrt{4x^2-1}}\,dx$, notice first that if we put 2x = cosh u, the square root in the denominator becomes $\sqrt{\cosh^2u-1} = \sinh u$. So we make the substitution x = (1/2) cosh u ; then dx = (1/2) sinh u du, and the integral becomes ${\displaystyle \int}\dfrac{2}{\sinh u}(1/2)\sinh u\,du = \Int1\,du = u + C$.
Since u = arccosh(2x), we obtain
$\displaystyle \int\dfrac{2}{\sqrt{4x^2-1}}\,dx = \arccosh(2x) + C$
(b) To find $\displaystyle \int\dfrac{1}{\sqrt{8x^2+3}}\,dx$, notice first that if we put $\sqrt{8\os}x = \sqrt{3\os}\sinh u$ the square root in the denominator becomes
$\sqrt{8\left[\left(\sqrt{3\os}/\sqrt{8\os}\right)\sinh u\right]^2+3} = \sqrt{3(\sinh^2u)+3} = \sqrt{3\os}\cosh u$
So we make the substitution $x = \sqrt{3/8\os}\sinh u$; then $dx = \sqrt{3/8\os}\cosh u\,du$, and the integral becomes
${\displaystyle \int}\dfrac{1}{\sqrt{3\os}\cosh u}\sqrt{3/8\os}\cosh u\,du = \dfrac{1}{\sqrt{8\os}}\Int1\,du = \dfrac{1}{\sqrt{8\os}}u + C$
Since $u = \arcsinh(\sqrt{8/3\os}x)$, we obtain
$\displaystyle \int\dfrac{1}{\sqrt{8x^2+3}}\,dx = \left(\dfrac{1}{\sqrt{8\os}}\right)\arcsinh\left(\sqrt{8/3\os}x\right) + C$
You can, of course, combine substitutions involving hyperbolic functions with the techniques of completing the square and splitting the numerator, in order to find even more integrals. For example, consider the integral
$\displaystyle I = \int\dfrac{1}{\sqrt{4x+x^2}}\,dx $
✦ Write the quadratic function 4x + x2 in completed square form.
✧ 4x + x2 = (x + 2)2 − 4
So we have
$\displaystyle I = \int\dfrac{1}{\sqrt{4x+x^2}}\,dx = \int\dfrac{1}{\sqrt{\smash[b]{(x+2)^2-4}}}\,dx$
We now make the substitution y = x + 2, to obtain
$\displaystyle I = \int\dfrac{1}{\sqrt{y^2-4}}\,dy$
✦ What substitution should we make in order to evaluate $\displaystyle \int\dfrac{1}{\sqrt{y^2-4}}\,dy$
✧ Since $\sqrt{4\cosh^2u - 4} = 2\sinh u$ we need to put y = 2 cosh u.
Making the substitution y = 2 cosh u, and writing dy = 2 sinh u du, we find
$\displaystyle I = \int\dfrac{1}{2\sinh u}2\sinh u\,du = u + C$
Finally, we express u in terms of x and obtain
$u = \arccosh(y/2) = \arccosh\left(\dfrac{x+2}{2}\right)$
so that
$I = \arccosh\left(\dfrac{x+2}{2}\right) + C$
Question T8
Find the integral $\displaystyle \int\dfrac{r}{\sqrt{r^2+2r-2}}\,dr$. i
[Hint: This question requires you to split the numerator; this will leave you with two integrals, one to be found by completing the square in the denominator and substituting a hyperbolic function.]
Answer T8
We first split the numerator. The derivative of the quadratic expression in the denominator is 2r + 2, so we write r = a (2r + 2) + b, from which we see that 2a = 1, 2a + b = 0, i.e. a = 1/2, b = −1.
So$\displaystyle \int\dfrac{r}{\sqrt{r^2+2r-2}}\,dr = \dfrac12\int\dfrac{(2r+2)}{\sqrt{r^2+2r-2}}\,dr - \int\dfrac{1}{\sqrt{r^2+2r-2}}\,dr$
The first integral here can be found by the substitution y = r2 + 2r − 2, with dy = (2r + 2) dr. It becomes
$\displaystyle \dfrac12\int\dfrac{1}{\sqrt{y\os}}\,dy = \sqrt{y\os} + C = \sqrt{r^2+2r-2} + C$
To find the second integral, we complete the square in the denominator: r2 + 2r − 2 = (r + 1)2 − 3
So$\displaystyle \int\dfrac{1}{\sqrt{r^2+2r-2}}\,dr = \int\dfrac{1}{\sqrt{\smash[b]{(r+1)^2-3}}}\,dr$
We make the substitution y = r + 1, which leaves us with $\displaystyle \int\dfrac{1}{\sqrt{y^2-3}}\,dy$ to find. We now make the substitution
$y = \sqrt{3\os}\cosh u$; then $y^2-3 = \sqrt{3\cosh^2u-3} = \sqrt{3\os}\sinh u\quad\text{and}\quad dy = \sqrt{3\os}\sinh u\,du$
so${\displaystyle \int}\dfrac{1}{\sqrt{y^2-3}}\,dy = \Int1\,du = u + C = \arccosh\left(\dfrac{y}{\sqrt{3\os}}\right) + C$
Hence$\displaystyle \int\dfrac{1}{\sqrt{r^2+2r-2}}\,dr = \arccosh\left(\dfrac{r+1}{\sqrt{3\os}}\right) + C$.
Finally we have
$\displaystyle \int\dfrac{r}{\sqrt{r^2+2r-2}}\,dr = \sqrt{r^2+2r-2} - \arccosh\left(\dfrac{r+1}{\sqrt{3\os}}\right) + C$.
We have seen that substitutions of hyperbolic functions enable us to find many integrals where the denominator of the integrand is the square root of a quadratic function. They can also be used to integrate other functions involving a square root of this sort, as in the following example.
Example 7
Find the integral $\displaystyle \int\sqrt{x^2-1}\,dx$.
Solution
We first try the substitution x = cosh u. Then $\sqrt{x^2 - 1} = \sinh u$ and dx = sinh u du. So our integral becomes $\Int\sinh^2u\,du$. This may not immediately seem like much of an improvement on the integral we started with. However, there is an identity involving hyperbolic functions which will help us here: the identity cosh(2u) = 1 + 2 sin h2 u. i Rearranging this gives us $\sinh^2 u = \frac12[\cosh(2u) - 1]$, and substituting this into the integral $\Int\sinh^2u\,du$ gives
$\Int\sinh^2u\,du = \frac12\Int\cosh(2u)\,du - \frac12\Int 1\,du = \frac14\underbrace{\sinh(2u)-\dfrac{u}{2}}_{\color{purple}{\large\substack{\text{We could put}\\[1pt] u = \arccosh x \text{ in here}}}} + C$ i
We now need to express our answer in terms of x. Of course, we could simply put u = arccosh x everywhere in the answer, but it is in fact possible to simplify the expression sinh(2 arccosh x) if we recall another identity, sinh(2u) = 2 cosh u sinh u, and use the result $\sinh u = \sqrt{\cosh^2u - 1}$.
Then we can write $\sinh(2u) = 2\cosh u\sqrt{\cosh^2u-1} = 2x\sqrt{x^2-1}$, and so the final answer is
$\displaystyle \int\sqrt{x^2-1}\,dx = \frac12\sqrt{x^2-1}-\frac12\arccosh x + C$
Study comment The indefinite integral in Example 7 was quite hard, partly because of the work required to express the final answer in terms of x. In the following question you are asked to evaluate a similar definite integral; if you transform the limits of integration when you make the substitution, you will not need to obtain a final answer in terms of x.
Question T9
The length of the section of the parabola y = x2 between the points (0, 0) and (1, 1) is given by the integral $\Int_0^1\sqrt{1+4x^2}\,dx$. Evaluate this integral, using the substitution $x = \frac12\sinh u$ and the identity cosh(2u) = 2 cosh2 u − 1.
Answer T9
With the substitution $x = \frac12\sinh u$ we have $\sqrt{1+4x^2} = \sqrt{1+\sinh^2u} = \cosh u$, and $dx = \frac12\cosh u\,du$. The limits of the original integral are 0 and 1, but u = arcsinh(2x) so that when x = 0 we have u = arcsinh(0) = 0 and when x = 1 we have u = arcsinh(2) = 1.4436. So the limits in the integral after the substitution are u = 0 and u = 1.4436, and we have
$\displaystyle \int_0^1\sqrt{1+4x^2}\,dx = \dfrac12\int_0^{1.4436}\cosh^2u\,du$
In order to evaluate the integral on the right we rearrange the given identity, cosh(2u) = 2 cosh2 u − 1, to obtain
$\cosh^2u = \frac12[1+\cosh(2u)]$
and substitute this in the integral over u, which gives us
$\begin{align}\displaystyle \int_0^1\sqrt{1+4x^2}\,dx & = \dfrac14\int_0^{1.4436}[1+ \cosh(2u)]\,du \\ & = \dfrac14\left[u + \dfrac12\sinh(2u)\right]_0^{1.4436} = \dfrac14\left(1.4436 + \dfrac12\sinh(2.8872) - 0\right) = 1.4789\end{align}$
We could carry on almost indefinitely, and work through many examples of integrals which can be found using the substitution of a hyperbolic function. (For example, the integral $\Int\sqrt{x^2-4x+1}\,dx$ can be found by the method described in Example 7, but you need to complete the square first.) However, we do not have the space; besides, it would become very tedious. You should simply bear in mind that whenever you encounter an integral that contains the square root of a quadratic function of x, a sinh or cosh substitution may well enable you to simplify it, if you cannot think of anything else. Of course, there may be quicker ways to do an integral of that sort!
✦ What is the quickest way to find the integral $\Int x\sqrt{x^2-1}\,dx$?
✧ This integral can be found using the substitution y = x2 − 1.
Then dy = 2x dx, so the integral becomes
$\frac12\Int y\,dy = \frac13y^{3/2}+C$
which gives
$\Int x\sqrt{x^2-1}\,dx = \frac13(x^2-1)^{3/2} + C$ i
2.5 Using trigonometric identities
You should already know how to find integrals like $\Int\cos x\sin^2 x\,dx$, but we will explain how it is done for the sake of completeness. Since cos x is the derivative of sin x, the substitution y = sin x can be used to simplify the integral; and with this substitution, the integral becomes $\Int y^2\,dy = \frac13y^3 + C = \frac13\sin^3x + C$. You may not yet have encountered similar integrals involving hyperbolic functions i, such as $\Int\cosh x\sinh^2x\,dx$, but the same sort of approach will work with those: cosh x is the derivative of sinh x, so, with the substitution y = sinh x this integral similarly becomes $\Int\cosh x\sinh^2x\,dx = \Int y^2\,dy = \frac13y^3 + C = \frac13\sinh^3x + C$.
How can we find the equally simple–looking integral $\Int\cos^3x\,dx$? If we use the trigonometric identity cos2 x + sin2 x =1, we can write this integral as the sum of two integrals that can be found. We proceed as follows:
$\Int\cos^3x\,dx = \Int\cos x\underbrace{\cos^2x}_{\color{purple}{\large{1-\sin^2x}}}\,dx = \Int\cos x(1-\sin^2x)\,dx$
$\phantom{\Int\cos^3x\,dx } = \Int\cos x\,dx - \Int\cos x\sin^2x\,dx = \sin x - \frac13\sin^3x + C$
A similar approach will enable you to integrate any product of powers of cos x and sin x in which either cos x or sin x (or both) is raised to an odd power. Here is an example.
Example 8
Find the integral $\Int\sin^6x\cos^5x\,dx$.
Solution
We write this integral as $\Int(\sin^6x\cos^4x)\cos x\,dx$. i We then express cos4 x in terms of sin x, writing cos4 x = (1 − sin2 x)2, so the integral becomes $\Int\sin^6x(1-\sin^2x)^2\cos x\,dx$. We now make the substitution y = sin x, dy = cos x dx, to obtain the integral
$\Int y^6(1-y^2)^2\,dy = \Int(y^6-2y^8+y^{10})\,dy = \dfrac17y^7 - \dfrac29y^9 + \dfrac{1}{11}y^{11} + C$
So finally, $\Int\sin^6x\cos^5x\,dx = \dfrac17\sin^7x - \dfrac29\sin^9x + \dfrac{1}{11}\sin^{11}x + C$
Question T10
Evaluate the definite integrals: (a) $\Int_0^\pi\sin^3x\,dx$ (b) $\Int_0^\pi\sin3x\cos^2x\,dx$ i
Answer T10
(a) We write the integral as $\Int_0^\pi(\sin^2x)\sin x\,dx$, and then substitute sin2 x = 1 – cos2 x to obtain
$\Int_0^\pi(1-\cos^2x)\sin x\,dx$. We now make the substitution y = cos x, dy = −sin x dx; the new limits of integration are 1 (lower limit) and −1 (upper limit), so that
$\Int_0^\pi(\sin^2x)\sin x\,dx = -\Int_1^{-1}(1-y^2)\,dy = -\left[y-\dfrac13y^3\right]_1^{-1} = \dfrac43$
(b) We write the integral as $\Int_0^\pi\cos^2x\underbrace{(\sin^2x\sin x)}_{\large\color{purple}{\text{this is }\sin^3x}}\,dx$, and substitute sin2 x = 1 − cos2 x to obtain
$\Int\cos^2x\underbrace{(1-\cos^2x)}_{\large\color{purple}{\text{this is }\sin^2x}}\sin x\,dx$
We now make the substitution y = cos x, dy = –sin x dx; the new limits of integration are 1 (lower limit) and
–1 (upper limit), so that
$\Int_0^\pi\sin^3x\cos^2x\,dx = -\Int_1^{-1}y^2(1-y^2)\,dy = -\left[\dfrac13y^3-\dfrac15y^5\right]_1^{-1} = \dfrac{4}{15}$
A very similar method can be used to find integrals of odd powers of cosh x or sinh x; you simply need to employ the identity cosh2 x − sinh2 x = 1.
✦ Find the integral $\Int\sinh^3x\,dx$.
✧ We write this as $\Int\sinh^2x \times \sinh x\,dx$ and put sinh2 x = cosh2 x − 1, to obtain
$\Int\sinh^3x\,dx = \Int\cosh^2x\sinh x\,dx -\Int\sinh x\,dx$
The first of these integrals, $\Int\cosh^2x\sinh x\,dx$, can be found by the substitution y = cosh x, dy = sinh x dx; it is equal to $\frac13\cosh^3x + C$. The second integral, $\Int\sinh x\,dx$ is cosh x + C.
So we have
$\Int\sinh^3x\,dx = \frac13\cosh^3x - \cosh x + C$
You now know how to integrate odd powers of cos x and sin x (or cosh x and sinh x); what about even powers? How can we find, for example, $\Int\cos^2x\,dx$ and $\Int\sin^2x\,dx$? Here we can make use of the identity
cos(2x) = 2 cos2 x − 1 = 1 − 2 sin 2 x
which can be rearranged to give two very useful relations:
$\cos^2x = \frac12[1+\cos(2x)]$(7a)
$\sin^2x = \frac12[1-\cos(2x)]$(7b)
We can use Equation 7a to find $\Int\cos^2x\,dx$. We write
$\Int\cos^2x\,dx = \frac12\Int[1+\cos(2x)]\,dx = \frac12\Int 1\,dx + \frac12\Int\cos(2x)\,dx$
The first of these integrals is equal to $\frac12x + C$ and the second is equal to $\frac14\sin(2x) + C$, so
$\Int\cos^2x\,dx = \frac12x + \frac14\sin(2x) + C$
✦ Use Equation 7b to find the integral $\Int\sin^2x\,dx$.
✧ $\Int\sin^2x\,dx = \frac12\Int[1-\cos(2x)]\,dx = \frac12x - \frac14\sin(2x) + C$
✦ Express cos2(x/2) in terms of cos x.
✧ We use Equation 7a,
$\cos^2x = \frac12[1 + \cos(2x)]$(Eqn 7a)
replacing x in that equation by x/2. This gives cos2 (x/2) = (1 + cos x)/2.
✦ Find $\Int\cos^2(x/2)\,dx$.
✧ $\Int\cos^2(x/2)\,dx = \frac12\Int(1+\cos x)\,dx = \frac12(x+\sin x) + C$
To evaluate higher even powers of cos x or sin x, we can simply use the identities in Equations 7a and 7b more than once, as in the following example.
Example 9
Find the integral $\Int\cos^4x\,dx$.
Solution
Using Equation 7a,
$\cos^2x = \frac12[1+\cos(2x)]$(Eqn 7a)
we have
$\Int\cos^4x\,dx = \frac14\Int[1+\cos(2x)]^2\,dx = \frac14\Int 1\,dx + \frac12\Int\cos(2x)\,dx + \frac14\Int\cos^2(2x)\,dx$(8)
We can easily integrate the first two terms here, and to deal with the last term we use Equation 7a again, with x in that equation replaced by 2x, giving $\cos^2(2x) = \frac12[1+\cos(4x)]$.
Substituting this in Equation 8 gives us
$\Int\cos^4x\,dx = \frac38\Int 1\,dx + \frac12\cos(2x)\,dx + \frac18\cos(4x)\,dx = \frac38x + \frac14\sin(2x) + \frac{1}{32}\sin(4x) + C$
With other integrals involving even powers of cos x and sin x, it may be necessary to use the identity cos2 x + sin2 x = 1, as well as the identities in Equations 7a and 7b. For example, consider the integral $\Int\cos^2x\sin^2x\,dx$. One way to evaluate this would be to replace sin2 x by 1 − cos2 x, thus turning the integral into $\Int\cos^2x\,dx - \Int\cos^4x\,dx$. These are both integrals that have been covered in this module.
Another way to evaluate $\Int\cos^2x\sin^2x\,dx$ is to make use of the identity
sin(2x) = 2 sin x cos x(9)
Since the integrand is simply (sin x cos x)2, we can write the integral as $\frac14\Int\sin^2(2x)\,dx$. You should also be familiar with this integral.
Identities analogous to those in Equations 7a, 7b
$\cos^2x = \frac12[1+\cos(2x)]$(Eqn 7a)
$\sin^2x = \frac12[1-\cos(2x)]$(Eqn 7b)
and Equation 9 hold for hyperbolic functions:
$\cosh^2x = \frac12[1+\cosh(2x)]$(10)
$\sinh^2x= \frac12[\cosh(2x)-1]$(11)
sinh(2x) = 2 sinh x cosh x(12)
These may be used to evaluate integrals of even powers of cosh x and sinh x. We have already used Equation 11 to evaluate $\Int\sinh^2x\,dx$ in Example 7. You can practise using these identities by trying the following question.
Question T11
Find the integral $\Int\sinh^4x\,dx$.
Answer T11
Using the identity in Equation 11, we write
$\Int\sinh^4x\,dx = \frac14\Int[\cosh(2x)-1]^2\,dx = \frac14\Int\cosh^2(2x)\,dx - \frac12\Int\cosh(2x)\,dx + \frac14\Int1\,dx$
To find $\Int\cosh^2(2x)\,dx$ we use the identity of Equation 10 (with x replaced by 2x), and write
$\Int\cosh^2(2x)\,dx = \frac12\Int1\,dx + \frac12\Int\cosh(4x)\,dx$
We then have
$\Int\sinh^4x\,dx = \frac18\Int\cosh(4x)\,dx - \frac12\Int\cosh(2x)\,dx + \frac38\Int1\,dx = \frac{1}{32}\sinh(4x) - \frac14\sinh(2x) + \frac38x + C$
Repeated use of the identities in Equations 7a, 7b and 9 to 12 can, however, become rather tedious in working out integrals of high even powers of cos x and sin x (or cosh x and sinh x). In the next subsection, we show you an alternative, less laborious, way of finding such integrals.
2.6 Reduction formulae
We have just shown you one way of finding the integral $\Int\cos^2x\,dx$. This integral can also be found using integration by parts, and the method is worth describing, as it will lead to an elegant means of finding integrals of high powers of cos x and sin x. We introduce the notation $I = \Int\cos^2x\,dx$. Applying the formula for integration by parts
$\Int f(x)g(x)\,dx = F(x)g(x) - \Int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(13)
and taking f (x) = g (x) = cos x, so that F (x) = sin x and $\dfrac{dg}{dx} = -\sin x$, we find
$I = \Int\underbrace{\cos x}_{\color{purple}{\large f(x)}}\underbrace{\cos x}_{\color{purple}{\large g(x)}}\,dx = \underbrace{\sin x}_{\color{purple}{\large F(x)}}\underbrace{\cos x}_{\color{purple}{\large g(x)}} - \Int\underbrace{\sin x}_{\color{purple}{\large F(x)}}\,\underbrace{(-\sin x)}_{\color{purple}{\large dg/dx}}\,dx$
i.e.$I = \sin x\cos x + \Int\sin^2x\,dx = \sin x\cos x + \Int[1-\cos^2x]\,dx = \sin x\cos x + \Int 1\,dx - \underbrace{\Int\cos^2x\,dx}_{\color{purple}{\large{\text{the integral } I}}}$
Pay particular attention to the fact that the integral I has appeared on the right–hand side of the final expression.
If we replace $\Int 1\,dx$ by x + C we can write the result of the above calculation in the form
I = sin x cos x + x + C − I
we can see that by rearranging this equation we have
2I = sin x cos x + x + C
so that the required integral is given by
$I = \Int\cos^2x\,dx = \frac12\sin x\cos x + \frac12x + C$(14) i
Let us see what would happen if we applied the same method to the integral of some other power of cos x. In fact, we will not specify the power; we will consider the general integral $I_n = \Int\cos^nx\,dx$ (where n is a positive integer greater than 1). i
We write In as $\Int(\cos x)(\cos^{n-1})\,dx$ and apply Equation 13, taking f (x) = cos x and g (x) = cosn−1 x. Then F (x) = sin x, and $\dfrac{dg}{dx} = -(n -1)\cos^{n-2}x\sin x$.
So Equation 13 gives the result
$I_n = \sin x\cos^{n-1}x + (n-1)\Int\cos^{n-2}x\underbrace{\sin^2x}_{\color{purple}{\large{\substack{\text{replaced by}\\1-\cos^2x}}}}\,dx$ i
$I_n = \sin x\cos^{n-1}x + (n-1)\Int\cos^{n-2}x(1-\cos^2x)\,dx$
$\phantom{I_n }= \sin x\cos^{n-1}x + (n-1)\Int\cos^{n-2}x\,dx - (n-1)\underbrace{\Int\cos^nx}_{\color{purple}{\large{\text{this is }I_n}}}\,dx$(15)
Again, the integral In that we are interested in appears on the right–hand side; unfortunately so does the integral $\Int\cos^{n-2}x\,dx$. This is not an integral that we can evaluate as it stands, but note that it is of the same form as the integral In that we are trying to find; we can call it In−2. With this notation, if we take all the terms in In to the left–hand side of Equation 15, it then becomes
nIn = sin x cosn−1 x + (n − 1)In−2
i.e.$\Int\cos^nx\,dx = \dfrac1n\sin x\cos^{n-1}x + \dfrac{n-1}{n}\Int\cos^{n-2}x\,dx$(16)
The reason why Equation 16 is useful is that if we have already evaluated $\Int\cos^{n-2}x\,dx$, it allows us to write down $\Int\cos^nx\,dx$ very quickly. In this way, it is possible to build up a whole sequence of integrals of powers of cos x. For example, we have already evaluated $\Int\cos^2x\,dx$ (see Equation 14); and we can use this to find $\Int\cos^4x\,dx$. We put n = 4 in Equation 16, to obtain
$\Int\cos^4x\,dx = \dfrac14\sin x\cos^3x + \dfrac34\Int\cos^2x\,dx = \dfrac{\sin x\cos^3x}{4} + \dfrac{3\sin x\cos x}{8} + \dfrac{3x}{8} + C$ i
Now that we know $\Int\cos^4x\,dx$, we can use it in Equation 16, setting n = 6, to find $\Int\cos^6x\,dx$, and so on.
✦ Substitute n = 3 in Equation 16, and hence find $\Int\cos^3x\,dx$.
✧ With n = 3, Equation 16,
i.e.$\Int\cos^nx\,dx = \dfrac1n\sin x\cos^{n-1}x + \dfrac{n-1}{n}\Int\cos^{n-2}x\,dx$(16)
becomes
$\begin{align}{\small\int}\cos^3x\,dx & = \dfrac13\sin x\cos^{3-1}x + \dfrac{3-1}{3}{\small\int}\cos^{3-3}x\,dx\\ & = \dfrac13\sin x\cos^2x + \dfrac23{\small\int}\cos x \,dx = \dfrac13\sin x\cos^2x + \dfrac23\sin x+C\end{align}$(Eqn 17)
✦ Find $\Int\cos^5x\,dx$ (you may make use of Equation 17).
$\begin{align}{\small\int}\cos^3x\,dx & = \dfrac13\sin x\cos^{3-1}x + \dfrac{3-1}{3}{\small\int}\cos^{3-3}x\,dx\\ & = \dfrac13\sin x\cos^2x + \dfrac23{\small\int}\cos x \,dx = \dfrac13\sin x\cos^2x + \dfrac23\sin x+C\end{align}$(Eqn 17)
✧ To do this, we put n = 5 in Equation 16,
i.e.$\Int\cos^nx\,dx = \dfrac1n\sin x\cos^{n-1}x + \dfrac{n-1}{n}\Int\cos^{n-2}x\,dx$(16)
so that it becomes
$\Int\cos^5x\,dx = \dfrac15\sin x\cos^4x + \dfrac45\Int\cos^3x\,dx$
Substituting the result for $\Int\cos^3x\,dx$ from Equation 17,
$\begin{align}{\small\int}\cos^3x\,dx & = \dfrac13\sin x\cos^{3-1}x + \dfrac{3-1}{3}{\small\int}\cos^{3-3}x\,dx\\ & = \dfrac13\sin x\cos^2x + \dfrac23{\small\int}\cos x \,dx = \dfrac13\sin x\cos^2x + \dfrac23\sin x+C\end{align}$(Eqn 17)
here gives us
$\Int\cos^5x\,dx = \dfrac15\sin x\cos^4x + \dfrac{4}{15}\sin x\cos^2x + \dfrac{8}{15}\sin x + C$
Formulae such as Equation 16, which relate an integral involving a power of some function (in the above case I n) to a similar integral involving a lower power of the same function (in the above case In−2), are known as reduction formulae. They enable us to build up a whole sequence of integrals, starting from an integral that is easy to evaluate. There is no need to memorize reduction formulae, but you should be aware that they exist, and be able to look them up and use them. We will present you here with two more examples of reduction formulae.
As you might expect, there also exists a reduction formula that enables us to find integrals of powers of sin x. Here it is:
$\Int\sin^nx\,dx = -\dfrac1n\cos x\sin^{n-1}x + \dfrac{n-1}{n}\Int\sin^{n-2}x\,dx$(18)
The derivation of this formula is very similar to the derivation of Equation 16, and we leave it for you to do in the following question.
Question T12
(a) Derive Equation 18. [Hint: Start by integrating $I_n = \Int\sin^nx\,dx$ by parts, taking f (x) = sin x and g (x) = sinn−1 x in Equation 13.]
$\Int f(x)g(x)\,dx = F(x)g(x) - \Int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 13)
(b) Use Equation 18 to find $\Int\sin^3x\,dx$.
Answer T12
(a) With f (x) = sin x and g (x) = sinn−1 x, F (x) = −cos x and $\dfrac{dg}{dx} = (n-1)\sin^{n-2}x\cos x$.
Substituting these expressions in Equation 13 gives
$\Int\sin^nx\,dx = -\cos x\sin^{n-1}x + (n-1)\Int\cos^2x\sin^{n-2}x\,dx$
We use the identity cos2 x = 1 − sin2 x in the integral on the right, to obtain
$\Int\sin^nx\,dx = -\cos x\sin^{n-1}x + (n-1)\Int\sin^{n-2}x\,dx - (n-1)\Int\sin^nx\,dx$
Collecting together the terms in $\Int\sin^nx\,dx$, we find
$n\Int\sin^nx\,dx = -\cos x\sin^{n-1}x + (n-1)\Int\sin^{n-2}x\,dx$
i.e.$\Int\sin^nx\,dx = -\dfrac1n\cos x\sin^{n-1}x + \dfrac{n-1}{n}\Int\sin^{n-2}x\,dx$
which is Equation 18.
(b) If we substitute n = 3 in Equation 18 we find
$\Int\sin^3x\,dx = -\frac13\cos x\sin^2x + \frac23\Int\sin x\,dx$
but$\Int\sin x\,dx = -\cos x + C$
so$\Int\sin^3x\,dx = -\frac13\cos x\sin^2x - \frac23\cos x + C$
A third useful reduction formula deals with integrals of the form $\Int x^n{\rm e}^{-ax}\,dx$ where a is a positive constant and n is a positive integer. Again we use integration by parts to derive the reduction formula. In the integral, we take
f (x) = e−ax and g (x) = x n, then $F(x) = -\dfrac1a{\rm e}^{-ax}$ and $\dfrac{dg}{dx} = nx^{n-1}$ and substituting these expressions into
Equation 13,
$\Int f(x)g(x)\,dx = F(x)g(x) - \Int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 13)
we obtain
$\Int \underbrace{{\rm e}^{-ax}}_{\color{purple}{\large f(x)}}\underbrace{x^n}_{\color{purple}{\large g(x)}}\,dx = \underbrace{\left(-\dfrac1a{\rm e}^{-ax}\right)}_{\color{purple}{\large F(x)}}\underbrace{x^n}_{\color{purple}{\large g(x)}} - {\displaystyle \int}\underbrace{nx^{n-1}}_{\color{purple}{\large dg/dx}}\underbrace{\left(-\dfrac1a{\rm e}^{-ax}\right)}_{\color{purple}{\large F(x)}}\,dx$
so that$\Int x^n{\rm e}^{-ax}\,dx = -x^n\dfrac1a{\rm e}^{-ax} + \dfrac na\Int x^{n-1}{\rm e}^{-ax}\,dx$(19) i
Equation 19 shows that we can express $\Int x^n{\rm e}^{-ax}\,dx$ in terms of $\Int x^{n-1}{\rm e}^{-ax}\,dx$, an integral involving one less power of x.
In the simplest case, if n = 1 in Equation 19, we can find $\Int x{\rm e}^{-ax}\,dx$, and so obtain
$\Int x{\rm e}^{-ax}\,dx = -\dfrac xa{\rm e}^{-ax} + \dfrac1a\Int{\rm e}^{-ax}\,dx = -\dfrac xa{\rm e}^{-ax} - \dfrac{1}{a^2}{\rm e}^{-ax} + C$
✦ Given that $\Int x{\rm e}^{-ax}\,dx = -\dfrac xa{\rm e}^{-ax} - \dfrac{1}{a^2}{\rm e}^{-ax} + C$, find $\Int x^2{\rm e}^{-ax}\,dx$.
✧ Let n = 2 in Equation 19,
$\Int x^n{\rm e}^{-ax}\,dx = -x^n\dfrac1a{\rm e}^{-ax} + \dfrac na\Int x^{n-1}{\rm e}^{-ax}\,dx$(Eqn 19)
which gives us
$\Int x^2{\rm e}^{-ax}\,dx = -\dfrac{x^2}{a}{\rm e}^{-ax} + \dfrac2a\Int x{\rm e}^{-ax}\,dx = -\dfrac{x^3}{a}{\rm e}^{-ax} - \dfrac{2}{a^2}{\rm e}^{-ax} - \dfrac{2}{a^3}{\rm e}^{-ax} + C$
2.7 Mixed examples
Aside You may be aware of the existence of algebraic computing programs such as: Mathematica, Reduce, Maple, Mathcad or Derive, which can find indefinite integrals, and evaluate definite integrals as functions of the parameters appearing in them. If so, you may be wondering why you should bother to learn advanced integration techniques; why not just key in the integral and let the program do the work? Such programs have their limitations. They may not give you the answer in the form you are expecting, for instance, in Example 6 we found
$\displaystyle \int\dfrac{1}{\sqrt{4+9x^2}}\,dx = \dfrac13\arcsinh\left(\dfrac{3x}{2}\right) + C$
but using Derive you would obtain
$\displaystyle \int\dfrac{1}{\sqrt{4+9x^2}}\,dx = \dfrac13\loge\sqrt{\smash[b]{(9x^2+4)+3x}} + C$
It is not immediately obvious that these two answers are the same.
In the case of improper but convergent integrals, the program may decide (incorrectly) that the integral cannot be evaluated, and you may have to make a substitution in order to make the integral acceptable to the program. Such programs can be very useful, and they certainly alleviate the tedious business of calculating unpleasant integrals, but you would be very unwise to use them without understanding the basic principles of integration.
How to tackle a general integral
You have learnt several tricks that will enable you to find a wide variety of integrals. We do not intend to summarize them here. First, their uses are so widespread that such a summary would be lengthy and boring; second (and more important) we do not want you to feel that you must learn by heart a long list of different types of integral and the methods that will work for them. Certainly you should have these methods as part of your ‘mathematical furniture’, but you should think of them as techniques to be applied in a ‘trial and error’ way. It is not a disaster if the first method you try does not work; you simply have to try something else. You should bear in mind too, that many integrals can only be found by a combination of the techniques you have learnt here; it may, for example, be necessary for you to use more than one substitution, and perhaps combine substitutions with algebraic manipulation or use of identities. As you gain more experience with integration, you will begin to see automatically what sort of approaches are likely to prove productive with a given integral.
The following two questions should serve as revision of the integration techniques we have discussed.
Question T13
Find the following integrals: i
(a) $\displaystyle \int\dfrac{1}{x^2 − 2x}\,dx$ [Hint: Use partial fractions.]
(b) $\Int\cos^7(2x)\sin^4(2x)\,dx$ [Hint: Use trigonometric identities.]
(c) $\displaystyle \int\dfrac{1-4x}{1+4x+2x^2}\,dx$ [Hint: Split the numerator; complete the square in the denominator; use a hyperbolic function substitution.]
(d) $\Int_1^2(x^2-1)^{3/2}\,dx$ [Hint: Substitute a hyperbolic function; use the answer to Question T11.]
Answer T13
(a) Write $\dfrac{1}{x^2-2x} = \dfrac{1}{x(x-2)} = \dfrac a2 + \dfrac{b}{x-2} = \dfrac{(a+b)x-2a}{x(x-2)}$,
from which it follows that a + b = 0, –2a = 1, so that a = –1/2 and b = 1/2. So
$\displaystyle \int\dfrac{1}{x^2-2x}\,dx = -\dfrac12\int x\,dx + \dfrac12\int\dfrac{1}{x-2}\,dx = -\dfrac12\loge x + \dfrac12\loge(x-2) + C$
(b) Write the integral as $\Int\cos^6(2x)\sin^4(2x) \times \cos(2x)\,dx$
and put cos2 (2x) = 1 − sin2 (2x), to obtain
$\Int[1-\sin^2(2x)]^3\sin^4(2x) \times \cos(2x)\,dx$
Now make the substitution y = sin(2x), dy = 2 cos(2x) dx; the integral becomes
$\frac12\Int(1-y^2)^3y^4\,dy = \frac12\Int(y^4-3y^6+3y^8-y^{10})\,dy = \frac{1}{10}y^5-\frac{3}{14}y^7+\frac16y^9-\frac{1}{22}y^{11}+C$
So$\Int\cos^7(2x)\sin^4(2x)\,dx = \frac{1}{10}\sin^5(2x)-\frac{3}{14}\sin^7(2x)+\frac16\sin^9(2x)-\frac{1}{22} \sin^{11}(2x)+C$
(c) First split the numerator. The derivative of the denominator is 4 + 4x; writing 1 − 4x = a (4 + 4x) + b, we find
4a = −4 and 4a + b = 1, so that a = −1 and b = 5.
So$\displaystyle \int\dfrac{1-4x}{\sqrt{1+4x+2x^2}}\,dx = -\int\dfrac{4+4x}{\sqrt{1+4x+2x^2}}\,dx + 5\int\dfrac{1}{\sqrt{1+4x+2x^2}}\,dx$
The first of these integrals can be found using the substitution y = 1 + 4x + 2x2, dy = (4 + 4x) dx; it becomes
$\displaystyle \int\dfrac{1}{\sqrt{y\os}}\,dy = -2\sqrt{y\os} + C = -2\sqrt{1+4x+2x^2} + C$
In the second integral, we complete the square in the denominator: 1 + 4x + 2x2 = 2 (x + 1)2 − 1.
So$\displaystyle 5\int\dfrac{1}{\sqrt{1+4x+2x^2}}\,dx = 5\int\dfrac{1}{\sqrt{\smash[b]{2(x+1)^2-1}}}\,dy$
We make the substitution y = x + 1, whereupon the integral becomes $\displaystyle 5\int\dfrac{1}{\sqrt{2y^2-1}}\,dy$, followed by the substitution $\sqrt{2\os}y = \cosh u, dy = \dfrac12\sinh u\,du$, after which this integral becomes $\displaystyle \dfrac{5}{\sqrt{2\os}}\int1\,du = \dfrac{5}{\sqrt{2\os}}u + C$
Expressing this answer in terms of x gives us $\dfrac{5}{\sqrt{2\os}}\arccosh\left[\sqrt{2\os}( x + 1)\right] + C$. So, finally,
$\displaystyle \int\dfrac{1-4x}{\sqrt{1+4x+2x^2}}\,dx = -2\sqrt{1+4x+2x^2} + \dfrac{5}{\sqrt{2\os}}\arccosh\left[\sqrt{2\os}( x + 1)\right] + C$
(d) Make the substitution x = cosh u. Then dx = sinh u du, and (x2 − 1)3/2 = sinh3 u. The new limits of integration are arccosh(1) = 0 and arccosh(2) = 1.3170.
So$\Int_1^2(x^2-1)^{3/2}\,dx = \Int_0^{1.3170}\sinh^4u\,du$
From the answer to Question T11,
$\begin{align}\Int_0^{1.3170}\sinh^4u\,du & = \left[\dfrac{1}{32}\sinh(4u) - \dfrac14\sinh(2u) + \dfrac38u\right]_0^{1.3170}\\ & = \dfrac{1}{32}((96.9949-0) - \dfrac14(6.9282-0) + \dfrac38(1.3170-0) = 1.7929\end{align}$
Question T14
Find the following integrals:
(a) $\displaystyle \int\dfrac{3x+2}{(x^2+2x+2)(x−1)}\,dx$ (b) $\Int_0^{\pi/2}\sin^6x\,dx$ (c) $\displaystyle \int\dfrac{x^2}{x^2-4}\,dx$
Answer T14
(a) First split the integrand into partial fractions, and write
$\dfrac{3x+2}{(x^2+2x+2)(x-1)} = \dfrac{ax+b}{x^2+2x+2} +\dfrac{d}{x-1} = \dfrac{(a+d)x^2+(2d+b-a)x+2d-b}{(x^2+2x+2)(x-1)}$
hencea + d = 0, 2d + b − a = 3, 2d − b = 2, which gives a = −1, b = 0 and d = 1.
So$\displaystyle \int\dfrac{3x+2}{(x^2+2x+2)(x-1)}\,dx = \int\dfrac{1}{x-1}\,dx - \int\dfrac{x}{x^2+2x+2}\,dx$
The first integral on the right is straightforward: $\displaystyle \int\dfrac{1}{x-1}\,dx= \loge(x-1) + C$
To evaluate the second integral, first split the numerator, and write
$\displaystyle \int\dfrac{x}{x^2+2x+2}\,dx = \dfrac12\int\dfrac{2x+2}{x^2+2x+2}\,dx - \int\dfrac{1}{x^2+2x+2}\,dx = \dfrac12\loge(x^2+2x+2) - \int\dfrac{1}{x^2+2x+2}\,dx$
Find the remaining integral by completing the square in the denominator:
$\displaystyle \int\dfrac{1}{x^2+2x+2}\,dx = \int\dfrac{1}{(x+1)^2+1}\,dx$
Now make the substitution y = x + 1, and obtain the standard integral
$\displaystyle \int\dfrac{1}{y^2+1}\,dy = \arctan y + C = \arctan(x+1) + C$
Therefore
$\displaystyle \int\dfrac{3x+2}{(x^2+2x+2)(x-1)}\,dx = \loge(x-1) - \dfrac12\loge(x^2+2x+2) + \arctan(x+1) + C$
(b) The quickest way to evaluate this integral is to use the reduction formula given in Equation 18,
$\Int\sin^nx\,dx = -\dfrac1n\cos x\sin^{n-1}x + \dfrac{n-1}{n}\Int\sin^{n-2}x\,dx$(Eqn 18)
Taking n = 6 there, and putting in the limits 0 and π/2 gives
$\displaystyle \int_0^{\pi/2}\sin^6x\,dx = -\dfrac16\left[\cos x\sin^5x\right]_0^{\pi/2} + \dfrac56\int_0^{\pi/2}\sin^4x\,dx$
The first term is zero, since cos(π/2) = 0 and sin 0 = 0; to evaluate the second integral, we use the same reduction formula again (with n = 4), to obtain
$\displaystyle \dfrac56\int_0^{\pi/2}\sin^4x\,dx = -\dfrac56\times\dfrac14\left[\cos x\sin^3x\right]_0^{\pi/2} + \dfrac56\times\dfrac34\int_0^{\pi/2}\sin^2x\,dx$
Once again the first term here is zero; use the reduction formula yet again to evaluate the remaining integral:
$\displaystyle \int_0^{\pi/2}\sin^2x\,dx = -\dfrac12\left[\sin x\cos x\right]_0^{\pi/2} + \dfrac12\int_0^{\pi/2}(\sin x)^0\,dx$
which is simply equal to $\displaystyle \dfrac12\int_0^{\pi/2}1\,dx = \dfrac{\pi\os}{4}$, because the first term vanishes and anything raised to the power zero is equal to 1. So finally
$\Int_0^{\pi/2}\sin^6x\,dx = \dfrac56\times\dfrac34\times\dfrac{\pi\os}{4} = \dfrac{5\pi\os}{32}$
(Alternatively, you could evaluate this integral by using trigonometric identities alone. If you managed to get the right answer this way, congratulations – it is quite a lengthy calculation. Bear in mind in future that reduction formulae are particularly useful when evaluating definite integrals between limits such that many terms vanish, as happens here.)
(c) To find this integral, we put x = 2 cosh u, dx = 2 sinh u du. The integral becomes
${\displaystyle \int}\dfrac{4\cosh^2u}{2\sinh u} \times 2\sinh u\,du = 4\Int\cosh^2u\,du$
and this integral can be found by using Equation 10,
$\cosh^2x = \frac12[1+\cosh(2x)]$(Eqn 10)
to give $4\Int\cosh^2u\,du = 2\Int[1+\cosh(2y)]\,du = 2u + \sinh(2u) + C$
We must now express this answer in terms of x. We can use Equation 12,
sinh(2x) = 2 sinh x cosh x(Eqn 12)
to simplify sinh(2u) (as we did at the end of Example 7): sinh(2u) = 2 sinh u cosh u, and cosh u = x/2, so
$\sinh(2u) = x\sqrt{\dfrac{x^2}{4}-1}$
So, finally, ${\displaystyle \int}\dfrac{x^2}{\sqrt{x^2-4}}\,dx = 2\arccosh\left(\dfrac{x}{2}\right) + x\sqrt{\dfrac{x^2}{4}-1} + C$
3 Some definite integrals
3.1 Integrals with an infinite upper or lower limit
Definite integrals in which one or both of the limits is infinite occur very often in physics. Here are some examples:
$\displaystyle V = \int_r^\infty\dfrac{Q}{4\pi\varepsilon_0x^2}\,dx$(20) i
$\displaystyle \int_{-\infty}^\infty\dfrac{1}{(x-x_0)^2 +a^2}\,dx$, where x0 and a are constants, and a > 0(21) i
$\langle v\rangle = 4\pi\left(\dfrac{m}{2\pi kT}\right)^{3/2}\Int_0^\infty v^3\exp(-mv^2/kT)\,dv$(22) i
$\Int_0^\infty x^n{\rm e}^{-ax}\,dx$, where n is a non–negative integer, and a > 0(23) i
Definite integrals over an infinite range of integration are known as improper integrals. The way to evaluate them is to replace the infinite limit by a very large (but finite) number, evaluate the integral in the usual way, and then see what happens to your result as the large number becomes larger still. More formally, we think of an improper integral as a limit:
$\Int_a^\infty\;f(x)\,dx = {\displaystyle \lim_{b\rightarrow\infty}}\;\Int_a^bf(x)\,dx$
and$\Int_{-\infty}^b\;f(x)\,dx = {\displaystyle \lim_{a\rightarrow\infty}}\;\Int_a^bf(x)\,dx$ i
If you can find the indefinite integral $F(x) + C = \Int f(x)\,dx$, evaluating an improper definite integral of the form $\Int_a^\infty f(x)\,dx$ simply requires you to know how the function F (x) behaves when x becomes very large. Often this is obvious. For example, to evaluate the integral in Equation 20,
$\displaystyle V = \int_r^\infty\dfrac{Q}{4\pi\varepsilon_0x^2}\,dx$(Eqn 20)
we think of it as the limit as R → ∞ of
$\displaystyle \int_r^R\dfrac{Q}{4\pi\varepsilon_0x^2}\,dx = \left[-\dfrac{Q}{4\pi\varepsilon_0x^2}\right]_r^R = -\dfrac{Q}{4\pi\varepsilon_0R} + \dfrac{Q}{4\pi\varepsilon_0r}$
As R becomes very large, 1/R becomes smaller and smaller, so that as R → ∞ the first term tends to zero. So we are left with
$\displaystyle V = \int_r^\infty\dfrac{Q}{4\pi\varepsilon_0x^2}\,dx =\dfrac{Q}{4\pi\varepsilon_0r}$
Sometimes it may not be immediately obvious what happens to F (x) as x becomes very large. For example, at the start of Subsection 2.1 we showed that
$\displaystyle \int\dfrac{1}{(x+1)(x+2)}\,dx = \loge(x+1)-\loge(x+2) + C$
Suppose that we want to find the definite integral $\displaystyle \int_0^\infty\dfrac{1}{(x+1)(x+2)}\,dx$. i We can express this integral as $\displaystyle \lim_{a\rightarrow\infty}\left[\loge(x+1) - \loge(x+2)\right]_0^a$; what happens to the difference between two logarithms when their arguments, i.e. (x +1) and (x + 2) both become very large? We can see what happens if we write this difference of logarithms as the logarithm of a fraction:
$\loge(x+1) - \loge(x+2) = \loge\left(\dfrac{x+1}{x+2}\right)$
As x becomes very large, the fraction tends towards the value 1, and its logarithm tends to zero.
So$\displaystyle \int_0^\infty\dfrac{1}{(x+1)(x+2)}\,dx = 0 - \loge\left(\dfrac{1}{2}\right) = 0.6931$
✦ What is the limit as x → ∞ of $\dfrac{3x^2+2x+5}{2x^2-4x-1}$?
✧ Dividing numerator and denominator by x2 we have
$\dfrac{3x^2+2x+5}{2x^2-4x-1} = \left.\left(3+\dfrac2x+\dfrac{5}{x^2}\right)\middle/\left(2-\dfrac4x-\dfrac{1}{x^2}\right)\right.$
and as x becomes very large, the numerator approaches 3 while the denominator approaches 2, so the fraction tends to 3/2.
Another potentially tricky situation arises when we consider the integral in Equation 23, namely $\Int_0^\infty x^n{\rm e}^{-ax}\,dx$.
We are already part of the way in evaluating the indefinite integral $\Int x^n{\rm e}^{-ax}\,dx$; we derived a reduction formula for it in Subsection 2.6:
$\Int x^n{\rm e}^{-ax}\,dx = -x^n\dfrac1a{\rm e}^{-ax} + \dfrac na\Int x^{n-1}{\rm e}^{-ax}\,dx$(Eqn 19)
We can easily convert Equation 19 into a reduction formula involving definite integrals between 0 and ∞, by putting in the limits:
$\Int_0^\infty x^n{\rm e}^{-ax}\,dx = -\dfrac1a\left[x^n{\rm e}^{-ax}\right]_0^\infty + \dfrac na\Int_0^\infty x^{n-1}{\rm e}^{-ax}\,dx$(24)
We now need to know what happens to the function x ne−ax as x becomes very large. There is something of a dilemma here: e−ax becomes very small for large x (remember that a is positive), but x n becomes very large; which one wins? Although we will not prove it here, the rule is as follows:
x ne−ax → 0 as x → ∞ for any n and any positive constant a(25) i
Using this rule to evaluate the term $\left[x^n{\rm e}^{-ax}\right]_0^\infty$ in Equation 24, we see that the function is zero at the upper limit; it is also zero at the lower limit (because of the factor x n). So Equation 24 becomes
$\Int_0^\infty x^n{\rm e}^{-ax}\,dx = \dfrac na\Int_0^\infty x^{n-1}{\rm e}^{-ax}\,dx$(26)
✦ Evaluate the integral $\Int_0^\infty{\rm e}^{-ax}\,dx$.
✧ $\Int_0^\infty {\rm e}^{-ax}\,dx = \left[\dfrac1a{\rm e}^{-ax}\right]_0^\infty = 1$, since e−ax → 0 as x → ∞.
✦ Evaluate the integrals $\Int_0^\infty x{\rm e}^{-ax}\,dx$ and $\Int_0^\infty x^2{\rm e}^{-ax}\,dx$, using Equation 26.
✧ Substituting n = 1 in Equation 26,
$\Int_0^\infty x^n{\rm e}^{-ax}\,dx = \dfrac na\Int_0^\infty x^{n-1}{\rm e}^{-ax}\,dx$(Eqn 26)
gives us
$\Int_0^\infty x{\rm e}^{-ax}\,dx = \dfrac1a\Int_0^\infty{\rm e}^{-ax}\,dx = \dfrac{1}{a^2}$
Substituting n = 2 in Equation 26, and using the above result, gives us
$\Int_0^\infty x^2{\rm e}^{-ax}\,dx = \dfrac2a\Int_0^\infty x{\rm e}^{-ax}\,dx = \dfrac{2}{a^3}$
You may be able to see a pattern emerging. If we now use Equation 26 to work out $\Int_0^\infty x^3{\rm e}^{-ax}\,dx$, we find
$\Int_0^\infty x^3{\rm e}^{-ax}\,dx = \dfrac{3\times 2\times 1}{a^4}, \Int_0^\infty x^4{\rm e}^{-ax}\,dx = \dfrac{4\times 3\times 2\times 1}{a^5}$ and so on.
The general result is
$\Int_0^\infty x^n{\rm e}^{-ax}\,dx = \dfrac{n!}{a^{n+1}}$(27) i
✦ Evaluate the integral $\Int_0^\infty x^7{\rm e}^{-ax}\,dx$.
✧ Taking n = 7 and a = 2 in Equation 27,
$\Int_0^\infty x^n{\rm e}^{-ax}\,dx = \dfrac{n!}{a^{n+1}}$(Eqn 27)
we obtain
$\Int_0^\infty x^7{\rm e}^{-2x}\,dx = \dfrac{7!}{2^8} = \dfrac{7\times 6\times 5\times 4\times 3\times 2\times 1}{2^8} = \dfrac{315}{16} = 19.6875$
So far, we have considered improper integrals which could be evaluated without using a substitution. Of course, if you want to evaluate an improper integral using a substitution, you will need to transform the infinite limit of integration appropriately. Sometimes it will turn into a finite quantity, as in the next example.
Example 10
Evaluate the integral $\displaystyle \int_{-\infty}^\infty\dfrac{1}{(x-x_0)^2 + a^2}\,dx$ appearing in Equation 21.
Solution
This integral can be found using the substitution x − x0 = a tan u. Then dx = a sec2 u du, and (x − x0)2 + a2 = a2 sec2 u. When x is very large and positive, so is x − x0 = a tan u. i
If a tan u is very large, then u is close to π/2, and as tan u tends to infinity, u tends to π/2; so the upper limit of integration becomes π/2. Similarly, the lower limit of integration becomes −π/2. Thus
${\displaystyle \int}_{-\infty}^\infty\dfrac{1}{(x-x_0)^2 + a^2}\,dx = \dfrac1a\Int_{-\pi/2}^{\pi/2}\Int 1\,du = a$
It is usually quite straightforward to change infinite limits of integration on making a substitution of the form u = g (x) or x = h (u); you need only ask yourself ‘What does u tend to as x gets very large?’ Of course, often you will find that the infinite limit of integration is still infinite. This is the case in the following question.
Question T15
Using the substitution u = v2, and Equation 27,
$\Int_0^\infty x^n{\rm e}^{-ax}\,dx = \dfrac{n!}{a^{n+1}}$(Eqn 27)
evaluate the integral $\Int_0^\infty v^3\exp(-mv^2/kT)\,dv$ that appears in Equation 22. i
Answer T15
With the substitution u = v2, du = 2v dv and the limits of integration are still 0 and ∞.
So$\Int_0^\infty v^3\exp(-mv^2/2kT)\,dv = \dfrac12{\displaystyle \int}_0^\infty u\exp(-mu/2kT)\,du$
Using Equation 27,
$\Int_0^\infty x^n{\rm e}^{-ax}\,dx = \dfrac{n!}{a^{n+1}}$(Eqn 27)
with n = 1, a = m/2kT gives us
$\Int_0^\infty v^3\exp(-mv^2/2kT)\,dv = 2\left(\dfrac{kT}{m}\right)^2$
3.2 Gaussian integrals
Integrals of the form $\Int_0^\infty x^r\exp(-ax^2)\,dx$, where r is a positive integer or zero, and a is a positive constant, are particularly common in physics. You have already seen one example of this sort in Equation 22,
$\langle v\rangle = 4\pi\left(\dfrac{m}{2\pi kT}\right)^{3/2}\Int_0^\infty v^3\exp(-mv^2/kT)\,dv$(Eqn 22)
(and evaluated it in Question T15). Many others like this arise in the kinetic_theory_of_ideal_gaseskinetic theory of gases, in quantum mechanics, and also in probabilityprobability theory (which you may find yourself using to analyse experimental data).
In the case where r is an odd integer, such integrals can easily be evaluated, using the same substitution that you employed in Question T15. To make it clear that r is odd, we will write r = 2n + 1, where n is any positive integer or zero, and consider the integral $\Int x^{2n+1}\exp(-ax^2)\,dx$ which we write as $\Int x^{2n}\exp(-ax^2)x\,dx$.
We now make the substitution y = x2. Then $x\,dx = \frac12\,dy$, and x2n = (x2) n = y n. So
$\Int_0^\infty x^{2n+1}\exp(-ax^2)\,dx = \dfrac12\Int_0^\infty y^n{\rm e}^{-ay}\,dy$
We know how to evaluate $\Int_0^\infty y^n{\rm e}^{-a}\,dy$; from Equation 27,
$\Int_0^\infty x^n{\rm e}^{-ax}\,dx = \dfrac{n!}{a^{n+1}}$(Eqn 27)
it is equal to $\dfrac{n!}{a^{n+1}}$. Thus:
$\Int_0^\infty x^{2n+1}\exp(-ax^2)\,dx = \dfrac{n!}{2a^{n+1}}$(28)
✦ Evaluate $\Int_0^\infty x^5\exp(-3x^2)\,dx$.
✧ Taking n = 2, a = 3 in Equation 28,
$\Int_0^\infty x^{2n+1}\exp(-ax^2)\,dx = \dfrac{n!}{2a^{n+1}}$(Eqn 28)
we obtain
$\Int_0^\infty x^5\exp(-3x^2)\,dx = \dfrac{2!}{2\times 3^3} = \dfrac{1}{27} = 0.0370$
Notice, too, that because we can relate $\Int x^{2n+1}\exp(-ax^2)\,dx$ to $\Int y^n{\rm e}^{ay}\,dy$ by the substitution y = x2, and we can find the latter integral (for any given value of n) by applying Equation 19,
$\Int x^n{\rm e}^{-ax}\,dx = -x^n\dfrac1a{\rm e}^{-ax} + \dfrac na\Int x^{n-1}{\rm e}^{-ax}\,dx$(Eqn 19)
as many times as is necessary, there is no problem in finding the indefinite integral $\Int x^{2n+1}\exp(-ax^2)\,dx$, should we want to do so.
The situation is very different for the indefinite integral $\Int x^r\exp(-ax^2)\,dx$ where r is an even integer. If you try the substitution x2 = y, you will quickly find that it does not help at all – there is an awkward factor of $\sqrt{y\os}$ left over in the integrand. In fact, such indefinite integrals cannot be evaluated in terms of familiar functions (such as exp, loge, powers of x and so forth). The simplest of these integrals (with r = 0, a = 1) is $\Int\exp(-x^2)\,dx$. This integral is in fact used to define a new function of x, known as the error function, erf(x); the precise definition is
$\erf(x) = \dfrac{2}{\sqrt{\pi\os}}{\displaystyle \int}_0^x\exp(-y^2/2)\,dy$
It is possible to evaluate this integral for different values of x by numerical techniques, and the results have been tabulated and can be looked up in books (indeed, some calculators have an ‘erf’ button). If you study advanced probability theory in future, you are bound to come across this function. However, here we will be concerned just with the definite integral $\Int_0^\infty\exp(-x^2)\,dx$, and definite integrals such as $\Int_0^\infty x^r\exp(-ax^2)\,dx$ (where r is an even integer) which can be related to it. Such integrals are called Gaussian integrals.
It is possible to evaluate $\Int_0^\infty\exp(-x^2)\,dx$ exactly by methods that are more advanced than those discussed in FLAP; we will present the answer here, and then show that a whole host of other Gaussian integrals can be found in terms of this integral. The basic result is
$\Int_0^\infty\exp(-x^2)\,dx = \dfrac12\sqrt{\pi\os}$(29)
We can use Equation 29 to find the integral $\Int_0^\infty\exp(-ax^2)\,dx$. We simply make the substitution y = ax. Then dx = a dy, and the limits of integration are still 0 and ∞. So $\Int_0^\infty\exp(-ax^2)\,dx = \dfrac{1}{\sqrt{a\os}}\Int_0^\infty\exp(-y^2)\,dy$ and from Equation 29,
$\Int_0^\infty\exp(-ax^2)\,dx = \dfrac12\sqrt{\dfrac{\pi\os}{a}}$(30)
✦ Evaluate $\Int_{-\infty}^\infty\exp(-ax^2)\,dx$.
✧ This is an even integral; so
$\Int_{-\infty}^\infty\exp(-ax^2)\,dx = 2\Int_0^\infty\exp(-ax^2)\,dx = \sqrt{\dfrac{\pi}{a}}$(31)
We can now use integration by parts to derive a reduction formula relating $\Int_0^\infty x^r\exp(-ax^2)\,dx$ to $\Int_0^\infty x^{r-2}\exp(-ax^2)\,dx$. To make it clear that r is an even integer, we write r = 2n, where n is any positive integer.
We can write the integral $\Int_0^\infty x^{2n}\exp(-ax^2)\,dx$ as $\Int_0^\infty x\exp(-ax^2)x^{2n-1}\,dx$, and apply Equation 13,
$\Int f(x)g(x)\,dx = F(x)g(x) - \Int F(x)\dfrac{dg}{dx}\,dx$ where $\dfrac{dF}{dx} = f(x)$(Eqn 13)
taking f (x) = x exp(−ax2) and g (x) = x2n−1
Then $F(x) = -\dfrac{1}{2a}\exp(-ax^2)$ (as you can easily check by differentiating), and $\dfrac{dg}{dx} = (2n-1)x^{2n-2}$.
So$\displaystyle \int_0^\infty x^{2n}\exp(-ax^2)\,dx = \left[−\dfrac{1}{2a}x^{2n-1}\exp(-ax^2)\right]_0^\infty + \dfrac{2n-1}{2a}\int_0^\infty x^{2n-2}\exp(-ax^2)\,dx$(32)
Now from the rule in Equation 25,
x ne−ax → 0 as x → ∞ for any n and any positive constant a(Eqn 25)
we know that x2n−1e−ax tends to zero as x tends to infinity; and since exp(−ax2) is smaller than e−ax when x is large, we can be sure that x2n−1exp(−ax2) also tends to zero as x tends to infinity.
Since n ≥ 1, x2n−1exp(−ax2) = 0 when x = 0. So the first term on the right–hand side of Equation 32 is zero, leaving us with the reduction formula
$\displaystyle \int_0^\infty x^{2n}\exp(-ax^2)\,dx = \dfrac{2n-1}{2a}\int_0^\infty x^{2n-2}\exp(-ax^2)\,dx$(33)
We can now use this reduction formula, and Equation 30 to work out values of $\Int_0^\infty x^{2n}\exp(-ax^2)\,dx$ for successively higher values of n.
✦ Evaluate $\Int_0^\infty x^2\exp(-ax^2)\,dx$.
✧ Substituting n = 1 in Equation 33,
$\displaystyle \int_0^\infty x^{2n}\exp(-ax^2)\,dx = \dfrac{2n-1}{2a}\int_0^\infty x^{2n-2}\exp(-ax^2)\,dx$(Eqn 33)
and using Equation 30,
$\Int_0^\infty\exp(-ax^2)\,dx = \dfrac12\sqrt{\dfrac{\pi\os}{a}}$(Eqn 30)
we have
$\Int x^2\exp(-ax)\,dx = \dfrac{1}{2a}{\displaystyle \int}_0^\infty\exp(-ax)\,dx = \dfrac{1}{4a}\sqrt{\dfrac{\pi}{a}}$
Gaussian integrals may sometimes appear in a disguised form. In the following question you have to make a substitution before it becomes clear that you are dealing with a Gaussian integral.
Question T16
Evaluate the integral $\Int_0^\infty x^{3/2}{\rm e}^{-5x}\,dx$. (Start by making the substitution x = y2).
Answer T16
If we let x = y2, dx = 2y dy, the integral becomes $2\Int_0^\infty y^4\exp(-5y^2)\,dy$. Substituting n = 2 and a = 5 in Equation 33,
$\displaystyle \int_0^\infty x^{2n}\exp(-ax^2)\,dx = \dfrac{2n-1}{2a}\int_0^\infty x^{2n-2}\exp(-ax^2)\,dx$(Eqn 33)
we find $\displaystyle 2\int_0^\infty y^4\exp(-5y^2)\,dy = \dfrac{3}{10}\int_0^\infty y^2\exp(-5y^2)\,dy$ and with n = 1 and a = 5 in Equation 33, we have
$\Int_0^\infty y^2\exp(-5y^2)\,dy = \dfrac{1}{10}{\displaystyle \int}_0^\infty\exp(-5y^2)\,dy = \dfrac{1}{20}\sqrt{\dfrac{\pi\os}{5}}$ from Equation 30,
$\Int_0^\infty\exp(-ax^2)\,dx = \dfrac12\sqrt{\dfrac{\pi\os}{a}}$(Eqn 30)
So$\Int_0^\infty x^{3/2}{\rm e}^-5x\,dx = 2\times \dfrac{3}{10}\times\dfrac{1}{10}\sqrt{\dfrac{\pi\os}{5}} = 0.04756.$
Finally, integrals of the form $\Int_{-\infty}^\infty\exp(-ax^2+bx)\,dx$ can be easily related to the integral appearing in Equation 31,
$\displaystyle \int_{-\infty}^\infty\exp(-ax^2)\,dx = 2\int_0^\infty\exp(-ax^2)\,dx = \sqrt{\dfrac{\pi}{a}}$(Eqn 31)
by the trick of completing the square in the exponent. The following example shows you how to proceed.
Example 11
Evaluate the integral $\Int_{-\infty}^\infty\exp(-2x^2+4x)\,dx$.
Solution
We write −2x2 + 4x in completed square form:
−2x2 + 4x = −2 (x2 − 2x) = −2 [(x − 1)2 − 1] = −2 (x − 1)2 + 2
Thus the integral can be written as $\Int_{-\infty}^\infty\exp[-2(x-1)^2{\rm e}^2\,dx$. We now make the substitution y = x − 1, dy = dx.
The limits of integration are still −∞ and ∞; so, taking the constant e2 outside the integral sign, we have
$\Int_{-\infty}^\infty\exp[-2(x-1)^2{\rm e}^2\,dx = {\rm e}^2\Int_{-\infty}^\infty\exp(-2y^2)\,dy$
Substituting a = 2 in Equation 31, we find that $\Int_{-\infty}^\infty\exp(-2y^2)\,dy = \sqrt{\dfrac{\pi}{2}}$
so$\Int_{-\infty}^\infty\exp(-2x^2+4x)\,dx = {\rm e}^2\sqrt{\dfrac{\pi}{2}} \approx 9.261$
Question T17
Evaluate the integral $\Int_{-\infty}^\infty\exp(-\frac12x^2-3x)\,dx$.
Answer T17
Write $-\frac12x^2-3x$ in completed square form:
$-\frac12x^2-3x = -\frac12(x^2+6x) = -\frac12\left[(x+3)^2-9\right] = -\frac12(x+3)^2+\frac92$
Thus the integral can be written as
$\Int_0^\infty\exp\left[-\frac12(x+3)^2\right]{\rm e}^{9/2}\,dx$
We now make the substitution y = x + 3, dy = dx. The limits of integration are still −∞ and ∞; so, taking the constant e9/2 outside the integral sign, we have
$\Int_0^\infty\exp\left[-\frac12(x+3)^2\right]{\rm e}^{9/2}\,dx = {\rm e}^{9/2}\Int\exp\left(-\frac12y^2\right)\,dy$
Substituting a = 1/2 in Equation 31,
$\displaystyle \int_{-\infty}^\infty\exp(-ax^2)\,dx = 2\int_0^\infty\exp(-ax^2)\,dx = \sqrt{\dfrac{\pi}{a}}$(Eqn 31)
we find that
$\Int\exp\left(-\frac12y^2\right)\,dy = \sqrt{2\pi\os}$
So$\Int_{-\infty}^\infty\exp(-\frac12x^2-3x)\,dx = {\rm e}^{9/2}\sqrt{2\pi\os} = 225.64$
3.3 Line integrals
This subsection discusses a type of definite integral that is known as a line integral. Line integrals can be used (among other applications) to evaluate the work done by a force, and we will introduce them in that context.
Suppose that an object moves along the x–axis under the influence of a constant force Fx in the x–direction. The work done by the force in moving the object from x = a to x = b is W = sxFx, where sx is the displacement of the object. If the force is not constant, but instead varies with x, Fx(x) say, then you may already know that the work done in moving the object from x = a to x = b is given by the definite integral $\Int_a^bF_x(x)\,dx$. To derive this result, we divide the interval a ≤ x ≤ b into many small subintervals: we introduce n + 1 values of x such that a = x1 < x2 < ... < xn < xn+1 = b, and we define ∆xi = xi+1 − xi, where i is any integer in the range 1 ≤ i ≤ n and let | ∆x | be the largest of these subintervals. We can then say that over any one of these small intervals, the force is approximately constant, so that the work done by the force in moving the object from xi to xi+1 is approximately equal to Fx(xi) ∆xi. Then the total work done by the force is approximately given by the sum
${\displaystyle \sum}_{i=1}^nF_x(x_i)\,\Delta x_i$(34)
As we increase the number n of subintervals, and let the size of each one become smaller and smaller, Equation 34 becomes a better and better approximation to the actual work done. In the limit as n tends to infinity and | ∆x | tends to zero, we have
$\displaystyle W = \lim_{\lvert\,\Delta x\,\rvert\rightarrow 0}F_x(x_i)\,\Delta x_i = \int_a^bF_x(x)\,dx$(35)
Figure 1 A constant force F moving an object along a straight line.
Let us now generalize these ideas to the case where the object is not constrained to move along the x–axis, but can move along a path in the (x, y) plane, and where the force is not in the same direction as the displacement of the object. First, we need to know the work done if a constant force F acts on the object so as to move it along a line that is not necessarily parallel to F, as in Figure 1. You may know that the work done is given by the scalar product of F and the displacement s of the object:
W = F ⋅ s(36) i
If we resolve both F and s into their components along the x and y axes, so that
F = (Fx, Fy) and s = (sx, sy)
we have the alternative expression for W:
W = Fxsx + Fysy(37)
✦ A force of 20 N acting in the y–direction moves an object along a straight line. The initial position of the object is x = 2 m, y = 3 m, and its final position is x = 4 m, y = 6 m. What is the work done by the force?
✧ Fx = 0 N, Fy = 20 N, sx = 4 m − 2 m = 2 m and sy = 6 m − 3 m = 3 m. So, using Equation 37, we have W = (0 × 2 + 20 × 3) J = 60 J.
Now consider the general case, where the object is constrained to move along a given curved path, and where the components of F may be functions of x and y. To show that the components of F are functions of x and y, we will write the vector F as
F(r) = (Fx(x, y), Fy(x, y))
To derive an expression for W, we proceed much as we did in deriving Equation 35. Essentially the procedure is to divide the curved path into a large number of straight sections, find the work done moving along each of these sections, then add together all these small contributions to find an estimate for the total work done.
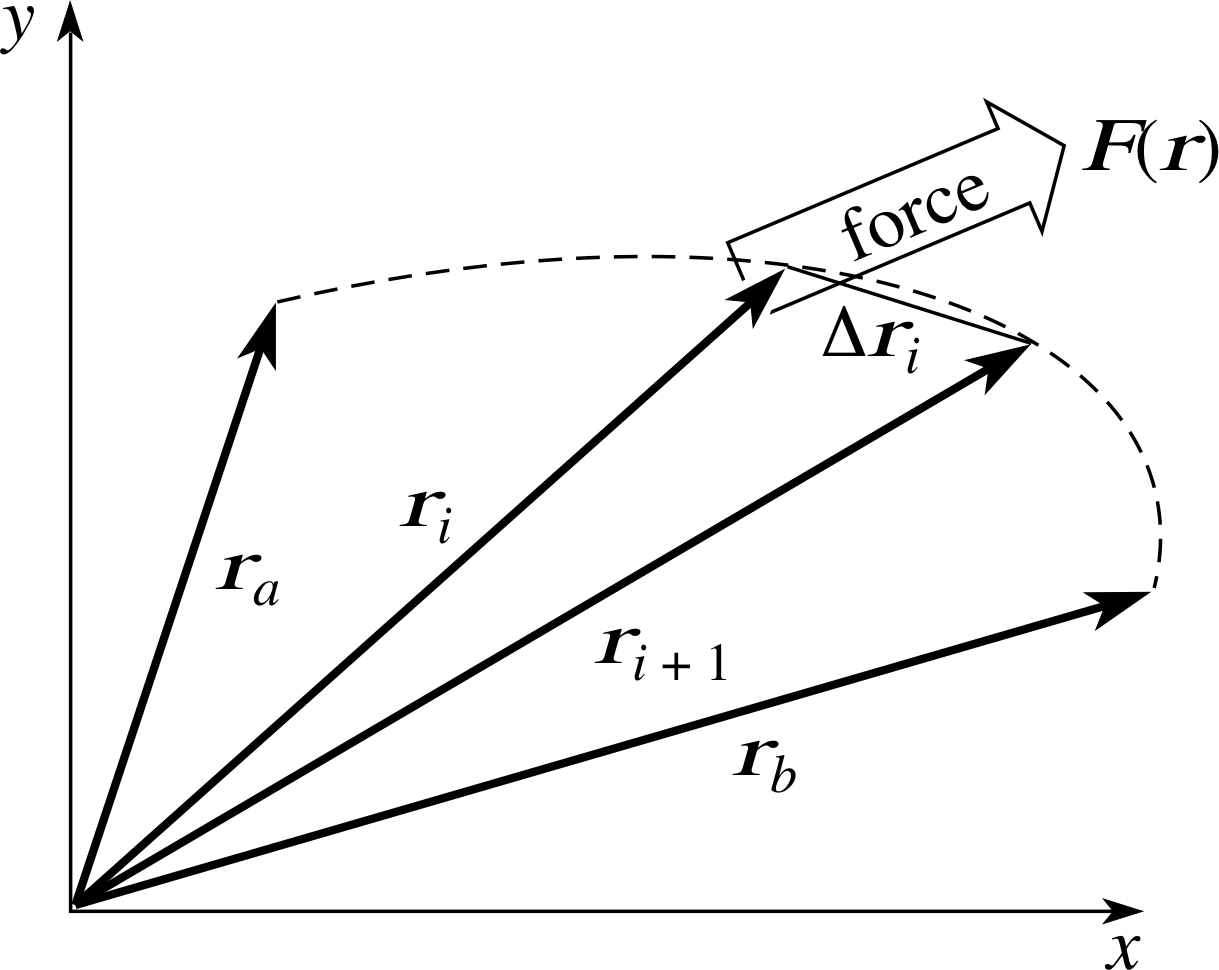
Figure 2 An object moving under the action of a variable force F(r).
We define an arbitrary position of the object by the vector r = (x, y), then suppose the initial position vector of the object is ra, and its final position vector is rb (see Figure 2). We divide the path of the object into n small subintervals. The position vector of the object at the start of the ith subinterval is ri−1, and at the end of it, the position vector is ri, where r0 = ra and rn = rb.We define ∆ri = ri+1− ri, and denote the components of ∆ri by ∆xi and ∆yi, so that ∆ri = (∆xi, ∆yi). We then let | ∆r | denote the size of the largest subinterval ∆ri. As before, over any one of these small intervals, the force is approximately constant, so we may use either Equation 36 or Equation 37 to derive an approximate expression for the work Wi done by the force in moving the object from ri to ri+1:
Wi = F (ri) ⋅ ∆ri(38)
which can be rewritten in the form
Wi = Fx(xi, yi) ∆xi + Fy(xi, yi) ∆yi(39)
The total work done in moving the object from ra to rb is given, to a good approximation, by the sum of all the Wi. As we allow the size of the largest subinterval, | ∆r |, to tend to zero (so that n tends to infinity), the approximation becomes more and more accurate, while the sums become integrals. We have two ways of writing the integral that results; using Equation 38, we have
$\displaystyle W = \lim_{\lvert\,\Delta \bi{r}\,\rvert\rightarrow 0}\sum_{i=1}^n\bi{F}_i(\bi{r}_i)\,\boldsymbol{\cdot}\,\Delta \bi{r_i} = \int_{\bi{r}_a}^{\bi{r}_b}\bi{F}(\bi{r})\,\boldsymbol{\cdot}\,(\bi{r})\,d\bi{r}$(40)
while using Equation 39 gives us
$\displaystyle W = \lim_{\lvert\,\Delta \bi{r}\,\rvert\rightarrow 0}\sum_{i=1}^n\left[F_x(x_i,\,y_i)\,\Delta x_i + F_y(x_i,\,y_i)\,\Delta y_i\right] = \int_{\bi{r}_a}^{\bi{r}_b}\left[F_x(x,\,y)\,dx + F_y(x,\,y)\,dy\right]$(41)
Equation 40 gives a very concise way of writing down the integral that determines W; but, as you will see, in practice we use Equation 41 to evaluate the integral.
An integral of the form
$\displaystyle \int_{\bi{r}_a}^{\bi{r}_b}\bi{F}(\bi{r})\,\boldsymbol{\cdot}\,(\bi{r})\,d\bi{r} = \int_{\bi{r}_a}^{\bi{r}_b}\left[F_x(x,\,y)\,dx + F_y(x,\,y)\,dy\right]$
is known as a line integral.
Study comment Many students have difficulties coming to grips with line integrals, and the source of the problems is often a matter of understanding. It is important to remember that a line integral is a limit of a sum – that is the definition, (and on the face of it, this has little to do with inverting the process of differentiation). Evaluating a line integral is a separate issue; it is a matter of turning the integral into a form that we recognize, and which we can calculate.
The path along which the object moves is crucial. If we know that the object’s path is determined by an equation y = f (x), then we can express both Fx and Fy as functions of x only; we can also express dy in Equation 41 in terms of dx. This means that the line integral becomes an ordinary definite integral – something that we know how to evaluate. A particular example should make the point clear.
Example 12
A force F = 2y i + 2x j i moves an object from the point (0, 0) to the point (1, 1) along the path y = x. What is the work done on the object by the force? What is the work done if the same force moves the object along the path y = x2?
Solution
We use Equation 41, substituting Fx(x, y) = 2y and Fy(x, y) = 2x. This gives $\Int_{\bi{r}_a}^{\bi{r}_b}(2y\,dx + 2x\,dy)$, where ra = 0 and rb = i + j. i
We need to evaluate this integral along two different paths.
(a) Along the path y = x, we have dy = dx. So we substitute y = x and dy = dx into Equation 41,
$\displaystyle W = \int_{\bi{r}_a}^{\bi{r}_b}\left[F_x(x,\,y)\,dx + F_y(x,\,y)\,dy\right] = \Int_{\bi{r}_a}^{\bi{r}_b}(\underbrace{2y}_{\large\color{purple}{F_x(x,\,y)}}\,dx + \underbrace{2x\us}_{\large\color{purple}{F_y(x,\,y)}}\,dy) $
$\displaystyle \phantom{W = \int_{\bi{r}_a}^{\bi{r}_b}\left[F_x(x,\,y)\,dx + F_y(x,\,y)\,dy\right]} = \Int_{\bi{r}_a}^{\bi{r}_b}(\underbrace{2y}_{\large\color{purple}{\text{let }y=x}}\,dx + 2x\,\underbrace{dy}_{\large\color{purple}{\text{let }dy=dx}}) = \Int_{\bi{r}_a}^{\bi{r}_b}(2x\,dx + 2x\,dx)$
On the right–hand side we now have a definite integral over x, and the limits of integration are the values of x at the points r = ra and r = rb, namely 0 and 1.
Thus$W = \Int_0^1(2x\,dx + 2x\,dx) = \Int_0^1 4x\,dx = \left[2x^2\right]_0^1 = 2$
(b) Along the path y = x2 we have dy = 2x dx, so in this case
$\displaystyle W = \int_{\bi{r}_a}^{\bi{r}_b}\left[F_x(x,\,y)\,dx + F_y(x,\,y)\,dy\right] = \Int_{\bi{r}_a}^{\bi{r}_b}(\underbrace{2y}_{\large\color{purple}{F_x(x,\,y)}}\,dx + \underbrace{2x\us}_{\large\color{purple}{F_y(x,\,y)}}\,dy) $
$\displaystyle \phantom{W = \int_{\bi{r}_a}^{\bi{r}_b}\left[F_x(x,\,y)\,dx + F_y(x,\,y)\,dy\right] }= \Int_{\bi{r}_a}^{\bi{r}_b}(\underbrace{2y}_{\large\color{purple}{\text{let }y=x^2}}\,dx + 2x\,\underbrace{dy}_{\large\color{purple}{\text{let }dy=2x\,dx}}) = \Int_{\bi{r}_a}^{\bi{r}_b}(2x^2\,dx + 4x^2\,dx)$
Again the expression on the right–hand side is just an ordinary integral, and once more the limits of integration are 0 and 1.
So$W = \Int_0^1(2x^2\,dx + 4x^2\,dx) = \Int_0^1 6x^2\,dx = \left[2x^3\right]_0^1 = 2$ i
Question T18
Find the work done when a force F = 2xy i − 3y j moves an object from the point (1, 2) to the point (2, 4) along the line y = 2x.
Answer T18
Substituting Fx(x, y) = 2xy and Fy(x, y) = −3y in Equation 41,
$\displaystyle W = \lim_{\lvert\,\Delta \bi{r}\,\rvert\rightarrow 0}\sum_{i=1}^n\left[F_x(x_i,\,y_i)\,\Delta x_i + F_y(x_i,\,y_i)\,\Delta y_i\right] = \int_{\bi{r}_a}^{\bi{r}_b}\left[F_x(x,\,y)\,dx + F_y(x,\,y)\,dy\right]$(Eqn 41)
we have
$W = \Int_{\bi{r}_a}^{\bi{r}_b}(2xy\,dx-3y\,dy)$
where ra and rb are the position vectors of the points (1, 2) and (2, 4). Along the given path, y = 2x and dy = 2 dx; substituting these expressions into the integral, and putting in the limits of integration 1 and 2, gives us
$W = \Int_1^2(4x^2-12x)\,dx = \left[\dfrac43x^3-6x^2\right]_1^2 = \dfrac43(8-1)-6(4-1) = -8.667$
We will finish with two comments.
First, although we have discussed line integrals only for paths that lie in the (x, y) plane, they can of course be
written down for paths in three dimensions. In that case, $\Int_{\bi{r}_a}^{\bi{r}_b}\bi{F}(\bi{r})\,\boldsymbol{\cdot}\,(\bi{r})\,d\bi{r}$ can be written as
$\Int_{\bi{r}_a}^{\bi{r}_b}\left[F_x(x,\,y,\,z)\,dx + F_y(x,\,y,\,z)\,dy + F_z(x,\,y,\,z)\,dz\right]$
To specify the path, we would need to know both y and z as functions of x; this knowledge would allow us to turn the line integral into a definite integral over x, as we did in Example 12.
Second, for some choices of the force F (r), the line integral $\Int_{\bi{r}_a}^{\bi{r}_b}\bi{F}(\bi{r})\,\boldsymbol{\cdot}\,(\bi{r})\,d\bi{r}$ is actually independent of the path chosen to evaluate the integral; it depends only on the coordinates of the endpoints of the path. (This is true of the force in Example 12). Forces of this sort are known as conservative forces. It is possible to specify necessary and sufficient conditions that the components of the force F must satisfy if F is to be conservative. This is beyond the scope of FLAP, but you are certain to meet them if you carry your study of physics further.
4 Closing items
4.1 Module summary
- 1
-
Integrals of the form $\displaystyle \int\dfrac{p(x)}{q(x)}\,dx$, where p (x) and q (x) are polynomials in x, may often be converted into sums of simpler integrals by writing the integrand in terms of its Subsection 2.1partial fractions.
- 2
-
If the method of partial fractions is to be useful, the denominator q (x) must factorize, at least partially. If q (x) is a quadratic function of x which does not factorize, the technique of writing q (x) in Subsection 2.2completed square form and making a substitution of the form x = tan u allows us to find the integral.
- 3
-
Completing the square in the denominator, and making a substitution of the form x = sin u, allows us to find integrals of the form $\displaystyle \int\dfrac{1}{\sqrt{a+bx-cx^2}}\,dx$, where c > 0.
- 4
-
By Subsection 2.3splitting the numerator, we can write integrals of the form $\displaystyle \int\dfrac{px+q}{\sqrt{a+bx-cx^2}}\,dx$ and (in the case where the denominator does not factorize) $\displaystyle \int\dfrac{px+q}{a+bx-cx^2}\,dx$ as sums of two simpler integrals.
- 5
-
Two standard integrals, which can be found by substitution of the Subsection 2.4hyperbolic functions x = sinh u and x = cosh u, respectively, are $\displaystyle \int\dfrac{1}{\sqrt{x^2+1}}\,dx = \arcsinh x + C$ and $\displaystyle \int\dfrac{1}{\sqrt{x^2-1}}\,dx = \arccosh x + C$, where C is a constant of integration.
Integrals of the form $\displaystyle \int\dfrac{1}{\sqrt{a+bx^2}}\,dx$ and $\displaystyle \int\dfrac{1}{\sqrt{bx^2-a}}\,dx$, where a, b are positive constants, can be found by the substitution x = d sinh u or x = d cosh u, where d is a suitably chosen constant.
- 6
-
Substitutions of hyperbolic functions may also be used to find many other integrals involving square roots of quadratic functions of x, especially when combined with the techniques of completing the square or splitting the numerator.
- 7
-
Trigonometric identities may be used to find integrals of products of powers of cos x and sin x (and the analogous identities for hyperbolic functions can similarly be used to find integrals of products of powers of cosh x and sinh x).
- 8
-
Subsection 2.6Reduction formulae are equations that relate an integral involving a power of x or some function of x to an integral of the same form but involving a lower power of x or the function of x. Two examples are
$\Int\cos^nx\,dx = \dfrac1n\sin x\cos^{n-1}x + \dfrac{n-1}{n}{\displaystyle \int}\cos^{n-2}x\,dx$
and$\Int\sin^nx\,dx = -\dfrac1n\cos x\sin^{n-1}x + \dfrac{n-1}{n}{\displaystyle \int}\sin^{n-2}x\,dx$
These are useful in finding integrals of high powers of cos x and sin x.
- 9
-
Definite integrals in which one or both of the limits of integration is infinite are known as improper integrals. They are to be found by treating the infinite limit as a very large number and allowing it to tend to infinity; formally, we have
$\Int_a^\infty f(x)\,dx = {\displaystyle \lim_{b\rightarrow\infty}}\Int_a^b f(x)\,dx\quad\text{and}\quad\Int_{-\infty}^b f(x)\,dx = {\displaystyle \lim_{a\rightarrow -\infty}}\Int_a^b f(x)\,dx$
- 10
-
Using the rule that x ne−ax → 0 as x → ∞, for any n and any positive constant a, and a reduction formula for the indefinite integral $\Int x^n{\rm e}^{-ax}\,dx$, we can derive a general result
$\Int_0^\infty x^n{\rm e}^{-ax}\,dx = \dfrac{n!}{a^{n+1}}$(Eqn 27)
Definite integrals of the form $\Int_0^\infty x^{2n+1}\exp(-ax^2)\,dx$ can be simply related to $\Int_0^\infty x^n{\rm e}^{-ax}\,dx$, allowing us to derive the general result
$\Int_0^\infty x^{2n+1}\exp(-ax^2)\,dx = \dfrac{n!}{2a^{n+1}}$(Eqn 28)
- 11
-
Subsection 3.2Gaussian integrals are definite integrals of the form $\Int_0^\infty x^{2n}\exp(-ax^2)\,dx$. They may all be evaluated in terms of the basic Gaussian integral, $\Int_0^\infty\exp(-x^2)\,dx = \dfrac12\sqrt{\pi\os}$, using the reduction formula
$\displaystyle \int_0^\infty x^{2n}\exp(-ax^2)\,dx = \dfrac{2n-1}{2a}\int_0^\infty x^{2n-2}\exp(-ax^2)\,dx$(Eqn 33)
- 12
-
A Subsection 3.3line integral of the form $\Int_{\bi{r}_a}^{\bi{r}_b}\bi{F}(\bi{r})\,\boldsymbol{\cdot}\,(\bi{r})\,d\bi{r}$ is defined as a limit of a sum along a particular path. It may be evaluated by using the equation of the path to convert the line integral into an ordinary definite integral.
4.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened.
- A2
-
Use algebraic techniques such as partial fractions, completing the square in the denominator, or splitting the numerator to find integrals of the form $\displaystyle \int\dfrac{p(x)}{q(x)}\,dx$, where p (x) and q (x) are polynomials in x.
- A3
-
Find integrals which involve square roots of quadratic functions of x using the substitution of an appropriate hyperbolic function or trigonometric function.
- A4
-
Use either trigonometric identities or reduction formulae to find integrals of products of powers of sin x and cos x (and use identities to find integrals of products of powers of sinh x and cosh x).
- A5
-
Choose, for a given integral, a method or combination of methods that will enable you to evaluate it – and be prepared to try another approach if your first one does not work.
- A6
-
Evaluate definite integrals in which one or both of the limits is infinite.
- A7
-
Use formulae such as $\Int_0^\infty x^n{\rm e}^{-ax}\,dx = \dfrac{n!}{a^{n+1}}$ and $\Int_0^\infty x^{2n+1}\exp(-ax^2)\,dx = \dfrac{n!}{2a^{n+1}}$ to evaluate definite integrals of these types.
- A8
-
Recognize Gaussian integrals, and integrals which can be related to these by means of a substitution or by completing the square in the exponent; and evaluate these using Equations 30 and 33.
- A9
-
Evaluate a line integral along a specified path in the (x, y) plane.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
4.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions, each of which tests one or more of the Achievements.
Question E1 (A2)
Find the integrals:
(a) $\displaystyle \int\dfrac{p}{x^2(x-p)}\,dx$, where p is a constant (b) $\displaystyle \int\dfrac{4x-3}{4x^2-4x+5}\,dx$
Answer E1
(a) Split the integrand into partial fractions
$\dfrac{p}{x^2(x-p)} = \dfrac ax + \dfrac{b}{x^2} + \dfrac{d}{x-p} = \dfrac{(a+d)x^2 + (b-pa)x - pb}{x^2(x-p)}$
From this we can see a + d = 0, b − pa = 0, so p = −pb which gives b = −1, a = –1/p and d = 1/p.
So$\displaystyle \int \dfrac{p}{x^2(x-p)}\,dx = -\dfrac 1p\int\dfrac 1x\,dx -\int\dfrac{1}{x^2}\,dx + \dfrac 1p\int \dfrac{1}{x-p}\,dx = -\dfrac 1p\loge x + \dfrac 1x + \dfrac 1p\loge(x-p) + C$
(b) First split the numerator. The derivative of 4x2 − 4x + 5 is 8x − 4; therefore we can write 4x − 3 = a (8x − 4) + b, from which we find a = 1/2 and b = −1.
So$\displaystyle \int\dfrac{4x-3}{4x^2-4x+5}\,dx = \dfrac12\int\dfrac{8x-4}{4x^2-4x+5}\,dx - \int\dfrac{1}{4x^2-4x+5}\,dx$
The first integral can be found by the substitution y = 4x2 − 4x + 5; it becomes
$\dfrac12\int 1\,dy = \dfrac12\loge y + C = \dfrac12\loge(4x^2-4x+5) + C$
To evaluate the second integral, we complete the square in the denominator, writing 4x2 − 4x + 5 = (2x −1)2 + 4. We substitute y = 2x − 1, so that the second integral now becomes
$\displaystyle -\dfrac12\int\dfrac{1}{y^2+4}\,dy = -\dfrac14\arctan y + C$
So, finally,
$\displaystyle \int\dfrac{4x-3}{4x^2-4x+5}\,dx = \dfrac12\loge(4x^2-4x+5) - \dfrac14\arctan\left(\dfrac{2x-1}{2}\right) + C$
(Reread Subsections 2.1 to 2.3 if you had difficulty with this question.)
Question E2 (A3)
Find the integral $\displaystyle \int\dfrac{1}{\sqrt{5+4x^2}}\,dx$
Answer E2
We make the substitution $2x = \sqrt{5\os}\sinh u$. Then $\sqrt{5 + 4x^2} = 5\cosh u$, and $dx = \dfrac{\sqrt{5\os}}{2}\cosh u\,du$, so that the integral becomes $\dfrac12\int 1\,du = \dfrac12 u + C$. Thus
$\displaystyle \int\dfrac{1}{\sqrt{5+4x^2}}\,dx = 2\arcsinh\left(\dfrac{2x}{\sqrt{5\os}}\right) + C$
(Reread Subsection 2.4 if you had difficulty with this question.)
Question E3 (A4)
Find the integrals:
(a) $\Int\cos^3(2x)\sin^4(2x)\,dx$, (b) $\Int_0^\pi\cos^8x\,dx$
Answer E3
(a) We write this integral as
$\Int\sin^4(2x)\cos^2(2x)\times \cos(2x)\,dx$
and let cos2 (2x) = 1 − sin2 (2x), so that the integral becomes
$\Int\sin^4(2x)[1-\sin^2(2x)]\cos(2x)\,dx$
With the substitution y = sin(2x), dy = 2 cos(2x) dx, so that we obtain
$\dfrac12\Int(y^4-y^6)\,dy = \dfrac{1}{10}y^5 - \dfrac{1}{14}y^7 + C$
Thus$\Int\sin^4(2x)\cos^3(2x)\,dx = \dfrac{1}{10}\sin^5(2x) - \dfrac{1}{14}\sin^7(2x) + C$
(b) Much the easiest way of evaluating this integral is to use Equation 16. Note that $\left[\sin x\cos^{n-1}x\right]_0^\pi = 0$, so that, when we put in limits of 0 and π, Equation 16,
$\Int\cos^nx\,dx = \dfrac1n\sin x\cos^{n-1}x + \dfrac{n-1}{n}\Int\cos^{n-2}x\,dx$(Eqn 16)
becomes $\Int_0^\pi\cos^nx\,dx = \dfrac{n-1}{n}\Int_0^\pi\cos^{n-2}x\,dx$. So, applying this equation with n = 8, 6, 4, 2 successively, we obtain
$\Int_0^\pi\cos^8x\,dx = \dfrac78\Int_0^\pi\cos^6x\,dx = \dfrac78\times\dfrac56\Int_0^\pi\cos^4x\,dx$
$\phantom{\Int_0^\pi\cos^8x\,dx }= \dfrac78\times\dfrac56\times\dfrac34\Int_0^\pi\cos^2x\,dx = \dfrac78\times\dfrac56\times\dfrac34\times\dfrac12\Int_0^\pi 1\,dx = \dfrac{105}{384}\pi= \dfrac{35}{128}\pi \approx 0.8590$
(Reread Subsections 2.5 and 2.6 if you had difficulty with this question.)
Question E4 (A5)
Find the integrals:
(a) $\displaystyle \int\dfrac{x+2}{\sqrt{13-6x-3^ 2}}\,dx$, (b) $\Int x\cosh^2x\,dx$.
Answer E4
(a) We start by splitting the numerator. The derivative of 13 – 6x − 3x2 is −6x − 6; so we write x + 2 = a (−6x − 6) + b, from which we find a = –1/6 and b = 1. So
$\displaystyle \int\dfrac{x+2}{\sqrt{13-6x-3x^2}}\,dx = -\dfrac16\int\dfrac{-6-6x}{\sqrt{13-6x-3x^2}}\,dx + \int\dfrac{1}{\sqrt{13-6x-3x^2}}\,dx$
The first integral here can be found using the substitution y = 13 − 6x − 3x2; it becomes
$\displaystyle -\dfrac16\int\dfrac{1}{\sqrt{y\os}}\,dy = -\dfrac13\sqrt{y\os} + C$, i.e. $-\dfrac13\sqrt{13-6x-3x^2} + C$
To find the second integral, we complete the square: 13 − 6x − 3x2 = 16 − 3 (x + 1)2; so this integral is equal to
$\displaystyle \int\dfrac{1}{\sqrt{\smash[b]{16-3(x+1)^2}}}\,dx$. We make the substitution y = x + 1, to obtain $\displaystyle \int\dfrac{1}{\sqrt{16-3y^2}}\,dx$, and then put $\sqrt{3\os}y = 4\sin u$, to obtain $\dfrac{1}{\sqrt{3\os}}\Int 1\,du = \dfrac{1}{\sqrt{3\os}}u + C$. Expressing this answer in terms of x gives $\dfrac{1}{\sqrt{3\os}}\arcsin\left(\dfrac{\sqrt{3\os}(x+1)}{4}\right) + C$. So, finally,
$\displaystyle \int\dfrac{x+2}{\sqrt{13-6x-3x^2}}\,dx = -\dfrac13\sqrt{13-6x-3x^2} + \dfrac{1}{\sqrt{3\os}}\arcsin\left(\dfrac{\sqrt{3\os}(x+1)}{4}\right) + C$
(b) Using Equation 10,
$\cosh^2x =\frac12[1+\cosh(2x)]$(Eqn 10)
the integral becomes
$\frac12\Int x[1+\cosh(2x)]\,dx = \frac12\Int x\,dx + \frac12\Int x\cosh(2x)\,dx$
The first of these integrals gives $\dfrac12\Int x\,dx = \dfrac14 x^2 + C$; and we may use integration by parts to find $\Int x\cosh(2x)\,dx$. Taking f (x) = cosh(2x), g (x) = x in Equation 13, we have $F(x) = \dfrac12\sinh(2x)$ and $\dfrac{dg}{dx} = 1$, so
$\Int x\cosh(2x)\,dx = \dfrac12 x\sinh(2x) - \dfrac12\Int\sinh(2x)\,dx = \dfrac12 x\sinh(2x) - \dfrac14\cosh(2x) + C$
Thus$\Int x\cosh^2x\,dx = \dfrac14x^2 + \dfrac14x\sinh(2x) - \dfrac18\cosh(2x) + C$
(Reread Section 2 if you had difficulty with this question.)
Question E5 (A3 and A6)
By substituting an appropriate hyperbolic function, evaluate the definite integral $\displaystyle \int\dfrac{1}{(x^2+a^2)^{3/2}}\,dx$. [Hint: You may find the answers to Questions R6 and R7 useful here.]
Answer E5
We make the substitution x = a sinh u. Then (a2 + x2 )3/2 = a3 cosh3 u, and dx = a cosh u du.
Since sinh u = x/a it follows that u tends to infinity as x tends to infinity; and sinh 0 = 0. So the limits of
integration are still 0 and ∞, and we have
$\displaystyle \int\dfrac{1}{(x^2+a^2)^{3/2}}\,dx = \dfrac{1}{a^2}\int\dfrac{1}{\cosh^2u}\,du = \dfrac{1}{a^2}\int\sech u\,du$
Since sech2 u is the derivative of tanh u, we see that
$\displaystyle \int\dfrac{1}{(x^2+a^2)^{3/2}}\,dx = \dfrac{1}{a^2}\left[\tanh u\right]_0^\infty$
Now recall that $\tanh u = \dfrac{\sinh u}{\cosh u} = \dfrac{{\rm e}^u-{\rm e}^{-u}}{{\rm e}^u+ {\rm e}^{-u}}$, so when u = 0, tanh u = 0, and as u becomes very large, tanh u tends to 1. Thus $\displaystyle \int\dfrac{1}{(x^2+a^2)^{3/2}}\,dx = \dfrac{1}{a^2}$
(Reread Subsection 3.1 if you had difficulty with this question.)
Question E6 (A7, A8)
The laplaces_equationLaplace transform i of a function f (x) is defined as the integral $\Int_0^\infty f(x){\rm e}^{-sx}\,dx$, where s > 0. Find the Laplace transforms of the functions (a) x3, (b) $\sqrt{x\os}$.
Answer E6
(a) We need to find the integral $\Int_0^\infty x^3{\rm e}^{-sx}\,dx$. Using Equation 27,
$\Int_0^\infty x^n{\rm e}^{-ax}\,dx = \dfrac{n!}{a^{n+1}}$(Eqn 27)
with n = 3 and a = s, we find $\Int_0^\infty x^3{\rm e}^{-sx}\,dx = \dfrac{3!}{s^4} = \dfrac{6}{s^4}$.
(b) We need to find the integral $\Int_0^\infty \sqrt{x\os}\;{\rm e}^{-sx}\,dx$. We make the substitution x = y2 so that dx = 2y dy, to obtain
$\Int \sqrt{x\os}{\rm e}^{-sx}\,dx = \Int \overbrace{y}^{\color{purple}{\large\sqrt{x\os}}}\exp(-sy^2)\overbrace{(2y\,dy)}^{\color{purple}{\large dx}} = 2\Int_0^\infty y^2\exp(-sy^2)\,dy$
Using Equation 33,
$\displaystyle \int_0^\infty x^{2n}\exp(-ax^2)\,dx = \dfrac{2n-1}{2a}\int_0^\infty x^{2n-2}\exp(-ax^2)\,dx$(Eqn 33)
with n = 1 and a = s, we find
$\Int_0^\infty y^2\exp(-sy^2)\,dy = \dfrac{1}{2s}{\displaystyle \int}_0^\infty\exp(-sy^2)\,dy$
and from Equation 30,
$\Int_0^\infty\exp(-ax^2)\,dx = \dfrac12\sqrt{\dfrac{\pi\os}{a}}$(Eqn 30)
$\Int_0^\infty\exp(-sy^2)\,dy = \dfrac12\sqrt{\dfrac{\pi\os}{s}}$ and so $\Int_0^\infty \sqrt{x\os}\;{\rm e}^{-sx}\,dx = \dfrac{1}{2s}\sqrt{\dfrac{\pi\os}{s}}$
(Reread Subsections 3.1 and 3.2 if you had difficulty with this question.)
Question E7 (A3 and A9)
A particle moves along the path $y = \sqrt{ x^2-4}$. It is acted upon by a force F = (−y i + x j) N. What is the work done by the force in moving the object from the point (2, 0) to the point (3, 5 )?
Answer E7
If we let Fx(x, y) = −y and Fy(x, y) = x in Equation 41,
$\displaystyle W = \lim_{\lvert\,\Delta \bi{r}\,\rvert\rightarrow 0}\sum_{i=1}^n\left[F_x(x_i,\,y_i)\,\Delta x_i + F_y(x_i,\,y_i)\,\Delta y_i\right] = \int_{\bi{r}_a}^{\bi{r}_b}\left[F_x(x,\,y)\,dx + F_y(x,\,y)\,dy\right]$(Eqn 41)
we obtain
$W = \Int_{\bi{r}_a}^{\bi{r}_b}(-y\,dx + x\,dy)$
Along the curve $y = \sqrt{x^2-4}$ we have $dy = \dfrac{x}{\sqrt{x^2-4}}\,dx$
so$-y\,dx + x\,dy = -\sqrt{x^2-4}\,dx + \dfrac{x^2}{\sqrt{x^2-4}}\,dx = \dfrac{4}{\sqrt{x^2-4}}\,dx$
The limits of integration are x = 2 and x = 3. Thus
$\displaystyle W = \int\dfrac{4}{\sqrt{x^2-4}}\,dx$
We evaluate this integral using the substitution x = 2 cosh u. Then $\sqrt{x^2-4} = 2\sinh u$ and dx = 2 sinh u du, while the limits of integration become arccosh 1 = 0 and arccosh(3/2) ≈ 0.9624.
So$W = 4 \Int_0^{0.9624} 1\,du = (4\times 0.9624)\,{\rm J} \approx 3.8497\,{\rm J}$
(Reread Subsections 3.3 and 2.4 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 5Closing items.