PHYS 11.1: Reflection and transmission at steps and barriers |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
In 1954, the Nobel Prize for physics was awarded to Cockcroft and Walton for their initiation of nuclear physics twenty years previously. They made use of quantum tunnelling to induce nuclear reactions in circumstances which classical physics deemed impossible. In 1973, the Nobel Prize was awarded to three scientists for their work in developing useful devices called tunnel diodes which depend for their operation on the same effect. These devices have opened up whole new areas of physics and technology. In 1986, another Nobel Prize was awarded to Binnig and Rohrer for their invention of the scanning tunnelling electron microscope. All these prizes have been awarded for the exploitation of one quantum effect, carried out with great ingenuity and insight.
The behaviour of particles such as electrons, photons and nucleons is determined by their quantum mechanical characteristics, and we rely on the Born probability hypothesis to relate particle position to the amplitude squared of the associated wavefunction. Such particles may therefore be expected to exhibit wave–like characteristics. When light waves encounter a boundary where the refractive index changes, there may be both a reflected and a transmitted wave. If the boundary is between a transparent and an opaque material, the wave will still penetrate into the opaque material for a distance roughly equal to the wavelength. It follows that light can be transmitted through a layer of a metal provided its thickness is less than the penetration depth of the wave.
A good example of this is the layer of silver a few atoms thick on a glass slide forming a semi–reflecting mirror. In the context of quantum mechanics we might expect particles to show similar behaviour.
In the quantum mechanical case, one can think of the particle potential energy as roughly analogous to a refractive index. If the potential energy changes suddenly with position, then there is usually both a transmitted and a reflected quantum wave at the boundary, and the particles will be transmitted or reflected with calculable probability. If the increase in potential energy is greater than the particle kinetic energy, then the quantum wave will penetrate into the classically forbidden region though its amplitude will rapidly decrease. In consequence, if the region of high potential energy is narrow enough, the wave will emerge with reduced amplitude on the other side and there is a probability that the associated particle will tunnel through. A narrow region of high potential energy is called a potential barrier. Quantum mechanics therefore predicts two effects totally alien to the classical mechanics based on Newton’s laws: (i) particles may be reflected by any sudden change in potential energy, and (ii) particles can tunnel through narrow potential barriers. Experiment confirms both of these remarkable predictions.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 5.1Module summary and the Subsection 5.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 5.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
A stationary state spatial wavefunction ψ (x) = A exp(ikx) represents a stream of particles. What is the number density of particles per unit length, the momentum of each particle, and the flux?
Answer F1
The wavefunction ψ (x) = A exp(ikx) is a momentum eigenfunction. It can represent a beam of electrons moving in the +x–direction, each with definite momentum $p = \hbar k$. The number of particles per unit length is then given by | A |2 and the flux by $F = \lvert\,A\,\rvert^2\hbar k/m$.
Question F2
A beam of electrons with kinetic energy 5 eV is incident on a region where the electron potential energy suddenly increases from 0 to 2.5 eV. Calculate the transmission and reflection coefficients at this ‘step’. Sketch the electron density as a function of position. Account for the sequence of maxima and minima before the step. Assume the potential is constant before and after the step.
Answer F2
The de Broglie wavelength λ = h/p, where p is the momentum, so that $k = 2\pi/\lambda = p/\hbar$. The momentum is calculated from the total energy E and the potential energy V: $E = \frac12m\upsilon^2 + V = p^2/(2m) + V$ so that $p = \sqrt{2m(E-V)\os}$.
Before the step, V = 0 and $k_1 = \sqrt{2mE\os}/\hbar$ with E = 5 eV. After the step, $k_2 = \sqrt{2m(E-V)\os}/\hbar$ with E − V = (5 − 2.5) eV = 2.5 eV.
Clearly $k_2 = k_1/\sqrt{2\os}$.
The reflection coefficient R and the transmission coefficient T are given by:
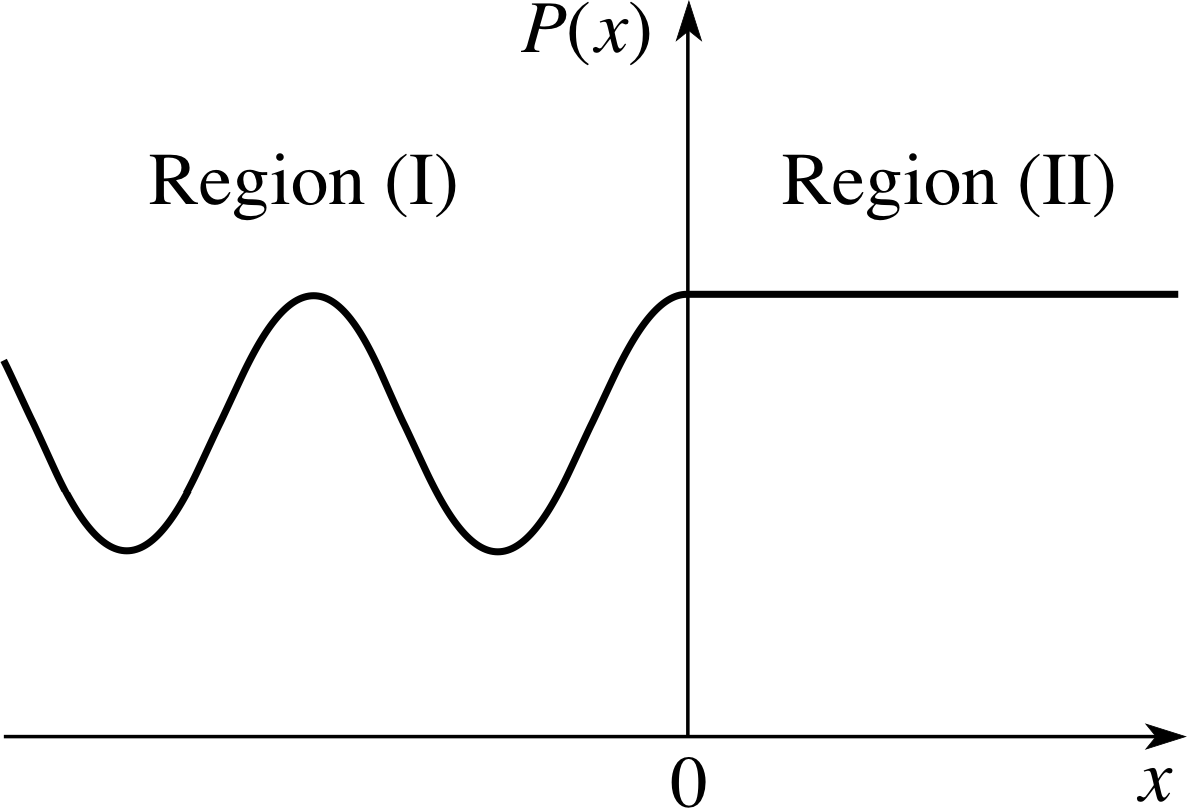
Figure 4 The particle density function P (x) in the region of a potential step (E > V). In region (I), P (x) shows a pattern of alternating maxima and minima caused by the interference of the incident and reflected waves.
$R = \dfrac{\text{reflected flux}}{\text{incident flux}} = \left(\dfrac{k_1-k_2}{k_1+k_2}\right)^2$
and$T = \dfrac{\text{transmitted flux}}{\text{incident flux}} = \dfrac{4k_1k_2}{(k_1+k_2)^2}$ with R + T = 1
We know that $k_2 = k_1/\sqrt{2\os}$ so that:
$R = \left(\dfrac{\sqrt{2\os}-1}{\sqrt{2\os}+1}\right)^2 = 0.029$
We have R + T = 1, so T = 0.971.
Your sketch of the electron density should look similar to Figure 4.
The series of maxima and minima in the density function before the step is caused by the interference of the incident and reflected waves. The amplitude of the reflected wave is smaller than the incident wave, so the minima are greater than zero.
Question F3
Estimate the fraction of 2.5 eV electrons that pass through a potential barrier height 5 eV and width 0.5 nm.
Answer F3
A good approximation for the transmission coefficient of particles with energy E incident on potential barrier width d and height V > E is T ≈ 4 exp(−2αd), where $\alpha = \sqrt{2m(V-E)\os}$
We have V − E = 2.5 eV and d = 0.5 nm.
Converting into joules: V − E = 2.5 × 1.6 × 10−19 J = 4.0 × 10−19 J
$\alpha = \rm \dfrac{\sqrt{2\times9.11\times10^{-31}\times4.0\times10^{-19}}}{1.05\times10^{-34}}\,m^{-1} = 0.813\times10^{10}\,m^{-1}$
T ≈ 4 exp(−2 × 0.813 × 1010 × 0.5 × 10−9) = 4 exp(−8.13) = 1.2 × 10−3
So approximately 0.1% of electrons will pass through this barrier.
1.3 Ready to study?
Study comment In order to study this module, you will need to be familiar with the following physics terms: de Broglie wave, eigenfunction (of momentum), time–independent Schrödinger equation, wavefunction, Born probability interpretation of the wavefunction, the (stationary state) probability density function P (x) = | ψ (x) |2. You should be familiar with the solutions of the Schrödinger equation for a particle moving in one dimension, in a region where the potential energy is constant. In particular, you should know the different forms of the solutions: (a) when the total energy of the particle is greater than the potential energy, and (b) when the total energy is less than the potential energy. Some knowledge of classical Newtonian mechanics is assumed, especially the treatment of particle motion in terms of the total energy, kinetic energy and potential energy. The module assumes some familiarity with the treatment of transverse waves on a string and the reflection of travelling waves at a boundary. If you are uncertain of any of these terms, you can review them now by referring to the Glossary which will indicate where in FLAP they are developed. We have to use complex numbers, so you must be familiar with them in cartesian_form_of_a_complex_numberCartesian form z = a + ib, polar form z = A (cos θ + isin θ) and exponential_form_of_a_complex_numberexponential form z = A exp(iθ). You must be confident using a spatial wavefunction written as a complex number: for example ψ (x) = A exp(ikx), and with the manipulation of complex numbers. We will frequently use calculusdifferential calculus, including differentiation of elementary functions such as sine, cosine and exponential. The following Ready to study questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
Write down the spatial part of the wavefunction of a particle travelling in the positive x–direction with definite momentum p. If the total energy of the particle is E and the potential energy has the constant value V, what is the relation between p, E, and V? What is the relation between the angular wavenumber k, i the de Broglie wavelength, and the momentum magnitude p?
Answer R1
The spatial wavefunction of a particle with definite momentum p is $\psi(x) = A\exp(ipx/\hbar)$.
The total energy is the sum of the kinetic energy and the potential energy:
$E = T + V = \frac12m\upsilon^2 + V$
but p = mυ, so that$E = \dfrac{p^2}{2m} + V$
Solving for p, we find$p = \sqrt{2m(E-V)\os}$
The de Broglie wavelength is given by λ = h/p, and the angular wavenumber k is given by k = 2π/λ, so that $k = p/\hbar$ where $\hbar = h/2\pi$.
Question R2
Write down the time–independent Schrödinger equation for a particle moving in one dimension (x) in a region of space where the total energy is less than the constant potential energy V. Show by substitution that the spatial wavefunction ψ (x) = A exp(−αx) + B exp(αx), where A and B are constants, is a solution of this equation and find α in terms of E and V.
Answer R2
The time–independent Schrödinger equation is:
$\dfrac{-\hbar^2}{2m\os}\dfrac{d\psi(x)}{dx^2} = (E-V)\psi(x)$ with E < V
Try the solution suggested, ψ (x) = A exp(−αx) + B exp(αx):
$\dfrac{d\psi}{dx} = -\alpha A\exp(-\alpha x) + \alpha B\exp(\alpha x)$
$\dfrac{d^2\psi}{dx^2} = +\alpha^2A\exp(-\alpha x) + \alpha^2B\exp(\alpha x)$
Therefore$\dfrac{-\hbar^2}{2m\os}\dfrac{d\psi(x)}{dx^2} = \dfrac{-\hbar^2\alpha^2\psi}{2m\os}$
Substituting in the Schrödinger equation, and assuming ψ ≠ 0:
$\alpha^2 = \dfrac{2m(V-E)}{\hbar^2}$
and since V > E $\alpha = \dfrac{\sqrt{2m(V-E)\os}}{\hbar}$
and ψ satisfies the time–independent Schrödinger equation.
Question R3
Define the (stationary state) probability density function P (x), for a particle moving in one dimension, and describe its physical interpretation. A particle has the spatial wavefunction ψ (x) = A exp(−αx), in the region x ≥ 0, with A and α real, and ψ (x) = 0 elsewhere. Write down an expression for the probability density P (x). Find a real positive value of A if the total probability of finding the particle somewhere between x = 0 and x → ∞ is one (i.e. normalize the wavefunction).
Answer R3
The probability_densityprobability density function for a stationary state is defined by P (x) = | ψ (x) |2 = ψ*(x) ψ (x).
If a particle has wavefunction ψ (x), then the probability of finding the particle in a small region of space ∆x near x is P (x) ∆x. The total probability of finding the particle is one, so that:
$\displaystyle \int_{-\infty}^{+\infty} P(x)\,dx = 1$
P (x) = A exp(−αx) A exp(−αx) = A2 exp(−2αx) for x ≥ 0; P (x) = 0 for x < 0.
Hence$\displaystyle \int_{-\infty}^{+\infty} P(x)\,dx = \int_{-\infty}^{+\infty} A^2\exp(-2\alpha x)\,dx = 1$
But the middle expression in the above equation may be written:
$\dfrac{A^2}{-2\alpha}\left[\exp(-2\alpha x)\right]_0^{\infty} = \dfrac{A^2}{-2\alpha}[0-1] = \dfrac{A^2}{2\alpha}$
and this must be equal to 1, so $A = \sqrt{2\alpha\os}$.
Question R4
(a) Write z = a + ib in the form z = A exp(iϕ) by relating A and ϕ to a and b.
(b) Show that the complex number $z = \dfrac{a - ib}{a + ib}$ may be written as z = exp(−2iϕ).
(c) Show that the complex number $z = \dfrac{2a}{a + ib}$ may be written z = 2 cos ϕ exp(−iϕ).
Answer R4
(a) In full detail, the calculation goes like this:
$z = a + ib = \sqrt{a^2+b^2}\left(\dfrac{a}{\sqrt{a^2+b^2}} + \dfrac{ib}{\sqrt{a^2+b^2}}\right) = A(\cos\phi+i\sin\phi)$
wheretan ϕ = b/a and $A = \sqrt{a^2+b^2}$.
Hencez = A exp(iϕ)
(b) Using the result of (a) and a similar calculation with b replaced by −b:
$z = \dfrac{a - ib}{a + ib} = \dfrac{A\exp(-i\phi)}{A\exp(i\phi)} = \exp(2-i\phi)$
where tan ϕ = b/a or ϕ = arctan(b/a).
(c) The method is similar to (a) and (b):
$z = \dfrac{2a}{a + ib} = \dfrac{2a}{\sqrt{a^2+b^2}\exp(i\phi)}$
where tanϕ = b/a and $\cos\phi = \dfrac{a}{\sqrt{a^2+b^2}}$
so that$z = \dfrac{2\cos\phi}{\exp(i\phi)} = 2\cos\phi\exp(-i\phi)$ as required.
(For details about complex numbers and their use consult the Glossary.)
2 Reflection and transmission at a potential step when E > V
2.1 Classical description of the problem
The physical situation we are modelling is quite simple. A particle is moving with constant velocity in the positive x–direction and encounters at some point a strong force directed in the negative x–direction. The force is constant in time and acts over a short distance d. It is usually best to represent the situation in classical (Newtonian) mechanics with a potential energy function U (x). The derivative of the potential energy function with respect to x gives the force component in the negative x–direction:
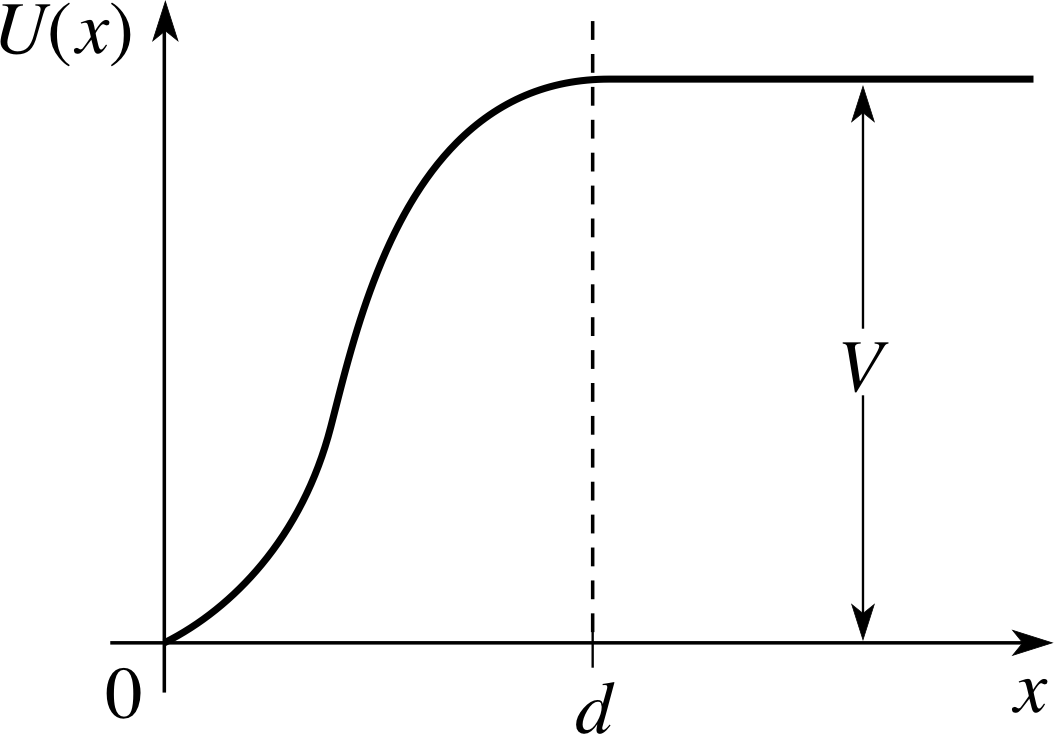
Figure 1 The potential energy function U (x) for a particle acted on by a repulsive force between x = 0 and x = d.
$F_x(x) = -\dfrac{U(x)}{dx}$
The potential energy function looks like that drawn in Figure 1. Notice that for convenience we have taken U (x) = 0 for x < 0 and U (x) = V for x ≥ d. It is the change in the potential energy that is physically significant, and the force acts in the region between 0 and d. For obvious reasons, the situation is referred to as a potential step, and we wish to know what happens to a particle encountering it.
Classical mechanics gives a definite answer, and all we need to know is the initial speed of the particle, its mass m and the potential energy function. Classically, the total energy E of the particle, kinetic plus potential, must be constant everywhere. So, if we let the speed of the particle be u as it approaches the step, and if we let υ be its speed beyond the step, then
$E = \frac12mu^2 + 0 = \frac12m\upsilon^2 + V$
Hence$\upsilon = \sqrt{\dfrac{2(E-V)}{m}}$ i
This equation has a real solution only if E ≥ V. The particle then passes across the step and continues with reduced speed. If the potential energy has a value greater than E beyond the step, then the solution for υ is purely imaginary_partimaginary and does not represent a physical situation. In fact, the particle is reflected from the step and is not seen in the region x ≥ d.
In the classical sense, reflected means that the repulsive force is so strong that the particle comes to rest and then moves back in the direction from which it came.
Question T1
Suppose the potential energy function in Figure 1 is U (x) = 0 for x < 0 and U (x) = 6 J for x ≥ d. A particle of mass 6 kg approaches from the left with speed 2 m s−1. Find its speed after the step.
Answer T1
We use the energy conservation for the motion. The initial total energy is $E =\frac12mu^2$, where u is the incident speed, since the potential energy is zero for x < 0. Let the speed after the step be υ, then:
$\frac12m\upsilon^2 + V = \frac12mu^2$
Solving for υ: $\upsilon = \sqrt{u^2 - \dfrac{2V}{m}}$
Substituting for u, V and m:
$\upsilon = \rm \sqrt{2^2 - \dfrac{2\times6}{6}}\,m\,s^{-1} = 1.4\,m\,s^{-1}$
If the force on the particle is in the positive x–direction, then the potential energy decreases and we have a step down rather than a step up! It is easy to show that the particle will always gain speed at this step and classical physics predicts that it will never be reflected.
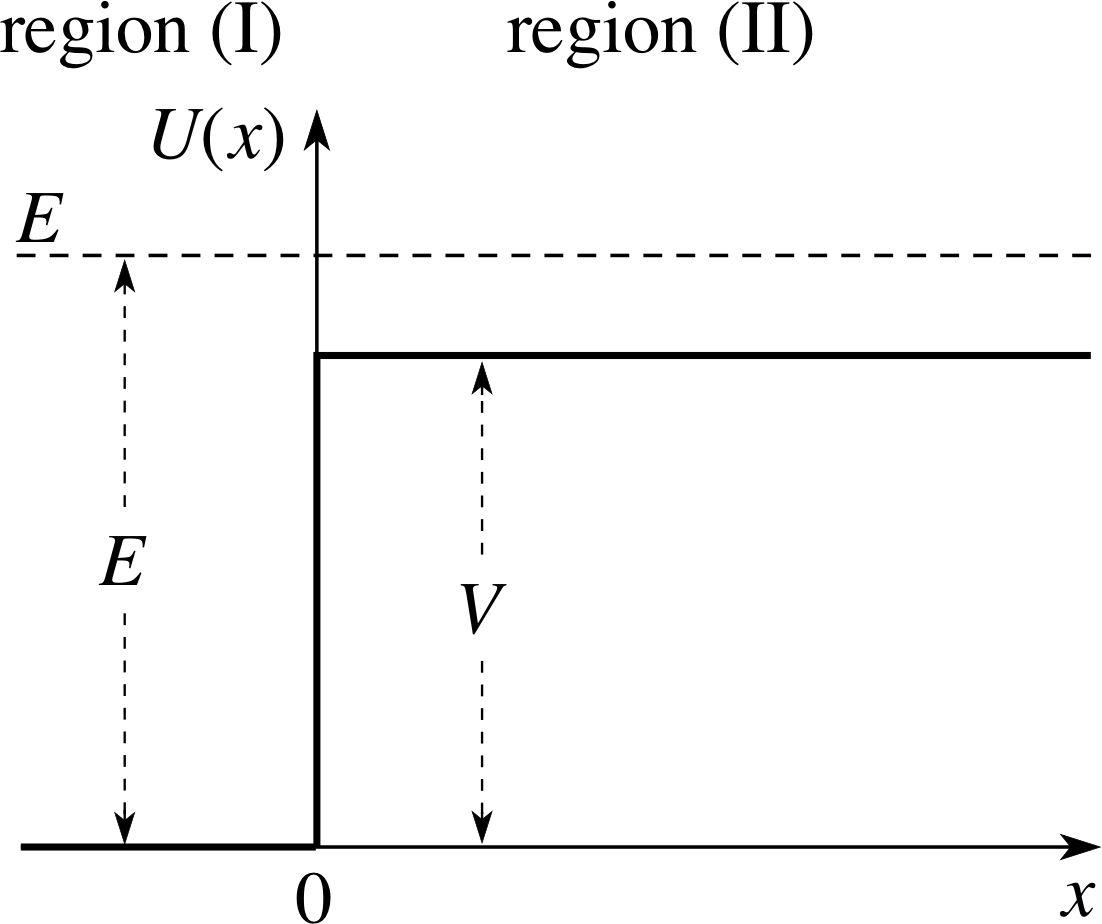
Figure 2 A schematic representation of a potential step. The distance over which the force acts is assumed to be negligible. The total energy of the particle is E.
Often we have to model this kind of situation when the distance d is small compared with any other dimension in the problem. Figure 2 represents a potential step with the distance d negligibly small; the potential suddenly increases at the origin from zero to a constant value V. Remember that this diagram can only be an approximation to the truth, since such a sudden increase in potential represents an infinite force acting over zero distance. However, it is a useful device, and it is also convenient to represent the total energy E on the diagram. Classical mechanics then makes the following definite predictions for a particle approaching from the left (x < 0) with zero potential energy initially:
Particle transmitted across the step if E > V and V > 0
Particle reflected at the step if E < V and V > 0
Particle always transmitted across step if V ≤ 0
2.2 The time–independent Schrödinger equation and its solutions
In order to find out what quantum mechanics can tell us about a physical situation, we have to make a simple model and then solve the Schrödinger equation to find the appropriate wave functions. As in classical mechanics, we model the potential function as a step and make the approximation that d is small, but small compared with what? i
The relevant dimension is now the de Broglie wavelength of the incident particle λ = h/p, where h is Planck’s constant and p is the magnitude of the particle momentum initially. The potential energy diagram is the same as Figure 2, and it is convenient to call the space x < 0 region (I) and the space x ≥ 0 region (II). The time–independent Schrödinger equation in one dimension is:
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} + U(x)\psi(x) = E\psi(x)$(1)
where E is the total energy of the particle, U (x) the potential energy function and ψ (x) the spatial part of the wavefunction.
Study comment The full wavefunction Ψ (x, t) is time–dependent and satisfies the time–dependent Schrödinger equation. For a stationary state of definite energy E the wavefunction takes the form
${\it\Psi}(x,\,t) = \psi(x)\exp\left(-i\dfrac{E}{\hbar}t\right)$
Since this module is entirely concerned with states of given energy E, we need only determine ψ (x), which we may therefore conveniently refer to as the wavefunction. The full wavefunction Ψ (x, t) follows immediately. Similarly, we may refer to Equation 1 as the Schrödinger equation.
In region (I), U (x) = 0 and ψ (x) = ψ1(x) so the Schrödinger equation is
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi_1(x)}{dx^2} = E\psi_1(x)$
The solution of this equation takes the form:
ψ1(x) = A exp(ik1x) + B exp(−ik1x)(2)
with A and B arbitrary complex constants and $k_1 = \sqrt{2mE/\hbar\os}$
In region (II), U (x) = V and the Schrödinger equation is:
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi_2(x)}{dx^2} = (E-V)\psi_2(x)$(3)
The solution then has the form:
ψ2(x) = C exp(ik2x) + D exp(−ik2x)
with C and D arbitrary complex constants and $k_2 = \sqrt{2m(E-V)/\hbar\os}$

Figure 2 A schematic representation of a potential step. The distance over which the force acts is assumed to be negligible. The total energy of the particle is E.
Notice that k2 is a real number because E > V. The first term on the right–hand side of Equation 2 represents a particle moving with momentum component $\hbar k_1$ in the x–direction, i and the second term represents a reflected particle moving with momentum component $-\hbar k_1$. The first term in Equation 3 represents a particle transmitted across the step moving with momentum component $\hbar k_2$, and the second term represents a particle moving in the negative x–direction. Clearly, we must set coefficient D = 0, since this physical problem involves a particle approaching the barrier from the left, not from the right and here it cannot return from infinity.
In summary, the solutions to the Schrödinger equation in the two regions are:
in region (I)ψ1 (x) = A exp(ik1x) + B exp(−ik1x)(4a)
in region (II)ψ2 (x) = C exp(ik2x)(4b)
The important question of normalization of the wavefunctions must be postponed until we have discussed fully the constraints imposed on the constants A, B and C by the conditions at the boundary between the two regions.
2.3 Relations imposed by the boundary conditions
General solutions of differential equations always contain arbitrary constants, and we can determine these from the conditions assumed to apply at certain positions or times. For example, the general solution of the wave equation for transverse waves on a string stretched between two fixed points has two arbitrary constants. i We can determine these constants from the initial configuration of the string including the requirement that its displacement is zero at the ends.
We can apply two boundary conditions, at x = 0, to the solutions of the Schrödinger equation in this application. We will state them and then make some justification.
boundary condition (1)ψ1(x) = ψ2(x) at x = 0
boundary condition (2)$\dfrac{d\psi_1(x)}{dx} = \dfrac{d\psi_2(x)}{dx}$ at x = 0
The first condition ensures that the wavefunction has a single value at x = 0. The Born probability hypothesis says that the probability density is given by | ψ (x) |2, so that the solution in region (I) must match the solution in region (II) at the boundary between the regions.
The second condition boundary condition is clear when we examine the Schrödinger equation itself,
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} + U(x)\psi(x) = E\psi(x)$(Eqn 1)
If both E and U (x) are finite quantities everywhere, then the second derivative d2ψ1(x)/dx2 must also be finite. This means that the first derivative of the wavefunction dψ1(x)/dx cannot suddenly change at any point, including the boundary at x = 0. Therefore the slope of the wavefunction in region (I) at x = 0 is equal to the slope of the wavefunction in region (II) also evaluated at x = 0.
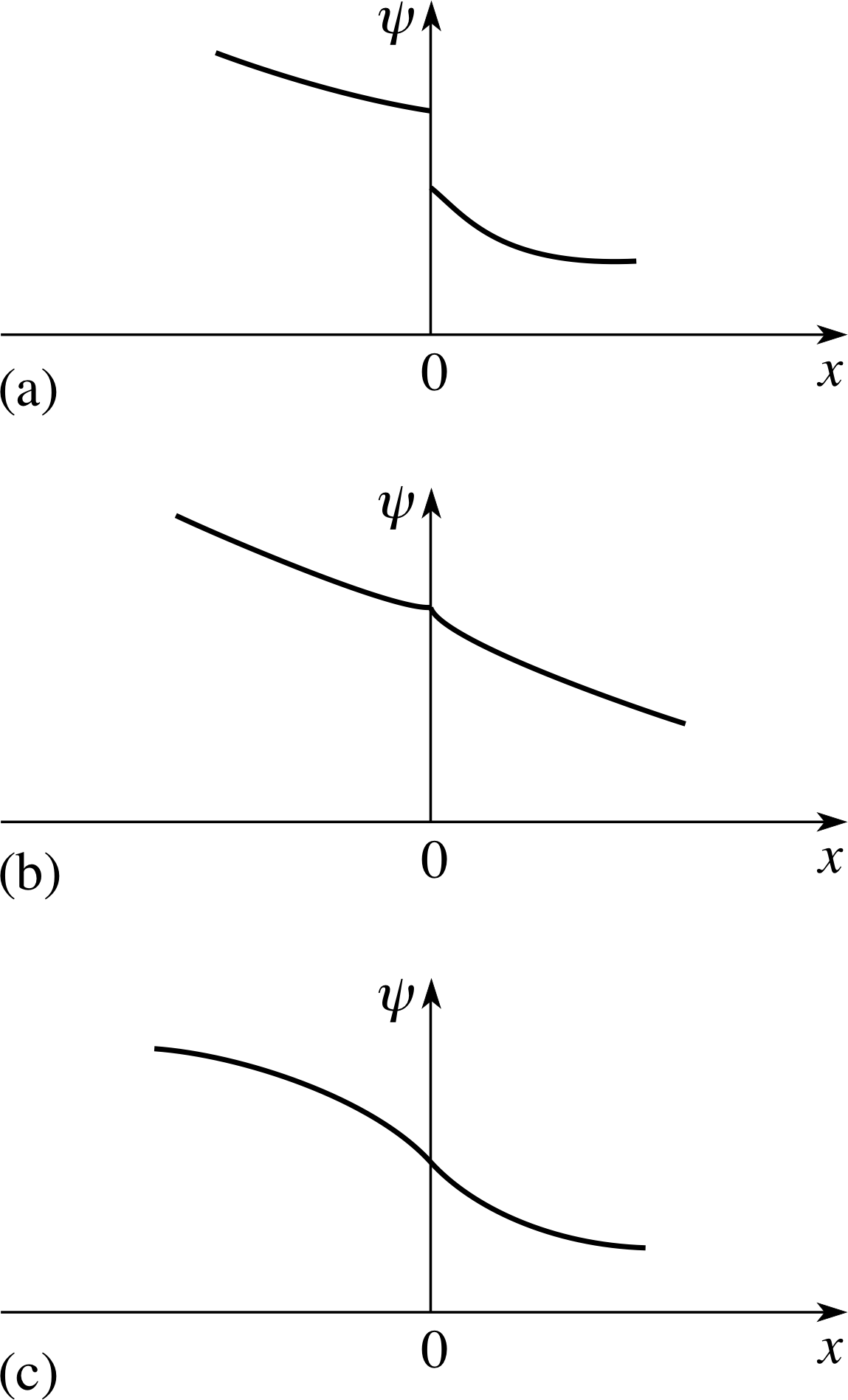
Figure 3 Boundary conditions at x = 0. Only (c) is allowed. (a) ψ1 ≠ ψ2, (b) ψ1 = ψ2 but dψ1/dx ≠ dψ2/dx, (c) ψ1 = ψ2 and dψ1/dx = dψ2/dx.
The possibilities are illustrated in Figure 3:
(a) shows a discontinuity in ψ at x = 0,
(b) has ψ continuous but dψ/dx discontinuous at x = 0,
and(c) both ψ and dψ/dx are continuous.
Only in case (c) can we say that ψ varies smoothly across the boundary, and this is what we require. i
Applying the boundary conditions gives us two equations linking A, B and C: Using Equations 4,
in region (I)ψ1 (x) = A exp(ik1x) + B exp(−ik1x)(Eqn 4a)
in region (II)ψ2 (x) = C exp(ik2x)(Eqn 4b)
boundary condition (1) gives:
ψ1(0) = ψ2(0)
so thatA exp 0 + B exp 0 = C exp 0 i.e. A + B = C(5)
Applying boundary condition (2):
A (ik1) exp 0 + B (−ik1) exp 0 = C (ik2) exp 0 i
so thatAk1 − Bk1 = Ck2(6)
Equations 5 and 6 can be used to determine the two ratios B/A and C/A:
$\dfrac BA = \dfrac{k_1-k_2}{k_1+k_2}$(7a)
$\dfrac CA = \dfrac{2k_1}{k_1+k_2}$(7b)
Question T2
Consider a string lying along the x–axis under tension F. The density per unit length of the string is ρ1 for x < 0 and ρ2 for x ≥ 0. Considering transverse waves on the string, describe how this problem in classical mechanics might be similar to the quantum–mechanical problem of particles incident on a potential step. (The speed of transverse waves is $\sqrt{F/\rho\os}$.)
Answer T2
The transverse waves on the string behave in a mathematically similar way to the quantum wavefunction. If the density of the string is ρ1 for x < 0 and ρ2 for x ≥ 0, then transverse waves from the left with frequency f will be partially reflected at the boundary. The incident, reflected and transmitted wave amplitudes are related by Equations 7:
$\dfrac BA = \dfrac{k_1-k_2}{k_1+k_2}$(Eqn 7a)
$\dfrac CA = \dfrac{2k_1}{k_1+k_2}$(Eqn 7b)
with $k_{1,2} = 2\pi f\sqrt{\left.\rho_{1,2}\middle/F\right.\os}$. Remember that the physical interpretation of a wavefunction is quite different from that of transverse waves on a string.
2.4 The wavefunctions in each region and the physical interpretation; normalization
In all our discussions of quantum mechanics so far, we have assumed that the wavefunction ψ (x) is normalized to unity and represents a single particle, so | ψ (x) |2 ∆x gives the probability of finding the particle in the range x to x + ∆x. Now it is convenient to modify the prescription and say that the wavefunction can represent more than one particle. In particular, the wavefunction ψ (x) = A exp(ikx) can represent a set of particles, moving in the x–direction, all with the same momentum $\hbar k$.
The position of any one particle is not specified (to do so violates the Heisenberg uncertainty principle), but we say the average number of particles per unit length is given by | ψ (x) |2. In this context, ‘average’ means the average of a large number of observations made on particles with this wavefunction. i
✦ The wavefunction ψ (x) = A exp(ikx) represents a stream of particles moving in the x–direction. Show that, on average, there are | A |2 particles per unit length.
✧ According to our new prescription, the average number N per unit length is given by:
N = | ψ (x) |2 = ψ*(x) ψ (x) = A* exp(−ikx) A exp(ikx) = A*A exp 0 = | A |2.
Now we must examine the wavefunctions,
in region (I)ψ1 (x) = A exp(ik1x) + B exp(−ik1x)(Eqn 4a)
in region (II)ψ2 (x) = C exp(ik2x)(Eqn 4b)
in the potential step problem in the light of the new prescription.
In region (I), we have the wavefunction:
ψ1(x) = A exp(ik1x) + B exp(−ik1x) with $k_1 = \sqrt{2mE\os}/\hbar$
The first term of this single wavefunction now represents a stream of particles moving in the positive x–direction towards the step; these are the incident particles. The second term represents a stream of particles moving in the negative x–direction away from the step, the reflected particles. The average number of incident particles per unit length is | A |2, and the average number of reflected particles is | B |2. Notice that the single wavefunction can represent both the incident and reflected particles.
In region (II), the wavefunction is:
ψ2(x) = C exp(ik2x) with $k_2 = \sqrt{2m(E-V)\os}/\hbar$
This simply represents a stream of particles moving in the positive x–direction away from the step, the transmitted particles. The average number of transmitted particles per unit length is | C |2.
A further simplification of the equations is made, with no loss of generality, if the wavefunctions are normalized_wavefunctionnormalized in a special way. If the coefficient A is set equal to one, then the average number of incident particles per unit length is equal to one.
Question T3
Electrons with kinetic energy 5 eV are moving in the positive x–direction in a region of constant potential. There are on average 5 × 106 electrons per millimetre. Find a suitable wavefunction i to describe them, and find A and k.
Answer T3
A suitable wavefunction is ψ (x) = A exp(ikx), and we have to find A and k. The particle density is given by | A |2 and we can choose A to be real: A2 = 5 × 106 × 103 m−1 = 5 × 109 m−2. Hence A = 7.1 ×104 m−1/2.
Remember that 1 eV is 1.60 × 10−19 J.
The angular wavenumber k is calculated from the kinetic energy E:
$k = \dfrac{\sqrt{2mE\os}}{\hbar} = \rm \dfrac{\sqrt{2\times9.11\times10^{-31}\times5\times1.60\times10^{-19}}}{1.05\times10^{-34}\,m^{-1}} = 1.15\times10^{10}\,m^{-1}$
You will have occasion to use this result in later questions.
2.5 Defining particle flux in the classical and quantum models
In classical mechanics, it is straightforward to define the concept of particle flux. We will restrict the discussion to motion in one dimension, but the extension to three dimensions is not difficult. If there are N particles per unit length and each one has speed u in the positive x–direction, then all the particles in a length u ∆t will pass a fixed point in time interval ∆t. The number passing a fixed point per unit time is the particle flux F:
$F = \dfrac{Nu\Delta t}{\Delta t} = Nu$
In quantum mechanics, the definition of particle flux is equally simple, provided we are dealing with wavefunctions of particles with definite momentum (i.e. momentum eigenfunctions). Consider a stream of particles represented by the wavefunction ψ (x) = A exp(ikx). The average number of particles per unit length is the constant | A |2, and their speed u is obtained from the momentum magnitude:
$p = \hbar k$ and u = p/m
so that:$u = \hbar k/m$
Since k > 0, so is u.
The flux is then given by:
$F = \vert\,A\,\rvert^2\dfrac{\hbar k}{m}$(8)
A word of warning is necessary here! Equation 8 can only be used when the wavefunction is a momentum eigenfunction; the momentum is then the same for all the particles, and the average number of particles per unit length is a constant, independent of position.
Question T4
What is the flux of electrons in Question T3?
[Electrons with kinetic energy 5 eV are moving in the positive x–direction in a region of constant potential. There are on average 5 × 106 electrons per millimetre.]
What is the corresponding current in amps?
[Hint: The current is the total charge in coulombs passing a point per second.]
Answer T4
The flux F is given by Equation 8:
$F = \dfrac{A^2\hbar k}{m} = \rm \dfrac{5\times10^9\times1.15\times10^{10}\times1.05\times10^{-34}}{9.11\times10^{-31}}\,s^{-1} = 6.63\times10^{15}\,s^{-1}$
The current I is then given by the flux (particles per second) multiplied by the charge on each electron:
I = 6.63 × 1015 × 1.6 × 10−19 A = 1.1 × 10−3 A.
This is just 1.1 mA.
2.6 Reflection and transmission in the quantum model

Figure 2 A schematic representation of a potential step. The distance over which the force acts is assumed to be negligible. The total energy of the particle is E.
We are now in a position to complete the quantum description of particle reflection and transmission at potential steps. Two coefficients are defined which characterize the behaviour of particles when they encounter a potential step such as that illustrated in Figure 2.
The reflection coefficient is defined as follows:
$R = \dfrac{\text{flux of reflected particles}}{\text{flux of incident particles}}$
The wavefunction in region (I) is:
ψ1(x) = A exp(ik1x) + B exp(−ik1x)
The first term represents the particles incident on the step, and, using Equation 8,
$F = \vert\,A\,\rvert^2\dfrac{\hbar k}{m}$(Eqn 8)
the incident flux is $\vert\,A\,\rvert^2\hbar k_1/m$
The second term
ψ1(x) = A exp(ik1x) + B exp(−ik1x)
represents the reflected particles which have average density | B |2 per unit length and the reflected flux is $\vert\,B\,\rvert^2\hbar k_1/m$. The reflection coefficient is therefore:
$R = \dfrac{\vert\,B\,\rvert^2\hbar k_1/m}{\vert\,A\,\rvert^2\hbar k_1/m} = \dfrac{\vert\,B\,\rvert^2}{\vert\,A\,\rvert^2}$
Using Equation 7a,
$\dfrac BA = \dfrac{k_1-k_2}{k_1+k_2}$(Eqn 7)
we get the result:
The reflection coefficient at a potential step with E > V
$R = \left(\dfrac{k_1-k_2}{k_1+k_2}\right)^2$(9)
The transmission coefficient is defined as:
$T = \dfrac{\text{flux of transmitted particles}}{\text{flux of incident particles}}$
The wavefunction in region (II) is ψ2(x) = C exp(ik2x), and this represents the particles transmitted across the step. The transmitted flux is given by $\vert\,C\,\rvert^2\hbar k_1/m$ and hence the transmission coefficient is:
$T = \dfrac{\vert\,C\,\rvert^2\hbar k_1/m}{\vert\,A\,\rvert^2\hbar k_1/m} = \dfrac{\vert\,C\,\rvert^2}{\vert\,A\,\rvert^2}$
Using Equations 7b,
$\dfrac CA = \dfrac{2k_1}{k_1+k_2}$(7b)
we get the result:
The transmission coefficient at a potential step with E > V
$T = \dfrac{4k_1k_2}{(k_1+k_2)^2}$(10)
In order to check that our equations for R and T are self-consistent, we must show that particles are not ‘lost’ at the step. The number of particles crossing the step per second (the transmitted flux) added to the number reflected per second (the reflected flux) must be equal to the incident flux. From the definitions of R and T, this means that R + T = 1. This is indeed the case!
Question T5
Use Equation 9 and Equation 10 to show that R + T = 1.
Answer T5
Equations 9 and 10 are:
$R = \left(\dfrac{k_1-k_2}{k_1+k_2}\right)^2$(Eqn 9)
$T = \dfrac{4k_1k_2}{(k_1+k_2)^2}$(Eqn 10)
$R + T = \dfrac{k_1^2-2k_1k_2+k_2^2+4k_1k2}{(k_1+k_2)^2} = \dfrac{k_1^2+2k_1k_2+k_2^2}{k_1^2+2k_1k_2+k_2^2} = 1$
as required.
Remember that R and T are both ratios of fluxes; this means that the formulae for R and T are unchanged whatever the value of A. It is also legitimate to regard R and T as reflection and transmission probabilities if you are dealing with the behaviour of a single particle at the step.
$R = \left(\dfrac{k_1-k_2}{k_1+k_2}\right)^2$(Eqn 9)
$T = \dfrac{4k_1k_2}{(k_1+k_2)^2}$(Eqn 10)
Notice that the reflection coefficient approaches the limit R = 1 and the transmission coefficient goes to zero, when k2 → 0. This happens when V is equal to the incident particle energy E.
The function P (x) = | ψ (x) |2 represents the probability density when ψ is the wavefunction for a single particle. However, when ψ represents a set of particles, the function P (x) = | ψ (x) |2 gives the average particle density at the position x. P (x) is then the particle density function and it is interesting to plot a graph of P (x) across the potential step.

Figure 4 The particle density function P (x) in the region of a potential step (E > V). In region (I), P (x) shows a pattern of alternating maxima and minima caused by the interference of the incident and reflected waves.
This is shown in Figure 4 for the case when A, B and C are real.
In region (I), we have to use the full expression for ψ1(x) (Equation 4):
in region (I)ψ1 (x) = A exp(ik1x) + B exp(−ik1x)(Eqn 4a)
in region (II)ψ2 (x) = C exp(ik2x)(Eqn 4b)
P1(x) = ψ1*(x) ψ1(x) = A2 + B2 + 2AB cos(2k1x)(11)
In region (II):
P2(x) = ψ2*(x) ψ2(x) = C2(12)
P1(x) and P2(x) join smoothly at x = 0 because of the boundary conditions,
A + B = C(Eqn 5)
Ak1 − Bk1 = Ck2(Eqn 6)
In region (I), P (x) has a cosine component due to the interference between the incident and reflected waves.
This example of quantum–mechanical interference with material particles is analogous to the interference of light beams reflected from boundaries between materials with different optical properties. The interference minima are not at zero because the amplitude of the reflected wave is less than the amplitude of the incident wave.
Question T6
Starting from Equations 4,
in region (I)ψ1 (x) = A exp(ik1x) + B exp(−ik1x)(Eqn 4a)
in region (II)ψ2 (x) = C exp(ik2x)(Eqn 4b)
verify Equations 11 and 12,
in region (I)P1(x) = ψ1*(x) ψ1(x) = A2 + B2 + 2AB cos(2k1x)(Eqn 11)
in region (II)P2(x) = ψ2*(x) ψ2(x) = C2(Eqn 12)
Show that P1(0) = P2(0). (Remember Equations 11 and 12 assume A, B and C are real.)
Answer T6
In region (I), the complete wavefunction is
ψ2(x) = A exp(ik2x) + B exp(−ik2x)
Multiply by the complex conjugate to get the modulus squared. In this case, both A and B are real.
P1(x) = ψ1*(x) ψ1(x) = [A exp(−ik1x) + B exp(ik1x)] × [A exp(ik1x) + B exp(−ik1x)]
P1(x) = A2 + B2 + AB [exp(−2ikx) + exp(+2ikx)]
P1(x) = A2 + B2 + 2AB cos(2kx)
In region (II), the wavefunction is ψ2(x) = C exp(ik2x) and the density is:
P2(x) = ψ2*(x) ψ2(x) = C exp(−ik2x) C exp(ik2x) = C2
At the boundary, x = 0:
P1(0) = A2 + B2 + 2AB cos 0 = (A + B)2
but from the boundary conditions, A + B = C.
HenceP1(0) = C2.
P2(x) = C2 everywhere, so that P1(0) = P2(0).
Question T7
Figure 4 shows clearly that the probability per unit length of finding a particle in region (II) is greater, on average, than the probability in region (I). How can that be when a fraction of the incident particles is reflected?
Answer T7
Remember that the speed of the particles decreases as they pass into region (II), since k1 > k2. The slower the particles, the greater the density for a given flux, i.e. the particles spend a longer time in any given interval. Even though the sum of the incident and reflected fluxes is greater than the transmitted flux, the average particle density is greater in region (II).
3 Reflection and transmission at a potential step when E < V
3.1 Classical description of the problem
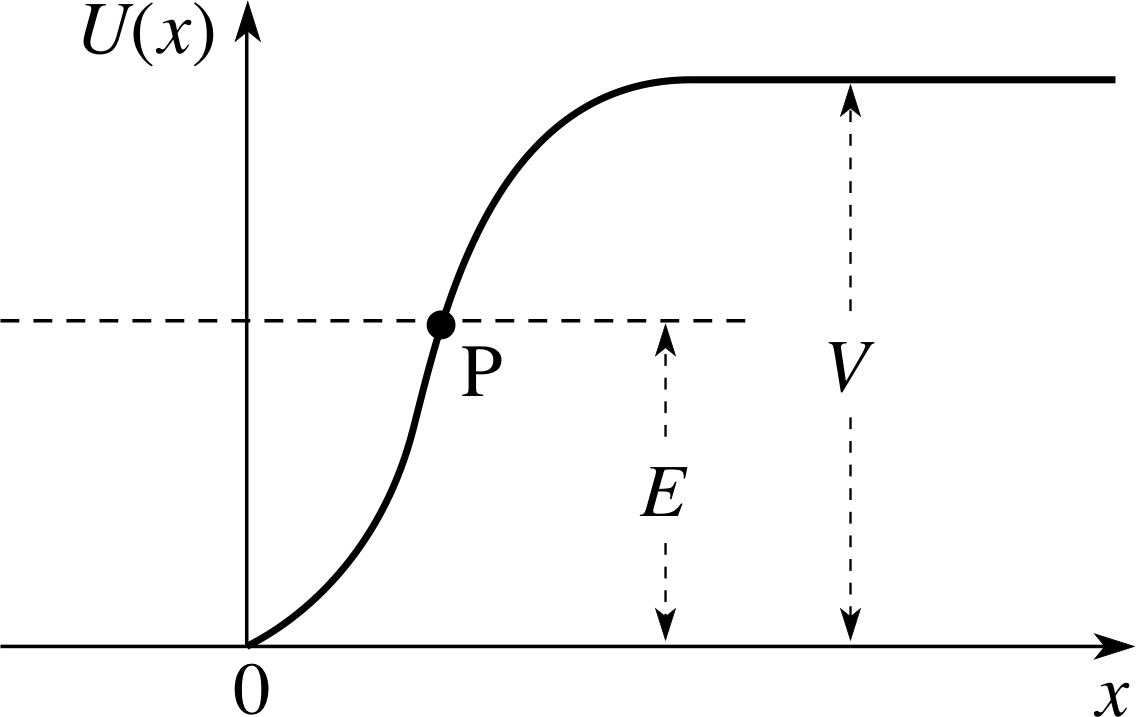
Figure 5 The function U (x) at a potential step. The height of the step V is greater than the energy E of each incident particle. According to classical mechanics, the particles reach the point P and are then reflected back.
A particle travelling in the positive x–direction encounters a step where the potential energy U (x) increases by an amount V greater than the particle energy. The physical situation is modelled by the illustration in Figure 5 and the total energy of a particle is represented by the horizontal dashed line. Applying the law of energy conservation to solve for the speed of the particle, we get:
$\frac12m\upsilon^2 = E - U(x)$
i.e.$\upsilon = \sqrt{\dfrac{2(E-U(x))}{m}}$
P marks the point where the total energy and the potential energy are equal, E = U (x) and υ = 0. There is no real–number solution to the speed equation anywhere to the right of P. According to classical mechanics, each particle will reach the point P and then be reflected back. The classical reflection coefficient is one.
3.2 The Schrödinger equation and the solutions in each region
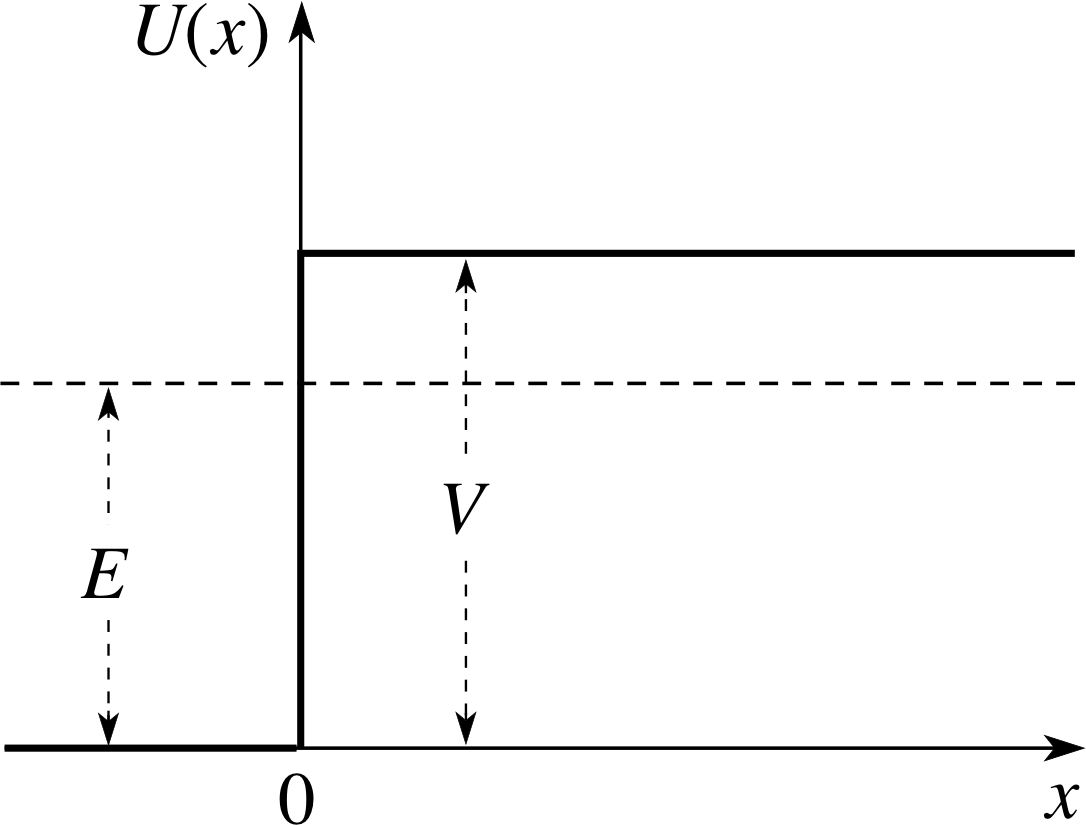
Figure 6 A schematic representation of a potential step with E < V. Particles are incident from the left.
For the quantum mechanical problem we again make the assumption that the distance over which the potential is increasing is small compared with the de Broglie wavelength of the incident particles. The situation is illustrated schematically in Figure 6 with the region x < 0 designated (I) and x ≥ 0 designated (II). The solution of the Schrödinger equation follows exactly as in Subsection 2.2, and we can write the solutions by referring to Equations 4:
in region (I)ψ1 (x) = A exp(ik1x) + B exp(−ik1x)(Eqn 4a)
in region (II)ψ2 (x) = C exp(ik2x)(Eqn 4b)
The angular wavenumbers k1and k2 are given by:
$k_1 = \dfrac{\sqrt{2mE\os}}{\hbar}\quad\text{and}\quad k_2 = \dfrac{\sqrt{2m(E-V)\os}}{\hbar}$
In this case it is clear that k2 is a purely imaginary number since E < V, but we cannot abandon this solution.
Remember that in quantum mechanics, the solutions make sense if the predictions for the values of physical observable quantities are real. We will continue the analysis and examine the form of the solution in region (II). If we replace k2 by iα, then α is a real number and we find:
ψ2(x) = C exp[i (iα)x] = C exp(−αx) since i2 = −1
The real constant α may be written in terms of E and V as follows:
α = k2/i = −ik2
However$k_2 = \dfrac{\sqrt{2m(E-V)\os}}{\hbar} = \dfrac{i\sqrt{2m(V-E)\os}}{\hbar}$
so that$\alpha = \dfrac{\sqrt{2m(E-V)\os}}{\hbar}$
In fact, there is a second part of the general solution in region (II) corresponding to a rising exponential rather than a falling exponential: ψ2(x) = C exp(−αx) + D exp(+αx). i The second term is ruled out as unphysical here because it predicts that the probability of observing the particles increases without limit as x → ∞.
In summary, we have:
in region (I)ψ1(x) = A exp(ik1x) + B exp(−ik1x)(13a)
in region (II)ψ2(x) = C exp(−αx)(13b) i
with$k_1 = \dfrac{\sqrt{2mE\os}}{\hbar}\quad\text{and}\quad\alpha = \dfrac{\sqrt{2m(E-V)\os}}{\hbar}$
3.3 Relationships imposed by the boundary conditions
The general requirements discussed in Subsection 2.3 that the wavefunction and its first derivative must both be continuous everywhere apply in this example. The relations between the arbitrary constants A, B and C are exactly the same as in Equations 7a and 7b:
$\dfrac BA = \dfrac{k_1-k_2}{k_1+k_2}$(Eqn 7a)
$\dfrac CA = \dfrac{2k_1}{k_1+k_2}$(Eqn 7b)
However now k2 is a purely imaginary number, and we have equated it to iα so:
$\dfrac BA = \dfrac{k_1-i\alpha}{k_1+i\alpha}$
$\dfrac CA = \dfrac{2k_1}{k_1+i\alpha}$
✦ Show that the complex number B/A can be written in the form: B/A = exp(−2iϕ) where tan ϕ = α/k1. Show also that | B | = | A |.
✧ We will need this important result later because it shows that the moduli of B and A are the same. Starting with the denominator
$k_1 + i\alpha = \sqrt{\smash[b]{k_1^2 + \alpha^2}}(\cos\phi + i\sin\phi) = \sqrt{\smash[b]{k_1^2+\alpha^2}}\exp(i\phi)$
where tan ϕ = α/k1.
Similarly, the numerator
$k_1 - i\alpha = \sqrt{\smash[b]{k_1^2+\alpha^2}}\exp(-i\phi)$
Hence
$\dfrac BA = \dfrac{k_1-i\alpha}{k_1+i\alpha} = \dfrac{\exp(-i\phi)}{\exp(i\phi)} = \exp(-2i\phi)$
From this, we see that | B/A | = | B | / | A | = 1
and so | B | = | A |.
Question T8
Show that the complex number C/A can be written in the form: C/A = 2 cos ϕ exp(−iϕ) and | C | = 2 | A |cos ϕ.
Answer T8
Starting with the equation $\dfrac CA = \dfrac{2k_1}{k_1 + i\alpha}$, we write the denominator in polar form:
$k_1 + i\alpha = \sqrt{\smash[b]{k_1^2+\alpha^2}}(\cos\phi + i\sin\phi) = \sqrt{\smash[b]{k_1^2+\alpha^2}}\exp(i\phi)$
Hence:$\dfrac CA = \dfrac{2k_1}{\sqrt{\smash[b]{k_1^2 + \alpha^2}}\exp(1\phi)} = \dfrac{2k_1\exp(-i\phi}{\sqrt{\smash[b]{k_1^2 + \alpha^2}}}$
but$\tan\phi = \dfrac{\alpha}{k_1}$, so $\cos\phi = \dfrac{k_1}{\sqrt{\smash[b]{k_1^2 + \alpha^2}}}$
HenceC/A = 2 cos ϕ exp(−iϕ)
The modulus of C/A is 2 cos ϕ, so that | C | = 2| A | cos ϕ.
In summary, we have the following relations for the ratios of the constants:
$\dfrac BA = \dfrac{k_1-i\alpha}{k_1+i\alpha} = \exp(-2i\phi)$so that $\dfrac{\lvert\,B\,\rvert}{\lvert\,A\,\rvert} = 1$(14a)
$\dfrac CA = \dfrac{2k_1}{k_1+i\alpha} = 2\cos\phi\exp(-\phi)$so that $\dfrac{\lvert\,C\,\rvert}{\lvert\,A\,\rvert} = 2\cos\phi$(14b)
with$\phi = \arctan\left(\dfrac{\alpha}{k_1}\right)$
3.4 The wavefunctions in each region and the physical interpretation
The wavefunctions for particles in regions (I) and (II) are given by Equations 13,
in region (I)ψ1(x) = A exp(ik1x) + B exp(−ik1x)(Eqn 13a)
in region (II)ψ2(x) = C exp(−αx)(Eqn 13b)
and the ratios of the constants B/A and C/A by Equations 14.
The incident beam A exp(ik1x) has an average density of | A |2 particles per unit length and the reflected beam B exp(−ik1x) has an average density | B |2. Our analysis showed that | B |2 = | A |2 (Equation 14a), and the densities of the reflected and incident particles are equal.
The transmitted particles are represented by the wavefunction in region (II):
ψ2(x) = C exp(−αx)
The density of transmitted particles is given by
| ψ2(x) |2 = | C |2 exp(−2αx)
This is a most important result: quantum mechanics makes the clear prediction that particles can be observed inside region (II). The particle density decreases exponentially with distance from the step. The scale of the penetration is set by the constant $\alpha = \sqrt{2m(V-E)\os}/\hbar$. In interesting cases, this is usually of the same order of magnitude as the angular wavenumber $k_1 = \sqrt{2mE\os}/\hbar$ in region (I).
It is helpful to visualize the situation by plotting a graph of the density function P (x) as we did at the end of Subsection 2.6.
We can simplify the algebra by setting A = 1 so that there is one incident particle per unit length. In region (I), we have with the help of Equations 14:
$\dfrac BA = \dfrac{k_1-i\alpha}{k_1+i\alpha} = \exp(-2i\phi)$so that $\dfrac{\lvert\,B\,\rvert}{\lvert\,A\,\rvert} = 1$(Eqn 14a)
$\dfrac CA = \dfrac{2k_1}{k_1+i\alpha} = 2\cos\phi\exp(-\phi)$so that $\dfrac{\lvert\,C\,\rvert}{\lvert\,A\,\rvert} = 2\cos\phi$(Eqn 14b)
in region (I)ψ1 (x) = A exp(ik1x) + B exp(−ik1x)(Eqn 4a)
and, since B = exp(−2iϕ):
ψ1 (x) = exp(ik1x) + exp[−i (2ϕ + k1x)]
NowP1(x) = ψ1*(x) ψ1(x)
so thatP1(x) = 2 + exp[i (2ϕ + 2k1x)] + exp[−i (2ϕ + 2k1x)]
P1(x) = 2 + 2 cos(2k1x + 2ϕ)(15)
In region (II), we have with the help of Question T8:
ψ2(x) = C exp(−αx)
P2(x) = ψ2*(x) ψ2(x) = | C |2 exp(−2αx)
and since C = 2 cos ϕ exp(−iϕ)
P2(x) = 4 cos2 ϕ exp(−2αx)(16)
The density function is drawn in Figure 7 using Equations 15 and 16. You can see a perfect interference pattern in region (I) with the regular array of maxima and minima. The amplitudes of the incident and reflected waves are equal so the maximum value of P1(x) is 4 and the minimum 0. At the boundary, P1(0) = P2(0) = 4 cos2 ϕ, and the density function passes smoothly to the decreasing exponential in region (II).
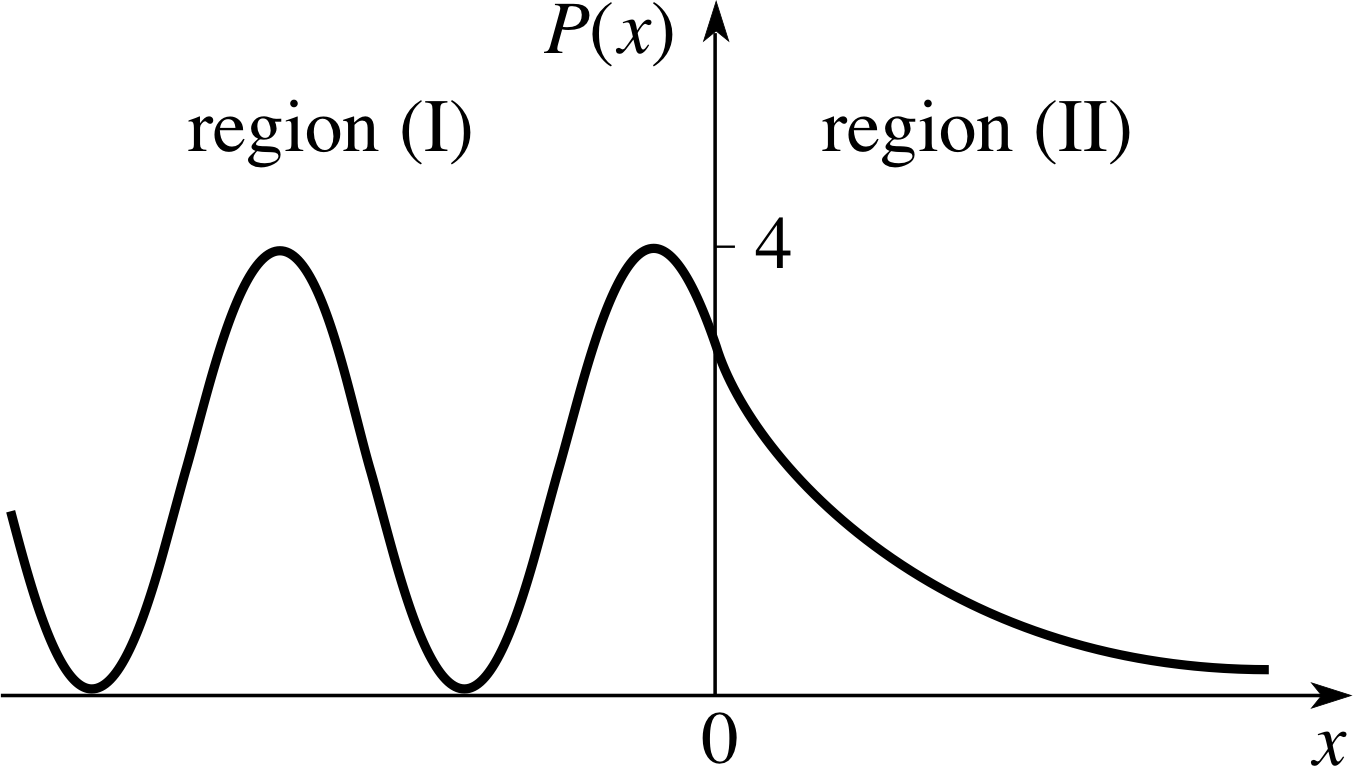
Figure 7 The density function P (x) in the region of a potential step at x = 0. The incident beam is from the left. The energy E of each particle is less than the height of the step V. In region (I), there is a pattern of maxima and minima due to the interference between incident and reflected waves of equal amplitude. In region (II), the density decreases exponentially.
Question T9
Why does the density function have a maximum of four particles per unit length in region (I) when the incident particle density is one per unit length?
Answer T9
In region (I), the incident and reflected waves interfere to produce an alternating pattern of maxima and minima. In an optical analogy, coherent beams would produce maxima and minima in light intensity, or maxima and minima in photon density. The incident and reflected waves have equal amplitudes, | A | = | B |, so that complete destructive interference takes place at the minima. The incident and reflected beams each have an average density of one particle per unit length so that the total density in region (I) must average two particles per unit length. The maxima must then be four if the minima are zero.
We can characterize the penetration of particles into region (II) by a distance D = 1/(2α). At this distance, the density, given by Equation 16 falls to 1/e of its value at x = 0:
P2(D) = P2(0) exp(−2αD) = P2(0) exp(−1) = P2(0)/e
The penetration depth is given in terms of E and V using Equation 13b,
in region (II)ψ2(x) = C exp(−αx)(Eqn 13b)
The penetration depth for particles incident on a potential step with E < V:
$D = \dfrac{1}{2\alpha} = \dfrac{\hbar}{2\sqrt{2m(V-E)\os}}$(17)
Question T10
A beam of electrons of energy 5 eV approaches a potential step of height 10 eV. Assume there is on average one incident particle per unit length. Calculate the following: (a) the average particle density at x = 0; (b) the point nearest the step where P1(x) is minimum; (c) the penetration depth D.
Answer T10
(a) Use Equation 15,
P1(x) = 2 + 2 cos(2k1x + 2ϕ)(Eqn 15)
to find P1(0):
P1(0) = 2 + 2 cos(2ϕ) with ϕ = arctan(α/k1)
We are given that E = 5 eV and V = 10 eV.
These numbers conveniently make α = k1, so using Equation 13b,
in region (II)ψ2(x) = C exp(−αx)(Equation 13b)
ϕ = π/4. Hence P1(0) = 2 + 2 cos(π/2) = 2.
(b) The minimum value of P1(x) occurs when the cosine term in Equation 15 has its minimum value of −1.
If cos(2k1x + 2ϕ) = −1, then 2k1x + 2ϕ = ±π, but ϕ = π/4, so x = −3π/4k1 (this is the minimum closest to the step).
Refer to Question T3 for the value of k1 at 5 eV:
$x = \rm \dfrac{-3\pi}{4\times1.15\times10^{10}\,m^{-1}} = -2.04\times10^{-10}\,m$
(c) The penetration depth is the distance into the step at which the particle density reduces to 1/e of its value at x = 0. Equation 17,
$D = \dfrac{1}{2\alpha} = \dfrac{\hbar}{2\sqrt{2m(V-E)\os}}$(Eqn 17)
gives:
$D = \dfrac{1}{2\alpha}\quad\text{where}\quad\alpha = \dfrac{\sqrt{2m(V-E)\os}}{\hbar}$
In this case, α = k1 = 1.15 × 1010 m−1, so that:
$D = \rm \dfrac{1}{2\times1.15\times10^{10}\,m^{-1}} = 0.43\times10^{-10}\,m$
This penetration depth is quite typical for problems at the atomic physics scale. It corresponds roughly to the size of a single atom and to the de Broglie wavelength of an electron with energy around 1 eV.
In this subsection, we have obtained two remarkable predictions of quantum mechanics. The predictions seem to defy common sense but they have been verified experimentally in many situations.
- Particles can penetrate into classically forbidden regions where V > E.
- Quantum-mechanical interference arises from a potential step and produces a regular set of points where the particle density is zero.
3.5 Reflection and transmission in the quantum model
The reflection coefficient R was defined in Subsection 2.6:
$R = \dfrac{\text{flux of reflected particles}}{\text{flux of incident particles}}$
The wavefunction in region (I) is:
ψ1(x) = A exp(ik1x) + B exp(−ik1x)
Equation 8 gives the incident flux $\vert\,A\,\rvert^2\hbar k/m$ and the reflected flux $\vert\,B\,\rvert^2\hbar k/m$. We have already demonstrated that when E < V, | B |2 = | A |2 (Equations 14), so that the reflected flux is equal to the incident flux and the reflection coefficient is one.
The reflection coefficient at a potential step with E < V:
R = 1(18)
This result agrees with the prediction of classical mechanics, but what can we say about the transmission coefficient? Particles can be observed across the step in the classically ‘forbidden’ region, but is there any flux? If particles are not to be created or destroyed at the boundary, then R + T = 1, and if R = 1, then T = 0. Even though particles are observed in region (II), there is no flux. Remember that the wavefunction ψ2(x) = C exp(−αx) is not an eigenfunction of momentum, and so does not represent a travelling wave with an associated momentum and an associated flux. Equation 8,
$F = \vert\,A\,\rvert^2\dfrac{\hbar k}{m}$(Eqn 8)
cannot be used to calculate flux since k is not defined.
The transmission coefficient at a potential step with E < V:
T = 0(19)
3.6 Summary of Sections 2 and 3
At a step where the potential energy increases by an amount V, classical mechanics makes definite predictions for the transmission and reflection of particles. If the total energy E of the incident particles is greater than V, then the particles are always transmitted across the step and are never reflected. If E is less than V, then the particles are always reflected and never transmitted.
When the distance over which the potential is changing is of the same order as, or smaller than, the de Broglie wavelength of the incident particles, then it is inappropriate to use classical mechanics. A quantum–mechanical treatment is required. Quantum mechanics makes some unexpected predictions which reveal the wave nature of particles in an interesting way. In the case E > V, there is always a finite probability that a particle will be reflected and the theory allows a calculation of the reflection and transmission coefficients, R and T:
$R = \left(\dfrac{k_1-k_2}{k_1+k_2}\right)^2$(Eqn 9)
$T = \dfrac{4k_1k_2}{(k_1+k_2)^2}$(Eqn 10)
In the case E < V, the quantum predictions for R and T agree with the classical predictions but there are important new features. There is always a finite probability of particles being found in the classically forbidden region beyond the step where the wavefunction has an exponential shape and the particle has no defined momentum. The theory allows a calculation of the penetration depth D in terms of E and V (Equation 17).
$D = \dfrac{1}{2\alpha} = \dfrac{\hbar}{2\sqrt{2m(V-E)\os}}$(17)

Figure 7 The density function P (x) in the region of a potential step at x = 0. The incident beam is from the left. The energy E of each particle is less than the height of the step V. In region (I), there is a pattern of maxima and minima due to the interference between incident and reflected waves of equal amplitude. In region (II), the density decreases exponentially.

Figure 4 The particle density function P (x) in the region of a potential step (E > V). In region (I), P (x) shows a pattern of alternating maxima and minima caused by the interference of the incident and reflected waves.
Critical elements in the theory are the selection of appropriate solutions of the Schrödinger equation in the regions before and after the potential step and the matching of the solutions at the boundary with both ψ (x) and dψ (x)/dx being continuous at the boundary.
The wave nature of material particles is made very clear by the appearance of ‘fringes’ caused by the interference of the incident and reflected waves. There is a regular pattern of points where the particle density is a minimum separated by points where the density is maximum (Figure 4 and Figure 7).
4 Reflection and transmission at a barrier when E < V
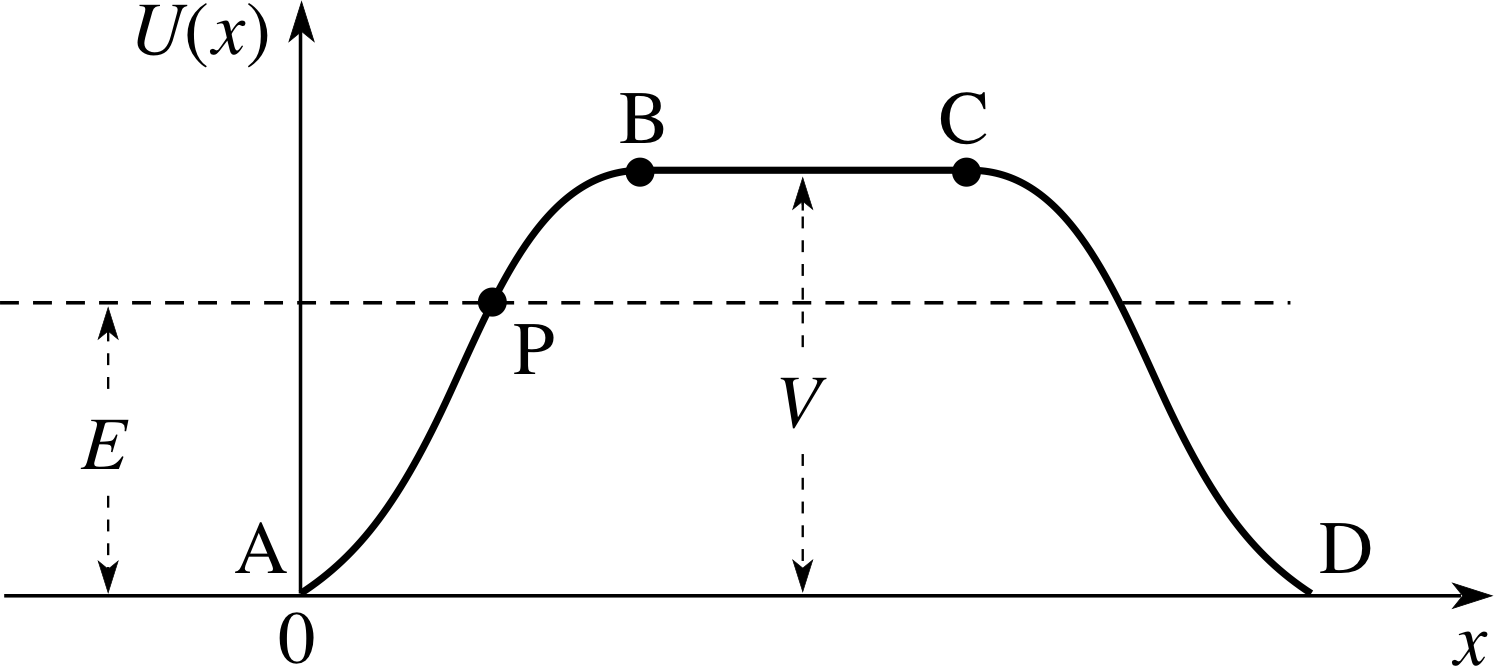
Figure 8 A potential barrier with height V. Particles with energy E are incident from the left and, according to classical theory, are reflected at the point P.
4.1 Classical description of the problem
We can now model a slightly more complicated physical situation by forming a potential barrier from two closely spaced steps. This is shown in Figure 8. The particles approach from the left and encounter first a negative force from point A to point B; from B to C there is no force, and from C to D there is a positive force. Particles with energy E < V will reach point P, according to classical mechanics, before being reflected back. The classical reflection coefficient for a barrier of this nature is one.
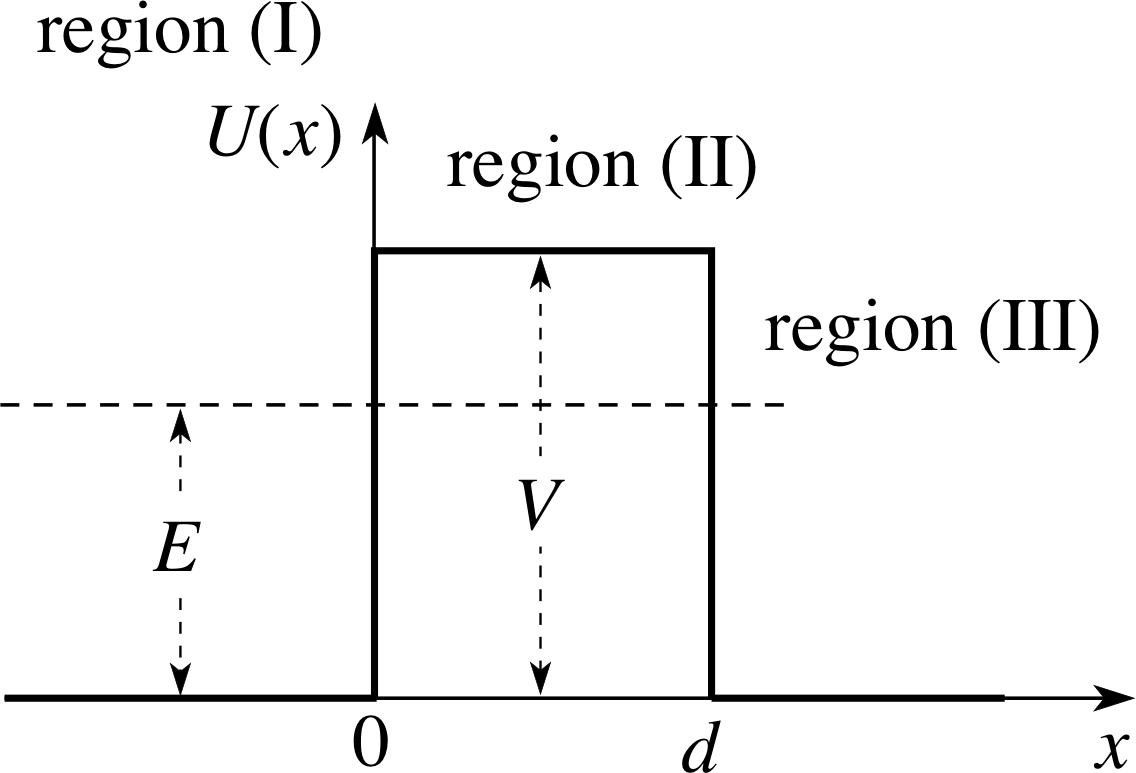
Figure 9 A schematic representation of a potential barrier width d. The energy E of each particle is less than the height of the barrier V.
4.2 The Schrödinger equation and the solutions in each region
A quantum treatment of this barrier problem is required if any of the distances AB, BC, CD in Figure 8 are of the same order as, or less than, the de Broglie wavelength of the incident particles. We will assume that the distances AB and CD are the ‘small’ ones and the barrier is then drawn schematically as in Figure 9.
In most physical situations, the width of the barrier, d, is greater than the de Broglie wavelength. The region x < 0 is designated (I), the region 0 ≤ x < d designated (II) and the region x ≥ d designated (III).
As usual, particles are incident on the barrier from the left with energy E. The solutions of the Schrödinger equation in regions (I) and (III), where the potential is zero, have the same form. You can refer back to Subsection 2.2 and Equation 2,
ψ1(x) = A exp(ik1x) + B exp(−ik1x)(Eqn 2)
i.e.
in region (I)ψ1 (x) = A exp(ikx) + B exp(−ikx)
in region (III)ψ3 (x) = G exp(ikx) + H exp(−ikx)
with$k = \dfrac{\sqrt{2mE\os}}{\hbar}$
We can immediately put H = 0 because particles cannot return from infinity. The general solution to the Schrödinger equation in region (II), where E < V, was derived in Subsection 3.2:
in region (II)ψ2(x) = C exp(−αx) + D exp(αx)
with$\alpha = \dfrac{\sqrt{2m(V-E)\os}}{\hbar}$
Notice that we have included the rising exponential term here because region (II) does not extend to infinity.
In summary, we have the general forms of the wavefunctions in the three regions:
in region (I)ψ1(x) = A exp(ikx) + B exp(−ikx)(20a)
in region (II)ψ2(x) = C exp(−αx) + D exp(αx)(20b)
in region (III)ψ3 (x) = G exp(ikx)(20c)
with$k = \dfrac{\sqrt{2mE\os}}{\hbar}\quad\text{and}\quad\alpha = \dfrac{\sqrt{2m(E-V)\os}}{\hbar}$
4.3 Relationships imposed by the boundary conditions
The situation now seems to be getting out of hand with five arbitrary complex constants and the boundary conditions to be applied at x = 0 and x = d. Matching the wavefunctions and their derivatives at the boundaries gives us four independent simultaneous equations which can, in principle, be solved for the four ratios B/A, C/A, D/A, and G/A. This piece of algebraic manipulation is extremely tedious, and we will not bore you with the details. We are interested mainly in the constant G because this tells us what the transmission coefficient is. We will quote the result and not even ask you to confirm it!
$\dfrac GA = \dfrac{4k\alpha\exp(-\alpha d)}{(k+i\alpha)^2 - (k-i\alpha)^2\exp(-2\alpha d)}$
Now look closely at the denominator of this expression. We have already stated that the width of the barrier d is usually much greater than the de Broglie wavelength of the incident particles. This in turn makes the argument of the exponential large and the second term in the denominator negligibly small compared with the first term. To a very good approximation, we have the following expression:
$\dfrac GA = \dfrac{4k\alpha\exp(-\alpha d)}{(k+i\alpha)^2}$(21)
This can be rewritten more conveniently as:
$\dfrac GA = \dfrac{4\exp(-\alpha d)\exp(-2i\phi)}{(k/\alpha+\alpha/k)^2}$(22)
Question T11
Show that Equation 21 can be written in the form of Equation 22.
What is the modulus of G/A when α = k?
Answer T11
Start with Equation 21,
$\dfrac GA = \dfrac{4k\alpha\exp(-\alpha d)}{(k+i\alpha)^2}$(Eqn 21)
and write the denominator in polar form:
$k + i\alpha = \sqrt{k^2 + \alpha^2}\exp(i\phi)$ with ϕ = arctan(α/k)
Therefore :
$\dfrac GA = \dfrac{4k\alpha\exp(-\alpha d)\exp(-2i\phi)}{(k^2+\alpha^2)} = \dfrac{4\exp(-\alpha d)}{(k/\alpha+\alpha/k)}\exp(-2i\phi)$
as required.
$\dfrac{\lvert\,G\,\rvert}{\lvert\,A\,\rvert} = \dfrac{4\exp(-\alpha d)}{(k/\alpha+\alpha/k)}$
When α = k, | G | / | A | = 2 exp(−kd) and | G | = 2 | A | exp(−kd).
The presence of the exponential factor exp(−αd) in the numerator of Equation 22 ensures that | G | / | A | is very small and very sensitive to the value of d.
We can now make similar approximations in region (II), and we find that the wavefunction is dominated by the falling exponential term, ψ2(x) = C exp(−αx), and the rising exponential makes a negligible contribution. The ratios B/A and C/A are then to a good approximation the same as for the potential step (Equations 14 in Subsection 3.3). In summary, we have the following results:
$\dfrac BA \approx \dfrac{k-i\alpha}{k+i\alpha} = \exp(-2i\phi)$and $\dfrac{\lvert\,B\,\rvert}{\lvert\,A\,\rvert}\approx 1$(23a)
$\dfrac CA \approx \dfrac{2k}{k+i\alpha} = 2\cos\phi \exp(-i\phi)$and $\dfrac{\lvert\,C\,\rvert}{\lvert\,A\,\rvert}\approx 2\cos\phi$(23b)
$\dfrac DA \approx 0$(23c)
$\dfrac GA = \dfrac{4\exp(-\alpha d)}{(k/\alpha+\alpha/k)^2}\exp(-2i\phi)$and $\dfrac{\lvert\,G\,\rvert}{\lvert\,A\,\rvert} \approx \dfrac{4\exp(\alpha d)}{k/\alpha + \alpha/k}$(23d)
with$\tan\phi = \dfrac{\alpha}{k}$
4.4 The wavefunctions in each region and the physical interpretation
The wavefunctions in the three regions are given by Equations 20, with the ratios of the constants given by Equations 23. Remember that we have made the assumption that the width of the barrier is much greater than the de Broglie wavelength. In region (I), the particles are represented by travelling waves, the incident particles by A exp(ikx) and the reflected particles by B exp(−ikx). The density of the reflected particles, | B |2, is almost equal to the density of the incident particles, | A |2, since | B/A | ≈ 1. In the classically forbidden region (II), the wavefunction is dominated by the falling exponential so that the density of particles is given approximately by | ψ2(x) |2 = | C |2 exp(−2αx). Finally, in region (III), the transmitted particles are represented by the travelling wave G exp(ikx), where | G | is much smaller than | A |. The density of the transmitted particles is consequently very much smaller than the density of the incident particles.
Quantum mechanics unambiguously predicts that particles can tunnel through a potential barrier and can be observed with reduced density but with their original momentum. This process is known as quantum tunnelling.
Question T12
Show that the density of particles in region (III) is constant and is given by $16\times\lvert\,A\,\rvert^2\dfrac{\exp(-2\alpha d)}{(k/\alpha+\alpha/k)^2}$.
Answer T12
The density of particles in region (III) is given by P3(x) = ψ3*(x) ψ3(x), where ψ3(x) = G exp(ikx).
ThereforeP3(x) = G* exp(−ikx) G exp(ikx) = | G |2 exp 0 = | G |2
Using Equation 23,
$\dfrac GA = \dfrac{4\exp(-\alpha d)}{(k/\alpha+\alpha/k)}\exp(-2i\phi)$(Eqn 23)
and
$\dfrac{\lvert\,G\,\rvert}{\lvert\,A\,\rvert} = \dfrac{4\exp(-\alpha d)}{(k/\alpha+\alpha/k)}$
we get: $P_3(x) = \dfrac{\lvert\,A\,\rvert^2 16\exp(-2\alpha d)}{(k/\alpha+\alpha/k)}$ as required.
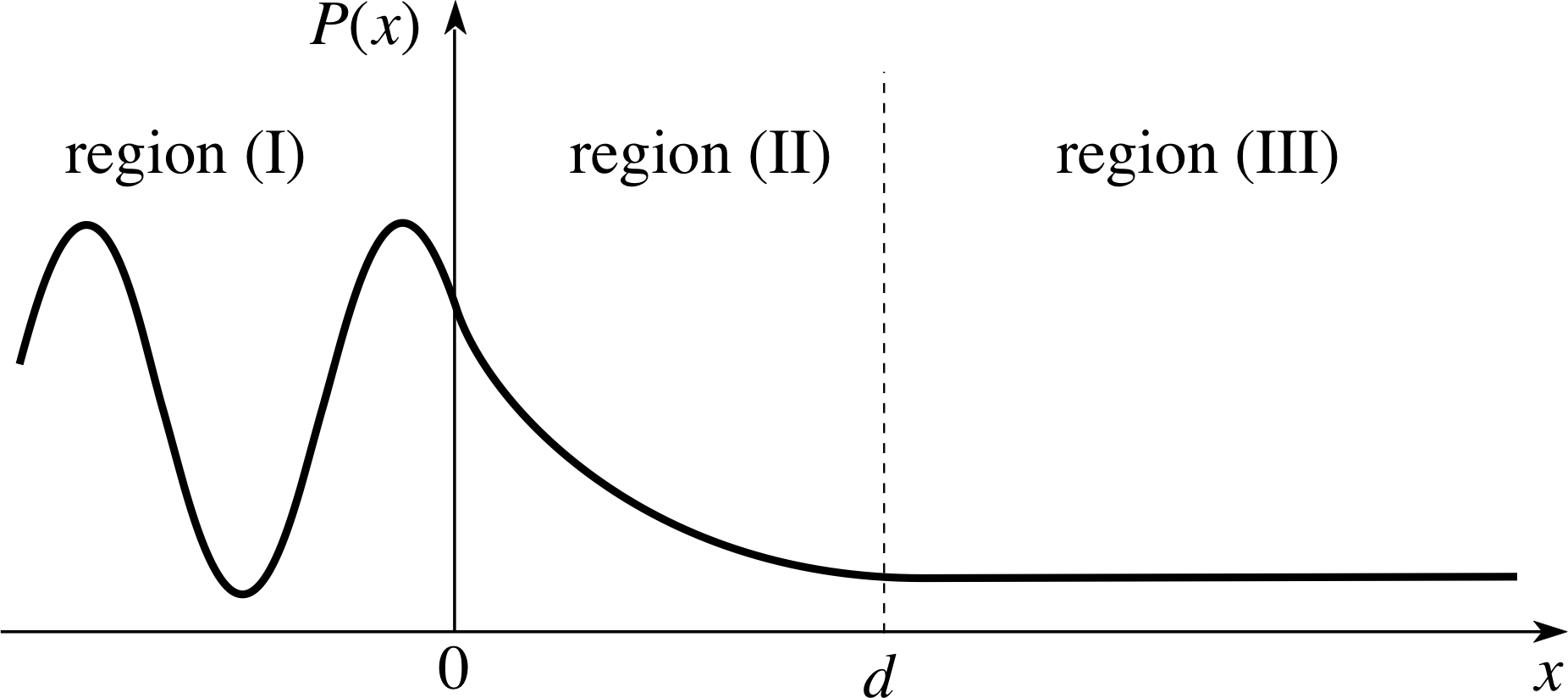
Figure 10 The particle density function P (x) near a potential barrier of height V. Particles are incident from the left, each with energy E less than V.
All these facts can be neatly represented by the graph of the density function P (x) = | ψ (x) |2 shown in Figure 10. The form of P (x) in regions (I) and (II) is very similar to that shown in Figure 7 for the potential step, because of the realistic approximations described in Subsection 4.3, so there is no need to repeat the calculations. In region (I), there is an almost perfect pattern due to the interference between incident and reflected waves of almost equal amplitude. At the boundary, x = d, P (x) has not quite fallen to zero and joins smoothly to its constant value in region (III). i
4.5 Transmission in the quantum model

Figure 9 A schematic representation of a potential barrier width d. The energy E of each particle is less than the height of the barrier V.
The method for finding the particle fluxes and hence the reflection and transmission coefficients follows from Equation 8,
$F = \lvert\,A\,\rvert^2\dfrac{\hbar k}{m}$(Eqn 8)
and the pattern set in Subsections 2.6 and 3.5. The transmission coefficient for the potential barrier illustrated in Figure 9 is given by:
$T = \dfrac{\text{flux of transmitted particles}}{\text{flux of incident particles}}$
The incident flux in region (I) is given by $\vert\,A\,\rvert^2\hbar k/m$ and the transmitted flux in region (III) by $\vert\,G\,\rvert^2\hbar k/m$. Consequently:
$T = \dfrac{\vert\,G\,\rvert^2}{\vert\,A\,\rvert^2}$
Equation 21,
$\dfrac GA = \dfrac{4k\alpha\exp(-\alpha d)}{(k+i\alpha)^2}$(Eqn 21)
gives the constant G in terms of A, and from this we can get the square modulus of G (see, for example, Question T12):
$\lvert\,G\,\rvert^2 = \dfrac{\lvert\,A\,\rvert^2 16\exp(-2\alpha d)}{(k/\alpha+\alpha/k)^2}$
It follows immediately that:
The transmission coefficient for a potential barrier :
$T \approx \dfrac{16\exp(-2\alpha d)}{(k/\alpha+\alpha/k)^2}$(24)
In many applications, the incident particle angular wavenumber k, and the factor α which characterizes the wavefunction inside the barrier, are the same order of magnitude. The denominator then takes a value of about 4, and the transmission coefficient has the approximate value:
An approximate value for the transmission coefficient when k ≈ α
T ≈ 4 exp(−αd)(25)
where $\alpha = \sqrt{2m(V-E)\os}{\hbar}$ and d is the barrier width.
This is a good equation to remember, because it usually gives a good estimate of the transmission coefficient of a barrier. The most important factor in calculating T is the exponential; remember that exponential functions can change by orders of magnitude for relatively small changes in the argument.
The reflection coefficient of the barrier R is of course very close to one because T is small with the approximations we have used. Application of the approximate formulae for | B | / | A | given in Equations 23, also gives R ≈ 1; a better approximation is obtained by using Equation 25 and putting R = 1 − T.
We can show that the phenomenon of barrier penetration is consistent with the Heisenberg uncertainty principle $\Delta E\,\Delta t \approx \hbar$.
The Heisenberg uncertainty principle tells us that a particle can ‘borrow’ energy ∆E sufficient to surmount the barrier provided it ‘repays’ the debt in a time ∆t of order $\hbar/\Delta E$. The value of ∆E is given by V − E. Let us assume a typical barrier of width d = 2/α so that T ≈ 4 exp(−4) = 0.07 (using Equation 25).
We estimate ∆t from the speed of the particle:
$\Delta t \approx \dfrac{d}{\upsilon}\quad\text{and}\quad\upsilon = \dfrac pm = \dfrac{\hbar k}{m}$
Hence$\Delta t \approx \dfrac{2/\alpha}{\hbar k/m} = \dfrac{2m}{\hbar k\alpha}$
However$\alpha = \dfrac{\sqrt{2m(E-V)\os}}{\hbar}\quad\text{and}\quad k = \dfrac{\sqrt{2mE\os}}{\hbar}$
Substituting these gives $\Delta t \approx \dfrac{\hbar}{\sqrt{E-V\os}}$
Both E and V − E are of the same order of magnitude, so that:
$\Delta t \approx \dfrac{\hbar}{V-E} \approx \dfrac{\hbar}{\Delta E}$
which is the required relation.
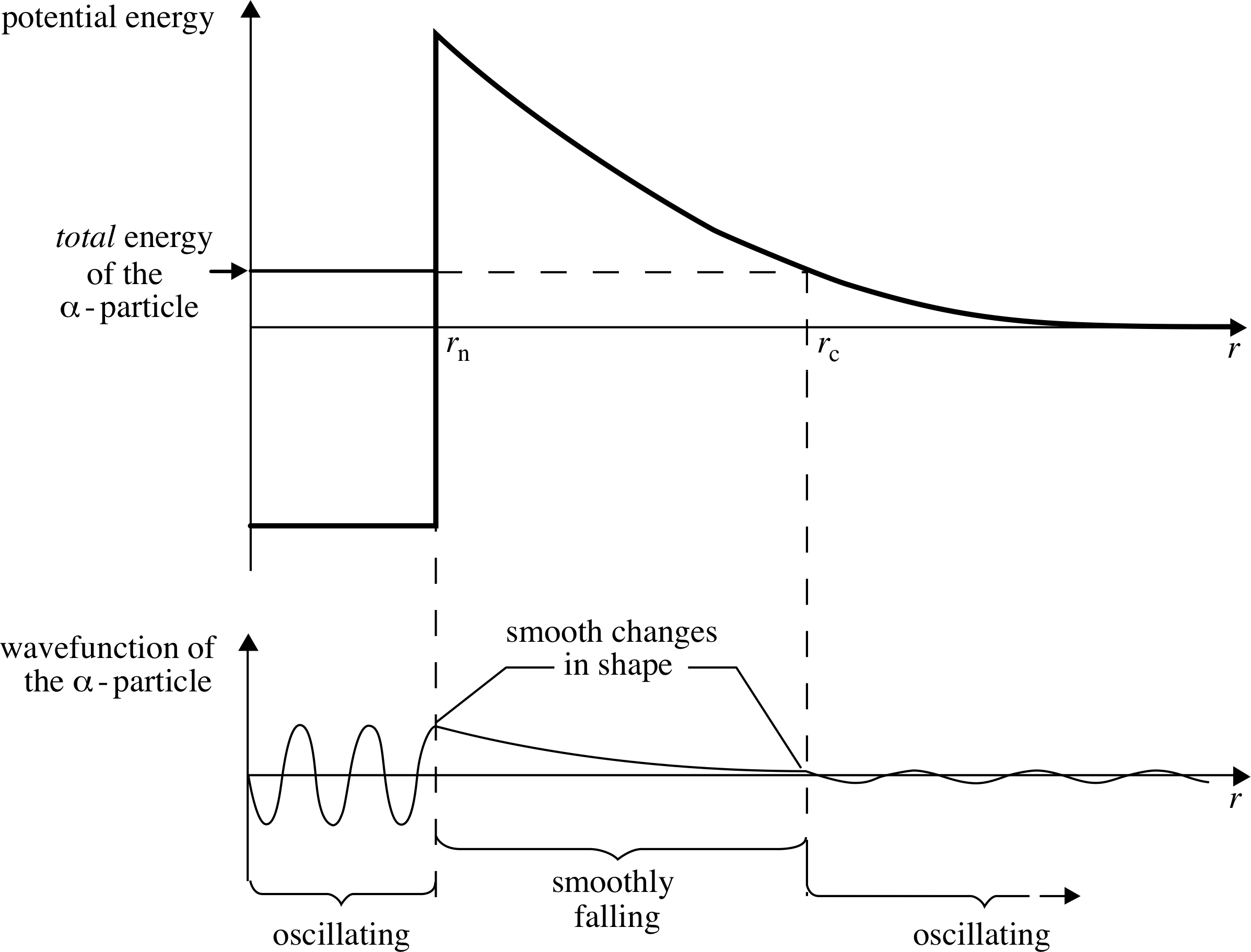
Figure 11 The potential barrier ‘seen’ by an α -particle in a radioactive nucleus.
4.6 Examples of quantum tunnelling
The idea of tunnelling was first used to explain α–decay in radioactive nuclei. α -particles may be formed within a nucleus. In heavy nuclei they may be formed with enough energy to escape. i They are held within the nucleus by a potential barrier which consists of an attractive part (due to nuclear forces), and a repulsive part (due to the electrostatic repulsion between the α–particle and the residual nucleus), as shown schematically in Figure 11.
This combination produces a potential well in which in which the α–particle is trapped. Notice that the energy is positive and states of this same energy exist outside the potential well of the nucleus, so the α–particle can tunnel out of its potential well and escape from the nucleus. This is alpha_decayα–decay.
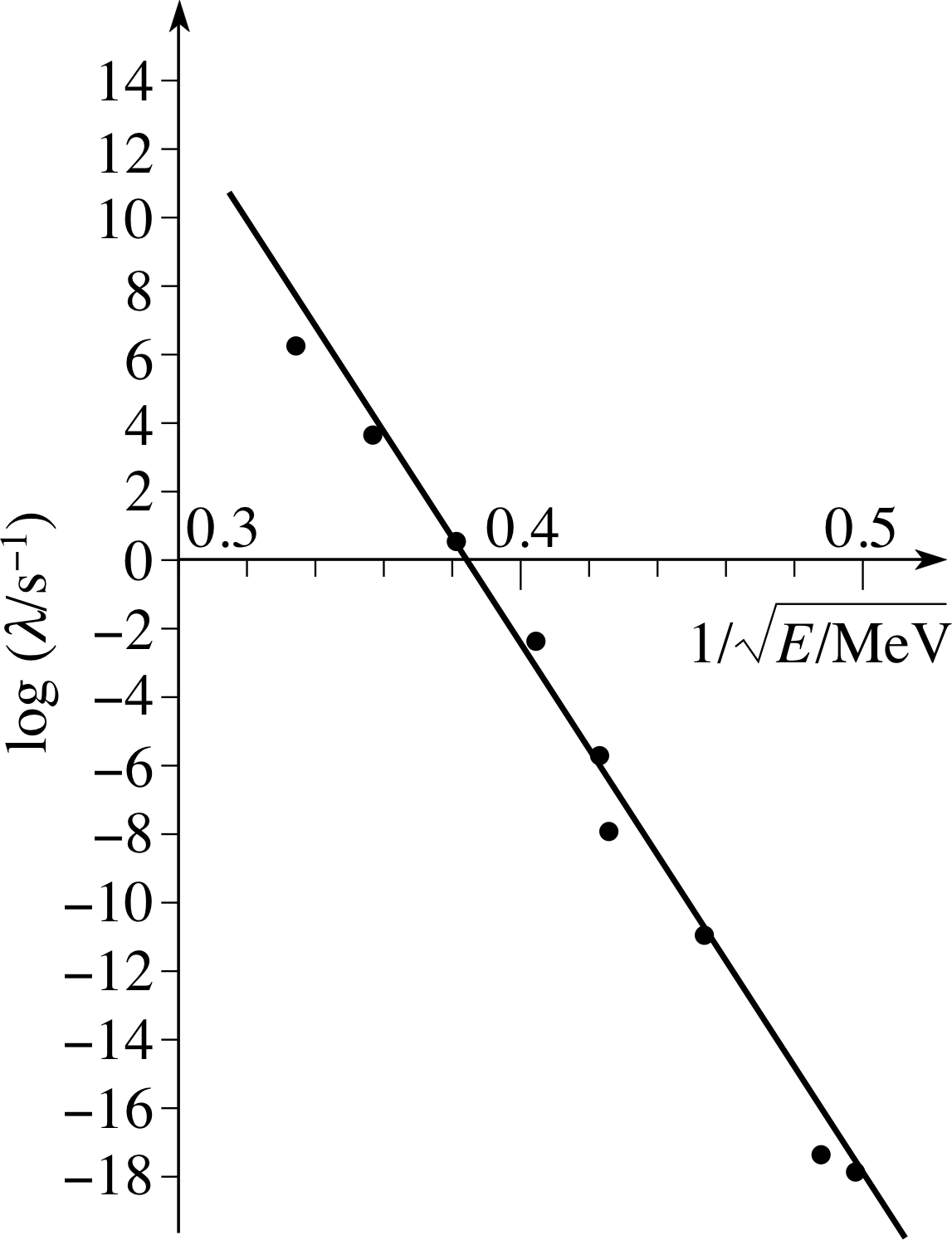
Figure 12 The variation in decay rate with α–particle energy for a number of radioactive nuclei.
The shape of the barrier is more complex than we have envisaged so far, but it should be clear that the higher the energy of the α–particle, the more likely it will be to penetrate the barrier, both directly because of the increased energy, and indirectly because of the decreased width of the barrier. These two effects lead to an extremely wide variation in decay rates for a relatively small change in energy. Figure 12 shows a variation of a factor 1024 in decay rates λ for a change of a factor 2 in energy. i
This same idea, used in reverse, suggested to Cockcroft and Walton that it would be possible to induce nuclear reactions using low–energy protons (about 0.5 MeV) without sufficient energy to overcome the electrostatic repulsion. This began the whole study of nuclear physics using particle accelerators.
The same process is involved in the nuclear reactions that supply the Sun’s energy. The principal reaction here involves the eventual formation of helium by the fusion of hydrogen nuclei (protons). It is essential to take tunnelling into account to be able to explain the rate of energy production. In laboratory fusion experiments the same principle allows nuclear fusion at attainable temperatures.

Figure 9 A schematic representation of a potential barrier width d. The energy E of each particle is less than the height of the barrier V.
An example of quantum tunnelling occurs when an electric current passes through a junction made by twisting two copper wires together. The surface of the copper, unless it is newly cleaned, is always covered with a thin layer of oxide – an insulator – so that in classical physics no current would flow; the potential energy of the electrons varies in the same way as in Figure 9. However, since the oxide layer is very thin, it is possible for electrons to tunnel through the barrier.
A development of this idea is the tunnel diode; in this device, the height of the potential barrier between two semiconductors is controlled externally, and the physical size of the junction is so small that the flow of electrons can be turned on or off very rapidly, within a few picoseconds. Further developments using superconductors have led to the Josephson junction and the SQUID (semiconducting quantum interference device), which can measure magnetic fields as small as 10−15 T.
The scanning tunnelling electron microscope was developed by Binnig and Rohrer, who were awarded the Nobel Prize in 1986. This remarkable device works by the tunnelling of electrons from the surface of a sample to the tip of a very fine needle. It is so sensitive that the detail of the surface can be resolved to distances much less than an atomic radius.
4.7 Summary of Section 4

Figure 10 The particle density function P (x) near a potential barrier of height V. Particles are incident from the left, each with energy E less than V.
This section describes one of the most powerful predictions of quantum mechanics. We have seen that material particles can penetrate into classically forbidden regions due to their wave nature. Here we go further and show that particles can penetrate through classically forbidden barriers (Figures 8 and 9). In most realistic situations, the width of the barrier is such that the transmission coefficient is small and considerable simplifications can be made in the theory. The nature of the particle wavefunctions is described in the regions before the barrier, inside the barrier and after the barrier. Matching the wavefunctions at the two boundaries allows the particle density ratios to be calculated. A graph of the particle density function near the barrier is given in Figure 10. Three features are important:
- The interference pattern due to the incident and reflected waves;
- The exponential decay within the barrier;
- The constant density beyond the barrier.
Finally, good approximations are derived for the transmission coefficient T. In our approximation, T is dominated by the exponential factor exp(−2αd).
5 Closing items
5.1 Module summary
- 1
-
A particle with kinetic energy E approaches a step where the potential increases by V. Classical mechanics predicts that if E > V then the particle will always pass over the step.
- 2
-
If the dimensions of the step are of the same order or less than the de Broglie wavelength of the incident particle, then quantum mechanics rather than classical mechanics must be used.

Figure 2 A schematic representation of a potential step. The distance over which the force acts is assumed to be negligible. The total energy of the particle is E.
- 3
-
A potential step where E > V is shown in Figure 2. The solutions of the Schrödinger equation are:
in region (I)ψ1 (x) = A exp(ik1x) + B exp(−ik1x)(Eqn 4a)
in region (II)ψ2 (x) = C exp(ik2x)Eqn (4b)
with$k_2 = \sqrt{2mE\os}/\hbar\quad\text{and}\quad k_2 = \sqrt{2m(E-V)\os}/\hbar$
The ratios of the coefficients are determined by boundary conditions. The wavefunction i and its slope must both be continuous at x = 0. This gives:
$\dfrac BA = \dfrac{k_1-k_2}{k_1+k_2}$(Eqn 7a)
$\dfrac CA = \dfrac{2k_1}{k_1+k_2}$(Eqn 7b)
- 4
-
The wavefunction ψ1(x) represents the incident particles, with density | A |2 per unit length, moving with momentum $\hbar k_1$ in the positive x–direction, and the reflected particles, with density | B |2 moving with momentum $-\hbar k_1$. The wavefunction ψ2(x) represents the transmitted particles, of density | C |2, moving with momentum $\hbar k_2$.
- 5
-
For a wavefunction ψ (x) = A exp(ikx), which is a momentum eigenfunction, the flux of particles is given by
$F = \vert\,A\,\rvert^2\dfrac{\hbar k}{m}$(Eqn 8)
- 6
-
At a potential step, the reflection coefficient R and the transmission coefficient T are defined:
$R = \dfrac{\text{flux of reflected particles}}{\text{flux of incident particles}}\quad\text{and}\quad T = \dfrac{\text{flux of transmitted particles}}{\text{flux of incident particles}}$

Figure 4 The particle density function P (x) in the region of a potential step (E > V). In region (I), P (x) shows a pattern of alternating maxima and minima caused by the interference of the incident and reflected waves.
If E > V, quantum mechanics predicts:
$R = \left(\dfrac{k_1-k_2}{k_1+k_2}\right)^2$(Eqn 9)
$T = \dfrac{4k_1k_2}{(k_1+k_2)^2}$(Eqn 10)
As expected R + T = 1. The prediction that R > 0 when E > V is a direct contradiction of classical mechanics.
- 7
-
The wave nature of particles is demonstrated by the particle density function P (x) in region (I), which shows the interference between the incident and reflected waves (Figure 4).
- 8
-

Figure 5 The function U (x) at a potential step. The height of the step V is greater than the energy E of each incident particle. According to classical mechanics, the particles reach the point P and are then reflected back.
A potential step where E < V is shown in Figure 5. The solutions of the Schrödinger equation are:
in region (I)ψ1(x) = A exp(ik1x) + B exp(−ik1x)(Eqn 13a)
in region (II)ψ2(x) = C exp(−αx)(Eqn 13b)
with$k_1 = \sqrt{2mE\os}/\hbar\quad\text{and}\quad\alpha = \sqrt{2m(V-E)\os}/\hbar$
The ratios of the constants are given by the boundary conditions at x = 0:
$\dfrac BA = \dfrac{k_1-i\alpha}{k_1+i\alpha} = \exp(-2i\phi)$so that$\dfrac{\lvert\,B\,\rvert}{\lvert\,A\,\rvert} = 1$(Eqn 14a)
$\dfrac CA = \dfrac{2k_1}{k_1+i\alpha} = 2\cos\phi\exp(-\phi)$so that $\dfrac{\lvert\,C\,\rvert}{\lvert\,A\,\rvert} = 2\cos\phi$(Eqn 14b)
with$\phi = \arctan\left(\dfrac{\alpha}{k_1}\right)$
- 9
-

Figure 7 The density function P (x) in the region of a potential step at x = 0. The incident beam is from the left. The energy E of each particle is less than the height of the step V. In region (I), there is a pattern of maxima and minima due to the interference between incident and reflected waves of equal amplitude. In region (II), the density decreases exponentially.
In region (I), the wavefunction ψ1(x) represents the incident and reflected particles with the same density, | B |2 = | A |2.
In region (II), the wavefunction ψ2(x) is not a momentum eigenfunction and there is no flux of particles. The particle density function P (x) (Figure 7) shows a perfect interference pattern in region (I) and joins smoothly to the falling exponential in region (II). There is a finite probability of particles being observed in the classically forbidden region: P2(x) = 4 cos2 ϕ exp(−2αx). At the penetration depth D = 1/(2α), the particle density is 1/e of its value at x = 0.
- 10
-
The reflection coefficient at the step where E < V is given by:
$R = \dfrac{\lvert\,B\,\rvert^2}{\lvert\,A\,\rvert^2} = 1$(Eqn 18)
This agrees with the classical prediction.
- 11
-

Figure 9 A schematic representation of a potential barrier width d. The energy E of each particle is less than the height of the barrier V.
A potential barrier with width d and V > E is shown schematically in Figure 9. The distances over which the potential is increasing or decreasing are assumed to be smaller than the de Broglie wavelength of the incident particles. The solutions of the Schrödinger equation are
in region (I)ψ1(x) = A exp(ikx) + B exp(−ikx)(Eqn 20a)
in region (II)ψ2(x) = C exp(−αx) + D exp(αx)(Eqn 20b)
in region (III)ψ3 (x) = G exp(ikx)(Eqn 20c)
with$k = \dfrac{\sqrt{2mE\os}}{\hbar}\quad\text{and}\quad\alpha = \dfrac{\sqrt{2m(E-V)\os}}{\hbar}$
The ratios of the constants are given by matching the wavefunctions and their slopes at the two boundaries.
With the assumption that d ≫ 1/α, the following approximations are valid:
$\dfrac BA \approx \dfrac{k-i\alpha}{k+i\alpha} = \exp(-2i\phi)$and $\dfrac{\lvert\,B\,\rvert}{\lvert\,A\,\rvert}\approx 1$(Eqn 23a)
$\dfrac CA \approx \dfrac{2k}{k+i\alpha} = 2\cos\phi \exp(-i\phi)$and $\dfrac{\lvert\,C\,\rvert}{\lvert\,A\,\rvert}\approx 2\cos\phi$(Eqn 23b)
$\dfrac DA \approx 0$(Eqn 23c)
$\dfrac GA = \dfrac{4\exp(-\alpha d)}{(k/\alpha+\alpha/k)^2}\exp(-2i\phi)$and $\dfrac{\lvert\,G\,\rvert}{\lvert\,A\,\rvert} \approx \dfrac{4\exp(\alpha d)}{k/\alpha + \alpha/k}$(Eqn 23d)
with$\tan\phi = \dfrac{\alpha}{k}$
- 12
-

Figure 10 The particle density function P (x) near a potential barrier of height V. Particles are incident from the left, each with energy E less than V.
In region (I), the wavefunction ψ1(x) represents both the incident and reflected particles with approximately the same density. In region (II), the wavefunction ψ2(x) is not a momentum eigenfunction. In region (III), the wavefunction ψ3(x) represents the transmitted particles. The density function P (x) (Figure 10) shows a typical interference pattern in region (I), falls exponentially in region (II) and joins smoothly to the constant value | G |2 in region (III).
- 13
-
The transmission coefficient at a barrier where V > E is given by T = | G |2/| A |2 so that:
$T \approx \dfrac{16\exp(-2\alpha d)}{(k/\alpha+\alpha/k)^2}$(Eqn 24)
When α and k are of the same order of magnitude, a good approximation is T ≈ 4 exp(−2αd). The transmission coefficient is normally much less than one so that the reflection coefficient R ≈ 1.
- 14
-
Subsection 4.6Quantum tunnelling also allows particles to tunnel into or out of a potential well. Such processes are responsible for nuclear fusion and also allow many technological developments.
5.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Describe the motion of a particle at a potential step using classical mechanics. Identify the circumstances when quantum mechanics should be used rather than classical mechanics.
- A3
-
Recall the form of the solutions of the Schrödinger equation for particles of energy E encountering an idealized potential step when E > V. Interpret the solutions in terms of the density and flux of the incident, reflected and transmitted particles.
- A4
-
Recall conditions on the wavefunctions at a boundary, and use the conditions to determine the relations between the constants appearing in the wavefunctions.
- A5
-
Derive expressions for the transmission and reflection coefficients at a potential step when E > V. Compare and contrast the predictions of quantum and classical mechanics.
- A6
-
Recall the form of the solutions of the Schrödinger equation for particles of energy E encountering an idealized potential step when E < V. Interpret the solutions in terms of the density and flux of the incident and reflected particles. Explain how these solutions predict that particles can penetrate into the classically forbidden region.
- A7
-
Use the theory to confirm that the reflection coefficient for a step is unity when E < V, in agreement with classical theory.
- A8
-
Recall the form of the solutions of the Schrödinger equation for particles of energy E < V encountering an idealized potential barrier of width d. Interpret the solutions in terms of the density and flux of the incident, reflected and transmitted particles.
- A9
-
Use the approximate formula for the transmission coefficient through a potential barrier.
- A10
-
Use the quantum theory results to calculate fluxes of particles transmitted by, and reflected from, specified steps and barriers.
- A11
-
Outline the use of barrier penetration, or tunnelling, in different physical situations.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
5.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions, each of which tests one or more of the Achievements.
Note We have used electron beams with energies in the eV region to illustrate the general principles of quantum mechanics applied to steps and barriers. This is an attempt to keep to a minimum the amount of repetitive arithmetic in the questions. You should be fully aware that similar examples can be generated using nuclear particles (e.g. protons or α–particles) with energies in the MeV region and lengths of the order of 10−15 m.
Question E1 (A2 and A10)
A beam of electrons, each with kinetic energy 5 eV, is incident on a step where the potential energy decreases by 2.5 eV. Calculate the transmission and reflection coefficients in the quantum model. What does classical mechanics predict? How can you decide which theory of mechanics to use?
Answer E1
You can find either the reflection coefficient or the transmission coefficient using Equation 9 or Equation 10,
$R = \left(\dfrac{k_1-k_2}{k_1+k_2}\right)^2$(Eqn 9)
$T = \dfrac{4k_1k_2}{(k_1+k_2)^2}$(Eqn 10)
then use R + T = 1.
Start with Equation 9 with:
$k_1 = \dfrac{\sqrt{2mE\os}}{\hbar}\quad\text{and}\quad k_2 = \dfrac{\sqrt{2m(E-V)\os}}{\hbar}$
Note, you didn’t need to rush into unnecessary calculations!
We have E = 5 eV and V = −2.5 eV, so that E − V = 1.5E.
Hence:$R = \left(\dfrac{\sqrt{E\os} - \sqrt{1.5E\os}}{\sqrt{E\os}+\sqrt{1.5E\os}}\right)^2 = \left(\dfrac{1-\sqrt{1.5\os}}{1+\sqrt{1.5\os}}\right)^2 = 0.01$
but R + T = 1, so that T = 1 − 0.01 = 0.99.
So 1% of the electrons are reflected and 99% of the electrons are transmitted at this falling step. The classical theory predicts that 100% of the electrons are transmitted. Quantum theory must be used if the distance over which the potential changes is of the same order or less than the de Broglie wavelength of the particles.
(Reread Subsection 2.6 if you had difficulty with this question.)
Question E2 (A4, A5 and A7)
Explain qualitatively how the boundary conditions on wavefunctions lead to Equations 5 and 6,
A + B = C(Eqn 5)
Ak1 − Bk1 = Ck2(Eqn 6)
Verify Equations 7,
$\dfrac BA = \dfrac{k_1-k_2}{k_1+k_2}$(Eqn 7a)
$\dfrac CA = \dfrac{2k_1}{k_1+k_2}$(Eqn 7b)
from Equations 5 and 6, and derive expressions for the transmission and reflection coefficients when V < E.
Show that for a potential step with V > E the ratio
$\dfrac BA = \dfrac{k_10i\alpha}{k_1+i\alpha}\quad\text{where}\quad\alpha = \dfrac{\sqrt{2m(V-E)\os}}{\hbar}$
Hence show that | B | = | A | and the reflection coefficient is one.
Answer E2

Figure 3 Boundary conditions at x = 0. Only (c) is allowed. (a) ψ1 ≠ ψ2, (b) ψ1 = ψ2 but dψ1/dx ≠ dψ2/dx, (c) ψ1 = ψ2 and dψ1/dx = dψ2/dx.
Refer to Figure 3 and to Equations 4:
in region (I)ψ1 (x) = A exp(ik1x) + B exp(−ik1x)(4a)
in region (II)ψ2 (x) = C exp(ik2x)(4b)
The wavefunctions must obey the following conditions if the potential energy is finite. First, the wavefunction itself must be continuous everywhere, and second, the derivative or slope of the wavefunction must be continuous. This means that at the boundary, x = 0, between regions (I) and (II):
$\psi_1(0) = \psi_2(0)\quad\text{and}\quad\left.\dfrac{d\psi_1(x)}{dx}\right\rvert_{x=0} = \left.\dfrac{d\psi_2(x)}{dx}\right\rvert_{x=0}$
So we have two equations to solve for the two ratios B/A and C/A.
Start with Equations 5 and 6: A + B = C and Ak1 − Bk1 = Ck2.
Substitute for C:
(A − B)k1 = (A + B)k2
soA (k1 − k2) = B (k1 + k2)
i.e.$\dfrac BA = \dfrac{k_1 - k_2}{k_1+k_2}$ as required.
Substitute for B:
$A + A\left(\dfrac{k_1 - k_2}{k_1+k_2}\right) = C$
soA (k1 + k2 + k1 − k2) = C (k1 + k2)
i.e.$\dfrac CA = \dfrac{2k_1}{k_1+k_2}$ as required.
The reflection and transmission coefficients follow immediately using the arguments leading up to Equations 9 and 10:
$R = \dfrac{\lvert\,B\,\rvert^2}{\lvert\,A\,\rvert^2} = \left(\dfrac{k_1 - k_2}{k_1+k_2}\right)^2\quad\text{and}\quad T = \dfrac{\lvert\,C\,\rvert^2k_2}{\lvert\,A\,\rvert^2k_1} = \dfrac{4k_1k_2}{(k_1+k_2)^2}$
When V > E, the angular wavenumber k2 is purely imaginary, so we make the substitution k2 = iα with α real
and positive. The result | B | = | A | follows immediately, since
| B | = | k1 − iα | = k12 + α2 and | A | = | k1 + iα | = k12 + α2
and in consequence R = 1.
(Reread Subsections 2.3, 3.2 and 3.3 if you had difficulty with this question.)
Question E3 (A3)
Find a suitable wavefunction to describe the incident electrons in Question E1 if the current is 10 µA.
[A beam of electrons, each with kinetic energy 5 eV, is incident on a step where the potential energy decreases by 2.5 eV.]
What is the current after the step?
Answer E3
A suitable wavefunction is an eigenfunction of momentum ψ (x) = A exp(ikx), in the region x < 0. The incident current I = 10 μA gives the incident flux F. The flux defines the constant A in Equation 8,
$F = \lvert\,A\,\rvert^2\dfrac{\hbar k}{m}$(Eqn 8)
and the angular wavenumber k = 1.15 × 1010 m−1 was found from the electron kinetic energy in Question T3.
$F = \dfrac{I}{\rm e} = \rm \dfrac{10\times10^{-6}\,A}{1.6\times10^{-19}\,C} = 6.25\times10^{13}\,s^{-1}$
So$A^2 = \dfrac{Fm}{\hbar k} = \rm \dfrac{6.25\times10^{13}\times9.11\times10^{-31}}{1.05\times10^{-34}\times1.15\times10^{10}}\,m{-1} = 4.72\times10^7\,m^{-1}\quad\text{and}\quad A = 6.9\times10^3\,m^{1/2}$
The current after the step is given by the incident current multiplied by the transmission coefficient T = 0.99. This is 9.9 μA.
(Reread Subsections 2.4 to 2.6 if you had difficulty with this question.)
Question E4 (A6)
At the junction between copper and an insulator, the potential energy of a conduction electron increases by 11.1 eV. Find the penetration depth, into the insulator, of a typical conduction electron with kinetic energy 7.0 eV.
Sketch the graph of the density function and account for the series of maxima and minima inside the copper.
Answer E4

Figure 7 The density function P (x) in the region of a potential step at x = 0. The incident beam is from the left. The energy E of each particle is less than the height of the step V. In region (I), there is a pattern of maxima and minima due to the interference between incident and reflected waves of equal amplitude. In region (II), the density decreases exponentially.
The penetration depth into the classically forbidden region is given by Equation 17,
$D = \dfrac{\hbar}{2\sqrt{2m(V-E)\os}}$(Eqn 17)
V = 11.1 eV and E = 7.0 eV, so:
$D = \rm \dfrac{1.05\times10^{-34}}{2\sqrt{2\times9.11\times10^{-31}\times(11.1-7.0)\times1.6\times10^{-19}}}\,m\\ \phantom{D }= 0.48\times10^{-10}\,m$
Your sketch of the density function should look like Figure 7. Region (I) is now the conducting copper and region (II) is the insulator. The series of maxima and minima within the copper conductor are caused by the interference of the incident and reflected waves. The conduction electrons penetrate a distance approximately one atomic radius into the insulator.
This effect accounts for the conduction of electric current between two conductors separated by a thin oxidized layer.
(Reread Subsection 3.4 if you had difficulty with this question.)
Question E5 (A8, A9 and A10)
A beam of electrons with kinetic energy 5 eV approaches a potential barrier of height 10 eV and width 1 nm. Sketch the graph of the density function near the barrier.
Calculate the transmission coefficient, T, according to Equation 24,
$T \approx \dfrac{16\exp(-2\alpha d)}{(k/\alpha+\alpha/k)^2}$(Eqn 24)
Are the approximations made to derive the formula valid in this case?
What is the value of T when the barrier potential is reduced to 6 eV?
Is Equation 25,
T ≈ 4 exp(−αd)(Eqn 25)
also a good approximation?
Answer E5

Figure 10 The particle density function P (x) near a potential barrier of height V. Particles are incident from the left, each with energy E less than V.
Your sketch of the density function should look similar to Figure 10. Significant features are the interference pattern in region (I), the exponential fall in region (II) and the constant value in region (III). The transmission coefficient is given by Equation 24 to a good approximation, provided the width of the barrier d is greater than 1/α:
$T \approx \dfrac{16\exp(-2\alpha d)}{(k/\alpha+\alpha/k)^2}$(Eqn 24)
We are given $k = \sqrt{2mE\os}/\hbar = \rm 1.15\times10^{10}\,m^{-1}$ (Question T3), $\alpha = \sqrt{2m(V-E)\os}/\hbar = 1.15\times10^{10}\,{\rm m}^{-1 } = k$, and d = 10−9 m.
The condition αd > 1 is satisfied, so we can proceed.
$T \approx \rm \dfrac{16\exp(-2\times1.15\times10^{10}\times10^{-9})}{(1+1)^2} = 4\exp(-23) = 4.1\times10^{-10}$
Transmission coefficients as small as this are quite normal in electronic applications. Now see what happens when the height of the barrier is reduced to 6 eV:
V − E = 1 eV
so that $\alpha = \rm \dfrac{1.15\times10^{10}}{\sqrt{5\os}}\,m^{-1} = 0.514\times10^{10}\,m^{-1}$.
$T \approx \rm \dfrac{16\exp(-2\times0.514\times10^{10}\times10^{-9})}{(1/\sqrt{5\os}+\sqrt{5\os}/1)^2} = \dfrac{16\exp(-10.3)}{7.20} = 7.62\times10^{-5}$
The transmission coefficient has increased by a factor of 105. In the tunnel diode, it is possible to reduce the barrier height within one nanosecond so a very fast current switch can be constructed.
Applying Equation 25,
T ≈ 4 exp(−αd)(Eqn 25)
instead of Equation 24 gives exactly the same result in the case when α = k.
However for the 6 eV barrier, we get:
T ≈ 4 exp(−2αd) = 4 exp(−2 × 0.514 × 1010 × 10−9) ≈ 13.7 × 10−5
The simpler approximate formula is wrong by a factor of two. This is not serious in most applications!
(Reread Section 4 if you had difficulty with this question.)
Question E6 (A9, A10 and A11)
In a modern scanning tunnelling microscope, the tip of a fine needle is 1 nm from a metal surface. The needle to metal gap behaves like a potential barrier of height 5 eV. Calculate the transmission coefficient T for electrons of energy 2.5 eV.
By what factor does T change when the gap increases to 1.1 nm? What is the significance of this result?
Answer E6
Since we are interested only in the change in the transmission factor we use the approximation given by Equation 25,
T ≈ 4 exp(−αd)(Eqn 25)
with $\alpha = \sqrt{2m(V-E)\os}/\hbar$.
It is given that V − E = 2.5 eV and d = 10−9 m.
At 5 eV, k = 1.15 × 1010 m−1 so that α = 0.813 × 1010 m−1.
T = 4 exp(−2 × 0.813 × 1010 × 10−9) = 4 exp(−16.3) ≈ 3.3 × 10−7
Now rework the calculation with d = 1.1 × 10−9 m.
T ≈ 4 exp(−2 × 0.813 × 1010 × 1.1 × 10−9) = 4 exp(−17.9) ≈ 0.7 × 10−7
The transmission factor has reduced by a factor of 5. This means that the scanning tunnelling microscope can readily detect single atoms in the surface of a metal (remember that atoms are typically 0.1 nm in size).
(Reread Subsection 4.5 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 5Closing items.