PHYS 1.2: Errors and uncertainty |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
Whenever you make a measurement, you should always be aware of the error or uncertainty in the result. This is an important principle for several reasons: first, unless you know how accurate your result is there is little point in performing the measurement at all; second, you might want to see if your result agrees with a theoretical prediction – exact agreement is unlikely, so you will usually need to know the extent to which your results are compatible with the prediction; third, you might want to compare your result with that obtained by another experimenter to see if the two are consistent, and again you would need to know the range of values which is compatible with your result.
This module is concerned with two particular aspects of error analysis. Section 2 concerns the uncertainty in a single quantity due to the random errors that cause repeated measurements of that quantity to differ from one another. This section is mainly concerned with statistical concepts such as mean, standard deviation and the standard error in the mean, and with the physical significance of these concepts. Section 3 deals with the errors that arise in compound quantities obtained by combining several other quantities that have known errors. This section also contains the rules for combining independent errors in a single quantity and for combining errors in sums, differences, products, quotients and powers. Section 4 completes the discussion with various hints and tips about the reduction and estimation of errors.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 5.1Module summary and the Subsection 5.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 5.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
Ten measurements of the period of a simple pendulum were as follows:
2.13 s, 2.07 s, 2.24 s, 2.20 s, 2.08 s, 2.11 s 2.15 s, 2.19 s, 2.22 s, 2.16 s
Calculate the mean (i.e. average) period, the standard deviation and the standard error in the mean. Given that the length of the pendulum is (1.15 ± 0.01) m, estimate g, the magnitude of the acceleration due to gravity.
[Hint: For a simple pendulum $T = 2\pi\sqrt{\smash[b]{l/g}}$ where T is the period and l is the length of the pendulum.]
Answer F1
Mean period = 2.16 s
Standard deviation = 0.0550 s
Standard error in the mean = 0.0183 s
It follows from the given equation for the period that g = (4π2l)/T 2. The fractional error in g is therefore given by
$\dfrac{\delta g}{g} = \sqrt{\left(\dfrac{\delta l}{l}\right)^2+\left(2\dfrac{\delta T}{T}\right)^2}$
The percentage error in T is
$\delta$T/T × 100% = (0.0183 × 100%)/2.155 = 0.85%.
So the percentage error in T 2 is
$\delta$T 2/T 2 × 100% = 2$\delta$T/T × 100% = 1.7%.
The percentage error in l is
$\delta$l/l × 100% = (0.01 × 100%)/1.15 = 0.9%.
Hence error in g is approximately
$\sqrt{\smash[b]{(0.9)^2 + (1.7)^2}}\% = 1.9\%$
Thus$\delta$g = 1.9 × g/100 = 0.2 m s−1
So the result is g = (9.8 ± 0.2) m s−2
Question F2
The electrical resistance R of a piece of wire of length L and diameter d is given by R = 4ρL/(πd2).
If ρ = 44.2 × 10−6 Ω m, L = (527.3 ± 0.1) cm, and d = (0.620 ± 0.010) mm, calculate R to three significant figures and estimate the error in your result.
Answer F2
$R = \dfrac{4\times(44.2\times 10^{-6}\,\rm{\Omega\,m})\times 5.273\,\rm{m}}{3.14159 \times(6.20\times 10^{-4}\,\rm{m})^2} = 772\,\rm{\Omega}$
We can either argue as follows:
The percentage error in L is about 0.02%; while that in d is about 1.6%.
So clearly the error in d dominates.
The percentage error in d2 is twice that in d, i.e. 3.2%, so the percentage error in R is also about 3.2%, i.e. R = (772 ± 25) Ω
or we can use the rules for combining errors:
$\dfrac{\delta L}{L} = \dfrac{0.1}{527.3} = 1.9\times 10^{-4}$
$\dfrac{\delta d}{d} = \dfrac{0.01}{0.62} = 1.6\times 10^{-2}$
so that$\dfrac{\delta d^2}{d^2} = 2\dfrac{\delta d}{d}=3.2 \times 10^{-2}$
Hence$\dfrac{\delta R}{R} = \sqrt{\smash[b]{(1.9)^2\times 10^{-8}+(3.2)^2\times 10^{-4}}} = 3.2/100$
so that$\delta$R = [(3.2/100) × 772] Ω = 25 Ω and R = (772 ± 25) Ω, as before.
1.3 Ready to study?
Study comment In order to study this module you will need to understand the following terms: modulus (i.e. absolute value), percentage, subject (of an equation) and significant figures. If you are uncertain of any of these terms you can review them by referring to the Glossary which will also indicate where in FLAP they are developed. In addition, you should be able to: rearrange equations, use a calculator to evaluate arithmetic expressions, work in decimal_notationdecimal or scientific notation (also known as powers–of–ten notation or standard form) and use basic SI units. The following questions will allow you to establish whether you need to review some of these topics before embarking on this module.
Question R1
Use your calculator to evaluate:
(a) $\dfrac{0.690\times10^3 + 167}{3.000\times10^{-3} + 5.200}$ (to three significant figures)
(b) (63.20 × 7.9600 × 2.400)/[0.6300 + (17.90 × 4.600 000)] (to four significant figures).
Answer R1
(a) 1.65 × 102 (b) 14.55
Question R2
Express the following fractions as percentages to the nearest whole number:
(a) 7/100 (b) 1/10 (c) 3/20 (d) 5/8 (e) 13/12 (f) 46/15
Answer R2
(a) 7% (b) 10% (c) 15% (d) 63% (e) 108% (f) 307%
Question R3
Rearrange the equation g = 2h/t2 to make (a) h, and (b) t, the subject.
Answer R3
(a) $h = gt^2/2$ (b) $t = \sqrt{\smash[b]{2h/g}}$
Question R4
Given the equation E = aP (T − t), find the value of a when P = 10, T = 70, t = 30 and E = 0.56.
Answer R4
0.56 = a × 10 (70 − 30)
Thus,a = 0.56/400 = 1.4 × 10−3
Question R5
The magnitude of the acceleration due to gravity, g, is measured in an experiment as 9.7 m s−2, with an error of ±0.2 m s−2. i Express the absolute value of the error (sometimes called the absolute error) as a fraction of the measured value and as a percentage of the measured value, thus determining (a) the fractional error, and (b) the percentage error, respectively.
Answer R5
(a) The fractional error is 0.02 (b) the percentage error is 2%
Comment If you had difficulty with any of the terms used in these Ready to study questions, consult the Glossary for further information.
2 Repeated measurements
2.1 Means and deviations from the mean
When you measure a particular quantity several times you usually get slightly different answers each time. Suppose, for example, that you have been measuring the rate at which water flows through a pipe by collecting the water that emerges in a measuring jug and recording the volume collected over a four–minute interval.
The results of five such measurements might be: 436.5 cm3, 437.3 cm3, 435.9 cm3, 436.4 cm3, 436.9 cm3. i
If we assume that there is nothing to choose between these measurements (i.e. they were all taken with the same care and skill, and with the same measuring instruments), then the best estimate they provide of the volume V collected over four minutes will be given by their average or mean. This is obtained by adding the measured values together and dividing the resulting sum by the number of measurements. Thus, denoting the mean of V by $\langle V \rangle$ i we find
$\langle V \rangle = \dfrac{436.5 + 437.3 + 435.9 + 436.4 + 436.9}{5}\rm{cm^3} = 436.6\,\rm{cm^3}$
More generally we can define the mean of a set of repeated measurements as follow:
The mean of n values of a quantity x (i.e. the mean of x1, x2, x3, x4, ... xn−2, xn−1, xn) is:
$\displaystyle \langle x \rangle = \dfrac{x_1+x_2+x_3+x_4+\ldots+x_{n-2}+x_{n-1}+x_n}{n} = \dfrac1n\sum_{i=1}^n x_i$(1) i
Given a set of repeated measurements and their mean it is interesting to know how far each individual measurement departs from the mean. The difference between any particular measurement and the mean is usually called the deviation of that measurement. In the case of the water flow experiment:
-
the deviation of the first measurement (436.5 cm3) from the mean is
436.5 cm3 − $\langle V \rangle$ = 436.5 cm3 − 436.6 cm3 = −0.1 cm3 -
and the deviation of the fifth measurement (436.9 cm3) from the mean is
436.9 cm3 − $\langle V \rangle$ = 436.9 cm3 − 436.6 cm3 = 0.3 cm3
On the basis of the available evidence, our best estimate of the volume V appears to be $\langle V \rangle$ = 436.6 cm3, but in view of the various deviations of the individual measurements this is unlikely to be exactly the ‘true value’ of V. It would therefore be sensible to use the available data to determine the range of values within which we might reasonably expect to find the true value. This can be done by determining the largest positive and negative deviations from the mean. The measurements are spread out between 435.9 cm3 and 437.3 cm3; that is from (436.6 − 0.7) cm3 to (436.6 + 0.7) cm3. So our first guess might be that the true value of V is within about 0.7 cm3 of the mean value, i.e. somewhere in the range 436.6 ± 0.7 cm3. However, the volume is unlikely to lie right at the ends of this range, so quoting a spread of ±0.7 cm3 would be unduly pessimistic. As a rough rule of thumb, we can take 2/3 of this spread as a more realistic estimate of the true value. So in this case the data indicate that the true value of V is probably in the range 436.6 ± 0.5 cm3. i
In view of the above discussion, if you were asked the value of V you might well say V = 436.6 ± 0.5 cm3. In making such a statement you are clearly indicating that there is some degree of uncertainty in your answer, as is appropriate in these circumstances. In fact, in this context the quantity ±0.5 cm3 is called the uncertainty or error in the measurement. We can summarize this in the following way:
Several repeated measurements of a single quantity x may be used to calculate the mean, $\langle x \rangle$, of that quantity and to estimate the error or uncertainty ±$\delta$x in that mean. The final result may therefore be written $\langle x \rangle$ ±$\delta$x.
Much of the remainder of this section will be devoted to finding a more reliable estimate of the error in the mean than that provided by the crude ‘rule of thumb’ introduced above. First though, we consider the problem of combining your results with those obtained in another experiment.
Combining results
Suppose a fellow student has made an independent determination of V and has found the value 436.0 cm3. Naturally you would both want to make the best possible estimate of V, so it would make sense to combine this new piece of information with your original data, but how should this be done? Should you take the mean of the two results? i.e.
(436.6 cm3 + 436.0 cm3)/2 = 436.3 cm3
If your fellow student had taken only one reading, of 436.0 cm3, you might naturally feel upset that a single reading taken by somebody else should carry as much weight as the mean of your five measurements. Clearly, as it stands, this would not be a sensible way of using the new information.
If the single new reading had the same reliability as any one of the readings you took, then the fairest result would obviously be obtained by treating the additional single reading as being of equal weight to any one of yours and then $\langle V \rangle$ would be given by
$\langle V \rangle = \dfrac{436.5 + 437.3 + 435.9 + 436.4 + 436.9 + 436.0}{6}\,\rm{cm^3} = 436.5\,\rm{cm^3}$
Alternatively, of course, the result obtained by your fellow student might have been the average of many readings, possibly more than you took.
✦ If your colleague’s value of 436.0 cm3 was the mean of 20 readings of the same reliability as yours, what would be the best estimate of $\langle V \rangle$?
✧ There is no need to know what the 20 individual readings were. If the average of 20 readings was 436.0 cm3, the sum of these 20 readings will be 20 × 436.0 cm3, whatever the individual readings were. And if the average of your five readings was 436.6, their sum will be 5 × 436.6 cm3, whatever the individual readings were. So the sum of all 25 readings is
(20 × 436.0 cm3) + (5 × 436.6 cm3) = 10 903 cm3
and so the new mean value is $\langle V \rangle$ = (10 903/25) cm3 = 436.1 cm3
It is reasonable to trust the value of 436.1 cm3 more than the values of 436.0 cm3 or 436.6 cm3, because it is based on a greater number of equally reliable readings, but what if the readings were not equally reliable? You might well attach greater weight to more reliable readings, but how can you recognize one set of readings as more deserving of extra weight than another?
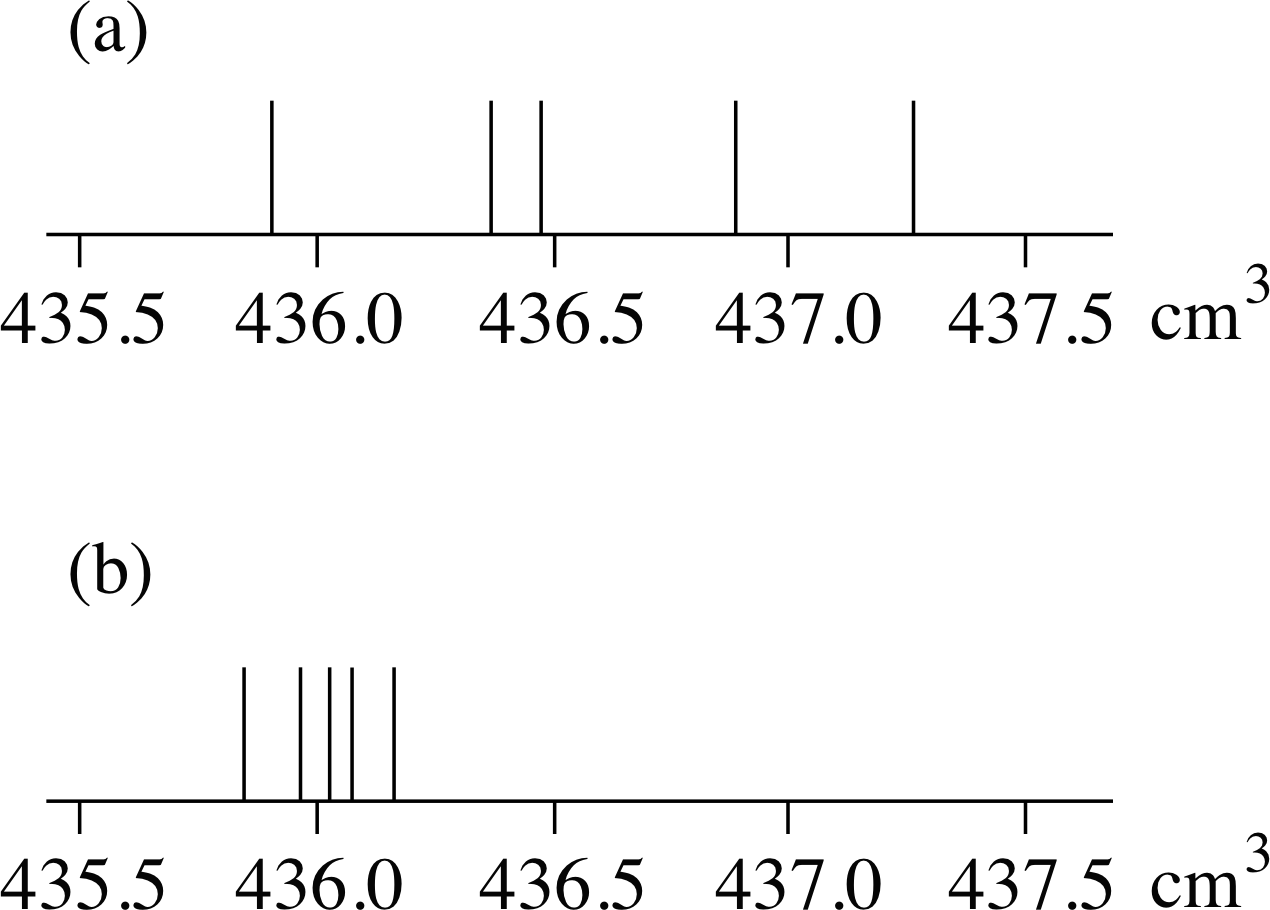
Figure 1 A set of five measurements of volume: (a) with a wide spread, (b) with a narrow spread.
Figure 1a shows the five readings that gave the original mean value of 436.6 cm3. In Figure 1b are five other possible readings giving a mean value of 436.0 cm3. If the number of readings were the sole criterion for judging the precision of a result, the two values – 436.6 cm3 and 436.0 cm3 – would carry the same weight. Does it look from Figure 1 as though they ought to? It would seem not. The measurements in the second set agree with each other more closely. Perhaps the second experimenter had a better means of cutting off the water flow at the end of the given time period than you. Whatever the cause, in seems only fair that the greater consistency of the new readings should be taken into account when combining the available data. Thus, the extent to which the readings are spread about the mean also has to be taken into account.
✦ You might feel that a way of assessing the relative spreads of two sets of readings would be to find the average deviation for each set and then compare these. Work out the average deviation for the five measurements taken for the volumes collected in the experiment described at the start of this subsection.
(436.5 cm3, 437.3 cm3, 435.9 cm3, 436.4 cm3, 436.9 cm3).
✧ The mean of the set is 436.6 cm3 and so the sum of the deviations of these five is
$\left(\dfrac{-0.1+0.7-0.7-0.2+0.3}{5}\right)\,\rm{cm^3} = 0\,\rm{cm^3}$
The mean deviation is always zero! This follows from the definition of the mean. If we wish to compare two sets of data then their average deviations, both zero, will not help.
You might next suggest comparing the magnitude of the two average deviations (disregarding the sign). This would be one way of proceeding, but it is not the preferred approach – which is to use the standard deviation, as is described in the next subsection.
2.2 Standard deviation
An objective measure of the extent to which n readings of a certain quantity are spread about their mean is given by the standard deviation, σn, of those readings. i This subsection gives the procedure for calculating the standard deviation of a set of readings and then explains the significance of that quantity.
To calculate σn, you need to know the total number of readings, n, and the individual readings, x1, x2, x3, x4, x5 ... xn. From these you can calculate the mean of the readings, $\langle x \rangle$, and the deviation between each reading and the mean (as discussed in Subsection 2.1). If these deviations are denoted d1, d2, d3 ... dn, then: d1 = x1 − $\langle x \rangle$, d2 = x2 − $\langle x \rangle$ and so on, up to dn = xn − $\langle x \rangle$. Given the deviations, the standard deviation can be calculated as follows:
- 1
-
take the square of each deviation;
- 2
-
divide the sum of these values by the total number of readings;
- 3
-
take the square root of the result.
We can summarize the whole procedure in the following way:
Given n measurements, x1, x2, x3, x4, x5 ... xn, of a quantity x, with mean $\langle x \rangle$, the deviation of the ith reading is $d_i = x_i - \langle x \rangle$, and the standard deviation σn is defined by
$\displaystyle \sigma_n = \sqrt{\dfrac{d_1^2+d_2^2+\ldots+d_n^2}{n}} = \left(\dfrac 1n \sum_{i=1}^n d_i^2\right)^{1/2}$(2) i
✦ What is the standard deviation of the five measurements of volume given at the beginning of Subsection 2.1?
(436.5 cm3, 437.3 cm3, 435.9 cm3, 436.4 cm3, 436.9 cm3. )
| V/cm3 | di /cm3 | di2/cm6 |
|---|---|---|
| 436.5 | −0.1 | 0.01 |
| 437.3 | +0.7 | 0.49 |
| 435.9 | −0.7 | 0.49 |
| 436.4 | −0.2 | 0.04 |
| 436.9 | +0.3 | 0.09 |
✧ The first step is to calculate the mean (436.6 cm3 in this case). Next, calculate the deviations, d1, d2, etc., between each reading and the mean, and then calculate the square $d_i^2$ of each of these deviations. (See Table 1; note that $d_i^2$ is always a positive quantity.)
Then add up all the values of di2 and divide this sum by the total number of measurements, n (five in this case). This gives σn2. Finally, take the square root of σn2 to get σn, the standard deviation and round off the result to an appropriate number of significant figures.
From the table, the sum of the squared deviations is
$\displaystyle \sum_{i=1}^5 d_i^2 = 1.12\,\rm{cm^6}$
Thus, using the formula for σn,
$\sigma_n = \sqrt{1.12\,\rm{cm^6}/5} = \sqrt{0.224\,\rm{cm^6}} = 0.5\,\rm{cm^3}$ (to one significant figure). i
When faced with many readings of the same quantity, it is difficult to make a quick assessment of the precision of an experiment and the likely mean value by examining a long list of numbers displayed in a table. In such circumstances it is more convenient to plot the readings in the form of a histogram – a graph composed of rectangular blocks, designed to show how often particular readings (or readings in a particular range) occur in a set of measurements.
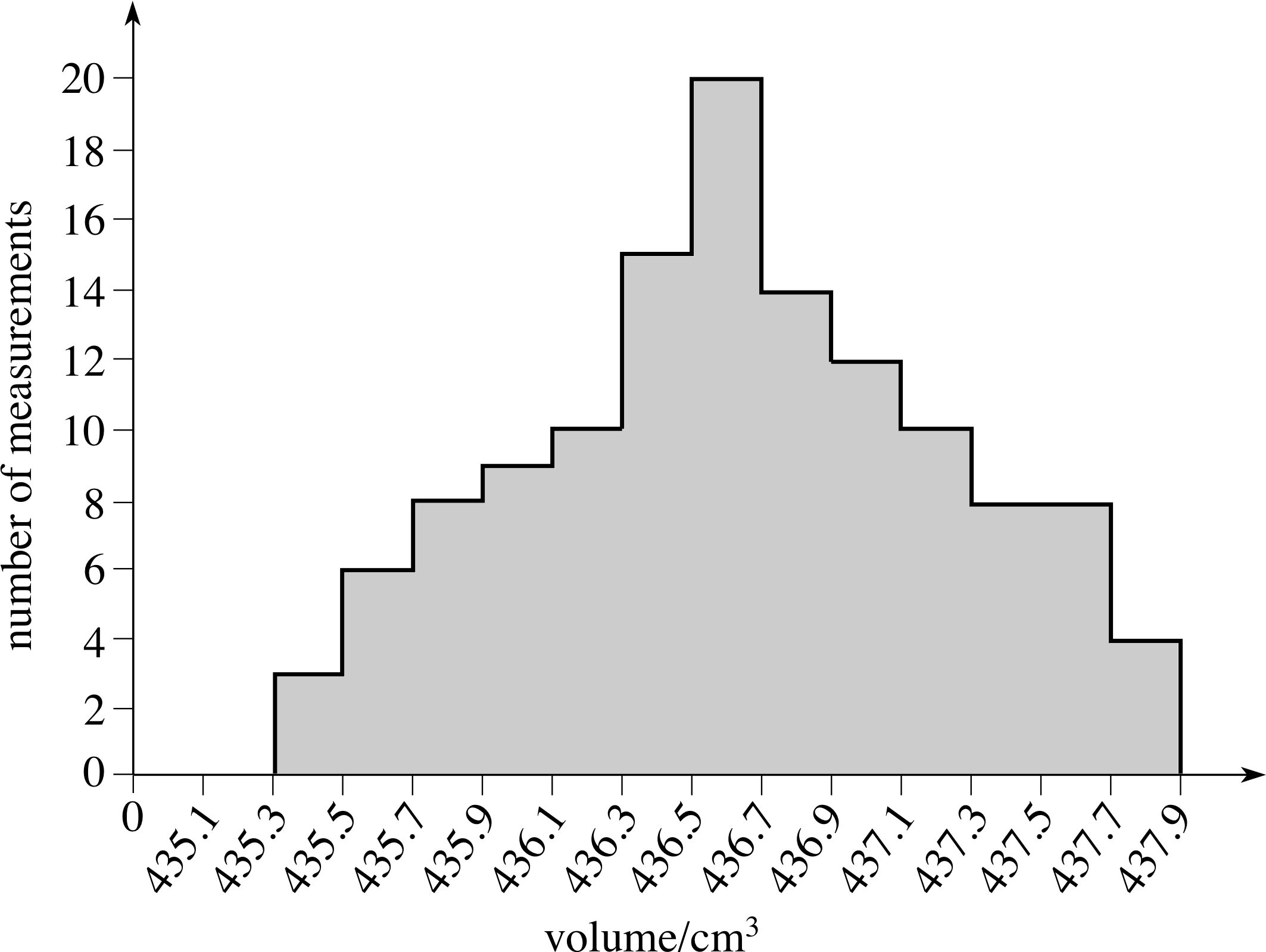
Figure 2 Histogram of measurements of water volume.
Figure 2 shows a histogram of 127 volume readings in our water flow experiment. The horizontal (volume) axis has been divided into equal intervals, representing 0.2 cm3, and the number of measurements in each interval has been used to determine the height of the block for that interval.
For instance, there are ten readings between 436.1 cm3 and 436.3 cm3. You can see at a glance from this histogram that the mean value is about 436.6 cm3 and the total spread is about ±1.2 cm3. Using the ‘rule of thumb’ introduced earlier, you might quote the result as (436.6 ± 0.7) cm3. However, the standard deviation calculated from the data works out to be ±0.5 cm3 which is somewhat less than the rule of thumb indicates. So, what is the significance of the standard deviation in this case? What feature of the spread of data does it represent?
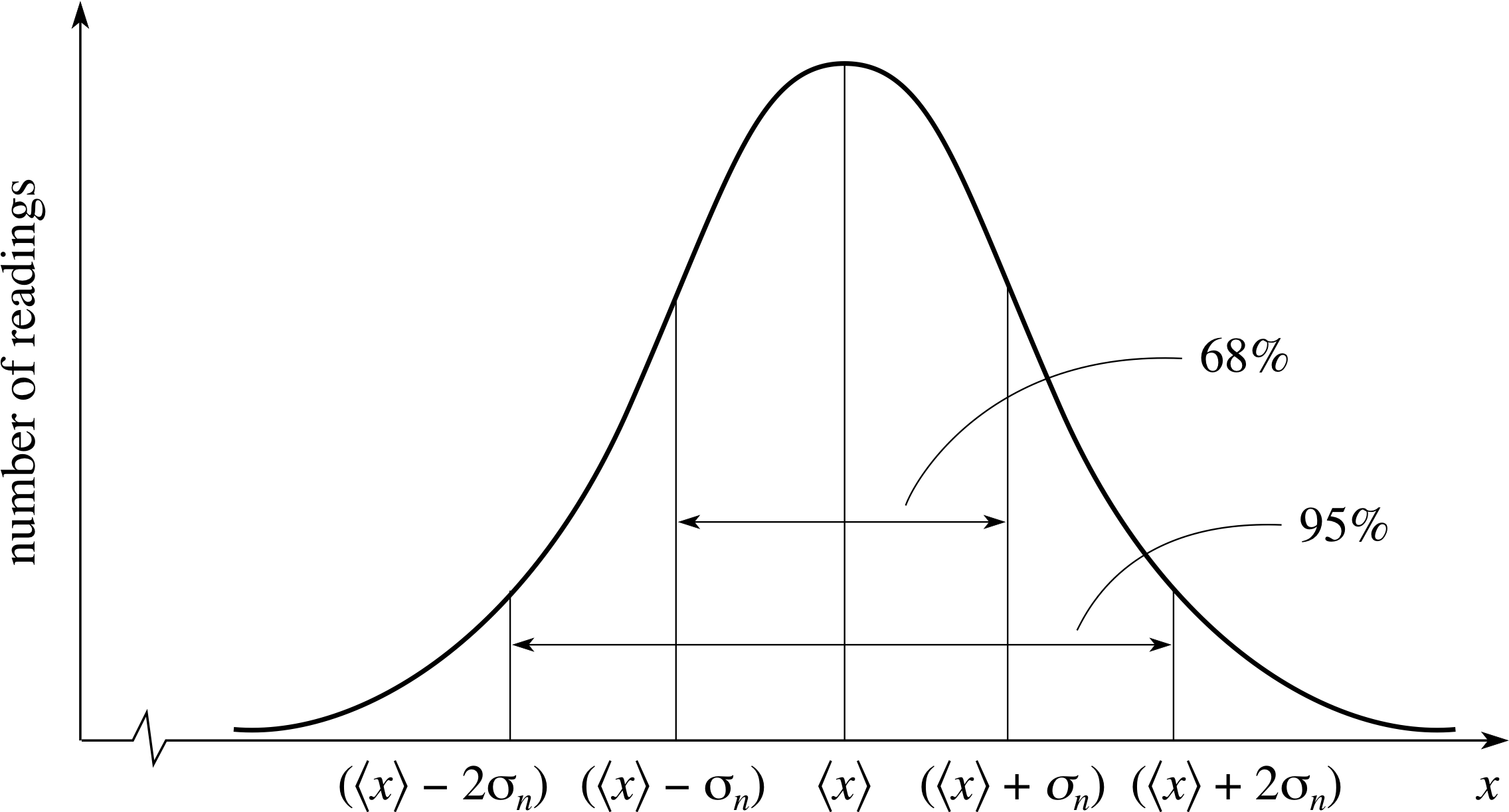
Figure 3 Distribution of a large number of readings about an average value.
Rather than answering these questions immediately, consider what would happen to the histogram if we took even more readings. As the number of readings is increased you can take smaller and smaller intervals and still have a reasonable number of readings in each. Eventually, the ‘step-like’ character of the histogram will no longer be noticeable and you will be left with a smooth curve as in Figure 3.
The distribution of readings represented by the bell–shaped curve in Figure 3 is actually of great importance and is called a gaussian_distributionGaussian or normal distribution. It is quite possible for a large number of readings of a quantity to be distributed in some other way, but in practice normal distributions (or at least close approximations to normal distributions) are a very common outcome of repeated measurements of a single quantity. i
In the rest of this module we will assume that a histogram showing the outcome of a large number of measurements of any quantity approaches a normal distribution. In other words we shall only consider normally distributed measurements.
The significance of the standard deviation of a large set of (normally distributed) readings is easy to explain: σn gives a measure of how far a typical reading is likely to be from the mean. In particular:
It can be shown that about 68% of the readings will lie within ±σn of the mean value, 95% within ± 2σn, and 99.7% within ± 3σn. i
The first two of these values are indicated in Figure 3.
Of course, in practice we often have to work with a very limited number of measurements where the precise percentages quoted above (for large samples) will not apply. Even so, the standard deviation continues to be used as a simple but effective indicator of the spread of the readings.
Question T1
Repeated measurements of the height of a building gave the following results, corrected to two decimal places (all these values are in metres):
33.48, 33.46, 33.49, 33.50, 33.49, 33.51, 33.48, 33.50, 33.47, 33.48, 33.49, 33.50, 33.47, 33.51, 33.50, 33.48
Calculate the mean and standard deviation of this set of measurements.
Answer T1
The mean is 33.490 m, the standard deviation is 0.014 m.
The standard deviation of a set of readings provides insight into the likelihood that any particular reading will have a given deviation from the mean. However, when evaluating the error or uncertainty in a quantity, what we are really interested in is the likely separation between the mean of the readings and the true value of the quantity we are trying to measure. This is the subject of the next subsection.
2.3 Standard error in the mean
Experimental measurements are generally subject to two kinds of error: random errors which are mainly responsible for the spread of the individual readings about the true value, and systematic errors which generally cause the mean to be consistently displaced above or below the true value. Systematic errors often arise from the failings in experimental design; consistently low temperatures obtained by using a wrongly calibrated thermometer would come into this category.
In the absence of systematic errors, we expect the mean of a set of readings to get closer and closer to the ‘true’ value as the number of measurements increases. We also expect that increasing the number of measurements will reduce the uncertainty in the result. This latter expectation is quite reasonable, but it is not a property of the standard deviation since σn tends towards a fixed value as the number of readings increases. The lesson to be drawn from this is that the standard deviation itself does not generally provide a good estimate of the uncertainty in the quoted mean result even though it describes the spread of the readings. A better indicator of the uncertainty, and the one generally adopted for scientific use is the standard error in the mean, sm. Unlike the standard deviation, this does decrease as the number of readings increases. The following procedure is used to estimate the standard error in the mean from the available data.
Given n readings of a quantity, with standard deviation σn, an estimate of the standard error in the mean, sm, is given by
$s_{\rm m} = \dfrac{\sigma_n}{\sqrt{\smash[b]{n-1\os}}}$(3) i
What is the significance of sm? Well, suppose you have a large number of (normally distributed) measurements of the quantity x, and that the mean of those measurements is $\langle x \rangle$. In the absence of systematic errors, this mean value has a 68% chance of lying within ±sm of the true value, a 95% chance of lying within ±2sm, and a 99.7% chance of lying within ±3sm. Thus, sm is a measure of how close the mean value of the readings, $\langle x \rangle$, is likely to be to the (unknown) true value which would be found from an infinite set of readings. Note the distinction between the standard error in the mean sm and the standard deviation σn which provides a measure of how close an individual reading is likely to be to the mean.
It should be noted from Equation 3 that as the number of readings n increases, the quantity n − 1 also increases and sm gets smaller. However, it does so relatively slowly as it is dependent on the square root of (n − 1). Thus, if you quadruple the number of readings, you halve the uncertainty sm; but a tenfold increase in the number of readings only reduces the uncertainty by a factor of 3.
A large number of inaccurate readings is therefore a rather poor substitute for taking care, and so keeping the spread of the individual readings, and hence σn, as small as possible.
✦ In the water flow experiment discussed earlier, we considered the mean of the original five measurements to be 436.6 cm3. Now calculate the standard error of this mean, using the value we have already calculated for σn, i.e. 0.5 cm3.
✧ For this problem, n has the value 5, and σn is 0.5 cm3.
So$s = \dfrac{0.5}{\sqrt{5-1\os}}\,\rm{cm^3}= \dfrac{0.5}{2}\,\rm{cm^3}= 0.3\,\rm{cm^3}$ to one significant figure.
Thus we can quote the final result as $\langle V \rangle$ = (436.6 ± 0.3) cm3. i
Question T2
Calculate the standard error in the mean of the measurements given in Question T1.
[Repeated measurements of the height of a building gave the following results, corrected to two decimal places (all these values are in metres):
33.48, 33.46, 33.49, 33.50, 33.49, 33.51, 33.48, 33.50, 33.47, 33.48, 33.49, 33.50, 33.47, 33.51, 33.50, 33.48]
How would you write the final result of the measurements?
Answer T2
The standard error in the mean is $(0.014/\sqrt{16-1\os})\,\rm{m} = 0.004\,\rm{m}$.
The final result of the measurements is (33.490 ± 0.004) m.
Just because one assigns a standard error sm to a result (for example, ±0.3 cm3 on a mean value of 436.6 cm3), it does not follow that the true value necessarily lies within the specified range, i.e. within the range 436.3 cm3 to 436.9 cm3. Quoting a standard error is understood by all scientists to mean that roughly speaking there is a 68% chance of the true value lying within ±sm of the mean value, and a 95% chance of the true value lying within ±2sm of the mean value.
Consequently, one important use of the standard error in the mean is in deciding on the significance of an experimental result. For instance, suppose that a new theory suggests that a particular physical quantity should have the value 100 units with an uncertainty of less than one unit, and an experiment is done in which a large number of measurements are made of this quantity. If the mean value of the measurements is found to be 90 units and the standard error in the mean ±11 units, what does this result tell us about the theory? Does the experiment refute the theory?
It is not possible to give a simple yes or no answer to this question but it is possible to gauge the likelihood of a prediction of 100 units being compatible with the experimental result. In order to do this note that the following two statements are equivalent:
- 1
-
The true value has a 68% chance of lying within ±sm of the mean value.
- 2
-
The mean value has a 68% chance of lying within ±sm of the true value.
If the true value actually is 100 units, then there is an approximately 68% chance that the mean will lie between 89 units and 111 units, i.e. within ±sm of the true value. Since the measured mean (90 units) is within this range there is a good chance that further measurements will continue to be compatible with the theory, and certainly no grounds for saying that the theory is wrong.
On the other hand, if the experimental result had been (90 ± 4) units, a true value of 100 units would differ from the mean by more than twice the standard error. Since the likelihood of this happening by chance is less than 5% it seems rather improbable that further measurement will support the theory, though it is still possible that it will do so.
A note of caution
You must use common sense when dealing with errors. It is tempting, when presented with a formula – such as that for the standard error in the mean – to just rush ahead without thinking, hoping that the formula will always be applicable and will always give the right answer. However, this attitude is never the right one to adopt and is especially dangerous in the context of errors. For instance, if you make several length measurements using a ruler you might feel that you can only read the ruler reliably to half of a scale division, 0.5 mm say, and you might record a set of repeated readings as 22.0 mm, 22.0 mm, 22.0 mm, 22.0 mm and 22.0 mm. If you apply the formulae for the mean and the standard error in the mean to these measurements you can easily see that they seem to imply a final result of (22.0 ± 0.0) mm. However, a little thought will show that all you have really done is to demonstrate convincingly that the measured length is closer to 22.0 mm than it is to 21.5 mm or 22.5 mm. Given the lack of variability in the results it makes no sense to use sophisticated statistical methods to analyse them. Similarly, there is seldom any point in carrying out a detailed investigation of random errors if they are swamped by systematic errors that are beyond your control.
3 Combining errors
3.1 Independent errors in a single quantity
Errors in a single measured quantity
In the majority of experiments, there will be more than one source of error. For instance, measurements of a single quantity may contain systematic errors (which we have largely ignored so far) in addition to the random errors that have been our main concern. We have already stressed the need to make a series of measurements, each as precise as possible, in order to determine and reduce the random errors, but the systematic errors are generally more difficult to deal with. Even so, it is important to distinguish between those systematic errors that can be measured and allowed for – and which, therefore, will not contribute to the error in the final result – and those systematic errors which cannot be eliminated from an experiment. In the latter case the best you can hope to do is to recognize their presence and estimate their effect. As an example of this let us return to the water flow experiment discussed in Subsection 2.1, and consider two different kinds of systematic error that might occur in timing each four–minute measurement interval.
- It could be that the stopwatch runs slow; comparing it with the telephone talking clock might show that it lost 10 s every hour, which is equivalent to (10/15) s lost in (60/15) min (i.e. 4 min) which is equal to 240 s. To allow for this, you could multiply the volumes collected by the factor [240 − (10 /15)]/240 ≈ 0.997, and this would mean that the slow running of the stopwatch did not contribute an error to the final modified result. i
- On the other hand you might have a tendency to start the stopwatch too early or too late each time. You might not be sure that you were making such a systematic error but you might feel it was sufficiently likely that it should be taken into account even though you didn’t know whether it was leading to readings that were systematically too long or systematically too short. (Note that we are imagining this systematic error to be quite independent of the random errors you will inevitably make in reading the stopwatch.) A reasonable estimate for the possible size of such a systematic error might be ±0.2 s – anything longer would probably be detected. This error of ±0.2 in 240 s, or ±1 part in 1200, would lead to an error of ±1 part in 1200 in the volume of water collected. As the average volume of water collected was 436.6 cm3, this would lead to a final systematic error of ±1436.6 cm3/1200 = ±0.4 cm3.
So the difference between these two types of systematic error is that we know that one is definitely present, and we can measure and correct for its effect, whereas the other may or may not be present, and we can only make an educated guess at its possible magnitude. Essentially, once we have identified, measured and corrected for the first type of error, it ceases to be a source of error in the final result. But the second type of error remains, and even when we have estimated its size we are left with the problem of working out its effect on the final result.
Combining errors in a single quantity
The example we have just considered raises a general question about the errors in a single quantity – whatever their cause. In every experiment there will be errors in the quantities that we measure, and those errors may have several contributory causes. Supposing that we can estimate the likely error from each cause, how should we combine those estimates in order to gauge their overall affect on the final result for any particular quantity we are attempting to measure?
In the particular case of the water flow experiment we have just estimated a systematic error of ±0.4 cm3, arising from the timing, and a random error of ±0.3 cm3. How should we combine those particular errors? The obvious answer would seem to be to add them directly to get a total error of ±0.7 cm3, but this is really being unduly pessimistic. Any systematic error in measuring time has nothing to do with the random error in this experiment – the two errors are independent. It is therefore highly unlikely (though possible, of course) that both errors will have their maximum positive value or their maximum negative value. There will generally be a partial cancellation of the errors, and this should be allowed for in any estimate of the total error in the final result. The rule for combining two independent errors in the same quantity, and we stress that it only applies if the errors are independent, is:
$E=\sqrt{\smash[b]{e_1^2+e_2^2}}$(4)
where ±E is the overall error, i and ±e1 and ±e2 are the individual errors that are to be combined.
Thus, in the water flow example,
$E= \sqrt{\smash[b]{(0.4\,\rm{cm^3})^2+(0.3\,\rm{cm^3})^2}} = \sqrt{(0.16\,\rm{cm^6})+(0.09\,\rm{cm^6})\os} = \sqrt{0.25\,\rm{cm^6}\os} = 0.5\,\rm{cm^3}$
This is obviously larger than either of the contributing errors, but considerably smaller than their sum. This calculated error is often referred to as a probable error.
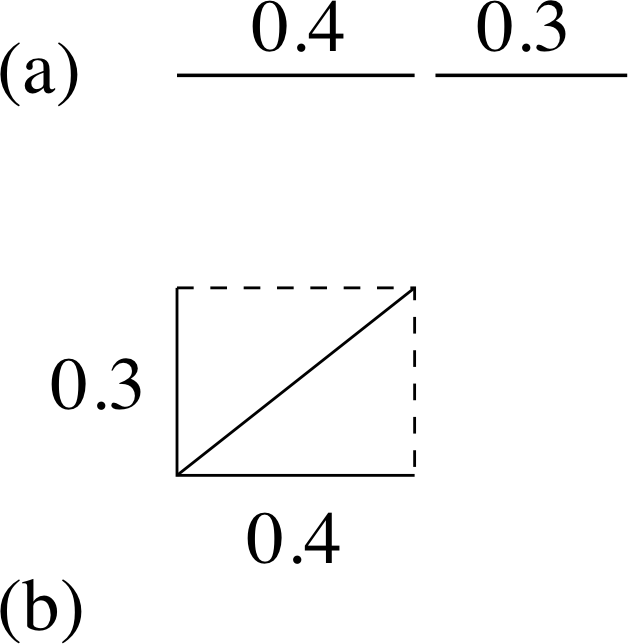
Figure 4 Adding directed lines: (a) in the same direction, and (b) at right angles.
You may find that the following argument which justifies this procedure helps you to remember the result. We can represent the individual errors by lines that have lengths proportional to the magnitude of the error. Direct addition can then be represented by putting the two lines together as illustrated in Figure 4a to produce a line equal to their sum. However, since the errors are independent, we need to add these lines in some way that shows their independence. This can be done if we arrange the lines at right angles, as in Figure 4b, and take their sum as being the diagonal of the rectangle.
(This is, in fact, the way we add forces that are acting in different directions.) The length of the diagonal is just given by Pythagoras’s theorem,
i.e. (diagonal)2 = (0.4 cm3)2 + (0.3 cm3)2
so, diagonal = $\sqrt{0.16 + 0.09\os}$ cm3 = 0.5 cm3
If more than two errors are involved, the method is still the same in principle. Suppose that, in addition to the above errors, we think that there may be another systematic error of ±0.5 cm3 in measuring the volume of water collected due to an error in the manufacture of the measuring device. Then the overall error is ±E, where
$E= \sqrt{\smash[b]{(0.5\,\rm{cm^3})^2+(0.4\,\rm{cm^3})^2+(0.3\,\rm{cm^3})^2}} = 0.7\,\rm{cm^3}$
which is, again, larger than the individual errors, but smaller than their sum.
Independent errors ±e1, ±e2, ±e3 ... ±en in a measured quantity will give rise to an overall error ±E of:
$E = \sqrt{\smash[b]{e_1^2+e_2^2+e_3^2+\ldots+e_n^2}} = (e_1^2+e_2^2+e_3^2+\ldots+e_n^2)^{1/2}$(5)
Question T3
A student measures the current through an electrical circuit using an ammeter, and obtains a value of 3.1 A. He thinks that the random error in reading the scale is about ±0.1 A. He is then told that there is a systematic error in the ammeter of ±14%. What is the total error?
Answer T3
The systematic error in his reading is [(4/100) × 3.1] A = 0.12 A.
Total error = $\sqrt{\smash[b]{(0.1)^2 + (0.12)^2}}\,\rm{A} = 0.16\,\rm{A}$.
3.2 Errors in sums, differences, products, quotients and powers
In Subsection 3.1, we were concerned with combining errors in a single measured quantity to find the total error in that quantity. Suppose now that you are conducting an investigation which involves measuring several different independent quantities. Naturally you would attempt to estimate the error in each of those quantities using the above method.
The next stage of your investigation might well involve the substitution of these measured quantities into a formula in order to obtain a final result. You know the errors in the individual quantities, but how can you determine the error in this final calculated result? How do errors propagate through a calculation using a formula? We will answer this question by considering in turn the behaviour of errors in sums, differences, products, quotients and powers; you should then be able to work out for yourself the effect of combining errors in a wide range of formulae.
Sums and differences
As an example, suppose we want to evaluate X = A + B, where A and B are independent quantities though they must have the same dimensions since they are being added together. How is the error in X related to the separate errors in A and B?
The reasoning here is exactly the same as given in the previous section on combining independent errors in a single quantity. The error in X is equal to the square root of the sum of the squares of the errors in A and B. We can represent this symbolically in the following way
$\delta X= \sqrt{\smash[b]{(\delta A)^2 +(\delta B)^2}}$(6) i
✦ An object is made from two parts. One part has mass M1 = (120 ± 5) kg and the other has mass M2 = (90 ± 3) kg. What is the total mass M, and the error $\delta$M in this mass?
✧ M = (M1 + M2) ±$\delta$M
= 120 kg + 90 kg ±$\delta$M = 210 kg ±$\delta$M
Since we are dealing with the error in a sum, we have
$\delta M= \sqrt{\smash[b]{(\delta M_1)^2+(\delta M_2)^2}} = \rm \sqrt{\smash[b]{(5\,kg)^2+ (3\,kg)^2}} = \sqrt{\smash[b]{34\,kg^2}} = 6\,kg$ (to one significant figure)
So the total mass is (210 ± 6) kg.
Suppose we now want the error in the difference between two quantities, say X = A − B. i
The error in the difference is not equal to the difference between the errors, or even to the square root of the difference between the squares of the two errors. Even when subtracting two quantities the resulting error must be larger than either of the individual errors. In fact the same rule applies, so:
If X = A + B, or X = A − B, the error in X is given by:
$\delta X= \sqrt{\smash[b]{(\delta A)^2 +(\delta B)^2}}$(Eqn 6)
✦ The temperature in a room before a heater is switched on is (16.2 ± 0.4)°C, and one hour after the heater is switched on it is (22.7 ± 0.4)°C. What is the temperature rise T?
✧ T = (22.7 − 16.2)°C ±$\delta$T = 6.5°C ±$\delta$T
where$\delta T = \sqrt{\smash[b]{(0.4°C)^2 + (0.4°C)^2}} = 0.6°C$
So we can quote the temperature difference as
T = (6.5 ± 0.6)°C
In error analysis it is common to use fractional errors or percentage errors in assessing the reliability of a measurement. If $\delta$A is the absolute error in A then the fractional error is defined as $\dfrac{\delta A}{A}$ and the percentage error as $\dfrac{\delta A}{A} \times 100$
When calculating differences between two quantities of similar size you should be alert to the very large percentage effect that errors in A and B can have on the difference quantity X. For example, in the example given here the percentage error in A is $\left(100 \times \dfrac{0.4}{22.7}\right) = 1.8\%$ and that in B is $\left(100 \times \dfrac{0.4}{16.2}\right) = 2.5\%$, yet the percentage error in X is $\left(100 \times \dfrac{0.6}{6.5}\right) = 9.2\%$. This scaling of the percentage error effect becomes very large as A and B approach the same size.
When dealing with sums and differences it is the numerical size of the errors that is relevant, not their sign, and so we use their absolute values (i.e. the values ignoring signs), these are called the absolute errors.
Question T4
Two objects have masses (100 ± 0.4) g and (98 ± 0.3) g. What is (i) the absolute error and (ii) the percentage error:
(a) on the sum of their masses, and (b) on the difference between their masses?
Answer T4
(a) error = [(0.4)2 + (0.3)2]1/2 g = (0.16 + 0.09)1/2 g = (0.25)1/2 g = 0.5 g; percentage error is
$\pm \left(\dfrac{0.5\,\rm{g}}{198\,\rm{g}}\right) \times 100 = 0.25\%$
(b) As in (a), error = 0.5 g; percentage error is
$\pm \left(\dfrac{0.5\,\rm{g}}{2\,\rm{g}}\right) \times 100 = 25\%$
Products and quotients
When estimating the errors arising from products and quotients it turns out that our computations involve the fractional errors, $\delta A/A$ and $\delta B/B$, rather than the absolute errors, $\delta A$ and $\delta B$.
Study comment We are here combining errors in quantities A and B which in general will have different dimensions, for example A could be a length and B a time. When we combine the errors we can only add quantities of the same dimension – it makes no sense to produce something which claims to add metres to seconds! So, when we combine the errors we must use dimensionless errors, either fractional errors or percentage errors, and never absolute errors (unless A and B happen to have the same dimensions).
If X = AB, or X = A/B, the error in X is given by:
$\delta X/X= \sqrt{\smash[b]{\smash[b]{(\delta A/A)^2 +(\delta B/B)^2}}}$(7)
✦ The speed υ of a train is measured as (80 ± 5) km h−1 over a measured time t of (0.20 ± 0.02) h. What distance s does the train travel in this time?
✧ In this case s = υ × t = (80 km h−1 × 0.20 h) ±$\delta$s = 16 km ±$\delta$s
and$\delta s/s = \sqrt{\smash[b]{(\delta \upsilon/\upsilon)^2+(\delta t/t)^2}} = \sqrt{\smash[b]{(5/80)^2+(0.02/0.20)^2}} = \sqrt{3.9\times10^{-3}+10^{-2}} = 0.12$
so$\delta$s = 0.12 × s = 0.12 × 16 km = 2 km
The result is therefore s = (16 ± 2) km i
Question T5
A motorist drives at a constant speed such that the reading on the speedometer is 40 miles per hour (i.e. 40 mph). The speedometer is assumed to be accurate to ±2 mph. At the end of the morning, he would like to know how far he has travelled but unfortunately he forgot to look at the mileage indicator when he set out. He reckoned that he had been driving for 4 h, give or take a quarter of an hour. Estimate how far he has travelled and assign an error to your result.
Answer T5
s = υt, where s = distance travelled, υ = speed, and t = time. Therefore, s = 40 mph × 4 h = 160 miles
$\delta$υ = 2 mph and $\delta$t = 0.25 h
So $\delta$s/s = [(2/40)2 + (0.25/4)2]1/2 = [(0.05)2 + (0.0625)2]1/2
$\delta$s/s = (0.0025 + 0.0039)1/2 = (0.0064)1/2 = 0.08
Thus $\delta$s = 0.08 × s = 0.08 × 160 miles = 12.8 miles ≈ 13 miles.
The motorist has therefore travelled (160 ± 13) miles.
What about products (or quotients) that involve constants?
If a constant k, which has no error associated with it, is involved, and X = kA
then $\delta$X = k$\delta$A(8)
and$\delta$X/X = $\delta$A/A(9)
So the constant has no effect on the fractional error.
Powers
The final important case to consider is when a measured quantity is raised to a power.
If X = A n, the error in X is given by:
$\delta$X/X = n ($\delta$A/A)(10)
Equation 10 can be derived using calculus, which is not required for the module. However, you can see that it is reasonable with the following example.
✦ The diameter of a sphere is measured as (7.2 ± 0.5) cm. What is its volume?
✧ The volume of a sphere of diameter d is given by,
V = (πd3)/6 = (π/6) × (7.2 cm)3 = 1.95 × 102 cm3
The value π/6 is a constant, so it doesn’t change the fractional error and so we only need to worry about the error in d3. From Equation 10,
$\delta$X/X = n ($\delta$A/A)(Eqn 10)
we can say
$\delta$V/V = 3$\delta$d/d = (3 × 0.5 cm)/7.2 cm = 0.21
therefore
$\delta$V = 0.21 × V = 0.21 × (1.95 × 102 cm3) = 41 cm3
Hence the volume of the sphere is
V = (2.0 ± 0.4) × 102 cm3.
If we now compare the fractional errors in V with that for d we find:
Fractional error in d is $\displaystyle \left(\pm \dfrac{0.5\,\rm{cm}}{7.2\,\rm{cm}}\right) \approx 0.07$
The maximum value for V is thus $\displaystyle \dfrac{\pi}{6}d_{\rm max}^3= \dfrac{\pi}{6}(7.7\,\rm{cm})^3= 2.39 \times 10^2\,\rm{cm^3}$
So $\delta$V = (2.39 × 102 − 1.95 × 102) cm3 = 44 cm3
Therefore, the fractional error in V for the maximum departure from the mean is
$\displaystyle \left(\pm \dfrac{44\,\rm{cm^3}}{195\,\rm{cm^3}}\right) \approx 0.23$
We note that the fractional error in V is approximately three times greater than that for d, in agreement with Equation 10.
$\delta$X/X = n ($\delta$A/A)(Eqn 10)
Note As you have just seen, the fractional error in a spherical volume is three times larger than the fractional error in the measured diameter. Because errors increase so rapidly when powers are involved, you should always take particular care to reduce errors when measuring quantities that will be raised to a power. Note also that it would be wrong to reason that
V = (π/6) × d × d × d
therefore$\delta V/V=\sqrt{\smash[b]{(\delta d/d)^2+(\delta d/d)^2+(\delta d/d)^2}} = 3(\delta d/d)$
The equation for the error in a product cannot be used in this case, because the three terms that have to be multiplied are exactly the same – and therefore are certainly not independent.
Question T6
The area of a circle is given by: A = πr2, where r is the radius. What is the error in the value of the area of a circle the radius of which is determined as (14.6 ± 0.5) cm?
Answer T6
A = [π × (14.6)2] cm2 = 669.7 cm2 ≈ 670 cm2
$\delta$A/A = 2$\delta$r/r
Therefore $\delta$A/670 cm2 = (2 × 0.5)/14.6
Therefore $\delta$A = 45.9 cm2 ≈ 46 cm2
So A = (670 ± 46) cm2
More than two quantities
When more than two quantities are involved in products and sums, the equations are extended in a straightforward way. The general results are given in the summary to this module, but you should not find it hard to see how the results should be extended from two to three quantities.
Question T7
Three objects have masses (100.0 ± 0.4) g, (50.0 ± 0.3) g and (200.0 ± 0.5) g. What is the error in their sum?
Answer T7
When there are more than two quantities, the same rule applies: the error is equal to the square root of the sum of the squares of the separate errors.
Error on the sum = [(0.4)2 + (0.3)2 + (0.5)2]1/2 g = (0.16 + 0.09 + 0.25)1/2 g = (0.50)1/2 g = 0.7 g
i.e. sum = (350.0 ± 0.7) g
Question T8
The volume of a rectangular block is calculated from the following measurements of its dimensions: (10.00 ± 0.10) cm, (5.00 ± 0.05) cm, and (4.00 ± 0.04) cm. What is the error in the value of the volume of the block assuming that the errors are independent?
Answer T8
V = abc, where V = volume, and a, b and c, are the dimensions of the block.
So V = (10.00 × 5.00 × 4.00) cm2 = 200 cm2
$\delta$V/V = [($\delta$a/a)2 + ($\delta$b/b)2 + ($\delta$c/c)2]1/2 = [(0.10/10.00)2 + (0.05/5.00)2 + (0.04/4.00)2]1/2
= (0.0001 + 0.0001 + 0.0001)1/2
= (3 × 0.0001)1/2 = $\sqrt{0.0003\os}$ = 0.017
Therefore $\delta$V = 0.017 × 200 cm2 = 3 cm2 and V = (200 ± 3) cm2
Basic functions
For the sake of completeness we note the following expressions for errors in functions:
| If | X = loge A | then | $\delta$X = $\delta$A/A | ||
| If | X = exp A | then | $\delta$X/X = $\delta$A | ||
| If | X = sin A | then | $\delta$X = cos A $\delta$A | $\bigg \rbrace$ | where A is in radians and $\delta$A is small |
| If | X = cos A | then | $\delta$X = −sin A $\delta$A |
3.3 Treatment of dependent errors
In the discussion up to now we have assumed that the errors we are combining are completely independent. For example, in the case of the water flow measurements (first introduced in Subsection 2.1), we assume that systematic errors in the measurements of time will not be related in any way to the random errors in the measurements of volume. However, it is by no means always true that errors are independent in this way. For example, suppose we are measuring the length and breadth of a piece of paper with a ruler in order to obtain the area (= length × breadth), and we know that there is a systematic error in the ruler. In this case the errors in both measurements will be in the same direction; if one is too high the other will also be too high. So when we come to combine the errors in length and breadth, we cannot assume that they are independent. In this case the overall error is more like the sum of the individual errors. In some situations it can happen that a large positive error in one quantity results in a large negative error in another quantity, thus causing cancellation and an overall error that is much smaller than the individual errors.
No precise rules can be given for dealing with dependent errors (except of course for the simple case of a number raised to a power, discussed above). You will have to consider each case on its merits using the general principles that have been introduced.
4 Miscellaneous tips about errors
4.1 Taking measurements so as to reduce errors
It has already been stressed that a few precise measurements are generally of more value than many imprecise measurements. Here are a few general points about how to achieve such measurements.
Concentrate on reducing the dominant errors As we have just shown, the largest errors will dominate the error in the final result, and small errors can often be neglected. This is particularly true since combining errors involves squaring and adding the squares. It is therefore, very important when doing experiments not to waste a lot of time reducing small errors when much larger errors are also present.
Find out as early as possible in an experiment what are the dominant errors, and then concentrate your time and effort on reducing them. Often a pilot experiment will achieve this, as will a look at the formula to be used for combining the measurements.
Take care when differences and powers are involved We saw the results of this in Subsection 3.2.
If calculating the result of an experiment involves taking the difference between two nearly equal measured quantities, or taking the power of a measured quantity, then pay particular attention to reducing the errors in those quantities.
4.2 Tips about error calculations
Don’t worry about errors in the errors Errors, by their very nature, cannot be precisely quantified. So a statement such as L = (2.732 ± 0.312) m is rather silly, an error of 0.312 pretends to be overly precise, and the result should be quoted as L = (2.7 ± 0.3) m. As a general rule:
Errors should usually be quoted only to one or (at most) two significant figures. You should bear this in mind when trying to assess the magnitude of errors, and when doing calculations involving errors. Don’t be concerned about errors (of say 30%) in your errors – they don’t really matter.
Neglecting small errors The total error in a result may be the combination of several contributing errors, and these contributing errors may have widely varying sizes. But, because the errors (or fractional errors) combine as the sum of the squares, the following general rule applies:
When calculating errors in sums and differences, as a rule of thumb, you may ignore any errors that are less than 1/3 of the largest error, and when calculating errors in products and quotients, ignore any fractional error that is less than 1/3 of the largest fractional error.
5 Closing items
5.1 Module summary
- 1
-
Measured values of physical quantities are generally subject to error or uncertainty.
- 2
-
Sources of error may be divided into two kinds: random and systematic. Random errors alone cause the measured values of a quantity to be distributed around the true value of that quantity and are revealed by repeated measurement. Systematic errors always affect a given measurement in the same way and are therefore not revealed by repeated measurement. Systematic errors will generally cause the measurements to be distributed about some value other than the true value.
- 3
-
The mean of n measured values of a quantity x (x1, x2, x3, x4, ... xn−2, xn−1, xn) is defined by
$\displaystyle \langle x \rangle = \dfrac{x_1+x_2+x_3+x_4+\ldots+x_{n-2}+x_{n-1}+x_n}{n} = \dfrac{1}{n} \sum_{i=1}^n x_i$(Eqn 1)
- 4
-
The Subsection 2.2standard deviation of n measured values of x, with a mean $\langle x \rangle$ is defined by
$\displaystyle \sigma_n=\sqrt{\dfrac{d_1^2+d_2^2+\ldots+d_n^2}{n}}=\left(\dfrac 1n \sum_{i=1}^n d_i^2\right)^{1/2}$(Eqn 2)
where $d_i= x_i - \langle x \rangle$ is the deviation of the ith measurement from the mean. For normally distributed readings σn provides an objective measure of the spread of the readings, in that roughly 68% of the readings would be expected to be in the range $\langle x \rangle \pm\sigma_n$ for a sufficiently large number of readings.
- 5
-
The Subsection 2.3standard error in the mean sm provides a measure of how close the mean $\langle x \rangle$ of a set of n measurements of a quantity x, with standard deviation σn is likely to be to the (unknown) true value of x, in the absence of systematic errors. The value of sm may be estimated from
$s_m = \dfrac{\sigma_n}{\sqrt{\smash[b]{n-1\os}}}$(Eqn 3)
This is often taken as the best estimate of the random error in the repeated measurements. For normally distributed readings there is a roughly 68% chance that the true value of the measured quantity will be in the range $\langle x \rangle \pm s_m$.
- 6
-
The rule for combining independent errors ±e1, ±e2 ... ±en in a single measured quantity to find the overall probable error ±E is
$E=\sqrt{\smash[b]{e_1^2+e_2^2+\ldots+e_n^2}}$(Eqn 5)
- 7
-
Assuming that independent measurements A and B, which have total errors $\delta$A and $\delta$B associated with them, are combined to give the result X, which has error $\delta$X, we find the rules for combining errors in an algebraic expression to be as follows:
Sums and differences
$\left.\substack{\large{\text{If}\quad\,X~=~A~+~B\\\text{or}\quad X~=A~-~B\us}}~\right\rbrace\quad\text{then}\quad\delta X = \sqrt{\smash[b]{(\delta A)^2+(\delta B)^2}}$
(A and B have the same dimensions)
Products and quotients
$\left.\substack{\large{\text{If}\quad\,X~=~AB\\\text{or}\quad X~=~A/B\us}}~\right\rbrace\quad\text{then}\quad\dfrac{\delta X}{X} = \sqrt{\left(\dfrac{\delta A}{A}\right)^2 + \left(\dfrac{\delta B}{B}\right)^2}$
(A and B may have different dimensions)
Powers
IfX = A n then $\dfrac{\delta X}{X} = n \dfrac{\delta A}{A}$
Constants
When a measurement A is multiplied by a constant k, which has no error associated with it, as in the formula
$X = kA\quad\text{then}\quad\delta X = k\delta A \quad\text{and}\quad\dfrac{\delta X}{X} = \dfrac{\delta A}{A}$
$\left.\substack{\large{\text{If}\quad\,X~=~kA~+~B\\\text{or}\quad X~=~kA~-~B\us}}~\right\rbrace\quad\text{then}\quad\delta X = \sqrt{\smash[b]{(k\delta A)^2+(\delta B)^2}}$
$\left.\substack{\large{\text{If}\quad X~=~kAB\\\text{or}\quad X~=~kA/B\us}}~\right\rbrace\quad\text{then}\quad\dfrac{\delta X}{X}=\sqrt{\left(\dfrac{\delta A}{A}\right)^2+\left(\dfrac{\delta B}{B}\right)^2}$
X = kAn then $\dfrac{\delta X}{X} = n\dfrac{\delta A}{A}$
(so the constant has no effect on the fractional error)
- 8
-
When more than two quantities are involved, the equations given above are extended in a straightforward way:
IfX = A ± B ± C ± D (e.g. X = A + B − C + D) then $\delta X = \sqrt{\smash[b]{(\delta A)^2+ (\delta B)^2+ (\delta C)^2+ (\delta D)^2}}$
(notice that only plus signs appear under the square root)
If$ X = \dfrac{A\times B}{C\times D}$ then $\dfrac{\delta X}{X} = \sqrt{\left(\dfrac{\delta A}{A}\right)^2+ \left(\dfrac{\delta B}{B}\right)^2+ \left(\dfrac{\delta C}{C}\right)^2+ \left(\dfrac{\delta D}{D}\right)^2}$
(again notice that only plus signs appear under the square root)
5.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Calculate the mean and standard deviation of a set of measurements.
- A3
-
Calculate the standard error in the mean of a set of measurements.
- A4
-
Combine several independent errors in a single quantity to produce an overall error.
- A5
-
Estimate the total error in a quantity that depends on several measured quantities, each with its own error.
Study comment You may now wish to take the Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
5.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions each of which tests one or more of the Achievements.
Question E1 (A2 and A3)
The masses in grams (g) of 20 copper spheres were as follows: 280, 275, 283, 264, 272, 280, 290, 287, 283, 276, 278, 282, 280, 288, 282, 265, 291, 282, 279, 278. All measurements were made to the nearest gram.
Calculate (a) the mean, (b) the standard deviation, and (c) the standard error in the mean.
Answer E1
(a) 279.75 g, (b) 6.9 g, (c) 1.6 g
(Reread Section 2 if you had difficulty with this question.)
Question E2 (A5)
The period T of a simple pendulum is given by the expression
$T=2\pi \sqrt{\smash[b]{L/g}}$
where L is the length of the pendulum and g is the magnitude of the acceleration due to gravity.
A pendulum of length (0.600 ± 0.002) m is used to determine the value of g. The value of T was found to be (1.55 ± 0.01) s. Find the percentage error in the value of g.
Answer E2
If the equation is rearranged to make g the subject, we find g = (4π2L)/T 2.
The fractional error in g is given by the equation:
$\delta$g/g = [($\delta$L/L)2 + ($\delta$(T 2)/T 2)2]1/2
Now$\delta$(T 2)/T 2 = 2$\delta$T/T
So$\delta$g/g = [($\delta$L/L)2 + (2$\delta$T/T)2]1/2
So$\delta$g/g = [(0.002/0.600)2 + (2 × 0.01/1.55)2]1/2 = 1.33 × 10−2
i.e.$\delta$g = 9.86 m s−2 × 1.33 × 10−2 = 0.13 m s−2
and the result of the experiment would be quoted as
g = (9.86 ± 0.13) m s−2
Percentage error = (0.13 × 100%)/9.86 = 1.3%
(Reread Section 3 if you had difficulty with this question.)
Question E3 (A5)
Two objects are weighed and each is found to be 200 g with an error of 0.5%. What is the percentage error in the sum of their masses?
Answer E3
The error in each mass determination = (0.5/100) × 200 g = 1 g.
Error on sum = 12 + 12 g = 2 g = 1.4 g
i.e. the sum of the masses = (400 ± 1.4) g
Percentage error = (1.4 × 100%)/(200 + 200) = 0.35%
(Reread Subsection 3.2 if you had difficulty with this question.)
Question E4 (A5)
(a) Given that υ = f λ, what is the value of υ if f = (2.0 ± 0.1) kHz and λ = (0.15 ± 0.02) m?
(b) Given that x = L − L0, what is the value of x if L = (1.10 ± 0.02) m and L0 = (1.01 ± 0.02) m?
(c) Given that a = mυ2/r, what is the value of a if m = (1.0 ± 0.1) kg, υ = (100 ± 4) m s−1 and r = (200 ± 10) m?
Answer E4
(a) υ = (300 ± 43) m s−1, (b) x = (0.09 ± 0.03) m, (c) a = (50 ± 7) kg m s−2
(Reread Subsection 3.2 if you had difficulty with this question.)
Question E5 (A5)
The pressure of a gas is the magnitude of the force exerted per unit area. If the force magnitude is (20.0 ± 0.5) N, and the area is rectangular with sides (5.0 ± 0.2) mm and (10.0 ± 0.5) mm, what is the fractional error on the value of the pressure and what is the pressure (in N m−2)?
Answer E5
P = F/(a × b), where P = pressure, F = force magnitude, a and b are the lengths of the sides of the area. Since the same rule applies for finding the errors on the quotients as on the products, the same rule will apply to a mixture of quotient and product.
$\delta$P/P = [($\delta$F/F)2 + ($\delta$a/a)2 + ($\delta$b/b)2]1/2 = [(0.5/20)2 + (0.2/5)2 + (0.5/10)2]1/2 = 0.0687 ≈ 0.069
$\delta$P = 0.069 × 4 × 105 N m−2 ≈ 0.3 × 105 N m−2
P = (4 ± 0.3) × 105 N m−2
(Reread Subsection 3.2 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 5Closing items.