PHYS 2.6: Circular motion |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
Why study circular motion?
For the ancient Greeks the circle symbolized perfection. The fact that the Sun, Moon and stars appeared to move around the Earth in circular paths was evidence of their status as ‘heavenly bodies’. Circular motion was supposedly their natural state. Today we know that the Greek picture of how things move was wrong. The ‘natural state’ of any body, heavenly or otherwise, is motion in a straight line at constant speed unless it is subject to a force. Why then do we need to study circular motion?
Although we don’t regard movement in a circle with the same reverence as did the ancient Greeks, it is still a very useful concept. If we restrict our discussion to circular motion at constant speed (called uniform circular motion), then its mathematical description turns out to be quite straightforward. There are many situations in nature which approximate to uniform circular motion; the motion of the Earth around the Sun, the orbits of the Moon and artificial satellites around the Earth, fairground rides, cars going around bends and the internal workings of washing machines are just some examples which come to mind.
This module deals with the physics of uniform circular motion and its applications. Some examples of uniform circular motion, e.g. artificial Earth satellites, are described in Section 2 to give you a ‘feel’ for what they have in common. This leads in to a more rigorous, mathematical description of circular motion in Section 3, where the terms angular speed and centripetal acceleration are introduced. Some practical applications of these ideas are discussed in Section 4.
Before you start to work through the material, here are a couple of questions you might like to ponder. By the time you reach the end of Section 3 you should be in a position to answer them yourself. Detailed explanations of the answers to these questions are given in Section 4.
Suppose you are designing a motorway. How can you ensure that the bends will not cause vehicles travelling at 70 mph to skid?
Communications satellites are most effective if they are permanently positioned above a particular point on the Earth’s surface. How is this possible? Can you position such a satellite above any point on the Earth’s surface? Could you, for example, have one permanently stationed over Britain?
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the Subsection 1.2Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 5.1Module summary and the Subsection 5.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 5.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
Show, from first principles, that an object undergoing uniform circular motion must be experiencing an acceleration which is directed towards the centre of the circle and has a magnitude υ2/r where υ is the speed of the object and r is the radius of the circle.
Answer F1
The proof of this very important result is given in Subsections 3.1 and 3.3 and is illustrated in Figures 6, 7 and 8. Compare this discussion with your own answer and revise the relevant subsections if necessary. In brief, the argument is first to show that a body in uniform circular motion has an acceleration towards the centre of the orbit. This is true both for the average acceleration between any two different points on the path and also for the instantaneous acceleration at any point on the path. This proof involves taking the limit as the interval tends to zero, and using the calculus notation. As a second stage, the magnitude of the acceleration (centripetal acceleration) is shown to equal υ2/r or the two equivalent expressions υω or rω2. This is an important argument and you should be sure that you are happy with it.
Question F2
A planet orbiting a star experiences a force of magnitude 3.0 × 1022 N due to the gravitational attraction of the star. If the planet has a speed of 2.0 × 1015 m s−1 and it takes 2.6 × 107 s to complete one orbit, calculate the mass of the planet and the radius of its orbit.
Answer F2
We are given the speed υ and the magnitude of the centripetal force F for the planet. We can calculate its angular speed ω from the orbital period T using
ω = 2π/T(Eqn 5)
In this case
$\omega = \dfrac{2\pi}{2.6\times 10^7}$ rad s−1 = 2.4 × 10−7 rad s−1
We can now calculate m using a rearrangement of Equation 10a
F = ma = mυω(Eqn 10a)
m = F/υω
Hence$m = \dfrac{3.0 \times 10^{22}}{2.0 \times 10^5 \times 2.4 \times 10^{-7}}$ kg = 6.3 × 10 kg
The radius of the orbit can be found from Equation 10c
F = ma = mrω2(Eqn 10c)
r = F/mω2
So,$r = \dfrac{3.0 \times 10^{22}}{6.3 \times 10^{23}\times 2.4 \times 10^{-7}}$ m = 8.3 × 10 m
1.3 Ready to study?
Study comment To study this module you will need to understand the following terms: acceleration, arc length, force, gravity, mass, Newton’s laws of motion, radian, radius, speed, tangent_to_a_curvetangent, velocity, weight. There are also some mathematical topics with which you will need to be familiar before starting to study: derivative, magnitude of a vector, Pythagoras’s theorem, scalar, triangle_ruletriangle rule for addition of vectors, trigonometry, vector. If you are uncertain about any of these ideas then you can review them now by reference to the Glossary, which will also indicate where in FLAP they are developed. The following questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
A cyclist moving along a straight road accelerates uniformly from 5.00 m/s to 10.0 m/s in 10.0 s. Calculate:
(a) the magnitude of the acceleration;
(b) the average speed over the interval;
(c) the distance travelled over the interval.
Answer R1
(a) If the acceleration is uniform, its magnitude_of_a_vector_or_vector_quantitymagnitude a can be expressed as
$a = \dfrac{\Delta\upsilon}{\Delta t}$
where ∆υ is the magnitude of the change in velocity during the time interval ∆t
$a = \dfrac{10.0 - 5.00}{10.0}$ m s−2 = 0.500 m s−2
(b) For uniform acceleration, the average speed $\langle\upsilon\rangle$ in the time interval ∆t is given by
$\langle\upsilon\rangle = \dfrac{\upsilon_0+\upsilon_1}{2}$
where υ0 and υ1 are the initial and final speeds, respectively. So for this case,
$\langle\upsilon\rangle = \dfrac{5.00+10.0}{2}$ m s−1 = 7.5 m s−1
(c) The distance travelled is ∆s = $\langle\upsilon\rangle$ ∆t = (7.50 × 10.0) m = 75.0 m
(If you are unclear about any of these terms consult the Glossary.)
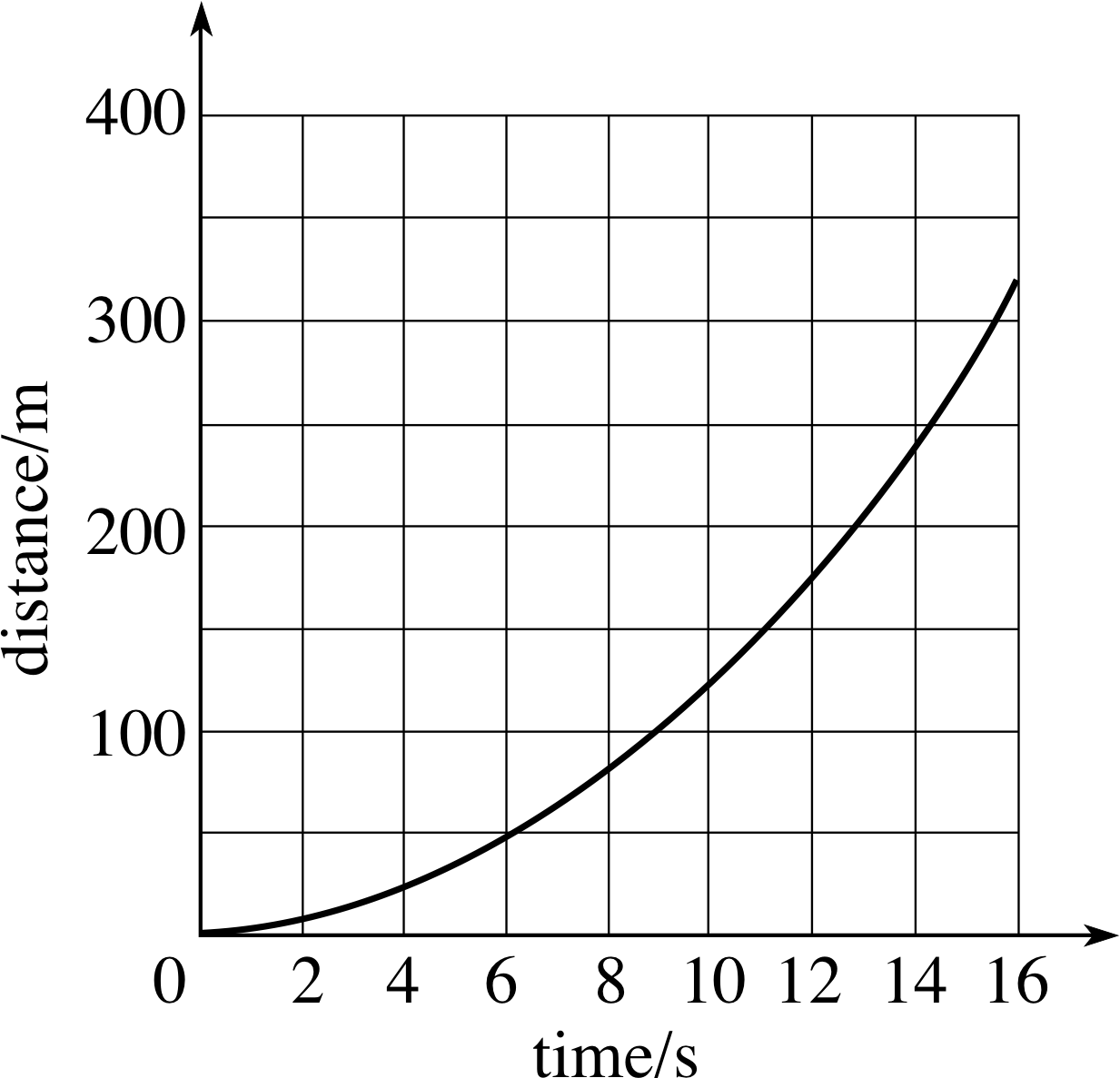
Figure 1 See Question R2.
Question R2
Figure 1 shows a graph of distance s travelled against time for an aircraft on a runway, accelerating towards take-off.
(a) Calculate the average speed between times t = 5 s and t = 15 s.
(b) Use the graph to estimate the instantaneous speeds at the same two times.
(c) Estimate the average acceleration between t = 5 s and t = 15 s.
Answer R2
(a) The average speed is $\langle\upsilon\rangle$ = ∆s/∆t where ∆s is the distance travelled in the time interval ∆t.
In this case $\langle\upsilon\rangle = \dfrac{270 - 40}{10}$ m s−1 = 23 m s−1
(b) The instantaneous speeds at t = 5 s and t = 15 s are obtained by drawing tangent_to_a_curvetangent lines to the graph at these points. This gives the following results
for t = 5 s υ5 = 12 m s−1
for t = 15 s υ15 = 36 m s−1
(c) The average acceleration in this time interval is
$\langle a \rangle = \dfrac{\left\lvert\,\Delta\upsilon\,\right\rvert}{\Delta d} = \dfrac{\left\vert\,\upsilon_{15}-\upsilon_5\,\right\rvert}{\Delta t} = \dfrac{36-12}{10}$ m s−2 = 2.4 m s−2
Comment Because these values are calculated from a graph, your answers to parts (b) and (c) may differ from those given here. Values within 10% of the quoted figures are acceptable. (If you are unclear about any of these terms consult the Glossary.)
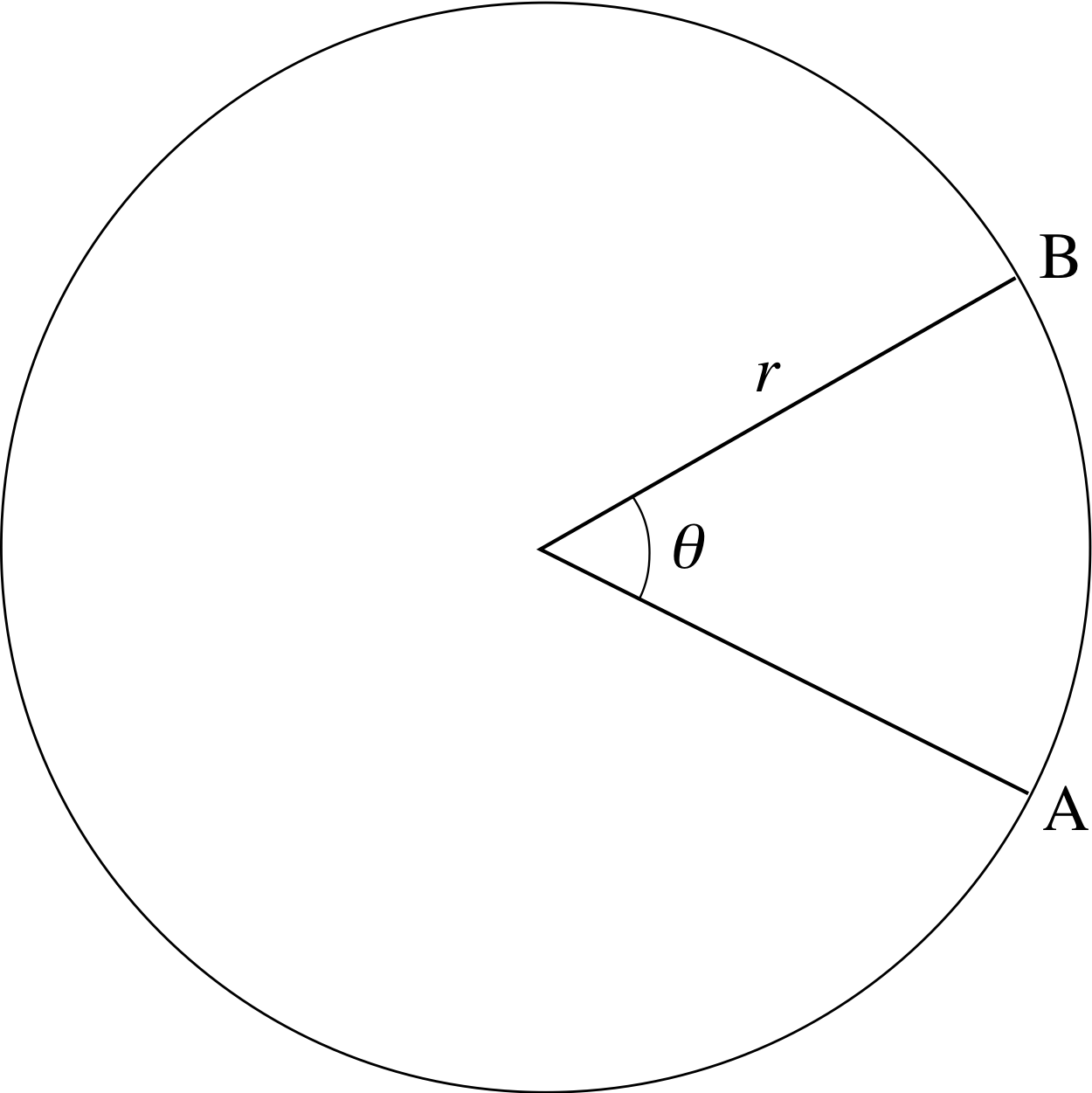
Figure 2 See Question R3.
Question R3
In Figure 2 if the arc length AB is 10 cm, and the radius r is 12 cm, calculate the angle θ in radians.
Answer R3
The value of an angle in radians can be calculated from the relationship s = rθ or θ = s/r, where s is the arc length and r is the radius.
In this case $\theta = \dfrac{10}{12}$ rad = 0.83 rad
Comment If you are unclear about any of these terms consult the Glossary.
Question R4
The vector a points North and has a magnitude_of_a_vector_or_vector_quantitymagnitude of 4 units; the vector b points East and has a magnitude of 3 units. Describe the vector c where c = a + b.
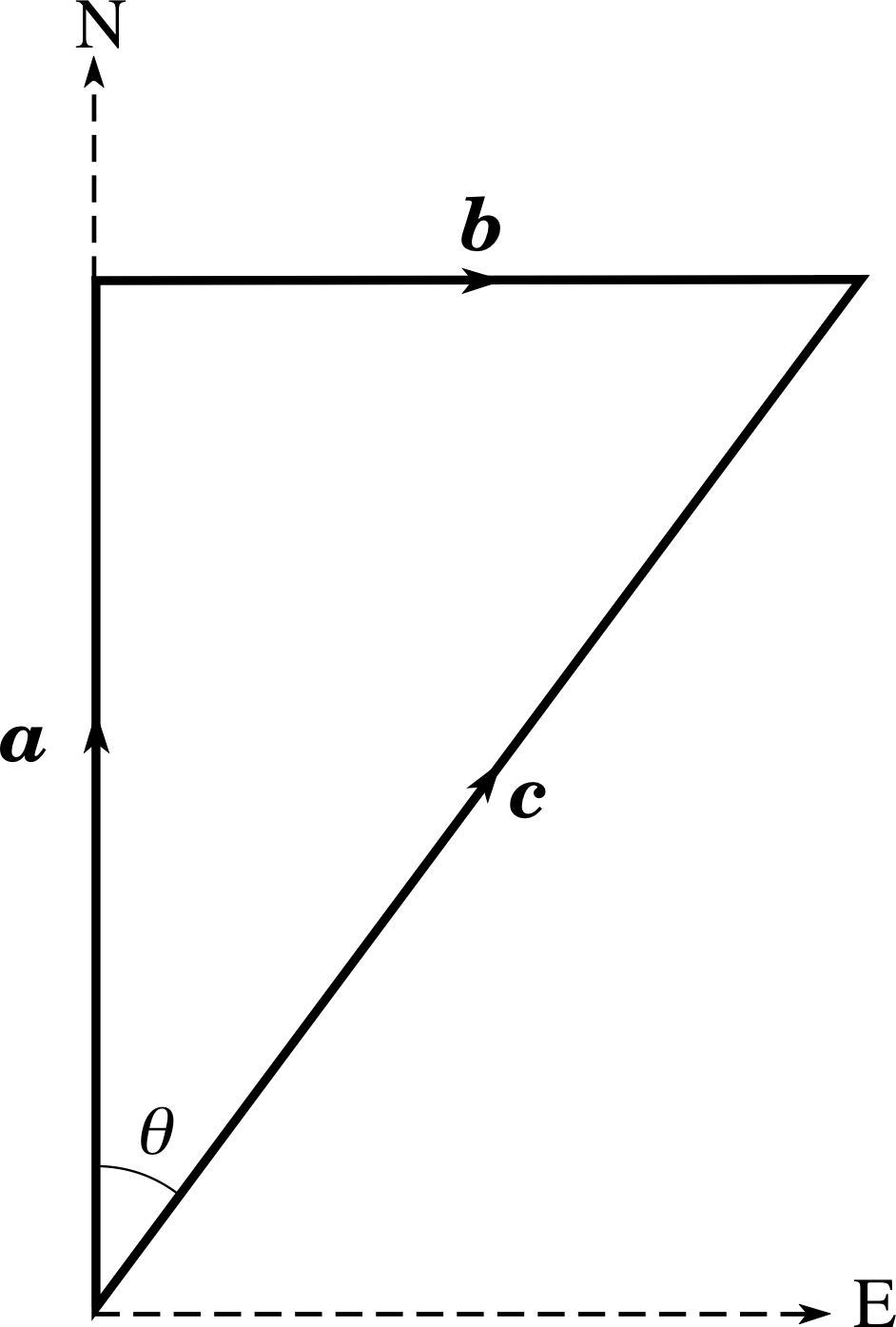
Figure 9 See Question R4.
Answer R4
The addition of a and b is carried out according to the usual triangle_ruletriangle rule for the addition of vectors. This is shown in Figure 9. From Figure 9, the vector c has a magnitude_of_a_vector_or_vector_quantitymagnitude of 5 units and a direction 37° East of North. This can be determined either by measurement from the figure or from Pythagoras’s theorem and trigonometry. Thus
$c^2 = a^2 + b^2$
$c = \sqrt{a^2+b^2} = \sqrt{4^2+3^2} = 5$
and$\sin\theta = \dfrac bc = \dfrac35$
Thereforeθ = 37°
Comment More information on this topic is contained in the maths strand of FLAP. (If you are unclear about any of these terms consult the Glossary.)
2 Characteristics of uniform circular motion
Uniform circular motion is simply motion in a circle at constant speed. In this section we will look at some of the situations in which this kind of motion occurs and we will consider some of its characteristics.
2.1 A satellite in a circular orbit

Figure 3a Launching a snowball.
Imagine yourself at the North Pole, throwing a snowball horizontally as hard as you can. It would hit the ground some distance away from you (Figure 3a) and if you knew its initial velocity you could easily work out how far it would travel by considering it as a projectile, moving along a parabolic path. i

Figure 3b/c Putting a snowball into orbit.

Figure 3b/c Putting a snowball into orbit.
If you were able to project it faster and faster (say from some kind of gun), it would travel further and further before touching down. At higher speeds you would have to take the curvature of the Earth into account in order to predict where it would land (Figure 3b). Finally, if you gave the snowball exactly the right horizontal velocity, you would find that the Earth’s surface would ‘fall away’ from the snowball, because of the curvature, at just the same rate as the snowball falls towards the Earth. It would then describe a circle around the Earth and arrive back at the starting point with exactly the same speed as when it set out (Figure 3c). For its whole journey, the snowball would be travelling at constant speed at the same fixed height above the Earth’s surface.
Could this really happen? I have to admit the answer is ‘No’. The snowball would be slowed down by air resistance, its path would be affected by the slightly non–spherical shape of the Earth and, travelling just above the ground, it would almost certainly collide with something. However, if it were to start off several hundred kilometres above the Earth’s surface, air resistance and the non–spherical shape of the Earth would be unimportant and a circular path would be feasible.
This is similar to an artificial Earth satellite (often abbreviated to ‘satellite’) being put into orbit. If it is sent up in a rocket to the desired height and given the appropriate velocity it will start to circle the Earth at constant speed.
Figure 4 Possible circular orbits for a satellite. All have the centre of the Earth at the centre of the orbital plane.
Notice that I said ‘appropriate velocity’. This means that both direction and speed must be correctly specified. The direction must be such that the satellite’s initial movement is parallel to the Earth’s surface and the centre of the Earth must lie at the centre of the plane of the orbit, as in Figure 4. The reason why the velocity has to be chosen so carefully will be explained in Subsection 4.2. For the moment, it is enough to say that if either the initial direction or speed is wrong then the path of the satellite will not be circular; such non–circular paths are outside the scope of this module.
We will now consider what controls this motion of the satellite; to do this we must revise briefly the idea of forces and their consequences.
2.2 A review of Newton’s first and second laws of motion
Newton’s insight into the motion of bodies was to recognize that if left to themselves bodies continue to move uniformly, that is to say with constant velocity – with constant speed in a straight line. This is a statement of Newton’s first law of motion.
To change the motion of a body requires the action of an unbalanced i force. When such a force acts on a body an acceleration of the body results, with the magnitude of the acceleration being proportional to the magnitude of the force and inversely proportional to the mass of the body; the acceleration is also in the same direction as the force. This is a statement of Newton’s second law of motion. This second law defines mass m and force F together in a common statement which can be written in mathematical terms as
F = ma(1)
This concise statement summarizes our experience that:
- If no unbalanced force acts (including friction) then a body moves with constant speed in a fixed direction (i.e. has zero acceleration).
- When an unbalanced force acts, the change in velocity (and therefore the acceleration) is along the direction of the force.
- For any given body, the larger the unbalanced force acting, the larger the resulting acceleration.
- For any given unbalanced force, the more massive the body, the smaller the resulting acceleration. i
Let us use these ideas to look at the satellite problem posed in Subsection 1.1, and in particular to consider what forces and accelerations are present.
✦ What is the main force acting on the satellite and how does the direction of this force relate to the direction of motion of the satellite?
✧ The only significant force which the satellite experiences is that due to the Earth’s gravitational attraction. Its direction is always towards the centre of the Earth – and therefore towards the centre of the circle which describes the satellite’s orbit. At all points in the orbit, the direction of the satellite’s motion is tangential, i.e. acting along a tangent_to_a_curvetangent to the circle. Since the force is radial, i.e. directed towards the centre of the circle, and the motion is tangential, it follows that at all points in the orbit the force acting on the satellite is perpendicular to its direction of motion.
✦ How does the magnitude of the force on the satellite vary as the satellite moves around the orbit?
✧ The force acting on the satellite arises from the gravitational attraction of the Earth. Later, in Subsection 4.2, we will discuss this quantitatively. For the moment we need to accept only that this force decreases in some way as distance from the Earth increases. Since in this case this distance is constant, it is reasonable to assume that the force has a constant magnitude.
2.3 A simple experiment
Figure 5 The ‘whirling pencil rubber’ experiment. (a) How to do it. (b) What you should see in fluorescent light.
Here is a short experiment you can carry out to look at circular motion in a different context. Take a piece of elastic about 20 cm in length and tie one end of it securely to a pencil rubber. Now, while holding the elastic, whirl the rubber round (carefully!) so that it moves in approximately horizontal circles at a uniform speed as in Figure 5a. You can check that it is moving at a roughly uniform speed by doing the experiment in fluorescent light. Because fluorescent light flashes on and off 100 times per second your eye should register a series of ‘still’ images of the elastic and rubber. If the images appear evenly spaced as in Figure 5b and the motion is circular, the rubber must be moving with a uniform speed.
We can ask the same questions here as we asked for the satellite in the previous section.
✦ What force causes the pencil rubber to move in a circle?
✧ The force responsible for the circular motion is the tension in the elastic due to the stretching of the elastic.
✦ How do the magnitude and direction of this force vary during the circular motion?
✧ You will know from experience that the tension in an elastic band increases as it is stretched. If the pencil rubber is moving with constant speed in a circle, the elastic will always have the same length, so the magnitude of the force it exerts on the pencil rubber will be constant. The direction of the force is obviously along the elastic and pulling inwards towards the centre of the circle. If the speed is increased the radius and the tension will increase as the elastic stretches more.
✦ What is the relationship between the direction of motion of the rubber and the direction of the force acting on it?
✧ As with the satellite discussed in the previous example, the motion is tangential while the force is radial with respect to the circle. So once again, the force is everywhere perpendicular to the direction of motion.
2.4 Circular motion in general
What we have been trying to show so far in this section is that the forces which cause uniform circular motion in two very different examples have certain things in common. In both cases the force has a constant magnitude and the direction of the force is always radially inwards towards the centre of the circle, which is to say perpendicular to the direction of motion. It turns out that this is true for all examples of uniform circular motion, so we can write a general statement:
An object moving in a circle at a constant speed is experiencing a force which is constant in magnitude and directed radially inwards towards the centre of the circle. This force, whatever its cause, is called the centripetal force.
Why is this always the case? To answer this question we need to look at things a little more deeply (and mathematically). That is the subject of the next section.
3 A mathematical description of circular motion
3.1 Speed, velocity and angular speed
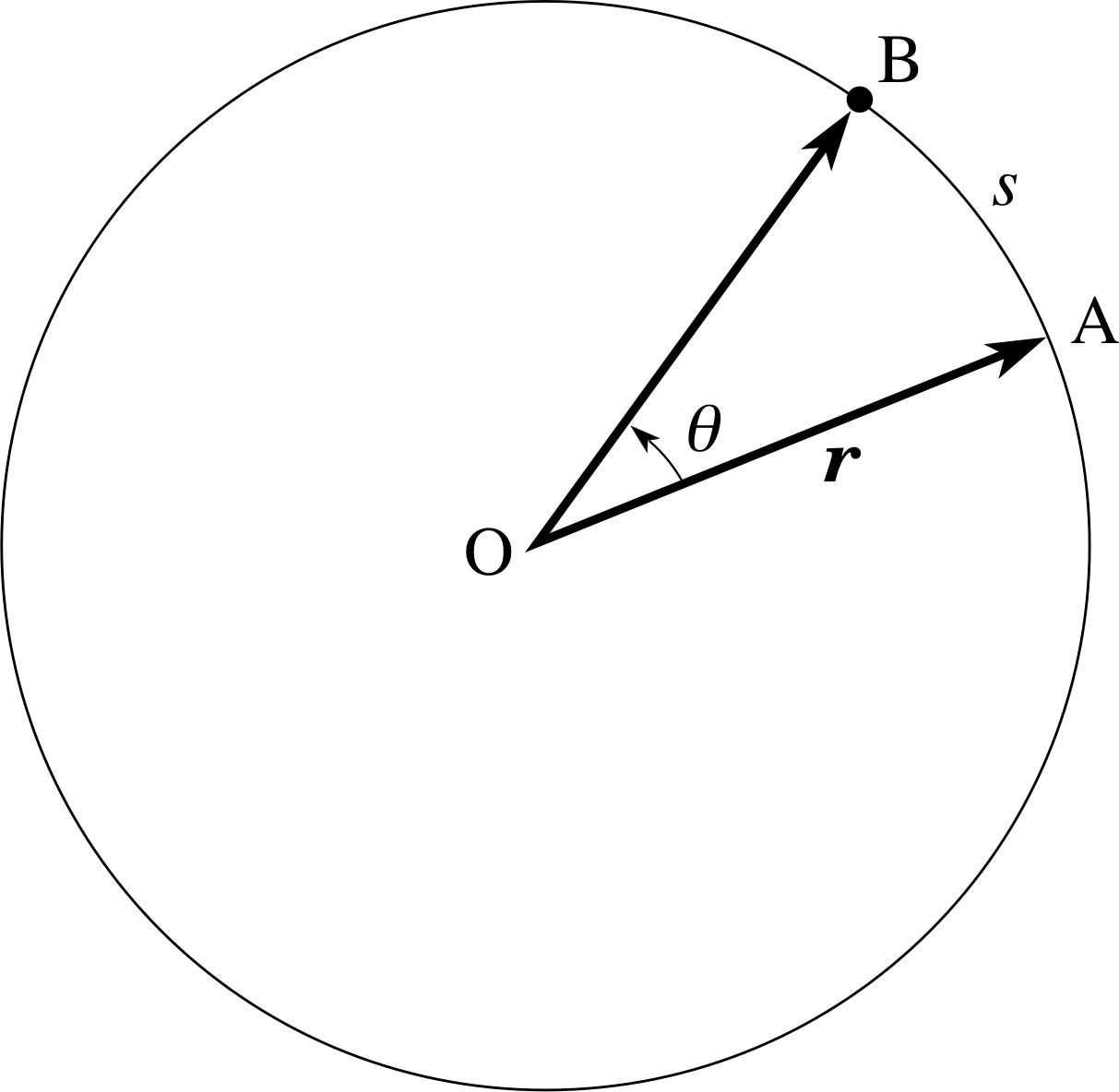
Figure 6 An object undergoing circular motion.
In order to describe circular motion more precisely it will be useful to think of the motion in terms of angles as well as distances. Figure 6 shows an object moving around the circumference of a circle. Its position vector r i relative to the centre of the circle is initially represented by $\overrightarrow {OA}$.
As the object moves from A to B along the arc of length s, the position vector r sweeps out an angle θ. The relationship between s, θ and the radius of the circle r is given by
s = rθ (θ in radians)(2) i
We can describe the progress of the object from A to B, either in terms of the speed or the angular speed of the object. The speed is the rate of coverage of distance measured along the arc, while the angular speed is the rate of change of angle θ with time.
If the speed or angular speed are varying we may define the average speed $\langle\upsilon\rangle$ and the average angular speed $\langle\omega\rangle$, (the angular brackets $\langle \rangle$ denote ‘the average of’) over the time interval t.
The average speed $\langle\upsilon\rangle$ is defined by
$\langle\upsilon\rangle = \dfrac st = \dfrac{r\theta}{t} = r\langle\omega\rangle$(3a) i
where $\langle\omega\rangle$ is defined as the average angle swept out by the position vector in unit time; in Figure 6 this is
$\langle\omega\rangle = \dfrac{\theta}{t}$(4a)
Question T1
What are the units of angular speed?
Answer T1
From Equation 4a,
$\langle\omega\rangle = \dfrac{\theta}{t}$(Eqn 4a)
the unit of angular speed should be the unit of angle divided by the unit of time. In the SI system, the standard unit of angle is the radian and the standard unit of time is the second. The unit of angular speed is therefore radians per second (rad s−1).
We have written down expressions for the average speed and the average angular speed above but it is often more useful to talk about the instantaneous values of these quantities at any particular point (say, at point A). The usual way to arrive at an instantaneous value at a point is to take the average over a very small time interval, ∆t, during which the angle changes by ∆θ. Then we consider what happens to the quantity (∆s/∆t) as ∆t becomes smaller and smaller. Mathematicians refer to this as a limiting process and use the derivative notation ds/dt to represent the result of the limiting process. Thus
$\dfrac{ds}{dt}$ = the limit of $\dfrac{\Delta s}{\Delta t}$ as ∆t approaches zero i
Using this standard notation the instantaneous speed at A, υA, is given as
υA = the limit of $\dfrac{\Delta s}{\Delta t}$ = the limit of $\dfrac{r\Delta \theta}{\Delta t}$ as ∆t approaches zero
and, since r is fixed
$\displaystyle \lim_{\Delta t\rightarrow 0}\left(r\dfrac{\Delta \theta}{\Delta t}\right) = r \lim_{\Delta t\rightarrow 0}\left(\dfrac{\Delta \theta}{\Delta t}\right) = r\dfrac{d\theta}{dt} = r\upsilon_A$
Thus using Equation 2,
s = rθ (θ in radians)(Eqn 2)
the instantaneous speed is
$\upsilon_A = \dfrac{ds}{dt} = r\dfrac{d\theta}{dt} = r\omega$(3b)
where the instantaneous angular speed ω is given by i
$\omega = \dfrac{d\theta}{dt}$(4b)
Question T2
The drum of a spin drier with an internal diameter of 0.50 m rotates at a constant 3500 revolutions per minute. Find:
(a) the instantaneous angular speed ω of the drum in units of rad/s ;
(b) the instantaneous speed (in m s−1) of a sock stuck to the inside surface of the drum of the drier.
Answer T2
(a) For the spin drier there are 3500 revolutions of the spin drier drum in one minute which means there are 3500/60 revolutions in one second. But there are 2π radians per revolution.
So,$\omega = \dfrac{3500 \times 2\pi}{60}$ rad s−1 = 366.5 rad s−1
(b) The speed of the sock is given by υ = rω
So,υ = 0.25 m × 366.5 rad s−1 = 92 m s−1

Figure 6 An object undergoing circular motion.
For uniform circular motion it makes no difference whether we speak of instantaneous or average speeds. The speed and angular speed (by definition) are constant so the instantaneous and average values are the same. However, it does make a difference to the velocity vector υ because the direction of the motion is continually changing.
Let us work out the direction of the instantaneous velocity vector at A in Figure 6. As θ gets smaller and smaller, the angle OA^B gets closer and closer to 90°. In the limit as θ approaches zero, OA^B = 90°. In other words, the direction of the velocity vector at A is perpendicular to the position vector at A, which means it must point along the tangent at A. There is nothing special about point A, so this must be true at any point on the circle.
For an object in uniform circular motion, the instantaneous velocity (a vector quantity) at any point is tangential to the circle at that point and its magnitude is equal to the product of the radius and the angular speed; υ = rω.
3.2 The period of circular motion
If we know the angular speed and that the motion is uniform, we can work out the time required to complete one revolution. This is known as the period of the motion. The period is usually represented by the letter T.
✦ For uniform circular motion, the period T and the angular speed ω should be related. What is the exact form of the relationship?
✧ ω is the angle (in radians) covered per second and 2π radians represents one complete revolution. So the time required for one revolution, the period T, is
$T = \dfrac{2\pi}{\omega}$(5) i
Question T3
Given that the radius of the Earth is 6.38 × 1016 m and that the radius of the Earth’s orbit around the Sun is 1.50 × 1011 m, calculate both the speed and angular speed for (a) a point on the Earth’s Equator, due only to the rotation of the Earth on its axis, and (b) the centre of the Earth, due to the motion of the Earth around the Sun.
Answer T3
(a) For a point on the surface of the Earth, the angular speed can be calculated from the period, which is of course 24 hours.
$\omega = \dfrac{2\pi}{T} = \dfrac{2\pi}{24 \times 3600}$ rad s−1 = 7.27 × 10−5rad s−1
The corresponding speed at the Equator is given by υ = rω
υ = 6.38 × 106 m × 7.27 × 10−5 rad s−1 = 4.64 × 102 m s−1
(b) For the centre of the Earth in its orbit, we repeat the calculations, this time with T = 1 year and r = 1.50 × 1011 m.
$\omega = \dfrac{2\pi}{365\times 24\times 3600}$ rad s−1 = 1.99 × 10−7rad s−1
andυ = rω, so
υ = 1.50 × 1011 m × 1.99 × 10−7 rad s−1 = 2.99 × 104 m s−1
3.3 Centripetal acceleration
Having considered speed, velocity and angular speed, we are now in a position to think more clearly about acceleration. For an object in uniform circular motion, its acceleration is known as the centripetal acceleration.
Question T4
How is it possible to talk about the acceleration of an object that is moving at constant speed?
Answer T4
This is not a contradiction. You should recall that in physics ‘acceleration’ is defined as the rate of change of velocity with time. Now velocity is a vector, so its direction is important as well as its magnitude. Thus an increase in speed, a decrease in speed or just a change in direction at constant speed can all be described as ‘accelerations’.
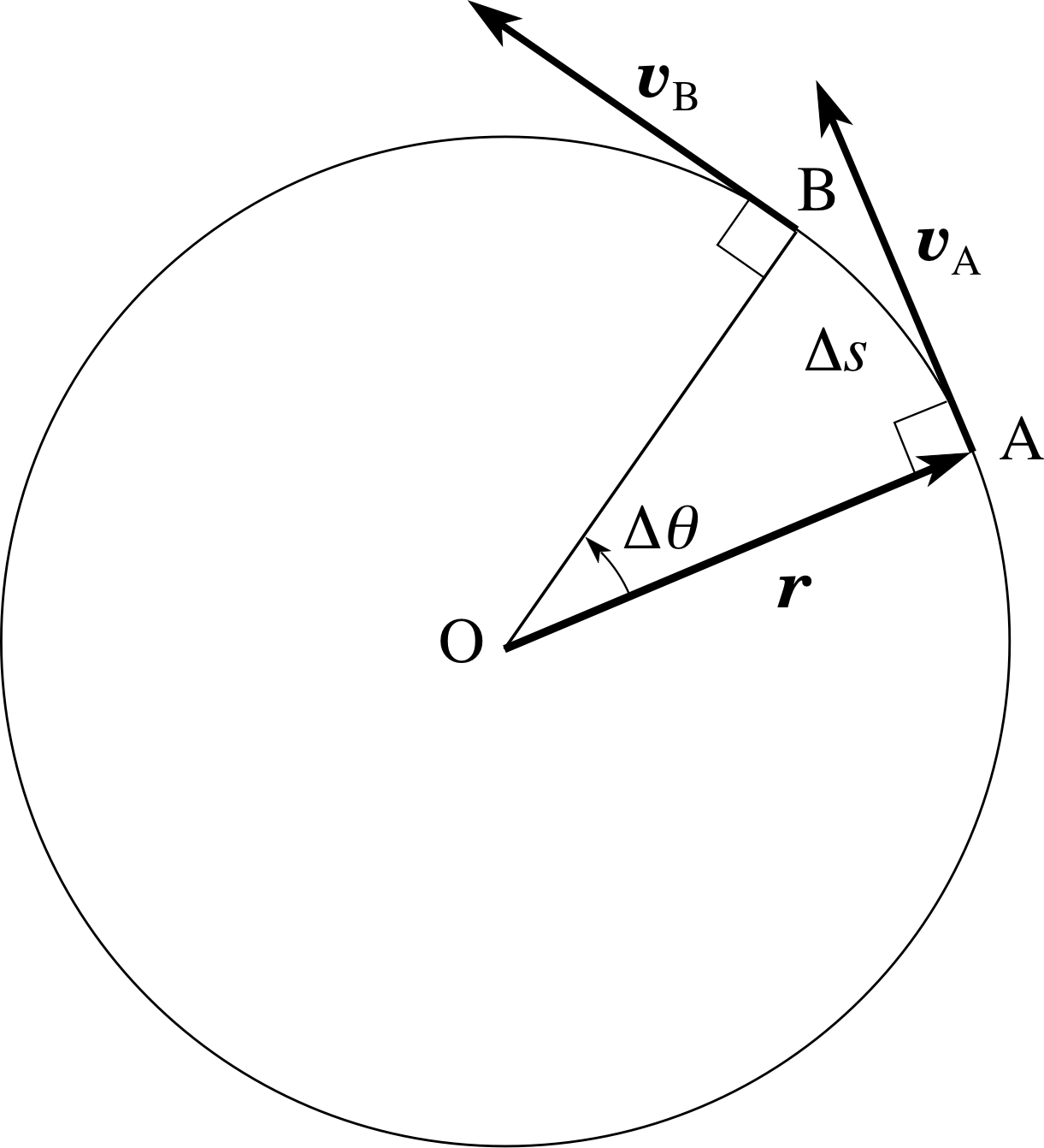
Figure 7 An object undergoing uniform circular motion with velocity vectors shown at A and B.
Let us think again about the orbiting object shown in Figure 6. It has been redrawn in Figure 7 with arrows representing the velocity vectors at A and at B (υA and υB). As is usual in drawing a vector, the arrow points in the direction of the vector and its length represents the magnitude of the vector. i
We are interested in the instantaneous value of the acceleration at A, so let’s look at what happens in a small time interval ∆t, as the object moves from A to B. Using the same notation as before, the average acceleration over the small distance AB can be written as
$\boldsymbol{a}_{\rm AB} = \dfrac{\Delta\upsilon_{\rm AB}}{\Delta t}$(6)
where ∆υAB is the change in velocity in the small time interval ∆t. Equation 6 shows that if we can work out ∆υAB we can use it to calculate aAB.
To calculate ∆υAB we have to carry out a vector subtraction
∆υAB = ∆υB − ∆υA
We can treat this as the addition of the vector ∆υB and the vector −∆υA, added according to the triangle_ruletriangle rule for vectors
∆υAB = υB + (−υA)
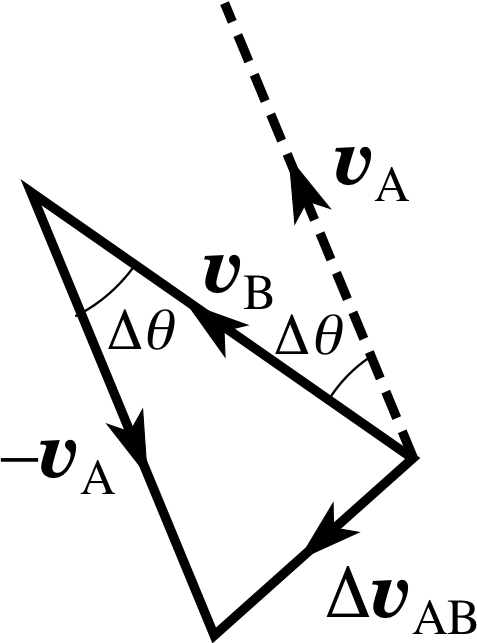
Figure 8 Triangle rule for the subtraction of υA from υB.
−υA has the same magnitude as υA but points in the opposite direction. This addition is illustrated in Figure 8.
Notice that the angle between υA and υB is the same as the angle between the lines OA and OB in Figure 7. This is because υA and υB are at the same angle of 90° to OA and OB respectively. As the position vector sweeps round through θ, from OA to OB, so the instantaneous velocity must also turn through an identical angle. We can use Figure 8 to find both the direction and the magnitude of the instantaneous acceleration. We shall do this in two separate steps, considering in each what happens as ∆θ approaches zero:
Step 1: the direction of the centripetal acceleration In the limit as ∆θ tends to zero, the angle between ∆υAB and υA becomes 90°. Since υA points along the tangent to the circle at A, ∆υAB must point towards the centre of the circle. Comparison of Figures 7 and 8 should convince you of this.
From the definition of acceleration (Equation 6) the acceleration vector a at A must point along the vector ∆υAB and so it too must point towards the centre of the circle. Again, there is nothing special about point A and so this must be true generally at any point on the circle. So, in uniform circular motion, the centripetal acceleration always acts radially inwards, towards the centre of the circle.
Step 2: the magnitude of the centripetal acceleration Look again at Figure 8.
Question T5
Write down an expression for the magnitude_of_a_vector_or_vector_quantitymagnitude | ∆υAB | i in Figure 8, in ∆υAB terms of the constant orbital speed υ (= υA = υB) and the angle ∆θ.

Figure 8 See Question T5.
Answer T5
The relationship between | ∆υAB |, υ and ∆θ is the same as the relationship between s, r and θ in Equation 2.
s = rθ (θ in radians)(Eqn 2)
That is
| ∆υAB | = υ∆θ
This can also be seen from the geometry of the (isoceles) triangle in Figure 8:
| ∆υAB | = ∆υAB = 2υ sin(∆θ/2) ≈ 2υ (∆θ/2) = υ∆θ (since ∆θ is small)
(This will become Equation 7).
It might worry you that s in Equation 2 is an arc length whereas ∆υAB is the magnitude of a vector which is represented as a straight line distance in the diagram, but the small size of the angle ∆θ allows us to do this. As ∆θ gets smaller and smaller, the arc length and the straight line distance become more and more nearly equal and in the limit as ∆θ approaches zero, we can regard them as being the same.
The expression (as given in Answer T5)
∆υAB = υ∆θ i
leads to the required result for the magnitude of the average centripetal acceleration, where the averages are taken over the time interval ∆t
$\langle a \rangle = \upsilon\dfrac{\Delta\theta}{\Delta t} = \upsilon\langle\omega\rangle$(8)
Again, taking the limit as ∆t tends to zero gives us the magnitude of the instantaneous centripetal acceleration at any point in the motion
$ a = \upsilon\dfrac{d\theta}{dt} = \upsilon\omega$(9a)
where we have used Equation 4b
$\omega - \dfrac{d\theta}{dt}$(Eqn 4b)
to identify ω.
Now we have the whole story for the centripetal acceleration. The instantaneous centripetal acceleration acts radially inwards and its magnitude is equal to the product of the speed and the angular speed; a = υω. i
Question T6
We can now use Equation 3b (υ = rω) to express Equation 9a
$ a = \upsilon\dfrac{d\theta}{dt} = \upsilon\omega$(9a)
in two other ways. Derive the two alternative versions of Equation 9a, one expressing the centripetal acceleration in terms of υ and r only and the other in terms of ω and r only.
Answer T6
If we substitute ω = υ/r in Equation 9a
$a = \upsilon\dfrac{d\theta}{dt} = \upsilon\omega$(Eqn 9a)
$a = \upsilon\omega = \upsilon\left(\dfrac{\upsilon}{r}\right) = \dfrac{\upsilon^2}{r}$
(This will become Equation 9b.)
If we substitute υ = rω in Equation 9a
a = υω = (rω)ω = 2rω2
(This will become Equation 9c.)
As you have just discovered in Answer T6, the two alternative expressions for the magnitude of centripetal acceleration are
$a = \dfrac{\upsilon^2}{r}$(9b)
anda = rω2(9c) i
3.4 Centripetal force
We have worked out the magnitude and direction of the centripetal acceleration which an object experiences during uniform circular motion. From Newton’s second law (Equation 1) we know that this centripetal acceleration must be caused by a force, the centripetal force, which we have already considered qualitatively in Subsection 2.4. Newton’s second law allows us to quantify this force.
Since F = ma(Eqn 1)
the force must be parallel to the centripetal acceleration and its magnitude F must equal the product of m and the magnitude of the centripetal acceleration. Thus:
The centripetal force must be directed towards the centre of the circle.
Its magnitude may be represented by any of the following three equivalent expressions
F = ma = mυω(10a)
or$F = ma = \dfrac{m\upsilon^2}{r}$(10b)
orF = ma = mrω2(10c) i
This mathematical description of centripetal force ties in very nicely with the observations in Subsection 2.2. Recall that in all the examples of uniform circular motion described, there was a force of constant magnitude which was acting perpendicular to the direction of motion. In Section 3 we have shown, from first principles, that the force should indeed be perpendicular to the direction of motion and, as υ and r are constant for uniform circular motion, this force must also have a constant magnitude.
Question T7
Calculate the magnitudes of the centripetal acceleration and centripetal force for a person of mass 80 kg standing on the Earth’s Equator, given that the radius of the Earth is 6.38 × 1016 m. What provides the centripetal force in this case?
Answer T7
From Answer T3 we already have a value of ω = 7.27 × 10−5 rad s−1 for a point on the Earth’s surface. From Equation 9c
a = rω2(Eqn 9c)
a = 6.38 × 106 × (7.27 × 10−5)2 m s−1
a = 3.37 × 10−2 m s−1
From Newton’s second law the magnitude of the force is given by
F = ma
Therefore, an 80 kg man standing on the Earth’s Equator will experience a centripetal force of magnitude
F = 80 × 3.37 × 10−2 N = 2.70 N
Both force and acceleration are directed towards the centre of the Earth. (Specifying the direction is a vital part of the answer.) The centripetal force is provided by the gravitational attraction of the Earth.
Question T8
Estimate the magnitudes of the centripetal accelerations and forces experienced by (a) the sock in Question T2 and (b) the pencil rubber which you used during the experiment in Subsection 2.3.
Answer T8
(a) From Answer T2, r = 0.25 m and ω = 367 rad s−1 for the spin drier drum. If the mass of a sock is estimated to be 0.05 kg, we have
a = rω2(Eqn 9c)
a = 0.25 × (367)2 m s−2 = 3.4 × 102 m s−2
andF = ma = 0.05 × 3.4 × 104 N = 1.7 × 103N (two significant figures).
(b) Suppose the rubber had a mass of 0.1 kg, its orbital period about 0.5 s, and radius of the orbit about 0.3 m.
If we use a = rω2(Eqn 9c)
withω = 2π/T(Eqn 5)
we get $a = \dfrac{4\pi^2r}{T^2} = \dfrac{4\pi^2 \times 0.3}{(0.5)^2}$ m s−2 = 47 m s−2
and the force (only justified to one significant figure)
F = ma = 0.1 × 47 kg m s−2 = 4.7 N ≈ 5N
Comment Your experimental values will probably differ from those given in (b).
Question T9
A student looking at Equation 9b
$a = \dfrac{\upsilon^2}{r}$(Eqn 9b)
concludes that centripetal acceleration decreases as the distance r increases because r appears in the denominator of the equation. Another student looking at Equation 9c
a = rω2(Eqn 9c)
reasons that the centripetal acceleration increases with increasing r because in this equation r appears in the numerator. Who is right?
Answer T9
Both students are partly correct although neither is telling the whole story. What the first student should say is, ‘If a = υ2/r then a will decrease with increasing r provided υ remains constant.’ The second student should say ‘If a = rω2, a will increase with increasing r provided ω remains constant.’ The statements are not contradictory as it is impossible for both υ and ω to remain constant if r is increasing. This follows from the relationship υ = rω. If υ is to remain constant as r increases, then ω must decrease proportionately. Similarly if ω is to remain constant, υ has to increase.
Equations 10a, b and c
F = ma = mυω(10a)
$F = ma = \dfrac{m\upsilon^2}{r}$(10b)
F = ma = mrω2(10c)
give the magnitude of the force required to keep an object moving with speed υ (or angular speed ω) in a circular path of radius r. Of course they can be rearranged to give the speed if r and F are known – or the radius if υ and F are known.
Question T10
Derive an expression for the speed υ of an object moving uniformly around a circle of radius r under the influence of a force with magnitude F. Your expression should involve only r, F and m.
Answer T10
If we rearrange Equation 10b
$F = ma = \dfrac{m\upsilon^2}{r}$(Eqn 10b)
it gives the speed as
$\upsilon = \sqrt{\dfrac{rF}{m}}$
Question T11
Calculate the speed with which the snowball in Subsection 2.1 must be thrown to orbit just above the Earth’s surface. (Neglect air resistance and anything else which gets in the way.)
Answer T11
From Answer T10
$\upsilon = \sqrt{\dfrac{rF}{m}\os} = \sqrt{ra\os}$
where a is the acceleration experienced by the body. For the snowball, the acceleration is the acceleration due to gravity close to the Earth’s surface. The required orbital speed is
$\upsilon = \rm \sqrt{6.38\times 10^6\times 9.8}\,m\,s^{-1} = 7.9\times10^3\,m\,s^{-1}$
4 Applications of circular motion
The analysis of uniform circular motion as outlined in Sections 2 and 3 can be applied to many practical problems. As a source of examples, we will return to the problems posed in Subsection 1.1 and see how the understanding developed in Sections 2 and 3 can be applied.
4.1 Designing safe bends for motorways
It is common knowledge that taking a bend too fast can cause a car to skid and the tighter the bend the more likely it is that skidding will occur. For a bend on a motorway to be ‘safe’, the curve must be sufficiently gentle that a car will not skid when travelling at the maximum allowable speed of 70 mph (given reasonable assumptions about the state of the road and car tyres). So how do we work out the tightest safe bend? To keep things simple we will assume a bend is always part of a circle, so the tightness of a bend is represented by the radius of the circle of which it forms a part. This is known as the radius of curvature of the bend. We will also assume the car is travelling at uniform speed.
The first question to ask is what provides the centripetal force which causes a car to follow the curved path? If the road surface is horizontal then the force comes entirely from friction between the wheels and the road. If the road is ‘banked’ or has a ‘camber’, other forces come into play which reduce the size of the frictional force needed – but that is beyond the scope of this module.
The reason why a car skids is that there is a limit to the size of the force that can be generated by friction between two surfaces. Fortunately, there is an easy way to calculate the magnitude of the maximum frictional force between two horizontal surfaces. In the case of a car on a horizontal road surface, the appropriate equation is
Fmax = μW
where Fmax is the magnitude of the maximum frictional force, W is the magnitude of the car’s weight and μ is a constant called the coefficient of static friction. The value of μ depends on the nature of the two surfaces. i The weight of an object is the force exerted on it by the Earth’s gravity. From Newton’s second law, the magnitude of the weight of an object of mass m is
W = mg(11)
where g is the magnitude of the acceleration due to gravity at the point. This gives the magnitude of the maximum frictional force (and therefore the magnitude of the maximum centripetal force) as
Fmax = μmg
How does this relate to the radius of curvature of the bend? The answer is found by combining this expression for Fmax
Fmax = μmg
with Equation 10b,
$F = ma = \dfrac{m\upsilon^2}{r}$(Eqn 10b)
$F_{\rm max} = \mu mg = \left(\dfrac{m\upsilon^2}{r}\right)_{\rm max} = m\left(\dfrac{\upsilon^2}{r}\right)_{\rm max}$(12)
Equation 12 tells us that for a particular value of Fmax there is a limit on the size of υ2/r which can be sustained; for a given speed there will be a minimum radius rmin, or for a given radius there will be a maximum permissible speed υmax to avoid skidding.
Equivalently, we can write
for a given radius r, $\upsilon_{\rm max} = \sqrt{\dfrac{rF_{\rm max}}{m}} = \sqrt{\dfrac{r\mu mg\os}{m}} = \sqrt{r\mu g\os}$(13)
or for a given speed υ, $r_{\rm min} = \dfrac{m\upsilon^2}{F_{\rm max}} = \dfrac{m\upsilon^2}{\mu mg} = \dfrac{\upsilon^2}{\mu g}$(14)
Even before we substitute values, Equations 13 and 14 tell us quite a lot. First, in Equation 14, the speed appears as a square. This means that the minimum r increases very rapidly as υ increases. Secondly, in both equations, m has cancelled out – so there is no dependence on mass. Heavy cars are just as likely to skid as light cars and the coefficient of friction plays the crucial role.
In calculating a suitable value for rmin (the tightest allowable bend in our motorway design), we obviously want to build in a suitable margin of safety. We should take a value for μ corresponding to poor tyres on a wet road surface (μ = 0.30) and then do the calculation say for 90 mph (i.e. 40 m s−1), rather than 70 mph, to allow a safety margin. From Equation 14 this gives r = 5.4 × 102 m.
Question T12
Calculate the maximum constant speed with which a car can take a bend with radius of curvature 3.0 × 102 m without skidding, if the value of μ is 0.40. (Take the value of g as 9.8 m s−2).
Answer T12
Equation 13 gives the relationship between speed and radius, just at the point of skidding,
$\upsilon_{\rm max} = \sqrt{r\mu g\os}$(Eqn 13)
$\upsilon_{\rm max} = \rm \sqrt{3.0\times10^2\times0.40\times9.8}\,m\,s^{-1} = 34\,m\,s^{-1}$
4.2 Satellites and communication satellites
Before discussing communication satellites in particular, we will return to a general point about satellite orbits which was raised in Subsection 2.1. There we said that for a satellite to be put into a circular orbit it must be set moving at the correct speed in a direction parallel to the Earth’s surface and with the centre of the Earth at the centre of the plane of the satellite’s orbit. We are now in a position to appreciate why this is so.
The satellite moves under the force due to Earth’s gravity, which acts towards the centre of the Earth. The satellite will only travel in a circular orbit if the magnitude and direction of this force exactly match the size and direction of the centripetal force required for that orbit. Therefore the satellite must be set moving in a way to ensure that this happens. How can this be done?
First, think about the direction of the satellite. In Subsection 3.4 you saw that for uniform circular motion the centripetal force must act towards the centre of the orbit. i As the gravitational force acts towards the centre of the Earth, the centre of the orbit must coincide with the centre of the Earth. Also, as the orbit is circular, the satellite’s path will be everywhere parallel to the Earth’s surface. An orbit which passes over both North and South poles is one example of such an orbit.
Now think about the speed of launch. The required centripetal force on the satellite must be provided by the gravitational force from the Earth. We can calculate this force by using Newton’s law of gravitation, which gives the magnitude of the gravitational force on a mass m1 due to another mass m2 (say satellite and Earth, respectively) separated by a distance r as
$F_{\rm grav} = \dfrac{Gm_1 m_2}{r^2}$(15) i
where G is the gravitational constant, which has an approximate value of 6.67 × 10−11 N m2 kg−2.
If we equate the magnitude of this force with that of the centripetal force given in Equation 10b,
$F = ma = \dfrac{m\upsilon^2}{r}$(Eqn 10b)
with m set equal to the satellite mass m1, we find
$\dfrac{Gm_1 m_2}{r^2} = \dfrac{m_1\upsilon^2}{r}$
Dividing both sides by m1, $\dfrac{Gm_1 m_2}{r^2} = \dfrac{m_1\upsilon^2}{r}$
and rearranging this equation, we can write the satellite’s speed as
$\upsilon = \sqrt{\dfrac{Gm_2}{r}}$(16)
Substitution of υ = rω from Equation 3b gives the satellite’s angular speed as
$\omega = \dfrac{\upsilon}{r} = \sqrt{\dfrac{Gm_2}{r^3}}$(17)
If we substitute T = 2π/ω from Equation 5, we find the satellite’s orbital period is
$T = \dfrac{2\pi}{\omega} = 2\pi\sqrt{\dfrac{r^3}{Gm_2}}$(18)
Equations 16, 17 and 18 are general results. Although we have derived them for a satellite in circular orbit around the Earth, they are generally true for any satellite or moon of any mass m1 in any circular orbit around any planet of mass m2. They are also equally valid for the planets themselves in orbit around the Sun, providing m2 is then taken as the mass of the Sun. i
Question T13
Calculate the speed of a satellite in circular orbit 1 000 km above the Earth’s surface. Take the mass of the Earth as 5.98 × 1024 kg.
Answer T13
From Equation 16,
$\upsilon = \sqrt{\dfrac{Gm_2}{r}}$(Eqn 16)
$\upsilon = \rm \sqrt{\dfrac{6.67\times 10^{-11}\times 5.98\times 10^{24}}{1\times 10^6 + 6.38\times 10^6}}\,m\,s^{-1} = 7.35\times10^3\,m\,s^{-1}$
Notice that this speed is slightly less than the orbital speed needed for the snowball in Answer T11. This is because the acceleration due to gravity at the satellite’s orbit is less than that at the Earth’s surface, or equivalently that the orbital radius is larger for the satellite than for the snowball.
We will now consider communication satellites and the many meteorological satellites in orbit around the Earth. In these cases it is usually an advantage if they orbit so that they are permanently located above a particular point on the Earth’s surface. To do so these satellites must travel with the same angular speed and rotate in the same direction as the Earth, and also lie in the Earth’s equatorial plane. An orbit of this kind is called a geostationary orbit (this is a special case of the more general geosynchronous orbit, which is inclined at an angle to the equatorial plane and may be elliptical) and the satellites in such orbits are said to be geostationary satellites.
Since the centre of any orbit around the Earth must be the centre of the Earth and since a geostationary satellite has its rotation matched to that of the Earth itself, it follows that such a satellite must be directly above the Equator. The direction of rotation and the angular speed of rotation of the satellite must also be the same as that of the Earth. i
If we use the general result given in Equation 17,
$\omega = \dfrac{\upsilon}{r} = \sqrt{\dfrac{Gm_2}{r^3}}$(Eqn 17)
with ω set equal to the Earth’s angular rotation speed (2π radians in 24 hours) we can calculate the orbital radius necessary for a geostationary satellite.
Equation 17 squared is $\omega^2 = \dfrac{Gm_2}{r^3}$
or$r = \sqrt[{\large\raise{6pt}3}]{\dfrac{Gm_2\os}{\omega^2}} = \rm \sqrt[{\large\raise{8pt}3}]{\dfrac{6.67\times10^{-11}\,N\,m^2\,kg^{-2}\times5.98\times10^{24}\, kg}{(7.27\times10^{-5}\,rad\,s^{-1})^2}} = 4.23\times10^7\,m$
However, this is the distance from the centre of the Earth. To find the height of the satellite above the Earth’s surface we have to subtract the Earth’s radius of 6.38 × 106 m. This gives the height for a geostationary orbit as 3.59 × 107 m, or about 36 000 km.
Question T14
Mars has a mass of 6.42 × 1023 kg and rotates with a period of 1.03 Earth days. At what distance from the centre of Mars should a satellite be put into orbit so that it remains located above a fixed point on the Martian surface?
Answer T14
Rearrange Equation 17 as before
$\omega = \dfrac{\upsilon}{r} = \sqrt{\dfrac{Gm_2}{r^3}}$(Eqn 17)
and then, using the result for the angular speed of the Earth from Answer T3, substitute the appropriate values for Mars
$r = \rm \sqrt[{\large\raise{8pt}3}]{\dfrac{6.67\times 10^{-11}\times 6.42\times 10^{23}}{(7.06\times 10^{-5})^2}}\,m = 2.05\times10^7\,m$
(Remember this is the distance from the centre of Mars.)
5 Closing items
5.1 Module summary
- 1
-
The analysis of uniform circular motion is important because there are many situations in the world around us which approximate to this kind of motion.
- 2
-
The mathematics of uniform circular motion is relatively straightforward. To keep an object in uniform circular motion, there must be a centripetal force which is constant in magnitude and always perpendicular to the direction of motion, directed radially inwards towards the centre of the circle.
- 3
-
The angular speed, ω = dθ/dt, of an object in uniform circular motion is equal to the angle swept out in unit time by the position vector from the centre of the circle to the object.
- 4
-
The speed υ and angular speed ω of an object in uniform circular motion are constant and related by the equation
υ = rω (ω in rad s−1)(Eqn 3)
where r is the radius of the circle.
- 5
-
The period T of uniform circular motion is related to the angular speed by the equation
$T = \dfrac{2\pi}{\omega}$ (ω in rad s−1)(Eqn 5)
- 6
-
The acceleration which is necessary to keep an object in uniform circular motion is known as the centripetal acceleration. It is directed radially inwards and has a magnitude given by the following equivalent expressions
$a = \upsilon\omega$ (ω in rad s−1)(Eqn 9a)
or$a = \dfrac{\upsilon^2}{r}$ (ω in rad s−1)(Eqn 9b)
or$a = r\omega^2$ (ω in rad s−1)(Eqn 9c)
- 7
-
The centripetal force is the force which gives rise to the centripetal acceleration. It is directed radially inwards with magnitude given by the following equivalent expressions (ω in rad s−1)
F = ma = mυω (ω in rad s−1)(Eqn 10a)
or$F = ma = \dfrac{m\upsilon^2}{r}$ (ω in rad s−1)(Eqn 10b)
orF = ma = mrω2 (ω in rad s−1)(Eqn 10c)
- 8
-
The analysis of uniform circular motion can be applied to many practical problems such as the radius of curvature for ‘safe’ bends on roads, and the orbits of geostationary and geosynchronous satellites.
5.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Demonstrate that for uniform circular motion the direction of the acceleration is radially inwards.
- A3
-
Recall that period T and angular speed ω are related by Equation 5.
- A4
-
Derive from first principles Equations 3, 9 (in each of its three forms) and 10 (in each of its three forms).
- A5
-
Carry out manipulations of the above equations and use them in simple calculations.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
5.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions each of which tests one or more of the Achievements.
Question E1 (A1 and A3)
A computer hard disk has a radius of 5 cm and rotates at 3000 revolutions per minute. Find the period of rotation of the disk and the speed of a point on the outer edge of the disk.
Answer E1
The disk rotates at 3000 revolutions per minute, i.e. 50 rev s−1. Therefore the period T of revolution is
(1/50) s = 0.02 s
The angular speed is related to the period by ω = 2π/T
Therefore ω = (2π/0.02) rad s−1 = 100π rad s−1
The speed is given by υ = rω. Hence (converting r to metres)
υ = 0.05 × 100π m s−1 = 5π m s−1 = 16 m s−1
(Reread Subsection 3.2 if you had difficulty with this question.)
Question E2 (A1 and A5)
An aircraft is circling over an airport, waiting for permission to land. If its speed is 120 m s−1 and it is executing circles of radius 5.00 km, calculate its angular speed, period and centripetal acceleration.
Answer E2
If we use the equation ω = υ/r for the angular speed, we have
$\omega = \dfrac{120}{5.00 \times 10^3}$ rad s−1 = 0.024 rad s−1
The period is calculated from T = 2π/ω
$T= \dfrac{2\pi}{0.0240}$ s = 262 s
The magnitude of the centripetal acceleration is given by
a = rω2
soa = 5.00 × 103 × 0.02402 m s−2 = 2.88 m s−2
(Reread Section 3 if you had difficulty with this question.)
Question E3 (A1)
In each pair of statements below, one is incorrect; say which you think it is, and why it is incorrect.
- (a)
-
(i) Uniform circular motion is any kind of motion where the path forms a perfect circle.
(ii) Uniform circular motion is motion in a circle at a constant speed.
- (b)
-
(i) Centripetal force is the force exerted by gravity on an object at the Earth’s Equator.
(ii) Centripetal force is the force required to maintain an object in uniform circular motion.
- (c)
-
(i) The period of a circular motion is the total length of time for which an object undergoes motion in a circle.
(ii) The period of a circular motion is the length of time required to complete one revolution.
- (d)
-
(i) The angular speed of an object in uniform circular motion is the angle swept out by its position vector in unit time.
(ii) The angular speed of an object in uniform circular motion is the length of time required for its position vector to sweep out an angle of 1 radian.
Answer E3
(a) Statement (i) is incorrect and statement (ii) is correct. The word uniform refers to the speed. The theory described in this module is only applicable to situations where the motion follows a circular path and the speed is constant. (See Section 2.)
(b) Statement (i) is incorrect and statement (ii) is correct. Although gravity provides the radially directed inward force for an object on the Equator, this is not an adequate general definition. Statement (ii) is correct; it is applicable to all situations involving uniform circular motion. (See Subsection 3.4.)
(c) Statement (i) is incorrect and statement (ii) is correct. Period is defined as the time to complete one revolution. (See Subsection 3.2.)
(d) Statement (ii) is incorrect and statement (i) is correct. Angular speed is defined by the rate of change of angle
$\omega = \dfrac{d\theta}{dt}$(Eqn 4b)
which, for uniform circular motion, is the change in angle divided by the time interval. (See Subsection 3.1.)
Question E4 (A4)
Starting from the definitions of speed υ and angular speed ω, show that for uniform circular motion the relationship between them is υ = rω, where r is the radius of the circle.
Answer E4
Speed is defined by υ = ds/dt = limit of (∆s/∆t) as ∆t approaches zero, and ∆s = r∆θ. If we combine these two we have υ = rdθ/dt = rω.
(Reread Subsection 3.1 if you had difficulty with this question.)
Question E5 (A1 and A5)
The strength of the gravitational force experienced by Io, one of Jupiter’s moons, is 5.19 × 1022 N. If it has a period of orbit of 1.77 Earth days and its distance from the centre of Jupiter is 4.22 × 1018 m, calculate its mass.
Answer E5
From Equation 10c,
F = ma = mrω2(10c)
the strength of the centripetal force can be written as
F = mrω2
Substituting 2π/T for ω (from Equation 5)
$T = \dfrac{2\pi}{\omega}$(Eqn 5)
and rearranging gives $m = \dfrac{FT^2}{4\pi^2r}$
so$m = \dfrac{5.19 \times 10^22 \times (1.77 \times 24 \times 3600)^2}{ 4\pi^2 \times4.22 \times 10^8}\,{\rm{kg}}$ = 7.29 × 1022 kg
(Reread Subsection 4.2 if you had difficulty with this question.)
Question E6 (A1)
Explain why a satellite cannot be put into a geostationary orbit directly over London.
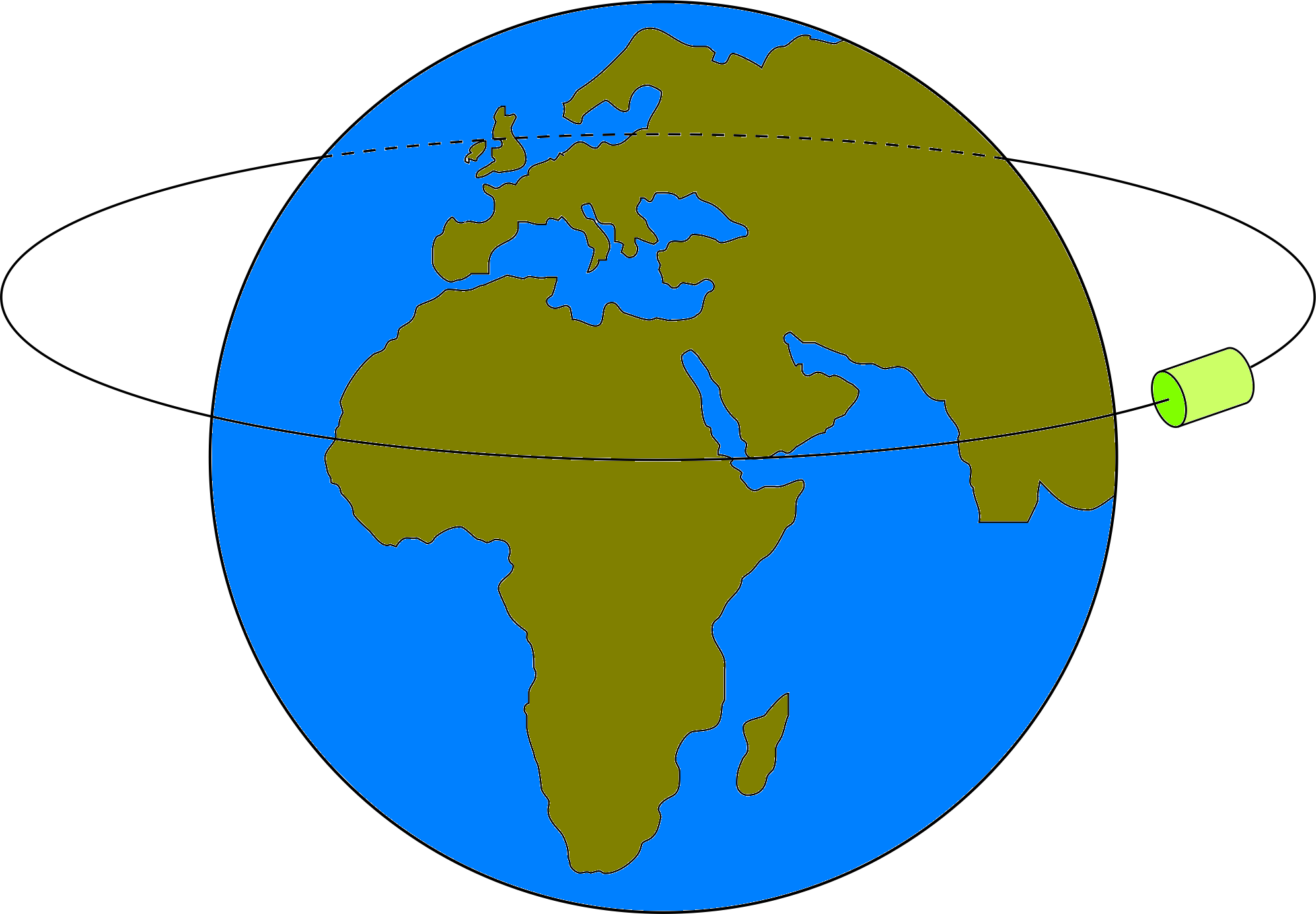
Figure 10 An impossible orbit; see the answer to Question E6.
Answer E6
For a satellite to be in geostationary orbit over London, it would have to follow the path shown in Figure 10. But this is in disagreement with the condition for a satellite orbit explained in Subsection 4.2, that the centre of the Earth must also be the centre of the orbital plane. It follows that geostationary orbits are only possible if the satellite is stationed over the Equator.
(Reread Subsection 4.2 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 5Closing items.