PHYS 3.2: Gravitation and orbits |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
In 1687 Newton formulated his law of universal gravitation in which he asserted that there is a gravitational interaction between all masses. In this module, we apply Newton’s law of gravitation to a variety of situations, beginning in Section 2 with the Cavendish experiment to measure the universal gravitational constant, G.
In Section 3 we concentrate on gravitational effects due to the Earth and see that, for an object close to the Earth, the gravitational force due to the Earth itself is much greater than that due to any other body. We see how the weight of an object on Earth is related to the Earth’s surface gravity (i.e. the surface gravitational field, or acceleration due to gravity). We also see that close to the Earth, the gravitational field can be treated as uniform, giving rise to a simple expression for changes in gravitational potential energy. However, for an object that travels from the Earth’s surface to an infinite distance from the Earth we need to take account of the variation in field strength with distance in order to derive an expression for the escape velocity.
In Section 4 we apply the law of gravitation and ideas about circular motion to the orbits of planets and satellites, and hence explain the basis of Kepler’s laws of planetary motion. We then use ideas about orbital motion to account for ocean tides and to explain how astronauts in an orbiting vehicle might detect the presence of a gravitational field despite feelings of ‘weightlessness’.
Sections 2 to 4, are concerned with the gravitational effects of those extended bodies which may be regarded as spheres, but we represent them by point masses located at their geometric centres. In Section 5, we use ideas about gravitational potential together with the principle of superposition to justify this procedure. This is a more technical section which assumes a greater knowledge of calculus and trigonometry than the rest of the module, but the method it uses and the result it derives are of importance in many areas of physics.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 6.1Module summary and the Subsection 6.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 6.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1 i
Calculate the surface gravity (acceleration due to gravity at the surface) of the Moon.
Answer F1
We need to find the gravitational field strength, or magnitude of the acceleration due to gravity gM, at the Moon’s surface. Treating the Moon as though all its mass were situated at its centre, and considering an object of mass m sitting on its surface, the magnitude of the gravitational force acting on the object towards the centre of the Moon is
$F_{\rm grav} = \dfrac{GM_{\rm M}m}{R_{\rm M}^2}$
where MM is the mass of the Moon and RM its radius.
Using Newton’s second law of motion, force = mass × acceleration, we find
$g_{\rm M} = \dfrac{GM_{\rm M}}{R_{\rm M}^2}$
so$g_{\rm M} = \rm \dfrac{6.67\times10^{-11}\,N\,m^2\,kg^{-2}\times 7.35\times 10^{22}\,kg}{(1.74\times10^6\,m)^2}$
i.e.gM = 1.62 m s−1, about one–sixth of the terrestrial value.
Question F2
Calculate the radius of the orbit of a geostationary satellite orbiting the Earth.
Answer F2
The satellite must revolve with the same period as the Earth, i.e. 1 day. The magnitude of the gravitational force between the satellite and the Earth is given by
$F_{\rm grav} = \dfrac{GM_{\rm E}m}{r^2}$
where r is the radius of the satellite’s orbit, m its mass and ME the mass of the Earth. For uniform motion in a circle, the centripetal acceleration (towards the centre of the orbit) is rω2 where ω is the angular speed, and the orbital period T = 2π/ω. Applying Newton’s second law to this case we have,
gravitational force = mass × radial acceleration:
so$F_{\rm grav} = \dfrac{GM_{\rm E}m}{r^2} = mr\omega^2$
i.e.$F_{\rm grav} =mr\dfrac{4\pi^2}{T^2}$
Rearranging to find r, we have
$r^3 = \dfrac{T^2GM_{\rm E}}{4\pi^2}$
Substituting values and putting 1 day = 24 × 60 × 60 s = 8.64 × 104 s, we have
r = 4.23 × 107 m
Question F3
Calculate the escape speed from the surface of the Moon.
Answer F3
An object of mass m on the surface of the Moon has gravitational potential energy $E_{\rm grav} = -\dfrac{GM_{\rm M}m}{R_{\rm M}}$ (relative to Egrav = 0 at an infinite distance from the Moon).
If it leaves the surface of the Moon with speed υe its kinetic energy is Ekin = ½ mυe2.
Provided no non–gravitational forces act, Egrav + Ekin must remain constant so
$\dfrac{1}{2}m\upsilon_e^2 - \dfrac{GM_{\rm M}m}{R_{\rm M}} =~\text{constant}$
If the object is just to reach infinity (where Egrav = 0) with zero speed (so Ekin = 0), we require that the constant should be zero; so in that case
$\dfrac{1}{2}m\upsilon_e^2 - \dfrac{GM_{\rm M}m}{R_{\rm M}} = 0$
Therefore lunar escape speed, $\upsilon_e = \left(\dfrac{2GM_{\rm M}}{R_{\rm M}}\right)^{1/2}$
Substituting values we have
$\upsilon_e = \rm \left(\dfrac{2\times 6.67\times10^{-11}\,N\,m^2\,kg^{-2}\times 7.35\times10^{22}\,kg}{1.74\times 10^{6}\,m}\right)^{1/2} = 2.37\,km\,s^{-1}$
1.3 Ready to study?
Study comment In order to study this module you will need to be familiar with the following terms: acceleration, conservation of energy, density, force, kinetic energy, mass, Newton’s laws of motion, position vector, potential energy, torque and work. You will be required to plot graphs, particularly straight–line graphs, and to use them to investigate relationships between variables. You will also need to be familiar with vectors, including the concept of a unit vector. Integration is used at one point in Section 3, but apart from this the use of calculus is confined to Section 5, which also uses implicit differentiation and the cosine rule of trigonometry. All the necessary concepts concerning gravitational field, gravitational potential and circular motion (angular speed, centripetal acceleration and centripetal force) are introduced at the appropriate points in this module, but some of those introductions are rather rapid and you will find it beneficial if you have studied such concepts before; they are all discussed in greater detail elsewhere in FLAP. If you are uncertain about any of these terms then you can review them now by reference to the Glossary, which also indicates where in FLAP they are developed. The following questions will help you to establish whether you need to review some of the above topics before embarking on this module.
Question R1
Evaluate the following integral between the limits given $\displaystyle \int_\infty^a \dfrac{dx}{x^2}$
Answer R1
$\displaystyle \int_{\infty}^a \dfrac{dx}{x^2} = -\left[\dfrac{1}{x}\right]_{\infty}^a = -\dfrac{1}{a}$
As x → ∞, 1/x → 0.
Consult integration in the Glossary for further information.
Question R2
(a) Sketch a graph of y against x for y2 = 2x3.
(b) What would you plot in order to obtain a straight–line graph from a set of (x, y) values that obeyed y2 = 2x3?
What would be the intercept and gradient of your graph?
Answer R2
(a) The graph of y against x is a curve (see Figure 12a). You can show this by plotting some specific points, e.g. x = 1, 2, 4. Note that the curve does not exist if x ≤ 0.
(b) Plotting y2 against x3 gives a straight line, which passes through the origin (so the intercept is zero) and has a gradient of 2 (see Figure 12b).
Consult gradient and intercept in the Glossary for further information.
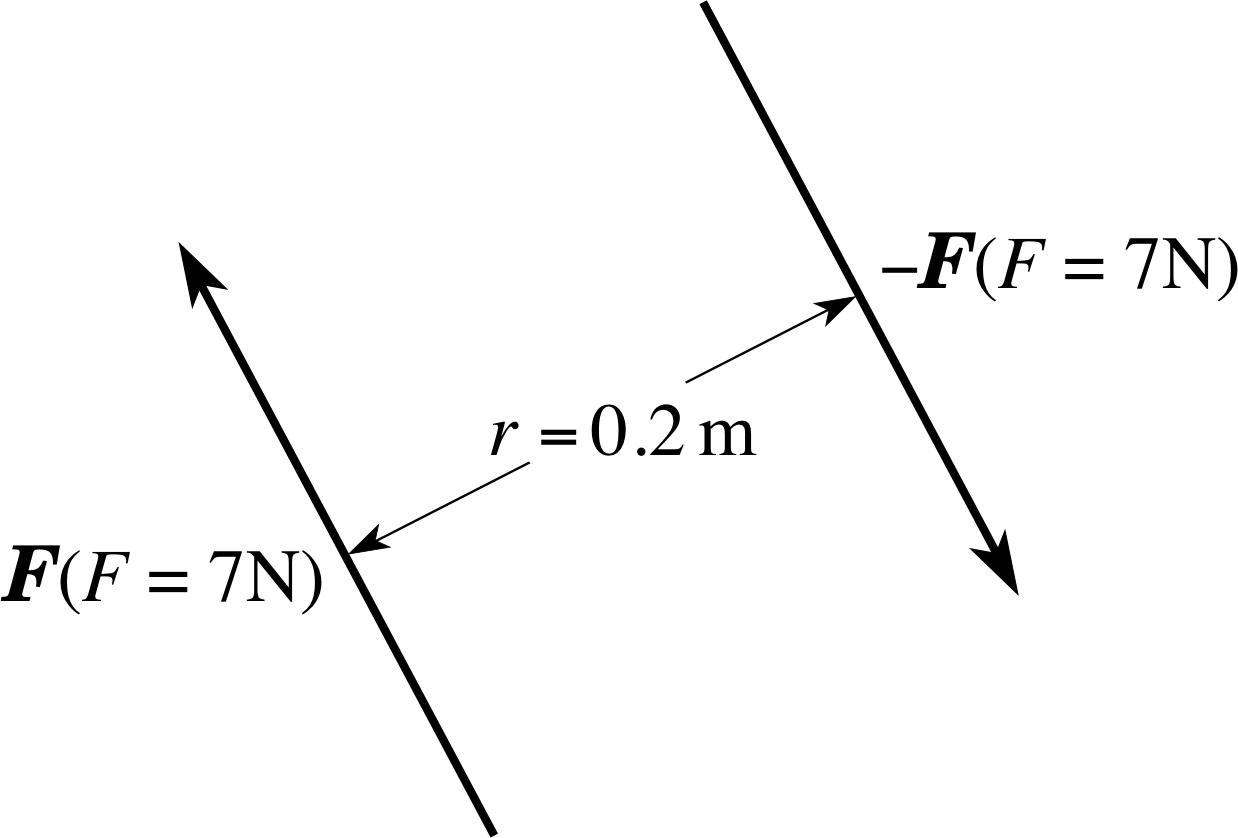
Figure 1 See Question R3.
Question R3
Calculate the magnitude of the torque (turning effect) produced by the forces shown in Figure 1 about a point midway between the lines of action of the two forces.
Answer R3
The magnitude of the torque, or turning effect, of two forces of magnitude F acting in opposite directions along lines separated by a perpendicular distance r is rF, i.e. in this case 1.4 N m. In this case the torque is independent of the point of action chosen.
Consult torque in the Glossary for further information.
Question R4
The mass of a lead sphere of diameter 100 mm is 5.92 kg. Calculate the density of lead.
(The volume of a sphere of radius r is $V = \dfrac{4}{3}\pi r^3$.)
Answer R4
Volume of sphere $V = \dfrac{4}{3}\pi r^3$ where r = 50 mm.
$V = \rm \dfrac{4}{3}\pi(50\times10^{-3}\,m)^3 = \dfrac{4}{3}\pi\times125\times10^{-6}\,m^3$
$\text{density} = \dfrac{\text{mass}}{\text{volume}} = \rm \dfrac{5.92\,kg\times 3}{4\pi\times125\times 10^{-6}\,m^3} = 1.13\times10^4\,kg\,m^{-3}$
2 Universal gravitation
2.1 Gravitational forces
We are all familiar with the notion of gravitational attraction. We know that the Earth, for example, exerts a ‘pull’ on objects in its vicinity. In 1687, Isaac Newton (1642–1727) published his explanation of this phenomenon in his Principia Mathematica. Having made clear what he meant generally by a ‘force’, in terms of the acceleration it would cause, he went on to introduce the concept of a gravitational force, which is described by his law of universal gravitation:
Every particle of matter in the Universe attracts every other particle with a force that is directly proportional to the product of the masses of the particles and inversely proportional to the square of the distance between them.
In modern vector notation, the gravitational force Fgrav on a particle of mass m2 due to a particle of mass m1 separated from it by a distance r is given by
${\boldsymbol F}_{\rm grav} = {\boldsymbol F}_{21} = -\dfrac{G m_1 m_2}{r^2} \hat{\boldsymbol r}$(1a)
where G = 6.673 × 10−11 N m2 kg−2 is the universal gravitational constant, and r^ is a dimensionless unit vector (i.e. a vector of magnitude 1) i directed from m1 to m2. The minus sign in Equation 1a signifies that the force is in the opposite direction to r^, i.e. that the force on m2 takes the form of an attraction towards m1. It follows from Equation 1a that the magnitude of the gravitational force is:
$\left|\,{\boldsymbol F}_{\rm grav}\,\right| = {\boldsymbol F}_{\rm grav} = \dfrac{G m_1 m_2}{r^2}$(1b)
Since the strength of the force is proportional to 1/r2 we say that the gravitational force obeys an inverse square law.
It is a big step to go from the force between two point–like particles to the force between two extended bodies, such as that between an apple and the Earth. However, you can probably imagine how such a step might be taken, at least in principle. In order to find the resultant force on the apple (or the oppositely directed force on the Earth) you would have to treat the extended bodies as large collections of particles and then use vector addition to sum all the forces that each particle in one body exerted on every particle in the other body. If you know the appropriate mathematical techniques this is not quite as daunting as it sounds, especially if the bodies involved are very simple. This is particularly true if the bodies are spherically symmetric, that is if the bodies are spheres, each with a density ρ that may vary with the distance r from the centre of the sphere, but which certainly doesn’t depend on direction. A spherically symmetric body with density ρ (r) i can be envisaged as something like a spherical onion; it consists of concentric layers that may have different densities, but it does not involve any other kind of density variation. The calculation of the gravitational force exerted by such a body is made simple by the following result:
The gravitational effect of any spherically symmetric body, outside its own surface, can be exactly reproduced by a single particle, with the same mass as that body, located at the body’s geometric centre.
This result may look at first like ‘common sense’, but its justification is not obvious – it took Newton almost 20 years to produce a satisfactory proof, and it is sometimes referred to as Newton’s theorem. The theorem will be proved in Section 5, but in the meantime we will simply accept that it is true and make use of it.
Study comment Section 5 uses ideas that are discussed in Sections 2 to 4, and is mathematically the most demanding section of this module, so we advise you to study the rest of the module first. However, if you really don’t like using unjustified results, and you are confident that you have a good grasp of all the mathematical prerequisites listed in Subsection 1.3, you may study Section 5 next and then return to Sections 2 to 4 later.
2.2 Determining the gravitational constant G
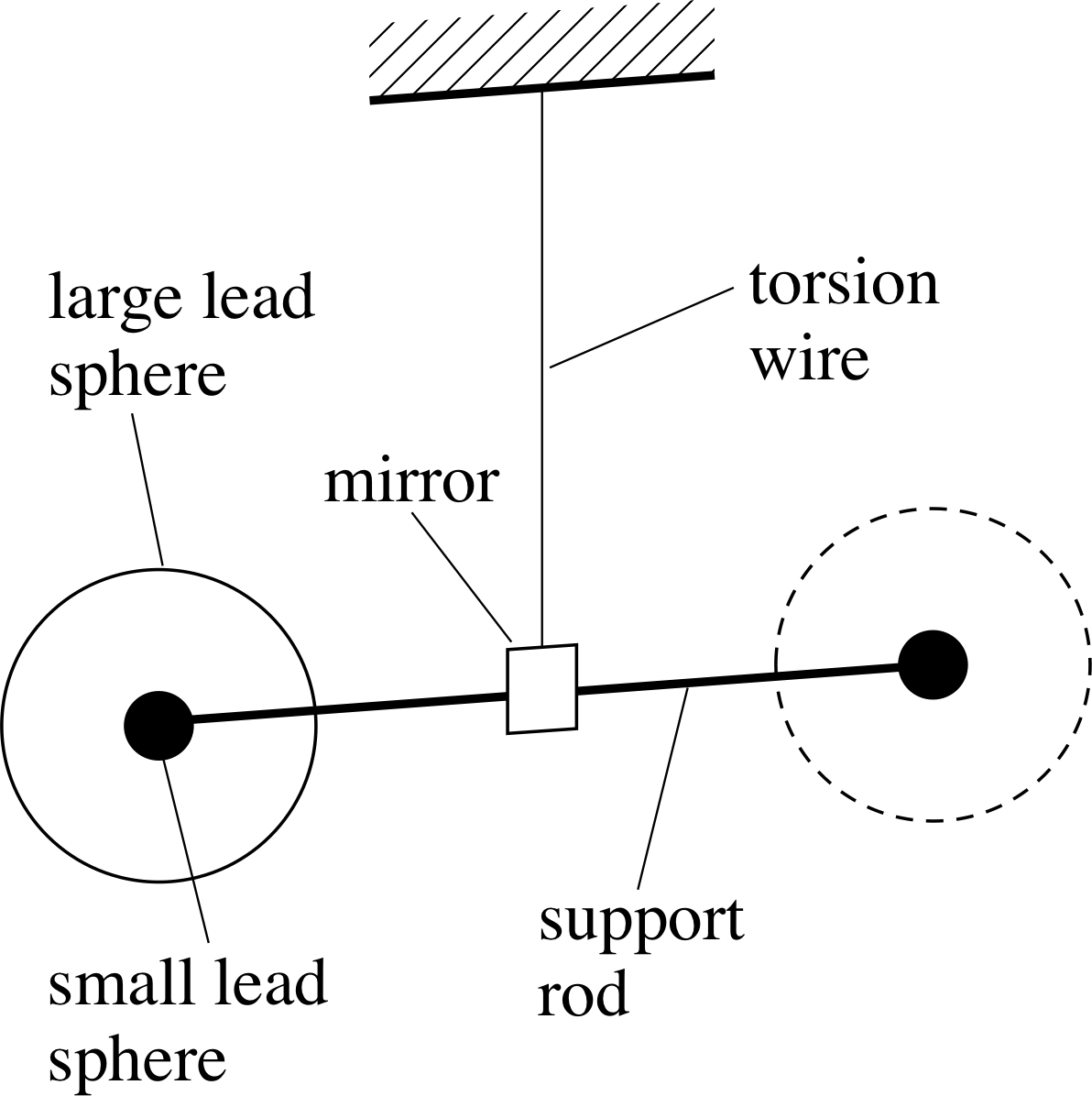
Figure 2 Schematic diagram of a Cavendish torsion balance. (From this side view, one of the large spheres is in front of a small sphere, the second is an equal distance behind the other small sphere.)
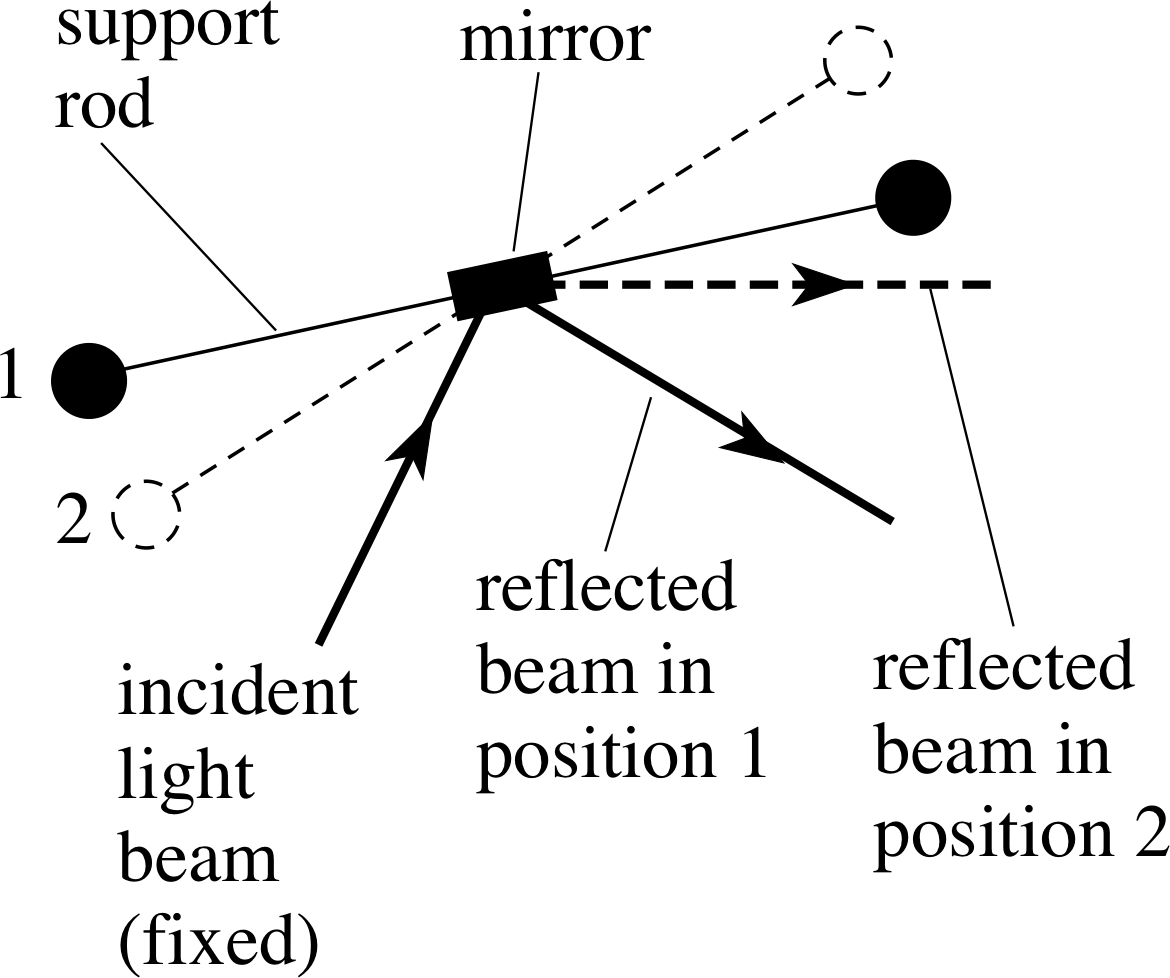
Figure 3 Use of a light beam to measure the rotation of the torsion balance.
The value of G, the universal gravitational constant, must be determined experimentally by measuring the gravitational force between known masses – currently there is no way to deduce its value theoretically. The gravitational forces between objects that we can handle in the laboratory are extremely weak (for example, the force between two 5 kg masses separated by 0.1 m has a magnitude of approximately 10−7 N) so they can be measured only with very sensitive apparatus. It is not surprising therefore that G is the least accurately known of all the fundamental constants.
Recent determinations all use the same basic technique as the experiment performed in 1798 by Henry Cavendish. i At the heart of the Cavendish’s experiment was a torsion balance of the kind shown schematically in Figure 2. In its simplest form such a balance consists of two small spheres of equal mass attached to the ends of a horizontal support rod. The rod is suspended at its centre by a fine vertical wire (or fibre), so it can turn in the horizontal plane but in doing so it will twist the wire and thus produce a torque that opposes the rotation.
The degree of twisting can be monitored by observing the behaviour of a beam of light that comes from a fixed source and is reflected from a small mirror attached to the centre of the support rod. At the start of a typical experiment the balance is shielded from draughts, vibrations and other external influences and allowed to settle into an equilibrium state in which the wire is untwisted. Once this has been achieved two large spherical masses are placed close to the small spheres, in the symmetrical arrangement shown in Figure 2. The gravitational forces between these large spheres and the torsion balance will cause the balance to turn in the horizontal plane until the increasing twist of the wire prevents further rotation. Left to itself, the system will eventually settle into a new equilibrium state as indicated in Figure 3.
The angle of rotation between the two equilibrium positions can be determined from the change in direction of the reflected light beam, and this angle together with the properties of the balance and the masses of the large spheres can be used to determine the value of G, as explained below.
When the large spheres are in position each of them will exert a horizontal gravitational force of magnitude Fgrav on the nearest small sphere. Assuming these are the only significant forces in the horizontal plane and that the spheres are positioned to ensure that the final position is one in which the gravitational forces are at right angles to the support rod, we can say that the final gravitational torque tending to rotate the balance is of magnitude FgravL, where L is the length of the support rod. As the support wire twists in response to the gravitational torque it will exert a restoring torque that tends to untwist the wire. In this sort of experiment the magnitude Γ of the restoring torque i will be proportional to the angle of rotation of the wire θ, so the quantity c = Γ/θ will be a constant and will be a characteristic property of the wire. The angle at which the balance eventually comes to rest will be such that the magnitudes of the gravitational torque and the restoring torque are equal, so it will be given by
FgravL = cθ(2)
If the mass of each small sphere is m1, the mass of each large sphere m2, and the distance between the centres of the small and large spheres r, then we can use Equation 1b,
$\left|\,{\boldsymbol F}_{\rm grav}\,\right| = {\boldsymbol F}_{\rm grav} = \dfrac{G m_1 m_2}{r^2}$(Eqn 1b)
to calculate the value of Fgrav in this case i, giving
$\dfrac{Gm_1 m_2}{r^2}L = c\theta$(3)
Now, m1, m2, L and c are determined by the equipment, θ can be measured and r (the final distance between the centre of either of the small spheres and the centre of its neighbouring large sphere) can be determined by simple geometry. Thus, using Equation 3, we can determine G from the experiment.
Question T1
What practical steps could you take to make θ as large as possible?
Answer T1
According to Equation 3,
$\dfrac{Gm_1 m_2}{r^2}L = c\theta$(Eqn 3)
to make θ large we require L to be large, r to be small (i.e. the masses close together), c to be small (which means a fine torsion wire) and m1m2 to be large. However, these requirements conflict to some extent, so we have to seek the best compromise. The small spheres must be supported by the (thin) wire, so their mass m1 must not be too large. A fine wire will be relatively weak so this will limit the size of L, as does the need to shield it from draughts and vibrations. The large spheres must be heavy, but mobile. However, their radius must not be any greater than necessary or it will force the final separation r to be unnecessarily large. To satisfy this requirement the large spheres should be made from a dense substance such as lead.
Modern accurate determinations of G, while based on the same principle of measurement, require clevermodifications and extremely elaborate precautions to reduce sources of error such as vibration.
3 Gravity and the Earth
3.1 Gravitational forces at the Earth’s surface
Study comment All the main results in this subsection are also discussed in greater detail elsewhere in the fields modules. See the Glossary for details.
Let us return to our apple on the surface of the Earth. We have seen how, using Newton’s theorem, we might calculate the force of attraction between the apple and the Earth, but according to Newton’s law of universal gravitation each object in the Universe is simultaneously attracted by all other objects in the Universe. How will other nearby objects affect the apple?
✦ Estimate the magnitudes of (a) the gravitational force between an apple of mass 300 g and a spherical boulder of mass 103 kg when their centres are separated by 10 m, and (b) the gravitational force between the apple and the Earth. i
✧ Treating all the objects as spherically symmetric and using Equation 1b,
$\vert\,{\boldsymbol F}_{\rm grav}\,\vert = F_{\rm grav} = \dfrac{Gm_1 m_2}{r^2}$
(a) $F_{\rm grav} = \dfrac{6.67\times 10^{-11}\,{\rm N\,m^2\,kg^{-2}}}{10^2\,{\rm m^2}} \times 10^3\,{\rm kg} \times 0.3\,{\rm kg} = 2.00\times 10^{-10}\,{\rm N}$
(b) $F_{\rm grav} = \dfrac{6.67\times 10^{-11}\,{\rm N\,m^2\,kg^{-2}}}{(6.38\times10^6\,{\rm m})^2}\times 5.98\times 10^{24}\,{\rm kg} \times 0.3\,{\rm kg} = 2.94\,{\rm N}$
The gravitational force due to the Earth is 1010 times larger than that due to the boulder, even though the centre of the Earth is much more distant – the Earth, though, has much the greater mass. If it is large masses which dominate the gravitational attraction, then shouldn’t the Moon and the Sun have considerable influence too?
✦ Compare the magnitudes of (a) the gravitational forces on the apple due to the Moon and the Earth, and (b) the magnitudes of the forces on the apple due to the Sun and the Earth. i
✧ (a) By writing down expressions for the two forces and taking their ratio, we find G and the apple’s mass both cancel. If FE is the magnitude of the force due to the Earth, and FM is that due to the Moon, we have
$\dfrac{F_{\rm M}}{F_{\rm E}} = \dfrac{M_{\rm M}}{M_{\rm E}}\dfrac{R_{\rm E}^2}{D_{\rm M}^2} = \rm \dfrac{7.35\times 10^{22}\,kg\,(6.38\times 10^6\,m)^2}{5.98\times 10^{24}\,kg\, (3.78\times 10^8\,m)^2} = 3.5\times 10^{-6}$
(b) Similarly, if FS is the magnitude of the force due to the Sun, we have
$\dfrac{F_{\rm S}}{F_{\rm E}} = \dfrac{M_{\rm S}}{M_{\rm E}}\dfrac{R_{\rm E}^2}{D_{\rm S}^2} = \rm \dfrac{1.99\times 10^{30}\,kg\,(6.38\times 10^6\,m)^2}{5.98\times 10^{24}\,kg\, (1.5\times 10^{11}\,m)^2} = 6.02\times 10^{-4}$
So the gravitational force due to the Moon is 3 × 105 times weaker than that due to the Earth and even that due to the Sun is nearly 2000 times smaller than that due to the Earth despite the Sun’s being nearly 106 times more massive. Although every object on the surface of the Earth feels a gravitational force that is the vector sum of an infinite number of forces from the whole Universe, in practically all everyday situations the only significant gravitational force on a small object near the Earth’s surface is that due to the Earth itself.
3.2 The Earth’s gravity close to its surface
In everyday life – and in laboratory experiments – we often need to deal with the effects of the Earth’s gravity close to its surface. In this subsection we look at various ways of describing these effects and, in doing so, summarize some concepts and definitions connected with gravitation.
The gravitational field and acceleration due to gravity
One way to describe the gravitational effect of the Earth is via its gravitational field. i The gravitational field at any point is a vector quantity which provides a quantitative measure of the gravitational force that would act on a point test mass m located at that point. (By a test mass we mean a mass sufficiently small that it will not significantly disturb the gravitational field we are using it to measure.) If the point we are interested in is defined by a position vector r, and if the gravitational force on a test mass m located at that point is Fgrav(on m at r), then we can define the gravitational field g (r) at that point by
${\boldsymbol g}({\boldsymbol r}) = \dfrac{{\boldsymbol F}_{\rm grav}({\rm on}~m~{\rm at}~{\boldsymbol r})}{m}$(4)
In other words, the gravitational field at any point is equal to the gravitational force per unit mass that would act on a point test mass at that point.
Treating the Earth as a spherically symmetric body we can use Equations 1a
${\boldsymbol F}_{\rm grav} = {\boldsymbol F}_{21} = -\dfrac{G m_1 m_2}{r^2} \hat{\boldsymbol r}$(Eqn 1a)
and Equation 4 to write down an expression for its gravitational field. In this case, the assumed spherical symmetry of the Earth will give rise to a gravitational field which is always directed towards the centre of the Earth and which has a magnitude that only varies with the distance from the centre of the Earth. If we take the centre of the Earth as our origin of coordinates, any point with position vector r will be at a distance r = | r | from the centre and we can write the gravitational field as
${\boldsymbol g}({\boldsymbol r}) = -\dfrac{GM_{\rm E}}{r^2}\hat{\boldsymbol r}$(5)
where ME is the mass of the Earth, r^ = r /| r | is a unit vector parallel to r, and the minus sign indicates that the field, like the force, points in the opposite direction to r^, i.e. towards the centre of the Earth.
It follows from Equation 5 that the magnitude of the field at the surface of the Earth, where r = RE, will be
$g(R_{\rm E}) = -\dfrac{GM_{\rm E}}{R_{\rm E}^2}$(6)
✦ What is the surface field strength predicted by Equation 6? Take care to include appropriate units of measurement.
✧ $g(R_{\rm E}) = \dfrac{6.67\times 10^{-11}\,{\rm N\,m^2\,kg^{-2}}\times 5.98\times 10^{24}\,{\rm kg}}{(6.38\times 10^6\,{\rm m})^2} = 9.80\,{\rm N\,kg^{-1}}$
Now imagine a small object somewhere in the Earth’s gravitational field subject only to gravitational forces. Such an object is said to be in free fall. Since there is an unbalanced force acting on the object it will accelerate and, according to Newton’s second law of motion, its acceleration must be equal to Fgrav/m. However this is just the quantity that defines the gravitational field. We can therefore identify the free fall acceleration of the object with the gravitational field at its location.
At the surface of the Earth, the free fall acceleration is usually referred to as the acceleration due to gravity, or the surface gravity, and its magnitude is denoted by g. It follows from Equation 6 that if the Earth was accurately spherically symmetric we would find that
$g = \dfrac{GM_{\rm E}}{R_{\rm E}^2}$(7)
✦ Confirm for yourself that the units of acceleration (m s−2) are identical to those of gravitational field strength (N kg−1).
✧ Remember that 1 N = 1 kg m s−2, therefore 1 N kg−1 = 1 m s−2 as required.
Of course, the Earth is not really spherically symmetric, so measured values of g vary from place to place, though departures from the value predicted by Equation 7 are never very great. Accurate measurements of g can be based on observations of the time t that a freely falling object, starting from rest, takes to cover a known distance s (since s = gt2/2), or on the period T of a freely swinging simple pendulum of length l (since $T=2\pi\sqrt{l/g}$).
Whichever technique is used, the measurements are usually made at fixed locations on the Earth’s surface, and are therefore influenced by the rotation of the Earth, which tends to reduce the effective value of g at the Equator relative to its value at the poles. i (This effect is similar to the apparent outward force experienced by the occupants of cars and buses as they go round corners.) Once a correction has been made to allow for this, the remaining variations in g are entirely due to departures from spherical symmetry and arise from factors such as the flattening of the Earth at its poles, the height above sea level and local variations in geology. The measured results are sometimes expressed as (small) departures from a standard reference value, which at latitude λ and height h above sea level is given by
g/m s−2 = 9.806 16 − 0.025 928 cos(2λ) + 0.000 069 cos2 (2λ) − 0.000 003h i
The sensitivity of g to local geology and the experimentally precise methods available make gravimetric surveying (the measurement of g over some specified area) an important technique in geophysics. Apart from being used to seek out various kinds of mineral deposit and other geological structures, short–term variations in g around volcanoes have even been used to assist in the prediction of eruptions. Despite the practical importance of variations in g we will ignore them throughout the rest of this module, simply using g = 9.81 m s−2 whenever we need a numerical value.
Now that we have a value for the magnitude of the field at all points on the Earth’s surface, we can say that the surface gravitational field is
g = − (9.81 m s−2) r^
In practice, we are often concerned with relatively restricted parts of the Earth’s surface that are sufficiently small to be considered a flat plane. In such cases the unit vector −r^, directed towards the centre of the Earth, may be replaced by a ‘downward’ directed unit vector $-\hat{\boldsymbol z}$ perpendicular to the flat plane, giving
g = − (9.81 m s−2)$\hat{\boldsymbol z}$
The ideas of gravitational field and acceleration due to gravity are closely related to that of weight. At the surface of the Earth, the weight of an object is usually taken to mean the gravitational force that acts on it, in which case we may write
W = mg(8)
where m is the mass of the object and g is the acceleration due to gravity. Some authors prefer to modify this slightly by allowing for the reduction in the effective value of g caused by the Earth’s rotation. We will have more to say about the significance of such a modification in the next subsection. Equation 8 enables us to find the gravitational force on an object at the Earth’s surface without explicitly using values of ME, RE or G.
Question T2
What is the weight of a 60 kg man on the surface of the Earth?
Answer T2
Assuming g = 9.81 m s−1, the magnitude of the weight will be
W = 60 kg × 9.81 N kg−2 = 589 N = 5.9 × 102 N (to two significant figures).
However weight is a vector quantity, so to answer the question fully we must also specify its direction, which will be downwards in this case.
Knowing g and G it is also possible to calculate the mass of the Earth and hence its average density – it is often said that Cavendish’s determination of G made it possible to ‘weigh the Earth’. (There is some truth in this, but Newton had previously estimated a value for ME that was within 0.5% of the currently accepted value! Newton used his estimate together with measured values of g and RE to determine G.)
Question T3
Derive an approximate expression for the Earth’s average density ρ in terms of G, g and RE.
Answer T3
Density of Earth, ρ = mass/volume
soρ = 3ME/4πRE3 (assuming Earth is spherical, i.e. it has a volume = 4πRE3/3)
$g = \dfrac{GM_{\rm E}}{R_{\rm E}^2}$(Eqn 7)
If we rearrange Equation 6 or 7,
$g(R_{\rm E}) = \dfrac{GM_{\rm E}}{R_{\rm E}^2}$(Eqn 6)
we find
$M_{\rm E} = \dfrac{gR_{\rm E}^2}{G}$
Substituting this equation for ME in the expression for ρ gives us an expression for the Earth’s density
$\rho = \dfrac{3g}{4\pi R_{\rm E}G}$
The gravitational potential and gravitational potential energy
An object of mass m in a gravitational field g (r) will be subject to a gravitational force F = mg(r). If such an object is displaced from one point to another within the field, a gravitational force will act on it throughout the displacement and may consequently do work as a result of the displacement. In any particular region of the Earth’s surface, where the gravitational field may be represented by the fixed vector −g$\hat{\boldsymbol z}$, the work done by the gravitational force when the object is displaced by an amount ∆z in the $\hat{\boldsymbol z}$ direction will be ∆W = −mg ∆z, where ∆z will be positive if the object is raised, and negative if it is lowered. i
✦ The 60 kg man (of Question T2) climbs a vertical height of 10 m. What is the work done by the gravitational force on the man as a result of the movement?
✧ Ignoring the tiny variation in g with height, the gravitational force on the person is his weight, 5.9 × 102 N, downwards. The work done by this force over a displacement of 10 m upwards is
∆W = −5.9 × 102 N × 10 m = −5.9 × 103 N m = −5.9 × 103 J
Notice that the answer is negative: the man might have to do a lot of positive work to raise himself through 10 m, but the gravitational force (weight) is opposed to the displacement, so it does negative work.
As a result of the work done when an object moves through a gravitational field, there may be a corresponding change in the gravitational potential energy that the object possesses by virtue of its position. i In general the change in the gravitational potential energy will be equal to minus the work done by the gravitational force, since the gravitational potential energy is a measure of the ability of the object to do work by virtue of its position. i
For an object of mass m close to the surface it follows that
∆Egrav = mg ∆z for ∆z ≪ RE
✦ What is the change in the gravitational potential energy of the 60 kg person as a result of his 10 m climb?
✧ ∆Egrav = −W = 5.9 × 103 J
Question T4
Calculate the changes in gravitational potential energy when a 5.0 kg bag of potatoes is (a) lifted from a supermarket floor and placed on a trolley 0.40 m above the floor, (b) wheeled 30 m across to the checkout, (c) taken in the trolley to an underground car park with a floor 6.0 m below the supermarket floor. In each case, say whether Egrav increases or decreases.
Answer T4
Use ∆Egrav = mg∆z, and mg = 5.0 kg × 9.81 N kg−1 = 49.05 N.
(a) Egrav increases by ∆Egrav = 49.05 N × 0.40 m = 19.6 J.
(b) ∆Egrav = 0, since Fgrav acts vertically and the potatoes are moved horizontally, there is no work done by Fgrav.
(c) Egrav decreases by ∆Egrav = 49.05 N × 6.0 m = 294 J.
The relation ∆Egrav = mg ∆z can be used to calculate potential energy changes in situations where ∆z is a few kilometres or less. Note that it only describes changes in gravitational potential energy – it says nothing about what the potential energy Egrav actually is at any point. We are therefore free to define Egrav = 0 at any convenient reference point, e.g. at the Earth’s surface, or at the floor of a laboratory. Once we have made the choice, though, the value of Egrav at all other points follows from the expression for ∆z.
If we choose to measure positive z vertically upwards (as we have done so far) from ground level, and we choose some point with z = 0 to be the point at which Egrav = 0, we can say that at a height z above the surface of the Earth
Egrav(z) = mgz i
A related quantity that is often used when characterizing the Earth’s gravitational field is the gravitational potential. Just as the gravitational field is defined as the gravitational force per unit mass, so the gravitational potential is the gravitational potential energy per unit mass. Thus, in the case of the gravitational field near the surface of the Earth, the gravitational potential is given by
$V_{\rm grav}(z) = \dfrac{E_{\rm grav}(z)}{m}$
It follows that the value of the gravitational potential close to the surface of the Earth is
Vgrav(z) = gz(9)
Note that the gravitational force on an object of mass m close to the Earth, and the corresponding gravitational potential energy depend on the properties of the Earth and the mass of the object, m. On the other hand, the gravitational field and the corresponding gravitational potential depend only on the Earth and are independent of the mass of the object.
Question T5
A ball of mass 500 g is thrown vertically upwards with a speed of 7 m s−1. If all its initial kinetic energy i is converted into gravitational potential energy, how far does it rise? Do you actually need to know the mass of the ball in order to answer this question?
Answer T5
Total mechanical energy remains constant for objects moving under the influence of gravity alone; the gravitational force is said to be conservative_forceconservative. Hence the gain in gravitational potential energy must equal the loss in kinetic energy
i.e.mgz = ½ mυ2
Cancelling m (so you don’t need to know the mass) and dividing by g we find:
$h = \dfrac{\upsilon^2}{2g} = \rm \dfrac{(7\,m\,s^{-1})^2}{2\times9.81\,m\,s^{-2}} = 2.5\,m$
3.3 The Earth’s gravity at large distances i
We saw in the last subsection that if we treat the Earth as a spherically symmetric body of radius RE then its
gravitational field at any distance r is given by
${\boldsymbol g}({\boldsymbol r}) = -\dfrac{GM_{\rm E}}{r^2}\hat{\boldsymbol r}$(Eqn 5)
provided r ≥ RE. It follows from the definition of the gravitational field (the gravitational force per unit mass that would act on a point test mass located at r) that the gravitational force on a mass m at a point with position vectorris
${\boldsymbol F}({\boldsymbol r}) = -\dfrac{GM_{\rm E}m}{r^2}\hat{\boldsymbol r}$(10)
If we are dealing with objects that move more than a few kilometres from the Earth’s surface we must take account of changes in gravitational force with distance implied by these formulae when calculating the gravitational potential and the gravitational potential energy.
In particular, it follows from Equation 10 that the radial component of the gravitational force at a distance r from the centre of the Earth, irrespective of direction, will be
$F(r) = -\dfrac{GM_{\rm E}}{r^2}$(11)
and the work done by the gravitational force when an object of mass m moves from a point with position vector r1, at which r = r1, to some other point r2, at which r = r2, will be given by the integral
$\displaystyle W = \int_{r_1}^{r_2} F_r(r)\,dr$(12)
and the corresponding change in the gravitational potential energy of the object will be
$\displaystyle \Delta E_{\rm grav} = -W = -\int_{r_1}^{r_2} F_r(r)\,dr$
So, using Equation 11 we can write
$\displaystyle \Delta E_{\rm grav} = \int_{r_1}^{r_2} \dfrac{GM_{\rm E}m}{r^2}$
Evaluating the integral we obtain
$\Delta E_{\rm grav} = -GM_{\rm E}m\left(\dfrac{1}{r_2}-\dfrac{1}{r_1}\right)$(13)
When dealing with the force specified by Equation 10 it is convenient to adopt the convention that Egrav = 0 where Fr = 0, i.e. at an infinite distance from Earth, where r = ∞.
The change in gravitational potential energy ∆Egrav in moving an object of mass m from r1 = ∞ to r2 = r will then be equal to the full value of the gravitational potential energy at r and we may write
$E_{\rm grav}(r) = -\dfrac{GM_{\rm E}m}{r}$(14)
Note that according to the convention we have adopted in this subsection, at the surface of the Earth, where r = RE, the gravitational potential energy is given by
$E_{\rm grav}(R{\rm E}) = -\dfrac{GM_{\rm E}m}{R_{\rm E}}$(15)
The fact that this is a negative quantity is of no direct significance, it is merely a consequence of our decision to let Egrav = 0 at r = ∞. Only differences in gravitational potential energy are physically meaningful, and they may be positive or negative.
With the aid of Equation 14 we can work out the minimum amount of energy required to enable a space probe to escape entirely from the Earth’s gravitational field. This minimum amount of energy will be equal to the change in the gravitational potential energy of the probe as it travels from r = RE to r = ∞. i
So, if the probe has mass m, the required energy will be Egrav(∞) − Egrav(RE), but since Egrav(∞) = 0 the required energy is just −Egrav(RE) = GMEm/RE.
This ‘escape energy’ as it is sometimes called can be used to compute the escape speed of the probe, i.e. the minimum speed at which the probe must be launched from the Earth (neglecting air resistance and any other non–gravitational effects) if it is to escape to infinity. Using the same approach as in Question T5, we simply equate the required escape energy with the initial kinetic energy of the probe, ½ mυe2.
Thus,$\dfrac{1}{2}m\upsilon_e^2 = \dfrac{GM_{\rm E}}{R_{\rm E}}$(16)
so, escape speed $\upsilon_e = \sqrt{\dfrac{2GM_{\rm E}}{R_{\rm E}}}$(17)
Note that this is independent of the mass of the probe!
Question T6
Evaluate the escape speed from the Earth. i Ignoring the atmosphere and any other non–gravitational influences, does the direction in which a space probe is launched have any influence on its escape speed?
Answer T6
Using Equation 17,
escape speed $\upsilon_e = \sqrt{\dfrac{2GM_{\rm E}}{R_{\rm E}}}$(Eqn 17)
we find
$\upsilon_{\rm e} = \rm \left(\dfrac{2\times6.67\times10^{-11}\,N\,m^2\,kg^{-2}\times 5.98\times10^{24}\,kg}{6.38\times10^6\,m}\right)^{1/2} = 11.2\,km\,s^{-1}$
The direction of launch makes no difference (as long as you ignore the atmosphere, don’t fire the probe into the ground and neglect all other non–gravitational effects). The argument that we used to deduce the escape speed was based on energy considerations, so for a spherically symmetric Earth it only depended on changes in the distance from the Earth’s centre; neither the direction of motion nor the nature of the path (straight line, spiral, etc.) had any bearing on the energy change.
If we know the escape speed from a planet’s surface we can work out whether the planet is able to retain an atmosphere. The speed of molecules depends on the temperature. i The average speed of hydrogen molecules at 300 K, for example, is 1.8 km s−1, whereas for oxygen molecules it is 0.4 km s−1. The actual molecular speeds are distributed above and below these values, so there will be some molecules of each species which are moving fast enough to escape from the Earth and, since the average speed for hydrogen is greater than that for oxygen, hydrogen molecules will escape at a much greater rate. The escape speed from the Moon is only 2.4 km s−1 and the rate of escape of gas molecules has been such that it has completely lost its original atmosphere. i
Using Equation 14,
$\displaystyle \Delta E_{\rm grav}(r) = -\dfrac{GM_{\rm E}m}{r}$(Eqn 14)
we can also evaluate the Earth’s gravitational potential (i.e. the gravitational potential energy per unit mass at any point in the field). According to the general definition of the gravitational potential
$V_{\rm grav}({\boldsymbol r}) = \dfrac{E_{\rm grav}({\rm of}~m~{\rm at}~{\boldsymbol r})}{m}$(18)
In the case of the Earth our assumption of spherical symmetry ensures that the gravitational potential will vary with distance from the Earth, but will be independent of direction. We may therefore write
$V_{\rm grav}({\boldsymbol r}) = \dfrac{E_{\rm grav}}{m}$
so, from Equation 14 we have
$V_{\rm grav}({\boldsymbol r}) = -\dfrac{GM_{\rm E}}{r}$(19)
Since Vgrav depends only on the field, and not on the mass of the object under consideration, we can use it to characterize a gravitational field. As you will see in Section 5, it can sometimes be easier to work with Vgrav(r) rather than the gravitational field g (r).
Question T7
Calculate the magnitudes of the following:
(a) the gravitational force between the Earth and a satellite of mass mS = 4.0 × 104 kg orbiting the Earth at a distance RS = 4.2 × 107 m from the centre of the Earth
(b) the Earth’s gravitational field strength at that distance
(c) the change in its gravitational potential energy when the satellite is put into orbit.
[Hint: Treat the Earth as a point mass situated at its centre.]
Answer T7
(a) $F_{\rm grav} = \dfrac{Gm_1 m_2}{r^2}$
At r = RS the magnitude of the force is
Fgrav = [6.67 × 10−11 N m2 kg−2 × 5.98 × 1024 kg × 4.0 × 104 kg]/(4.2 × 107 m)2 = 9.04 × 103 N
(b) Field strength g is the magnitude of the gravitational force per unit mass (or, equivalently, the magnitude of the gravitational acceleration) so
g = Fgrav/mS
i.e.g = 2.3 × 10−1 N kg−1
(c) Gravitational potential energy Egrav = −GmSME/r (relative to Egrav = 0 at infinite distance from Earth) so the change in potential energy is
$\Delta E_{\rm grav} = GM_{\rm E}m_{\rm S}\left[\dfrac{1}{R_{\rm E}}-\dfrac{1}{R_{\rm S}}\right]$
i.e.$\Delta E_{\rm grav} = GM_{\rm E}m_{\rm S}\left[\dfrac{R_{\rm S}-R_{\rm E}}{R_{\rm E}R_{\rm S}}\right]$
$\phantom{\Delta E_{\rm grav}} = \rm \dfrac{6.67\times10^{-11}\,N\,m^2\,kg^{-2}\times 5.98\times10^{24}\,kg\times4.0\times10^4\,kg\times35.6\times10^6\,m}{4.2\times10^7\,m\times6.38\times10^6\,m}$
$\phantom{\Delta E_{\rm grav}} = \rm \dfrac{6.67\times5.98\times4.0\times35.6}{4.2\times 6.38}\times\dfrac{10^{-11}\times10^{24}\times 10^4\times10^6}{10^7\times 10^6}\,N\,m$
$\phantom{\Delta E_{\rm grav}} = \rm 2.12\times10^{12}\,J$
4 Gravity and orbits
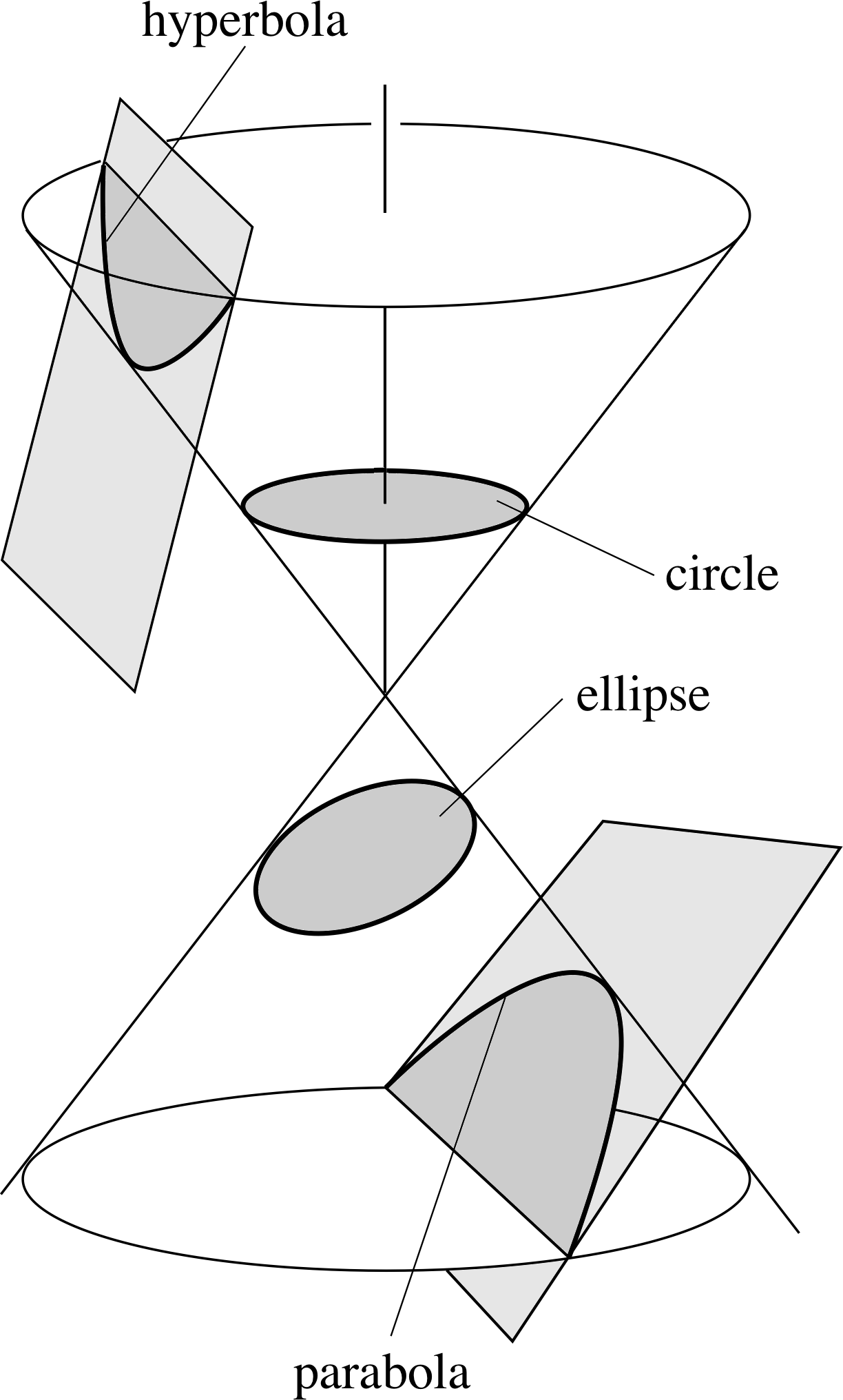
Figure 4 The conic sections obtained by slicing a double cone.
By combining Newton’s laws of motion with his law of universal gravitation, it is possible to work out the path that a body such as a planet will follow as it moves under the gravitational influence of another body such as the Sun. Such investigations show that these paths, or orbits as they are called, are members of a family of curves called conic sections. As Figure 4 indicates, this family includes circles, ellipses, parabolas and hyperbolas. In this section we examine some of these orbits in greater detail, beginning with simple circular orbits.
4.1 Orbital periods and circular orbits
Perfectly circular orbits are quite rare in nature, certainly amongst natural astronomical bodies such as planets and their moons. However, many bodies, including the Earth, have orbits that closely approximate circles. Moreover, circular orbits are easy to describe and investigate. For both of these reasons circular orbits provide a good starting point for a more general study of orbits and deserve close attention.
If a body moves in a circle of radius r with constant speed υ, and takes a time T to complete each orbit, then we say that T is its orbital period, and its angular speed ω (measured in rad s−1) is given by i
$\omega = \dfrac{2\pi\,\text{radians}}{T}$
Since the total distance travelled in time T is equal to the circumference of the circle we can say that
υT = 2πr
so$\dfrac{\upsilon}{r} = \dfrac{2\pi}{T}$
and hence υ = rω
In order to keep the body moving in a circle it must always be subject to an acceleration towards the centre of the circle. This centrally directed acceleration is called the centripetal acceleration and has magnitude
$a = r\omega^2 = \upsilon\omega = \dfrac{\upsilon^2}{r}$
The centrally directed force needed to maintain this acceleration is called the centripetal force. If the circling body has mass m, the magnitude of this force will be
$F = mr\omega^2 = m\upsilon\omega = m\dfrac{\upsilon^2}{r}$
If the body is held in its circular orbit by the gravitational attraction of some other body of mass M, then the centripetal force is provided by the gravitational force on the orbiting body and we may write
F = Fgrav
i.e.$mr\omega^2 = \dfrac{GMm}{r^2}$(20) i
Dividing both sides by m and rearranging the equation we obtain
$\dfrac{1}{\omega^2} = \dfrac{r^3}{GM}$(21)
Recalling that the orbital period of the circular motion is T = 2π/ω, we can write
$T^2 = \dfrac{4\pi^2}{GM}r^3$(22)
Notice that T does not depend on the mass m of the orbiting object, so the mass M can be calculated from measurements of T and r.
Question T8
The radius of the Earth’s orbit around the Sun is 1.496 × 1011 m. Calculate the mass of the Sun. i
Answer T8
Rearranging Equation 22,
$T^2 = \dfrac{4\pi^2}{GM}r^3$(Eqn 22)
gives the mass of the ‘parent’ body
$M = \dfrac{4\pi^2r^3}{GT^2}$
T is the Earth’s orbital period of 1 year (= 3.15 × 107 s).
Hence the mass of the Sun
$M = \rm \dfrac{4\pi^2\times(1.496\times 10^{11}\,m)^3}{6.67\times10^{-11}\,N\,m^2\,kg^{-2}\times(3.15\times 10^7\,s)^2} = 1.99\times10^{30}\,kg$
Question T9
Many communications satellites orbit the Earth with a period of exactly 1 day so that they can always remain in a fixed position relative to the rotating Earth. Such an orbit is known as a ‘geostationary’ orbit. Calculate the orbital speed of such a satellite.
Answer T9
Orbital speed υ = rω = r2π/T. Substituting r = υT/2π into Equation 22:
$T^2 = \dfrac{4\pi^2}{GM}r^3$(Eqn 22)
$T^2 = \dfrac{4\pi^2}{GM}\left[\dfrac{\upsilon T}{2\pi}\right]^3$
Hence$\upsilon^3 = \dfrac{2\pi GM}{T}$
For the satellite to maintain its position above the Earth, T = 1 day = 8.64 × 102 s, hence
$\upsilon^3 = \rm \dfrac{2\pi\times6.67\times10^{-11}\,N\,m^2\,kg^{-2}\times5.98\times 10^{24}\,kg}{8.64\times 10^4\,s}$
Therefore the orbital speed υ = 3.07 × 103 m s−1.
4.2 Kepler’s laws and elliptical orbits

Figure 5a Illustration of Kepler’s laws. (a) A point P that moves in such a way that the sum of its distances from two fixed points F1 and F2 is constant, will follow an ellipse. F1 and F2 are the focii of the ellipse and a is its semi–major axis and b is the semi–minor axis. The planets move in elliptical orbits with the Sun at one focus.

Figure 5b Illustration of Kepler’s laws. (b) A radial line from a planet to the Sun sweeps out equal areas in equal amounts of time.

Figure 5c Illustration of Kepler’s laws. (c) The square of a planet’s orbital period is proportional to the cube of its semi–major axis.
Newton’s investigations of orbital motion under gravity provided an explanation of Kepler’s laws of planetary motion. Johannes Kepler (1571–1630) had arrived at these laws early in the 17th century by careful analysis of observational data on planetary motion collected by the Danish astronomer Tycho Brahe (1546–1601).
Kepler’s first law: The orbits of the planets in the solar system are ellipses with the Sun at one focus (see Figure 5a).
An ellipse may be obtained by plotting all the points (x, y) that satisfy the equation
$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$
Such an ellipse has a semi–major axis of length a, and focus_of_a_conic_sectionfoci F1 and F2 located at the points (ae, 0) and (−ae, 0), where $e = \dfrac{1}{a}\sqrt{a^2 - b^2}$ is the eccentricity of the ellipse. A circle may be regarded as a limiting case of an ellipse, in which a = b and e = 0.
Of the nine planets that orbit the Sun, only two (Mercury and Pluto) have eccentricities greater than 0.10 (b/a < 0.995), all the others (especially Venus, Earth and Neptune) have very nearly circular orbits.
Kepler’s second law: A radial line from the Sun to a planet sweeps out equal areas in equal intervals of time (see Figure 5b).
This law implies that a planet moves more quickly as it gets closer to the Sun. In the context of Newtonian mechanics, Kepler’s second law may be viewed as a consequence of the conservation of angular momentum, a basic physical principle that is discussed elsewhere in FLAP.
Kepler’s third law: The square of the orbital period of each planet is proportional to the cube of its semi–major axis, i.e. T 2 = ka3 (see Figure 5c).
This law is a generalization of Equation 22 to elliptical orbits:
$T^2 = \left (\dfrac{4\pi^2}{GM}\right)r^3$(Eqn 22)
We can therefore identify the constant of proportionality k with the $4\pi^2/(GM)$ that appeared in that earlier equation, at least to the extent that we are justified in neglecting the masses of the planets relative to that of the Sun
Thus,$T^2 = \left(\dfrac{4\pi^2}{GM}\right)a^3$(23)
| Planet | Mean distance from the Sun, a/106 km | Orbital period, T/years |
|---|---|---|
| Mercury | 57.9 | 0.241 |
| Venus | 108 | 0.615 |
| Earth | 150 | 1.00 |
| Mars | 228 | 1.88 |
| Jupiter | 778 | 11.9 |
| Saturn | 1430 | 29.5 |
As we have already said, Kepler deduced his laws from observational data. Given the data in Table 1 relating to the six inner planets (the only ones known in Kepler’s time) think about how you might deduce Kepler’s third law.
(The following question may help.)
✦ If T 2 is proportional to a3, how can we present the data on a graph to produce a straight line?
✧ A graph of T 2 against a3 will give a straight line. Alternatively, by taking the square root of both sides of Equation 23,
$T^2 = \dfrac{4\pi^2}{GM}a^3$(Eqn 23)
we see that T is proportional to a3/2. i
Question T10
(a) Plot a graph of T versus a3/2 for the six inner planets. Do the data agree with Kepler’s third law?
(b) What would be the orbital period of an asteroid (a small rocky body orbiting the Sun) in an elliptical orbit with a semi–major axis of 300 × 106 km?
Answer T10
| Planet | a3/2/1012 km3/2 |
|---|---|
| Mercury | 0.44 |
| Venus | 1.12 |
| Earth | 1.84 |
| Mars | 3.44 |
| Jupiter | 21.7 |
| Saturn | 54.1 |
(a) Table 2 lists values of a2, which when plotted as in Figure 13 give a straight line and hence show that the data do obey Kepler’s third law.
(b) If a = 300 × 102 km, then a2 = 5.196 × 102 km2 and hence from Figure 13 T ≈ 2.5 years.
Comment To fit all the data on to a manageable scale, it would be better to plot a logarithmic graph. Consult the maths strand of FLAP for further discussion.
Newton was able to show that Kepler’s laws agreed with the expected behaviour of two bodies interacting in the way described by the inverse square law of gravitation. This was a great success for Newton’s general approach, and it was made even more impressive by the quantitative agreement that it provided with a range of astronomical measurements. However, as Newton was well aware, the planets are not isolated bodies; the motion of each is influenced by all the other bodies in the Solar System as well as by the Sun.
As you might expect, these additional interactions are relatively small, but they give rise to observable departures from the simple behaviour described by Kepler’s laws. Moreover, these departures from Keplerian behaviour are, in principle at least, calculable on the basis of Newton’s laws of motion and the law of gravitation.
Following the publication of Newton’s Principia scientists and mathematicians were able to make increasingly accurate analyses of orbital motion and thereby uncovered many new phenomena. Perhaps the most notable was the discovery of Neptune, the eighth planet from the Sun. The seventh planet, Uranus, was discovered observationally by William Herschel (1738–1822) in 1781, but small unexplained irregularities in its motion suggested that it might be acted upon by some other planet yet further from the Sun. John Couch Adams (1819–1892) and Urbain Le Verrier (1811–1877), working independently in England and in France, calculated the position that such a planet might occupy, and in 1846 Neptune was found only about a degree from its predicted position!
4.3 Energy and parabolic orbits
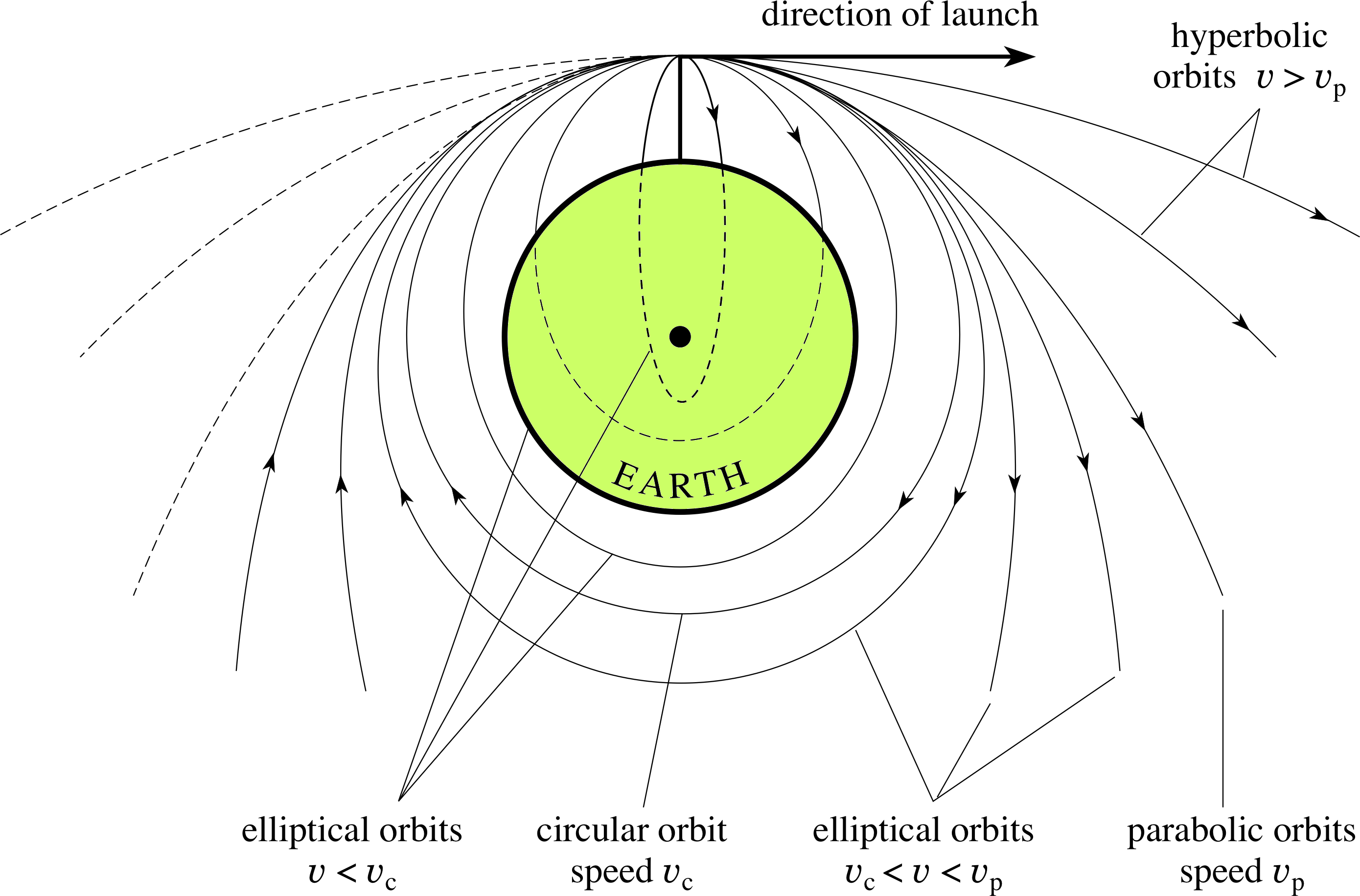
Figure 6 The effect of launching a body horizontally at different speeds (where υ is the launch speed).
Figure 6 shows the effect of launching a body horizontally from the top of a tall vertical tower at a variety of different speeds, neglecting non–gravitational effects such as air resistance and treating the Earth as a point mass concentrated at its geometric centre.
As you can see, the orbits are all conic sections, the precise shapes of which are determined by the speed of launch.
If υc is the speed required to attain a circular orbit, any lesser speed will produce an elliptical orbit with the centre of the Earth at the farthest focus of the ellipse.
Launch speeds increasingly greater than υc will first produce elliptical orbits with the Earth’s centre at the nearer focus, then (at speed υp) a parabolic orbit, and finally a range of hyperbolic orbits.
The different speeds shown in Figure 6 have an important influence on the energy associated with each orbit.
The gravitational field is a conservative_forceconservative field, so if we ignore all non–gravitational effects the mechanical energy of each orbit (the sum of the kinetic and potential energies at any point) will be constant. Since the bodies are being launched from the same position they all have the same potential energy at that point, so their energies differ by amounts that are determined by their respective speeds. It follows that the increasing launch speeds indicate increasing orbital energies.
✦ In the case of the circular orbit, write down an expression for the sum of the kinetic and potential energies of a body of mass m, and then use it to show that the total energy of the circling body is $E = -\dfrac{GmM_{\rm E}}{2r}$, where ME is the mass of the Earth and r is the distance of the launch point from the centre of the Earth.
✧ Using the expression for gravitational potential energy given in Equation 14,
$E_{\rm grav}(r) = -\dfrac{GM_{\rm E}m}{r}$(Eqn 14)
we have
$E = E_{\rm kin} + E_{\rm grav} =\dfrac{1}{2}m\upsilon_c^2 + \left(-\dfrac{GmM_{\rm E}}{r}\right)$
and by writing υc = rω and using Equation 20,
$mr\omega^2 = \dfrac{GMm}{r^2}$)(Eqn 20)
we see that
$\dfrac{1}{2}m\upsilon_c^2 = \dfrac{1}{2}mr\omega^2 = \dfrac{1}{2} \left(-\dfrac{GmM_{\rm E}}{r}\right)$
so
$\dfrac{1}{2} \left(-\dfrac{GmM_{\rm E}}{r}\right) + \left(-\dfrac{GmM_{\rm E}}{r}\right) = \left(-\dfrac{GmM_{\rm E}}{2r}\right)$
as required.
Note that in a circular orbit the kinetic energy (which is always positive) has exactly half the magnitude of the potential energy (which is negative), and the total energy is negative. This ensures that a body in a circular path can never escape to infinity where its potential energy would be zero and its total energy non-negative.
In fact, we can see from Figure 6 that the lowest energy orbit that does permit escape to infinity is the parabolic orbit. This must be the orbit with a total energy of zero. The closed elliptical orbits must therefore all have negative total energy, and the open hyperbolic orbits must have all positive total energy.
The zero energy parabolic orbit marks an important dividing line between open and closed orbits.
✦ What is the speed υp that corresponds to the parabolic orbit?
✧ Since this is the minimum speed required to reach infinity we can obtain its value from the condition
E = Ekin + Egrav = 0
i.e.$\dfrac{1}{2}m\upsilon_p^2 + \left(-\dfrac{GmM_{\rm E}}{r}\right) = 0$
This is just how we worked out the escape speed in Subsection 3.3, so we can write
$\upsilon_p = \sqrt{\dfrac{2GM_{\rm E}}{r}}$
4.4 Weightlessness and tidal effects
Astronauts in an orbiting space shuttle float around the vehicle and feel ‘weightless’, even though they are close to the Earth and must therefore be affected by its gravitational field. How can this be?
In Subsection 3.2 we noted that measurements made by observers located at fixed points on the rotating Earth have to allow for a reduction in the effective value of g, the acceleration due to gravity. This apparent reduction is actually caused by the rotation of the observers and their experimental equipment. A similar effect is at work in an orbiting spacecraft. The crucial point is that both the observers on the turning Earth and the observers in an orbiting spacecraft are accelerating. Such observers, when using Newton’s laws of motion, must always make allowances for the effects of their own acceleration. In the case of observers on the Earth these effects are small and can often be ignored, but for orbiting observers the effects are much larger. The orbital motion has no effect on the mass of an object, and in a low Earth orbit, 100 to 150 km above the Earth’s surface, the gravitational force on an object is very similar to its surface weight, but the effective weight, as observed by the occupants of the spacecraft, will be zero. It is in this sense that orbiting objects may be said to be weightless, though it would probably be better to describe them as being in ‘free fall’ under gravity.
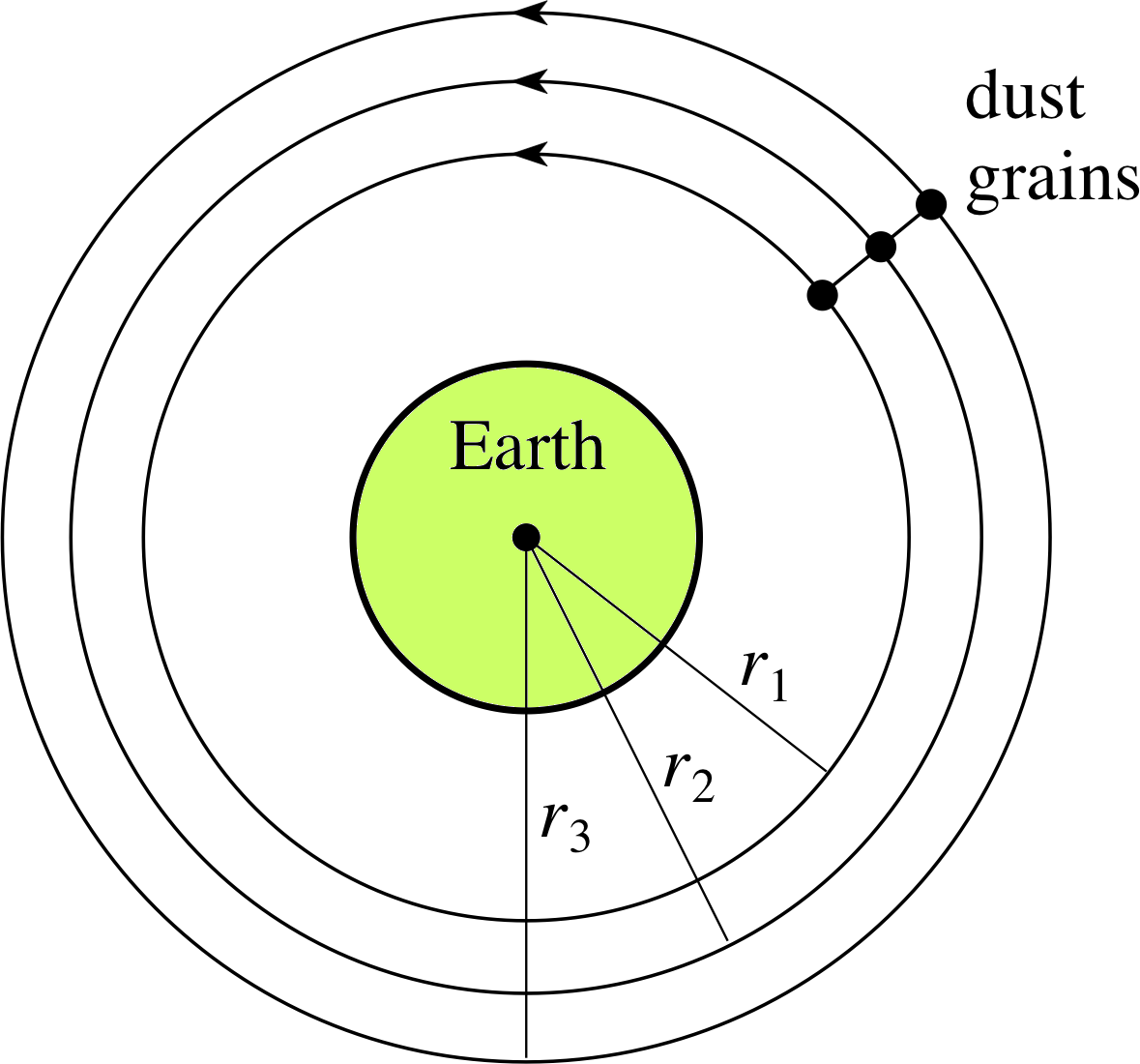
Figure 7 Dust grains in an orbiting space vehicle. The grains are assumed to be moving at a common angular speed, but are at differing distances from the centre of the Earth.
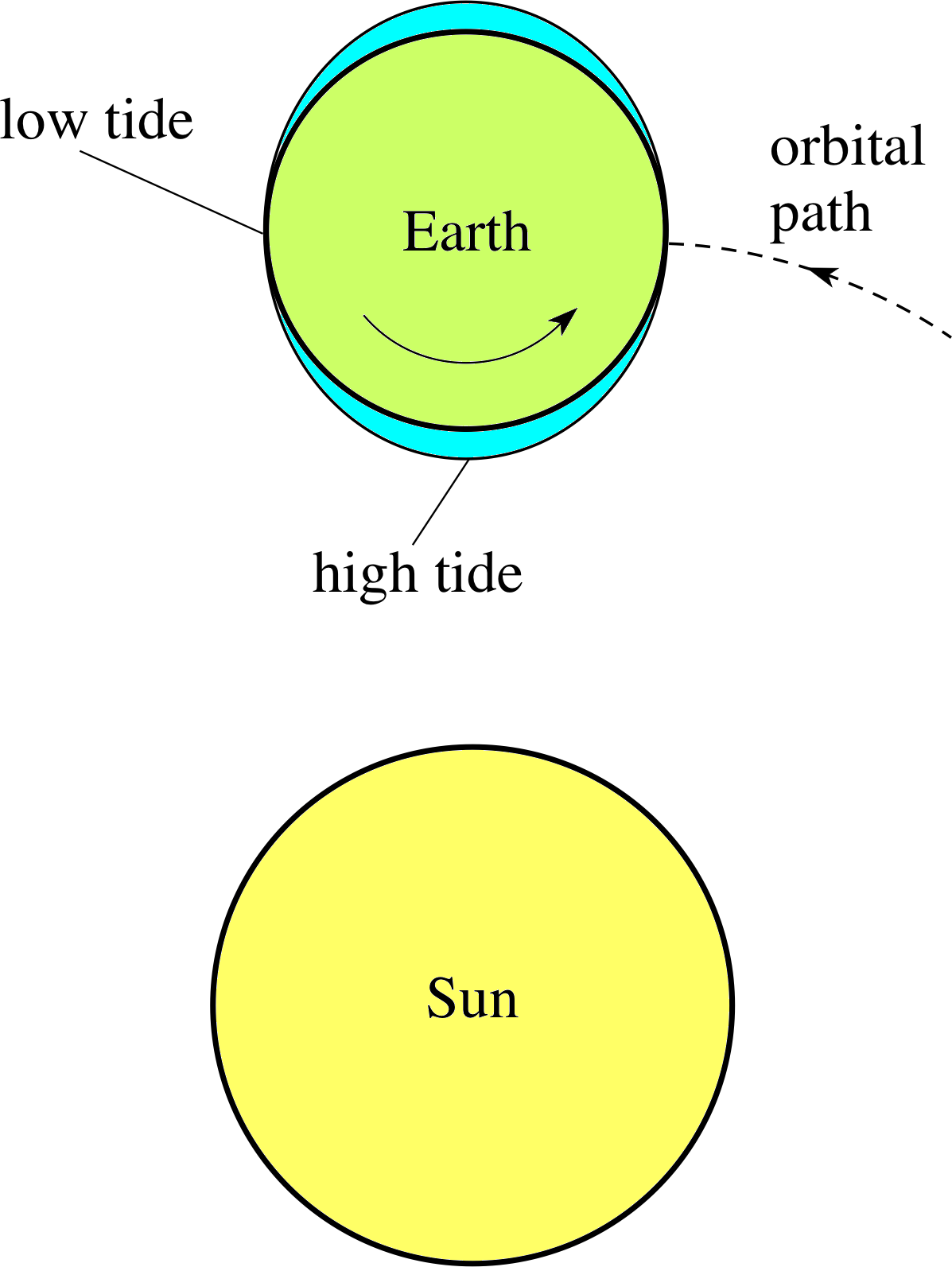
Figure 8 Ocean tides.
In reality, orbiting astronauts are not quite in free fall and they can, in principle at least, tell that they are in the Earth’s gravitational field even without looking out of the window. In the above discussion we treated the spacecraft as though it were a point mass orbiting at a precise distance from the Earth, but it is actually extended and so some parts are closer to the Earth than others. The Earth’s gravitational field decreases with distance so the parts of the vehicle nearest the Earth will be in a slightly stronger gravitational field than those parts that are further away. Within the vehicle, small objects (e.g. dust grains) at the centre of the craft will be subjected to the gravitational force needed to keep them in the orbit they are following, but grains on the Earthward side of the craft will experience a slightly stronger field than is necessary to keep them in their somewhat smaller ‘orbit’, and grains that are on the side of the ship away from the Earth will experience a weaker force than necessary. The result of this is that grains on the Earthward side tend to move towards the Earth while grains on the away side move away. The situation of three such grains forced to follow circular paths of different radii at a common angular speed is shown in Figure 7. The central grain is held in a true circular orbit by the gravitational field that acts upon it, but the circular paths of the other two grains are not true orbits since the gravitational force that acts on them is either too great or too small to provide the necessary centripetal force.
An astronaut would be able to deduce, from the behaviour of the dust, that his or her vehicle was in a gravitational field.
You may be thinking that the movement of dust in a space shuttle is a very esoteric effect, but the tides commonly observed in the Earth’s oceans have a very similar cause. Ocean tides are complicated by factors such as local geography and ocean depth, but their basic cause is the variation in the strength of the gravitational fields of the Moon and the Sun across the diameter of the Earth. Ocean water is not rigidly attached to the Earth, so it can move towards or away from these bodies just as the dust grains in a space shuttle can move towards or away from the Earth (Figure 8). The gravitational fields (together with geographical factors) determine the ’shape’ of the oceans, and the solid Earth rotates within that deformed body of water, causing the high tides and low tides that are actually observed. i
Question T11
Suggest a reason why the Moon has a greater influence on the Earth’s ocean tides than does the Sun (despite the fact that the gravitational field due to the Sun is stronger, at the Earth, than that due to the Moon).
Answer T11
Tides are produced because the gravitational acceleration towards the Moon (or Sun) varies between one side of the Earth and the other. The greater the difference in field strength across the Earth’s diameter, the greater the tidal effect. Field strength varies as 1/r2: when r is small, the field changes rapidly with distance, but at large r the change is more gradual. The Moon is much closer to the Earth than is the Sun, and hence there is a greater fractional change in its field strength over the diameter of the Earth, which more than compensates for the fact that the actual strength of the Moon’s field at the Earth is much less than that of the Sun.
(The tidal effect produced by the Moon is about twice that produced by the Sun.)
5 Gravity and extended bodies
Throughout this module, we have used the fact that the gravitational effects outside a spherically symmetric body are identical to those of a single particle, of the same mass located at its centre. In this final section, we will derive that result and also consider the gravitational field inside a spherical body.
Study comment This section is more mathematically demanding than the rest of the module. The results that it contains are an important part of the module but the techniques used to obtain those results are not the subject of any the achievements listed at the end of the module. Do not allow any difficulties you may have following the detailed arguments to cause unnecessary delays. If you encounter problems, consult your tutor.
5.1 Approaching the task
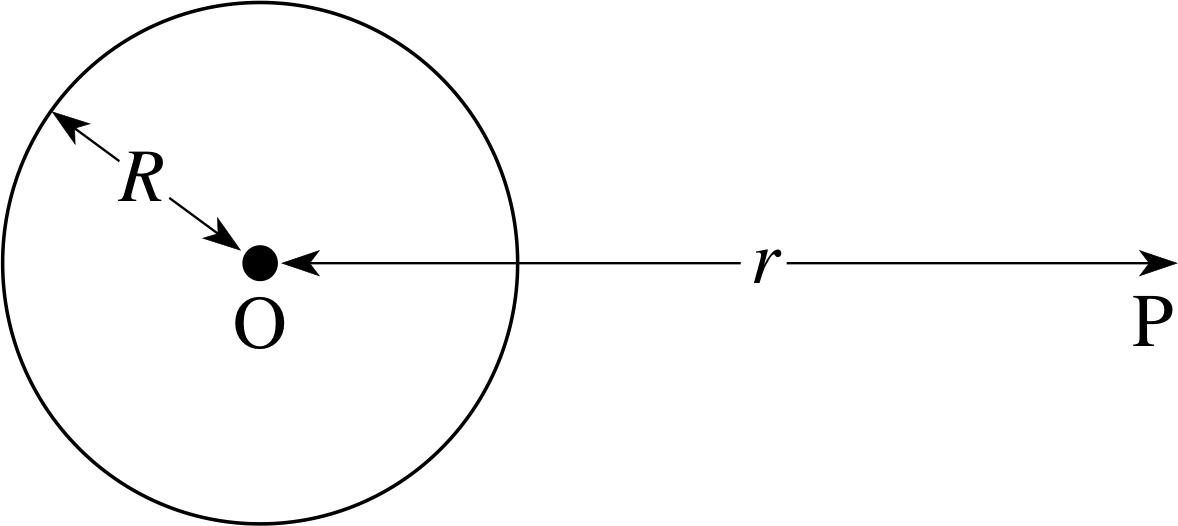
Figure 9 A sphere of radius R with a point P at a distance r from its centre.
What we are trying to find is an expression for the gravitational field at some point P outside a spherical body (Figure 9). One way of approaching the problem would be to treat the whole sphere as a collection of tiny elements, each with its own individual mass ∆mi. We could then work out the gravitational field at P due to each tiny element and add them all together using vector addition. i
However, this calculation gets rather cumbersome, so instead of working with gravitational fields and getting involved in vector additions, it is easier to work in terms of gravitational potentials since these are scalar quantities. The resultant potential at any point due to a collection of particles is simply the algebraic sum of all the contributions. The gravitational field at P may be determined fairly straightforwardly once we have an expression for the gravitational potential, so this is the approach we will adopt.
The problem of finding the gravitational potential due to a general spherically symmetric body is still quite demanding, so we will start by considering the potential due to a thin spherical shell of uniform composition.
5.2 Gravitational field due to a thin spherical shell
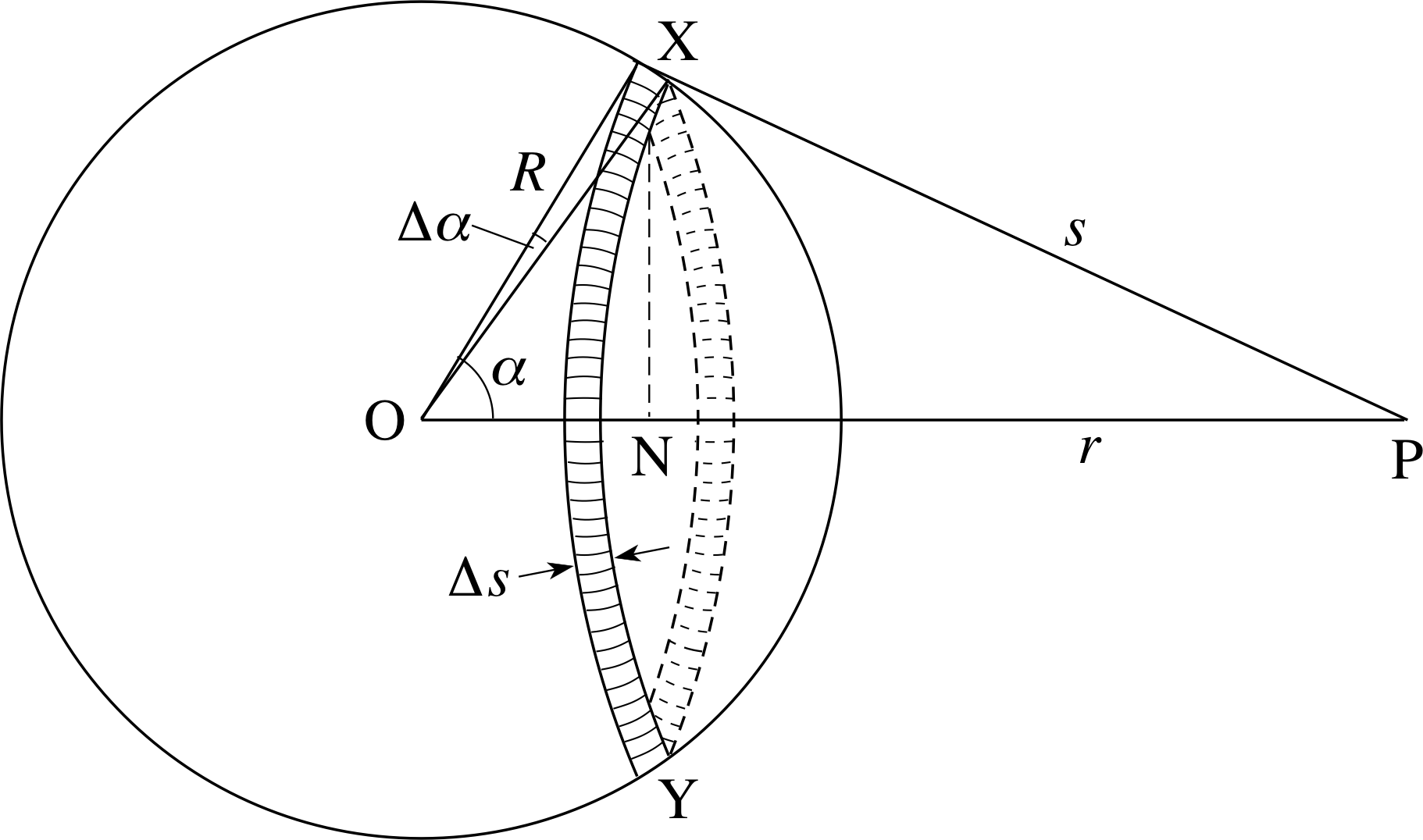
Figure 10 A narrow ring passing through the points XY on the surface of a thin spherical shell of radius R. The width of the ring subtends a small angle ∆α at the centre of the sphere.
A spherical shell can be divided into narrow rings in such a way that all the points on each ring are effectively at the same distance from P. This is indicated in Figure 10, where all the points on the ring through X and Y are at a distance s from P. The radius of the ring, NX, is R sin α and the width of the ring, measured along the surface of the shell, is R ∆α. It follows that the area of the ring is (2πR sin α) × (R ∆α). i Consequently, if the mass per unit area of the shell’s surface is σ, i we can say that the mass of the ring will be 2πσR2sin(α) ∆α. Since all the points on the ring are at the same distance from P it then follows from our usual expression for the gravitational potential due to a point mass that the gravitational potential produced at P by the whole ring will be
$\Delta V = - \dfrac{G2\pi\sigma R^2\sin(\alpha)\Delta\alpha}{s}$(24)
In principle we can use this expression to compare the potential due to any two rings, but doing so is complicated because any other ring will correspond to different values of the two related variables α and s. In order to simplify the expression we need to eliminate one or other of these variables. To do so we can use the cosine rule which tells us that
s2 = R2 + r2 − 2Rr cos α
If this is then differentiated (implicitly) i we obtain the rate of change of s with respect to α
$2s \dfrac{ds}{d\alpha} = 2Rr\sin\alpha\,d\alpha$
so$\dfrac{ds}{d\alpha} = \dfrac{Rr\sin\alpha}{s}$
and it therefore follows from this that the increase in s that corresponds to a small increase ∆α in α is
$\Delta s = \dfrac{ds}{d\alpha}\Delta \alpha = \dfrac{Rs\sin{\alpha}\,\Delta\alpha}{s}$
Substituting this into Equation 24 we find
$\Delta V = -\dfrac{2G\pi\sigma R\Delta s}{r}$
The material of the sphere provides rings at all values of s between r − R and r + R. We can add their r contributions together to find the total gravitational potential V (r) at P by performing the following integral
$\displaystyle V(r) = -\dfrac{2G\sigma\pi R}{r} \int_{r-R}^{r+R} ds$
$\displaystyle V(r) = -\dfrac{2G\sigma\pi R}{r} \left[s\right]_{r-R}^{r+R} = -\dfrac{2G\sigma\pi R}{r}\left[(r+R)-(r-R)\right]$
$\displaystyle V(r) = -\dfrac{2G\sigma\pi R}{r}2R = -\dfrac{4\pi R^2\sigma G}{r}$(26)
Now, the surface area of the shell is 4πR2, so its total mass M is given by
M = 4πR2σ(27)
Hence, the gravitational potential due to a uniform spherical shell of mass M at an external point at a distance r from the shell’s centre will be
$V(r) = -\dfrac{GM}{r}$(28)
Note that this is independent of the radius of the shell. You should recognize this expression – it is identical to the expression for the gravitational potential at a distance r from a point mass M. We therefore come to the perhaps surprising conclusion that:
The gravitational effect of a hollow sphere whose mass M is uniformly spread over its surface is the same as if all its mass were concentrated in a point at the centre of the sphere.
This important result means we can use the expression for the gravitational field g (r) at a distance r from a point mass (see Equation 5)
${\boldsymbol g}({\boldsymbol r}) = -\dfrac{GM_{\rm E}}{r^2}\hat{\boldsymbol r}$(Eqn 5)
to represent the gravitational field outside a uniform spherical shell. At a point with position vector r
${\boldsymbol g}({\boldsymbol r}) = -\dfrac{GM}{r^2}\hat{\boldsymbol r}$(29)
We now know about gravitational effects outside a hollow sphere – but what happens inside?
✦ Can you deduce what the field will be exactly at the centre of the shell, point O?
✧ The field is zero. We can see that this is so if we consider placing a small mass at O. It will be pulled equally in all directions by the uniform mass surrounding it, so the net force acting on it will be zero. Hence the field is zero.
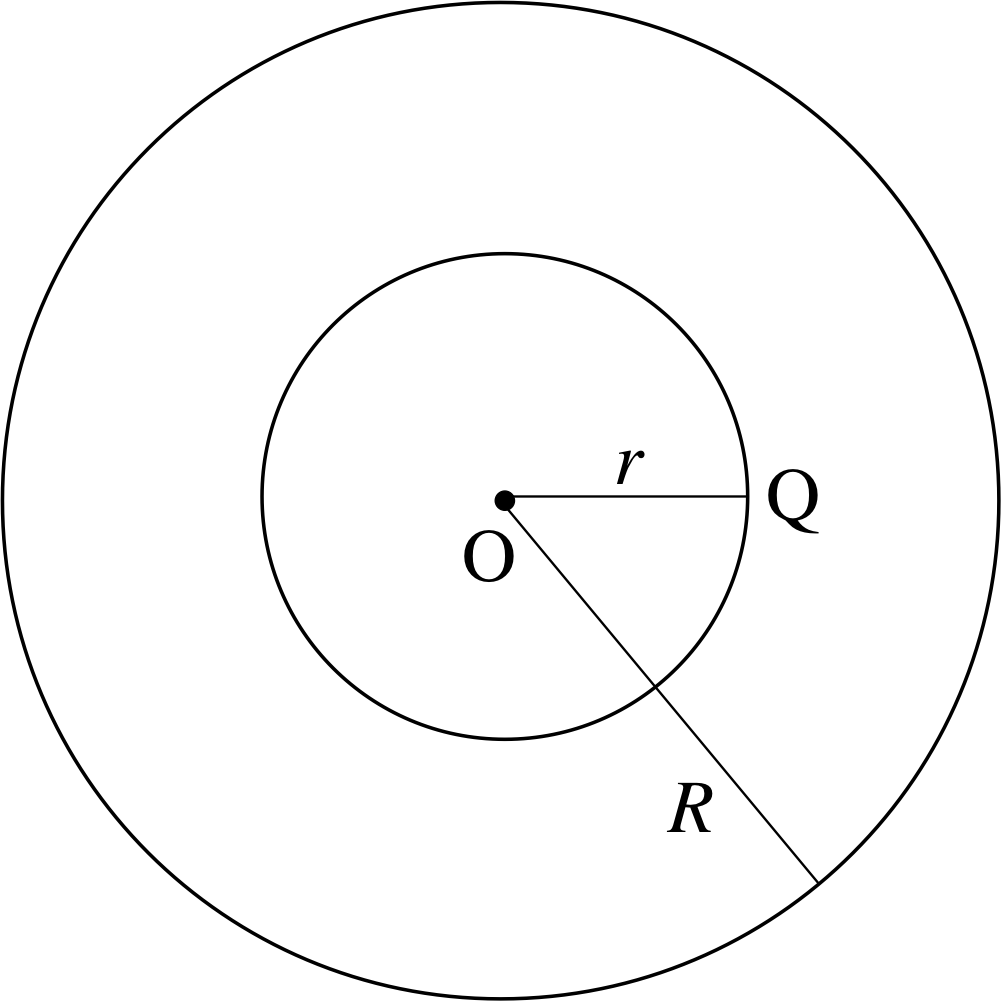
Figure 11 Point Q inside a uniform solid sphere, distance r from the centre O.
Suppose we now move off centre to a point Q, to the right of O (see Figure 11). Now although there’s more mass on the left–hand side of Q, it is generally further away than the mass on the right–hand side, so again the forces cancel and the field at Q is zero. It is possible to show, by summing the contributions from each mass element, that:
There is no gravitational field inside any spherically symmetric hollow sphere. i
This does not mean that the shell shields the space inside it from gravitational fields due to other masses; it means simply that its own field is zero, i.e. a mass inside the shell doesn’t feel any net force due to the mass of the surrounding shell.
Question T12
Sketch the variation of the gravitational field due to a shell of radius R as a function of the distance r from the centre O of the shell. Include distances r both less than and greater than R.
Answer T12
The sketch is given in Figure 14. Notice that the field between O and R is zero; from R onwards it falls off as 1/r2 and is negative.
5.3 Gravitational field due to a solid sphere
We are now in a position to return to a solid sphere, which we can think of as a series of shells one inside the other, like the layers of an onion. For each, the field at a point P outside the sphere is as though the shell’s mass were at the centre O.
The gravitational effect of any spherically symmetric body of total mass M, at any point outside that body, is identical to the effect of a point mass M located at the geometric centre of the sphere. i
What is the gravitational field inside a uniform solid sphere? We will assume that the sphere is of uniform density, and think about point Q in Figure 11. Point Q is inside all the shells making up the solid sphere with radii between r and R so there will be no effect due to these shells. For the mass inside Q, i.e. within a sphere of radius r, its effect is as though it were all concentrated at the centre. Since the density of the sphere is uniform, the mass m of the sphere of radius r is given by
$m = \dfrac{Mr^3}{R^3}$(30)
It follows that the field at Q is the field at a point r, a distance r from a point mass m:
i.e.${\boldsymbol g}({\boldsymbol r}) = -\dfrac{Gm}{r^2}\hat{\boldsymbol r}$
so${\boldsymbol g}({\boldsymbol r}) = -\dfrac{G}{r^2}\left(\dfrac{Mr^3}{R^3}\right)\hat{\boldsymbol r}$
i.e.inside a uniform solid sphere
${\boldsymbol g}({\boldsymbol r}) = -\dfrac{GMr}{R^3}\hat{\boldsymbol r}$(31)
Question T13
Sketch a graph showing the magnitude of the gravitational field as a function of distance from the centre of a uniform solid sphere of radius R for points inside and outside the sphere.
Answer T13
The sketch is given in Figure 15. Inside the sphere g (r) is proportional to r and from R outwards, it varies as 1/r2. Note that g (r) is always negative.
In this section we have only considered one simple solid object – a sphere. However, in principle, we can find the gravitational effects of an object of any shape by dividing it up into pieces that are simpler to deal with, then summing their contributions to the total gravitational potential. The maths can sometimes get very complicated, but the principle is always the same. In the case of the sphere we were able to use its particular symmetry to deduce the field that corresponded to the potential. In general there will be no such symmetry, but it is always the case that the field can be deduced from the potential, generally by investigating its rate of change in various directions.
Study comment If you have studied Section 5 before completing Sections 2 to 4 then you should return now to Section 2.2. Otherwise you can now move on to the following Closing items.
6 Closing items
6.1 Module summary
- 1
-
1 According to the law of universal gravitation, the gravitational force Fgrav on a particle of mass m2 due to a particle of mass m1 separated from it by a distance r is given by
${\boldsymbol F}_{\rm grav} = {\boldsymbol F}_{21} = -\dfrac{G m_1 m_2}{r^2} \hat{\boldsymbol r}$(Eqn 1)
where G = 6.673 × 10−11 N m2 kg−2 is the universal gravitational constant, and r^ is a unit vector directed from m1 to m2.
- 2
-
2 According to Newton’s theorem: the gravitational effect of any spherically symmetric body, outside its own surface, can be exactly reproduced by a single particle, with the same mass as that body, located at the body’s geometric centre.
- 3
-
The gravitational field at a pointris the gravitational force per unit mass that would act on a point test mass at that point
${\boldsymbol g}({\boldsymbol r}) = \dfrac{{\boldsymbol F}_{\rm grav}({\rm on}~m~{\rm at}~{\boldsymbol r})}{m}$(Eqn 4)
- 4
-
The gravitational field of a spherically symmetric Earth at an external point a distance r from its centre would be
${\boldsymbol g}({\boldsymbol r}) = -\dfrac{GM_{\rm E}}{r^2}\hat{\boldsymbol r}$(Eqn 5)
where ME is the mass of the Earth. Over a localized region close to the surface of the Earth the field may be approximated by
g = −g z^
where g is the local magnitude of the acceleration due to gravity (9.81 m s−2 in the UK). For the spherically symmetric Earth
$g = \dfrac{GM_{\rm E}}{R_{\rm E}^2}$(Eqn 7)
- 5
-
The gravitational potential energy of a body is the energy that it possess by virtue of its position in a gravitational field.
- 6
-
The gravitational potential energy of a body of mass m at an external point a distance r from the centre of a spherically symmetric Earth would be
$\displaystyle \Delta E_{\rm grav}(r) = -\dfrac{GM_{\rm E}m}{r}$ (with Egrav = 0 at r = ∞)(Eqn 14)
Over a localized region close to the surface of the Earth this may be approximated by
Egrav(z) = mgz (with Egrav = 0 at z = 0)
- 7
-
The gravitational potential at a pointris the gravitational potential energy per unit mass at that point.
$V_{\rm grav}({\boldsymbol r}) = \dfrac{E_{\rm grav}({\rm of}~m~{\rm at}~{\boldsymbol r})}{m}$(Eqn 18)
so for a spherically symmetric Earth
$V_{\rm grav}({\boldsymbol r}) = -\dfrac{GM_{\rm E}}{r}$(Eqn 19)
and over a localized part of the surface
Vgrav(z) = gz(Eqn 9)
- 8
-
The escape speed for a planet (or satellite) is the least speed at which a body must be launched from its surface in order to escape to an infinite distance. The body can only escape if its initial kinetic energy is at least as great as the increase in gravitational potential energy associated with moving from the surface to an infinite distance.
- 9
-
When a body moves about a fixed point under the influence of a force that satisfies an inverse square law (such as the gravitational force due to a much more massive body) its orbit is a conic section; an ellipse, a circle, a parabola or a hyperbola, according to the energy of the body.
- 10
-
According to Kepler’s laws of planetary motion:
(1) Planets orbit the Sun in ellipses with the Sun at oneFigure 5afocus.
(2) A radial line from the Sun to a planet sweeps out equal areas in equal intervals of time.
(3) The square of the orbital period T of each planet is proportional to the cube of the semi–major axis a of the ellipse.
- 11
-
Astronauts in an orbiting vehicle experience weightlessness because they, along with the contents of their space vehicle, are falling freely under gravity.
- 12
-
Ocean tides arise because of the difference in strength of the gravitational fields of the Moon and of the Sun across the Earth’s diameter.
- 13
-
The gravitational field inside a spherically symmetric hollow sphere is zero.
6.2 Achievements
Having completed this module, you should be able to:
- A1
-
A1 Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Describe and explain the principles of the Cavendish experiment for measuring the universal gravitational constant G.
- A3
-
Calculate the surface gravity of a spherically symmetric body (such as a planet), and determine the gravitational field of that body.
- A4
-
Calculate the change in potential energy when an object is raised a small distance from the surface of the Earth.
- A5
-
Calculate the gravitational potential energy of an object due to a spherically symmetric body (such as a planet), and determine the gravitational potential of that body.
- A6
-
Apply the principle of conservation of energy to a body moving in a gravitational field, and relate the shape of an orbit to its energy in simple cases.
- A7
-
Explain what is meant by escape speed, and calculate the escape speed from the surface of a planet or satellite.
- A8
-
Describe the orbital motion of planets around the Sun and of satellites around their ‘parent’ body and apply the equations of uniform circular motion to planetary motion.
- A9
-
Quote the general relationship between the orbital period and the mean radius of the orbit (Kepler’s third law).
- A10
-
Explain why astronauts in an orbiting vehicle experience weightlessness.
- A11
-
Explain the origin of the Earth’s ocean tides.
- A12
-
Calculate (not derive) the gravitational force between two bodies, if the bodies are point particles, hollow spheres or solid spheres.
- A13
-
Calculate (not derive) the gravitational field due to a uniform sphere both inside and outside its surface, and state the value of the gravitational field produced inside a hollow spherically symmetric sphere.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
6.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions, each of which tests one or more of the Achievements. i
Question E1 (A2 and A12)
In a Cavendish torsion balance experiment to measure G the distance between the centres of the large and small spheres is reduced from 100 mm to 70 mm. What effect does this have on the angle of rotation of the torsion fibre?
Answer E1
In equilibrium we have
$\left|\,{\boldsymbol F}_{\rm grav}\,\right| = {\boldsymbol F}_{\rm grav} = \dfrac{G m_1 m_2}{r^2}$(Eqn 1b)
andFgravL = cθ(Eqn 2)
Hence θ is proportional to 1/r2. So if we decrease r from 100 to 70 mm, the angle of rotation θ will increase by (100/70)2, i.e. approximately double.
(Reread Subsections 2.1 and 2.2 if you had difficulty with this question.)
Question E2 (A3 and A8)
A small satellite of Saturn has a mass of 3.8 × 1019 kg and a diameter of 50 km N. Calculate the maximum angular speed with which it can rotate if loose rocks sitting on its surface at its equator are not to fly off.
Answer E2
If loose rocks are not to fly off, we require the gravitational force towards the centre of the satellite to be at least as great as the centripetal force to maintain their circular motion
i.e.mg ≥ mRsω2
where RS is the radius of the satellite, ω is the angular speed in radians per second and g the acceleration due to gravity on the surface of the satellite is given by adapting Equation 6,
$g(R_{\rm E}) = -\dfrac{GM_{\rm E}}{R_{\rm E}^2}$(Eqn 6)
where MS = mass of Saturn’s satellite.
Hence we require
$\omega^2 \le \dfrac{g}{R_{\rm S}} \le \dfrac{GM_{\rm S}}{R_{\rm S}^3}$
$\omega^2 \le \dfrac{6.67\times 10^{-11}\,{\rm N\,m^2\,kg^{-2}})\times 3.8\times 10^{19}\,{\rm kg}}{(2.5\times 10^5\,{\rm m})^3}$
Maximum angular speed ω = 4.03 × 10−4 rad s−1.
(Reread Subsections 3.1 and 4.1 if you had difficulty with this question.)
Question E3 (A4, A5 and A6)
Calculate the gravitational potential energy of a 5 kg mass on the surface of the Earth, taking the zero of potential energy to be at infinity and compare this with the change in potential energy when the mass is lifted a height of 500 m above the surface of the Earth.
What would be the minimum launch speed of a missile required to reach a height of 500 m above the Earth’s surface?
Answer E3
The gravitational potential energy at the surface is
$E_{\rm grav}(R_{\rm E}) = -\dfrac{GM_{\rm E}m}{R_{\rm E}}$(15)
$\phantom{E_{\rm grav}(R_{\rm E})} = -\dfrac{-6.67\times10^{-11}\,{\rm N\,m^2\,kg^{-2}}\times 5.98\times 10^{24}\,{\rm kg}\times 5\,{\rm kg}}{6.38\times 10^6\,{\rm m}} = -3.13\times 10^8\,{\rm J}$
The height of 500 m is much smaller than the Earth’s radius, so g does not change significantly over this distance, therefore
∆Egrav = mgh = 5 kg × 9.81 m s−2 × 500 m = 2.45 × 104 J
ThereforeEgrav ≈ 13 000 × ∆Egrav.
Total energy remains constant, so
gain in Egrav = loss in Ekin
i.e.mgh = ½ mυ2 where υ is the launch speed.
Hence υ2 = 2gh = 2 × 9.81 m s−2 × 500 m = 9.81 × 103 m2 s−2
and soυ = 99 m s−1
(Reread Subsections 3.2 and 3.3 if you had difficulty with this question.)
Question E4 (A8 and A9)
What orbital period does Kepler’s third law predict for the planet Uranus, whose mean orbital radius (semi-major axis) is 19.14 times the Earth’s orbital radius?
Answer E4
By Kepler’s third law, (orbital time period)2 is proportional to (orbital radius)3 so
$\dfrac{T_{\rm U}}{T_{\rm E}} = \left(\dfrac{r_{\rm U}}{r_{\rm E}}\right)^{3/2}$
TE = 1 year
hence for Uranus,
TU = (rU/rE)3/2 years = (19.14)3/2 = 83.7 years
(Reread Subsection 4.2 if you had difficulty with this question.)
Question E5 (A11)
Why is the tidal range (the difference between the depth of water at high and low tides) greatest when the Moon is full or new, and least when the Moon is mid way between these phases? i
Answer E5
When there is a full or new Moon (Figures 16a and b, respectively), the solar and lunar tidal effects reinforce each other, whereas between these phases (Figure 16c) the two effects partially cancel each other.
(Reread Subsection 4.3 if you had difficulty with this question.)
Question E6 (A13)
The gravitational field at the surface of a uniform solid sphere of mass M, radius R is −g. What is the value of the field at a distance R/10 below the surface of the sphere?
Answer E6
The magnitude of the field at the surface of the sphere is (from Equation 5) g(r) = − GME rˆ
${\boldsymbol g}({\boldsymbol r}) = -\dfrac{GM_{\rm E}}{r^2}\hat{\boldsymbol r}$(Eqn 5)
$g = \dfrac{GM}{R^2}$
At depth X, we require the gravitational field g1 at the surface of a solid sphere of radius r, where r = 9R/10, since the mass outside this radius does not contribute to the field.
The mass m of the inner sphere is m = M (r/R)3, so the magnitude of g1 is
$g_1 = \dfrac{GMr^3}{r^2R^3}$
i.e.$g_1 = g\dfrac{r}{R} = \dfrac{9g}{10}$
(Reread Subsections 3.1 and 5.3 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.


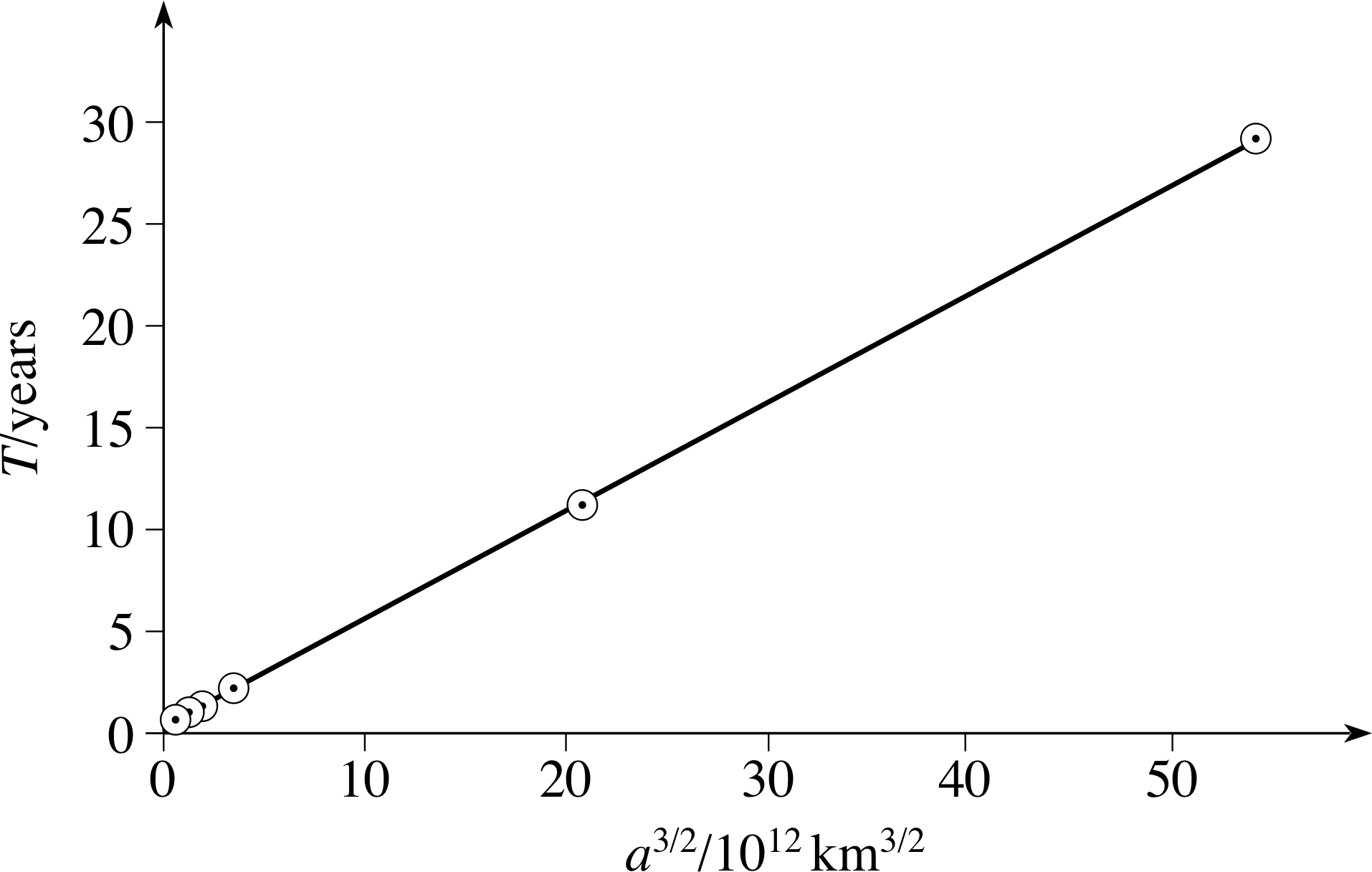
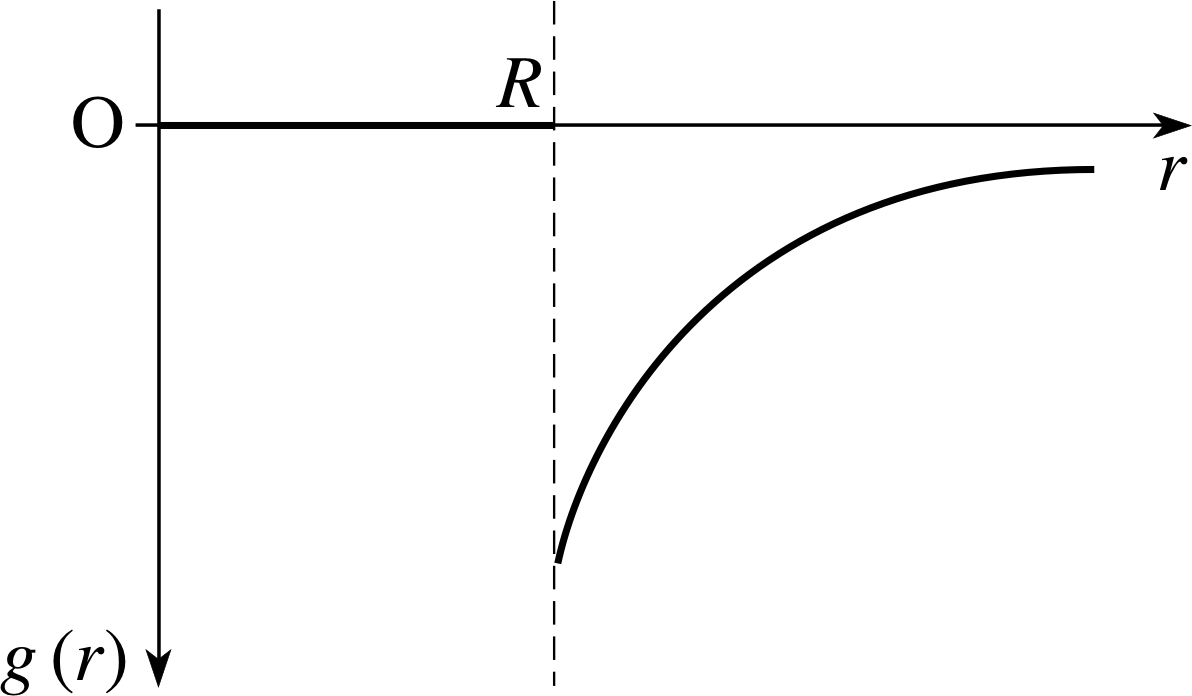
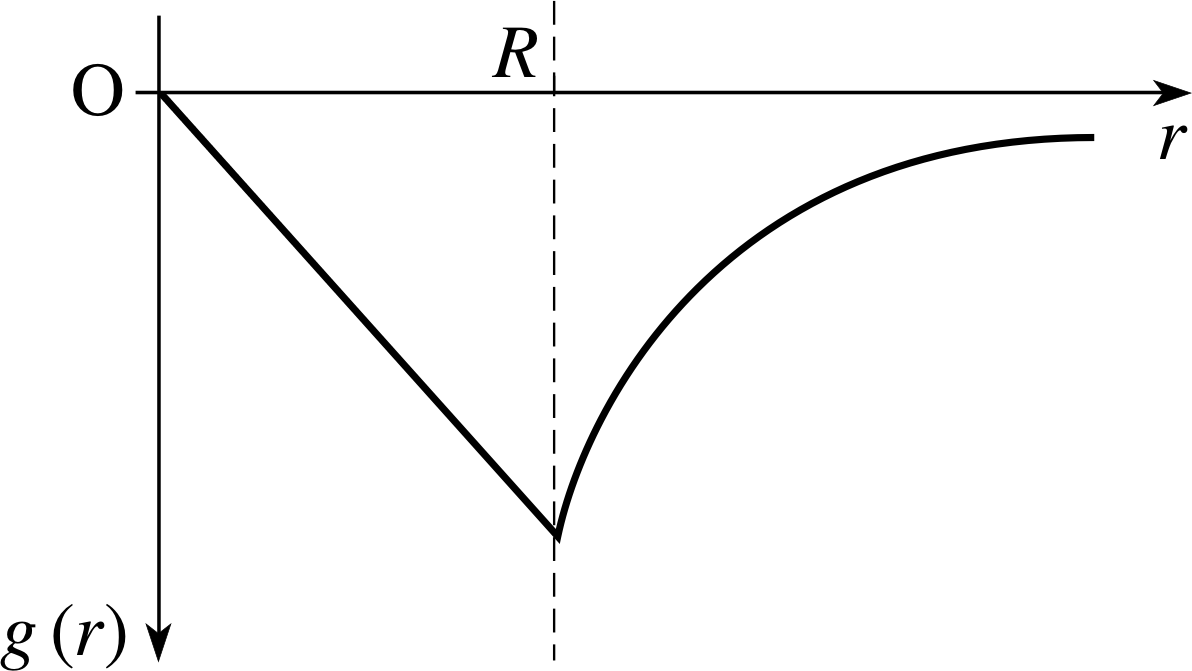
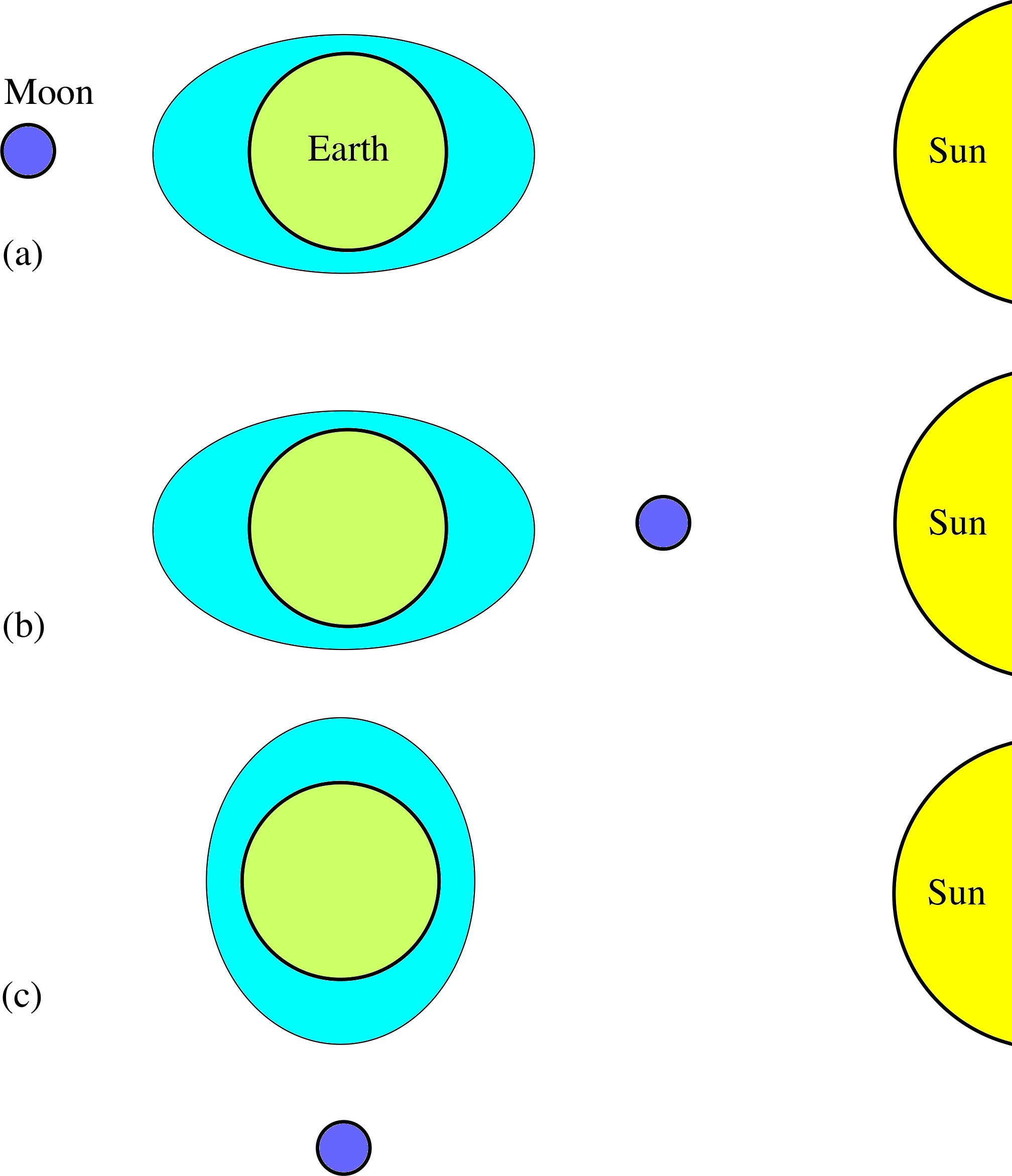
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 6Closing items.