PHYS 9.3: Nuclear fission and fusion and radiation hazards |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
Two separate topics are covered in this module – the use of nuclear reactions for power generation (both nuclear fission and nuclear fusion) and the hazards of radioactivity. The topics are related in that current nuclear power generation produces radioactive waste material. The debate concerning the safety of the nuclear industry is still raging. We will approach the subject of radiation hazard from the point of view of the underlying physics and, as far as possible, give a quantitative presentation.
We begin (in Section 2) by considering the process of nuclear fission and we see how thermal neutrons can sustain a nuclear chain reaction. In Subsection 2.2 we outline design features that allow a nuclear reactor to be maintained in a critical state, by means of control rods and a suitable moderator. This is followed, in Subsection 2.3 by a summary of the various types of radioactive waste produced in fission reactors, and of the treatment (including reprocessing) of this material.
Power generation by nuclear fusion is the ultimate objective of intense international research effort which, if successful, will produce nuclear power with much less radioactive hazard than existing nuclear fission reactors. In Section 3 we describe the underlying physical principles of power generation by fusion, including the use of deuterium and tritium as fuels, and the need for a very high temperature plasma and the consequent problems of heating and confinement, both magnetic confinement and inertial confinement.
Finally in Section 4, we consider the hazards associated with radioactivity. We see how ionizing radiation affects living tissue, and how the effects of different types of radiation can be characterized by a radiation weighting factor. Various units for measuring radiation dose are introduced, and we end with a survey of the various sources of ionizing radiation to which we are exposed.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 5.1Module summary and the Subsection 5.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 5.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
What is meant by the statement that the radiation weighting factor for α–particles is 20? Could a small source of α–particles give rise to: (a) a damaging external dose? or (b) a damaging internal dose?
Make clear the reason for any difference between these two cases.
Answer F1
A radiation weighting factor (RWF) of 20 for α–particles means that α–particles are 20 times as effective at ionizing tissue as are X–rays, for the same energy absorbed. α–particles are strongly ionizing and so have a very short range in tissue, unable even to penetrate the skin if the source is external. In case (a) there will be no appreciable damage. In case (b) where the source is ingested, the α–particles can reach vulnerable tissue and can cause severe damage.
Question F2
What is induced nuclear fission? Why might a chain reaction follow an induced fission in a fissile material?
Answer F2
Fission is the name given to the spitting of a heavy nucleus into two medium–mass nuclei. A fission is said to be induced if it results from the absorption of a neutron to form an unstable nucleus that decays by fission. The induced fission usually produces further neutrons accompanying the fission fragments. A chain reaction is possible since these neutrons may in turn induce fission of neighbouring fissionable nuclei.
Question F3
What are the two classes of radioactive nuclei that constitute the main portion of waste from a nuclear fission reactor? What are the main reasons why these elements are especially hazardous?
Answer F3
The two categories are the fission products (medium-mass) and the actinides (high-mass). The actinides are heavy nuclei produced by neutron absorption reactions in the nuclear reactor. The actinides are hazardous as they are produced in large amounts and many have very long half–lives so the waste remains hazardous for many human life-spans.
Question F4
One fusion reaction is:
21H + 21H → 31H + 11H + 4.0 MeV
What is the source of the 4.0 MeV when two low–energy deuterons react in this way? Why does power generation from this reaction require a plasma?
Answer F4
The energy released in the fusion reaction comes from the release of binding energy. The triton (31H) has a higher binding energy per nucleon than the deuteron and the difference appears first as kinetic energy of the products and then as heat, as they are brought to rest.
To fuse, the two positively–charged deuterons must have sufficient kinetic energy to overcome their mutual electric repulsion and approach within range of the strong nuclear force. Elastic scattering remains a more probable outcome of the collision and to avoid this reducing the average kinetic energy per particle below the threshold for fusion it is necessary to have plasma conditions, with a temperature exceeding about 100 × 106 K.
1.3 Ready to study?
Study comment In order to study this module you will need to be familiar with the following terms: atomic mass, atomic number, binding_energy_of_a_nucleusbinding energy, charge, Einstein’s mass–energy equation, electric potential energy, electromagnetic radiation, electron, conservation_of_energyenergy conservation, half–life, ionization, isotope, kinetic energy, magnetic field, mass number A, neutron, nucleon, nuclide, photon, proton, Q–value (i.e. energy released), radioactive decay (α–, β– and γ–decay), strong nuclear force. You should be familiar with the electronvolt (eV) energy unit and with masses expressed in atomic mass units (u) and in MeV/c2 and should be able to use conventional symbols for nuclides (e.g. 42He). If you are uncertain about any of these terms then you can review them by referring to the Glossary, which will indicate where in FLAP they are developed. The following questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
Calculate the binding energy in MeV of the nucleus 42He.
Answer R1
The mass equivalent of the binding energy of a nucleus is equal to the mass of its constituent nucleons minus the nuclear mass. Therefore, for 42He the mass equivalent of the binding energy is the mass defect, given by:
mass defect = 2 × 1.007 276 u + 2 × 1.008 665 u − 4.002 603 u = 0.029 279 u
So the binding energy is = 0.029 279 u × 931.502 MeV/u = 27.27 MeV
Question R2
A nucleus of radon 22286Rn decays into a nucleus of polonium (Po) and an α–particle.
(a) What are the atomic number and the mass number of the polonium nucleus? How many nucleons does it contain?
(b) Write down the reaction for the decay. (c) Calculate the energy released (Q–value) in the decay.
Answer R2
(a) atomic number = 84, mass number = 218, and it contains 218 nucleons.
(b) The decay is: 22286Rn → 21884Po + 42He
(c) The mass difference is given by
222.017 574 u − 218.008 964 u − 4.002 603 u = 0.006 007 u = 5.596 MeV/c2
The Q–value is 5.596 MeV.
Mass data for Questions R1 and R2:
proton mass = 1.007 276 uneutron mass = 1.008 665 u
mass of a 42He nucleus = 4.002 603 umass of a polonium nucleus = 218.008 964 u
mass of a 22286Rn nucleus = 222.017 574 u1 u = 931.502 MeV/c2
magnitude of the charge on the electron e = 1.6 × 10−19 C
2 Nuclear fission
2.1 Spontaneous and induced nuclear fission
Nuclei with atomic numbers greater than 83 are unstable although some have very long half-lives. Above this value of Z, the repulsive electrical force between the protons is greater than the attractive strong nuclear force between the nucleons, and the nuclei disintegrate. For most naturally–occurring nuclei, the decay is by spontaneous α– or β–decay, and these are often accompanied by γ–decay. However there are other possibilities:
In some cases a very heavy parent nucleus decays into two (medium mass) daughter nuclei. This is called nuclear fission and a material containing nuclei that undergo fission is said to be a fissile material. i
Natural or spontaneous fission is also common in artificially–produced nuclei. For example, the fermium-256 nucleus may undergo spontaneous fission into a xenon nucleus, a palladium nucleus and four neutrons:
256100Fm → 14054Xe + 11246Pd + 410n(1)

Figure 1 The nuclear binding energy graph with some nuclei shown explicitly.
The mass energy of any nucleus is always less than the sum of the mass energies of its constituent nucleons and the binding_energy_of_a_nucleusbinding energy of the nucleus is equal to this difference. The binding energy per nucleon is a measure of the stability of a nucleus; the larger this energy the more stable the nucleus. i Figure 1 shows the binding energy per nucleon plotted against the mass number A for each nucleus.
We can see from Figure 1 that a consequence of a fission reaction, such as the one represented by Reaction 1 (Equation 1), is that the binding energy per nucleon for each of the daughter nuclei is larger than that of the original nucleus. As a result fission is energetically favoured and is therefore likely to occur, with the consequent release of the energy difference (called the Q–value of the reaction). i
This energy difference is carried away as kinetic energy by the decay products. In the case of Reaction 1, the Q–value is about 150 MeV, and the process can be represented as:
256100Fm → 14054Xe + 11246Pd + 410n + 150 MeV(2)
In some cases a heavy nucleus becomes unstable if it captures an incident neutron or proton. If it then undergoes fission this process is called induced fission. An example of induced fission is the fission of 23592U following neutron capture. This process is the basis of present energy generation from nuclear fission. i
✦ What nucleus is formed in the capture of a neutron by 23592U?
✧ The atomic number (92) is unchanged (so it is still a uranium nucleus) but the mass number increases by one. The nucleus produced is therefore 23692U.
The nucleus 23692U is unstable and decays rapidly by fission. There are many possible decays or nuclear decay channels for this process. One possibility is:
10n + 23592U → 23692U → 14155Cs + 19337Rb + 210n + 180 MeV(3)
The probability that a neutron will be captured by a 23592U nucleus, and hence that fission will take place, depends critically upon the energy of the incident neutron. Most neutrons which collide with the uranium nucleus simply scatter elastic_collisionelastically from the nucleus, without any reaction taking place. The probability of capture is much higher for a very low–energy neutron than for a high–energy neutron. For instance, the probability that fission will be induced by a 0.04 eV neutron is about 600 times larger than for a 1 MeV neutron, under otherwise identical circumstances. Neutrons with energies of the order 0.04 eV are known as thermal neutrons. To understand this term we can draw on a result from kinetic theory which tells us that at temperature T the average translational kinetic energy per particle, $\langle\varepsilon_{\rm tran}\rangle$, is $\frac32kT$ where k is Boltzmann’s constant. i
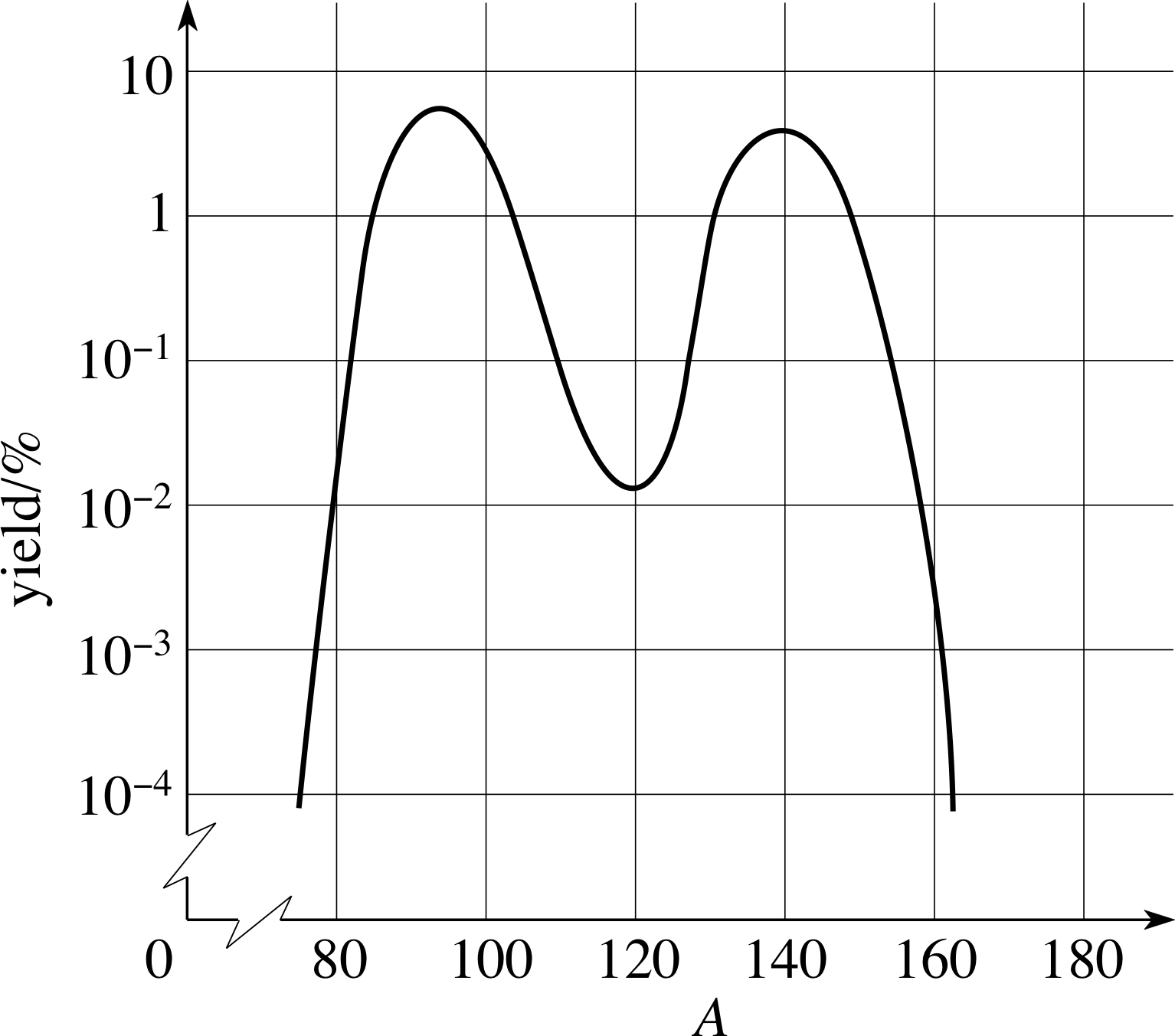
Figure 2 The mass distribution of fragments from the fission of 23692U by thermal neutrons.
From this, we know that at T = 300 K, $\langle\varepsilon_{\rm tran}\rangle$ = 0.04 eV, in other words, the energy of neutrons in thermal equilibrium with their surroundings at room temperature is about 0.04 eV.
Reaction 3 shows one of many possible fission paths of a nucleus 23692U into two fragments.
The distribution of the masses of the fragments following the fission of 23692U by thermal neutrons is shown in Figure 2.
The vast majority of 23692U fissions result in one fragment with mass number A in the region 90 to 100 and the other with a mass number in the region 130 to 145. Usually, two, three, or four neutrons accompany the two fission fragments with, on average, 2.42 neutrons emitted per 23692U fission.
Question T1
What is the equation for the reaction when a nucleus of 23592U absorbs a neutron, splitting into the nuclei 14156Ba and 9236Kr?
Answer T1
Conservation of mass number means that the reaction must be:
23592U + 10n → 23692U → 14156Ba + 9236Kr + 310n
Question T2
The reaction referred to in Question T1 has a Q–value of 173 MeV. How much energy would be released if all the nuclei in 1.0 kg of 23592U underwent this reaction? (Take the mass of each 23592U atom to be 235 u, 1 u = 1.66 × 10−27 kg, 921 MeV = 1.60 × 10−13 J.) Express your answer in joules and in MeV.
Answer T2
The 23592U atomic mass is 235 u = 235 × 1.66 × 10−27 kg. The number of nuclei in the sample is then
1.0 kg/(235 × 1.66 × 10−27 kg) = 2.6 × 1024
Energy released = 2.6 × 1024 × 173 MeV = 4.4 × 1026 MeV = 7.1 × 1013 J.
2.2 Energy from nuclear fission
The energy released when a single heavy nucleus undergoes fission is typically 100–200 MeV – about a hundred times greater than the energy released when a nucleus undergoes α–decay, and millions of times greater than the energy released per atom in a chemical reaction, such as the burning of fossil fuels. This large energy release is the main advantage of nuclear power. Other advantages include the fact that the process does not consume valuable fossil fuels, and does not produce the greenhouse gas, CO2.
All current nuclear reactors use uranium as fuel. Natural uranium has the composition 0.72% 23592U and 99.28% 23892U. It is the 23592U that is the desired isotope as it readily captures thermal neutrons and undergoes fission.
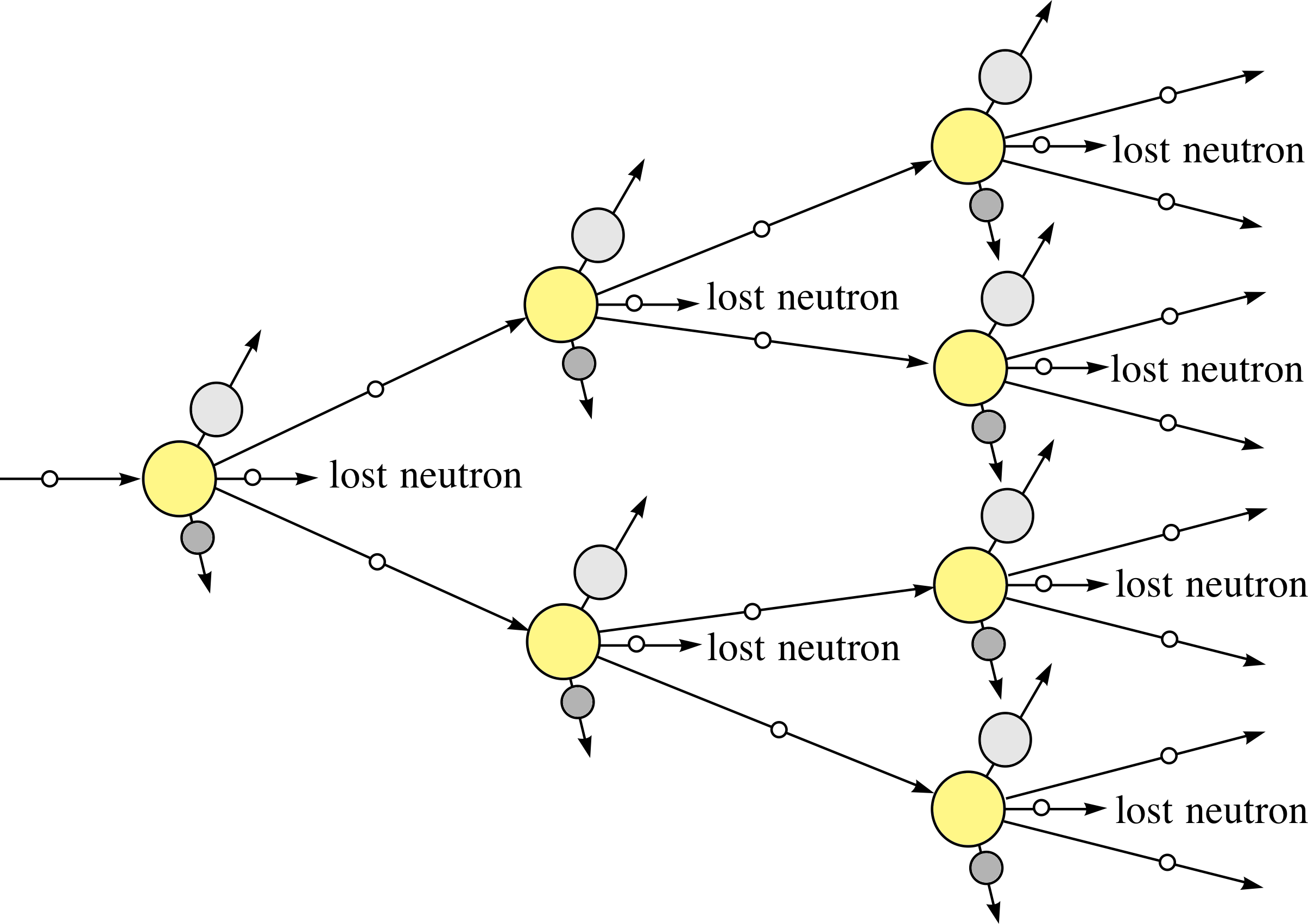
Figure 3 Schematic visualization of the chain reaction in a sample of 23592U following the fission of one 23592U nucleus by a neutron.
The isotope 23892U makes little contribution to the fission process. As a consequence of this, modern reactors use enriched uranium fuel rods, which have a 23592U content of between 2% and 3%.
The fact that each fission induced by a single neutron gives rise to several more neutrons in the fission process, brings with it the possibility of a self–sustaining nuclear chain reaction.
If some of the emitted neutrons produce the fission of neighbouring uranium nuclei in a sample, then there will be a nuclear chain reaction, as shown schematically in Figure 3.
✦ What will happen if, on average, two neutrons from a fission process go on to produce further fission (as illustrated in Figure 3)?
✧ There will be a rapid increase of energy release. One fission in the first step produces two in the second, 4 (= 22) in the third, and so on. The energy released at each step is double that at the previous one.
For example, after only 10 steps of such a process, the energy released will be equivalent to 1 + 2 + 22 + 23 + ... + 210 = 211 − 1 = 2047 times the energy released from a single fission. This is the basis of a self-perpetuating, uncontrolled chain reaction which underlies the operation of a nuclear fission bomb. i
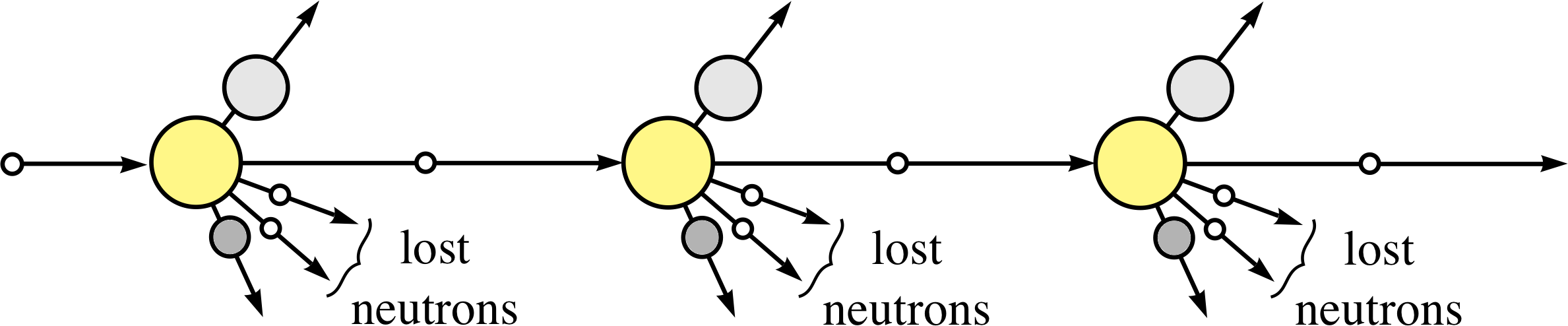
Figure 4 Schematic visualization of a controlled self–sustaining chain reaction (to be compared with the uncontrolled reaction shown in Figure 3).
To harness the energy release from fission, the chain reaction must be controlled, as represented schematically in Figure 4. In the controlled self–sustaining chain reaction there must, on average, be just one new neutron that will produce fission at each step.
This will lead to a steady release of energy that can be used to produce the steam that ultimately drives the generators in a power station. But if too few of the neutrons produce further fission – because they have been absorbed in non–fission reactions or have escaped from the surface of the uranium sample – then the process will fizzle out, no useful energy is obtained and the reactor is said to be subcritical. On the other hand, if too many neutrons produce further fission the reactor is said to be supercritical – it will overheat and could melt–down or even explode, as happened at Chernobyl. i A practical nuclear reactor must maintain a critical state, i.e. have a controlled balance between the subcritical and supercritical states, and this is achieved by various factors that are crucial in reactor design.
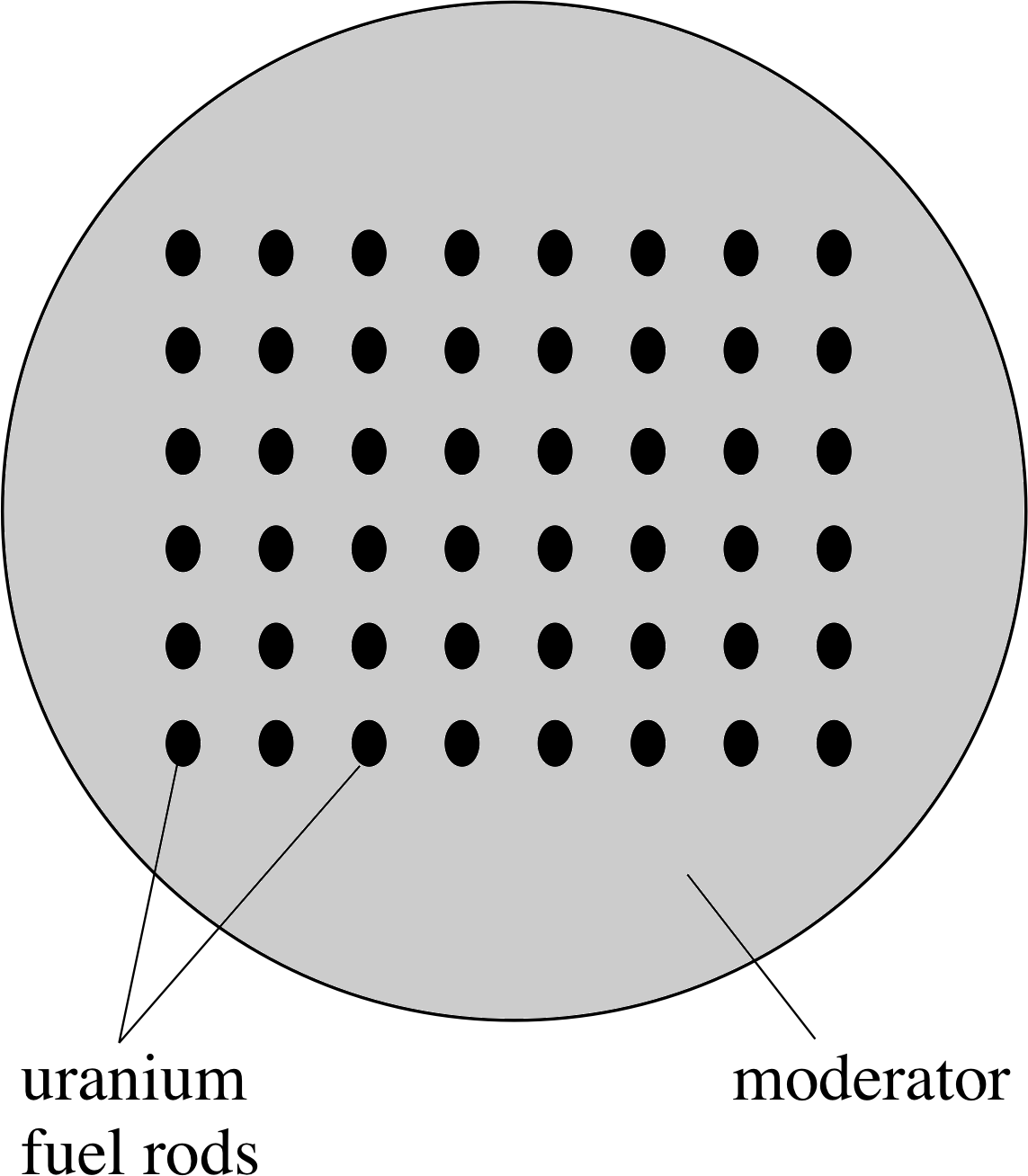
Figure 5 Schematic representation of a nuclear reactor core. A cross section through a cylindrical core is shown.
The heart of the reactor, known as the core, is where the fission reactions take place. All nuclear reactor cores use a similar principle, which is shown schematically in Figure 5. The uranium fuel used is often uranium oxide pellets packed in cylindrical cans. These are the fuel rods and they are separated by a material called a moderator, whose function will be described shortly.
If a sample of fissile material is small, neutrons will have a high probability of escaping from the sample rather than being absorbed by another nucleus, and the sample will therefore be subcritical. In a large sample, neutrons released in the interior are very likely to be absorbed by another nucleus before they can reach the surface and escape. The mass that is just large enough to ensure that enough neutrons are absorbed to sustain a chain reaction is called the critical mass. For enriched uranium the critical mass is about 15 kg – enough to make a sphere about 12 cm in diameter. If the mass exceeds this critical mass, the sample becomes supercritical and will explode. In principle, the operation of a nuclear fission bomb simply requires this amount of fissile material to be concentrated together.
✦ What influences the upper limit on the size of a fuel rod?
✧ Clearly, reactor fuel rods must not be so large as to become supercritical themselves. In fact the rods are cylindrical, not spherical, so the mass limit is not simply 15 kg, but their size must be carefully chosen.
The two or more neutrons produced as a result of a fission have energies of the order of MeV. As they are not thermal neutrons, they will be ineffective in producing further fissions to keep the chain reaction going. The function of the moderator is to slow the fission neutrons down to thermal energies before they enter another fuel rod, enabling them to sustain a chain reaction.
Neutrons, being uncharged, can lose energy only by colliding with the nuclei in the moderator. The moderator is chosen to make this process as effective as possible. We can draw on a result from mechanics which tells us that the optimum condition is when the incident and target particles have the same mass. i Energy would still be lost from the neutron if it were to collide with a heavier nucleus but this would not be ideal, as more collisions would be required to reduce the neutron energy by a given amount and so a larger amount of moderator would be needed.
Ideally, a moderator should have the following properties:
- 1
-
Its atoms should have a mass number as close to unity as possible, i.e. to be close to that of the fission neutron.
- 2
-
It should be a solid or liquid, resulting in a high density of target nuclei.
- 3
-
It must not absorb the chain reaction neutrons via other nuclear reactions.
- 4
-
It must be chemically stable, cheap and abundant.
No single material satisfies all these criteria perfectly, but two commonly–used moderators are graphite and water.
✦ Why is water a suitable material for a moderator?
✧ Water (by virtue of the hydrogen in H2O molecules) satisfies criterion 1 as well as criteria 2 and 4.
- 1
- Its atoms should have a mass number as close to unity as possible, i.e. to be close to that of the fission neutron.
- 2
- It should be a solid or liquid, resulting in a high density of target nuclei.
- 3
- It must not absorb the chain reaction neutrons via other nuclear reactions.
- 4
- It must be chemically stable, cheap and abundant.
Water does less well on criterion 3, since there is some neutron absorption through the process:
10n + 11H → 21H + γ
Graphite (carbon) does not satisfy criterion 1 very well but it has a high specific heat i and so is a good absorber of heat; in the event of an accident in the cooling system, its temperature would rise relatively slowly. Also, as a solid, it cannot leak from the reactor. You shouldn’t need much convincing that, notwithstanding criteria 1 and 2, liquid hydrogen itself is not a wise choice of moderator – the combination of a nuclear reactor and a rocket fuel does not commend itself!
The reactor core, as depicted in Figure 5, lacks any control over the numbers of thermal neutrons. This would be dangerous. The reactor has to be maintained in a critical condition for steady power production. There must be a means of rapidly removing thermal neutrons if there were to be any danger of the reactor becoming supercritical. This control of the rate of the reaction is exercised by control rods, which are made from a material that absorbs thermal neutrons very readily. The control rods can be moved in and out of the core as rapidly as is required. i
A commonly–used material for control rods is boron steel, where the boron in the steel absorbs neutrons via the reaction:
105B + 10n → 115B
The energy released in the fission appears first as kinetic energy of the fission fragments and neutrons released, then as heat energy in the fuel rods, moderator and control rods. This energy is extracted using a coolant. The function of the coolant is two-fold. It must keep these components cool, so that they do not melt and eventually evaporate, and it must also provide a means of transferring the energy to a heat exchanger where water is heated to produce steam, which then drives the turbines in the electricity generator. i Nuclear power generation differs in principle from coal– or gas–fired generation only in the source of primary heat. Water or gases at high pressure are commonly used coolants.
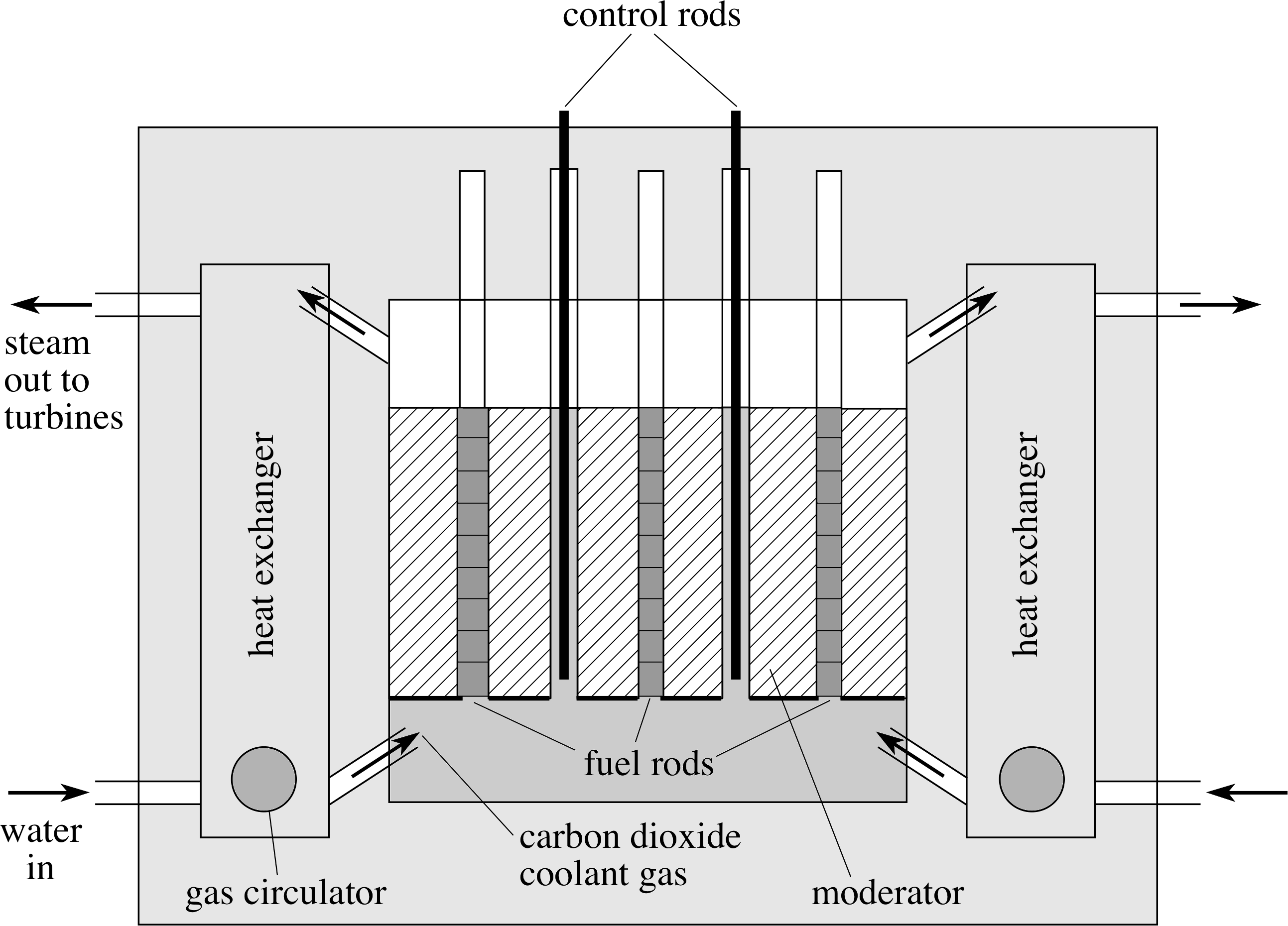
Figure 6 A schematic diagram of an advanced gas–cooled reactor.
Figure 6 shows a schematic diagram of one type of nuclear reactor in common use – the advanced gas–cooled reactor (AGR). i Another type, the pressurized water reactor (PWR), is based on the same physical principles but uses pressurized water as both coolant and moderator.
Yet another type of fission reactor uses a much smaller core with plutonium as the fissile material, surrounded by a blanket of natural uranium. The principles of this reactor are similar to those already discussed except that plutonium fission does not require thermal neutrons but can establish a chain reaction with the fast neutrons produced directly in the fission. For this reason this type of reactor is known as a fast reactor or breeder reactor. The second name stems from the ability of this type of reactor to generate plutonium within the uranium blanket, as fast neutrons escaping from the core are captured. The reactor can, in principle, be designed either to be a net consumer or a net producer of plutonium. There are several prototype fast breeder reactors in existence but there are some technological problems with their operation and it is debatable whether they will ever become commercially viable. i
Question T3
Nuclear reactors and nuclear bombs both rely on nuclear chain reactions, yet the nuclear industry assures the public that nuclear reactors cannot explode like a nuclear bomb. Give arguments for this claim, based on features of conventional reactor core design.
Answer T3
First, the control rods can be lowered into the core to absorb thermal neutrons and hence stop the nuclear chain reaction. Also, in a reactor core, the fissile material is spread out within the moderator, whereas in a bomb it is concentrated. However, the events at Chernobyl are a warning that explosions at a nuclear reactor present a serious threat.
2.3 Radioactive waste
Nuclear power stations produce waste material that is radioactive and must be disposed of safely. However, nuclear power stations are not the only source of the waste: others include hospitals as well as industry and research laboratories. Radioactive waste is classified as high–, intermediate– or low–level waste, with high–level waste being that which is most radioactive and hence presents the greatest hazard. Low–level waste is classified as that having an activity below 4 × 109 Bq (4 GBq) i for α–emitters, and below 12 GBq for β– and γ–emitters. In this subsection, we describe first how high–level waste arises from nuclear fission and then outline some strategies for dealing with various types of radioactive waste. i
| (a) Actinides | (b) Fission products | ||||
|---|---|---|---|---|---|
| Nuclide | Half-life /yr | Amount /kg yr−1 | Nuclide | Half-life /yr | Amount /kg yr−1 |
| 23793Np | 2.1 × 106 | 14.5 | 7934Se | 6.5 × 104 | 0.2 |
| 23894Pu | 88 | 4.5 | 8536Kr | 11 | 0.4 |
| 23994Pu | 2.4 × 104 | 166.0 | 9038Sr | 29 | 13.4 |
| 24094Pu | 6.6 × 103 | 76.7 | 9940Zr | 1.5 × 106 | 23.2 |
| 24194Pu | 14 | 25.4 | 10743Tc | 2.1 × 105 | 24.7 |
| 24294Pu | 3.8 × 105 | 15.5 | 12646Pd | 6.5 × 106 | 7.3 |
| 24195Am | 432 | 16.6 | 12950Sn | 1.0 × 105 | 1.0 |
| 24395Am | 7.4 × 103 | 3.0 | 12953I | 1.6 × 107 | 5.8 |
| 24496Cm | 18 | 0.6 | 13555Cs | 3.0 × 106 | 9.4 |
| 13755Cs | 30 | 31.8 | |||
| 15162Sm | 90 | 0.4 | |||
| total: 322.8 | total: 117.6 | ||||
| The units kg yr−1 represent the average rate at which these materials are produced by a reactor. | |||||
The fission process in a nuclear reactor involves the destruction of the 23592U nuclei and hence the depletion of the active isotope. After a few years of operation a fuel rod becomes significantly less effective and must be replaced. The fuel rods are normally made from enriched uranium, often as uranium oxide pellets packed in stainless steel cans. The spent fuel rods are highly radioactive and the cans themselves also present a radiation hazard. i
Table 1 lists the main isotopes found in spent fuel rods from one type of reactor. The largest component is plutonium, particularly 23994Pu, which is produced when 23592U absorbs a neutron.
The other isotopes listed in Table 1 (a) are produced from 23892U by successive absorption of neutrons, sometimes followed by α– or β–decay of the resulting unstable nucleus. All these high–mass isotopes are actinides, i.e. members of the family of elements with atomic numbers 89–102, all of which are radioactive.
The lower mass nuclides, listed in Table 1(b), are the fission products. For example, the fission shown in Reaction 3 produces 14155Cs and 9337Rb:
10n + 23592U → 23692U → 14155Cs + 9337Rb + 210n + 18 MeV(Eqn 3)
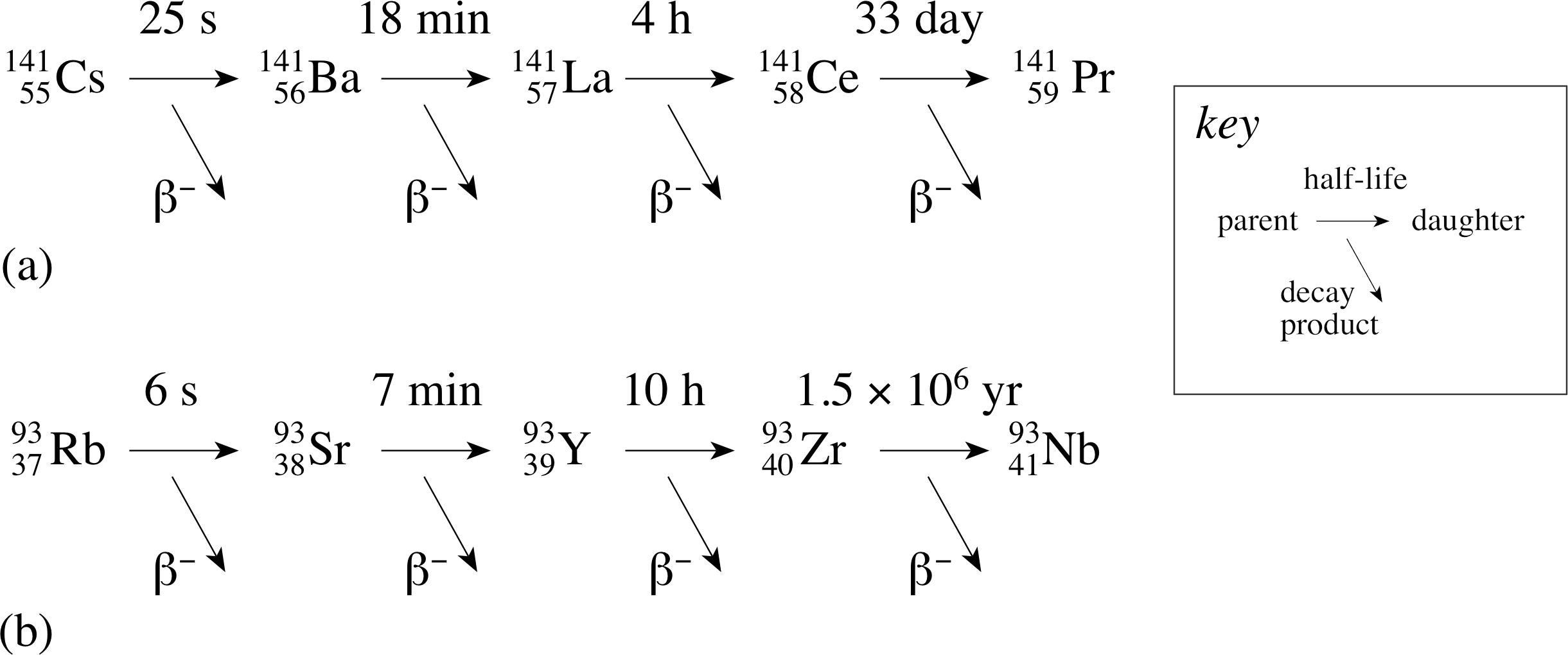
Figure 7 The decay chains of the fission fragments (a) 14155Cs and (b) 9337Rb.
The decay modes of these two products are shown in Figure 7.
From this single fission of a 23592U nucleus at least eight different radioactive isotopes are produced.
✦ What indications are there in Figure 7 and Table 1 that some nuclides will present serious disposal problems?
✧ Nuclides with very short half-lives, for example most of those shown in Figure 7, do not present a great problem since they will decay after only a short period of storage. i However, many of the nuclides listed in Table 1 have extremely long half–lives and it is the presence of these long–lived nuclides in waste material that presents a serious problem.
The plutonium in spent fuel rods is particularly hazardous, as it is also chemically highly toxic and a potential ingredient for bomb-making. The rods also contain other valuable materials, such as uranium. Techniques have been developed for reprocessing the rods, to recover these materials, before they are disposed of. These techniques involve dissolving the rods in a mixture of ‘oily’ and ‘watery’ solvents, chosen so that the uranium and plutonium dissolve in the oily solvent, and the other materials in the watery solvent. When the liquids are allowed to settle, the oil floats on top of the water and hence the two solutions can be separated.
The long half–lives of the ‘waste’ isotopes and the quantities produced in nuclear reactors presents a serious problem. At present, in the UK, this high–level liquid waste is stored in shielded, double-walled, stainless steel tanks at Sellafield. The volume of the waste can be reduced by converting it into solid glass blocks – a process known as vitrification.
Another promising treatment of radioactive waste from nuclear power stations involves bombarding the waste with thermal neutrons. These interact with the actinides and fission products by absorption or fission, and transmute them into shorter–lived or inactive isotopes. This research is at an early stage but an eventual advantage might be that this ‘burning’ of the actinide and fission products could be built into the design of each reactor, avoiding transportation for reprocessing.
Intermediate-level waste has much lower activity than the high–level waste. It consists of material such as fuel rod casing. At Sellafield this waste is encased in cement inside steel drums which are stored in vaults.
Low-level waste consists of things such as clothing and equipment that has been used in areas where radioactive materials are handled. Low–level waste is also produced by hospitals as well as industry and research laboratories. i It is proposed that in future, intermediate–level and solid low–level waste should be stored deep underground in sites with appropriate geological stability. Liquid low–level waste, such as the water from the cooling ponds in which spent fuel rods have been stored initially, is treated and eventually discharged. There are government regulations on the amounts of such waste that may be released in this way.
3 Nuclear fusion

Figure 1 The nuclear binding energy graph with some nuclei shown explicitly.
3.1 Fusion of light nuclei
When a very heavy nucleus undergoes fission, energy is released because there is a net loss of mass energy and hence an increase in kinetic energy. This is equivalent to saying that there is a net increase in the average binding energy per nucleon. From Figure 1 you will see that such an increase can also be achieved by having two light nuclei coalesce to form a heavier one.
The joining of two light nuclei is called nuclear fusion.
One example of a nuclear fusion reaction is:
21H + 21H → 32He + 10n(4)
| Isotope | Rest mass /(MeV/c2) |
|---|---|
| 11H hydrogen | 938.3 |
| 10n neutron | 939.6 |
| 21H deuterium | 1876.1 |
| 31H tritium | 2809.4 |
| 32He helium-3 | 2809.4 |
| 42He helium-4 | 3728.3 |
Each nucleus on the left of the reaction equation has a lower binding energy per nucleon than the nucleus on the right–hand side. The amount of energy released in the reaction may be found from the rest masses of the participants. i Using the atomic rest masses given in Table 2, the Q–value for the reaction is:
2 × 1876.1 MeV − 2809.4 MeV − 939.6 MeV = 3.2 MeV
The reaction is thus:
21H + 21H → 32He + 10n + 3.2 MeV(5)
Several other possible fusion interactions exist between the lightest nuclei; these often involve the hydrogen isotopes 21H and 31H. The hydrogen isotope with mass number 2 is commonly called deuterium or ‘heavy hydrogen’ and its nucleus, known as a deuteron, is represented by the symbol D. The hydrogen isotope with mass number 3 is called tritium, and its nucleus, known as a triton, is represented as T. Reaction 5 (Equation 5) is then an example of a D–D reaction; a reaction between a deuteron and a triton is a D–T reaction. i
As with fission, nuclear fusion is a possible source of energy. Reactions that have been studied as potential power sources include Reaction 5 and also:
21H + 21H → 31H + 11Hn + 4.5 MeV(6)
and21H + 31H → 42He + 10n + Q(7)
Question T4
Use the data in Table 2 to find the Q–value for the reaction represented by Reaction 7 (Equation 7).
Answer T4
From Table 2:
Q = 1876. MeV + 2809.4 MeV − 3728.3 MeV − 939.6 MeV= 17.6 MeV.
The high–energy yield comes from the production of the tightly bound 42He nucleus.
Question T5
In comparing the energy production potential of fission and fusion, a fair comparison is in terms of the energy yield per atomic mass unit of fuel used. Use Reactions 3 and 7,
10n + 23592U → 23692U → 14155Cs + 9337Rb + 210n + 18 MeV(Eqn 3)
21H + 31H → 42He + 10n + Q(Eqn 7)
and the answer to Question T4 to make this comparison, approximately.
Answer T5
From Equation 3 each 23592U fission releases approximately 180 MeV. The yield is approximately:
$\rm \dfrac{180\,MeV}{235\,u} = 0.766\,MeV\,u^{-1}$
From Equation 7 and the answer to Question T4, each D–T fusion releases 17.6 MeV. This yield is approximately:
$\rm \dfrac{17.6\,MeV}{5\,u} = 3.52\,MeV\,u^{-1}$
So D–T fusion has a higher yield per unit mass by the factor 3.52/0.766 = 4.60.
3.2 Energy from nuclear fusion
In many respects fusion offers a more attractive nuclear power source than fission, and it is the subject of major research programmes in the United States, Russia, Europe and Japan. The potential advantages of fusion over fission are considerable and fairly obvious from inspection of Reactions 5, 6 and 7:
21H + 21H → 32He + 10n + 3.2 MeV(Eqn 5)
21H + 21H → 31H + 11Hn + 4.5 MeV(Eqn 6)
21H + 31H → 42He + 10n + 17.6 MeV(Eqn 7)
These advantages also remove most of the concerns presently expressed about nuclear power. They are briefly stated as follows:
- 1
-
There are few problems concerning radioactive waste. The final product of the deuterium fusion reactions (42He) is not radioactive; it is, in contrast, quite a valuable by–product of the fusion. i
- 2
-
The initial deuterium fuel is cheap and readily available. Seawater is a natural mixture of H2O and D2O and although the relative abundance of deuterium to hydrogen is only about 0.015%, its extraction is relatively easy and there is plenty of seawater around – enough deuterium to satisfy the present global energy requirements for billions of years!
- 3
-
There are no fuel security problems; the fuel is neither hazardous nor valuable – potential thieves would be well advised to take a bucket to the seaside and collect their own!
- 4
-
Since deuterium is gaseous, there would be very little fuel mass in a reactor and no danger of a runaway reaction. Similarly, any terrorist attack on a reactor would pose no major environmental threat.
- 5
-
Fusion is more fuel–efficient than fission, producing more energy per kilogram of fuel.
This list is so impressive that you may wonder what we are waiting for! As you might suspect, it is not that simple. In practice, fusion power is much more difficult to achieve than fission power. Despite massive research efforts, huge problems remain to be solved. Laboratory fusion is not too difficult to achieve but the transition from this to a practical fusion reactor is a major challenge; the problems faced are technical as much as scientific.
The difficulties in fusion all stem from one rather obvious difference between fission and fusion. In fission, an uncharged neutron infiltrates the positive nucleus and induces its disintegration. The nucleus puts up no resistance since there is no electric force between them and so the nucleus does not respond to the approach of the neutron – even a very low–energy neutron is able to breach the defences of the nucleus. By contrast, in fusion both nuclei are positively charged and so there is a strong electrical repulsion between them. Only if the two nuclei can overcome this repulsion, and approach within range of the strong nuclear attractive force, will they fuse and release nuclear energy. This may happen if the two deuterons have sufficient kinetic energy to approach within range of the nuclear force before being brought to rest by the repulsive electric force. We can estimate the required kinetic energy, from the conservation_of_energyprinciple of energy conservation, by equating the total kinetic energy of the two particles to the electric potential energy at the position of closest approach. The electric potential energy of two deuterons (charge +e) a distance r apart is given from Coulomb’s law as
$E_{\rm pot} = \dfrac{e^2}{4\pi\varepsilon_0r}$
where ε0 = 8.85 × 10−12 C2 N−1 m−2 is the permittivity of free space. We can estimate the required distance of closest approach since we know that the strong nuclear force operates only over distances comparable to the diameter of a nucleus, say 10−14 m, so r must be less than this for fusion to occur.
Question T6
From the data just given, and the magnitude of the electronic charge e = 1.60 × 10−19 °C, estimate the minimum total kinetic energy for two deuterons to fuse in a head–on collision. (Ignore recoil.)
Answer T6
The electric potential energy for two charges +e, separated by a distance r = 10−14 m is given from Coulomb’s law as $E_{\rm pot} = \dfrac{e^2}{4\pi\varepsilon_0r}$. This must also be equal to the required total initial kinetic energy, Ekin so:
$E_{\rm kin} = \rm \dfrac{(1.60\times10^{-19}\,C)^2}{4\pi\times8.85\times10^{-12}\,C^2\,N^{-1}\,m^{-2}\times10^{-14}\,m} = 2.30\times10^{-14}\,J = 144\,keV$
This crude calculation in Answer T6 provides no more than a rough estimate (70 keV for each deuteron) of the required particle kinetic energies. i The prediction from more reliable calculations is that D−D laboratory fusion will require particle kinetic energies of about 150 keV (although in the core of the Sun such reactions seem to thrive with average kinetic energies as low as 4 keV – we will return to this problem shortly).
It is not particularly difficult to produce a beam of deuterons from ionized deuterium, accelerate them through say 200 kV, to give them kinetic energy of 200 keV, and then allow them to strike a stationary deuterium target. This energy should allow fusion to take place; do we then have a fusion reactor?
Unfortunately, the answer is no. The problem is that even when a fusion collision is energetically possible it is still an extremely unlikely event. A far more likely event is the elastic_collisionelastic scattering of the fast deuterons in the beam from the stationary deuterons in the target.
As we discussed in Subsection 2.2, when a particle scatters elastically from a stationary particle of the same mass a substantial fraction of the incident kinetic energy is transferred to the stationary particle. On average the energy is shared equally, so that one elastic scattering of a 200 keV deuteron will produce two deuterons, each of 100 keV – each below the threshold to cause fusion. The production of fusion by firing a beam of deuterons at a deuterium target would require far more energy to accelerate the beam than would be made available from the fusions that occurred – a completely impractical reactor!
The problem of elastic scattering can be overcome if both colliding deuterons are moving, each with about the same kinetic energy. In this case if one deuteron loses kinetic energy in the collision then the other must gain this kinetic energy, so the average kinetic energy per particle remains above the threshold for fusion. If a sample of deuterium gas is heated to a high temperature so that the average particle energy is around 150 keV the collisions which will occur naturally will preserve the average particle kinetic energy above threshold and eventually a fusion collision will occur; all we have to do is to wait! How long we have to wait will be determined by the collision rate (i.e. by the pressure or density of the gas) and the average kinetic energy of the particles (i.e. by the gas temperature). The probability of a fusion reaction in a collision increases rapidly as the kinetic energy rises above the threshold, so the best plan is to heat the gas as much as possible and hope that we recoup more energy from fusion than we invest in the heating.
We can estimate the temperature required from the same kinetic theory result which we invoked in Subsection 2.1. This gave the average particle translational kinetic energy $\langle\varepsilon_{\rm tran}\rangle$ in terms of the temperature T (in kelvin) by $\langle\varepsilon_{\rm tran}\rangle = \frac32kT$ where k is Boltzmann’s constant.
Question T7
Using the average particle translational kinetic energy as 150 keV estimate the required temperature for D–D fusion.
Answer T7
The required kinetic energy per particle is 150 keV. From the kinetic theory result that each particle has $\langle\varepsilon_{\rm tran}\rangle = \frac32kT$ we have a required temperature given by:
$\frac32T = 150\times10^3\times1.6\times10^{-19}\,{\rm J}$
So$T = \rm \dfrac{2\times150\times10^3\times1.6\times10^{-19}\,J}{3\times1.38\times10^{-23}\,J\,K^{-1}} = 1.16\times10^9\,K$ or about 1000 MK.
It is clear that laboratory D–D fusion will require temperatures of about 1000 MK and that this will be difficult to achieve. Also, there will be a serious problem of containment of the gas at these temperatures, since no vessel walls could withstand contact with material at 1000 MK. i
Plasmas
So far we have referred to the hot deuterium as a gas, but the word ‘gas’ is misleading. The temperature and the particle energies are so great that interparticle elastic collisions are sufficiently violent to remove many of the electrons normally bound within the atoms. The ‘gas’ formed then consists not of neutral atoms and molecules, but rather positive ions and electrons – charged particles. A ‘gas’ of charged particles behaves quite differently from a normal gas of neutral atoms and molecules – it is a fourth state of matter, distinct from solids, liquids or gases and is called a plasma. The problems to be addressed are therefore ones of plasma production, plasma heating and plasma confinement.
In a plasma there are strong electric forces between the charged particles, unlike the rather weak electric forces between the neutral molecules of a normal gas. i This leads to several surprising properties of a hot, highly ionized plasma and illustrates why such a plasma qualifies as a different state of matter and why it is difficult to control and confine:
- 1
-
The plasma particles distribute themselves so as to produce overall charge neutrality in any local region with, at most, only tiny electric fields within the plasma. If we try to apply an external electric field to a plasma the particles move to nullify its effect within the plasma – the electric field is almost completely shielded out by the plasma. In this respect the plasma behaves more like a metal than a gas or a liquid. i
- 2
-
Charged particles move freely in response to any applied electric field and this motion constitutes an electric current. A very hot plasma is an excellent electrical conductor, with an conductivityelectrical conductivity which is higher than that of copper at room temperature!
- 3
-
Plasmas can be controlled by magnetic fields via the magnetic forces on the moving charges. Suitable magnetic fields can prevent the plasma from reaching the walls of a containment vessel and hence allow magnetic confinement of the plasma, as is discussed Subsection 3.3. This behaviour is unique to plasmas; normal gas molecules move around freely, but cannot be controlled like this, whereas, in solids and liquids there may be charged particles which will react to an externally applied magnetic field, but their motions are constrained to a fixed volume.
- 4
-
The strong electric forces between the particles cause the plasma to act in a cooperative way – if one part of the plasma is disturbed the whole plasma may become unstable. These strong forces make the plasma behave in some respects more like a liquid or a solid than a gas, e.g. ripple waves can travel through a plasma, rather like on water. A plasma also has some rigidity, rather like a solid and unlike a liquid, so that shear_stressshear forces can also be transmitted and waves, like those on a string, can travel through a plasma. All of these aspects make confinement of a plasma extremely difficult.
The plasma state of matter is a good deal more common than you might imagine. Many ionized states of matter can be described as a plasma, whether or not the temperature is high. Although uncommon on Earth, it is believed that plasmas form more than 99% of the visible matter in the universe (including the stars and the interstellar medium between them). i Our own star, the Sun, is nothing other than an enormous ball of plasma 1.4 × 106 km in diameter with a mass of about 2 × 1030 kg.
The Sun is almost our role–model of an ideal fusion reactor, consuming hydrogen and forming helium in its core, and doing so at a temperature of only 30 MK. Fusion at this relatively ‘low’ temperature is made possible by the particular way in which the Sun solves the problem of confining the plasma. In the case of the Sun (as in all stars) it is gravity that holds the huge mass of plasma together. So high is the plasma density in the core of the Sun and so permanent the confinement that a temperature of 30 MK is sufficient to let the Sun produce the energy it eventually radiates into space as sunlight. Sadly such conditions do not pertain in terrestrial laboratories, where the mass of plasma is far too small for gravitational confinement to work.
The time scale for successful confinement in a laboratory is also very different from that in the Sun. The solar plasma has been around for about 5 billion years. In the laboratory we must achieve viable fusion conditions within the time over which we can sustain the temperature, density and plasma stability – in practice this means over a few tens of seconds. The price we have to pay for the low density and for the unseemly haste is that laboratory fusion plasmas must be much hotter than the Sun’s core. i
Fortunately we can improve on the Sun a little by using the D–T reaction (Reaction 7),
21H + 31H → 42He + 10n + 17.6 MeV(Eqn 7)
with a fuel mixture of deuterium and tritium. At a working temperature of 200 MK this reaction rate is about 200 times higher than that for the D–D reaction that dominates solar fusion. Unfortunately, tritium does not occur naturally and its high cost requires any viable reactor to regenerate the tritium it consumes during operation.
The fundamental problem of fusion power is simply put – the plasma must be produced, heated to an extreme temperature and the conditions of density and temperature must be maintained for sufficient time to allow fusion collisions to provide enough energy to maintain the plasma temperature against energy losses – conditions usually referred to as ‘break even’. In other words, we must get enough energy out to repay the energy expended in raising and maintaining the temperature in the first place. This condition is often stated in terms of reaching the Lawson criterion, requiring the product of the number density of nuclei in the plasma and the confinement time to be greater than a given value. i This value depends on the reaction concerned and on the temperature. For D−T reactions it is about 5 × 1019 m−3 s at 200 MK, but for D−D reactions it is 1021 m−3 s at 1000 MK. Some of the attempts that have been made to solve the confinement problem and meet the Lawson criterion are described in the next subsection.
3.3 Plasma confinement
In this subsection, two lines of approach to confinement will be discussed: magnetic confinement and inertial confinement. In both cases we will discuss the broad principles only.
Magnetic confinement
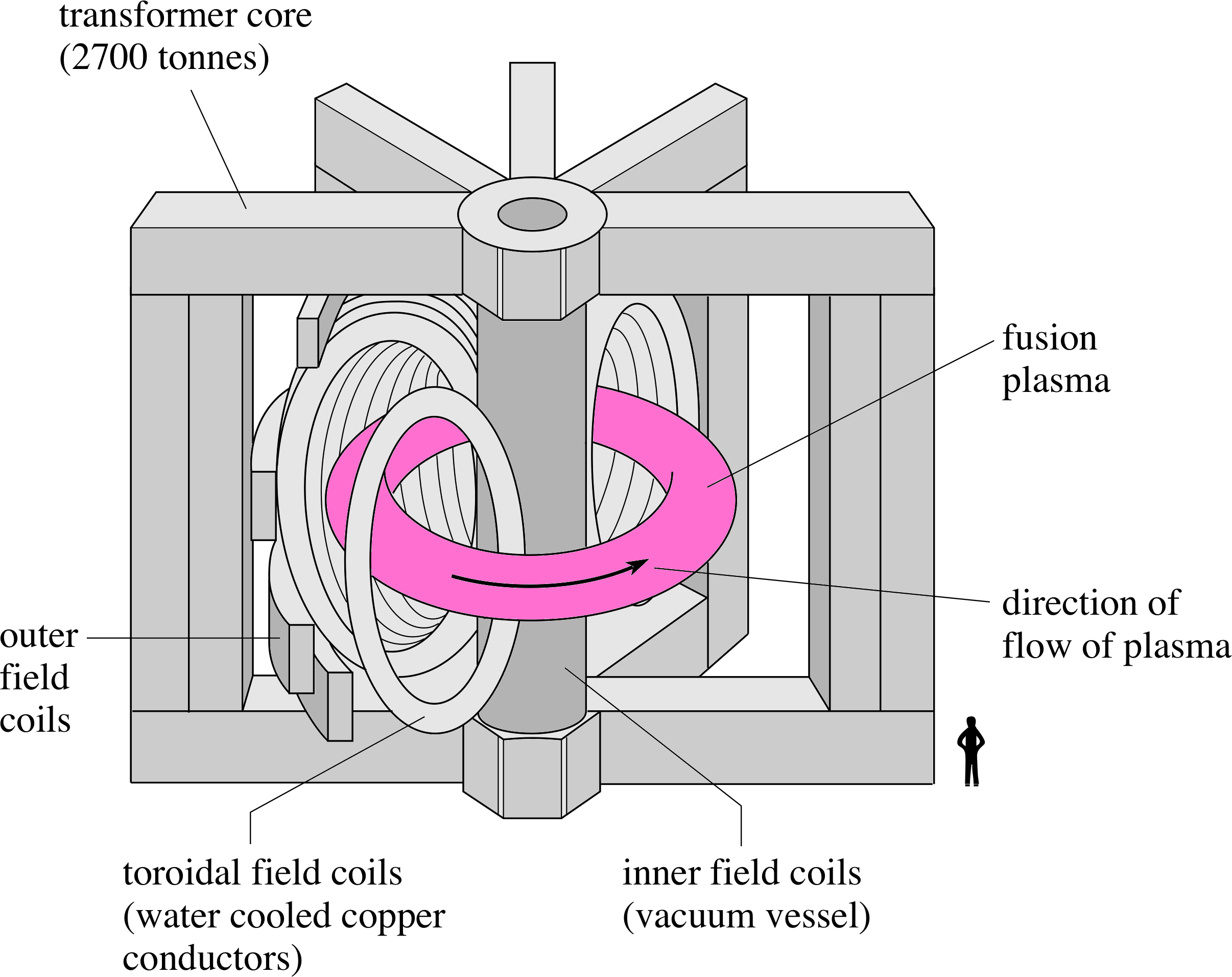
Figure 8 Schematic diagram of the JET torus.
Magnetic confinement uses the magnetic forces on the moving charged particles to prevent the particles reaching the walls of the vessel. The electromagnetic force is always at right angles both to the direction of motion of the charge and to the magnetic field. i One magnetic field configuration used to confine a plasma is illustrated in the European JET project (Joint European Torus), at Culham Laboratory in Oxfordshire.
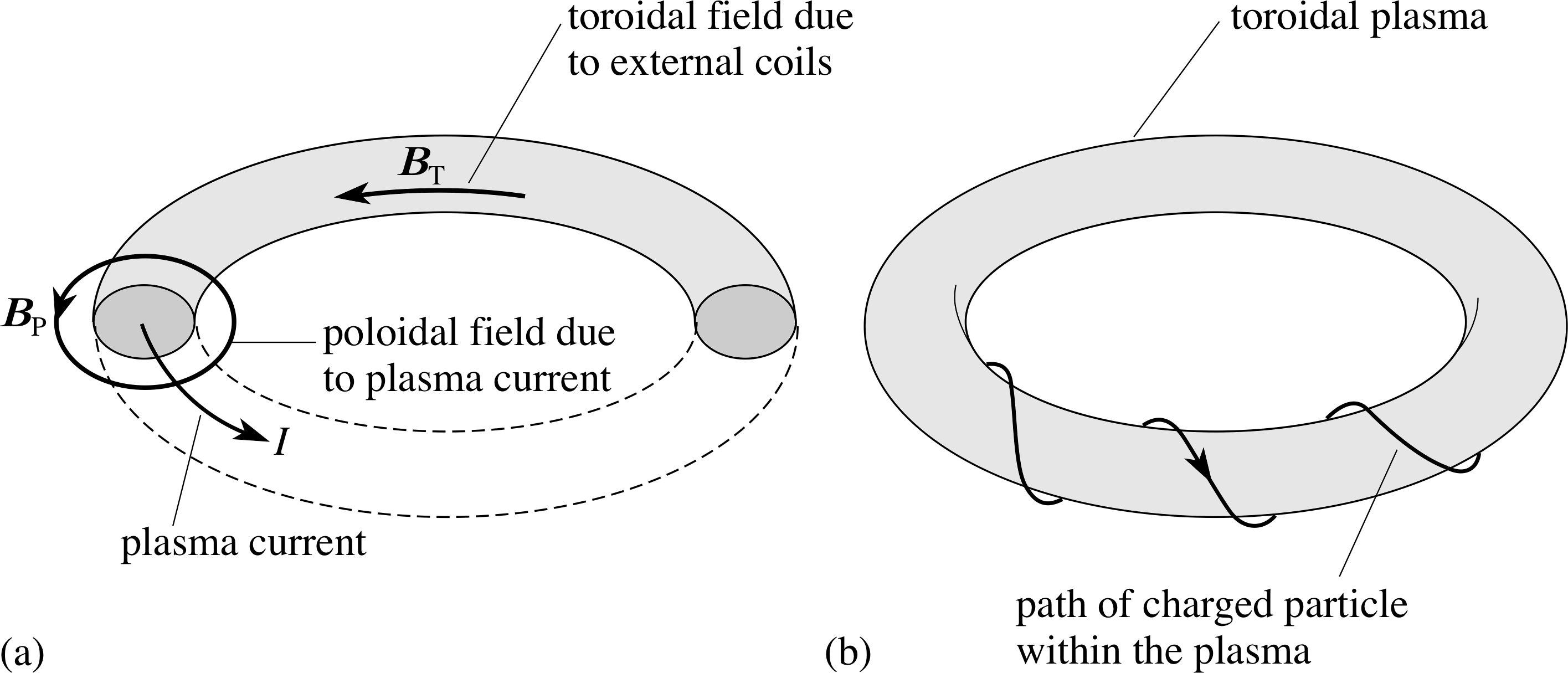
Figure 9 (a) The toroidal and poloidal fields in the JET torus. (b) Motion of a plasma particle in the combined toroidal and poloidal magnetic fields.
In JET the plasma is contained in a toroidal stainless steel vessel (Figure 8) i through which there are two main confining magnetic fields. A toroidal field (predominantly horizontal and directed parallel to the toroidal axis) is produced by electric currents in vertical coils around the torus. A poloidal field (predominantly vertical and directed at right angles to the toroidal axis) is produced by a combination of electric currents flowing through horizontal coils inner central coil), around the vertical axis (including an inner central coil), and by a large current flowing through the plasma (Figure 9a). The combination of these two fields produces helical field lines (Figure 9b) i which wrap around the toroidal plasma and constrain the motion of the particles along these helical field lines, keeping the plasma away from the walls of the containment vessel.
An additional vertical magnetic field, perpendicular to the plane of the torus, stabilizes the plasma current by producing forces towards the centre of the current ring.
The scale of this machine should be appreciated. The stainless steel torus is 6 m in diameter, and the whole machine has a mass of more than 3 × 106 kg. The plasma current consists of 20 or 30 s pulses of about 5 × 106 A, induced by transformer action. i The highly conducting plasma forms a single secondary turn of a transformer, with the plasma current initiated by a current pulse through the inner poloidal coil as a primary coil. The energy needed for the primary current pulse comes from the energy stored in two 8 × 105 kg flywheels, each of which has been accelerated to spin at over 200 rpm using electrical power from the National Grid drawn over a period of time. Any attempt to drive the primary pulse directly from the National Grid could put out the lights in the whole of the south of England!
The JET plasma is heated by a combination of processes. First, the plasma current itself heats the plasma in the same way that currents produce heat in any conductor. i This heating is limited because as the plasma heats up it becomes a better and better conductor. Later stages of heating involve launching 30 MW of electromagnetic wave power into the plasma and also 10 MW of high energy neutral deuterium atoms. The details of these processes need not concern us here but the outcome is that the JET project has already achieved temperatures in excess of 100 MK and, with the addition of tritium, has demonstrated fusion power. Unfortunately, there is still a long way to go to produce a practical fusion reactor for the future, but certainly the results so far are encouraging.
Inertial confinement
Research is also underway on a completely different approach to plasma confinement. In this approach, no attempt is made to confine the plasma by external means but fusion conditions are attempted by extreme compression of a D−T target using intense pulsed lasers or electron or ion beams. i The idea is to create such intense conditions within the target that the time needed for the target to disrupt is still long enough to meet the Lawson criterion and allow fusion. The disruption time is set by the mass or inertia i of the target and so this approach is described as inertial confinement. A fuel pellet, consisting of a D−T gas mixture, held in a small spherical container (diameter about 1 mm), is subjected to symmetrical compression from the incident beams. For fusion within the pellet it is necessary that the gas should be compressed to a density of about 1000 times normal liquid density and that there should be a central hot spot where particle energies exceed about 5 keV. To achieve these conditions, the incident beam needs to deliver megajoules of energy in nanosecond pulses. i The processes involved in the compression are not yet well understood and the problems involved appear to be at least as difficult as those for magnetic confinement, but research into this approach also continues apace and optimism about this line of attack has recently grown.
Question T8
Justify the claim that a plasma is genuinely a fourth state of matter, different from a gas, a liquid or a solid.
Answer T8
In a plasma the particles are mobile, able to travel widely, and when unrestrained by any external forces will fill any container in which they are placed; in this a plasma resembles a gas. However, the particles are charged rather than neutral and they interact strongly with each other through electric forces. Because mobile charged particles can carry electric currents plasmas are excellent electrical conductors, unlike a normal gas and more like a metal (in fact their electrical conductivities can exceed that of any metal at room temperature). With the high conductivity comes the ability to shield out externally applied electric fields, in the same way as a metal. The strong forces between particles allow plasmas to act in a cooperative way, with the whole plasma affected by any local disturbance. Wave transmission through plasmas shows many of the features of waves in a gas or a liquid or a solid (e.g. compressional waves such as sound, ripple waves on the surface, and transverse waves as on a string).
Question T9
Use the Lawson criterion for D−T fusion i to estimate, (a) the required plasma number density in JET, given a containment time of 10 s, and (b) the effective containment time for inertial confinement, given the compressed density must reach 1000 times greater than a typical liquid density (i.e. 1000 × 103 kg m−3). Take the deuteron mass as mD = 3 × 10−27 kg.
Answer T9
The Lawson criterion gives the required product of number density and containment time for D−T fusion as 5 × 1019 m−3 s.
(a) For JET the required number density is therefore 5 × 1019 m−3 s/10 s = 5 × 1018 m−3.
(b) For inertial confinement we first need to calculate the required number density nρ from the mass density ρ and the atomic mass of deuterium mD (3 × 10−27 kg). This number density is:
nρ = ρ/mD = 106 kg m−3/(3 × 10−27) kg = 3.3 × 1032 m−3
The minimum containment time is then = 5 × 1019 m−3 s/(3.3 × 1032) m−3 = 1.5 × 10−13 s = 0.15 ps.
The fuel pellet must not disrupt within this time if fusion is to begin.
3.4 Tritium as a fuel
Whether magnetic or inertial confinement is eventually successful, it is likely that tritium will form part of the fuel, and regeneration or recycling of this very expensive and scarce material will be crucial in any practical fusion reactor of the future. The solution to this problem is likely to involve lithium and its ability to absorb neutrons and create tritium. Lithium has two stable isotopes, 73Li and 63Li. These isotopes react with neutrons via:
10n + 63Li → 31H + 42He + 4.8 MeV(8)
and10n + 73Li → 31H + 42He + 10n − 2.5 MeV(9) i
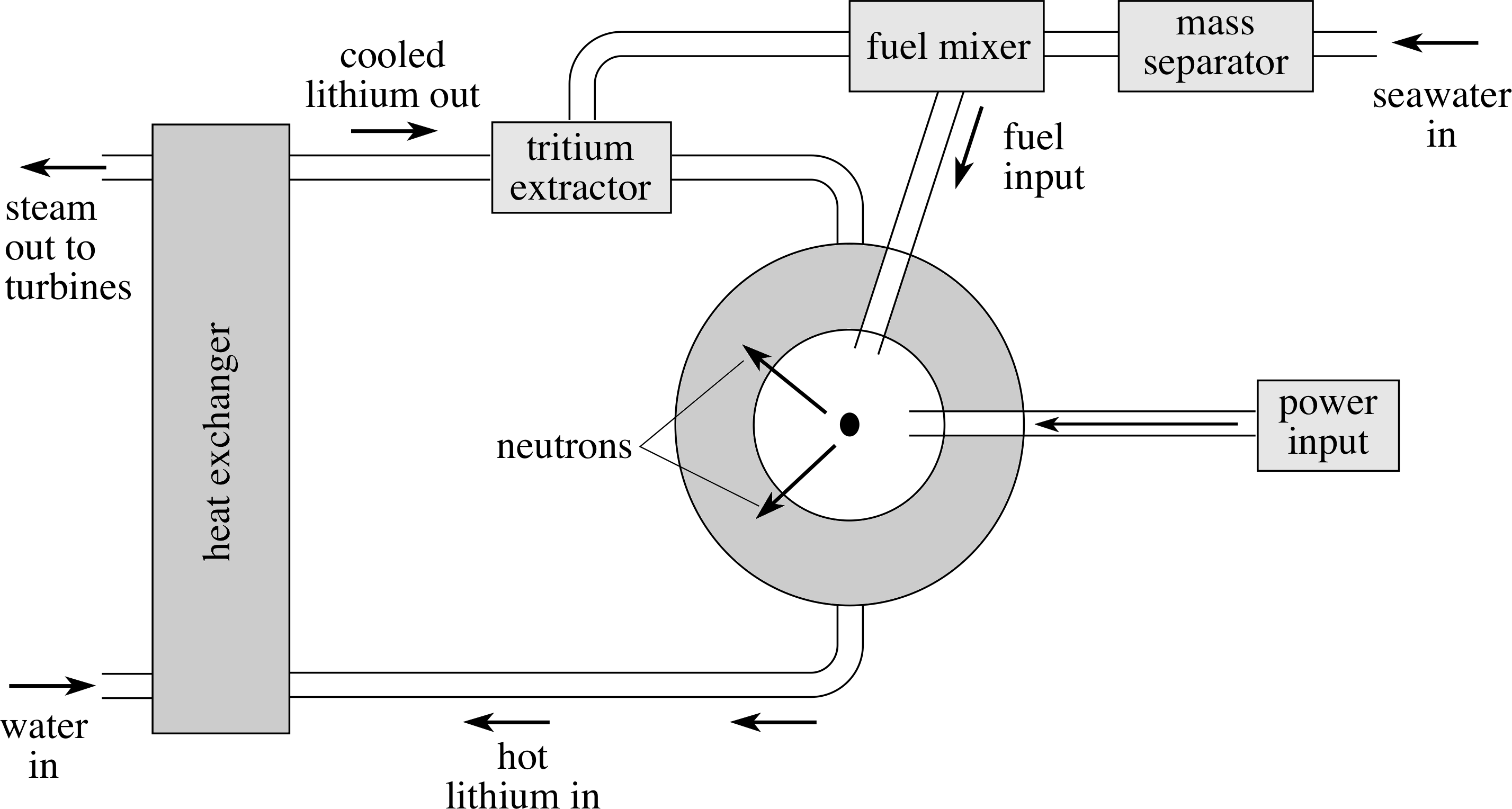
Figure 10 A schematic representation of a nuclear fusion reactor.
These breeder reactions can produce tritium fuel for the reactor while absorbing potentially harmful neutrons, which might otherwise be absorbed elsewhere in the structure of the reactor and cause it to become radioactive. If we use liquid lithium (metal) also as the coolant in the reactor then we have three benefits for the price of one! As a bonus, seawater also contains plenty of lithium as well as the basic deuterium fuel.
A schematic of such a reactor is shown in Figure 10.
4 Radiation hazards
4.1 Radioactivity – friend and foe
Radiation can cause great damage as shown by the fall–out from nuclear weapons, but on the other hand γ–rays and radioactive tracers have been used beneficially in medicine and in archaeological dating and are vital in much of research (within biology, genetics, chemistry and physics). In recent times, the explosion at Chernobyl and possible leukaemia clusters near Sellafield have focused attention on radiation hazards to living organisms. As with all human activity, the risks associated with nuclear power generation must be balanced against the benefits that may stem from it.
Radioactive processes produce α– and β–radiations, which are charged particles, and γ–rays, which are a form of high–energy electromagnetic radiation. To these must be added X–rays, which are also high–energy electromagnetic radiation, but their production is via an atomic rather than a nuclear process. i All these ionizing radiations can damage living tissue by ionization or by excitation of the molecules that make up the cells of the body.
We live in an environment that naturally includes low levels of ionizing radiation which come from the decay of naturally–occurring radioactive isotopes and from cosmic rays, high–energy particles (mainly protons) which enter the Earth’s upper atmosphere from space. Overall, the natural radioactivity of the Earth must be considered a bonus since it is the decay of radioactive nuclei within the Earth that keeps our planet geologically active. In the distant past, when short–lived isotopes would have been more abundant, the heat provided by this source would have been much greater and it can even be argued that without its influence life on Earth would never have arisen.
Although we are right to be concerned about any additional artificial ionizing radiations, at very low levels it is difficult to distinguish between any damage from this and damage caused by the effects of the natural background radiation. In this section we can give only an introductory account of radiation hazards, but we will approach the subject quantitatively as far as possible.
4.2 Radiation dose
In order to classify the hazard in any exposure to ionizing radiation we need to have a measure of the potential damage caused by this radiation. The words ‘damage’ and ‘hazard’ are words which do not easily succumb to quantitative measure. They have no obvious unit of measure, and the damage can take many forms; it may not be apparent immediately or it may be local initially but later have repercussions for the whole body. Notwithstanding these difficulties, we will work towards a definition of radiation dose as a measure of the potential hazard. The damage caused by radiation depends on several factors – the total energy of the radiation which is absorbed, the individual energies of the particles (including photons i) involved, how strongly ionizing it is, how far it can travel (its range) in tissue, and whether it is targeted on specific parts of the body (e.g. if the source is ingested).
| Type of ionizing radiation | Range in tissue |
|---|---|
| α–particles | 10 to 100 μm |
| β–particles | 1 to 10 mm |
| γ– and X–rays | through body |
There is an inverse relationship between range and ionizing strength – the more strongly ionizing the radiation, the more rapidly the energy is transferred to tissue, the shorter the range and the more localized is the initial damage. Ranges of the various radiations in tissue are shown in Table 3. From this we can see that α–particles are strongly ionizing and cannot even penetrate the skin from outside the body (although if ingested the damage can be very serious). At the other extreme, γ–rays are weakly ionizing, very penetrating, and can pass right through the body. i
Note Our best protection against any radiation source is the inverse square law – keep well away from it, if possible!
The inverse square law states that the radiation intensity falls in proportion to the square of the distance from the source. This law applies equally to ionizing radiation as it does to light. For γ–radiation the application is complicated because γ–rays scatter effectively from surfaces such as walls and ceilings – so the received dose may be higher than you might predict from the inverse square law.
| Type of ionizing radiation | Radiation weighting factor |
|---|---|
| X–rays, γ–rays, electrons and muons i | 1 |
| neutrons, of various kinetic energies Ekin: | |
| Ekin ≤ 10 keV | 5 |
| 10 keV < Ekin ≤ 100 keV | 10 |
| 100 keV < Ekin ≤ 2 MeV | 20 |
| 2 MeV < Ekin ≤ 20 MeV | 10 |
| Ekin > 20 MeV | 5 |
| protons | 5 |
| α–particles, fission fragments, heavy nuclei | 20 |
The efficiency with which a given type of radiation causes ionization in tissue (by creating ions along its path), is characterized by the radiation weighting factor (RWF). The larger the RWF, the more damaging is the radiation for a given total energy input. X–rays are defined to have a RWF of 1 and the other radiations have their RWF determined relative to X–rays. The RWF values are shown in Table 4. As opposed to what is expected from the range, α–particles are potentially very much more damaging than, say, γ–rays. An α–source outside the body will pose no risk to internal organs, but if the same source were to be inhaled into the lungs its high ionization strength would present a very grave risk to that organ.
Apart from the ionizing strength of the radiation, the other quantity involved in the hazard is the total absorbed energy. This is a clear–cut physical quantity, called the absorbed dose, and it is measured by the energy absorbed per kilogram of tissue; the unit for this is the gray (Gy), with 1 Gy = 1 J kg−1. The overall hazard (the biological effect of the radiation) is then measured in terms of the dose equivalent, which is the product of the absorbed dose and the radiation weighting factor. The sievert (Sv) is the unit of dose equivalent and is defined as that dose with the same biological effect as a 1 Gy dose of X–rays. So, for any particular type of radiation:
(dose equivalent/Sv) = (absorbed dose/Gy) × RWF(10)
The two units, Gy and Sv, have the same dimensions (equivalent to J kg−1), and are related through the RWF, which is a dimensionless numerical factor.
Question T10
In Subsection 2.3 it was stated that β– and γ–emitting waste with an activity below 12 GBq is classed as low-level, while α–emitting waste can only be classed as low–level if its activity is below 4 GBq. Suggest a reason for these different limits.
Answer T10
α–radiation can cause more damage to living tissue than β– or γ–radiation, because of its ionizing efficiency. For the same activity, α–emitting waste is therefore a greater potential hazard than β– or γ–emitting waste. The ratio of the classification boundaries (3 to 1) is not simply the inverse ratio of the RWFs (20 to 1), since α–sources would need to be ingested to develop their full hazard.
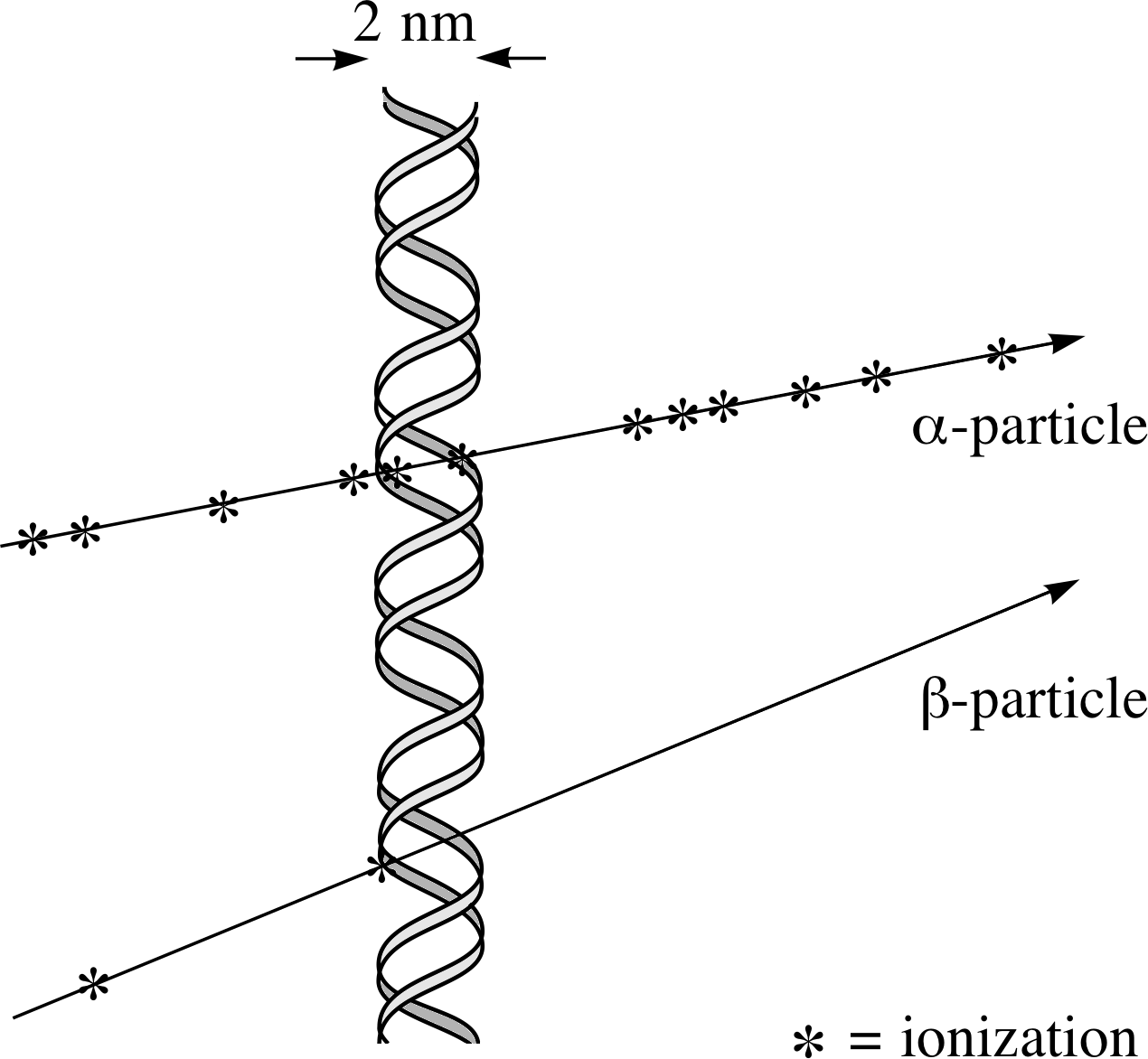
Figure 11 Ionization damage to a DNA molecule.
4.3 Biological effects of radiation
Radiation damage in living tissue arises through ionization or excitation of molecules. Excitation can produce very reactive ‘free radicals’ i, which attack sensitive biomolecules and interfere with the body’s chemistry. Ionization is most hazardous where it involves the DNA in the body’s cells.
If a strand of the DNA double helix i in the nucleus of a cell is damaged (see Figure 11) this may lead to the death of the cell; this is serious if the cell cannot be replaced but otherwise it may not be too serious. The body has well–developed mechanisms for repairing DNA damage and the damaged cell may not die. Sometimes this repair is ineffective or is incorrect. Such damage can lead to changes in the ‘genetic message’ coded in the DNA – this change is known as a ‘mutation’. If the damage is to a part of the DNA which is responsible for controlling cell replication then an uncontrolled replication of cells, or a cancer, may occur.
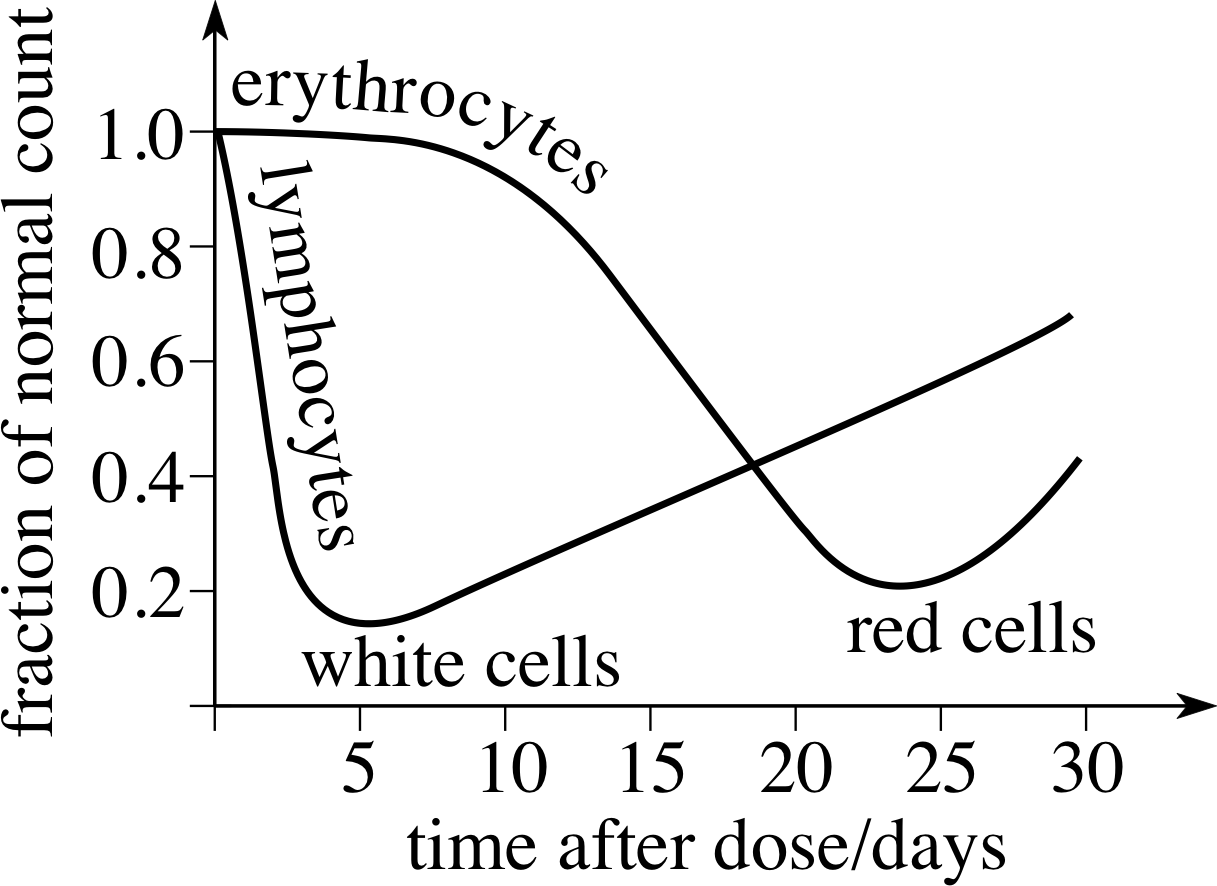
Figure 12 The effect of a single large dose of X–rays on lymphocytes (white cells) and erythrocytes (red cells) in the blood.
Where mutations affect those specialized cells involved in reproduction (gametes) there may be repercussions for future generations. Natural mutations have played a key part in human evolution but it is clearly important to avoid additional mutations caused by radiations of artificial origin – however difficult it may be to quantify such long–term effects.
Aside A gamete is a cell, namely a sperm or an ovum (egg) in a human being, that is involved in the reproduction of offspring and is hence responsible for transferring genetic information to the offspring.
In a so–called whole–body dose, cells throughout the body may be affected by radiation. If only replaceable cells are destroyed, such as the red or white cells in the blood, short–term recoverable damage occurs. This is illustrated in Figure 12, which shows how a large dose of X–rays will affect the red and white blood cells.
| Dose equivalent/Sv | Chance of survival |
|---|---|
| 1 | ≈100% |
| 3 | ≈80% |
| 5 | ≈50% |
| > 6 | ≈0% |
Table 5 gives the approximate chance of survival of the individual from a single external whole–body dose. i Recovery may take weeks or months, or the dose may be fatal depending on its level. The recoverable cases will suffer from what has become known as radiation sickness, with symptoms that include skin disorders and hair loss. Since the white blood cells, for instance, are involved in the immune system, their destruction may lead to illness or death from secondary causes, which the body cannot then fight successfully. With damage of this type, chances of recovery depend not only on the cumulative dose but also on the time period over which it is administered.
Radiation from an external source may also cause skin burns, which may be localized or extensive, depending on the source. The damage may not be permanent since skin cells can be replaced.
If irreplaceable cells are destroyed, such as brain and bone marrow cells, then long–term permanent damage results. The time before serious effects are evident from the loss of these cells may be up to 20 years.
| Class | Example | Half-life | Emissions | Damaging effect |
|---|---|---|---|---|
| very highly toxic | 9038Sr | 29 years | β− | long-lived bone-seeker |
| highly toxic | 4520Ca | 165 days | β− | much shorter–lived bone-seeker |
| moderately toxic | 2411Na | 15 hours | β−, γ | not targeted on a critical organ |
| slightly toxic | 146C | 5730 years | β− | not targeted on a critical organ |
Radioactive substances are also classified according to their harmful effect if taken internally. This depends on their chemical nature, their radiation type and their half-life. For instance, an ingested isotope of calcium or strontium is potentially harmful because it will be preferentially absorbed in the bones. Similarly, iodine would concentrate in the thyroid gland. Table 6 lists some radioactive substances, classified according to this hazard. Some substances affect specific organs initially, whereas others affect the whole body. This property of chemical targeting can also be used in medical applications.
Question T11
What would be the approximate chances of surviving each of the following absorbed radiation doses? (a) 3 Gy of X–rays, (b) 1 Gy of 25 MeV neutrons, (c) 1 Gy of α–particles.
| Type of ionizing radiation | Radiation weighting factor |
|---|---|
| X–rays, γ–rays, electrons and muons i | 1 |
| neutrons, of various kinetic energies Ekin: | |
| Ekin ≤ 10 keV | 5 |
| 10 keV < Ekin ≤ 100 keV | 10 |
| 100 keV < Ekin ≤ 2 MeV | 20 |
| 2 MeV < Ekin ≤ 20 MeV | 10 |
| Ekin > 20 MeV | 5 |
| protons | 5 |
| α–particles, fission fragments, heavy nuclei | 20 |
Answer T11
From Tables 4 and 5:
(a) dose equivalent = 3 Sv; survival chance ≈ 80%
(b) dose equivalent = 5 Sv; survival chance ≈ 50%
(c) dose equivalent = 20 Sv; survival chance ≈ 0.
| Dose equivalent/Sv | Chance of survival |
|---|---|
| 1 | ≈100% |
| 3 | ≈80% |
| 5 | ≈50% |
| > 6 | ≈0% |
4.4 Natural and artificial sources of ionizing radiation
The monitoring of average radiation doses received by individuals in the UK is undertaken by the National Radiological Protection Board (NRPB).
In the UK the average annual dose equivalent is approximately 2.5 mSv (millisieverts) per individual per year. This consists of about 85% from natural sources and 15% from artificial sources, although there are very wide variations regionally, by occupation and lifestyle.
Information about annual dose is summarized in Figure 13.

Figure 14 The UK regional variation in annual dose equivalent due to radioactive gases.
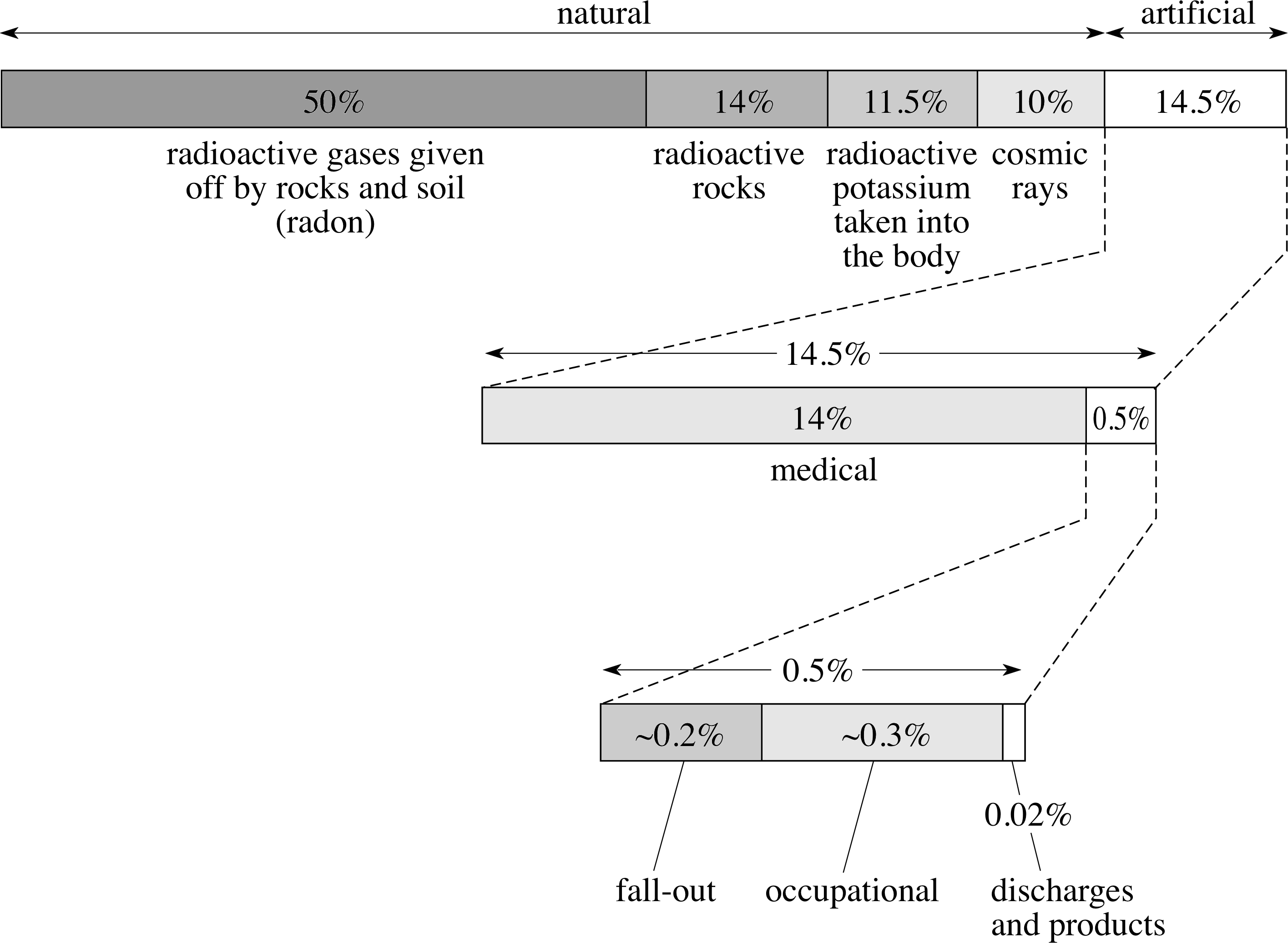
Figure 13 Average annual doses of sources of radiation in the UK. (Source: ‘Radiation exposure in the UK’, S. Hughes, Radiological Protection Bulletin, No. 145, September 93, pp. 10–12. Radiological Protection Board, Chilton)
The detailed breakdown of the natural sources of radiations is as follows:
Radioactive gases given off by rocks and soil (50%)
The gases radon and thoron are relatively short–lived α–emitters, produced in the decay of radium. They are much denser than air. In the open air they are rapidly dispersed but higher concentrations may accumulate within a confined space, such as a building or in a mine. There are wide regional variations in dose from this source, as is shown in Figure 14. Radium is a minor constituent of granite, so radon levels are high in regions where granite is common, such as Cornwall, but much lower in the clays around the London region. Radon test kits are available and, in high–risk areas, radon levels are monitored by NRPB.
γ–rays from radioactive rocks and building materials (14%)
The material of the Earth’s crust is slightly radioactive. Building materials may therefore also be radioactive since they are extracted from the Earth.
Note There are also regional variations in this γ–ray background level, with a similar distribution (but less pronounced) to that of radon activity.
Radioactive potassium taken into the body (11.5%)
Potassium-40 is the major source of radioactivity taken into the body as foodstuffs. 4019K forms 0.01% of naturally–occurring potassium.
Note Shellfish tend to develop higher levels of radioactivity as they feed on the sea floor. This can produce dosages about 50% higher than the average under this heading.
Cosmic rays (10%)
The Earth is constantly being bombarded by very high–energy particles, mainly protons, from space. These collide with nuclei in the atmosphere, producing radioactive isotopes. The dose increases with altitude, and the value quoted here is at sea level.
Note As you might expect, aircrew receive higher average levels under this heading – at 10 km altitude, where aircraft usually fly, the cosmic ray contribution can be almost 200 times that at ground level and for Concorde, which cruised at 15 km, it was almost 400 times this level.
From Figure 13, we see that the remaining 15% of average annual dosage is attributable to the following artificial sources:
Medical (14%)
Radiation doses within this category mainly arise from diagnostic X–rays, γ–radiation used in the treatment of cancer and radioisotopes injected into the body as tracers or for other treatments.
Note The average for medical exposure is of little relevance. Many people have little or no exposure under this heading, whilst a few have considerably more than this average.
Fall-out (0.2%)
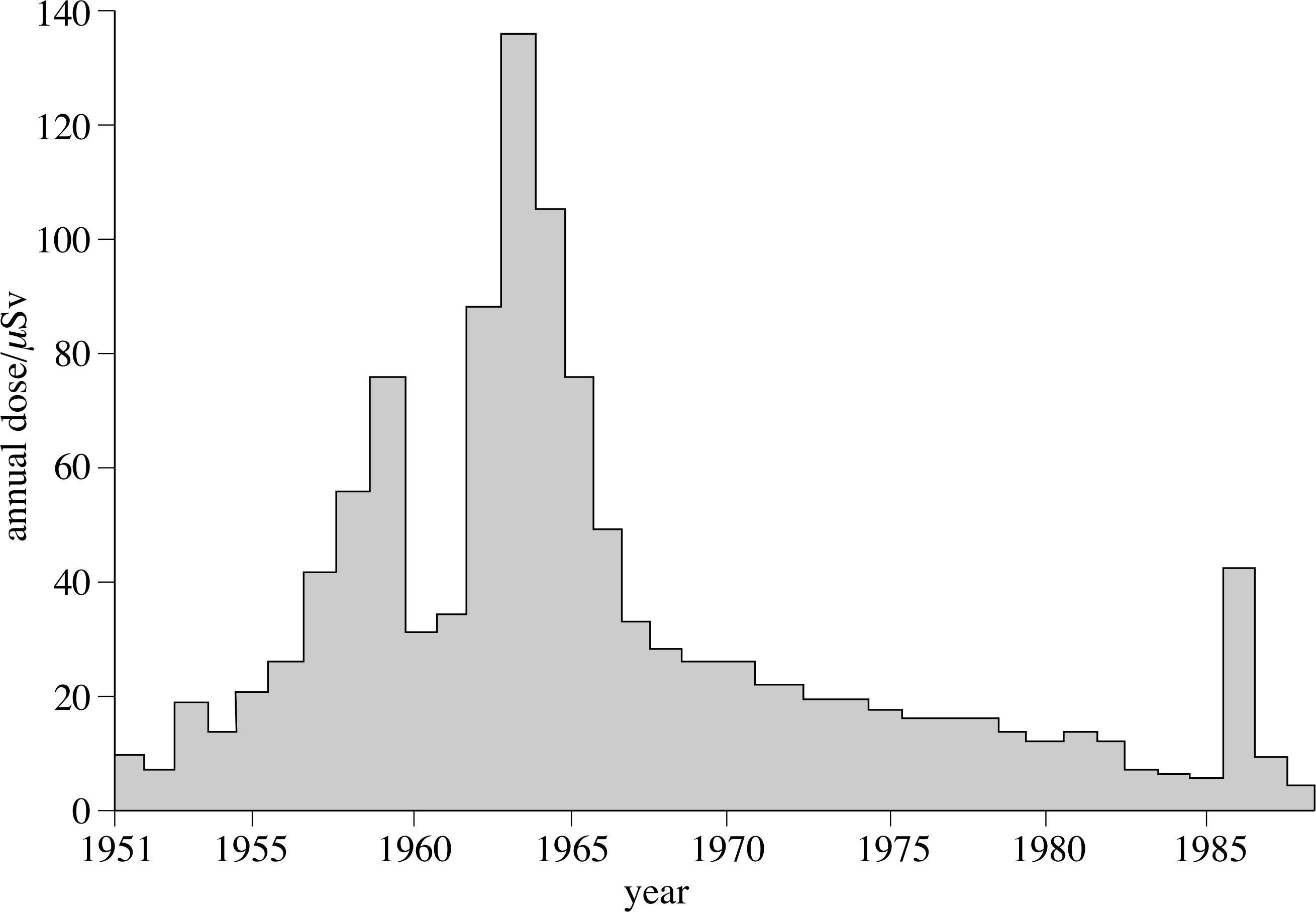
Figure 15 The variation in average annual dose from fall-out; the effect of Chernobyl, in 1986, is clearly seen.
Radioactive materials were produced by the testing of 120 nuclear weapons in the atmosphere prior to the Test Ban Treaty of 1963. These materials are now spread world–wide in the atmosphere, and have been very much reduced since the treaty, as can be seen in Figure 15.
Miscellaneous sources, such as air travel and commercial products (0.5%)
Some products make use of radioactive materials, e.g. smoke detectors and, where essential, luminous dials.
Occupational (0.3%)
Many occupations involve contact with radioactive substances – in industry, in medicine and in research. Clearly the doses here vary substantially between occupations and the average dose of 0.3% can be misleading as a measure of its importance. Monitoring of exposure is strictly controlled under the ‘Ionizing Radiation Regulations’. Ordinarily the maximum dose permissible for whole–body radiation is 12.5 mSv over a three–month period, but there are constraints on the proportion of this dose that may be received over shorter periods. Detailed provisions are made for different categories of worker, according to their usual level of exposure and workplace areas are categorized in terms of the radiation levels in them.
Discharges (0.02%)
This category includes the burning of coal. Coal contains radioactive carbon and traces of other radioactive elements, including uranium, released into the atmosphere on burning. Also, routine discharges of small amounts of radioactive materials by the nuclear power industry are permitted. This radioactivity arises from the preparation of the fuel, its use in the reactor and the subsequent reprocessing of the spent fuel.
The account given here and in the preceding subsection is, of course, a shallow sketch of a very complex field. It can be summed up by saying that the probability of damage by natural radiation is relatively low – the human race could hardly have survived over millennia if it had been otherwise – but the consequences of very large doses are horrendous. The risk to an individual from irradiation at levels only slightly above the natural level are hard to quantify, and the risks to succeeding generations even harder.
Question T12
Which one of the following statements is correct? Say briefly why the other statements are false.
(a) The terms ionizing radiation and electromagnetic radiation are synonymous.
(b) When ionization damages a DNA molecule in the nucleus of a cell, the damage is always permanent.
(c) For the majority of people living in the UK the average annual dose of ionizing radiation is mainly due to natural background sources.
(d) The only known effect of ionizing radiation on humans is the induction of cancer.
Answer T12
Statement (a) is incorrect: ionizing radiation is radiation that can ionize matter. Types of ionizing radiation include α– and β–particles, neither of which are electro–magnetic radiation. Some electromagnetic radiation (X–rays and γ–rays) is ionizing, but other types (e.g. radiowaves) are not.
Statement (b) is incorrect because DNA damage may be repaired by the body; also some cells are replaceable.
Statement (c) is correct (see Figure 13).
Statement (d) is incorrect because the damaged cell in the body could be a gamete, which may transmit inherited disorders to future generations. Lesser damage – e.g. radiation burns to the skin – may also be inflicted. Also a damaged immune system can lead to secondary illness.
5 Closing items
5.1 Module summary
- 1
-
section 2Nuclear fission involves the decay of a heavy nucleus into two medium–mass nuclei plus several neutrons, with the conversion of some mass energy into kinetic energy.
- 2
-
Fission may be induced by the absorption of a neutron. A nuclear chain reaction may be set up if the neutrons released cause further fissions.
- 3
-
The steady release of the energy from nuclear fission required in a nuclear power station is achieved by controlling the numbers of thermal neutrons in the core and hence maintaining a critical state.
- 4
-
The basic constituents of a nuclear reactor are the fuel rods containing fissionable uranium nuclei, the moderator which slows the neutrons to thermal energies and the control rods which regulate the numbers of neutrons in the reactor core. A coolant flows around the core and this transfers the energy which is then used to raise steam to drive turbines.
- 5
-
Spent fuel rods are highly radioactive with by–products of fission including isotopes with very long half-lives. reprocessingReprocessing spent rods enables some uranium and plutonium to be recovered, leaving high–level waste that must be disposed of safely.
- 6
-
section 3Nuclear fusion involves the coalescence of two very light nuclei, such as deuterium, to form a heavier nucleus, with the conversion of some mass energy into kinetic energy. It is the power source within the Sun.
- 7
-
Fusion reactors require temperatures of at least 200 MK in their fuel and the production and plasma confinementconfinement of the resulting plasma at relatively high density. Plasmas are described as the fourth state of matter since they have unique combinations of properties which are separately characteristic of solids, liquids or gases. Plasma confinement methods include magnetic confinement (as in JET) or inertial confinement (as in laser or particle beam compression).
- 8
-
Fusion power is not yet commercially feasible but it has been scientifically demonstrated. If successfully developed, it would have advantages over fission power in that the fuel is safe and readily available and relatively little radioactive waste would be produced.
- 9
-
Radiation causes damage to living cells by ionization. The seriousness of the damage depends on the nature and energy of the radiation, and the location and function of the damaged cells, and can vary in extent from burning of the skin to death. The damage may be immediate or long–term – such as cancer or genetic mutations, which may be passed on to later generations.
- 10
-
The hazard from a dose of ionizing radiation is measured in terms of the radiation dose equivalent (in units of sieverts, Sv), which is the product of the absorbed radiation dose (energy absorbed per kilogram of tissue, in units of graygrays with 1 Gy = 1 J kg−1) and the radiation weighting factor, which takes account of the ionizing strength of the radiation concerned.
- 11
-
Radiation is received from both natural and artificial sources. In the UK about 85% of the total dose is from natural sources, but there are wide variations with region, individual lifestyle and occupation.
Acknowledgements
Grateful acknowledgement is made to the following sources for permission to reproduce material in this module:
Figure 8: Sang, Dr D. (1990), ‘JET torus’, Nuclear Physics, Bath Science series, Thomas Nelson and Sons Ltd 1990; Figure 14: Selfe, J. and Nicholl, B. (N. S. Education Consultants) ‘Our radioactive world’, Snippets, 16, United Kingdom Atomic Energy Authority Education Service; Figure 15: ‘Radioactive fallout’, Radiation Doses – Maps and Magnitudes, At-A-Glance series, NRPB. © National Radiological Protection Board. Second edition 1994.
5.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Explain energy production from nuclear fission and nuclear fusion.
- A3
-
Explain how a fission chain reaction may be established and distinguish between a subcritical, a critical and a supercritical chain reaction.
- A4
-
Describe the function of a moderator in a fission reactor and the main characteristics required of a moderator material.
- A5
-
Describe the function of the control rods in a fission reactor.
- A6
-
State in general terms the kinds of waste that are produced by a nuclear reactor, and describe how the problems they present are addressed.
- A7
-
Explain why the fuel in a fusion reactor will be a plasma and describe the plasma state of matter and its main characteristics.
- A8
-
Describe in general terms magnetic confinement and inertial confinement.
- A9
-
State the main sources of ionizing radiation dose for the general population in the UK.
- A10
-
Explain why the hazard posed by radioactive material depends on the type and energy of the radiation it emits and on whether this radiation is received internally or externally.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
5.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions each of which tests one or more of the Achievements.

Figure 1 The nuclear binding energy graph with some nuclei shown explicitly.
Question E1 (A2)
(a) Explain, by referring to Figure 1, but without doing any calculations, whether each of the following reactions would result in a release of energy:
(i)126C + 126C → 2412Mg
(ii)5326Fe → 2814Si + 2412Mg + 10n
(iii)24094Pu → 14556Ba + 9338Sr + 210n
(b) For each of the energy–releasing reactions above what can you say about the practical difficulties of using it in a reactor.
Answer E1
(a) Reactions (i) and (iii) would both release energy, because they each lead to a net increase in the average binding energy per nucleon (Figure 1) or a decrease in mass energy, with some mass energy converted into kinetic energy.
Reaction (ii) would not lead to a release of energy since it would lead to a decrease in binding energy and would hence require energy input.
(b) Reaction (i) would require a very high kinetic energy, and hence a very high temperature, because of the electrical repulsion between the two nuclei, each of which has a charge of +6e. It would therefore be very difficult to make the reaction happen in a reactor on Earth (but it does occur in the cores of some very hot stars).
You cannot say whether reaction (iii) takes place readily without knowing whether this isotope of plutonium is fissile (in fact the reaction does occur, e.g. in fast fission reactors that use plutonium as fuel, where it is initiated by a nucleus of 23994Pu absorbing a neutron).
(Reread Subsection 2.1Subsections 2.1, Subsection 2.22.2, Subsection 3.13.1 and Subsection 3.23.2 if you had difficulty with this question.)
Question E2 (A3)
Explain the meaning of the phrase, ‘a chain reaction resulted from the induced fission of uranium’. What is the difference between critical, supercritical and subcritical chain reactions?
Answer E2
A chain reaction occurs when the product of a reaction causes another reaction of the same kind, which in turn causes a reaction of the same kind and so on. In this case, the fission induced by a neutron leads to the production of further neutrons, some of which go on to induce further fission. However, not all of these neutrons will cause further fissions. Some will be absorbed without producing fission, others will escape from the surface of the fissile material.
The chain reaction is supercritical if on average more than one neutron produces a further fission, leading to a rapid build–up of energy release; it is subcritical if less than one neutron does so, and the reaction fizzles out; it is critical if precisely one neutron causes a further fission, maintaining a steady rate of energy release.
(Reread Subsection 2.2 if you had difficulty with this question.)
Question E3 (A4 and A5)
In not more than three or four sentences for each, explain the purpose in a fission reactor of (a) the moderator and (b) the control rods.
Answer E3
(a) To cause further fissions efficiently, neutrons must have thermal energies (approximately 0.04 eV). Neutrons produced by fission have high (MeV) energies. The function of the moderator is to slow the fast neutrons down to thermal energies.
(b) To produce energy at a steady rate the chain reaction must be critical. The control rods – which are made of materials that readily absorb thermal neutrons – are inserted or withdrawn from the reactor core so as to keep the balance between the subcritical and the supercritical state. They may also be rapidly inserted fully to close down the reactor in case of emergency.
(Reread Subsection 2.2 if you had difficulty with this question.)
Question E4 (A4)
What physical characteristic would make 2412Mg a better moderator than 5626Fe? Explain in one sentence why, in practice, neither is used in this role.
Answer E4
A neutron loses energy by transferring it to another particle in an elastic collision. The greatest energy transfer in such a collision is between particles of the same mass. Since the neutron mass is about 1 u, the nearer the target mass is to this, the greater will be the energy transfer. Therefore 2412Mg is a better moderator than 5626Fe. Neither is used because both nuclei are much heavier than neutrons and many materials exist with lighter nuclei.
(Reread Subsection 2.2 if you had difficulty with this question.)
| Nuclide | Half-life /yr | Amount /kg yr−1 |
|---|---|---|
| 23793Np | 2.1 × 106 | 14.5 |
| 23894Pu | 88 | 4.5 |
| 23994Pu | 2.4 × 104 | 166.0 |
| 24094Pu | 6.6 × 103 | 76.7 |
| 24194Pu | 14 | 25.4 |
| 24294Pu | 3.8 × 105 | 15.5 |
| 24195Am | 432 | 16.6 |
| 24395Am | 7.4 × 103 | 3.0 |
| 24496Cm | 18 | 0.6 |
| total: 322.8 |
Question E5 (A6)
Using only information from Table 1, say which of the listed actinides pose the greatest problems of waste disposal. Give your reasons.
Answer E5
Nuclides present a problem of waste disposal because they are produced in large quantity and they are very long-lived. On the first criterion, the actinides are a problem, worst first, in the order: 23994Pu, 24094Pu, 24194Pu, 24195Am, 24294Pu, 23793Np. On the second criterion, the order is: 23793Np, 24294Pu, 23994Pu, 24395Am, 24094Pu. Nuclides that occur in both lists are a particular problem. This does not take into account the type of radiation emitted, which cannot be deduced from Table 1.
(Reread Subsection 2.3 if you had difficulty with this question.)
Question E6 (A7)
The reactions in a fusion reactor take place in a deuterium or a deuterium–tritium plasma. Explain the term plasma and explain why the plasma state is necessary for a fusion reactor.
Answer E6
A plasma consists of freely–moving ions and electrons and occurs when electrons are stripped from their atoms, for example by collisions at high temperature. For fusion to take place, the deuterons must approach each other to within a typical nuclear diameter. Deuterons are positively charged, so repel each other. To overcome this repulsion they must approach each other with high energy. Deuterons with sufficient energy are available only if the ‘gas’ is at the very high temperature of a plasma.
(Reread Subsection 3.2 if you had difficulty with this question.)
Question E7 (A8)
Explain why confinement is a problem for a fusion reactor. Outline the physical principles underlying two methods for confining a plasma.
Answer E7
The temperature necessary to produce high rates of fusion is far above the temperature that any material vessel could tolerate, so the hot plasma must be kept away from the walls of its containing vessel. Magnetic confinement exploits the fact that the plasma consists of moving charged particles, which experience a force in a magnetic field. In inertial confinement, intense laser or particle beam radiation is focused on to a sphere containing fusionable matter. The fuel pellet is compressed, leading to fusion–producing temperatures and densities at the centre, in a time which is less than the time for disruption of the pellet.
(Reread Subsection 3.2Subsections 3.2 and Section 3.33.3 if you had difficulty with this question.)
Question E8 (A9)
What types of radiation dose are likely to be similar for a farmer in Cornwall and a radiologist in a London hospital? What levels might be significantly different?
Answer E8
Similar levels of radiation are from food and drink, from cosmic rays, from medical sources as a patient (for a similar health record) and from nuclear power. Significant differences might arise because (i) Cornwall is largely on granite whereas London is largely on clay. Dose from rocks and building materials, and especially from radon escaping from rocks, are likely to be significantly higher in Cornwall than in London. (ii) The radiologist will have occupational exposure to radiation (X–rays or γ–rays) which the farmer will not.
(Reread Subsection 4.3Subsections 4.3 and Section 4.44.4 if you had difficulty with this question.)
Question E9 (A10)
A person receives a radiation dose of 10 mGy. What is the effective dose in mSv if the radiation absorbed is (a) γ–rays and (b) α–particles?
Answer E9
Using Equation 10,
(dose equivalent/Sv) = (absorbed dose/Gy) × RWF(Eqn 10)
| Type of ionizing radiation | Radiation weighting factor |
|---|---|
| X–rays, γ–rays, electrons and muons i | 1 |
| neutrons, of various kinetic energies Ekin: | |
| Ekin ≤ 10 keV | 5 |
| 10 keV < Ekin ≤ 100 keV | 10 |
| 100 keV < Ekin ≤ 2 MeV | 20 |
| 2 MeV < Ekin ≤ 20 MeV | 10 |
| Ekin > 20 MeV | 5 |
| protons | 5 |
| α–particles, fission fragments, heavy nuclei | 20 |
and Table 4:
(a) γ–rays have RWF = 1, so the effective dose = 10 mSv.
(b) α–particles have RWF = 20, so the effective dose = 200 mSv.
(Reread Subsection 4.2Subsections 4.2 if you had difficulty with this question.)
Question E10 (A10)
Distinguish between external whole–body doses of radiation and internal doses. In terms of these two categories evaluate a dose from (a) an α–emitting gas, (b) a β–emitting liquid, and (c) a γ–emitting solid. Is the chemical nature of the material significant?
Answer E10
An external whole–body dose is one from a source outside the body. An internal dose is one from a source which has been ingested.
(a) An α–emitting gas would be a relatively harmless source outside the body since α–particles do not penetrate the skin and therefore cannot cause harm to any vital internal organs. If the gas were breathed into the lungs then the α–particles could cause substantial damage.
(b) A β–emitting liquid, because of the higher penetrating power of the rays, would be a potential source of damage outside as well as inside the body but it would be more hazardous if ingested.
(c) γ–rays are much less effective ionizers than α– or β–particles but their great penetrating power would make the solid an almost equal hazard outside or inside the body (at about the same distance). The chemical nature of the material is significant only as an internal dose and where there is a targeting or higher concentration in a particular organ or site.
(Reread Subsection 4.2Subsections 4.2 and Subsection 4.34.3 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 5Closing items.