1. Introduction
It is possible to determine a function ƒ (x) from its derivative ƒ (x) by calculating the anti-derivative or integral of ƒ (x), i.e.:
| if dFdx = ƒ (x), then ƒ (x) = ∫ ƒ (x) dx + C |
- where C is an integration constant (see the module on Indefinite Integration).
In this module we will see how to use integration to calculate the area under a curve.
As a revision exercise, try this quiz on indefinite integration:
Quiz 1: Select the indefinite integral of ∫ (3x2 − 12x) dx with respect to x:
Hint: If n ≠ −1, the integral of xn is xn + 1(n + 1).
Explanation: To find the indefinite integral ∫ (3x2 − 12x) dx we use the sum rule for integrals, rewriting it as the sum of two integrals:
| ∫ (3x2 − 12x) dx | = | ∫ 3x2 dx − ∫ (− 12x) dx |
| = | 3 ∫ x2 dx − 12 ∫ x dx |
Using ∫ xn dx = 1n+1 xn+1; n ≠ −1 with n = 2 in the first integral and n = 1 in the second gives:
| 3 ∫ x2 dx − 12 ∫ x dx | = | 3 × 11 + 2 x1+2 − 12 × 11 + 1 x1+1 + C |
| = | 33 x3 − 12(1 + 1) x2 + C = x3 − 14 x2 + C |
It can be checked that differentiation of this result gives 3x2 − 12x
2. Definite Integration
We define the definite integral of the function ƒ(x) with respect to x from x = a to x = b to be:
| b∫a ƒ (x) dx = ƒ (x) = ƒ (b) − ƒ (a) |
- where ƒ (x) is the anti-derivative of ƒ(x). We call a and b the lower and upper limits of integration, respectively. The function being integrated, ƒ(x), is called the integrand. Note the minus sign!
Note: integration constants are not written in definite integrals since they always cancel in them:
| b∫a ƒ (x) dx | = | ƒ (x) |
| = | (ƒ (b) + C) − (ƒ (a) + C) | |
| = | ƒ (b) − ƒ (a) |
Example 1: Calculate the definite integral 2∫1 x3 dx
Solution: From the rule ∫xndx = 1n+1 xn+1 we have:
| 2∫1 | = | 13 + 1 x3+1 |
| = | 14 x4 = 14 × 24 − 14 × 14 | |
| = | 14 × 16 − 14 = 4 − 14 = 154 |
Exercise 1: Calculate the following definite integrals:
Solution: To calculate 3∫0 x dx use the formula:
with n = 1. This yields:
| 3∫0 x dx | = | 11 + 1 x1+1 = 12x2 |
| = | 12 × (3)2 − 12 × (0)2 | |
| = | 12 × 9 − 0 = 92 |
Solution: To calculate 2∫−1 x dx use the formula for the definite integral:
with n = 1. This yields:
| 2∫−1 x dx | = | 11 + 1 x1+1 = 12 x2 |
| = | 12 × (2)2 − 12 × (−1)2 | |
| = | 12 × 4 − 12 × (+1) = 2 − 12 = 32 |
Solution: To evaluate the definite integral 2∫1 (x2 − x) dx we rewrite it as the sum of two integrals and use ∫xndx = 1n+1 xn+1, with n = 2 in the first integral and n = 1 in the second one:
| 2∫1 x2 dx − 2∫1 x dx | = | 13 x3 − 12 x2 = 13 23 − 13 13 − ( 12 22 − 12 12 ) |
| = | 13 × 8 − 13 × 1 − ( 12 × 4 − 12 × 1 ) | |
| = | 73 − 32 = 146 − 96 = 56 |
Solution: To find the integral 2∫−1 (x2 − x) dx, we rewrite it as the sum of two integrals and use the result of the previous part to write is as:
| 2∫−1x2 dx − 2∫−1x dx | = | 13 x3 − 12 x2 = 13 23 − 13 (−1)3 − (12 22 − 12 (−1)2) |
| = | 13 × 8 + 13 × 1 − ( 12 × 4 − 12 × 1 ) | |
| = | 93 − 32 = 3 − 32 = 32 |
Click on questions to reveal their solution
3. The Area Under a Curve
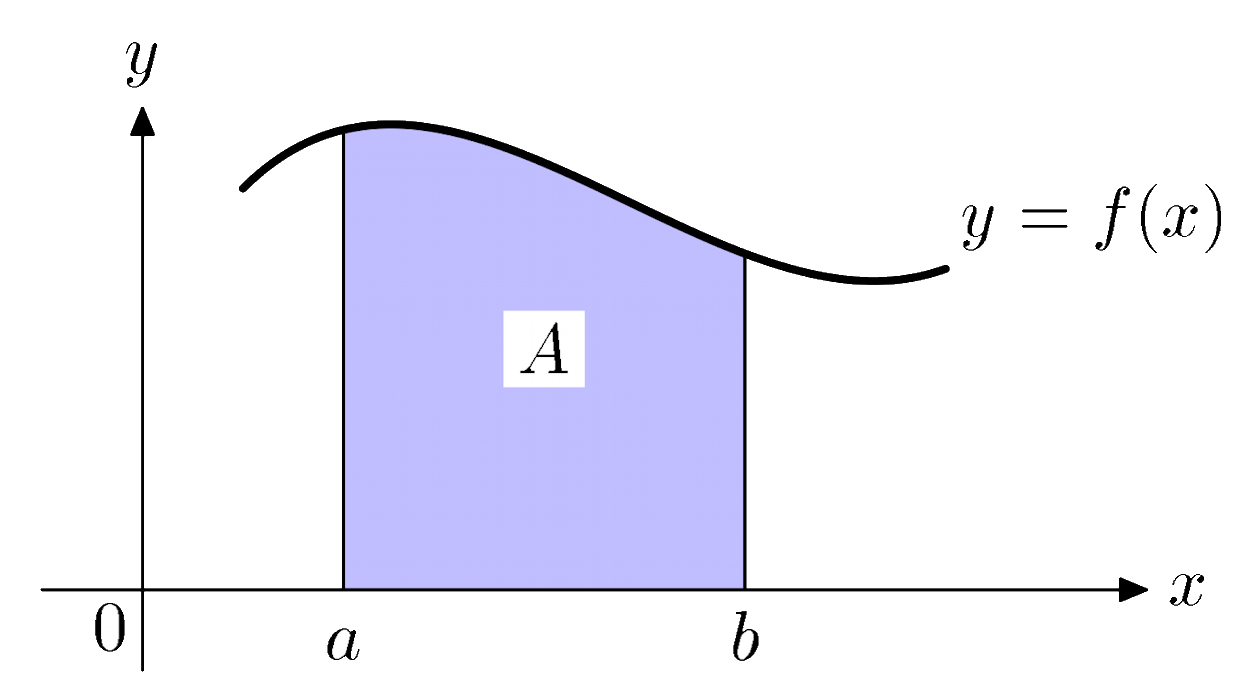
The definite integral of a function ƒ(x) which lies above the x-axis can be interpreted as the area under the curve of ƒ(x). Thus the area shaded blue in the figure on the right is given by the definite integral:
b∫a ƒ (x) dx = ƒ (x) = ƒ (b) − ƒ (a)
This is demonstrated as follows: |
|
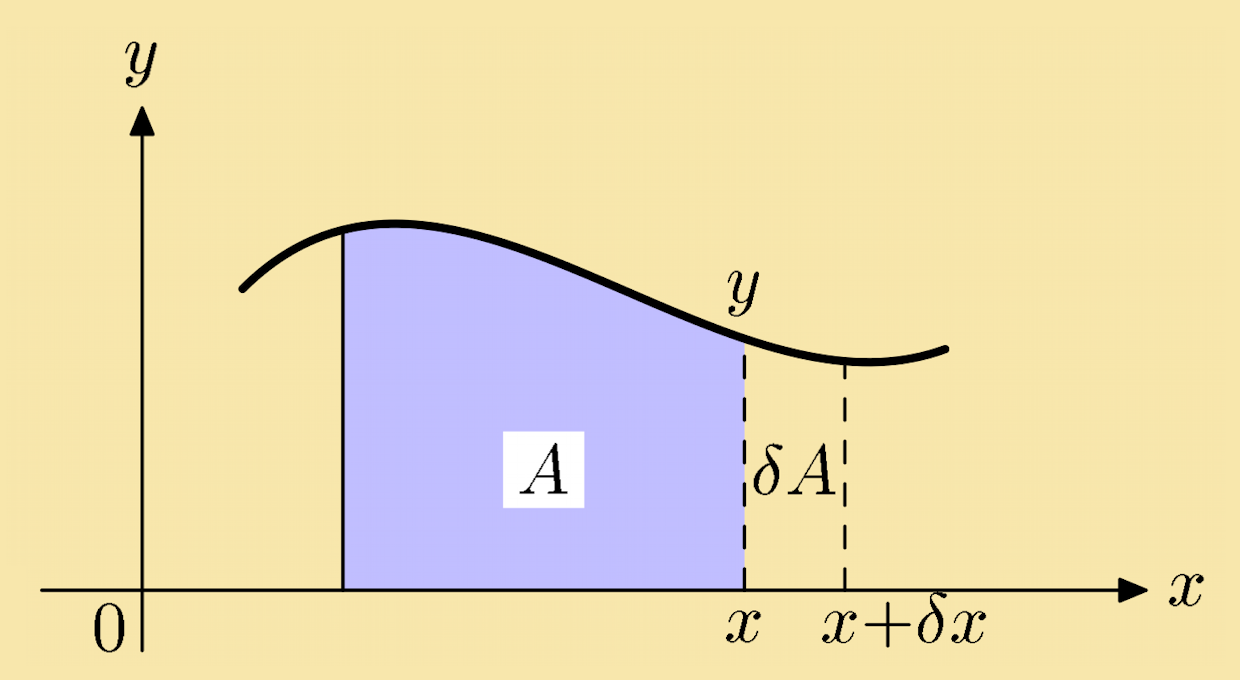
Consider the area, A, under the curve y = ƒ (x)in the figure on the right. If we increase the value of x by δx, then the increase in area, δA, is approximately:
δA = y δx → δAδx = y
Here we approximate the area of the thin strip by a rectangle of width δx and height y. In the limit as the strips become thin, δx → 0, this means:
dAdx = limδx → 0 δAδx = y
|
|
The function (height of the curve) is the derivative of the area and the area below the curve is an anti-derivative or integral of the function.
Note: So far we have assumed that y = ƒ (x) lies above the x-axis.
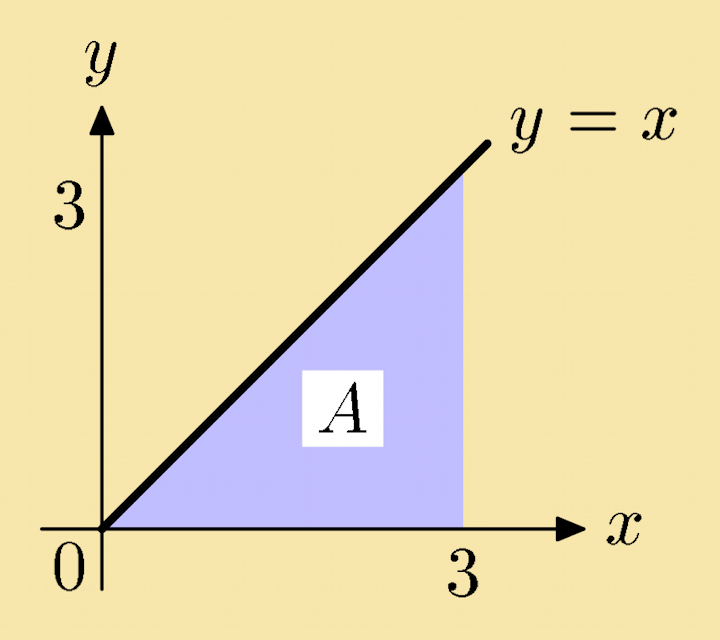
Example 2: Consider the integral 3∫0 x dx. The integrand y = x (a straight line) is shown in the figure on the right. The area A underneath the line is the blue shaded triangle. The area of any triangle is half its base times the height. For the blue shaded triangle, this is:
A = 12 × 3 × 3 = 92
As expected, the integral yields the same result:
3∫0 x dx = x22 = 322 − 022 = 92 −
0
= 92
|
|
Here is a quiz on this relation between definite integrals and the area under a curve:
Quiz 2:
Select the value of the definite integral 3∫1 2 dx, shown here:
(a)6Incorrect - please try again!
(b)2Incorrect - please try again!
(c)4Correct - well done!
(d)8Incorrect - please try again!
Hint: 2 may be written as 2x0, since x0 = 1. |

|
Explanation: Using 2 = 2x0, the integral is:
| 3∫12 dx | = | 2 3∫1 x0 dx = 2x |
| = | 2 × 3 − 2 × 1 | |
| = | 6 − 2 = 4 |
This can be confirmed by inspecting the figure. The area under the curve between the integration limits is the area of a square of side 2, which has area 22 = 4.
Example 3: Consider the two lines: y = 3 and y = −3. Let us integrate these functions in turn from x = 0 to x = 2. For y = +3: 2∫0 (+3) dx = 3x = 3 × 2 − 3 × 0 = 6 - and 6 is indeed the area of the rectangle of height 3 and length 2. However, for y = −3: 2∫0 (−3) dx = −3x = −3 × 2 − (−3 × 0) = −6 |

|
Although both rectangles have the same area, the sign of this result is negative because the curve y = −3 lies below the x-axis. This indicates the sign convention:
| If a function lies below the x-axis, its integral is negative |
|---|
| If a function lies above the x-axis, its integral is positive |
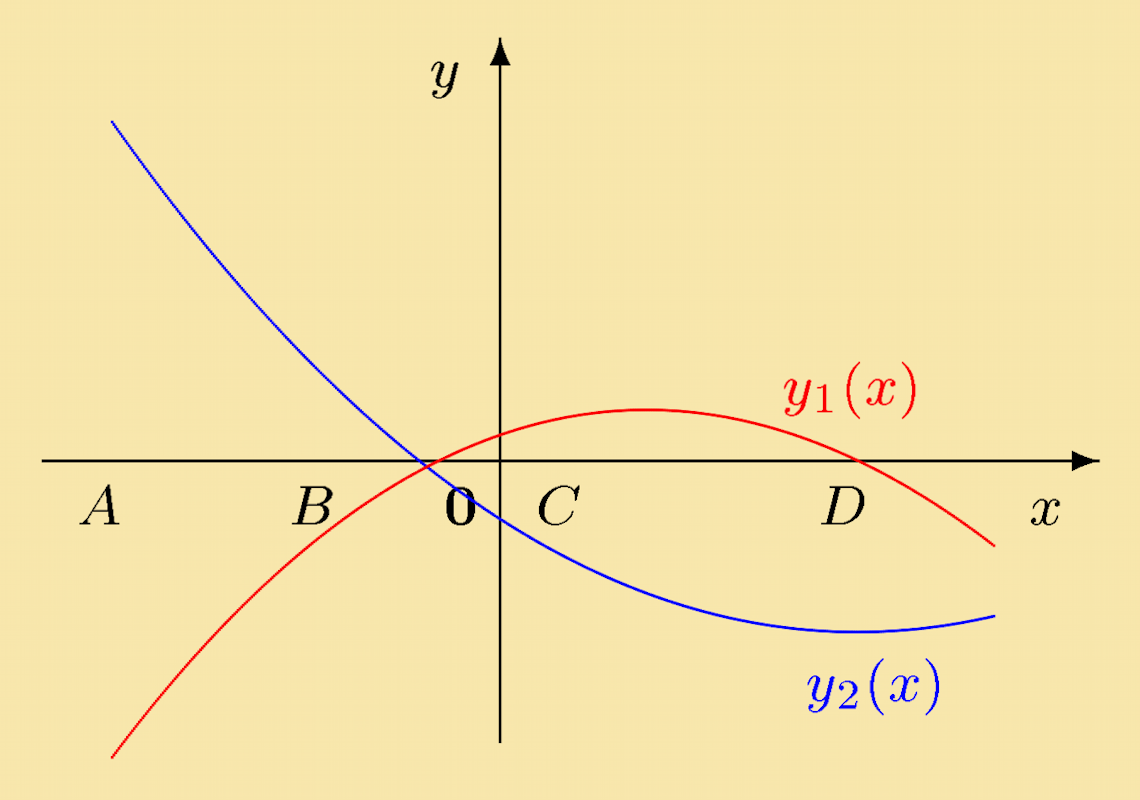
Exercise 2: From the figure on the right, what can you say about the signs of the following definite integrals?
(a) B∫A y1 dx
Solution: The sign of the definite integral, B∫A y1 dx, must be negative. This is because the function y1(x) is negative for all values of x between A and B. The area is all below the x-axis.
(b) D∫B y1 dx
Solution: The sign of the definite integral, D∫B y1 dx, must be positive. This is because, between the integration limits B and D, there is more area above the x-axis than below it.
(c) O∫A y2 dx
Solution: The sign of the definite integral, O∫A y2 dx, must be positive. This is because, between the integration limits A and O, there is more area above the x-axis than below it.
(d) D∫C y2 dx
Solution: The sign of the definite integral, D∫C y2 dx, must be negative. This is because, between the integration limits C and D, the integrand y2(x) is always negative. Click on questions to reveal their solution |
|
Example 4: To calculate −2∫−6 6x2 dx, use ∫axndx = an+1 xn+1. Thus:
| −2∫−6 6x2 dx | = | 62 + 1 x2+1 |
| = | 63 x3 = 2x3 | |
| = | 2 × (−2)3 − 2 × (−4)3 = −16 + 128 = 112 |
Note: Even though the integration range is for negative x (from −4 to −2), the integrand, ƒ(x) = 6x2, is a positive function. The definite integral of a positive function is positive. Similarly, it is negative for a negative function.
Quiz 3: Select the definite integral of y = 5x4 with respect to x if the lower limit of the integral is x = −2 and the upper limit is x = −1:
Explanation: The definite integral of y = 5x4 with respect to x if the lower limit of the integral is x = −2 and the upper limit is x = −1 can be written as:
From the basic result B ∫Aaxndx = an+1 xn+1 we obtain:
| −1∫−2 5x4 dx | = | 55 x5 |
| = | (−1)5 − (−2)5 | |
| = | −1 − (−32) | |
| = | −1 + 32 = 31 |
Note: Since the integrand 5x4 is positive for all x, the negative suggested solutions could not be correct.
Exercise 3: Use the integrals listed below to calculate the following definite integrals:
| ƒ (x) | xn for n ≠ −1 | sin (ax) | cos (ax) | eax | 1x |
|---|---|---|---|---|---|
| ∫ ƒ (x) dx | 1n + 1 xn+1 | − 1a cos (ax) | 1a sin (ax) | 1a eax | ln (x) |
Solution: To calculate the definite integral 9 ∫4 3 √t dt we rewrite it as:
and use ∫xndx = 1n+1 xn+1, with n = ½:
| 3 × 9 ∫4 t½ dt | = | 1½ + 1 t½+1 = 3 × 1 3 ⁄ 2 t3 ⁄ 2 = 3 × 2 3 t3 ⁄ 2 |
| = | 2t3 ⁄ 2 | |
| = | 2 × (9)3 ⁄ 2 − 2 × (4)3 ⁄ 2 = 2 × (9½)3 − (4½)3 | |
| = | 2 × (9)3 ⁄ 2 − 2 × (4)3 ⁄ 2 = 2 × 33 − 2 × (2)3 = 2 × 27 − 2 × 8 = 54 − 16 = 38 |
Note: Dividing by a fraction is equivalent to multiplying by its inverse (see the module on Fractions).
Solution: To calculate the definite integral 1 ∫−1 (x2 − 2x + 4) dx we rewrite it as a sum of integrals:
1 ∫−1 x2 dx − 2 × 1 ∫−1 x dx + 4 × 1 ∫−1 dx, and use ∫xndx = 1n+1 xn+1, with n = 2 in the first integral:
with n = 1 in the second integral:
and with n = 0 in the second integral:
Summing up these numbers we obtain 2 ⁄ 3 + 0 + 8 = 26 ⁄ 3.
Solution: To calculate the definite integral π∫0 sin (x) dx we note from the table that:
This yields (with a = 1):
| π∫0 sin (x) dx | = | − cos (x) |
| = | − (cos (π) − cos (0)) = − ((−1) − 1) = 2 |
Note: It is worth emphasizing that the angles in calculus formulae for trigonometric functions are measured in radians.
Solution: To calculate the definite integral 3∫0 4 e2x dx rewrite it as:
and use from the table:
This gives, for a = 2:
| 4 × 3∫0 e2x dx | = | 4 × 12 e2x = 2 e2x |
| = | 2 e(2×3) − 2 e(2×0) = 2 e6 − 2 e0 = 2 e6 − 2 ×1 = 2 e6 − 2 |
Solution: To evaluate the definite integral 2 ∫1 3t dt we write:
and use:
This yields:
| 3 × 2 ∫1 1t dt | = | 3 × ln (t) |
| = | 3 × ln (2) − 3 × ln (1) | |
| = | 3 × ln (2) − 3 × 0 | |
| = | 3 ln (2) |
Note: ln (0) = 1, since e0 = 1.
Solution: To find the definite integral π ⁄ 2 ∫π ⁄ 4 2 cos (4w)dw use
and
| 2 × π ⁄ 2 ∫π ⁄ 4 cos (4w)dw | = | 2 × 14 sin (4w) = 12 sin (4w) |
| = | 12 sin (4 × π2) − 12 sin (4 × π4) | |
| = | 12 sin (2π) − 12 sin (π) | |
| = | 12 × 0 − 12 × 0 = 0 |
Click on questions to reveal their solution
Quiz 4: Which is the correct result for the definite integral 2b ∫ax2 dx?
Explanation: To caclulate the definite integral 2b∫a x2 dx use the basic indefinite integral:
with n = 2. This gives:
| 2b∫a x2 dx | = | 12 + 1 x(2+1) = 13x3 |
| = | 13 × (2b)3 − 13 × 1(a)3 | |
| = | 13 × (2)3 × b3 − 13 × a3 | |
| = | 13 × 8 × b3 − 13 × a3 | |
| = | 83b3 − 13a3 |
Quiz 5: Which is the correct answer for the definite integral 3∫2 1x2 dx?
Explanation: To evaluate the definite integral 3∫2 1x2 dx = 3∫2 x−2 dx
use B∫A xndx = 1n+1 xn+1 with n = −2:
| 3∫2 x−2 dx | = | 1−2 + 1 x(−2+1) = 1(−1)x−1 |
| = | (−1) × 1x = − 1x = − 13 − (12) | |
| = | − 13 + 12 = − 26 + 36 | |
| = | −2 + 36 =16 |
4. Quiz on Definite Integrals
Choose the solutions from the options given
