The ansatz method of infinite summation of higher order diagrams
given in Shukla and Cowley, Phys. Rev.
58, 2596, (1998), is
extended to the self-consistent phonon theory. We demonstrate the high
accuracy of this approach with respect to the first order
self-consistent (SC1) and improved self-consistent (ISC) phonon theories,
by comparing the results from the ansatz method with their
exact counterparts. The ISC theory is then extended to include the
remaining diagrams of
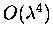
,
which could not be included in
its earlier formulation. This makes the ISC theory consistent, at
least to
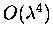
.
The new ISC theory offers a substantial
improvement over the current ISC theory. The results of the equation
of state for a face centered cubic (fcc) nearest neighbor interaction
Lennard-Jones solid from the new ISC theory are shown to be in
excellent agreement with the results of the classical Monte Carlo
method also obtained for the same model.
We have presented a detailed analysis of the higher order anharmonic
contributions to the average square atomic displacement
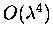 or Debye Waller factor by the diagrammatic method and the
Zubarev type Green's function method. The Hamiltonian employed in
the detailed analysis contains the anharmonic terms up to
or Debye Waller factor by the diagrammatic method and the
Zubarev type Green's function method. The Hamiltonian employed in
the detailed analysis contains the anharmonic terms up to
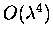 ,
i.e. the cubic, quartic, quintic, and sextic terms
which arise from the Taylor expansion of the potential energy.
Thus the various contributions to
,
i.e. the cubic, quartic, quintic, and sextic terms
which arise from the Taylor expansion of the potential energy.
Thus the various contributions to
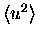 of
of
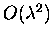 and
and
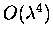 ,
presented in the diagrammatic
language arise from the first, second, third, and the fourth
order perturbation theory. This analysis establishing
interrelationships between the Helmholtz free energy (F),
self-energy, and
,
presented in the diagrammatic
language arise from the first, second, third, and the fourth
order perturbation theory. This analysis establishing
interrelationships between the Helmholtz free energy (F),
self-energy, and
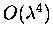 reveals that a total of 16
diagrams contribute to
reveals that a total of 16
diagrams contribute to
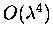 for a Bravais lattice or
a lattice with a basis where every atom is at a site of inversion
symmetry. A simple prescription is given for the derivation of
for a Bravais lattice or
a lattice with a basis where every atom is at a site of inversion
symmetry. A simple prescription is given for the derivation of
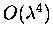 diagrams from the F diagrams. Out of 16
diagrams 2 are of
diagrams from the F diagrams. Out of 16
diagrams 2 are of
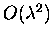 and 14 of
and 14 of
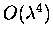 where
where
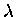 is a perturbation expansion parameter. It is also shown
that at least up to
is a perturbation expansion parameter. It is also shown
that at least up to
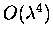 the contributions to
the contributions to
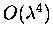 from 9 out of 16 diagrams are included in the Green's
function iterative solution if the latter is generated from the
anharmonic Hamiltonian containing the cubic and quartic terms.
Exact and approximate numerical magnitudes for all the diagrams are
obtained for a nearest-neighbour 6-12 Lennard-Jones fcc solid by
extrapolating the Brillouin Zone (BZ) sums to the
from 9 out of 16 diagrams are included in the Green's
function iterative solution if the latter is generated from the
anharmonic Hamiltonian containing the cubic and quartic terms.
Exact and approximate numerical magnitudes for all the diagrams are
obtained for a nearest-neighbour 6-12 Lennard-Jones fcc solid by
extrapolating the Brillouin Zone (BZ) sums to the
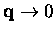 limit. A disproportionate contribution to
the BZ sums comes from this region of
limit. A disproportionate contribution to
the BZ sums comes from this region of 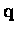 space in the
calculation of
space in the
calculation of
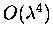 .
In the context of
.
In the context of
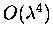 the importance of the various self-energy
diagrams involving the same type of anharmonic vertices is established.
It is shown that there exists a heavy cancellation among these
14 diagrams, nevertheless their total contribution to
the importance of the various self-energy
diagrams involving the same type of anharmonic vertices is established.
It is shown that there exists a heavy cancellation among these
14 diagrams, nevertheless their total contribution to
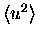 is sufficient to bring
it in almost exact agreement with the classical Monte Carlo
(MC) results which are also obtained for the same model.
is sufficient to bring
it in almost exact agreement with the classical Monte Carlo
(MC) results which are also obtained for the same model.
Phil. Mag. B, August, 2000
We present a critical assessment of the equation of state results
for a fcc Lennard-Jones (LJ) solid calculated from two entirely
different summation procedures for an infinite set of free energy
diagrams. The first is the recent procedure given by Shukla and Cowley
(R.C. Shukla and E.R. Cowley, Phys. Rev. B
58, 2596 (1998))
where the diagrams of the same order of magnitude generated from the
Van Hove ordering scheme, but arising in different orders of
perturbation theory (PT), are summed to infinity. The second procedure
is the self-consistent phonon theory (SC) which has been in use for
some time. In the first order version of this theory (SC1) only the
first order PT diagrams are summed and in the improved self-consistent
(ISC) theory the first important contribution (cubic term) arising from
the second order PT, omitted in SC1, is included as a correction to the
SC1 free energy. We have calculated the equation of state results from
the ISC theory by averaging the cubic tensor force constant and also
without averaging this constant (ISCU). This brings out the effect of
averaging which is a necessary requirement in the SC1 theory but
not in ISC. The results from SC1 and ISCU are poor. The results from
ISC and Shukla-Cowley summation procedures agree with each other
at low temperature. At high temperatures, the ISC results are in
poor agreement with the classical Monte Carlo (MC) results whereas
the Shukla-Cowley procedure yields results in excellent agreement
with MC.
Phys. Rev. B, 60, 14 500-2, 1999.
We present a method of calculating the Helmholtz free energy of an anharmonic crystal. The exact
expression for F, obtained by summing an infinite series of contributions, from all the
loops and bubbles (quartic and cubic contributions to the self-energy of the Green's function), is
evaluated numerically and the equation of state results for a Lennard-Jones solid are compared with the
lambda-squared perturbation theory (PT) which contains only the lowest-order cubic and quartic contributions.
It is shown that the infinite sum results are considerably improved over the lambda-squared PT results for
higher temperatures. Next, we have presented a powerful ansatz approach of evaluating the same sum. The
numerical results from this method are shown to be identical to the exact sum except at near
T_m where they are very slightly different. The ansatz method is then extended to the
higher-order lambda-to-the-fourth diagrams and here too the numerical results are found to be improved over the
results from the lambda-to-the-fourth PT. The ansatz procedure is then extended to the propagator renormalization
and the numerical results obtained seem to have the best agreement with the results of classical
Monte Carlo simulations.
Phys. Rev. B, 58, 2596-602, 1998.
We have presented a new method for the derivation of the Helmholtz free energy (F of an
anharmonic crystal from the Zubarev type Green's function. The hamiltonian (H) employed
in the derivation contains the contributions from all the even terms of the Taylor's
expansion of the crystal potential energy. In the language of perturbation theory (PT) these are
essentially all the first order PT contributions summed to infinity to the free energy,
the self-energy of the Green's function, and the renormalized phonon frequencies. The
self-consistency condition arises because in evaluating the correlation functions from the
Zubarev type Green's functions the full Hamiltonian is required instead of the usual harmonic
Hamiltonian. The final equations which determine F and the self-consistent phonon
frequencies are shown to be identical to those of the first order self-consistent phonon (SC1) theory.
phys. stat. sol. (b) 205, 481-92, 1998.
It is shown that a practical procedure for including both anharmonic and quantum effects in the
calculation of the properties of solids is to combine classical molecular-dynamics simulations with
quantum corrections obtained with the quasiharmonic approximation. The procedure is simple to
implement and possesses an ordered set of anharmonic quantum corrections. It is tested by calculations
on a Lennard-Jones model for solid Ar with nearest-neighbor interactions. The results obtained are
competitive with the predictions of effective-potential Monte Carlo (EPMC) and are in very good
agreement with path-integral Monte Carlo results, which were obtained with a constant-pressure
algorithm that includes higher-order corrections to the Trotter expansion. The lowest-order
perturbative correction to EPMC is shown to be the same as the cubic part of the anharmonic quantum
correction.
Phys. Rev. B, 57, 833-8, 1998.
A perturbation theory (PT) is developed in the classical limit which is based on an infinite series
of diagrams composed of the loops and bubbles arising from the first- and second-order matrix elements
of the PT, respectively. This theory leads to a closed form expression for the free energy, which on
expansion gives an infinite power series in the temperature. Results from this theory are obtained
for a Hamiltonian in which the Taylor expansion of the potential energy is truncated at the quartic
term. These results are compared with results of finite summation versions of the theory up to
O(lambda-to-the-eighth), with results of standard PT of O(lambda-squared) and O(lambda-to-the-fourth), and with results of
molecular dynamics (MD) simulations carried out for the same potential energy surface (i.e., the
potential energy expansion truncated at the quartic term). The results show that the theory which
includes all powers of temperature gives better agreement with the MD results throughout a wide
temperature range than does the standard PT of O(lambda-squared) and O(lambda-to-the-fourth).
J. Chem. Phys., 107, 7409-17, 1997.
Phys. Rev. B, 54, 15548-97, 1997.
Molecular dynamics simulations are carried out on a Lennard-Jones crystal,
for the potential energy surfaces generated from the full Hamiltonian and
the Taylor expansion of the potential energy truncated at the quartic
term, to determine the accuracy of the quartic truncation with regard to
the thermodynamic properties of a crystal. The results show that the errors
arising from the quartic truncation become significant only for
temperatures T > 0.2 Tm, and are only on the order of 5% at
T = 0.8Tm, where Tm is the melting temperature. The
quartic truncation represents a significant improvement over the quadratic
(harmonic) truncation, and the errors associated with the quadratic
truncation are decreased by 75%. The sources of error in the lambda-squared
perturbation theory are investigated; the errors are found to arise from
the truncation of the potential energy expansion at low temperatures, and
primarily from the truncation of the perturbation expansion at high
temperatures.
J. Chem. Phys., 105, 4185-90, 1996.
We have calculated the Debye-Waller factor (DWF) of Cu from a model that was used
successfully in earlier calculations of anharmonicity by Cowley and Shukla. The present
calculation has been carried out using quasiharmonic theory, the lowest-order (lambda-squared) anharmonic
perturbation theory and a Green's function (GF) method which sums an infinite series of the
lambda-squared-type anharmonic terms. The static approximation in the cubic contribution to the
self-energy of the GF, introduced in the earlier work on the DWF by Shukla and Hübschle is
further justified by showing that in the high-temperature limit the exact results for the
cubic and quartic anharmonic contributions to the Helmholtz free energy are given in this
approximation. Results for the DWF are also obtained for a modified version of the Morse
potential with lambda-squared perturbation theory (PT) and the GF method. The GF results are in
excellent agreement with the experimental Mössbauer and X-ray data in the entire temperature
range, 300 K < T <1200 K. The GF and lambda-squared PT results for the Morse potential agree very well
with each other but are lower than the experimental values in the high-temperature range,
T > 600 K.
Phil. Mag. B, 74, 1-11, 1996.
We present a derivation of the finite-temperature expressions for the lowest-order anharmonic
(lambda^2)
contributions to the atomic mean-square displacement (MSD) from the Green's function (GF) method
and show that there is no contribution to MSD from the polarization mixing in the self-energy of
the GF. These contributions arise from the cubic- and quartic-phonon shifts and the cubic-phonon
width for a phonon mode. Since the present MSD expressions are valid for all temperatures they
can be used in numerical evaluation of the lambda-squared contributions for Ne and other quantum
crystals where the high-temperature expressions are not valid. In the high-temperature limit
the total MSD from the cubic shift and width agrees with the cubic contribution to MSD derived
in the classical limit by Maradudin and Flinn (MF) and the cubic MSD derived in the limit of the
self-energy of the GF by Shukla and Hübschle (SH). The quartic contribution
to MSD in the high-temperature limit similarly agrees with those derived by MF and SH. Thus it is
shown that the static approximation limit employed by SH leads to the exact result for MSD in the
high-temperature limit.
Phil. Mag. B, 74, 13-23, 1996.
Highly accurate results for the mean-square displacement (MSD) of an atom for a nearest-neighbor
Lennard-Jones model of a fcc solid are presented. These results are obtained from the Monte-Carlo
(MC) method and the Green's function method. The dependence of MSD on the sample size (N) in
the MC method and similarly the dependence of MSD on the number of wave vectors used in the
calculation by the Green's function method is discussed in detail. The results are presented by both
methods for the infinite sample size limit as well as for the finite sizes, i.e., 32-, 108-, and
256- atom sample sizes and the same number of corresponding wave vectors. It is shown that an
analytical method like the Green's function method reproduces almost exactly the results of the MC
method (a completely numerical procedure) for all temperatures except at the melting point
(T_m). The computing time required in the former method is only a fraction of the latter one.
phys. stat. sol. (b) 195, 73-83, 1996.
The anharmonic contribution to the Helmholtz free energy (F_A) is calculated as a
function of temperature (T) and volume (V) for a fcc crystal of atoms
interacting via a nearest-neighbor 6-12 Lennard-Jones potential, by the molecular-dynamics
(MD) method and by perturbation theory (PT) to O (lambda-squared) and O
(lambda-to-the-fourth). The volume-dependent coefficients for the T^2 and T^3 terms
of (F_A) terms have been extracted from the MD results, and compared with the corresponding
coefficients of lambda-squared and lambda-to-the-fourth PT. The agreement between the results of the
MD and PT methods is excellent. The coefficient of the T^4 term of F_A is also
extracted from the MD results, to give an approximation to the corresponding term in O
(lambda-to-the-sixth) PT.
Various thermodynamic properties are calculated from this approximation and are compared to exact
MD results to provide a picture of the convergence properties of PT. The results suggest that
lambda-to-the-sixth PT would be accurate up to approximately 60% of the melting temperature.
Phys. Rev. B, 54, 3266-72, 1996.
We present a method for the calculation of the atomic mean-square displacement of an anharmonic
crystal from potentials involving repulsive interactions. The quasiharmonic and the lowest-order
cubic and quartic anharmonic contributions are evaluated from the knowledge of seven Brillouin zone
(BZ) sums which are tabulated in the interval-0.1 < a_1 <0.0. the parameter a_1
characterizes the volume dependence of the BZ sums and is negative for repulsive potential. All the
BZ sums are evaluated in the limit L to infinity, where L is the step length from
the origin to the boundary of the BZ. The method is applicable to a nearest-neighbor central force
model of the fcc lattice, and it can be extended to a bcc lattice. We present two applications of the
method. One is the calculation of ....from .... repulsive potential, and our results are in good
agreements with those obtained by Monte Carlo methods. The other is to the nearest-neighbor
Born-Mayer potential with a volume-dependent effective coefficient alpha. In the case of Cu, the
agreement with other theoretical calculations as well as the experimental values from X-ray data at
300 and 400 K is excellent.
Phil. Mag. Lett., 73, 79-84, 1996.
Phys. Rev. B, 52, 168-76, 1995.
In two recent letters, one by Zoli in 1991, and the other by Schober in
1992, the evaluation of the quasiharmonic and anharmonic contributions to
the atomic mean-square displacement (MSD) for fcc metals has been
discussed. In Zoli's work, the difference in the two contributions is
found to be 91%. Schober, on the other hand, has not evaluated the
explicit anharmonic contribution to MSD. The huge difference in Zoli's
work is shown here to be due to an inaccurate evaluation of the explicit
anharmonic contribution to MSD. A proper self-contained method as
presented here, which employs the same model in the quasiharmonic and
anharmonic calculations of MSD or Debye-Waller factor, indeed shows that the
two contributions differ from each other by 10-15% depending on the
temperature. Larger differences exist at higher temperatures. Some
numerical results are given for a model of the fcc lattice, namely a
nearest-neighbor central force model employing a Lennard-Jones potential
(applicable to rare-gas solids) and the Morse potential as a model for Cu.
Phil. Mag. Lett., 70, 255-9, 1994.
The equations for determining the free energy of a solid with two-body
interactions in the uncorrelated-factors approximation (UFA) are derived
from the correlated-factors theorem. A self-consistent choice of the
parameters in the harmonic Hamiltonian causes the approximation to be
accurate through second order. The specific heat, thermal expansion, and
bulk modulus of an fcc Lennard-Jones solid with nearest-neighbor
interactions only are calculated in the UFA and the results are compared
with the predictions of lowest-order and improved self-consistent phonon
theory (SC1 and ISC), perturbation theory through fourth order, and other
approximations. The predictions of the UFA are in very good agreement with
new classical Monte Carlo estimates and with recent effective potential
Monte Carlo results. The calculational effort required in the UFA is similar
to that in SC1, while the accuracy of the predictions is similar to that of
ISC.
Phys. Rev. B, 49, 8732-7, 1994.
The Mössbauer recoilless fraction is calculated from the lowest-order
anharmonic-perturbation theory, the Green's function method, which sums the
lowest-order anharmonic contributions to all orders, and the Monte Carlo
method. In all cases we have employed a nearest-neighbor-interaction
Lennard-Jones and Morse potential. Excellent agreement is shown to exist
between the theory and the Mössbauer and x-ray experimental results.
Phys. Rev. B, 49, 9966-8, 1994.
Monte Carlo (MC) and anharmonic-lattice-dynamics (the lambda-squared and
lambda-to-the-fourth) perturbation-theory (PT) calculations of the
thermodynamic properties of Xe are presented for the temperature range
60-160 K using a nearest-neighbor central-force (NNCF) model of the fcc
crystal with atoms interacting via a Morse potential. In particular, we
calculate the equilibrium lattice parameter at zero pressure and the
corresponding specific heats at constant volume and at constant pressure,
volume expansivity, adiabatic and isothermal bulk moduli, and
Grüneisen parameter. We also calculate the atomic mean-square
displacement (MSD) from the MC method and the lowest-order (lambda-squared)
PT for the same NNCF model and the Morse potential. For the thermodynamic
properties, the MC results are found to agree more closely with the
lambda-squared PT and the lambda-to-the-fourth PT results. Similarly, the
MSD results from the MC method agree quite well with those from the
lambda-squared theory. This may be due to the fact that the exact solution
of the Schrödinger equation for the vibrational states of the Morse
potential for a one-dimensional or an isotropic three-dimensional model
agrees exactly with the lambda-squared PT. We show that this is indeed
true by evaluating the lambda-squared and lambda-to-the-fourth
contributions to vibrational energy for the above model of the Morse
potential and showing that all the lambda-to-the-fourth contributions add up
to zero and that the total lambda-squared contribution is in agreement with
the solutions of the Schrödinger equation.
Phys. Rev. B, 45, 12812-20, 1992.
We have compared the Debye-Waller factor of sodium calculated by three
different theoretical methods with the recent measured values in the
temperature range 80-295 K, using the Mössbauer gamma-ray-scattering
technique. The Mössbauer results are also compared with the two sets
of earlier x-ray measurements, one of which extends to 365 K. The three
theoretical methods are the following: the lowest-order anharmonic
perturbation theory, a Green's-function method that includes anharmonic
contributions of the lowest-order perturbation theory summed to infinity,
and the molecular-dynamics method, which includes the anharmonic
contributions to all orders. In all three methods the Ashcroft
pseudopotential with the Vashihta-Singwi screening function is employed to
generate the real-space two-body potential function whose range is cut off
at the sixth-neighbor distance. Excellent agreement is found between the
results of these three methods and the Mössbauer experimental results.
The x-ray results are also in very good agreement with the Mössbauer
data where the temperatures overlap in the measurements.
Phys. Rev. B, 45, 10765-8, 1992.