• Increased efficiency: e^xtrema's dual mode of operation offers both ease-of-use and power. For easy or routine tasks, use the Graphical User Interface. For more complex tasks, or for large-volume, repetitive jobs, use the built-in command language or scripting mode.
• Increased productivity: e^xtrema has been designed with ease-of-use as a priority. Within hours, you will be able to interactively manipulate and plot your data, customize the output, and easily import it directly into your papers.
• Increased confidence: The e^xtrema technology was developed for nuclear and particle physics research, among the most demanding fields of data analysis there are. It is also proven in a wide variety of other scientific fields at many leading universities, national laboratories, government agencies, and industry.

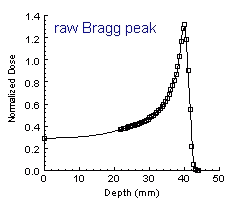The Problem: The radiation dose resulting from a proton passing through living tissue has a sharp, narrow peak, known as a Bragg peak. In certain cancer therapies, the desired radiation dose should have a broad, flat peak, where the flat section corresponds to the extent of the tumour being treated. The problem is how to deliver the dosage in a broad, flat distribution when the radiation is naturally deposited in narrow Bragg peaks.

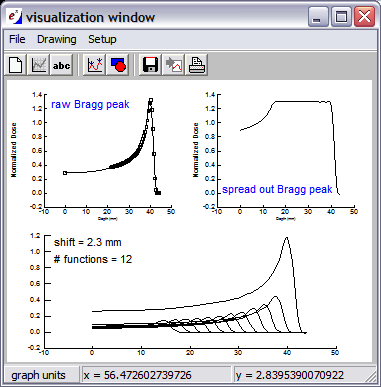
This problem was solved using e^xtrema: see the solution

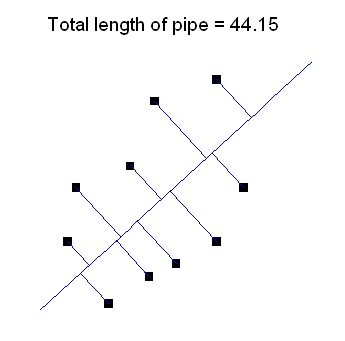
The Problem: We were given the job of figuring out the minimum amount of water pipe necessary to connect up the houses on a street to a water main. We had to determine where to dig a straight trench down the street for the water main pipe. The houses are set back from the street by varying distances, and ideally each house should be about 5 meters from the water main. The problem was to find the trench that would result in the minimum usage of water pipe segments from the main to the houses, and the total length of the pipe needed.

This problem was solved using e^xtrema: see the solution

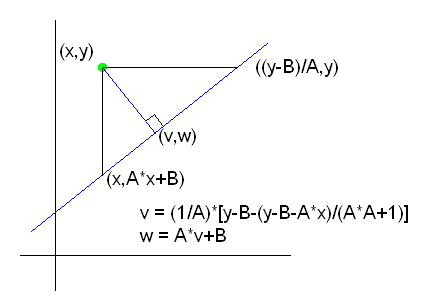
Solution: We have the (x,y) coordinates of the connections to the houses stored in a file, houses.dat. Remember from plane geometry that the distance from point (x,y) to a straight line with slope A and y-intercept B is given by $$ D = \frac{|A*x+B-y|}{\sqrt{A^2+1}} $$

We want to minimize the connecting pipe lengths by varying the free parameters A and B. The following short script does just that:

LENGTH_GOAL = 5                       ! try to achieve this goal
READ\-MESSAGES houses.dat X Y         ! read in the house positions
SCALAR\FIT A B                        ! declare the free parameters
A = 1                                 ! initialize
B = 1                                 ! initialize
D[1:LEN(X)] = LENGTH_GOAL             ! 
DISTANCE = 'ABS(A*X+B-Y)/SQRT(A*A+1)' !
FIT\-MESSAGES D=SQRT(DISTANCE)        ! do the fit
FIT\UPDATE PIECES                     ! redo using calculated A and B
STATISTICS PIECES PSUM\SUM            ! the total length of pipe needed
DISPLAY 'Total length of pipe = '//RCHAR(PSUM,'%4.2f')

Since least squares is used for fitting, we take the square root of the expression. Note that we have more than one independent variable in the expression. Extension to multidimensional cases is straightforward. The problem of fitting to a scattered set of points with a straight line which is, on the average, a fixed number of units away will, in general, have two solutions, and which one you get will depend on the starting values of the free parameters.

Try it yourself: e^xtrema macro performs the analysis using this raw data file, houses.dat

• A rich graphical user interface lets you quickly tackle one-off problems.
• For more elaborate tasks, the intuitive command language makes script writing easy. For example, to graph two data vectors x and y against each other, just type "graph x y".
• Automatic script-writing mode will create a script based on your GUI point-and-click actions. Write scripts without typing a single command!
• Data manipulation is easy with e^xtrema's automatic expression evaluation. For instance, if you have 10,000 (x,y) data coordinates stored in vectors x and y, you can instantly compute each of their distances from the origin with "d = sqrt(x^2 + y^2)".
• Simple, easy-to-understand programming constructs allow you to write code with little or no programming experience.
• The GUI gives you ALL the power of the low-level language, and vice versa.

• Contour plots: colour, legend, area/volume tabulations, control over contour label size, colour, separation, etc.
• Density plots: derivatives, random point type, box type, colour filled regions, dithering patterns with automatic or user defined patterns, diffusion type, profiles, legend, area/volume tabulations, etc.

• Customized 2-D line graphs, scatter plots, horizontal or vertical bar charts, each with a large variety of type styles and fonts of any size and color
• Customized or automatic legends
• Multiple axes with arbitrary axis positioning
• Fill the area between data curves or fill individual histogram bars
• Logarithmic axes, to any base, including e
• Axis scaling can be automatic or user set (including commensurate axes)
• Labels can optionally follow the curves on rescaling a graph
• Many plotting symbols, with control over size, colour and angle
• Complete control over axis appearance (short/long tic mark length and angle, separation between tic marks and axis labels, axis angle, length and location, axis labels size, colour, font, number of digits, etc.)

• Differentiate/Integrate an arbitrary expression
• Interpolate 1-D or 2-D data using various methods (linear, Lagrange, weighted splines under tension, Fritsch-Carlson, etc.)
• Smooth data using various methods (weighted splines under tension, Savitzky-Golay filters, etc.)
• Convolution and deconvolution of data
• Integral transforms of arbitrary expressions
• Fast Fourier Transforms and Inverse FFT's
• Reorganize data (sort, step, roll, wrap, etc.)
• Weighted (re-)binning of 1-D or 2-D data into automatic or user defined bins (specified by centres or edges)
• Find multiple real roots of an expression
• Recursive and non-recursive digital filters
• Manual or automatic determination of data extrema using graphics cursor
• Fit data with an arbitrary, non-linear, expression involving up to 25 variable parameters
• Ellipse fitting
• Calculation of parameters for least-squares fit using adjustable parameters
• User defined and named variables (scalars, vectors, matrices, strings, arrays of strings)
• Full indexing on variables and expressions
• Literal vectors may be specified as a list or a range
• Boolean operators (<, >, &, etc.)
• Array operators (inner/outer product, matrix transpose, etc.)
• Over 200 built-in functions including: scalar type (Bessel, Clebsch-Gordan, etc.); array type (sum, product, loop, where, etc.); string type (case, date/time, etc.)
• Mathematical/character expressions may appear in any suitable command parameter
• Use character variables to substitute for complicated expression substrings

• Display the history of variables
• Read data from binary or ASCII files by formats or space/tab/comma separated columns
• Output data to binary or ASCII files by formats or in columns
• Dynamic allocation of arrays
• Digitize data from a displayed plot

• Scripting capability with up to 20 nesting levels and with parameter passing
• Script library of `super' commands
• Nested looping, branching and conditional statements in scripts
• Display messages, prompt for user input from within a script
• Return to interactive mode from within a script, and later resume script execution
• Create a script interactively

• Unlimited text capabilities for titles, labels, and annotations
• Multiple windows within the graphing area
• Any number of charts of any mixed type on a single picture
• High quality graphics display
• Interactive entry of lines, arcs, geometric figures, and text

• Comprehensive on-line documentation: instant help for any command, or interactive browsing through help library
• Keyword searching
• Save/Restore an entire e^xtrema session, including graphics
• Keep a journal file of all command input and message output
• Dynamic input line recall buffers allow recall/edit of commands using the arrow keys