Performing Quadrature

For any scattering length density profiles it is possible to calculate the reflectivity by subdividing the SLD profile into small slices, and then using either Parratt's recursion relation, or Abele's matrix method to calculate the reflectivity.

This is exactly what yanera does for every model type, except for the simple case of homogeneous layers with gaussian roughness.

Unlike most other reflectivity software, the method of breaking the profile into small slices is done through adaptive quadrature, rather than simply dividing the total sample thickness into a large number of slices of equal thickness. This means that regions of large gradient in SLD have many small slices, and regions of constant SLD have few, larger slices. This cuts down on the total number of slices.

Adaptive quadrature starts by calculating the two-point numerical integrals of the SLD profile over a region 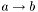$a\rightarrow b$ , by trapazoidal rule and midpoint rule

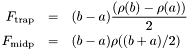
$\begin{eqnarray*} F_{\mathrm{trap}} &=& (b-a)\frac{(\rho(b)-\rho(a))}{2} \\ F_{\mathrm{midp}} &=& (b-a)\rho((b+a)/2) \\ \end{eqnarray*}$

If the difference in these areas is above a user-supplied tolerance, (<quadrature_error/>) then the region 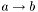$a\rightarrow b$ is cut in two and the smaller regions are tested. This is applied iterativly until the whole region is subdivided.

A small tolerance

This method may fail for multi-layer stacks, for example, a layer of material that has the structure ABABA. If the region 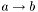$a\rightarrow b$ overlaps one or more repeating layers (AXAXA), then the tolerance can be satisfied and misses the stuff in the middle (XAX). In this case, the user sets a value for the largest slice allowed in the quadrature (<quadrature_thik/>) to be just smaller than the smallest layer thickness, and adaptive quadrature works quite well for repeating multilayers. If the model does not have repeating multilayers, then it is okay to leave this parameter to be large.