XML syntax - data

Data Section

Information about the data to be fitted goes between <data_section/> tags, which is also a child of <yanera/> as is the <model_section/>.

Each data set is specified by a set of <data/> tags, which are the only children of <data_section/>.

<data_section>
  <data data_id="data0">
    <file_name>mydata.dat</file_name>
    <resolution>
       <type>RESOLUTION_NONE</type>
       <value/>
       <file_name/>
    </resolution>
  </data>
</data_section>

The <data/> tags have only two children, <file_name/> tags and <resolution/> tags. The first specifies the name of the file containing the data to be fitted. The second contains information regarding the instrumental resolution.

Data

Data files are expected to be in 2 or 3 columns, sorting order is unimportant. The columns should be in the order: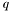 $q$

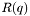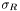, and optionally the error in the reflectivity, $\sigma_R$ .

The <data/> tags must have a data_id property that will correspond to the data_idref of only one <model/>. Any alpha-numeric string will work for this property.

Resolution

The calculated reflectivity can be smeared out to account for the instrumental resolution. It was decided to place resolution information in the data section because; 1. There are no adjustable parameters. 2. The resolution is more closely related to the data and its collection than the model.

Users can choose resolution smearing types from the list/

RESOLUTION_NONE
RESOLUTION_CONSTANT
RESOLUTION_RELATIVE
RESOLUTION_ARRAY_CONSTANT
RESOLUTION_ARRAY_RELATIVE

The first does not apply any resolution smearing and is the default.

Other options are for instrumental resolution determined by calculating the reflectivity averaged over several points with Gaussian weights. It's a method that was borrowed and made more general from Parratt32. It works by the following, assuming a 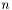$n$ point average,

$\begin{eqnarray*} R(q) &=& {\sum_{a=-n}^{n} w_a R(q[1+\frac{a}{n}\frac{\delta q}{q}])}/ {\sum_{a=-n}^{n} w_a} \\ \mathrm{or} &=& {\sum_{a=-n}^{n} w_a R(q+\frac{a}{n}\delta q)}/ {\sum_{a=-n}^{n} w_a} \\ w_a &=& \exp\left(-2\left(\frac{a}{n}\right)^2\right) \end{eqnarray*}$

For RESOLUTION_RELATIVE, we can specify the instrumental resolution due to continually varying slits, 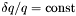$\delta q/q=\mathrm{const}$ . Otherwise, the resolution RESOLUTION_CONSTANT can be specified as 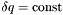$\delta q=\mathrm{const}$ . Specify the value of the resolution by <value/> tags.

If the resolution changes during the course of the scan, you can specify an array of values by a two column file, and include the file's name with <file_name/> tags, such as;

      <resolution>
        <type>RESOLUTION_ARRAY_CONSTANT</type>
        <file_name>resolution.dat</file_name>
      </resolution>

In the file, supply the ranges of 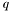$q$ for each value of the resolution by the minimum 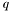$q$ , e.g. from 0 to 0.02, from 0.02 to 0.08, and from 0.08 to 0.12 would look like:

0.00 0.1
0.02 0.12
0.08 0.15

Alternatively, if you know the resolution at every data point, you could have as many data points in the resolution file as in the data file, and select RESOLUTION_ARRAY_CONSTANT.

Application of resolution smearing slows the fitting a fair bit. Try fitting without resolution first.